Study on the Hydraulic Characteristics of the Trapezoidal Energy Dissipation Baffle Block-Step Combination Energy Dissipator
Abstract
:1. Introduction
2. Construction of Mathematical Models
2.1. Turbulence Model
2.2. Air Entrainment Related Models
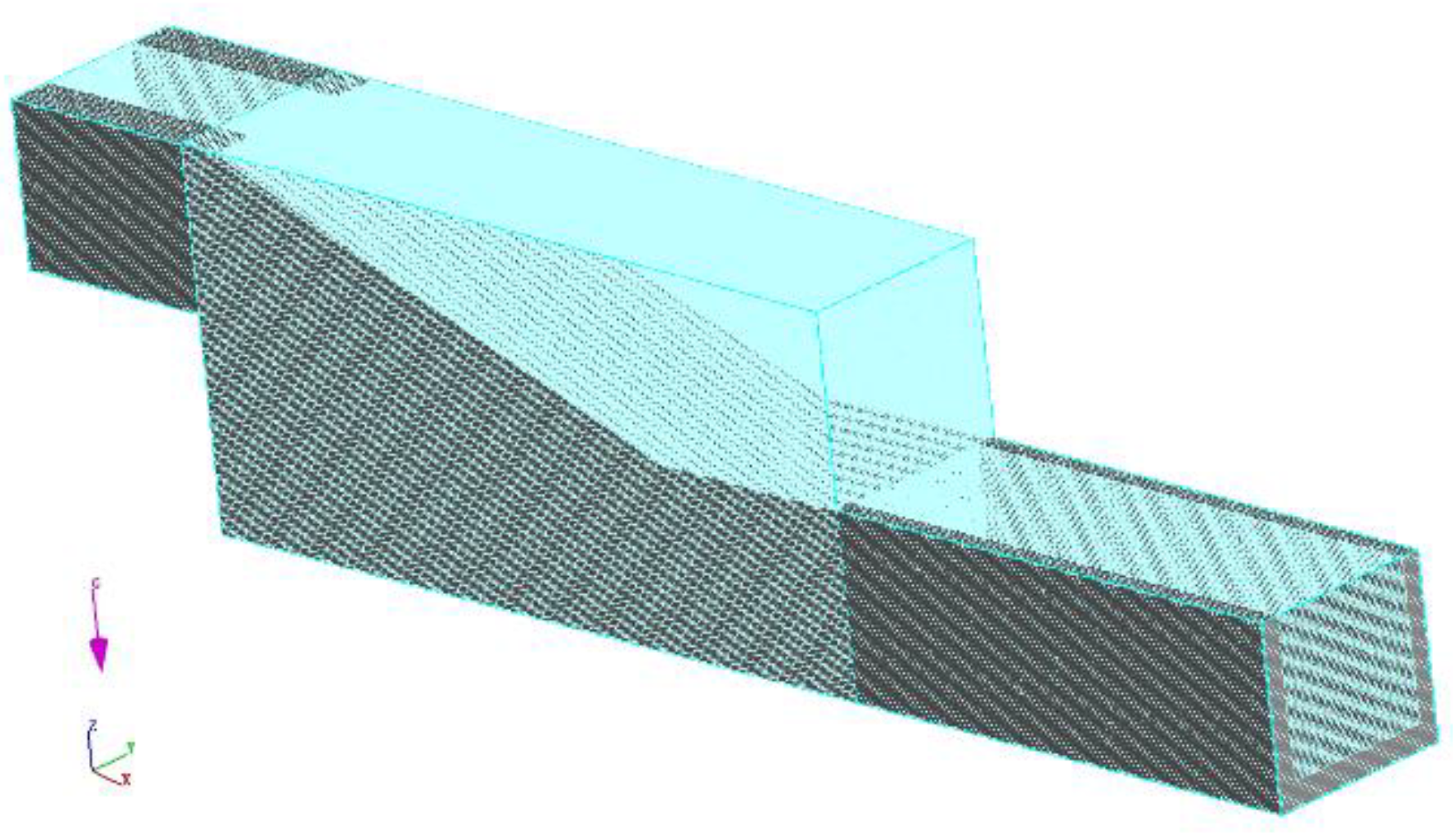
2.3. Meshing and Boundary Conditions
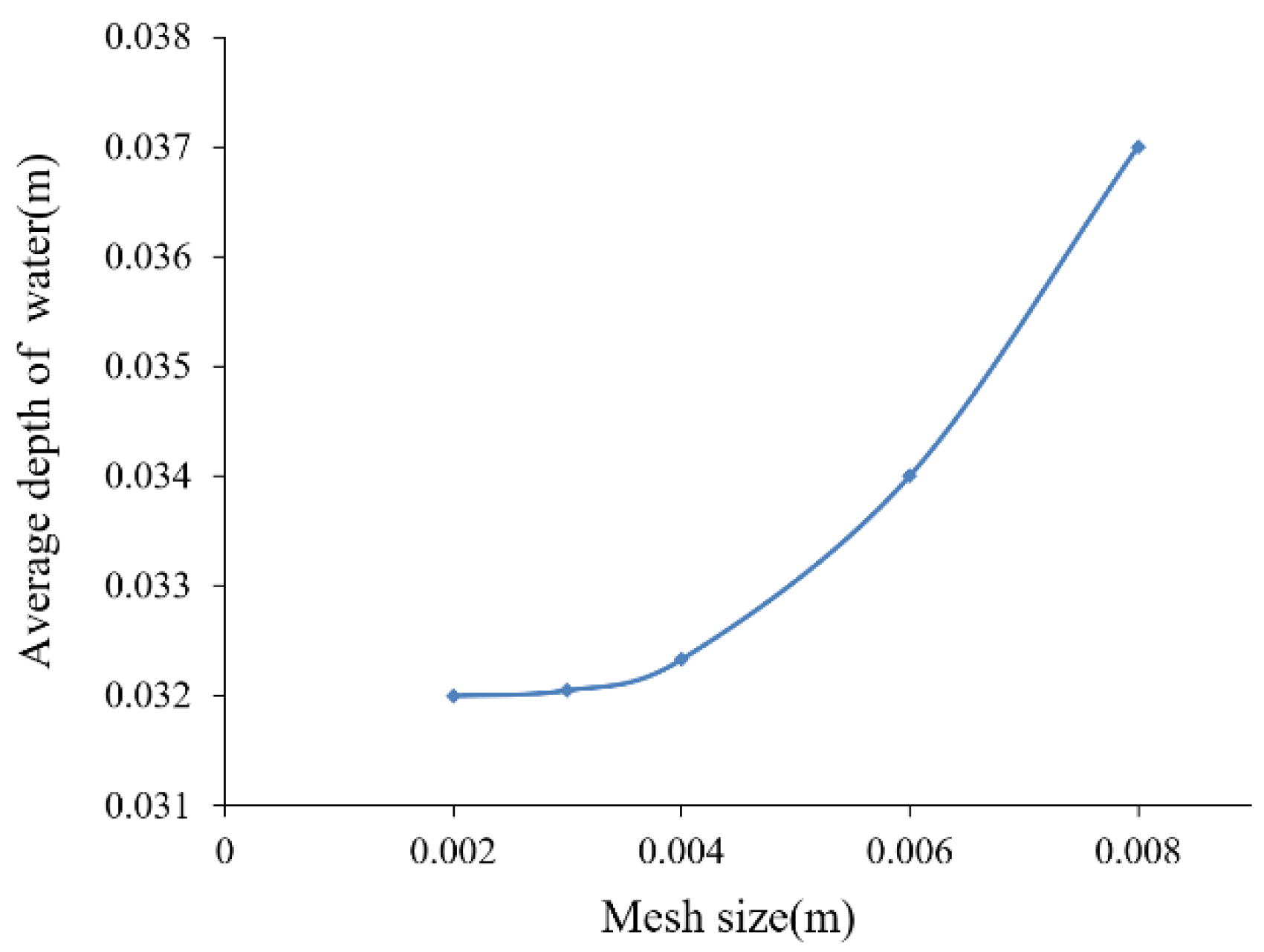
2.4. Sensitivity Analysis of Grids
3. Experimental Validation of Mathematical Models
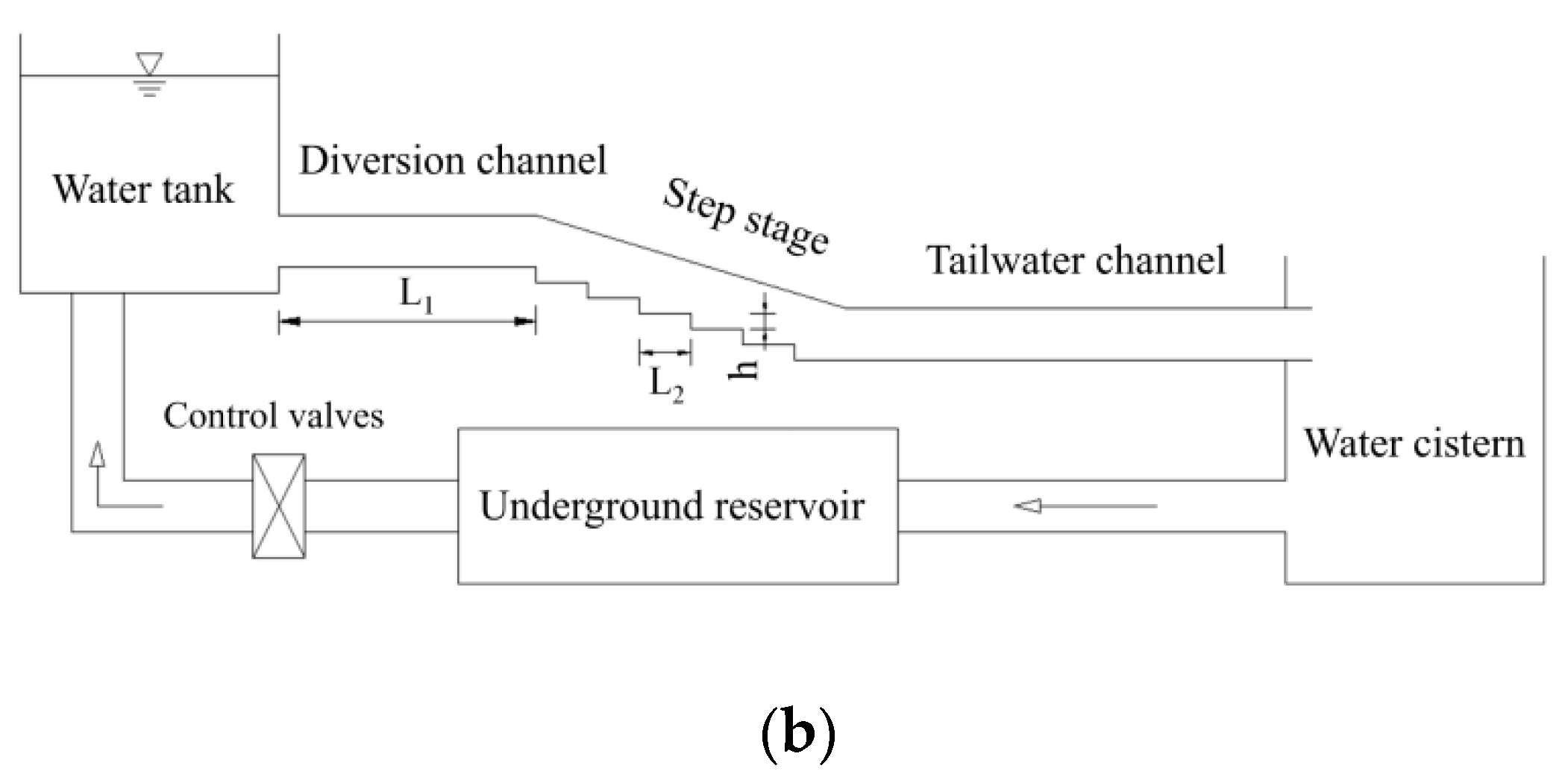
3.1. Experimental Systems
3.2. Model Validation
4. Results and Discussion
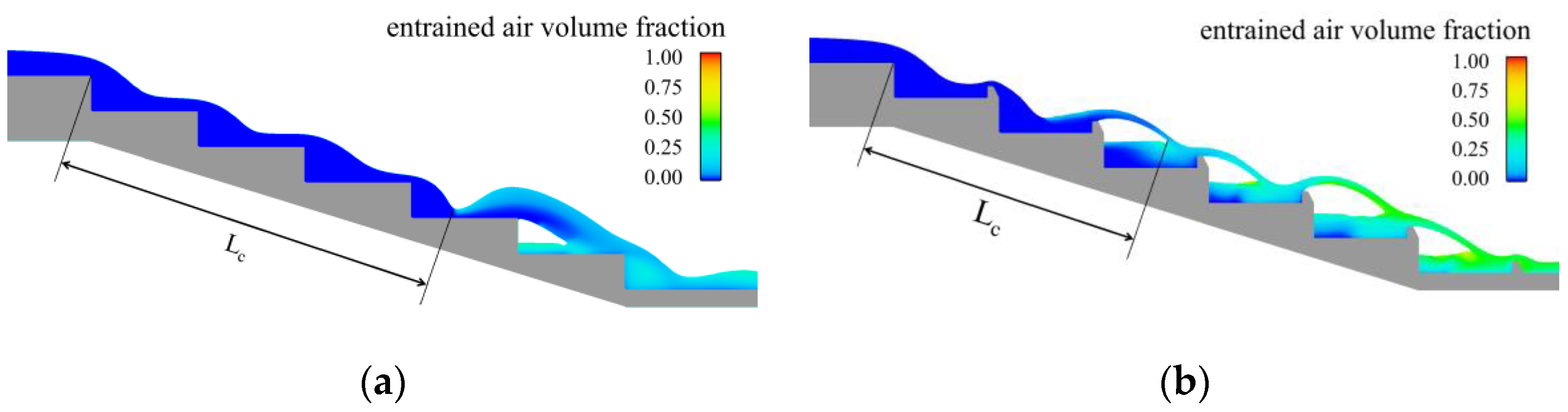
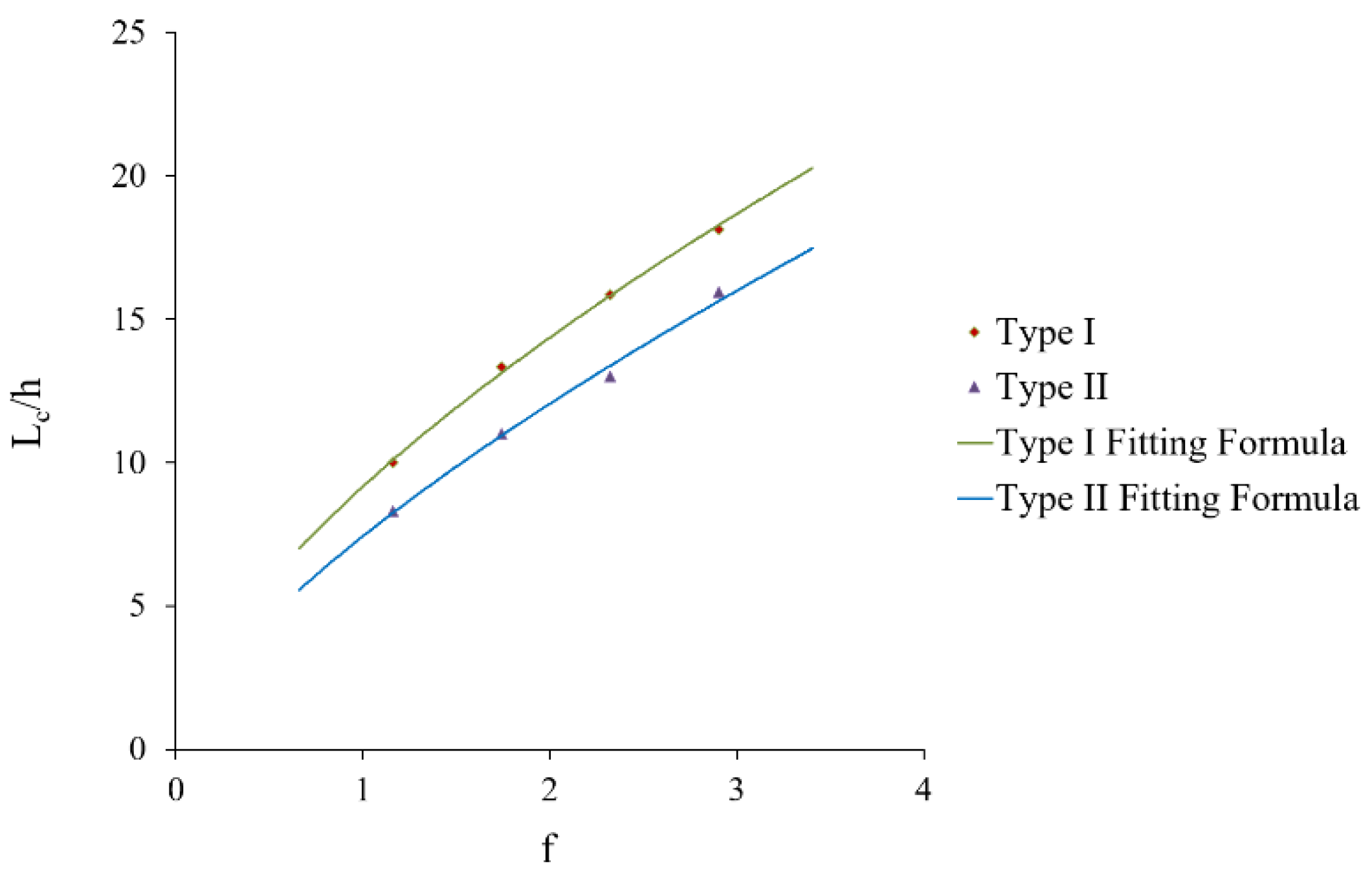
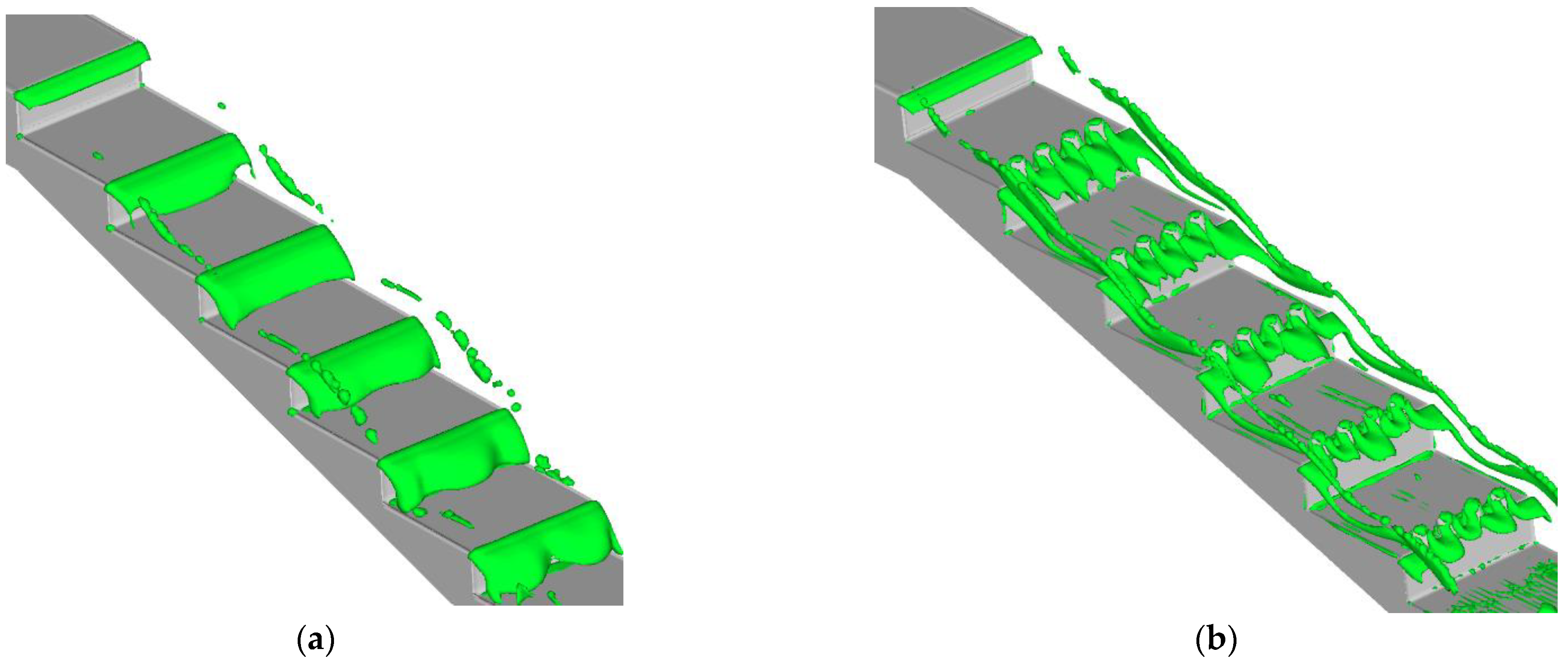
4.1. Air Entrainment Characteristics
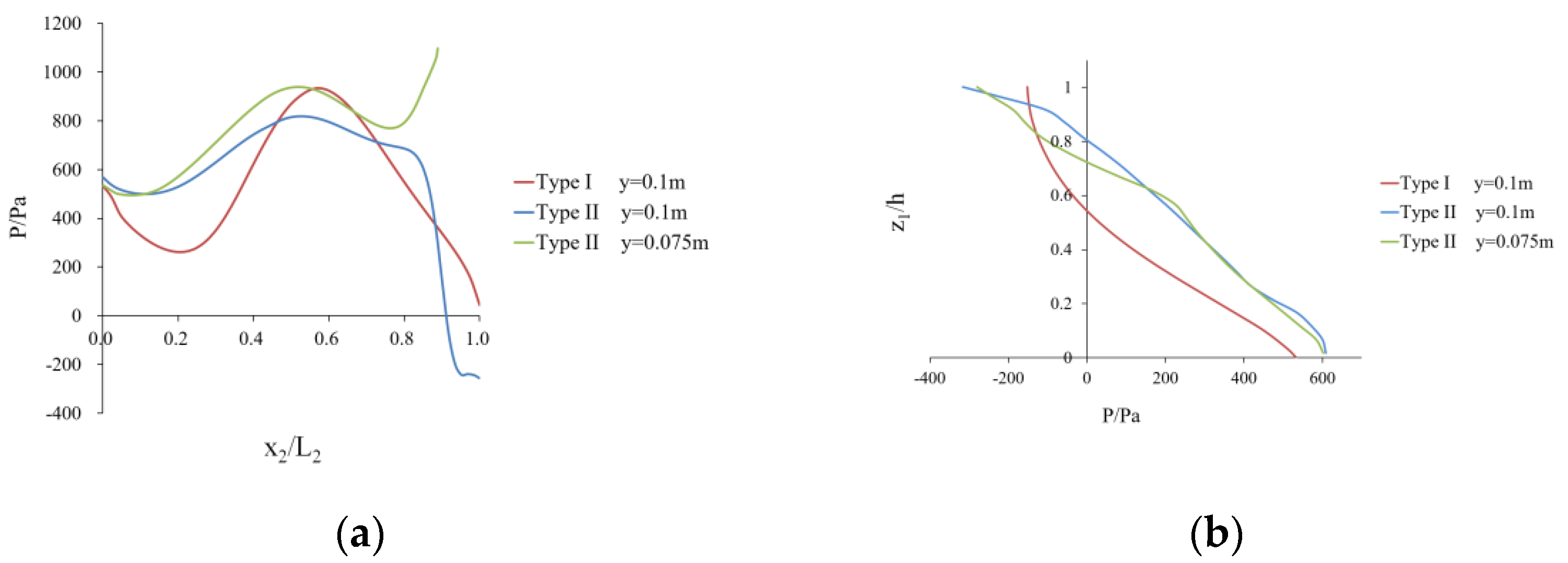
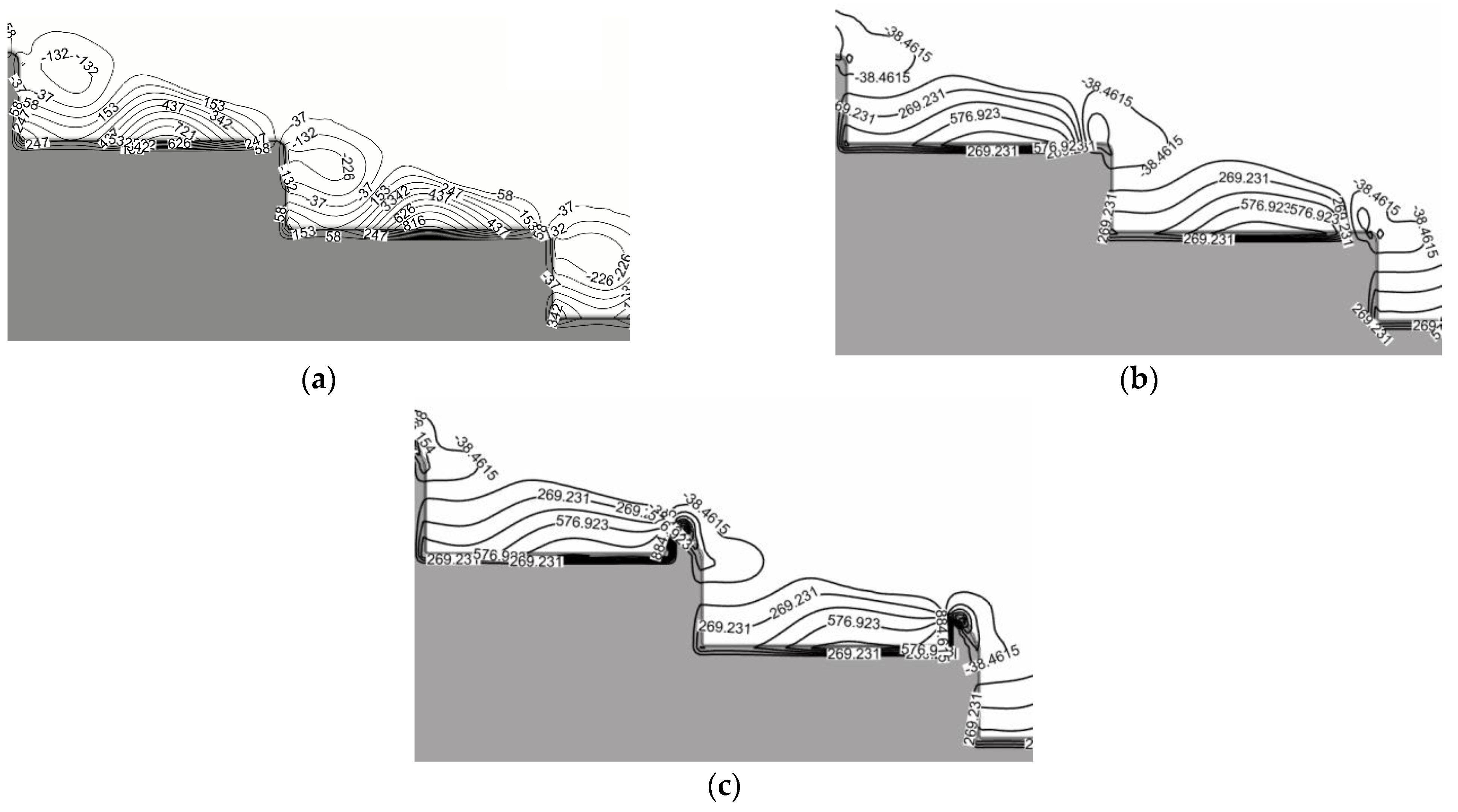
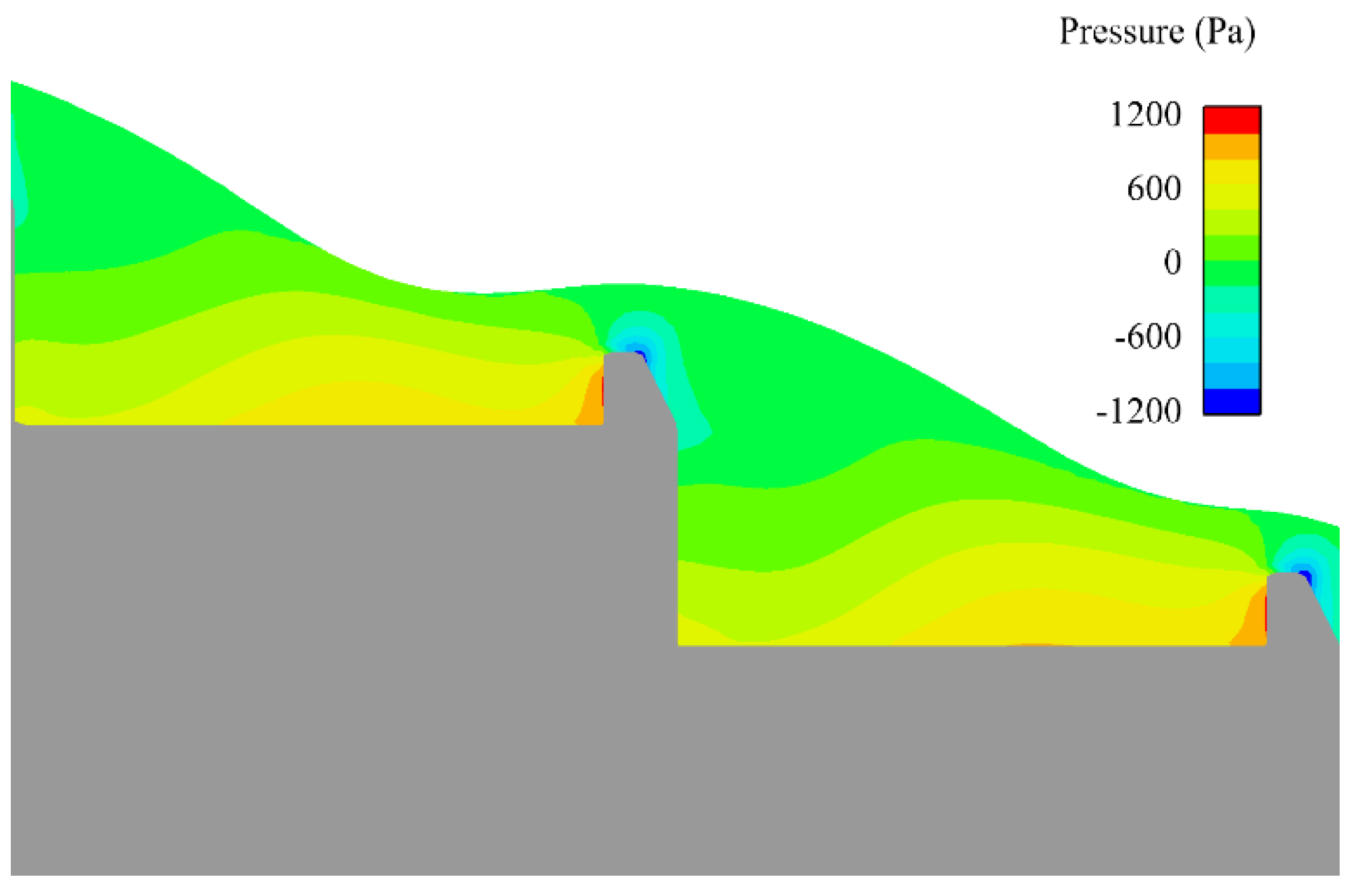
4.2. Pressure Distribution
4.3. Flow Velocity Distribution
4.4. Energy Dissipation Rate Analysis
5. Conclusions
- (1)
- Compared with the traditional step energy dissipator, the trapezoidal energy dissipation baffle block-step combination energy dissipator can increase the energy dissipation rate by about 6.67%, with better energy dissipation characteristics. The use of a trapezoidal energy dissipation baffle block to improve the hydraulic characteristics of the step energy dissipator is feasible.
- (2)
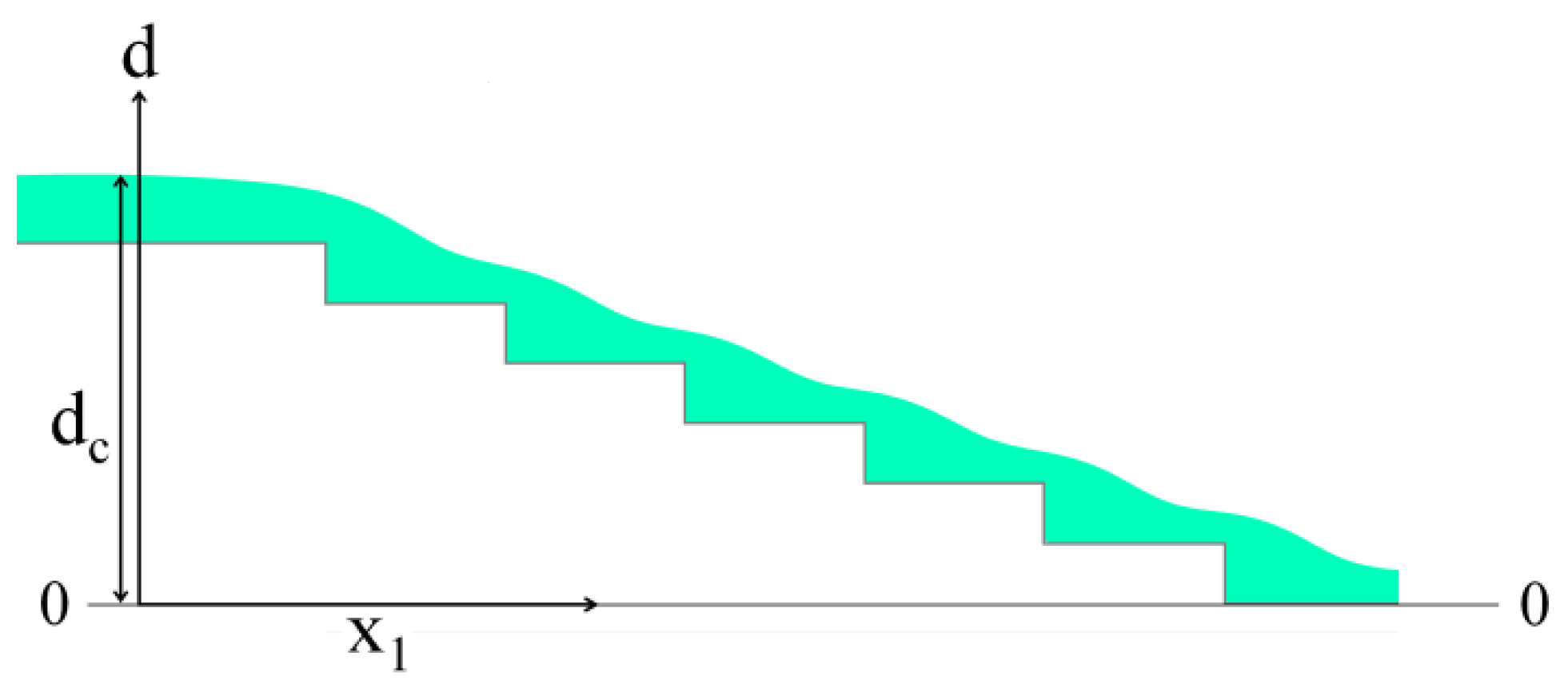
- The trapezoidal energy dissipation baffle block-step combination energy dissipator has a better air entrainment effect. Compared with the traditional step energy dissipator, the trapezoidal energy dissipation baffle block-step combination energy dissipator can advance the initial aeration point by one step and increase the air entrainment volume of the flow. We also proposed the calculation formula of the initial aeration point of the trapezoidal energy dissipation baffle block-step combination energy dissipator.
- (3)
- The trapezoidal energy dissipation baffle block-step combination energy dissipator has a lower risk of cavitation. By adding trapezoidal energy dissipation baffle blocks at the convex corner of the step, the pressure variation law of the horizontal and vertical surfaces of the traditional step is changed, which reduces the extreme value of the pressure on the horizontal surface of the step and reduces the distribution area of the negative pressure on the vertical surface of the step, thus reducing the risk of cavitation of the step. The top and the backwater surface of the trapezoidal energy dissipation baffle block have negative pressure, which can easily cause cavitation damage, and certain protective measures will be needed for the actual project.
- (4)
- The trapezoidal energy dissipation baffle block-step combination energy dissipator has a lower flow velocity. The trapezoidal energy dissipation baffle block-step combination energy dissipator mainstream cross-sectional flow velocity still follows the law of a small bottom layer and large surface layer. However, compared with the traditional step energy dissipator, the trapezoidal energy dissipation baffle block-step combination energy dissipator mainstream section flow velocity change amplitude is higher, the flow velocity is lower, the concave angle roll area low-flow-velocity range is higher, and the energy dissipation effect is better. The trapezoidal energy dissipation baffle block-step combination energy dissipator makes the vortex structure more distributed in the vicinity of the trapezoidal energy dissipation baffle block, which helps the energy dissipation of the step energy dissipator.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ap | the cross-sectional area of the bubble (m2) |
| C1ε | constant terms (-) |
| C2ε | constant terms (-) |
| Cd | the custom resistance coefficient (-) |
| c | the air admixture density (-) |
| Dc | the diffusion coefficient (-) |
| d | the elevation head of the water flow (m) |
| dc | the total elevation of the step dissipator (m) |
| f | friction coefficient (-) |
| Gk | the turbulent kinetic energy generation term (kg/m/s−3) |
| gn | the gravitational normal component to the water surface (m/s2) |
| h | step height (m) |
| hk | critical water depth (m) |
| K | interphase resistance coefficient (-) |
| Kair | scale factor (-) |
| K* | roughness (m) |
| L1 | length of diversion channel (m) |
| L2 | step length (m) |
| Lc | initial air entrainment point distance (m) |
| LT | turbulence length scale (m) |
| la1 | energy dissipating baffle block bottom length (m) |
| la2 | energy dissipating baffle block upper length (m) |
| lb | energy dissipating baffle block width (m) |
| lc | energy dissipating baffle block height (m) |
| q | single wide flow (m3/s) |
| Rp | air bubble radius (m) |
| Sa | volume of gas blended into the grid per unit time (-) |
| t | time (s) |
| Uai | velocity of motion of gas phase (m/s) |
| Ur | slip speed (m/s) |
| ui | i-direction velocity component (m/s) |
| uj | j-direction velocity component (m/s) |
| V | cross-sectional flow rate (m/s) |
| Vb | grid volume (-) |
| Vc | critical flow rate (m/s) |
| Vp | volume of a single bubble (-) |
| W | width of diversion channel (m) |
| x1 | location upstream from the step (m) |
| x2 | distance from the horizontal plane of the concave angle of the step (m) |
| xi | i-directional coordinate components (-) |
| xj | j-directional coordinate components (-) |
| y | steps in different longitudinal sections (m) |
| z1 | distance from the vertical plane of the concave angle of the step (m) |
| z2 | water depth perpendicular to the virtual substrate (m) |
| zmax | maximum water depth at section (m) |
| α | slope (-) |
| ζ | dimensionless parameters (-) |
| η | energy dissipation (-) |
| μ | molecular viscosity coefficient (-) |
| μc | power viscosity of continuous phase (N∙s/m2) |
| μt | turbulent viscosity coefficient (-) |
| ρ | density (kg/m3) |
| ρa | density of air (-) |
| ρb | average density of water and gas phases (kg/m3) |
| ρc | density of continuous phase (-) |
| ρm | mixed-phase density (kg/m3) |
| ρw | density of water (kg/m3) |
| σ | surface tension coefficient (-) |
| σk | the Prandtl number corresponding to the k (-) |
| σε | the Prandtl number corresponding to the ε (-) |
References
- Wang, Y.H.; Ma, Y.H.; Xu, L. Problems with reinforcement of small reservoirs and recommendations. China Water Resour. 2021, 22, 51–52. [Google Scholar]
- Chanson, H. Hydraulic design of stepped spillways and downstream energy dissipators. Dam Eng. 2001, 11, 205–242. [Google Scholar]
- Ohtsu, I.; Yasuda, Y.; Takahashi, M. Flow characteristics of skimming flows in stepped channels. J. Hydraul. Eng. 2004, 130, 860–869. [Google Scholar] [CrossRef] [Green Version]
- Matos, J.; Novakoski, C.K.; Ferla, R.; Marques, M.G.; Dai Prá, M.; Canellas, A.V.B.; Teixeira, E.D. Extreme pressures and risk of cavitation in steeply sloping stepped spillways of large dams. Water 2022, 14, 306. [Google Scholar] [CrossRef]
- Sanchez-Juny, M.; Blade, E.; Dolz, J. Analysis of pressures on a stepped spillway. J. Hydraul. Res. 2008, 46, 410–414. [Google Scholar] [CrossRef]
- Amador, A.; Sánchez-Juny, M.; Dolz, J. Developing flow region and pressure fluctuations on steeply sloping stepped spillways. J. Hydraul. Eng. 2009, 135, 1092–1100. [Google Scholar] [CrossRef]
- Frizell, K.W.; Renna, F.M.; Matos, J. Cavitation potential of flow on stepped spillways. J. Hydraul. Eng. 2013, 139, 630–636. [Google Scholar] [CrossRef]
- Novakoski, C. Análise da macroturbulência do escoamento sobre vertedouro em degraus com aeração induzida por defletor e câmara de ar. Ph.D. Thesis, Universidade Federal do Rio Grande do Sul (UFRGS), Porto Alegre, Brazil, 2021. [Google Scholar]
- Wu, X.S. Study on toe velocity of stepped overflow dam. J. Hydraul. Eng. 2001, 2, 73–78. [Google Scholar]
- Dong, Z.; Wang, J.; Vetsch, D.F.; Boes, R.M.; Tan, G. Numerical simulation of air–water two-phase flow on stepped spillways behind x-shaped flaring gate piers under very high unit discharge. Water 2019, 11, 1956. [Google Scholar] [CrossRef] [Green Version]
- Chanson, H.; Toombes, L. Experimental investigations of air entrainment in transition and skimming flows down a stepped chute. Can. J. Civil. Eng. 2002, 29, 145–156. [Google Scholar] [CrossRef] [Green Version]
- Bung, D.B. Developing flow in skimming flow regime on embankment stepped spillways. J. Hydraul. Res. 2011, 49, 639–648. [Google Scholar] [CrossRef]
- Ghaderi, A.; Abbasi, S.; Abraham, J.; Azamathulla, H.M. Efficiency of trapezoidal labyrinth shaped stepped spillways. Flow Meas. Instrum. 2020, 72, 101711. [Google Scholar] [CrossRef]
- Raza, A.; Wan, W.; Mehmood, K. Stepped spillway slope effect on air entrainment and inception point location. Water 2021, 13, 1428. [Google Scholar] [CrossRef]
- Hubert, C. Stepped spillway flows and air entrainment. Can. J. Civ. Eng. 1993, 20, 422–435. [Google Scholar]
- Salmasi, F.; Abraham, J. Effect of slope on energy dissipation for flow over a stepped spillway. Water Supply 2022, 22, 5056–5069. [Google Scholar] [CrossRef]
- Nikseresht, A.H.; Talebbeydokhti, N.; Rezaei, M.J. Numerical simulation of two-phase flow on step-pool spillways. Sci. Iran. 2013, 2, 222–230. [Google Scholar]
- Ghaderi, A.; Abbasi, S.; Francesco, S.D. Numerical study on the hydraulic properties of flow over different pooled stepped spillways. Water 2021, 13, 710. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Effects of step pool porosity upon flow aeration and energy dissipation on pooled stepped spillways. J. Hydraul. Eng. 2014, 140, 04014002. [Google Scholar] [CrossRef] [Green Version]
- Morovati, K.; Eghbalzadeh, A. Study of inception point, void fraction and pressure over pooled stepped spillways using flow-3d. Int. J. Numer. Methods Heat Fluid Flow 2017, 28, 982–998. [Google Scholar] [CrossRef]
- Sarkardeh, H.; Marosi, M.; Roshan, R. Stepped spillway optimization through numerical and physical modeling. Int. J. Energy Environ. 2015, 6, 597–606. [Google Scholar]
- Hekmatzadeh, A.A.; Papari, S.; Amiri, S.M. Investigation of energy dissipation on various configurations of stepped spillways considering several rans turbulence models. Iran. J. Sci. Technol. Trans. Civ. Eng. 2018, 42, 97–109. [Google Scholar] [CrossRef]
- Hien, L.T.T.; Duc, D.H. Numerical simulation of free surface flow on spillways and channel chutes with wall and step abutments by coupling turbulence and air entrainment models. Water 2020, 12, 3036. [Google Scholar] [CrossRef]
- Wan, W.; Raza, A.; Chen, X. Effect of height and geometry of stepped spillway on inception point location. Appl. Sci. 2019, 9, 2091. [Google Scholar] [CrossRef] [Green Version]
- Hunt, J.; Wray, A.; Moin, P. Eddies, streams, and convergence zones in turbulent flows. Cent. Turbul. Res. 1988, 193–208. [Google Scholar]
- Nakagawa, H.; Nezu, I. Experimental investigation on turbulent structure of backward-facing step flow in an open channel. J. Hydraul. Res. 1987, 25, 67–88. [Google Scholar] [CrossRef]
- Liang, S.C.; Zhang, X.D.; Kang, S.; Ren, H.L.; Wang, J.Y.; Fan, Z.Y.; Zhao, Y.F. Des simulation of the flow around a cube and analysis of the vortex structure. J. Eng. Thermophys. 2015, 36, 535–540. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Li, Y.; Sun, X. Study on the Hydraulic Characteristics of the Trapezoidal Energy Dissipation Baffle Block-Step Combination Energy Dissipator. Water 2022, 14, 2239. https://doi.org/10.3390/w14142239
Tian Y, Li Y, Sun X. Study on the Hydraulic Characteristics of the Trapezoidal Energy Dissipation Baffle Block-Step Combination Energy Dissipator. Water. 2022; 14(14):2239. https://doi.org/10.3390/w14142239
Chicago/Turabian StyleTian, Yu, Yongye Li, and Xihuan Sun. 2022. "Study on the Hydraulic Characteristics of the Trapezoidal Energy Dissipation Baffle Block-Step Combination Energy Dissipator" Water 14, no. 14: 2239. https://doi.org/10.3390/w14142239




