1. Introduction
Around the world, damage from natural disasters is increasing due to the abnormal climate caused by global warming, and it is expected that the frequency and intensity of natural disasters will continue to increase [
1,
2]. Compared to the 20 years from 1980 to 1999, both the number of and amount of damage caused by natural disasters during the 20-year period from 2000 to 2019 has increased. In particular, the increase in damage from floods and storms was higher than that of other natural disasters.
Figure 1 compares the amount of damage caused by natural disasters during the period from 1980 to 1999 and from 2000 to 2019 [
3]. In the case of the United States, the loss due to natural disasters occurred at an all-time high in 2017, with more than
$306 billion in losses due to hurricanes and heavy rains [
4].
In order to reduce the damage caused by flooding, it is necessary to accurately predict the flood and evacuate people and property located in the flood-damaged area at an appropriate time [
5,
6]. However, flood prediction has many difficulties in forecasting because there are many variables to consider, and each element has spatial and temporal correlations. Methods for flood prediction are continuously being studied, and there are mainly hydrological models and data-driven intelligent models.
In the case of the hydrological model, it is a model that analyzes the characteristics of the hydrological gate and physically describes the discharge confluence point. It is based on the theory of fluid mechanics and is a method for researchers to derive a confluence equation by combining physical laws such as mass, momentum, and conservation of energy. It has been used in the past for flood prediction and management even before studies through machine learning and deep learning were actively conducted, and various studies have been conducted using the model [
7,
8,
9,
10,
11,
12]. However, the model requires a deep hydrological knowledge of the researcher, and there is variability due to erosion of the topography over time, so it is difficult to use it in the long term. In addition, it is difficult to construct input data with various variables, and low prediction accuracy is obtained due to non-linearity. Furthermore, since each river has different characteristics of the watershed, it is necessary to create an individual model applied to each river, so there is a lack of versatility [
13].
In the case of a data-based intelligent model, it is a method of predicting water level and runoff through data analysis based on observed data. Data analysis and data mining technologies are being researched in many fields and are rapidly developing [
14]. Regardless of fields such as medicine [
15], economy [
16,
17], environment [
18], and tourism [
19,
20], a great deal of research is being conducted by applying machine learning and deep learning, and it has been confirmed that it shows excellent performance. One of the data-based intelligent models applied in the hydrological field for predicting and managing floods is the artificial neural network (ANN) model. The ANN model developed by [
21] uses water level and meteorological data as input data and estimates the water flow by applying harmony search (HS) [
22] and differential evolution (DE) [
23]. By utilizing HS and DE, overfitting was prevented by updating the parameters of the architecture and selecting important features. Compared with the radial basis function neural network (BRFNN) [
24] and multi-layer perceptron (MLP) [
25] models, ANN with HS and DE was confirmed to show good performance, and it was proved that the ANN model can be used for water flow prediction. In addition, many studies have been conducted to predict key factors of flooding using models such as ANN-based water level prediction models and runoff prediction models [
26,
27,
28,
29,
30]. However, most of the related studies utilize hydrological data and meteorological data, which are categories of time series data, as input data [
31,
32]. In the case of the ANN model, there is a problem of insufficient memory when operating on sequential data and time series data and it is difficult to find an optimal parameter in the learning process [
33,
34].
Recently, deep neural network (DNN) data-based intelligent models with two or more hidden layers that have improved some problems of the ANN model have been extensively studied. In this case, LSTM and GRU models based on recurrent neural networks (RNN), which show excellent performance in time series data processing, are being widely used. Le et al. [
35] proposed an LSTM model for flood forecasting. In this study, daily runoff and rainfall data were used as input datasets, and a performance comparison experiment was conducted according to the input data of the model. An experiment was conducted in the Da River basin of Vietnam, and the performance comparison experiment of the model according to the input data was conducted using the runoff and precipitation data sets. The output of the model was configured to predict the amount of runoff for 1, 2, and 3 days into the future. The performance evaluation was conducted using the Nash–Sutcliffe efficiency (NSE) and root mean squared error (RMSE) indicators [
36]. Finally, the NSE value of the first day data was around 99.1%, the NSE value of the second day was 94.9%, and the 3rd day NSE value was 87.2%, so it was possible to obtain more than 87.2% accuracy for all output data. Through this study, it was confirmed that the LSTM model, which is widely used for time series data processing, performed well enough for flood prediction. In addition, RNN-based LSTM and GRU models are continuously being studied for flood prediction and are showing good performance as they are specialized models for time series data prediction [
37,
38,
39,
40,
41,
42]. In addition, there are many studies using artificial intelligence such as ANN and RNN for flood management which consider the ratio of training data and validation data [
43] or which compare the performance according to the size of the input data of the model [
44]. All of these studies greatly affect the performance of the model, and the difference in the current paper is that other types of meteorological data are used to conduct a performance comparison experiment according to the meteorological data. As a result of the experiment, the best data set for the study area obtained the best results when water level data and ASOS data were used. There are two or more types of meteorological data measured in most research areas. Therefore, as suggested in this paper, it is considered that there is a possibility that the performance of the model will be improved if appropriate meteorological data are used in the papers related to water level prediction.
In this paper, we propose an LSTM-GRU-based water level prediction model using water level data and meteorological data as input data. In addition, two types of weather data provided by the Korea Meteorological Administration, the Automated Synoptic Observing System (ASOS) data set and the Automatic Weather System (AWS) data set, are used to test which data are more suitable for the study area. In addition, for water level data, data from upstream and downstream of Yeojubo, Icheon-si, Gyeonggi province, Republic of Korea were used, and performance comparison experiments of the multi-LSTM model, multi-GRU model, and LSTM-GRU model were conducted. A total of three evaluation indicators were used: MSE, NSE, and MAE, and the maximum water level prediction error was additionally used. The LSTM-GRU model proposed in this paper showed the best performance among all cases. The mean squared error (MSE) value of the LSTM-GRU model was 3.92, the Nash–Sutcliffe coefficient of efficiency (NSE) value was 0.942, the mean absolute error (MAE) value was 2.22, and the maximum water level error was 55.49, confirming the best performance in all indicators.
Section 2 describes the study area, training data, and deep learning techniques used in model development. Experimental scenarios and model design are described in
Section 3, and a model performance comparison is conducted in
Section 4. Finally,
Section 5 reviews and concludes the results of this study.
2. Methodology
2.1. Study Area
One of the main causes of flooding is localized heavy rain which is accompanied by a large amount of rainfall in a short period of time. To select a test area where extensive damage occurred due to rainfall, the data on the current situation of heavy rain damage by region, published by the Ministry of Public Administration and Security of the Republic of Korea, were used. The Ministry of Public Administration and Security is the central administrative agency of the Republic of Korea in charge of affairs related to disaster prevention, such as establishing, generalizing, and co-ordinating safety and disaster policies. The current status of heavy rain damage by region over the past 30 years was investigated.
Figure 2 shows the amount of rain damage and the frequency of occurrence of rain damage for each city in Korea.
In Gyeonggi province, the amount of rain damage recovery amount was the second highest among all cities, and in the case of occurrence frequency, rainfall occurred with the highest frequency among all cities. In addition, due to the geographical characteristics of the Gyeonggi province region, it surrounds the capital of the Republic of Korea, which has the highest population density, and a large population is also distributed in Gyeonggi-do.
Figure 3 shows the population density and total population of each city as of 2020.
As described above, the Gyeonggi-do region, which is expected to receive extensive damage in case of heavy rain and flood, was selected as the test bed area. Due to the nature of rivers and the water flows from upstream to downstream, excessive runoff due to rainfall occurs, causing flooding in the downstream area. Yeojubo, in Gyeonggi-do, was selected as the final test bed for this study because there are measuring stations upstream and downstream of the city.
2.2. Meteorological Dataset and Water Level Dataset
For the water level dataset, the Korea Water Management Information System (WAMIS) [
45] was referred to, and the water level measurement station used data from upstream and downstream water level measurement stations in Yeojubo. The water level dataset and the meteorological dataset are used as input data for the water level prediction model in this paper, and data were measured at 1 h intervals from 2 October 2013 to 9 June 2022. The total dataset for upstream and downstream consists of 71,136 rows each and can be confirmed by visualizing the entire dataset upstream and downstream through
Figure 4.
The upstream and downstream datasets maintain an appropriate water level except in the summer when there is high rainfall; nevertheless, they have the same characteristic in that the water level increases rapidly in the summer when there is high rainfall. However, in the case of upstream of Yeojubo, it was confirmed that the amount of increase when rainfall occurred compared to the water level in the period when there was little rainfall was significant compared to the downstream recordings.
In this paper, two types of data provided by the Korea Meteorological Administration were used for meteorological training data for the model. The Korea Meteorological Administration uses a variety of meteorological equipment to observe the weather in the field, such as ground, high-rise, marine, and aviation. In this paper, data from the Automatic Weather System (AWS) and the Automated Synoptic Observing System (ASOS) were used to observe the weather on the ground. In the case of the AWS, it is a device designed for automatic observation without human observation, and it automatically handles all processes such as real-time measurement, calculation, storage, and display. The items to be observed include air pressure, temperature, humidity, wind direction, wind speed, precipitation, etc., and are observed in real time. Both ASOS and AWS datasets used temperature, humidity, and precipitation parameters as input data. Furthermore, as with the water level data set, data measurements were carried out at 1-h intervals.
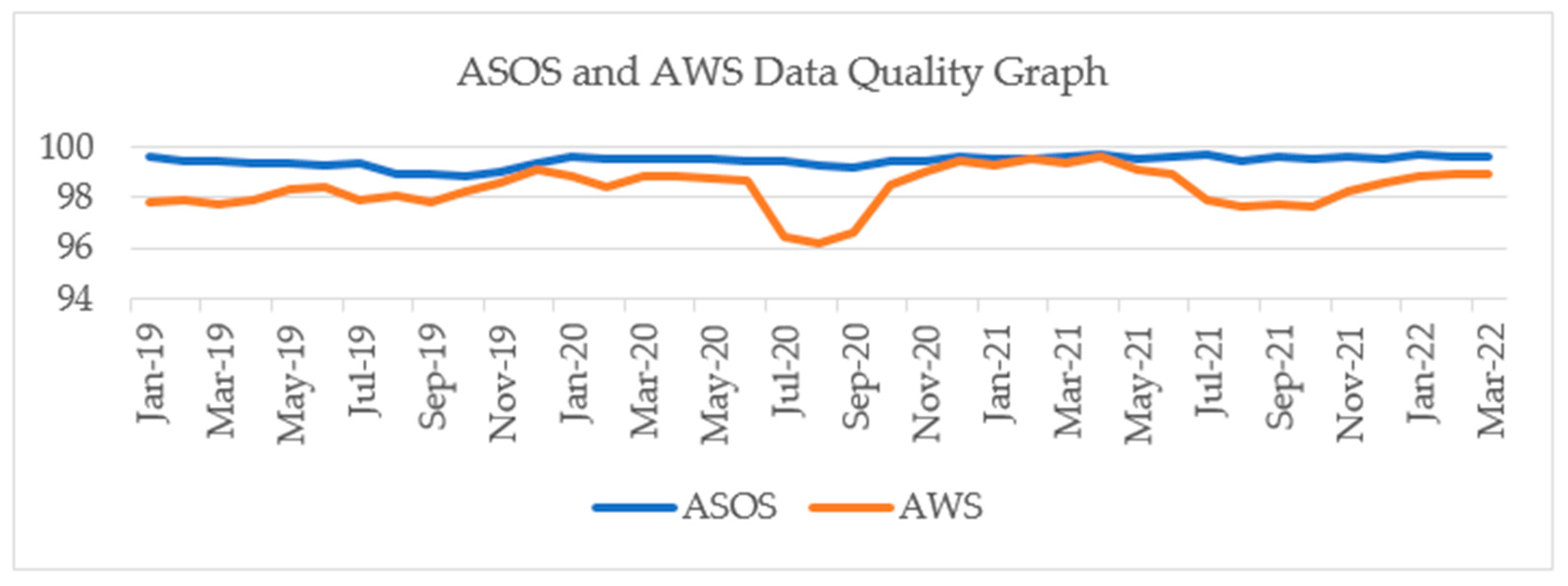
Figure 5 shows the quality information of AWS and ASOS data provided by the Korea Meteorological Administration [
46]. Korea has a hot and humid climate in summer, which causes high rainfall and a large number of typhoons, and it can be seen that the accuracy of AWS data operated unattended during the corresponding period is lower than that of other periods or ASOS observation equipment. However, the location of the nearest AWS observatory is located about 8 km away from Yeojubo, the actual test area, and the location of the nearest ASOS observatory is about 20 km away from Yeojubo.
Figure 6 shows the locations of the water level and meteorological data stations in the test area.
In the case of torrential downpours in summer, there is a characteristic that a large amount of rainfall continues in a narrow range. Due to these characteristics, it was determined that the distance between the actual test bed and the meteorological data observation point would affect the model performance. Therefore, we intend to conduct a performance comparison experiment of the model according to the type of meteorological data used as input data.
Table 1 shows the information of the hydrology and meteorology stations used and the datasets used.
2.3. LSTM (Long Short-Term Memory)
LSTM is one of the recurrent neural network (RNN) architectures used in many fields for time series data processing [
47]. RNN is mainly used for temporally correlated data. It considers the correlation between previous data and current data and predicts future data through past data while having a structure in which signals cycle to predict future data. However, there is a problem that the past data cannot be remembered for a long time [
48,
49]. LSTM is an architecture that has emerged to compensate for these problems. There are a total of six parameters, and through the structure of four gates, not only short-term memory but also long-term memory can be resolved, and the structure of the LSTM can be confirmed in
Figure 7.
The LSTM network has the same chain structure as the RNN, but the repeating modules of the RNN are structured to exchange information with each other through four layers, not just one tanh layer. The state in the LSTM cell is divided into two vectors, where means a short-term state and means a long-term state. Data can be added to or removed from the cell state through sigmoid gates, each gate having an individual weight, similar to a layer or series of matrix operations. It is designed to solve the problem of long-term dependencies, as gates can also retain information from long-term historical data.
The first step in an LSTM network is to identify and decide which unnecessary information to omit from the cell. The corresponding cell is called a forget gate, and the process determines the output of the last LSTM cell () at and the current input () at the current time by a sigmoid function. In this instance, the value that comes out through the sigmoid function has a value between (0~1). In this case, the larger the value, the more intact is the information of the previous state that is memorized. The smaller the value, the more information about the previous state is forgotten, and the part to omit from the previous output is decided.
After going through the forget gate, it goes through the process of selecting information to store. Through the forget gate, the memory cell ( of the previous time is forgotten, new information to be remembered is added, and the value of each element is determined as newly added information. In this case, appropriate choices are made rather than unconditionally accepting new information. A gate that performs a corresponding role is called an input gate. In this instance, the sigmoid function is taken through the last LSTM cell ( and the current value , and the function, which is an activation function, is added. In this instance, after going through the sigmoid layer, the value is between (0~1) and represents the degree to which new information is updated, and the value after going through the tanh function has a value between (−1~1) and has a weight representative of the importance given to it. Finally, the input gate performs the Hadamard product operation on the two values, and the corresponding new memory is added to the previous cell state () to become .
After judging the value of new information through the input gate and selecting the information to remember, the next process is to select the output information. The corresponding gate is called an output gate, and a sigmoid function is obtained through the value of the current time (
and the value of the last LSTM cell (
. The result value through the sigmoid function performs the operation of the current cell state (
) and Hadamard product, and the effect of filtering the value occurs and it becomes a hidden state.
Here, denotes a sigmoid function, denotes a weight matrix, and denotes a bias. denotes the cell state of the current time, denotes the cell state of the previous time, and means Hadamard product operation. Equation (1) refers to the process of going through the forgetting gate, and in the process of going through the input data, the cell state is updated through Equations (2)–(4). Next, it goes through the output gate indicated by Equation (5), and the LSTM operates in a structure in which the final hidden layer state is updated through Equation (6).
2.4. GRU (Gated Recurrent Units)
As one of the RNN architectures, GRU is a model inspired by LSTM. It is a model that improves the problem of RNN and reduces the computation of updating the hidden state while maintaining the solution to the long-term dependency problem of LSTM. The performance is similar to that of LSTM [
50]. In the case of LSTM, there is a problem that overfitting occurs when there is insufficient data, because more parameters are required compared to the existing RNN to solve the long-term dependency problem. GRU improved this shortcoming through a LSTM structure change. GRU improved this shortcoming through the structural change of LSTM. The structure of GRU is shown in
Figure 8.
In
Figure 8 it can see that the structure is more concise than the LSTM structure of
Figure 7. The main difference from the LSTM is that GRU integrates the LSTM’s forget gate and input gate and replaces it with an update gate. In addition, it has a simpler structure than the LSTM by integrating the cell state and the hidden state, and the calculation cost is low because the number of parameters is smaller than that of the LSTM.
The process corresponding to
r in
Figure 8 means the reset gate, and the hidden state of the network is calculated through this process. The result of going through the reset gate is calculated with the information of the past hidden layer to calculate the candidate group for the hidden state. Next, the part corresponding to z means the update gate. Through this part, the functions of forget gate and input gate of LSTM are performed, and how much current information is used is decided. The value calculated through the corresponding gate is calculated with the candidate of the previously calculated hidden state to determine the final hidden state. Equation (7) below corresponds to a reset gate, Equation (8) corresponds to an update gate, and Equations (9) and (10) are equations for determining hidden state candidates and the final hidden state.
Since it cannot be concluded that either GRU or LSTM is better in terms of model performance, in this paper, we conduct an experiment based on LSTM and GRU, and compare their performance.
2.5. Performance Indicators
In this paper, three types of performance comparison indicators of the water level prediction model are MSE (mean squared error), NSE (Nash–Sutcliffe coefficient of efficiency), and MAE (mean absolute error). MSE is a widely used method for evaluating the performance of a regression model. It is the square of the difference between the actual observed value and the predicted value. The indicator is sensitive to outliers because the difference between the observed and predicted values is squared. In the case of the hydrologic model, the MSE index was selected because it can cause human casualties if an outlier occurs in the prediction. In the case of NSE, it is a widely used indicator to evaluate the performance of hydrological models. NSE has a value of (−∞~1) as an index frequently used to evaluate the performance of hydrological models. A value closer to 1 means better model performance. In the case of MAE, it means the average of all absolute errors of the observed and predicted values and has the advantage of intuitively checking the performance of the model. The equations for the performance comparison metrics are given as follows:
In this paper, performance evaluation is performed according to LSTM, GRU model, and meteorological data through three indicators. Information on each piece of experiment is described in
Section 3.
4. Results
The water level and meteorological data sets described in
Section 2 were used for the data for the experiment, and the experiment was conducted using the input data and model consisting of nine types of input data using the three models described in
Section 3.
The total collection period of all training and test data was measured at 1-h intervals from 2 October 2013 to 9 June 2022. Of the data consisting of a total of 76,152 rows, 57,114 rows (75%) were used as training data and validation data, and the remaining 19,018 rows (25%) were used as test data. In the case of a flood prediction model, it is important to predict a high-water level due to a rapid increase. In this instance, the maximum value among all the measured water levels exists in the test data, so that the validity of the model can be verified.
4.1. Training and Validation Result
MSE was used as the basic loss function for model training, and NSE and MAE indicators were used as auxiliary indicators for actual test data to compare observed values and predicted values. In addition, Adam was used as the optimization function, the number of units of the LSTM and GRU models was 256, and the number of training iterations (epoch) was 200, which was performed under the same conditions. The reason for selecting the parameters of the model was to derive the optimal values through preliminary experiments. In the case of the learning model, a total of nine cases were carried out as in the case summarized in
Table 2, information on each model training and validation can be checked in
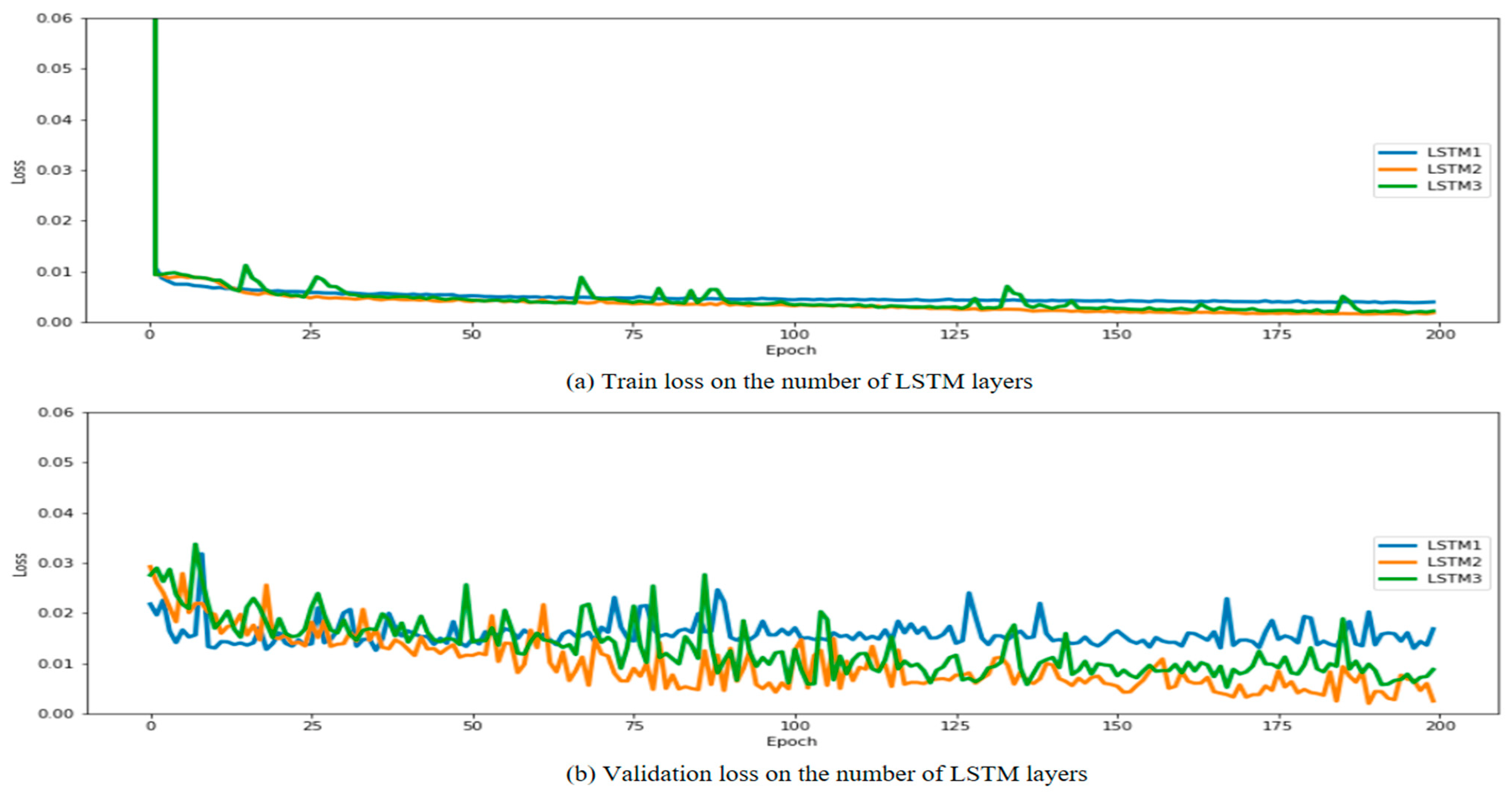
Table 3, and the change in loss value according to epoch during model training is shown in
Figure 10. In the case of the learning model, a total of nine cases were performed as in the case summarized in
Table 2 and
Table 3 and shows information about each model learning and validation.
Figure 10 shows the change in loss value according to epoch during model training.
According to the characteristics of the LSTM model, the multi-LSTM model had the largest number of hyperparameters, and the multi-GRU model had the smallest number of hyperparameters. In the case of training time, the GRU model took the least amount of time, but it was confirmed that the number of hyperparameters and the training time were not proportional. In addition, looking at
Figure 14, the loss value converges to close to 0 according to the epoch in all cases, and it was determined that the learning was well accomplished. It was considered that overfitting occurred, but for equality with other models, the epochs were maintained at 200 and the experiment was conducted. In the case of the MSE value used as the loss function, differences were found according to the input data characteristics for each model. In the case of the multi-LSTM model, there was no significant difference depending on the input data; however, in the case of multi-GRU and LSTM–GRU, it was confirmed that the performance difference occurred depending on the input data. In the case of the multi-GRU model, it was confirmed that the performance of the S2 and S3 cases, including the weather data in the training data, was lower than that of the S1 case, and it was confirmed that the performance was poor among the nine cases. When checking the training and validation results, it was confirmed that GRU showed good performance for S1 data with a small number of dimensions, but poor performance for S2 and S3 with a large number of dimensions. However, in the case of the LSTM–GRU model, it was confirmed that the verification MSE of the S1 model with a small dimension of training data showed the lowest performance. Finally, the worst performing case was S3_GRU which showed the worst results with 0.39 for training and 1.80 for validation, and the case with the best performance showed the best results with S3_LSTM_GRU, 0.15 for training and 0.19 for validation.
4.2. Test Result
The data set for the test has the highest water level data during the entire data collection period, and the performance of the model is judged by comparing the MSE, NSE, and MAE indicators with the highest water level prediction error. In this instance, the highest water level in the observed data was 3552.38 cm. The test results are shown in
Table 4, and the difference between the observed value and the predicted value according to the training data for each model are shown in
Figure 15,
Figure 16 and
Figure 17.
The test results are similar to the model training and validation results. In the multi-LSTM model, no significant difference was found depending on the input data, but the NSE value obtained the best result when the data corresponding to the S1 case were used as the input data. In addition, it was confirmed that the difference in the predicted maximum water level included in the test data was 91.27 cm in the S1 case, which obtained the best result. Among the LSTM models, when the S2 case data were used, the NSE was 0.834, which was slightly lower than those of the S1 and S3 cases, and the maximum water level prediction error was also the lowest at 117.87 cm.
In the case of the multi-GRU model, the lowest performance was confirmed in all cases compared to other models. Similarly, in the results of verification it was confirmed that the GRU-based water level prediction model effectively learned S1 with a small number of dimensions from the experimental results but showed poor performance when the input data had a large number of dimensions. When the data of S1 case were used, the best results were obtained in the GRU model, but it was confirmed that the results were inferior compared to other models. For S2 and S3, the NSE values were 0.2 and 0.3, respectively, which were the lowest among the nine cases. Furthermore, in the case of S3, it was confirmed that the maximum water level prediction error was 211.77, being the lowest result among all scenarios.
The LSTM–GRU model showed the best performance on average among the three models, and in the case of S1, it was confirmed that the NSE was slightly lower than that of the LSTM model. However, in the case of S2 and S3, the NSE values were 0.920 and 0.942, respectively, and the maximum water level error was 79.64 and 55.49, which showed much better performance than other models.
Of these, when the S3 case was used, the best results were obtained among the nine models in all evaluation indicators, including MSE, NSE, MAE, and maximum water level prediction error. Therefore, it is determined that the most suitable weather data for the test bed, Yeojubo, is the ASOS data corresponding to the S3 case in view of the model’s performance.
5. Discussion
Due to global warming and abnormal climate changes, the frequency of and damage from floods are steadily increasing. Therefore, many studies are being conducted for flood management to minimize flood damage. Hydrological models and data-based intelligent models are mainly used to predict the water level, the most important parameter of flooding. In this paper, we propose the LSTM–GRU water level prediction model included in the data-based intelligent model. In this study, Yeojubo in Gyeonggi-do, Korea was selected as the test area, and the water level datasets upstream and downstream of Yeojubo were used. In addition, using meteorological data, comparison experiments between ASOS data and AWS data were conducted.
First, we conducted two experiments to find the most suitable parameters for the LSTM–GRU model. The two experiments were as follows: 1. experiment according to the number of units of the LSTM and GRU layers; and 2. performance comparison experiment according to input data size. As a result of the experiment, the best results were obtained when the number of units was 256, and the best performance was obtained when the size of the input data was used for the past 20 h. Next, to select a comparative model, a model composed of LSTM and GRU, which shows good performance in time-series data processing, was used. In this case, a performance comparison experiment was conducted according to the number of hidden layers to find the most suitable model configuration. When both LSTM and GRU were composed of two hidden layers, the best performance was shown, and multi-LSTM and multi-GRU models were selected as comparative models.
Next, a comparison experiment was conducted according to the three input data sets, and the three data sets consist of the following: 1. water level dataset; 2. water level dataset + AWS dataset; and 3. water level dataset + ASOS dataset. Experiments were conducted on nine scenarios using three datasets for a total of three models, and the model performance was evaluated using MSE, NSE, MAE, and maximum water level error. In the case of MSE, as an evaluation index sensitive to outliers, it was selected because a fatal error can occur if an outlier occurs in response to a rapidly rising water level. In the case of NSE, it is a model widely used for performance evaluation of hydrological models, and MAE has the strength of intuitively checking errors. Lastly, the reason for using the maximum water level error is that the historical highest water level of Yeojubo in the test data set occurred, so it was used as an evaluation index to check to what extent the water level can be predicted. In this instance, the LSTM–GRU model proposed in this study obtained the best results among nine scenarios when the water level dataset and the ASOS dataset were combined as input data. If the LSTM–GRU model proposed in this paper is used, it is considered that it can be used as a preliminary study of a flood management system that can predict the water level in advance, and evacuate through risk assessment.
6. Conclusions
In this paper, we propose an approach for data-based water level prediction using actual observation data. In order to predict the data of the 21st hour using the data of the past 20 h through the data of the upstream and downstream of Yeojubo in Gyeonggi-do, Republic of Korea, a model was constructed using the LSTM and GRU models, and a performance comparison experiment was conducted according to the input data. For comparative experiments, a model composed of LSTM and GRU was used. In this instance, the optimal model configuration was selected through experiments, and LSTM composed of two layers and GRU composed of two layers were selected as final comparative models. The existing hydrological method used for flood prediction has a problem in that it is difficult to build a model because various factors, including soil and watershed characteristics, must be considered, and there is a disadvantage that requires high hydrological competence of the researcher. The water level prediction model proposed in this paper has the advantage of being able to predict the water level more easily by using only the meteorological data set and the water level data set. Multi-LSTM, multi-GRU, and LSTM–GRU models were used to conduct a performance comparison experiment according to a total of nine cases, and it was confirmed that there was a significant performance difference when the input data was configured differently according to each model. The three types of input data are: S1 case using water level data only, S2 case using water level data and AWS data provided by the Korea Meteorological Administration, and ASOS data provided by the Korea Meteorological Administration. When looking at the data quality information provided by the Korea Meteorological Administration, the quality of the ASOS data was higher, but due to the concentrated heavy rain that fell in a narrow range in a short period of time in summer due to the seasonal nature of Korea, the AWS data were used in the comparative experiment. The LSTM and LSTM–GRU-based models confirmed good results for all three data types, but in the case of the GRU model, it was confirmed that the results were slightly inferior when the data of S2 and S3 cases with large input data dimensions were used. It was determined that the GRU, which reduced the number of parameters by simplifying the LSTM, did not effectively learn the characteristics of the training data used in this paper. In this instance, the case that obtained the best results used ASOS data and water level data, which are S3 cases, as training data, and the water level prediction model learned through the LSTM–GRU model obtained the best results. The test MSE of this model was 3.92, NSE was 0.942, and MAE was 2.22, showing the best performance in all evaluation indicators, and the maximum water level prediction error was 55.49 cm, which was the best result. In order to predict floods, the ability to predict a sudden rise in water level due to heavy rainfall, etc. is a very important factor, so the model is judged to be the most suitable among the nine cases. The NSE of the LSTM–GRU model proposed in this paper confirmed a high score of 0.942, and it is considered that it can be used for flood management.