Geospatial Artificial Intelligence (GeoAI) in the Integrated Hydrological and Fluvial Systems Modeling: Review of Current Applications and Trends
Abstract
:1. Introduction
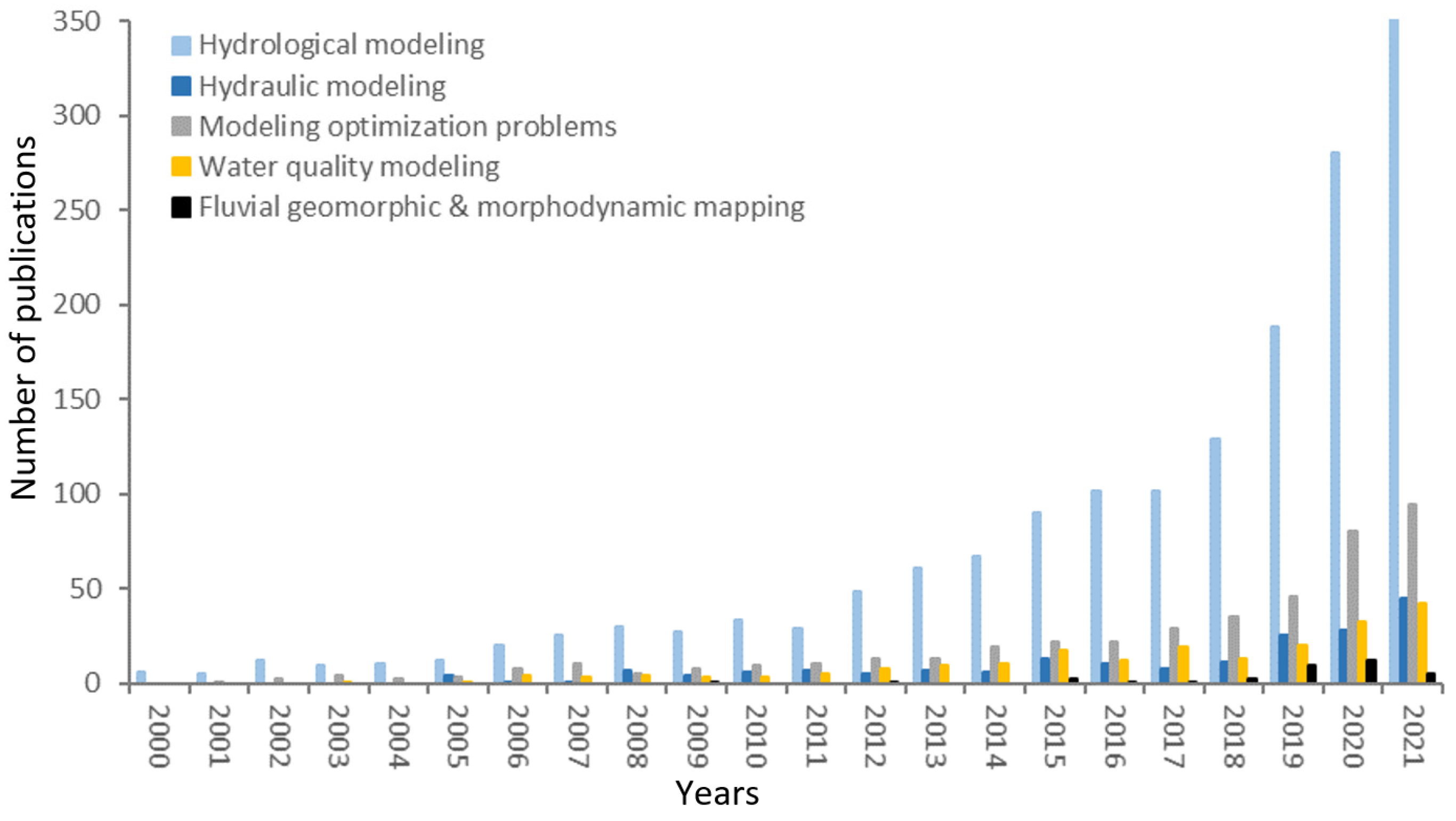
2. Review Methodology and Outline
3. Brief Introduction to Geospatial Artificial Intelligence
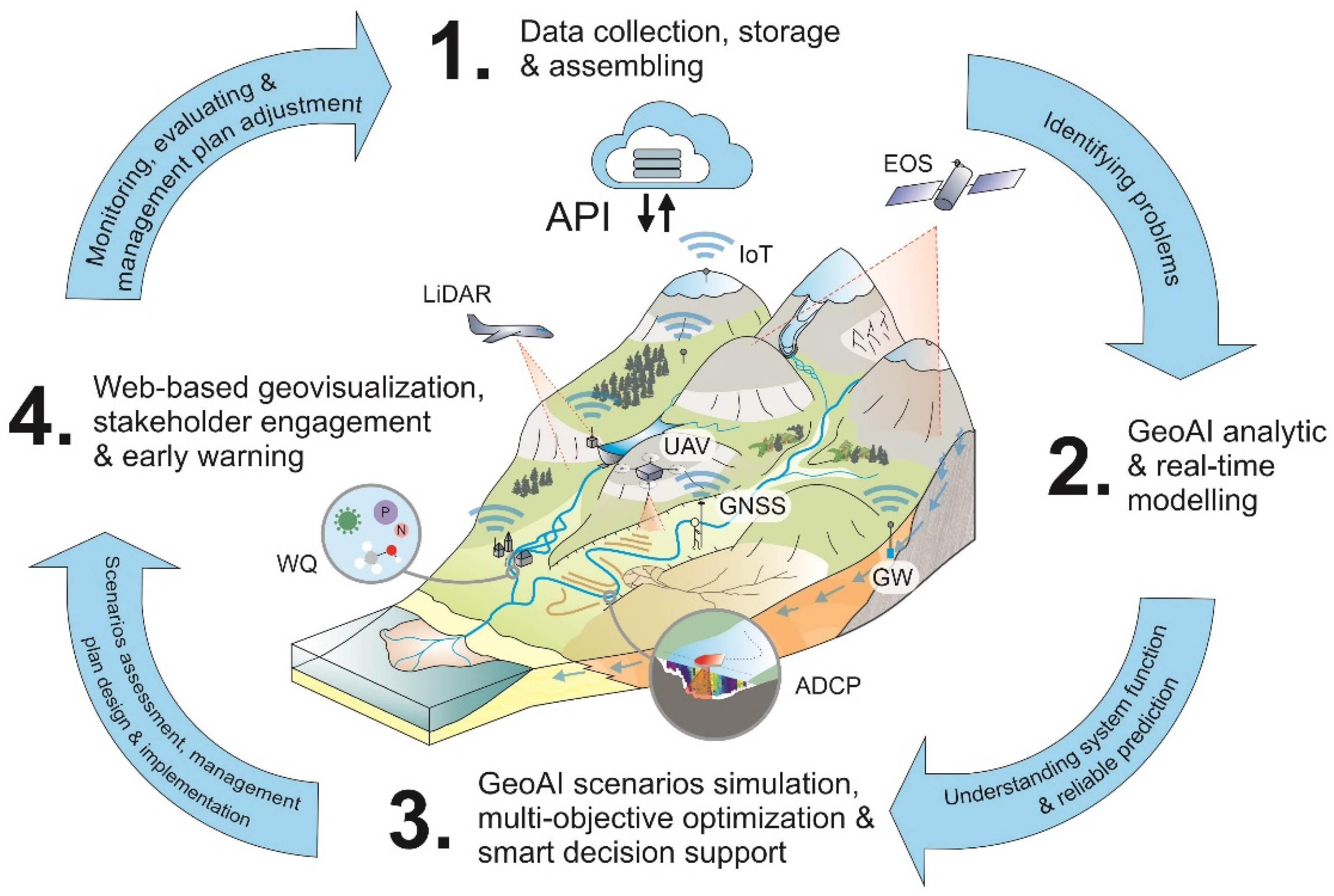
4. Current GeoAI Applications in Integrated Hydrological and Fluvial Systems Modeling
4.1. Hydrological and Hydraulic Modeling
4.1.1. Hydrological System Classification
4.1.2. Hydrological Data Fusion and Geospatial Downscaling
4.1.3. Spatial Prediction of Hydrological Variables
4.1.4. Hydrological Process Modeling
4.1.5. Hydraulic Modeling
4.1.6. Hydrological Data Assimilation
4.2. Modeling Optimization Problems for Hydrological Model Calibration and Decision Support System
4.2.1. Hydrological Model Calibration
4.2.2. Decision Support System for Integrated Water Resources Management
4.3. Automatic Water Quality Monitoring and Spatio-Temporal Prediction
4.3.1. Automatic Water Quality Monitoring
4.3.2. Spatio-Temporal Water Quality Prediction
4.4. Machine Learning in Fluvial Geomorphic and Morphodynamic Mapping
5. GeoAI Causal and Predictive Inference Capability
5.1. Renewed Data-Driven Research
5.2. Generalization of GeoAI Prediction
5.3. GeoAI Data Requirement for Reliably Prediction
5.4. GeoAI Capacity to Provide Novel Physical Insights
6. GeoAI Research Trends in Integrated Hydrological and Fluvial Systems Modeling
6.1. Toward Transdisciplinary GeoAI Research in Hydrological Modeling
6.2. Augmenting GeoAI Prediction Capability with Open Data and Crowdsourced Data
6.3. From Physical-Based and GeoAI Hybrid Models to Fully Integrated GeoAI–Physical-Based Models
6.4. From Small-Scale to Global-Scale Hydrological Modeling
6.5. Automation of Hydrological and Fluvial System Modeling
6.6. GeoAI-Based Multi-Dimensional Geo-Visualization and Digital Twin
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| CNN | Convolution Neural Network |
| DA | Data Assimilation |
| DEM | Digital Elevation Model |
| GA | Genetic Algorithm |
| GAN | Generative Adversarial Networks |
| GeoAI | Geospatial Artificial Intelligence |
| GP | Genetic programing |
| IoT | Internet of Things |
| IWRM | Integrated Water Resources Management |
| LiDAR | Light Detection and Ranging |
| LSTM | Long Short-term Memory Networks |
| ML | Machine Learning |
| RF | Random Forest (RF) |
| RL | Reinforced Learning |
| RNN | Recurrent Neural Network (RNN) |
| SVM | Support Vector Machine (SVM) |
| UAV | Unmanned Aerial Vehicles |
| WQ | Water Quality |
References
- Beven, K. Towards a Methodology for Testing Models as Hypotheses in the Inexact Sciences. Proc. R. Soc. Math. Phys. Eng. Sci. 2019, 475, 20180862. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McMillan, H.K.; Westerberg, I.K.; Krueger, T. Hydrological Data Uncertainty and Its Implications. WIREs Water 2018, 5, e1319. [Google Scholar] [CrossRef] [Green Version]
- Sun, A.Y.; Scanlon, B.R. How Can Big Data and Machine Learning Benefit Environment and Water Management: A Survey of Methods, Applications, and Future Directions. Environ. Res. Lett. 2019, 14, 073001. [Google Scholar] [CrossRef]
- Todini, E. History and Perspectives of Hydrological Catchment Modelling. Hydrol. Res. 2011, 42, 73–85. [Google Scholar] [CrossRef]
- Coulthard, T.J.; Van De Wiel, M.J. Modelling River History and Evolution. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2012, 370, 2123–2142. [Google Scholar] [CrossRef]
- Singh, V.P. Hydrologic Modeling: Progress and Future Directions. Geosci. Lett. 2018, 5, 15. [Google Scholar] [CrossRef]
- Koren, V.; Smith, M.; Cui, Z. Physically-Based Modifications to the Sacramento Soil Moisture Accounting Model. Part A: Modeling the Effects of Frozen Ground on the Runoff Generation Process. J. Hydrol. 2014, 519, 3475–3491. [Google Scholar] [CrossRef]
- Arnold, J.; Moriasi, D.; Gassman, P.; Abbaspour, K.; White, M.; Srinivasan, R.; Santhi, C.; Harmel, R.; van Griensven, A.; Van Liew, M.; et al. SWAT: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Gochis, D.J.; Yu, W.; Yates, D. The WRF-Hydro Model Technical Description and User-s Guide. NCAR Tech. Doc. 2013. [Google Scholar] [CrossRef]
- Brunner, P.; Simmons, C.T. HydroGeoSphere: A Fully Integrated, Physically Based Hydrological Model. Groundwater 2012, 50, 170–176. [Google Scholar] [CrossRef] [Green Version]
- Lane, S.N.; Ferguson, R.I. Modelling Reach-Scale Fluvial Flows. In Computational Fluid Dynamics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005; pp. 215–269. ISBN 978-0-470-01519-3. [Google Scholar]
- Clark, M.P.; Bierkens, M.F.P.; Samaniego, L.; Woods, R.A.; Uijlenhoet, R.; Bennett, K.E.; Pauwels, V.R.N.; Cai, X.; Wood, A.W.; Peters-Lidard, C.D. The Evolution of Process-Based Hydrologic Models: Historical Challenges and the Collective Quest for Physical Realism. Hydrol. Earth Syst. Sci. 2017, 21, 3427–3440. [Google Scholar] [CrossRef] [Green Version]
- Hauswirth, S.M.; Bierkens, M.F.P.; Beijk, V.; Wanders, N. The Potential of Data Driven Approaches for Quantifying Hydrological Extremes. Adv. Water Resour. 2021, 155, 104017. [Google Scholar] [CrossRef]
- Noori, N.; Kalin, L. Coupling SWAT and ANN Models for Enhanced Daily Streamflow Prediction. J. Hydrol. 2016, 533, 141–151. [Google Scholar] [CrossRef]
- Li, X.; Yan, D.; Wang, K.; Weng, B.; Qin, T.; Liu, S. Flood Risk Assessment of Global Watersheds Based on Multiple Machine Learning Models. Water 2019, 11, 1654. [Google Scholar] [CrossRef] [Green Version]
- Hsu, K.; Gupta, H.V.; Sorooshian, S. Artificial Neural Network Modeling of the Rainfall-Runoff Process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Prabhat Deep Learning and Process Understanding for Data-Driven Earth System Science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Razavi, S. Deep Learning, Explained: Fundamentals, Explainability, and Bridgeability to Process-Based Modelling. Environ. Model. Softw. 2021, 144, 105159. [Google Scholar] [CrossRef]
- Hosseiny, H.; Nazari, F.; Smith, V.; Nataraj, C. A Framework for Modeling Flood Depth Using a Hybrid of Hydraulics and Machine Learning. Sci. Rep. 2020, 10, 8222. [Google Scholar] [CrossRef]
- Tsai, W.-P.; Feng, D.; Pan, M.; Beck, H.; Lawson, K.; Yang, Y.; Liu, J.; Shen, C. From Calibration to Parameter Learning: Harnessing the Scaling Effects of Big Data in Geoscientific Modeling. Nat. Commun. 2021, 12, 5988. [Google Scholar] [CrossRef]
- Hanson, P.C.; Stillman, A.B.; Jia, X.; Karpatne, A.; Dugan, H.A.; Carey, C.C.; Stachelek, J.; Ward, N.K.; Zhang, Y.; Read, J.S.; et al. Predicting Lake Surface Water Phosphorus Dynamics Using Process-Guided Machine Learning. Ecol. Model. 2020, 430, 109136. [Google Scholar] [CrossRef]
- Lu, D.; Konapala, G.; Painter, S.L.; Kao, S.-C.; Gangrade, S. Streamflow Simulation in Data-Scarce Basins Using Bayesian and Physics-Informed Machine Learning Models. J. Hydrometeorol. 2021, 22, 1421–1438. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Condon, L.E.; Melchior, P. A Physics-Informed, Machine Learning Emulator of a 2D Surface Water Model: What Temporal Networks and Simulation-Based Inference Can Help Us Learn about Hydrologic Processes. Water 2021, 13, 3633. [Google Scholar] [CrossRef]
- Tran, H.; Leonarduzzi, E.; De la Fuente, L.; Hull, R.B.; Bansal, V.; Chennault, C.; Gentine, P.; Melchior, P.; Condon, L.E.; Maxwell, R.M. Development of a Deep Learning Emulator for a Distributed Groundwater–Surface Water Model: ParFlow-ML. Water 2021, 13, 3393. [Google Scholar] [CrossRef]
- Madaeni, F.; Lhissou, R.; Chokmani, K.; Raymond, S.; Gauthier, Y. Ice Jam Formation, Breakup and Prediction Methods Based on Hydroclimatic Data Using Artificial Intelligence: A Review. Cold Reg. Sci. Technol. 2020, 174, 103032. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Matta, E.; Cominola, A.; Xia, X.; Zhang, Q.; Liang, Q.; Hinkelmann, R. Neurocomputing in Surface Water Hydrology and Hydraulics: A Review of Two Decades Retrospective, Current Status and Future Prospects. J. Hydrol. 2020, 588, 125085. [Google Scholar] [CrossRef]
- Rajaee, T.; Khani, S.; Ravansalar, M. Artificial Intelligence-Based Single and Hybrid Models for Prediction of Water Quality in Rivers: A Review. Chemom. Intell. Lab. Syst. 2020, 200, 103978. [Google Scholar] [CrossRef]
- Najah Ahmed, A.; Binti Othman, F.; Abdulmohsin Afan, H.; Khaleel Ibrahim, R.; Ming Fai, C.; Shabbir Hossain, M.; Ehteram, M.; Elshafie, A. Machine Learning Methods for Better Water Quality Prediction. J. Hydrol. 2019, 578, 124084. [Google Scholar] [CrossRef]
- Naloufi, M.; Lucas, F.S.; Souihi, S.; Servais, P.; Janne, A.; Wanderley Matos De Abreu, T. Evaluating the Performance of Machine Learning Approaches to Predict the Microbial Quality of Surface Waters and to Optimize the Sampling Effort. Water 2021, 13, 2457. [Google Scholar] [CrossRef]
- Nourani, V.; Hosseini Baghanam, A.; Adamowski, J.; Kisi, O. Applications of Hybrid Wavelet–Artificial Intelligence Models in Hydrology: A Review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A Comprehensive Review of Deep Learning Applications in Hydrology and Water Resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef]
- Kambalimath, S.; Deka, P.C. A Basic Review of Fuzzy Logic Applications in Hydrology and Water Resources. Appl. Water Sci. 2020, 10, 191. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Batelaan, O.; Fadaee, M.; Hinkelmann, R. Ensemble Machine Learning Paradigms in Hydrology: A Review. J. Hydrol. 2021, 598, 126266. [Google Scholar] [CrossRef]
- Pham, M.T.; Rajić, A.; Greig, J.D.; Sargeant, J.M.; Papadopoulos, A.; McEwen, S.A. A Scoping Review of Scoping Reviews: Advancing the Approach and Enhancing the Consistency. Res. Synth. Methods 2014, 5, 371–385. [Google Scholar] [CrossRef] [PubMed]
- Sucharew, H.; Macaluso, M. Methods for Research Evidence Synthesis: The Scoping Review Approach. J. Hosp. Med. 2019, 14, 416–418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- VoPham, T.; Hart, J.E.; Laden, F.; Chiang, Y.-Y. Emerging Trends in Geospatial Artificial Intelligence (GeoAI): Potential Applications for Environmental Epidemiology. Environ. Health 2018, 17, 40. [Google Scholar] [CrossRef]
- Janowicz, K.; Gao, S.; McKenzie, G.; Hu, Y.; Bhaduri, B. GeoAI: Spatially Explicit Artificial Intelligence Techniques for Geographic Knowledge Discovery and Beyond. Int. J. Geogr. Inf. Sci. 2020, 34, 625–636. [Google Scholar] [CrossRef]
- Hu, Y.; Gao, S.; Lunga, D.; Li, W.; Newsam, S.; Bhaduri, B. GeoAI at ACM SIGSPATIAL: Progress, Challenges, and Future Directions. Sigspatial Spec. 2019, 11, 5–15. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Introduction. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Hastie, T., Tibshirani, R., Friedman, J., Eds.; Springer Series in Statistics; Springer: New York, NY, USA, 2009; pp. 1–8. ISBN 978-0-387-84858-7. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2016; ISBN 978-0-262-03561-3. [Google Scholar]
- Lee, T.; Singh, V.P.; Cho, K.H. Deep Learning for Hydrometeorology and Environmental Science; Water Science and Technology Library; Springer International Publishing: Cham, Switzerland, 2021; ISBN 978-3-030-64776-6. [Google Scholar]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef]
- Nicholaus, I.T.; Park, J.R.; Jung, K.; Lee, J.S.; Kang, D.-K. Anomaly Detection of Water Level Using Deep Autoencoder. Sensors 2021, 21, 6679. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A Working Guide to Boosted Regression Trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Ibrahim, K.S.M.H.; Huang, Y.F.; Ahmed, A.N.; Koo, C.H.; El-Shafie, A. A Review of the Hybrid Artificial Intelligence and Optimization Modelling of Hydrological Streamflow Forecasting. Alex. Eng. J. 2022, 61, 279–303. [Google Scholar] [CrossRef]
- Jia, J.; Wang, W. Review of Reinforcement Learning Research. In Proceedings of the 2020 35th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Zhanjiang, China, 16–18 October 2020; pp. 186–191. [Google Scholar]
- Lange, H.; Sippel, S. Machine Learning Applications in Hydrology. In Forest-Water Interactions; Levia, D.F., Carlyle-Moses, D.E., Iida, S., Michalzik, B., Nanko, K., Tischer, A., Eds.; Ecological Studies; Springer International Publishing: Cham, Switzerland, 2020; pp. 233–257. ISBN 978-3-030-26086-6. [Google Scholar]
- Troch, P.A.; Carrillo, G.A.; Heidbüchel, I.; Rajagopal, S.; Switanek, M.; Volkmann, T.H.M.; Yaeger, M. Dealing with Landscape Heterogeneity in Watershed Hydrology: A Review of Recent Progress toward New Hydrological Theory. Geogr. Compass 2009, 3, 375–392. [Google Scholar] [CrossRef]
- Sivakumar, B. Nonlinear Dynamics and Chaos in Hydrologic Systems: Latest Developments and a Look Forward. Stoch. Environ. Res. Risk Assess. 2009, 23, 1027–1036. [Google Scholar] [CrossRef]
- Schmidt, L.; Heße, F.; Attinger, S.; Kumar, R. Challenges in Applying Machine Learning Models for Hydrological Inference: A Case Study for Flooding Events Across Germany. Water Resour. Res. 2020, 56, e2019WR025924. [Google Scholar] [CrossRef]
- Badrzadeh, H.; Sarukkalige, R.; Jayawardena, A.W. Hourly Runoff Forecasting for Flood Risk Management: Application of Various Computational Intelligence Models. J. Hydrol. 2015, 529, 1633–1643. [Google Scholar] [CrossRef]
- Schoppa, L.; Disse, M.; Bachmair, S. Evaluating the Performance of Random Forest for Large-Scale Flood Discharge Simulation. J. Hydrol. 2020, 590, 125531. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, Y.; Zhang, C.; Wang, B. Are Hybrid Models Integrated with Data Preprocessing Techniques Suitable for Monthly Streamflow Forecasting? Some Experiment Evidences. J. Hydrol. 2015, 530, 137–152. [Google Scholar] [CrossRef]
- Iwashita, F.; Friedel, M.J.; Ferreira, F.J.F. A Self-Organizing Map Approach to Characterize Hydrogeology of the Fractured Serra-Geral Transboundary Aquifer. Hydrol. Res. 2017, 49, 794–814. [Google Scholar] [CrossRef]
- Kimura, N.; Yoshinaga, I.; Sekijima, K.; Azechi, I.; Baba, D. Convolutional Neural Network Coupled with a Transfer-Learning Approach for Time-Series Flood Predictions. Water 2020, 12, 96. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.I.; Han, K.Y. Urban Flood Prediction Using Deep Neural Network with Data Augmentation. Water 2020, 12, 899. [Google Scholar] [CrossRef] [Green Version]
- Sun, A.Y.; Scanlon, B.R.; Zhang, Z.; Walling, D.; Bhanja, S.N.; Mukherjee, A.; Zhong, Z. Combining Physically Based Modeling and Deep Learning for Fusing GRACE Satellite Data: Can We Learn From Mismatch? Water Resour. Res. 2019, 55, 1179–1195. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Z.; Yan, J.; Demir, I. A Rainfall-Runoff Model With LSTM-Based Sequence-to-Sequence Learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Tennant, C.; Larsen, L.; Bellugi, D.; Moges, E.; Zhang, L.; Ma, H. The Utility of Information Flow in Formulating Discharge Forecast Models: A Case Study From an Arid Snow-Dominated Catchment. Water Resour. Res. 2020, 56, e2019WR024908. [Google Scholar] [CrossRef]
- Kan, G.; Liang, K.; Yu, H.; Sun, B.; Ding, L.; Li, J.; He, X.; Shen, C. Hybrid Machine Learning Hydrological Model for Flood Forecast Purpose. Open Geosci. 2020, 12, 813–820. [Google Scholar] [CrossRef]
- Boucher, M.-A.; Quilty, J.; Adamowski, J. Data Assimilation for Streamflow Forecasting Using Extreme Learning Machines and Multilayer Perceptrons. Water Resour. Res. 2020, 56, e2019WR026226. [Google Scholar] [CrossRef]
- Hernández, F.; Liang, X. Hybridizing Bayesian and Variational Data Assimilation for High-Resolution Hydrologic Forecasting. Hydrol. Earth Syst. Sci. 2018, 22, 5759–5779. [Google Scholar] [CrossRef] [Green Version]
- Aytaç, E. Unsupervised Learning Approach in Defining the Similarity of Catchments: Hydrological Response Unit Based k-Means Clustering, a Demonstration on Western Black Sea Region of Turkey. Int. Soil Water Conserv. Res. 2020, 8, 321–331. [Google Scholar] [CrossRef]
- Ley, R.; Casper, M.C.; Hellebrand, H.; Merz, R. Catchment Classification by Runoff Behaviour with Self-Organizing Maps (SOM). Hydrol. Earth Syst. Sci. 2011, 15, 2947–2962. [Google Scholar] [CrossRef] [Green Version]
- Ley, R.; Hellebrand, H.; Casper, M.C.; Fenicia, F. Is Catchment Classification Possible by Means of Multiple Model Structures? A Case Study Based on 99 Catchments in Germany. Hydrology 2016, 3, 22. [Google Scholar] [CrossRef] [Green Version]
- Swain, J.B.; Sahoo, M.M.; Patra, K.C. Homogeneous Region Determination Using Linear and Nonlinear Techniques. Phys. Geogr. 2016, 37, 361–384. [Google Scholar] [CrossRef]
- Chen, I.-T.; Chang, L.-C.; Chang, F.-J. Exploring the Spatio-Temporal Interrelation between Groundwater and Surface Water by Using the Self-Organizing Maps. J. Hydrol. 2018, 556, 131–142. [Google Scholar] [CrossRef]
- Chang, L.-C.; Chang, F.-J.; Yang, S.-N.; Tsai, F.-H.; Chang, T.-H.; Herricks, E.E. Self-Organizing Maps of Typhoon Tracks Allow for Flood Forecasts up to Two Days in Advance. Nat. Commun. 2020, 11, 1983. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prinzio, M.; Castellarin, A.; Toth, E. Data-Driven Catchment Classification: Combining Linear and Non-Linear Approaches to Improve Hydrological Predictions in Ungauged Catchments. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 22–27 April 2012; p. 11717. [Google Scholar]
- Brown, S.C.; Lester, R.E.; Versace, V.L.; Fawcett, J.; Laurenson, L. Hydrologic Landscape Regionalisation Using Deductive Classification and Random Forests. PLoS ONE 2014, 9, e112856. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Hu, T.; Zheng, G.; Shen, L.; Fan, J.; Zhang, D. An Improved Simplified Urban Storm Inundation Model Based on Urban Terrain and Catchment Modification. Water 2019, 11, 2335. [Google Scholar] [CrossRef] [Green Version]
- Ebtehaj, A.M.; Foufoula-Georgiou, E. On Variational Downscaling, Fusion, and Assimilation of Hydrometeorological States: A Unified Framework via Regularization. Water Resour. Res. 2013, 49, 5944–5963. [Google Scholar] [CrossRef] [Green Version]
- See, L. Data Fusion Methods for Integrating Data-Driven Hydrological Models. In Quantitative Information Fusion for Hydrological Sciences; Cai, X., Yeh, T.-C.J., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–18. ISBN 978-3-540-75384-1. [Google Scholar]
- Meng, T.; Jing, X.; Yan, Z.; Pedrycz, W. A Survey on Machine Learning for Data Fusion. Inf. Fusion 2020, 57, 115–129. [Google Scholar] [CrossRef]
- Qian, S.S.; Reckhow, K.H.; Zhai, J.; McMahon, G. Nonlinear Regression Modeling of Nutrient Loads in Streams: A Bayesian Approach. Water Resour. Res. 2005, 41, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Rawat, S.; Rawat, S. Multi-Sensor Data Fusion by a Hybrid Methodology—A Comparative Study. Comput. Ind. 2016, 75, 27–34. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep Learning in Environmental Remote Sensing: Achievements and Challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Sist, M.; Schiavon, G.; Del Frate, F. A New Data Fusion Neural Network Scheme for Rainfall Retrieval Using Passive Microwave and Visible/Infrared Satellite Data. Appl. Sci. 2021, 11, 4686. [Google Scholar] [CrossRef]
- Zhuo, L.; Han, D. Multi-Source Hydrological Soil Moisture State Estimation Using Data Fusion Optimisation. Hydrol. Earth Syst. Sci. 2017, 21, 3267–3285. [Google Scholar] [CrossRef] [Green Version]
- Fehri, R.; Bogaert, P.; Khlifi, S.; Vanclooster, M. Data Fusion of Citizen-Generated Smartphone Discharge Measurements in Tunisia. J. Hydrol. 2020, 590, 125518. [Google Scholar] [CrossRef]
- Abbaszadeh, P.; Moradkhani, H.; Zhan, X. Downscaling SMAP Radiometer Soil Moisture Over the CONUS Using an Ensemble Learning Method. Water Resour. Res. 2019, 55, 324–344. [Google Scholar] [CrossRef] [Green Version]
- Serifi, A.; Günther, T.; Ban, N. Spatio-Temporal Downscaling of Climate Data Using Convolutional and Error-Predicting Neural Networks. Front. Clim. 2021, 3, 26. [Google Scholar] [CrossRef]
- Sun, A.Y.; Tang, G. Downscaling Satellite and Reanalysis Precipitation Products Using Attention-Based Deep Convolutional Neural Nets. Front. Water 2020, 2, 56. [Google Scholar] [CrossRef]
- Rittger, K.; Krock, M.; Kleiber, W.; Bair, E.H.; Brodzik, M.J.; Stephenson, T.R.; Rajagopalan, B.; Bormann, K.J.; Painter, T.H. Multi-Sensor Fusion Using Random Forests for Daily Fractional Snow Cover at 30 m. Remote Sens. Environ. 2021, 264, 112608. [Google Scholar] [CrossRef]
- Tang, K.; Zhu, H.; Ni, P. Spatial Downscaling of Land Surface Temperature over Heterogeneous Regions Using Random Forest Regression Considering Spatial Features. Remote Sens. 2021, 13, 3645. [Google Scholar] [CrossRef]
- Tran, H.; Nguyen, P.; Ombadi, M.; Hsu, K.; Sorooshian, S.; Qing, X. A Cloud-Free MODIS Snow Cover Dataset for the Contiguous United States from 2000 to 2017. Sci. Data 2019, 6, 180300. [Google Scholar] [CrossRef]
- Miao, Q.; Pan, B.; Wang, H.; Hsu, K.; Sorooshian, S. Improving Monsoon Precipitation Prediction Using Combined Convolutional and Long Short Term Memory Neural Network. Water 2019, 11, 977. [Google Scholar] [CrossRef] [Green Version]
- Lei, X.; Chen, W.; Panahi, M.; Falah, F.; Rahmati, O.; Uuemaa, E.; Kalantari, Z.; Ferreira, C.S.S.; Rezaie, F.; Tiefenbacher, J.P.; et al. Urban Flood Modeling Using Deep-Learning Approaches in Seoul, South Korea. J. Hydrol. 2021, 601, 126684. [Google Scholar] [CrossRef]
- Veettil, A.V.; Konapala, G.; Mishra, A.K.; Li, H.-Y. Sensitivity of Drought Resilience-Vulnerability-Exposure to Hydrologic Ratios in Contiguous United States. J. Hydrol. 2018, 564, 294–306. [Google Scholar] [CrossRef]
- Tran, H.; Nguyen, P.; Ombadi, M.; Hsu, K.; Sorooshian, S.; Andreadis, K. Improving Hydrologic Modeling Using Cloud-Free MODIS Flood Maps. J. Hydrometeorol. 2019, 20, 2203–2214. [Google Scholar] [CrossRef] [Green Version]
- Mosavi, A.; Ozturk, P.; Chau, K. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef] [Green Version]
- Shahabi, H.; Shirzadi, A.; Ghaderi, K.; Omidvar, E.; Al-Ansari, N.; Clague, J.J.; Geertsema, M.; Khosravi, K.; Amini, A.; Bahrami, S.; et al. Flood Detection and Susceptibility Mapping Using Sentinel-1 Remote Sensing Data and a Machine Learning Approach: Hybrid Intelligence of Bagging Ensemble Based on K-Nearest Neighbor Classifier. Remote Sens. 2020, 12, 266. [Google Scholar] [CrossRef] [Green Version]
- Lin, Q.; Leandro, J.; Wu, W.; Bhola, P.; Disse, M. Prediction of Maximum Flood Inundation Extents With Resilient Backpropagation Neural Network: Case Study of Kulmbach. Front. Earth Sci. 2020, 8, 332. [Google Scholar] [CrossRef]
- Löwe, R.; Böhm, J.; Jensen, D.G.; Leandro, J.; Rasmussen, S.H. U-FLOOD—Topographic Deep Learning for Predicting Urban Pluvial Flood Water Depth. J. Hydrol. 2021, 603, 126898. [Google Scholar] [CrossRef]
- Sahoo, S.; Russo, T.A.; Elliott, J.; Foster, I. Machine Learning Algorithms for Modeling Groundwater Level Changes in Agricultural Regions of the U.S. Water Resour. Res. 2017, 53, 3878–3895. [Google Scholar] [CrossRef]
- Bui, D.T.; Panahi, M.; Shahabi, H.; Singh, V.P.; Shirzadi, A.; Chapi, K.; Khosravi, K.; Chen, W.; Panahi, S.; Li, S.; et al. Novel Hybrid Evolutionary Algorithms for Spatial Prediction of Floods. Sci. Rep. 2018, 8, 15364. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Guo, S.; Chang, F.-J. Explore an Evolutionary Recurrent ANFIS for Modelling Multi-Step-Ahead Flood Forecasts. J. Hydrol. 2019, 570, 343–355. [Google Scholar] [CrossRef]
- Chang, F.-J.; Chiang, Y.-M.; Tsai, M.-J.; Shieh, M.-C.; Hsu, K.-L.; Sorooshian, S. Watershed Rainfall Forecasting Using Neuro-Fuzzy Networks with the Assimilation of Multi-Sensor Information. J. Hydrol. 2014, 508, 374–384. [Google Scholar] [CrossRef] [Green Version]
- Araya, S.N.; Ghezzehei, T.A. Using Machine Learning for Prediction of Saturated Hydraulic Conductivity and Its Sensitivity to Soil Structural Perturbations. Water Resour. Res. 2019, 55, 5715–5737. [Google Scholar] [CrossRef]
- Jian, J.; Shiklomanov, A.; Shuster, W.D.; Stewart, R.D. Predicting Near-Saturated Hydraulic Conductivity in Urban Soils. J. Hydrol. 2021, 595, 126051. [Google Scholar] [CrossRef]
- Watt-Meyer, O.; Brenowitz, N.D.; Clark, S.K.; Henn, B.; Kwa, A.; McGibbon, J.; Perkins, W.A.; Bretherton, C.S. Correcting Weather and Climate Models by Machine Learning Nudged Historical Simulations. Geophys. Res. Lett. 2021, 48, e2021GL092555. [Google Scholar] [CrossRef]
- Xu, T.; Liang, F. Machine Learning for Hydrologic Sciences: An Introductory Overview. WIREs Water 2021, 8, e1533. [Google Scholar] [CrossRef]
- Koch, J.; Gotfredsen, J.; Schneider, R.; Troldborg, L.; Stisen, S.; Henriksen, H.J. High Resolution Water Table Modeling of the Shallow Groundwater Using a Knowledge-Guided Gradient Boosting Decision Tree Model. Front. Water 2021, 3. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Groundwater Level Forecasting with Artificial Neural Networks: A Comparison of Long Short-Term Memory (LSTM), Convolutional Neural Networks (CNNs), and Non-Linear Autoregressive Networks with Exogenous Input (NARX). Hydrol. Earth Syst. Sci. 2021, 25, 1671–1687. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–Runoff Modelling Using Long Short-Term Memory (LSTM) Networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Jiang, Y.; Zhang, X.; Li, Y.; Zhang, R.; Fu, G. Using Long Short-Term Memory Networks for River Flow Prediction. Hydrol. Res. 2020, 51, 1358–1376. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J.; Krebs, P. Prediction of Flow Based on a CNN-LSTM Combined Deep Learning Approach. Water 2022, 14, 993. [Google Scholar] [CrossRef]
- Lees, T.; Reece, S.; Kratzert, F.; Klotz, D.; Gauch, M.; De Bruijn, J.; Kumar Sahu, R.; Greve, P.; Slater, L.; Dadson, S.J. Hydrological Concept Formation inside Long Short-Term Memory (LSTM) Networks. Hydrol. Earth Syst. Sci. 2022, 26, 3079–3101. [Google Scholar] [CrossRef]
- Hussain, D.; Hussain, T.; Khan, A.A.; Naqvi, S.A.A.; Jamil, A. A Deep Learning Approach for Hydrological Time-Series Prediction: A Case Study of Gilgit River Basin. Earth Sci. Inform. 2020, 13, 915–927. [Google Scholar] [CrossRef]
- Anderson, S.; Radić, V. Evaluation and Interpretation of Convolutional Long Short-Term Memory Networks for Regional Hydrological Modelling. Hydrol. Earth Syst. Sci. 2022, 26, 795–825. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and Rainfall Forecasting by Two Long Short-Term Memory-Based Models. J. Hydrol. 2020, 583, 124296. [Google Scholar] [CrossRef]
- Young, C.-C.; Liu, W.-C.; Wu, M.-C. A Physically Based and Machine Learning Hybrid Approach for Accurate Rainfall-Runoff Modeling during Extreme Typhoon Events. Appl. Soft Comput. 2017, 53, 205–216. [Google Scholar] [CrossRef]
- Tamiru, H.; Dinka, M.O. Application of ANN and HEC-RAS Model for Flood Inundation Mapping in Lower Baro Akobo River Basin, Ethiopia. J. Hydrol. Reg. Stud. 2021, 36, 100855. [Google Scholar] [CrossRef]
- Wagenaar, D.; Curran, A.; Balbi, M.; Bhardwaj, A.; Soden, R.; Hartato, E.; Mestav Sarica, G.; Ruangpan, L.; Molinario, G.; Lallemant, D. Invited Perspectives: How Machine Learning Will Change Flood Risk and Impact Assessment. Nat. Hazards Earth Syst. Sci. 2020, 20, 1149–1161. [Google Scholar] [CrossRef]
- Williams, R.D.; Brasington, J.; Hicks, D.M. Numerical Modelling of Braided River Morphodynamics: Review and Future Challenges. Geogr. Compass 2016, 10, 102–127. [Google Scholar] [CrossRef] [Green Version]
- Flora, K.; Khosronejad, A. On the Impact of Bed-Bathymetry Resolution and Bank Vegetation on the Flood Flow Field of the American River, California: Insights Gained Using Data-Driven Large-Eddy Simulation. J. Irrig. Drain. Eng. 2021, 147, 04021036. [Google Scholar] [CrossRef]
- Williams, R.D.; Measures, R.; Hicks, D.M.; Brasington, J. Assessment of a Numerical Model to Reproduce Event-Scale Erosion and Deposition Distributions in a Braided River. Water Resour. Res. 2016, 52, 6621–6642. [Google Scholar] [CrossRef]
- Perrin, O.; Christophe, S.; Jacquinod, F.; Payrastre, O. Visual Analysis of Inconsistencies in Hydraulic Simulation Data. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Hannover, Germany, 25 August 2020; Copernicus GmbH: Goettingen, Germany, 2020; Volume XLIII-B4-2020, pp. 795–801. [Google Scholar]
- Mirza Alipour, S.; Leal, J. Emulation of 2D Hydrodynamic Flood Simulations at Catchment Scale Using ANN and SVR. Water 2021, 13, 2858. [Google Scholar] [CrossRef]
- Ardourel, V.; Jebeile, J. Numerical Instability and Dynamical Systems. Eur. J. Philos. Sci. 2021, 11, 49. [Google Scholar] [CrossRef]
- Hosseiny, H. A Deep Learning Model for Predicting River Flood Depth and Extent. Environ. Model. Softw. 2021, 145, 105186. [Google Scholar] [CrossRef]
- Forghani, M.; Qian, Y.; Lee, J.; Farthing, M.W.; Hesser, T.; Kitanidis, P.K.; Darve, E.F. Application of Deep Learning to Large Scale Riverine Flow Velocity Estimation. Stoch. Environ. Res. Risk Assess. 2021, 35, 1069–1088. [Google Scholar] [CrossRef]
- Cheng, C.; Zhang, G.-T. Deep Learning Method Based on Physics Informed Neural Network with Resnet Block for Solving Fluid Flow Problems. Water 2021, 13, 423. [Google Scholar] [CrossRef]
- Fukami, K.; Fukagata, K.; Taira, K. Machine-Learning-Based Spatio-Temporal Super Resolution Reconstruction of Turbulent Flows. J. Fluid Mech. 2021, 909, 1–24. [Google Scholar] [CrossRef]
- Buzzicotti, M.; Bonaccorso, F.; Di Leoni, P.C.; Biferale, L. Reconstruction of Turbulent Data with Deep Generative Models for Semantic Inpainting from TURB-Rot Database. Phys. Rev. Fluids 2021, 6, 050503. [Google Scholar] [CrossRef]
- Baracchini, T.; Chu, P.Y.; Šukys, J.; Lieberherr, G.; Wunderle, S.; Wüest, A.; Bouffard, D. Data Assimilation of in Situ and Satellite Remote Sensing Data to 3D Hydrodynamic Lake Models: A Case Study Using Delft3D-FLOW v4.03 and OpenDA v2.4. Geosci. Model Dev. 2020, 13, 1267–1284. [Google Scholar] [CrossRef] [Green Version]
- Carrassi, A.; Bocquet, M.; Bertino, L.; Evensen, G. Data Assimilation in the Geosciences: An Overview of Methods, Issues, and Perspectives. WIREs Clim. Chang. 2018, 9, e535. [Google Scholar] [CrossRef] [Green Version]
- Houser, P.; Lannoy, G.; Walker, J. Hydrologic Data Assimilation. In Advances in Water Science Methodologies; CRC Press: Boca Raton, FL, USA, 2012; ISBN 978-953-51-0294-6. [Google Scholar]
- Nearing, G.S.; Kratzert, F.; Sampson, A.K.; Pelissier, C.S.; Klotz, D.; Frame, J.M.; Prieto, C.; Gupta, H.V. What Role Does Hydrological Science Play in the Age of Machine Learning? Water Resour. Res. 2021, 57, e2020WR028091. [Google Scholar] [CrossRef]
- Xiong, Z.; Sang, J.; Sun, X.; Zhang, B.; Li, J. Comparisons of Performance Using Data Assimilation and Data Fusion Approaches in Acquiring Precipitable Water Vapor: A Case Study of a Western United States of America Area. Water 2020, 12, 2943. [Google Scholar] [CrossRef]
- Farchi, A.; Laloyaux, P.; Bonavita, M.; Bocquet, M. Using Machine Learning to Correct Model Error in Data Assimilation and Forecast Applications. Q. J. R. Meteorol. Soc. 2021, 147, 3067–3084. [Google Scholar] [CrossRef]
- Arcucci, R.; Zhu, J.; Hu, S.; Guo, Y.-K. Deep Data Assimilation: Integrating Deep Learning with Data Assimilation. Appl. Sci. 2021, 11, 1114. [Google Scholar] [CrossRef]
- Geer, A. Learning Earth System Models from Observations: Machine Learning or Data Assimilation? Philos. Trans. R. Soc. A 2021, 379, 20200089. [Google Scholar] [CrossRef] [PubMed]
- Wagener, T.; Boyle, D.P.; Lees, M.J.; Wheater, H.S.; Gupta, H.V.; Sorooshian, S. A Framework for Development and Application of Hydrological Models. Hydrol. Earth Syst. Sci. 2001, 5, 13–26. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Stauffer, P.H.; Wöhling, T.; Robinson, B.A.; Vesselinov, V.V. Inverse Modeling of Subsurface Flow and Transport Properties: A Review with New Developments. Vadose Zone J. 2008, 7, 843–864. [Google Scholar] [CrossRef]
- Carrera, J.; Alcolea, A.; Medina, A.; Hidalgo, J.; Slooten, L.J. Inverse Problem in Hydrogeology. Hydrogeol. J. 2005, 13, 206–222. [Google Scholar] [CrossRef]
- Beven, K. A Manifesto for the Equifinality Thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef] [Green Version]
- Mostafaie, A.; Forootan, E.; Safari, A.; Schumacher, M. Comparing Multi-Objective Optimization Techniques to Calibrate a Conceptual Hydrological Model Using In Situ Runoff and Daily GRACE Data. Comput. Geosci. 2018, 22, 789–814. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Zhou, J.; Lu, J.; Zou, Q.; Zhang, H.; Bi, S. Multi-Objective Optimization of Empirical Hydrological Model for Streamflow Prediction. J. Hydrol. 2014, 511, 242–253. [Google Scholar] [CrossRef]
- Huang, X.; Lei, X.; Jiang, Y. Comparison of Three Multi-Objective Optimization Algorithms for Hydrological Model. In Proceedings of the International Symposium on Intelligence Computation and Applications, Wuhan, China, 27–28 October 2012; Li, Z., Li, X., Liu, Y., Cai, Z., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 209–216. [Google Scholar]
- Vrugt, J.A.; Gupta, H.V.; Bastidas, L.A.; Bouten, W.; Sorooshian, S. Effective and Efficient Algorithm for Multiobjective Optimization of Hydrologic Models. Water Resour. Res. 2003, 39, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Essenfelder, A.H.; Giupponi, C. A Coupled Hydrologic-Machine Learning Modelling Framework to Support Hydrologic Modelling in River Basins under Interbasin Water Transfer Regimes. Environ. Model. Softw. 2020, 131, 104779. [Google Scholar] [CrossRef]
- Barnhart, B.L.; Sawicz, K.A.; Ficklin, D.L.; Whittaker, G.W. MOESHA: A Genetic Algorithm for Automatic Calibration and Estimation of Parameter Uncertainty and Sensitivity of Hydrologic Models. Trans. ASABE 2017, 60, 1259–1269. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Srinivasan, R.; Liew, M.V. On the Use of Multi-Algorithm, Genetically Adaptive Multi-Objective Method for Multi-Site Calibration of the SWAT Model. Hydrol. Process. 2010, 24, 955–969. [Google Scholar] [CrossRef]
- Kamali, B.; Mousavi, S.J.; Abbaspour, K.C. Automatic Calibration of HEC-HMS Using Single-Objective and Multi-Objective PSO Algorithms. Hydrol. Process. 2013, 27, 4028–4042. [Google Scholar] [CrossRef]
- Krapu, C.; Borsuk, M.; Kumar, M. Gradient-Based Inverse Estimation for a Rainfall-Runoff Model. Water Resour. Res. 2019, 55, 6625–6639. [Google Scholar] [CrossRef]
- Navarro-Hellín, H.; Martínez-del-Rincon, J.; Domingo-Miguel, R.; Soto-Valles, F.; Torres-Sánchez, R. A Decision Support System for Managing Irrigation in Agriculture. Comput. Electron. Agric. 2016, 124, 121–131. [Google Scholar] [CrossRef] [Green Version]
- Mullapudi, A.; Lewis, M.J.; Gruden, C.L.; Kerkez, B. Deep Reinforcement Learning for the Real Time Control of Stormwater Systems. Adv. Water Resour. 2020, 140, 103600. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Yusoff, Y.; Ngadiman, M.S.; Zain, A.M. Overview of NSGA-II for Optimizing Machining Process Parameters. Procedia Eng. 2011, 15, 3978–3983. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, L.; Dorigo, M.; Gambardella, L.M.; Gutjahr, W.J. A Survey on Metaheuristics for Stochastic Combinatorial Optimization. Nat. Comput. 2009, 8, 239–287. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; Robinson, B.A. Improved Evolutionary Optimization from Genetically Adaptive Multimethod Search. Proc. Natl. Acad. Sci. USA 2007, 104, 708–711. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Confesor, R.B., Jr.; Whittaker, G.W. Automatic Calibration of Hydrologic Models With Multi-Objective Evolutionary Algorithm and Pareto Optimization1. JAWRA J. Am. Water Resour. Assoc. 2007, 43, 981–989. [Google Scholar] [CrossRef]
- Ercan, M.B.; Goodall, J.L. Design and Implementation of a General Software Library for Using NSGA-II with SWAT for Multi-Objective Model Calibration. Environ. Model. Softw. 2016, 84, 112–120. [Google Scholar] [CrossRef] [Green Version]
- Saravanan, V.S.; McDonald, G.T.; Mollinga, P.P. Critical Review of Integrated Water Resources Management: Moving beyond Polarised Discourse. Nat. Resour. Forum 2009, 33, 76–86. [Google Scholar] [CrossRef]
- Sun, R.; Hernández, F.; Liang, X.; Yuan, H. A Calibration Framework for High-Resolution Hydrological Models Using a Multiresolution and Heterogeneous Strategy. Water Resour. Res. 2020, 56, e2019WR026541. [Google Scholar] [CrossRef]
- Ahmad, A.; El-Shafie, A.; Razali, S.F.M.; Mohamad, Z.S. Reservoir Optimization in Water Resources: A Review. Water Resour. Manag. 2014, 28, 3391–3405. [Google Scholar] [CrossRef]
- Xiang, X.; Li, Q.; Khan, S.; Khalaf, O.I. Urban Water Resource Management for Sustainable Environment Planning Using Artificial Intelligence Techniques. Environ. Impact Assess. Rev. 2021, 86, 106515. [Google Scholar] [CrossRef]
- Chaves, P.; Chang, F.-J. Intelligent Reservoir Operation System Based on Evolving Artificial Neural Networks. Adv. Water Resour. 2008, 31, 926–936. [Google Scholar] [CrossRef]
- Cai, Y.; Wang, H.; Yue, W.; Xie, Y.; Liang, Q. An Integrated Approach for Reducing Spatially Coupled Water-Shortage Risks of Beijing-Tianjin-Hebei Urban Agglomeration in China. J. Hydrol. 2021, 603, 127123. [Google Scholar] [CrossRef]
- Zhang, D.; Peng, Q.; Lin, J.; Wang, D.; Liu, X.; Zhuang, J. Simulating Reservoir Operation Using a Recurrent Neural Network Algorithm. Water 2019, 11, 865. [Google Scholar] [CrossRef] [Green Version]
- Zarei, M.; Bozorg-Haddad, O.; Baghban, S.; Delpasand, M.; Goharian, E.; Loáiciga, H.A. Machine-Learning Algorithms for Forecast-Informed Reservoir Operation (FIRO) to Reduce Flood Damages. Sci. Rep. 2021, 11, 24295. [Google Scholar] [CrossRef] [PubMed]
- Munawar, H.S.; Hammad, A.W.A.; Waller, S.T.; Thaheem, M.J.; Shrestha, A. An Integrated Approach for Post-Disaster Flood Management Via the Use of Cutting-Edge Technologies and UAVs: A Review. Sustainability 2021, 13, 7925. [Google Scholar] [CrossRef]
- Abraham, A. Adaptation of Fuzzy Inference System Using Neural Learning. In Fuzzy Systems Engineering: Theory and Practice; Nedjah, N., de Macedo Mourelle, L., Eds.; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2005; pp. 53–83. ISBN 978-3-540-32397-6. [Google Scholar]
- Ighalo, J.O.; Adeniyi, A.G.; Marques, G. Internet of Things for Water Quality Monitoring and Assessment: A Comprehensive Review. In Artificial Intelligence for Sustainable Development: Theory, Practice and Future Applications; Hassanien, A.E., Bhatnagar, R., Darwish, A., Eds.; Studies in Computational Intelligence; Springer International Publishing: Cham, Switzerland, 2021; pp. 245–259. ISBN 978-3-030-51920-9. [Google Scholar]
- Jan, F.; Min-Allah, N.; Düştegör, D. IoT Based Smart Water Quality Monitoring: Recent Techniques, Trends and Challenges for Domestic Applications. Water 2021, 13, 1729. [Google Scholar] [CrossRef]
- Leigh, C.; Kandanaarachchi, S.; McGree, J.M.; Hyndman, R.J.; Alsibai, O.; Mengersen, K.; Peterson, E.E. Predicting Sediment and Nutrient Concentrations from High-Frequency Water-Quality Data. PLoS ONE 2019, 14, e0215503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mathany, T.M.; Saraceno, J.F.; Kulongoski, J.T. Guidelines and Standard Procedures for High-Frequency Groundwater-Quality Monitoring Stations—Design, Operation, and Record Computation; Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2019; Volume 1-D7, p. 66.
- Seifert-Dähnn, I.; Furuseth, I.S.; Vondolia, G.K.; Gal, G.; de Eyto, E.; Jennings, E.; Pierson, D. Costs and Benefits of Automated High-Frequency Environmental Monitoring—The Case of Lake Water Management. J. Environ. Manag. 2021, 285, 112108. [Google Scholar] [CrossRef] [PubMed]
- Jung, H.; Senf, C.; Jordan, P.; Krueger, T. Benchmarking Inference Methods for Water Quality Monitoring and Status Classification. Environ. Monit. Assess. 2020, 192, 261. [Google Scholar] [CrossRef] [Green Version]
- Jesus, G.; Casimiro, A.; Oliveira, A. A Survey on Data Quality for Dependable Monitoring in Wireless Sensor Networks. Sensors 2017, 17, 2010. [Google Scholar] [CrossRef]
- Khatri, P.; Gupta, K.K.; Gupta, R.K. Drift Compensation of Commercial Water Quality Sensors Using Machine Learning to Extend the Calibration Lifetime. J. Ambient Intell. Humaniz. Comput. 2021, 12, 3091–3099. [Google Scholar] [CrossRef]
- Kahiluoto, J.; Hirvonen, J.; Näykki, T. Automatic Real-Time Uncertainty Estimation for Online Measurements: A Case Study on Water Turbidity. Environ. Monit. Assess. 2019, 191, 259. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Perez, J.; Leigh, C.; Liquet, B.; Kermorvant, C.; Peterson, E.; Sous, D.; Mengersen, K. Detecting Technical Anomalies in High-Frequency Water-Quality Data Using Artificial Neural Networks. Environ. Sci. Technol. 2020, 54, 13719–13730. [Google Scholar] [CrossRef]
- Jiang, J.; Tang, S.; Han, D.; Fu, G.; Solomatine, D.; Zheng, Y. A Comprehensive Review on the Design and Optimization of Surface Water Quality Monitoring Networks. Environ. Model. Softw. 2020, 132, 104792. [Google Scholar] [CrossRef]
- Chachuła, K.; Słojewski, T.M.; Nowak, R. Multisensor Data Fusion for Localization of Pollution Sources in Wastewater Networks. Sensors 2022, 22, 387. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Guo, Z.; Wang, S.; Cheng, H.; Zhan, C. Intelligent Wide-Area Water Quality Monitoring and Analysis System Exploiting Unmanned Surface Vehicles and Ensemble Learning. Water 2020, 12, 681. [Google Scholar] [CrossRef]
- Huang, W.; Yang, Y. Water Quality Sensor Model Based on an Optimization Method of RBF Neural Network. Comput. Water Energy Environ. Eng. 2019, 9, 1. [Google Scholar] [CrossRef] [Green Version]
- Jafari, H.; Rajaee, T.; Kisi, O. Improved Water Quality Prediction with Hybrid Wavelet-Genetic Programming Model and Shannon Entropy. Nat. Resour. Res. 2020, 29, 3819–3840. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, C.; Sun, L.; Guo, D.; Zhang, Y.; Wang, W. A Deep Learning Algorithm for Multi-Source Data Fusion to Predict Water Quality of Urban Sewer Networks. J. Clean. Prod. 2021, 318, 128533. [Google Scholar] [CrossRef]
- Pattnaik, B.S.; Pattanayak, A.S.; Udgata, S.K.; Panda, A.K. Machine Learning Based Soft Sensor Model for BOD Estimation Using Intelligence at Edge. Complex Intell. Syst. 2021, 7, 961–976. [Google Scholar] [CrossRef]
- Lu, H.; Ma, X. Hybrid Decision Tree-Based Machine Learning Models for Short-Term Water Quality Prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef]
- Chen, K.; Chen, H.; Zhou, C.; Huang, Y.; Qi, X.; Shen, R.; Liu, F.; Zuo, M.; Zou, X.; Wang, J.; et al. Comparative Analysis of Surface Water Quality Prediction Performance and Identification of Key Water Parameters Using Different Machine Learning Models Based on Big Data. Water Res. 2020, 171, 115454. [Google Scholar] [CrossRef]
- Castrillo, M.; García, Á.L. Estimation of High Frequency Nutrient Concentrations from Water Quality Surrogates Using Machine Learning Methods. Water Res. 2020, 172, 115490. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Yao, J.; Wang, G.; Hao, F.; Shrestha, S.; Xue, B.; Xie, G.; Peng, Y. Exploring the Application of Artificial Intelligence Technology for Identification of Water Pollution Characteristics and Tracing the Source of Water Quality Pollutants. Sci. Total Environ. 2019, 693, 133440. [Google Scholar] [CrossRef] [PubMed]
- Holmberg, M.; Forsius, M.; Starr, M.; Huttunen, M. An Application of Artificial Neural Networks to Carbon, Nitrogen and Phosphorus Concentrations in Three Boreal Streams and Impacts of Climate Change. Ecol. Model. 2006, 195, 51–60. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Ghaemi, A. Prediction of the Five-Day Biochemical Oxygen Demand and Chemical Oxygen Demand in Natural Streams Using Machine Learning Methods. Environ. Monit. Assess. 2019, 191, 380. [Google Scholar] [CrossRef] [PubMed]
- Noori, N.; Kalin, L.; Isik, S. Water Quality Prediction Using SWAT-ANN Coupled Approach. J. Hydrol. 2020, 590, 125220. [Google Scholar] [CrossRef]
- Haghiabi, A.H.; Nasrolahi, A.H.; Parsaie, A. Water Quality Prediction Using Machine Learning Methods. Water Qual. Res. J. 2018, 53, 3–13. [Google Scholar] [CrossRef]
- Bui, D.T.; Khosravi, K.; Tiefenbacher, J.; Nguyen, H.; Kazakis, N. Improving Prediction of Water Quality Indices Using Novel Hybrid Machine-Learning Algorithms. Sci. Total Environ. 2020, 721, 137612. [Google Scholar] [CrossRef]
- Green, M.B.; Pardo, L.H.; Bailey, S.W.; Campbell, J.L.; McDowell, W.H.; Bernhardt, E.S.; Rosi, E.J. Predicting High-Frequency Variation in Stream Solute Concentrations with Water Quality Sensors and Machine Learning. Hydrol. Process. 2021, 35, e14000. [Google Scholar] [CrossRef]
- Chang, N.-B.; Bai, K.; Chen, C.-F. Integrating Multisensor Satellite Data Merging and Image Reconstruction in Support of Machine Learning for Better Water Quality Management. J. Environ. Manag. 2017, 201, 227–240. [Google Scholar] [CrossRef]
- Hamshaw, S.D.; Dewoolkar, M.M.; Schroth, A.W.; Wemple, B.C.; Rizzo, D.M. A New Machine-Learning Approach for Classifying Hysteresis in Suspended-Sediment Discharge Relationships Using High-Frequency Monitoring Data. Water Resour. Res. 2018, 54, 4040–4058. [Google Scholar] [CrossRef]
- Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A Review of the Artificial Neural Network Models for Water Quality Prediction. Appl. Sci. 2020, 10, 5776. [Google Scholar] [CrossRef]
- Shi, P.; Li, G.; Yuan, Y.; Kuang, L. Data Fusion Using Improved Support Degree Function in Aquaculture Wireless Sensor Networks. Sensors 2018, 18, 3851. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, L.Q.; Amatulli, G.; Sethi, T.; Raymond, P.; Domisch, S. Estimating Nitrogen and Phosphorus Concentrations in Streams and Rivers, within a Machine Learning Framework. Sci. Data 2020, 7, 161. [Google Scholar] [CrossRef] [PubMed]
- Sperotto, A.; Molina, J.L.; Torresan, S.; Critto, A.; Pulido-Velazquez, M.; Marcomini, A. A Bayesian Networks Approach for the Assessment of Climate Change Impacts on Nutrients Loading. Environ. Sci. Policy 2019, 100, 21–36. [Google Scholar] [CrossRef]
- Song, C.; Yao, L.; Hua, C.; Ni, Q. A Novel Hybrid Model for Water Quality Prediction Based on Synchrosqueezed Wavelet Transform Technique and Improved Long Short-Term Memory. J. Hydrol. 2021, 603, 126879. [Google Scholar] [CrossRef]
- Zhou, J.; Chu, F.; Li, X.; Ma, H.; Xiao, F.; Sun, L. Water Quality Prediction Approach Based on T-SNE and SA-BiLSTM. In Proceedings of the 2020 IEEE 22nd International Conference on High Performance Computing and Communications; IEEE 18th International Conference on Smart City; IEEE 6th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Yanuca Island, Fiji, 14–16 December 2020; pp. 708–714. [Google Scholar]
- Milošević, D.; Medeiros, A.S.; Stojković Piperac, M.; Cvijanović, D.; Soininen, J.; Milosavljević, A.; Predić, B. The Application of Uniform Manifold Approximation and Projection (UMAP) for Unconstrained Ordination and Classification of Biological Indicators in Aquatic Ecology. Sci. Total Environ. 2022, 815, 152365. [Google Scholar] [CrossRef]
- Baker, V.R. The Modern Evolution of Geomorphology—Binghamton and Personal Perspectives, 1970–2019 and Beyond. Geomorphology 2020, 366, 106684. [Google Scholar] [CrossRef]
- Flener, C.; Vaaja, M.; Jaakkola, A.; Krooks, A.; Kaartinen, H.; Kukko, A.; Kasvi, E.; Hyyppä, H.; Hyyppä, J.; Alho, P. Seamless Mapping of River Channels at High Resolution Using Mobile LiDAR and UAV-Photography. Remote Sens. 2013, 5, 6382–6407. [Google Scholar] [CrossRef] [Green Version]
- Tonina, D.; McKean, J.A.; Benjankar, R.M.; Wright, C.W.; Goode, J.R.; Chen, Q.; Reeder, W.J.; Carmichael, R.A.; Edmondson, M.R. Mapping River Bathymetries: Evaluating Topobathymetric LiDAR Survey. Earth Surf. Process. Landf. 2019, 44, 507–520. [Google Scholar] [CrossRef]
- Emanuele, P.; Nives, G.; Andrea, C.; Carlo, C.; Paolo, D.; Andrea Maria, L. Bathymetric Detection of Fluvial Environments through UASs and Machine Learning Systems. Remote Sens. 2020, 12, 4148. [Google Scholar] [CrossRef]
- Carbonneau, P.E.; Dugdale, S.J.; Breckon, T.P.; Dietrich, J.T.; Fonstad, M.A.; Miyamoto, H.; Woodget, A.S. Adopting Deep Learning Methods for Airborne RGB Fluvial Scene Classification. Remote Sens. Environ. 2020, 251, 112107. [Google Scholar] [CrossRef]
- Carbonneau, P.E.; Belletti, B.; Micotti, M.; Lastoria, B.; Casaioli, M.; Mariani, S.; Marchetti, G.; Bizzi, S. UAV-Based Training for Fully Fuzzy Classification of Sentinel-2 Fluvial Scenes. Earth Surf. Process. Landf. 2020, 45, 3120–3140. [Google Scholar] [CrossRef]
- Rivas Casado, M.; Ballesteros Gonzalez, R.; Kriechbaumer, T.; Veal, A. Automated Identification of River Hydromorphological Features Using UAV High Resolution Aerial Imagery. Sensors 2015, 15, 27969–27989. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ling, F.; Boyd, D.; Ge, Y.; Foody, G.M.; Li, X.; Wang, L.; Zhang, Y.; Shi, L.; Shang, C.; Li, X.; et al. Measuring River Wetted Width From Remotely Sensed Imagery at the Subpixel Scale With a Deep Convolutional Neural Network. Water Resour. Res. 2019, 55, 5631–5649. [Google Scholar] [CrossRef]
- Demarchi, L.; van de Bund, W.; Pistocchi, A. Object-Based Ensemble Learning for Pan-European Riverscape Units Mapping Based on Copernicus VHR and EU-DEM Data Fusion. Remote Sens. 2020, 12, 1222. [Google Scholar] [CrossRef] [Green Version]
- Szabo, Z.C.; Mikita, T.; Negyesi, G.; Varga, O.G.; Burai, P.; Takacs-Szilagyi, L.; Szabo, S. Uncertainty and Overfitting in Fluvial Landform Classification Using Laser Scanned Data and Machine Learning: A Comparison of Pixel and Object-Based Approaches. Remote Sens. 2020, 12, 3652. [Google Scholar] [CrossRef]
- Demarchi, L.; Bizzi, S.; Piegay, H. Hierarchical Object-Based Mapping of Riverscape Units and in-Stream Mesohabitats Using LiDAR and VHR Imagery. Remote Sens. 2016, 8, 97. [Google Scholar] [CrossRef] [Green Version]
- Khan, S.; Fryirs, K.A. Application of Globally Available, Coarse-Resolution Digital Elevation Models for Delineating Valley Bottom Segments of Varying Length across a Catchment. Earth Surf. Process. Landf. 2020, 45, 2788–2803. [Google Scholar] [CrossRef]
- Moody, D.I.; Brumby, S.P.; Rowland, J.C.; Gangodagamage, C. Undercomplete Learned Dictionaries for Land Cover Classification in Multispectral Imagery of Arctic Landscapes Using CoSA: Clustering of Sparse Approximations. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery Xix; Shen, S.S., Lewis, P.E., Eds.; SPIE: Baltimore, MD, USA, 2013; Volume 8743, ISBN 978-0-8194-9534-1. [Google Scholar]
- Guillon, H.; Byrne, C.F.; Lane, B.A.; Solis, S.S.; Pasternack, G.B. Machine Learning Predicts Reach-Scale Channel Types From Coarse-Scale Geospatial Data in a Large River Basin. Water Resour. Res. 2020, 56, e2019WR026691. [Google Scholar] [CrossRef]
- De Souza, C.M.P.; de Figueredo, N.A.; da Costa, L.M.; Veloso, G.V.; de Almeida, M.I.S.; Ferreira, E.J. Machine Learning Algorithm In The Prediction Of Geomorphic Indices For Appraisal The Influence Of Landscape Structure On Fluvial Systems, Southeastern-Brazil. Rev. Bras. Geomorfol. 2020, 21, 365–380. [Google Scholar] [CrossRef]
- Guneralp, I.; Filippi, A.M.; Hales, B. Influence of River Channel Morphology and Bank Characteristics on Water Surface Boundary Delineation Using High-Resolution Passive Remote Sensing and Template Matching. Earth Surf. Process. Landf. 2014, 39, 977–986. [Google Scholar] [CrossRef]
- Heasley, E.L.; Millington, J.D.A.; Clifford, N.J.; Chadwick, M.A. A Waterbody Typology Derived from Catchment Controls Using Self-Organising Maps. Water 2020, 12, 78. [Google Scholar] [CrossRef] [Green Version]
- Mandlburger, G.; Kölle, M.; Nübel, H.; Soergel, U. BathyNet: A Deep Neural Network for Water Depth Mapping from Multispectral Aerial Images. PFG—J. Photogramm. Remote Sens. Geoinf. Sci. 2021, 89, 71–89. [Google Scholar] [CrossRef]
- Corenblit, D.; Vautier, F.; González, E.; Steiger, J. Formation and Dynamics of Vegetated Fluvial Landforms Follow the Biogeomorphological Succession Model in a Channelized River. Earth Surf. Process. Landf. 2020, 45, 2020–2035. [Google Scholar] [CrossRef]
- Díaz Gómez, R.; Pasternack, G.B.; Guillon, H.; Byrne, C.F.; Schwindt, S.; Larrieu, K.G.; Solis, S.S. Mapping Subaerial Sand-Gravel-Cobble Fluvial Sediment Facies Using Airborne Lidar and Machine Learning. Geomorphology 2022, 401, 108106. [Google Scholar] [CrossRef]
- Clubb, F.J.; Bookhagen, B.; Rheinwalt, A. Clustering River Profiles to Classify Geomorphic Domains. J. Geophys. Res. Earth Surf. 2019, 124, 1417–1439. [Google Scholar] [CrossRef]
- Harrison, L.R.; Legleiter, C.J.; Overstreet, B.T.; Bell, T.W.; Hannon, J. Assessing the Potential for Spectrally Based Remote Sensing of Salmon Spawning Locations. River Res. Appl. 2020, 36, 1618–1632. [Google Scholar] [CrossRef]
- Alfredsen, K.; Dalsgård, A.; Shamsaliei, S.; Halleraker, J.H.; Gundersen, O.E. Towards an Automatic Characterization of Riverscape Development by Deep Learning. River Res. Appl. 2022, 38, 810–816. [Google Scholar] [CrossRef]
- González-Castro, J.A.; Muste, M. Framework for Estimating Uncertainty of ADCP Measurements from a Moving Boat by Standardized Uncertainty Analysis. J. Hydraul. Eng. 2007, 133, 1390–1410. [Google Scholar] [CrossRef]
- Pan, Z.; Glennie, C.; Hartzell, P.; Fernandez-Diaz, J.C.; Legleiter, C.; Overstreet, B. Performance Assessment of High Resolution Airborne Full Waveform LiDAR for Shallow River Bathymetry. Remote Sens. 2015, 7, 5133–5159. [Google Scholar] [CrossRef] [Green Version]
- Bandini, F.; Olesen, D.; Jakobsen, J.; Kittel, C.M.M.; Wang, S.; Garcia, M.; Bauer-Gottwein, P. Technical Note: Bathymetry Observations of Inland Water Bodies Using a Tethered Single-Beam Sonar Controlled by an Unmanned Aerial Vehicle. Hydrol. Earth Syst. Sci. 2018, 22, 4165–4181. [Google Scholar] [CrossRef] [Green Version]
- Alvarez, L.V.; Moreno, H.A.; Segales, A.R.; Pham, T.G.; Pillar-Little, E.A.; Chilson, P.B. Merging Unmanned Aerial Systems (UAS) Imagery and Echo Soundings with an Adaptive Sampling Technique for Bathymetric Surveys. Remote Sens. 2018, 10, 1362. [Google Scholar] [CrossRef] [Green Version]
- Van Iersel, W.; Straatsma, M.; Middelkoop, H.; Addink, E. Multitemporal Classification of River Floodplain Vegetation Using Time Series of UAV Images. Remote Sens. 2018, 10, 1144. [Google Scholar] [CrossRef] [Green Version]
- Hemmelder, S.; Marra, W.; Markies, H.; De Jong, S.M. Monitoring River Morphology & Bank Erosion Using UAV Imagery—A Case Study of the River Buëch, Hautes-Alpes, France. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 428–437. [Google Scholar] [CrossRef]
- Boothroyd, R.J.; Williams, R.D.; Hoey, T.B.; Barrett, B.; Prasojo, O.A. Applications of Google Earth Engine in Fluvial Geomorphology for Detecting River Channel Change. WIREs Water 2021, 8, e21496. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, M.; Zhang, R.; Chen, S.; Zhan, Z. Change Detection Based on Artificial Intelligence: State-of-the-Art and Challenges. Remote Sens. 2020, 12, 1688. [Google Scholar] [CrossRef]
- Wheaton, J.M.; Fryirs, K.A.; Brierley, G.; Bangen, S.G.; Bouwes, N.; O’Brien, G. Geomorphic Mapping and Taxonomy of Fluvial Landforms. Geomorphology 2015, 248, 273–295. [Google Scholar] [CrossRef]
- Polidori, L.; El Hage, M. Digital Elevation Model Quality Assessment Methods: A Critical Review. Remote Sens. 2020, 12, 3522. [Google Scholar] [CrossRef]
- Paniconi, C.; Putti, M. Physically Based Modeling in Catchment Hydrology at 50: Survey and Outlook. Water Resour. Res. 2015, 51, 7090–7129. [Google Scholar] [CrossRef] [Green Version]
- Marçais, J.; de Dreuzy, J.-R. Prospective Interest of Deep Learning for Hydrological Inference. Groundwater 2017, 55, 688–692. [Google Scholar] [CrossRef]
- Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Definitions, Methods, and Applications in Interpretable Machine Learning. Proc. Natl. Acad. Sci. USA 2019, 116, 22071–22080. [Google Scholar] [CrossRef] [Green Version]
- Pearl, J. The Seven Tools of Causal Inference, with Reflections on Machine Learning. Commun. ACM 2019, 62, 54–60. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, E.B.; Coco, G.; Plant, N.G. A Review of Machine Learning Applications to Coastal Sediment Transport and Morphodynamics. Earth-Sci. Rev. 2019, 194, 97–108. [Google Scholar] [CrossRef] [Green Version]
- Tharwat, A. Parameter Investigation of Support Vector Machine Classifier with Kernel Functions. Knowl. Inf. Syst. 2019, 61, 1269–1302. [Google Scholar] [CrossRef]
- Shen, C.; Laloy, E.; Elshorbagy, A.; Albert, A.; Bales, J.; Chang, F.-J.; Ganguly, S.; Hsu, K.-L.; Kifer, D.; Fang, Z.; et al. HESS Opinions: Incubating Deep-Learning-Powered Hydrologic Science Advances as a Community. Hydrol. Earth Syst. Sci. 2018, 22, 5639–5656. [Google Scholar] [CrossRef] [Green Version]
- Lindersson, S.; Brandimarte, L.; Mård, J.; Baldassarre, G.D. A Review of Freely Accessible Global Datasets for the Study of Floods, Droughts and Their Interactions with Human Societies. WIREs Water 2020, 7, e1424. [Google Scholar] [CrossRef] [Green Version]
- Pitts, J.; Gopal, S.; Ma, Y.; Koch, M.; Boumans, R.M.; Kaufman, L. Leveraging Big Data and Analytics to Improve Food, Energy, and Water System Sustainability. Front. Big Data 2020, 3, 13. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Towards Learning Universal, Regional, and Local Hydrological Behaviors via Machine Learning Applied to Large-Sample Datasets. Hydrol. Earth Syst. Sci. 2019, 23, 5089–5110. [Google Scholar] [CrossRef] [Green Version]
- Hagen, J.S.; Leblois, E.; Lawrence, D.; Solomatine, D.; Sorteberg, A. Identifying Major Drivers of Daily Streamflow from Large-Scale Atmospheric Circulation with Machine Learning. J. Hydrol. 2021, 596, 126086. [Google Scholar] [CrossRef]
- Sahraei, A.; Chamorro, A.; Kraft, P.; Breuer, L. Application of Machine Learning Models to Predict Maximum Event Water Fractions in Streamflow. Front. Water 2021, 3, 652100. [Google Scholar] [CrossRef]
- Sudmanns, M.; Tiede, D.; Lang, S.; Bergstedt, H.; Trost, G.; Augustin, H.; Baraldi, A.; Blaschke, T. Big Earth Data: Disruptive Changes in Earth Observation Data Management and Analysis? Int. J. Digit. Earth 2020, 13, 832–850. [Google Scholar] [CrossRef]
- Le Coz, J.; Patalano, A.; Collins, D.; Guillén, N.F.; García, C.M.; Smart, G.M.; Bind, J.; Chiaverini, A.; Le Boursicaud, R.; Dramais, G.; et al. Crowdsourced Data for Flood Hydrology: Feedback from Recent Citizen Science Projects in Argentina, France and New Zealand. J. Hydrol. 2016, 541, 766–777. [Google Scholar] [CrossRef] [Green Version]
- Lowry, C.S.; Fienen, M.N.; Hall, D.M.; Stepenuck, K.F. Growing Pains of Crowdsourced Stream Stage Monitoring Using Mobile Phones: The Development of CrowdHydrology. Front. Earth Sci. 2019, 7, 128. [Google Scholar] [CrossRef] [Green Version]
- Etter, S.; Strobl, B.; van Meerveld, I.; Seibert, J. Quality and Timing of Crowd-Based Water Level Class Observations. Hydrol. Process. 2020, 34, 4365–4378. [Google Scholar] [CrossRef]
- Njue, N.; Stenfert Kroese, J.; Gräf, J.; Jacobs, S.R.; Weeser, B.; Breuer, L.; Rufino, M.C. Citizen Science in Hydrological Monitoring and Ecosystem Services Management: State of the Art and Future Prospects. Sci. Total Environ. 2019, 693, 133531. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Yang, D.; Chen, J.; Santisirisomboon, J.; Lu, W.; Zhao, B. A Physical Process and Machine Learning Combined Hydrological Model for Daily Streamflow Simulations of Large Watersheds with Limited Observation Data. J. Hydrol. 2020, 590, 125206. [Google Scholar] [CrossRef]
- Yang, T.; Sun, F.; Gentine, P.; Liu, W.; Wang, H.; Yin, J.; Du, M.; Liu, C. Evaluation and Machine Learning Improvement of Global Hydrological Model-Based Flood Simulations. Environ. Res. Lett. 2019, 14, 114027. [Google Scholar] [CrossRef]
- Souffront Alcantara, M.A.; Nelson, E.J.; Shakya, K.; Edwards, C.; Roberts, W.; Krewson, C.; Ames, D.P.; Jones, N.L.; Gutierrez, A. Hydrologic Modeling as a Service (HMaaS): A New Approach to Address Hydroinformatic Challenges in Developing Countries. Front. Environ. Sci. 2019, 7, 158. [Google Scholar] [CrossRef]
- Kraft, B.; Jung, M.; Körner, M.; Koirala, S.; Reichstein, M. Towards Hybrid Modeling of the Global Hydrological Cycle. Hydrol. Earth Syst. Sci. Discuss. 2021, 26, 1579–1614. [Google Scholar] [CrossRef]
- Gomes, V.C.F.; Queiroz, G.R.; Ferreira, K.R. An Overview of Platforms for Big Earth Observation Data Management and Analysis. Remote Sens. 2020, 12, 1253. [Google Scholar] [CrossRef] [Green Version]
- Sperna Weiland, F.C.; Vrugt, J.A.; van Beek, R.P.H.; Weerts, A.H.; Bierkens, M.F.P. Significant Uncertainty in Global Scale Hydrological Modeling from Precipitation Data Errors. J. Hydrol. 2015, 529, 1095–1115. [Google Scholar] [CrossRef] [Green Version]
- Marthews, T.R.; Blyth, E.M.; Martínez-de la Torre, A.; Veldkamp, T.I.E. A Global-Scale Evaluation of Extreme Event Uncertainty in the EartH2Observe Project. Hydrol. Earth Syst. Sci. 2020, 24, 75–92. [Google Scholar] [CrossRef] [Green Version]
- Pagano, T.C.; Pappenberger, F.; Wood, A.W.; Ramos, M.-H.; Persson, A.; Anderson, B. Automation and Human Expertise in Operational River Forecasting. WIREs Water 2016, 3, 692–705. [Google Scholar] [CrossRef] [Green Version]
- Mulligan, M. WaterWorld: A Self-Parameterising, Physically Based Model for Application in Data-Poor but Problem-Rich Environments Globally. Hydrol. Res. 2012, 44, 748–769. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, X.; Huang, C. Automatic Calibration a Hydrological Model Using a Master–Slave Swarms Shuffling Evolution Algorithm Based on Self-Adaptive Particle Swarm Optimization. Expert Syst. Appl. 2013, 40, 752–757. [Google Scholar] [CrossRef]
- Nandi, S.; Janga Reddy, M. Comparative Performance Evaluation of Self-Adaptive Differential Evolution with GA, SCE and DE Algorithms for the Automatic Calibration of a Computationally Intensive Distributed Hydrological Model. H2Open J. 2020, 3, 306–327. [Google Scholar] [CrossRef]
- Koch, P.; Golovidov, O.; Gardner, S.; Wujek, B.; Griffin, J.; Xu, Y. Autotune: A Derivative-Free Optimization Framework for Hyperparameter Tuning. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 443–452. [Google Scholar]
- Feurer, M.; Klein, A.; Eggensperger, K.; Springenberg, J.T.; Blum, M.; Hutter, F. Auto-Sklearn: Efficient and Robust Automated Machine Learning. In Automated Machine Learning: Methods, Systems, Challenges; Hutter, F., Kotthoff, L., Vanschoren, J., Eds.; The Springer Series on Challenges in Machine Learning; Springer International Publishing: Cham, Switzerland, 2019; pp. 113–134. ISBN 978-3-030-05318-5. [Google Scholar]
- Zürn, J.; Burgard, W.; Valada, A. Self-Supervised Visual Terrain Classification From Unsupervised Acoustic Feature Learning. IEEE Trans. Robot. 2021, 37, 466–481. [Google Scholar] [CrossRef]
- Wittscher, L.; Diers, J.; Pigorsch, C. Improving Image Classification Robustness Using Self-Supervision. Stat 2022, 11, e455. [Google Scholar] [CrossRef]
- Pintelas, E.; Livieris, I.E.; Pintelas, P.E. A Convolutional Autoencoder Topology for Classification in High-Dimensional Noisy Image Datasets. Sensors 2021, 21, 7731. [Google Scholar] [CrossRef]
- Feng, J.; Feng, X.; Chen, J.; Cao, X.; Zhang, X.; Jiao, L.; Yu, T. Generative Adversarial Networks Based on Collaborative Learning and Attention Mechanism for Hyperspectral Image Classification. Remote Sens. 2020, 12, 1149. [Google Scholar] [CrossRef] [Green Version]
- He, Z.; He, D.; Mei, X.; Hu, S. Wetland Classification Based on a New Efficient Generative Adversarial Network and Jilin-1 Satellite Image. Remote Sens. 2019, 11, 2455. [Google Scholar] [CrossRef] [Green Version]
- Hofmann, J.; Schüttrumpf, H. FloodGAN: Using Deep Adversarial Learning to Predict Pluvial Flooding in Real Time. Water 2021, 13, 2255. [Google Scholar] [CrossRef]
- Dong, H.; Ma, W.; Wu, Y.; Zhang, J.; Jiao, L. Self-Supervised Representation Learning for Remote Sensing Image Change Detection Based on Temporal Prediction. Remote Sens. 2020, 12, 1868. [Google Scholar] [CrossRef]
- Xu, Z.; Du, J.; Wang, J.; Jiang, C.; Ren, Y. Satellite Image Prediction Relying on GAN and LSTM Neural Networks. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Kao, I.-F.; Liou, J.-Y.; Lee, M.-H.; Chang, F.-J. Fusing Stacked Autoencoder and Long Short-Term Memory for Regional Multistep-Ahead Flood Inundation Forecasts. J. Hydrol. 2021, 598, 126371. [Google Scholar] [CrossRef]
- Kao, I.-F.; Zhou, Y.; Chang, L.-C.; Chang, F.-J. Exploring a Long Short-Term Memory Based Encoder-Decoder Framework for Multi-Step-Ahead Flood Forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Li, X.; Song, G.; Du, Z. Hybrid Model of Generative Adversarial Network and Takagi-Sugeno for Multidimensional Incomplete Hydrological Big Data Prediction. Concurr. Comput. Pract. Exp. 2021, 33, e5713. [Google Scholar] [CrossRef]
- Mazher, A. Visualization Framework for High-Dimensional Spatio-Temporal Hydrological Gridded Datasets Using Machine-Learning Techniques. Water 2020, 12, 590. [Google Scholar] [CrossRef] [Green Version]
- Van Oosterom, P.; Stoter, J. 5D Data Modelling: Full Integration of 2D/3D Space, Time and Scale Dimensions. In Proceedings of the International Conference on Geographic Information Science, Zurich, Switzerland, 14–17 September 2010; Fabrikant, S.I., Reichenbacher, T., van Kreveld, M., Schlieder, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 310–324. [Google Scholar]
- Bauer, P.; Stevens, B.; Hazeleger, W. A Digital Twin of Earth for the Green Transition. Nat. Clim. Chang. 2021, 11, 80–83. [Google Scholar] [CrossRef]
- Bartos, M.; Kerkez, B. Pipedream: An Interactive Digital Twin Model for Natural and Urban Drainage Systems. Environ. Model. Softw. 2021, 144, 105120. [Google Scholar] [CrossRef]
- Veenendaal, B.; Brovelli, M.A.; Li, S. Review of Web Mapping: Eras, Trends and Directions. ISPRS Int. J. Geo-Inf. 2017, 6, 317. [Google Scholar] [CrossRef]
| Unsupervised Learning | Supervised Learning | Modeling Optimization Problems |
|---|---|---|
| Clustering: | Regression and Classification: | Evolutionary Computing: |
|
| Genetic algorithm (GA)
|
| Dimension reduction unsupervised/semi-supervised depth learning: | Metaheuristic methods: | |
| Particle swan optimization (PSO) algorithm Artificial bee colony (ABC) Ant colony optimization (ACO) Gray wolf optimization algorithm Whale optimization algorithm (WOA) | |
| Self-supervised learning/Reinforced learning (RL) | ||
| Single agent/Multi-agent RL Model-based RL Model-free RL |
| Method and Software | Objectives, Advantages, and Limitations | Reference |
|---|---|---|
| ANN and RF and permuted feature importance Software: Coded in r, available online: https://gitlab.com/lennartschmidt/floodmagnitude (accessed on 21 June 2022). | Objective: To compare ANN and RF flood prediction at the national level in Germany Advantages: ANN and RF achieved higher prediction accuracy for a large area with a large dataset than linear models. They reflect basic hydrological principles. Limitations: Heterogeneity of results across algorithms. The non-uniqueness/equifinality problem was identified due to the ML model setting. | [50] |
| ANN, ANFIS, wavelet neural networks, and hybrid ANFIS with wavelets transformation Software: MATLAB toolboxes | Objective: Hourly rainfall-runoff forecasting in Richmond River, Australia Advantages: Several ML methods compared, showing that hybrid ANFIS wavelet-based models significantly outperform ANFIS and ANN. Limitations: Only rainfall and runoff data were used in the modeling. Catchment physical features were not included. | [51] |
| RF and hybrid RF and the hydromad hydrological model. Software: RF package in R and hydromad package (available online: https://hydromad.catchment.org) (accessed on 21 June 2022). | Objective: To study the RF model performance vs. hydromad conceptual models in USA and Canada. Advantages: The RF model is simple and outperformed existing conceptual flood-forecasting models, predicting low and medium flood magnitudes. Limitations: The RF models exhibit inaccuracies for higher flood events, and their performance depends on the catchment characteristics. | [52] |
| ANN Software: Matlab toolboxes (e.g., wavelet) | Objective: Comparison of ANN and ARMA, combining them with wavelet analysis, empirical model decomposition, and singular spectrum analysis, for hindcasting and forecasting of monthly streamflow in two Chinese basins. Advantages: In hindcasting, the hybrid ANN and ARAM models performed better than the non-hybrid ones. Limitations: Hybrid models were not suitable for monthly streamflow forecasting, needing further refinement. | [53] |
| SOM and modified SOM (MSOM) Software: Not stated | Objective: To compare SOM and the MSOM clustering approaches, to deal with missing values, identifying groundwater exchange areas between the Serra Geral and Guarani aquifers (Brazil). Advantages: The MSOM showed higher accuracy in mapping hydrochemistry and groundwater physical properties, quantifying relationships in a large set of variables, which would not be revealed with conventional multivariate statistics. Limitations: SOM requires extensive data to obtain accurate and informative clusters. | [54] |
| CNN with transfer learning in time-series flood prediction Software: Not stated | Objective: To introduce a new CNN transfer-learning model as a conversion tool between time-series and image data to predict water levels in flood events. Advantages: CNN showed acceptable agreement with the observed water level data. Quantitative improvement in the CNN transfer learning appeared in the reduction in computational costs. Limitations: CNN captured higher peaks poorly. CNN was not as good as a fully connected deep neural network or RNN, especially when predicting the highest peaks. | [55] |
| Deep neural network (DNN) and data augmentation. Software: Not stated | Objective: To assess the feasibility of DNN in urban flood mapping, integrated with the stormwater management model (SWMM). Study area was two small urban catchments in Seoul, Korea. Advantages: The DNN was about 300 times faster than SWMM. Data augmentation could improve the poor predictive power of DNN. Limitations: Limited amount of input data needed to be improved by applying data augmentation. | [56] |
| CNN-based segmentation, VGG16, U-net, and Segnet Software: Not stated | Objective: To learn the spatiotemporal patterns of the mismatch between total water storage anomalies derived from the GRACE satellite mission and those simulated by the NOAH land surface model. Study area was India. Advantages: CNN models significantly improve the match with modeled and satellite-based observations of terrestrial total water storage. Limitations: Current grid resolution is relatively coarse. | [57] |
| LSTM and sequence-to-sequence (seq2seq) model Software: uses the Keras and TensorFlow packages in Python 3 | Objective: To present a prediction model based on LSTM and the seq2seq structure to estimate hourly rainfall-runoff. Study area was two small watersheds in Iowa, US. Advantages: The LSTM-based seq2seq model was demonstrated to be an effective method for rainfall-runoff predictions and applicable to different watersheds. Limitations: Needs sufficient predictive power. | [58] |
| Transfer entropy (TE), ANN, LSTM, random forest regression (RFR), and support vector regression (SVR) Software: Not stated | Objective: To predict discharge with ML models and identify dominant drivers of discharge and their timescales using sensor data and TE. Study area was the Dry Creek Experimental Watershed, ID, USA. Advantages: The LSTM model is effective in identifying the key lag and aggregation scales for predicting discharge. TE was able to identify dominant streamflow controls and the relative importance of different mechanisms of streamflow generation. Limitations: Restricting ML models based on dominant timescales undercuts their skill at learning these timescales internally. | [59] |
| ANN and K-nearest neighbor Software: Not stated | Objective: To introduce the coupled ANN with the K-nearest neighbor hybrid machine learning (HML) for flood forecast. The study area was the Tunxi watershed, Anhui, China. Advantages: HML model showed satisfactory performance and reliable stability and predicted discharge continuously without accuracy loss. Limitations: Peak flow was not well captured. | [60] |
| Extreme learning machine (ELM) and the multilayer perceptron (MLP) for data assimilation with GR4J lumped hydrological model. Software: Not stated | Objective: To test two new ELM and MLP data assimilation methods in the rainfall-runoff models. The study catchments were Mistassibi (Canada), Schwuerbitz (Germany), Ourthe (Belgium), and Los Idolos (Mexico). Advantages: It shows that ELM and MLP can be successfully used for data assimilation, with a noticeable improvement over the GR4J and OpenLoop hydrological models for all studied catchments. Limitations: The ELM, MLP, and hydrological models are loosely coupled and simulated on an open-loop approach, and no feedback from the model output is considered. Furthermore, few observed variables in the ANN training are used (discharge and temperature). | [61] |
| Bayesian and variational data assimilation hybrid algorithm called OPTIMISTS (Optimized PareTo Inverse Modeling through Integrated STochastic Search) Software: code available online: https://github.com/felherc/OPTIMISTS (accessed on 21 June 2022). | Objective: To introduce the new data assimilation algorithm OPTIMISTS and to test it using the DHSVM hydrological models in the Blue River and Indiantown watershed, USA. Advantages: OPTIMISTS combines the features from Bayesian and variational approaches. OPTIMISTS produced probabilistic forecasts efficiently, with the combined advantages of allowing for fast, non-Gaussian, non-linear, and high-resolution prediction and for the balancing of the imperfect observation. Limitations: The model seems to be under development. | [62] |
| ML Method | Objectives, Advantages, and Limitations | Reference |
|---|---|---|
| Non-dominated sorting genetic algorithm II (NSGA-II), particle swarm optimization (MPSO), the Pareto envelope-based selection algorithm II (PESA-II), the strength Pareto evolutionary algorithm II (SPEA-II) with the combined objective function and genetic algorithm. Software: Not stated | Objective: To compare optimization techniques to calibrate conceptual hydrological models. Advantages: All techniques perform well, better results gained than when using a single-objective algorithm. The NSGA-II with two indicators performed better than the MPSO with one indicator. Limitations: Depending on the selected performance indicators, the best model varied. | [138] |
| The multi-objective evolution algorithm MODE-ACM and the enhanced Pareto multi-objective differential evolution algorithm (EPMODE). Software: Not stated | Objective: To introduce the MODE-ACM and the enhanced EPMODE model. To test model efficacy by comparing the NSGA-II and SPEA2 model. Advantages: The EPMODE and the MODE-ACM were both reliable and showed better performance than the NSGA-II and SPEA2 models. Limitation: Very complex model. | [139] |
| The multi-objective particle swarm optimization (MOPSO), NSGA-II and the multi-objective shuffled complex evolution metropolis (MOSCEM-UA). Software: Not stated | Objective: Comparison of three multi-objective algorithms for hydrological model calibration. Advantages: All three algorithms are able to find Pareto sets of solutions. The most uniform distribution of the solutions was derived with MOSCEM-U as the NSGA-II has the shortest Pareto optimal front and the MOPSO has the maximal extent of the obtained non-dominated front. Limitations: The rate of convergence with the optimal solutions varies across the three algorithms. | [140] |
| MOSCEM-UA and shuffled complex evolution metropolis (SCEM-UA). Software: Not stated | Objective: To calibrate hydrological models using more effective and efficient multi-objective algorithms called MOSCEM-UA. Advantages: MOSCEM-UA allows multi-objective calibration, preventing the collapse of the algorithm to a single region of highest attraction. It combines the complex shuffling and the probabilistic covariance-annealing search procedure of the SCEM-UA algorithm. Limitations: Challenging to make sure that a diverse and large initial population size is provided, which supports multiple objective approaches. | [141] |
| ANN coupled with SWAT model. Software: SWAT-ANN, available online: https://zenodo.org/record/3699658#.YewXid_RZaQ (accessed on 21 June 2022). | Objective: Evaluation of SWAT-ANN rainfall-runoff simulation in a catchment, Italy. Advantages: The SWAT-ANN prediction accuracy was acceptable and useful in the absence of observational data. Limitations: The overall model calibration is only evaluated by model residual error. | [142] |
| Genetic algorithm Software: Multi-objective evolutionary sensitivity handling algorithm (MOESHA), programed in Python | Objective: River discharge modeling with a hydrological model called EXP-HYDRO, applied in a small catchment in Wales, UK. Advantages: The MOESHA algorithm determines well the optimal distribution of the model parameters that maximize model robustness and minimize error; it also estimates model parameter uncertainty. Disadvantages: Computationally expensive. | [143] |
| Multi-algorithm, genetically adaptive multi-objective method (AMALGAM), single evolutionary multi-objective optimization (SPEA-II and NSGA-II). Software: AMALGAM code in Visual Basic | Objective: Comparative study of SWAT model calibration using single- and multi-evolutionary optimization algorithms. The study areas are the Yellow River Headwaters Watershed (Tibet Plateau, China), the Reynolds Creek Experimental Watershed (Idaho, USA), the Little River Experimental Watershed (Georgia, USA), and the Mahantango Creek Experimental Watershed (Pennsylvania, USA). Advantage: The advantage of the multi-evolutionary algorithm AMALGAM calibrating the SWAT model has been demonstrated. AMALGAM provides fast, reliable, and computationally efficient solutions to multi-objective optimization problems. Limitations: With a small number of run schemes, multiple trials might be needed for implementing AMALGAM. The solution contribution of the different algorithms used in AMALGAM varies in the different watersheds. | [144] |
| Single-objective and multi-objective particle swarm optimization (PSO) algorithms. Software: Not stated | Objective: Automatic calibration of hydrologic engineering center- hydrologic modeling systems (HEC-HMS) rainfall-runoff model. The study area is the Tamar sub-basin of the Gorganroud River Basin, Iran. Advantages: Multi-objective PSO calibration outperforms the single-objective one. However, an appropriate combination of objective functions is essential in multi-objective calibration. Limitations: Increasing the number of objective functions did not necessarily lead to a better performance than the bi-objective calibration. The increasing number of objective functions also introduces computational challenges. Insufficient data and flood events seriously affect the calibration performance. | [145] |
| The deep learning gradient-based optimizer. Software: Python code, available online: https://github.com/ckrapu/gr4j_theano (accessed on 21 June 2022). | Objective: Estimating unknown parameters for GR4J conceptual hydrological model. Advantages: The deep learning gradient-based optimizer is effective for high-dimensional inverse estimation problems for hydrological models. Limitations: Need for hydrological model to be established at the site and high computational effort. | [146] |
| Partial least squares regression (PLSR) and ANFIS. Software: Not stated | Objective: Development of a smart irrigation decision support system, using PLSR and ANFIS as reasoning engines. The study area is in the southeast of Spain. Advantages: ANFIS prediction was better than PLSR for water requirement estimation and identifying timely crop irrigation needs. Limitations: The model has been tested with a few soil and weather variables. | [147] |
| Reinforcement learning (RL) Software: Python code, available online: https://github.com/kLabUM/rl-storm-control (accessed on 21 June 2022). | Objective: To implement a smart stormwater real-time system control based on RL. Advantages: The RL-based model learned the control valve strategy in a distributed stormwater system by interacting with the system it controls under thousands of simulated storm scenarios. It effectively tries various control strategies until it achieves target water level and flow set points. Limitations: RL performance is highly sensitive to the RL agent reward formulation and requires a significant amount of computational resources to achieve a good performance. | [148] |
| Method and Software | Objective, Advantages, and Limitations | Reference |
|---|---|---|
| ANN Software: ANNs computed and fitted with the Keras package in R. Available online: https://github.com/benoit-liquet/AD_ANN (accessed on 21 June 2022). | Objective: To use ANN to detect anomalies caused by the technical error of in situ sensor monitoring of conductivity and turbidity. Advantage: Semi-supervised ANN very well suited to identifying short-term anomalous events. Supervised classification able to identify long-term anomalies. Limitations: High rate of false positive detection. Large dataset required due to relative scarcity of anomalous events to train data. | [174] |
| MLP, SVM-SMO, lazy-instance-based learning K nearest-neighbor (IBK), KStar, RF, random tree, and REPTree. Software: Python | Objective: To compare ML techniques for soft sensor monitoring of biological oxygen demand (BOD). Advantage: IBK algorithm was best for estimating BOD based on turbidity, dissolved oxygen, pH, and water temperature sensors. IBK algorithm can also be used within a low-cost system to allow incorporation into IoT-based WQ systems. Limitations: Overloading of servers may occur in IoT-based systems if prediction algorithms run on the cloud for a large number of sensing nodes. | [181] |
| Feed-forward ANN (FF-ANN). Software: Python using the scikit-learn library. | Objective: To compare FF-ANN and traditional methods for drift correction. Advantages: The FF-ANN model outperformed traditional methods for drift calibration and may increase calibration lifetime and reduce calibration frequency for water quality sensors. Limitations: High error rate apparent when using logistic function. | [172] |
| RF, SVM, and logistic regression Software: Python | Objective: Evaluation of 3D wide-area WQ monitoring and analysis systems, using unmanned surface vehicles (USV) and ML algorithms. Advantage: RF demonstrated high precision for estimating WQ status, using WQ measured data (turbidity, total dissolved solid, and pH) by USV at multiple points and different water depth levels. Limitations: USV drifting control, working performance, and system accuracy were evaluated just in one environmental condition (a small lake) and for a few WQ parameters. | [177] |
| Gradient boosting (XGBoost), RF, coupled with denoising model called CEEMDAN. Software: Not stated | Objective: Hourly prediction of several WQ parameters in Tualatin River, Oregon, USA. Advantages: The best model performance depended on the predicted WQ variable. CEEMDAN-RF and CEEMDAN-XGBoost show better performance, less errors, and higher stability than simple RF and XGBoost. New error metric is introduced for model performance evaluation and compared with conventional methods of model evaluation. Limitations: The prediction model only depends on time-series data and no other explanatory variables were included. | [182] |
| Multi-layer perceptron, radial basis function ANN, ANFIS, and ANFIS with wavelet denoising technique (WDT-ANFIS). Software: wavelet and fuzzy logic toolboxes of MATLAB | Objective: Prediction of WQ parameters such as ammoniacal nitrogen, suspended solid, and pH in Johor river, Malaysia. Advantages: Several ML algorithms were compared, where the WDT-ANFIS model advantage was well illustrated. Limitations: Complex models and not possible to identify a single network structure that can best predict WQ parameters. | [28] |
| Decision tree (DT), RF, and deep cascade forest (DCF), trained by big data. Software: Python. RF and DT built using the package Scikit-learn v.019. DCF was built with the package gcForest | Objective: Comparison of 7 traditional learning models vs. 3 ensemble models for prediction of 6 levels of WQ parameters for major rivers and lakes in China. Advantages: DT, RF, DCF trained by big data all had significantly better prediction of WQ compared with traditional learning models. DCF had the best performance overall for prediction of all 6 levels of WQ. Limitations: DCF unable to learn directly from big raw data. | [183] |
| RF Software: Python using the libraries Scikit-Learn (0.20.1) and MLxtend (0.13.0) | Objective: Comparison of random forest to multiple linear regression for estimation of high-frequency nutrient concentration. Advantages: RF outperformed linear models when more than one predictor was included. Limitations: At least 3 predictors required to identify clear benefit of using RF compared to multiple linear regressions. | [184] |
| Integrated LSTM, using cross-correlation and association rules (apriori). Software: Not stated | Objective: GeoAI system to identify and trace point sources of pollution in Shandong Province, China. Advantages: LSTM algorithm had high prediction accuracy for tracing the main point sources of pollution. Limitations: GeoAI model was not aware of the change in aquatic environment conditions. It requires multi-dimensional and multi-spatial perspectives to identify, analyze, and respond to data. | [185] |
| ANN Software: Mathematica | Objective: Modeling daily total organic carbon (TOC), total nitrogen (TN), total phosphorous (TP), and predicting future fluxes under climate change scenarios for two streams in Finland. Advantages: ANN model managed to recreate most dynamics in TOC, TN, and TP. Limitations: ANN model struggled to capture extreme values for TOC, TN, and TP. | [186] |
| Least square-SVM (LS-SVM) and multivariate adaptive regression spline (MARS). Software: Not stated | Objective: Prediction of 5-day biochemical oxygen demand (BOD) and chemical oxygen demand (COD) in natural streams in Karoun River, southwest Iran. Advantages: LS-SVM and MARS models performed better in terms of external validation criteria and F test compared with multiple-regression-based models and ANN and ANFIS equations. Limitations: Intensive amount of data collection required for a wide variety of parameters. | [187] |
| ANN using feed-forward network with Levenberg–Marquardt back-propagation learning. Software: Not stated | Objective: Hybrid approach using a SWAT model as an input to an ANN to simulate monthly nitrate, ammonium, and phosphate loads in Atlanta, GA, USA. Advantages: Hybrid model outperformed standalone SWAT and ANN models for prediction of monthly loads. Hybrid models are useful for predictions in unmonitored catchments. Limitations: Hybrid model for nitrate had substantially better predictions than the ammonium and phosphate models. Large peaks of ammonium and phosphate were underestimated. | [188] |
| ANN compared with SVM and group method of data handling (GMDH). Software: Not stated | Objective: ML techniques compared for predicting various WQ components in Tireh River, southwest Iran. Advantages: SVM models were most accurate, with less data dispersion. Limitations: All models overestimated some properties. | [189] |
| Twelve hybrid data mining algorithms compared, spanning two main groups. Group one featured decision tree algorithms, and group two featured meta-classifier or hybrid algorithms. Software: Not stated | Objective: Comparison of 12 hybrid GeoAI models predicting WQ indices in Talar Catchment, Iran. Advantages: Hybrid models showed improved predictive power compared to standalone algorithms. Hybrid bagging random tree (BA-RT) model showed greatest predictive power and was able to produce reliable results despite a dataset spanning a short time period. Limitations: BA-RT model struggled to accurately predict extreme WQ index values, while most models also overestimated WQI values. | [190] |
| SVM and RF Software: e1071 R package used to build SVM model and random forest R package used to build RF model. | Objective: SVM and RF algorithms compared to predict high-frequency variation in stream solutes in Hubbard Brook, New Hampshire, USA. Advantages: Both ML algorithms were capable of effectively predicting concentrations of major ions. Limitations: Solutes with atmospheric, episodic, or strong biotic and abiotic controls were much more poorly predicted than solutes least affected by ecosystem dynamics. | [191] |
| Method and Software | Objective, Advantages and Limitations | Reference |
|---|---|---|
| NASNet CNN Software: Python based. CNN supervised classification available for PyQGIS | Objective: To classify fluvial scenes in 11 rivers in Canada, Italy, Japan, the United Kingdom, and Costa Rica. Advantages: The NasNet-CNN model outperformed other supervised classifiers, e.g., maximum likelihood, MLP, and RF. The NasNet-CNN model can be transferable to other rivers with no training data, obtaining good classification accuracy of fluvial land cover. Limitations: CNN is sensitive to the hyperparameters definition. CNN was also affected by imbalanced training data size in land cover classes. Some features were misclassified. | [205] |
| Fuzzy-CNN Software: Python based. Dependency packages: TensorFlow | Objective: To predict vegetation, bare sediment, and water bodies at a sub-pixel scale with Sentinel-2 images, trained with high resolution UAV images. Study areas were Sesia, Po, and Paglia Rivers in Italy. Advantages: Fuzzy-CNN models were successfully used to provide continuous and crisp subpixel classification of Sentinel-2 imagery. The model was transferable to satellite images with different acquisition time. It can be used for annual change detection. Limitations: UAV reference data obtained with manual OBIA was highly time-consuming. The process was computationally expensive due to the “super-resolution” process used to feed the CNN. The model was tested only in Mediterranean drainage basins. | [206] |
| ANN Software: MATLAB-based software. Leaf area index calculation (LAIC) | Objective: Hydromorphological features classification using very high resolution UAV images (2.5 cm) in a reach of the River Dee, Wales, UK. Advantages: ANN LAIC model showed satisfactory classification accuracy and potential to identify multiple hydromorphological classes that can be attributed to site features based, e.g., on their hydraulic, habitat, or vegetation types. The model settings seem to be transferable to other rivers without training data. Limitations: The algorithm showed misclassification of small fluvial entities, e.g., shallow water areas with rippled surface, water areas affected by tree shadow, and vegetated banks and/or areas obscured by brown submerged vegetation. The authors provided very limited information about the model parameter setting in the paper. | [207] |
| CNN Software: Matlab- based software. Visualization and image processing for environmental research (VIPER) | Objective: To measure river wetted width (RWW) with a novel approach at the subpixel scale by using MODIS and Landsat OLI images in Bay of Bengal, India, and Landsat TM in Columbia River, USA. Advantages: CNN-based sub-pixel scale classification resulted in a more accurate estimation of RWW than the conventional hard image classification. Limitations: No full spectral unmixing was possible due to the spectral variations of land cover classes and the nonlinear mixture phenomenon. Misclassification issues were reported when shadows, bridges, or trees were located along riverbanks. In such situations, RWW was unmeasured. | [208] |
| GEOBIA, EL, RF, extra tree (ET), gradient tree boosting (GTB), extreme gradient boosting (XGB). Then, it was combined with a voting classifier. Software: Python-based with scikit-learn package. | Objective: To map the main hydromorphological types that characterize fluvial landscapes in Europe by using Copernicus image mosaic and EU DEM. Target classes: water, sediment bars, riparian vegetation, other floodplain units. Advantages: RF outperformed any other tested classifier, e.g., ET, GTB, and XGB. Hierarchical object-based segmentation is robust for combining spectral and topographical data at different spatial resolutions and enhancing low spectral resolutions. Area-based validations were the preferred method to validate the quality of the object-based maps. Limitations: Vegetation units and sediment bars were not very well classified. Main source of error was related to the high mixture of riparian vegetation, sediment bars, and other floodplain features. | [209] |
| Object-based RF and pixel-based RF, combined with recursive feature elimination and PCAs Software: rpart and caret R packages, and EnMAP-Box (environmental mapping and analysis program) 2.1.1 software. | Objective: To reveal uncertainty, overfitting, and efficiency of terrain attribute identification in fluvial landforms using morphometric variables derived from a LiDAR DTM from Tisza River, Hungary. Advantages: Object-based RF method had a better classification accuracy (95%) than the pixel-based RF method (78%) when identifying 4 different river landforms (crevasse channels, swales, point bars, levees). Overfitting was controlled in the study by limiting the number of input variables. Limitations: Object-based RF classifications needed visual interpretation, field observations, and high-resolution data. PCAs did not help to select more efficient and important variables. | [210] |
| RF and SVM Software: eCognition developer 9 software. | Objective: Semi-automatic map of riverscape units and in-stream microhabitats, providing continuous, objective, and multi-scale classification using very-high-resolution near-infrared aerial imagery and LiDAR DTM from the Orco River, Italy. Advantages: RF better identified riverscape elements, e.g., channel and bars, while SVM did better when classifying in-stream meso-habitats. Topographical data, in particular detrended DTM (DDTM), was a relevant data source for an accurate classification of the riverscape units. Near-infrared imagery combined with DDTM was the best predictor. Limitations: Extensive expert-based training was necessary for detailed post-classification. Several subjective rules added to the process. Most confusion in the classification was detected between the floodplain and sparse vegetation classes, where the DDTM was not helpful. | [211] |
| K-means clustering Software: ArcGIS based. Geoprocessing tool (multivariate clustering) | Objective: To delineate valley bottom extent across large catchments and automatically classify valley bottom segments of variable length by using DEM-based derivatives from Richmond River, Australia. Advantages: The k-means successfully clustered the entire river network into 6 valley bottom segments of varying length. Limitations: The resulting cluster is unlabeled and needs expert recognition. Only used a low number of the variables selected (slope and valley bottom width). The model was validated with a basin-scale expert mapping of valley types. This is time-consuming and not available for other areas. The model was only proposed as a preliminary assessment for further studies. | [212] |
| Modified Hebbian algorithms and k-mean clustering. Software: On-line batch Hebbian algorithm and CoSA (clustering of sparse approximations) packages. | Objective: To investigate the applicability of ML classifier in Arctic regions using DigitalGlobe Worldview-2 visible/near-infrared, high-resolution imagery from Mackenzie River, Canada, and Selawik and Barrow Rivers in Alaska (USA). Advantages: Allows automatic discretization of landscape units in large areas. Useful as a preliminary method to learn which scale of clustering is suitable to study different processes or focuses of the study (e.g., hydrology versus vegetation). Capable of detecting vegetation changes as it recognizes vegetation levels in different classes. Limitations: No error assessment was performed, nor was there ground truth validation. The selection of an appropriate number of clusters depends on the expert’s decision. | [213] |
| SVM, RF, ANN, partial least squares, multivariate adaptive regression splines, flexible discriminant analysis, k-NN, regression tree, bagged trees, linear discriminant analysis, regularized linear discriminant analysis, and naive Bayes. Software: Caret and h2o R packages. | Objective: To extrapolate a geomorphic classification of channel types to a regional stream network using DEMs and thematic maps (e.g., lithology, soil, stream network, etc.) from Sacramento River, USA. Advantages: Multiple algorithms compared. RF outperformed other models with more accuracy and stability and lower entropy in reach-scale river type classification. Rigorous approach in model design and evaluation of performance with 20 × 10-fold cross validation used for clarification of some black box aspects of ML. Limitations: Needs large expert-based field survey data. It is unclear if ML is able to integrate predictors at different scales and to show different uncertainty across the watershed. | [214] |
| RF and RF combined with recursive feature elimination (RF-RFE). Software: R program | Objective: To detect structural and/or neotectonic controls influencing the knickpoints of the drainage network using DEM and thematic maps (geology and geomorphology) from Abaeté Watershed, Brazil. Advantages: Simple and reproducible methodology that provides causal relationship of knickpoint formation to lithological contacts and neotectonic configuration and activity. RF succeeded in partially predicting geomorphic indices (e.g., stream length gradient index or normalized channel steepness index) and can be used to predict them in unsampled areas without overfitting. Limitations: Low performance of the methods, obtaining R2 = 0.38 as the highest correlation between predicted and direct estimation values of geomorphic indices. It may have been affected by the selection of the covariables. | [215] |
| Template-matching (object-based) algorithm (TMA) and pixel-based SVM. Software: Feature Analyst (Overwatch Systems Ltd.). Not specified for SVM. | Objective: To delineate water surface boundaries and assess the influence of river and bank characteristics in the efficacy of a template-matching compared to a pixel-based algorithm, using high-resolution images with false-color infrared, from the Brazos River, USA. Advantages: Both algorithms adequately delineate the water surface. SVM performed better and handled complex and noisy class relationships. TMA performed better than SVM in spatially complex channel morphologies (e.g., partially submerged sediment deposits, sediment bar structures) due to its capability to incorporate both spectral and spatial information. Limitations: Validation relies on expert knowledge and previous maps. Selection of ancillary data types depends on expert decision and the delineation accuracy of TMA. In addition, the low spectral dimension of the images limited the pixel-based classification. Both algorithms encounter problems when classifying multiple complex features (e.g., overhanging trees) and illumination conditions (e.g., shading). The TMA performance was less spatially consistent than that of SVM. | [216] |
| SOM Software: R based (R v3.5.1). Package “kohonen” v3.0.7 | Objective: To produce waterbody typology from 22 GIS-derived continuous catchment characteristics to capture the dominant controls that influence river reaches across England and Wales. Advantages: SOM-based water body topology reflects catchment functional feature controls on river reaches. The method is extendable to other areas where reach-level monitoring is relevant. The SOM combined with hierarchical clustering can be applied over a wide range of catchment, e.g., a national-level waterbody typology map. Limitations: The method could not isolate individual effects from catchment controls as they are dependent on each other. It does not detect temporal change and local controls such as dams, channelization, and others not taken into account. | [217] |
| U-Net convolutional neural networks (CNNs). Software: Not stated. | Objective: To introduce the BathyNet framework, a photogrammetry and radiometric-based combined retrieval of water depth using U-Net CNNs. Study area was Lech river, Augsburg, Bavaria, Germany. Advantages: U-Net CNNs approximate arbitrary functions and include spatial context. The U-Net CNN-based depth retrieval outperformed traditional regression-based optical inversion methods. Limitations: U-Net CNNs require large amounts of training data and their application might be unfeasible in areas with scarce water-depth field samples. | [218] |
| Process-Based Model | GeoAI Model |
|---|---|
| Based on general physical laws. | A data-driven approach, inductive model building, may not fully respect physical laws. |
| All input variables and parameter ranges are well-structured and known. | Unstructured data, not all input variables’ role in the model is known, making the output less interpretable. |
| Limited to the current state-of-the-art. | Able to reveal unknown associations and patterns. |
| It is a deductive, hypothesis testing approach. It can be used for causal inference. | It is an inductive, exploratory approach. Their use in causal inference depends on the GeoAI model building and selected variables. |
| No uniqueness problem due to inverse modeling in model parameterization. | No uniqueness problem due to GeoAI hyper-parameter optimizations. |
| Mostly deterministic, the system is represented by the average values of variables. | Deterministic and probabilistic, depending on the GeoAI method, variables can be treated as probabilistic. |
| Reductionist, considerable simplification of complex processes which can result in prediction bias. | Integrative, GeoAI can be integrated into several types of observation and may be able to reveal patterns not represented by a physical-based model. Therefore, GeoAI prediction can be less biased. |
| It is assumed to be of general application. | It is assumed to be applied only within the range of the training data. |
| Fixed to the model basis data requirement, and unable to deal with multisource data. | Flexible to data input, from minimal input to big data. GeoAI can maximize the use of all types of available data, from different sources, types, and quality. |
| High computing demand for high-frequency and large-scale modeling. | High computing efficiency and suitable for high-frequency and large-scale modeling. |
| One-time calibration, once the model is calibrated, the parameters are usually fixed. | Continuous learning model, the model calibration is constantly updated with past and new data. |
| Well-defined framework for model performance, uncertainty, and error propagation evaluation. | Diverse and developing approaches for model performance, uncertainty, and error propagation evaluation. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzales-Inca, C.; Calle, M.; Croghan, D.; Torabi Haghighi, A.; Marttila, H.; Silander, J.; Alho, P. Geospatial Artificial Intelligence (GeoAI) in the Integrated Hydrological and Fluvial Systems Modeling: Review of Current Applications and Trends. Water 2022, 14, 2211. https://doi.org/10.3390/w14142211
Gonzales-Inca C, Calle M, Croghan D, Torabi Haghighi A, Marttila H, Silander J, Alho P. Geospatial Artificial Intelligence (GeoAI) in the Integrated Hydrological and Fluvial Systems Modeling: Review of Current Applications and Trends. Water. 2022; 14(14):2211. https://doi.org/10.3390/w14142211
Chicago/Turabian StyleGonzales-Inca, Carlos, Mikel Calle, Danny Croghan, Ali Torabi Haghighi, Hannu Marttila, Jari Silander, and Petteri Alho. 2022. "Geospatial Artificial Intelligence (GeoAI) in the Integrated Hydrological and Fluvial Systems Modeling: Review of Current Applications and Trends" Water 14, no. 14: 2211. https://doi.org/10.3390/w14142211






