Modeling the 2D Inundation Simulation Based on the ANN-Derived Model with Real-Time Measurements at Roadside IoT Sensors
Abstract
:1. Introduction
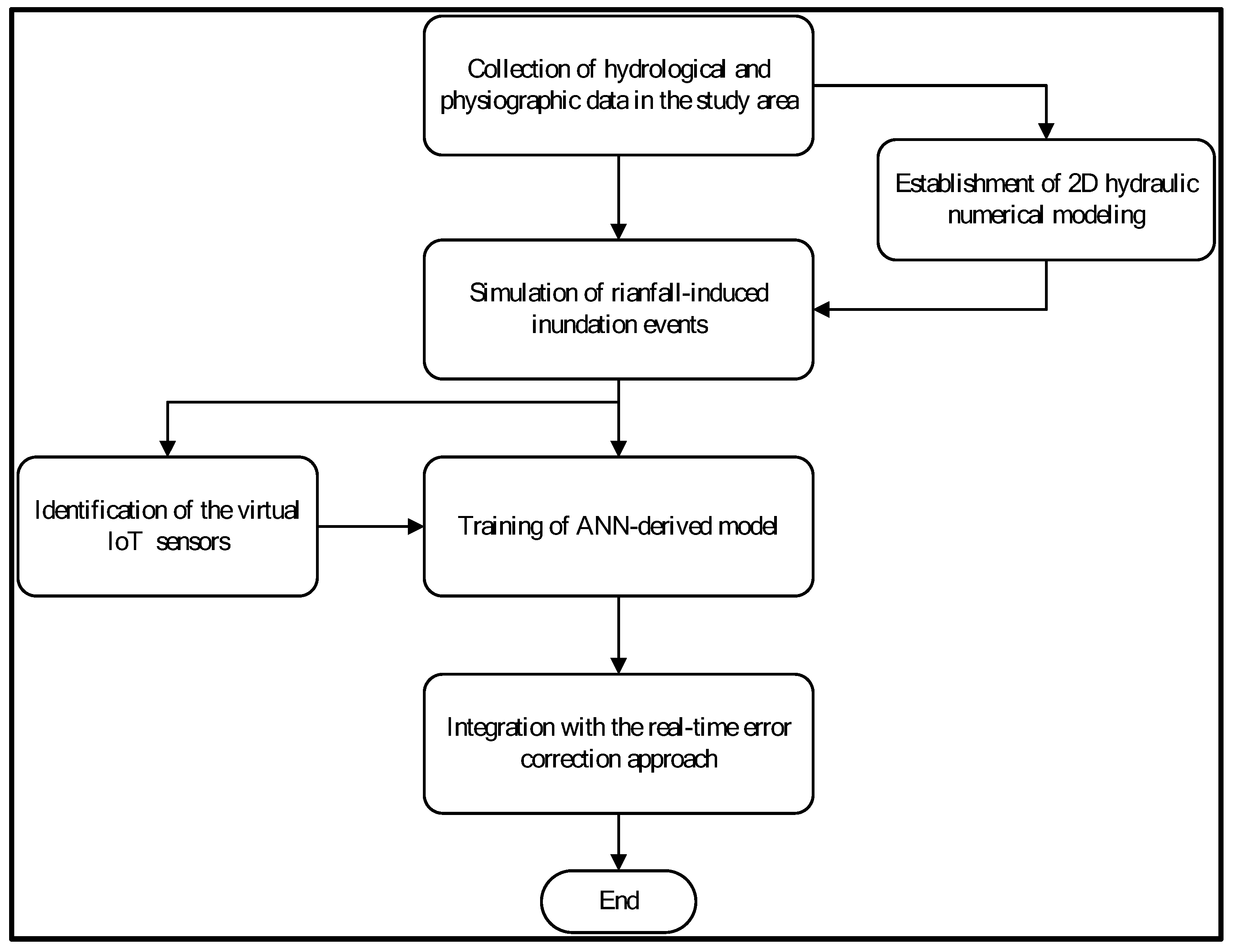
2. Methodology
2.1. Model Concept
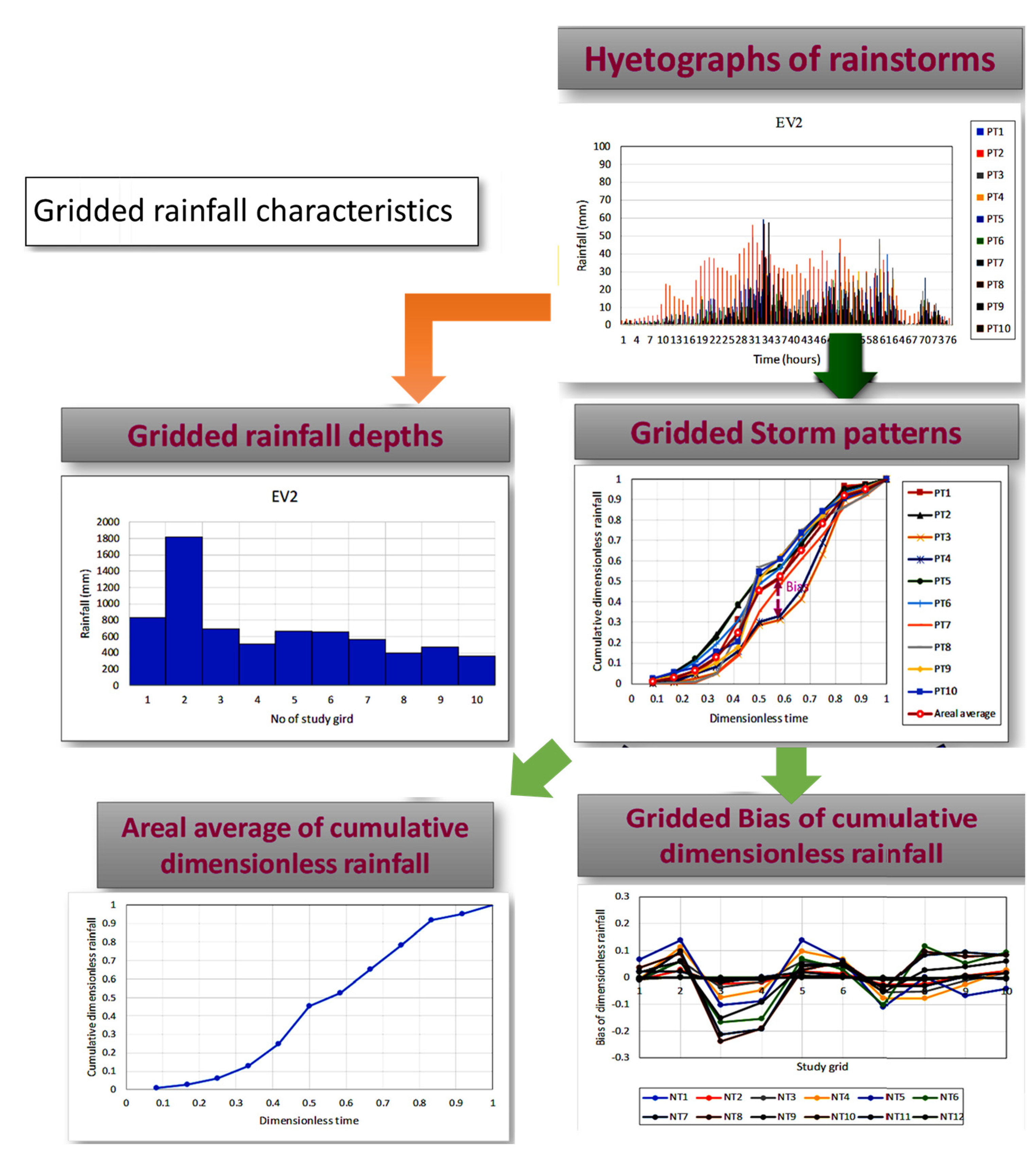
2.2. Simulation of Rainfall-Induced Inundation Events
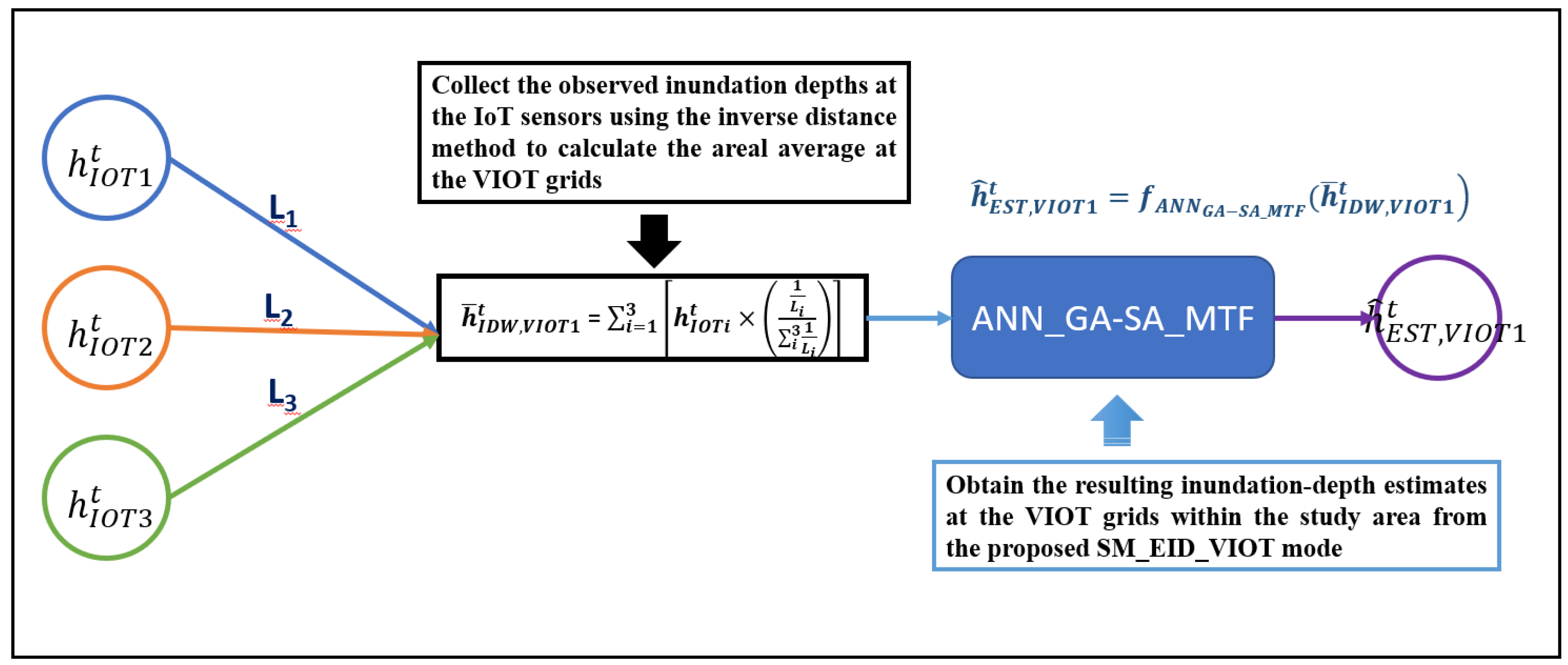
2.3. Identification of the Virtual IoT (VIOT) Grids
2.4. Artificial Neural Network Model Associated with Multiple Transfer Functions
2.5. Integration with Real-Time Correction Approach
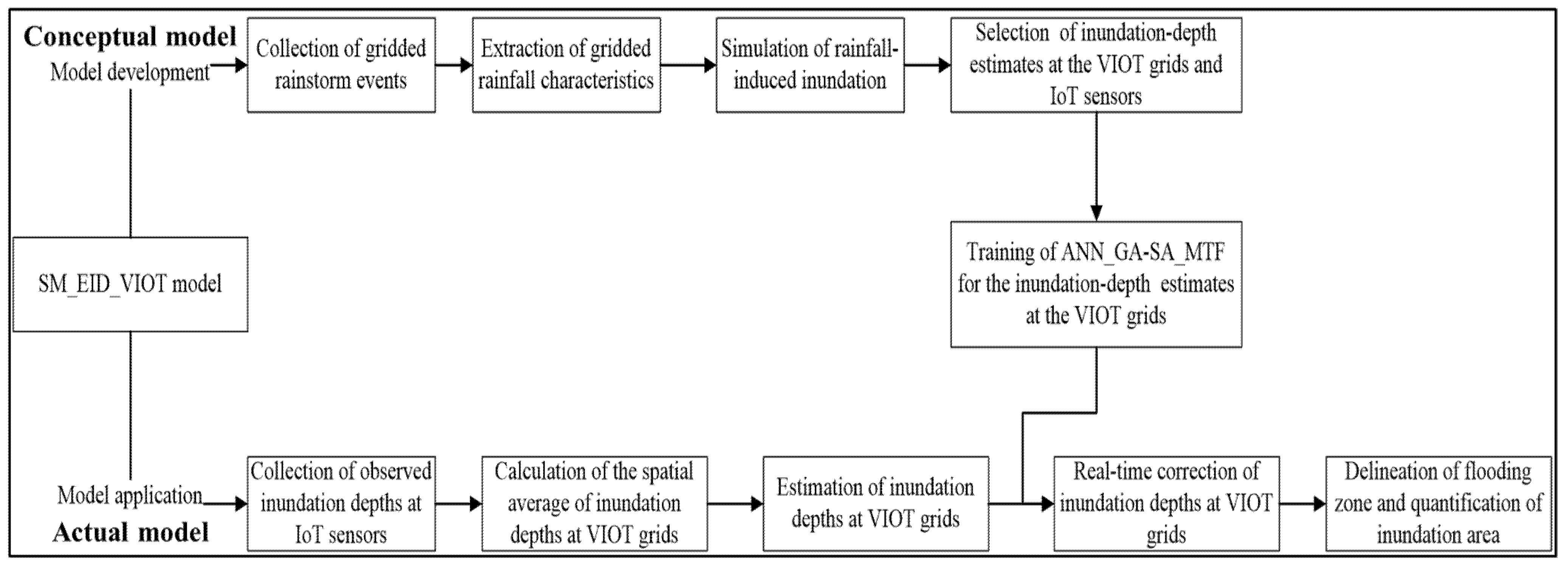
2.6. Model Framework
2.6.1. Conceptual Model
2.6.2. Actual Model
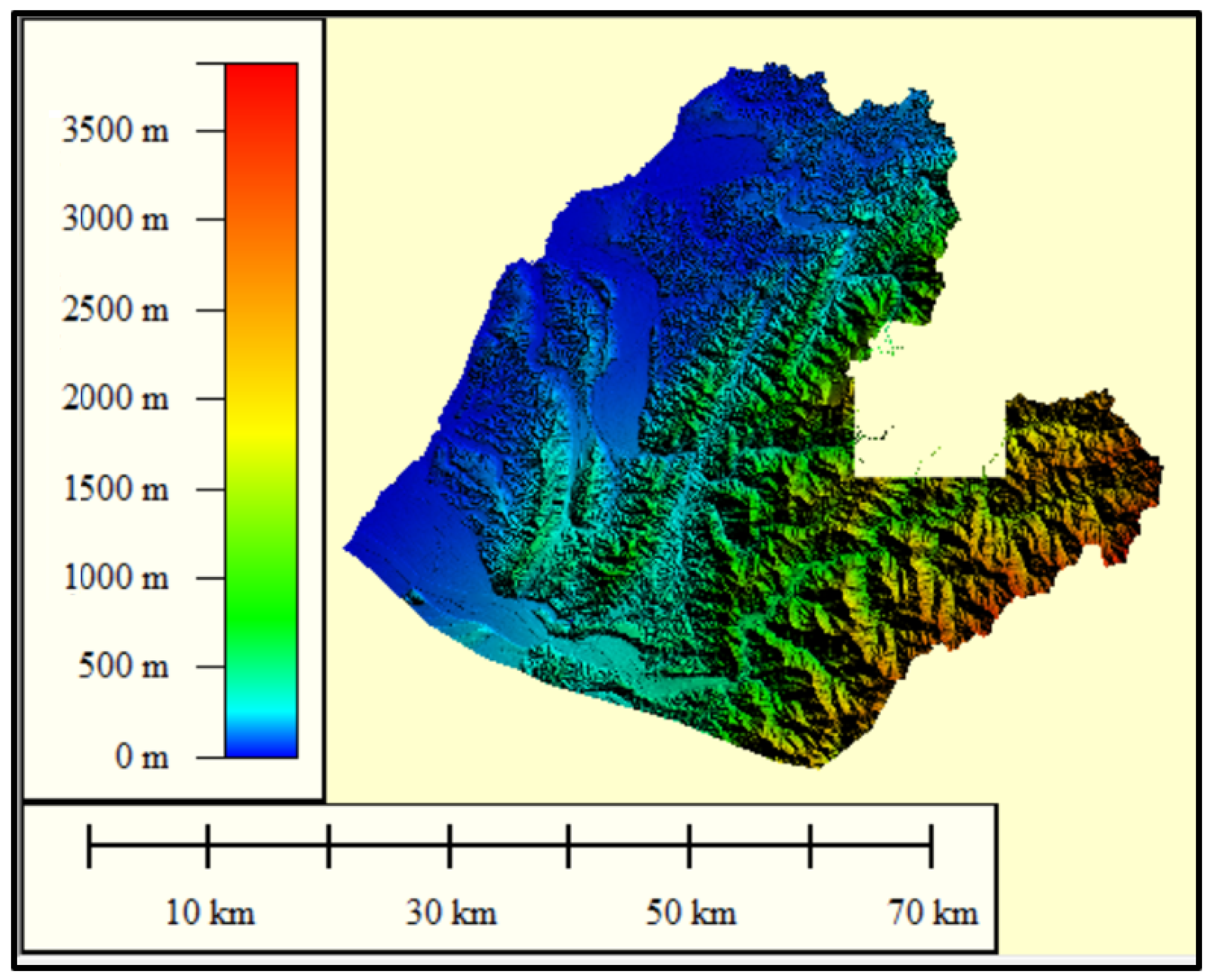
3. Study Area and Data
4. Results and Discussions
4.1. Simulation of Rainfall-Induced Inundation
4.1.1. Extraction of Gridded Rainstorms
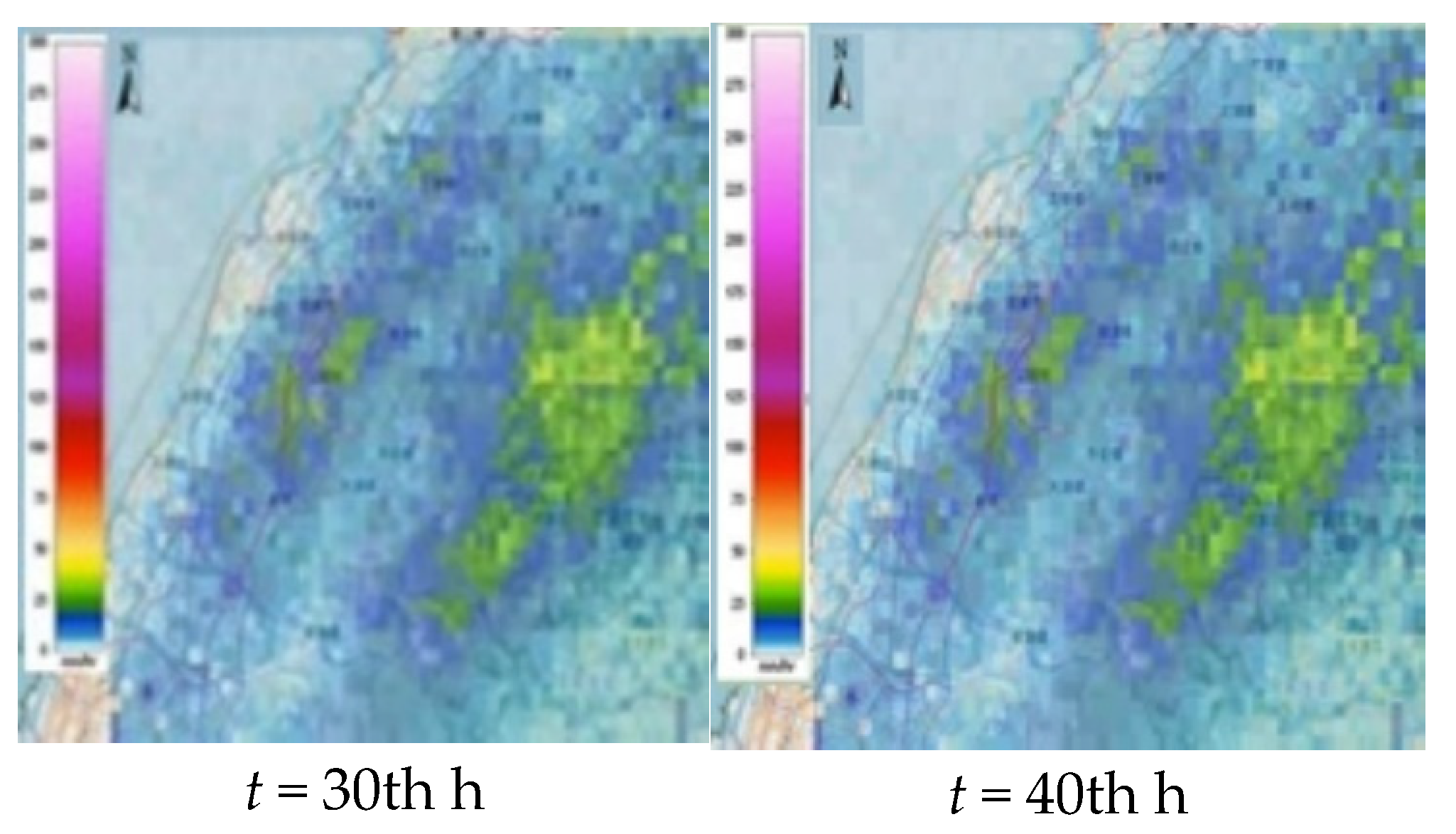
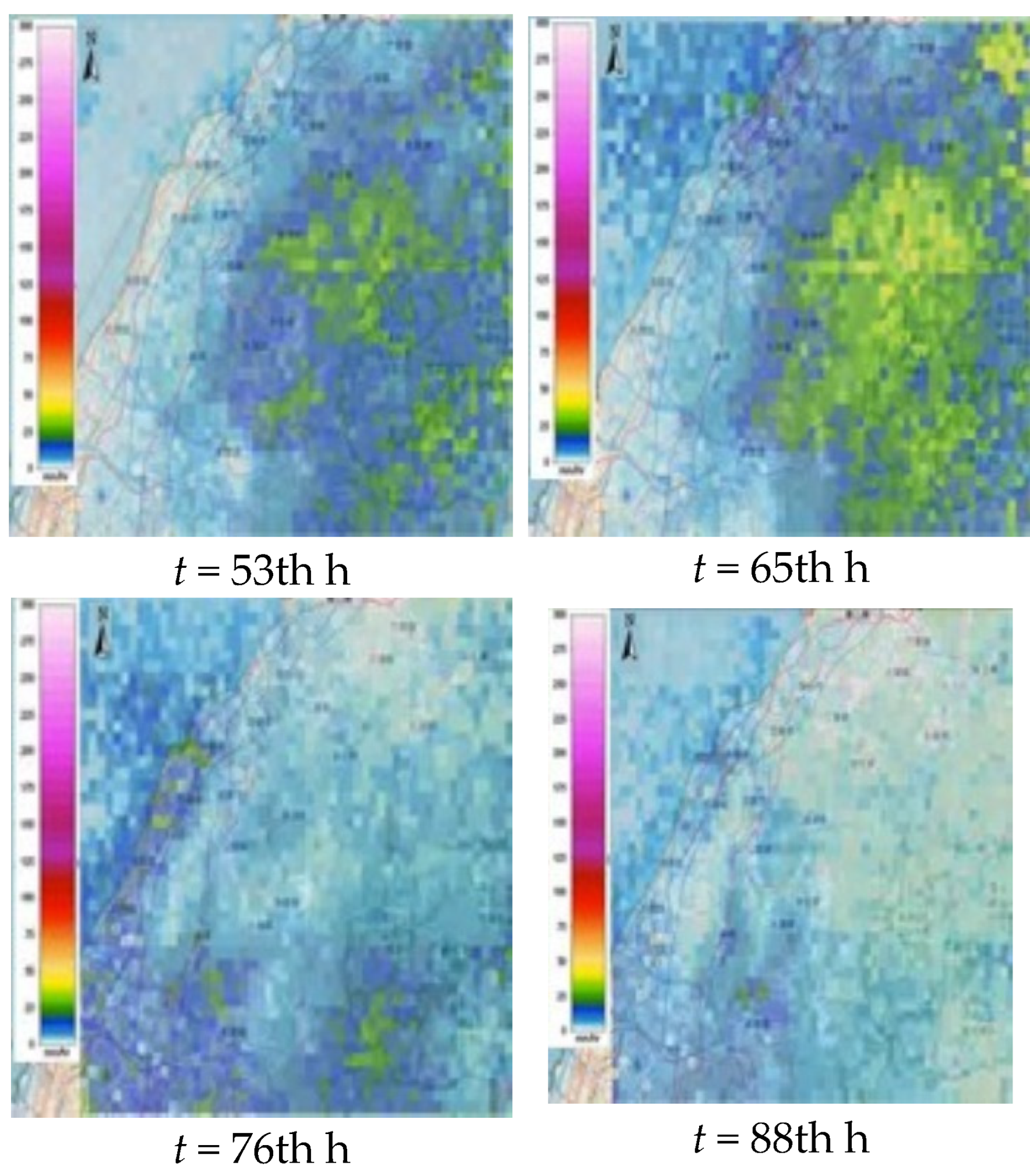
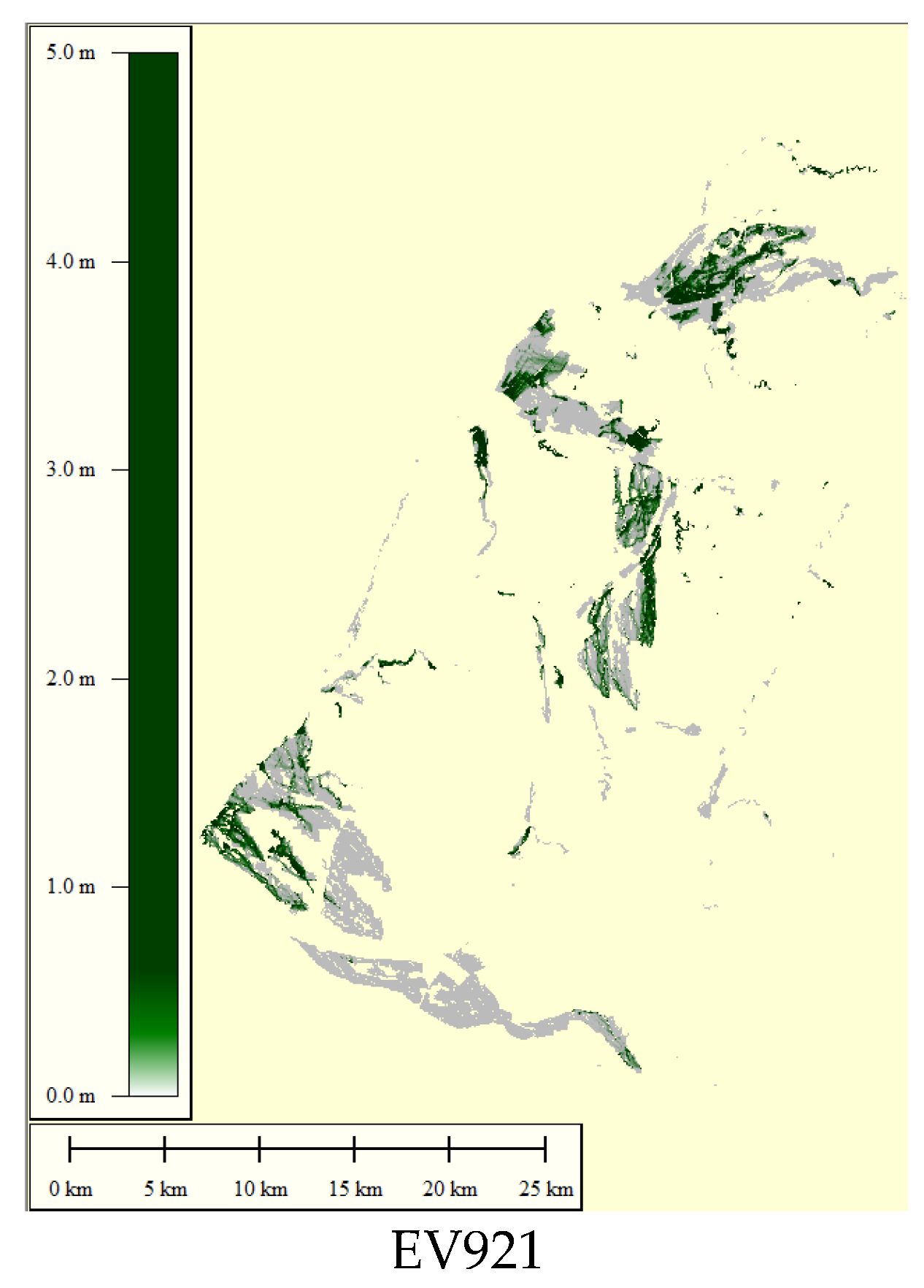
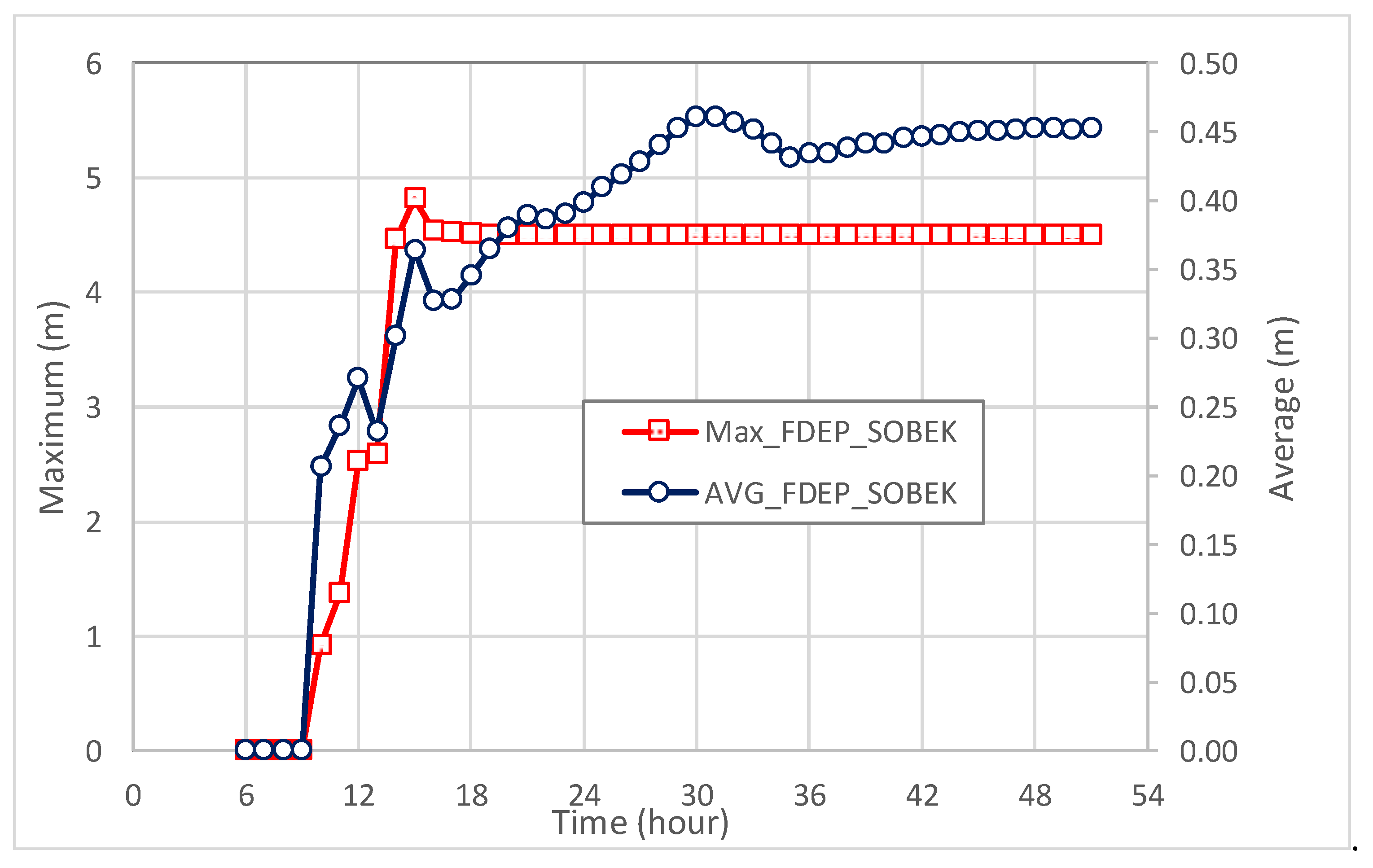
4.1.2. Simulation of Rainfall-Induced Inundation Events
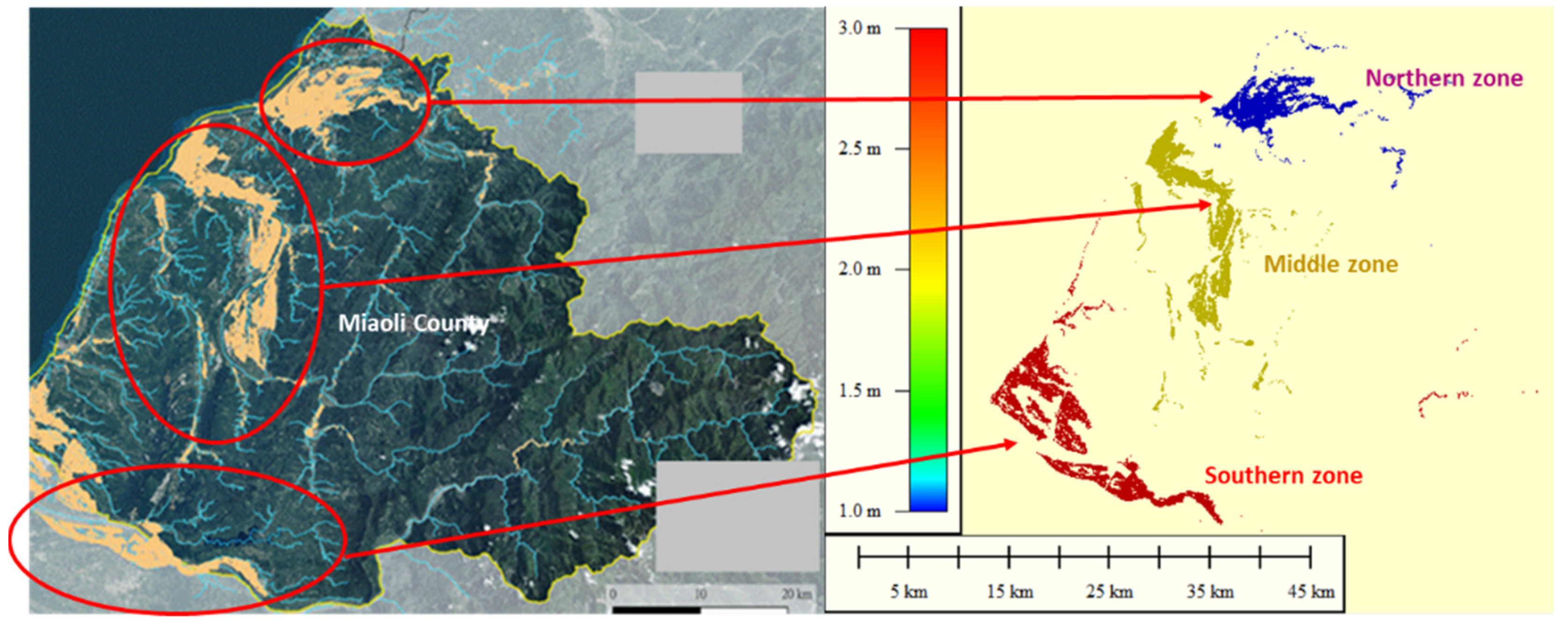
4.2. Identification of Ungauged Locations as VIOT Grids
4.3. Training of ANN-Derived Model
4.4. Model Validation
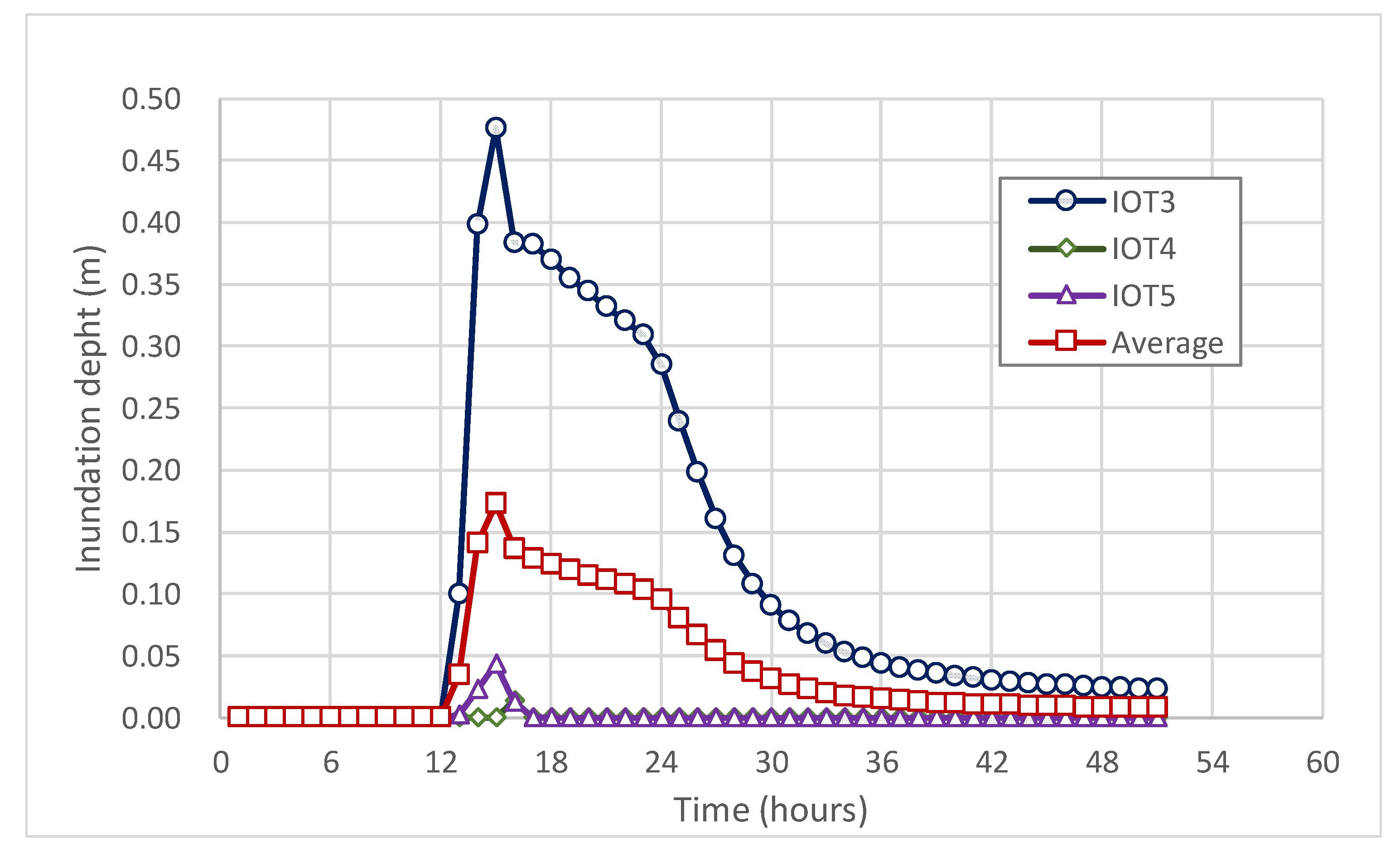
4.4.1. Extraction of Validation Data
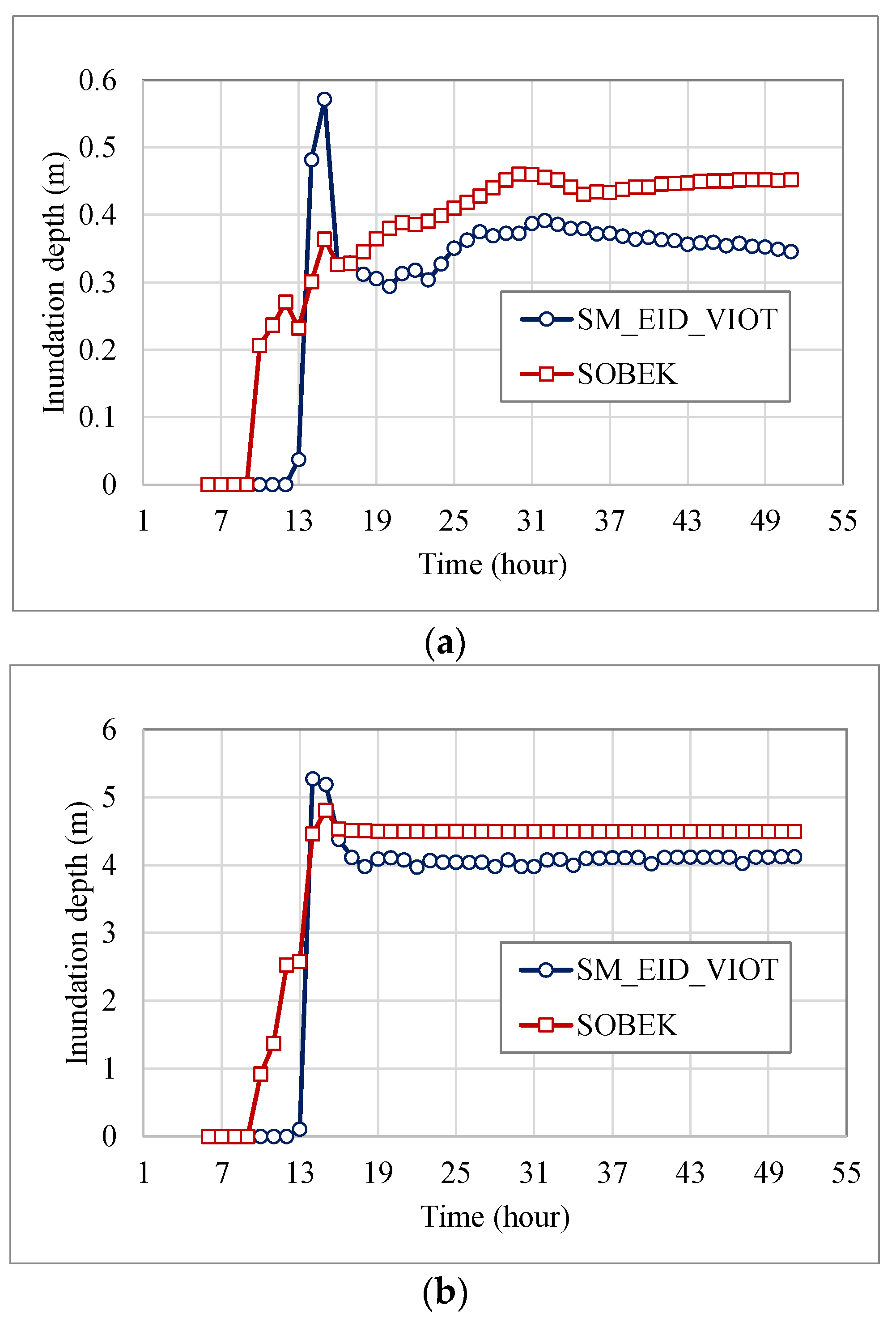
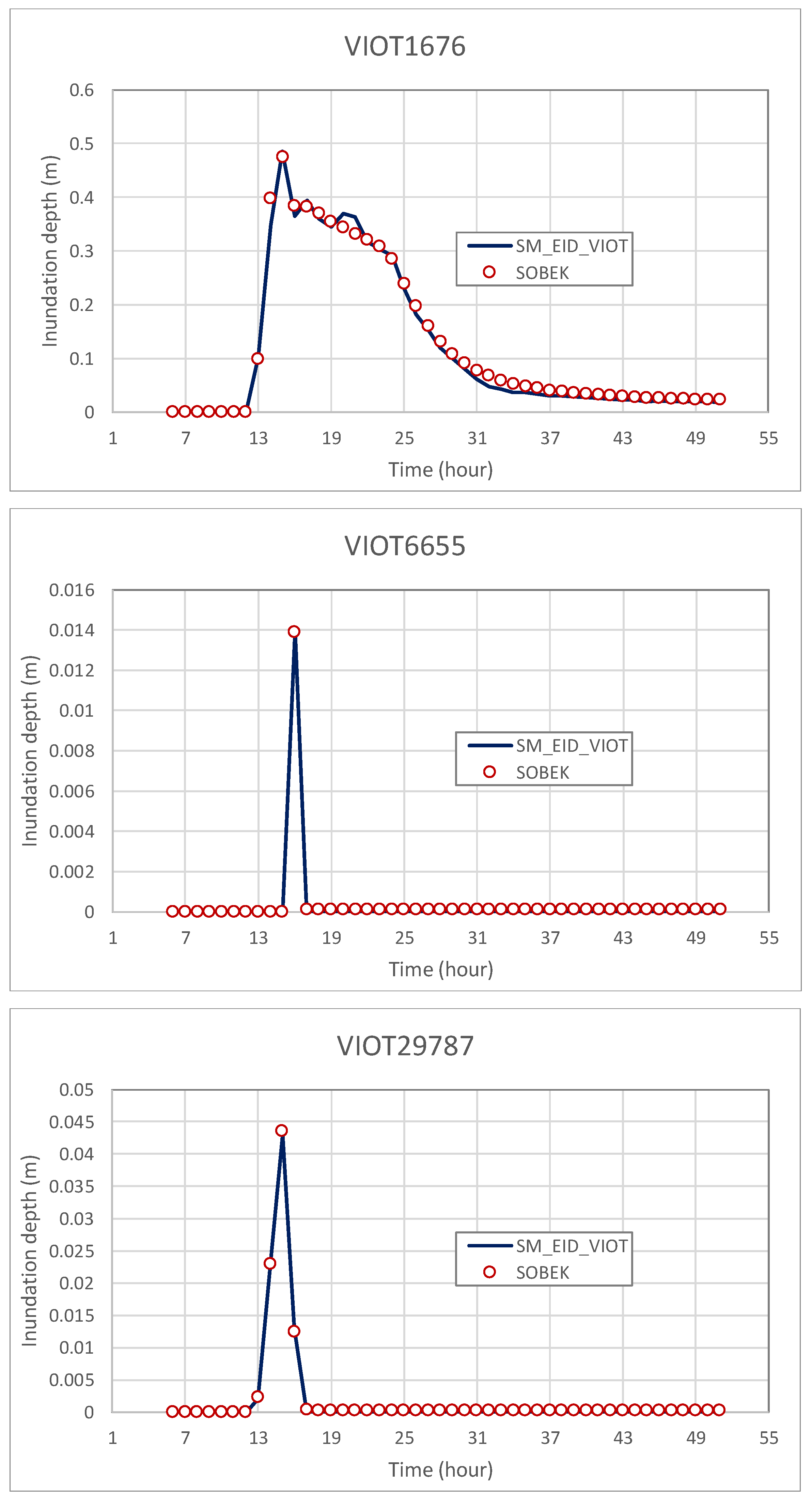
4.4.2. Evaluation of the Inundation-Depth Estimates
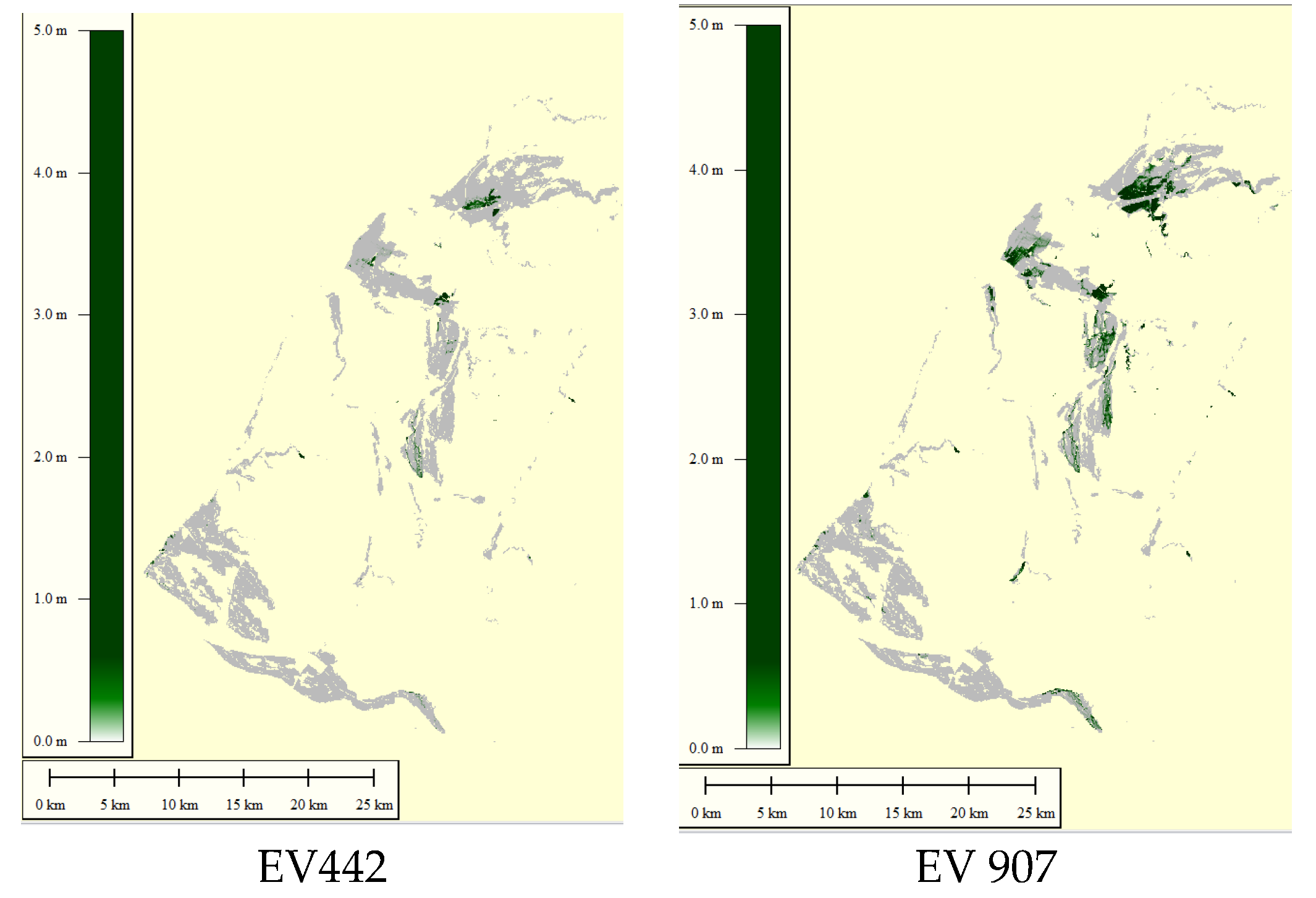
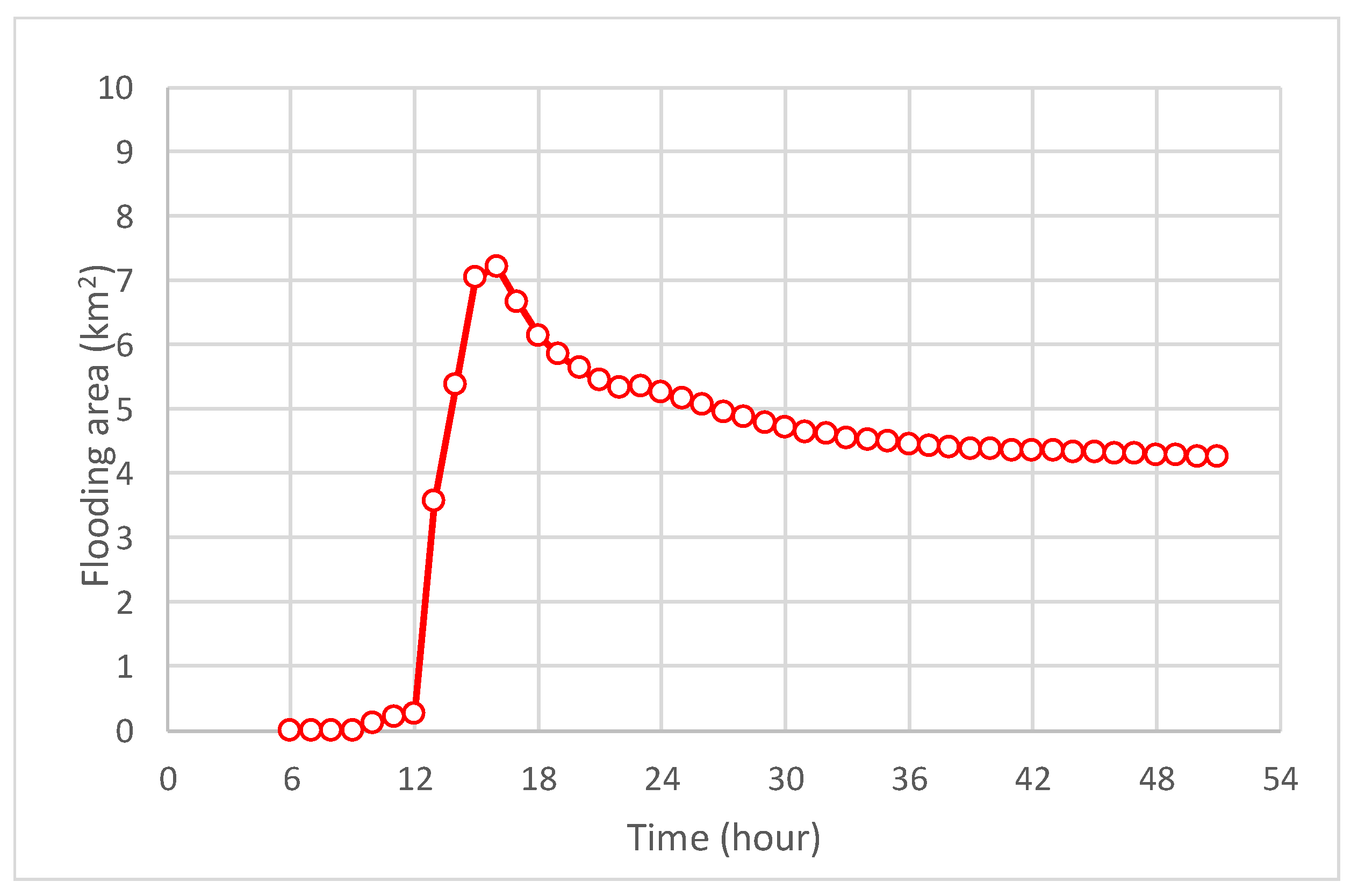
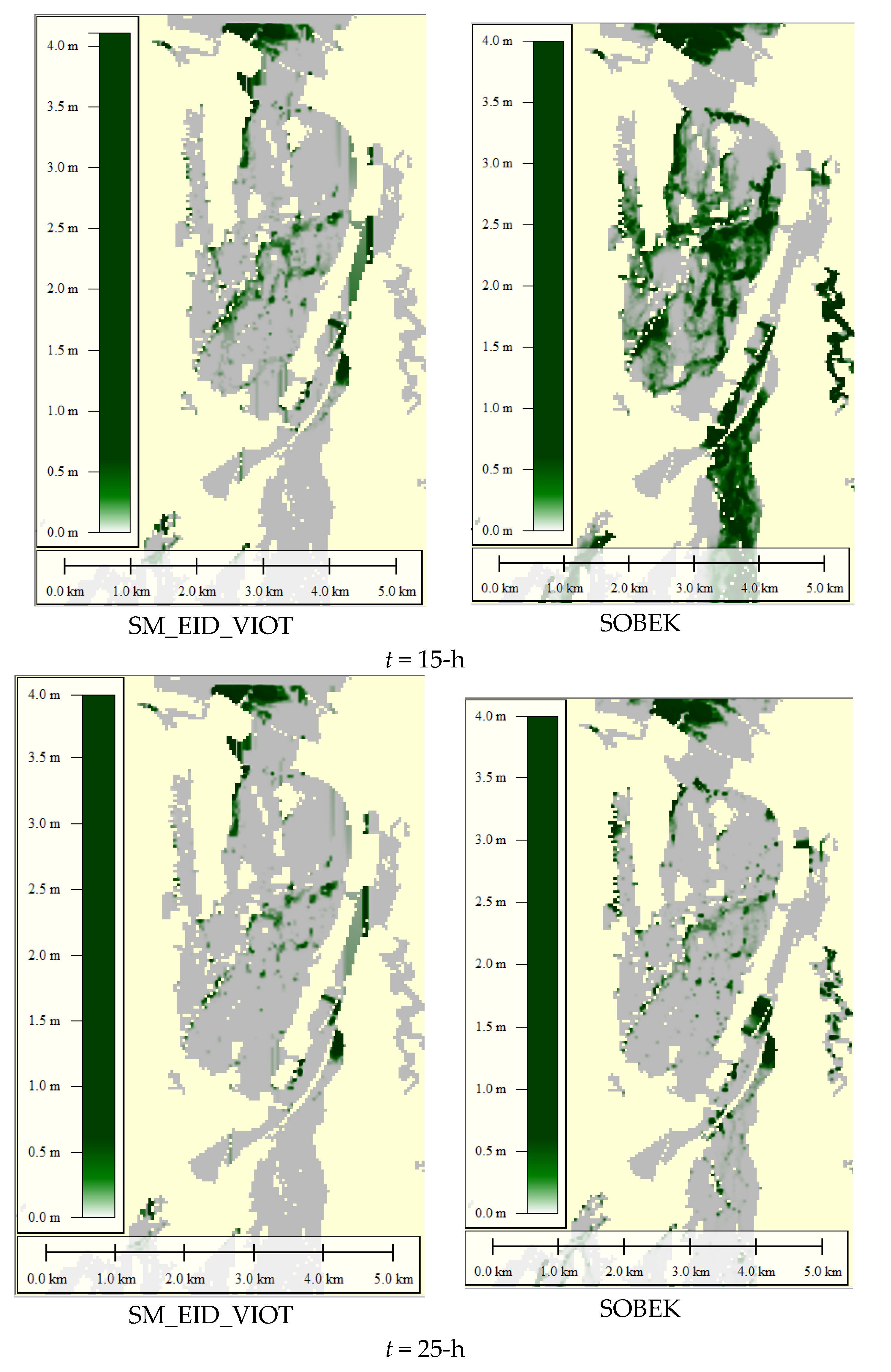
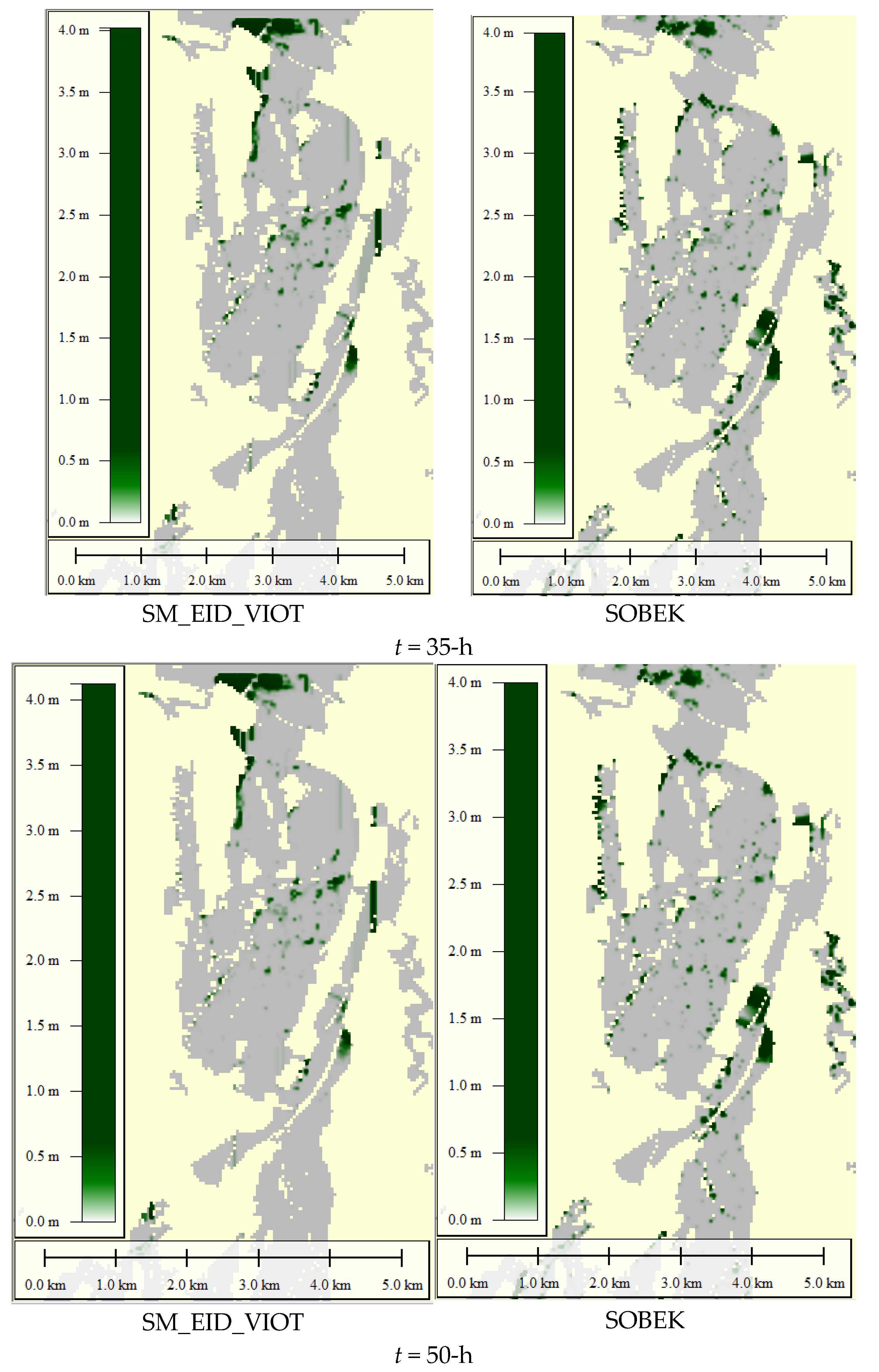
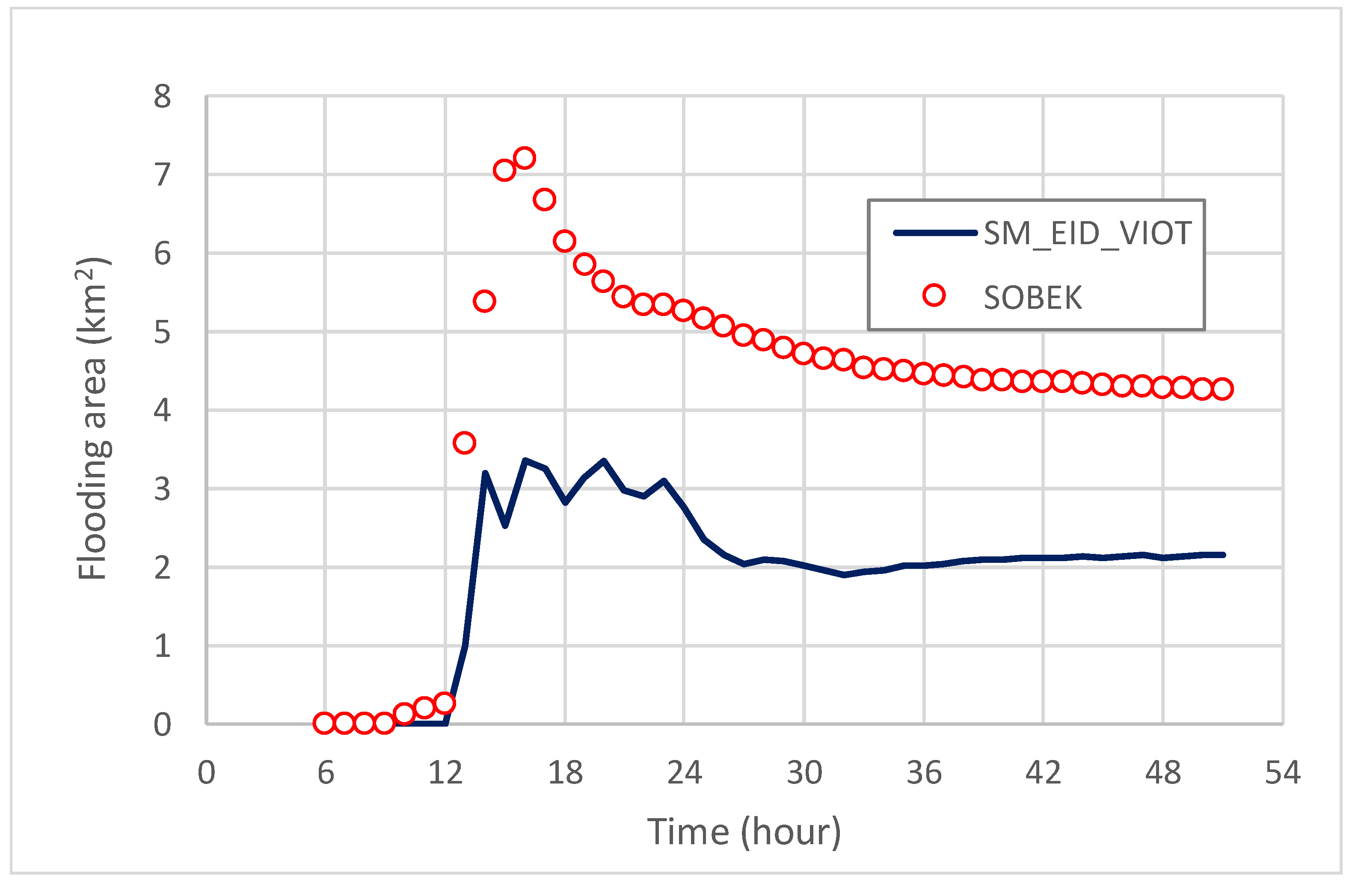
4.4.3. Assessment of the Flooding Area
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, S.J.; Hsu, C.T.; Chang, C.H. Stochastic modeling of artificial neural networks for real-Time hydrological forecasts based on uncertainties in transfer Functions and ANN weights. Hydrol. Res. 2021, 52, 1490–1525. [Google Scholar] [CrossRef]
- Wu, S.J.; Chang, C.H.; Hsu, C.T. Real-time error correction of two-dimensional flood-inundation simulations during rainstorm events. Stoch. Environ. Res. Risk Assess. 2020, 34, 641–667. [Google Scholar] [CrossRef]
- Kabir, S.; Patidar, S.; Xia, X.; Liang, Q.; Jeffrey Neal, J.; Gareth Pender, G. A deep convolutional neural network model for rapid prediction of fluvial flood inundation. J. Hydrol. 2020, 560, 125841. [Google Scholar] [CrossRef]
- Chen, Y.C.; Chang, T.Y.; Chow, H.Y.; Li, S.L.; Ou, C.Y. Using convolutional neural networks to build a lightweight flood height prediction model with grid-cam for the selection of key grid cells in radar echo maps. Water 2020, 14, 155. [Google Scholar] [CrossRef]
- Ming, X.; Liang, Q.; Xia, X.; Li, D.; Fowler, H.J. Real-time flood forecasting based on a high-performance 2-D hydrodynamic model and numerical weather predictions. Water Resour. Res. 2019, 56, e2019WR025583. [Google Scholar] [CrossRef]
- Ongdas, N.; Akiyanova, F.; Karakulov, Y.; Muratbayeva, A.; Zinabdin, N. Application of HEC-RAS (2D) for Flood Hazard Maps Generation for Yesil (Ishim) River in Kazakhstan. Water 2020, 12, 2672. [Google Scholar] [CrossRef]
- Chang, C.H.; Chung, M.K.; Yang, S.Y.; Chih-Tsung Hsu, C.T.; Wu, S.J. A Case Study for the Application of an Operational Two-Dimensional Real-Time Flooding Forecasting System and Smart Water Level Gauges on Roads in Tainan City, Taiwan. Water 2018, 10, 574. [Google Scholar] [CrossRef] [Green Version]
- Chu, H.; Wu, W.; Wang, Q.J.; Nathan, R.; Wei, J. An ANN-based emulation modelling framework for flood inundation modelling: Application, challenges and future directions. Environ. Model. Softw. 2020, 124, 104587. [Google Scholar] [CrossRef]
- Kwon, S.H.; Kim, J.H. Machine learning and urban drainage systems: State-of –the-art review. Water 2021, 12, 3545. [Google Scholar] [CrossRef]
- Wang, W.C.; Chau, K.W.; Cheng, C.T.; Qiu, L. A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef] [Green Version]
- Ioannou, K.; Myronidis, D.; Lefakis, P.; Stathis, D. The use of artificial neural networks (ANNs) for the forecast of precipitation levels of lake Doirani (N. Greece). Fresenius Environ. Bull. 2010, 19, 1921–1927. [Google Scholar]
- Chang, L.C.; Shen, H.Y.; Chang, F.J. Regional flood inundation nowcast using hybrid SOM and dynamic neural networks. J. Hydrol. 2014, 519, 476–489. [Google Scholar] [CrossRef]
- Huashi, A.O.; Abdirahman, A.A.; Elmi, M.A.; Hashi, S.Z.M.; Rodriguez, O.E.R. A real-time flood detection system based on machine learning algorithms with emphasis on deep learning. Int. J. Eng. Trends Technol. 2021, 69, 219–256. [Google Scholar]
- Wu, S.J.; Hsu, C.T.; Chang, C.H. Stochastic Modeling for Estimating Real-Time Inundation Depths at Roadside IoT Sensors Using the ANN-Derived Model. Water 2021, 12, 3128. [Google Scholar] [CrossRef]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef]
- Khashei, M.; Bijiai, M. An artificial neural network (p, d, q) model for timeseries forecasting. Expert Syst. Appl. 2010, 37, 479–489. [Google Scholar] [CrossRef]
- Mustafa, M.R.; Rezaur, R.B.; Rahardjo, H.; Isa, M.H.; Arif, A. Artificial Neural Network Modeling for Spatial and Temporal Variations of Pore-Water Pressure Responses to Rainfall. Adv. Meteorol. 2015, 2015, 273730. [Google Scholar] [CrossRef] [Green Version]
- Chang, L.C.; Amin, M.Z.M.; Yang, S.N.; Chang, F.J. Building ANN-Based Regional Multi-Step-Ahead Flood Inundation Forecast Models. Water 2018, 10, 1283. [Google Scholar] [CrossRef] [Green Version]
- Tu, J.V. Advantages and disadvantages of using artificial neural networks versus logistic Regression for predicting medical outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Zahiri, A. Neuro-Fuzzy GMDH-Based Evolutionary Algorithms to Predict Flow Discharge in Straight Compound Channels. J. Hydrol. Eng. 2015, 20, 04015035. [Google Scholar] [CrossRef]
- Delasalles, E.; Ziat, A.; Denoyer, L.; Gallinari, P. Spatio-temporal neural networks for space-time data modeling and relation discovery. Knowl. Inf. Syst. 2019, 61, 1241–1267. [Google Scholar] [CrossRef]
- Amiri, M.A.; Zmerian, Y.; Mesgari, M.S. Spatial and temporal monthly precipitation forecasting using wavelet transform and neural network, Qara-Qum catchment, Iran. Arab. J. Geosci. 2016, 9, 421–438. [Google Scholar] [CrossRef]
- Wu, S.J.; Hsu, C.T.; Chang, C.H. Stochastic modeling of gridded short-term rainstorms. Hydrol. Res. 2021, 52, 876–904. [Google Scholar] [CrossRef]
- Delft Hydraulics. SOBEK Software User’s Manual; WL|Delft Hydraulics: Delft, The Netherlands, 2013; Available online: https://content.oss.deltares.nl/delft3d/manuals/SOBEK_User_Manual.pdf (accessed on 6 June 2022).
- Chang, C.H.; Yang, J.C.; Tung, Y.K. Incorporate marginal distributions in point estimate methods for uncertainty analysis. J. Hydraul. Eng. 1997, 123, 244–251. [Google Scholar] [CrossRef] [Green Version]
- Nataf, A. Determination des distributions don’t les marges sontdonnees. Comptes Rendus L’académie Sci. 1962, 225, 42–43. [Google Scholar]
- Wu, S.J.; Lien, H.C.; Chang, C.H. Calibration of a conceptual Rainfall-Runoff Model using a Genetic Algorithm Integrated with Runoff Estimation Sensitivity to Parameters. J. Hydroinform. 2011, 14, 497–511. [Google Scholar] [CrossRef]
- Wu, S.J.; Lien, H.C.; Chang, C.H.; Shen, J.C. Real-Time Correction of Water Stage Forecast during Rainstorm Events Using Combination of Forecast Errors. Stoch. Environ. Res. Risk Assess. 2012, 26, 519–531. [Google Scholar] [CrossRef]
- Wu, S.J.; Chen, P.H.; Yang, J.C. Application of Weighted Semivariogram Model (WSVM) based on fitness to experimental semivariogram on estimation of rainfall amount. Hydrol. Earth Syst. Sci. Discuss. 2011, 8, 4229–4259. [Google Scholar]










| No of Formula | Formula |
|---|---|
| 1 | |
| 2 | |
| 3 | +1 |
| 4 | |
| 5 | |
| 6 |
| Transfer Function | Formula | Derivative | |
|---|---|---|---|
| TF1 | Logistic(soft step, Sigmoid) | ||
| TF2 | Tanh | ||
| TF3 | Arctan | ||
| TF4 | Identity | x | |
| TF5 | Rectified linear unit (ReLU) | ||
| TF6 | Parameteric rectified linear unit (PReLU, leaky ReLU) | ||
| TF7 | Exponential linear unit(ELU) | ||
| TF8 | Inverse abs (IA) | ||
| TF9 | Rootsig (RS) | ||
| TF10 | Sech function (SF) | ||
| Function | Facilities | Number |
|---|---|---|
| Hydraulic analysis | Sub-basins | 4731 |
| Cross-sections | 9838 | |
| Gates | 62 | |
| Bridges | 9018 | |
| Sewer | 68.6 km | |
| Maintenance of sewer system | 1382 | |
| Hydrological analysis | Rainfall-runoff node | 4097 |
| Parameters | Definition | ||
|---|---|---|---|
| Transfer functions used | TF1-TF10 | ||
| Input factors | Resulting areal average of Inundation depth from IoT sensors | ||
| Output factor | Inundation depth at VIOT grids | ||
| Number of hidden levels | 1 | ||
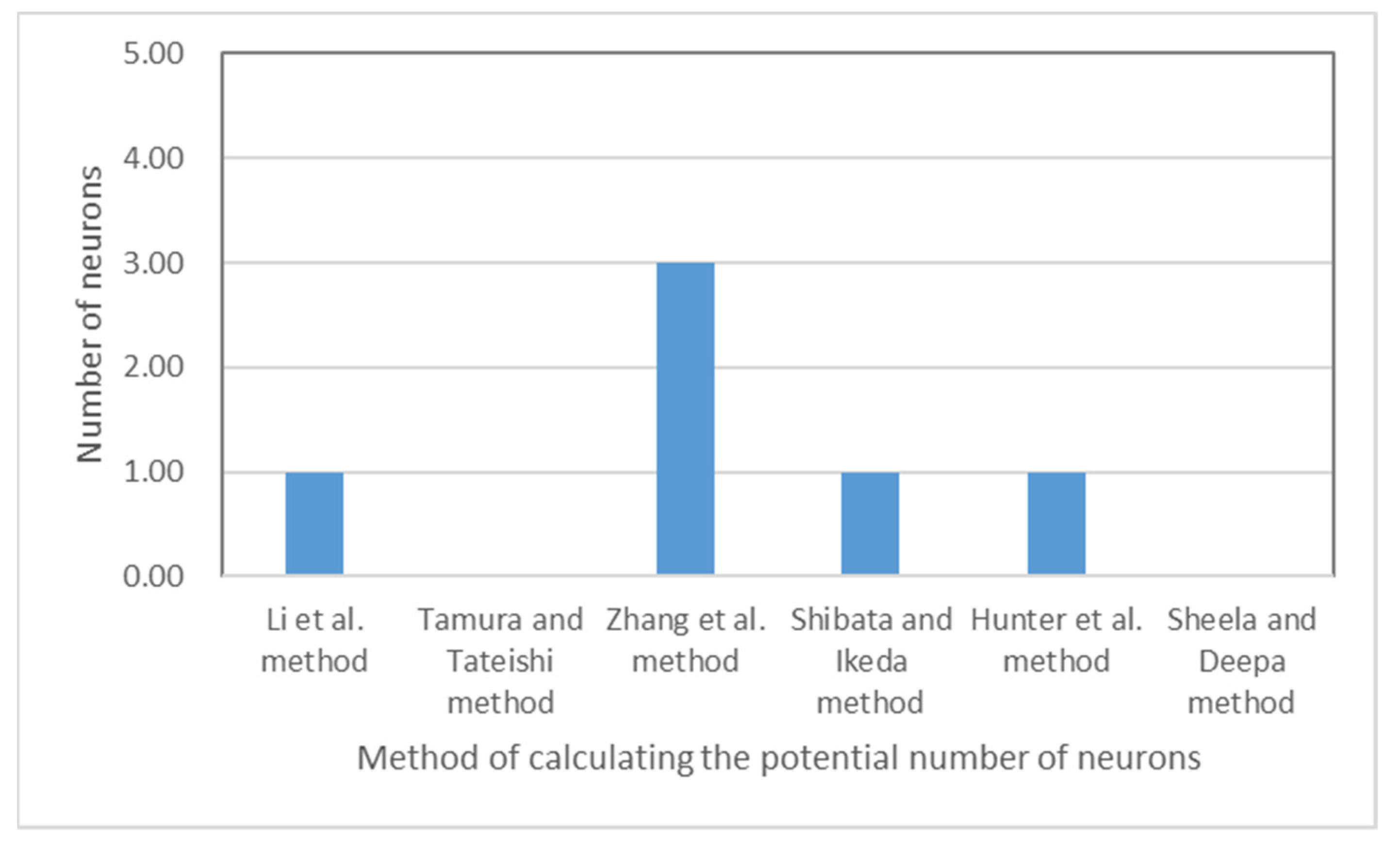
| Number of neurons | 3 | ||
| Calibration of parameters of transfer function | Number of optimizations | 10 | |
| Mean | 1 | ||
| Standard deviation | 3 | ||
| Mean | 0 | ||
| Standard deviation | 1 | ||
| Mean | 1 | ||
| Standard deviation | 0.005 | ||
| Transfer Function | No of Optimization | Adjust Factor | 1.00113 | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | OPT1 | Weights of | The 1st hidden layer | Input factors | ||||
| 1 | Bias | |||||||
| Neuron | 1 | 2.27251 | −1.14272 | |||||
| 2 | 0.58986 | −2.71961 | ||||||
| 3 | 4.56974 | −4.28293 | ||||||
| Output layer | The 1st hidden layer | |||||||
| 1 | 2 | 3 | Bias | |||||
| Input factor | 1 | −0.87316 | 1.04999 | 0.08291 | −0.21039 | |||
| Performance Index | Inundation Depth | ||||
| Average | Maximum | VIOT1676 | VIOT6655 | VIOT2978 | |
| Root mean square error RMSE (m) | 0.103 | 0.015 | 0.002 | 0.000 | 0.000 |
| Coefficient of determination (R2) | 0.891 | 0.703 | 0.993 | 1.000 | 1.000 |
| Performance Index | Precision Index | Recall Index | F1 | RMSE (km2) | R2 | |
|---|---|---|---|---|---|---|
| Statistical properties | Mean | 0.669 | 0.364 | 0.461 | 0.161 | 0.65 |
| Standard deviation | 0.209 | 0.220 | 0.208 | |||
| Maximum | 1.000 | 1.000 | 1.000 | |||
| Minimum | 0.000 | 0.000 | 0.000 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.-J.; Hsu, C.-T.; Shen, J.-C.; Chang, C.-H. Modeling the 2D Inundation Simulation Based on the ANN-Derived Model with Real-Time Measurements at Roadside IoT Sensors. Water 2022, 14, 2189. https://doi.org/10.3390/w14142189
Wu S-J, Hsu C-T, Shen J-C, Chang C-H. Modeling the 2D Inundation Simulation Based on the ANN-Derived Model with Real-Time Measurements at Roadside IoT Sensors. Water. 2022; 14(14):2189. https://doi.org/10.3390/w14142189
Chicago/Turabian StyleWu, Shiang-Jen, Chih-Tsu Hsu, Jhih-Cyuan Shen, and Che-Hao Chang. 2022. "Modeling the 2D Inundation Simulation Based on the ANN-Derived Model with Real-Time Measurements at Roadside IoT Sensors" Water 14, no. 14: 2189. https://doi.org/10.3390/w14142189
APA StyleWu, S.-J., Hsu, C.-T., Shen, J.-C., & Chang, C.-H. (2022). Modeling the 2D Inundation Simulation Based on the ANN-Derived Model with Real-Time Measurements at Roadside IoT Sensors. Water, 14(14), 2189. https://doi.org/10.3390/w14142189





