Numerical Investigation of the Scaling Effects for a Point Absorber
Abstract
:1. Introduction
Wave Energy Converter
2. Wave Theories
2.1. Airy Wave Theory
2.2. Stokes Wave Theories
Validity Regions
3. Numerical Model
3.1. Numerical Wave Tank Characteristics
3.2. Solver Settings
3.3. Boundary Conditions
3.4. Mesh
- Case A: Waves , , and without WEC, for the scale 1:1 and 1:50;
- Case B: Waves , , and , including the WEC, for the scale 1:1 and 1:50.
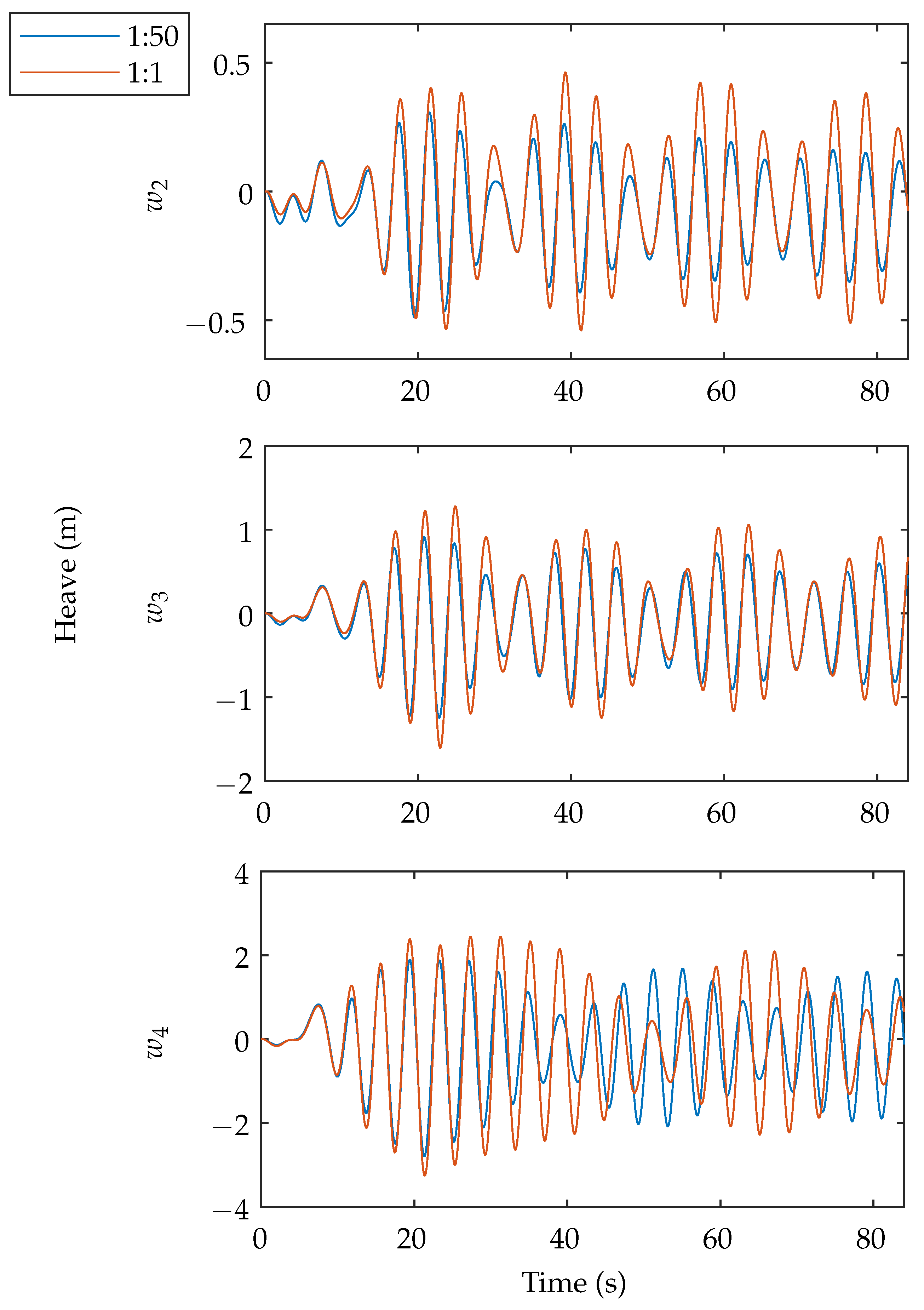
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| DOF | Degree Of Freedom |
| FSE | Free Surface Elevation |
| LWT | Linear Wave Theory |
| OWC | Oscillating Wave Surge Converter |
| OCWBC | Open Channel Wave Boundary Condition |
| PA-WEC | Point Absorber Wave Energy Converter |
| RANS | Reynolds-Averaged Navier-Stokes |
| SPH | Smoothed-particle hydrodynamics |
| TLR | Technology readiness level |
| VOF | Volume of Fluid |
| WEC | Wave Energy Converter |
References
- Salter, S. Wave power. Nature 1974, 7720, 249–260. [Google Scholar] [CrossRef]
- Mørk, G.; Barstow, S.; Kabuth, A.; Pontes, M.T. Assessing the global wave energy potential. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Shanghai, China, 6–11 June 2010; Volume 3, pp. 447–454. [Google Scholar]
- Noble, D.R.; O’Shea, M.; Judge, F.; Robles, E.; Martinez, R.; Khalid, F.; Thies, P.R.; Johanning, L.; Corlay, Y.; Gabl, R.; et al. Standardising Marine Renewable Energy Testing: Gap Analysis and Recommendations for Development of Standards. J. Mar. Sci. Eng. 2021, 9, 971. [Google Scholar] [CrossRef]
- Ticona Rollano, F.; Tran, T.T.; Yu, Y.H.; García-Medina, G.; Yang, Z. Influence of Time and Frequency Domain Wave Forcing on the Power Estimation of a Wave Energy Converter Array. J. Mar. Sci. Eng. 2020, 8, 171. [Google Scholar] [CrossRef] [Green Version]
- Cabral, T.; Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F.; Morais, T.; Belga, F.; Cestaro, H. Performance Assessment of a Hybrid Wave Energy Converter Integrated into a Harbor Breakwater. Energies 2020, 13, 236. [Google Scholar] [CrossRef] [Green Version]
- Musiedlak, P.H.; Ransley, E.J.; Hann, M.; Child, B.; Greaves, D.M. Time-Splitting Coupling of WaveDyn with OpenFOAM by Fidelity Limit Identified from a WEC in Extreme Waves. Energies 2020, 13, 3431. [Google Scholar] [CrossRef]
- Quartier, N.; Ropero-Giralda, P.; Domínguez, J.M.; Stratigaki, V.; Troch, P. Influence of the Drag Force on the Average Absorbed Power of Heaving Wave Energy Converters Using Smoothed Particle Hydrodynamics. Water 2021, 13, 384. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.J.C.; Coe, R.G.; Tagliafierro, B.; Domínguez, J.M.; Bacelli, G.; Gómez-Gesteira, M. Modelling a Heaving Point-Absorber with a Closed-Loop Control System Using the DualSPHysics Code. Energies 2021, 14, 760. [Google Scholar] [CrossRef]
- Verao Fernandez, G.; Stratigaki, V.; Quartier, N.; Troch, P. Influence of Power Take-Off Modelling on the Far-Field Effects of Wave Energy Converter Farms. Water 2021, 13, 429. [Google Scholar] [CrossRef]
- Balitsky, P.; Quartier, N.; Stratigaki, V.; Verao Fernandez, G.; Vasarmidis, P.; Troch, P. Analysing the Near-Field Effects and the Power Production of Near-Shore WEC Array Using a New Wave-to-Wire Model. Water 2019, 11, 1137. [Google Scholar] [CrossRef] [Green Version]
- Šljivac, D.; Temiz, I.; Nakomčić-Smaragdakis, B.; Žnidarec, M. Integration of Wave Power Farms into Power Systems of the Adriatic Islands: Technical Possibilities and Cross-Cutting Aspects. Water 2021, 13, 13. [Google Scholar] [CrossRef]
- Sheng, W.; Alcorn, R.; Lewis, T. Physical modelling of wave energy converters. Ocean. Eng. 2014, 84, 29–36. [Google Scholar] [CrossRef]
- IEC TS 62600; Wave, Tidal and Other Water Current Converters—Part 103: Guidelines for the Early Stage Development of Wave Energy Converters—Best Practices and Recommended Procedures for the Testing of Pre-Prototype Devices. International Electrotechnical Commission: Geneva, Switzerland, 2018.
- Davey, T.; Sarmiento, J.; Ohana, J.; Thiebaut, F.; Haquin, S.; Weber, M.; Gueydon, S.; Judge, F.; Lyden, E.; O’Shea, M.; et al. Round Robin Testing: Exploring Experimental Uncertainties through a Multifacility Comparison of a Hinged Raft Wave Energy Converter. J. Mar. Sci. Eng. 2021, 9, 946. [Google Scholar] [CrossRef]
- Assessment of Experimental Uncertainty for a Floating Wind Semisubmersible Under Hydrodynamic Loading. Volume 10: Ocean Renewable Energy. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [CrossRef]
- BMT Fluid Mechanics Ltd. Review of Model Testing Requirements for FPSO’s; BMT Fluid Mechanics Ltd.: Teddington, UK, 2001; pp. 1–80. [Google Scholar]
- Heller, V. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar] [CrossRef]
- Schmitt, P.; Elsäßer, B. The application of Froude scaling to model tests of Oscillating Wave Surge Converters. Ocean. Eng. 2017, 141, 108–115. [Google Scholar] [CrossRef] [Green Version]
- Palm, J.; Eskilsson, C.; Bergdahl, L.; Bensow, R.E. Assessment of scale effects, viscous forces and induced drag on a point-absorbing wave energy converter by CFD simulations. J. Mar. Sci. Eng. 2018, 6, 124. [Google Scholar] [CrossRef] [Green Version]
- Windt, C.; Ringwood, J.V.; Davidson, J.; Schmitt, P. Contribution to the ccp-wsi blind test series 3: Analysis of scaling effects of moored point-absorber wave energy converters in a cfd-based numerical wave tank. In Proceedings of the International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019; Volume 3, pp. 3051–3058. [Google Scholar]
- Windt, C.; Davidson, J.; Ringwood, J.V. Numerical analysis of the hydrodynamic scaling effects for the Wavestar wave energy converter. J. Fluids Struct. 2021, 105, 103328. [Google Scholar] [CrossRef]
- Le Méhauté, B. An Introduction to Hydrodynamics and Water Waves; Springer: New York, NY, USA, 1976. [Google Scholar]
- Hedges, T.; URSELL. Regions of validity of analytical wave theories. Proc. Inst. Civ. Eng.-Water Marit. Energy 1995, 112, 111–114. [Google Scholar] [CrossRef]
- Finnegan, W.; Rosa-Santos, P.; Taveira-Pinto, F.; Goggins, J. Development of a numerical model of the CECO wave energy converter using computational fluid dynamics. Ocean. Eng. 2021, 219, 108416. [Google Scholar] [CrossRef]
- Schubert, B.W.; Robertson, W.S.; Cazzolato, B.S.; Ghayesh, M.H. Linear and nonlinear hydrodynamic models for dynamics of a submerged point absorber wave energy converter. Ocean. Eng. 2020, 197, 106828. [Google Scholar] [CrossRef]
- Sjökvist, L.; Wu, J.; Ransley, E.; Engström, J.; Eriksson, M.; Göteman, M. Numerical models for the motion and forces of point-absorbing wave energy converters in extreme waves. Ocean. Eng. 2017, 145, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Al Shami, E.; Wang, Z.; Wang, X. Non-linear dynamic simulations of two-body wave energy converters via identification of viscous drag coefficients of different shapes of the submerged body based on numerical wave tank CFD simulation. Renew. Energy 2021, 179, 983–997. [Google Scholar] [CrossRef]
- Bharath, A.; Nader, J.R.; Penesis, I.; Macfarlane, G. Nonlinear hydrodynamic effects on a generic spherical wave energy converter. Renew. Energy 2018, 118, 56–70. [Google Scholar] [CrossRef]
- Benites-Munoz, D.; Huang, L.; Anderlini, E.; Marín-Lopez, J.R.; Thomas, G. Hydrodynamic modelling of an oscillating wave surge converter including power take-off. J. Mar. Sci. Eng. 2020, 8, 771. [Google Scholar] [CrossRef]
- Airy, G. Tides and Waves. Encycl. Metrop. 1845, 5, 341–396. [Google Scholar]
- Fluent, A. ANSYS Fluent Theory Guide 2019R3; ANSYS: Canonsburg, PA, USA, 2019; pp. 561–734. [Google Scholar]
- Stokes, G. On the theory of oscillatory waves. Trans. Camb. Philos. Soc. 1847, 8, 441–455. [Google Scholar]
- Fenton, J.D. Nonlinear wave theories. Sea 1990, 9, 3–25. [Google Scholar]
- Penalba, M.; Giorgi, G.; Ringwood, J.V. Mathematical modelling of wave energy converters: A review of nonlinear approaches. Renew. Sustain. Energy Rev. 2017, 78, 1188–1207. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Yu, Y.H. A synthesis of numerical methods for modeling wave energy converter-point absorbers. Renew. Sustain. Energy Rev. 2012, 16, 4352–4364. [Google Scholar] [CrossRef]
- Martínez-Ferrer, P.J.; Qian, L.; Ma, Z.; Causon, D.M.; Mingham, C.G. Improved numerical wave generation for modelling ocean and coastal engineering problems. Ocean. Eng. 2018, 152, 257–272. [Google Scholar] [CrossRef] [Green Version]
- Bharath, A.; Penesis, I.; Nader, J.r.; Macfarlane, G. Non-Linear CFD Modelling of a Submerged Sphere Wave Energy Converter. In Proceedings of the 3rd Asian Wave and Tidal Energy Conference, Singapore, 24–28 October 2016; pp. 1–10. [Google Scholar]
- Bouali, B.; Larbi, S. Contribution to the geometry optimization of an oscillating water column wave energy converter. Energy Procedia 2013, 36, 565–573. [Google Scholar] [CrossRef] [Green Version]
- Martin, D.; Parker, R.G.; Tafti, D.K. Hydrodynamic Design Optimization and Wave Tank Testing of a Self-Reacting Two-Body Wave Energy Converter. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2017. [Google Scholar]
- Khedkar, K.; Nangia, N.; Thirumalaisamy, R.; Bhalla, A.P.S. The inertial sea wave energy converter (ISWEC) technology: Device-physics, multiphase modeling and simulations. Ocean. Eng. 2021, 229, 108879. [Google Scholar] [CrossRef]
- Yu, Y.H.; Li, Y. Reynolds-Averaged Navier-Stokes simulation of the heave performance of a two-body floating-point absorber wave energy system. Comput. Fluids 2013, 73, 104–114. [Google Scholar] [CrossRef]
- Devolder, B.; Stratigaki, V.; Troch, P.; Rauwoens, P. CFD simulations of floating point absorber wave energy converter arrays subjected to regular waves. Energies 2018, 11, 641. [Google Scholar] [CrossRef] [Green Version]
- Bhinder, M.A.; Babarit, A.; Gentaz, L.; Ferrant, P. Assessment of Viscous Damping via 3D-CFD Modelling of a Floating Wave Energy Device. In Proceedings of the European Wave and Tidal Energy Conference, EWTEC, Southampton, UK, 5–9 September 2011; pp. 1–6. [Google Scholar]









| Scale | h | L | ||||||
|---|---|---|---|---|---|---|---|---|
| 1:1 | 15 | 29.58 | 24 | 82.0 | 44.5 | 3 | 3.9 | 1.1695 |
| 1:50 | 0.300 | 0.5916 | 0.48 | 1.64 | 0.89 | 0.06 | 0.078 | 0.02339 |
| Parameter | Value | Units |
|---|---|---|
| Total mass | 0.235 | Kg |
| Construction method | 3D printed | - |
| Material | Polylactic Acid (PLA) | - |
| Surface treatment | Epoxy adhesive | - |
| Support method | Axial bearings | - |
| Parameter | Value | Units |
|---|---|---|
| Time step | adaptive | s |
| Turbulence model | realisable | - |
| WEC density | 574 | kg/m3 |
| Water-Air surface tension | 0.074 | mN/m |
| Scale | Height | Length () | Period () | |||
|---|---|---|---|---|---|---|
| 1:1 | 4.200 m | 30 m | 4.394 s | 0.0793 | 0.0222 | |
| 1:50 | 0.084 m | 0.6 m | 0.621 s | 0.0793 | 0.0222 | |
| 1:1 | 2.400 m | 30 m | 4.394 s | 0.0793 | 0.0127 | |
| 1:50 | 0.048 m | 0.6 m | 0.621 s | 0.0793 | 0.0127 | |
| 1:1 | 1.000 m | 30 m | 4.394 s | 0.0793 | 0.0053 | |
| 1:50 | 0.020 m | 0.6 m | 0.621 s | 0.0793 | 0.0053 |
| Zone | Boundary Condition |
|---|---|
| Top | Pressure Outlet |
| Inlet | Velocity Inlet and OCWBC |
| Outlet | Pressure Outlet and OCWBC |
| Walls and buoy | No-slip Wall |
| N° Ele/ | Scale | Mesh 1 | Mesh 2 | Mesh 3 | |||
|---|---|---|---|---|---|---|---|
| Total | Zone 1 | Total | Zone 1 | Total | Zone 1 | ||
| Case A | 1:1 | 9758 | 3955 | 13,292 | 5707 | 3736 | 23,575 |
| 1:50 | 350,334 | 142,026 | 664,648 | 285,439 | 2,007,075 | 1,270,300 | |
| Total | Zone 1 + 2 | Total | Zone 1 + 2 | Total | Zone 1 + 2 | ||
| Case B | 1:1 | 14,265 | 10,613 | 17,001 | 14,445 | 34,560 | 27,661 |
| 1:50 | 715,819 | 532,584 | 1,284,762 | 1,025,800 | 1,434,264 | 1,148,041 | |
| Scale | Wave | Mesh 1/Mesh 2 | Mesh 2/Mesh 3 | |
|---|---|---|---|---|
| Case A | 1:1 | 0.470% | 0.079% | |
| 0.036% | 0.109% | |||
| 0.107% | 1.152% | |||
| 1:50 | 0.016% | 0.202% | ||
| 0.014% | 0.021% | |||
| 1.041% | 0.434% | |||
| Case B | 1:1 | 0.035% | 0.452% | |
| 0.213% | 0.085% | |||
| 0.292% | 0.021% | |||
| 1:50 | 2.073% | 0.322% | ||
| 0.234% | 0.846% | |||
| 0.875% | 0.034% | |||
| Heave | 1:1 | 0.012% | 1.931% | |
| 0.134% | 0.705% | |||
| 0.383% | 0.473% | |||
| 1:50 | 2.076% | 0.854% | ||
| 0.348% | 0.034% | |||
| 0.871% | 0.084% |
| Parameter | Froude Scaling Ratio |
|---|---|
| Length | |
| Time | |
| Mass | |
| Power |
| Case A FSE | 1.09% | 0.58% | 3.05% |
| Case B FSE | 6.46% | 3.00% | 0.59% |
| Case B Heave | 38.0% | 30.0% | 56.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pierart, F.G.; Fernandez, J.; Olivos, J.; Gabl, R.; Davey, T. Numerical Investigation of the Scaling Effects for a Point Absorber. Water 2022, 14, 2156. https://doi.org/10.3390/w14142156
Pierart FG, Fernandez J, Olivos J, Gabl R, Davey T. Numerical Investigation of the Scaling Effects for a Point Absorber. Water. 2022; 14(14):2156. https://doi.org/10.3390/w14142156
Chicago/Turabian StylePierart, Fabián G., Joaquín Fernandez, Juan Olivos, Roman Gabl, and Thomas Davey. 2022. "Numerical Investigation of the Scaling Effects for a Point Absorber" Water 14, no. 14: 2156. https://doi.org/10.3390/w14142156







