Rainfall Runoff Balance Enhanced Model Applied to Tropical Hydrology
Abstract
1. Introduction
2. Materials and Methods
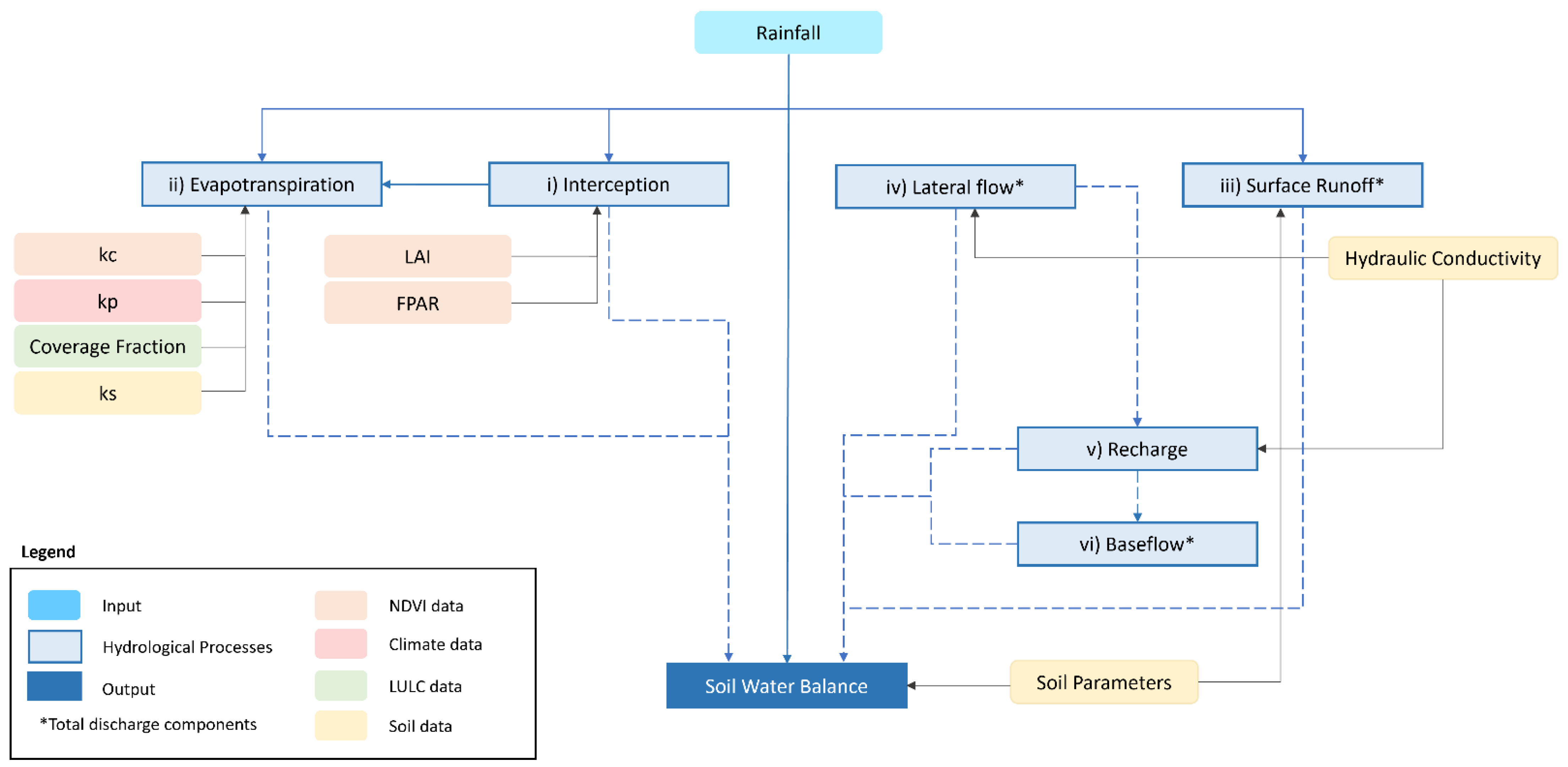
2.1. Model Overview
2.2. Model Development
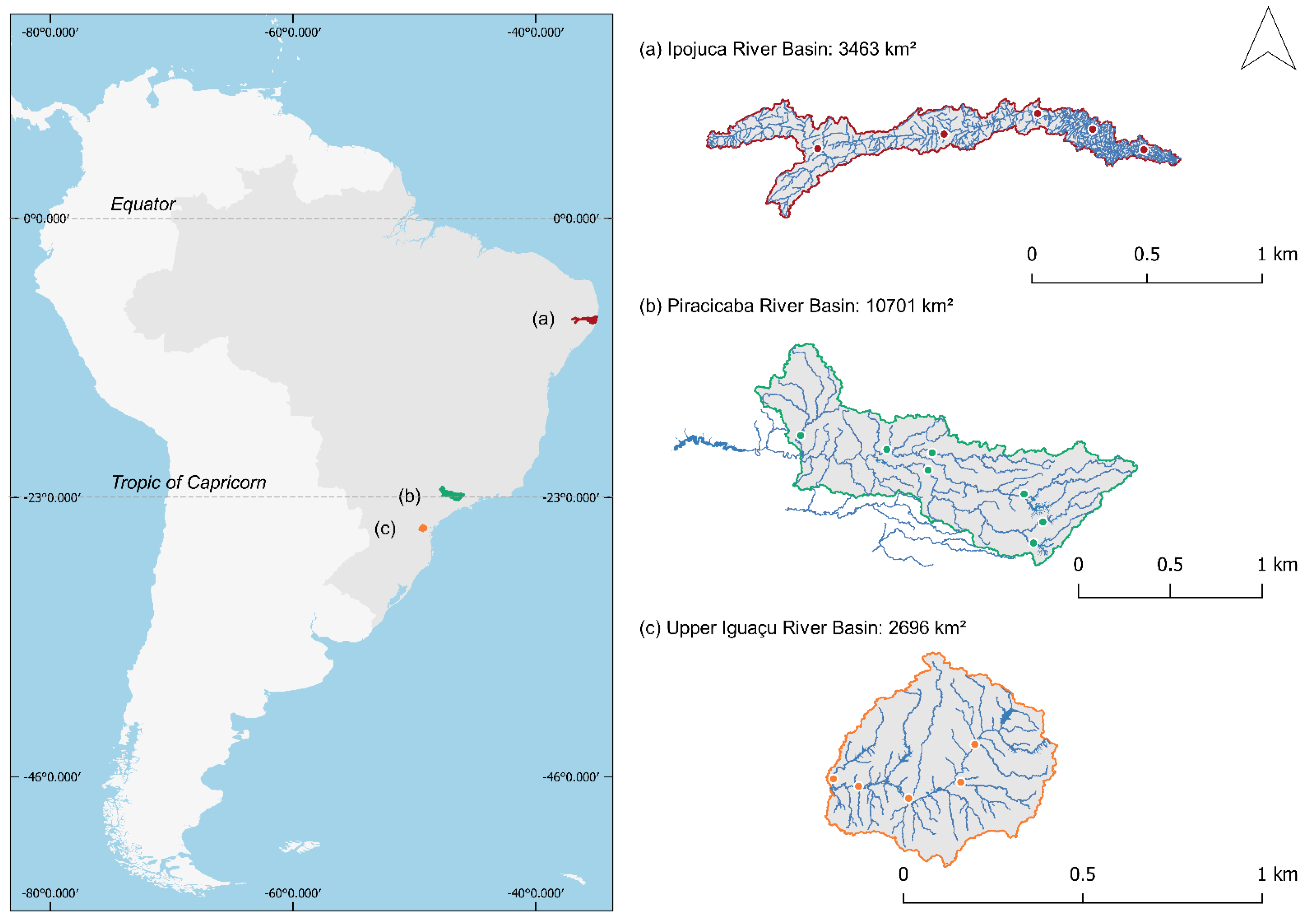
2.3. Model Aplication
2.4. Calibration and Validation
3. Results
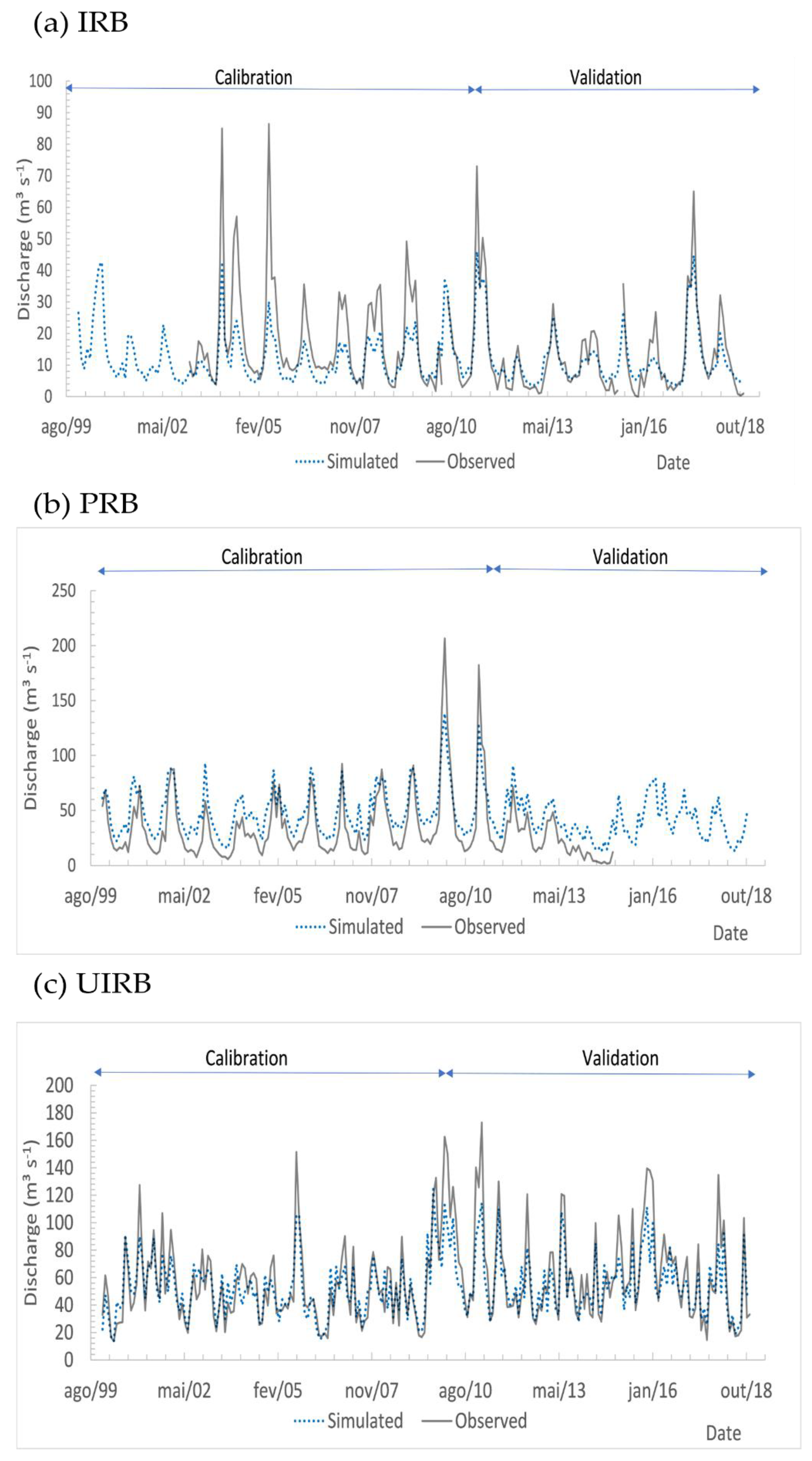
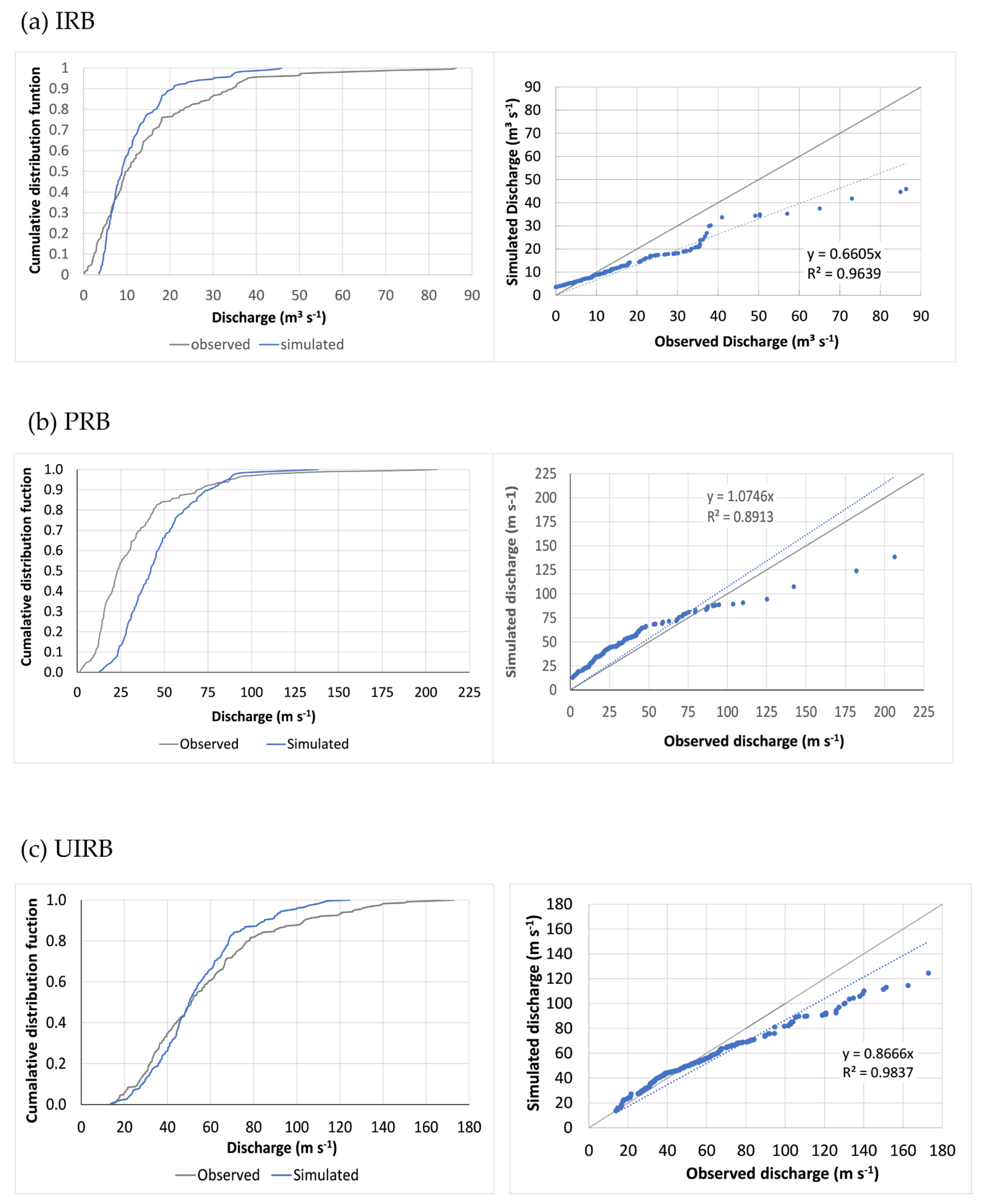
3.1. Calibration and Validation
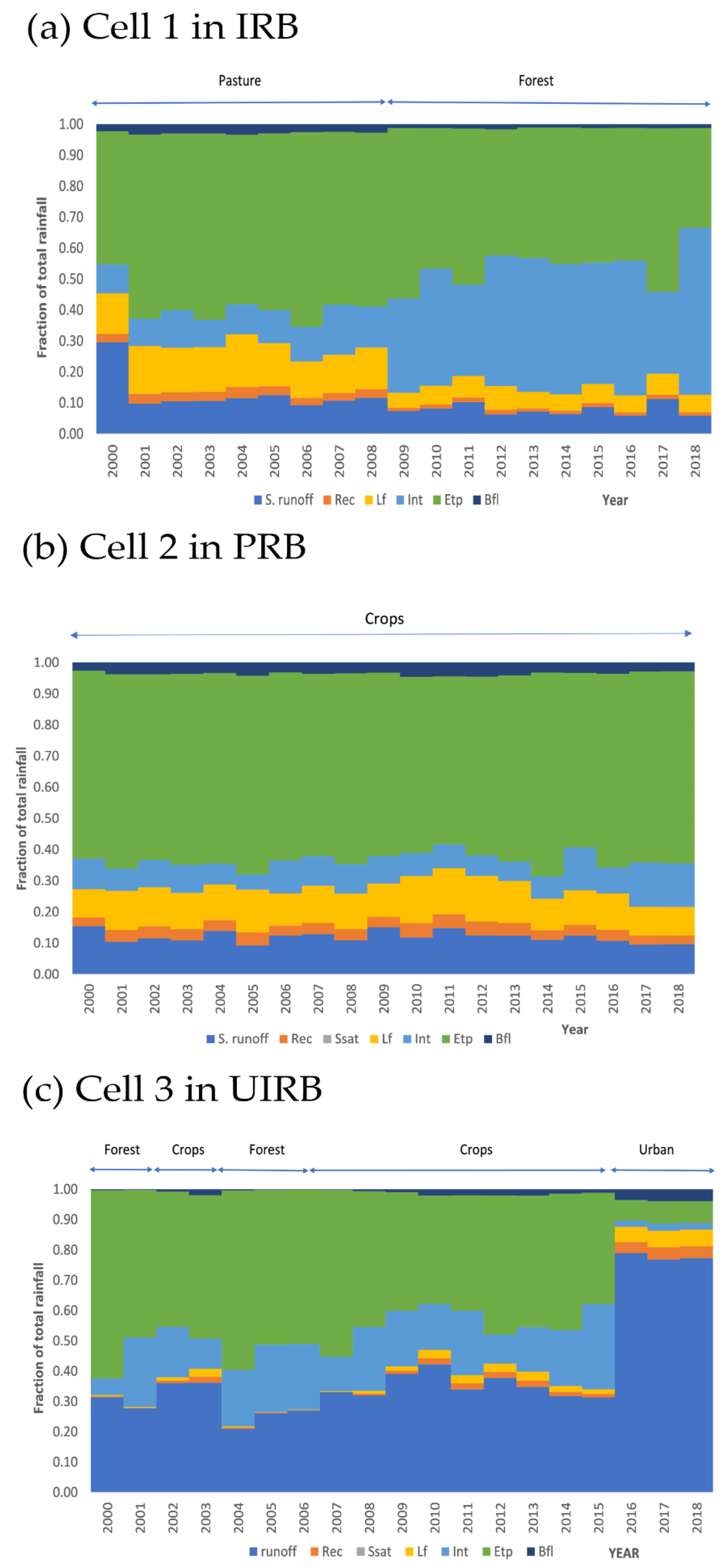
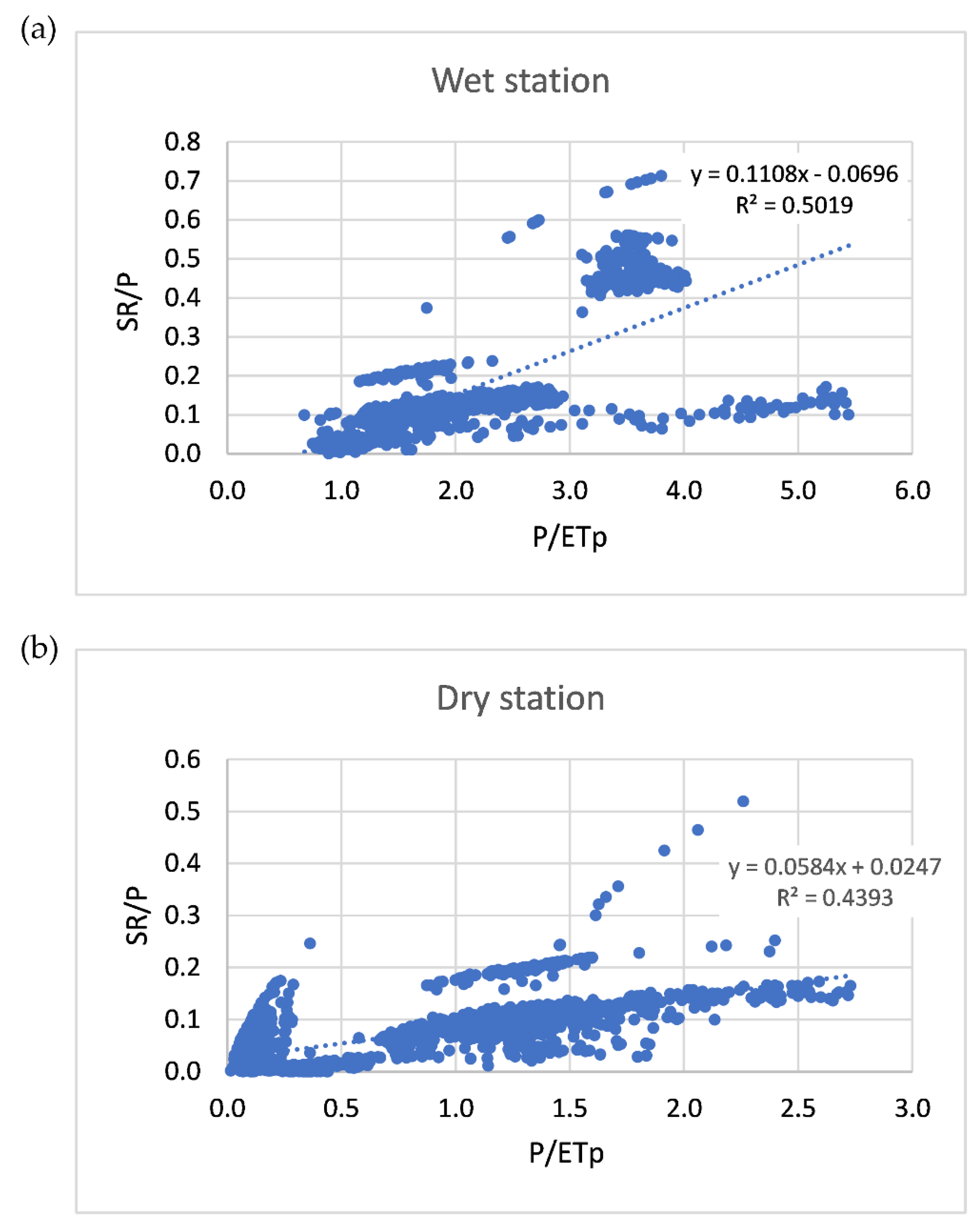
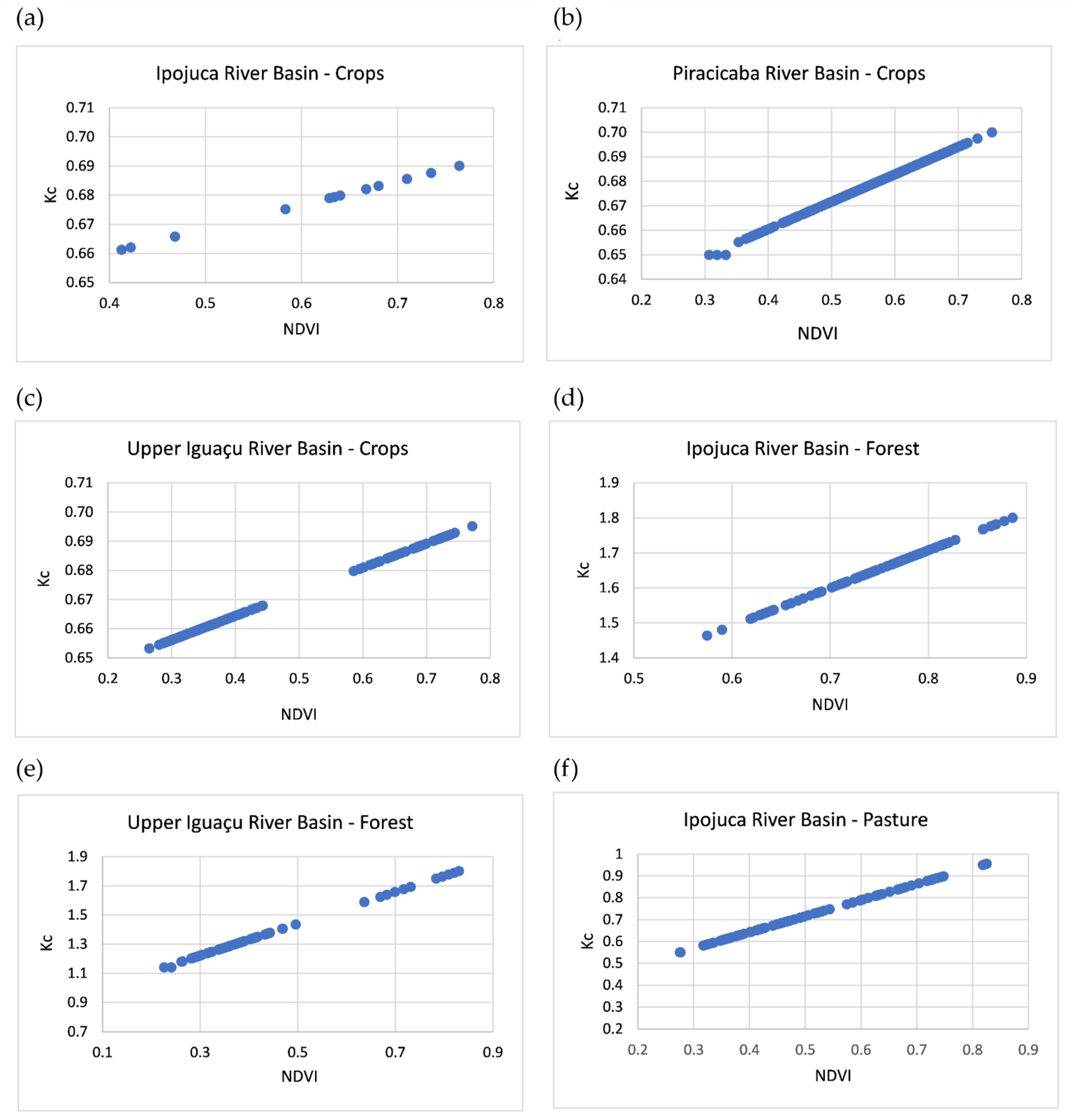
3.2. Soil and LULC Heterogeneities Analysis
4. Discussion
4.1. Calibration and Validation
4.2. Soil and LULC Heterogeneities
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Garg, V.; Nikam, B.R.; Thakur, P.K.; Aggarwal, S.P.; Gupta, P.K.; Srivastav, S.K. Human-Induced Land Use Land Cover Change and Its Impact on Hydrology. HydroResearch 2019, 1, 48–56. [Google Scholar] [CrossRef]
- Pokhrel, Y.; Burbano, M.; Roush, J.; Kang, H.; Sridhar, V.; Hyndman, D. A Review of the Integrated Effects of Changing Climate, Land Use, and Dams on Mekong River Hydrology. Water 2018, 10, 266. [Google Scholar] [CrossRef]
- Fendrich, A.N.; Barretto, A.; de Faria, V.G.; de Bastiani, F.; Tenneson, K.; Guedes Pinto, L.F.; Sparovek, G. Disclosing Contrasting Scenarios for Future Land Cover in Brazil: Results from a High-Resolution Spatiotemporal Model. Sci. Total Environ. 2020, 742, 140477. [Google Scholar] [CrossRef]
- Woolhiser, D.A. Search for Physically Based Runoff Model—A Hydrologic El Dorado? J. Hydraul. Eng. 1996, 122, 122–129. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A Simple Hydrologically Based Model of Land Surface Water and Energy Fluxes for General Circulation Models. J. Geophys. Res. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R.; King, K.W. Soil and Water Assessment Tool (SWAT) User’s Manual, Version 2000, Grassland Soil and Water Research Laboratory. Texas Water Resour. Institute Coll. Stn. 2002, 13, 52–55. [Google Scholar]
- Batelaan, O.; De Smedt, F. WetSpass: A Flexible, GIS Based, Distributed Recharge Methodology for Regional Groundwater Modelling. In Impact of Human Activity on Groundwater Dynamics; Gehrels, H., Peters, N.E., Hoehn, E., Jensen, K., Leibundgut, C., Griffioen, J., Webb, B., Zaadnoordijk, W.J., Eds.; IAHS Publication 269; IAHS Press: Wallingford, UK, 2001; pp. 11–18. ISBN 1-901502-56-2. [Google Scholar]
- Collischonn, W.; Allasia, D.; da Silva, B.C.; Tucci, C.E.M. The MGB-IPH Model for Large-Scale Rainfall-Runoff Modelling. Hydrol. Sci. J. 2007, 52, 878–895. [Google Scholar] [CrossRef]
- Yates, D.; Sieber, J.; Purkey, D.; Huber-Lee, A. WEAP21—A Demand-, Priority-, and Preference-Driven Water Planning Model. Part 1: Model Characteristics. Water Int. 2005, 30, 487–500. [Google Scholar] [CrossRef]
- Terink, W.; Lutz, A.F.; Simons, G.W.H.; Immerzeel, W.W.; Droogers, P. SPHY v2.0: Spatial Processes in HYdrology. Geosci. Model Dev. 2015, 8, 2009–2034. [Google Scholar] [CrossRef]
- Bierkensi, M.F.P.; Van Beek, L.P.H. Seasonal Predictability of European Discharge: NAO and Hydrological Response Time. J. Hydrometeorol. 2009, 10, 953–968. [Google Scholar] [CrossRef]
- Sperna Weiland, F.C.; Van Beek, L.P.H.; Kwadijk, J.C.J.; Bierkens, M.F.P. The Ability of a GCM-Forced Hydrological Model to Reproduce Global Discharge Variability. Hydrol. Earth Syst. Sci. 2010, 14, 1595–1621. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An Introduction to the European Hydrological System—Systeme Hydrologique Europeen, “SHE”, 2: Structure of a Physically-Based, Distributed Modelling System. J. Hydrol. 1986, 87, 61–77. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An Introduction to the European Hydrological System—Systeme Hydrologique Europeen, “SHE”, 1: History and Philosophy of a Physically-Based, Distributed Modelling System. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Refshaard, J.C.; Storm, B. MIKE SHE. Comput. Model. Watershed Hydrol. 1995, 3, 809–846. [Google Scholar]
- Oogathoo, S.; Prasher, S.O.; Rudra, R.; Patel, R.M. Calibration and Validation of the MIKE SHE Model in Canagagigue Creek Watershed. In Agricultural and Biosystems Engineering for a Sustainable World, Proceedings of the International Conference on Agricultural Engineering, Hersonissos, Greece, 23–25 June 2008; European Society of Agricultural Engineers (AgEng): Silsoe, UK, 2008. [Google Scholar]
- Shukla, M. Soil Hydrology, Land Use and Agriculture: Measurement and Modelling; CABI: Wallingford, UK, 2011; ISBN 978-1-84593-877-2. [Google Scholar]
- Wang, L.; Wang, Z.; Liu, C.; Bai, P.; Liu, X. A Flexible Framework Hydroinformatic Modeling System-HIMS. Water 2018, 10, 962. [Google Scholar] [CrossRef]
- Beven, K.; Calver, A.; Morris, E.M. The Institute of Hydrology Distributed Model; Report 98; Ministry of Agriculture, Fisheries and Food: Wallingford, UK, 1987.
- Kite, G.W.; Kouwen, N. Watershed Modeling Using Land Classifications. Water Resour. Res. 1992, 28, 3193–3200. [Google Scholar] [CrossRef]
- Ren-Jun, Z. The Xinanjiang Model Applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Van der Kwaak, J.E.; Loague, K. Hydrologic-Response Simulations for the R-5 Catchment with a Comprehensive Physics-Based Model. Water Resour. Res. 2001, 37, 999–1013. [Google Scholar] [CrossRef]
- Qu, Y.; Duffy, C.J. A Semidiscrete Finite Volume Formulation for Multiprocess Watershed Simulation. Water Resour. Res. 2007, 43, 5752. [Google Scholar] [CrossRef]
- Droogers, P.; Bouma, J. Simulation Modelling for Water Governance in Basins. Int. J. Water Resour. Dev. 2014, 30, 475–494. [Google Scholar] [CrossRef]
- Smith, M.B.; Seo, D.J.; Koren, V.I.; Reed, S.M.; Zhang, Z.; Duan, Q.; Moreda, F.; Cong, S. The Distributed Model Intercomparison Project (DMIP): Motivation and Experiment Design. J. Hydrol. 2004, 298, 4–26. [Google Scholar] [CrossRef]
- Smith, M.B.; Koren, V.; Zhang, Z.; Zhang, Y.; Reed, S.M.; Cui, Z.; Moreda, F.; Cosgrove, B.A.; Mizukami, N.; Anderson, E.A. Results of the DMIP 2 Oklahoma Experiments. J. Hydrol. 2012, 418–419, 17–48. [Google Scholar] [CrossRef]
- Moges, E.; Demissie, Y.; Larsen, L.; Yassin, F. Review: Sources of Hydrological Model Uncertainties and Advances in Their Analysis. Water 2021, 13, 28. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Peel, M.C.; Fowler, K.J.A.; Woods, R.A. A Brief Analysis of Conceptual Model Structure Uncertainty Using 36 Models and 559 Catchments. Water Resour. Res. 2020, 56, 5975. [Google Scholar] [CrossRef]
- Francke, T.; Baroni, G.; Brosinsky, A.; Foerster, S.; López-Tarazón, J.A.; Sommerer, E.; Bronstert, A. What Did Really Improve Our Mesoscale Hydrological Model? A Multidimensional Analysis Based on Real Observations. Water Resour. Res. 2018, 54, 8594–8612. [Google Scholar] [CrossRef]
- Clark, M.P.; Slater, A.G.; Rupp, D.E.; Woods, R.A.; Vrugt, J.A.; Gupta, H.V.; Wagener, T.; Hay, L.E. Framework for Understanding Structural Errors (FUSE): A Modular Framework to Diagnose Differences between Hydrological Models. Water Resour. Res. 2008, 44, 6735. [Google Scholar] [CrossRef]
- Fenicia, F.; McDonnell, J.J.; Savenije, H.H.G. Learning from Model Improvement: On the Contribution of Complementary Data to Process Understanding. Water Resour. Res. 2008, 44, 6386. [Google Scholar] [CrossRef]
- Wood, E.F.; Sivapalan, M.; Beven, K. Similarity and Scale in Catchment Storm Response. Rev. Geophys. 1990, 28, 1–18. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The Future of Distributed Models: Model Calibration and Uncertainty Prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Singh, V.P. Computer Models of Watershed Hydrology; Water Resources Publications: Littleton, CO, USA, 1995; ISBN 978-0-918334-91-6. [Google Scholar]
- Shaw, E.M.; Beven, K.J.; Chappell, N.A.; Lamb, R. Hydrology in Practice, 4th ed.; CRC Press: London, UK, 2017; ISBN 978-1-4822-6570-5. [Google Scholar]
- Richter, M. Tropical Forestry Handbook, 2nd ed.; Pancel, L., Kökl, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 285–291. ISBN 978-3-642-54601-3. [Google Scholar]
- Latrubesse, E.M.; Stevaux, J.C.; Sinha, R. Tropical Rivers. Geomorphology 2005, 70, 187–206. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL): 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.F.; Roerink, G.J.; Van Der Wal, T. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL): 2. Validation. J. Hydrol. 1998, 212–213, 213–229. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A Review of Global Terrestrial Evapotranspiration: Observation, Modeling, Climatology, and Climatic Variability. Rev. Geophys. 2012, 50, 373. [Google Scholar] [CrossRef]
- Hoegh-Guldberg, O.; Jacob, D.; Bindi, M.; Brown, S.; Camilloni, I.; Diedhiou, A.; Djalante, R.; Ebi, K.; Engelbrecht, F.; Guiot, J.; et al. Impacts of 1.5 °C Global Warming on Natural and Human Systems. In Global Warming of 1.5°C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; Special Report of the Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2018; pp. 175–311. [Google Scholar]
- Greve, P.; Gudmundsson, L.; Seneviratne, S.I. Regional Scaling of Annual Mean Precipitation and Water Availability with Global Temperature Change. Earth Syst. Dyn. 2018, 9, 227–240. [Google Scholar] [CrossRef]
- Singh, V.P.; Frevert, D.K. (Eds.) Watershed Models, 1st ed.; CRC Press: Boca Raton, FL, USA, 2006; pp. 3–19. ISBN 978-0-8493-3609-6. [Google Scholar]
- Sitterson, J.; Knightes, C.; Parmar, R.; Wolfe, K.; Avant, B.; Muche, M. An Overview of Rainfall-Runoff Model Types. In Proceedings of the 9th International Congress on Environmental Modelling & Software (iEMS 2018), Collins, CO, USA, 24–28 June 2018. [Google Scholar]
- Chow, V.T.; Albertson, M.L.; Ven Te Chow, P.D. Handbook of Applied Hydrology: A Compendium of Water-Resources Technology, 1st ed.; McGraw-Hill: New York, NY, USA, 1964; Volume 1, pp. 1–171. ISBN 978-0-07-010774-8. [Google Scholar]
- Abdollahi, K.; Bashir, I.; Verbeiren, B.; Harouna, M.R.; Van Griensven, A.; Huysmans, M.; Batelaan, O. A Distributed Monthly Water Balance Model: Formulation and Application on Black Volta Basin. Environ. Earth Sci. 2017, 76, 198. [Google Scholar] [CrossRef]
- Mello, C.R.; Ávila, L.F.; Lin, H.; Terra, M.C.N.S.; Chappell, N.A. Water Balance in a Neotropical Forest Catchment of Southeastern Brazil. Catena 2019, 173, 9–21. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements. In FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; Volume 300, ISBN 92-5-104219-5. [Google Scholar]
- Souza, C.M.; Shimbo, J.Z.; Rosa, M.R.; Parente, L.L.; Alencar, A.A.; Rudorff, B.F.T.; Hasenack, H.; Matsumoto, M.; Ferreira, L.G.; Souza-Filho, P.W.M.; et al. Reconstructing Three Decades of Land Use and Land Cover Changes in Brazilian Biomes with Landsat Archive and Earth Engine. Remote Sens. 2020, 12, 2735. [Google Scholar] [CrossRef]
- Smith, M.; Steduto, P. Yield Response to Water: The Original FAO Water Production Function. In FAO Irrigation and Drainage Paper 66; Food and Agriculture Organization of the United Nations: Rome, Italy, 2012; pp. 6–13. ISBN 978-92-5-107274-5. [Google Scholar]
- Kaboosi, K.; Kaveh, F. Sensitivity Analysis of FAO 33 Crop Water Production Function. Irrig. Sci. 2012, 30, 89–100. [Google Scholar] [CrossRef]
- Karssenberg, D.; Schmitz, O.; Salamon, P.; de Jong, K.; Bierkens, M.F.P. A Software Framework for Construction of Process-Based Stochastic Spatio-Temporal Models and Data Assimilation. Environ. Model. Softw. 2010, 25, 489–502. [Google Scholar] [CrossRef]
- Ottoni, M.V. HYBRAS Hydrophysical Database for Brazilian Soils: Banco de Dados Hidrofísicos em Solos no Brasil para o Desenvolvimento de Funções de Pedotransferências de Propriedades Hidráulicas: Ver. 1.0: Relatório; CPRM: Rio de Janeiro, Brazil, 2018; ISBN 978-85-7499-370-6. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance Evaluation of Hydrological Models: Statistical Significance for Reducing Subjectivity in Goodness-of-Fit Assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Machado, A.R. Alternativas de Restauração de Florestas Ripárias Para o Fornecimento de Serviços Ecossistêmicos. Ph.D. Thesis, Universidade de São Paulo, São Paulo, Brazil, 2017. [Google Scholar] [CrossRef]
- Olivos, L.M.O. Sustentabilidade do Uso dos Recursos Hídricos Superficiais e Subterrâneos no Município de São Carlos—SP. Master’s Dissertation, Universidade de São Paulo, São Paulo, Brazil, 2017. [Google Scholar] [CrossRef]
- McCuen, R.H.; Knight, Z.; Cutter, A.G. Evaluation of the Nash–Sutcliffe Efficiency Index. J. Hydrol. Eng. 2006, 11, 597–602. [Google Scholar] [CrossRef]
- O’Brien, T.P.; Sornette, D.; McPherron, R.L. Statistical Asynchronous Regression: Determining the Relationship between Two Quantities That Are Not Measured Simultaneously. J. Geophys. Res. Sp. Phys. 2001, 106, 13247–13259. [Google Scholar] [CrossRef]
- Tena, T.M.; Mwaanga, P.; Nguvulu, A. Hydrological Modelling and Water Resources Assessment of Chongwe River Catchment Using WEAP Model. Water 2019, 11, 839. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrological Modeling of the Iroquois River Watershed Using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- McCuen, R.H.; Snyder, W.M. A Proposed Index for Comparing Hydrographs. Water Resour. Res. 1975, 11, 1021–1024. [Google Scholar] [CrossRef]
- Fukunaga, D.C.; Cecílio, R.A.; Zanetti, S.S.; Oliveira, L.T.; Caiado, M.A.C. Application of the SWAT Hydrologic Model to a Tropical Watershed at Brazil. Catena 2015, 125, 206–213. [Google Scholar] [CrossRef]
- Bloomfield, J.P.; Allen, D.J.; Griffiths, K.J. Examining Geological Controls on Baseflow Index (BFI) Using Regression Analysis: An Illustration from the Thames Basin, UK. J. Hydrol. 2009, 373, 164–176. [Google Scholar] [CrossRef]
- Wagener, T.; Sivapalan, M.; Troch, P.; Woods, R. Catchment Classification and Hydrologic Similarity. Geogr. Compass 2007, 1, 901–931. [Google Scholar] [CrossRef]
- Bloomfield, J.P.; Bricker, S.H.; Newell, A.J. Some Relationships between Lithology, Basin Form and Hydrology: A Case Study from the Thames Basin, UK. Hydrol. Process. 2011, 25, 2518–2530. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic Implications of Dynamical and Statistical Approaches to Downscaling Climate Model Outputs. Clim. Change 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Dettinger, M.D.; Cayan, D.R.; Meyer, M.K.; Jeton, A. Simulated Hydrologic Responses to Climate Variations and Change in the Merced, Carson, and American River Basins, Sierra Nevada, California, 1900–2099. Clim. Change 2004, 62, 283–317. [Google Scholar] [CrossRef]
- Chen, C.; Kalra, A.; Ahmad, S. Hydrologic Responses to Climate Change Using Downscaled GCM Data on a Watershed Scale. J. Water Clim. Change 2019, 10, 63–77. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Ricard, S.; Bourdillon, R.; Roussel, D.; Turcotte, R. Global Calibration of Distributed Hydrological Models for Large-Scale Applications. J. Hydrol. Eng. 2013, 18, 719–721. [Google Scholar] [CrossRef]
- Te Linde, A.H.; Aerts, J.C.J.H.; Hurkmans, R.T.W.L.; Eberle, M. Comparing Model Performance of Two Rainfall-Runoff Models in the Rhine Basin Using Different Atmospheric Forcing Data Sets. Hydrol. Earth Syst. Sci. 2008, 12, 943–957. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale Issues in Hydrological Modelling: A Review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Almeida, C.T.; Oliveira-Júnior, J.F.; Delgado, R.C.; Cubo, P.; Ramos, M.C. Spatiotemporal Rainfall and Temperature Trends throughout the Brazilian Legal Amazon, 1973–2013. Int. J. Climatol. 2017, 37, 2013–2026. [Google Scholar] [CrossRef]
- Bressiani, D.D.A.; Gassman, P.W.; Fernandes, J.G.; Garbossa, L.H.P.; Srinivasan, R.; Bonumá, N.B.; Mendiondo, E.M. A Review of Soil and Water Assessment Tool (SWAT) Applications in Brazil: Challenges and Prospects. Int. J. Agric. Biol. Eng. 2015, 8, 1–27. [Google Scholar] [CrossRef]
- Butts, M.B.; Payne, J.T.; Kristensen, M.; Madsen, H. An Evaluation of the Impact of Model Structure on Hydrological Modelling Uncertainty for Streamflow Simulation. J. Hydrol. 2004, 298, 242–266. [Google Scholar] [CrossRef]
- Spieler, D.; Mai, J.; Craig, J.R.; Tolson, B.A.; Schütze, N. Automatic Model Structure Identification for Conceptual Hydrologic Models. Water Resour. Res. 2020, 56, 7009. [Google Scholar] [CrossRef]
- Dias, S.H.B.; Filgueiras, R.; Filho, E.I.F.; Arcanjo, G.S.; Da Silva, G.H.; Mantovani, E.C.; Da Cunha, F.F. Reference Evapotranspiration of Brazil Modeled with Machine Learning Techniques and Remote Sensing. PLoS ONE 2021, 16, e0245834. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, G.D.; Moraes, E.C.; Brunsell, N.A.; Shimabukuro, Y.E.; Mataveli, G.A.V.; dos Santos, T.V. Analysis of Precipitation and Evapotranspiration in Atlantic Rainforest Remnants in Southeastern Brazil from Remote Sensing Data. Trop. For.-Chall. Maint. Ecosyst. Serv. Manag. Landsc. 2016, 6, 93–112. [Google Scholar] [CrossRef]
- Santos, L.D.C.; José, J.V.; Alves, D.S.; Nitsche, P.R.; Reis, E.F.D.; Bender, F.D. Variabilidade Espaço-Temporal da Evapotranspiração e Precipitação para o Estado do Paraná. Rev. Ambient. Água 2017, 12, 743–759. [Google Scholar] [CrossRef]
- Kamble, B.; Kilic, A.; Hubbard, K. Estimating Crop Coefficients Using Remote Sensing-Based Vegetation Index. Remote Sens. 2013, 5, 1588–1602. [Google Scholar] [CrossRef]
- Duchemin, B.; Hadria, R.; Erraki, S.; Boulet, G.; Maisongrande, P.; Chehbouni, A.; Escadafal, R.; Ezzahar, J.; Hoedjes, J.C.B.; Kharrou, M.H.; et al. Monitoring Wheat Phenology and Irrigation in Central Morocco: On the Use of Relationships between Evapotranspiration, Crops Coefficients, Leaf Area Index and Remotely-Sensed Vegetation Indices. Agric. Water Manag. 2006, 79, 1–27. [Google Scholar] [CrossRef]
- Almeida, A.C.D.; Soares, J.V. Comparação Entre Uso de Água em Plantações de Eucalyptus Grandis e Floresta Ombrófila Densa (Mata Atlântica) na Costa Leste do Brasil. Rev. Árvore 2003, 27, 159–170. [Google Scholar] [CrossRef]
- Dorman, J.L.; Sellers, P.J. A Global Climatology of Albedo, Roughness Length and Stomatal Resistance for Atmospheric General Circulation Models as Represented by the Simple Biosphere Model (SiB). J. Appl. Meteorol. 1989, 28, 833–855. [Google Scholar] [CrossRef]
- Dieguez, J.; Smith, R. Flood Breach Analysis Using ArcMap & HEC-RAS 5.0; U.S. Department of Agriculture, Natural Resources Conservation Service: Nashville, TN, USA, 2016.
- Peng, D.; Zhang, B.; Liu, L. Comparing Spatiotemporal Patterns in Eurasian FPAR Derived from Two NDVI-Based Methods. Int. J. Digit. Earth 2012, 5, 283–298. [Google Scholar] [CrossRef]
- Profill-Rhama Consortium. Plano de Recursos Hídricos das Bacias Hidrográficas dos Rios Piracicaba, Capivari e Jundiaí, 2020 a 2035: Relatório Síntese; Technical Report for Comitês PCJ/Agência das Bacias PCJ: Piracicaba, Brazil, September 2020; ISBN 978-65-88688-01-4. Available online: https://plano.agencia.baciaspcj.org.br/o-plano/documentos/relat%C3%B3rio-final (accessed on 11 November 2020).
- RDR Consultores Associados. Plano das Bacias do Alto Iguaçu e Afluentes do Alto Ribeira: Relatório Técnico-v1. Technical Report for Superintendência de Desenvolvimento de Recursos Hídricos e Saneamento Ambiental do Estado do Paraná: Curitiba, Brazil; November 2007. Available online: https://www.iat.pr.gov.br/Pagina/Comite-das-Bacias-do-Alto-Iguacu-e-Afluentes-do-Alto-Ribeira-COALIAR (accessed on 11 November 2020).
- dos Santos, H.G.; de Junior, W.C.; de Dart, R.O.; Aglio, M.L.D.; de Souza, J.S.; Pares, J.G.; Fontana, A.; Martins, A.L.d.S.; de Oliveira, A.P. O Novo Mapa de Solos do Brasil: Legenda Atualizada. In Documentos 130; Embrapa Solos; Empresa Brasileira de Pesquisa Agropecuária: Rio de Janeiro, Brazil, 2011; Available online: https://ainfo.cnptia.embrapa.br/digital/bitstream/item/123772/1/DOC-130-O-novo-mapa-de-solos-do-Brasil.pdf (accessed on 29 September 2020).
- Azevedo, J.A. Relações Físico-Hídricas em Solos de Terraço e de Meia Encosta de Viçosa (MG). Master’s Thesis, Universidade Federal de Viçosa, Viçosa, Brazil, 1976. [Google Scholar]
- Moreira, J.A.A.; Silva, C.J.C.G.d. Características de retenção de água de um solo Podzólico Vermelho-Amarelo de Goiana, Pernambuco. Pesq. Agropec. Bras. 1987, 22, 411–418. [Google Scholar]
- Ottoni, M.V. Classificação Físico-Hídrica de Solos e Determinação da Capacidade de Campo In Situ a Partir de Testes de Infiltração. Master’s Thesis, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil, October 2005. Available online: https://rigeo.cprm.gov.br/handle/doc/301 (accessed on 2 June 2020).
- Souza, L.D.S.; Souza, L.D.; Centro Nacional de Pesquisa de Mandioca e Fruticultura Tropical. Caracterização físico-hídrica de solos da área do Centro Nacional de Pesquisa de Mandioca e Fruticultura Tropical. In Boletim de Pesquisa e Desenvolvimento 20; Empresa Brasileira de Pesquisa Agropecuária: Cruz das Almas, Brazil, 2001; pp. 5–56. [Google Scholar]
- Cooper, M.; Medeiros, J.C.; Rosa, J.D.; Soria, J.E.; Toma, R.S. Soil Functioning in a Toposequence under Rainforest in São Paulo, Brazil. Rev. Bras. Ciência Do Solo 2013, 37, 392–399. [Google Scholar] [CrossRef]
- da Silva, M.A.S.; Mafra, Á.L.; Albuquerque, J.A.; Bayer, C.; Mielniczuk, J. Atributos Físicos Do Solo Relacionados Ao Armazenamento de Água Em Um Argissolo Vermelho Sob Diferentes Sistemas de Preparo. Ciência Rural. 2005, 35, 544–552. [Google Scholar] [CrossRef]
- Toma, R.S. Evolução do Funcionamento Físico-Hídrico do Solo em Diferentes Sistemas de Manejo em Áreas de Agricultura Familiar na Região do Vale do Ribeira, SP. Ph.D. Thesis, Universidade de São Paulo, São Paulo, Brazil, July 2012. [Google Scholar] [CrossRef]
- Leal, I.F. Classificação e Mapeamento Físico-Hídrico de Solos do Assentamento Agrícola Sebastião Lan II, Silva Jardim – RJ. Master’s Thesis, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil, March 2011. Available online: http://objdig.ufrj.br/60/teses/coppe_m/IsaiasFagundesLeal.pdf (accessed on 16 June 2020).
- Ferreira, I.C.D.M. Associações Entre Solos e Remanescentes de Vegetação Nativa em Campinas, SP. Master’s Thesis, Instituo Agronômico, Campinas, Brazil, April 2007. Available online: http://www.iac.sp.gov.br/areadoinstituto/posgraduacao/repositorio/storage/pb1203705.pdf (accessed on 16 June 2020).
- Nebel, Á.L.C.; Timm, L.C.; Cornelis, W.; Gabriels, D.; Reichardt, K.; Aquino, L.S.; Pauletto, E.A.; Reinert, D.J. Pedotransfer Functions Related to Spatial Variability of Water Retention Attributes for Lowland Soils. Rev. Bras. Cienc. Do Solo 2010, 34, 669–680. [Google Scholar] [CrossRef][Green Version]
- Marques, J.D.d.O.; Teixeira, W.G.; Reis, A.M.; Junior, O.F.C.; Batista, S.M.; Afonso, M.A.C.B. Atributos Químicos, Físico-Hídricos e Mineralogia da Fração Argila em Solos do Baixo Amazonas: Serra de Parintins. Acta Amaz. 2010, 40, 1–12. [Google Scholar] [CrossRef]
- Andrade, R.d.S.; Stone, L.F. Uso do Índice S da Determinação da Condutividade Hidráulica Não-Saturada de Solos do Cerrado Brasileiro. Rev. Bras. Eng. Agrícola Ambient. 2009, 13, 376–381. [Google Scholar] [CrossRef]
- Araujo-Junior, C.F.; Dias Junior, M.S.; Guimarães, P.T.G.; Alcântara, E.N. Sistema Poroso e Capacidade de Retenção de Água em Latossolo Submetido a Diferentes Manejos de Plantas Invasoras em uma Lavoura Cafeeira. Planta Daninha 2011, 29, 499–513. [Google Scholar] [CrossRef]
- Serviço Nacional de Levantamento e Conservação de Solos; Empresa Brasileira de Pesquisa Agropecuária; Ministério da Agricultura, Pecuária e Abastecimento, BR; Food and Agriculture Organization of the United Nations. Caracterização Físico Hídrica dos Principais Solos da Amazônia Legal: I Estado do Pará; Empresa Brasileira de Pesquisa Agropecuária: Belém, Brazil, 1991.
- Rosseti, R.A.C. Estimativa da Capacidade de Campo e do Ponto de Murcha Permanente por Meio de Pedofunções para o Centro Sul de Mato Grosso. Master’s Thesis, Universidade Federal de Mato Grosso, Cuiabá, Brazil, December 2017. Available online: https://www.ufmt.br/ppgat/images/uploads/Dissertações-Teses/Dissertações/2017/DISSERTAÇÃO-RAFAELROSSETI.pdf (accessed on 10 June 2020).
- Spera, S.; Reatto, A.; Martins, É.; Correia, J.; Cunha, T.; Embrapa Cerrados. Solos Areno-Quarzosos no Cerrado: Problemas, Características e Limitação ao Uso. In Documentos 7; Empresa Brasileira de Pesquisa Agropecuária: Planaltina, Brazil, 1999; Available online: https://ainfo.cnptia.embrapa.br/digital/bitstream/item/101733/1/doc-07.pdf (accessed on 10 June 2020).
- Souza, M.S. de Caracterização do Intervalo Hídrico Ótimo de Três Solos da Região Norte Fluminense. Master’s Thesis, Universidade Estadual do Norte Fluminense Darcy Ribeiro, Campos dos Goytacazes, Brazil, April 2004. Available online: https://uenf.br/ccta/lsol/files/2018/03/Marcelo-Sobreira-de-Souza-Prof.-Cl%c3%a1udio.pdf (accessed on 10 June 2020).
- Parahyba, R.d.B.V. Geoambientes, Litotopossequências e Características Físico-Hídricas de Solos Arenosos da Bacia do Tucano, Bahia. Ph.D. Thesis, Universidade Federal de Pernambuco, Recife, Brazil, January 2013. Available online: https://repositorio.ufpe.br/handle/123456789/10683 (accessed on 16 June 2020).
- Scopel, I.; Sousa, M.S.; Peixinho, D.M. Uso e Manejo de Solos Arenosos e Recuperação de Áreas Degradadas com Areais no Sudoeste Goiano. Research Report: Jataí, Brazil. September 2011. Available online: https://geoinfo.jatai.ufg.br/p/20548-avaliacao-e-controle-das-areas-degradadas-com-areais-no-sudoeste-goiano (accessed on 24 June 2020).
- Ruiz, H.A.; Ferreira, G.B.; Pereira, J.B.M. Estimativa da Capacidade de Campo de Latossolos e Neossolos Quartzarênicos pela Determinação do Equivalente de Umidade. Rev. Bras. Ciência Do Solo 2003, 27, 389–393. [Google Scholar] [CrossRef][Green Version]
- Scardua, R. Porosidade Livre de Água de Dois Solos do Município de Piracicaba, SP. Master’s Thesis, Universidade de São Paulo, São Paulo, Brazil, 1972. [Google Scholar]
- Costa, A.C.S.d. Balanço Hídrico das Culturas de Feijão (Phaseolus vulgaris, L.) e Milho (Zea mays, L.) em Condições de Campo. Master’s Thesis, Universidade de São Paulo, São Paulo, Brazil, 1986. [Google Scholar]
- de Sousa, J.R.; Queiroz, J.E.; Gheyi, H.R. Variabilidade Espacial de Características Físico-Hídricas e de Água Disponível em um Solo Aluvial no Semi-Árido Paraibano. Rev. Bras. Eng. Agrícola Ambient. 1999, 3, 140–144. [Google Scholar] [CrossRef]
- Grego, C.R.; Coelho, R.M.; Vieira, S.R. Critérios Morfológicos e Taxonômicos de Latossolo e Nitossolo Validados por Propriedades Físicas Mensuráveis Analisadas em Parte pela Geoestatística. Rev. Bras. Cienc. Do Solo 2011, 35, 337–350. [Google Scholar] [CrossRef]
- Vasconcellos, E.B. Levantamento dos Atributos Físicos e Hídricos de Três Solos de Várzea do Rio Grande do Sul. Master’s Thesis, Universidade Federal de Pelotas, Pelotas, Brazil, 1983. [Google Scholar]
- Costa, A.E.M.d. Quantificação de Atributos Físico de Solos de Várzea, Relacionados com a Disponibilidade de Água, o Espaço Aéreo e a Consistência do Solo. Master’s Thesis, Universidade Federal de Pelotas, Pelotas, Brazil, 1993. [Google Scholar]
- Parfitt, J.M.B. Impacto da Sistematização Sobre Atributos Físicos, Químicos e Biológico em Solos de Várzea. Ph.D. Thesis, Universidade Federal de Pelotas, Pelotas, Brazil, June 2009. Available online: http://guaiaca.ufpel.edu.br/handle/123456789/2452 (accessed on 30 April 2021).
- Rossi, M.; Mattos, I.F.A. Solos de Mangue do Estado de São Paulo: Caracterização Química e Física. Geogr. Dep. Univ. Sao Paulo 2002, 15, 101–113. [Google Scholar] [CrossRef]
- de Aguiar, M.I. Qualidade Física do Solo em Sistemas Agroflorestais. Master’s Thesis, Universidade Federal de Viçosa, Viçosa, Brazil, February 2008. Available online: https://www.locus.ufv.br/handle/123456789/5396 (accessed on 30 April 2021).
- Rojas, C.A.L.; Lier, Q.d.J.V. Alterações Físicas e Hídricas de um Podzólico em Função de Sistemas de Preparo. Pesqui. Agropecuária Gaúcha 1999, 5, 105–115. [Google Scholar]
- Macedo, J.R.d.; Otonni Filho, T.B.; Meneguelli, N.D.A. Variabilidade de Características Físicas, Químicas e Físico-Hídricas em Solo Podzólico Vermelho-Amarelo de Seropédica, RJ. Pesqui. Agropecu. Bras. 1998, 33, 2043–2053. [Google Scholar]
- Juhász, C.E.P.; Cooper, M.; Cursi, P.R.; Ketzer, A.O.; Toma, R.S. Savanna Woodland Soil Micromorphology Related to Water Retention. Sci. Agric. 2007, 64, 344–354. [Google Scholar] [CrossRef]
- Carducci, C.E.; de Oliveira, G.C.; Severiano, E.d.C.; Zeviani, W.M. Modelagem da Curva de Retenção de Água de Latossolos Utilizando a Equação Duplo Van Genuchten. Rev. Bras. Ciência Do Solo 2011, 35, 77–86. [Google Scholar] [CrossRef]
- Souto Filho, S.N. Variação de Armazenagem de Água num Latossolo de Cerrado em Recuperação. Master’s Thesis, Universidade Estadual Paulista, São Paul, Brazil, February 2012. Available online: https://repositorio.unesp.br/handle/11449/98800 (accessed on 26 October 2020).
- Scheer, M.B.; Curcio, G.R.; Roderjan, C.V. Funcionalidades Ambientais de Solos Altomontanos na Serra da Igreja, Paraná. Rev. Bras. Cienc. Do Solo 2011, 35, 1113–1126. [Google Scholar] [CrossRef]
- Jensen, J.R. Sensoriamento Remoto do Ambiente-Uma Perspectiva em Recursos Terrestres, 2nd ed.; Parêntese: São José dos Campos, Brazil, 2009; ISBN 978-85-60507-06-1. [Google Scholar]
- Projetec Consortium. Plano Hidroambiental da Bacia Hidrográfica do rio Ipojuca: TOMO I–Diagnóstico Hidroambiental. Technical Report for Secretaria de Recursos Hídricos do Estado de Pernambuco: Recife, Brazil; 2010. Available online: http://www.sirh.srh.pe.gov.br/hidroambiental/files/ipojuca/ (accessed on 1 February 2021).
| Data | Description | Type | Source |
|---|---|---|---|
| Hydrological | Historic rainfall and runoff, monthly rainy days | Raster (.map or .tif) and tabular (.txt) | National Water Agency (ANA)–Hidroweb |
| Climate | Historic evapotranspiration and Class A Pan coefficient (kp) | Raster (.map or .tif) | National Water Agency (ANA)–Hidroweb |
| Soil | Soil types used for aquifer recharge calculation | Raster (.map or .tif) | CPRM HYBRAS [54] |
| Ground Elevation (DEM) | Digital Elevation Model used to calculate Local Drain Direction (LDD) | Raster (.map or .tif) | NASADEM |
| LULC | Land Use and Land Cover Data, area fractions and Manning’s Roughness Coefficient | Raster (.map or .tif) and tabular (.txt) | MapBiomas |
| NDVI | Normalized Difference Vegetation Index used in evapotranspiration’s calculation | Raster (.map or .tif) | MODIS |
| Parameter | Description | Restriction |
|---|---|---|
| Interception Parameter (α) | The interception parameter value. It represents the daily interception threshold that depends on land use. | 0.01 ≤ α ≤ 10 |
| Parameter related to Soil Moisture (b) | Exponent value that represents the effect of the condition of moisture in the soil. | 0.01 ≤ b ≤ 1 |
| Land Use Factor Weight (w1) | Weight of land-use factor. It measures the effect of the land use on the potential runoff produced. | w1+ w2+ w3 = 1 |
| Moisture Soil Factor Weight (w2) | Weight of moisture soil factor in the permanent wilting point. It measures the effect of the soil classes on the potential surface runoff produced. | w1+w2+ w3 = 1 |
| Slope Factor Weight (w3) | Weight of slope factor. It measures the effect of the slope on the potential runoff produced. | w1+w2+ w3 = 1 |
| Regional Consecutive Dryness Level (RCD) | Regional Consecutive Dryness level incorporates the intensity of rain and the number of consecutive days in runoff calculation. | 1 ≤ RCD ≤ 10 |
| Flow Direction Factor (f) | It is used to partition the flow out of the root zone between interflow and flow to the saturated zone. | 0.01 ≤ f ≤ 1 |
| Baseflow Recession Coefficient (αgw) | Decimal value refers to the recession coefficient of the baseflow. The lower values show areas that react slowly to groundwater drainage, while the higher values show areas that react rapidly. | 0.01 ≤ αgw ≤ 1 |
| Flow Recession Coefficient (x) | Flow recession coefficient value incorporates a flow delay in the accumulated amount of water that flows out of the cell into its neighboring downstream cell (0 means that during a month with no rainfall, there will be no surface runoff). | 0 ≤ x ≤ 1 |
| Parameter | IRB | PRB | UIRB |
|---|---|---|---|
| Interception parameter (α) | 4.415 | 1.049 | 9.771 |
| Parameter related to soil moisture (b) | 0.078 | 0.152 | 0.181 |
| Land use factor weight (w1) | 0.51 | 0.47 | 0.46 |
| Soil factor weight (w2) | 0.12 | 0.35 | 0.43 |
| Slope factor weight (w3) | 0.37 | 0.18 | 0.11 |
| Regional Consecutive Dryness level (RCD) | 5.375 | 7.957 | 8.342 |
| Flow direction factor (f) | 0.581 | 0.767 | 0.831 |
| Baseflow recession coefficient (αgw) | 0.922 | 0.782 | 0.552 |
| Flow recession coefficient (x) | 0.307 | 0.219 | 0.107 |
| Basin | Area (km2) | Calibration Period | Validation Period | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| N | SD | RMSE | NSE | RB | N | SD | RMSE | NSE | RB | ||
| IRB | 672 | 58 | 3.357 | 3.078 | 0.159 | 0.315 | 80 | 0.194 | 1.528 | −61.2 | 12.71 |
| 2000 | 100 | 6.517 | 4.225 | 0.58 | 0.781 | 104 | 3.316 | 1.123 | 0.885 | 2.041 | |
| 2650 | 105 | 7.145 | 5.355 | 0.438 | 0.818 | 68 | 6.712 | 6.258 | 0.131 | 1.03 | |
| 2960 | 117 | 11.285 | 6.847 | 0.632 | 0.01 | 104 | 9.328 | 5.057 | 0.706 | 0.342 | |
| 3310 | 82 | 16.144 | 12.32 | 0.417 | −0.397 | 105 | 9.070 | 5.355 | 0.652 | 0.007 | |
| PRB | 358 | 120 | 2.409 | 1.494 | 0.615 | −0.238 | 96 | 3.183 | 1.849 | 0.663 | −0.01 |
| 431 | 120 | 3.539 | 1.846 | 0.728 | 0.056 | 96 | 4.090 | 2.341 | 0.672 | 0.104 | |
| 928 | 82 | 10.073 | 6.552 | 0.577 | −0.227 | 56 | 11.602 | 6.541 | 0.682 | −0.18 | |
| 1350 | 120 | 12.113 | 7.541 | 0.612 | −0.205 | 96 | 13.906 | 9.601 | 0.523 | 0.22 | |
| 1580 | 105 | 16.493 | 9.327 | 0.68 | −0.134 | 40 | 15.834 | 9.575 | 0.634 | −0.2 | |
| 2490 | 85 | 13.245 | 9.923 | 0.439 | 0.41 | 60 | 22.769 | 9.874 | 0.812 | 0.23 | |
| 3400 | 120 | 23.524 | 17.47 | 0.448 | 0.468 | 60 | 39.926 | 21.303 | 0.715 | 0.348 | |
| UIRB | 231 | 120 | 2.468 | 1.423 | 0.667 | −0.005 | 60 | 3.235 | 1.709 | 0.721 | −0.09 |
| 272 | 120 | 3.913 | 2.928 | 0.44 | −0.226 | 56 | 2.547 | 2.723 | −0.142 | −0.23 | |
| 564 | 120 | 4.401 | 4.587 | −0.09 | 0.48 | 62 | 5.683 | 3.395 | 0.643 | 0.177 | |
| 1930 | 120 | 21.904 | 11.62 | 0.719 | −0.078 | 25 | 22.625 | 8.411 | 0.862 | −0.29 | |
| 2330 | 120 | 26.250 | 13.37 | 0.741 | −0.027 | 108 | 22.702 | 8.072 | 0.874 | −0.14 | |
| Coverage | Basin | Season | |||
|---|---|---|---|---|---|
| Wet | Dry | ||||
| N. Cells | r | N. Cells | R | ||
| IRB | 12 | 11 | |||
| Forest | PRB | 245 | 0.77 | 251 | 0.72 |
| UIRB | 83 | 84 | |||
| IRB | 82 | 72 | |||
| Savanna | PRB | 1 | 0.63 | 2 | 0.85 |
| UIRB | - | - | |||
| IRB | 166 | 168 | |||
| Pasture | PRB | 358 | 0.76 | 144 | 0.90 |
| UIRB | 31 | 31 | |||
| IRB | 24 | 26 | |||
| Crop | PRB | 167 | 0.55 | 181 | 0.74 |
| UIRB | 41 | 41 | |||
| IRB | 25 | 29 | |||
| Agriculture and Pasture | PRB | 153 | 0.53 | 135 | 0.75 |
| UIRB | 28 | 29 | |||
| IRB | 7 | 10 | |||
| Urban | PRB | 61 | 0.98 | 67 | 0.86 |
| UIRB | 59 | 56 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Méllo Júnior, A.V.; Olivos, L.M.O.; Billerbeck, C.; Marcellini, S.S.; Vichete, W.D.; Pasetti, D.M.; da Silva, L.M.; Soares, G.A.d.S.; Tercini, J.R.B. Rainfall Runoff Balance Enhanced Model Applied to Tropical Hydrology. Water 2022, 14, 1958. https://doi.org/10.3390/w14121958
Méllo Júnior AV, Olivos LMO, Billerbeck C, Marcellini SS, Vichete WD, Pasetti DM, da Silva LM, Soares GAdS, Tercini JRB. Rainfall Runoff Balance Enhanced Model Applied to Tropical Hydrology. Water. 2022; 14(12):1958. https://doi.org/10.3390/w14121958
Chicago/Turabian StyleMéllo Júnior, Arisvaldo Vieira, Lina Maria Osorio Olivos, Camila Billerbeck, Silvana Susko Marcellini, William Dantas Vichete, Daniel Manabe Pasetti, Ligia Monteiro da Silva, Gabriel Anísio dos Santos Soares, and João Rafael Bergamaschi Tercini. 2022. "Rainfall Runoff Balance Enhanced Model Applied to Tropical Hydrology" Water 14, no. 12: 1958. https://doi.org/10.3390/w14121958
APA StyleMéllo Júnior, A. V., Olivos, L. M. O., Billerbeck, C., Marcellini, S. S., Vichete, W. D., Pasetti, D. M., da Silva, L. M., Soares, G. A. d. S., & Tercini, J. R. B. (2022). Rainfall Runoff Balance Enhanced Model Applied to Tropical Hydrology. Water, 14(12), 1958. https://doi.org/10.3390/w14121958







