LSTM-Based Model for Predicting Inland River Runoff in Arid Region: A Case Study on Yarkant River, Northwest China
Abstract
:1. Introduction
2. Methods and Data Sources
2.1. Study Area
2.2. Data Sources
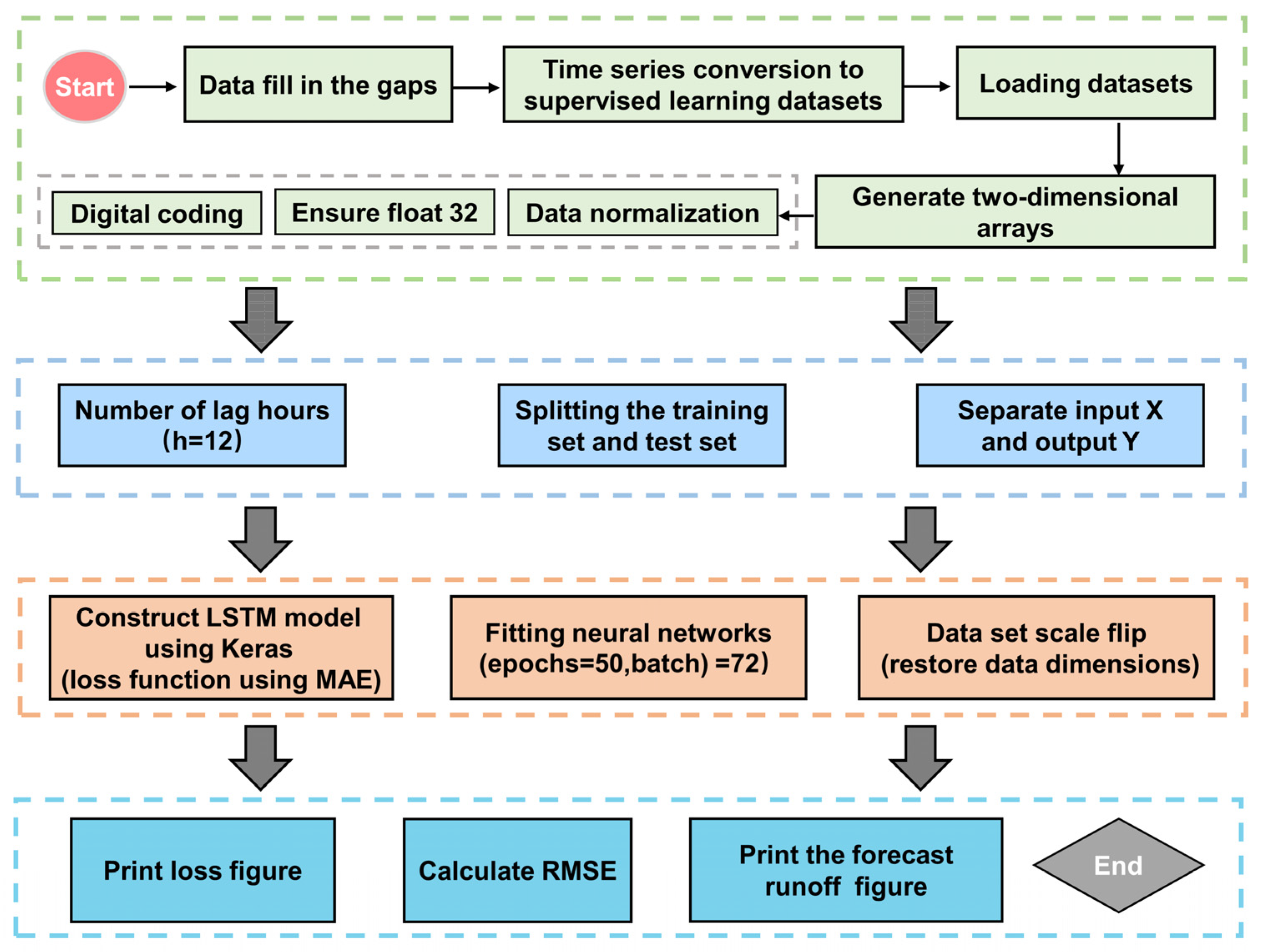
2.3. Methods
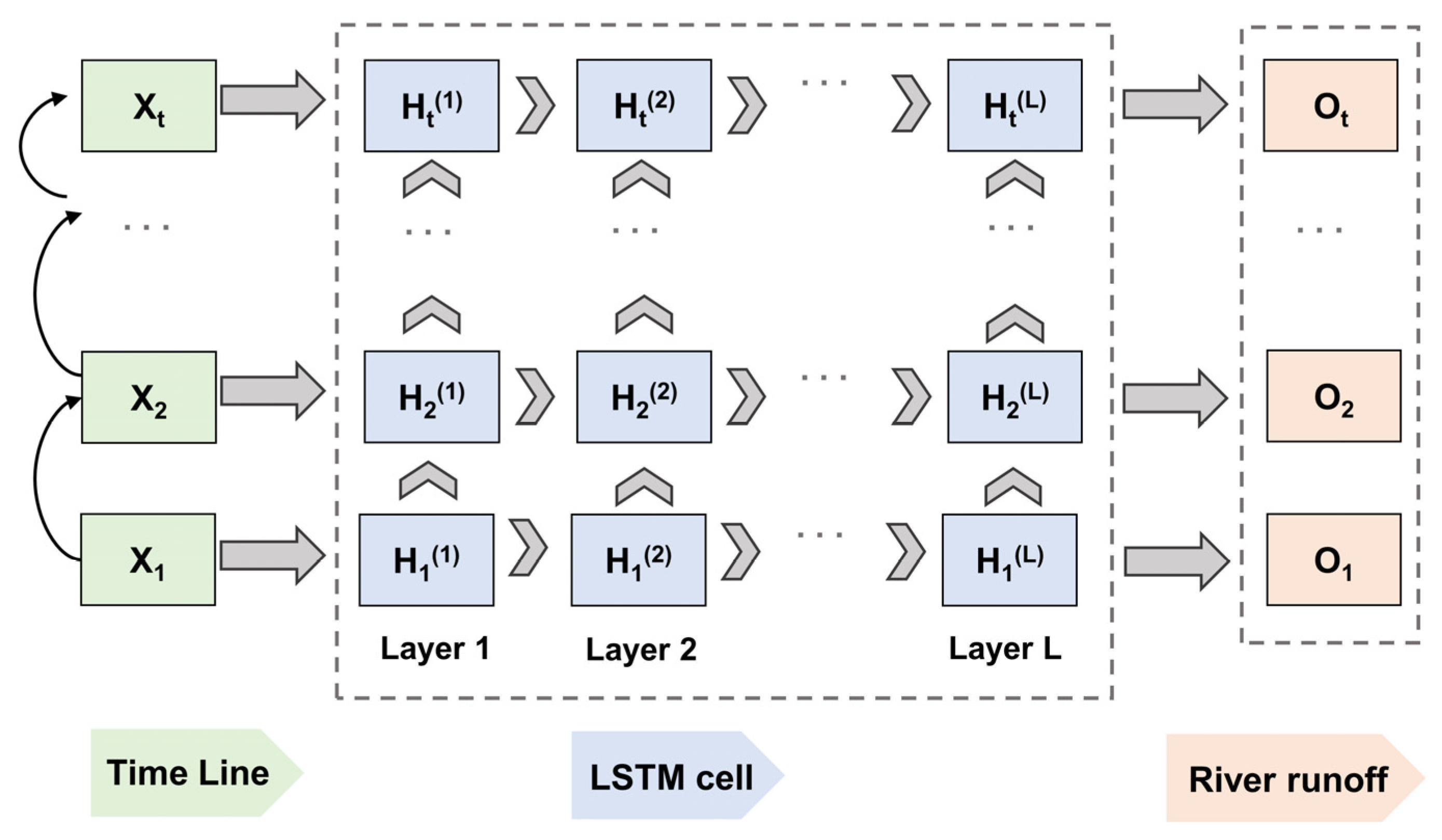
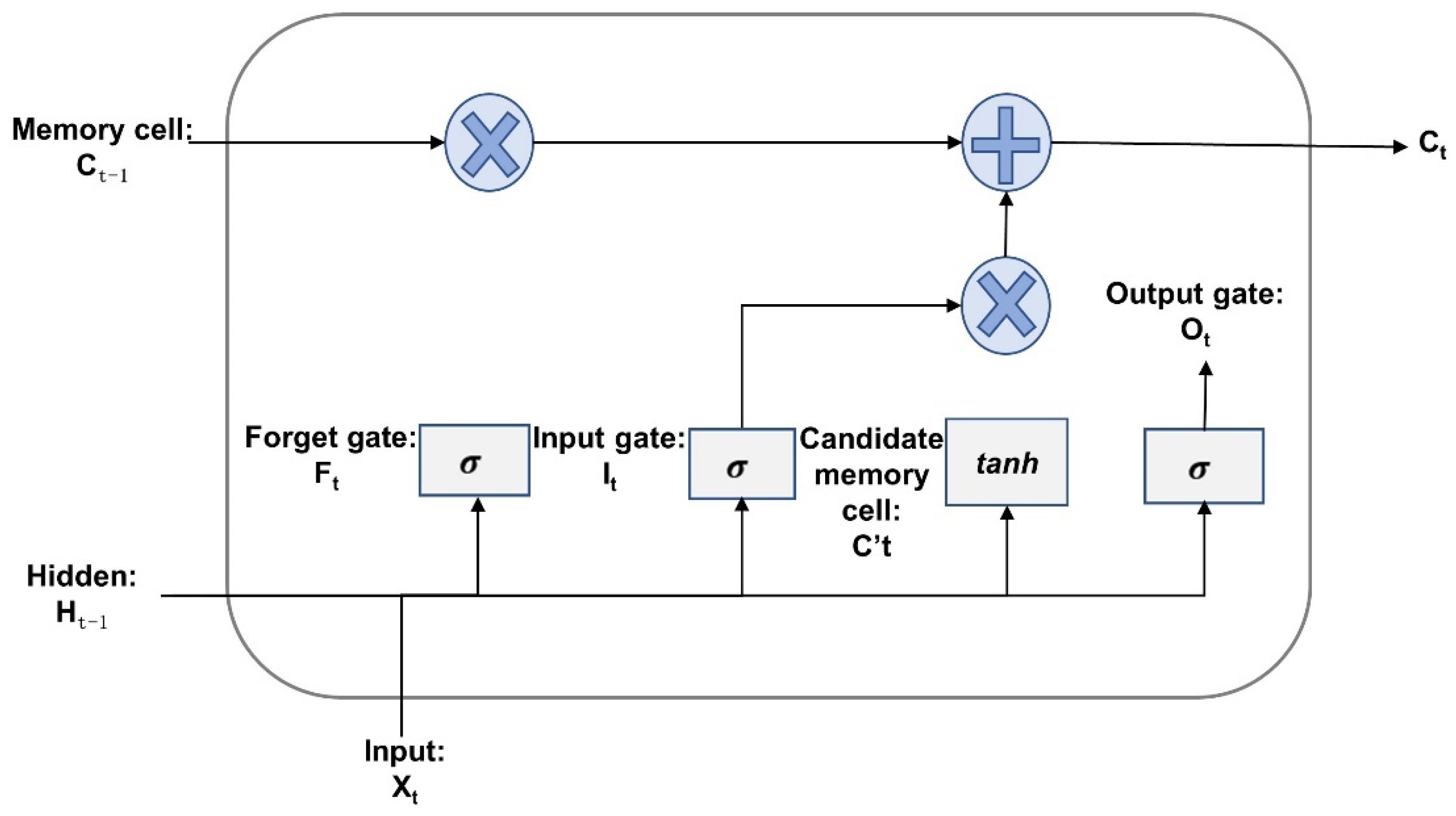
2.3.1. LSTM Method
2.3.2. System Structure
2.4. Evaluation Methods
3. Results
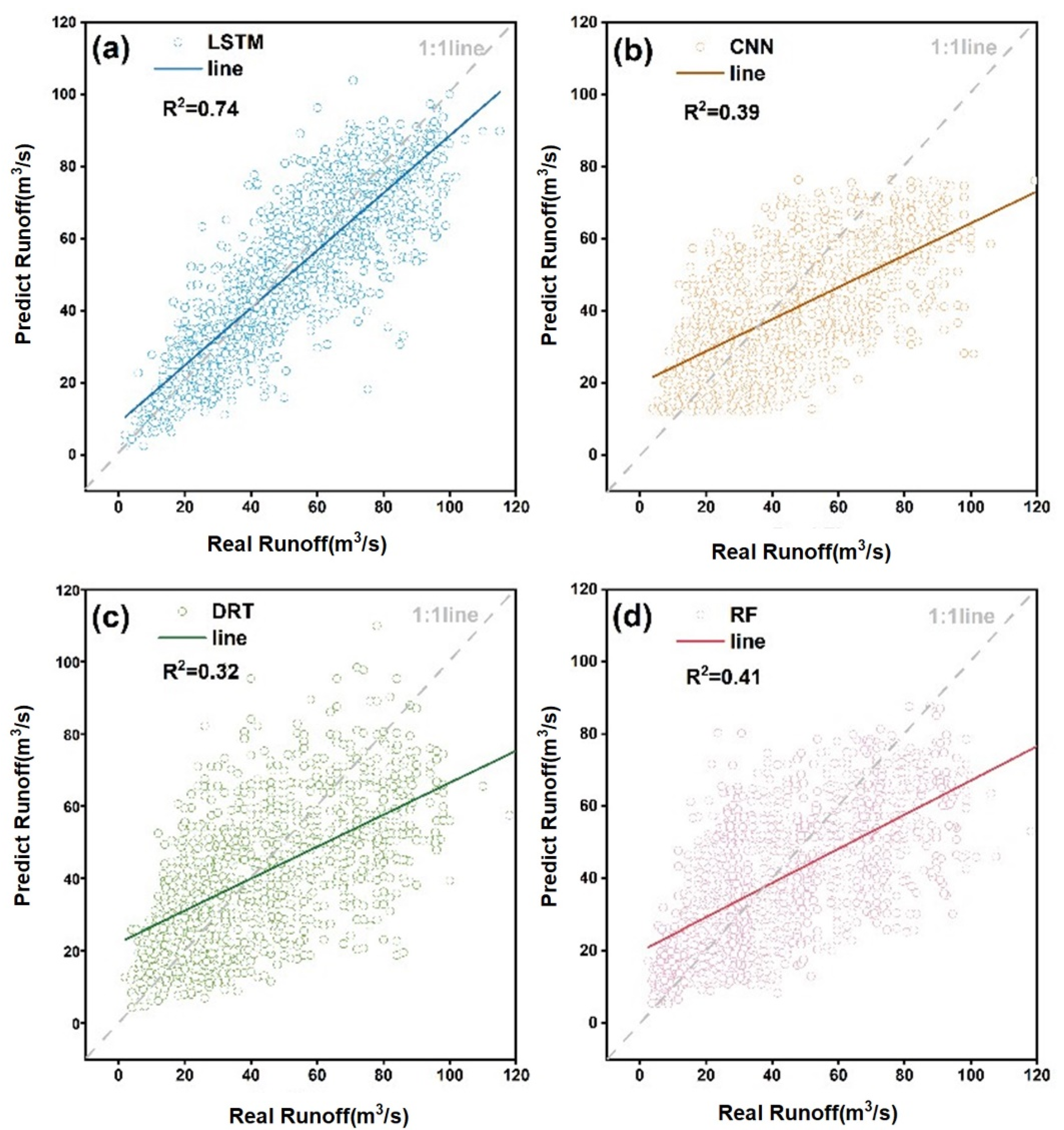
3.1. Comparison with Other Models
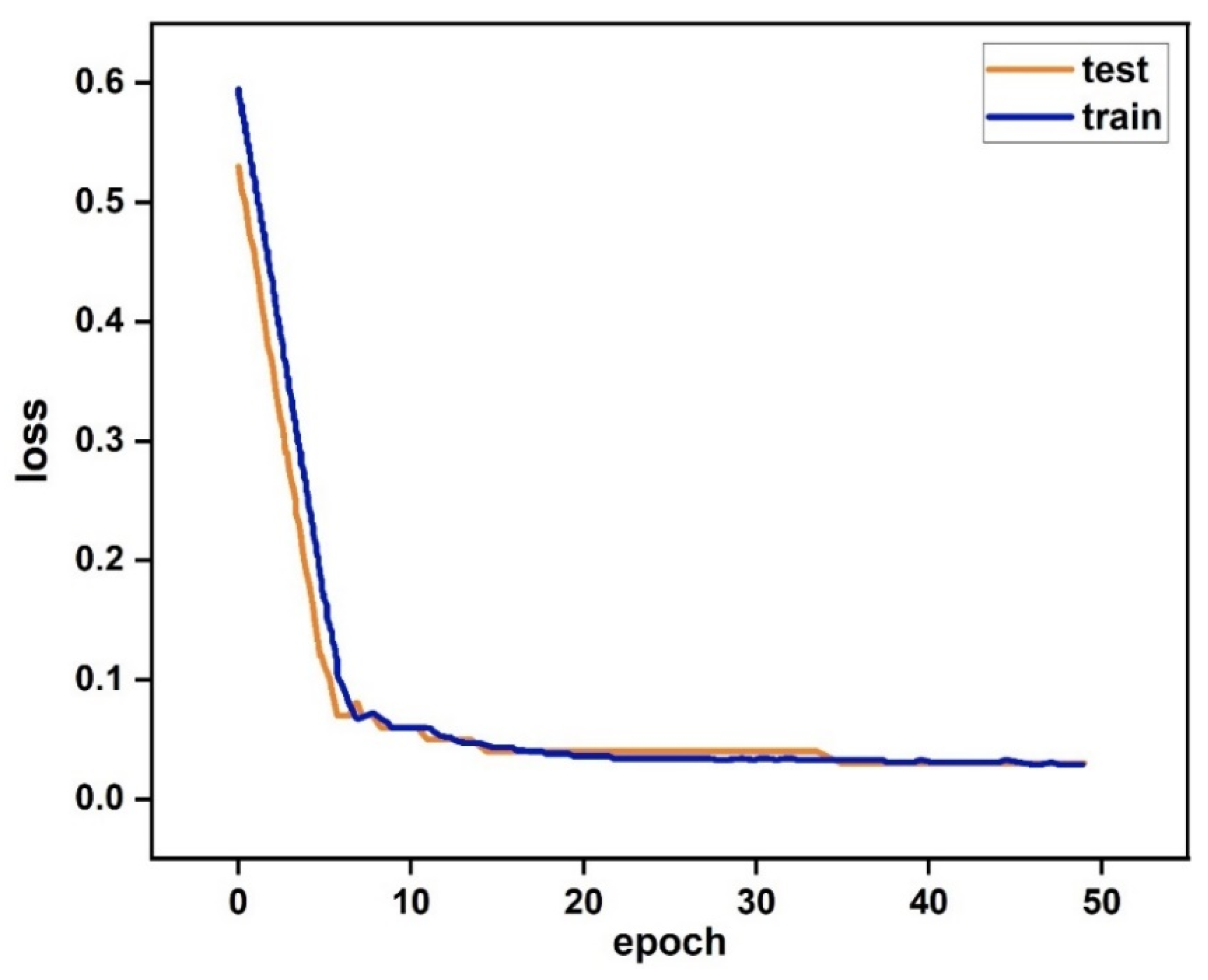
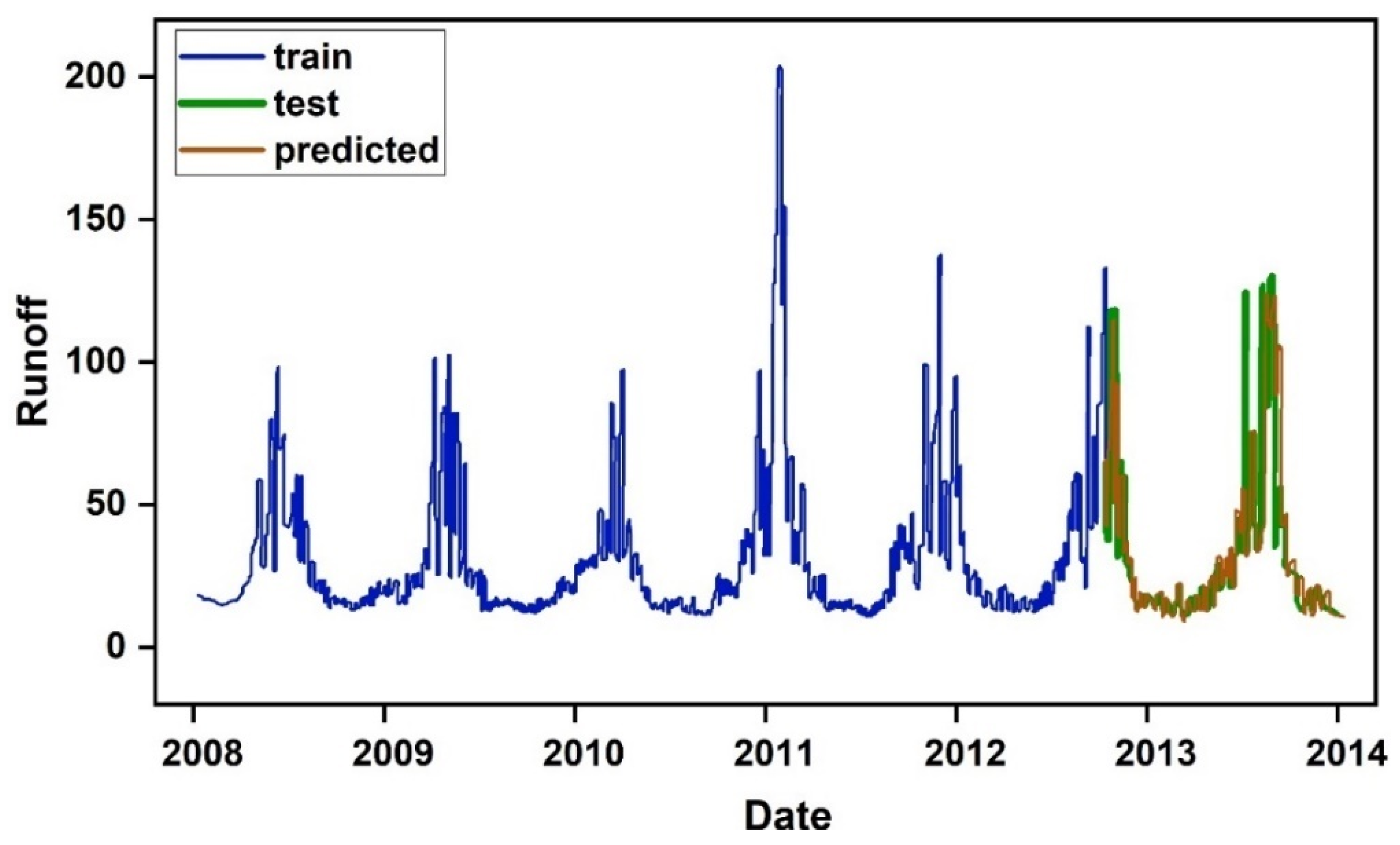
3.2. LSTM Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al-Fugara, A.K.; Ahmadlou, M.; Shatnawi, R.; AlAyyash, S.; Al-Adamat, R.; Al-Shabeeb, A.A.-R.; Soni, S. Novel hybrid models combining meta-heuristic algorithms with support vector regression (SVR) for groundwater potential mapping. Geocarto Int. 2020, 1–20. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Pan, Y.; Li, W. Spatial and temporal variability of drought in the arid region of China and its relationships to teleconnection indices. J. Hydrol. 2015, 523, 283–296. [Google Scholar] [CrossRef]
- Ryu, Y.; Jiang, C.; Kobayashi, H.; Detto, M. MODIS-derived global land products of shortwave radiation and diffuse and total photosynthetically active radiation at 5 km resolution from 2000. Remote Sens. Environ. 2018, 204, 812–825. [Google Scholar] [CrossRef]
- Yang, Y.; Bai, L.; Wang, B.; Wu, J.; Fu, S. Reliability of the global climate models during 1961–1999 in arid and semiarid regions of China. Sci. Total Environ. 2019, 667, 271–286. [Google Scholar] [CrossRef] [PubMed]
- Gaur, M.K.; Squires, V.R. Geographic extent and characteristics of the world’s arid zones and their peoples. In Climate Variability Impacts on Land Use and Livelihoods in Drylands; Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–20. [Google Scholar]
- Hatibu, N. Rainwater Management: Strategies for Improving Water Availability and Productivity in Semi-Arid and Arid Areas; International Water Management Institute: Anand, India, 2002. [Google Scholar]
- Giles, D.M.; Sinyuk, A.; Sorokin, M.G.; Schafer, J.S.; Smirnov, A.; Slutsker, I.; Eck, T.F.; Holben, B.N.; Lewis, J.R.; Campbell, J.R.; et al. Advancements in the Aerosol Robotic Network (AERONET) Version 3 database—Automated near-real-time quality control algorithm with improved cloud screening for Sun photometer aerosol optical depth (AOD) measurements. Atmos. Meas. Tech. 2019, 12, 169–209. [Google Scholar] [CrossRef] [Green Version]
- Lu, N.; Wang, M.; Ning, B.; Yu, D.; Fu, B. Research advances in ecosystem services in drylands under global environmental changes. Curr. Opin. Environ. Sustain. 2018, 33, 92–98. [Google Scholar] [CrossRef]
- Magalhaes, A.R. Sustainable development planning and semi-arid regions. Glob. Environ. Change 1994, 4, 275–279. [Google Scholar] [CrossRef]
- Lourenço, N.; Russo Machado, C. Water Resources and Sustainable Development: Factors and Constraints for Improving Human Well-Being in Water-Stressed Regions; School of the Environment of Nanjing University: Nanjing, China, 2005. [Google Scholar]
- Liu, Y.; Du, J.; Ding, B.; Liu, Y.; Liu, W.; Xia, A.; Huo, R.; Ran, Q.; Hao, Y.; Cui, X. Water resource conservation promotes synergy between economy and environment in China’s northern drylands. Front. Environ. Sci. Eng. 2022, 16, 1–12. [Google Scholar] [CrossRef]
- Stringer, L.C.; Mirzabaev, A.; Benjaminsen, T.A.; Harris, R.M.; Jafari, M.; Lissner, T.K.; Stevens, N.; Tirado-von Der Pahlen, C. Climate change impacts on water security in global drylands. One Earth 2021, 4, 851–864. [Google Scholar] [CrossRef]
- Ma, J.; Wang, X.; Edmunds, W. The characteristics of ground-water resources and their changes under the impacts of human activity in the arid Northwest China—A case study of the Shiyang River Basin. J. Arid Environ. 2005, 61, 277–295. [Google Scholar] [CrossRef]
- Rockström, J.; Falkenmark, M.; Allan, T.; Folke, C.; Gordon, L.; Jägerskog, A.; Kummu, M.; Lannerstad, M.; Meybeck, M.; Molden, D. The unfolding water drama in the Anthropocene: Towards a resilience-based perspective on water for global sustainability. Ecohydrology 2014, 7, 1249–1261. [Google Scholar] [CrossRef]
- Cassardo, C.; Jones, J.A.A. Managing Water in a Changing World; Molecular Diversity Preservation International: Basel, Switzerland, 2011; Volume 3, pp. 618–628. [Google Scholar]
- Van Dijk, A.I.; Beck, H.E.; Crosbie, R.S.; de Jeu, R.A.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The Millennium Drought in southeast Australia (2001–2009): Natural and human causes and implications for water resources, ecosystems, economy, and society. Water Resour. Res. 2013, 49, 1040–1057. [Google Scholar] [CrossRef]
- Jury, W.A.; Vaux, H.J., Jr. The emerging global water crisis: Managing scarcity and conflict between water users. Adv. Agron. 2007, 95, 1–76. [Google Scholar]
- Richter, B.D.; Mathews, R.; Harrison, D.L.; Wigington, R. Ecologically sustainable water management: Managing river flows for ecological integrity. Ecol. Appl. 2003, 13, 206–224. [Google Scholar] [CrossRef]
- Wu, G.; Li, L.; Ahmad, S.; Chen, X.; Pan, X. A dynamic model for vulnerability assessment of regional water resources in arid areas: A case study of Bayingolin, China. Water Resour. Manag. 2013, 27, 3085–3101. [Google Scholar] [CrossRef]
- Grundmann, J.; Schütze, N.; Schmitz, G.H.; Al-Shaqsi, S. Towards an integrated arid zone water management using simulation-based optimisation. Environ. Earth Sci. 2012, 65, 1381–1394. [Google Scholar] [CrossRef]
- Ragab, R.; Prudhomme, C. Sw—soil and Water: Climate change and water resources management in arid and semi-arid regions: Prospective and challenges for the 21st century. Biosyst. Eng. 2002, 81, 3–34. [Google Scholar]
- Chen, Y.; Li, Z.; Fan, Y.; Wang, H.; Deng, H. Progress and prospects of climate change impacts on hydrology in the arid region of northwest China. Environ. Res. 2015, 139, 11–19. [Google Scholar] [CrossRef]
- Pilgrim, D.; Chapman, T.; Doran, D. Problems of rainfall-runoff modelling in arid and semiarid regions. Hydrol. Sci. J. 1988, 33, 379–400. [Google Scholar] [CrossRef]
- Derdour, A.; Bouanani, A.; Babahamed, K. Modelling rainfall runoff relations using HEC-HMS in a semi-arid region: Case study in Ain Sefra watershed, Ksour Mountains (SW Algeria). J. Water Land Dev. 2018, 36, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Muneer, A.S.; Sayl, K.N.; Kamel, A.H. Modeling of runoff in the arid regions using remote sensing and geographic information system (GIS). Int. J. Des. Nat. Ecodynamics 2020, 15, 691–700. [Google Scholar] [CrossRef]
- Chen, Y.; Li, B.; Li, Z.; Li, W. Water resource formation and conversion and water security in arid region of Northwest China. J. Geogr. Sci. 2016, 26, 939–952. [Google Scholar] [CrossRef] [Green Version]
- Silva, T.A.; Ferreira, J.; Calijuri, M.L.; dos Santos, V.J.; do Carmo Alves, S.; de Siqueira Castro, J. Efficiency of technologies to live with drought in agricultural development in Brazil’s semi-arid regions. J. Arid Environ. 2021, 192, 104538. [Google Scholar] [CrossRef]
- Yang, T.; Wang, S.; Li, X.; Wu, T.; Li, L.; Chen, J. River habitat assessment for ecological restoration of Wei River Basin, China. Environ. Sci. Pollut. Res. 2018, 25, 17077–17090. [Google Scholar] [CrossRef]
- Wu, W.; Xu, Z.; Zhan, C.; Yin, X.; Yu, S. A new framework to evaluate ecosystem health: A case study in the Wei River basin, China. Environ. Monit. Assess. 2015, 187, 1–15. [Google Scholar] [CrossRef]
- Saadati, H.; Gholami, S.A.; Sharifi, F.; AYOUBZADEH, S.A. An investigation of the effects of land use change on simulating surface runoff using SWAT mathematical model (case study: Kasilian catchment area). Iran. J. Nat. Resour. 2006, 59, 301–313. [Google Scholar]
- Singh, V.P.; Woolhiser, D.A. Mathematical modeling of watershed hydrology. J. Hydrol. Eng. 2002, 7, 270–292. [Google Scholar] [CrossRef] [Green Version]
- Shende, S. A conceptual rainfall-runoff mathematical model to simulate runoff using daily amount of rainfall for arid and semi-arid region. In Proceedings of Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; p. 022017. [Google Scholar]
- Abdessamed, D.; Abderrazak, B. Coupling HEC-RAS and HEC-HMS in rainfall–runoff modeling and evaluating floodplain inundation maps in arid environments: Case study of Ain Sefra city, Ksour Mountain. SW of Algeria. Environ. Earth Sci. 2019, 78, 586. [Google Scholar] [CrossRef]
- Lange, H.; Sippel, S. Machine learning applications in hydrology. In Forest-Water Interactions; Springer: Berlin/Heidelberg, Germany, 2020; pp. 233–257. [Google Scholar]
- Gimblett, H.R. Integrating geographic information systems and agent-based technologies for modeling and simulating social and ecological phenomena. In Integrating Geographic Information Systems and Agent-Based Modeling Techniques for Understanding Social and Ecological Processes; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Hosseini, F.S.; Choubin, B.; Mosavi, A.; Nabipour, N.; Shamshirband, S.; Darabi, H.; Haghighi, A.T. Flash-flood hazard assessment using ensembles and Bayesian-based machine learning models: Application of the simulated annealing feature selection method. Sci. Total Environ. 2020, 711, 135161. [Google Scholar] [CrossRef]
- Tanty, R.; Desmukh, T.S. Application of artificial neural network in hydrology—A review. Int. J. Eng. Technol. Res. 2015, 4, 184–188. [Google Scholar]
- Solomatine, D.P.; Ostfeld, A. Data-driven modelling: Some past experiences and new approaches. J. Hydroinform. 2008, 10, 3–22. [Google Scholar] [CrossRef] [Green Version]
- Fa, W.; Wieczorek, M.A.; Heggy, E. Modeling polarimetric radar scattering from the lunar surface: Study on the effect of physical properties of the regolith layer. J. Geophys. Res. Planets 2011, 116. [Google Scholar] [CrossRef]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, A.; Singh, R. Runoff modelling through back propagation artificial neural network with variable rainfall-runoff data. Water Resour. Manag. 2004, 18, 285–300. [Google Scholar] [CrossRef]
- Boulmaiz, T.; Ouerdachi, L.; Boutoutaou, D.; Boutaghane, H. Single neural network and neuro-updating conceptual model for forecasting runoff. Int. J. Hydrol. Sci. Technol. 2016, 6, 344–358. [Google Scholar] [CrossRef]
- Van, S.P.; Le, H.M.; Thanh, D.V.; Dang, T.D.; Loc, H.H.; Anh, D.T. Deep learning convolutional neural network in rainfall–runoff modelling. J. Hydroinform. 2020, 22, 541–561. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef] [Green Version]
- Gers, F.A.; Schraudolph, N.N.; Schmidhuber, J. Learning precise timing with LSTM recurrent networks. J. Mach. Learn. Res. 2002, 3, 115–143. [Google Scholar]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Wang, J.; Li, H.; Hao, X. Responses of snowmelt runoff to climatic change in an inland river basin, Northwestern China, over the past 50 years. Hydrol. Earth Syst. Sci. 2010, 14, 1979–1987. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Xu, C.-Y.; Tao, H.; Jiang, T.; Chen, Y.D. Climate changes and their impacts on water resources in the arid regions: A case study of the Tarim River basin, China. Stoch. Environ. Res. Risk Assess. 2010, 24, 349–358. [Google Scholar] [CrossRef]
- Butterworth, J.; Warner, J.; Moriarty, P.; Smits, S.; Batchelor, C. Finding practical approaches to integrated water resources management. Water Altern. 2010, 3, 68–81. [Google Scholar]
- Wei, R.-j.; Peng, L.; Liang, C.; Haemmig, C.; Huss, M.; Mu, Z.-x.; He, Y. Analysis of temporal and spatial variations in hydrometeorological elements in the Yarkant River Basin, China. J. Water Clim. Change 2019, 10, 167–180. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Yan, W.; Zhao, C.; Kundzewicz, Z.W. Snow-cover area and runoff variation under climate change in the West Kunlun Mountains. Water-Sui 2019, 11, 2246. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Xu, C.; Chen, Y.; Li, W.; Liu, J. Response of glacial-lake outburst floods to climate change in the Yarkant River basin on northern slope of Karakoram Mountains, China. Quat. Int. 2010, 226, 75–81. [Google Scholar] [CrossRef]
- Yaning, C.; Changchun, X.; Xingming, H.; Weihong, L.; Yapeng, C.; Chenggang, Z.; Zhaoxia, Y. Fifty-year climate change and its effect on annual runoff in the Tarim River Basin, China. Quat. Int. 2009, 208, 53–61. [Google Scholar]
- Fan, Y.; Chen, Y.; Liu, Y.; Li, W. Variation of baseflows in the headstreams of the Tarim River Basin during 1960–2007. J. Hydrol. 2013, 487, 98–108. [Google Scholar] [CrossRef]
- Chen, Y.-n.; Li, W.-h.; Xu, C.-c.; Hao, X.-m. Effects of climate change on water resources in Tarim River Basin, Northwest China. J. Environ. Sci. 2007, 19, 488–493. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, Y.; Chen, Y.; Zhang, Q. Impact of Climate Change on the Hydrological Regime of the Yarkant River Basin, China: An Assessment Using Three SSP Scenarios of CMIP6 GCMs. Remote Sens. 2021, 14, 115. [Google Scholar] [CrossRef]
- Kan, B.; Su, F.; Xu, B.; Xie, Y.; Li, J.; Zhang, H. Generation of high mountain precipitation and temperature data for a quantitative assessment of flow regime in the Upper Yarkant basin in the Karakoram. J. Geophys. Res. Atmos. 2018, 123, 8462–8486. [Google Scholar] [CrossRef]
- Fan, Z.; Xia, X.; Shen, Y.; Alishir, K.; Wang, R.; Li, S.; Ma, Y. Utilization of water resources, ecological balance and land desertification in the Tarim Basin, Xinjiang. Sci. China Ser. D Earth Sci. 2002, 45, 102–108. [Google Scholar] [CrossRef]
- Bruelheide, H.; Jandt, U.; Gries, D.; Thomas, F.M.; Foetzki, A.; Bürkert, A.; Wang, G.; Zhang, X.; Runge, M. Vegetation Changes in a River Oasis on the Southern Rim of the Taklamakan Desert in China between 1956 and 2000; Borntraeger: Stuttgart, Germany, 2003. [Google Scholar]
- Li, D.; Xu, E.; Zhang, H. Influence of ecological land change on wind erosion prevention service in arid area of northwest China from 1990 to 2015. Ecol. Indic. 2020, 117, 106686. [Google Scholar] [CrossRef]
- Wang, B.; Dong, X.; Wang, Z.; Qin, G. Characterizing spatiotemporal variations of soil salinization and its relationship with eco-hydrological parameters at the Regional Scale in the Kashi Area of Xinjiang, China from 2000 to 2017. Water 2021, 13, 1075. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, F.; Hu, H.; Sivapalan, M. Socio-hydrologic perspectives of the co-evolution of humans and water in the Tarim River basin, Western China: The Taiji–Tire model. Hydrol. Earth Syst. Sci. 2014, 18, 1289–1303. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Li, S.; Chen, Y.; Qi, Y.; Zhang, S. Estimation of regional irrigation water requirement and water supply risk in the arid region of Northwestern China 1989–2010. Agric. Water Manag. 2013, 128, 55–64. [Google Scholar] [CrossRef]
- Yang, F.; Xue, L.; Wei, G.; Chi, Y.; Yang, G. Study on the dominant causes of streamflow alteration and effects of the current water diversion in the Tarim River Basin, China. Hydrol. Processes 2018, 32, 3391–3401. [Google Scholar] [CrossRef]
- Abdulrazzaq, Z.T.; Hasan, R.H.; Aziz, N.A. Integrated TRMM data and standardized precipitation index to monitor the meteorological drought. Civ. Eng. J. 2019, 5, 1590–1598. [Google Scholar] [CrossRef] [Green Version]
- Legates, D.R.; Willmott, C.J. Mean seasonal and spatial variability in global surface air temperature. Theor. Appl. Climatol. 1990, 41, 11–21. [Google Scholar] [CrossRef]
- Suarez-Alvarez, M.M.; Pham, D.-T.; Prostov, M.Y.; Prostov, Y.I. Statistical approach to normalization of feature vectors and clustering of mixed datasets. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 2630–2651. [Google Scholar] [CrossRef]
- Liu, M.; Huang, Y.; Li, Z.; Tong, B.; Liu, Z.; Sun, M.; Jiang, F.; Zhang, H. The applicability of LSTM-KNN model for real-time flood forecasting in different climate zones in China. Water 2020, 12, 440. [Google Scholar] [CrossRef] [Green Version]
- Papacharalampous, G.; Tyralis, H.; Papalexiou, S.M.; Langousis, A.; Khatami, S.; Volpi, E.; Grimaldi, S. Global-scale massive feature extraction from monthly hydroclimatic time series: Statistical characterizations, spatial patterns and hydrological similarity. Sci. Total Environ. 2021, 767, 144612. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Bezak, N.; Zeng, B.; Li, C.; Sapač, K.; Zhang, J. Daily runoff forecasting using a cascade long short-term memory model that considers different variables. Water Resour. Manag. 2021, 35, 1167–1181. [Google Scholar]
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and rainfall forecasting by two long short-term memory-based models. J. Hydrol. 2020, 583, 124296. [Google Scholar] [CrossRef]
- Li, F.; Ma, G.; Chen, S.; Huang, W. An Ensemble Modeling Approach to Forecast Daily Reservoir Inflow Using Bidirectional Long-and Short-Term Memory (Bi-LSTM), Variational Mode Decomposition (VMD), and Energy Entropy Method. Water Resour. Manag. 2021, 35, 2941–2963. [Google Scholar] [CrossRef]
- Jing, X.; Luo, J.; Zhang, S.; Wei, N. Runoff forecasting model based on variational mode decomposition and artificial neural networks. Math. Biosci. Eng. 2022, 19, 1633–1648. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Benchmarking a catchment-aware long short-term memory network (LSTM) for large-scale hydrological modeling. Hydrol. Earth Syst. Sci. Discuss. 2019, 1–32. [Google Scholar]
- Chen, Y.-C.; Gao, J.-J.; Bin, Z.-H.; Qian, J.-Z.; Pei, R.-L.; Zhu, H. Application study of IFAS and LSTM models on runoff simulation and flood prediction in the Tokachi River basin. J. Hydroinform. 2021, 23, 1098–1111. [Google Scholar] [CrossRef]
- Tao, S.; Fang, J.; Ma, S.; Cai, Q.; Xiong, X.; Tian, D.; Zhao, X.; Fang, L.; Zhang, H.; Zhu, J.J.N.S.R. Changes in China’s lakes: Climate and human impacts. Natl. Sci. Rev. 2020, 7, 132–140. [Google Scholar] [CrossRef] [Green Version]
- Yozgatligil, C.; Aslan, S.; Iyigun, C.; Batmaz, I. Comparison of missing value imputation methods in time series: The case of Turkish meteorological data. Theor. Appl. Climatol. 2013, 112, 143–167. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Y. Analysis of the mean absolute error (MAE) and the root mean square error (RMSE) in assessing rounding model. In Proceedings of IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; p. 012049. [Google Scholar]
- Gauch, M.; Kratzert, F.; Klotz, D.; Nearing, G.; Lin, J.; Hochreiter, S. Rainfall–runoff prediction at multiple timescales with a single Long Short-Term Memory network. Hydrol. Earth Syst. Sci. 2021, 25, 2045–2062. [Google Scholar] [CrossRef]
- Han, H.; Morrison, R.R. Data-driven approaches for runoff prediction using distributed data. Stoch. Environ. Res. Risk Assess. 2021, 1–19. [Google Scholar] [CrossRef]
- Nasser, A.A.; Rashad, M.Z.; Hussein, S.E. A two-layer water demand prediction system in urban areas based on micro-services and LSTM neural networks. IEEE Access 2020, 8, 147647–147661. [Google Scholar] [CrossRef]
- Quan, Q.; Hao, Z.; Xifeng, H.; Jingchun, L. Research on water temperature prediction based on improved support vector regression. Neural Comput. Appl. 2020, 34, 8501–8510. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Liu, Y.; Jiang, Z.; Yang, X. Runoff Prediction Model Based on Improved Convolutional Neural Network. Water Resour. Manag. 2021. Reprint. [Google Scholar] [CrossRef]
- Contreras, P.; Orellana-Alvear, J.; Muñoz, P.; Bendix, J.; Célleri, R. Influence of random forest hyperparameterization on short-term runoff forecasting in an andean mountain catchment. Atmosphere 2021, 12, 238. [Google Scholar] [CrossRef]
- Oppel, H.; Schumann, A.H. Machine learning based identification of dominant controls on runoff dynamics. Hydrol. Processes 2020, 34, 2450–2465. [Google Scholar] [CrossRef]
- Müftüoğlu, R.F. Monthly runoff generation by non-linear models. J. Hydrol. 1991, 125, 277–291. [Google Scholar] [CrossRef]
- Chen, S.; Dong, S.; Cao, Z.; Guo, J. A compound approach for monthly runoff forecasting based on multiscale analysis and deep network with sequential structure. Water 2020, 12, 2274. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J.; Krebs, P. Prediction of Flow Based on a CNN-LSTM Combined Deep Learning Approach. Water 2022, 14, 993. [Google Scholar] [CrossRef]
- Raman, H.; Sunilkumar, N. Multivariate modelling of water resources time series using artificial neural networks. Hydrol. Sci. J. 1995, 40, 145–163. [Google Scholar] [CrossRef]
- Nawaz, N.; Adeloye, A. Evaluation of monthly runoff estimated by a rainfall-runoff regression model for reservoir yield assessment. Hydrol. Sci. J. 1999, 44, 113–134. [Google Scholar] [CrossRef] [Green Version]
- Özelkan, E.C.; Duckstein, L. Fuzzy conceptual rainfall–runoff models. J. Hydrol. 2001, 253, 41–68. [Google Scholar] [CrossRef]
- Willems, P. A time series tool to support the multi-criteria performance evaluation of rainfall-runoff models. Environ. Model. Softw. 2009, 24, 311–321. [Google Scholar] [CrossRef]
- Wang, W.-C.; Chau, K.-W.; Xu, D.-M.; Chen, X.-Y. Improving forecasting accuracy of annual runoff time series using ARIMA based on EEMD decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
- Trivedi, H.; Singh, J. Application of grey system theory in the development of a runoff prediction model. Biosyst. Eng. 2005, 92, 521–526. [Google Scholar] [CrossRef]
- Yu, P.S.; Chen, C.J.; Chen, S.J.; Lin, S.C. Application of Grey Model toward Runoff Forecasting 1. JAWRA J. Am. Water Resour. Assoc. 2001, 37, 151–166. [Google Scholar] [CrossRef]
- Alvisi, S.; Bernini, A.; Franchini, M. A conceptual grey rainfall-runoff model for simulation with uncertainty. J. Hydroinform. 2013, 15, 1–20. [Google Scholar] [CrossRef]
- Dawson, C.W.; Wilby, R. An artificial neural network approach to rainfall-runoff modelling. Hydrol. Sci. J. 1998, 43, 47–66. [Google Scholar] [CrossRef]
- Riad, S.; Mania, J.; Bouchaou, L.; Najjar, Y. Rainfall-runoff model usingan artificial neural network approach. Math. Comput. Model. 2004, 40, 839–846. [Google Scholar] [CrossRef]
- Bray, M.; Han, D. Identification of support vector machines for runoff modelling. J. Hydroinformatics 2004, 6, 265–280. [Google Scholar] [CrossRef] [Green Version]
- Han, D.W.; Cluckie, I. Support vector machines identification for runoff modelling. In Hydroinformatics: (In 2 Volumes, with CD-ROM); World Scientific: Singapore, 2004; pp. 1597–1604. [Google Scholar]
- Herath, H.; Chadalawada, J.; Babovic, V. Hydrologically informed machine learning for rainfall-runoff modelling: Towards distributed modelling. Hydrol. Earth Syst. Sci. Discuss. 2020, 2020, 1–42. [Google Scholar] [CrossRef]
- Mohammadi, B. A review on the applications of machine learning for runoff modeling. Sustain. Water Resour. Manag. 2021, 7, 1–11. [Google Scholar] [CrossRef]
- Li, W.; Kiaghadi, A.; Dawson, C. High temporal resolution rainfall–runoff modeling using long-short-term-memory (LSTM) networks. Neural Comput. Appl. 2021, 33, 1261–1278. [Google Scholar] [CrossRef]
- Lees, T.; Buechel, M.; Anderson, B.; Slater, L.; Reece, S.; Coxon, G.; Dadson, S.J. Benchmarking Data-Driven Rainfall-Runoff Models in Great Britain: A comparison of LSTM-based models with four lumped conceptual models. Hydrol. Earth Syst. Sci. 2021, 25, 5517–5534. [Google Scholar] [CrossRef]
- Fan, H.; Jiang, M.; Xu, L.; Zhu, H.; Cheng, J.; Jiang, J. Comparison of long short term memory networks and the hydrological model in runoff simulation. Water 2020, 12, 175. [Google Scholar] [CrossRef] [Green Version]
- Klotz, D.; Kratzert, F.; Gauch, M.; Keefe Sampson, A.; Brandstetter, J.; Klambauer, G.; Hochreiter, S.; Nearing, G. Uncertainty estimation with deep learning for rainfall–runoff modelling. Hydrol. Earth Syst. Sci. Discuss. 2021, 26, 1673–1693. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, T.; Kang, A.; Li, J.; Lei, X. Research on runoff simulations using deep-learning methods. Sustainability 2021, 13, 1336. [Google Scholar] [CrossRef]
- Redondo, J.; Ibarra-Vega, D.; Catumba-Ruíz, J.; Sánchez-Muñoz, M. Hydrological system modeling: Approach for analysis with dynamical systems. In Proceedings of Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; p. 012013. [Google Scholar]
- Li, Z.; Kang, L.; Zhou, L.; Zhu, M. Deep learning framework with time series analysis methods for runoff prediction. Water 2021, 13, 575. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Hochreiter, S. A Glimpse into the Unobserved: Runoff Simulation for Ungauged Catchments with LSTMs. 2018. Available online: https://openreview.net/forum?id=Bylhm72oKX (accessed on 25 May 2022).
- Zhang, D.; Hølland, E.S.; Lindholm, G.; Ratnaweera, H. Hydraulic modeling and deep learning based flow forecasting for optimizing inter catchment wastewater transfer. J. Hydrol. 2018, 567, 792–802. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Processing Syst. 2015, 28. [Google Scholar] [CrossRef]
- Guan, Y.; Lu, H.; Jiang, Y.; Tian, P.; Qiu, L.; Pellikka, P.; Heiskanen, J. Changes in global climate heterogeneity under the 21st century global warming. Ecol. Indic. 2021, 130, 108075. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Qin, D.-H. Influence of climate change and human activity on water resources in arid region of Northwest China: An overview. Adv. Clim. Change Res. 2017, 8, 268–278. [Google Scholar] [CrossRef]
- Frenierre, J.L.; Mark, B.G. A review of methods for estimating the contribution of glacial meltwater to total watershed discharge. Prog. Phys. Geogr. 2014, 38, 173–200. [Google Scholar] [CrossRef]
- Kezer, K.; Matsuyama, H. Decrease of river runoff in the Lake Balkhash basin in Central Asia. Hydrol. Processes Int. J. 2006, 20, 1407–1423. [Google Scholar] [CrossRef]
- Lang, H. Forecasting meltwater runoff from snow-covered areas and from glacier basins. In River Flow Modelling and Forecasting; Springer: Berlin/Heidelberg, Germany, 1986; pp. 99–127. [Google Scholar]
- Liu, G.; Tang, Z.; Qin, H.; Liu, S.; Shen, Q.; Qu, Y.; Zhou, J. Short-term runoff prediction using deep learning multi-dimensional ensemble method. J. Hydrol. 2022, 609, 127762. [Google Scholar] [CrossRef]

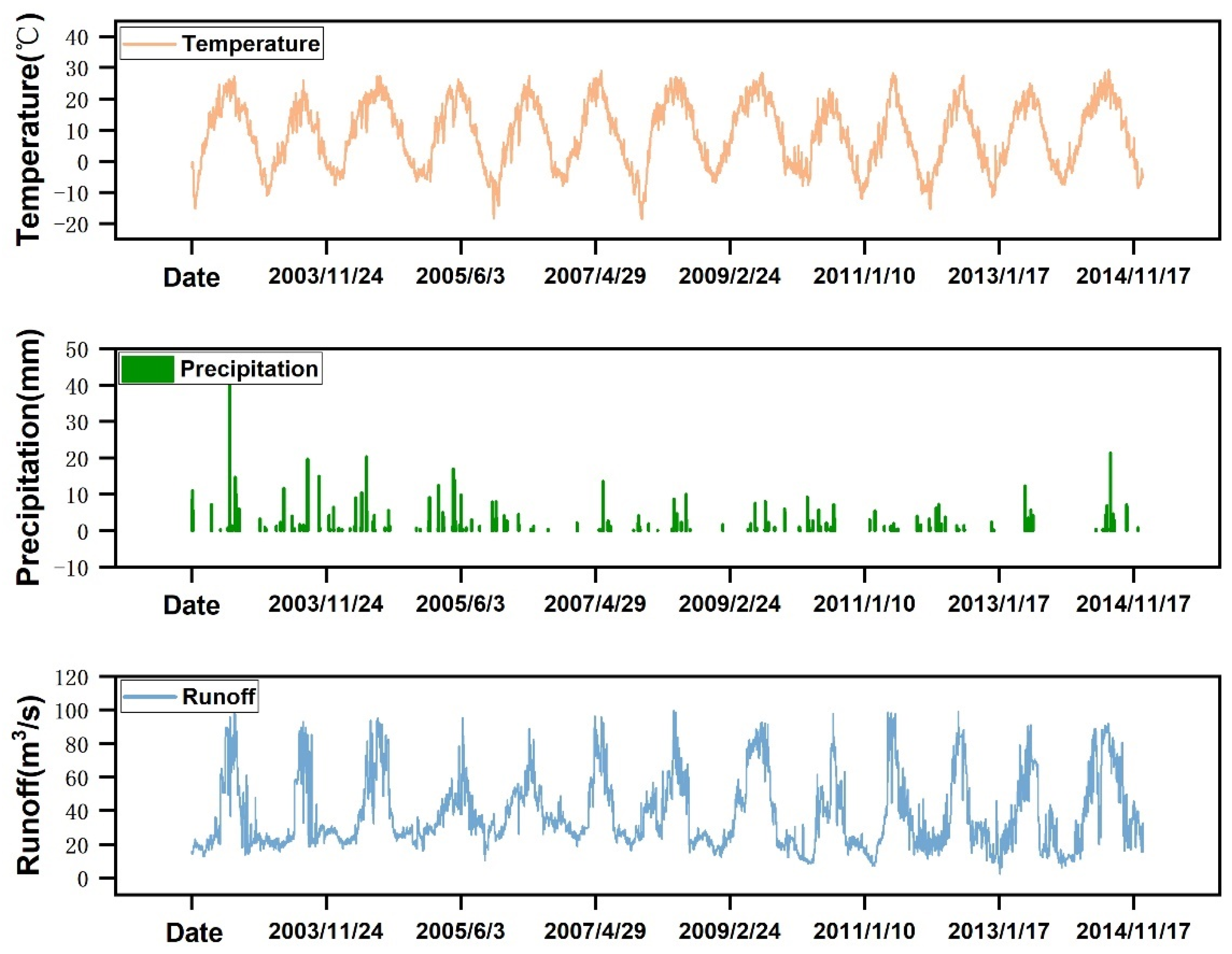

| Date | Runoff | Temperature | Precipitation | |
|---|---|---|---|---|
| 1 | 1 January 1957 | 5.1 | −7.2 | 0 |
| 2 | 2 January 1957 | 6.06 | −6.5 | 0 |
| 3 | 3 January 1957 | 7.05 | −5.1 | 0 |
| 4 | 4 January 1957 | 7.25 | −6.6 | 0 |
| 5 | 5 January 1957 | 7.75 | −7.7 | 0 |
| 14,409 | 22 December 2014 | 15.5 | −4.4 | 0 |
| Runoff (t − 1) | Temperature (t) | Precipitation (t) | Runoff (t) | |
|---|---|---|---|---|
| 1 | 0.240343 | 0.040205 | 0.0 | 0.267382 |
| 2 | 0.267382 | 0.041920 | 0.0 | 0.214592 |
| 3 | 0.214592 | 0.041920 | 0.0 | 0.206009 |
| 4 | 0.206009 | 0.045615 | 0.0 | 0.206009 |
| 5 | 0.206009 | 0.045351 | 0.0 | 0.178112 |
| Model | MAE | RMSE |
|---|---|---|
| LSTM | 3.633 | 7.337 |
| CNN | 8.961 | 12.650 |
| DTR | 9.282 | 13.557 |
| RF | 9.403 | 13.658 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Qian, K.; Liu, Y.; Yan, W.; Yang, X.; Luo, G.; Ma, X. LSTM-Based Model for Predicting Inland River Runoff in Arid Region: A Case Study on Yarkant River, Northwest China. Water 2022, 14, 1745. https://doi.org/10.3390/w14111745
Li J, Qian K, Liu Y, Yan W, Yang X, Luo G, Ma X. LSTM-Based Model for Predicting Inland River Runoff in Arid Region: A Case Study on Yarkant River, Northwest China. Water. 2022; 14(11):1745. https://doi.org/10.3390/w14111745
Chicago/Turabian StyleLi, Jiaxin, Kaixuan Qian, Yuan Liu, Wei Yan, Xiuyun Yang, Geping Luo, and Xiaofei Ma. 2022. "LSTM-Based Model for Predicting Inland River Runoff in Arid Region: A Case Study on Yarkant River, Northwest China" Water 14, no. 11: 1745. https://doi.org/10.3390/w14111745
APA StyleLi, J., Qian, K., Liu, Y., Yan, W., Yang, X., Luo, G., & Ma, X. (2022). LSTM-Based Model for Predicting Inland River Runoff in Arid Region: A Case Study on Yarkant River, Northwest China. Water, 14(11), 1745. https://doi.org/10.3390/w14111745









