Analysis of One-Dimensional Consolidation Considering Non-Darcian Flow Described by Non-Newtonian Index Incorporating Impeded Drainage Boundaries

Abstract

The nonlinear flow law and soil boundaries greatly affect the dissipation process of soil consolidation. Thus, to study the impact of nonlinear flow under impeded drainage boundaries, the classical non-Darcian flow model described by non-Newtonian index was introduced. The numerical solutions are derived in detail by the finite difference method (FDM) for one-dimensional (1-D) consolidation incorporating the impeded boundaries, and the computer program is compiled. Then, comparing two analytical solutions based on Darcy’s law and a numerical case of Forchheimeer’s flow, the validity of the present method was verified. The numerical results indicate that there is a critical depth phenomenon for the non-Darcian flow incorporating impeded drainage boundaries. The excess pore water pressure of the soil below the critical depth dissipates more slowly than that of Darcy’s law, whereas the pore pressure of the soil above the critical depth dissipates more quickly than that of Darcy’s law. Moreover, considering that the non-Darcian flow with the non-Newtonian index will still delay the overall consolidation rate of the soft ground, the greater the nondimensional parameter I₀ is, the more obvious the lagging phenomenon of the overall dissipation of pore pressure is.

1. Introduction

As one of the common issues in geotechnical engineering, soil consolidation has captured a lot of attention from geotechnical engineers since the 1920s [1]. To obtain the analytical solutions or numerical solutions more conveniently, the boundary of the soft soil layer is usually simplified as completely permeable (the first kind of drainage boundary) or absolutely impermeable (the second kind of drainage boundary) [2,3,4,5]. In fact, the drainage at the boundaries of the soil layer is partially permeable, i.e., is impeded [6]. For example, the sand cushion covering the soil layer and the underlying layer at the bottom of the soft soil will become partially permeable when its drainage path is clogged by the fine particles released from the soil layer. Therefore, it is of practical engineering importance to study the consolidation characteristics considering non-Darcian flow in foundations under semi-permeable boundaries.

In view of this, Gray [7] first proposed the definition of impeded drainage boundary in Darcy’s law, which can be described as:

$$\frac{R}{H}\frac{u}{{\gamma }_w}=\frac{1}{{\gamma }_w}\frac{\partial u}{\partial z}$$

(1)

where H is the height of the soil layer, u and ${\gamma }_w$ are the excess pore water pressure and the weight of water in order, and R is a dimensionless parameter that can reflect the drainage capacity of the impeded drainage boundary. When R tends to infinity or is equal to zero, Equation (1) can be simplified into the first kind of drainage boundary (i.e., complete drainage) or the second kind of drainage boundary (i.e., absolutely undrained). Thus, it is a more general boundary than the first and second kinds of boundary conditions. Using impeded drainage boundaries, Schiffman and Stein [8] studied the consolidation of soils with variable compressibility and permeability coefficients. Xie [9] conducted a fully explicit analytical solution of 1-D consolidation of double-layered soil under constant loads. Cai [10] used the Laplace transform to obtain the analytical solution of the viscoelastic soil layer under cyclic loadings. Recently, researchers [11,12] have also introduced the impede drainage boundaries into the consolidation theory of unsaturated soils and discussed the consolidation characteristics in 1-D and 2-D plane strain states.

So far, most of the studies, including those mentioned above, have been conducted under the assumption that the flow of pore water conforms to Darcy’s law. However, many penetration tests have shown [13,14,15,16,17,18] that for saturated soft clay or fine-grained soil with a low permeability coefficient under the low hydraulic slope, there are large deviations between actual flow and Darcy’s law at low hydraulic gradients. These nonlinear flow characteristics were first called non-Darcian flow by Hansbo [13], and he introduced a piecewise function to describe it. Based on this flow model, scholars [19,20] have successively analyzed the non-Darcian factors in 1-D or 2-D consolidation, and some reasonable explanations have been given to problems that cannot be explained by linear Darcy’s law. However, the above nonlinear flow model is described in the form of a piecewise function, which makes it complicated to determine the piecewise interval. Given this, Swartzendruber [21] proposed a non-Darcian flow model described by a continuous function, which is expressed as:

$$v=-K\left[i-i_0\left(1-e^{-i/i_0}\right)\right]$$

(2)

where v is penetration velocity, K represents the permeability coefficient, i₀ is the slope and intercept of the asymptotics of the v~i curve, and i₀ is the non-Newtonian index. When i₀ = 0, the upper formula degenerates into Darcian flow.

The expression of this flow model described by the non-Newtonian index is relatively simple, and it also fits well with the experimental data. Scholars [22,23] have analyzed the influence of the flow parameters on 1-D consolidation or viscoelastic consolidation. However, to the best of the knowledge of this study’s authors, these non-Darcy flow studies above ignored the impeded drainage boundary conditions, which is this paper’s starting point.

Based on the classical non-Darcian flow with non-Newtonian index, this paper deduces the finite difference expression of the 1-D consolidation equation of non-Darcian flow under impeded boundary drainage conditions. Then, the program of 1-D consolidation incorporating impeded boundaries is compiled. The method in this paper and the existing analytical solutions are used to verify the solution method’s rationality and the programming’s correctness. Finally, the program developed in this paper is used to analyze the 1-D consolidation characteristics with non-Darcian flow by incorporating a semi-permeable boundary.

2. Material Model and Methods

2.1. Problem Description

A simplified model of the 1-D consolidation incorporating impeded boundaries is shown in Figure 1. Assuming that the soil layer thickness of H has been fully consolidated under the stress of self-weight, the flow of pore water during consolidation is described in Equation (2). The thicknesses of the sand cushion at the top and the underlying layer at the bottom base are L_t and L_b, respectively, and the corresponding permeability coefficients are k_b and k_t, respectively. Other assumptions used in this study are parallel to those used in the consolidation theory of saturated soil [18,19,20]. The main assumptions are summarized as follows: (i) The soil layer is saturated and homogeneous; (ii) the load p(t) is an infinite uniform load applied instantaneously; (iii) the compression and flow are assumed to occur along the vertical direction only; and (iv) the coefficients of permeability is constant during the consolidation process. The consolidation deformation of the soil layer is small, and the influence of the secondary consolidation is omitted.

For the variable loading condition, the corresponding consolidation equation for 1-D consolidation of soft soil layer can be written as [20,22]:

$$\frac{K}{{\gamma }_w}\cdot \frac{{\partial }^{2}u}{\partial z^2}\left(1-e^{-\frac{1}{i_0{\gamma }_w}\frac{\partial u}{\partial z}}\right)=\frac{a}{1+e_0}\left(\frac{\partial u}{\partial t}-\frac{\partial p}{\partial t}\right)$$

(3)

where e₀ is the initial void ratio and a is the compression coefficient of soil.

The initial conditions for this subject is:

$$u\left(z,0\right)=u_0=p_0,0\le z\le H$$

(4)

The impeded drainage boundaries considering non-Darcian flow with non-Newtonian index can be rewritten as follows according to Equation (1):

When z = 0,

$$\frac{R_{\mathrm{t}}}{H}\frac{u}{{\gamma }_w}=\frac{1}{{\gamma }_w}{\frac{\partial u}{\partial z}|}_{z=0}-i_0\left(1-e^{-\frac{1}{i_0{\gamma }_w}{\frac{\partial u}{\partial z}|}_{z=0}}\right)$$

(5)

and when z = H,

$$-\frac{R_b}{H}\frac{u}{{\gamma }_w}=\frac{1}{{\gamma }_w}{\frac{\partial u}{\partial z}|}_{z=H}-i_0\left(1-e^{-\frac{1}{i_0{\gamma }_w}{\frac{\partial u}{\partial z}|}_{z=h}}\right)$$

(6)

where $R_t=\frac{k_{t}H}{K{L}_t}$, $R_b=\frac{k_{b}H}{K{L}_b}$, which can respectively reflect the drainage capacity of the top and bottom of the soft soil layer. It can be seen from Formula (5)–(6) that when i₀ = 0, the above formula degenerates to Formula (1), which is the impeded drainage boundaries corresponding to Darcy’s law.

For the convenience of analysis, the following nondimensional variables are introduced:

$$Z=\frac{z}{H},U=\frac{u}{p_u},T=\frac{C_{v}t}{H^2},I_0=\frac{i_0{\gamma }_{w}H}{p_u},P\left(T\right)=\frac{p\left(t\right)}{p_u},C_v=\frac{K\left(1+e_0\right)}{a{\gamma }_w}$$

(7)

where Z is the nondimensional depth; P_u is the maximum applied load; and H is a reference length of soil thickness, which is nonconsistent with the drainage length in Terzaghi’s 1-D solution. U is the nondimensional pore pressure; T represents nondimensional time; I₀ is nondimensional flow parameter; P(T) denotes nondimensional variable load; and C_v is the vertical consolidation coefficient of soil.

In this way, Equations (3)–(6) can be successively transformed into:

$$\frac{U_{j-1,i^{\prime }+1}-2U_{j,i^{\prime }+1}+U_{j+1,i^{\prime }+1}}{\mathsf{\Delta }{Z}^2}\left(1-e^{-\frac{1}{I_0}\frac{U_{j+1,i^{\prime }+1}-U_{j-1,i^{\prime }+1}}{2\mathsf{\Delta }Z}}\right)=\frac{U_{j,i^{\prime }+1}-U_{j,i^{\prime }}}{\mathsf{\Delta }T}-\frac{p_{i^{\prime }+1}-p_{i^{\prime }}}{\mathsf{\Delta }T}$$

(8)

$$U\left(Z,0\right)=U_0=p_0/p_u,0<Z<1$$

(9)

$$R_{t}U={\frac{\partial U}{\partial Z}|}_{Z=0}-I_0\left(1-e^{-\frac{1}{I_0}{\frac{\partial U}{\partial Z}|}_{Z=0}}\right)$$

(10)

$$-R_{b}U={\frac{\partial U}{\partial Z}|}_{Z=H}-I_0\left(1-e^{-\frac{1}{I_0}{\frac{\partial U}{\partial Z}|}_{Z=H}}\right)$$

(11)

where j is the discrete points along with the depth and i’ is time the axis discrete points.

2.2. Differential Iteration Format of The Governing Equation

The soil layer is evenly divided into the n − 1 layer from the top to the bottom base, with nodes numbered 1 to n. The time step is taken as Δt and numbered from 1. This section adopts an implicit format for linear partial differential equations, and the differential equation corresponding to the governing equation can be expressed as:

$$\frac{U_{j-1,i^{\prime }+1}-2U_{j,i^{\prime }+1}+U_{j+1,i^{\prime }+1}}{\mathsf{\Delta }{Z}^2}\left(1-e^{-\frac{1}{I_0}\frac{U_{j+1,i^{\prime }+1}-U_{j-1,i^{\prime }+1}}{2\mathsf{\Delta }Z}}\right)=\frac{U_{j,i^{\prime }+1}-U_{j,i^{\prime }}}{\mathsf{\Delta }T}$$

(12)

The corresponding initial conditions and boundary conditions can be represented by discrete points in turn as

$$U_{j,1}=P_0$$

(13)

$$-\left(\frac{1}{\mathsf{\Delta }Z}+R_1\right)U_{1,i^{\prime }+1}+\frac{U_{2,i^{\prime }+1}}{\mathsf{\Delta }Z}=I_0\left(1-e^{-\frac{1}{I_0}\frac{U_{2,i^{\prime }+1}-U_{1,i^{\prime }+1}}{\mathsf{\Delta }Z}}\right)$$

(14)

$$-\frac{U_{k-1,i^{\prime }+1}}{\mathsf{\Delta }Z}+\left(R_2+\frac{1}{\mathsf{\Delta }Z}\right)U_{k,i^{\prime }+1}=I_0\left(1-e^{-\frac{1}{I_0}\frac{U_{k,i^{\prime }+1}-U_{k-1,i^{\prime }+1}}{\mathsf{\Delta }Z}}\right)$$

(15)

Thus, Equations (12)–(15) can be formed into a tridiagonal matrix equation set in the form of AX = B, and the elements of matrix A are expressions related to pore pressure, and it can be calculated and solved by an iterative method.

2.3. Degrees of Consolidation

For homogeneous elastic soils, the degree of consolidation defined by deformation and the degree of consolidation defined by pore pressure are equal. For the convenience of comparison and discussion, the consolidation degree U_p, which reflects the dissipation of soil pore pressure, is introduced here:

$$U_s=U_p=\frac{p\left(t\right)}{p_u}=P_{i^{\prime }+1}-\mathsf{\Delta }z{\displaystyle \sum _{j=1}^{n-1}\frac{U_{j,i^{\prime }}+U_{j-1,i^{\prime }}}{2}}$$

(16)

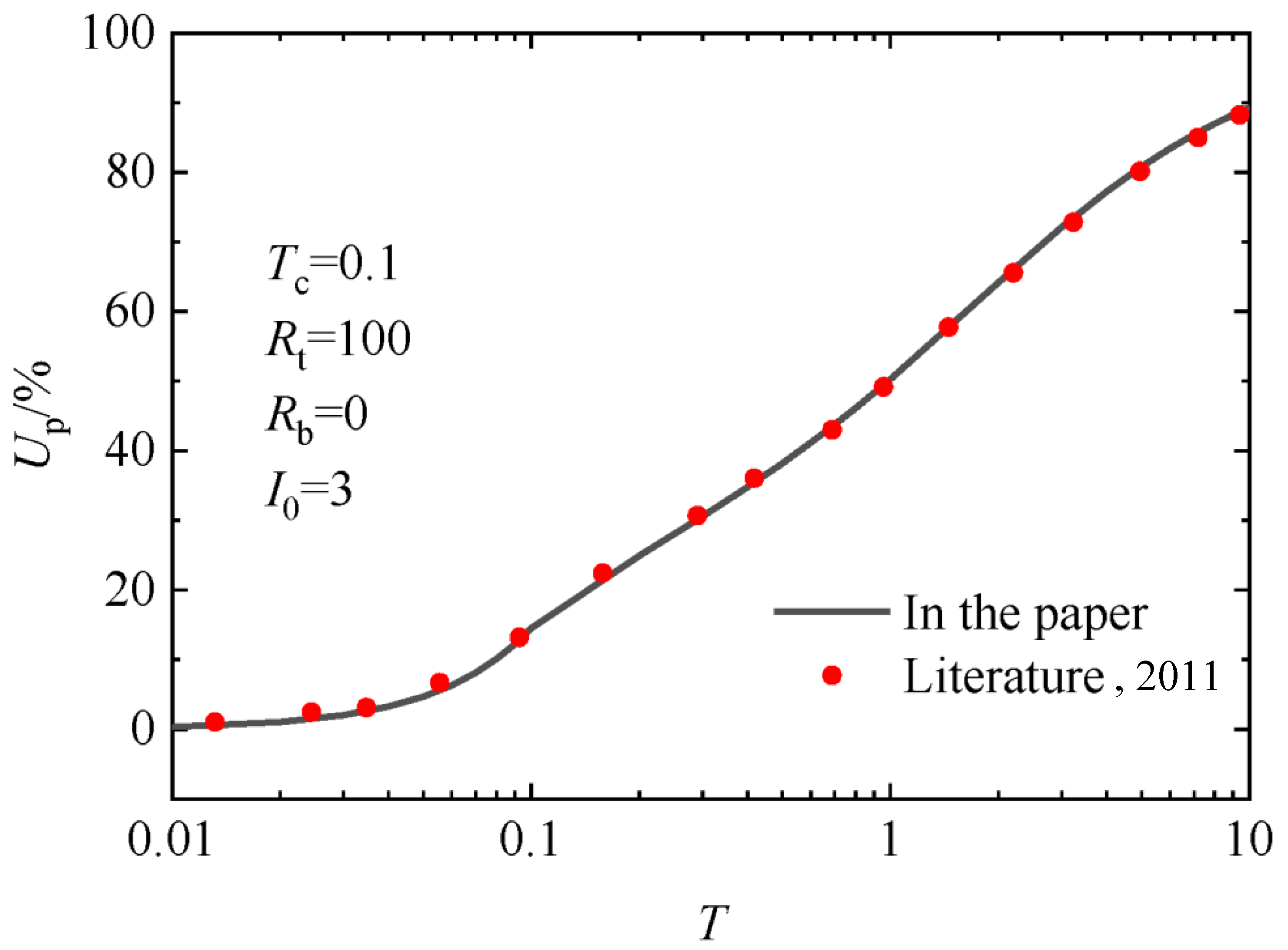
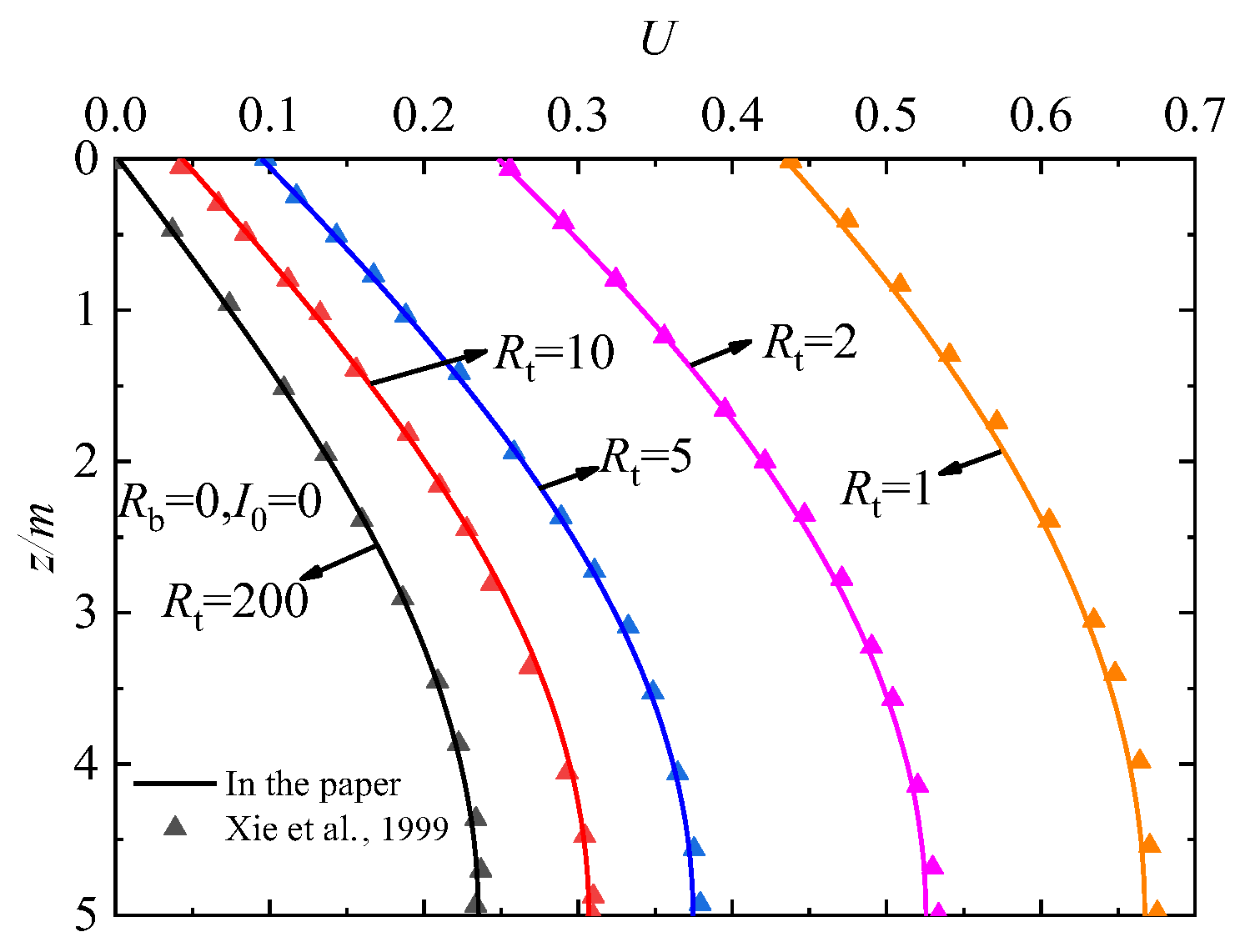
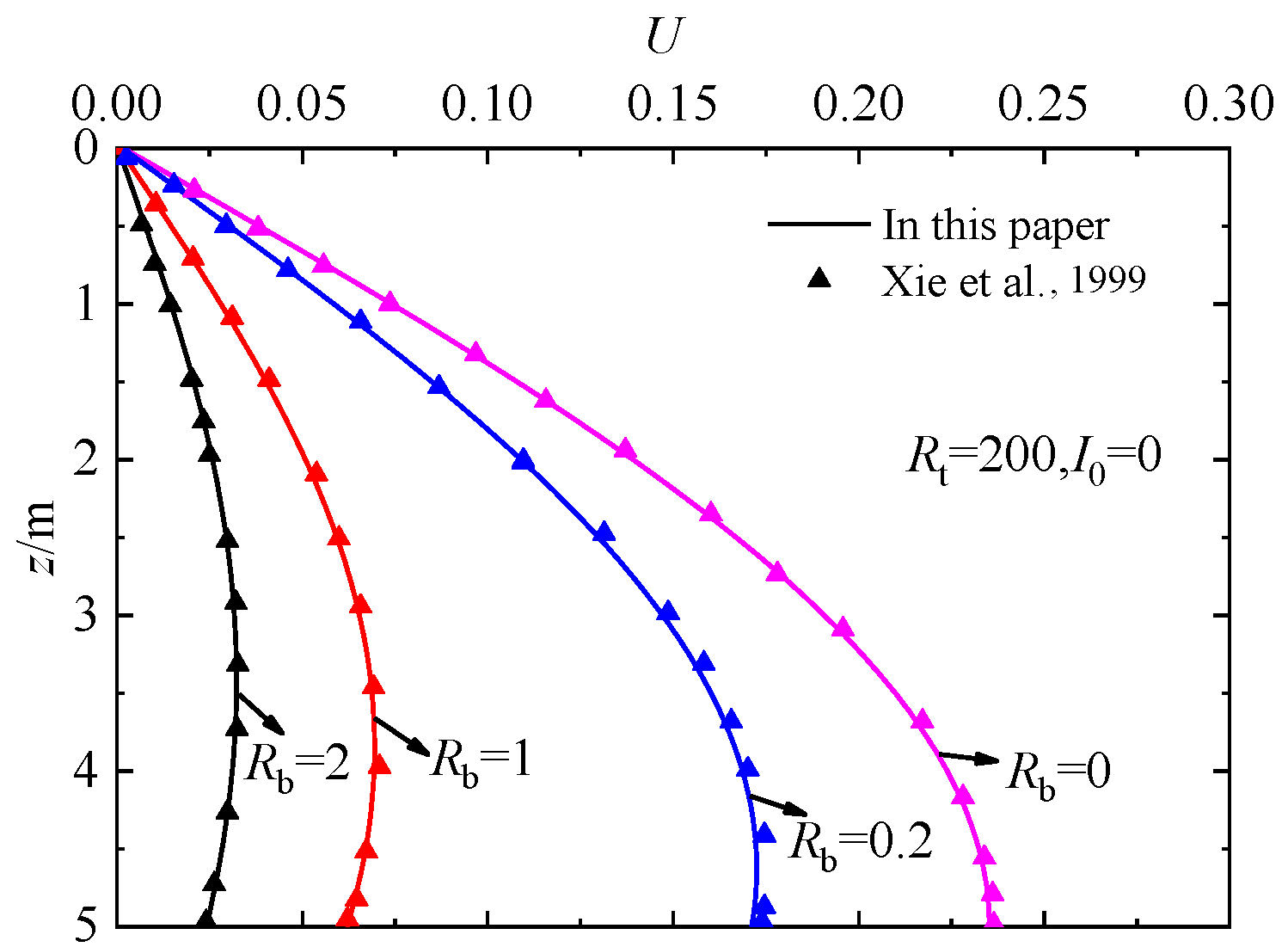
3. Verification of the Solution

When R_t = ∞, R_b = 0, the subject of this paper degenerates to a 1-D consolidation problem considering the non-Darcian flow described by the non-Newtonian index under the condition of a single-sided full-drainage boundary. The effect of single-stage linear loading on this consolidation problem has been studied by Li [22] using the C-N finite-difference format, where the dimensionless parameter n₀ = 1 corresponds to the condition where the vertical additional stress is uniformly distributed along with the depth. To verify the validity of the algorithm in this paper for nonlinear flow, the linear loading duration T_vc = 0.1 and I₀ = 3 are calculated according to the method in this paper, and the results are shown in Figure 2. For the convenience of comparison, the data corresponding to n₀ = 1 in the literature [22] are also presented in Figure 2. Then, it can be found that the results of both are quite consistent

Xie [9] gave an analytical solution for the 1-D consolidation of double-layered soil under the condition of Darcy’s law considering impeded drainage boundaries. If the parameters of the double-layered soil are the same, it can degenerate into a single-layer soil problem. As mentioned above, when I₀ = 0 and the external load p(t) is constant, the solution in the paper is simplified to the impeded drainage boundaries of Darcy’s law under constant load. To further verify the validity of the solution in this paper and the correctness of the programming, two calculation examples in the literature [9] are analyzed, using the analytical solution and the numerical method in this paper, and the corresponding results are shown in Figure 3 and Figure 4. In the two calculation examples, the thickness of the soil layer is taken as 5 m, the permeability coefficient K = 2 × 10⁻⁹ m/s, the modulus of compressibility is Es = 2 MPa, and the instantaneous load is 100 kPa. A total of 100 equal-length units are divided along with the depth, the time calculation step is taken as 1 day (i.e., T = 1.3824 × 10³), and the iteration error is set as 10⁻⁶.

Figure 3 and Figure 4 respectively show the dissipation of pore pressure along with the depth under the single-sided and double-sided impeded drainage boundaries at 500 days. It can be seen from the two figures that the numerical solutions in this paper are quite consistent with the literature solutions under either the single-sided or double-sided impeded drainage boundaries, which fully verifies the rationality of the solution in this paper and the correctness of the programming.

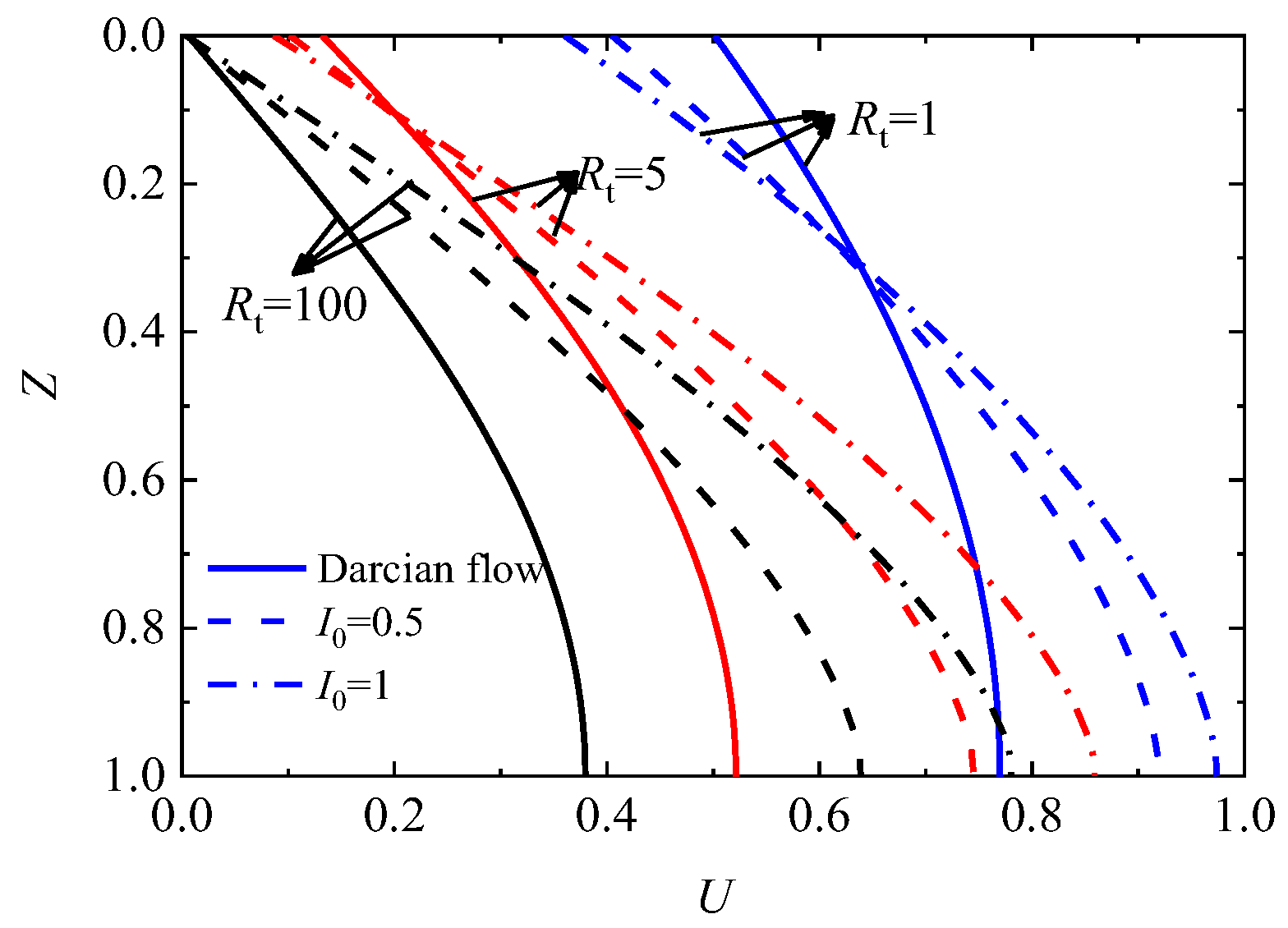
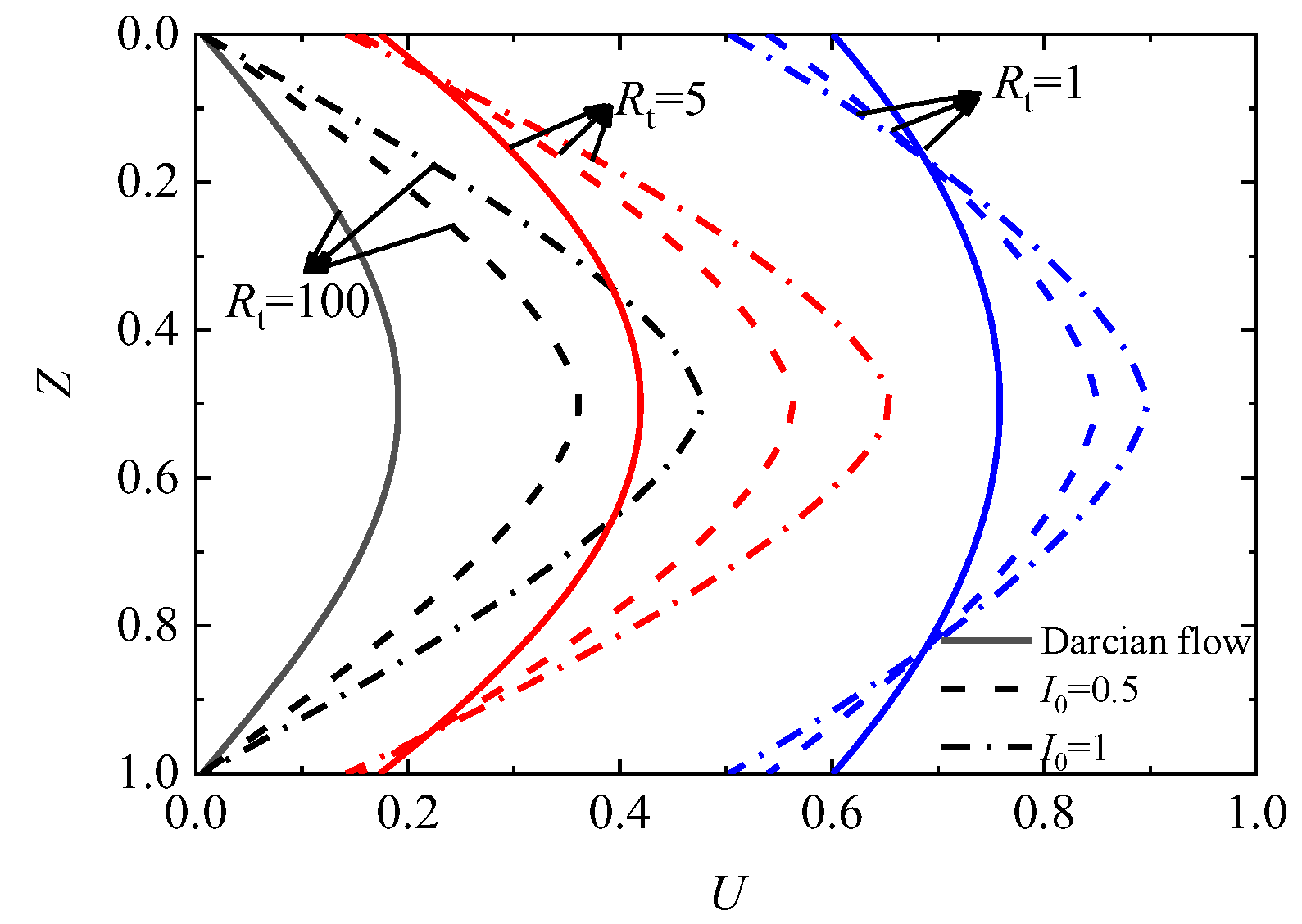
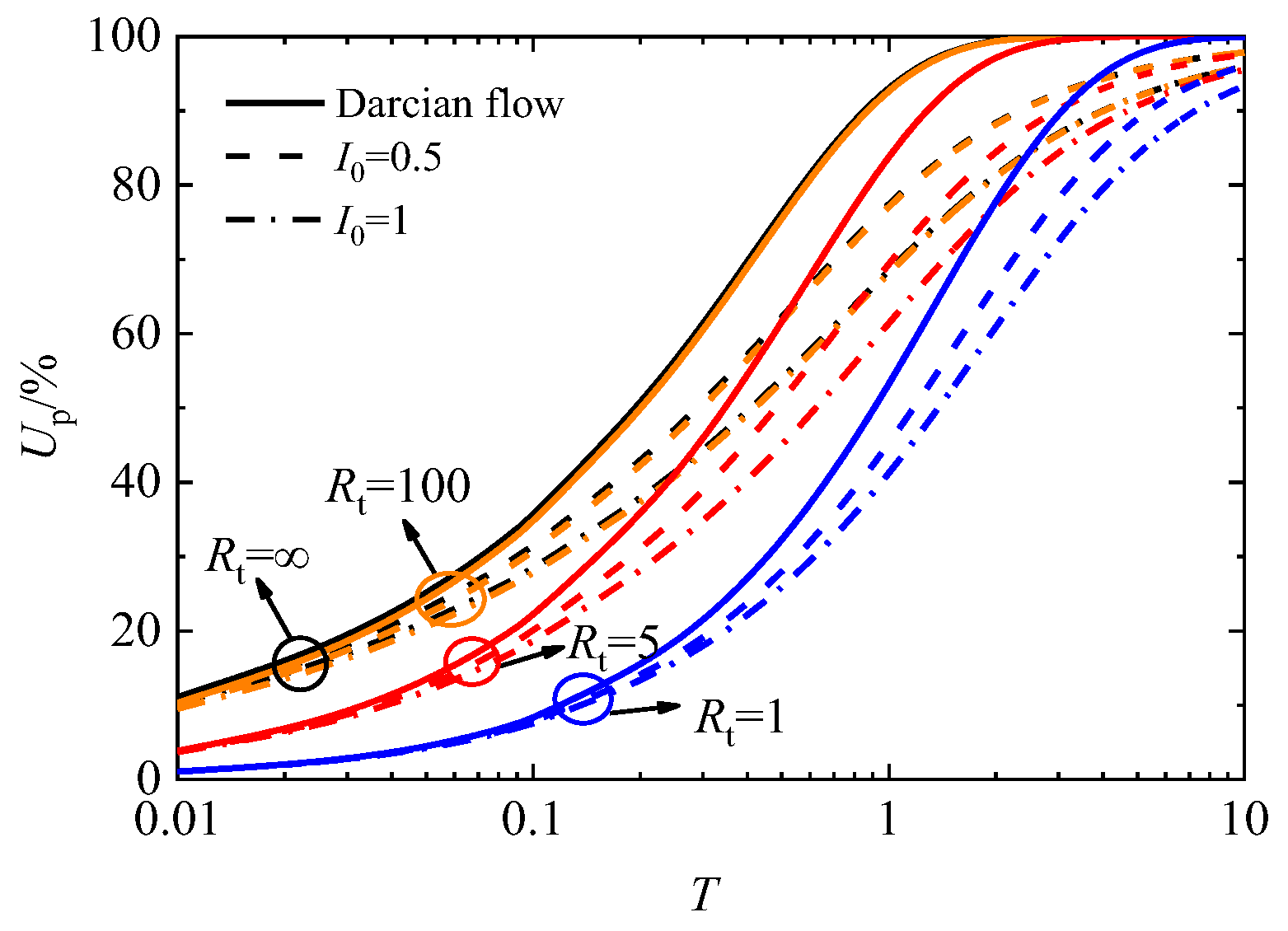
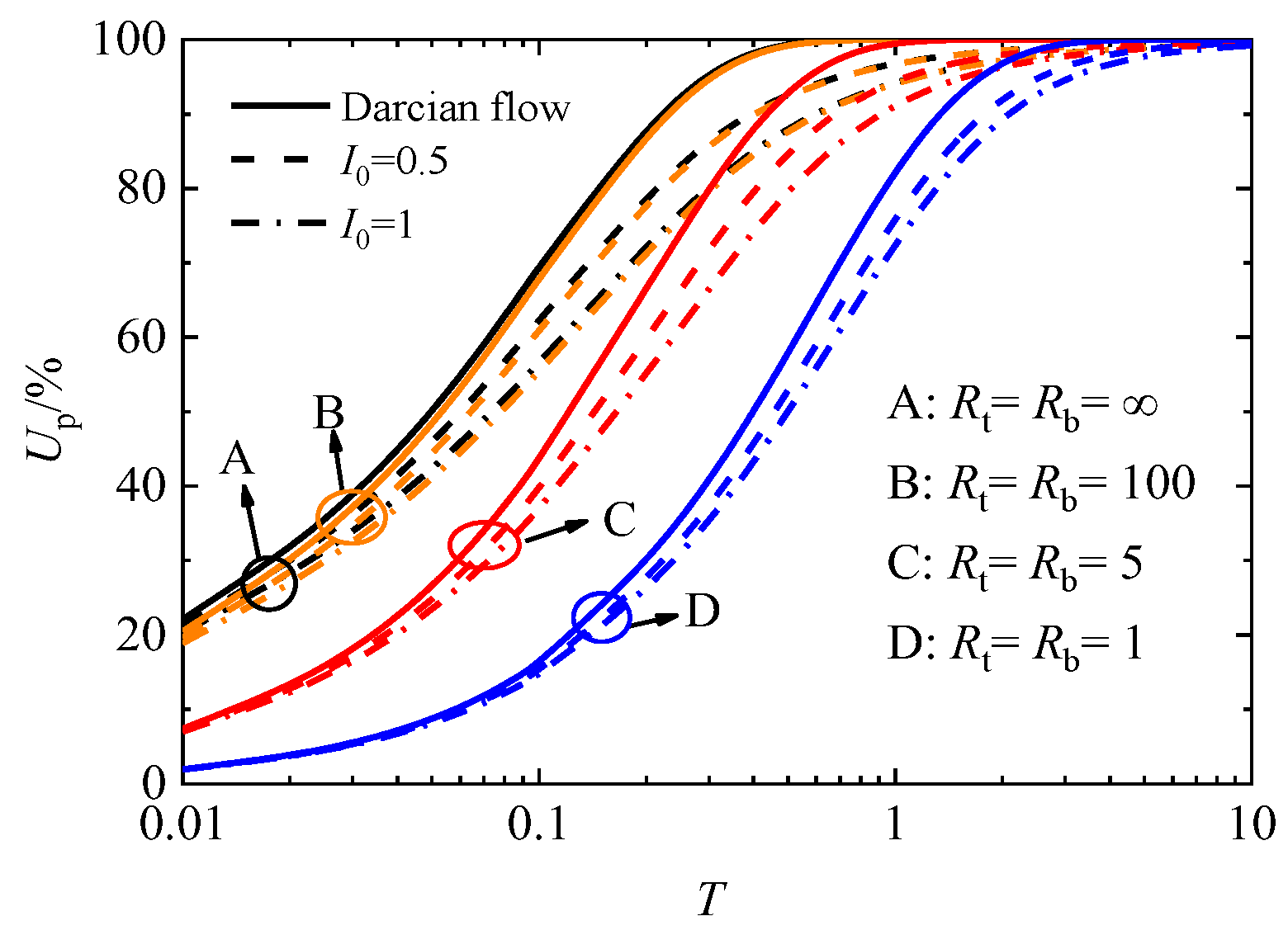
4. Consolidation Characteristics Analysis

For the convenience of discussion, this paper only discusses the case where p(t) is a constant.

Figure 5 and Figure 6 show the comparisons of pore pressure of Darcy flow (I₀ = 0) and non-Darcian flow rule (I₀ = 0.5) under single-sided and double-sided impeded drainage boundaries, respectively. It can be seen from Figure 5 that when R_t = 100, the pore pressure in Darcy’s law is faster than that in non-Darcian flow described by the non-Newtonian index along with the full depth. In contrast, when R_t =0.5, 1, 5, a different law is exhibited: There is a critical depth phenomenon, and below the critical depth, the pore pressure of Darcy’s law dissipates faster than it does under non-Darcian flow. In contrast, above the critical depth, the opposite phenomenon occurs, that is, when considering the non-Darcian flow, the excess pore water pressure dissipates faster than it does under Darcy’s flow rule, and the critical depth decreases gradually with the increase of R_t.

In fact, it is not difficult to understand from the definition of Equation (5) that when I₀ > 0, the initial pore pressure at the drainage boundary is less than I₀ = 0. That is to say, when considering non-Darcian flow, the pore pressure near the impeded drainage boundaries dissipates faster. However, in essence, this is due to the impeded drainage boundary condition because for a larger R_t, such as R_t = 100, there does not exist critical depth. For a smaller R_t, such as R_t = 1 and R_t = 5, the dissipation value of pore pressure becomes small. Then, along the depth direction of the soil layer, the dissipation rate of the pore pressure is gradually delayed when considering non-Darcian flow, i.e., it is gradually slower than Darcy’s law. It can be further seen from Figure 5 that when R_t = 100, the initial pore pressures at Z = 0 under the conditions of Darcy flow and non-Darcian flow are both equal to 0, which means it already can be treated as a completely permeable boundary. That is, in this scenario, whereas previous scholars [22,23] concluded that the dissipation of pore pressure under the condition of non-Darcian flow is always slower than that of Darcy’s law along with the depth of the soil layer, the present authors in fact believe that this phenomenon is due to the special void structure and mineral composition of cohesive soil on the one hand and the viscous resistance of bound water in cohesive soil on the other hand, which leads to the macro phenomenon of considering nonlinear flow delays the dissipation process of pore pressure.

Figure 7 and Figure 8 show the comparison of the pore pressure along with the depth for different I₀ values at the single-sided and the double-sided impeded drainage boundaries, respectively. It can be seen from the figures that when R_t is 1, 5, and 100, with the increase of flow parameter I₀, the dissipation of pore pressure along the full depth becomes slower, i.e., the greater the value of I₀ is, the more obvious the delay phenomenon of the pore pressure along with the depth is, which also indicates that the dissipation rate of pore pressure will be overestimated if the non-Darcy flow effect of flow is ignored. As also shown in Figure 7 and Figure 8, the larger the boundary parameter R is, the stronger the boundary drainage capacity of impeded drainage boundaries and the faster the consolidation rate of the soft clay ground under the same value of percolation parameter I₀.

In order to investigate the influence of impeded drainage boundary parameters on the consolidation process, the curves of the dimensionless parameter I₀ on the average consolidation degree under the single-sided and double-sided impeded drainage boundaries are depicted in Figure 9 and Figure 10, respectively. It can be seen from the two figures that both the impeded drainage boundary parameters and flow parameters have a significant influence on the consolidation process. Under the same boundary drainage parameters, the consolidation rate slows with the increase of I₀. As mentioned above, whether it is a single-sided or a double-sided impeded drainage boundary, there is a critical depth phenomenon in the dissipation of pore pressure, i.e., above the critical depth, the dissipation of pore pressure along the depth is faster than that of Darcy’s law when the non-Darcian flow is considered. However, it can be seen from Figure 9 and Figure 10 that the overall dissipation rate of the foundation soil under the above parameters still shows that non-Darcian flow slows down the consolidation process, and the larger the value of I₀, the more obvious the delay in the overall consolidation process. The authors suggest that the pore water pressure considering non-Darcian flow above the critical depth differs little from Darcy’s law. Then, the overall influence on the foundation soil is not enough to affect the overall consolidation rate of the soil layer after the pore pressure is averaged along with the depth.

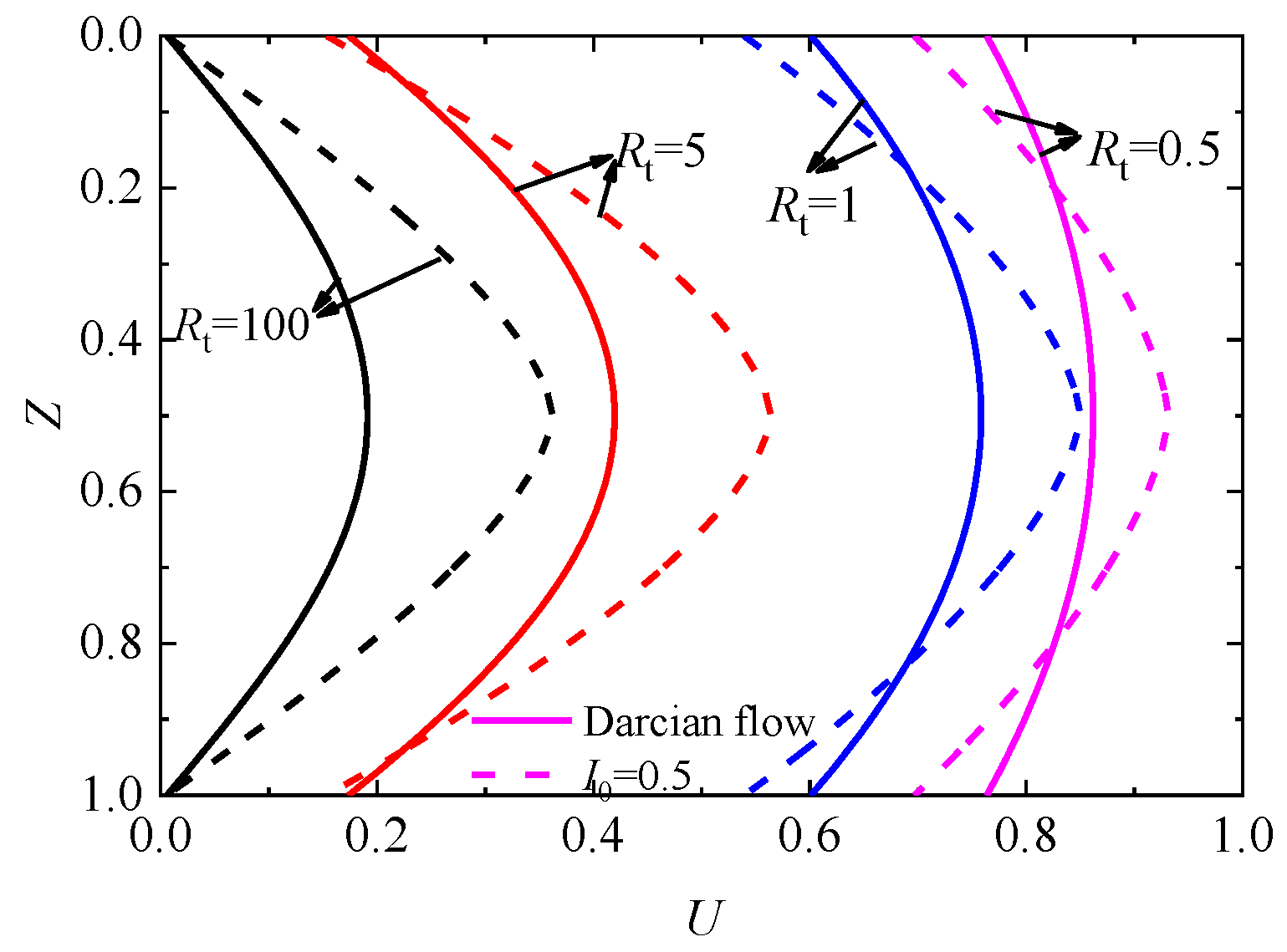
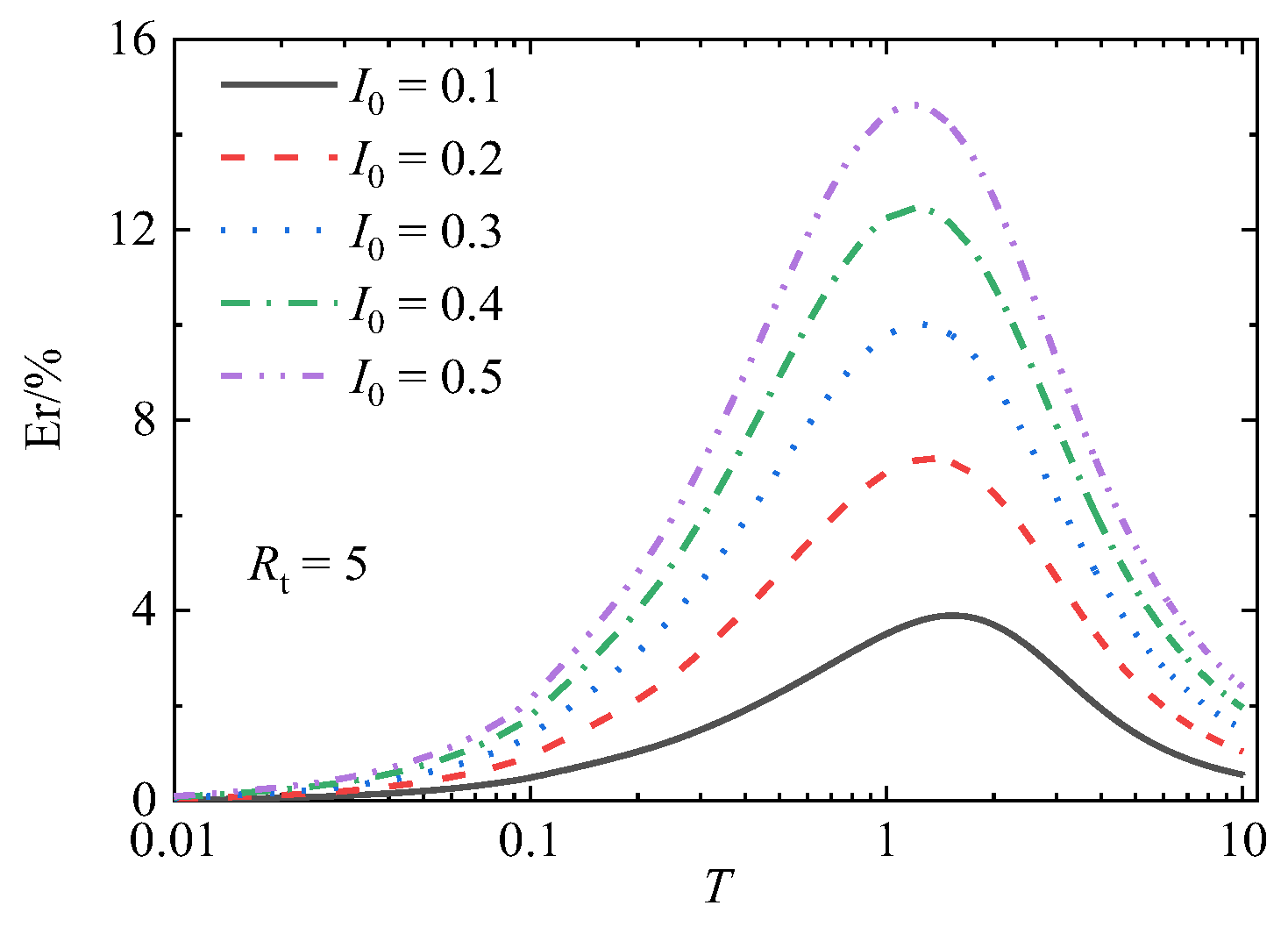
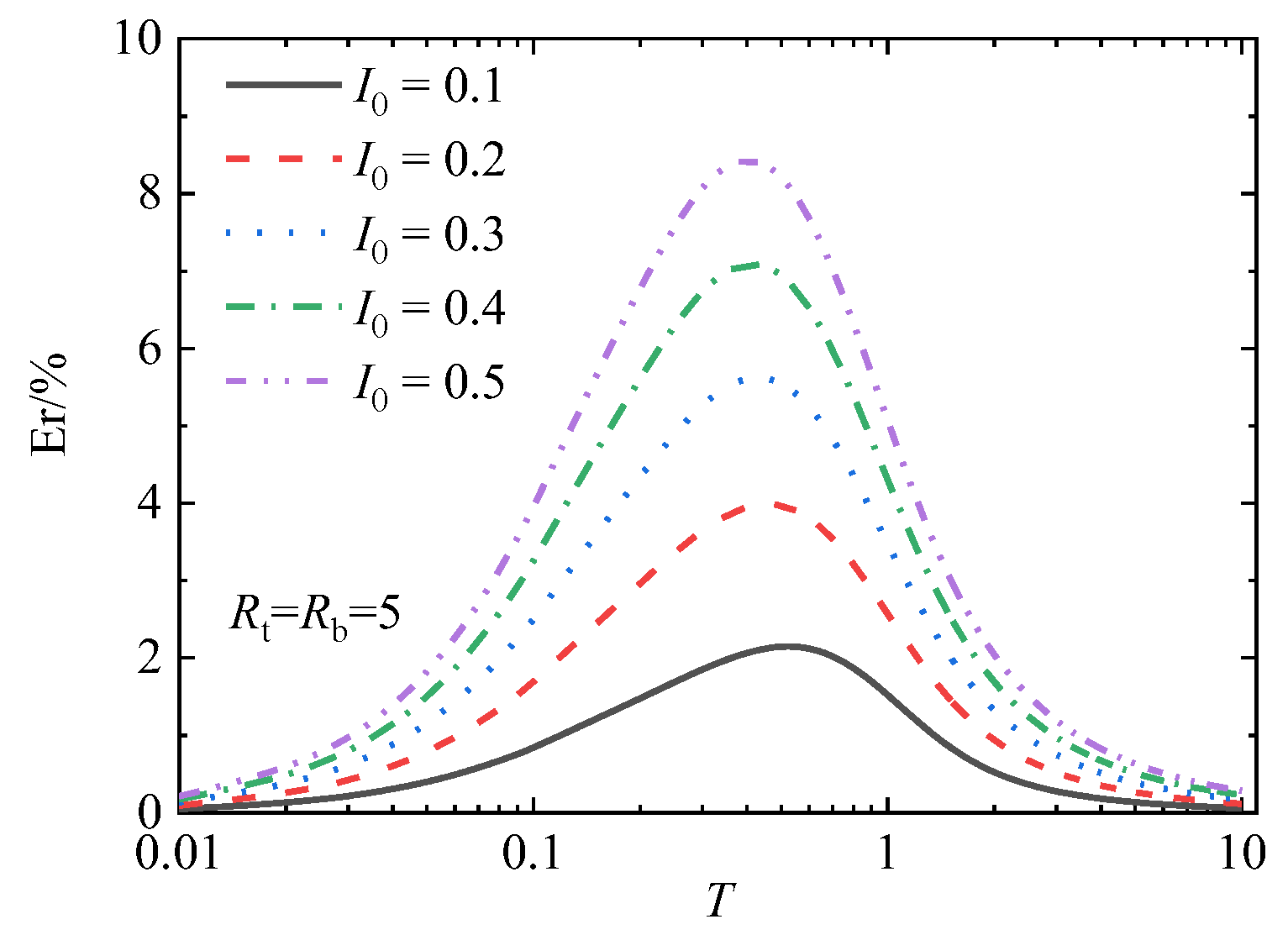
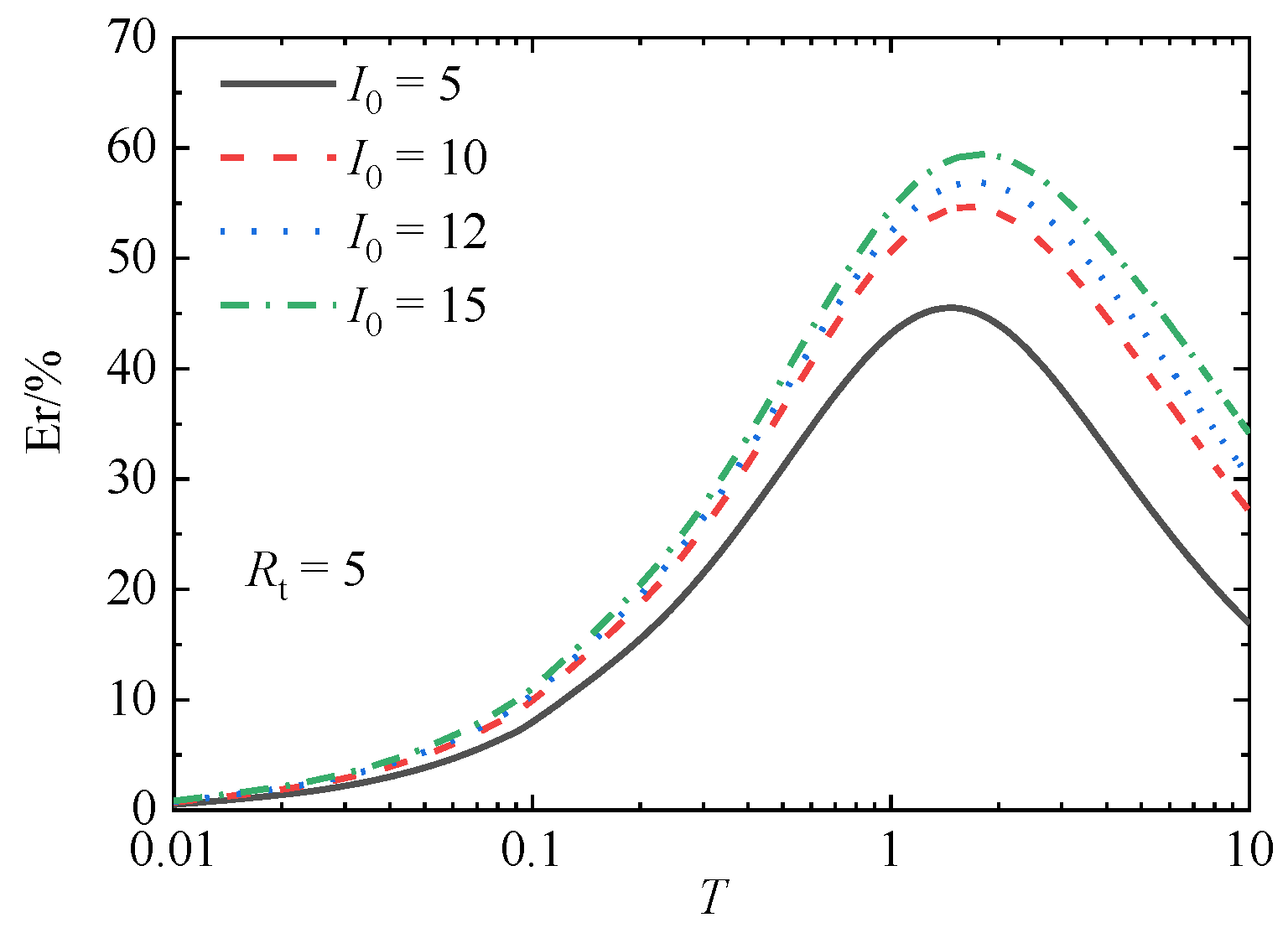
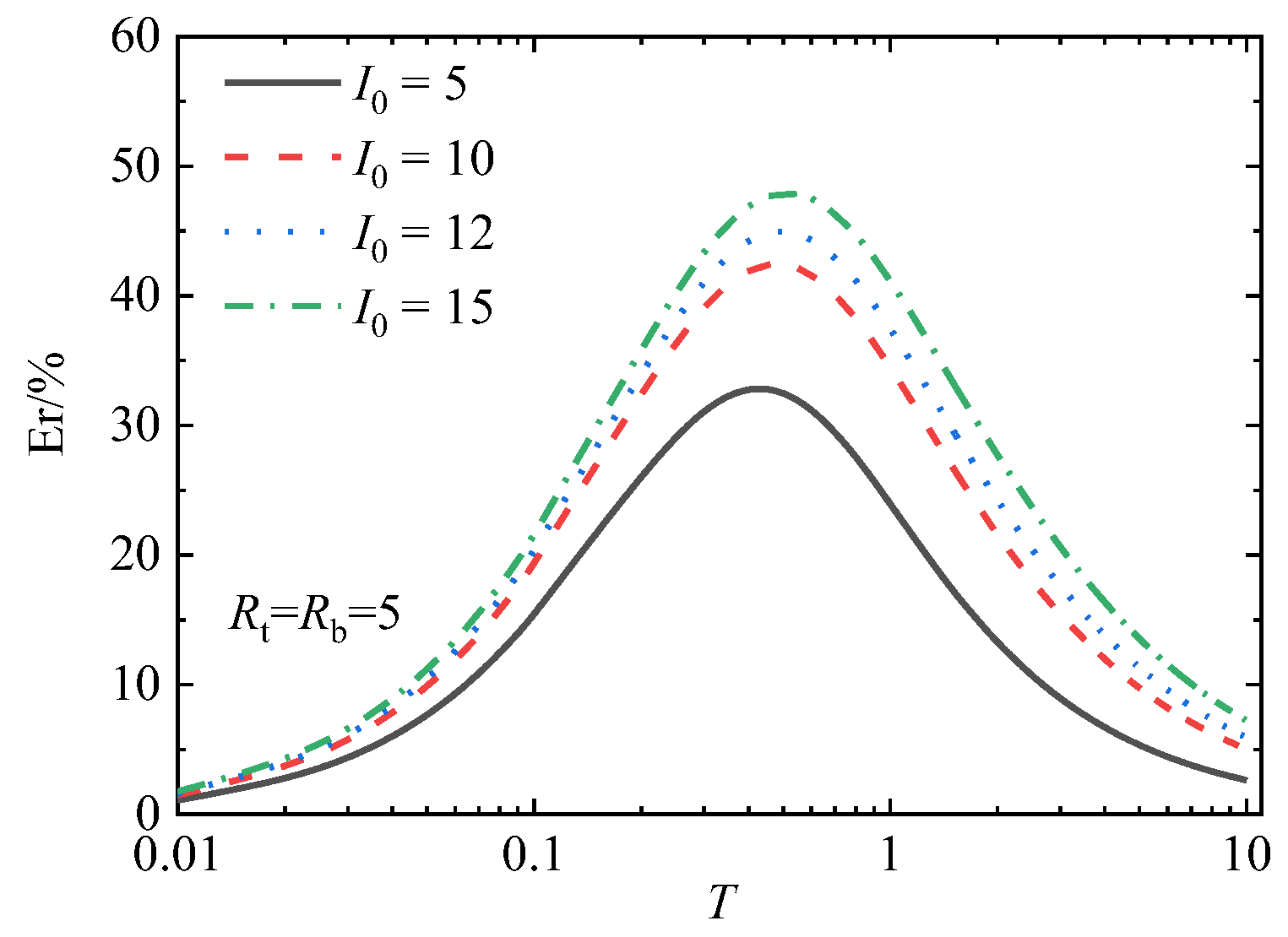
5. Discussion of the Applicability of Darcy’s Law

Li [22] discussed that the common variation range of flow parameter i₀ is concentrated in the range of 1–12. Considering its degradation form, it can be concluded that the general discussion range of i₀ is 0–12. Additionally, combined with the expression of I₀, it is believed that its variation range is generally 0–20 [22] and that its common range is 0–5 [20,24,25]. The thickness of foundation soil is generally 0–15 m, and the overburden load usually varies in the range of 100–200 kPa, and the common variation range of I₀ is summarized here. In this part of the error analysis, the variation range of I₀ is 0–15.

From Figure 9 and Figure 10, it can be concluded that when I₀ is small enough, the error caused by Darcy’s flow is acceptable in engineering practice; the deviation errors of Darcy’s law and non-Darcian flow with non-Newtonian index are shown in Figure 11 and Figure 12 (lower I₀) and Figure 13 and Figure 14 (larger I₀) under a single-sided and a double-sided impeded drainage boundary, respectively. As shown in Figure 11, under the condition of a one-sided impeded drainage boundary, when I₀ = 0.1, the maximum deviation of the non-Darcian flow described by the non-Newtonian index with Darcy’s flow is less than 4%, and when I₀ = 0.2, the maximum deviation of the two cases is less than 8%. Under the condition of a double-sided impeded drainage boundary, when I₀ = 0.1, the maximum deviation of Darcy’s flow is about 2%, and when I₀ = 0.5, the deviation is about 8.5%. As shown in Figure 13 and Figure 14, under the condition of one-sided and double-sided impeded drainage boundaries, when I₀ = 12, the maximum deviations of the non-Darcian flow with Darcy’s flow are more than 56.8% and 44.9%, respectively, and when I₀ = 15, the maximum deviation of the two cases exceeded 59.5% and 48.0% in sequence. Therefore, when the soil layer is very thin and the load acting on the soil layer is large (at this time, the I₀ value is very small), it is acceptable to apply Darcy’s law to calculate consolidation deformation in engineering. On the contrary, when the soft soil layer is very thick, and the load acting on it is small, the consolidation deformation is calculated by non-Darcian flow to avoid causing great calculation error, especially when the time factor T changes from 0.1 to 1.5.

6. Conclusions

(1)

Whether it is a single-sided or a double-sided impeded drainage boundary, there will be a critical depth phenomenon when considering non-Darcian flow incorporating impeded drainage boundaries.

(2)

Below the critical depth, the distribution of pore pressure along the depth considering non-Darcian flow with the non-Newtonian index will be slower than that of Darcy’s law, while above the critical depth, the pore pressure will dissipate faster when the non-Darcian flow rule is considered. When the impeded drainage parameter R_t or R_b increases, the critical depth gradually decreases, but the effect of this above-critical-depth phenomenon on the overall dissipation of pore pressure is not enough to affect the overall consolidation rate of the soil layer, that is, the overall dissipation rate of the soft soil layer still reflects that the overall consolidation process is delayed when considering non-Darcian flow.

(3)

Both the impeded drainage boundary parameters and flow parameters have obvious effects on the 1-D consolidation of soft soils. The larger the impeded drainage boundary parameters are, the faster the overall consolidation rate of the soft clay ground is, and when the drainage is greater than 100, it no longer has a significant effect on the consolidation process; that is, the boundary can be regarded as full drainage. Considering non-Darcian flow will delay the consolidation rate of the soft soils, and the larger the nondimensional flow parameter I₀ is, the more obvious this delay phenomenon will be.

(4)

When the value of I₀ is small (less than 0.1 under the condition of a one-sided impeded drainage boundary and less than 0.2 under the condition of a double-sided impeded drainage boundary), the maximum deviation caused by Darcy’s law for consolidation calculation is less than 5%.