Utilizing Optical Satellite Imagery to Monitor Temporal and Spatial Changes of Crop Water Stress: A Case Study in Alfalfa
Abstract
:1. Introduction
2. Materials and Methods
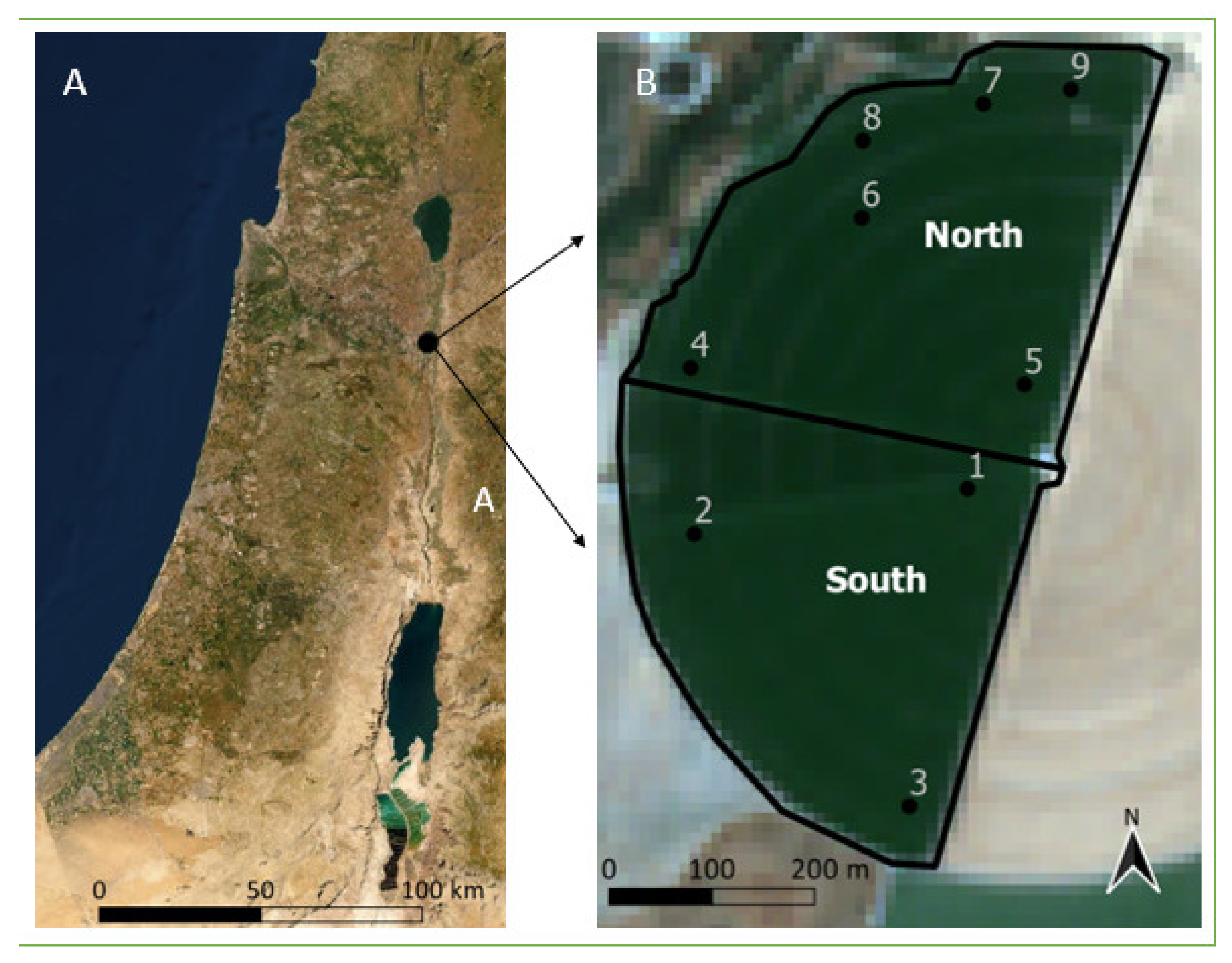
2.1. Study Area
2.2. Crop Measurements
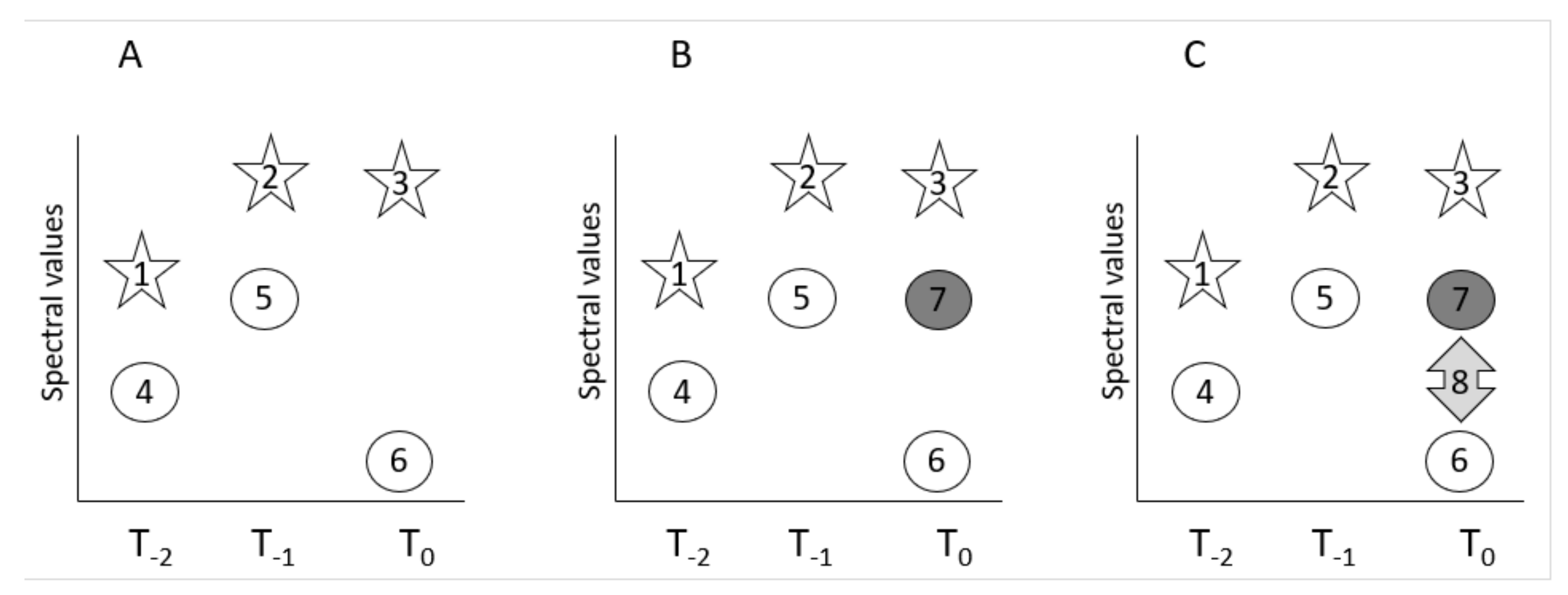
2.3. Remote Sensing
2.4. Statistical Analyses
3. Results
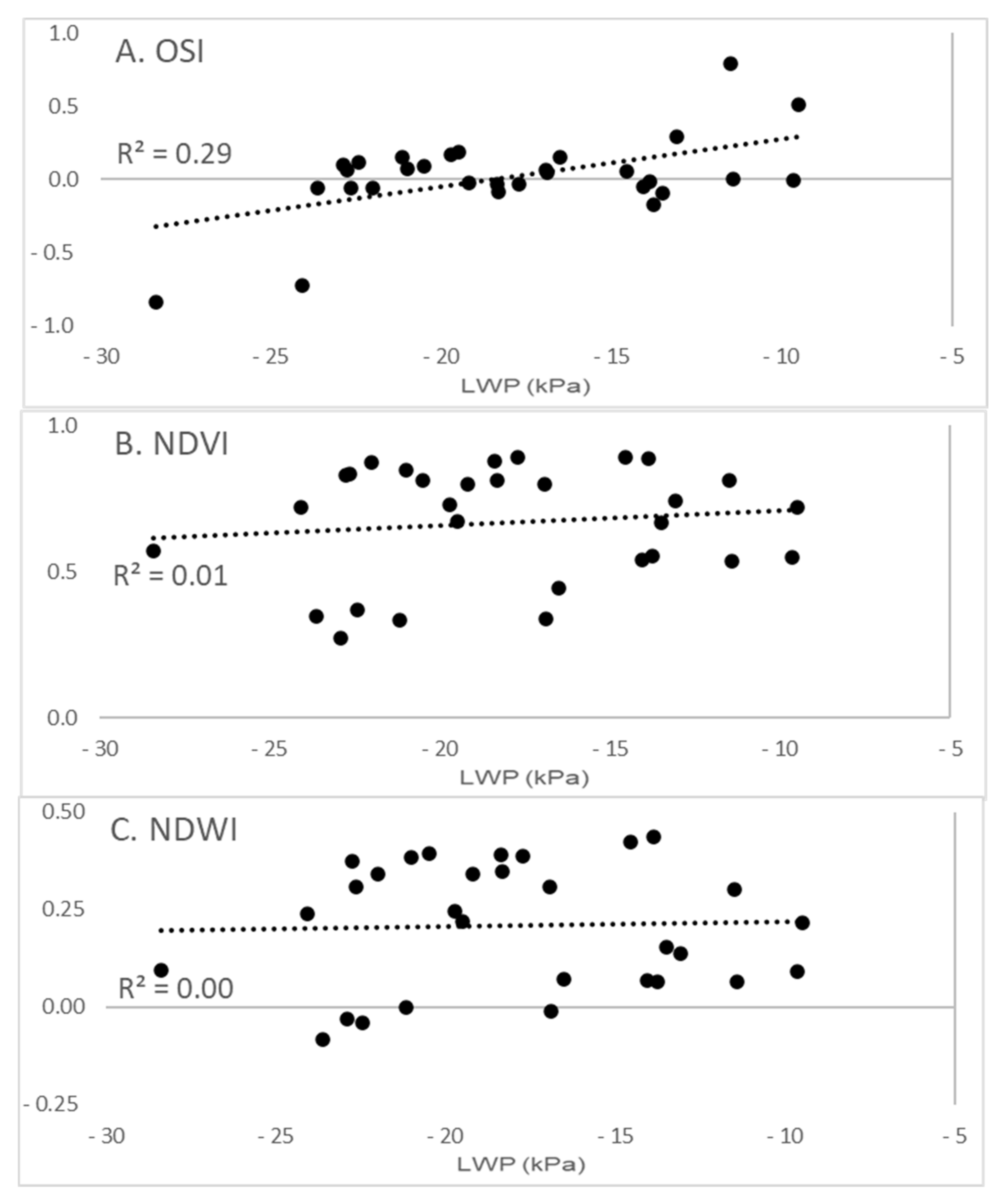
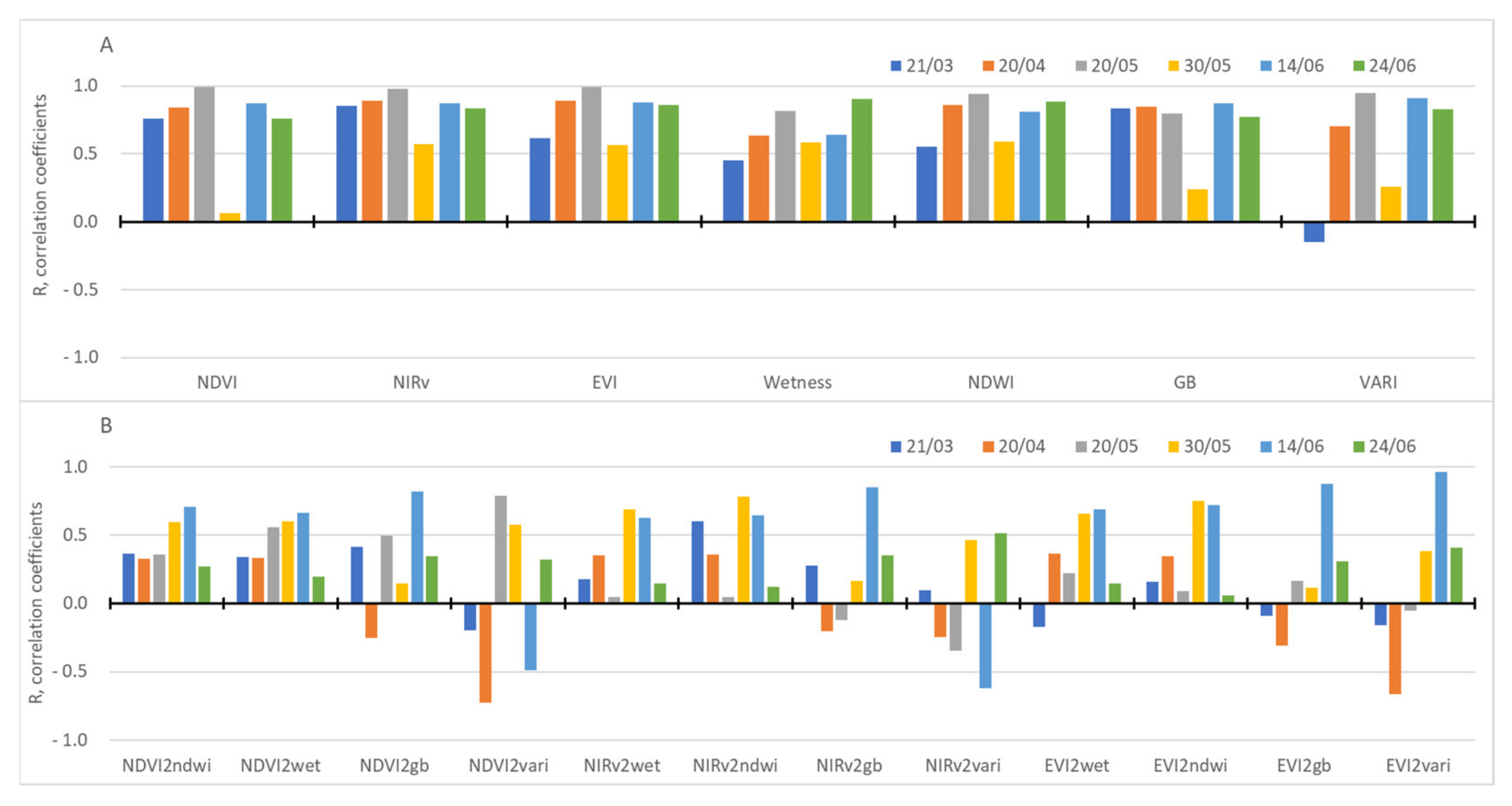
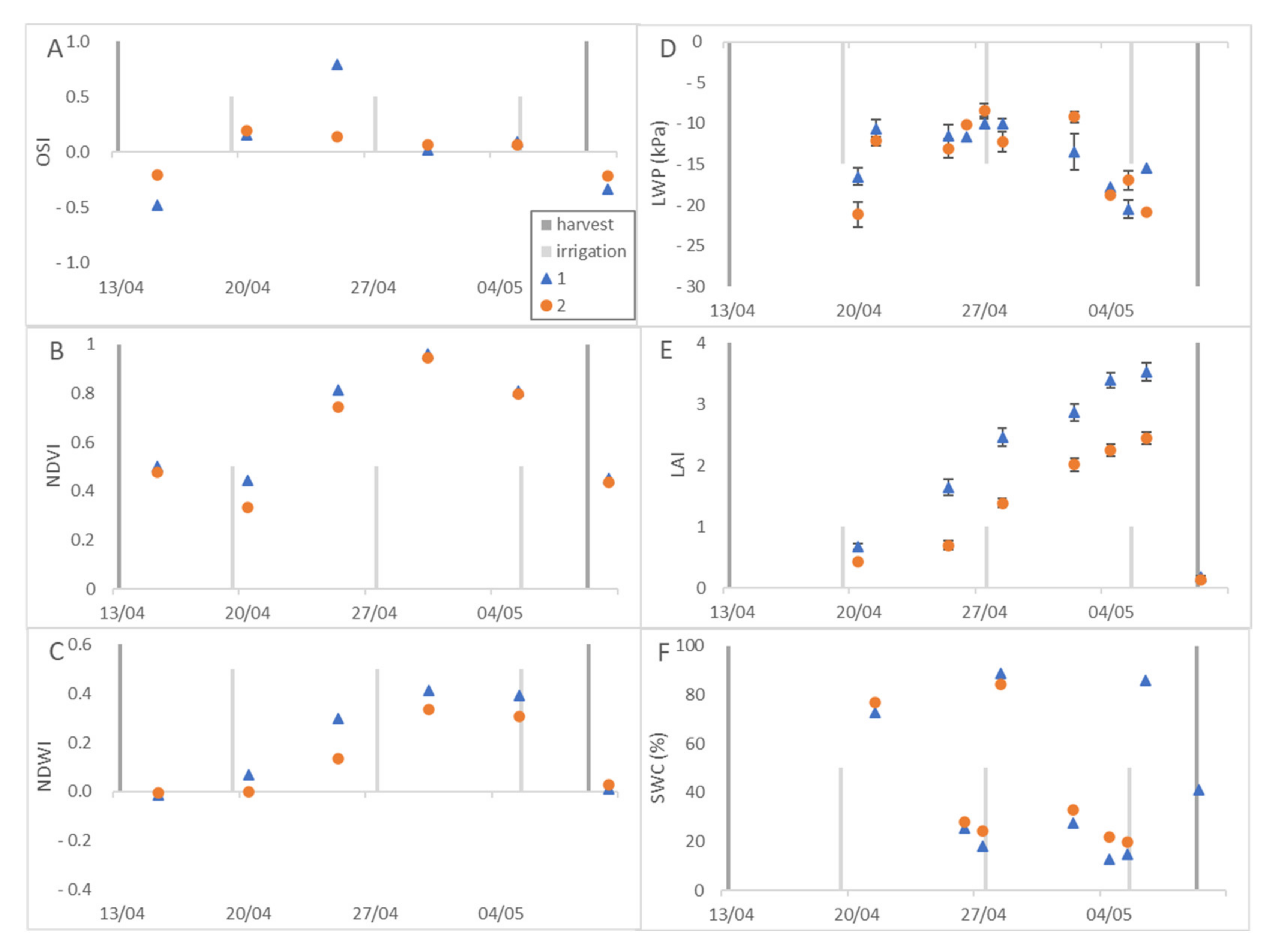
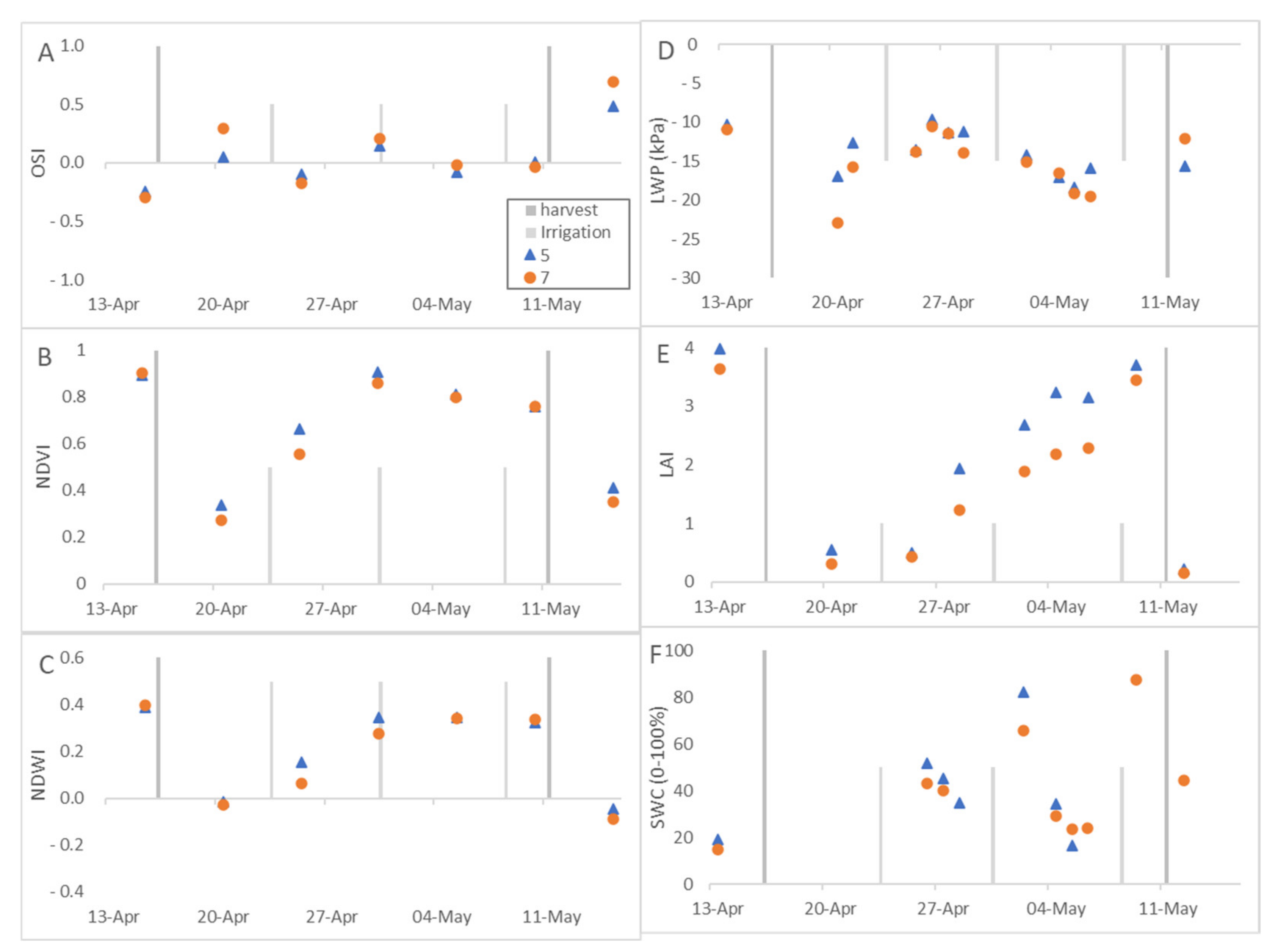
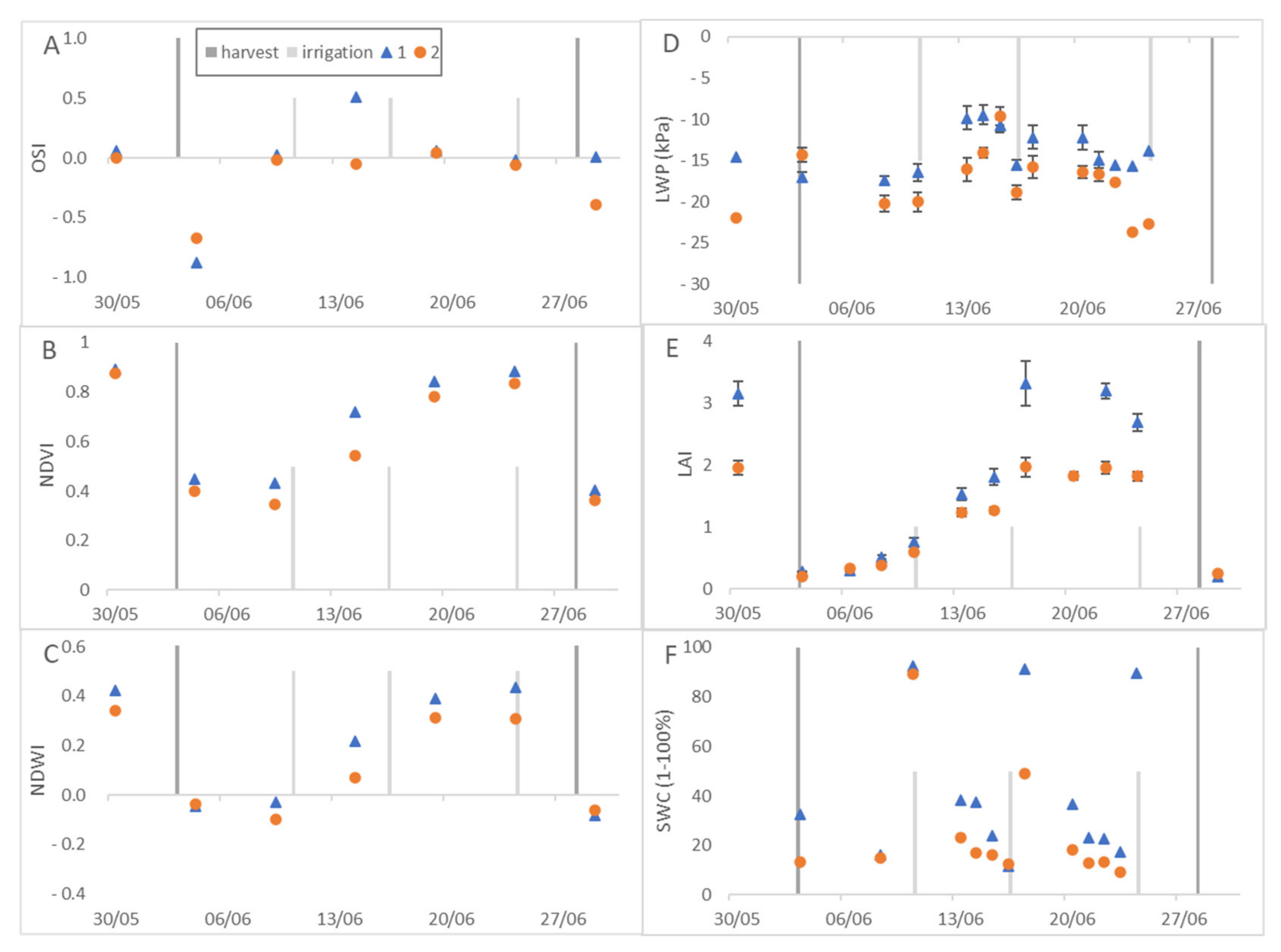
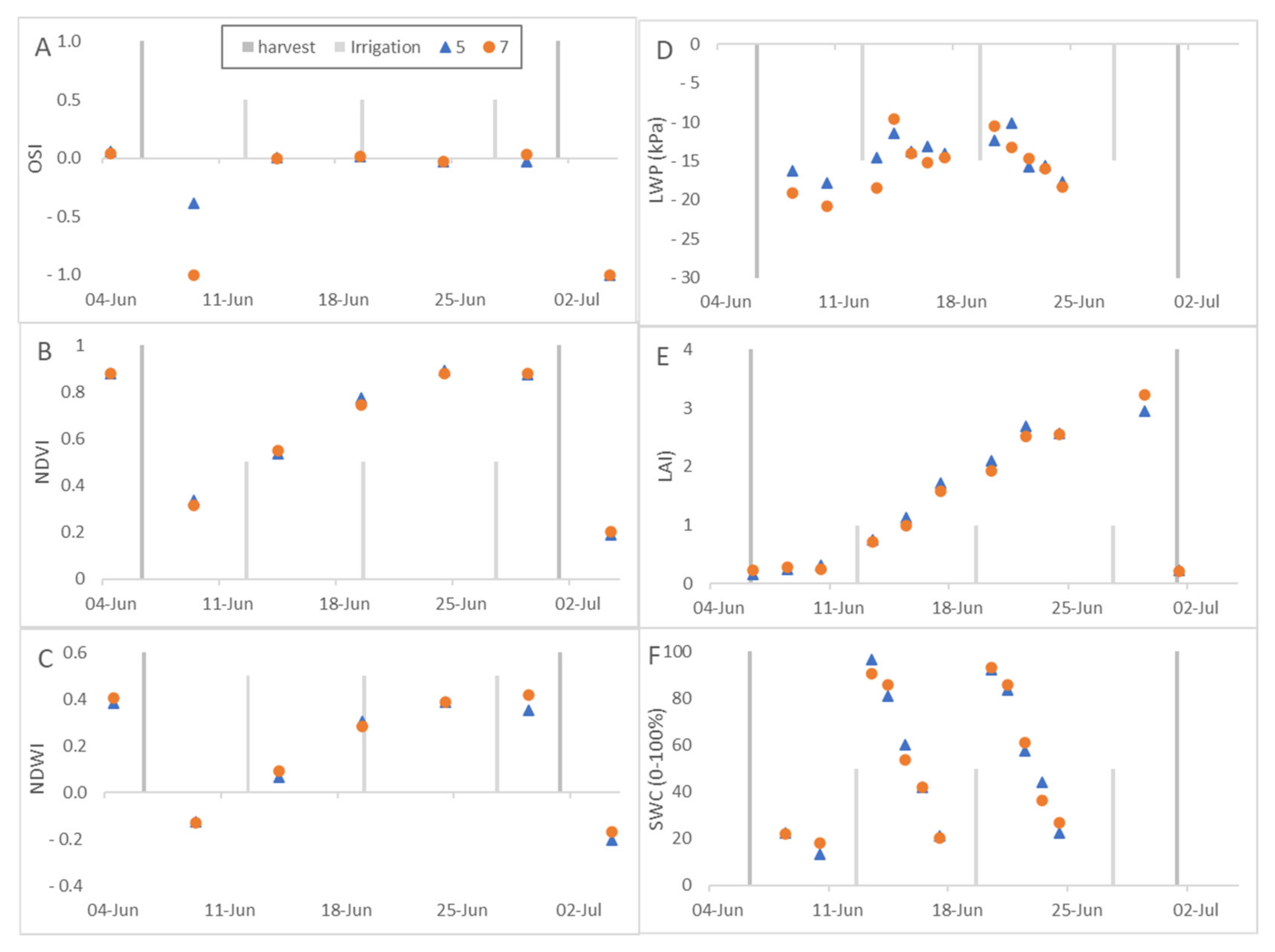
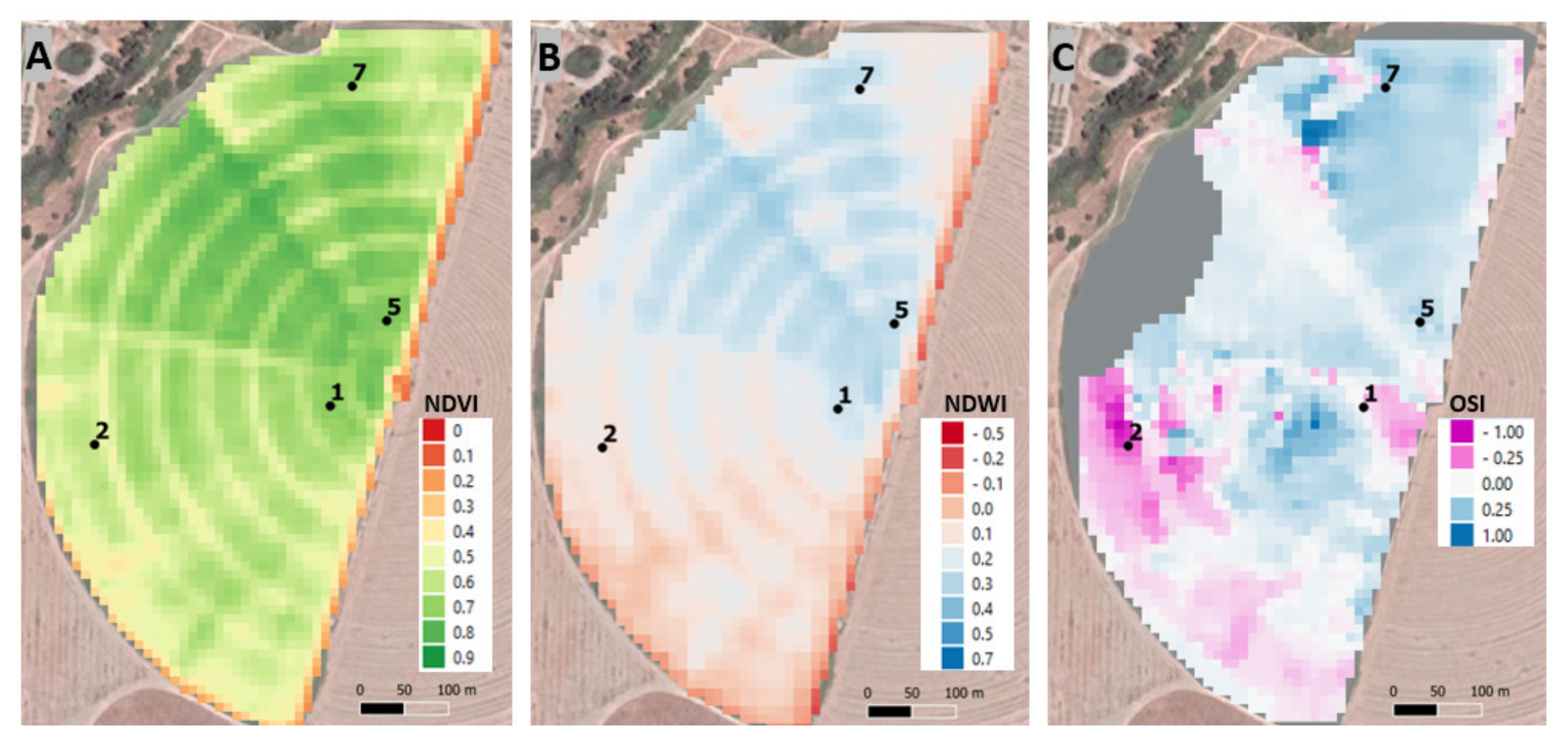
3.1. Spatial Variability of the Spectral Data: Alfalfa LWP and LAI Measurements
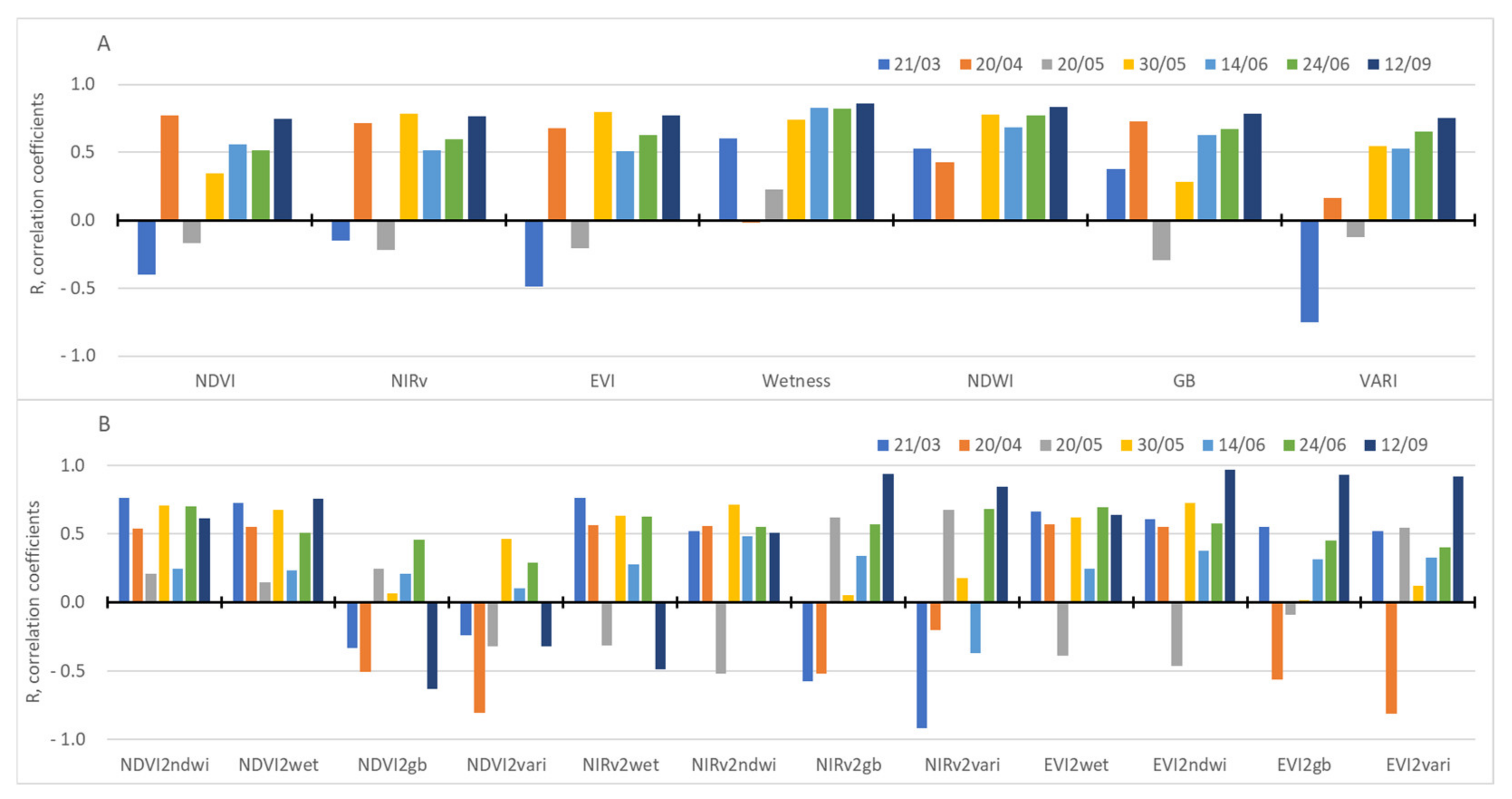
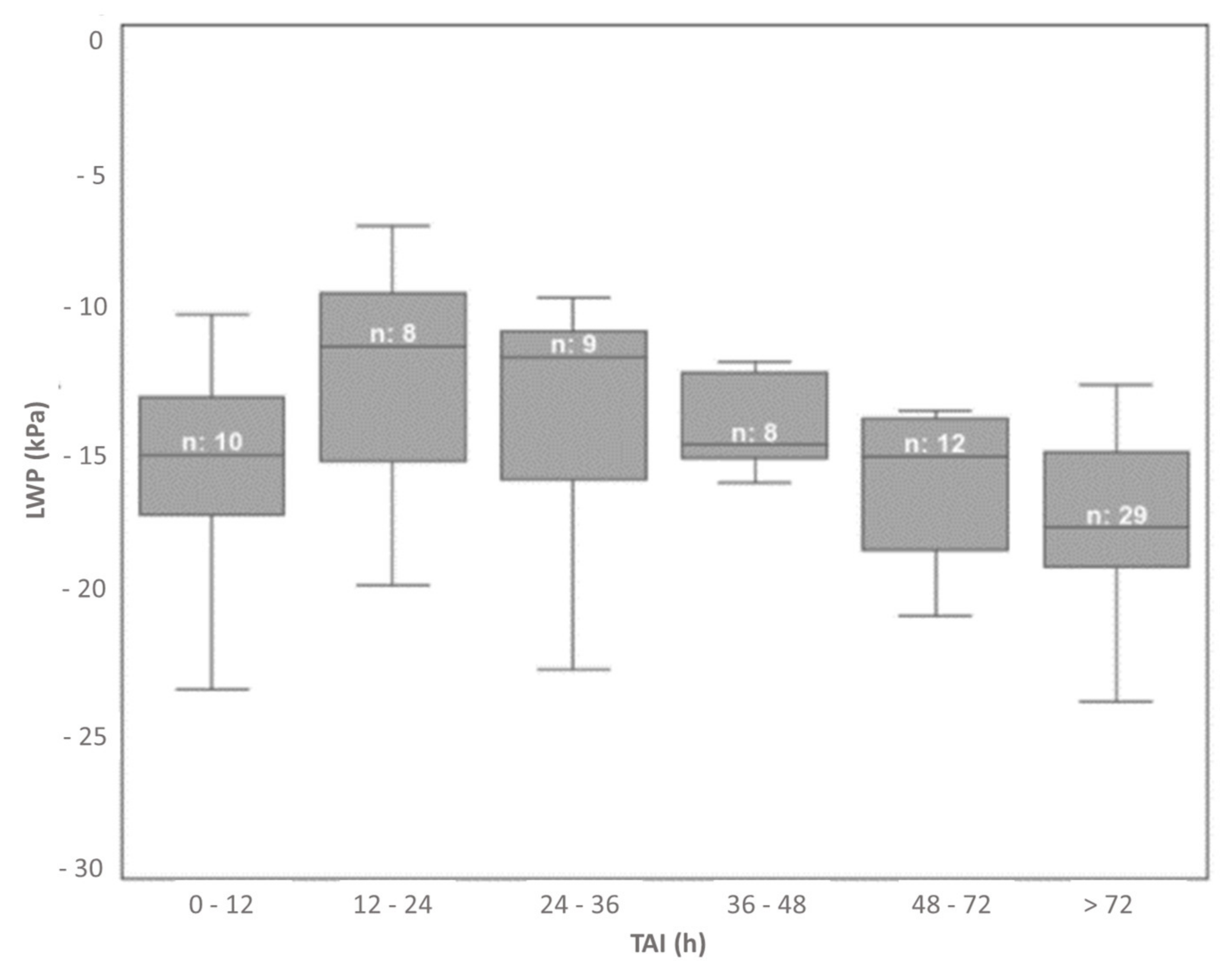
3.2. Temporal Variability of the OSI and the Crop Parameters
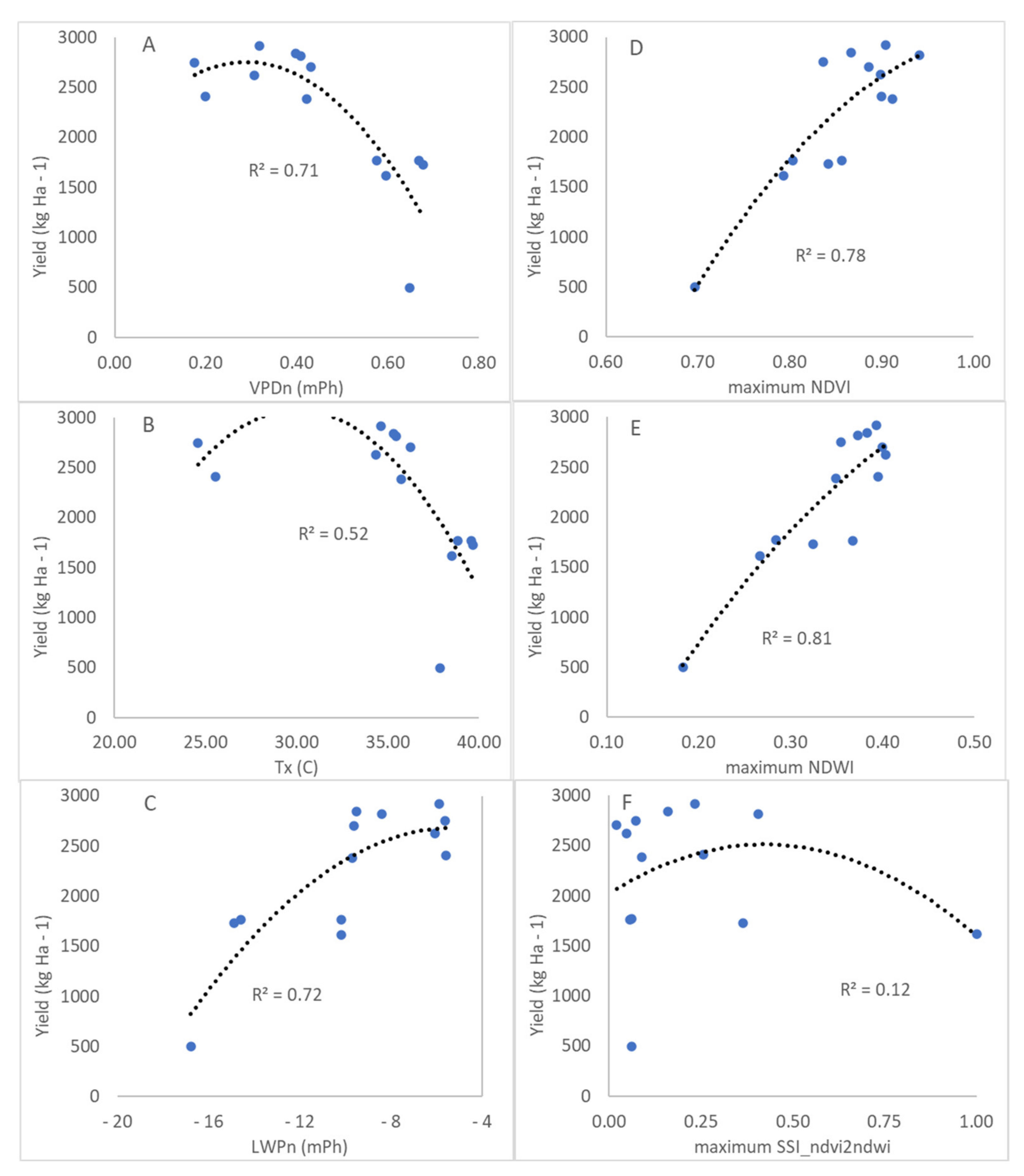
3.3. Temporal Variability of the Alfalfa Yield
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Cycle # | Dates |
|---|---|
| 1 | 6 March, 16 March, 21 March, 31 March, 5 April |
| 2 | 15 April, 20 April, 25 April, 30 April, 5 May |
| 3 | 10 May, 15 May, 20 May, 25 May, 30 May |
| 4 | 4 June, 9 June, 14 June, 19 June, 24 June, 29 June |
| 5 | 4 July, 9 July, 14 July, 19 July |
| 6 | 29 July, 3 August, 13 August |
| 7 | 18 August, 23 August, 28 August, 2 September, 7 September, 12 September |
Appendix B
| df | sum_sq | mean_sq | F | p | |
|---|---|---|---|---|---|
| TAI | 5.00 | 210.79 | 42.16 | 2.78 | 0.02 |
| Residual | 70.00 | 1061.93 | 15.17 |
| df | sum_sq | mean_sq | F | p | |
|---|---|---|---|---|---|
| TAI | 5.00 | 2.27 | 0.45 | 0.85 | 0.53 |
| Residual | 38.00 | 20.36 | 0.54 |
Appendix C
References
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and Drainage Paper No 56: Crop Evapotranspiration; United Nations FAO: Rome, Italy, 1998. [Google Scholar]
- Naor, A. Irrigation Scheduling and Evaluation of Tree Water Status in Deciduous Orchards. In Horticultural Reviews; Janick, J., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; Volume 32, pp. 111–165. ISBN 9780470767986. [Google Scholar]
- Munitz, S.; Schwartz, A.; Netzer, Y. Water consumption, crop coefficient and leaf area relations of a Vitis vinifera cv. “Cabernet Sauvignon” vineyard. Agric. Water Manag. 2019, 219, 86–94. [Google Scholar] [CrossRef]
- Halim, R.A.; Buxton, D.R.; Hattendorf, M.J.; Carlson, R.E. Water-Stress Effects on Alfalfa Forage Quality after Adjustment for Maturity Differences. Agron. J. 1989, 81, 189–194. [Google Scholar] [CrossRef]
- Teviotdale, B.L.; Goldhamer, D.A.; Viveros, M. Effects of deficit irrigation on hull rot disease of almond trees caused by Monilinia fructicola and Rhizopus stolonifer. Plant Dis. 2001, 85, 399–403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sanden, B.; Hanson, B.; Bali, K. Key irrigation management practices for alfalfa. In Proceedings of the 2012 Alfalfa & Forage Conference; UC Cooperative Extension, Plant Sciences Department, University of California: Davis, CA, USA; Sacramento, CA, USA, 2011. [Google Scholar]
- Mouradi, M.; Bouizgaren, A.; Farissi, M.; Ghoulam, C. Assessment of Deficit Irrigation Responses of Moroccan Alfalfa (Medicago sativa L.) Landraces Grown Under Field Conditions. Irrig. Drain. 2018, 67, 179–190. [Google Scholar] [CrossRef]
- Zeyliger, A.M.; Ermolaeva, O.S. Water stress regime of irrigated crops based on remote sensing and ground-based data. Agronomy 2021, 11, 1117. [Google Scholar] [CrossRef]
- Kanatas, P.; Gazoulis, I.; Travlos, I. Irrigation timing as a practice of effective weed management in established Alfalfa (Medicago sativa L.) crop. Agronomy 2021, 11, 550. [Google Scholar] [CrossRef]
- Idso, S.B. Non-water-stress baselines: A key to measuring and interpreting plant water stress. Agric. Meteorol. 1982, 27, 59–70. [Google Scholar] [CrossRef]
- Lazaridou, M.; Noitsakis, V. The effect of cutting on water balance of alfalfa plants. J. Biol. Res. 2005, 4, 189–195. [Google Scholar]
- Moran, M.; Clarke, T.; Inoue, Y.; Vidal, A. Estimating crop water efficiency using the relation between surface minus air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Chandel, A.K.; Khot, L.R.; Yu, L.-X. Alfalfa (Medicago sativa L.) crop vigor and yield characterization using high-resolution aerial multispectral and thermal infrared imaging technique. Comput. Electron. Agric. 2021, 182, 105999. [Google Scholar] [CrossRef]
- Kauth, R.J.; Thomas, G.S. The tasseled cap—A graphic description of the spectral-temporal development of agricultural crops as seen in Landsat. In Proceedings of the Symposium on Machine Processing of Remotely Sensed Data, West Lafayette, IN, USA, 29 June–1 July 1976; pp. 41–51. [Google Scholar]
- Hardisky, M.A.; Klemas, V.; Smart, R.M. The influence of soft salinity, growth form, mad leaf moisture on the spectral reflectance of Spartina alterniflora canopies. Photogramm. Eng. Remote Sens. 1983, 49, 77–83. [Google Scholar]
- Ballester, C.; Brinkhoff, J.; Quayle, W.C.; Hornbuckle, J. Monitoring the effects of water stress in cotton using the green red vegetation index and red edge ratio. Remote Sens. 2019, 11, 873. [Google Scholar] [CrossRef] [Green Version]
- Moran, M.S. Irrigation management in Arizona using satellite and airplane. Irrig. Sci. 1994, 15, 35–44. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plans with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 10–14 December 1973; pp. 309–316. [Google Scholar]
- Badgley, G.; Anderegg, L.D.L.; Berry, J.A.; Field, C.B. Terrestrial gross primary production: Using NIRV to scale from site to globe. Glob. Chang. Biol. 2019, 25, 3731–3740. [Google Scholar] [CrossRef] [PubMed]
- Huete, A.; Justice, C.; Liu, H. Development of vegetation and soil indices for MODIS-EOS. Remote Sens. Environ. 1994, 49, 224–234. [Google Scholar] [CrossRef]
- Beeri, O.; May-tal, S.; Raz, Y.; Rud, R.; Pelta, R. Detecting variability in plant water potential with multi- spectral satellite imagery. In Proceedings of the 14th International Conference on Precision Agriculture, Montreal, Canada, 24–27 June 2018. [Google Scholar]
- Gitelson, A.A.; Stark, R.; Rundquist, D.; Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel Algorithms for Remote Estimation of Vegetation Fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef] [Green Version]
- Kelly, Z.; Kemal, T. Silverman, Stuart Correlation and simple linear regression. J. Vet. Clin. 2010, 27, 427–434. [Google Scholar] [CrossRef]
- Idso, S.B.; Reginato, R.J.; Reicosky, D.C.; Hatfield, J.L. Determining Soil-Induced Plant Water Potential Depressions in Alfalfa by Means of Infrared Thermometry 1. Agron. J. 1981, 73, 826–830. [Google Scholar] [CrossRef]
- Schneider, P.; Roberts, D.A.; Kyriakidis, P.C. A VARI-based relative greenness from MODIS data for computing the Fire Potential Index. Remote Sens. Environ. 2008, 112, 1151–1167. [Google Scholar] [CrossRef]
- Anderson, M.C.; Neale, C.M.U.; Li, F.; Norman, J.M.; Kustas, W.P.; Jayanthi, H.; Chavez, J. Upscaling ground observations of vegetation water content, canopy height, and leaf area index during SMEX02 using aircraft and Landsat imagery. Remote. Sens. Environ. 2004, 92, 447–464. [Google Scholar] [CrossRef]
- Zarate-valdez, J.L.; Whiting, M.L.; Lampinen, B.D.; Metcalf, S.; Ustin, S.L.; Brown, P.H. Prediction of leaf area index in almonds by vegetation indexes. Comput. Electron. Agric. 2012, 85, 24–32. [Google Scholar] [CrossRef]
- Brown, P.W.; Tanner, C.B. Alfalfa Stem and Leaf Growth during Water Stress 1. Agron. J. 1983, 75, 799–805. [Google Scholar] [CrossRef]
- Sharratt, B.S.; Reicosky, D.C.; Idso, S.B.; Baker, D.C. Relationships between leaf water potential, canopy temperature and evapotranspiration in irrigated and nonirrigated Alfalfa. Agron. J. 1983, 75, 891–894. [Google Scholar] [CrossRef]
- Beeri, O.; Pelta, R.; Shilo, T.; Mey-Tal, S. Assessing infield temporal and spatial variability of leaf water potential. In Proceedings of the Precision agriculture 2019; Stafford, J., Ed.; Wageningen Academic Publishers: Wageningen, The Netherlands, 2019; pp. 263–270. [Google Scholar]
- Drechsler, K.; Kisekka, I.; Upadhyaya, S. A comprehensive stress indicator for evaluating plant water status in almond trees. Agric. Water Manag. 2019, 216, 214–223. [Google Scholar] [CrossRef]
- Moran, M.S.; Inoue, Y.; Barnes, E.M. Opportunities and Limitations for Image-Based Remote Sensing in Precision Crop Management. Remote Sens. Environ. 2000, 61, 319–346. [Google Scholar] [CrossRef]

| # | Harvest Date | Yield (kg ha−1) | Tx (Co) | Tn (Co) | VPDx (kPa) | VPDn (kPa) | ETo (mm day−1) |
|---|---|---|---|---|---|---|---|
| Southern zone | |||||||
| 1 | 13 April | 2750 | 24.59 | 10.78 | 2.83 | 0.17 | 4.16 |
| 2 | 9 May | 2817 | 35.48 | 16.01 | 4.92 | 0.41 | 7.34 |
| 3 | 3 June | 2917 | 34.64 | 18.19 | 4.54 | 0.32 | 7.72 |
| 4 | 28 June | 2842 | 35.35 | 20.15 | 4.60 | 0.40 | 8.00 |
| 5 | 23 July | 1770 | 38.85 | 24.11 | 5.32 | 0.57 | 8.47 |
| 6 | 16 August | 1730 | 39.67 | 25.20 | 5.45 | 0.68 | 8.12 |
| 7 | 14 September | 500 | 37.89 | 24.22 | 5.01 | 0.65 | 7.31 |
| Northern zone | |||||||
| 1 | 16 April | 2407 | 25.53 | 10.90 | 3.02 | 0.20 | 4.52 |
| 2 | 11 May | 2385 | 35.76 | 16.89 | 4.94 | 0.42 | 7.40 |
| 3 | 6 June | 2625 | 34.37 | 17.93 | 4.49 | 0.31 | 7.65 |
| 4 | 1 July | 2704 | 36.24 | 20.83 | 4.80 | 0.43 | 8.14 |
| 5 | 26 July | 1615 | 38.52 | 24.48 | 5.21 | 0.60 | 8.32 |
| 6 | 19 August | 1766 | 39.61 | 24.98 | 5.45 | 0.67 | 8.14 |
| 7 | 14 September | 37.95 | 24.19 | 5.03 | 0.64 | 7.26 | |
| Name | Equation | Source | |
|---|---|---|---|
| Remotely sensed growth index | |||
| 1 | Normalized difference vegetation index (NDVI) | (B8 − B4)/(B8 + B4) | [18] |
| 2 | Near infrared vegetation (NIRv) | B8 × ((B8 − B4)/(B8 + B4)) | [19] |
| 3 | Enhanced vegetation index (EVI) | 2.5 × (B8 − B4)/ (B8 + 6.0 × B4 + 7.5 + B2 + 1) | [20] |
| Remotely sensed water stress index | |||
| 4 | Modified tasseled cap wetness | ((B2 × 0.14 + B3 × 0.18 + B4 × 0.33 + B8 × 0.34 − B11 × 0.62 − B12 × 0.42)/a + b) × c | Originally from [14] ** |
| 5 | Normalized difference water index (NDWI) | (B8 − B11)/(B8 + B11) | [15] |
| 6 | Green-Blue (GB) | (B3 − B2)/(B3 + B2) | [21] |
| 7 | Visible Atmospherically Resistant Index (VARI) | (B3 − B4)/(B3 + B4 − B2) | [22] |
| NDVI | NIRv | EVI | Wetness | NDWI | GB | VARI | ndvi2wet | |
|---|---|---|---|---|---|---|---|---|
| NIRv | 0.97 | |||||||
| EVI | 0.96 | 0.98 | ||||||
| Wetness | 0.91 | 0.92 | 0.94 | |||||
| NDWI | 0.97 | 0.97 | 0.97 | 0.98 | ||||
| GB | 0.69 | 0.69 | 0.56 | 0.53 | 0.62 | |||
| VARI | 0.95 | 0.95 | 0.96 | 0.90 | 0.94 | 0.63 | ||
| OSI ndvi2wet | 0.35 | 0.35 | 0.38 | 0.38 | 0.37 | 0.19 | 0.34 | |
| OSI ndvi2ndwi | 0.35 | 0.33 | 0.35 | 0.36 | 0.36 | 0.20 | 0.33 | 0.88 |
| Weather Parameters | r | LWP Values | r |
|---|---|---|---|
| Average Ta minimum | −0.65 | Maximum LWP | 0.81 |
| Average Ta maximum | −0.49 | Minimum LWP | 0.68 |
| Average VPD minimum | −0.76 | ||
| Average VPD maximum | −0.45 | ||
| Average ETo | −0.24 |
| Index | r for the Minimum Value | r for the Maximum Value |
|---|---|---|
| NDVI | 0.59 | 0.87 |
| NIRv | 0.59 | 0.88 |
| EVI | 0.57 | 0.89 |
| Wetness | 0.41 | 0.89 |
| NDWI | 0.55 | 0.90 |
| GB | 0.67 | 0.40 |
| VARI | 0.65 | 0.43 |
| ndvi2wet | −0.52 | 0.11 |
| ndvi2ndwi | −0.55 | −0.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beeri, O.; Tarshish, R.; Pelta, R.; Shilo, T. Utilizing Optical Satellite Imagery to Monitor Temporal and Spatial Changes of Crop Water Stress: A Case Study in Alfalfa. Water 2022, 14, 1676. https://doi.org/10.3390/w14111676
Beeri O, Tarshish R, Pelta R, Shilo T. Utilizing Optical Satellite Imagery to Monitor Temporal and Spatial Changes of Crop Water Stress: A Case Study in Alfalfa. Water. 2022; 14(11):1676. https://doi.org/10.3390/w14111676
Chicago/Turabian StyleBeeri, Ofer, Rom Tarshish, Ran Pelta, and Tal Shilo. 2022. "Utilizing Optical Satellite Imagery to Monitor Temporal and Spatial Changes of Crop Water Stress: A Case Study in Alfalfa" Water 14, no. 11: 1676. https://doi.org/10.3390/w14111676
APA StyleBeeri, O., Tarshish, R., Pelta, R., & Shilo, T. (2022). Utilizing Optical Satellite Imagery to Monitor Temporal and Spatial Changes of Crop Water Stress: A Case Study in Alfalfa. Water, 14(11), 1676. https://doi.org/10.3390/w14111676





