Interpreting Self-Potential Signal during Reactive Transport: Application to Calcite Dissolution and Precipitation
Abstract
1. Introduction
2. Theoretical Workflow
2.1. Reactive Transport in Carbonaceous System
2.1.1. Carbonate Material Reactivity
2.1.2. Flow and Transport
2.2. The Electrical Conductivity
2.2.1. The Pore Water EC
2.2.2. The Sample EC
2.3. The Self-Potential Method
2.3.1. The Electrokinetic Contribution
2.3.2. The Electro-Diffusive Contribution
2.3.3. Development of a New Model for the Electro-Diffusive Potential in a Multi-Ionic System
3. Materials and Methods
3.1. One-Dimensional Reactive Transport Simulations Using CrunchFlow
3.1.1. Thermodynamic and Kinetic Data
3.1.2. Initial Chemical Compositions
3.1.3. Flow and Transport Properties
3.1.4. Discretization
3.1.5. Specific Reactive Surface Area
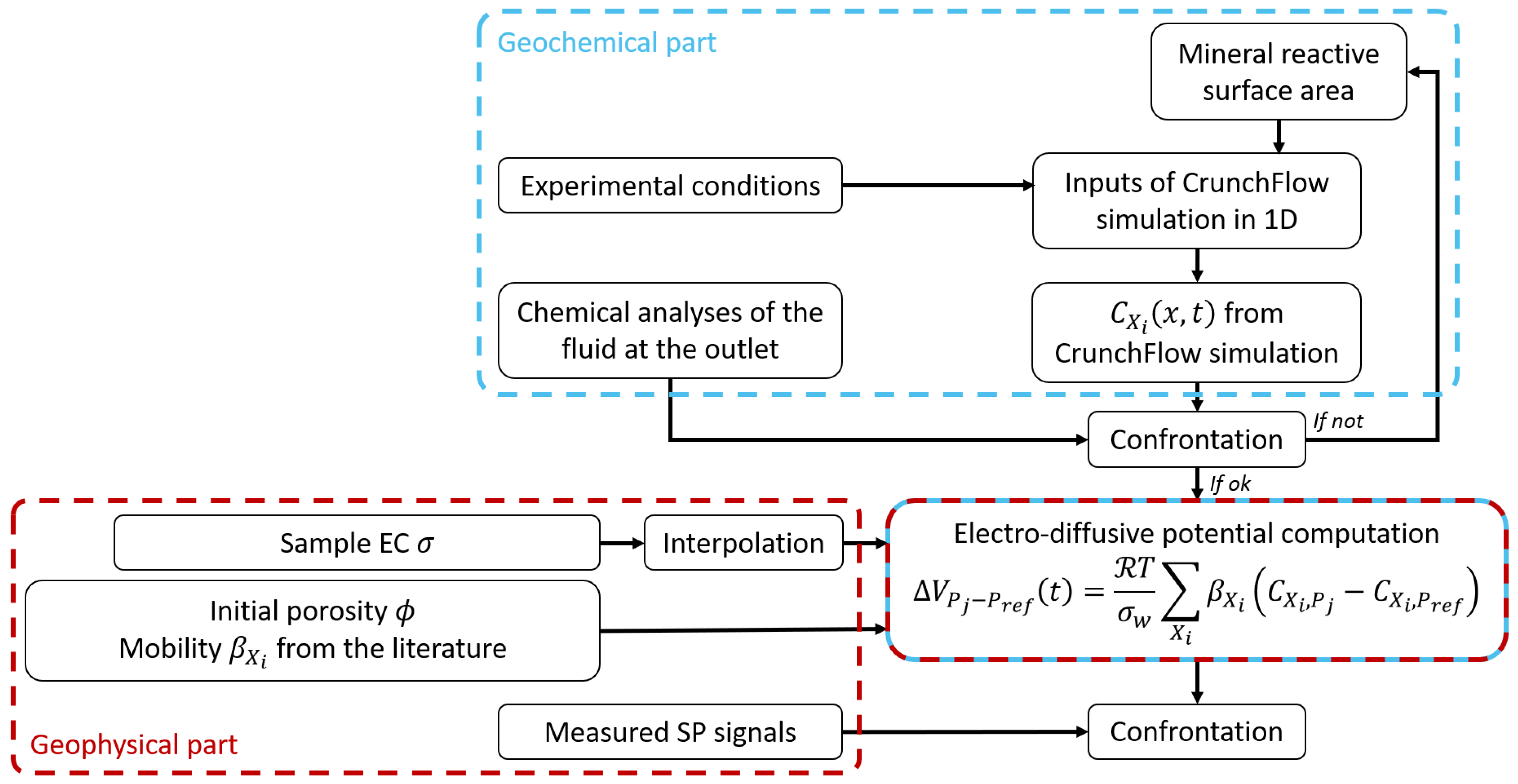
3.2. Fully Coupled Numerical Workflow for Multi-Ionic Modeling of Electro-Diffusive Potential
3.3. Experimental Setup
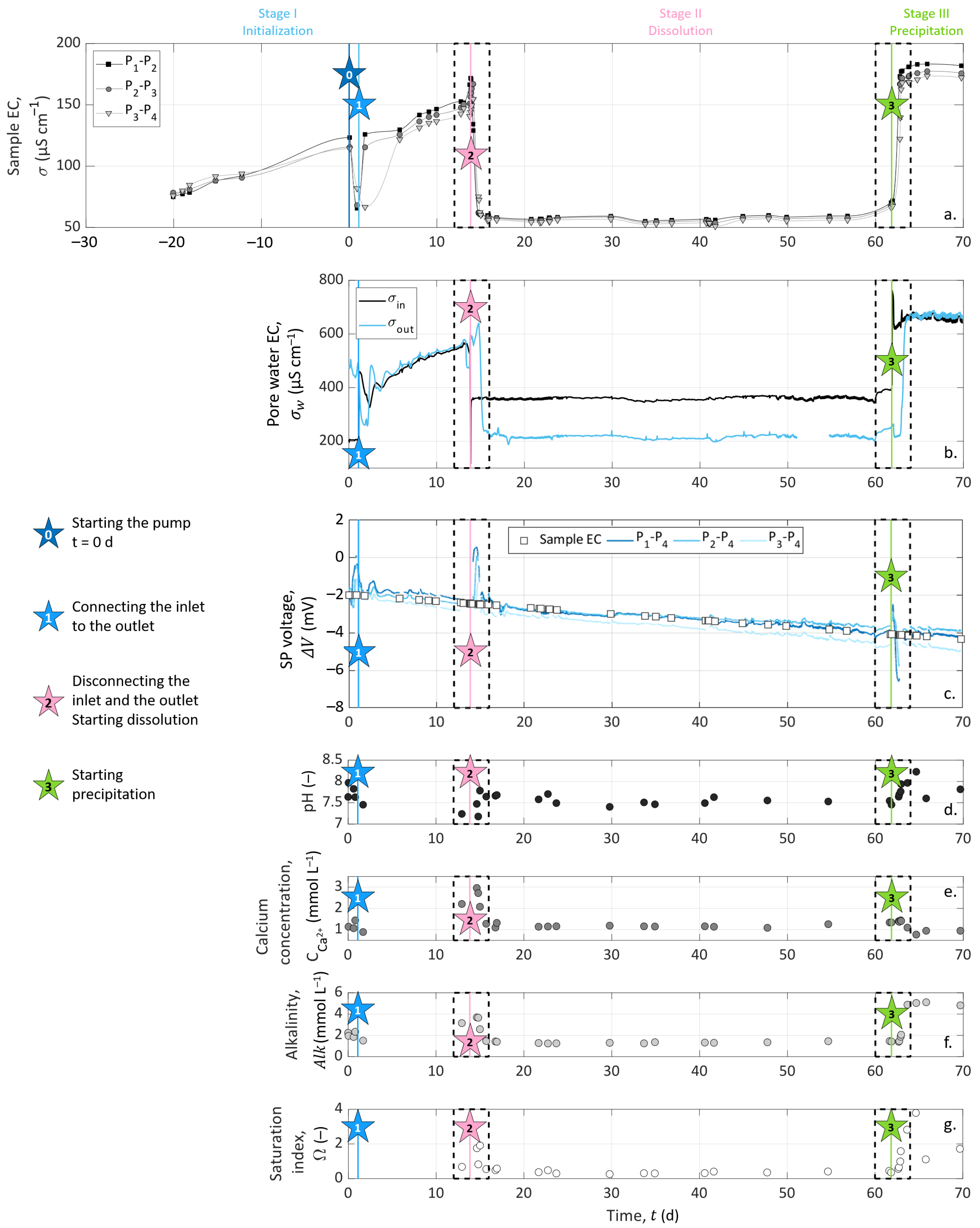
3.4. Experimental Timeline
4. Results and Discussion
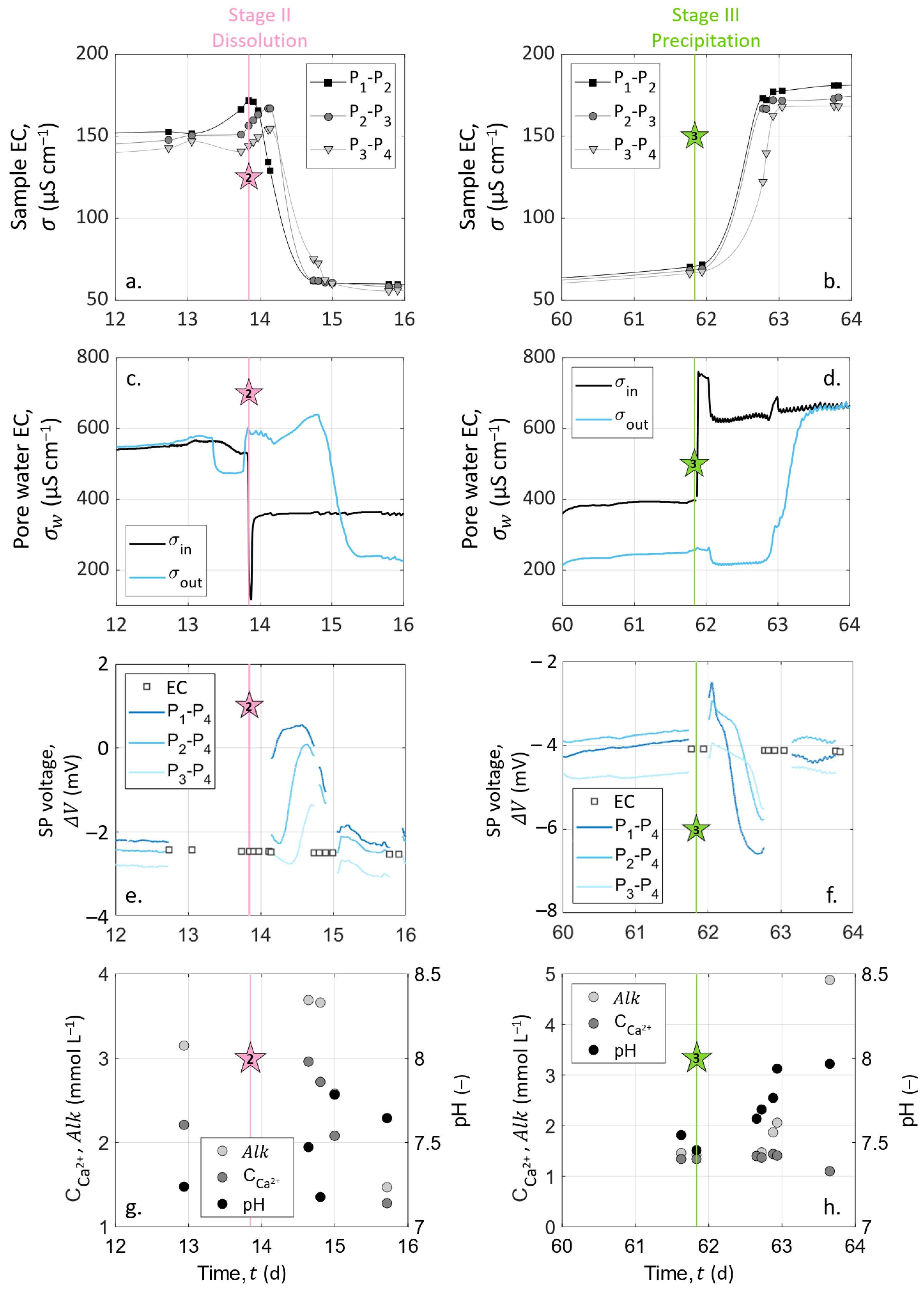
4.1. Pore Water EC Monitoring
4.2. Chemical Analysis on Outlet Water Samples
4.3. Column Sample EC Measurements
4.4. SP Monitoring
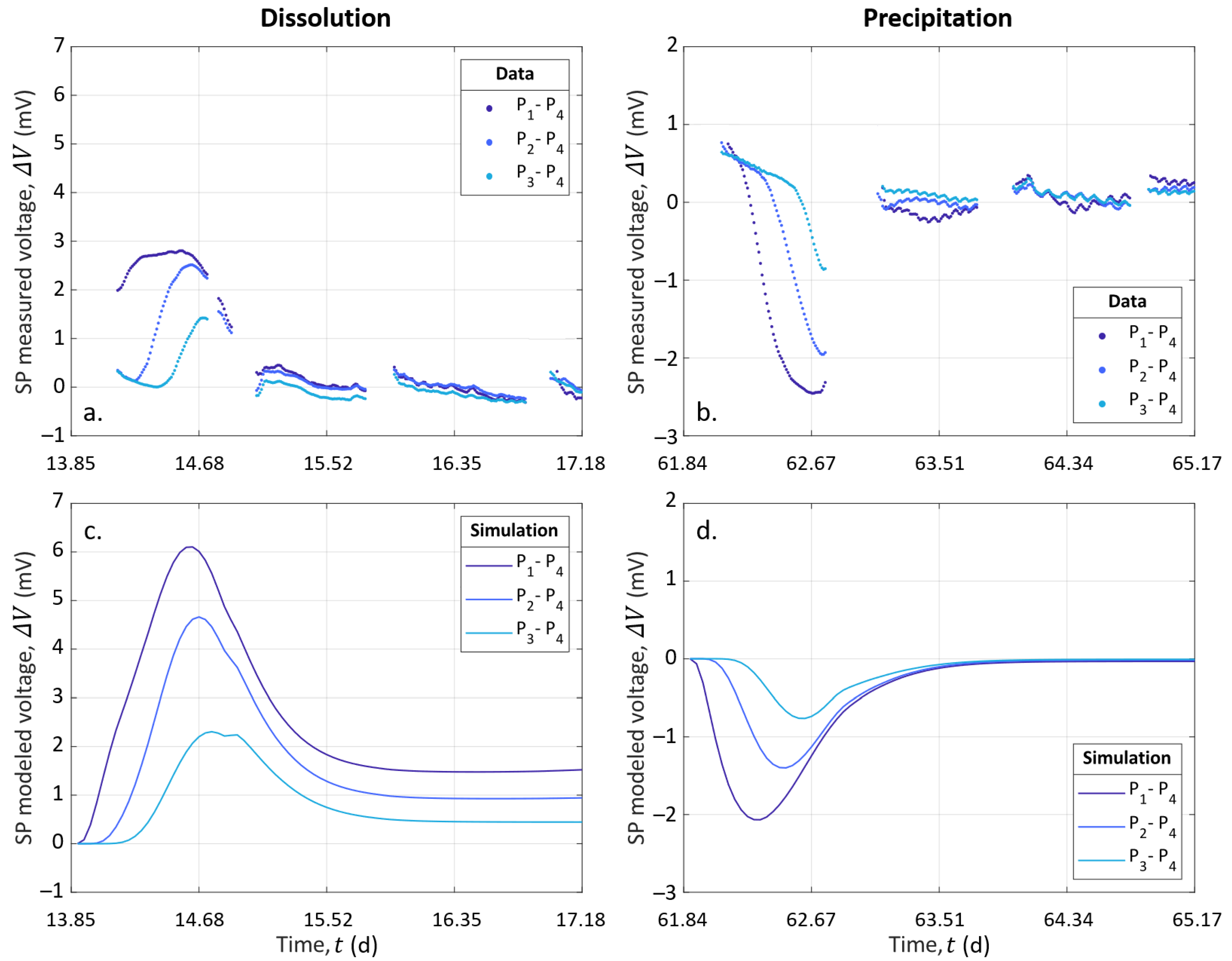
4.4.1. Experimental Results
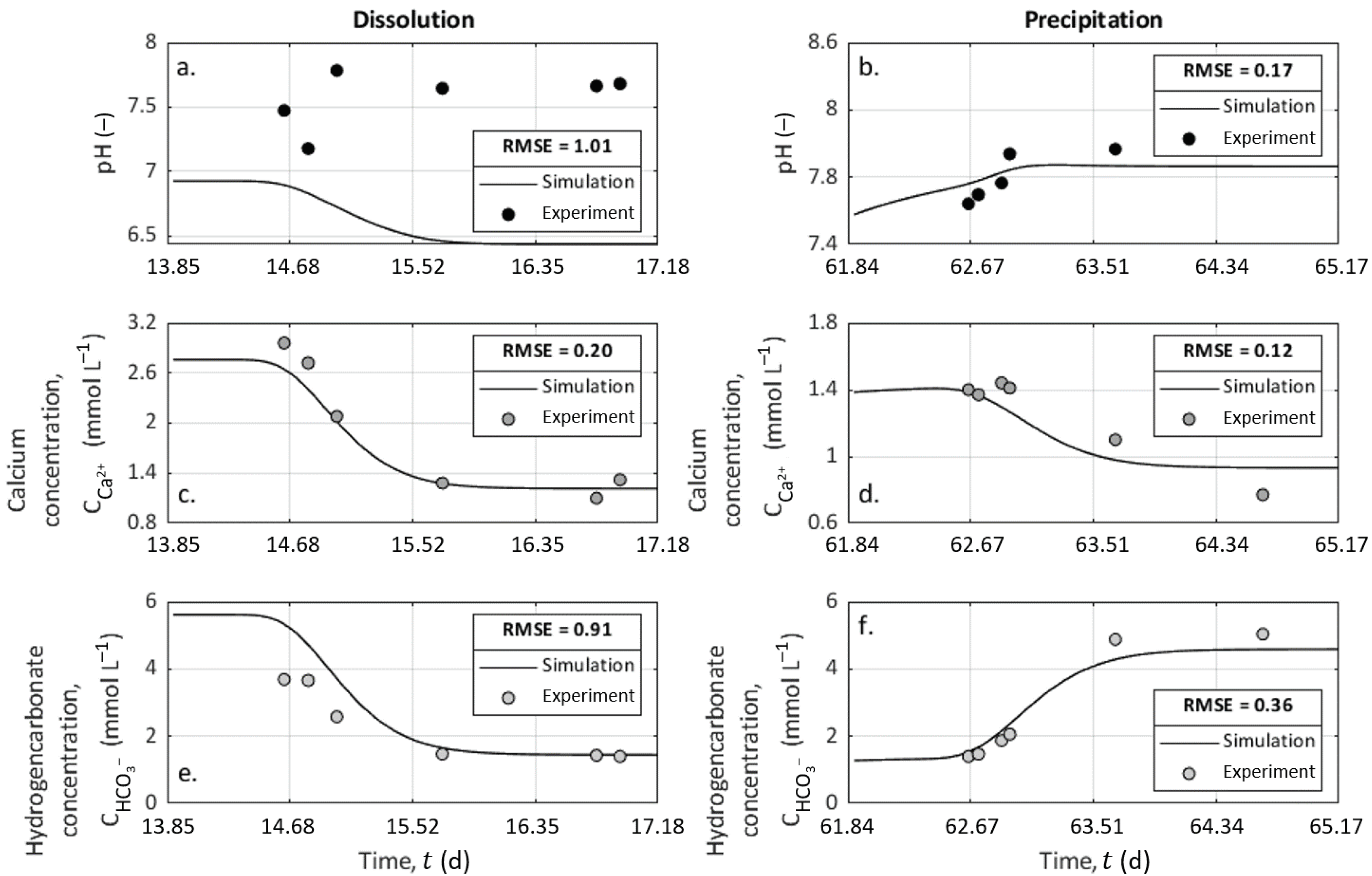
4.4.2. CrunchFlow Simulation Results for the Reactive Transport
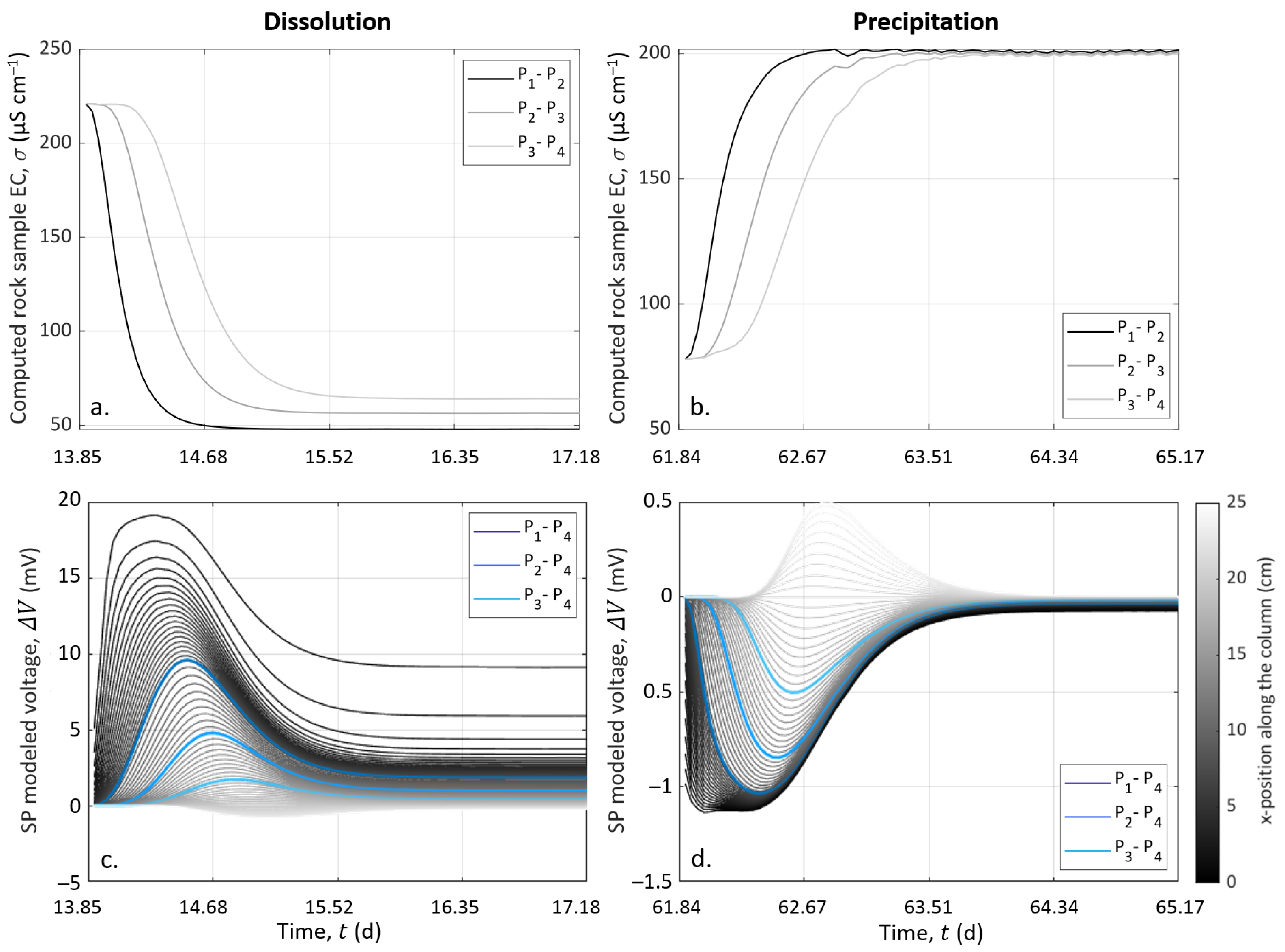
4.4.3. Results from the Electro-Diffusive Potential Modeling
4.5. Location of the Reactive Zone
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Notations
| Symbol | Definition (unit) |
| Alkalinity ( ) | |
| Electro-diffusive coupling coefficient () | |
| Mobility on ion ( ) | |
| C | Ionic concentration of the solution ( ) |
| Standard concentration ( ) | |
| Ionic concentration of ion ( ) | |
| Electrokinetic coupling coefficient ( ) | |
| Mean grain diameter () | |
| Diffusion coefficient of ion ( ) | |
| Time step for the calculation of the cumulative porosity () | |
| Electric voltage () | |
| E | Electric field ( ) |
| Water dynamic viscosity ( ) | |
| f | Frequency () |
| F | Formation factor (–) |
| Faraday constant ( ) | |
| Activity coefficient of the ion (–) | |
| Source current density ( ) | |
| Electrochemical coupling current density from ionic concentration gradients ( ) | |
| Electrokinetic coupling current density ( ) | |
| Total electric current density ( ) | |
| Boltzmann constant ( ) | |
| Acidity constant of bicarbonate ion (–) | |
| Acidity constant of carbonate ion (–) | |
| Hydration constant (–) | |
| Solubility product of calcite (–) | |
| Molar conductivity of ion ( ) | |
| m | Cementation exponent (–) |
| Cumulative mass of calcium (g) | |
| Angular frequency ( ) | |
| Saturation index (–) | |
| Empirical parameter for temperature compensation (–) | |
| Péclet number (–) | |
| One of the measurement electrodes | |
| Reference electrode | |
| Porosity (–) | |
| Final porosity (–) | |
| Initial porosity (–) | |
| Q | Flow rate ( ) |
| Volumetric excess charge ( ) | |
| Molar gas constant ( ) | |
| REV | Representative elementary volume |
| Calcite volumetric mass ( ) | |
| Sample EC ( ) | |
| Bulk conductivity ( ) | |
| Inlet pore water EC ( ) | |
| Outlet pore water EC ( ) | |
| Surface conductivity ( ) | |
| Pore water electrical conductivity ( ) | |
| t | Time () |
| T | Temperature () |
| Transference number (–) | |
| Temperature () | |
| U | Darcy velocity ( ) |
| v | Particle velocity ( ) |
| V | Electric potential () |
| Volume of the column () | |
| Ionic activity of the ion (–) | |
| Valence of the ion (–) |
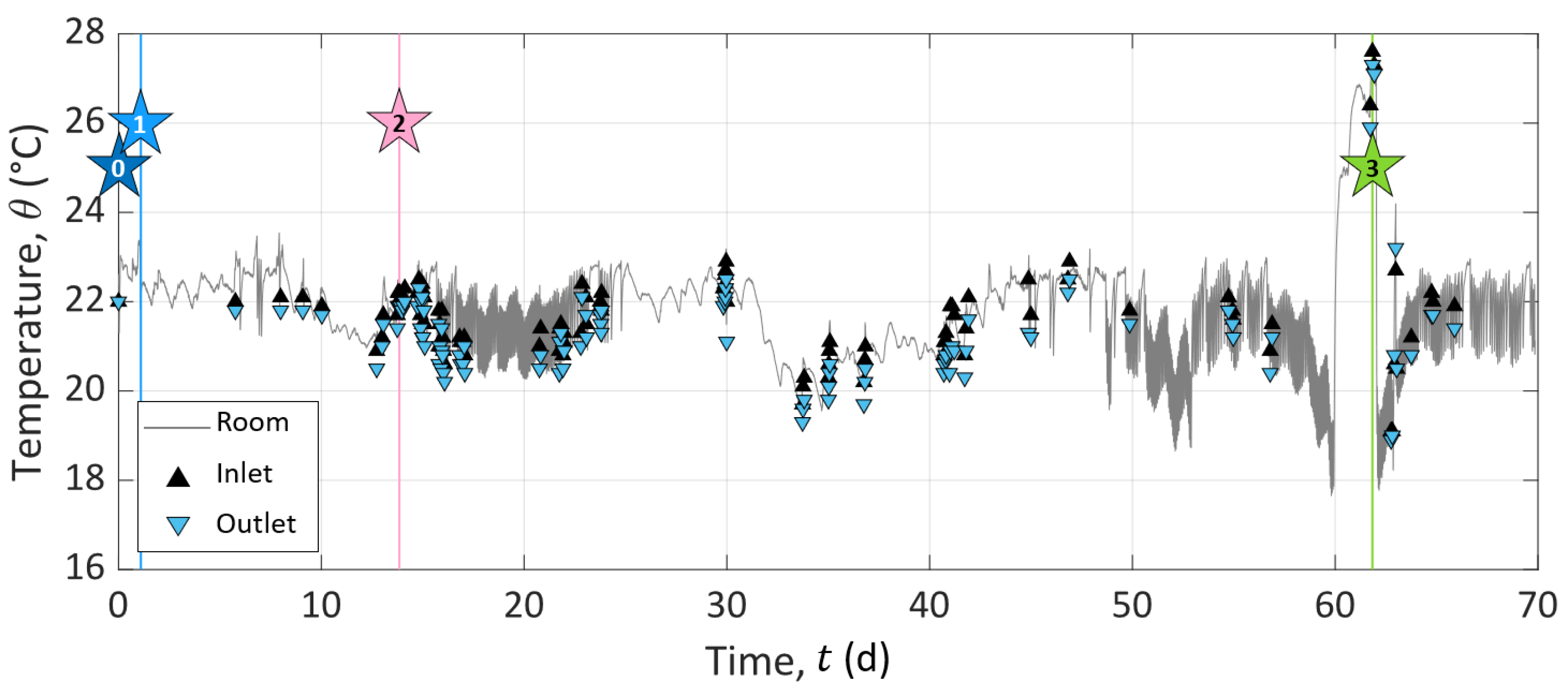
Appendix A. Temperature Monitoring
Appendix B. Electro-Diffusive Coupling Computation from Pore Water EC Computation
References
- Goldscheider, N.; Meiman, J.; Pronk, M.; Smart, C. Tracer tests in karst hydrogeology and speleology. Int. J. Speleol. 2008, 37, 27–40. [Google Scholar] [CrossRef]
- Hubbard, S.S.; Linde, N. 2.15-Hydrogeophysics. In Treatise on Water Science; Wilderer, P., Ed.; Elsevier: Oxford, UK, 2011; pp. 401–434. [Google Scholar] [CrossRef]
- Revil, A.; Karaoulis, M.; Johnson, T.; Kemna, A. Some low-frequency electrical methods for subsurface characterization and monitoring in hydrogeology. Hydrogeol. J. 2012, 20, 617–658. [Google Scholar] [CrossRef]
- Binley, A.; Hubbard, A.S.; Huisman, J.A.; Revil, A.; Robinson, D.A.; Singha, K.; Slater, L.D. The emergence of hydrogeophysics for improved understanding of subsurface processes over multiple scales. Water Resour. Res. 2015, 51, 3837–3866. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Goldscheider, N.; Auler, A.S.; Bakalowicz, M. The World karst aquifer mapping project: Concept, mapping procedure and map of Europe. Hydrogeol. J. 2017, 25, 771–785. [Google Scholar] [CrossRef]
- Luquot, L.; Gouze, P. Experimental determination of porosity and permeability changes induced by injection of CO2 into carbonate rocks. Chem. Geol. 2009, 265, 148–159. [Google Scholar] [CrossRef]
- Cherubini, A.; Garcia, B.; Cerepi, A.; Revil, A. Influence of CO2 on the electrical conductivity and streaming potential of carbonate rocks. J. Geophys. Res. Solid Earth 2019, 124, 10056–10073. [Google Scholar] [CrossRef]
- Kačaroǧlu, F. Review of groundwater pollution and protection in karst areas. Water Air Soil Pollut. 1999, 113, 337–356. [Google Scholar] [CrossRef]
- Bakalowicz, M. Karst groundwater: A challenge for new resources. Hydrogeol. J. 2005, 13, 148–160. [Google Scholar] [CrossRef]
- Montanari, D.; Minissale, A.; Doveri, M.; Gola, G.; Trumpy, E.; Santilano, A.; Manzella, A. Geothermal resources within carbonate reservoirs in western Sicily (Italy): A review. Earth Sci. Rev. 2017, 169, 180–201. [Google Scholar] [CrossRef]
- Burchette, T.P. Carbonate rocks and petroleum reservoirs: A geological perspective from the industry. Geol. Soc. Lond. Spec. Publ. 2012, 370, 17–37. [Google Scholar] [CrossRef]
- Drew, D.; Lamoreaux, P.E.; Coxon, C.; Wess, J.W.; Slattery, L.D.; Bosch, A.P.; Hötzl, H. Karst Hydrogeology and Human Activities: Impacts, Consequences and Implications: IAH International Contributions to Hydrogeology 20, 5th ed.; Drew, D., Hötzl, H., Eds.; Routledge: London, UK, 2017. [Google Scholar] [CrossRef]
- Buckerfield, S.J.; Quilliam, R.S.; Bussiere, L.; Waldron, S.; Naylor, L.A.; Li, S.; Oliver, D.M. Chronic urban hotspots and agricultural drainage drive microbial pollution of karst water resources in rural developing regions. Sci. Total Environ. 2020, 744, 140898. [Google Scholar] [CrossRef] [PubMed]
- Jouniaux, L.; Maineult, A.; Naudet, V.; Pessel, M.; Sailhac, P. Review of self-potential methods in hydrogeophysics. Comptes Rendus Geosci. 2009, 341, 928–936. [Google Scholar] [CrossRef]
- Revil, A.; Jardani, A. The Self-Potential Method: Theory and Applications in Environmental Geosciences; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Jougnot, D.; Roubinet, D.; Guarracino, L.; Maineult, A. Modeling streaming potential in porous and fractured media, description and benefits of the effective excess charge density approach. In Advances in Modeling and Interpretation in Near Surface Geophysics; Biswas, A., Sharma, S., Eds.; Springer Geophysics; Springer: Cham, Switzerland, 2020; Chapter 4; pp. 61–96. [Google Scholar] [CrossRef]
- Guichet, X.; Jouniaux, L.; Catel, N. Modification of streaming potential by precipitation of calcite in a sand-water system: Laboratory measurements in the pH range from 4 to 12. Geophys. J. Int. 2006, 166, 445–460. [Google Scholar] [CrossRef]
- Hidayat, M.; Sarmadivaleh, M.; Derksen, J.; Vega-Maza, D.; Iglauer, S.; Vinogradov, J. Zeta potential of CO2-rich aqueous solutions in contact with intact sandstone sample at temperatures of 23 °C and 40 °C and pressures up to 10.0 MPa. J. Colloid Interface Sci. 2022, 607, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Revil, A. Ionic diffusivity, electrical conductivity, membrane and thermoelectric potentials in colloids and granular porous media: A unified model. J. Colloid Interface Sci. 1999, 212, 503–522. [Google Scholar] [CrossRef]
- Maineult, A.; Bernabé, Y.; Ackerer, P. Detection of advected concentration and pH fronts from self-potential measurements. J. Geophys. Res. 2005, 110, B11205. [Google Scholar] [CrossRef]
- Korom, S.F.; Seaman, J.C. When “conservative” anionic tracers aren’t. Groundwater 2012, 50, 820–824. [Google Scholar] [CrossRef]
- Graham, M.T.; MacAllister, D.J.; Vinogradov, J.; Jackson, M.D.; Butler, A.P. Self-potential as a predictor of seawater intrusion in coastal groundwater boreholes. Water Resour. Res. 2018, 54, 6055–6071. [Google Scholar] [CrossRef]
- MacAllister, D.J.; Jackson, M.D.; Butler, A.P.; Vinogradov, J. Remote detection of saline intrusion in a coastal aquifer using borehole measurements of self-potential. Water Resour. Res. 2018, 54, 1669–1687. [Google Scholar] [CrossRef]
- Gulamali, M.Y.; Leinov, E.; Jackson, M.D. Self-potential anomalies induced by water injection into hydrocarbon reservoirs. Geophysics 2011, 76, F283–F292. [Google Scholar] [CrossRef]
- Revil, A.; Leroy, P. Constitutive equations for ionic transport in porous shales. J. Geophys. Res. 2004, 109, B03208. [Google Scholar] [CrossRef]
- Linde, N.; Doetsch, J.; Jougnot, D.; Genoni, O.; Dürst, Y.; Minsley, B.J.; Vogt, T.; Pasquale, N.; Luster, J. Self-potential investigations of a gravel bar in a restored river corridor. Hydrol. Earth Syst. Sci. 2011, 15, 729–742. [Google Scholar] [CrossRef]
- Bautista-Anguiano, J.; Torres-Verdin, C. Estimation of in situ hydrocarbon saturation of porous rocks fromborehole measurements of spontaneous potential. Geophysics 2020, 85, D199–D217. [Google Scholar] [CrossRef]
- Revil, A.; Linde, N. Chemico-electromechanical coupling in microporous media. J. Colloid Interface Sci. 2006, 302, 682–694. [Google Scholar] [CrossRef]
- Revil, A.; Jougnot, D. Diffusion of ions in unsaturated porous materials. J. Colloid Interface Sci. 2008, 319, 226–235. [Google Scholar] [CrossRef]
- Plummer, L.N.; Busenberg, E. The solubilities of calcite, aragonite and vaterite in CO2-H2O solutions between 0 and 90 °C, and an evaluation of the aqueous model for the system CaCO3-CO2-H2O. Geochim. Cosmochim. Acta 1982, 46, 1011–1040. [Google Scholar] [CrossRef]
- Cohen, E.R.; Cvitaš, T.; Frey, J.G.; Holmström, B.; Kuchitsu, K.; Marquardt, R.; Mills, I.; Pavese, F.; Quack, M.; Stohner, J.; et al. Quantities, Units and Symbols in Physical Chemistry, 3rd ed.; Royal Society of Chemistry: Cambridge, UK, 2007. [Google Scholar]
- De Marsily, G. Quantitative Hydrogeology: Groundwater Hydrology for Engineers, 2nd ed.; Paris School of Mines: Fontainebleau, France, 1986; p. 440. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier: New York, NY, USA, 1988. [Google Scholar]
- Vialle, S.; Contraires, S.; Zinzsner, B.; Clavaud, J.B.; Mahiouz, K.; Zuddas, P.; Zamora, M. Percolation of CO2-rich fluids in a limestone sample: Evolution of hydraulic, electrical, chemical, and structural properties. J. Geophys. Res. Solid Earth 2014, 119, 2828–2847. [Google Scholar] [CrossRef]
- Leger, M.; Roubinet, D.; Jamet, M.; Luquot, L. Impact of hydro-chemical conditions on structural and hydro-mechanical properties of chalk samples during dissolution experiments. Chem. Geol. 2022, 594, 120763. [Google Scholar] [CrossRef]
- McCleskey, R.B.; Nordstrom, D.K.; Ryan, J.N. Comparison of electrical conductivity calculation methods for natural waters. Limnol. Oceanogr. Methods 2012, 10, 952–967. [Google Scholar] [CrossRef]
- Atkins, P.; de Paula, J. Atkins’ Physical Chemistry; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Robinson, R.A.; Chia, C.L. The diffusion coefficient of calcium chloride in aqueous solution at 25. J. Am. Chem. Soc. 1952, 74, 2776–2777. [Google Scholar] [CrossRef]
- Gregory, T.M.; Chow, L.C.; Carey, C.M. A mathematical model for dental caries: A coupled dissolution-diffusion process. J. Res. Natl. Inst. Stand. Technol. 1991, 96, 593–604. [Google Scholar] [CrossRef] [PubMed]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3: A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; Technical Report; US Geological Survey: Denver, CO, USA, 2013. [CrossRef]
- Hunter, R.J. Zeta Potential in Colloid Science: Principles and Applications; Academic Press London: London, UK, 1981; Volume 2, p. 391. [Google Scholar] [CrossRef]
- Chelidze, T.L.; Gueguen, Y. Electrical spectroscopy of porous rocks: A review-I. Theoretical models. Geophys. J. Int. 1999, 137, 1–15. [Google Scholar] [CrossRef]
- Leroy, P.; Revil, A. A triple layer model of the surface electrochemical properties of clay minerals. J. Colloid Interface Sci. 2004, 270, 371–380. [Google Scholar] [CrossRef] [PubMed]
- Bolève, A.; Crespy, A.; Revil, A.; Janod, F.; Mattiuzzo, J.L. Streaming potentials of granular media: Influence of the Dukhin and Reynolds numbers. J. Geophys. Res. 2007, 112, 204–217. [Google Scholar] [CrossRef]
- Soueid Ahmed, A.; Revil, A.; Abdulsamad, F.; Steck, B.; Vergniault, C.; Guihard, V. Induced polarization as a tool to non-intrusively characterize embankment hydraulic properties. Eng. Geol. 2020, 271, 105604. [Google Scholar] [CrossRef]
- Waxman, M.H.; Smits, L.J.M. Electrical conductivities in oil bearing shaly sands. Soc. Pet. Eng. J. 1968, 8, 107–122. [Google Scholar] [CrossRef]
- Weller, A.; Slater, L.; Nordsiek, S. On the relationship between induced polarization and surface conductivity: Implications for petrophysical interpretation of electrical measurements. Geophysics 2013, 78, D315–D325. [Google Scholar] [CrossRef]
- Revil, A.; Kessouri, P.; Torres-Verdin, C. Electrical conductivity, induced polarization, and permeability of the fontainebleau sandstone. Geophysics 2014, 79, D301–D318. [Google Scholar] [CrossRef]
- Rembert, F.; Jougnot, D.; Guarracino, L. A fractal model for the electrical conductivity of water-saturated porous media during mineral precipitation-dissolution processes. Adv. Water Resour. 2020, 145, 103742. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Pfannkuch, H.O. On the correlation of electrical conductivity properties of porous systems with viscous flow transport coefficients. Dev. Soil Sci. 1972, 2, 42–54. [Google Scholar] [CrossRef]
- Thanh, L.D.; Jougnot, D.; Phan, V.D.; Nguyen, V.N.A. A physically based model for the electrical conductivity of water-saturated porous media. Geophys. J. Int. 2019, 219, 866–876. [Google Scholar] [CrossRef]
- Berg, C.F.; Kennedy, W.D.; Herrick, D.C. Conductivity in partially saturated porous media described by porosity, electrolyte saturation and saturation-dependent tortuosity and constriction factor. Geophys. Prospect. 2022, 70, 400–420. [Google Scholar] [CrossRef]
- Sill, W.R. Self-potential modeling from primary flows. Geophysics 1983, 48, 76–86. [Google Scholar] [CrossRef]
- Jougnot, D.; Linde, N. Self-potentials in partially saturated media: The importance of explicit modeling of electrode effects. Vadose Zone J. 2013, 12, 1–21. [Google Scholar] [CrossRef]
- Kormiltsev, V.V.; Ratushnyak, A.N.; Shapiro, V.A. Three-dimensional modeling of electric and magnetic fields induced by the fluid flow movement in porous media. Phys. Earth Planet. Inter. 1998, 105, 109–118. [Google Scholar] [CrossRef]
- Jardani, A.; Revil, A.; Bolève, A.; Cespy, A.; Dupont, J.P.; Barrash, W.; Malama, B. Tomography of the Darcy velocity from self-potential measurements. Geophys. Res. Lett. 2007, 34, 403–408. [Google Scholar] [CrossRef]
- Cherubini, A.; Garcia, B.; Cerepi, A.; Revil, A. Streaming potential coupling coefficient and transport properties of unsaturated carbonate rocks. Vadose Zone J. 2018, 17, 180030. [Google Scholar] [CrossRef]
- Guarracino, L.; Jougnot, D. A physically based analytical model to describe effective excess charge for streaming potential generation in water saturated porous media. J. Geophys. Res. Solid Earth 2018, 123, 52–65. [Google Scholar] [CrossRef]
- Jougnot, D.; Mendieta, A.; Leroy, P.; Maineult, A. Exploring the effect of the pore size distribution on the streaming potential generation in saturated porous media, insight from pore network simulations. J. Geophys. Res. Solid Earth 2019, 124, 5315–5335. [Google Scholar] [CrossRef]
- Von Smoluchowski, M. Contribution à la théorie de l’endosmose électrique et de quelques phénomènes corrélatifs. Bull. Int. L’Académie Sci. Crac. 1903, 8, 182–200. [Google Scholar]
- Leinov, E.; Jackson, M.D. Experimental measurements of the SP response to concentration and temperature gradients in sandstones with application to subsurface geophysical monitoring. J. Geophys. Res. Solid Earth 2014, 119, 6855–6876. [Google Scholar] [CrossRef]
- MacAllister, D.J.; Graham, M.T.; Vinogradov, J.; Butler, A.P.; Jackson, M.D. Characterizing the self-potential response to concentration gradients in heterogeneous subsurface environments. J. Geophys. Res. Solid Earth 2019, 124, 7918–7933. [Google Scholar] [CrossRef]
- Henderson, P. The thermodynamics of liquid cells. Z. Für Phys. Chem. 1907, 59, 118–127. [Google Scholar] [CrossRef]
- Guggenheim, E.A. A study of cells with liquid–liquid junctions. J. Am. Chem. Soc. 1930, 52, 1315–1337. [Google Scholar] [CrossRef]
- Strathmann, H. Electrochemical and thermodynamic fundamentals. In Ion-Exchange Membrane Separation Processes; Elsevier: Amsterdam, The Netherlands, 2004; Volume 9, Chapter 2; pp. 23–88. [Google Scholar] [CrossRef]
- Daintith, J. (Ed.) A Dictionary of Chemistry, 6th ed.; Oxford University Press: Oxford, UK, 2008. [Google Scholar] [CrossRef]
- Steefel, C.I. CrunchFlow. Software for Modeling Multicomponent Reactive Flow and Transport. User’s Manual; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2009.
- Molins, S.; Trebotich, D.; Yang, L.; Ajo-Franklin, J.B.; Ligocki, T.J.; Shen, C.; Steefel, C.I. Pore-scale controls on calcite dissolution rates from flow-through laboratory and numerical experiments. Environ. Sci. Technol. 2014, 48, 7453–7460. [Google Scholar] [CrossRef]
- Garcia-Rios, M.; Cama, J.; Luquot, L.; Soler, J.M. Interaction between CO2-rich sulfate solutions and carbonate reservoir rocks from atmospheric to supercritical CO2 conditions: Experiments and modeling. Chem. Geol. 2014, 383, 107–122. [Google Scholar] [CrossRef]
- Palandri, J.L.; Kharaka, Y.K. A Compilation of Rate Parameters of Water-Mineral Interaction Kinetics for Application to Geochemical Modeling; Technical Report; Geological Survey: Menlo Park, CA, USA, 2004.
- Schulze-Makuch, D. Longitudinal dispersivity data and implications for scaling behavior. Ground Water 2005, 43, 443–546. [Google Scholar] [CrossRef]
- Chakraborty, P.; Bhabani, S.D. Measurement and modeling of longitudinal dispersivity in undisturbed saturated soil: An experimental approach. Soil Sci. Soc. Am. J. 2018, 83, 1117–1123. [Google Scholar] [CrossRef]
- Petiau, G.; Dupis, A. Noise, temperature coefficient, and long time stability of electrodes for telluric observations. Geophys. Prospect. 1980, 28, 792–804. [Google Scholar] [CrossRef]
- Sorensen, J.A.; Glass, G.E. Ion and temperature dependence of electrical conductance for natural waters. Anal. Chem. 1987, 59, 1594–1597. [Google Scholar] [CrossRef]
- Hayashi, M. Temperature-electrical conductivity relation of water for environmental monitoring and geophysical data inversion. Environ. Monit. Assess. 2004, 96, 119–128. [Google Scholar] [CrossRef] [PubMed]
- Smart, C.C. Temperature compensation of electrical conductivity in glacial meltwaters. J. Glaciol. 1992, 38, 9–12. [Google Scholar] [CrossRef][Green Version]
- Friedman, S.P. Soil properties influencing apparent electrical conductivity: A review. Comput. Electron. Agric. 2005, 46, 45–70. [Google Scholar] [CrossRef]
- Oliveira, T.D.S.; Blunt, M.J.; Bijeljic, B. Multispecies reactive transport in a microporous rock: Impact of flow heterogeneity and reversibility of reaction. Water Resour. Res. 2020, 56, e2020WR027317. [Google Scholar] [CrossRef]
- Gawel, K.; Wenner, S.; Edvardsen, L. Effect of carbonation on bulk resistivity of cement/carbon nanofiber composites. Constr. Build. Mater. 2021, 305, 124794. [Google Scholar] [CrossRef]
- Saneiyan, S.; Ntarlagiannis, D.; Ohan, J.; Lee, J.; Colwell, F.; Burns, S. Induced polarization as a monitoring tool for in-situ microbial induced carbonate precipitation (MICP) processes. Ecol. Eng. 2019, 127, 36–47. [Google Scholar] [CrossRef]
- Hong, D.; Cao, J.; Wu, T.; Dang, S.; Hu, W.; Yao, S. Authigenic clay minerals and calcite dissolution influence reservoir quality in tight sandstones: Insights from the central Junggar Basin, NW China. Energy Geosci. 2020, 1, 8–19. [Google Scholar] [CrossRef]
- Zhang, C.; Slater, L.; Redden, G.; Fujita, Y.; Johnson, T.; Fox, D. Spectral induced polarization signatures of hydroxide adsorption and mineral precipitation in porous media. Environ. Sci. Technol. 2012, 46, 4357–4364. [Google Scholar] [CrossRef]




| Equations | Thermodynamic Constants (25 C) |
|---|---|
| CO + HO ↔ HCO | |
| HCO ↔ H + HCO | |
| HCO ↔ H + CO | |
| Ca + CO ↔ CaCO |
| Ionic Species | Molar Conductivity | Mobility |
|---|---|---|
| ( ) | ( ) | |
| Ca | 119.1 | 0.62 |
| H | 349.6 | 3.62 |
| Na | 50.0 | 0.52 |
| CaCl | 50.9 | 0.53 |
| CaHCO | 19.0 | 0.20 |
| CaOH | 39.1 | 0.41 |
| Cl | 76.2 | 0.79 |
| HCO | 44.3 | 0.46 |
| CO | 143.5 | 0.74 |
| NaCO | 22.0 | 0.23 |
| HO | 197.9 | 2.05 |
| Experiment | Dissolution | Precipitation |
|---|---|---|
| Rock composition | Calcite | |
| Reactive specific surface area (m/m) | 1.5 | |
| Temperature () | from experimental measurements | |
| Initial pore water properties | ||
| pH | 6.9 | 7.4 |
| ( ) | 2.9 | 1.4 |
| ( ) | 7.1 | 1.4 |
| ( ) | 2.0 | 1.0 |
| ( ) | 2.0 | 0.0 |
| Inlet solutions properties | ||
| pH | 3.0 | 8.5 |
| ( ) | 1.2 | |
| ( ) | 1.4 | 4.8 |
| ( ) | 1.0 | 2.4 |
| ( ) | 4.9 | |
| Flow and transport properties | ||
| Effective diffusion coefficient ( ) | 3.0 | |
| Dispersivity () | 0.9 | |
| Darcy velocity ( ) | 2.7 | |
| Experiment | Dissolution | Precipitation |
|---|---|---|
| Experimental conditions | ||
| Temperature () | 21.8 ± 1.14 | |
| Pressure () | 1 | |
| pCO () | 10 | |
| Sample | Crushed and sifted calcite with diameter | |
| ranging from 125 to 250 | ||
| Inlet solution | S1 | S2 |
| Diluted hydrochloric acid | Over-saturated brine | |
| Inlet solutions’ properties | ||
| pH | 3.0 | 8.5 |
| ( ) | 0 | 1.2 |
| ( ) | - | 4.8 |
| ( ) | 1.0 | 2.4 |
| ( ) | 0 | 4.9 |
| Saturation index and activity coefficients | ||
| 0 | 14 | |
| 0.96 | 0.90 | |
| - | 0.67 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rembert, F.; Jougnot, D.; Luquot, L.; Guérin, R. Interpreting Self-Potential Signal during Reactive Transport: Application to Calcite Dissolution and Precipitation. Water 2022, 14, 1632. https://doi.org/10.3390/w14101632
Rembert F, Jougnot D, Luquot L, Guérin R. Interpreting Self-Potential Signal during Reactive Transport: Application to Calcite Dissolution and Precipitation. Water. 2022; 14(10):1632. https://doi.org/10.3390/w14101632
Chicago/Turabian StyleRembert, Flore, Damien Jougnot, Linda Luquot, and Roger Guérin. 2022. "Interpreting Self-Potential Signal during Reactive Transport: Application to Calcite Dissolution and Precipitation" Water 14, no. 10: 1632. https://doi.org/10.3390/w14101632
APA StyleRembert, F., Jougnot, D., Luquot, L., & Guérin, R. (2022). Interpreting Self-Potential Signal during Reactive Transport: Application to Calcite Dissolution and Precipitation. Water, 14(10), 1632. https://doi.org/10.3390/w14101632