A Novel Surge Damping Method for Hydraulic Transients with Operating Pump Using an Optimized Valve Control Strategy
Abstract
:1. Introduction
2. Simulation Model
2.1. One-Dimensional Unsteady Friction Model
- (1)
- The liquid fluid complies with cross-section-averaged properties.
- (2)
- The water liquid is considered to be single phase without entrained air.
- (3)
- The pipe is elastic, and the fluid is compressible.
- (4)
- The pipe flow is assumed to be adiabatic flow.
2.2. Physical Model and Solution Method
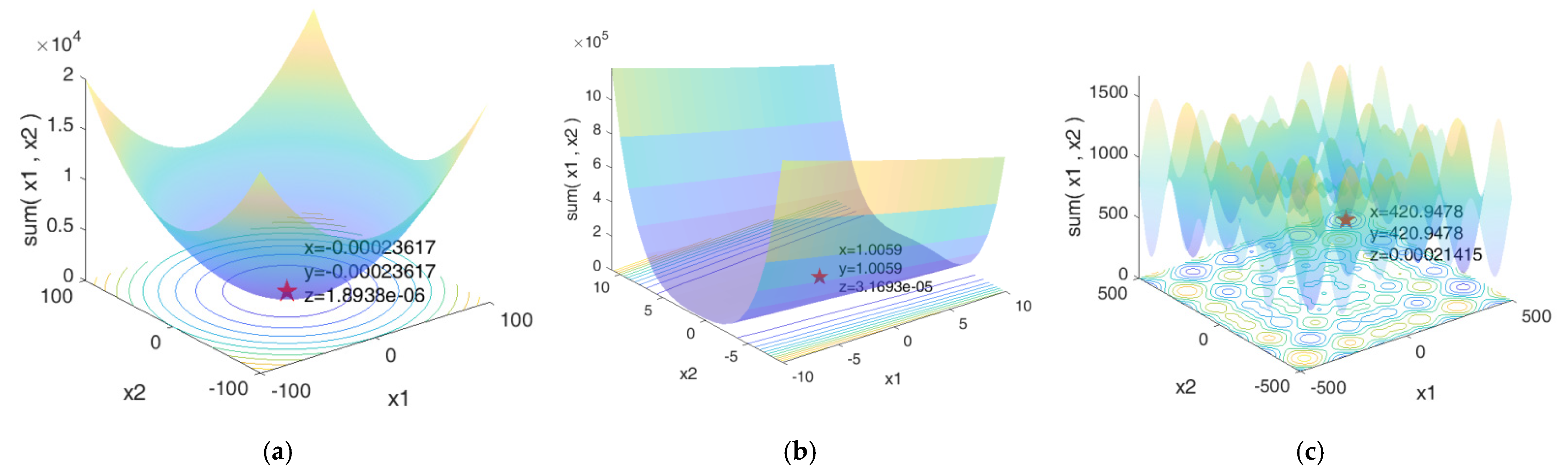
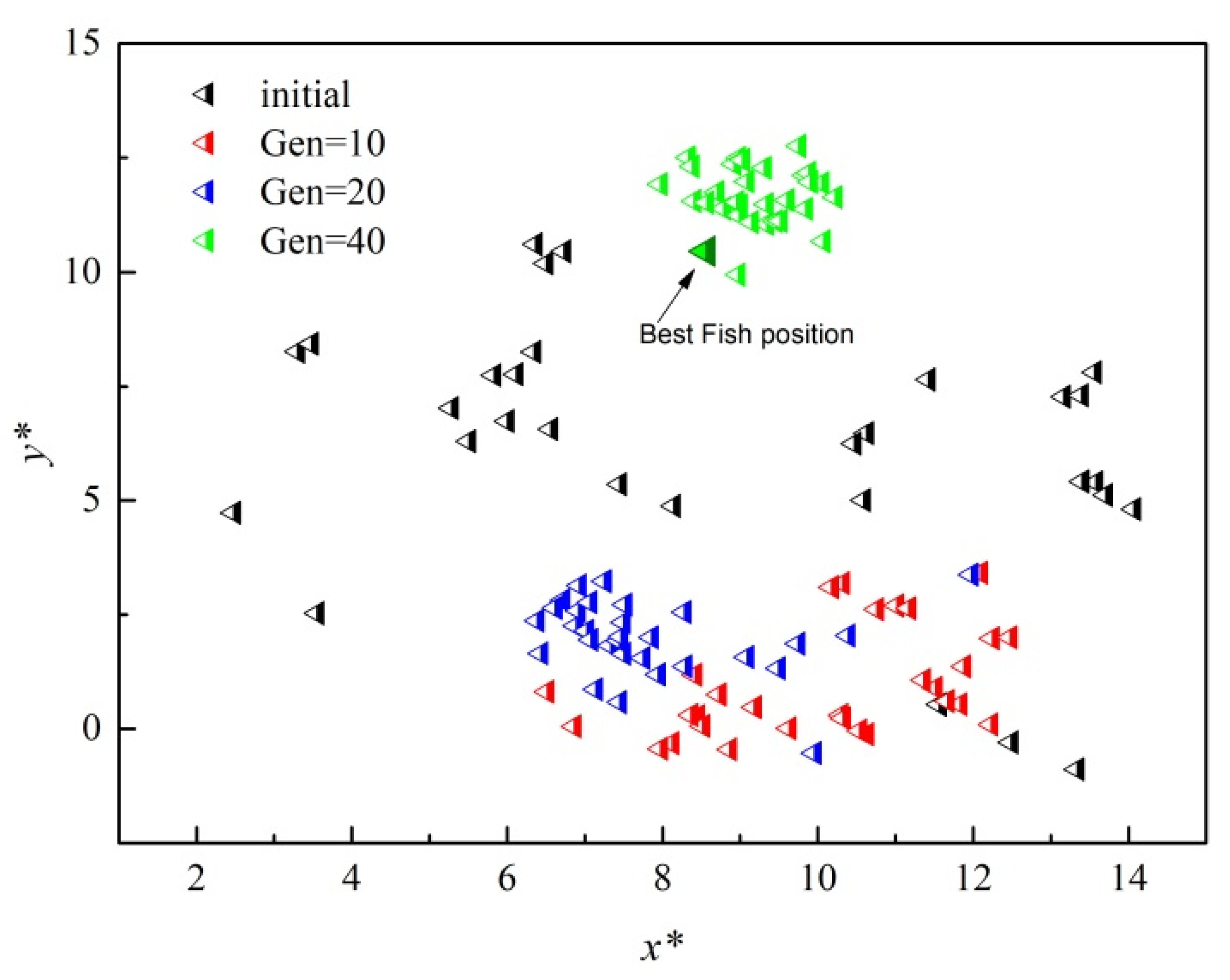
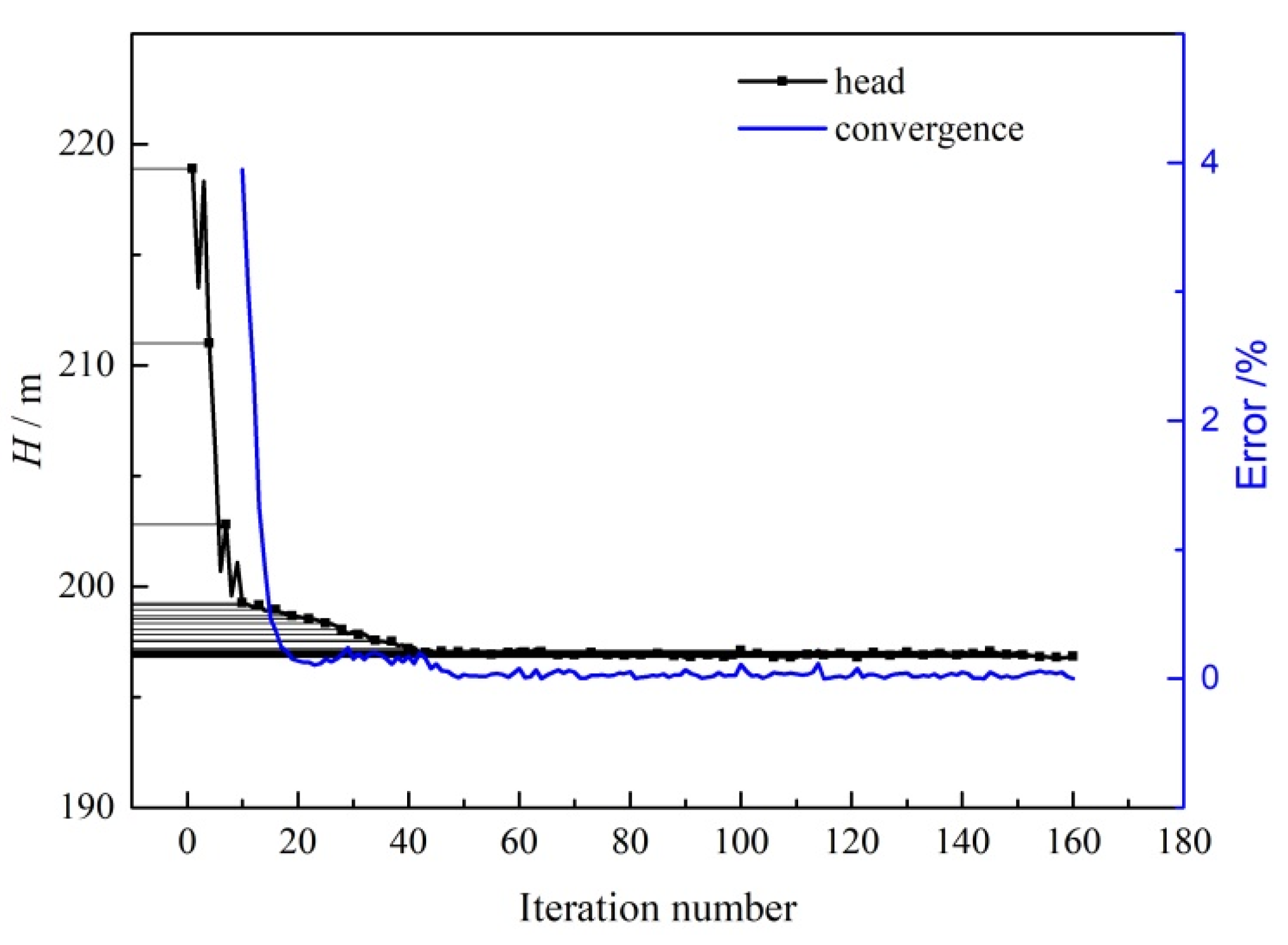
3. Optimization Scheme Using ASFA
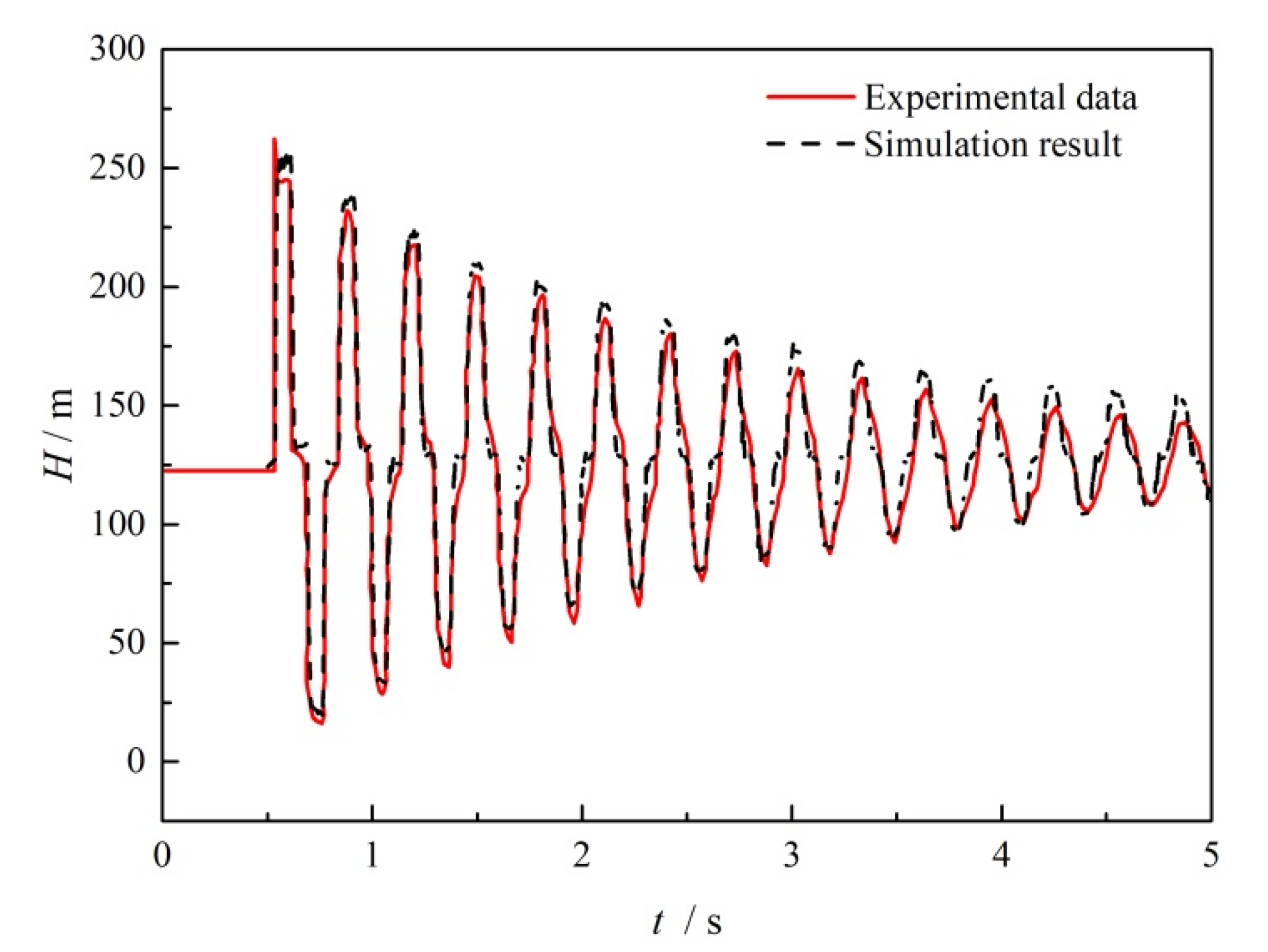
4. Model Validation
5. Results
5.1. Wave Damping Case without Pump Operation
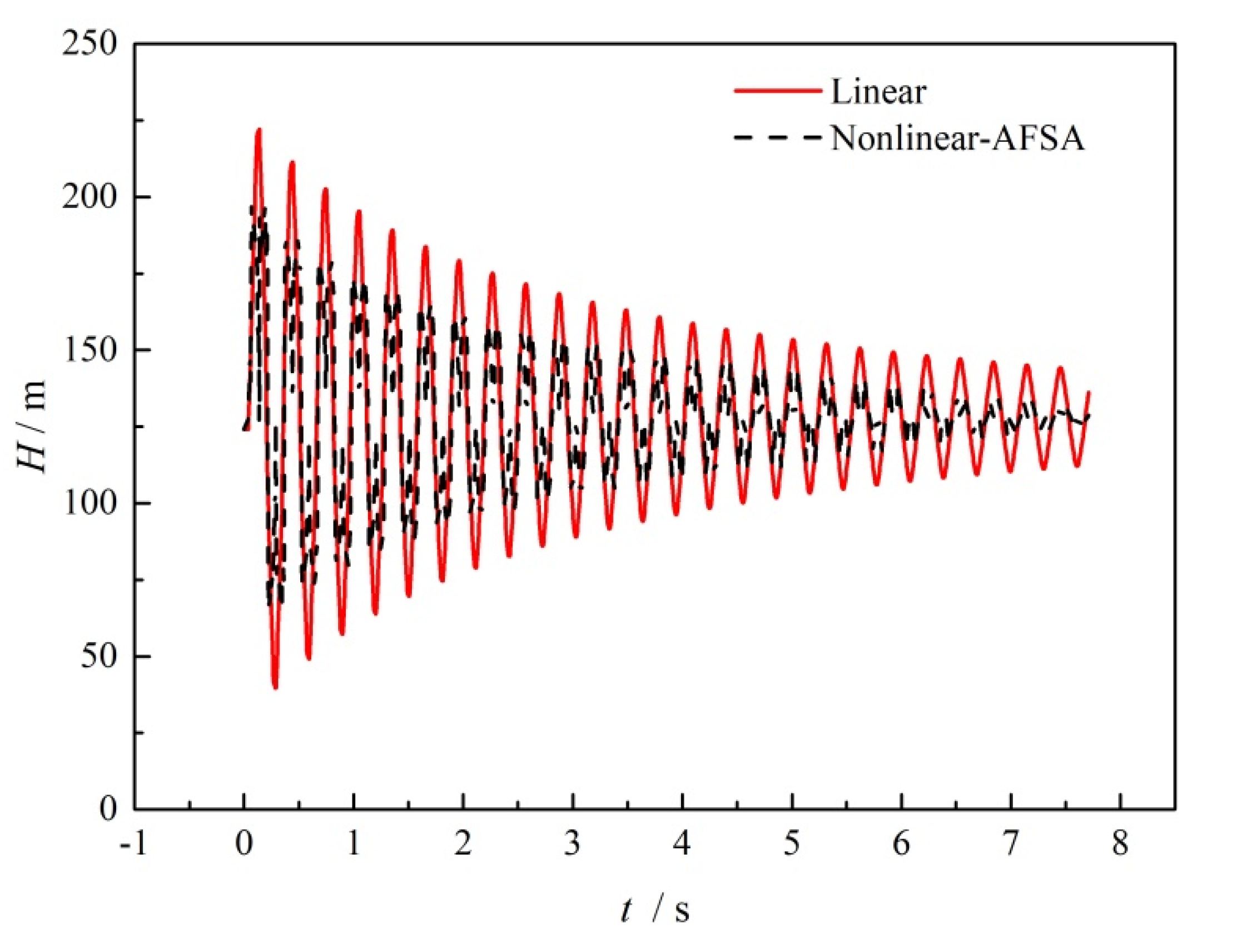
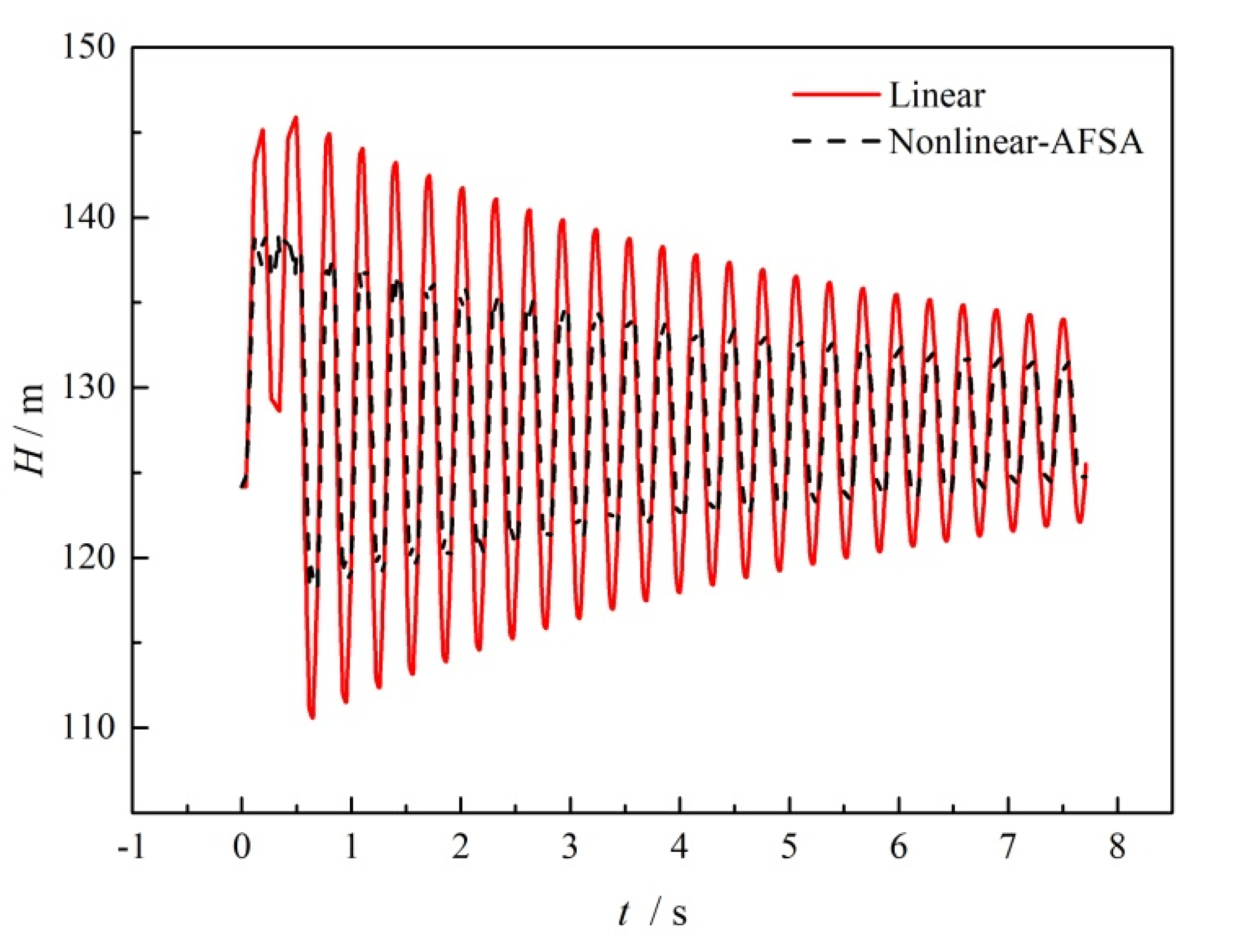
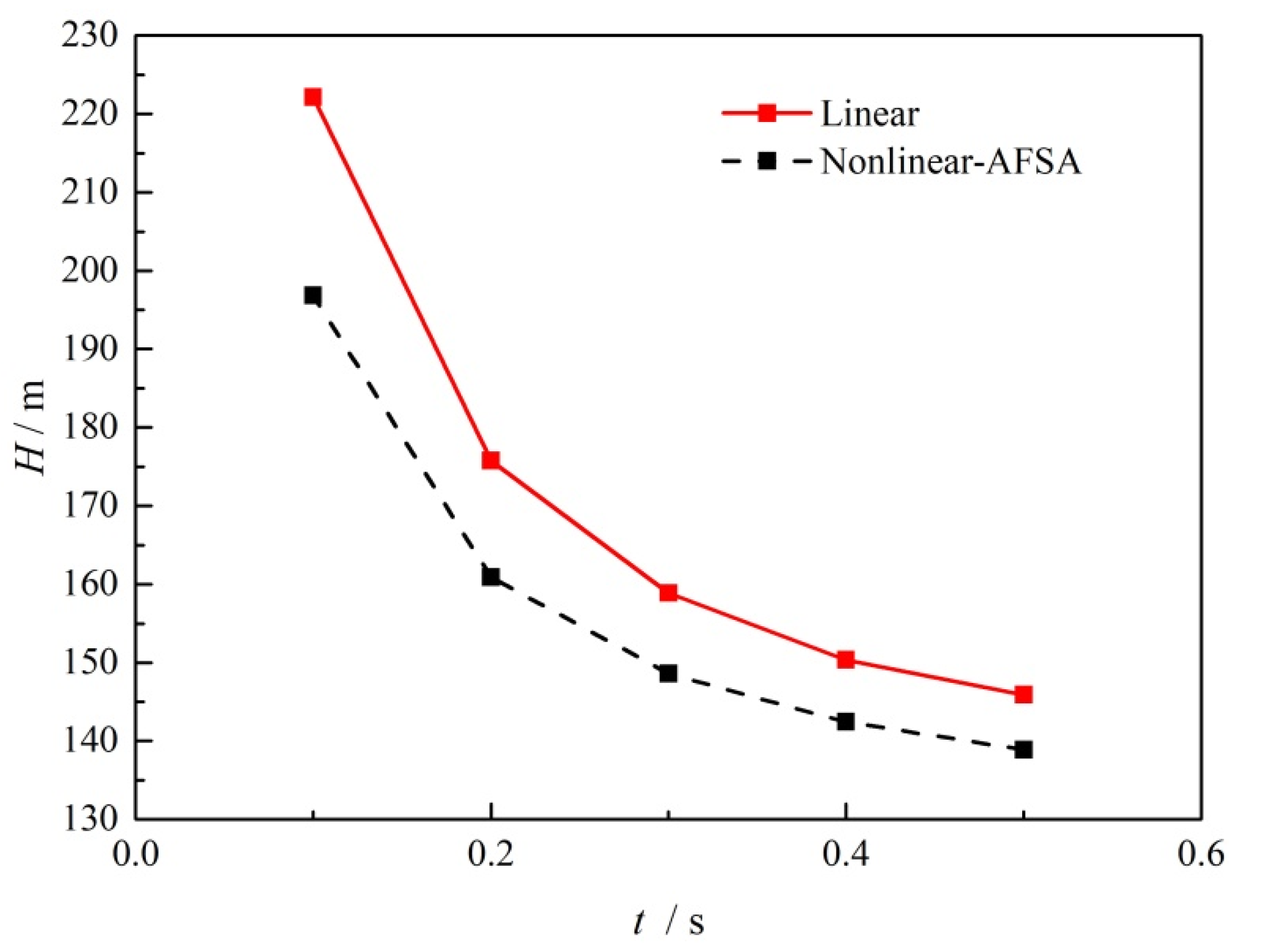
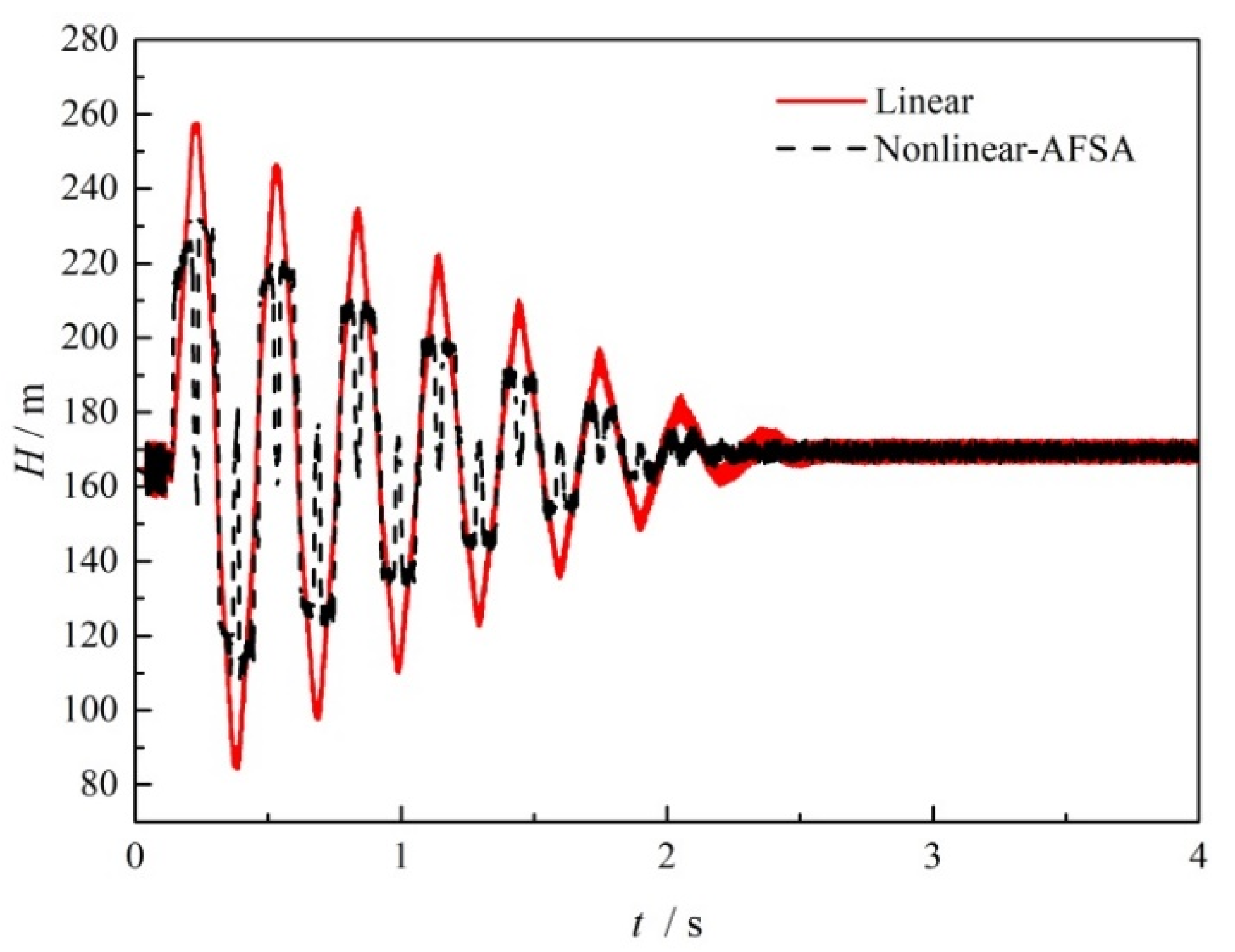
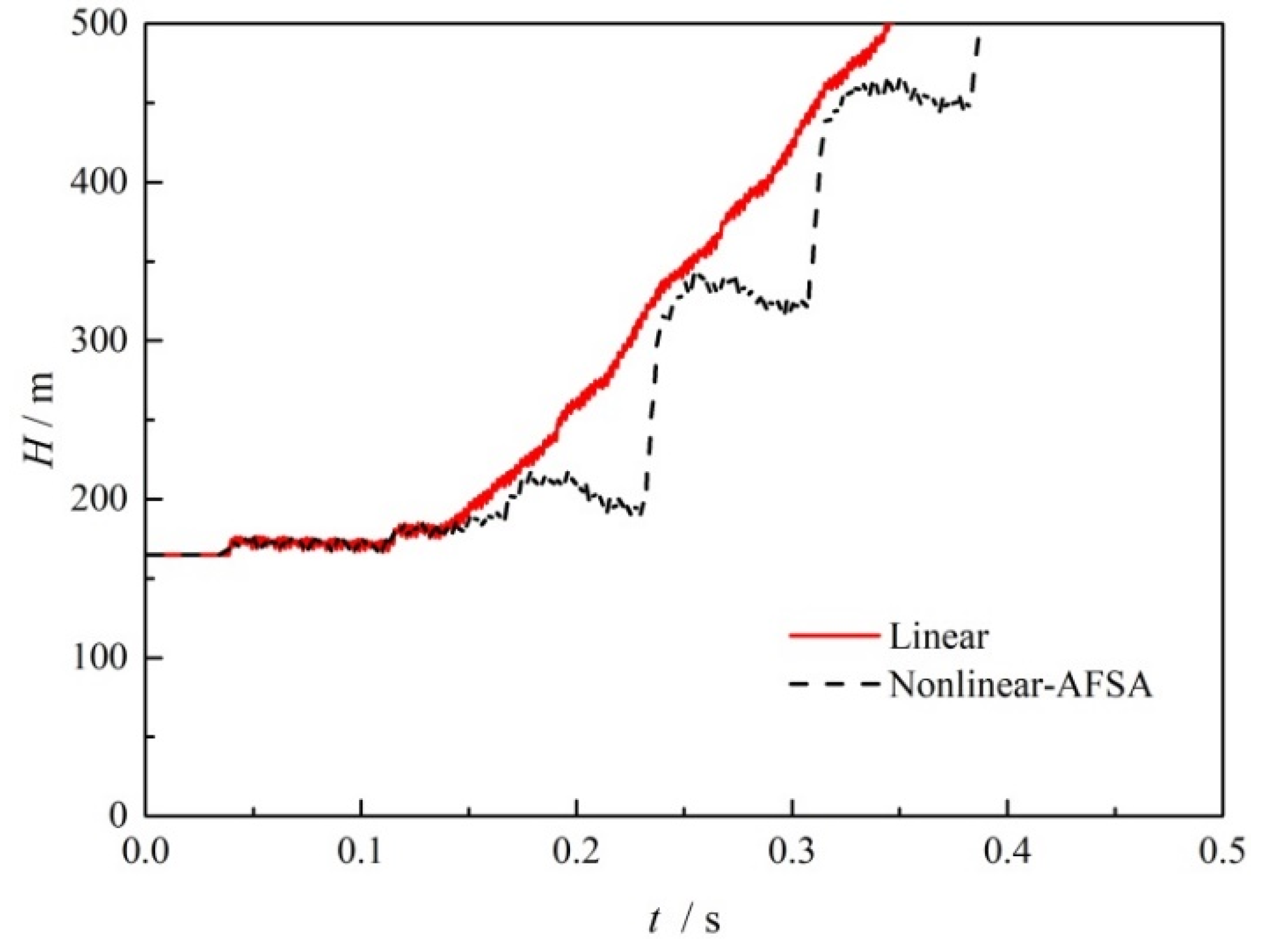
5.2. Wave Damping Case with Centrifugal Pump Operation
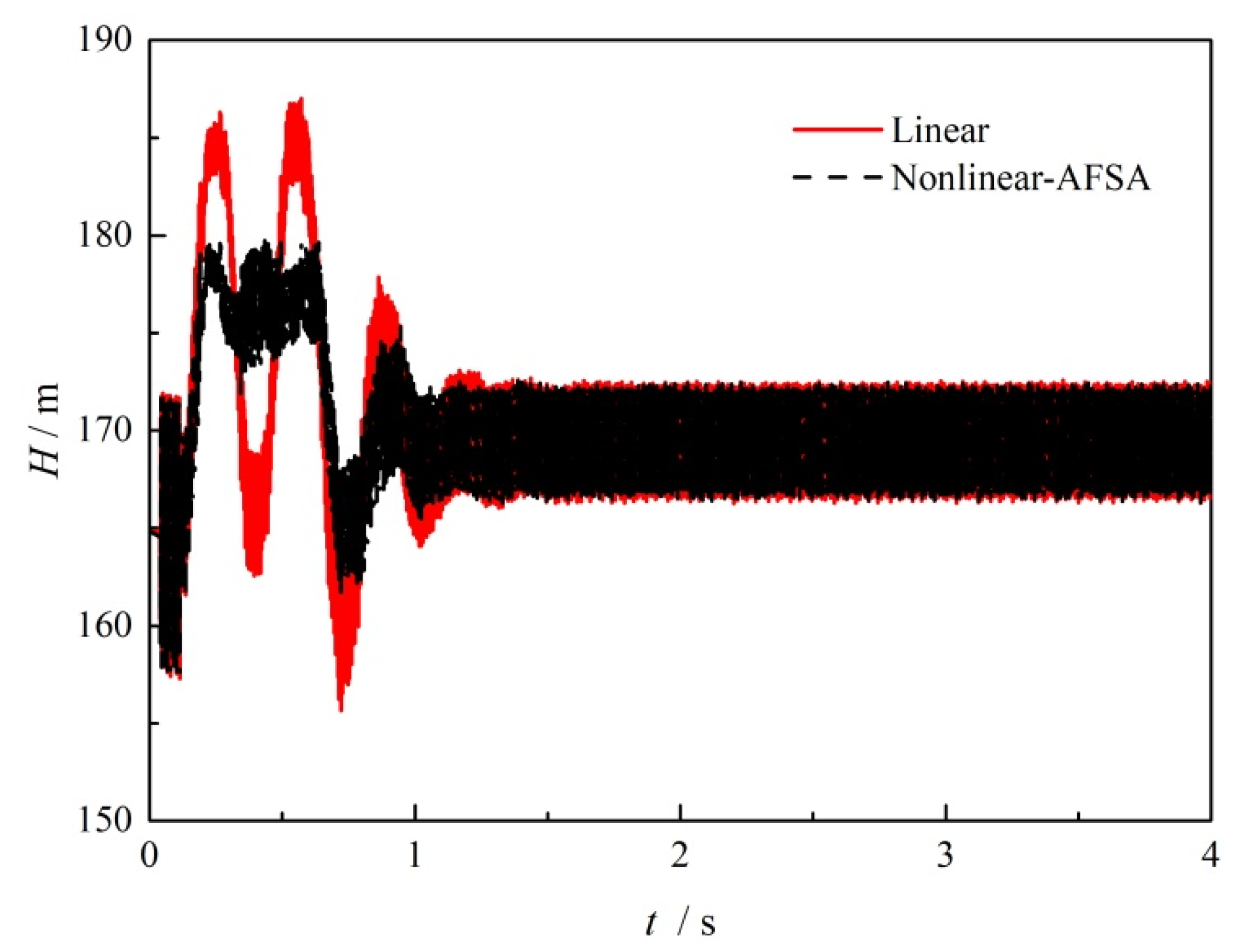
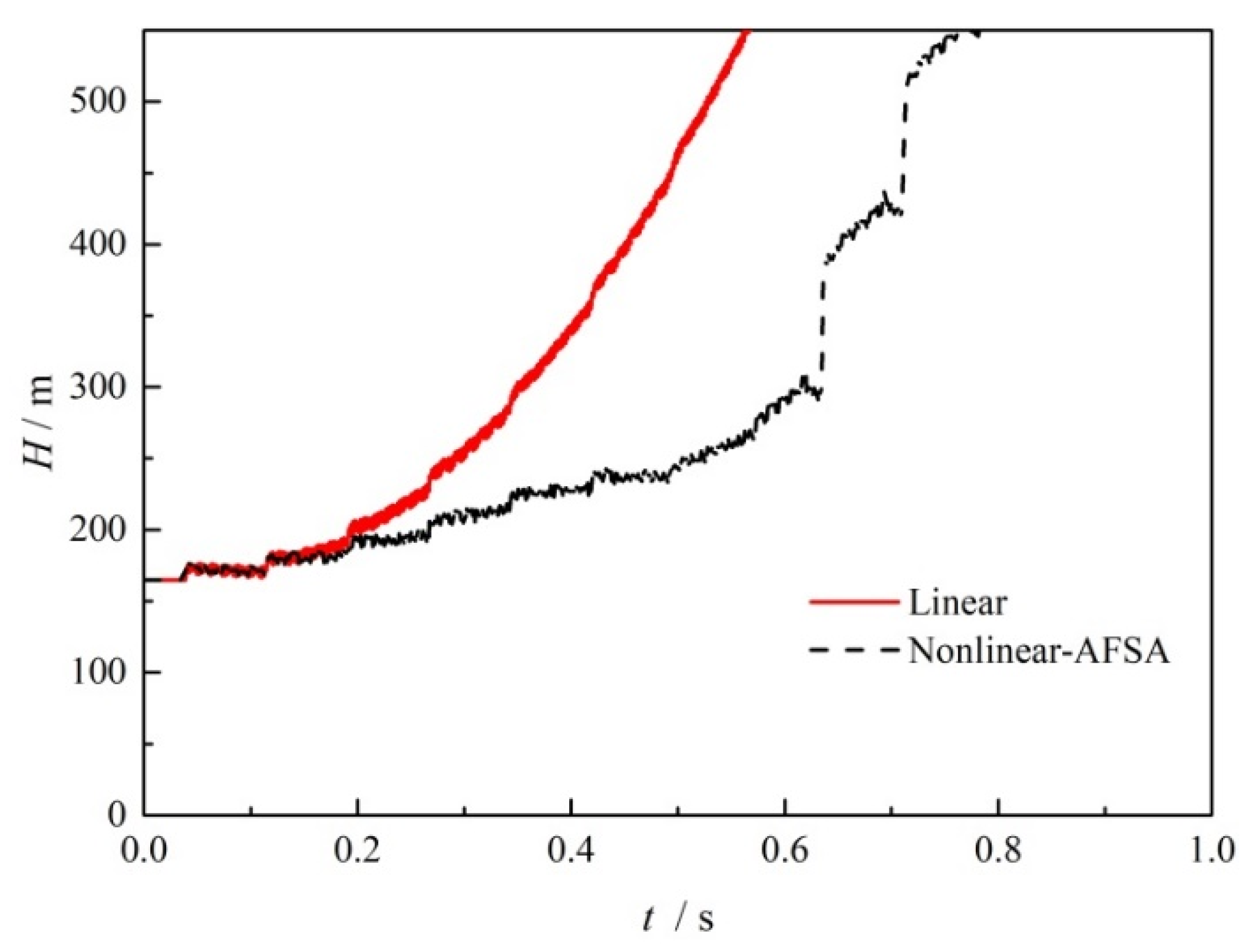
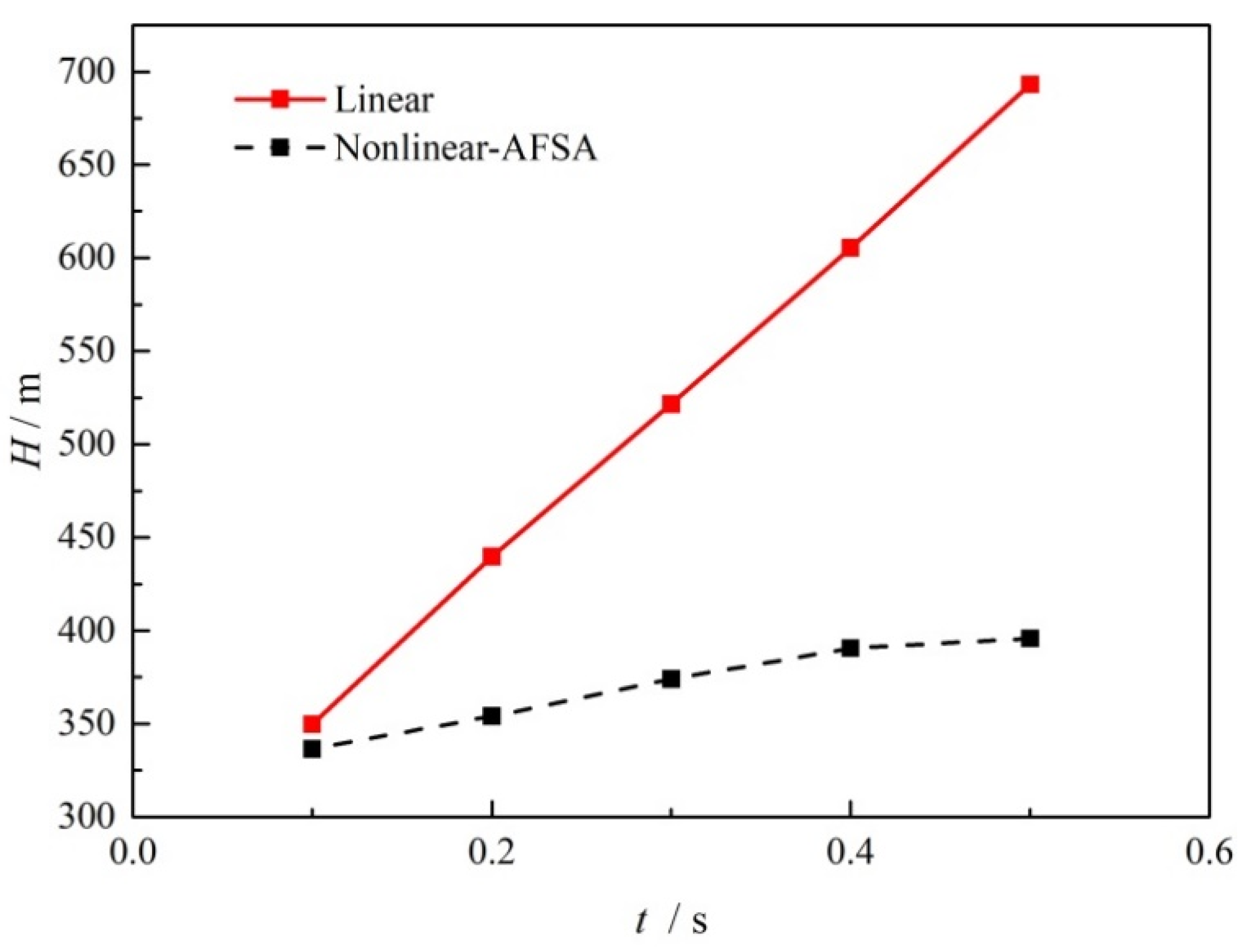
5.3. Wave Damping Case with Positive Displacement Pump Operation
6. Conclusions
- (1)
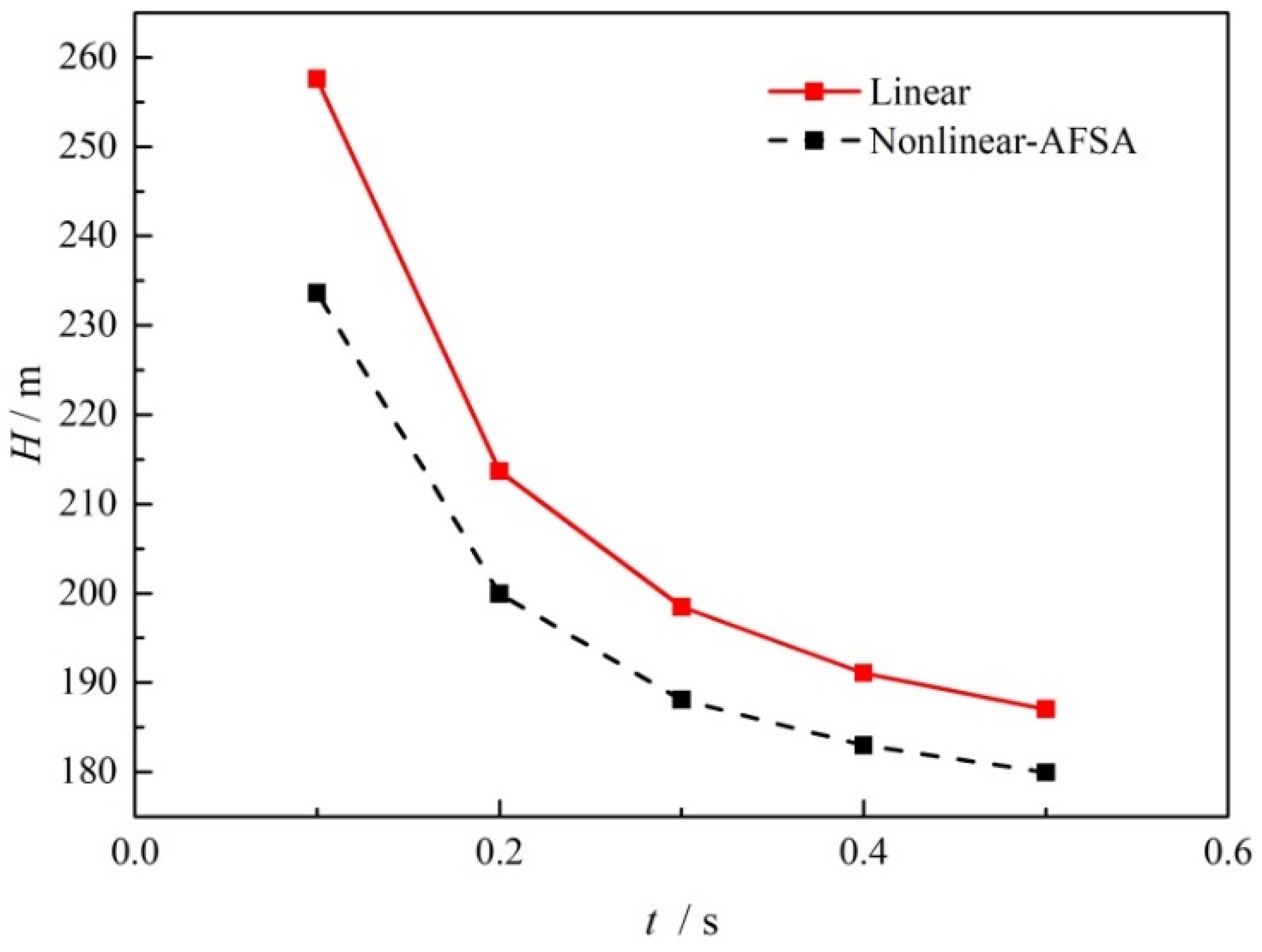
- The transient wave surge can be reduced through nonlinear valve closure without adding additional damping devices. For transient flow with and without a centrifugal pump running, surge reduction of 9.3% and 11.4% could be obtained in the most severe valve closure case. Even with increasing pressure with positive displacement pump operation, the surge damping method was able to achieve a 34% time margin for reaching the head limit and a maximum reduction in the surge amplitude of 75.2%.
- (2)
- With increasing valve closing time, the surge amplitude caused by valve closure decreases for the transient flow with and without the centrifugal pump running, and the rate of surge amplitude decrease also decreases. For positive displacement pumps, the surge amplitude increases with increasing valve closing time, but at a significantly slower rate of increase with the optimized nonlinear valve closure.
- (3)
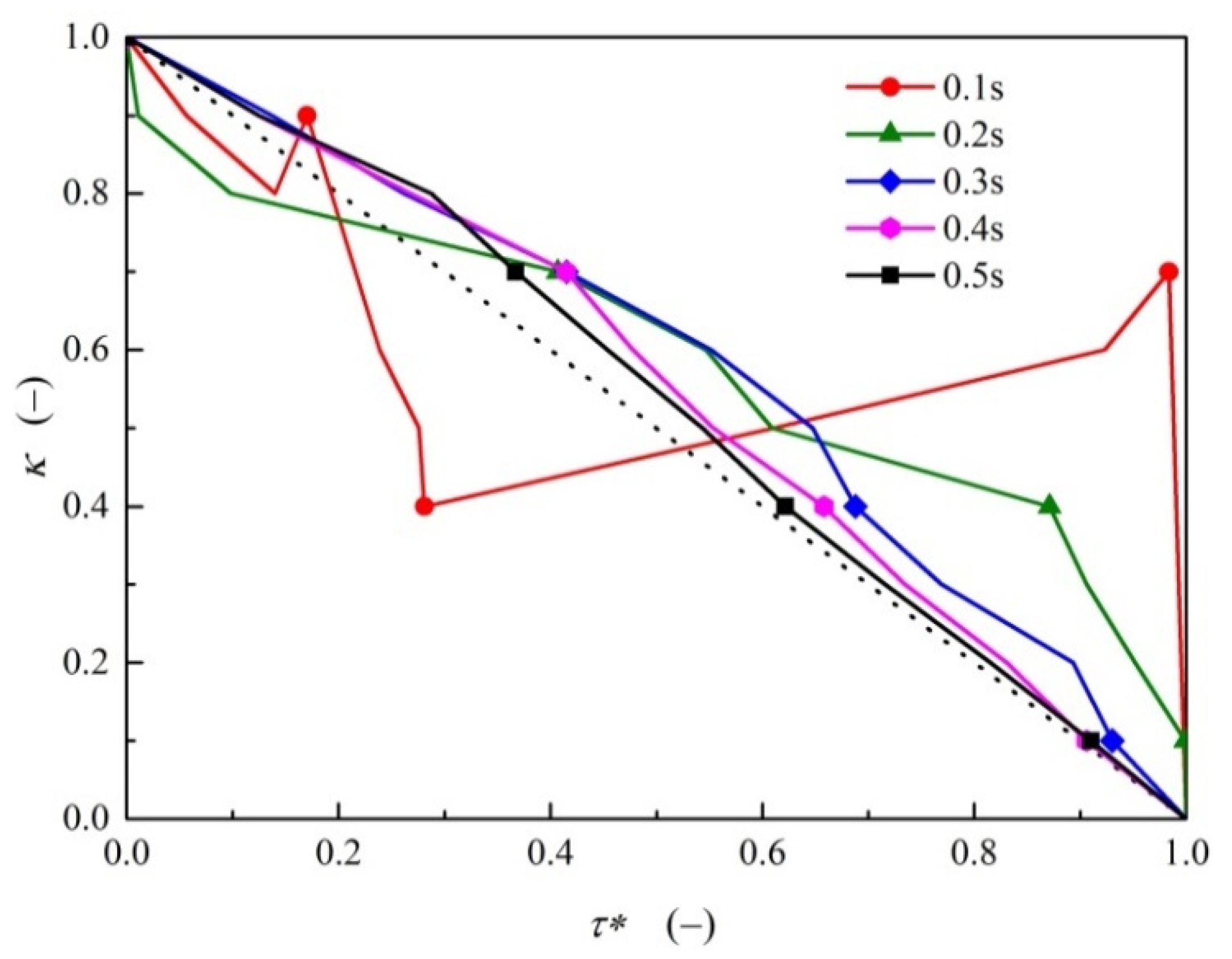
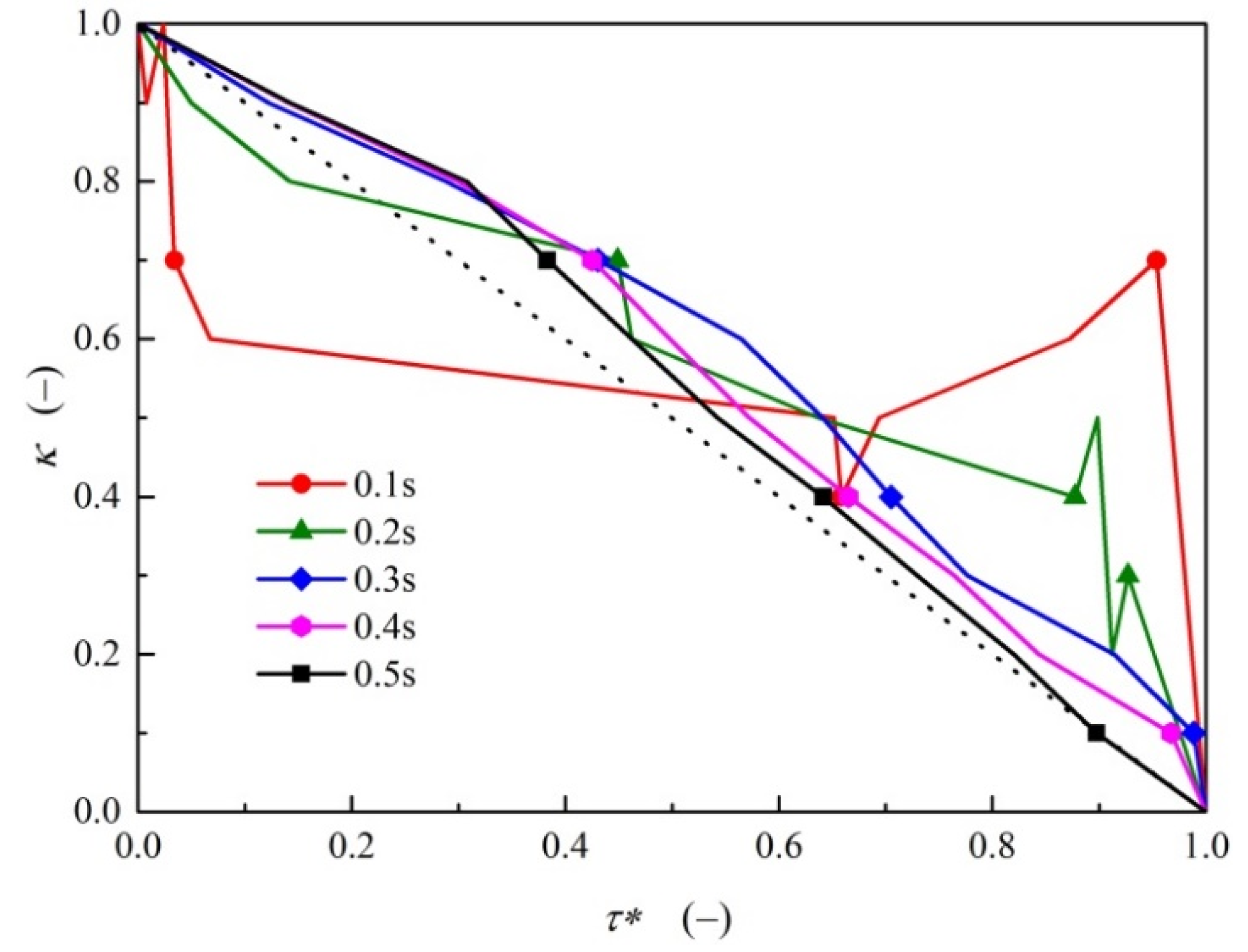
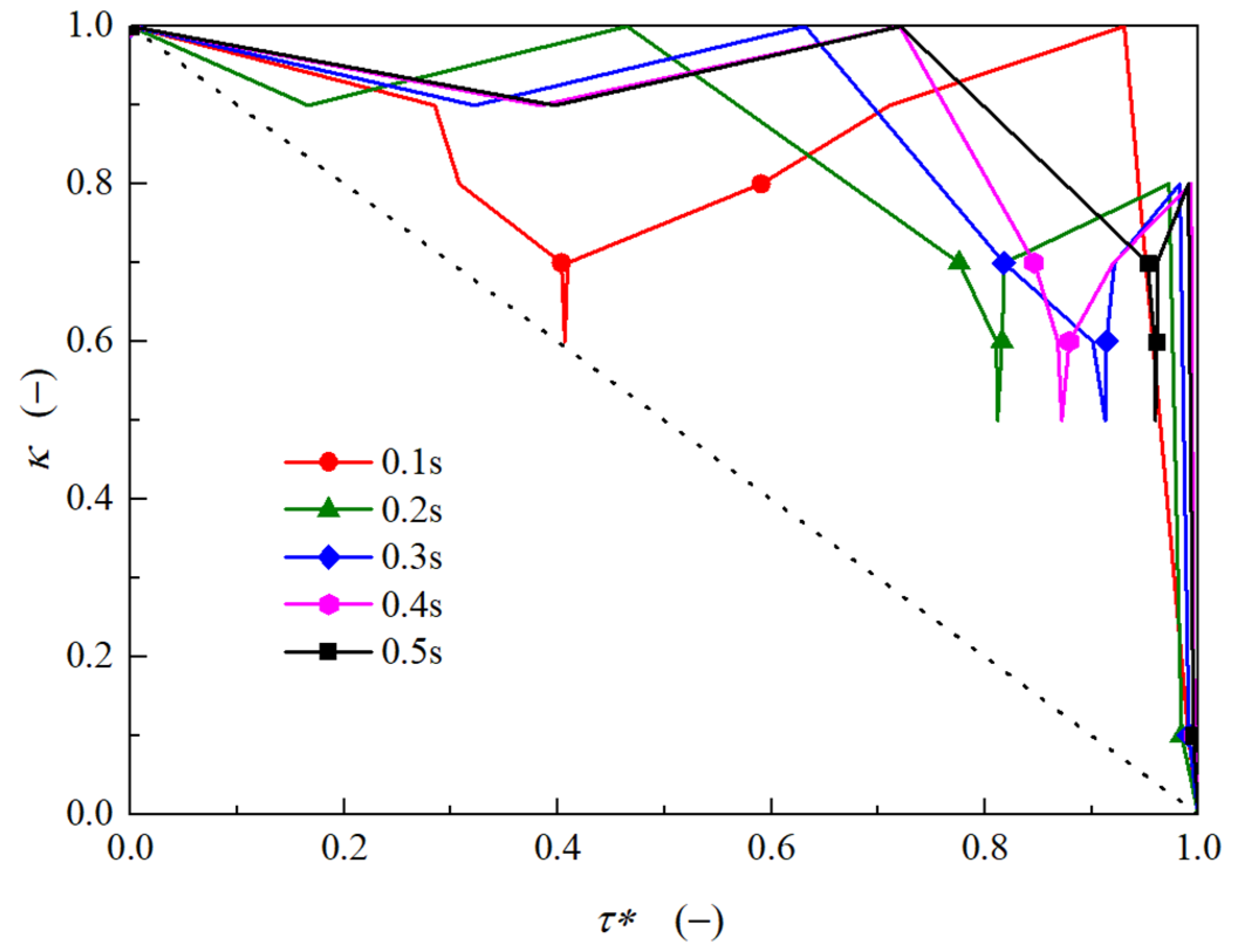
- For rapid valve closure in 0.1 s, the optimized nonlinear closing motion performs a similar “И” shape. For other valve closure cases in the present study, the optimized valve opening curves show a relatively smooth variation during the initial stage before decreasing rapidly to full closure during valve operation.
- (4)
- The valve closure process can be abstracted into a traveling salesman problem, and further optimization using an artificial fish swarm algorithm was demonstrated to be beneficial for wave damping. The strategy proposed in the present study could help for either guiding real-time valve control or serve as a design reference for novel valve structures for the purpose of surge protection.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFSA | artificial fish swarm algorithm |
| CB | convolution-based |
| CE | compression–expansion |
| CFD | computational fluid dynamics |
| IAB | instantaneous accelerations-based |
| MOC | method of characteristics |
| ODE | ordinary differential equation |
| TSP | traveling salesman problem |
| 1-D | one-dimensional |
| Notation | |
| a | wave speed (m∙s−1) |
| a1, a2 | pump coefficient constants (-) |
| A | cross sectional area (m2) |
| B | pipeline characteristic impedance (-) |
| D | pipe diameter (m) |
| f | Darcy–Weisbach friction factor (-) |
| g | gravitational acceleration (m∙s−2) |
| H | pressure head (m) |
| Js | steady friction loss term (-) |
| Ju | unsteady friction loss term (-) |
| k | empirical decay coefficient (-) |
| kd | second viscosity coefficient (-) |
| L | pipe length (m) |
| n | artificial fish number (-) |
| P | cross-section-average pressure (Pa) |
| Q | flowrate (m3∙s−1) |
| R | pipeline resistance coefficient (-) |
| r | radial coordinate (m) |
| Re | Reynolds number (-) |
| V | cross-section-average velocity (m∙s−1) |
| ϖ | phase velocity in fluctuation (rad∙s−1) |
| t | time (s) |
| τ | valve opening (-) |
| ρ | fluid density (kg∙m−3) |
| dynamic viscosity (Pa∙s) | |
| the second viscosity (Pa∙s) | |
| x | coordinate along the pipe axis (m) |
| X | artificial fish position (-) |
References
- Mandhare, N.A.; Karunamurthy, K.; Ismail, S. Compendious Review on “Internal Flow Physics and Minimization of Flow Instabilities Through Design Modifications in a Centrifugal Pump”. ASME J. Press. Vessel. Technol. 2019, 141, 051601. [Google Scholar] [CrossRef]
- Tanaka, T.; Tsukamoto, H. Transient behavior of a cavitating centrifugal pump at rapid change in operating conditions—Part 1: Transient phenomena at opening/closure of discharge valve. ASME J. Fluids Eng. 1999, 121, 841–849. [Google Scholar] [CrossRef]
- Duan, H.F.; Lee, P.J.; Che, T.C.; Ghidaoui, M.S.; Karney, B.W.; Kolyshkin, A.A. The influence of non-uniform blockages on transient wave behavior and blockage detection in pressurized water pipelines. J. Hydro-Environ. Res. 2017, 17, 1–7. [Google Scholar] [CrossRef]
- Duan, H.F.; Ghidaoui, M.S.; Lee, P.J.; Tung, Y.K. Relevance of unsteady friction to pipe size and length in pipe fluid transients. J. Hydraul. Eng. 2012, 138, 154–166. [Google Scholar] [CrossRef]
- Ghidaoui, M.; Mansour, S.; Zhao, M. Applicability of quasi steady axisymmetric turbulence models in water hammer. J. Hydraul. Eng. 2002, 128, 917–924. [Google Scholar] [CrossRef]
- Zielke, W. Frequency-dependent friction in transient pipe flow. J. Basic Eng. 1968, 90, 109–115. [Google Scholar] [CrossRef]
- Urbanowicz, K. Fast and accurate modelling of frictional transient pipe flow. Z. Angew. Math. Mech. 2018, 5, 802–823. [Google Scholar]
- Trikha, A.K. An efficient method for simulating frequency dependent friction in transient liquid flow. J. Fluids Eng. 1975, 97, 97–105. [Google Scholar] [CrossRef]
- Vardy, A.E.; Brown, J.M.B. Transient turbulent friction in fully rough pipe flows. J. Sound Vib. 2004, 270, 233–257. [Google Scholar] [CrossRef]
- Zarzycki, Z.; Kudzma, S. Simulation of transient flows in a hydraulic system with a long liquid line. J. Theor. App. Mech. 2007, 45, 853–871. [Google Scholar]
- Vitkovsky, J.P.; Stephens, M.; Bergant, A.; Simpson, A.R.; Lambert, M.F. Numerical error in weighting function-based unsteady friction models for pipe transients. J. Hydraul. Eng. 2006, 132, 709–721. [Google Scholar] [CrossRef] [Green Version]
- Brunone, B.; Golia, U.M.; Greco, M. Effects of two dimensionality on pipe transients modeling. J. Hydraul. Eng. 1995, 121, 906–912. [Google Scholar] [CrossRef]
- Pezzinga, G. Evaluation of Unsteady Flow Resistances by Quasi-2D or 1D Models. J. Hydraul. Eng. 2000, 126, 778–785. [Google Scholar] [CrossRef]
- Ramos, H.; Covas, D.; Borga, A.; Loureiro, D. Surge damping analysis in pipe systems: Modelling and experiments. J. Hydraul. Res. 2004, 42, 413–425. [Google Scholar] [CrossRef]
- Duan, H.F.; Meniconi, S.; Lee, P.J.; Brunone, B.; Ghidaoui, M.S. Local and integral energy-based evaluation for the unsteady friction relevance in transient pipe flows. J. Hydraul. Eng. 2017, 143, 04017015. [Google Scholar] [CrossRef] [Green Version]
- Nault, J.D.; Karney, B.W. Comprehensive adaptive modelling of 1-D unsteady pipe network hydraulics. J. Hydraul. Res. 2021, 59, 263–279. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, Z.; Deng, J.; Guo, X.; Lu, L. Unsteady friction model modified with compression–expansion effects in transient pipe flow. AQUA—Water Infrastruct. Ecosyst. Soc. 2022, 71, 330–344. [Google Scholar] [CrossRef]
- Wu, D.; Yang, S.; Wu, P.; Wang, L. MOC-CFD coupled approach for the analysis of the fluid dynamic interaction between water hammer and pump. J. Hydraul. Eng. 2015, 141, 06015003. [Google Scholar] [CrossRef]
- He, L.; Wen, K.; Gong, J.; Wu, C. A multi-model ensemble digital twin solution for real-time unsteady flow state estimation of a pumping station. ISA Trans. 2021. online ahead of print. [Google Scholar] [CrossRef]
- Vítkovský, J.P.; Bergant, A.; Simpson, A.R.; Lambert, M.F. Systematic evaluation of one-dimensional unsteady friction models in simple pipelines. J. Hydraul. Eng. 2006, 132, 696–708. [Google Scholar] [CrossRef] [Green Version]
- Bettaieb, N.; Taieb, E.H. Assessment of failure modes caused by water hammer and investigation of convenient control measures. J. Pipeline Syst. Eng. Pract. 2020, 11, 04020006. [Google Scholar] [CrossRef]
- Garg, R.K.; Kumar, A.; Abbas, A. Analysis of wave damping in pipeline having different pipe materials configuration under water hammer conditions. Res. Sq. 2021, 1–30. [Google Scholar] [CrossRef]
- Urbanowicz, K.; Stosiak, M.; Towarnicki, K.; Bergant, A. Theoretical and experimental investigations of transient flow in oil-hydraulic small-diameter pipe system. Eng. Fail. Anal. 2021, 128, 105607. [Google Scholar]
- Wan, W.; Huang, W. Investigation on complete characteristics and hydraulic transient of centrifugal pump. J. Mech. Sci. Technol 2011, 25, 2583–2590. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Chen, S.; Shi, L.; Zhao, W.; Wang, S. Valve closure based on pump runaway characteristics in long distance pressurized systems. AQUA—Water Infrastruct. Ecosyst. Soc. 2021, 70, 493–506. [Google Scholar] [CrossRef]
- Tian, W.; Su, G.H.; Wang, G.; Qiu, S.; Xiao, Z. Numerical simulation and optimization on valve-induced water hammer characteristics for parallel pump feedwater system. Ann. Nucl. Energy 2008, 35, 2280–2287. [Google Scholar] [CrossRef]
- Triki, A.; Essaidi, B. Investigation of Pump Failure-Induced Waterhammer Waves: A Case Study. J. Press. Vessel Technol. 2022, 144, 061403. [Google Scholar] [CrossRef]
- Sattar, A.M.A.; Soliman, M.; El-Ansary, A. Preliminary sizing of surge vessels on pumping mains. Urban. Water J. 2019, 16, 738–748. [Google Scholar] [CrossRef]
- Kubrak, M.; Malesińska, A.; Kodura, A.; Urbanowicz, K.; Bury, P.; Stosiak, M. Water Hammer Control Using Additional Branched HDPE Pipe. Energies 2021, 14, 8008. [Google Scholar] [CrossRef]
- Bostan, M.; Akhtari, A.A.; Bonakdari, H.; Gharabaghi, B.; Noori, O. Investigation of a new shock damper system efficiency in reducing water hammer excess pressure due to the sudden closure of a control valve. ISH J. Hydraul. Eng. 2020, 26, 258–266. [Google Scholar]
- Triki, A.; Trabelsi, M. On the in-series and branching dual-technique-based water-hammer control strategy. Urban. Water J. 2021, 18, 631–639. [Google Scholar] [CrossRef]
- Triki, A. Comparative assessment of the inline and branching design strategies based on the compound-technique. AQUA-Water Infrastruct. Ecosyst. Soc. 2021, 70, 155–170. [Google Scholar] [CrossRef]
- Reddy, H.P.; Araya, W.F.; Chaudhry, M.H. Estimation of decay coefficients for unsteady friction for instantaneous, acceleration-based models. J. Hydraul. Eng. 2012, 138, 260–271. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, Z.; Shi, G.; Huang, Y. Effects of rotational speeds on the performance of a centrifugal pump with a variable-pitch inducer. J. Hydrodynam. 2017, 29, 854–862. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients; Springer: New York, NY, USA, 2014. [Google Scholar]
- Barrio, R.; Blanco, E.; Keller, J.; Parrondo, J.; Ferna’ndez, J. Numerical determination of the acoustic impedance of a centrifugal pump. In Proceedings of the Fluids Engineering Division Summer Meeting, Hamamatsu, Japan, 24–29 July 2011; pp. 405–412. [Google Scholar]
- Hu, J.; Yang, J.; Zeng, W.; Yang, J. Transient pressure analysis of a prototype pump turbine: Field tests and simulation. J. Fluids Eng. 2018, 140, 071102. [Google Scholar]
- Zhang, J.; Yang, H.; Liu, H.; Xu, L.; Lv, Y. Pressure Fluctuation Characteristics of High-Speed Centrifugal Pump with Enlarged Flow Design. Processes 2021, 9, 2261. [Google Scholar] [CrossRef]
- Li, X. A new Intelligent Optimization Method-Artificial Fish School Algorithm. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2003. (In Chinese). [Google Scholar]
- Adamkowski, A.; Lewandowski, M. Experimental examination of unsteady friction models for transient pipe flow Simulation. J. Fluids Eng. 2006, 128, 1351. [Google Scholar] [CrossRef]
- Azizi, R. Empirical study of artificial fish swarm algorithm. Int. J. Comput. Netw. Commun. 2014, 3, 1–7. [Google Scholar]
- Martin, C.S. Representation of Pump Characteristics for Transient Analysis. In Proceedings of the ASME, Symposium on Performance Characteristics of Hydraulic Turbines and Pumps, Winter Annual Meeting, Boston, MA, USA, 13–18 November 1983; pp. 1–13. [Google Scholar]
- Donsky, B. Complete pump characteristics and the effects of specific speeds on hydraulic transients. J. Basic Eng. 1961, 83, 685–696. [Google Scholar]
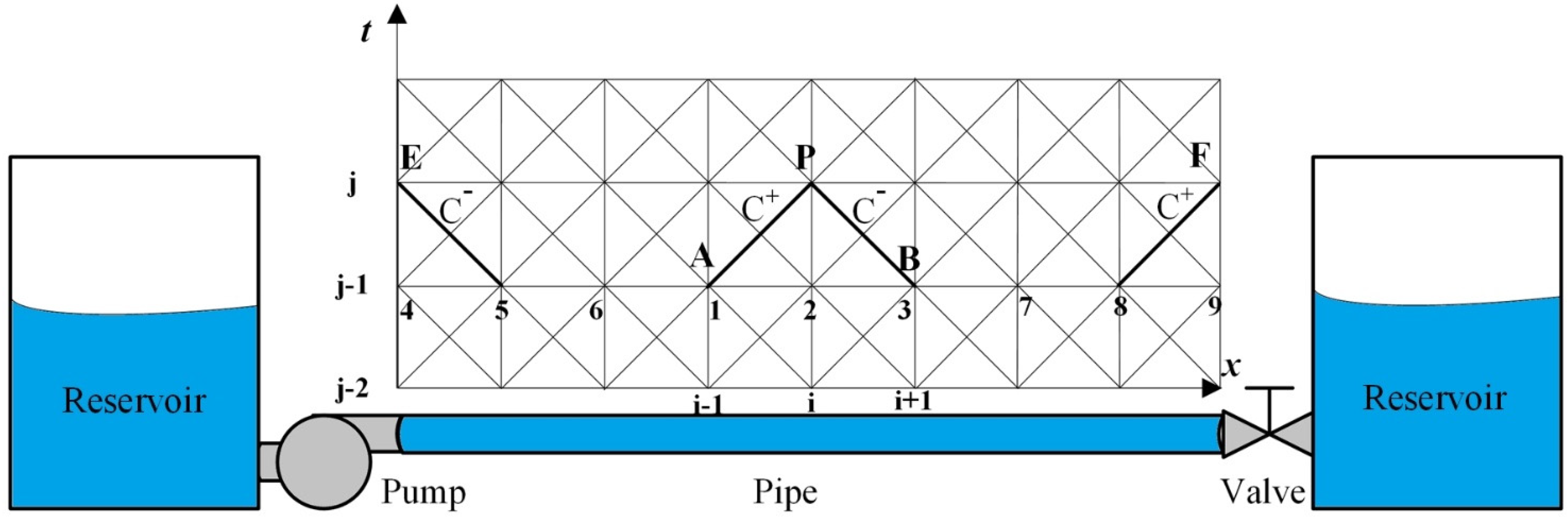
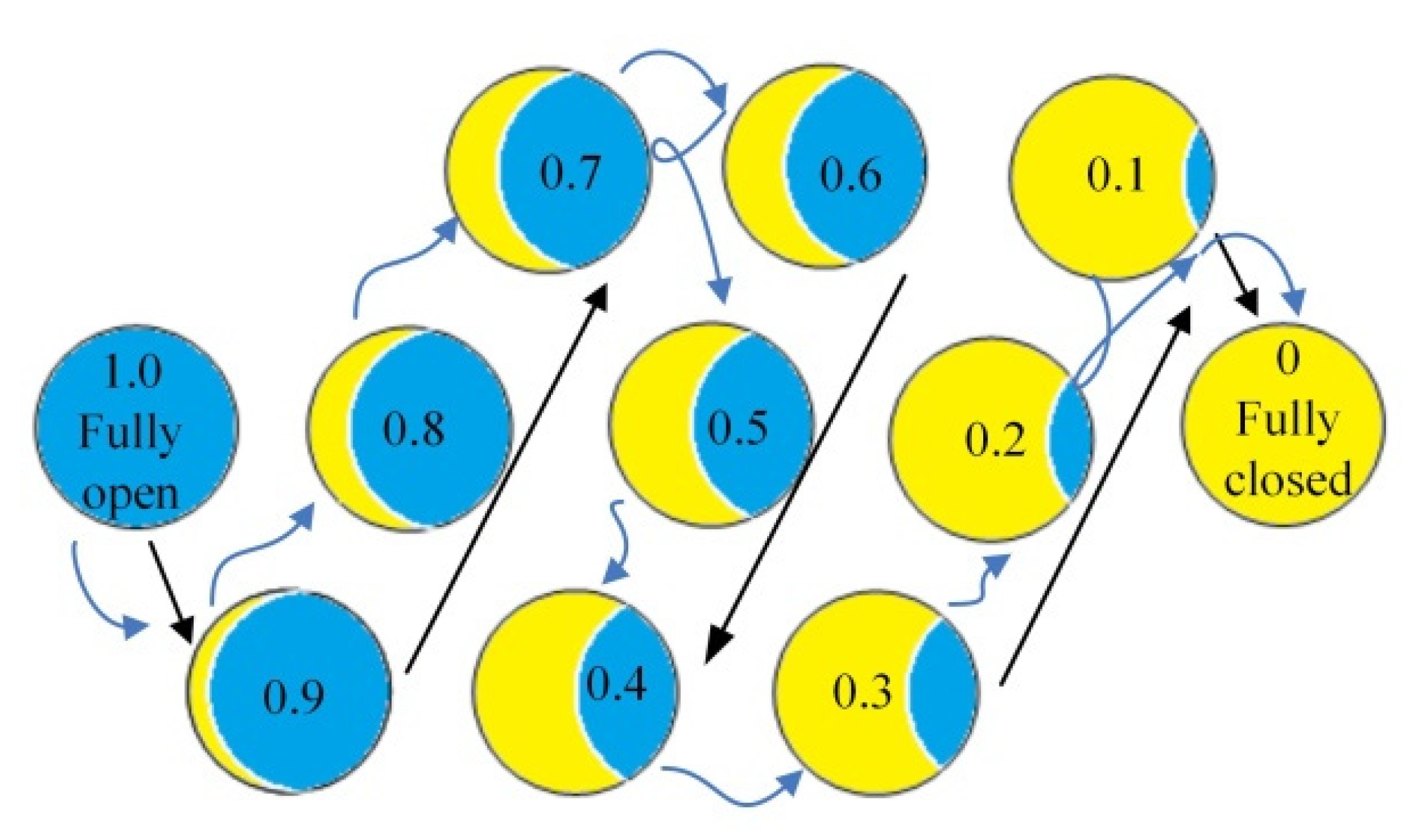
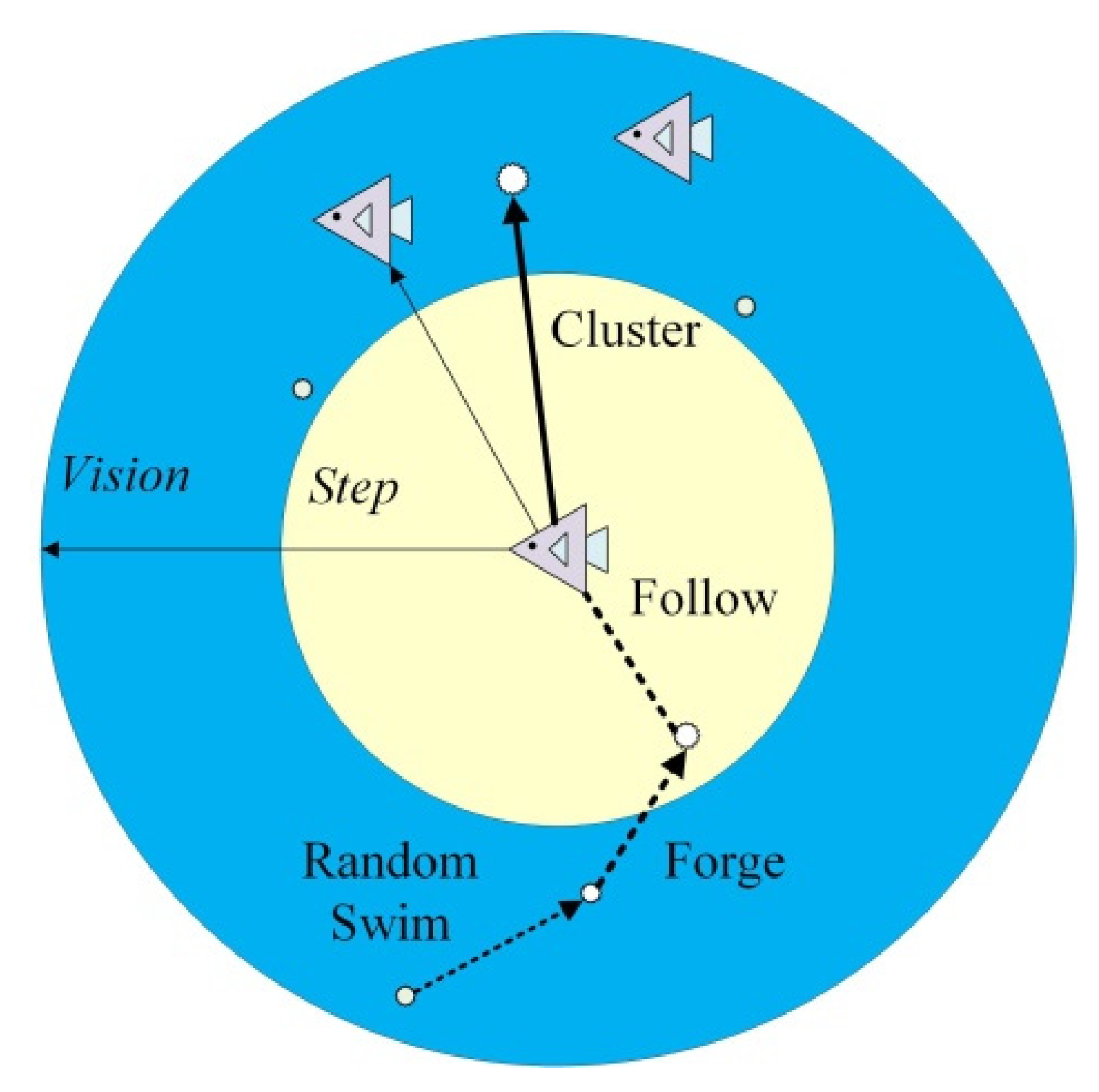
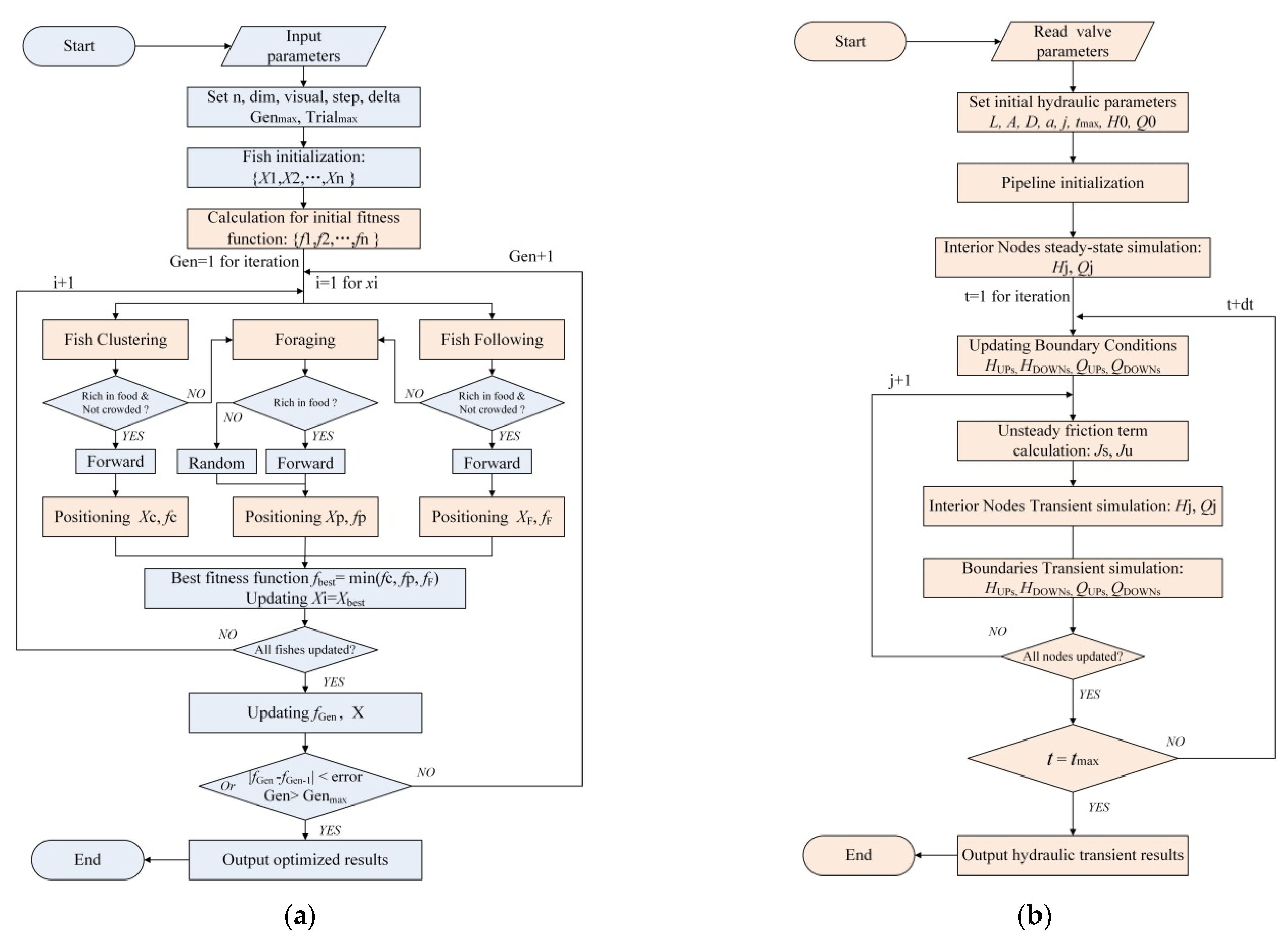
| Parameters (Unit) | Values |
|---|---|
| Initial tank head, Hres (m) | 128 |
| Initial flow velocity, V0 (m/s) | 0.94 |
| Pipeline length, L (m) Wave speed, a (m/s) | 98.11 1298.4 |
| Pump rotational speed, npump (r/min) Pump designed head, Hpump (m) Pump designed velocity, Vpump (m/s) | 8000 165.9 0.88 |
| blade numbers | 8 |
| Valve closing time, tc (s) | 0.1~0.5 |
| (kg/m3) | 997.59 |
| ) | 0.947 × 10−3 |
| empirical coefficient k second viscosity coefficient kd Darcy–Weisbach friction factor, f | 0.0138 20.258 0.0224 |
| Parameters | Description | Values |
|---|---|---|
| Vision | visual radius | 0.1 |
| step | moving distance | 0.01 |
| n | artificial fish quatities | 30 |
| dim | artificial fish dimension | 10 |
| delta Trailmax Genmax | fish swarm crowdness maximum trial number maximum iteration number | 27 30 500 |
| error | convergence error | 1 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Xia, Q.; Guo, X.; Lu, L.; Deng, J. A Novel Surge Damping Method for Hydraulic Transients with Operating Pump Using an Optimized Valve Control Strategy. Water 2022, 14, 1576. https://doi.org/10.3390/w14101576
Cao Z, Xia Q, Guo X, Lu L, Deng J. A Novel Surge Damping Method for Hydraulic Transients with Operating Pump Using an Optimized Valve Control Strategy. Water. 2022; 14(10):1576. https://doi.org/10.3390/w14101576
Chicago/Turabian StyleCao, Zheng, Qi Xia, Xijian Guo, Lin Lu, and Jianqiang Deng. 2022. "A Novel Surge Damping Method for Hydraulic Transients with Operating Pump Using an Optimized Valve Control Strategy" Water 14, no. 10: 1576. https://doi.org/10.3390/w14101576
APA StyleCao, Z., Xia, Q., Guo, X., Lu, L., & Deng, J. (2022). A Novel Surge Damping Method for Hydraulic Transients with Operating Pump Using an Optimized Valve Control Strategy. Water, 14(10), 1576. https://doi.org/10.3390/w14101576







