Development and Assessment of Water-Level Prediction Models for Small Reservoirs Using a Deep Learning Algorithm
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
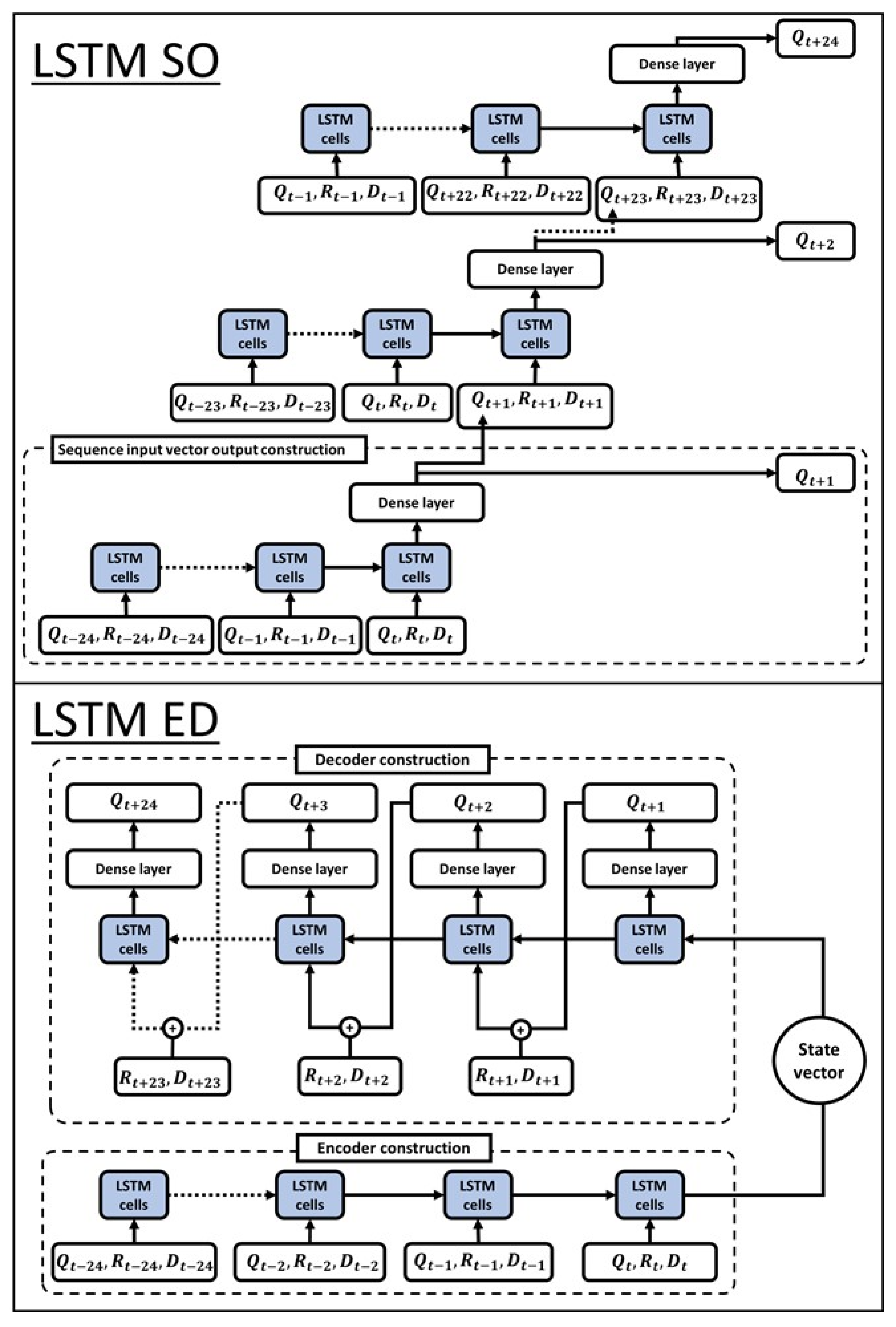
2.2. LSTM Model Development
2.3. LSTM Model Assessment
2.4. Ensemble Learning Method
2.5. Comparing the Performances of Different Models
3. Results and Discussion
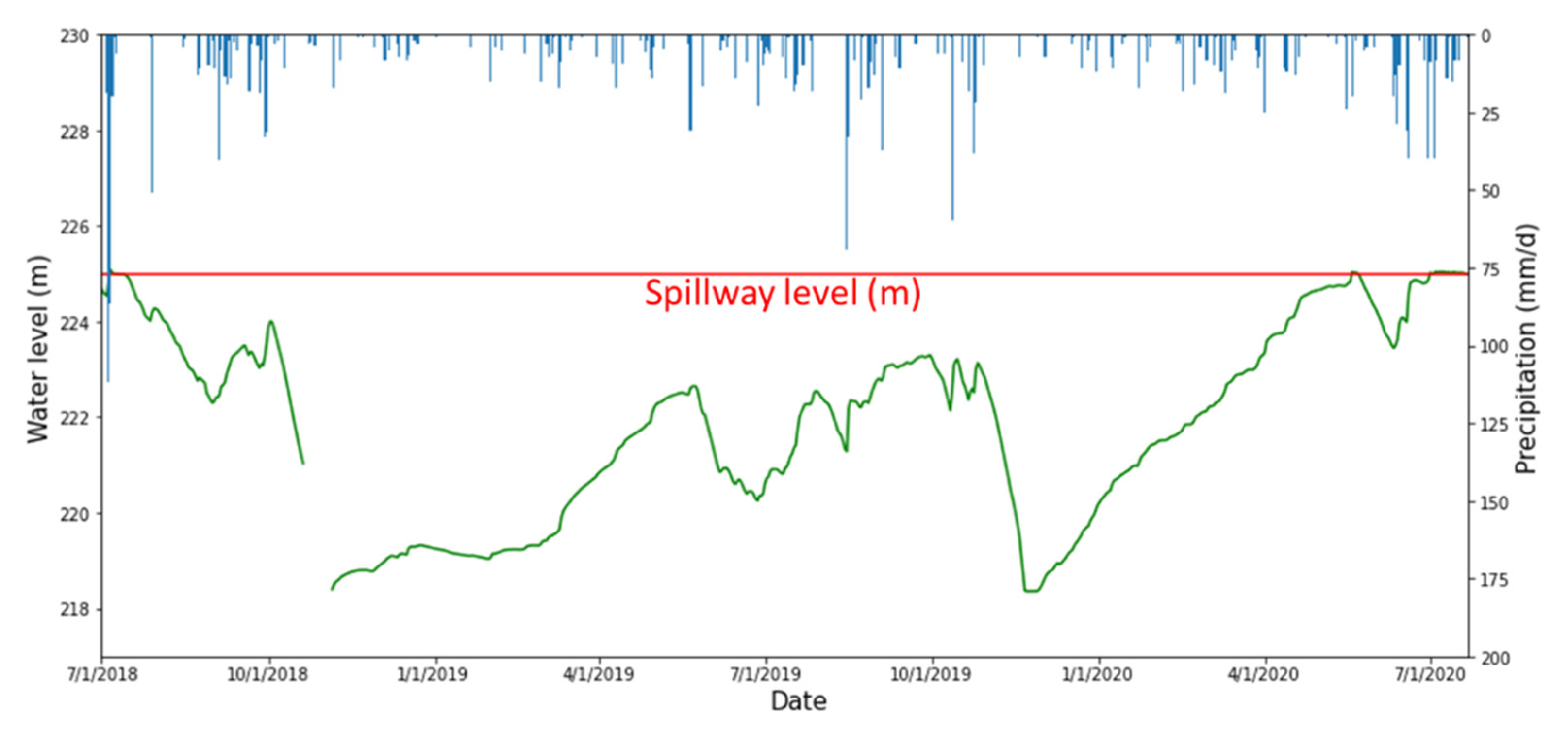
3.1. Field Data
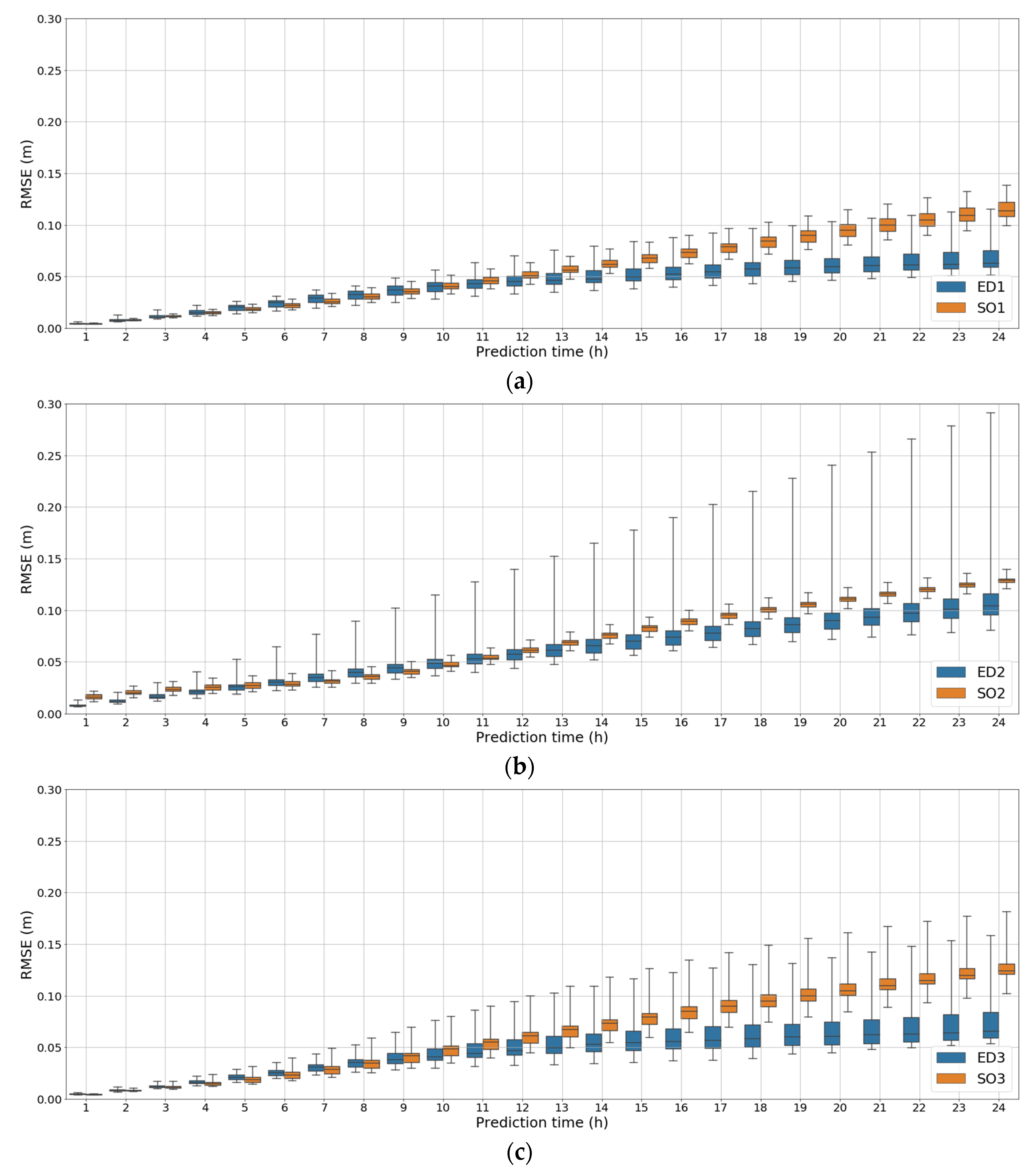
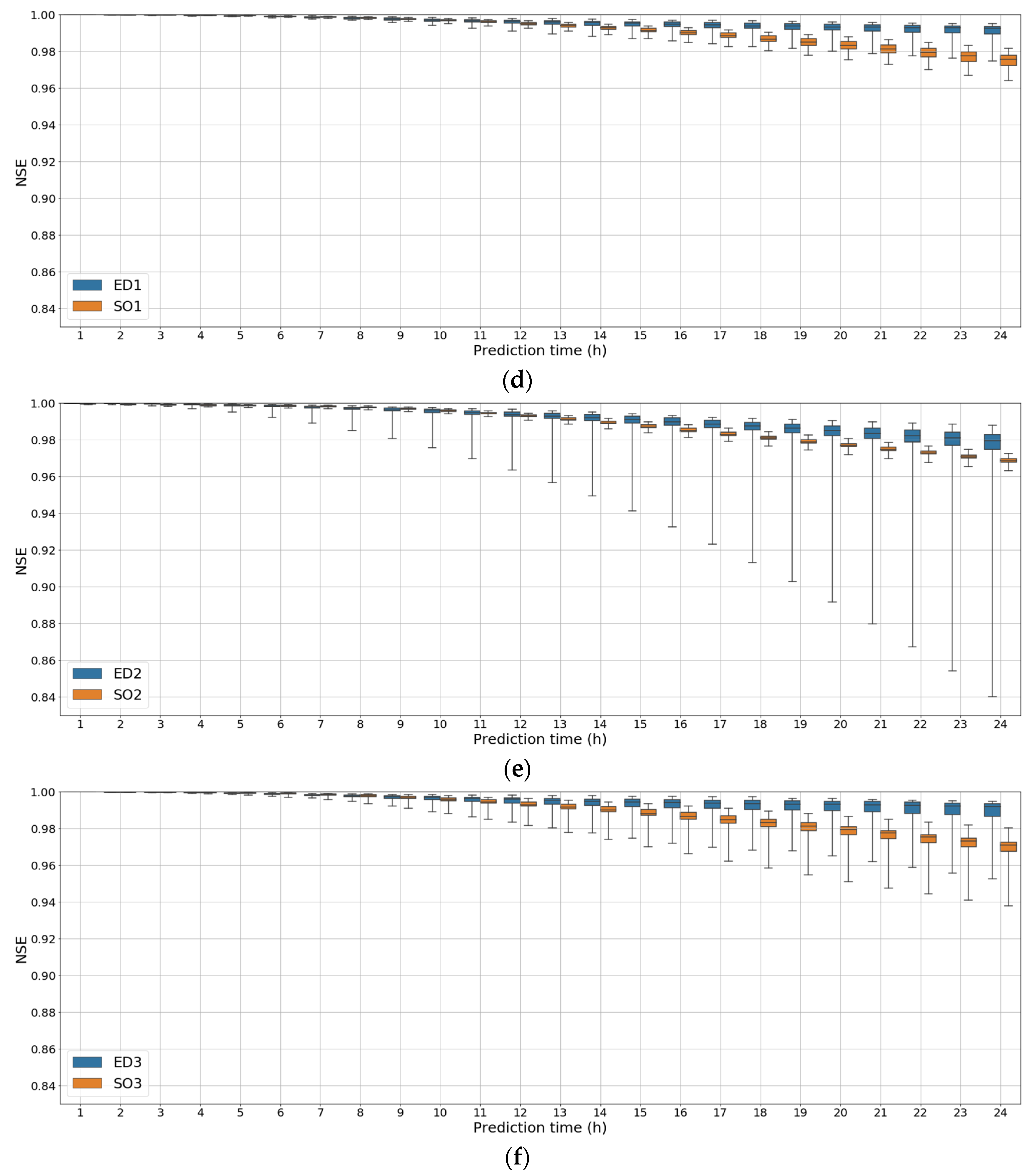
3.2. Comparison of the LSTM Models
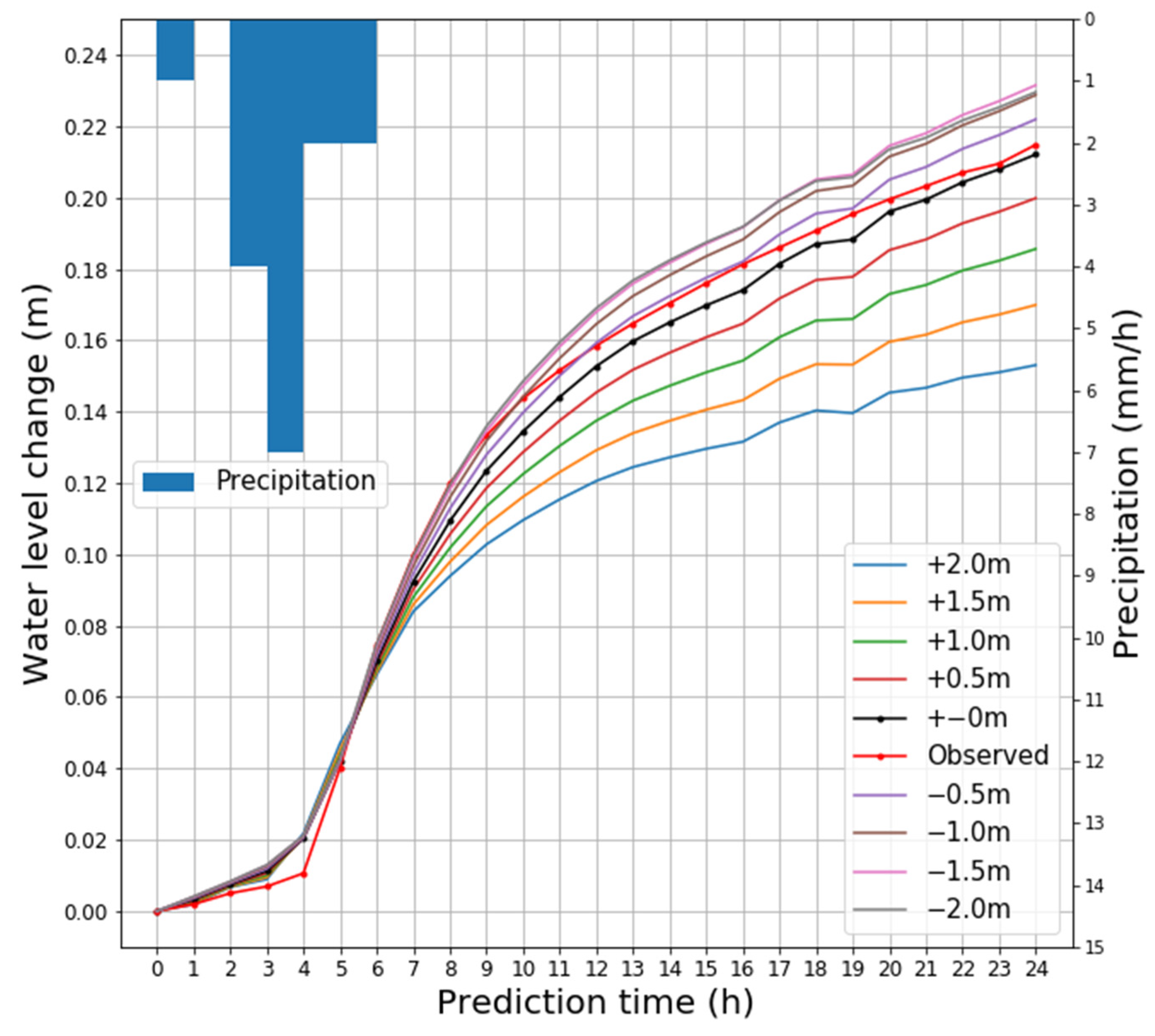
3.3. Relationship between Water-Level Changes and the Reservoir Capacity
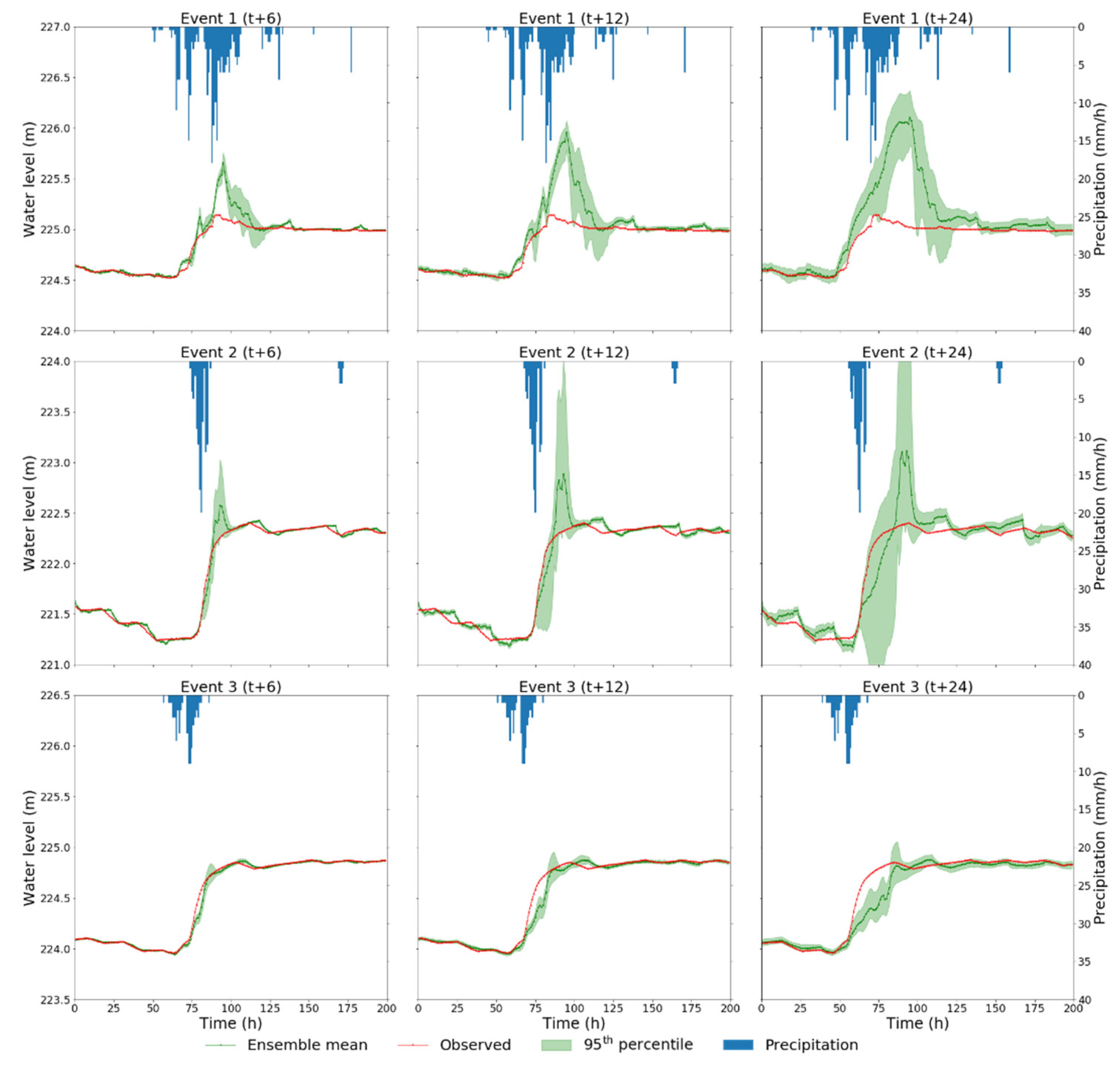
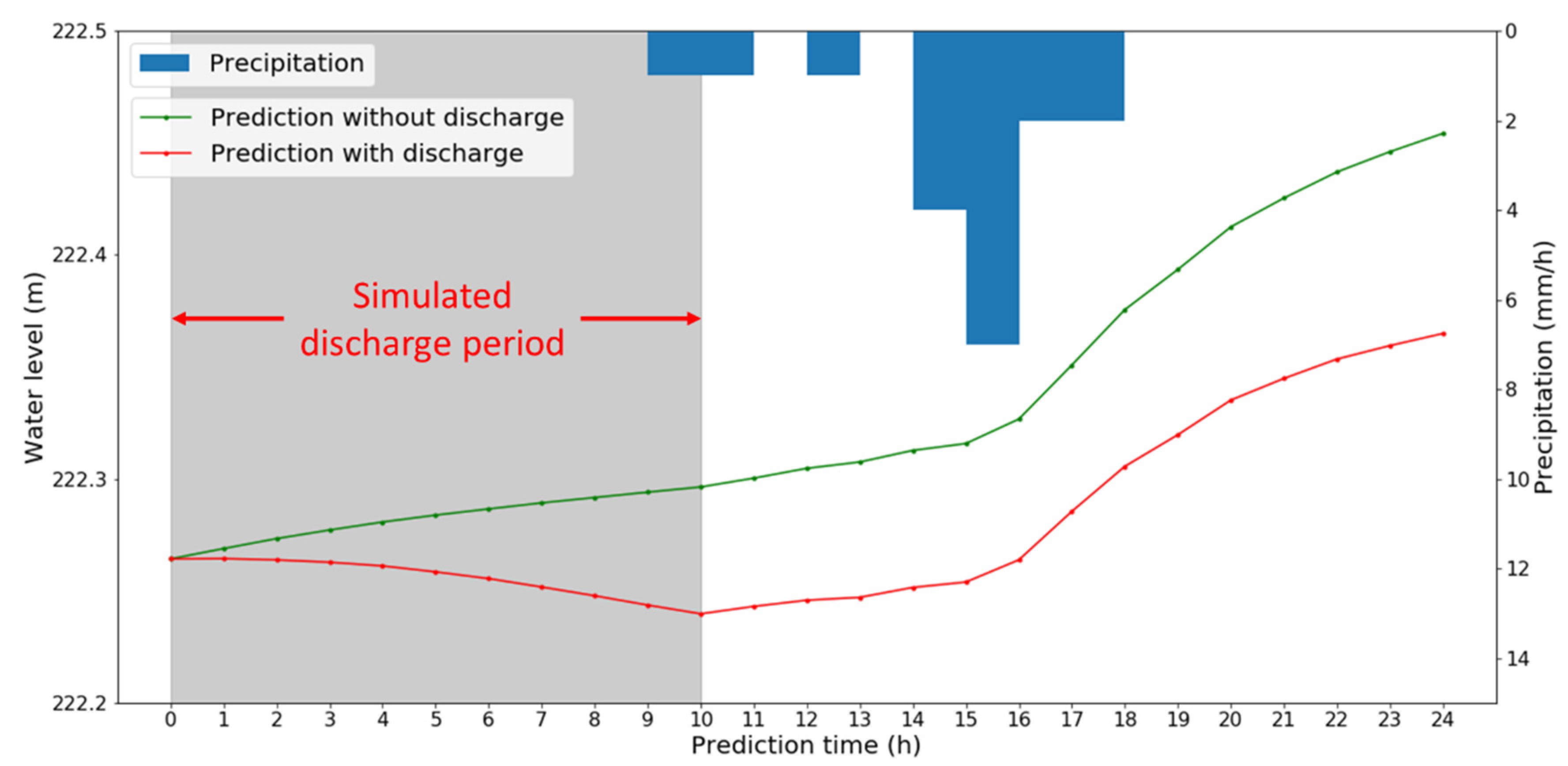
3.4. Assessment of the LSTM ED1 Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baup, F.; Frappart, F.; Maubant, J. Combining High-Resolution Satellite Images and Altimetry to Estimate the Volume of Small Lakes. Hydrol. Earth Syst. Sci. 2014, 18, 2007–2020. [Google Scholar] [CrossRef] [Green Version]
- Ogilvie, A.; Belaud, G.; Massuel, S.; Mulligan, M.; Le Goulven, P.; Malaterre, P.O.; Calvez, R. Combining Landsat Observations with Hydrological Modelling for Improved Surface Water Monitoring of Small Lakes. J. Hydrol. 2018, 566, 109–121. [Google Scholar] [CrossRef]
- Li, K.; Wan, D.; Zhu, Y.; Yao, C.; Yu, Y.; Si, C.; Ruan, X. The Applicability of ASCS_LSTM_ATT Model for Water Level Prediction in Small- and Medium-Sized Basins in China. J. Hydroinform. 2020, 22, 1693–1717. [Google Scholar] [CrossRef]
- Liu, M.; Huang, Y.; Li, Z.; Tong, B.; Liu, Z.; Sun, M.; Jiang, F.; Zhang, H. The Applicability of LSTM-KNN Model for Real-Time Flood Forecasting in Different Climate Zones in China. Water 2020, 12, 440. [Google Scholar] [CrossRef] [Green Version]
- Sajedi-Hosseini, F.; Malekian, A.; Choubin, B.; Rahmati, O.; Cipullo, S.; Coulon, F.; Pradhan, B. A Novel Machine Learning-Based Approach for the Risk Assessment of Nitrate Groundwater Contamination. Sci. Total Environ. 2018, 644, 954–962. [Google Scholar] [CrossRef] [Green Version]
- Kuo, Y.M.; Liu, C.W.; Lin, K.H. Evaluation of the Ability of an Artificial Neural Network Model to Assess the Variation of Groundwater Quality in an Area of Blackfoot Disease in Taiwan. Water Res. 2004, 38, 148–158. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Homaei, F.; Mohamadi, S. Reliability Evaluation of Groundwater Quality Index Using Data-Driven Models. Environ. Sci. Pollut. Res. Int. 2021. [Google Scholar] [CrossRef]
- Barzkar, A.; Najafzadeh, M.; Homaei, F. Evaluation of Drought Events in Various Climatic Conditions Using Data-Driven Models and a Reliability-Based Probabilistic Model. Nat. Hazards 2021. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-Term SPI Drought Forecasting in the Awash River Basin in Ethiopia Using Wavelet Neural Network and Wavelet Support Vector Regression Models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. Application of the Extreme Learning Machine Algorithm for the Prediction of Monthly Effective Drought Index in Eastern Australia. Atmos. Res. 2015, 153, 512–525. [Google Scholar] [CrossRef] [Green Version]
- Deo, R.C.; Tiwari, M.K.; Adamowski, J.F.; Quilty, J.M. Forecasting Effective Drought Index Using a Wavelet Extreme Learning Machine (W-ELM) Model. Stoch. Environ. Res. Risk Assess. 2017, 31, 1211–1240. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. Application of the Artificial Neural Network model for prediction of monthly Standardized Precipitation and Evapotranspiration Index using hydrometeorological parameters and climate indices in eastern Australia. Atmos. Res. 2015, 161–162, 65–81. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F. Forecasting Evapotranspiration in Different Climates Using Ensembles of Recurrent Neural Networks. Agric. Water Manag. 2021, 255, 107040. [Google Scholar] [CrossRef]
- Yin, J.; Deng, Z.; Ines, A.V.M.; Wu, J.; Rasu, E. Forecast of Short-Term Daily Reference Evapotranspiration Under Limited Meteorological Variables Using a Hybrid Bi-Directional Long Short-Term Memory Model (Bi-LSTM). Agric. Water Manag. 2020, 242, 106386. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Pollack, J.B. Recursive Distributed Representations. Artif. Intell. 1990, 46, 77–105. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; van Merrienboer, B.; Gülçehre, Ç.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Shewalkar, A.; Nyavanandi, D.; Ludwig, S.A. Performance Evaluation of Deep Neural Networks Applied to Speech Recognition: Rnn, LSTM and GRU. J. Artif. Intell. Soft Comput. Res. 2019, 9, 235–245. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Qiu, X.; Huang, X. Recurrent Neural Network for Text Classification with Multi-Task Learning. In Proceedings of the 25th International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016; pp. 2873–2879. [Google Scholar]
- Xu, J.; Chen, D.; Qiu, X.; Huang, X. Cached Long Short-Term Memory Neural Networks for Document-Level Sentiment Classification. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Austin, TX, USA, 1–5 November 2016. [Google Scholar]
- Huang, Z.; Xu, W.; Yu, K. Bidirectional LSTM-CRF Models for Sequence Tagging. arXiv 2015, arXiv:1508.01991. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional Recurrent Neural Networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef] [Green Version]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 2, pp. 3104–3112. [Google Scholar]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A Comprehensive Review of Deep Learning Applications in Hydrology and Water Resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef] [Green Version]
- Fu, M.; Fan, T.; Ding, Z.; Salih, S.Q.; Al-Ansari, N.; Yaseen, Z.M. Deep Learning Data-Intelligence Model Based on Adjusted Forecasting Window Scale: Application in Daily Streamflow Simulation. IEEE Access 2020, 8, 32632–32651. [Google Scholar] [CrossRef]
- Li, W.; Kiaghadi, A.; Dawson, C. High Temporal Resolution Rainfall–Runoff Modeling Using Long-Short-Term-Memory (LSTM) Networks. Neural Comput. Appl. 2021, 33, 1261–1278. [Google Scholar] [CrossRef]
- Xu, W.; Jiang, Y.; Zhang, X.; Li, Y.; Zhang, R.; Fu, G. Using Long Short-Term Memory Networks for River Flow Prediction. Hydrol. Res. 2020, 51, 1358–1376. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-Runoff Modelling Using Long Short-Term Memory (LSTM) Networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, T.; Sorooshian, S.; Liu, X.; Zhuang, J. Modeling and Simulating of Reservoir Operation Using the Artificial Neural Network, Support Vector Regression, Deep Learning Algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Yang, D.; Chen, J.; Zhao, B. Real-Time Reservoir Operation Using Recurrent Neural Networks and Inflow Forecast from a Distributed Hydrological Model. J. Hydrol. 2019, 579, 124229. [Google Scholar] [CrossRef]
- Hrnjica, B.; Bonacci, O. Lake Level Prediction Using Feed Forward and Recurrent Neural Networks. Water Resour. Manag. 2019, 33, 2471–2484. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-Term Water Quality Variable Prediction Using a Hybrid CNN–LSTM Deep Learning Model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Zhu, S.; Luo, X.; Yuan, X.; Xu, Z. An Improved Long Short-Term Memory Network for Streamflow Forecasting in the Upper Yangtze River. Stoch. Environ. Res. Risk Assess. 2020, 34, 1313–1329. [Google Scholar] [CrossRef]
- Li, W.; Kiaghadi, A.; Dawson, C. Exploring the Best Sequence LSTM Modeling Architecture for Flood Prediction. Neural Comput. Appl. 2021, 33, 5571–5580. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A Rainfall-Runoff Model with LSTM-Based Sequence-to-Sequence Learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Kao, I.F.; Zhou, Y.; Chang, L.C.; Chang, F.J. Exploring a Long Short-Term Memory Based Encoder-Decoder Framework for Multi-Step-Ahead Flood Forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Kingma, B.D.; Ba, L.J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980v9. [Google Scholar]
- Opitz, D.; Maclin, R. Popular Ensemble Methods: An Empirical Study. J. Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
- Geron, A. Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow, 2nd ed.; O’Reilly Media, Inc.: Sebastopol, ON, Canada, 2019; p. 134. [Google Scholar]
- Saberi-Movahed, F.; Najafzadeh, M.; Mehrpooya, A. Receiving More Accurate Predictions for Longitudinal Dispersion Coefficients in Water Pipelines: Training Group Method of Data Handling Using Extreme Learning Machine Conceptions. Water Resour. Manag. 2020, 34, 529–561. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
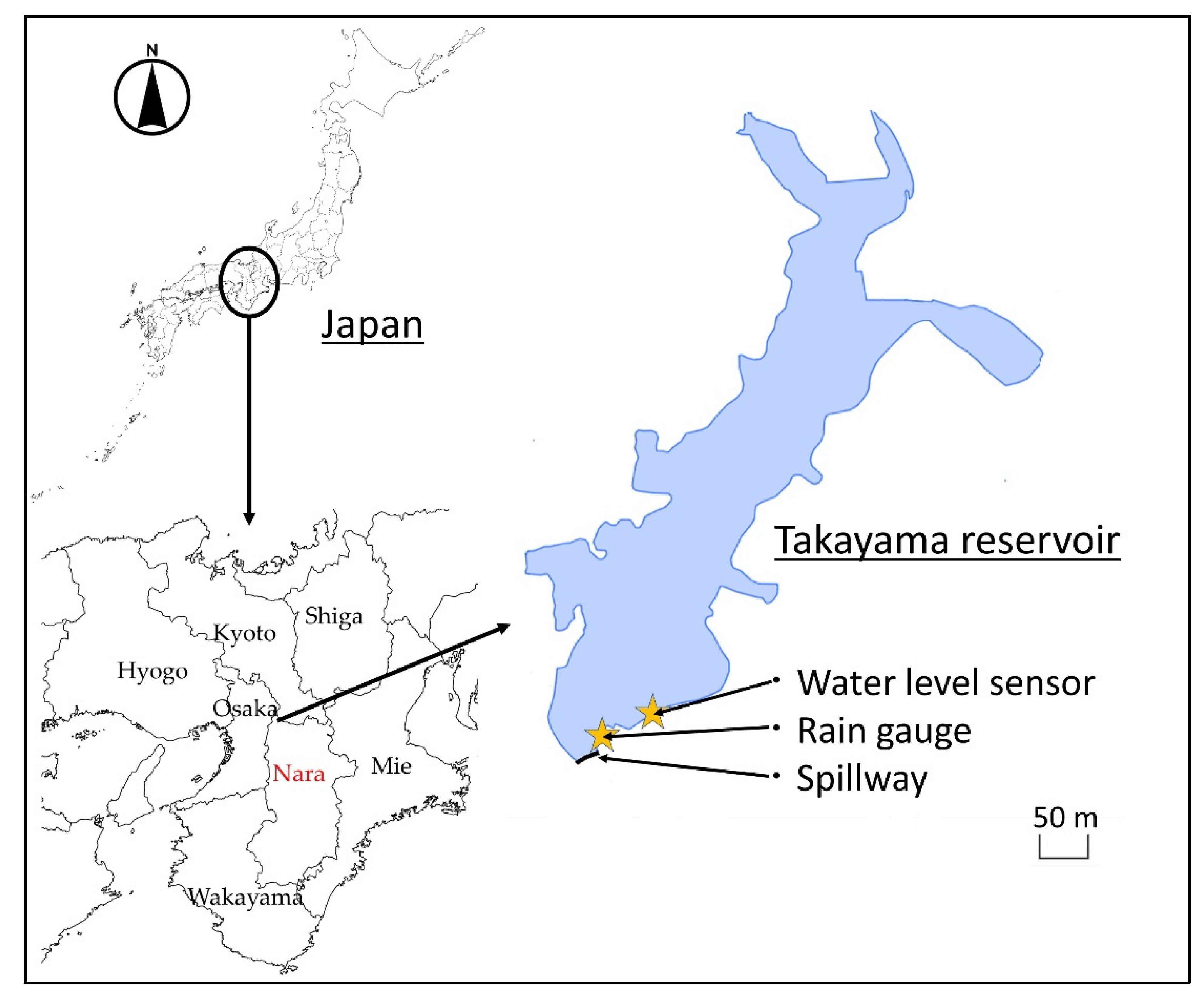
| Capacity | Surface Area | Catchment Area |
| 580,000 m3 | 90,000 m2 | 2.3 km2 |
| Beneficiary Area | Embankment Height | Embankment Length |
| 530 ha | 23 m | 135 m |
| Model Type | Model Name | Input Variable | Output Variable |
|---|---|---|---|
| LSTM Single-output | SO1 | Precipitation (mm/h) Discharge event (0 or 1) Water level (m) Water-level change (m/h) | Water-level change (m) |
| SO2 | Precipitation (mm/h) Discharge event (0 or 1) Water level (m) | Water level (m) | |
| SO3 | Precipitation (mm/h) Discharge event (0 or 1) Water-level change (m/h) | Water-level change (m) | |
| LSTME ncoder-decoder | ED1 | Precipitation (mm/h) Discharge event (0 or 1) Water level (m) Water-level change (m/h) | Water-level change (m) |
| ED2 | Precipitation (mm/h) Discharge event (0 or 1) Water level (m) | Water level (m) | |
| ED3 | Precipitation (mm/h) Discharge event (0 or 1) Water-level change (m/h) | Water-level change (m) |
| Type Name | Hidden Unit | Batch Size | Optimizer | Loss Function | Epochs (Early Stopping) | Input Length (h) | Output Length (h) |
|---|---|---|---|---|---|---|---|
| LSTM SO1 to SO3 | 20 | 64 | Adam | Mean squared error | 150 | 25 | 1 |
| LSTM ED1 to ED3 | 20 | 64 | Adam | Mean squared error | 200 | 25 | 24 |
| Item | Counts | Mean | Standard Deviation | Max | Min | Total Discharge Time |
|---|---|---|---|---|---|---|
| Water level (m) | 17,690 | 221.86 | 1.95 | 225.14 | 218.35 | - |
| Precipitation (mm/h) | 18,072 | 0.12 | 0.76 | 28.00 | 0.00 | - |
| Discharge | 17,690 | - | - | - | - | 6171 |
| Period Number | Period | Rainfall Event | Water Level | ||||
|---|---|---|---|---|---|---|---|
| Number of Events | Max Rainfall (mm/event) | Mean Rainfall (mm/event) | Max (m) | Min (m) | Mean (m) | ||
| 1 | 1 Jul. 2018–16 Sep. 2018 | 11 | 213.0 | 37.9 | 225.14 | 222.25 | 223.74 |
| 2 | 16 Sep. 2018–3 Dec. 2018 | 9 | 33.0 | 18.8 | 224.01 | 218.40 | 221.05 |
| 3 | 3 Dec. 2018–19 Feb. 2019 | 7 | 15.0 | 8.6 | 219.33 | 218.97 | 219.17 |
| 4 | 19 Feb. 2019–8 May 2019 | 10 | 26.0 | 12.9 | 222.40 | 219.28 | 220.75 |
| 5 | 8 May 2019–25 Jul. 2019 | 14 | 33.0 | 14.0 | 222.65 | 220.21 | 221.39 |
| 6 | 25 Jul. 2019–11 Oct. 2019 | 13 | 102.0 | 18.7 | 223.30 | 221.24 | 222.63 |
| 7 | 11 Oct. 2019–28 Dec. 2019 | 9 | 61.0 | 20.6 | 223.25 | 218.35 | 220.47 |
| 8 | 28 Dec. 2019–15 Mar. 2020 | 13 | 19.0 | 11.8 | 222.82 | 219.89 | 221.45 |
| 9 | 15 Mar. 2020–1 Jun. 2020 | 11 | 25.0 | 12.6 | 225.09 | 222.82 | 224.57 |
| 10 | 1 Jun. 2020–22 Jul. 2020 | 11 | 70.0 | 25.9 | 225.09 | 223.43 | 224.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kusudo, T.; Yamamoto, A.; Kimura, M.; Matsuno, Y. Development and Assessment of Water-Level Prediction Models for Small Reservoirs Using a Deep Learning Algorithm. Water 2022, 14, 55. https://doi.org/10.3390/w14010055
Kusudo T, Yamamoto A, Kimura M, Matsuno Y. Development and Assessment of Water-Level Prediction Models for Small Reservoirs Using a Deep Learning Algorithm. Water. 2022; 14(1):55. https://doi.org/10.3390/w14010055
Chicago/Turabian StyleKusudo, Tsumugu, Atsushi Yamamoto, Masaomi Kimura, and Yutaka Matsuno. 2022. "Development and Assessment of Water-Level Prediction Models for Small Reservoirs Using a Deep Learning Algorithm" Water 14, no. 1: 55. https://doi.org/10.3390/w14010055
APA StyleKusudo, T., Yamamoto, A., Kimura, M., & Matsuno, Y. (2022). Development and Assessment of Water-Level Prediction Models for Small Reservoirs Using a Deep Learning Algorithm. Water, 14(1), 55. https://doi.org/10.3390/w14010055






