1. Introduction
Water distribution systems (WDSs) are an energy-intensive consumer [
1]. About 7–8% of the world’s total generated energy is used for drinking water production and distribution [
2]. A major portion of this energy is used for distribution, i.e., pumping, chlorination, and maintenance activities. Therefore, increasing WDSs efficiency yields both economic and environmental benefits. Energy is usually invested into the system via pumps and dissipated mainly due to friction within the pipes and components. The amount of energy invested in the systems is dictated to supply the demand with sufficient pressure to the most low-pressure sensitive consumer. Yet, it frequently results in a high residual pressure elsewhere in the system. Surplus residual pressure in WDSs contributes to water and energy inefficiencies and shortens the average lifespan of pipes and components [
3].
Improving the management of WDSs, in terms of energy and resource efficiency, is a crucial step towards more sustainable use of water, and in general towards a more sustainable consumption and development strategy. In addition, minimizing the energy consumption helps decrease the associated carbon dioxide emissions providing a more sustainable system. Significant research has been focused on sustainable WDSs operation [
4,
5] and optimal placement and management of network pressure control devices to reduce excess pressure to better manage water leakage and other pressure- related phenomena [
6,
7,
8,
9,
10,
11,
12,
13,
14,
15]. Water leakage remains a major cause of water loss in water distribution systems (WDSs), particularly in developing countries. In addition to self-evident economic losses, water leakage poses environmental, sustainability and health risks [
16]. Among the factors that amplify leakages are bad pipe connections, internal or external pipe corrosion or mechanical damage, ground movement, high system pressure, damage due to excavation, pipe age, winter temperature, defects in pipes, ground conditions, and poor quality of workmanship. Commonly, leakage is related to pressure as described by the orifice equation, where the flow rate is correlated to the pressure at the orifice at the power of α. Several field studies (e.g., [
17,
18]) reported that α can vary between 0.5 and 2.79. Hence, leakage in WDS is much more sensitive to pressure than might be intuitively assumed.
Most common approaches in the literature discuss installing pressure reducing valves (PRVs) to dissipate surplus energy. Different studies have analyzed how and where PRVs should be installed along the systems [
19,
20,
21]. Moreover, another common approach is subdividing the network into pressure management zones to operate them as district metered areas (DMAs). Nonetheless, it is beneficial to integrate PRVs and DMAs in a two-prong approach. Additionally, incorporating micro-hydropower turbines, or pumps as turbines (PAT), within water distribution networks has been shown as a viable option for pressure reduction and enhancing the energy efficiency of the water systems [
22,
23,
24,
25,
26,
27]. In addition, Ramos et al. [
28] suggests coupling the water-energy generation with other non-water-related energy-consumption systems, for more sustainable city management.
However, the installation of micro-hydroelectric plants in distribution systems is mainly limited to the larger transmission pipelines, in which the hydraulic characteristics are almost constant, and the power recovery is considerable [
29,
30,
31]. Nevertheless, micro-hydroelectric plants installation in WDSs are still challenging due to the limited available power, the high cost of miniaturized energy production devices, and the larger variability of the hydraulic characteristics [
32].
This work presents an innovative approach to integrating Hydrams into modern distribution systems for better pressure management and reduction in operational costs. Unlike micro-hydroelectric plants, Hydrams are relatively cheap and easy to maintain. The automatic hydraulic ram pump, also referred to as Hydram in the literature, is a device for pumping water, powered solely by the potential energy of the supply. The Hydram main concept is to exploit the momentum of a driving stream of water undergoing a head drop to pump a small portion of the stream to a head considerably greater than that of the supply. To the authors’ best knowledge, the integration of Hydrams in modern distribution systems was never considered, nor was the use of Hydrams for pressure reduction and management. Moreover, this study presents a novel pumping unit that combines both centrifugal and Hydram pumps.
The first hydraulic ram pump invented by J. Whitehurst in 1772 was not automatic, it was rather operated manually, to supply fresh water for a brewery. Building on Whitehurst’s work, Montgolfier introduced in 1796 a check valve in the hydraulic ram pump as the waste valve and realized the automatic operation. Two decades later, Pierce designed a snifter valve to allow small air bubbles to enter the air chamber automatically and periodically to replenish air dissolved in the delivery flow. Numerous Hydrams designs were introduced since, yet the main operation principles did not change for over two centuries.
A well-designed Hydram is very durable and can operate for decades. This is mainly because it includes only two check valves as moving parts, a drive valve, and a waste valve, both of which operate automatically from the fluid dynamic actions of the pumping cycle [
33]. Besides its satisfactory durability, the Hydram is also an environmentally friendly equipment due to no consumption of fossil fuels [
34]. However, the fact to be kept in mind is that the hydraulic ram pump can lift only a small portion of the inflow to a higher or farther place and the rest of the water must flow downstream under gravity, which is called wastewater.
In the 19th and 20th centuries, Hydrams were widely used around the world and provided much needed fresh water for residents and farmlands for drinking and irrigation. Nevertheless, Hydrams became outdated and obsolete with the introduction of water distribution networks and electrical supplies to rural areas. Recently, however, enthusiasm for low-cost, low-maintenance, environmentally friendly devices using a renewable energy resource has revived interest in the 200 years old technology and its use for water supply in developing countries [
35].
2. Materials and Methods
The model formulation described below is composed of a description of the physical model for the Hydram including friction in the delivery and discharge pipes, the Hybrid configuration with the centrifugal pump. This is followed by a presentation of the optimization method and fitness function. The Hydram could be integrated into the system as an active or passive element. Conventionally, Hydrams are installed as a passive element, where there is no need for an input from the operator besides the initial triggering. In this case, the Hydram performance and pumping capabilities are dictated by the system’s hydraulics (i.e., the available flow and head upstream) and the consumers’ elevation. This passive installation presents challenges in system operation and water supply reliability. This is especially true for systems with high fluctuating demands. Thus, the optimization process can include only sizing parameters (e.g., tanks volume, height, Hydram size) rather than operational parameters. Nonetheless, if the Hydram is installed as an active element, the operator can actively decide whether to direct the flow through the Hydram by opening the feed valve, or to divert it through a different element or path. Ideally, the flow is diverted to another pumping unit or a storage facility. This approach introduces scheduling options, subsequently introducing flexibility into the system, and presents new management and sizing optimization opportunities. In this work, the Hydram is installed and operated as an active element.
2.1. Hydram Frictionless Model
This model describes the performance of the Hydram neglecting the effect of pipes friction. The flow and head supplied by the Hydram needs to be calculated according to the following Equation (1):
where
H and
Q are the supply head and flow at the upstream of the Hydram, and
h and
q are their counterparts at the downstream end of the Hydram.
η is the efficiency of the Hydram, and it can range from 35% to 66%. The q is dictated by the demands at the elevated consumers where h is the height (Lift) that the water needs to reach, thus dictated by the topography of the network.
Usually, in an inurbane setting, the line friction does not play a major role in the calculation since there are a lot of unknown factors, inaccuracies, and uncertainties. Thus, accurate calculations are not justified. Moreover, the incoming flow rate is mostly unpredicted, and the consumption model is usually poor or non-existing. However, in urban water distribution systems, most of these factors are known to a certain accuracy. Hence, the implementation of Hydram in such a setting requires more calculations and less simplification to supply the required demands reliably.
2.2. Hydram-Comprehensive Model
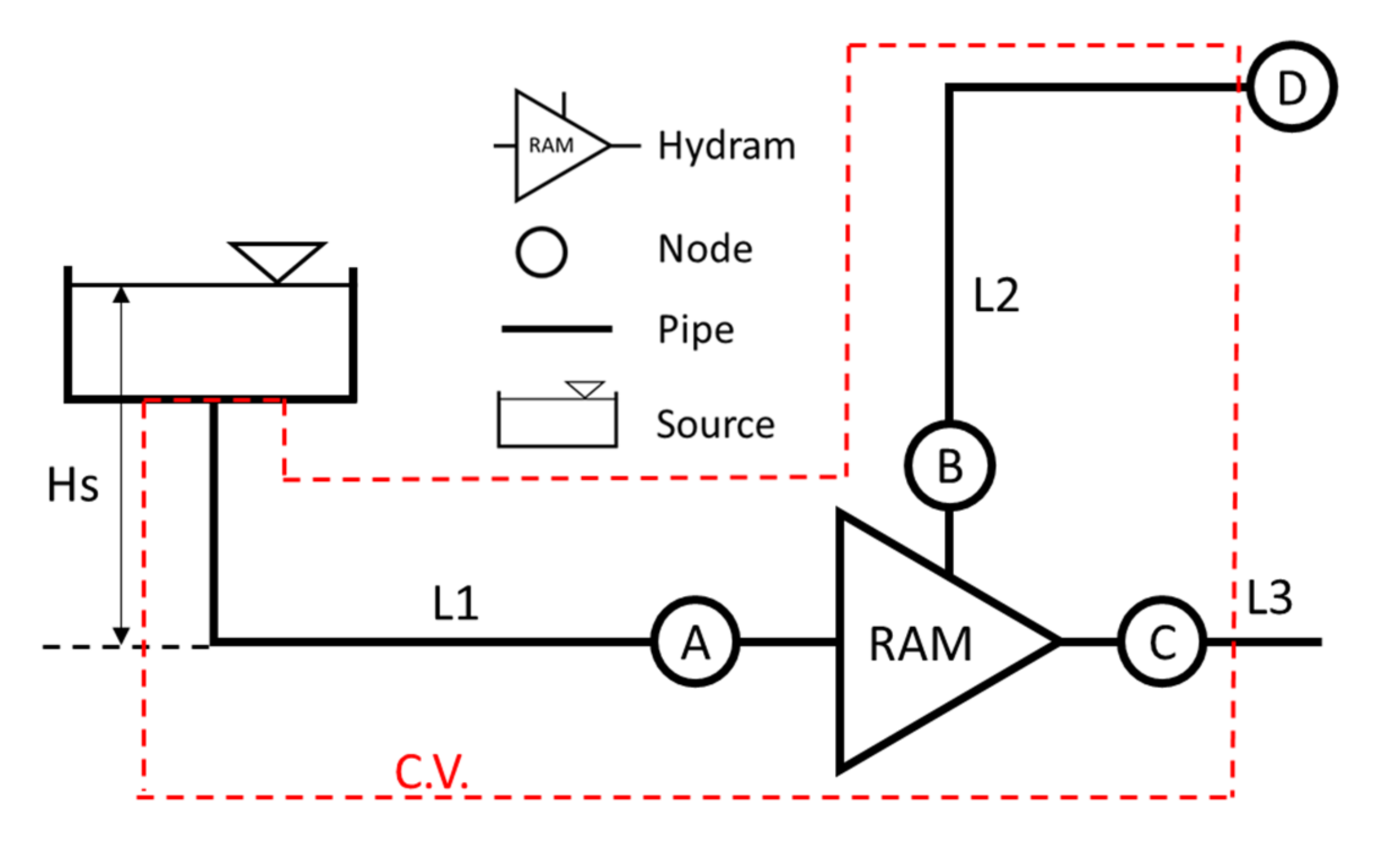
The Hydram’s head and flow are calculated using the mass and energy balance over the whole control volume (C.V.) including the delivery and discharge pipes, rather than the Hydram alone. The control volume is confined within red dashed lines as presented in
Figure 1. While using this model, Hydram’s performance is expected to diminish due to friction losses at the delivery and discharge pipes.
The mass balance equation is written as a volume balance, under the assumption of constant density and zero water loss through the system.
The Energy balance over the control volume, where the energy at node B is equal to the energy at node A times the efficiency
can be written as follows:
The friction losses are calculated using the Darcy equation, R represents the pipes’ resistance for convenience, and it is a function of the Darcy friction factor (
), the flow through the pipe (Q), the pipes Length (L) and its Diameter (D). Additionally,
stands for the elevation difference (positive value) between node B and D in metes.
by substituting Equations (5) and (6) into Equation (3), the following term is achieved:
by substituting Equation (5) into Equation (2), the following term is achieved:
After organizing the Equation (8), the following term is achieved:
is the flow at the inflow of the Hydram, is the flow at the uphill consumer, while is the demand of the downhill consumer. stands for the Head at node i, stands for the resistance of the pipe i. The Darcy equation is used to describe the head loss. For each iteration, the Newtown-Raphson method is used to solve Equation (9) for when the demand is known, consequently solving for .
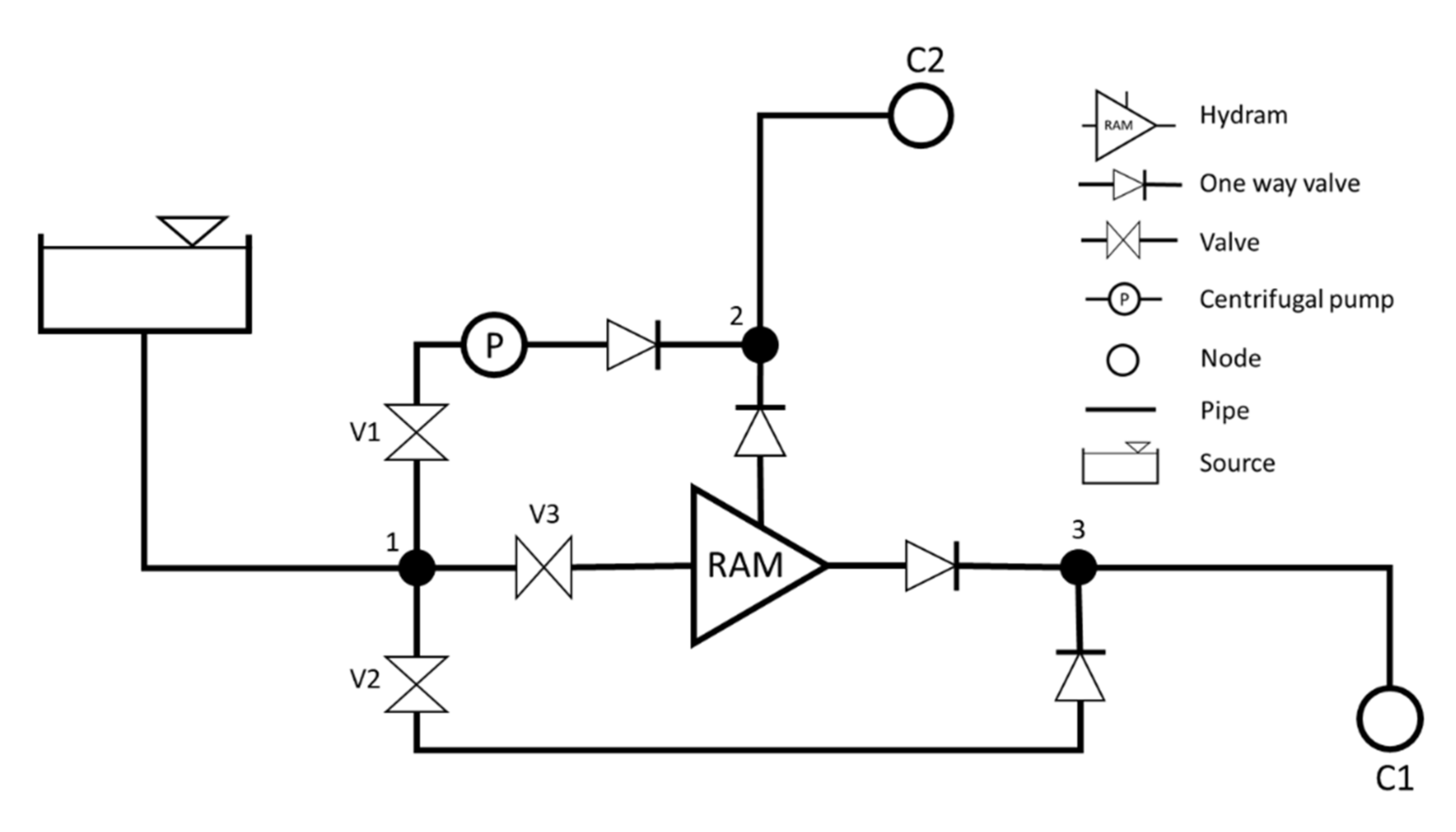
Figure 2 depicts the basic configuration for the Hybrid Pumping Unit (HPU) where the water source is connected to junction 1. From junction 1 the flow can take different paths depending on the valves’ configuration, hereby referred to as modes. If valves V1 and V2 are closed while V3 is open, the system directs the flow through the Hydram to the consumers at C1 and C2, this configuration is referred to as “Ram configuration”. When operating in Ram configuration, the centrifugal pump is silenced while the Hydram is activated, and the storage unit receives the amount of water dictated by Equation (9). In the second configuration, referred to as “Pump configuration”, the valves V1 and V2 are open and V3 is closed. While operating in Pump configuration, the Hydram is silenced, and the centrifugal pump is activated to supply water to the storage unit. The flow is directed to it through valve V1, and to the downhill consumer through valve V2. This mode is created to cover for the low-demand periods at the downhill consumer, providing needed water to consumer C2. Such an option widens the range of feasible solutions and introduces a more realistic approach for integrating Hydrams in modern water distribution systems. The last configuration is referred to as “off configuration” where both valve V1 and V3 are closed and only valve V2 is open. In this case, both the Hydram and centrifugal pump are silenced, and no water flows to the storage unit. This helps overcome overflow problems in the storage unit and adds more flexibility into the system, further allowing the satisfaction of different constraints.
2.3. Optimization and Fitness Function
All investments are converted into annual costs. The following section describes the equations and their parameters.
The decision variables represent the configuration of the HPU at each time step t. When , the HPU is operating at Ram mode and only the Hydram is active. When , the HPU is operating at Pump mode and only the centrifugal pump is active, and when none of the pumps are active.
The main objective of the optimization is minimizing capital costs associated with the operation of WDSs as written in Equation (10). The overall annual cost consists of three main parts; the Hydram and storage tank annual installation costs, and the operational cost, denoted as
,
,
, respectively. The price values presented in this work are in New Israeli Shekel currency (NIS), during which the USD to NIS rate was 3.5.
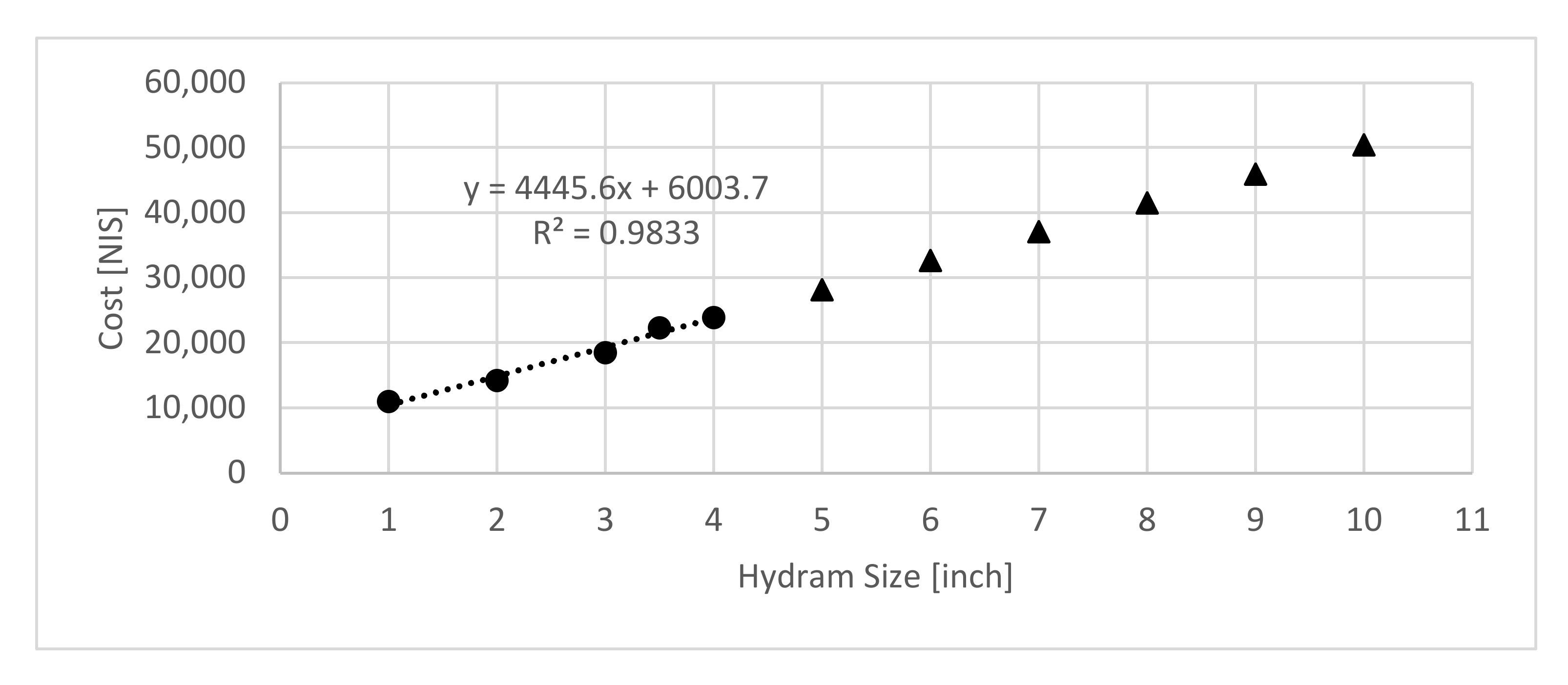
The Hydram annuity is calculated for a 20-year lifespan with an interest of 5% using Equation (11), where the capital cost is multiplied by the relevant Capital Recovery Factor (CRF). The Hydram capital cost used in this work relies on the prices found on the Blake’s Hydram website.
Appendix A Figure A1 presents the available data, its trendline, and the speculated prices for larger pump sizes. The Hydram cost
depends on its size
, which is dictated by the highest flow it supplies
. To the authors’ best knowledge, there are no available data nor estimated costs regarding the Hydrams maintenance costs. It is critical to note that the maintenance was not included in the fitness function and optimization process.
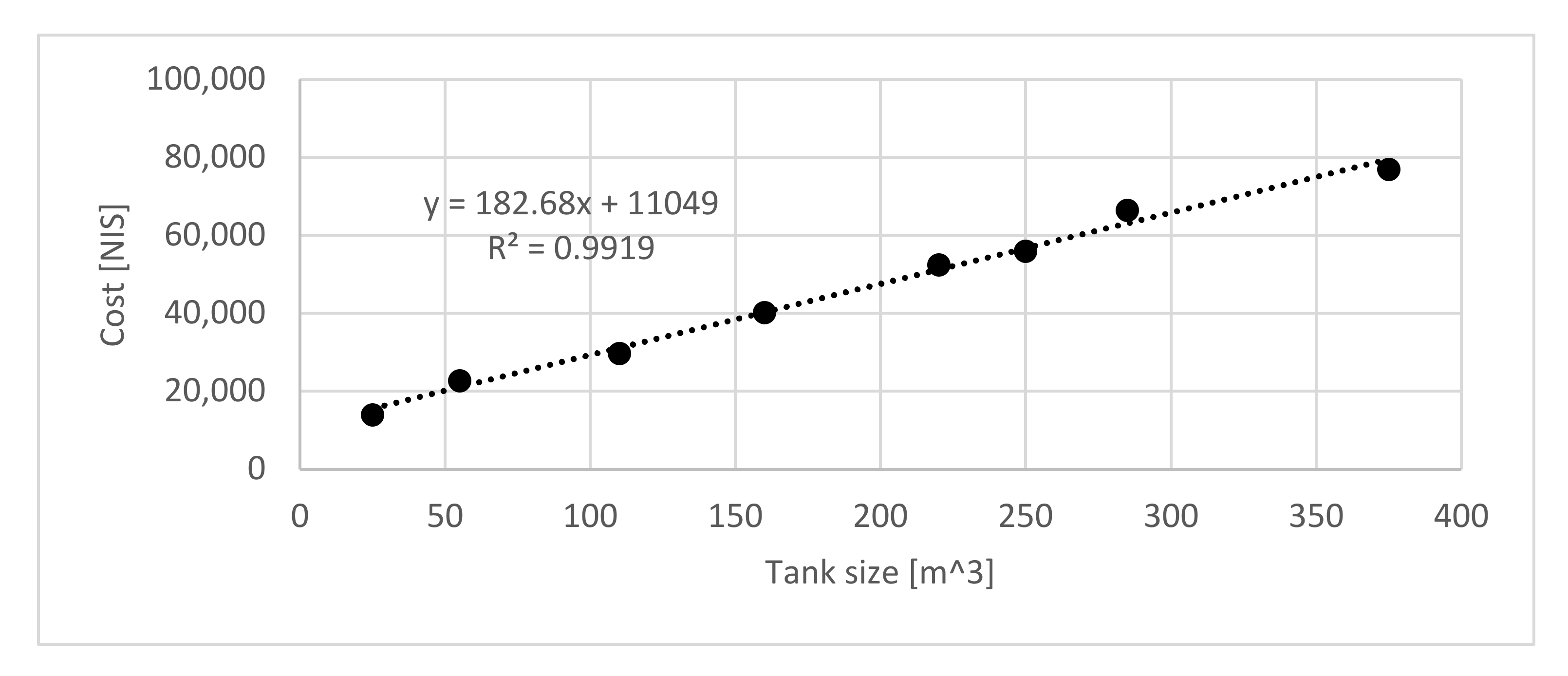
The storage tank annuity is calculated for a 20-year lifespan as well with the same interest of 5% using Equation (13), where the capital cost is multiplied by the relevant CRF. The storage tank capital cost formula used in this work relies on the prices of steel tanks within a size range of 25–375
.
Appendix B Figure A2 presents the available data and the price to size formula. The tank cost
is in correlation to the tank’s volume
, and it is described in the following equation:
where
and
stand for the highest and lowest volume differences between the accumulated inlet and outlet flow of the storage tank. The operational cost
is described as follows:
where
(kW) is the centrifugal pump power,
is the electricity base cost,
is the energy cost tariff at every time step, over the simulation period. The main constraints are minimum pressure of 25 m at each node and the tank level cycle over the simulation period with a tolerance of 5%.
The genetic algorithm provided in MATLAB version R2019b was utilized to determine the optimum HPU operation pattern to minimize annual costs for each operation-mode. It is essential to mention that there is no guarantee that the found solution will be the most accurate or optimal for the given problem, rather a good enough solution in most cases. The genetic algorithm parameters such as population size and maximum number of generations have a significant impact on the optimization process, its outcomes, and running durations. For instance, as further described subsequently, a population size of 50, with 30 generations was sufficient to solve the first network at a running time duration of roughly 8 min. Whereas for the second network, a population of 100, with 100 generations was required, resulting in a running time above 40 min.
3. Results and Discussion
In this section, the Hydram integration into WDSs is investigated through two WDS examples of increasing complexity and are depicted in
Figure 2 and Figure 5. To better demonstrate the HPU capabilities, a sensitivity analysis was performed for the second WDS case study where the influence of the uphill demand and the consumers’ patterns were examined. The sensitivity analysis is thoroughly discussed in the second case study.
3.1. Case Study 01—Proof of Concept
The first case study consists of a water source at an elevation of 120 m, the hybrid pumping unit at 100 m, the storage tank at 200 m, and the downhill consumer at 50 m. The system’s layout matches the one described in
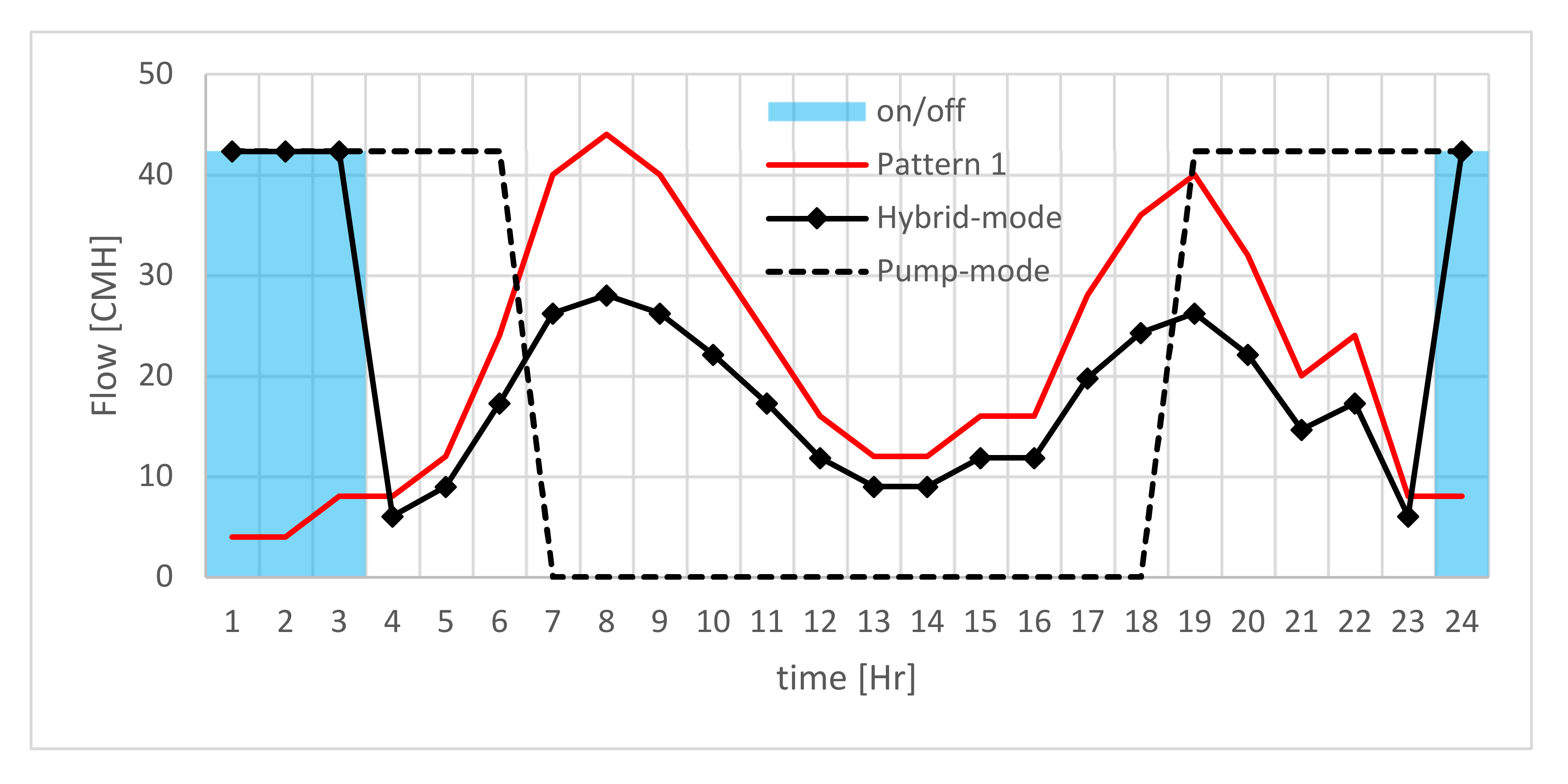
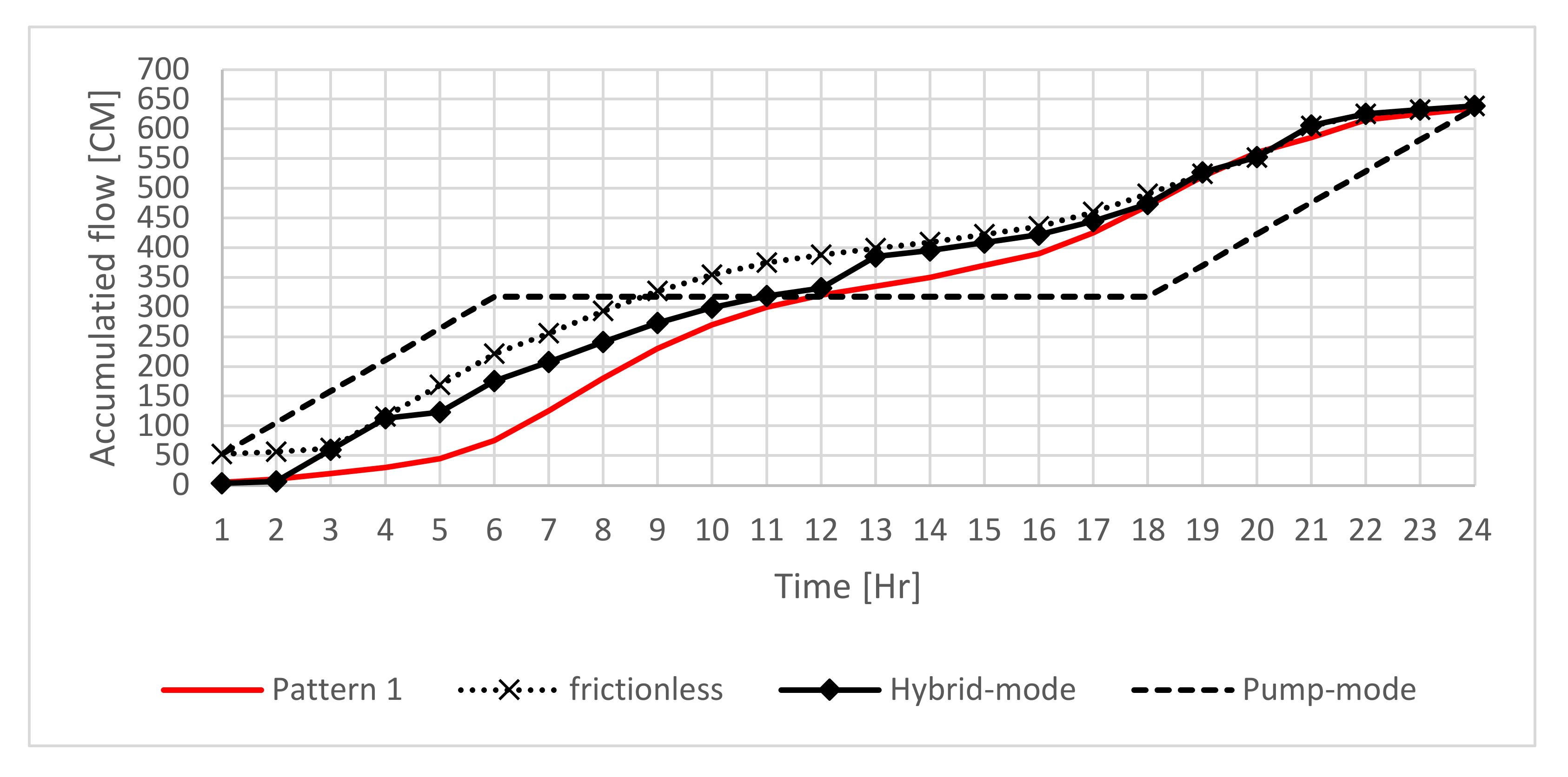
Figure 2. The base demand of the uphill and downhill consumers are 40 CMH and 200 CMH, respectively. Both demands are distributed within 24 h according to Pattern 1 described in
Figure 3. The drive pipe is a 500 m long, 240 mm in diameter HDPE pipe. The delivery discharge pipe is 500 m HDPE as well, but with a smaller diameter of 100 mm. The Darcy friction factor for both pipes is 0.01. When examining case study 01, only two operational modes are available; that is the Hybrid-mode and the Pump-mode, while the Null-mode is not considered in the decision-making of this case study.
As shown in
Figure 3, the red line describes the uphill consumer demand as well as the outflow of the storage tank, while the black continuous line with diamond markers describes the incoming flow to the tank when activating the Hybrid-mode. The dashed line, however, describes the in-flow to the tank in the Pump-mode. The blue columns represent the flow delivered by the pumps in the Hybrid-mode and highlight the pump’s activation period.
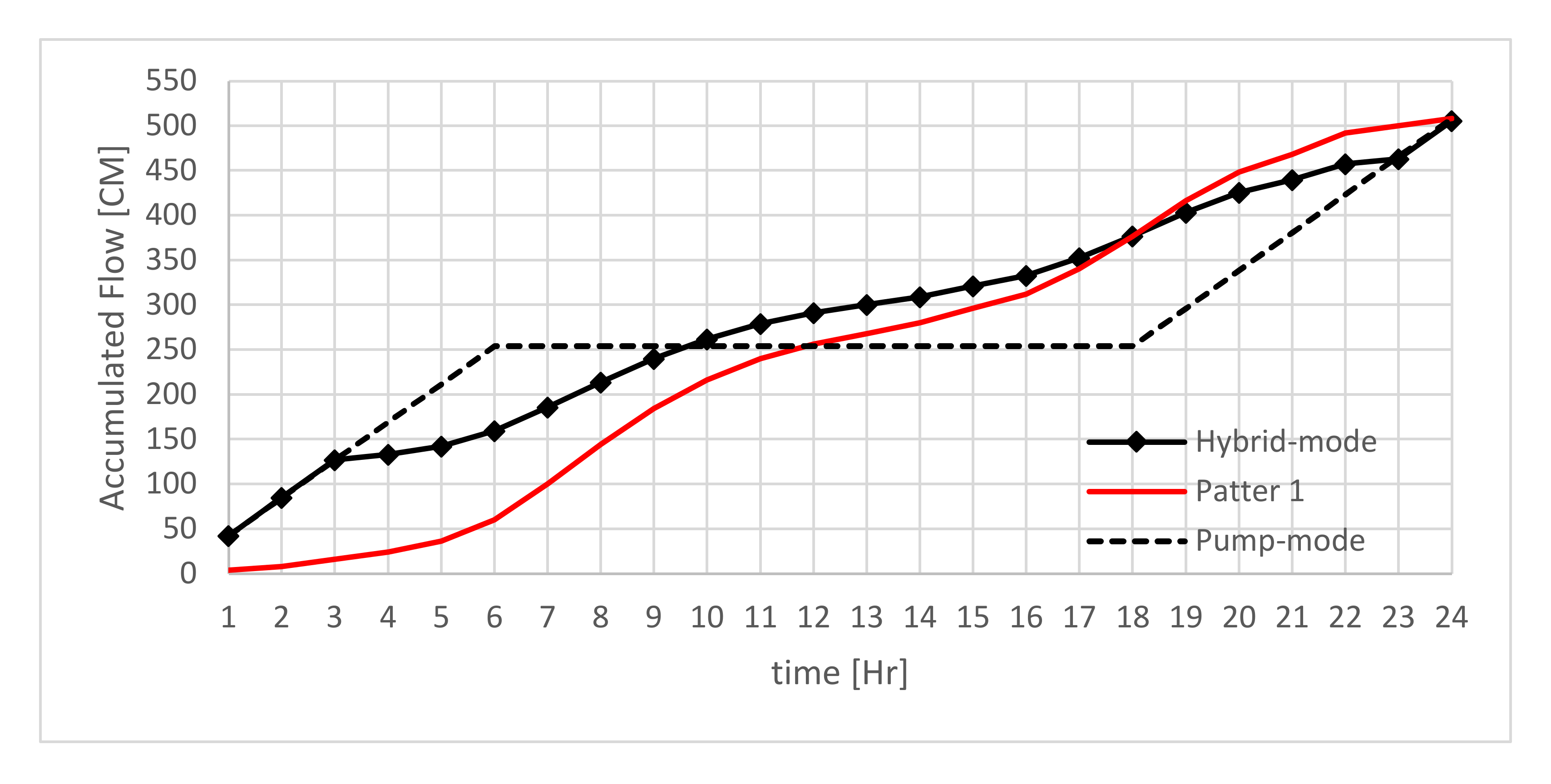
Figure 4 depicts the Accumulated flows in and out of the storage tank for both Hybrid and Pump modes. It is shown that the overall inflow delivered meets the overall daily demand, indicating that the tank water level returns to its original height, within the approved tolerance, at the end of each day. The lines’ colors and characteristics are consistent with the description in
Figure 3.
For the first case study, the chosen population (50) was set to be about 2 times the variables number (24). The genetic algorithm was set to run for 30 generations under 0.8 crossover and 0.01 mutation. However, the max generation stall was set to 20 generations. That is, if the function score did not improve for 20 consecutive generations the algorithm ceased. The obtained flows at the storage tank are illustrated in
Figure 3 and
Figure 4. The retrieved operational patterns are shown in
Table 1.
In order to examine and compare the different operation modes, the annual cost of each element including the storage tank, the Hydram, and energy invested in each mode as well as the percentage of demands met daily are presented in
Table 2. As shown, when operating in Pump-mode, meaning that only the centrifugal pumps are working, the energy cost is much higher than the Hybrid-mode, where the Hydram is also activated. Moreover, the Hybrid-mode is deemed economically superior to the Pump-mode, since the Hydram’s estimated annual cost is far less than the energy cost difference when comparing the two. When activating the Ram-mode, where only the Hydram is operational, the annual costs are relatively low, yet only 70% of the daily demand is met. This exercise helps demonstrate the shortcomings and advantages for each of the individual pumping units, and the potential of operating them interchangeably.
To better examine the sustainability and environmental effects for the different operation modes, additional sustainability indicators were adopted from Camilo et al. [
36], such as Annual consumed energy (IAE), Consumed energy per unit volume (IEFW), and Energy cost per unit volume (IEC).
Table 3 presents the annual water and energy consumption for each operational mode, and the sustainable indicators listed above.
The Hybrid-mode is clearly more energy efficient when compared to the pump-mode, where the energy consumption stands at ~15 MW·h rather than ~45 MW·h. Subsequently, the amount of energy required for supplying a cubic meter of water drops down from 89 to 29 kW·h (lower by ~67%). Additionally, since the Hydram adds flexibility into the operation hours, the percentage of energy cost drop is even greater (lower by ~72%).
3.2. Case Study 02—Water Distribution Network
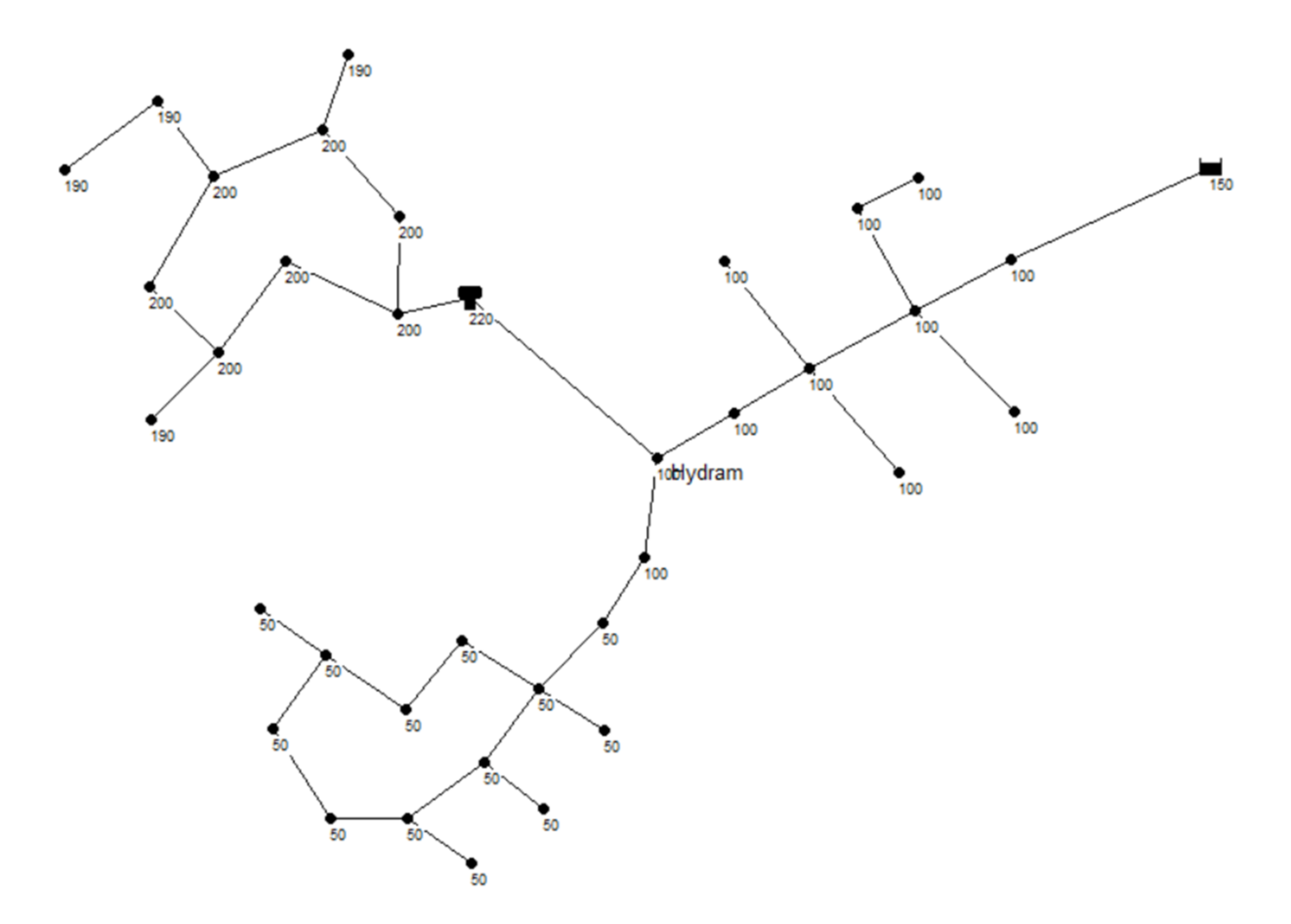
The second case study represents a water distribution-like system, with more nodes, edges, branches, and loops. The layout at
Figure 5 depicts a distribution system where the water source is at 150 m, the downhill consumer is at 50 m while the storage tank for the uphill consumer is at 220 m and stands 10 m high (total head of 230). The Hybrid pumping unit is located at the intersection in between at 100 m. In this case study, the performance of the integrated HPU is examined. It is essential to state that the layout and terrains modeled in case study 02 are such that the HPU performance is optimal. This is done to examine the systems at their peak performance, rather than their limitations. Moreover, it is worth noting that such terrains and conditions are not common nor typical in distribution systems. In this case study, the three operation modes are available; that is the Hybrid, Pump, and Null modes.
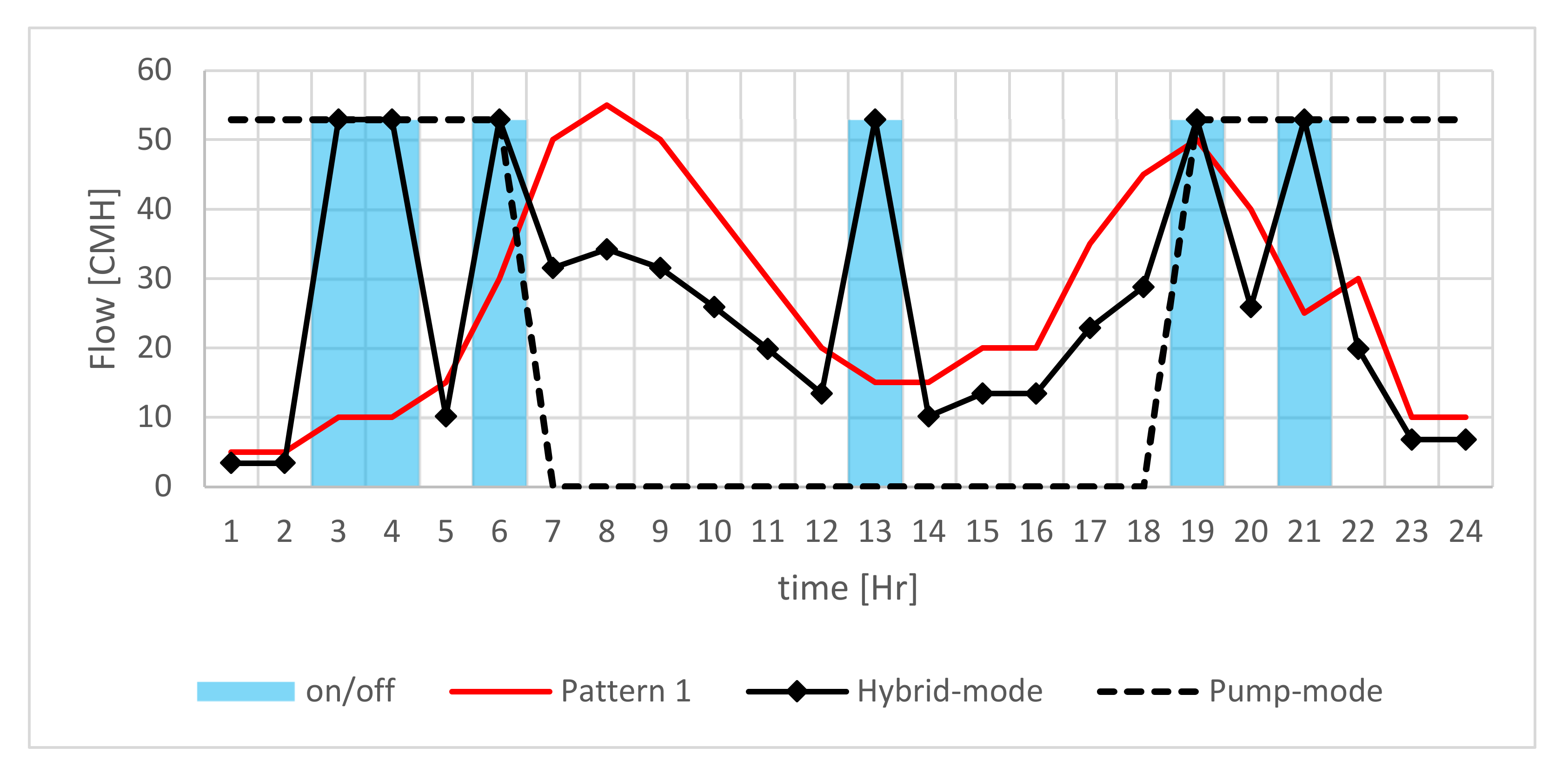
A genetic algorithm was utilized to determine the optimum HPU operation pattern to minimize annual costs for each operation-mode. The chosen population (100) was set to be about 4 times the variable number (24). The GA would run for 100 generations under 0.8 crossover and 0.01 mutation. However, the max generation stall was set to 30 generations. The obtained flows and water levels at the storage tank are illustrated in
Figure 6 and
Figure 7. The retrieved operational patterns are shown in
Table 4. The trade-off in the optimization is mainly between the Energy and investment costs, while the main constraints are the minimum pressure at the nodes (2.5 atm) and the tank level cycle. The red line in
Figure 6 describes the outflow from the tank while the black diamond line describes the incoming flow for the Hybrid-mode. The blue columns depict the centrifugal pump activation periods. The inflow for the Pump-mode is plotted as dashed lines to better emphasize the operational differences.
Figure 7 shows the accumulated inflows-outflows for the storage tank for all operation modes. The lines’ colors and characteristics are consistent with those of
Figure 6. It shows that the overall inflow supplied meets the overall daily demand, indicating that the tank water level returns to its original height, within the approved tolerance, at the end of each simulation period.
To better emphasize the importance of accounting for pipe friction, the system was operated in Hybrid-mode while neglecting the head losses in the drive and discharge pipes. The accumulated outflow at the storage tank for this test is plotted in
Figure 7 as X-marked dashed lines. The results are further presented in
Table 5 under a frictionless column. As shown in
Table 5, the total annual cost in the frictionless-mode is 22% lower than the Hybrid-mode, and the energy costs are lower by 37%. These results help demonstrate the importance of incorporating the pipes’ friction in the overall model to prevent unaccounted expenses.
As shown in
Table 5, the total annual cost for the Pump-mode exceeds the Hybrid-mode by 64%. This is mainly due to energy costs (~77% higher) and the larger storage tank required. The Hybrid-mode shows promising potential in reducing both the energy and the storage unit investment costs. Moreover, the frictionless model here shows the importance of including the friction effect in both drive and discharge pipes to better estimate the annual costs. Ignoring said friction can have severe economical and operational consequences. The Ram-mode here managed to supply only 65% of the daily demand, showing it as a promising solution in emergency scenarios.
As shown in
Table 6, the Hybrid-mode is clearly more energy efficient when compared to the pump-mode, where the energy consumption stands at ~28 MW·h rather than ~56 MW·h. Subsequently, the amount of energy required for supplying a cubic meter of water drops down from 88.4 to 44
(lower by ~50%). Unlike the previous case study, the flexibility introduced by the Hydram, in terms of operation hours, did not influence a further decrease in the operational cost (lower by ~44%).
3.3. Case Study 02—Sensitivity Analysis
The HPU was tested under different loading conditions (hereby referred to as scenarios) to evaluate its capabilities. The different scenarios numbered from 01 to 07 are shown in
Table 7. Scenario 01 acts as the baseline for comparison. The uphill consumption is half of the downhill one, and both consumers’ demand is distributed by pattern 1. The already existing centrifugal pump (12.8 kW) can supply the uphill demand in 12 h. Scenarios 02 and 03 inspect the influence of the demand distribution on the different costs. Scenario 04 examines a system with a more powerful pump (15.4 kW) that can supply the Uphill demand is in 10 h. Scenarios 05, 06, and 07 explore the performance of the HPU in case the uphill demand is larger than the downhill one, and address the important question, if installing a Hydram pump is still economically justified.
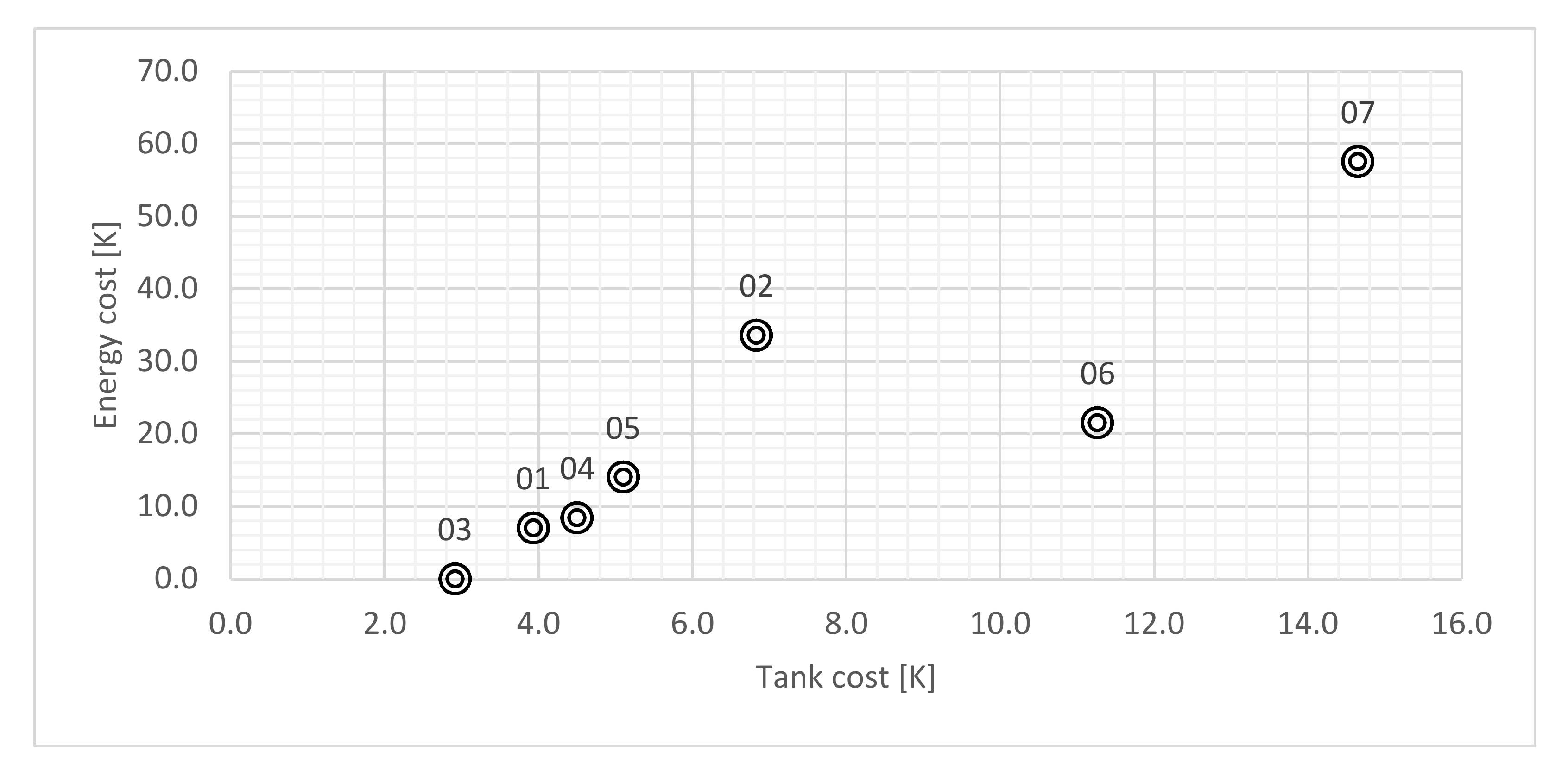
In
Figure 8, the results for the different scenarios are plotted as a Pareto graph for visual comparison. The horizontal axis represents the tank annual cost, and the vertical axis represents the annual energy cost, as mentioned previously, scenario 01 acts as the baseline for comparison. As seen in
Figure 8, scenario 02 is more expensive in both spectrums while scenario 03 is cheaper compared to the baseline. That is expected since the uniformity of the uphill demand creates water stress during the low demands of the downhill consumer. This is because the Hydram is least effective during those periods and provides insignificant flows. Meanwhile in scenario 03, the constant downhill demand supplies sufficient flow through the Hydram for longer periods, reducing the use of the centrifugal pumps and cutting the costs. Moreover, it requires a smaller buffer, thus a smaller storage tank. Scenario 04 is slightly more expensive compared with the baseline; however, the difference is mainly in the tank annual cost. The higher pump power dictates a different pattern which, in this case, is more expensive. However, it does not have to be in this manner when considering different powers, loading conditions, and layouts.
Scenarios 05, 06, and 07 show a noticeable increase in both spectrums, suggesting that with higher demand-differences come higher costs. This is to be expected since a higher uphill demand builds more stress on the system and requires the intervention of the centrifugal pumps more often to compensate for the high demands.
The annuities of the different cost components are presented in
Table 8 for all the tested scenarios for further examination. It is instructive to note that, in scenario 03 there was no need for the centrifugal pump intervention at any time during the simulation. The entire uphill demand was delivered completely by the Hydram. Thus, all the sustainability indexes are equal to zero. The sustainability indexes and the centrifugal pump details are presented in
Table 8 as well, where the pumping hours stands for the number of hours the centrifugal pump was activated annually. Subsequently, the greater the pumping hours, the greater the energy consumptions and the CO
2 emissions. The water volume stands for the annual amount of water [m
3] pumped to the uphill consumer, by both the Hydram and the centrifugal pump.
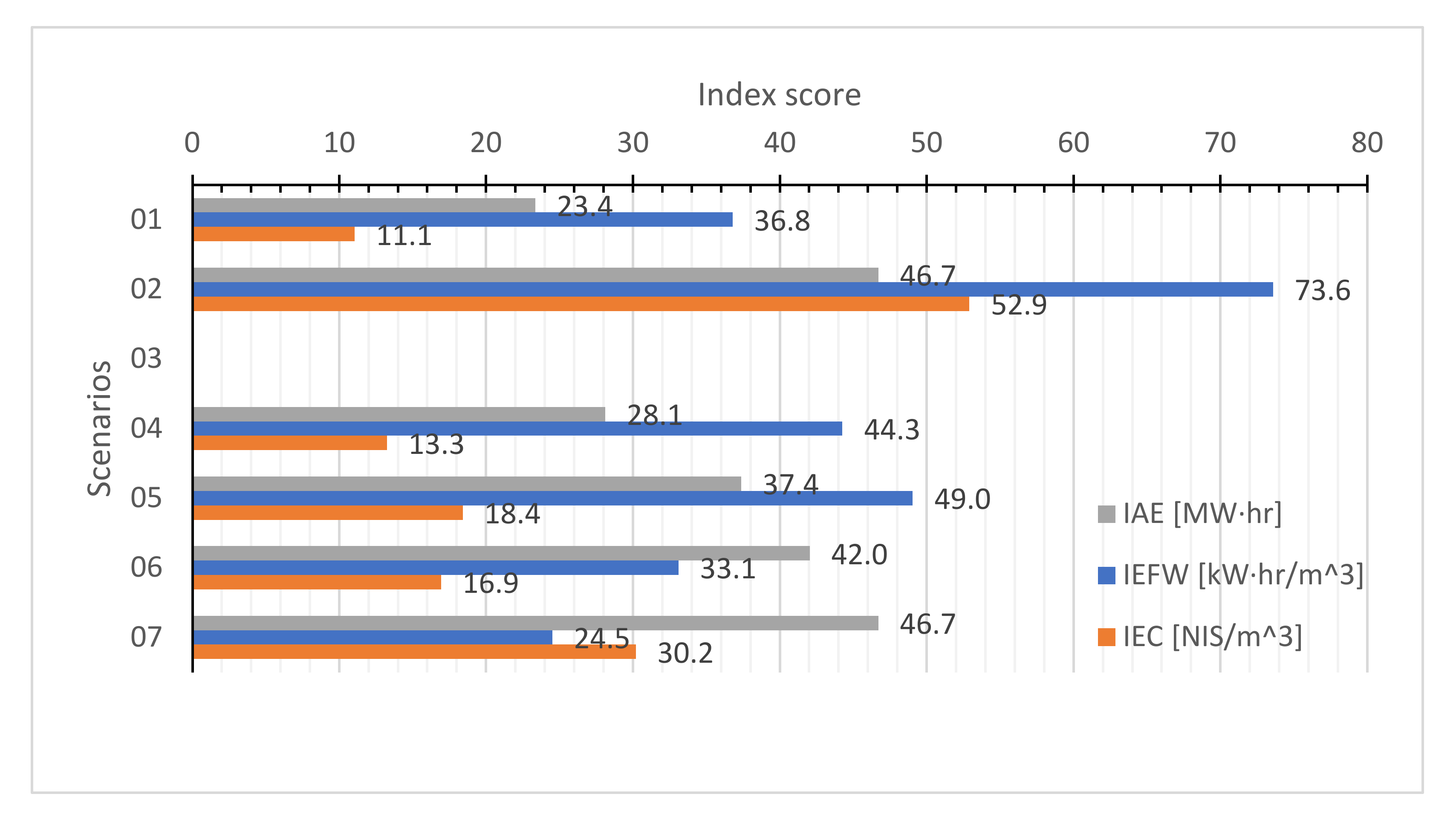
The sustainability indexes introduced previously are depicted in
Figure 9 for better analysis. The IAE index [MW·h] portrays the sustainability of the system. It indicates the amount of energy consumed during operation, thus the carbon footprint related to it. Hence, the higher the IAE, the less sustainable the system. The IEFW index [
] however, depicts the efficiency of the system in terms of pumping. Higher IEFW values translate to a less efficient system, which requires more energy to deliver a cubic meter of water to the consumer. Nonetheless, the IEC [
] portray the system’s economical aspect, where higher IEC values indicate higher energy cost for delivering water to the consumer, however, it does not necessarily indicate higher energy consumption.
When comparing scenario 02 and 07, interesting results are observed, although they seem counterintuitive at first. In scenario 02 the water demand stands at 50 CMH compared to 150 CMH in scenario 07, however, in both scenarios the energy consumption stands at 46.7 MW·h. Subsequently, the sustainability indexes at scenario 07 are significantly lower than the ones at scenario 02. The reason behind this lies in the operation patterns. When optimizing the operation pattern of scenario 02, the genetic algorithm deactivated both pumps (Null-mode) for a total of 6 h during the day, compared to only 2 h in scenario 07. This is due to the oversized pump at scenario 02 that does not allow optimal pumping operation. Since the fitness function is purely economical, it pushes the algorithm to cease pumping from both units to reduce tank size and associated costs. It is essential to note that the uphill demand at scenario 02 is constant while the downhill is distributed, which in turn applies more stress on the system. This comparison highlights the importance of pairing the Hydram with the right centrifugal pump size. Another approach would suggest attaching adjustable frequency drives (AFDs) to the centrifugal pump, enabling control over the pump’s speed and power to increase overall efficiency.
4. Conclusions
Previous works have implemented numerous approaches for reducing and recovering energy from water distribution systems. Approaches include pressure reducing valves, micro-hydroelectric plants, or a combination of them. However, these approaches either deplete energy from the system or require complex infrastructure to recover it. In this study, we examined the integration of Hydrams into water distribution systems for energy recovery applications. The introduction of Hydram into the system did not eliminate the traditional centrifugal pumps, on the contrary, both pumps operate interchangeably, creating a better and more efficient pumping unit. Thus, the new concept of an interchangeable hybrid pumping unit is introduced, where an evolutionary genetic algorithm is utilized to optimize the operation patterns.
The model’s applicability is illustrated by applying it to two networks of increasing complexity. The findings showed that in both cases, the interchangeable operation caused substantial energy and cost reduction without threatening the consumers’ demand. Even when solely operated, the Hydram managed to supply up to 65% of the requested demand. This study has several limitations which need to be considered. The examined networks are built with terrains so as to highlight the potential of Hydram pumps rather than its limitations. Moreover, it is worth noting that such terrains and conditions, however common in mountainous areas, are not common nor typical in more flat distribution systems. Therefore, implementing this approach is restricted to specific hydraulic conditions and terrains. Future research should incorporate more complex networks and integrate different approaches (i.e., PRVs and PATs) alongside Hydrams, for Multiobjective problems.