Analysis of the Intake Locations of Salinity Gradient Plants Using Hydrodynamic and Membrane Models
Abstract
1. Introduction
2. Methods
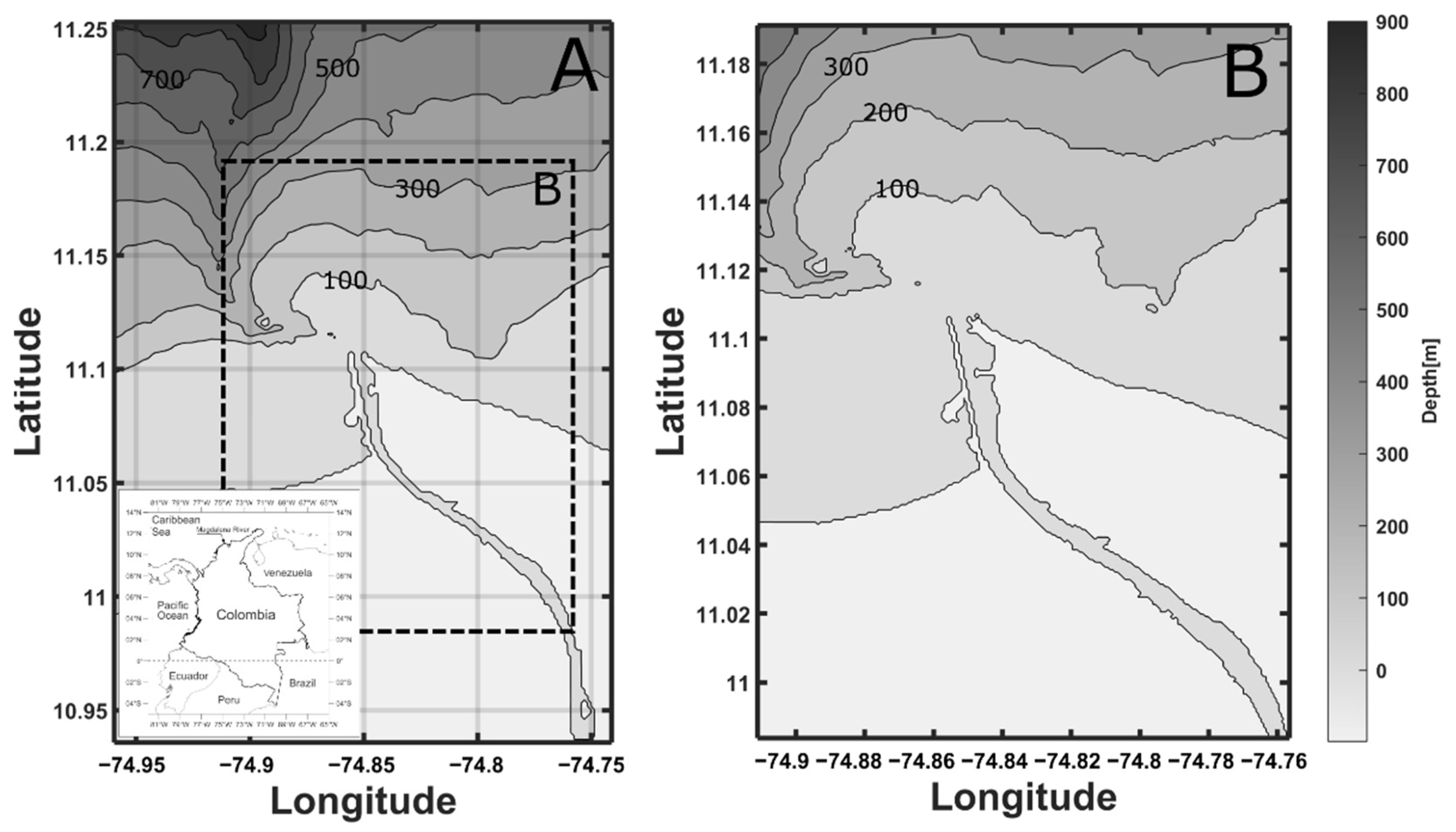
2.1. Development of a Hydrodynamic Model of the River Mouth
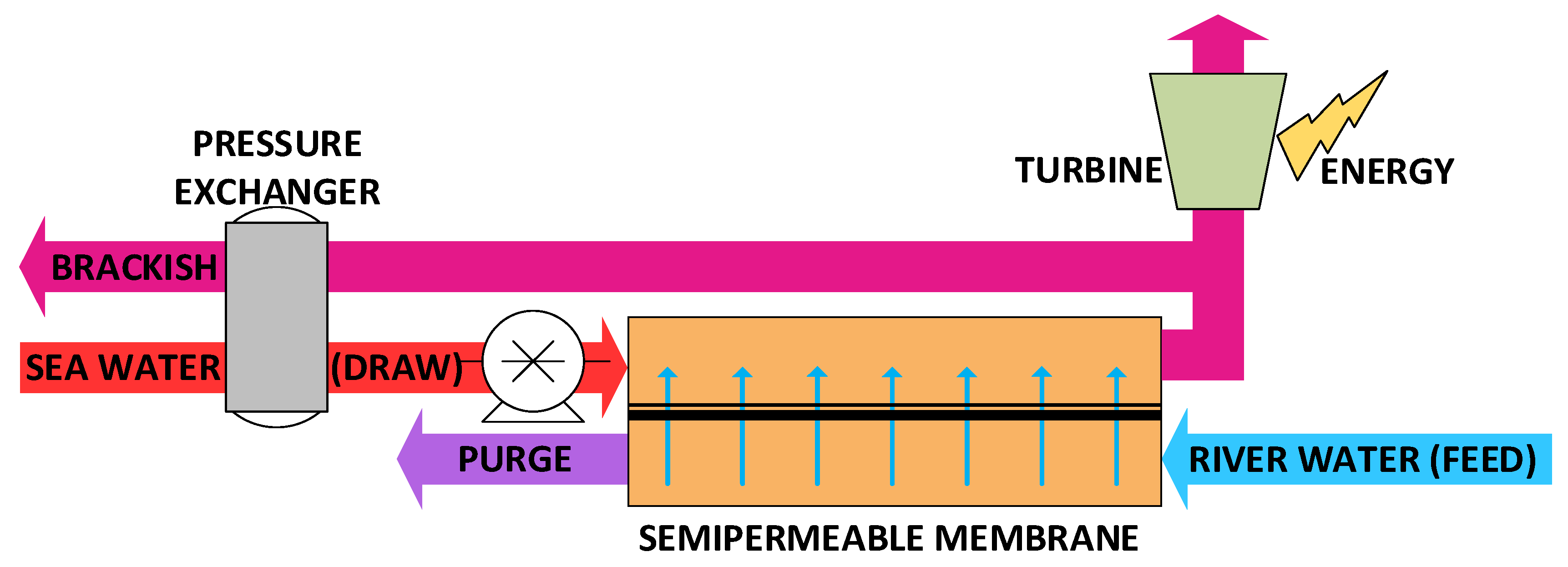
2.2. Evaluation of Power Consumed and Power Produced
2.3. Selection of the Intakes Location
3. Results and Discussion
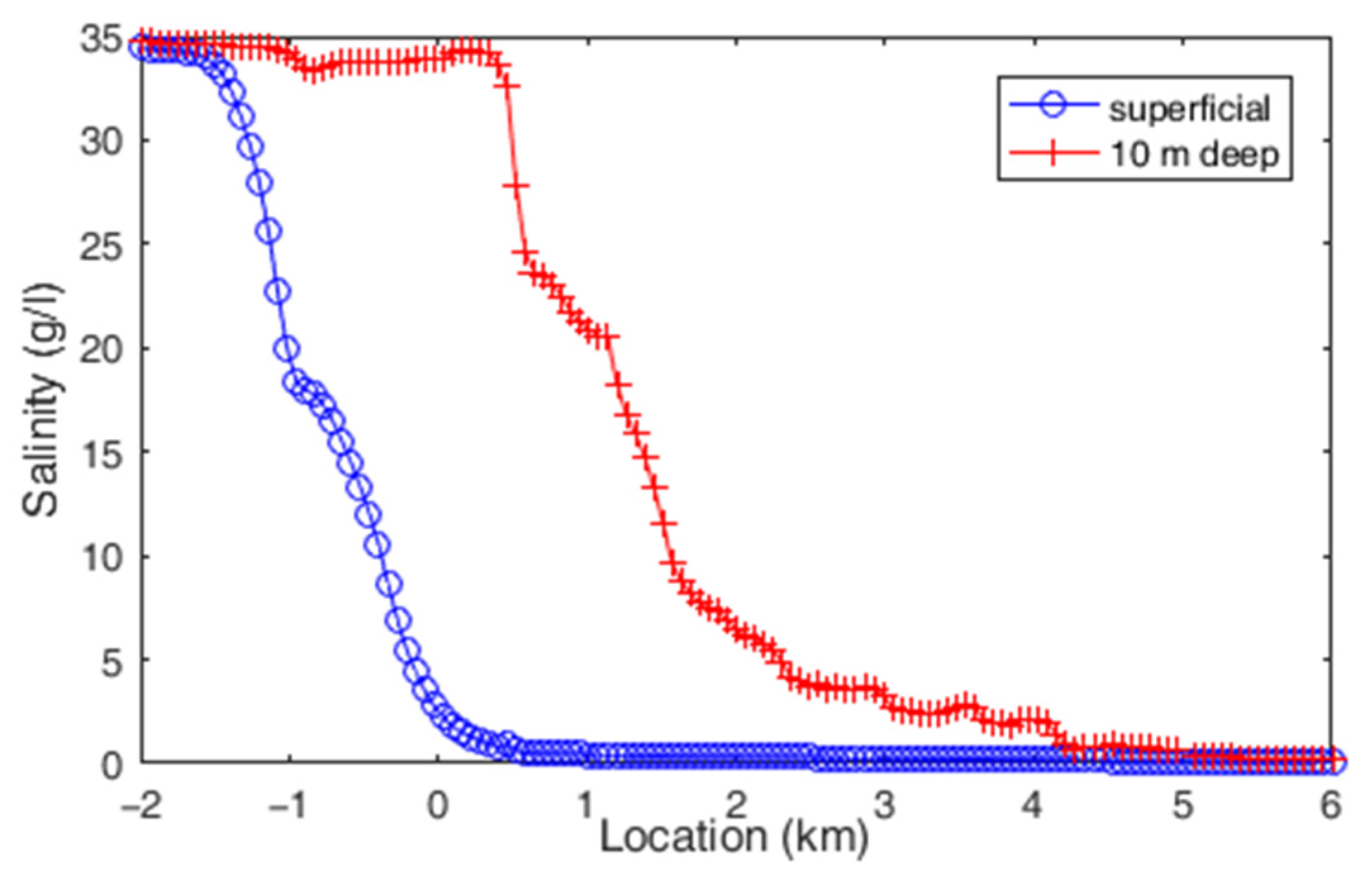
3.1. Hydrodynamic Model
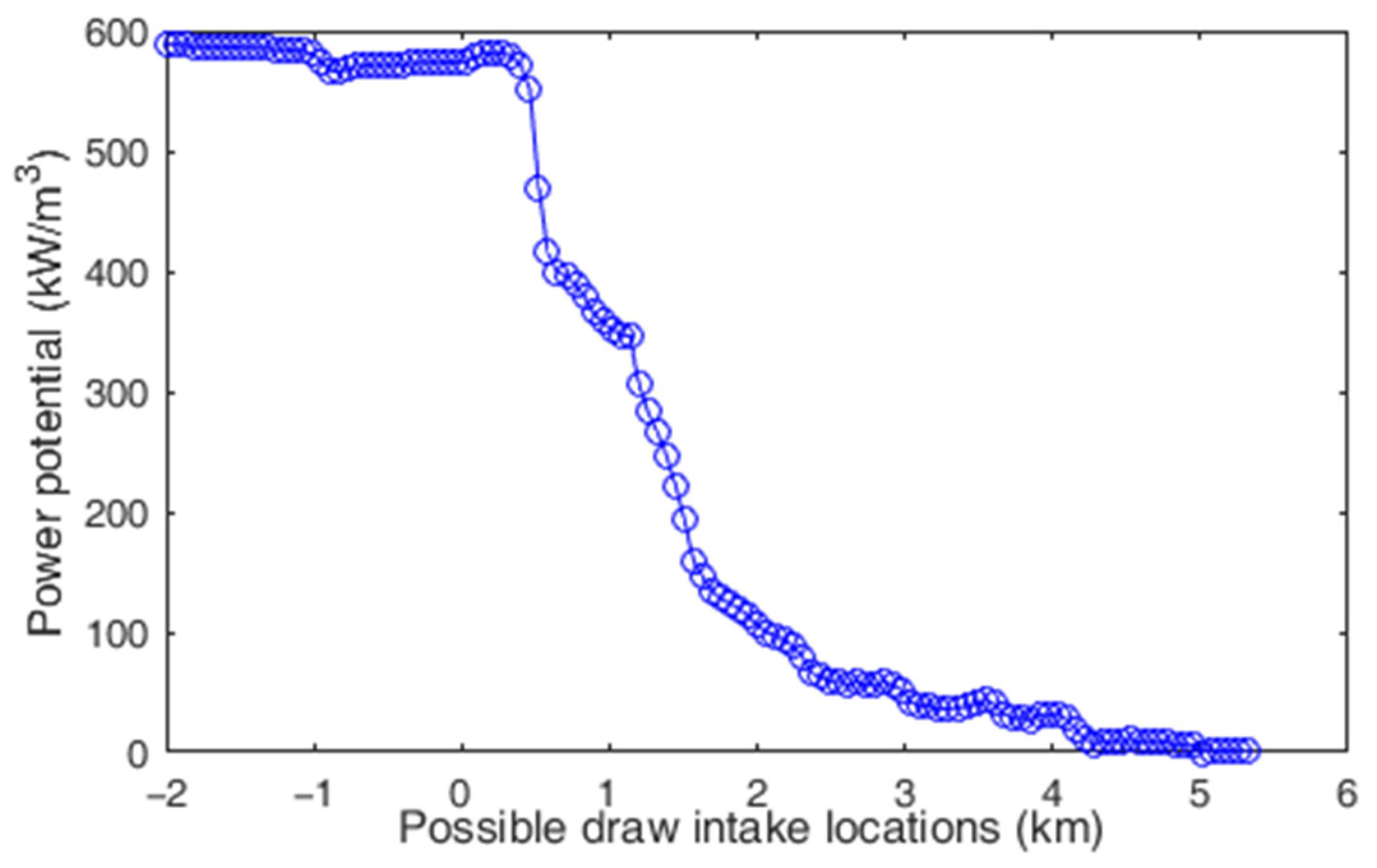
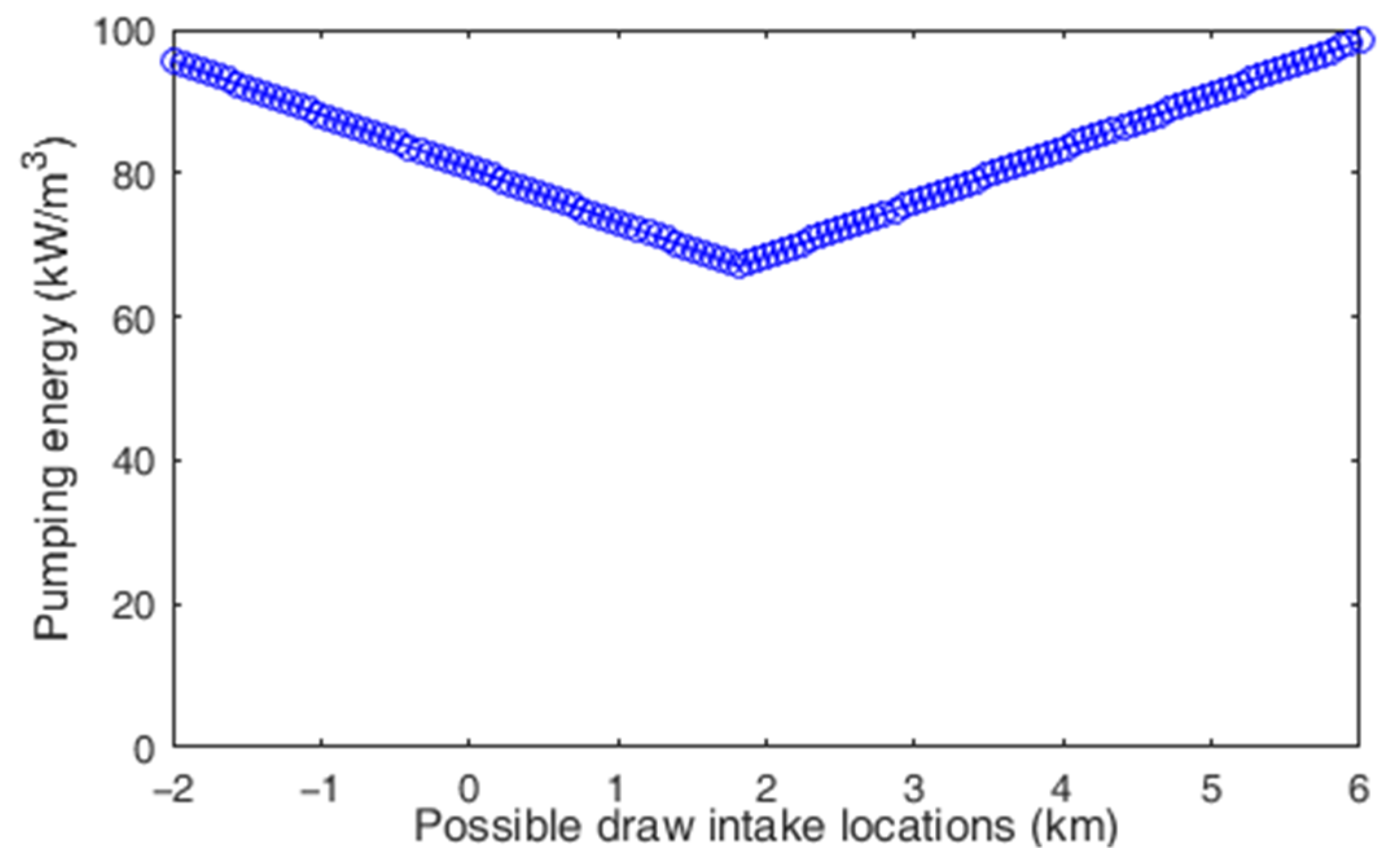
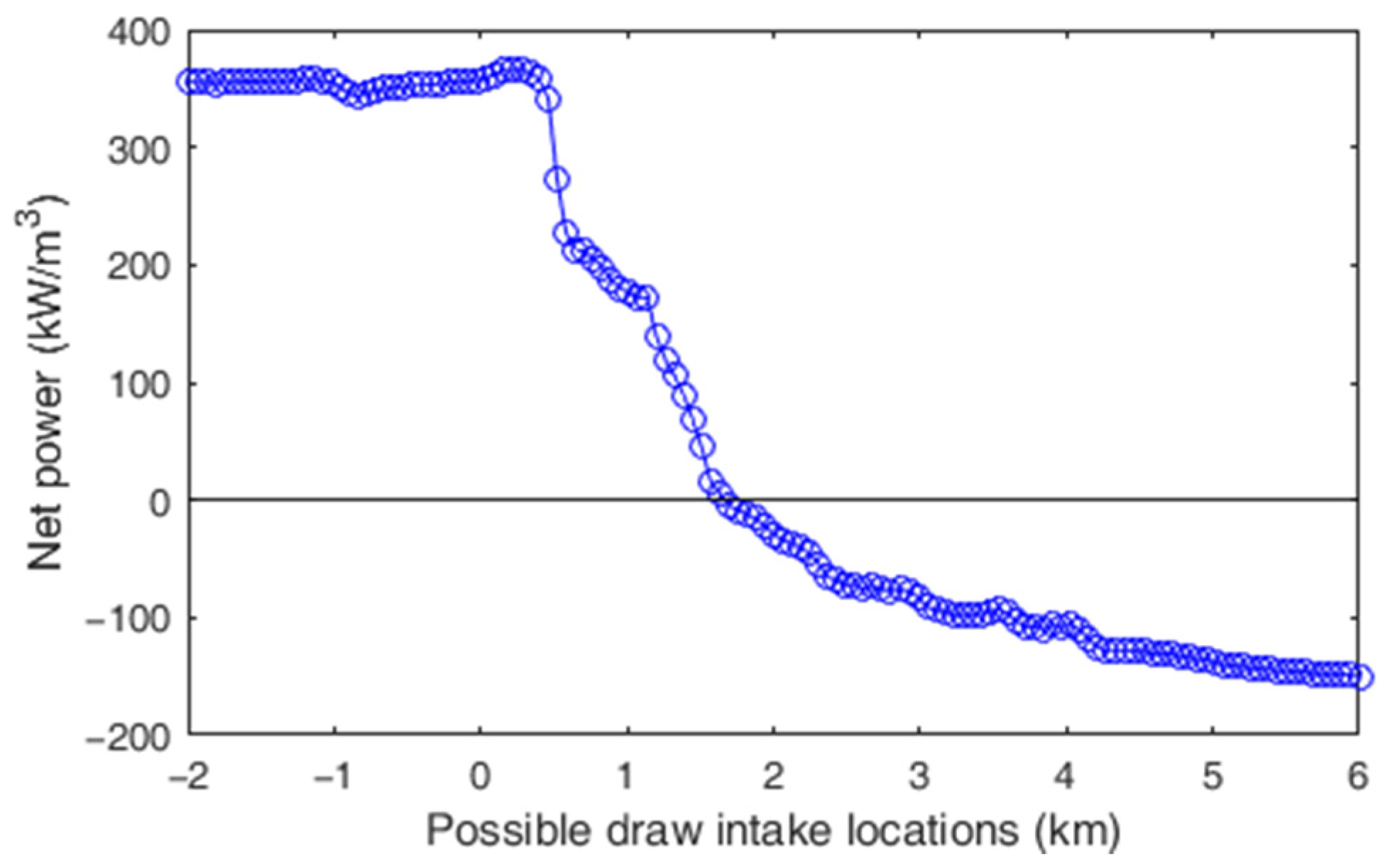
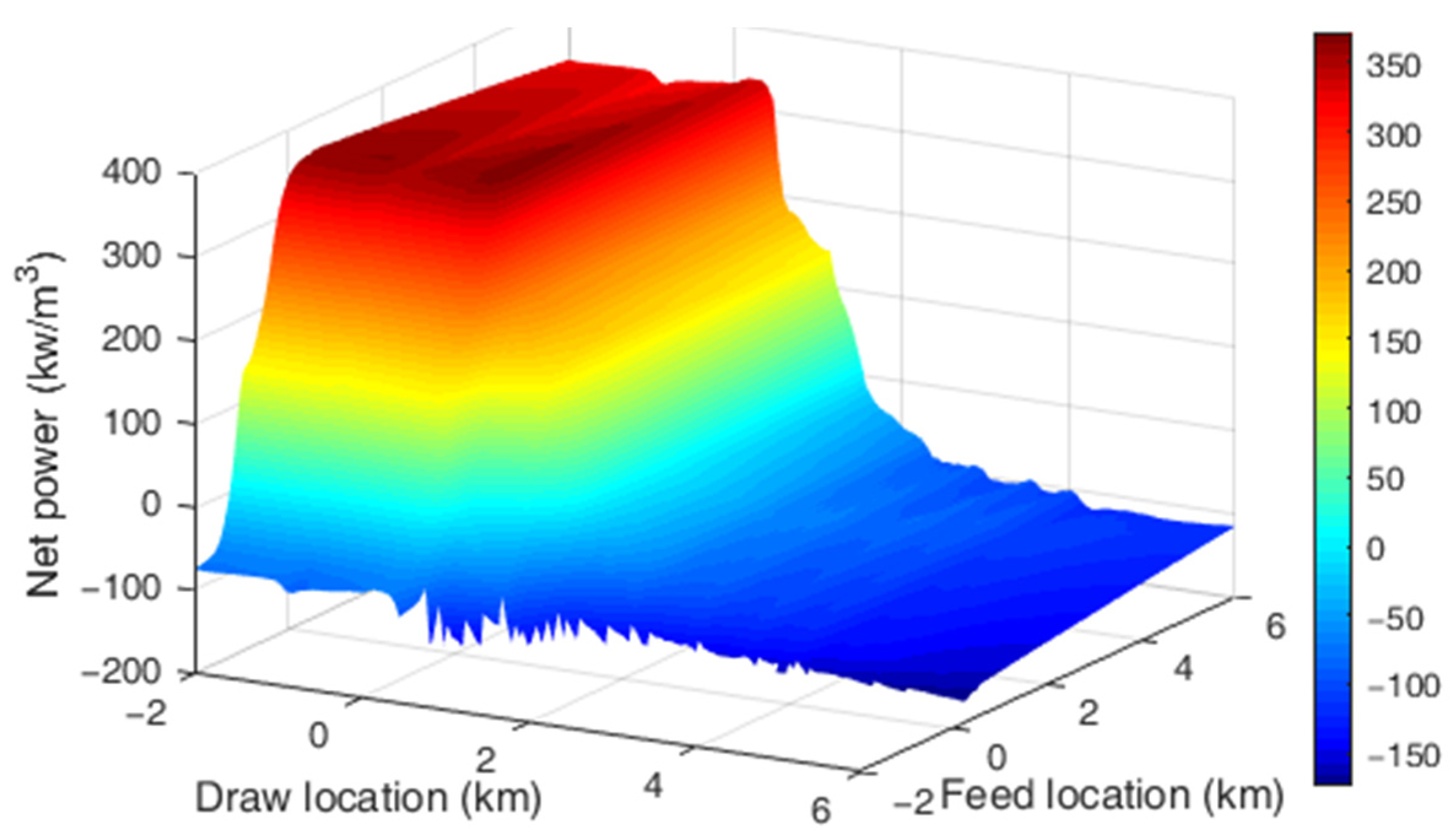
3.2. PRO Power Production and Pumping Costs
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Gross, M.; Rüdiger, M. Renewable Energies; Routledge: London, UK, 2014. [Google Scholar]
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Mikulcic, H.; Kalogirou, S. Sustainable development using renewable energy technology. Renew. Energy 2020, 146, 2430–2437. [Google Scholar] [CrossRef]
- Twidell, J. Tony Weir. In Renewable Energy Resources; Routledge: London, UK, 2015. [Google Scholar]
- Halkos, G.E.; Eleni-Christina, G. Reviewing Usage, Potentials, and Limitations of Renewable Energy Sources. Energies 2020, 13, 2906. [Google Scholar] [CrossRef]
- Hussain, A.; Syed, M.A.; Muhammad, A. Emerging renewable and sustainable energy technologies: State of the art. Renew. Sustain. Energy Rev. 2017, 71, 12–28. [Google Scholar] [CrossRef]
- Micale, G.; Cipollina, A.; Tamburini, A. Salinity gradient energy. In Sustainable Energy from Salinity Gradients; Woodhead Publishing: Sawston, UK, 2016; pp. 1–17. [Google Scholar]
- Touati, K.; Tadeo, F.; Kim, J.H.; Silva, O.A.A.; Chae, S.H. Pressure Retarded Osmosis: Renewable Energy Generation and Recovery; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Alvarez-Silva, A.; Osorio, A.F.; Winter, C. Practical global salinity gradient energy potential. Renew. Sustain. Energy Rev. 2016, 60, 1387–1395. [Google Scholar] [CrossRef]
- Sandbach, S.D.; Nicholas, A.P.; Ashworth, P.J.; Best, J.L.; Keevil, C.E.; Parsons, D.R.; Simpson, C.J. Hydrodynamic modelling of tidal-fluvial flows in a large river estuary. Estuar. Coast. Shelf Sci. 2018, 212, 176–188. [Google Scholar] [CrossRef]
- Panchenko, E.; Max, L.; Serafima, L. Hydrodynamic modelling of the Onega River tidal estuary. E3S Web Conf. 2020, 163, 01-008. [Google Scholar] [CrossRef]
- Restrepo, J.C.; Ortiz, J.C.; Pierini, J. Freshwater discharge into the Caribbean Sea from the rivers of Northwestern South America (Colombia): Magnitude, variability and recent changes. J. Hydrol. 2014, 509, 266–281. [Google Scholar] [CrossRef]
- Leitao, P.; Mateus, M.; Braunschweig, L.; Fernandes, L.; Neves, R. Modelling Coastal Systems: The MOHID Water Numerical Lab, Perspectives on Integrated Coastal Zone Management in South America; IST Press: Lisboa, Portugal, 2008. [Google Scholar]
- Martins, F.; Leitao, P.; Silva, A.; Neves, R. 3D modelling in the Sado estuary using a new generic vertical discretization approach. Oceanol. Acta 2001, 24, 51–62. [Google Scholar] [CrossRef]
- Available online: https://www.aviso.altimetry.fr/en/data/products/auxiliary-products/global-tide-fes/description-fes2012.html (accessed on 16 April 2021).
- Available online: https://www.ncdc.noaa.gov/data-access/model-data/model-datasets/global-forcast-system-gfs (accessed on 16 April 2021).
- Skote, M. Studies of Turbulent Boundary Layer Flow through Direct Numerical Simulation; Technical Report; Royal Institute of Technology, Department of Mechanics: Stockholm, Sweden, 2001. [Google Scholar]
- Canuto, V.M.; Howard, A.; Cheng, Y.; Dubovikov, M.S. Ocean Turbulence. Part I: One-point closure model momentum and heat vertical diffusivities. J. Phys. Oceanogr. 2001, 31, 1413–1426. [Google Scholar] [CrossRef]
- Touati, K.; Hänel, C.; Tadeo, F.; Schiestel, T. Effect of the feed and draw solution temperatures on PRO performance: Theoretical and experimental study. Desalination 2015, 365, 182–195. [Google Scholar] [CrossRef]
- Gonzales, R.R.; Abdel-Wahab, A.; Adham, S.; Dong, S.H.; Phuntsho, S.; Suwaileh, W.; Hilalf, N.; Shon, H.K. Salinity gradient energy generation by pressure retarded osmosis: A review. Desalination 2021, 500, 114841. [Google Scholar] [CrossRef]
- Salamanca, J.M.; Álvarez-Silva, O.; Tadeo, F. Potential and analysis of an osmotic power plant in the Magdalena River using experimental field-data. Energy 2019, 180, 548–555. [Google Scholar] [CrossRef]
- Seme, S.; Sredensk, K.; Praunseis, Z.; Stumberger, B.; Hadziselimovic, M. Optimal price of electricity of solar power plants and small hydro power plants–Technical and economical part of investments. Energy 2018, 157, 87–95. [Google Scholar] [CrossRef]
- Abbasi-Garravand, E.; Catherine, N.; Mulligan, C.B.; Laflamme, G.C. Role of two different pretreatment methods in osmotic power (salinity gradient energy) generation. Renew. Energy 2016, 96, 98–119. [Google Scholar] [CrossRef]
- Roldan-Carvajal, M.; Vallejo-Castaño, S.; Álvarez-Silva, O.; Bernal-García, S.; Arango-Aramburo, S.; Sánchez-Sáenz, C.I.; Osorio, A.F. Salinity gradient power by reverse electrodialysis: A multidisciplinary assessment in the Colombian context. Desalination 2021, 503, 114933. [Google Scholar] [CrossRef]
- Alvarez-Silva, O.; Maturana, A.Y.; Pacheco-Bustos, C.A.; Osorio, A.F. Effects of water pretreatment on the extractable salinity gradient energy at river mouths: The case of Magdalena River, Caribbean Sea. J. Ocean Eng. Marine Energy 2019, 5, 227–240. [Google Scholar] [CrossRef]
- Ortega, S.; Stenzel, P.; Alvarez-Silva, O.; Osorio, A.F. Site-specific potential analysis for pressure retarded osmosis (PRO) power plants–The León River example. Renew. Energy 2014, 68, 466–474. [Google Scholar] [CrossRef]
- Alvarez-Silva, A.; Winter, C.; Osorio, A.F. Salinity gradient energy at river mouths. Environ. Sci. J. Technol. Lett. 2014, 1, 410–415. [Google Scholar] [CrossRef]
- Geyer, W.R.; Ralston, D.K. The dynamics of strongly stratified estuaries. In Treatise on Estuarine and Coastal Science; Elsevier: Amsterdam, The Netherlands, 2011; pp. 37–52. [Google Scholar]
- Ospino, S.; Restrepo, J.C.; Otero, L.; Pierini, J.; Alvarez-Silva, O. Saltwater Intrusion into a River with High Fluvial Discharge: A Microtidal Estuary of the Magdalena River, Colombia. J. Coast. Res. 2018, 34, 1273–1288. [Google Scholar]
| Symbol | Variable | Units |
|---|---|---|
| A | Water permeability | m/s·Pa |
| B | Salt permeability | m/s |
| CD | Salinity in draw stream | mol/m3 |
| CF | Salinity in feed stream | mol/m3 |
| JW | Transmembrane flow density | m/s |
| Js | Transmembrane salt flow density | mol/m2·s |
| K | Solute resistivity | s/m |
| kD | Mass transfer coefficient (membrane draw side) | m/s |
| kF | Mass transfer coefficient (membrane feed side) | m/s |
| R | Universal ideal gas constant | J/mol·K |
| TD | Draw temperature | K |
| TF | Feed temperature | K |
| WPRO | Power density from pressure retarded osmosis | W/m2 |
| βvH | van’t Hoff coefficient | - |
| Δx | Hydrodynamic model mesh width | m |
| Δy | Hydrodynamic model mesh length | m |
| ΔP | Draw external pressure | Pa |
| Δt | Hydrodynamic model time step | s |
| πD | Osmotic pressure of draw stream | Pa |
| πF | Osmotic pressure of feed stream | Pa |
| Water permeability A | 1.1 × 10−11 m3/m2·s·Pa |
| Salt permeability B | 1.2 × 10−7 m3/m2·s |
| Average osmotic gradient | 19.7 bar |
| Membrane area requirement | 1.5 × 105 m2/m3feed/s |
| Average power density | Up to 6.4 W/m2 |
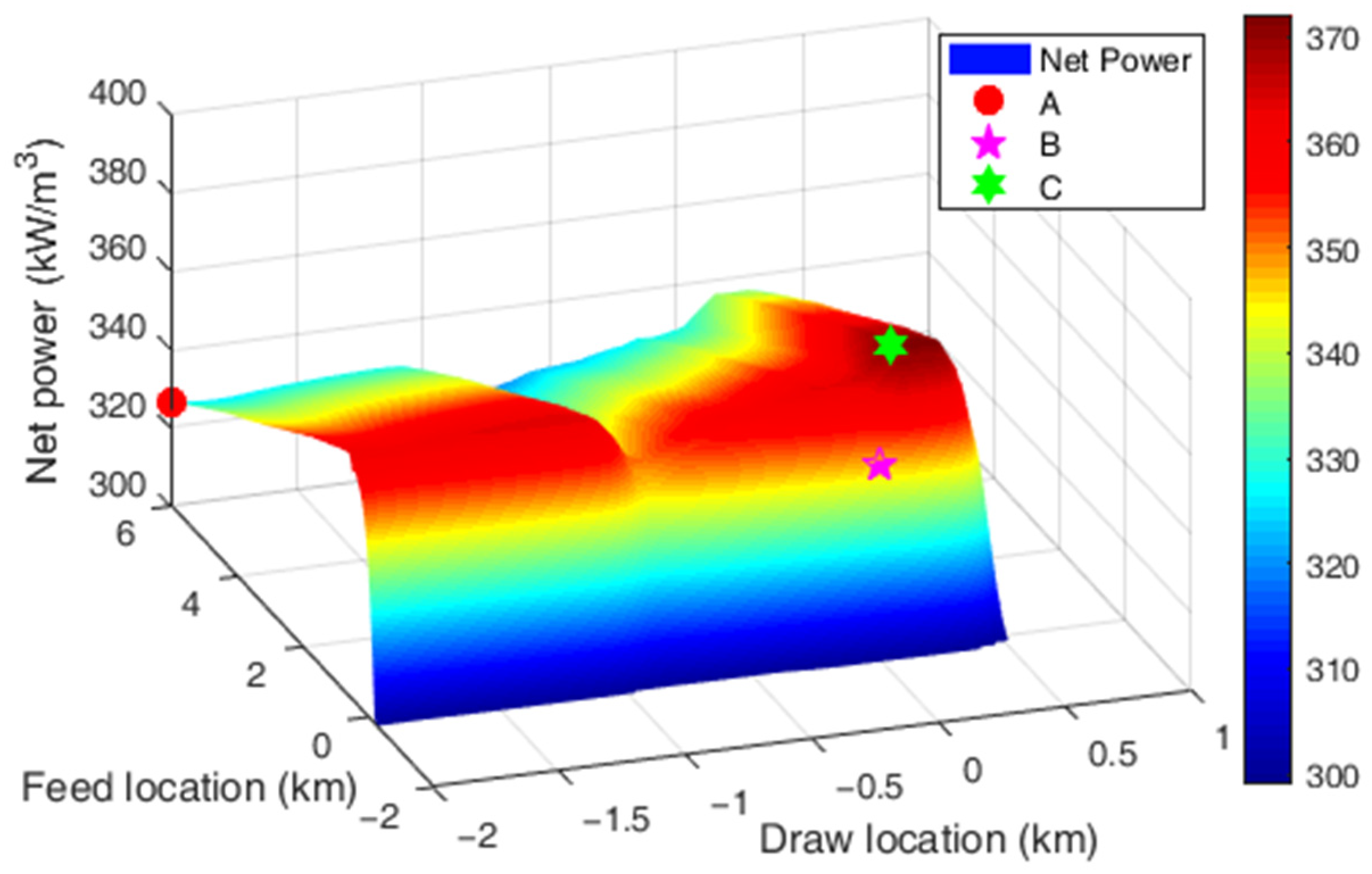
| A: Highest Power | B: Lowest Pumping | C: Best Efficiency | |
|---|---|---|---|
| Feed intake (km) | 6.0 | 0.03 | 0.58 |
| Draw intake (km) | −2.0 | 0.03 | 0.15 |
| Relative Distance (km) | 8.0 | 0 | 0.43 |
| Feed mean salinity (g/L) | 0.11 | 1.9 | 0.28 |
| Draw mean salinity (g/L) | 34.8 | 33.9 | 34.3 |
| Gross power potential (kW/m3) | 593 | 546 | 579 |
| Pumping power (kW/m3) | 166 | 106 | 109 |
| Net power (kW/m3) | 327 | 347 | 373 |
| Scenario | Base Case | D: +1 °C | E: −1 °C | F: +1 g/L Feed | G: +1 g/L Draw | H: −1 g/L Draw |
|---|---|---|---|---|---|---|
| Net power (kW/m3) | 373 | 375 | 371 | 314 | 388 | 353 |
| % variation | +0.6% | −0.6% | −15.8% | +3.9% | −5.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salamanca, J.M.; Álvarez-Silva, O.; Higgins, A.; Tadeo, F. Analysis of the Intake Locations of Salinity Gradient Plants Using Hydrodynamic and Membrane Models. Water 2021, 13, 1133. https://doi.org/10.3390/w13091133
Salamanca JM, Álvarez-Silva O, Higgins A, Tadeo F. Analysis of the Intake Locations of Salinity Gradient Plants Using Hydrodynamic and Membrane Models. Water. 2021; 13(9):1133. https://doi.org/10.3390/w13091133
Chicago/Turabian StyleSalamanca, Jacobo M., Oscar Álvarez-Silva, Aldemar Higgins, and Fernando Tadeo. 2021. "Analysis of the Intake Locations of Salinity Gradient Plants Using Hydrodynamic and Membrane Models" Water 13, no. 9: 1133. https://doi.org/10.3390/w13091133
APA StyleSalamanca, J. M., Álvarez-Silva, O., Higgins, A., & Tadeo, F. (2021). Analysis of the Intake Locations of Salinity Gradient Plants Using Hydrodynamic and Membrane Models. Water, 13(9), 1133. https://doi.org/10.3390/w13091133







