Evaluation of Incipient Motion of Sand Particles by Different Indirect Methods in Erosion Function Apparatus
Abstract
:1. Introduction
1.1. Threshold Shear Stress in Erosion Function Apparatus (EFA)
1.2. Threshold Shear Stress in Other Experimental Facilities
1.3. Importance of Resistance Coefficients in EFA and Other Experimental Facilities
2. Materials and Methods
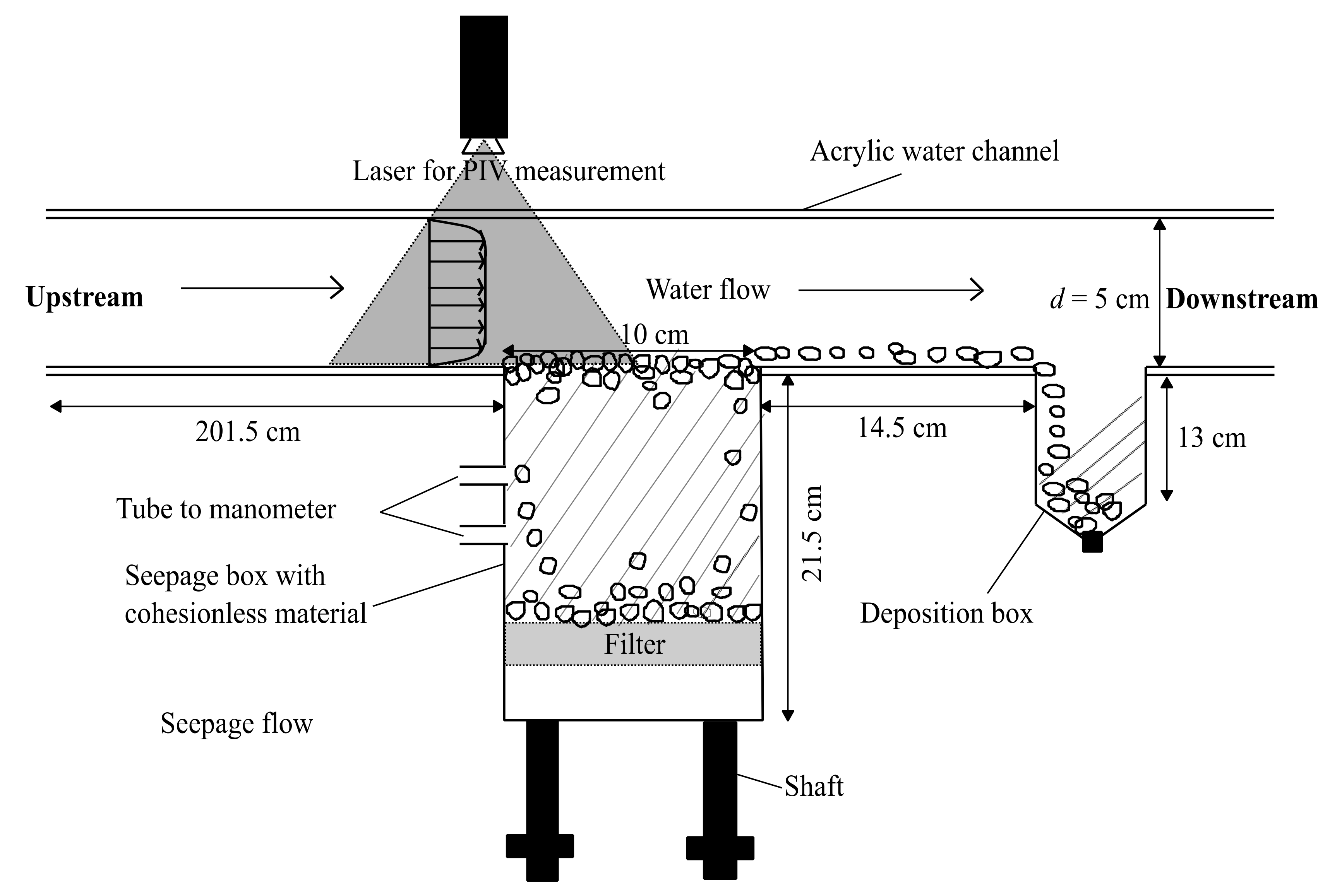
2.1. Experiment and Procedure
2.2. Indirect Methods to Estimate Shear Velocity
2.2.1. Log-Law Method
2.2.2. Reynolds Shear Stress Method
2.2.3. Turbulence Intensity Method
3. Results and Discussion
3.1. Streamwise Flow Velocity in Closed Conduit
3.2. Universal Characteristics of Turbulence Flow in Closed Conduit
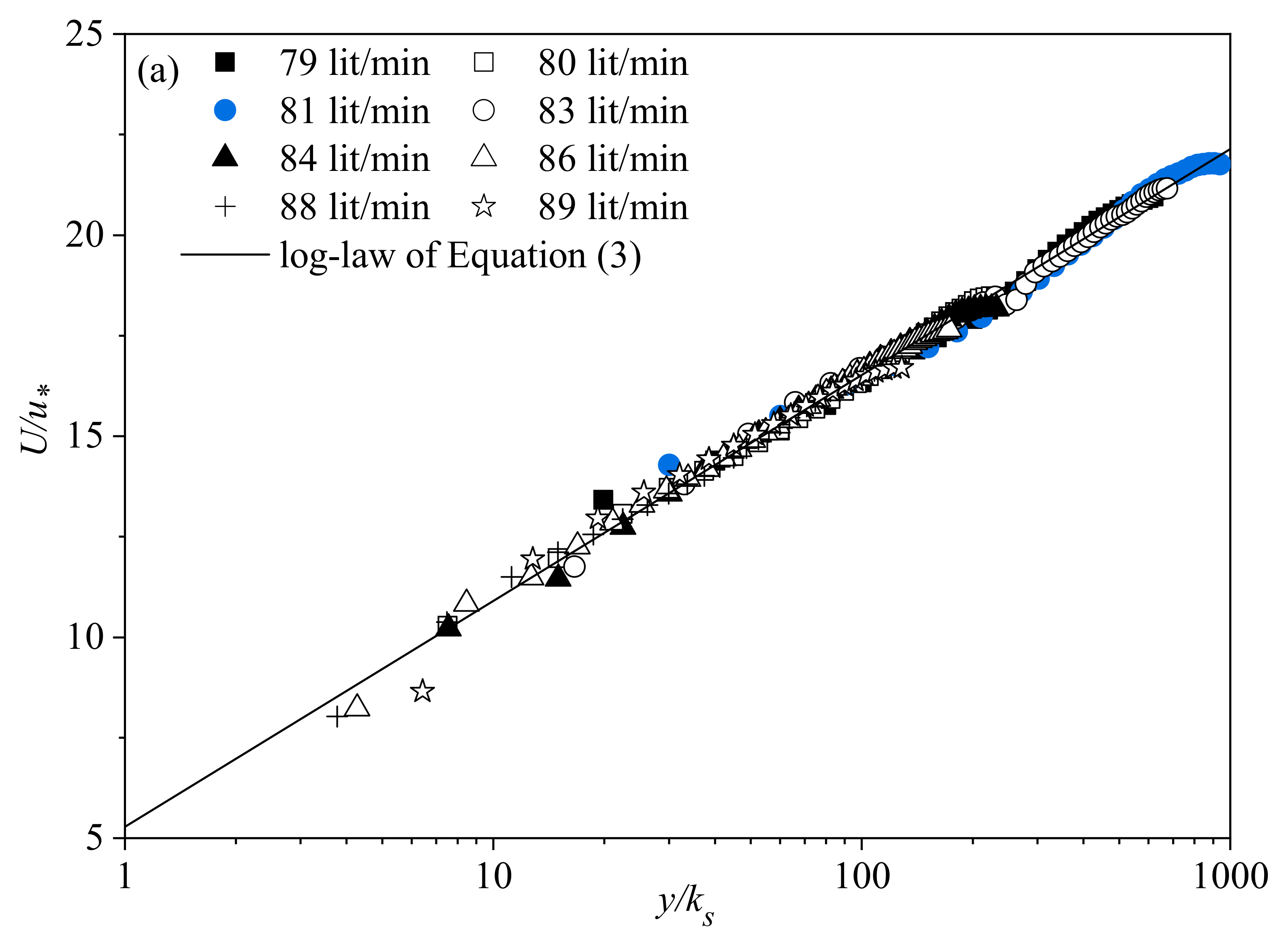
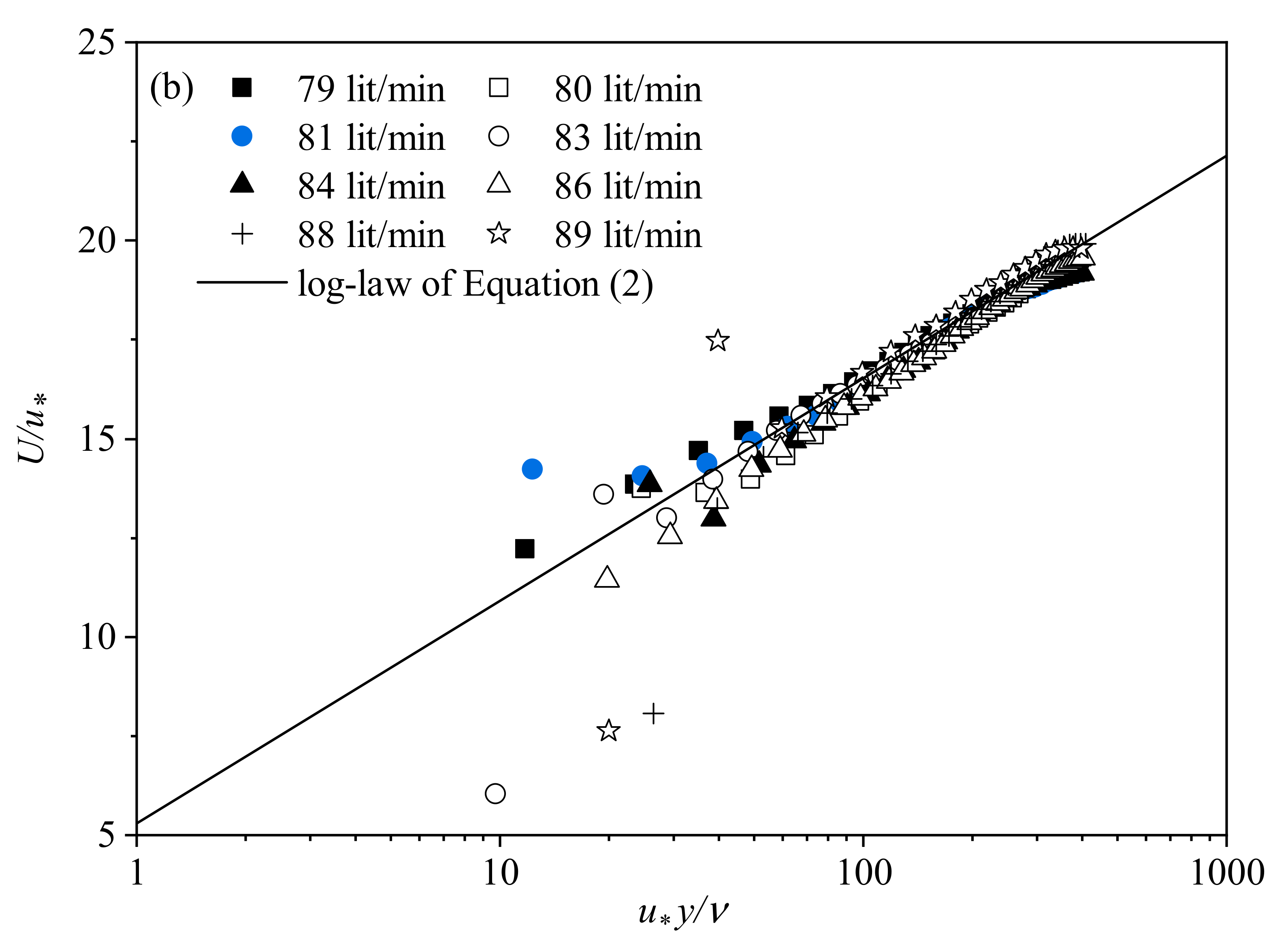
3.2.1. Logarithmic Distributions of Flow Profiles
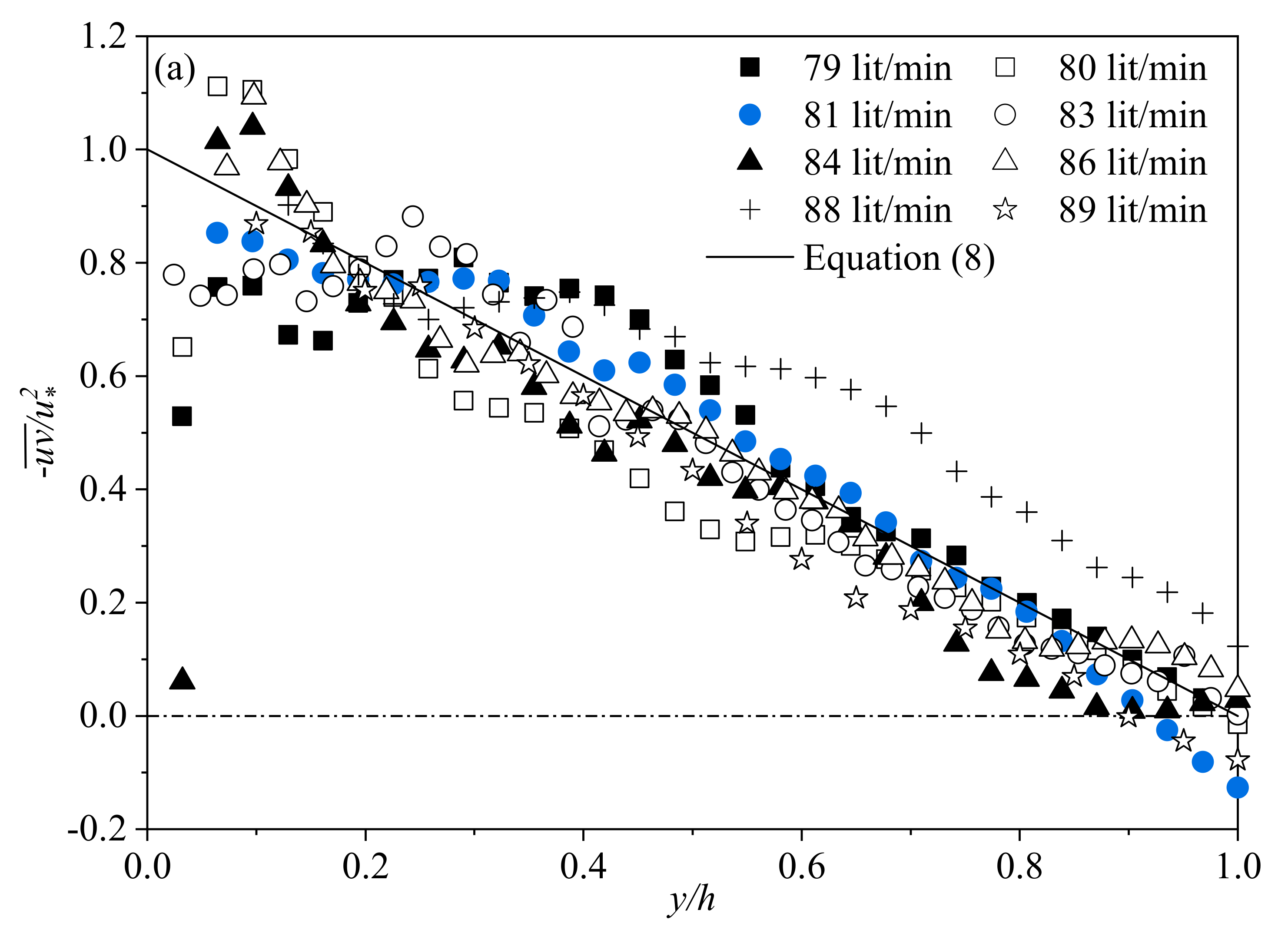
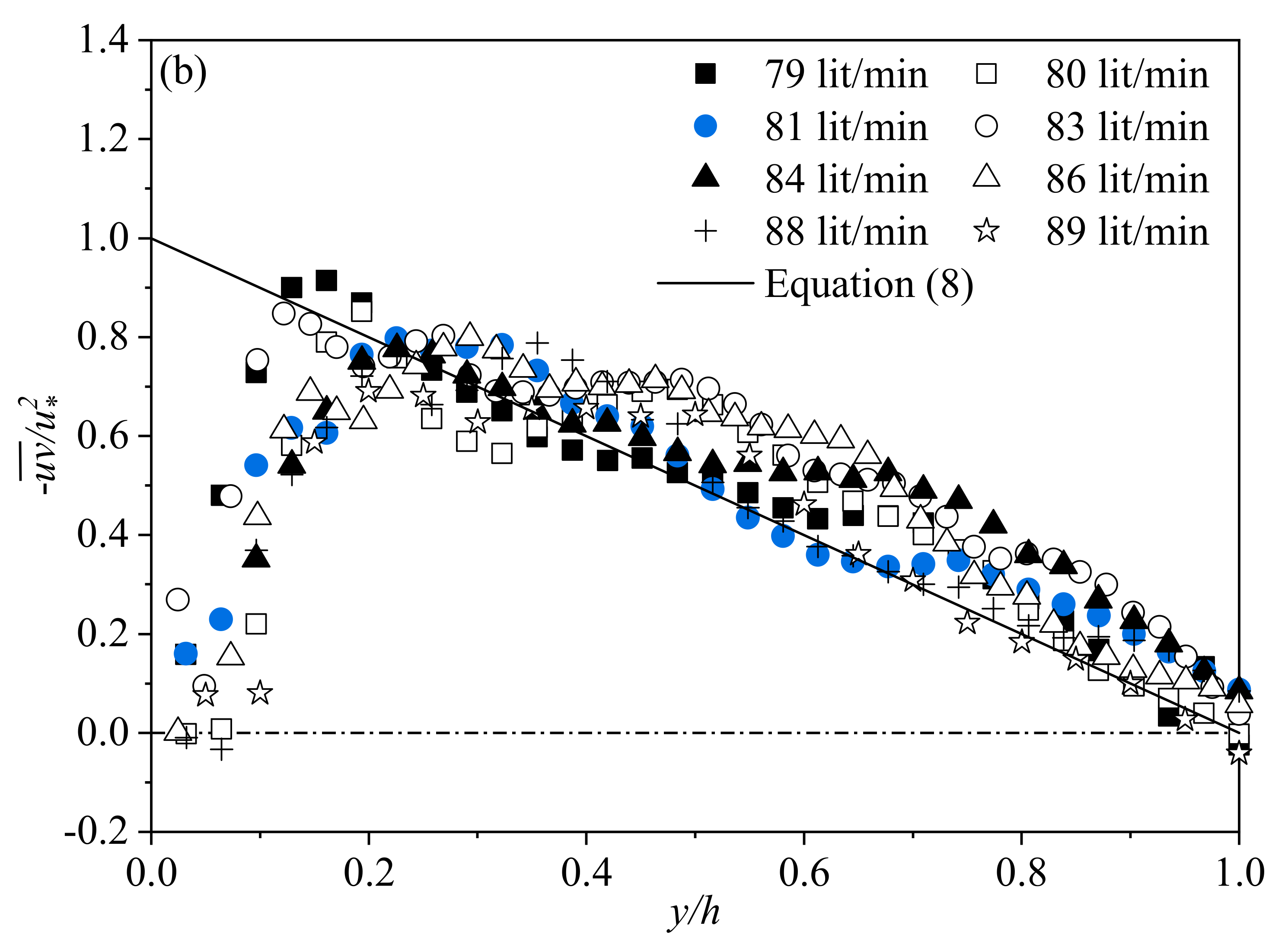
3.2.2. Reynolds Shear Stress Distribution of Flow Profiles
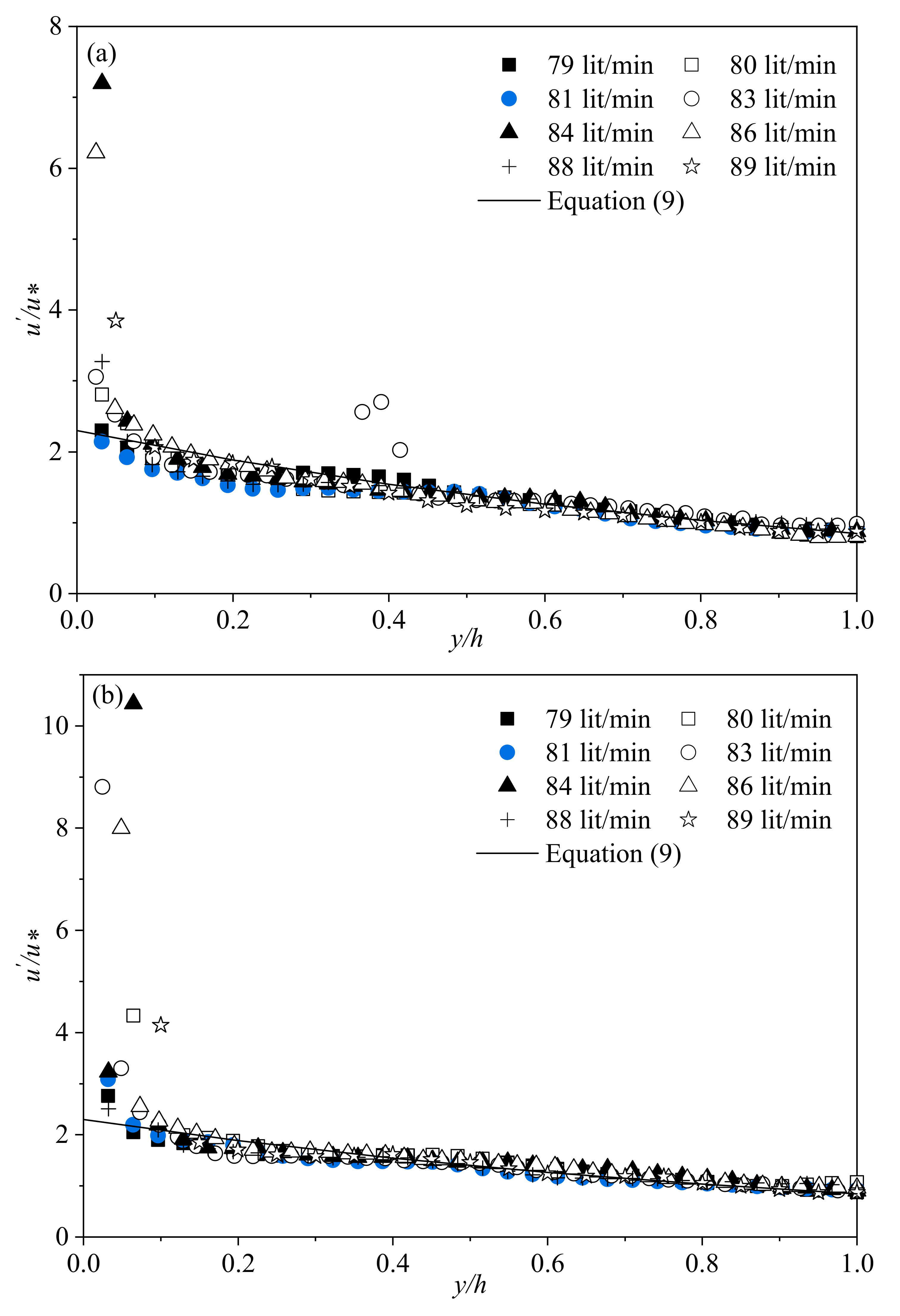
3.2.3. Turbulence Intensity Distribution of Flow Profiles
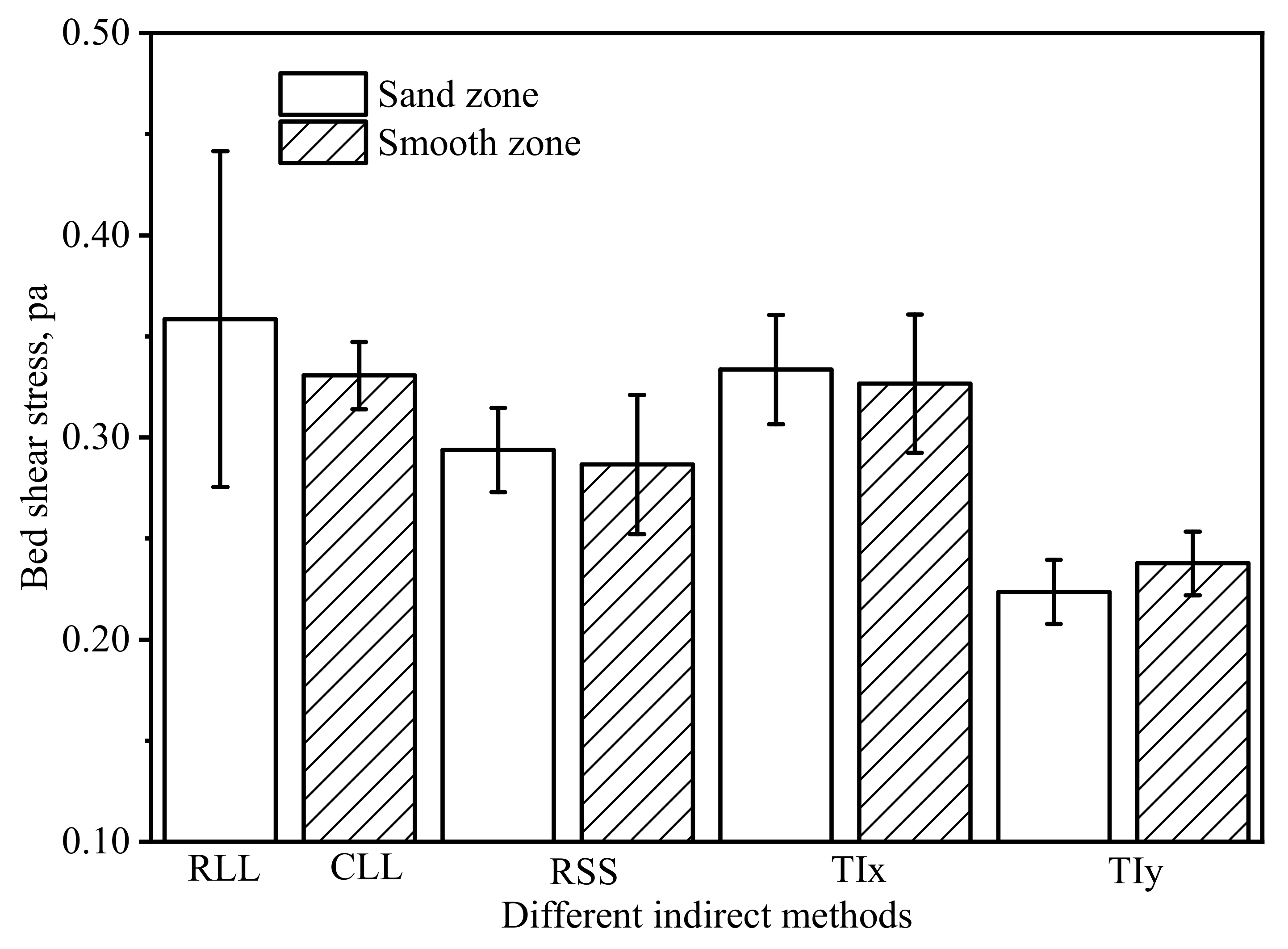
3.3. Shear Velocity and Bed Shear Stress of Flow
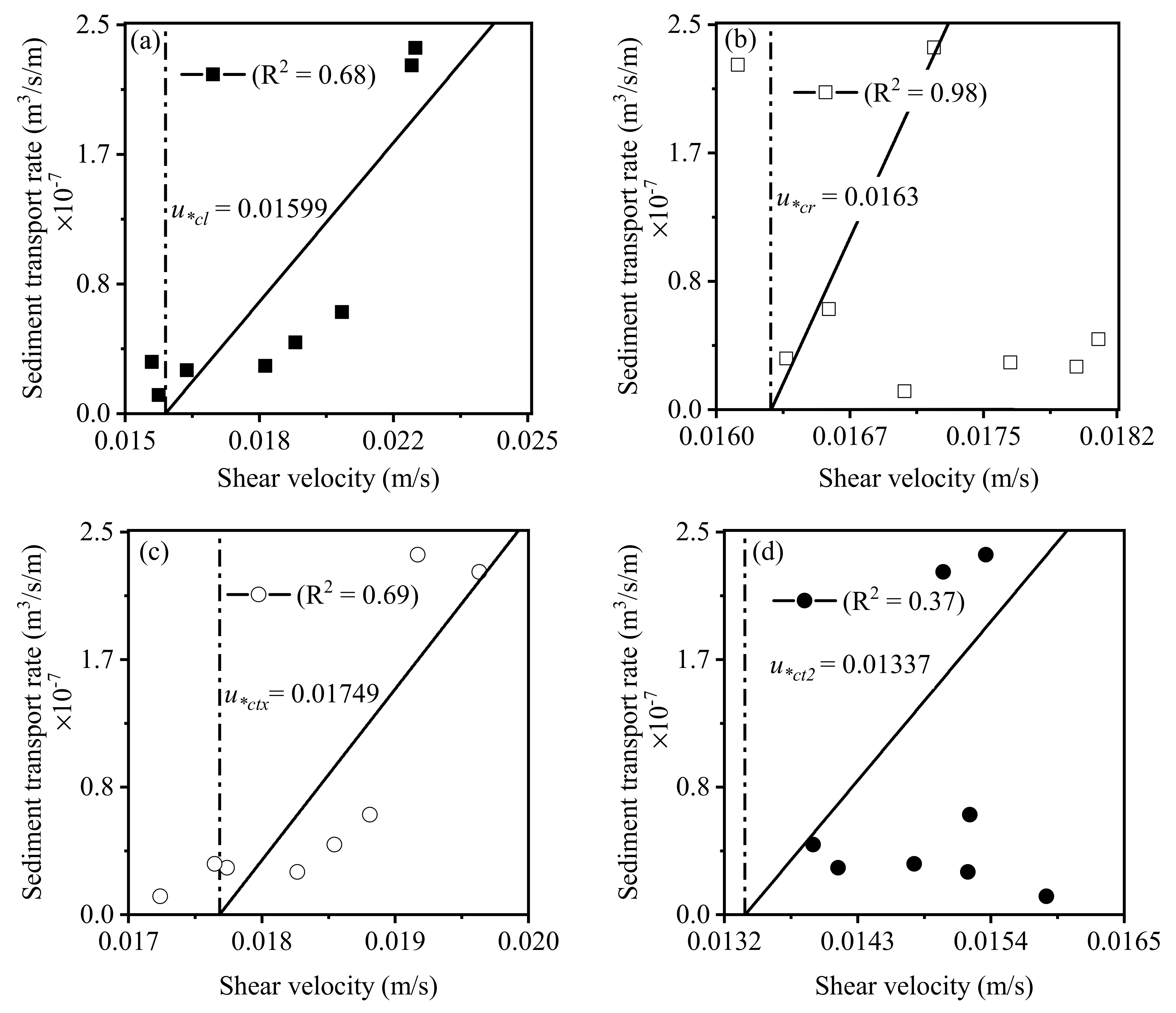
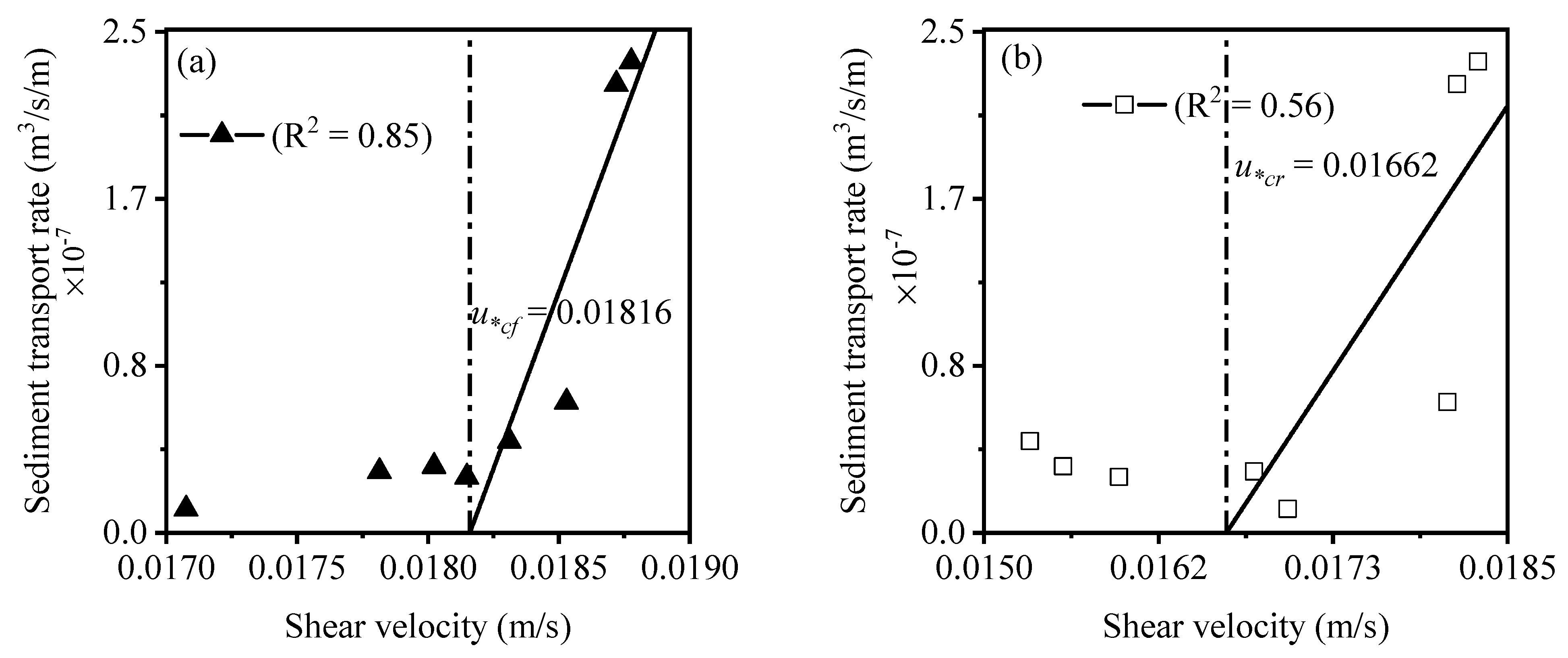
3.4. Determination of Critical Shear Velocity
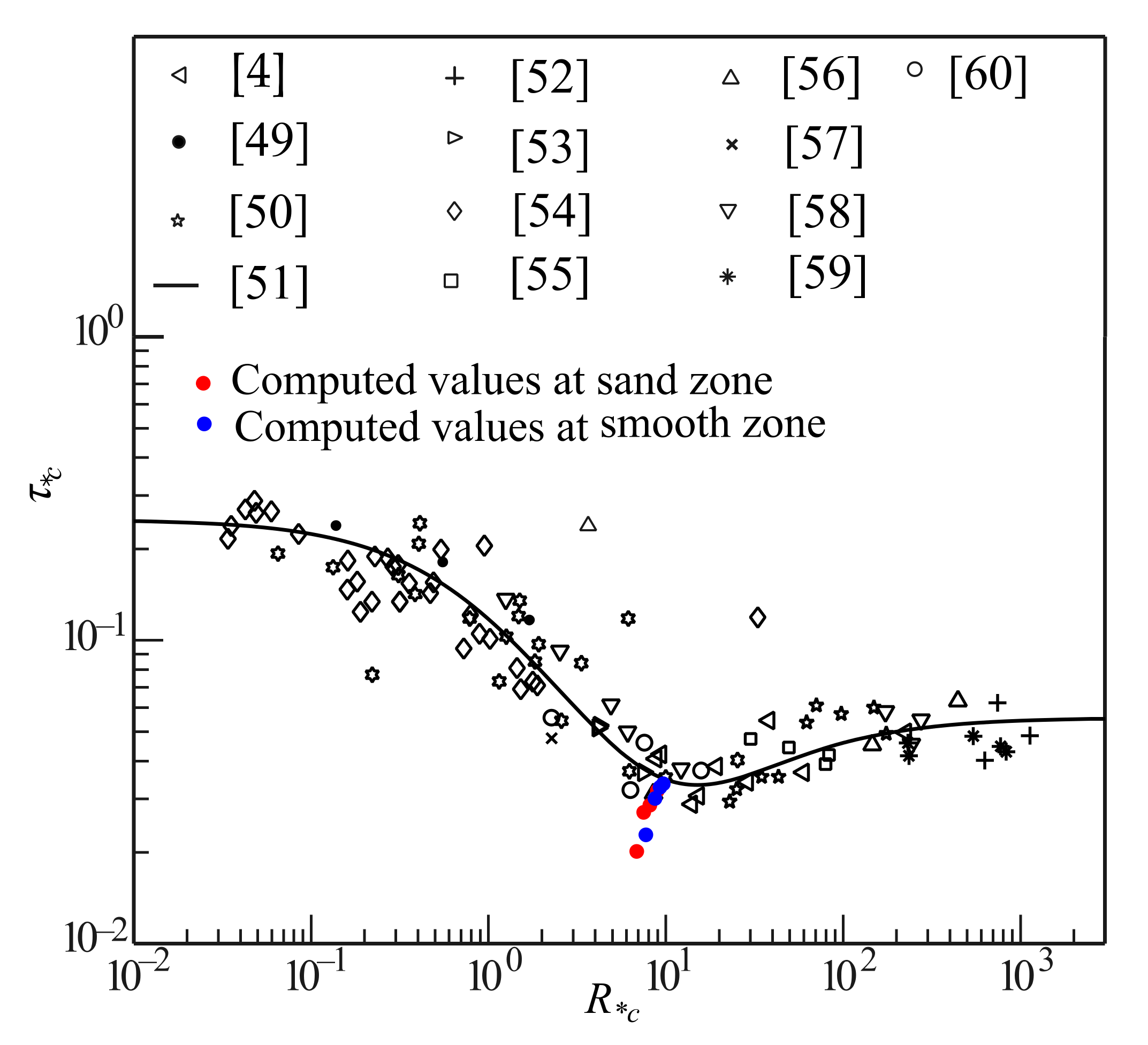
3.5. Determination of Dimensionless Critical Bed Shear Stress
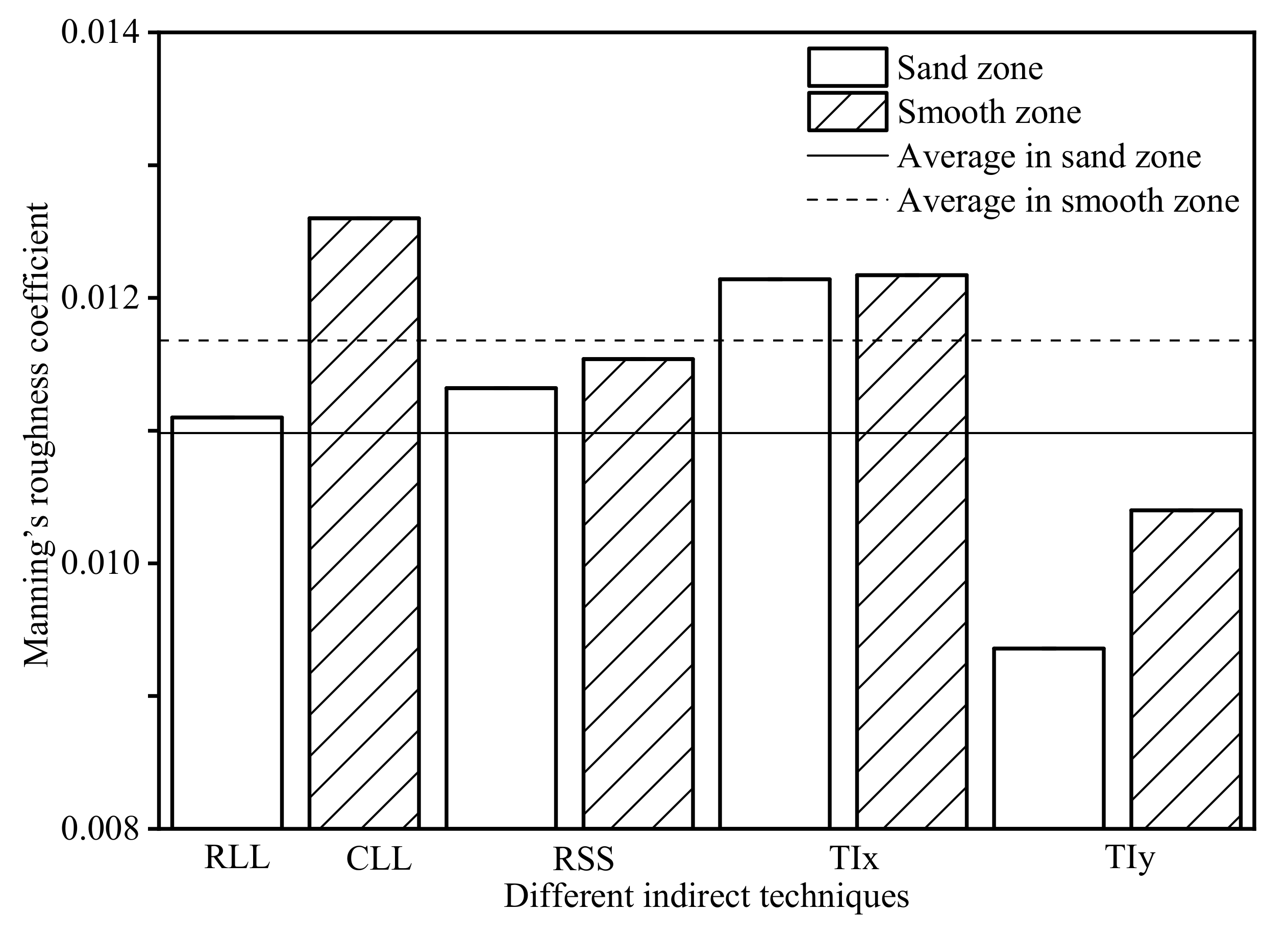
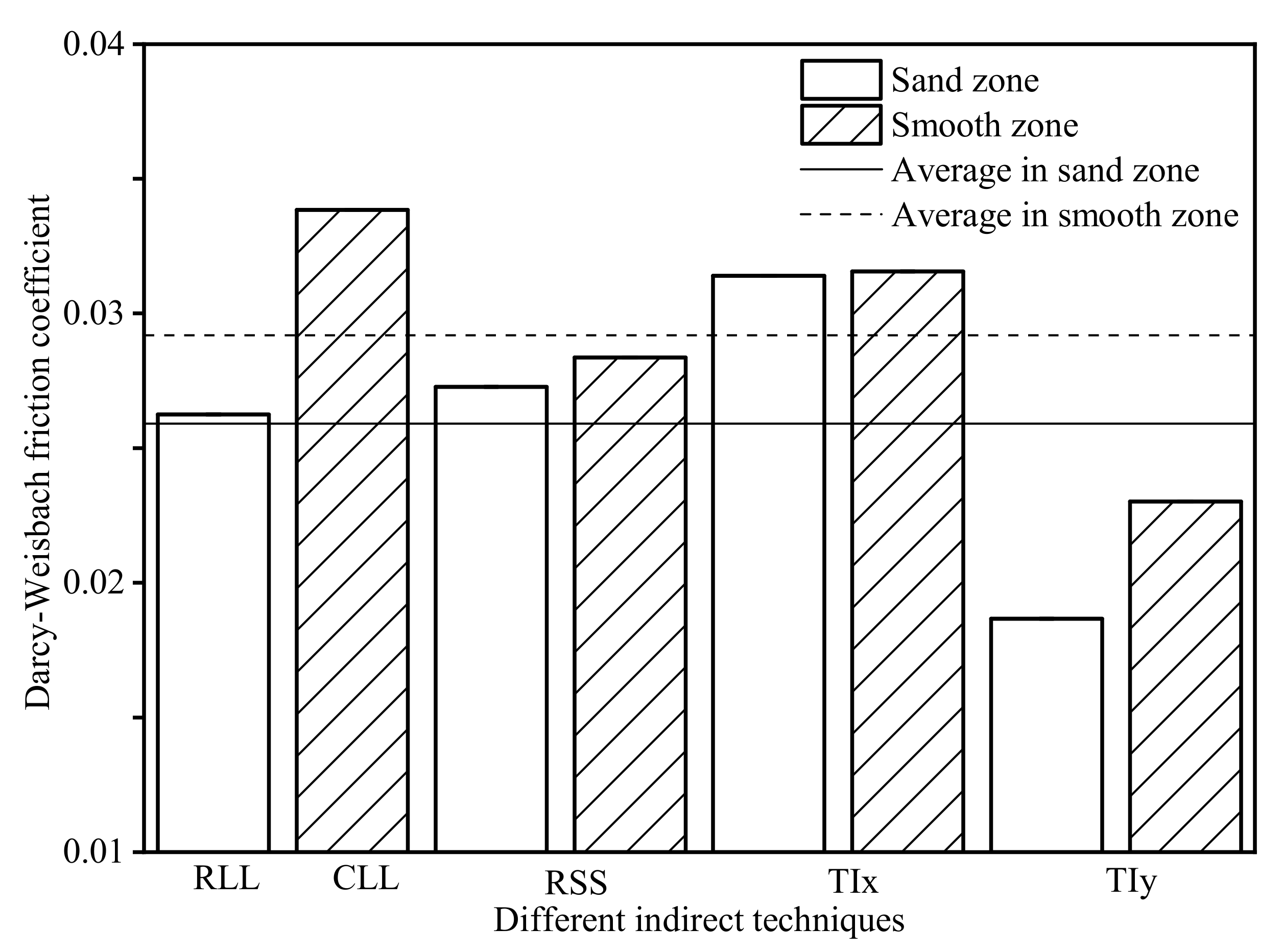
3.6. Determination of Resistance Coefficients
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pähtz, T.; Clark, A.H.; Valyrakis, M.; Durán, O. The Physics of Sediment Transport Initiation, Cessation, and Entrainment Across Aeolian and Fluvial Environments. Rev. Geophys. 2020, 58. [Google Scholar] [CrossRef]
- Safari, M.J.S.; Aksoy, H.; Unal, N.E.; Mohammadi, M. Experimental analysis of sediment incipient motion in rigid boundary open channels. Environ. Fluid Mech. 2017, 17, 1281–1298. [Google Scholar] [CrossRef]
- Vollmer, S.; Kleinhans, M.G. Predicting incipient motion, including the effect of turbulent pressure fluctuations in the bed. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Shields, A. Application of Similarity Principles and Turbulence Research to Bed-Load Movement; Ott, W.P.; Uchelen, J.C., Translators; California Institute of Technology: Pasadena, CA, USA, 1936. [Google Scholar]
- Briaud, J.L.; Ting, F.C.K.; Chen, H.C.; Cao, Y.; Han, S.W.; Kwak, K.W. Erosion Function Apparatus for Scour Rate Predictions. J. Geotech. Geoenviron. Eng. 2001, 127, 105–113. [Google Scholar] [CrossRef]
- Kang, G.-O.; Tsuchida, T.; Hashimoto, R.; Awazu, S.; Kim, Y.-S. Erosion resistance capacity of dredged marine clay treated with basic oxygen furnace slag. Soils Found. 2020. [Google Scholar] [CrossRef]
- Flack, K.A.; Schultz, M.P. Roughness effects on wall-bounded turbulent flows. Phys. Fluids 2014. [Google Scholar] [CrossRef] [Green Version]
- Cheng, N.-S.; Chiew, Y.-M. Incipient sediment motion with upward seepage. J. Hydraul. Res. 1999, 37, 665–681. [Google Scholar] [CrossRef]
- Southard, J.B.; Boguchwal, L.A. Bed configuration in steady unidirectional water flows; Part 2, Synthesis of flume data. J. Sediment. Res. 1990, 60, 658–679. [Google Scholar] [CrossRef]
- Costello, W.R.; Southard, J.B. Flume Experiments on Lower-Flow-Regime Bed Forms in Coarse Sand. SEPM J. Sediment. Res. 1981, 51, 849–864. [Google Scholar]
- Rees, A.I. Some Flume Experiments with A Fine Silt. Sedimentology 1966, 6, 209–240. [Google Scholar] [CrossRef]
- Ljunggren, P.; Sundborg, Ä. Some Aspects on Fluvial Sediments and Fluvial Morphology I. General Views and Graphic Methods. Geogr. Ann. Ser. A Phys. Geogr. 1967, 49, 333. [Google Scholar]
- Ashley, G.M. Classification of large-scale subaqueous bedforms; a new look at an old problem. J. Sediment. Res. 1990, 60, 160–172. [Google Scholar]
- Dyer, K.R. Coastal and Estuarine Sediment Dynamics; Wiley: Chichester, UK, 1986. [Google Scholar]
- Whitehouse, R.J.; Hardisty, J. Experimental assessment of two theories for the effect of bedslope on the threshold of bedload transport. Mar. Geol. 1988, 79, 135–139. [Google Scholar] [CrossRef]
- Chiew, Y.-M.; Parker, G. Incipient sediment motion on non-horizontal slopes. J. Hydraul. Res. 1994, 32, 649–660. [Google Scholar] [CrossRef]
- Parker, G.; Klingeman, P.C.; McLean, D.G. Bedload and size distribution in paved gravel-bed streams. J. Hydraul. Div. ASCE 1982. [Google Scholar] [CrossRef]
- Wilcock, P.R.; Southard, J.B. Experimental study of incipient motion in mixed-size sediment. Water Resour. Res. 1988, 24, 1137–1151. [Google Scholar] [CrossRef] [Green Version]
- Kuhnle, R.A. Incipient Motion of Sand-Gravel Sediment Mixtures. J. Hydraul. Eng. 1993, 119, 1400–1415. [Google Scholar] [CrossRef]
- Wilcock, P.R. Estimating Local Bed Shear Stress from Velocity Observations. Water Resour. Res. 1996, 32, 3361–3366. [Google Scholar] [CrossRef]
- Wei, T.; Schmidt, R.; McMurtry, P. Comment on the Clauser chart method for determining the friction velocity. Exp. Fluids 2005, 38, 695–699. [Google Scholar] [CrossRef]
- Kim, S.-C.; Friedrichs, C.T.; Maa, J.P.-Y.; Wright, L.D. Estimating Bottom Stress in Tidal Boundary Layer from Acoustic Doppler Velocimeter Data. J. Hydraul. Eng. 2000, 126, 399–406. [Google Scholar] [CrossRef] [Green Version]
- Nikora, V.; Goring, D. Flow turbulence over fixed and weakly mobile gravel beds. J. Hydraul. Eng. 2000. [Google Scholar] [CrossRef]
- Song, T.; Chiew, Y.M. Turbulence Measurement in Nonuniform Open-Channel Flow Using Acoustic Doppler Velocimeter (ADV). J. Eng. Mech. 2001, 127, 219–232. [Google Scholar] [CrossRef]
- Strom, K.B.; Papanicolaou, A.N. ADV Measurements around a Cluster Microform in a Shallow Mountain Stream. J. Hydraul. Eng. 2007, 133, 1379–1389. [Google Scholar] [CrossRef]
- Tominaga, A.; Sakaki, T. Evaluation of bed shear stress from velocity measurements in gravel-bed river with local non-uniformity. In Proceedings of the River Flow 2010: International Conference on Fluvial Hydraulics, Braunschweig, Germany, 8–10 September 2010; Bundesanstalt für Wasserbau: Karlsruhe, Germany, 2010. [Google Scholar]
- Al Faruque, M.A.; Balachandar, R. Seepage effects on turbulence characteristics in an open channel flow. Can. J. Civ. Eng. 2011, 38, 785–799. [Google Scholar]
- Balachandar, R.; Patel, V.C. Flow over a fixed rough dune. Can. J. Civ. Eng. 2008, 35, 511–520. [Google Scholar] [CrossRef]
- Cheng, N.S. Seepage effect on open-channel flow and incipient sediment motion. Ph.D. Thesis, Nanyang Technological University, Singapore, 1997. [Google Scholar]
- Hanmaiahgari, P.R.; Roussinova, V.; Balachandar, R. Turbulence characteristics of flow in an open channel with temporally varying mobile bedforms. J. Hydrol. Hydromech. 2017, 65, 35–48. [Google Scholar] [CrossRef] [Green Version]
- Robert, A.; Uhlman, W. An experimental study on the ripple-dune transition. Earth Surf. Process Landf. 2001. [Google Scholar] [CrossRef]
- Jewel, A.; Fujisawa, K.; Murakami, A. Effect of seepage flow on incipient motion of sand particles in a bed subjected to surface flow. J. Hydrol. 2019, 579. [Google Scholar] [CrossRef]
- Smart, G.M. Turbulent Velocity Profiles and Boundary Shear in Gravel Bed Rivers. J. Hydraul. Eng. 1999, 125, 106–116. [Google Scholar] [CrossRef]
- Roussinova, V.; Biswas, N.; Balachandar, R. Revisiting turbulence in smooth uniform open channel flow. J. Hydraul. Res. 2008, 46 (Suppl. 1), 36–48. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R.V. Characteristics of Loose Rough Boundary Streams at Near-Threshold. J. Hydraul. Eng. 2007, 133, 288–304. [Google Scholar] [CrossRef]
- Zanoun, E.-S.; Durst, F.; Nagib, H. Evaluating the law of the wall in two-dimensional fully developed turbulent channel flows. Phys. Fluids 2003, 15, 3079. [Google Scholar] [CrossRef]
- Cheng, N.S. Power-law index for velocity profiles in open channel flows. Adv. Water Resour. 2007, 30, 1775–1784. [Google Scholar] [CrossRef]
- Schultz, M.P.; Flack, K.A. The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 2007. [Google Scholar] [CrossRef] [Green Version]
- Nezu, I.; Nakagawa, H. (Eds.) Turbulence in Open-Channel Flows; IAHR Monographs; CRC Press/Balkema: Boca Raton, FL, USA, 1993. [Google Scholar]
- Fransson, J.H.M.; Matsubara, M.; Alfredsson, P.H. Transition induced by free-stream turbulence. J. Fluid Mech. 2005, 527, 1–25. [Google Scholar] [CrossRef]
- Hollingsworth, D.K.; Bourgogne, H.-A. The development of a turbulent boundary layer in high free-stream turbulence produced by a two-stream mixing layer. Exp. Therm. Fluid Sci. 1995, 11, 210–222. [Google Scholar] [CrossRef]
- Scheichl, B.; Kluwick, A.; Smith, F.T. Break-away separation for high turbulence intensity and large Reynolds number. J. Fluid Mech. 2011, 670, 260–300. [Google Scholar] [CrossRef] [Green Version]
- Degraaff, D.B.; Eaton, J.K. Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 2000, 422, 319–346. [Google Scholar] [CrossRef]
- Miller, M.C.; Mccave, I.N.; Komar, P.D. Threshold of sediment motion under unidirectional currents. Sedimentology 1977, 24, 507–527. [Google Scholar] [CrossRef]
- Koster, E. Transverse Ribs: Their Characteristics, Origin and Paleohydraulic Significance. In Fluvial Sedimentology; Memoir 5; Miall, A.D., Ed.; Canadian Society of Petroleum Geologists: Calgary, AL, CA, 1978; pp. 161–186. [Google Scholar]
- Biron, P.M.; Robson, C.; Lapointe, M.F.; Gaskin, S.J. Comparing different methods of bed shear stress estimates in simple and complex flow fields. Earth Surf. Process Landf. 2004. [Google Scholar] [CrossRef]
- Julien, P.Y. Erosion and Sedimentation; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Southard, J. Introduction to Fluid Motions and Sediment Transport; Massachusetts Institute of Technology: Cambridge, MA, USA, 2019. [Google Scholar]
- Mantz, P.A. Incipient transport of fine grains and flakes by fluids-extended Shields diagram. J. Hydraul. Div. 1977. [Google Scholar] [CrossRef]
- Yalin, M.S.; Karahan, E. Inception of sediment transport. J. Hydraul. Div. 1979. [Google Scholar] [CrossRef]
- Guo, J. Empirical model for Shields diagram and its applications. J. Hydraul. Eng. 2020, 146. [Google Scholar] [CrossRef]
- Kramer, H. Modellgeschiebe und Schleppkraft; Preuss. Versuchsanst. f. Wasserbau u. Schiffbau: Berlin, Germany, 1932; [In German]. [Google Scholar]
- Kramer, H. Sand mixtures and sand movement in fluvial models. Trans. Am. Soc. Civ. Eng. 1935, 100, 798–838. [Google Scholar] [CrossRef]
- Neill, C.R. Mean velocity criterion for scour of course uniform bed material. In Proceedings of the 12th Congress of the Int. Association for Hydraulic Research, 46–54 Fort Collins, CO, USA, 11–14 September 1967; International Association for Hydraulic Research: Madrid, Spain, 1967; Volume 3. [Google Scholar]
- USWES. Study of Riverbed Material and Their Use with Special Reference to the Lower Mississippi River; Mississippi River Commission Print: St. Louis, MO, USA, 1935. [Google Scholar]
- White, C.M. The equilibrium of grains on the bed of a stream. Proc. R. Soc. London 1940, 174, 322–338. [Google Scholar]
- Casey, H.J. About Bedload Movement. Ph.D. Thesis, Prussian Laboratory of Hydraulics and Shipbuilding, Technischen Hochschule, Berlin, Germany, 1935. [Google Scholar]
- Gilbert, G.K. The Transportaton of Debris by Running Water; US Government Printing Office: Washington, DC, USA, 1914. [Google Scholar]
- Grass, A. Initial Instability of Fine Bed Sand. J. Hydraul. Div. 1970. [Google Scholar] [CrossRef]
- Karahan, E. Initiation of motion for uniform and nonuniform materials. Ph.D. Thesis, Dept. of Civil Engineering, Istanbul Technical University, Istanbul, Turkey, 1975. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill Book Co: New York, NY, USA, 1959. [Google Scholar]




| Flow Rate, Q lit/min | Reynolds Number, ReQ | Froude Number, Fr | Sediment Transport Rate, m3/s/m |
|---|---|---|---|
| 79 | 15,419 | 0.37600 | 1.188 × 10−8 |
| 80 | 16,028 | 0.38076 | 3.053 × 10−8 |
| 81 | 15,395 | 0.38552 | 3.296 × 10−8 |
| 83 | 16,199 | 0.39504 | 2.768 × 10−8 |
| 84 | 15,965 | 0.39980 | 4.551 × 10−8 |
| 86 | 16,346 | 0.40932 | 6.506 × 10−8 |
| 88 | 16,280 | 0.41883 | 2.229 × 10−7 |
| 89 | 16,916 | 0.42359 | 2.341 × 10−7 |
| Streamwise Flow Velocity (m/s) at y = 0.1h | Streamwise Flow Velocity (m/s) at y = 0.3h | Streamwise Flow Velocity (m/s) at y = 0.5h | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Q | Sand Zone | Smooth Zone | % Increase | Sand Zone | Smooth Zone | % Increase | Sand Zone | Smooth Zone | % Increase |
| 79 | 0.26551 | 0.27041 | 1.81262 | 0.31508 | 0.31384 | −0.39417 | 0.33174 | 0.33291 | 0.35159 |
| 80 | 0.26749 | 0.26908 | 0.59237 | 0.32124 | 0.32613 | 1.49949 | 0.34062 | 0.34212 | 0.43965 |
| 81 | 0.27569 | 0.28101 | 1.89063 | 0.32900 | 0.33291 | 1.17555 | 0.34084 | 0.34540 | 1.32219 |
| 83 | 0.28509 | 0.28829 | 1.11192 | 0.32967 | 0.33512 | 1.62635 | 0.34966 | 0.35272 | 0.86715 |
| 84 | 0.28174 | 0.28187 | 0.04605 | 0.33515 | 0.34073 | 1.63793 | 0.34877 | 0.35135 | 0.73566 |
| 86 | 0.28345 | 0.28691 | 1.20682 | 0.33945 | 0.34327 | 1.11349 | 0.35914 | 0.36232 | 0.87720 |
| 88 | 0.28540 | 0.29273 | 2.50730 | 0.34715 | 0.35344 | 1.77765 | 0.36852 | 0.37292 | 1.17770 |
| 89 | 0.30106 | 0.30128 | 0.07154 | 0.35669 | 0.35916 | 0.68581 | 0.36971 | 0.37168 | 0.53083 |
| Average | 0.28068 | 0.28395 | 0.33418 | 0.33807 | 0.35112 | 0.35393 | |||
| St. dev. | 0.01058 | 0.01014 | 0.01267 | 0.01360 | 0.01281 | 0.01327 | |||
| Zone | Q (lit/min) | Shear Velocity (m/s) | Bed Shear Stress (pa) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sand zone | 79 | 0.01583 | 0.01703 | 0.01701 | 0.01586 | 0.25059 | 0.29002 | 0.28934 | 0.25154 |
| 80 | 0.01845 | 0.01761 | 0.01755 | 0.01414 | 0.34040 | 0.31011 | 0.30800 | 0.19994 | |
| 81 | 0.01566 | 0.01638 | 0.01745 | 0.01477 | 0.24524 | 0.26830 | 0.30450 | 0.21815 | |
| 83 | 0.01652 | 0.01797 | 0.01812 | 0.01521 | 0.27291 | 0.32292 | 0.32833 | 0.23134 | |
| 84 | 0.01919 | 0.01809 | 0.01842 | 0.01393 | 0.36826 | 0.32725 | 0.33930 | 0.19404 | |
| 86 | 0.02034 | 0.01662 | 0.01871 | 0.01523 | 0.41372 | 0.27622 | 0.35006 | 0.23195 | |
| 88 | 0.02206 | 0.01612 | 0.01960 | 0.01501 | 0.48664 | 0.25985 | 0.38416 | 0.22530 | |
| 89 | 0.02214 | 0.01719 | 0.01910 | 0.01536 | 0.49018 | 0.29550 | 0.36481 | 0.23593 | |
| Average | 0.01877 | 0.01713 | 0.01825 | 0.01494 | 0.35849 | 0.29377 | 0.33356 | 0.22353 | |
| St. dev. | 0.00246 | 0.00068 | 0.00083 | 0.00060 | 0.09289 | 0.02335 | 0.03025 | 0.01778 | |
| Smooth zone | 79 | 0.01708 | 0.01703 | 0.01755 | 0.01446 | 0.29173 | 0.29002 | 0.30800 | 0.20909 |
| 80 | 0.01781 | 0.01680 | 0.01687 | 0.01545 | 0.31720 | 0.28224 | 0.28460 | 0.23870 | |
| 81 | 0.01802 | 0.01553 | 0.01667 | 0.01542 | 0.32472 | 0.24118 | 0.27789 | 0.23778 | |
| 83 | 0.01815 | 0.01590 | 0.01767 | 0.01531 | 0.32942 | 0.25281 | 0.31223 | 0.23440 | |
| 84 | 0.01831 | 0.01531 | 0.01787 | 0.01526 | 0.33526 | 0.23440 | 0.31934 | 0.23287 | |
| 86 | 0.01853 | 0.01810 | 0.01850 | 0.01617 | 0.34336 | 0.32761 | 0.34225 | 0.26147 | |
| 88 | 0.01872 | 0.01816 | 0.01950 | 0.01488 | 0.35044 | 0.32979 | 0.38025 | 0.22141 | |
| 89 | 0.01878 | 0.01830 | 0.01970 | 0.01630 | 0.35269 | 0.33489 | 0.38809 | 0.26569 | |
| Average | 0.01818 | 0.01689 | 0.01804 | 0.01541 | 0.33060 | 0.28662 | 0.32658 | 0.23768 | |
| St. dev. | 0.00052 | 0.00114 | 0.00105 | 0.00057 | 0.01868 | 0.03847 | 0.03816 | 0.01756 | |
| Zone | Critical Shear Velocity (m/s) | ||||
|---|---|---|---|---|---|
| Sand zone | 0.01599 | - | 0.01630 | 0.01749 | 0.01337 |
| Smooth zone | - | 0.01816 | 0.01662 | 0.01753 | 0.01497 |
| Zone | Dimensionless Critical Bed Shear Stress | ||||
|---|---|---|---|---|---|
| Sand zone | 0.02740 | - | 0.02847 | 0.03277 | 0.01949 |
| Smooth zone | - | 0.03533 | 0.02960 | 0.03294 | 0.02403 |
| Zone | Manning Roughness Coefficient | ||||
|---|---|---|---|---|---|
| Sand zone | 0.01110 | - | 0.01132 | 0.01214 | 0.00936 |
| Smooth zone | - | 0.01260 | 0.01154 | 0.01217 | 0.01040 |
| Friction Coefficient for Darcy–Weisbach Formula | |||||
| Sand zone | 0.02625 | - | 0.02727 | 0.03139 | 0.01867 |
| Smooth zone | - | 0.03384 | 0.02836 | 0.03155 | 0.02302 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jewel, A.; Fujisawa, K.; Murakami, A. Evaluation of Incipient Motion of Sand Particles by Different Indirect Methods in Erosion Function Apparatus. Water 2021, 13, 1118. https://doi.org/10.3390/w13081118
Jewel A, Fujisawa K, Murakami A. Evaluation of Incipient Motion of Sand Particles by Different Indirect Methods in Erosion Function Apparatus. Water. 2021; 13(8):1118. https://doi.org/10.3390/w13081118
Chicago/Turabian StyleJewel, Arif, Kazunori Fujisawa, and Akira Murakami. 2021. "Evaluation of Incipient Motion of Sand Particles by Different Indirect Methods in Erosion Function Apparatus" Water 13, no. 8: 1118. https://doi.org/10.3390/w13081118