Surface Water Temperature Predictions at a Mid-Latitude Reservoir under Long-Term Climate Change Impacts Using a Deep Neural Network Coupled with a Transfer Learning Approach
Abstract
:1. Introduction
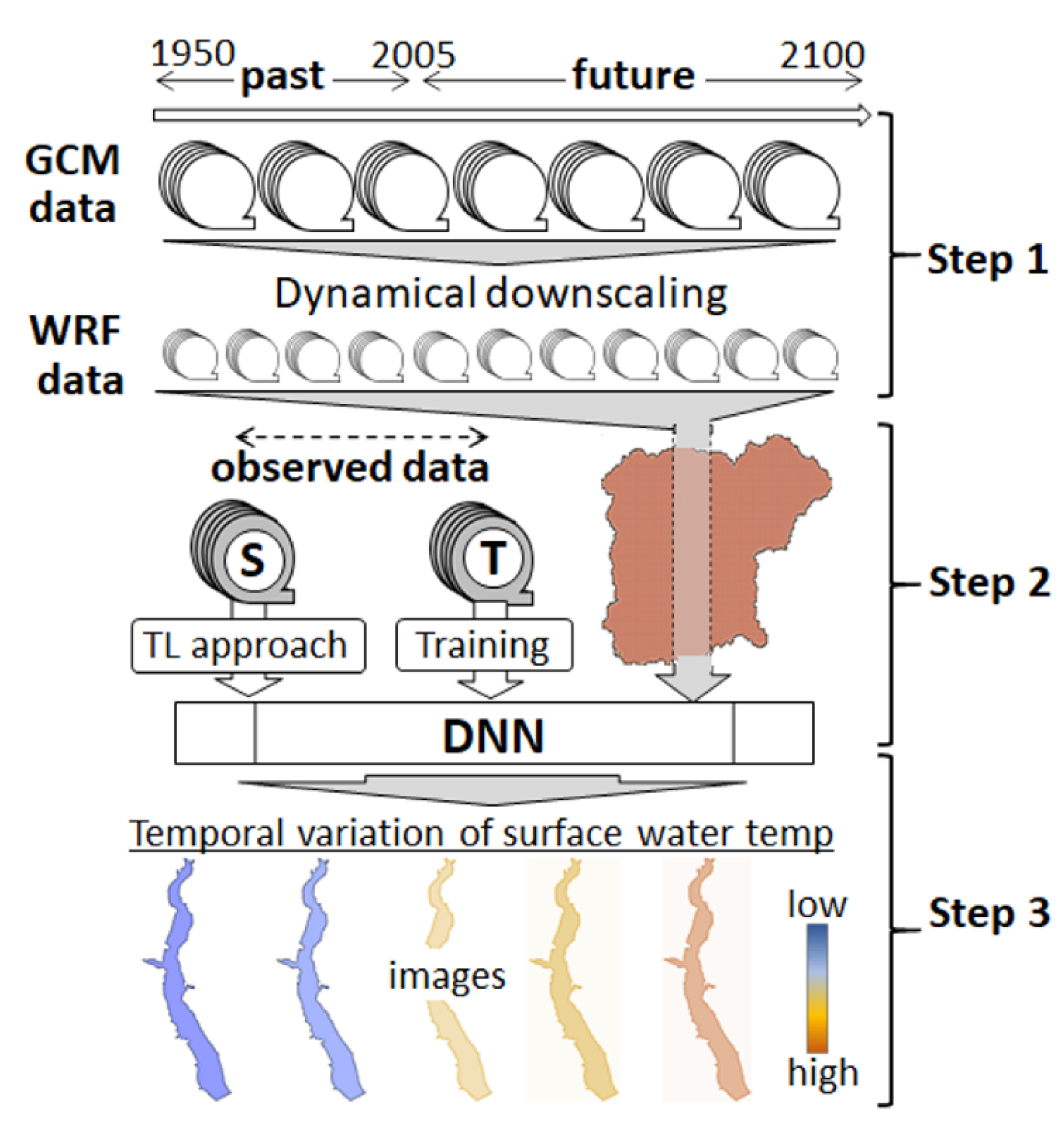
2. Materials and Methods
2.1. Data Acquisition
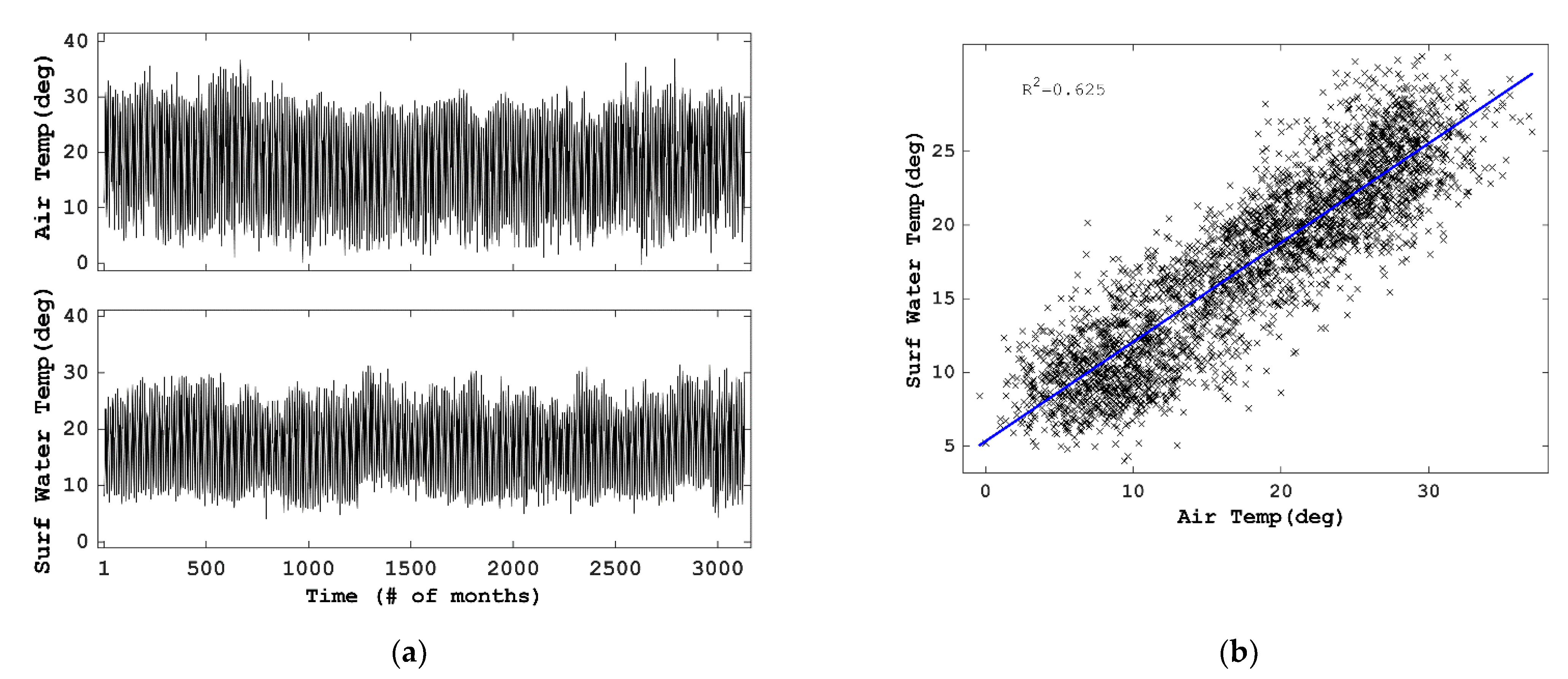
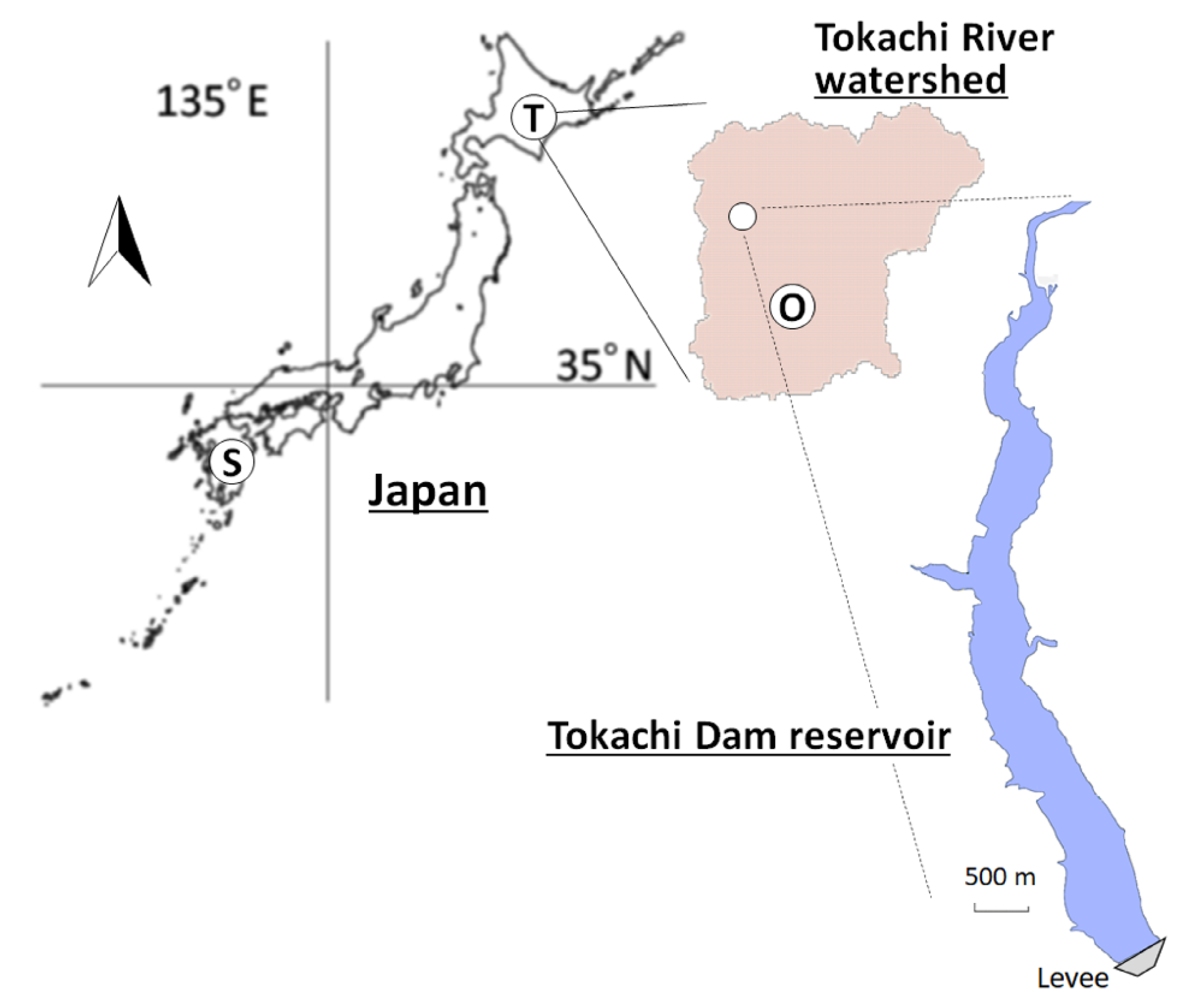
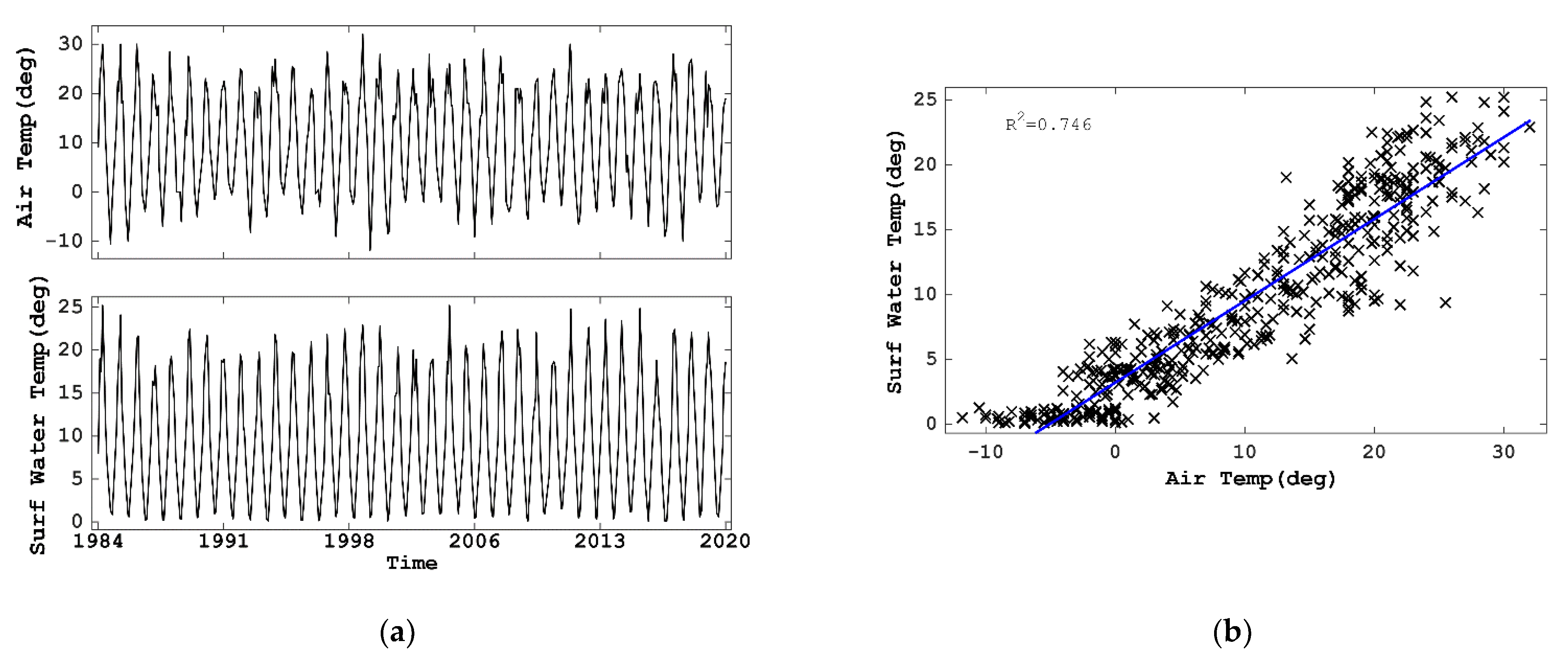
2.1.1. Target Site and Observed Data
2.1.2. General Circulation Model and Weather Research and Forecast Model Data
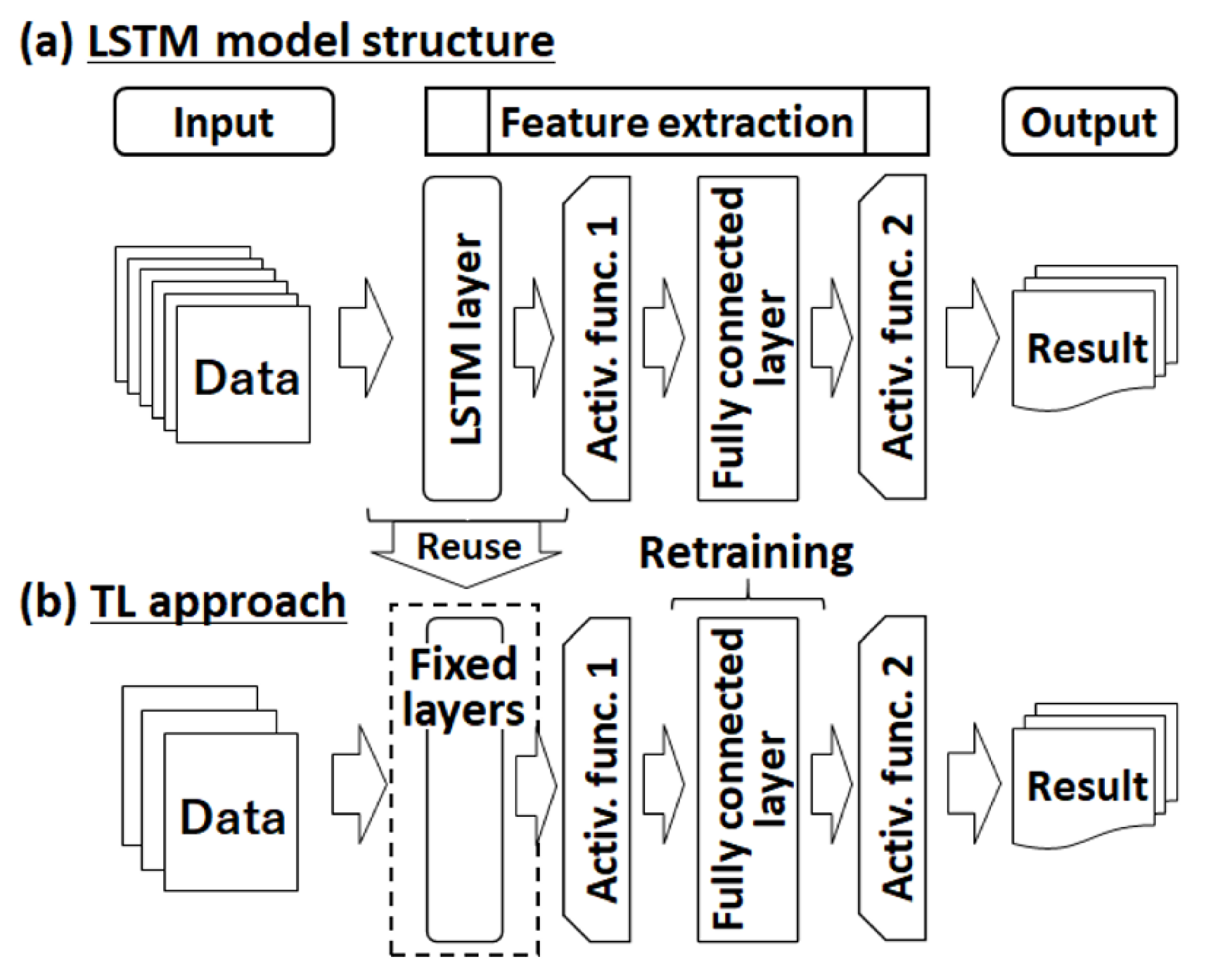
2.2. Long Short-Term Memory Model
2.3. Transfer Learning (TL) Approach
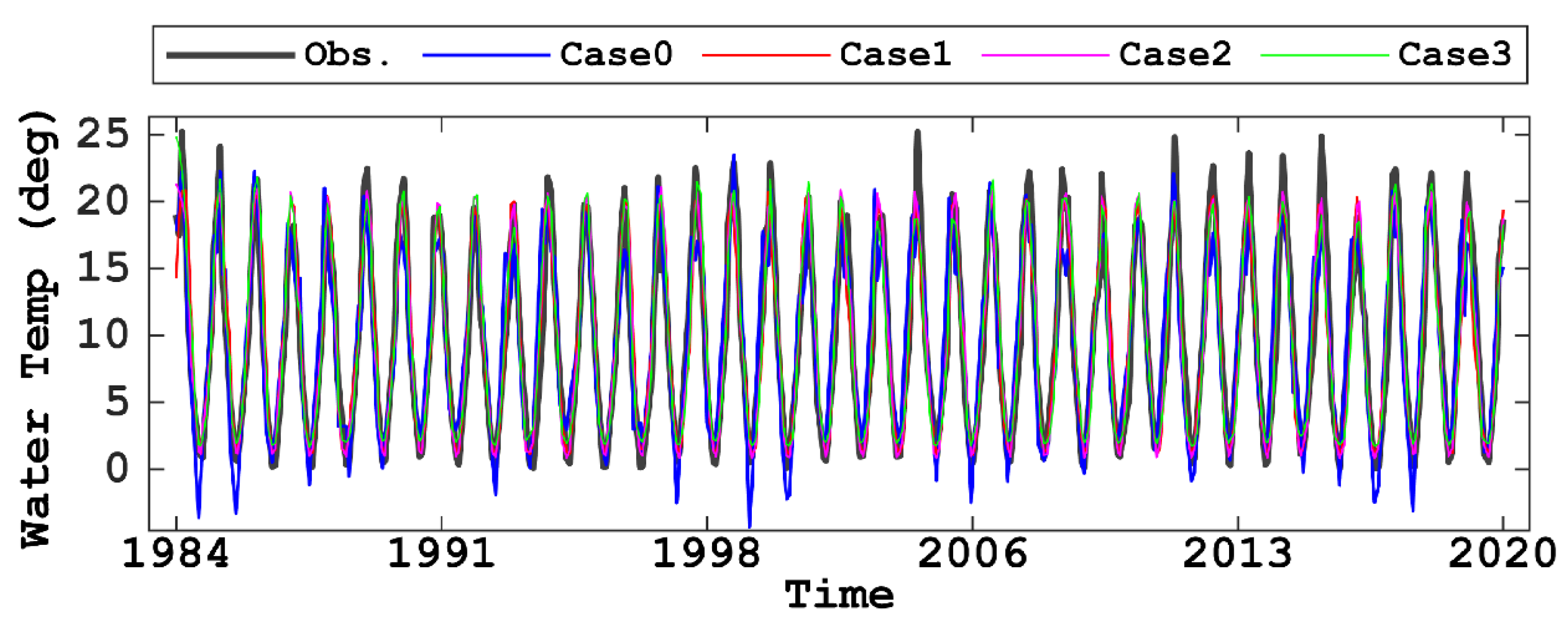
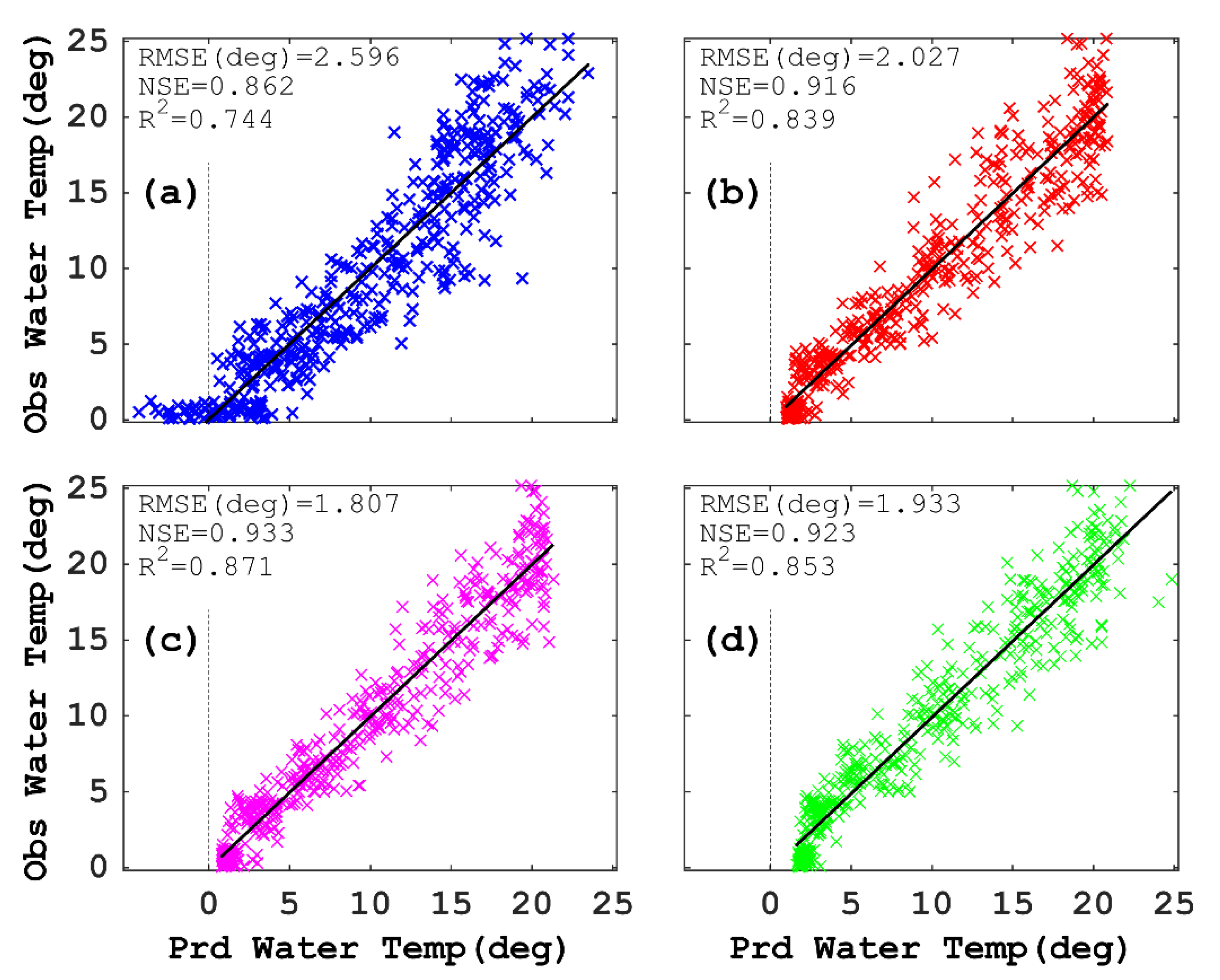
2.4. Evaluation
2.5. Procedures and Setups of the Computation
- air temperature strongly affects the surface water temperature;
- the humid subarctic climate in the Tokachi River watershed (the target) changes into a humid subtropical climate at Kyushu (the source). Note that the TL approach possibly adjusts the source climate to the target climate, although past air temperature at the source was significantly higher than that at the target;
- the effect of water level variations is involved in the variations of surface water temperature;
- no sediment accumulation affects the topographical aspects of the reservoir;
- no geological changes occur in the surrounding environments;
- the effect of the presence or absence of ice cover is included in the values of the surface water temperature;
- the effect of the air−water interaction on surface water temperature is homogeneous among lakes.
3. Results
4. Discussion
5. Conclusions
- The LSTM model that was validated with the observed data achieved accurate reproducibility calculations with R2 > 0.8 and NSE > 0.9. In particular, Case 2 with two input datasets, i.e., air temperature and difference in air temperature, was marginally better than the other cases.
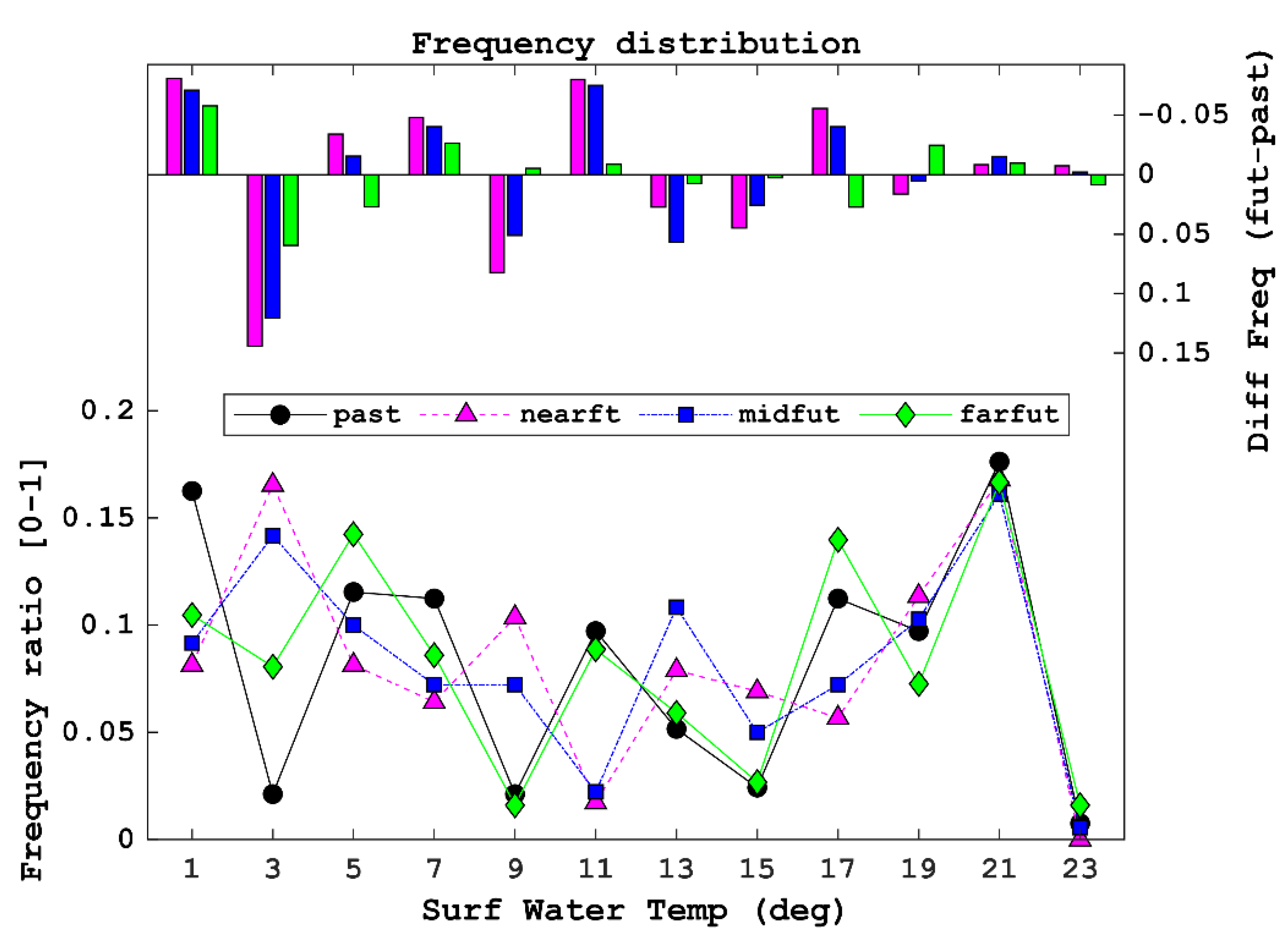
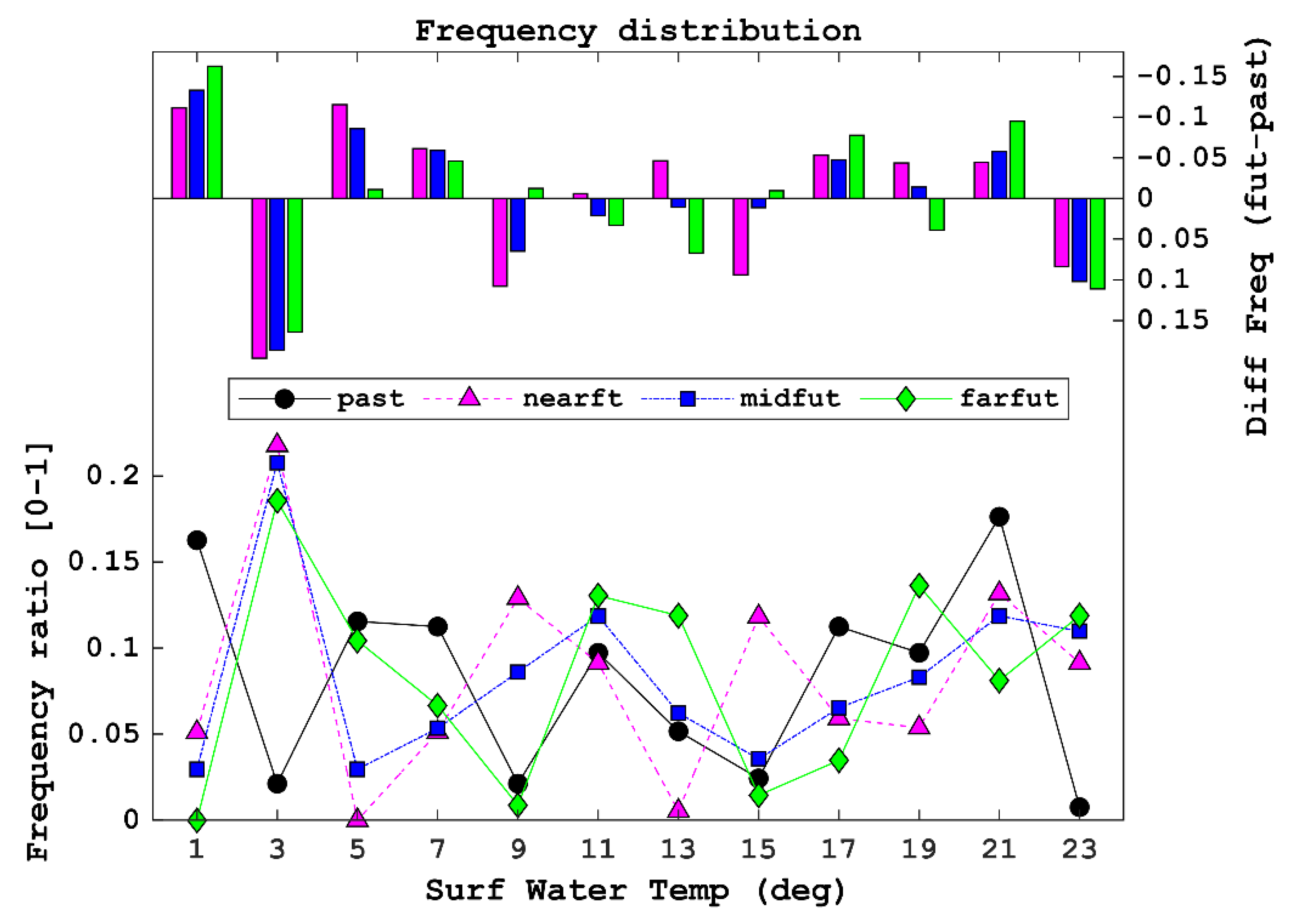
- Past and future predictions with locally downscaled data showed that the LSTM model with the TL approach (Case 3 model) was more realistic for future prediction than that without the TL approach based on the difference between past and future air temperatures. The Case 3 model suggested that the frequency ratios with respect to the predicted surface water temperature were increased in the highest range of water temperature and decreased in the lowest range, because the model predicted higher water temperatures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Name | Location | Total Capacity (m3) | Surface Area (km2) | Catchment Area (km2) |
|---|---|---|---|---|
| Ayakita | 32.0975° N, 131.1422° E | 21,300,000 | 0.82 | 149.3 |
| Ayanann | 32.0578° N, 131.1217° E | 38,000,000 | 1.36 | 101.0 |
| Dokawa | 32.3553° N, 131.3453° E | 33,900,000 | 1.54 | 143.0 |
| Hikawa | 32.5714° N, 130.7865° E | 6,300,000 | 0.35 | 57.4 |
| Hirowatari | 31.7167° N, 131.2675° E | 6,400,000 | 0.38 | 34.4 |
| Houri | 32.7158° N, 131.5736° E | 5,774,000 | 0.28 | 45.2 |
| Ichifusa | 32.3200° N, 131.0128° E | 40,200,000 | 1.65 | 157.8 |
| Iwase | 31.9428° N, 131.1403° E | 57,000,000 | 4.13 | 354.0 |
| Kawabe | 31.4450° N, 130.4456° E | 2,920,000 | 0.23 | 30.2 |
| Matsuo | 32.2839° N, 131.3714° E | 45,202,000 | 1.95 | 304.1 |
| Midorikawa | 32.6273° N, 130.9089° E | 46,000,000 | 1.81 | 359.0 |
| Hase-miyazaki | 32.1458° N, 131.3403° E | 2,250,000 | 0.14 | 11.8 |
| Nichinann | 31.6369° N, 131.2758° E | 6,000,000 | 0.41 | 59.2 |
| Okita | 32.5506° N, 131.6192° E | 2,750,000 | 0.27 | 8.8 |
| Tachibana | 32.1322° N, 131.2700° E | 10,000,000 | 0.29 | 70.5 |
| Tashirobae | 32.1367° N, 131.1197° E | 19,270,000 | 1.02 | 131.5 |
| Turuta (old) | 31.9853° N, 130.4958° E | 123,000,000 | 3.61 | 805.0 |
| Urita | 31.9267° N, 131.3086° E | 720,000 | 0.07 | 4.4 |
References
- Intergovernmental Panel on Climate Change (IPCC) Climate Change 2014: Synthesis report. In Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core writing team; Pachauri, R.K.; Meyer, L.A. (Eds.) IPCC: Geneva, Switzerland, 2014; 151p. [Google Scholar]
- Hoshino, T.; Yamada, T.J. Analysis of annual maximum precipitation over first-class river basins in Japan using a large-ensemble dataset(d4PDF). J. JSCE Hydraul. Engr. 2018, 74, I_187–I_192. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, N.; Kiri, H.; Kanada, S.; Kitagawa, I.; Yoshinaga, I.; Aiki, H. Flood simulations in mid-latitude agricultural land using regional current and future extreme weathers. Water 2019, 11, 2421. [Google Scholar] [CrossRef] [Green Version]
- Umeda, M.; Ochiai, Y. Assessment of Water Quality Changes in Reservoirs in Japan Affected by Global Warming. J. Japan Soc. Civil Eng. 2012, 68, I_127–I_135. (In Japanese) [Google Scholar] [CrossRef]
- Ito, U.; Oda, S.; Momii, K. Global warming and heat-feature change in Lake Ikeda. In Proceedings of the Annual Meeting of Japan Society of Hydrology and Water Resources, Miyazaki, Japan, 25–28 September 2014. (In Japanese). [Google Scholar]
- Lewis, W.M.; McCutchan, J.H.; Roberson, J. Effects of climatic change on temperature and thermal structure of a mountain reservoir. Water Resour. Res. 2019, 55, 1988–1999. [Google Scholar] [CrossRef]
- Mudelsee, M. Trend analysis of climate time series: A review of methods. Earth Sci. Rev. 2019, 190, 310–322. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Read, J.S.; Jia, X.; Willard, J.; Appling, A.P.; Zwart, J.A.; Oliver, S.K.; Karpatne, A.; Hansen, G.J.; Hanson, P.C.; Watkins, W.; et al. Process-guided deep learning predictions of lake water temperature. Water Resour. Res. 2019, 55, 9173–9190. [Google Scholar] [CrossRef] [Green Version]
- Peterson, K.T.; Sagan, V.; Sloan, J.J. Deep learning-based water quality estimation and anomaly detection using Landsat-8/ Sentinel-2 virtual constellation and cloud computing. GISci. Remote Sens. 2020, 57, 510–525. [Google Scholar] [CrossRef]
- Pratt, L.Y. Discriminability-based transfer between neural networks. In Proceedings of the Conference of the Advances in NIPS 5, Denver, CO, USA, 30 November–3 December 1992; pp. 154–196. [Google Scholar]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- Kimura, N.; Yoshinaga, I.; Sekijima, K.; Azechi, I.; Baba, D. Convolutional neural network coupled with a transfer-learning approach for time-series flood predictions. Water 2020, 12, 96. [Google Scholar] [CrossRef] [Green Version]
- Database of Dams in Japan. Available online: http://mudam.nilim.go.jp/home (accessed on 28 February 2021). (In Japanese).
- Mizuta, R.; Yoshimura, H.; Murakami, H.; Matsueda, M.; Endo, H.; Ose, T.; Kamiguchi, K.; Hosaka, M.; Sugi, M.; Yukimoto, S.; et al. Climate simulations using MRI-AGCM3.2 with 20-km grid. J. Meteor. Soc. Japan 2012, 90A, 233–258. [Google Scholar] [CrossRef] [Green Version]
- Yukimoto, S.; Adachi, Y.; Hosaka, M.; Sskami, T.; Yoshimura, H.; Hirabara, M.; Tanaka, T.Y.; Shindo, E.; Tsujino, H.; Deushi, M.; et al. A new global climate model of the meteorological research institute: MRI-CGCM3—Model description and basic performance. J. Meteor. Soc. Japan 2012, 90A, 23–64. [Google Scholar] [CrossRef] [Green Version]
- Weather Research and Forecasting (WRF) Model. Available online: https://www.mmm.ucar.edu/weather-research-and-forecasting-model (accessed on 28 February 2021).
- Shamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Technical Note: Boulder, CO, USA, 2008. [Google Scholar] [CrossRef]
- Ishida, K.; Tanaka, K. Analysis of future changes in precipitation over watersheds in the Hokkaido region, Japan by means of dynamical downscaling. In Proceedings of the Poster, AGU Fall Meeting 2019, San Francisco, CA, USA, 9–13 December 2019. [Google Scholar]
- Ishida, K.; Tanaka, K.; Hama, T. Sensitivity analysis of convective parameterizations of a regional climate model in higher-resolution domains for long-term precipitation reconstruction. J. Water Clim. Chang. 2020, 11, 1467–1480. [Google Scholar] [CrossRef]
- Past Weather Database. Available online: http://www.data.jma.go.jp/gmd/risk/obsdl/index.php (accessed on 28 February 2021). (In Japanese).
- Hochreiter, P.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kimura, N.; Yoshinaga, I.; Sekijima, K.; Azechi, I.; Kiri, H.; Baba, D. Recurrent neural network predictions for water levels at drainage pumping stations in an agricultural lowland. Japan Agr. Res. Quart. 2021, 55. [Google Scholar] [CrossRef]
- Geisser, S. Predictive Inference: An Introduction, Mono-Graphs on Statistics and Applied Probability 55; Chapman and Hall: NewYork, NY, USA, 1993; 240p. [Google Scholar]
- Teegavarapu, R.S.V. Modeling climate change uncertainties in water resources management models. Environ. Modell. Software 2010, 25, 1261–1265. [Google Scholar] [CrossRef]
- Keras. Available online: http://keras.io/ (accessed on 28 February 2021).
- Jia, X.; Willard, J.; Karpatne, A.; Read, J.S.; Zwart, J.; Steinbach, M.; Kumar, V. Physics guided RNNs for modeling dynamical systems: A case study in simulating lake temperature profiles. In Proceedings of the 2019 SIAM International Conference on Data Mining, Calgary, AB, Canada, 2–4 May 2019; pp. 558–566. [Google Scholar] [CrossRef] [Green Version]
- Modiri-Gharehveran, M.; Etemad-Shahidi, A.; Jabbari, E. Effects of climate change on the thermal regime of a reservoir. Proceedings of the Institution of Civil Engineers. Water Manag. 2014, 167, 601–811. [Google Scholar] [CrossRef] [Green Version]
- Mi, C.; Shatwell, T.; Ma, J.; Xu, Y.; Su, F.; Rinke, K. Ensemble warming projections in Germany’s largest drinking water reservoir and potential adaptation strategies. Sci. Total Environ. 2020, 748, 141366. [Google Scholar] [CrossRef] [PubMed]

| Hyperparameters and Function | Values or Equations | Remarks |
|---|---|---|
| Number of LSTM layers | 1 | |
| Number of nodes | 20 | |
| Past and present time in input | 6 to 0 | Time interval = month |
| Lead time in output | 1 | Time interval = month |
| Batch size | 100 | |
| Number of epochs | 1000 | Retaining the TL approach and has the same number |
| Learning rate | 0.01 | |
| Dropout rate | 0.0 | |
| Reproducibility | None | |
| Optimizer | Stochastic gradient descent (SGD) | |
| Activation function | Sigmoid Hyperbolic tangent | Range from 0 to 1 Range from −1 to 1 |
| Loss function | Sum of squared residuals = | ci = model calculation, oi = observed data, N1 = the number of data |
| Error evaluation functions | RMSE = | Same as above |
| NSE = | Same as above, and <*> = average |
| Name | Model | Input Data | Transfer Learning |
|---|---|---|---|
| Case 0 | Linear regression | Air temperature | No |
| Case 1 | LSTM | Air temperature | No |
| Case 2 | LSTM | Air temperature, difference in air temperature | No |
| Case 3 | LSTM | Same as above | Yes |
| Result | Pre-Trained Model Applied to the Past WRF Data | Pre-Trained Model Applied to the Future WRF data | * Net Heat-Related Factor (Ratio °C) | ||
|---|---|---|---|---|---|
| Near Future | Mid Future | Far Future | |||
| Figure 8 | Case 2 | Case 2 | −0.27 | −0.23 | 0.04 |
| Figure 9 | Case 2 | Case 3 | 0.03 | 0.06 | 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kimura, N.; Ishida, K.; Baba, D. Surface Water Temperature Predictions at a Mid-Latitude Reservoir under Long-Term Climate Change Impacts Using a Deep Neural Network Coupled with a Transfer Learning Approach. Water 2021, 13, 1109. https://doi.org/10.3390/w13081109
Kimura N, Ishida K, Baba D. Surface Water Temperature Predictions at a Mid-Latitude Reservoir under Long-Term Climate Change Impacts Using a Deep Neural Network Coupled with a Transfer Learning Approach. Water. 2021; 13(8):1109. https://doi.org/10.3390/w13081109
Chicago/Turabian StyleKimura, Nobuaki, Kei Ishida, and Daichi Baba. 2021. "Surface Water Temperature Predictions at a Mid-Latitude Reservoir under Long-Term Climate Change Impacts Using a Deep Neural Network Coupled with a Transfer Learning Approach" Water 13, no. 8: 1109. https://doi.org/10.3390/w13081109
APA StyleKimura, N., Ishida, K., & Baba, D. (2021). Surface Water Temperature Predictions at a Mid-Latitude Reservoir under Long-Term Climate Change Impacts Using a Deep Neural Network Coupled with a Transfer Learning Approach. Water, 13(8), 1109. https://doi.org/10.3390/w13081109






