Analytical Models of Velocity, Reynolds Stress and Turbulence Intensity in Ice-Covered Channels
Abstract
:1. Introduction
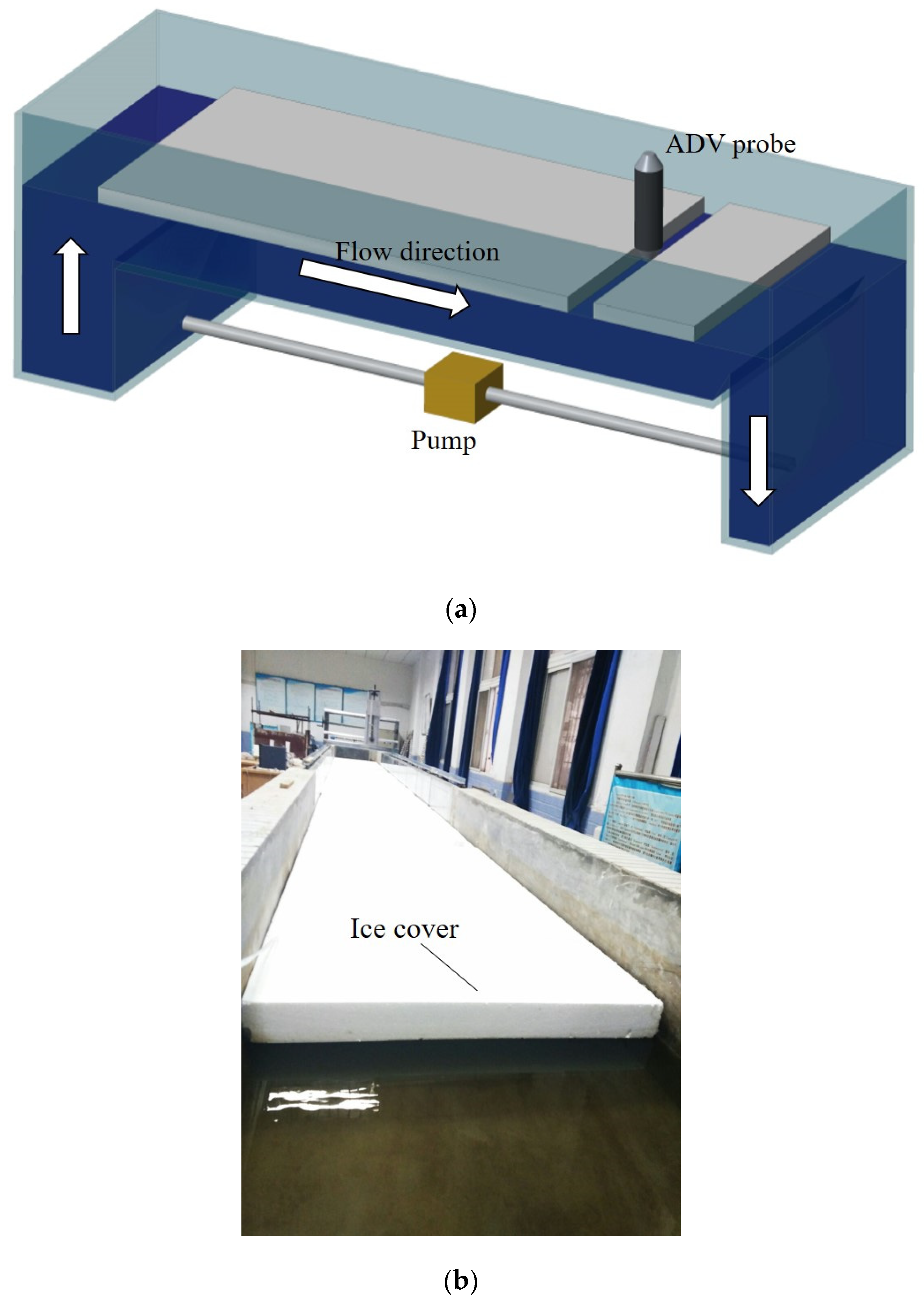
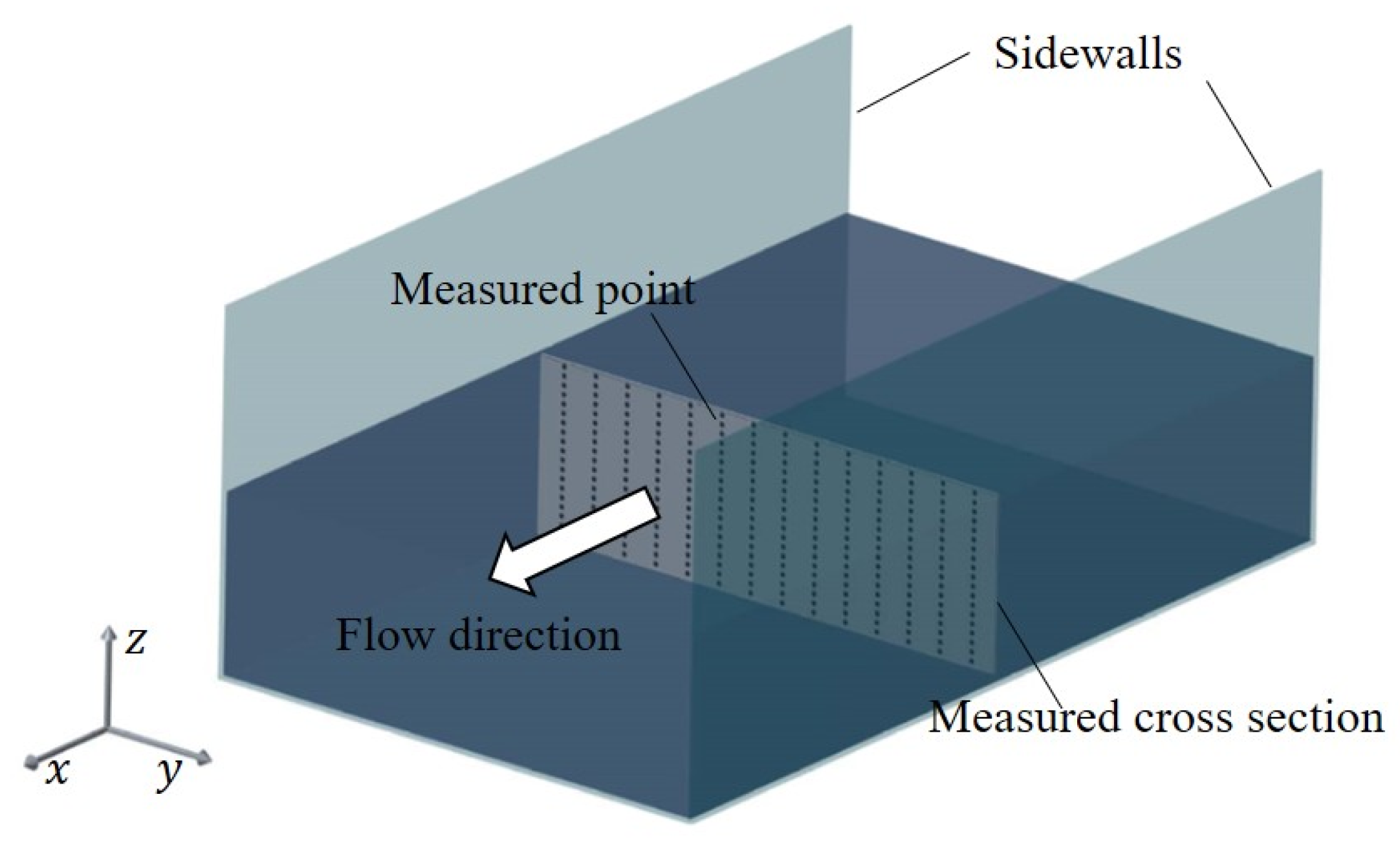
2. Material and Methods
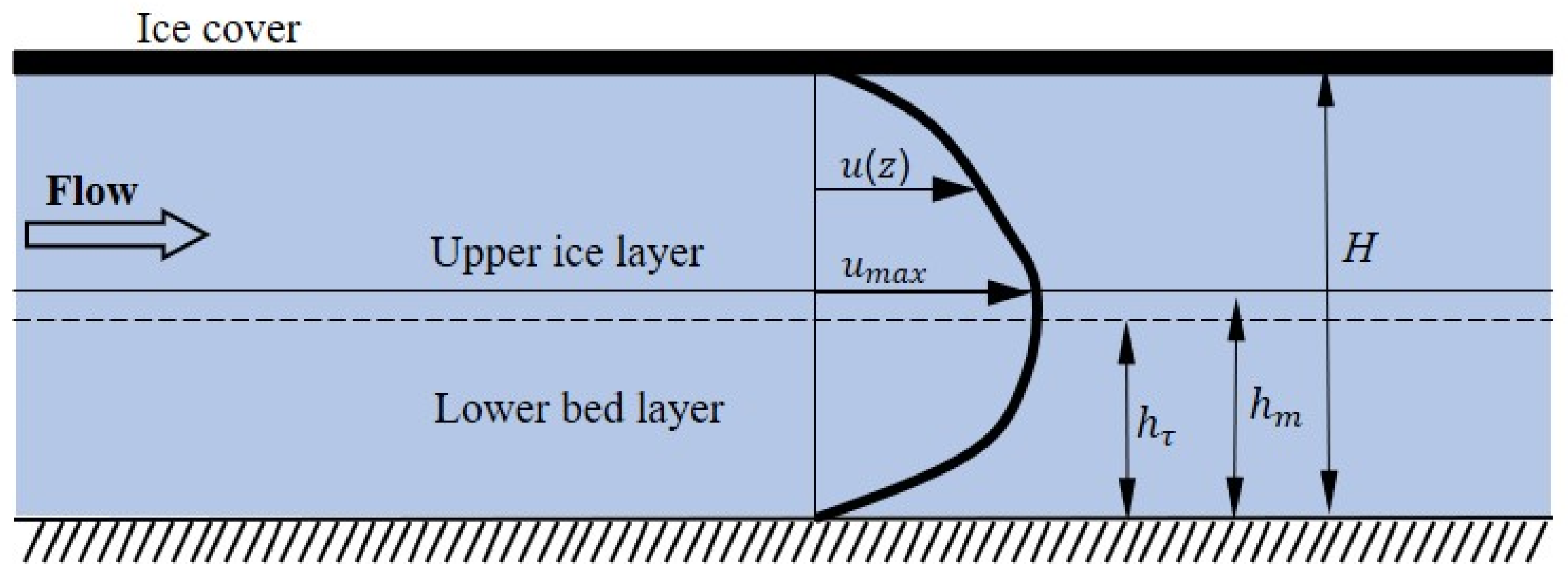
2.1. Vertical Distribution of Longitudinal Velocity
2.2. Vertical Distribution of Reynolds Stress
2.3. Vertical Distribution of Turbulence Intensity
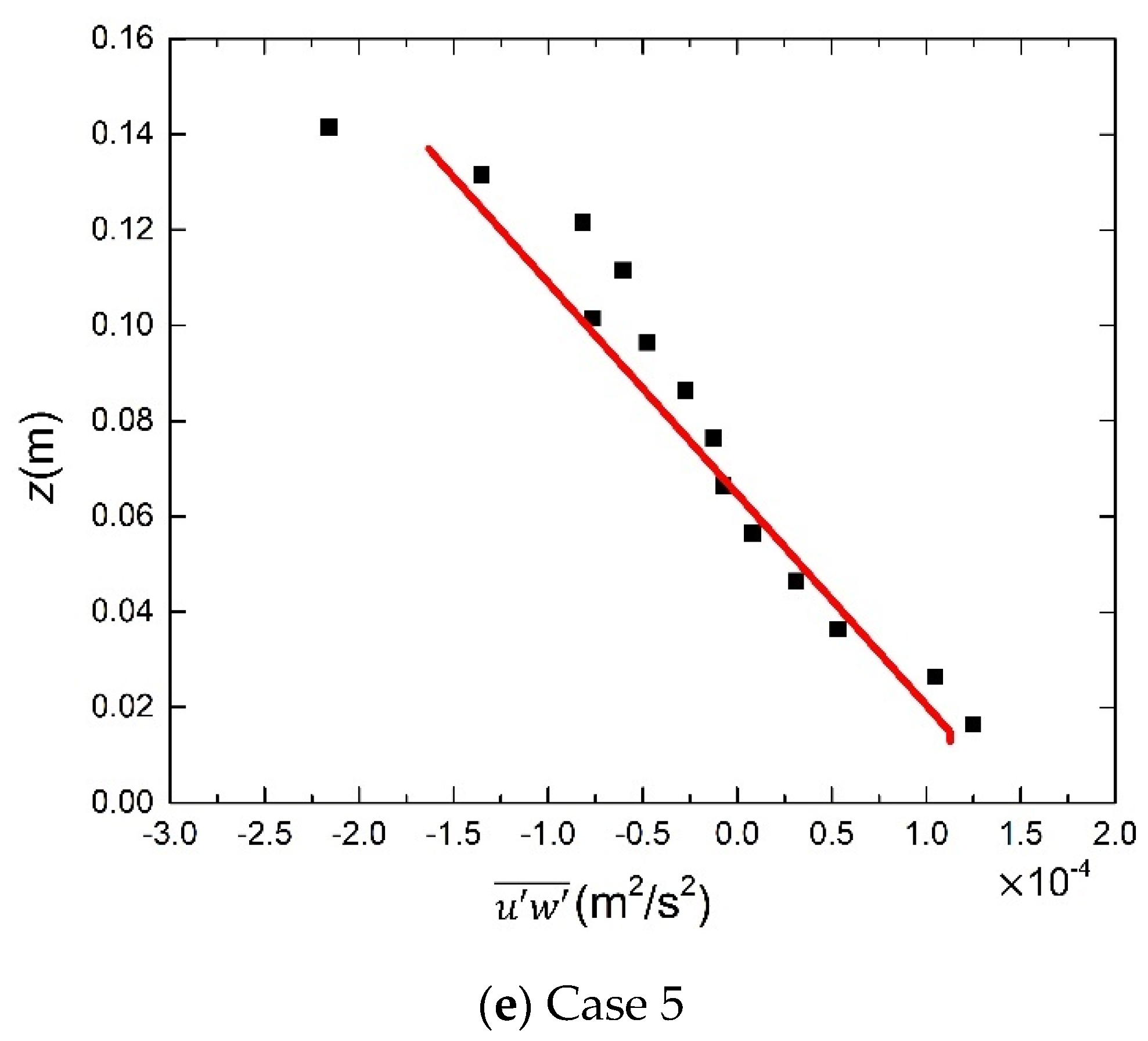
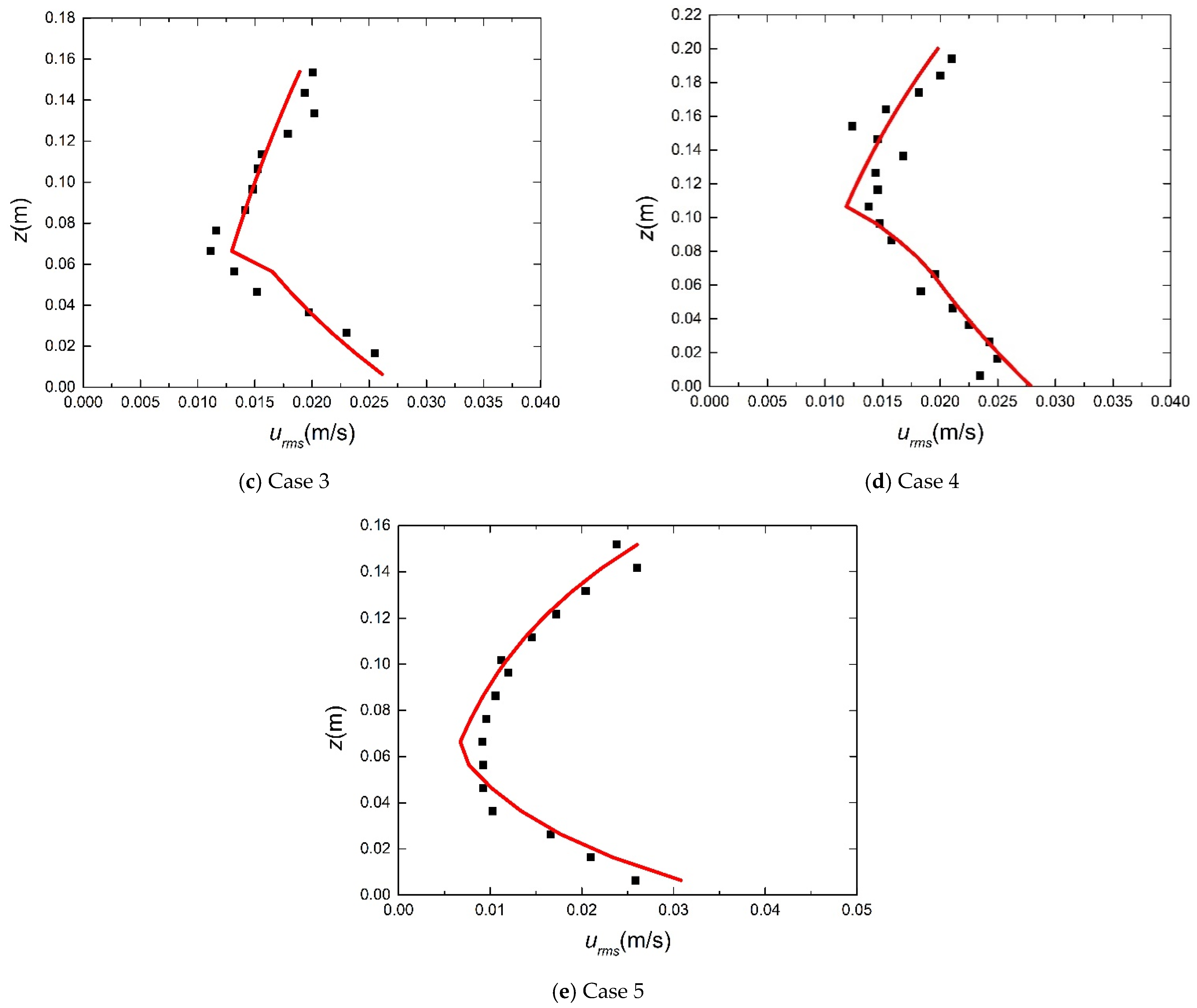
3. Experimental Verification
4. Model Parameters
4.1. and
4.2. and
4.3.
5. Results and Discussion
5.1. Model Verification
5.2. Discussion
5.2.1. Manning’s Coefficients and
5.2.2. Flow Parameters and
5.2.3. Comparison of and
5.2.4. Empirical Constants , , and
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Davar, K.S.; Elhadi, N.A. Management of ice-covered rivers: Problems and perspectives. J. Hydrol. 1981, 51, 245–253. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z.; Zhu, D.; Liu, Z. Longitudinal dispersion coefficient in ice-covered rivers. J. Hydraul. Res. 2016, 54, 558–566. [Google Scholar] [CrossRef]
- Chen, G.; Gu, S.; Li, B.; Zhou, M.; Huai, W. Physically based coefficient for streamflow estimation in ice-covered channels. J. Hydrol. 2018, 563, 470–479. [Google Scholar] [CrossRef]
- Knack, I.; Shen, H.-T. Sediment transport in ice-covered channels. Int. J. Sediment Res. 2015, 30, 63–67. [Google Scholar] [CrossRef]
- Lee, M.; Moser, R.D. Direct numerical simulation of turbulent channel flow up to Reτ ≈ 5200. J. Fluid Mech. 2015, 774, 395–415. [Google Scholar] [CrossRef]
- Lotsari, E.; Tarsa, T.; Mri, M.K.; Alho, P.; Kasvi, E. Spatial variation of flow characteristics in a subarctic meandering river in ice-covered and open-channel conditions: A 2d hydrodynamic modelling approach. Earth Surf. Process. Landf. 2019, 44, 1509–1529. [Google Scholar] [CrossRef] [Green Version]
- Turcotte, B.; Morse, B.; Bergeron, N.E.; Roy, A.G. Sediment transport in ice-affected rivers. J. Hydrol. 2011, 409, 561–577. [Google Scholar] [CrossRef]
- Wang, F.; Huai, W.; Liu, M.; Fu, X. Modeling depth-averaged streamwise velocity in straight trapezoidal compound channels with ice cover. J. Hydrol. 2020, 585, 124336. [Google Scholar] [CrossRef]
- Smith, B.T.; Ettema, R. Flow Resistance in Ice-Covered Alluvial Channels. J. Hydraul. Eng. 1997, 123, 592–599. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Sui, J.; Karney, B. Formation and movement of ice accumulation waves under ice cover—An experimental study. J. Hydrol. Hydromech. 2019, 67, 171–178. [Google Scholar] [CrossRef] [Green Version]
- Namaee, M.R.; Sui, J. Velocity profiles and turbulence intensities around side-by-side bridge piers under ice-covered flow condition. J. Hydrol. Hydromech. 2020, 68, 70–82. [Google Scholar] [CrossRef] [Green Version]
- Hanjalić, K.; Launder, B.E. Fully developed asymmetric flow in a plane channel. J. Fluid Mech. 1972, 51, 301–335. [Google Scholar] [CrossRef]
- Parthasarathy, R.N.; Muste, M. Velocity Measurements in Asymmetric Turbulent Channel Flows. J. Hydraul. Eng. 1994, 120, 1000–1020. [Google Scholar] [CrossRef]
- Tatinclaux, J.; Gogus, M. Asymmetric Plane Flow with Application to Ice Jams. J. Hydraul. Eng. 1983, 109, 1540–1554. [Google Scholar] [CrossRef]
- Lau, Y.L.; Krishnappan, B.G. Sediment Transport Under Ice Cover. J. Hydraul. Eng. 1985, 111, 934–950. [Google Scholar] [CrossRef]
- Muste, M.; Braileanu, F.; Ettema, R. Flow and sediment transport measurements in a simulated ice-covered channel. Water Resour. Res. 2000, 36, 2711–2720. [Google Scholar] [CrossRef]
- Robert, A.; Tran, T. Mean and turbulent flow fields in a simulated ice-covered channel with a gravel bed: Some laboratory observations. Earth Surf. Process. Landforms 2012, 37, 951–956. [Google Scholar] [CrossRef]
- Tao, L. Experimental Study on vertical velocity distribution of water flow under ice sheet. Eng. Constr. 2015, 29, 370–371. [Google Scholar]
- Shen, H.T.; Harden, T.O. The effect of ice cover on vertical transfer in stream channels. J. Am. Water Resour. Assoc. 1978, 14, 1429–1439. [Google Scholar] [CrossRef]
- Lau, Y.L.; Krishnappan, B.G. Ice Cover Effects on Stream Flows and Mixing. J. Hydraul. Div. 1981, 107, 1225–1242. [Google Scholar] [CrossRef]
- Chen, G.; Gu, S.; Huai, W.; Zhang, Y. Boundary Shear Stress in Rectangular Ice-Covered Channels. J. Hydraul. Eng. 2015, 141, 06015005. [Google Scholar] [CrossRef]
- Attar, S.; Li, S. Data-fitted velocity profiles for ice-covered rivers. Can. J. Civ. Eng. 2012, 39, 334–338. [Google Scholar] [CrossRef]
- Sui, J.; Wang, J.; Yun, H.E.; Krol, F. Velocity profiles and incipient motion of frazil particles under ice cover. Int. J. Sediment Res. 2010, 25, 39–51. [Google Scholar] [CrossRef]
- Larsen, P.A. Head losses caused by an ice cover on open channels. J. Boston Soc. Civ. Eng. 1969, 56, 45–67. [Google Scholar]
- Sayre, W.W.; Song, G.B. Effects of Ice Covers on Alluvial Channel Flow and Sediment Transport Processes. IIHR Report No. 218, University of Lowa. Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a066991.pdf (accessed on 16 April 2021).
- Uzuner, M.S. The composite roughness of ice covered streams. J. Hydraul. Res. 1975, 13, 79–102. [Google Scholar] [CrossRef]
- Teal, M.J.; Ettema, R.; Walker, J.F. Estimation of Mean Flow Velocity in Ice-Covered Channels. J. Hydraul. Eng. 1994, 120, 1385–1400. [Google Scholar] [CrossRef]
- Tsai, W.; Ettema, R. Modified Eddy Viscosity Model in Fully Developed Asymmetric Channel Flows. J. Eng. Mech. 1994, 120, 720–732. [Google Scholar] [CrossRef]
- Li, Q.; Zeng, Y.-H.; Bai, Y. Mean flow and turbulence structure of open channel flow with suspended vegetation. J. Hydrodyn. 2020, 32, 314–325. [Google Scholar] [CrossRef]
- Zhang, J.; Lei, J.; Huai, W.; Nepf, H. Turbulence and Particle Deposition Under Steady Flow Along a Submerged Seagrass Meadow. J. Geophys. Res. Oceans 2020, 125, 2019–015985. [Google Scholar] [CrossRef]
- Rowiński, P.M.; Kubrak, J. A mixing-length model for predicting vertical velocity distribution in flows through emergent vegetation. Hydrol. Sci. J. 2002, 47, 893–904. [Google Scholar] [CrossRef] [Green Version]
- Nezu, I.; Rodi, W. Open-channel Flow Measurements with a Laser Doppler Anemometer. J. Hydraul. Eng. 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Zhong, Y.; Huai, W.; Chen, G. Analytical Model for Lateral Depth-Averaged Velocity Distributions in Rectangular Ice-Covered Channels. J. Hydraul. Eng. 2019, 145, 04018080. [Google Scholar] [CrossRef]
- Huai, W.-X.; Xu, Z.-G.; Yang, Z.-H.; Zeng, Y.-H. Two dimensional analytical solution for a partially vegetated compound channel flow. Appl. Math. Mech. 2008, 29, 1077–1084. [Google Scholar] [CrossRef]
- Bonakdari, H.; Larrarte, F.; Lassabatere, L.; Joannis, C. Turbulent velocity profile in fully-developed open channel flows. Environ. Fluid Mech. 2008, 8, 1–17. [Google Scholar] [CrossRef]
- Zare, S.G.A.; Moore, S.A.; Rennie, C.D.; Seidou, O.; Ahmari, H.; Malenchak, J. Estimation of composite hydraulic resistance in ice-covered alluvial streams. Water Resour. Res. 2016, 52, 1306–1327. [Google Scholar] [CrossRef] [Green Version]
- Han, L.; Zeng, Y.; Chen, L.; Li, M. Modeling streamwise velocity and boundary shear stress of vegetation-covered flow. Ecol. Indic. 2018, 92, 379–387. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Elhakeem, M.; Hilldale, R. Secondary current effects on cohesive river bank erosion. Water Resour. Res. 2007, 43, 497–507. [Google Scholar] [CrossRef]
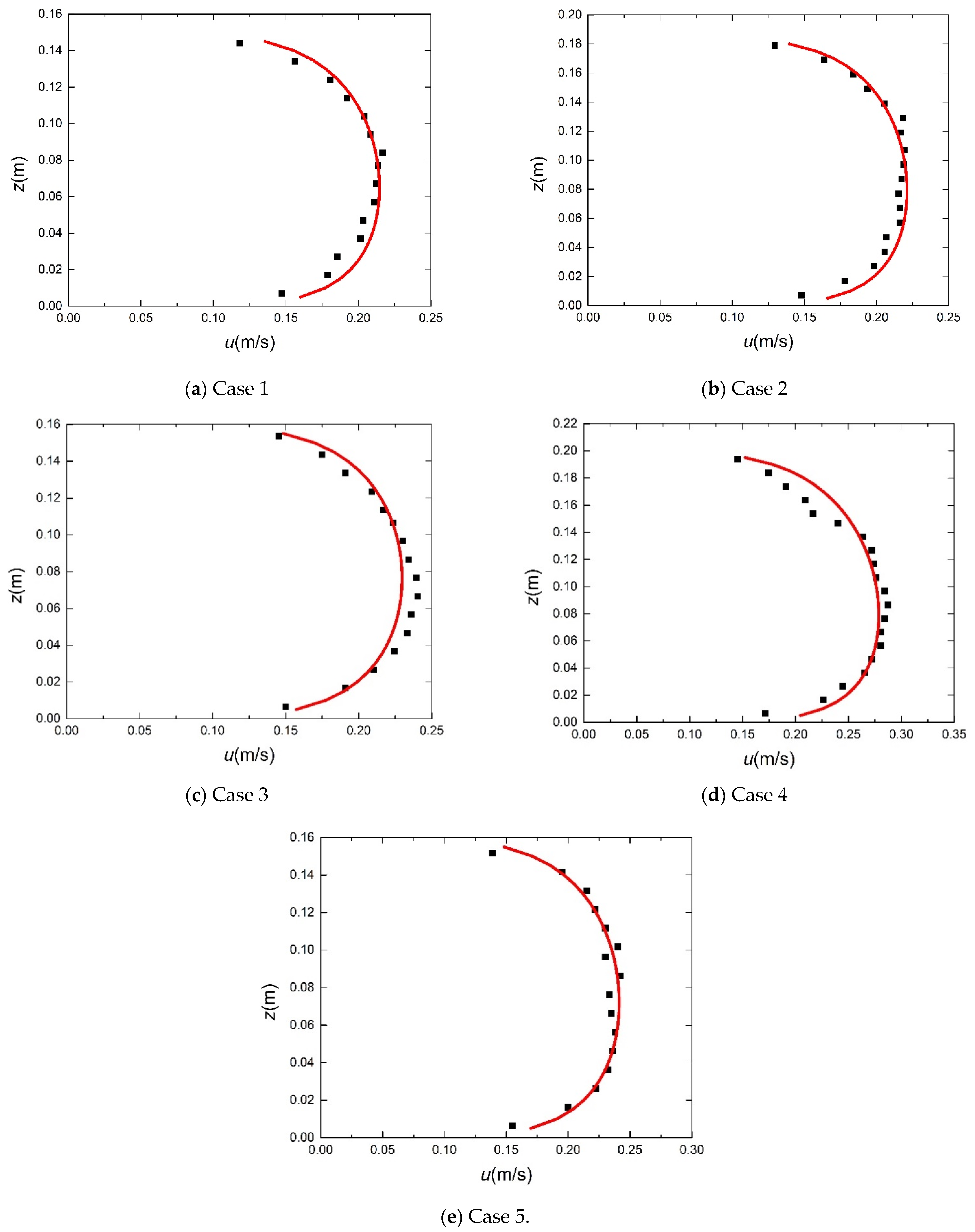


| Cases | Cover Condition | (m) | (m) | ||
|---|---|---|---|---|---|
| 1 | Full ice cover | 1 | 0.15 | 0.001 | 25590 |
| 2 | Full ice cover | 1 | 0.185 | 0.001 | 33725 |
| 3 | Symmetrical shore cover | 1 | 0.16 | 0.001 | 32480 |
| 4 | Symmetrical shore cover | 1 | 0.20 | 0.001 | 49160 |
| 5 | Asymmetrical shore cover | 1 | 0.16 | 0.001 | 31888 |
| Cases | Velocity | Reynolds Stress | Turbulence Intensity | |||
|---|---|---|---|---|---|---|
| 1 | 0.0065 | 3.99 | 0.036 | 7.01 | 0.0013 | 10.52 |
| 2 | 0.0057 | 3.18 | 0.038 | 10.00 | 0.0011 | 8.09 |
| 3 | 0.0059 | 2.86 | 0.050 | 9.11 | 0.0012 | 8.05 |
| 4 | 0.011 | 5.25 | 0.082 | 8.42 | 0.0012 | 6.99 |
| 5 | 0.019 | 10.97 | 0.093 | 13.63 | 0.0019 | 12.54 |
| Cases | ||||||||
|---|---|---|---|---|---|---|---|---|
| Calculated | Measured | Calculated | Measured | |||||
| 1 | 0.013 | 0.018 | 6.35 | 4.84 | 0.43 | 0.56 | 0.37 | 0.35 |
| 2 | 0.012 | 0.017 | 7.13 | 5.31 | 0.43 | 0.58 | 0.43 | 0.44 |
| 3 | 0.015 | 0.017 | 5.41 | 4.96 | 0.48 | 0.42 | 0.43 | 0.43 |
| 4 | 0.014 | 0.02 | 6.57 | 4.30 | 0.40 | 0.44 | 0.39 | 0.44 |
| 5 | 0.015 | 0.019 | 5.63 | 4.59 | 0.45 | 0.54 | 0.39 | 0.39 |
| Cases | ||||
| 1 | 2.22 | 1.44 | 2.06 | 1.82 |
| 2 | 2.21 | 1.46 | 2.13 | 1.87 |
| 3 | 2.22 | 1.73 | 2.24 | 1.50 |
| 4 | 2.15 | 1.00 | 2.21 | 1.83 |
| 5 | 2.31 | 1.81 | 2.16 | 1.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, W.; Li, Z.; Li, Q.; Zhong, Y.; Xia, Z.; Qiu, H. Analytical Models of Velocity, Reynolds Stress and Turbulence Intensity in Ice-Covered Channels. Water 2021, 13, 1107. https://doi.org/10.3390/w13081107
Zhang J, Wang W, Li Z, Li Q, Zhong Y, Xia Z, Qiu H. Analytical Models of Velocity, Reynolds Stress and Turbulence Intensity in Ice-Covered Channels. Water. 2021; 13(8):1107. https://doi.org/10.3390/w13081107
Chicago/Turabian StyleZhang, Jiao, Wen Wang, Zhanbin Li, Qian Li, Ya Zhong, Zhaohui Xia, and Hunan Qiu. 2021. "Analytical Models of Velocity, Reynolds Stress and Turbulence Intensity in Ice-Covered Channels" Water 13, no. 8: 1107. https://doi.org/10.3390/w13081107





