The Performance of Physically Based and Conceptual Hydrologic Models: A Case Study for Makkah Watershed, Saudi Arabia
Abstract
:1. Introduction
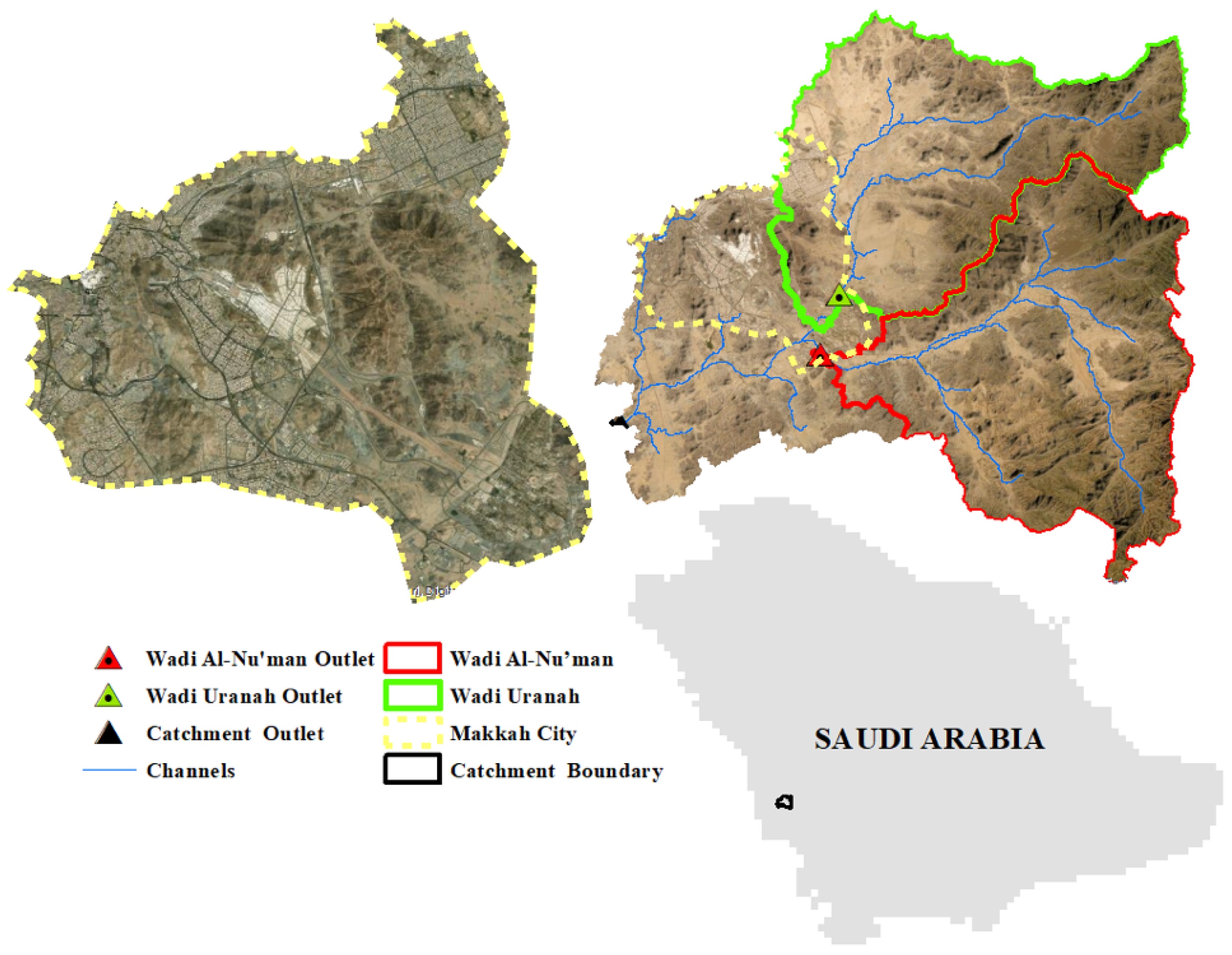
2. Study Area
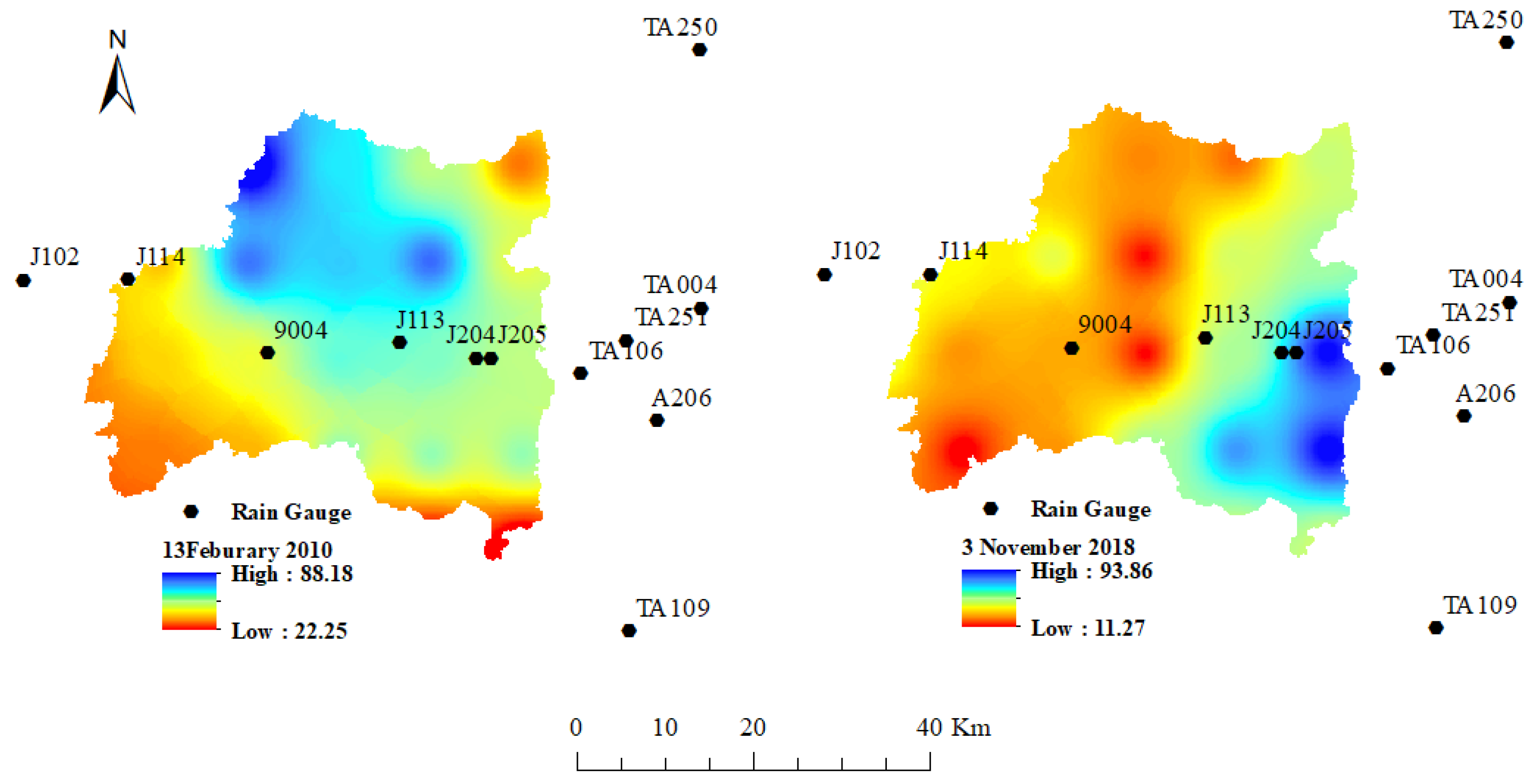
3. Rainfall Events
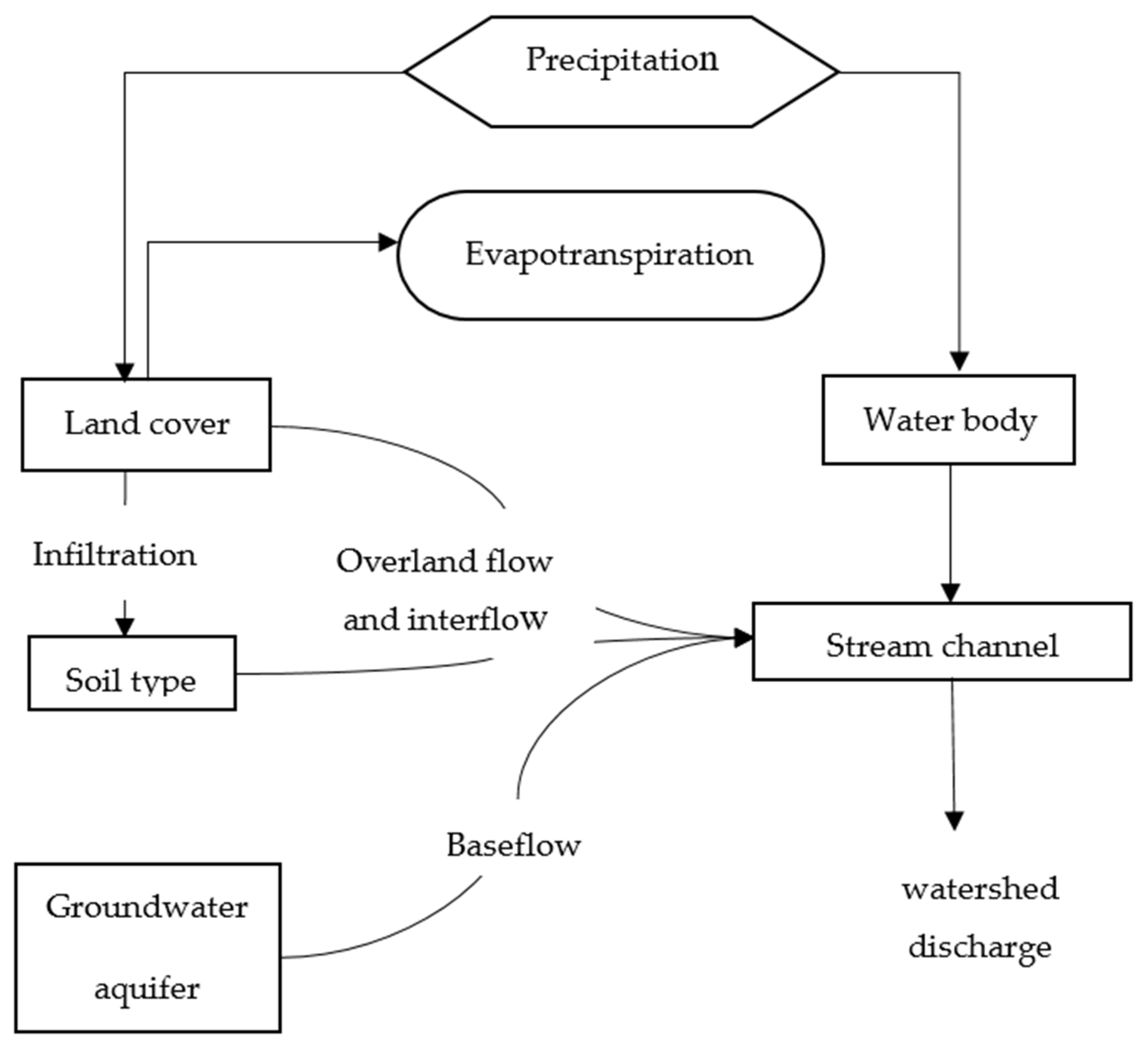
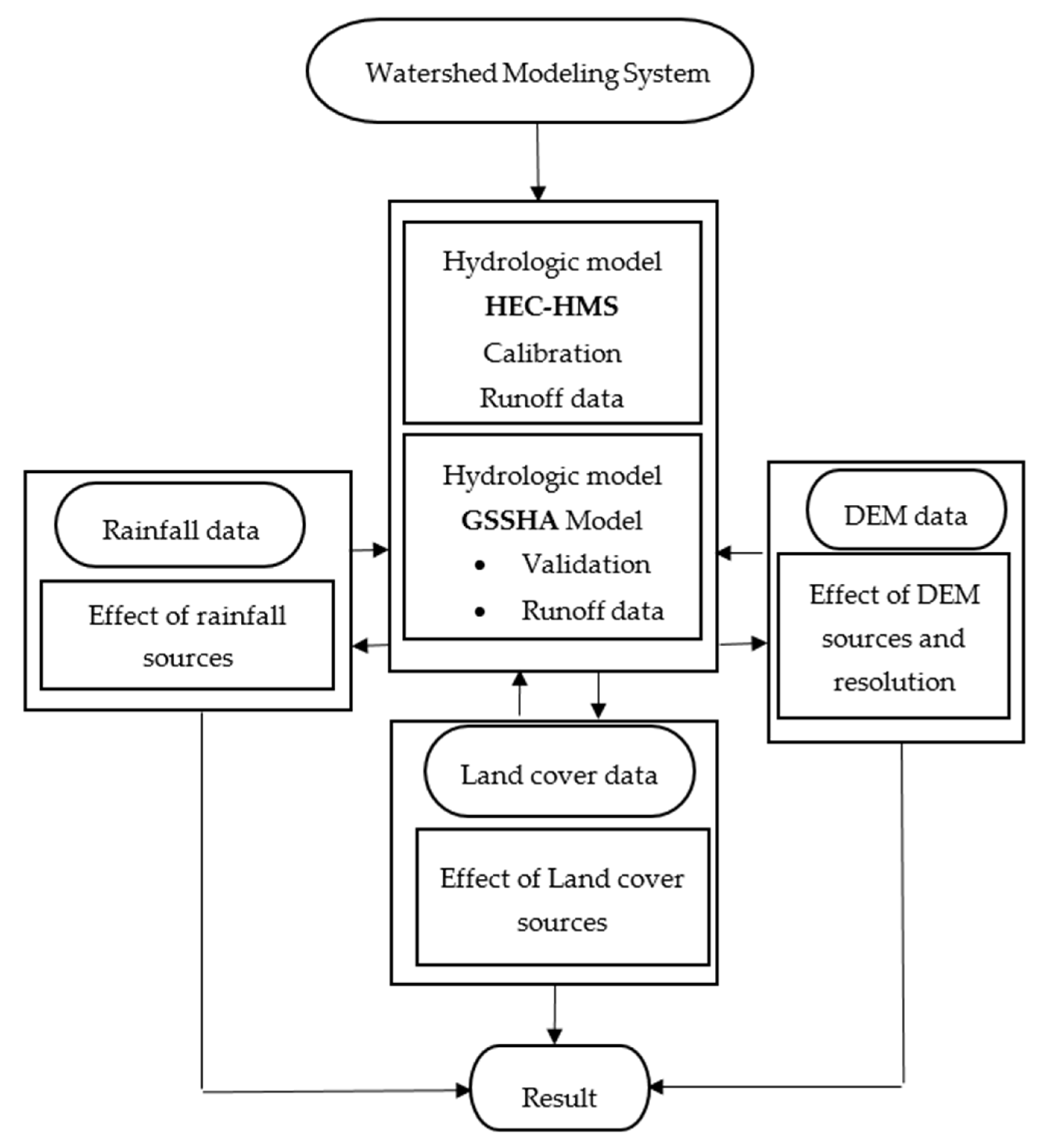
4. Models Description
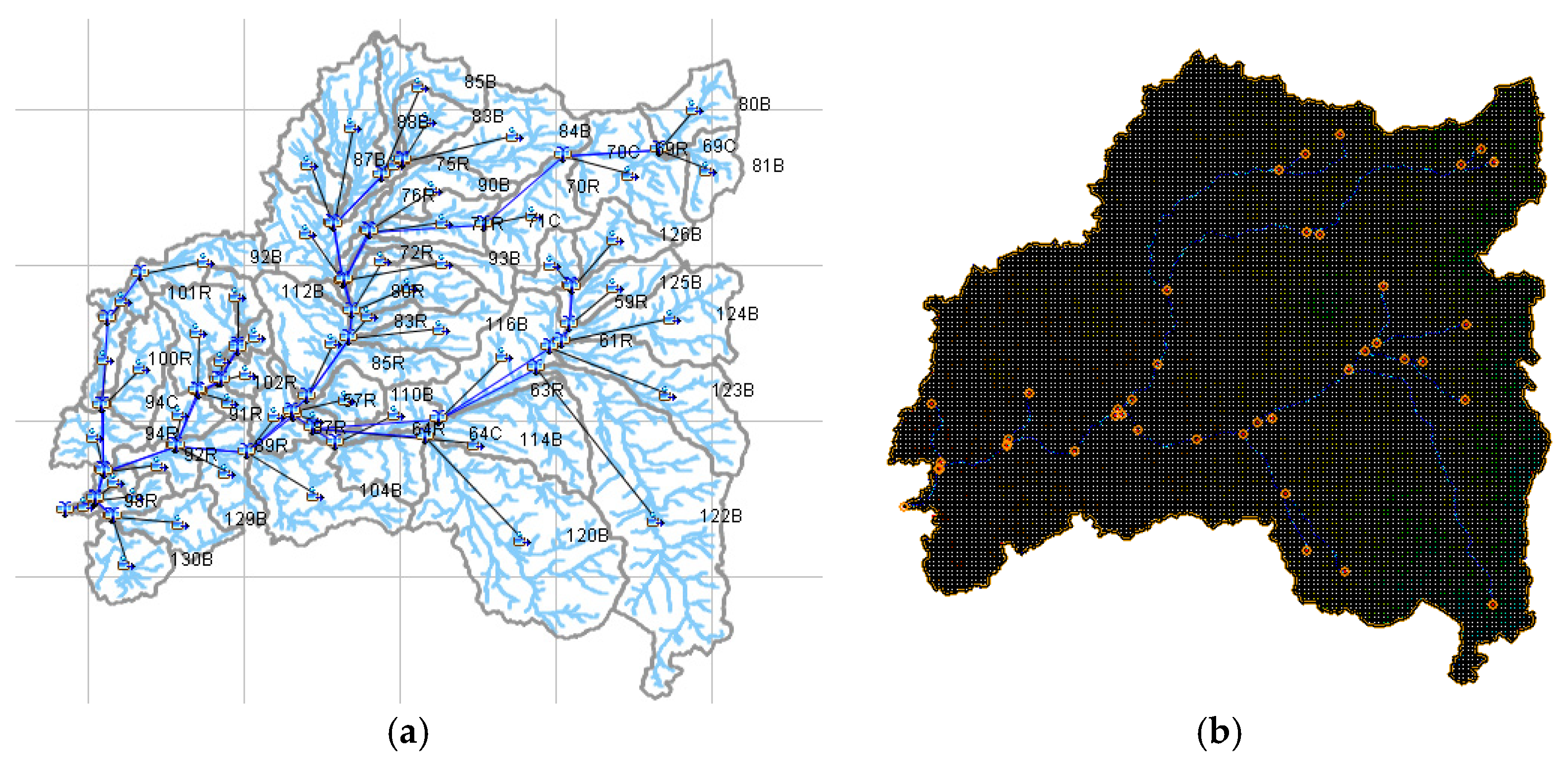
4.1. Semi-Distributed Modeling (HEC-HMS Model)
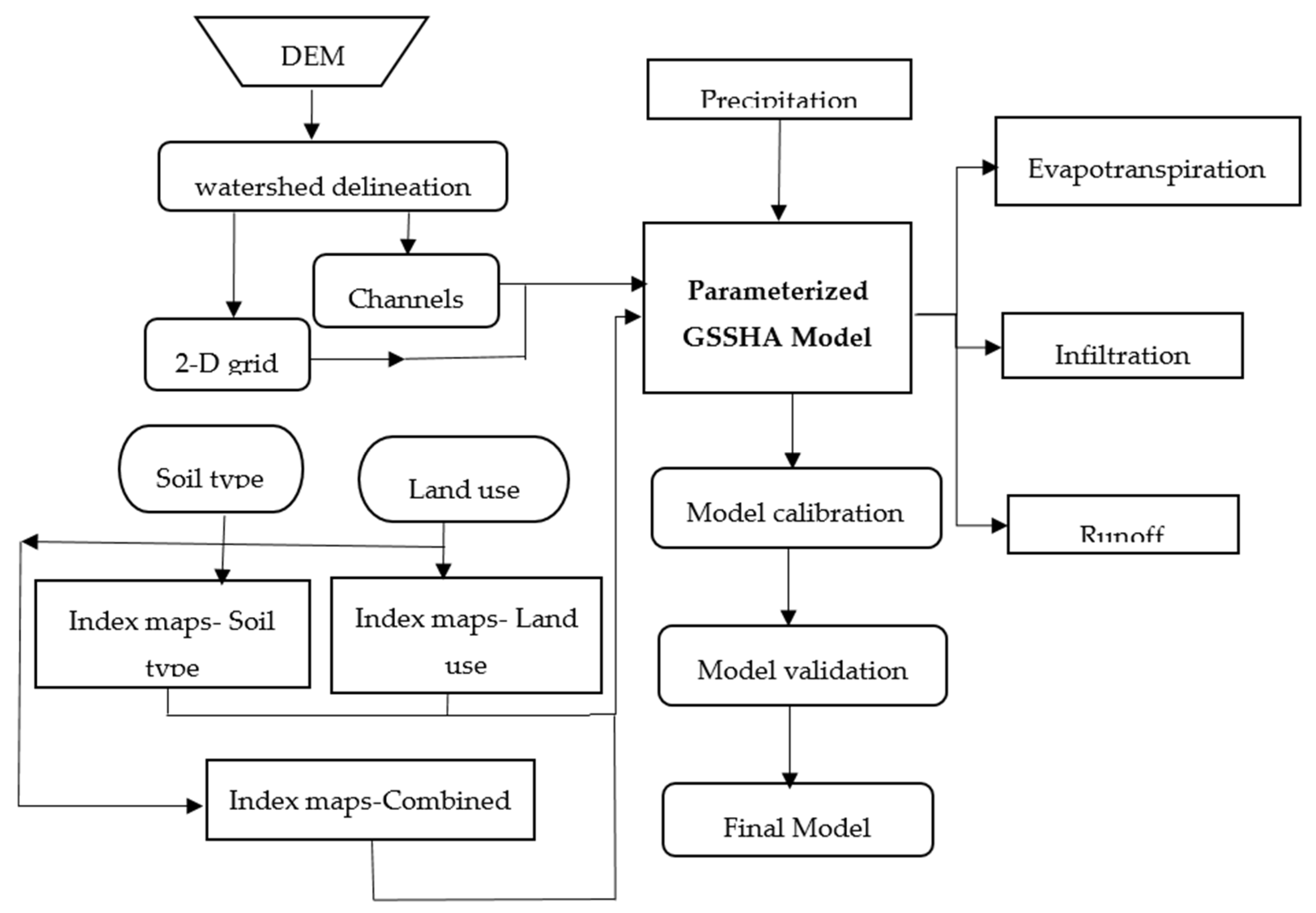
4.2. The Physically-Based, Fully Distributed Hydrologic Model (GSSHA)
- = lateral flow (m2/s)
- = flow exchange between the channel and groundwater (m2/s)
- = the computed inter-cell flows from depths (h) in the longitudinal (x), at the Nth time level.
- f (t) = Infiltration Rate (cm/hr)
- Sf = wetting front suction head (cm)
- K = effective hydraulic conductivity (cm/hr)
- θi = initial soil moisture content
- θs = water content of the soil at natural saturation.
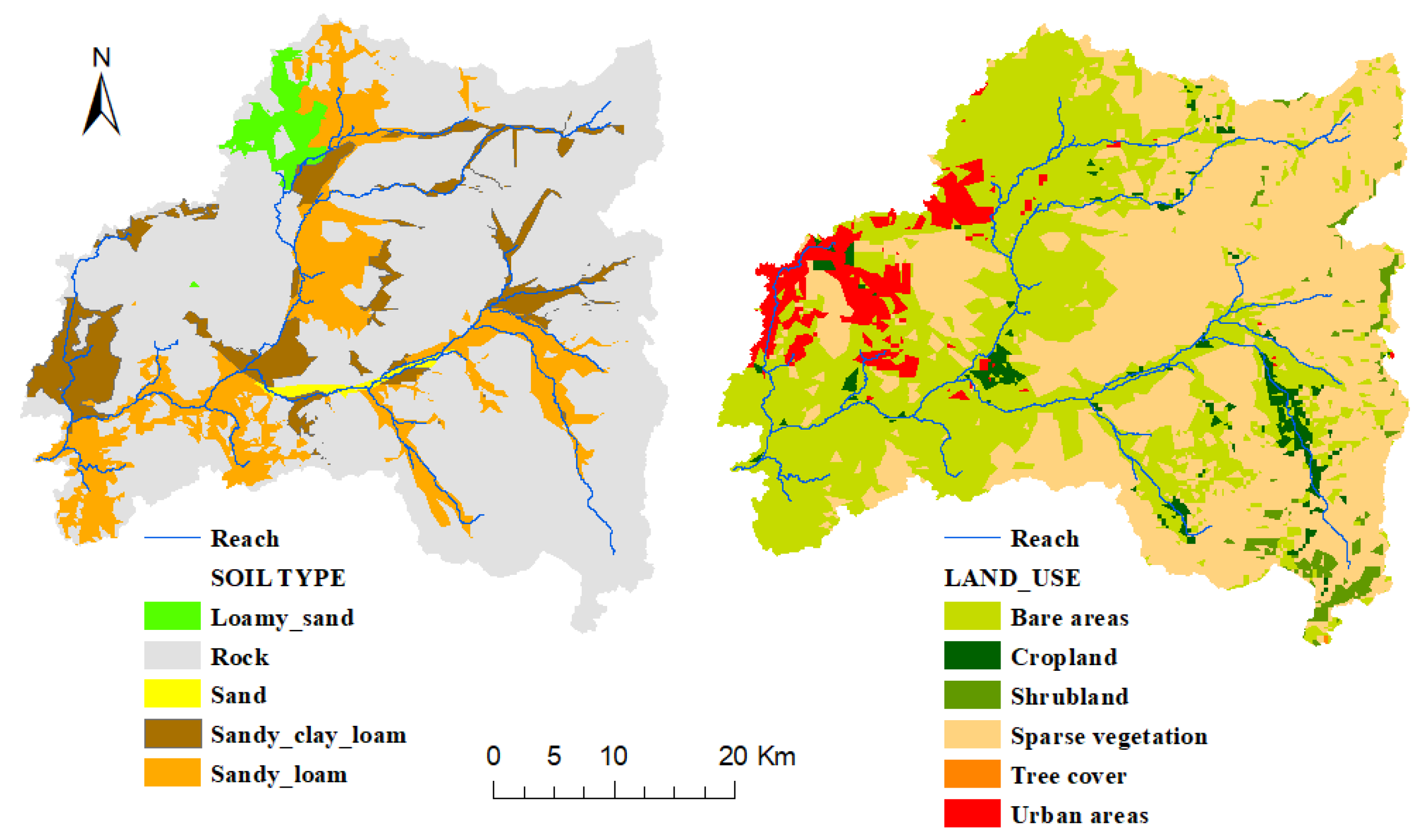
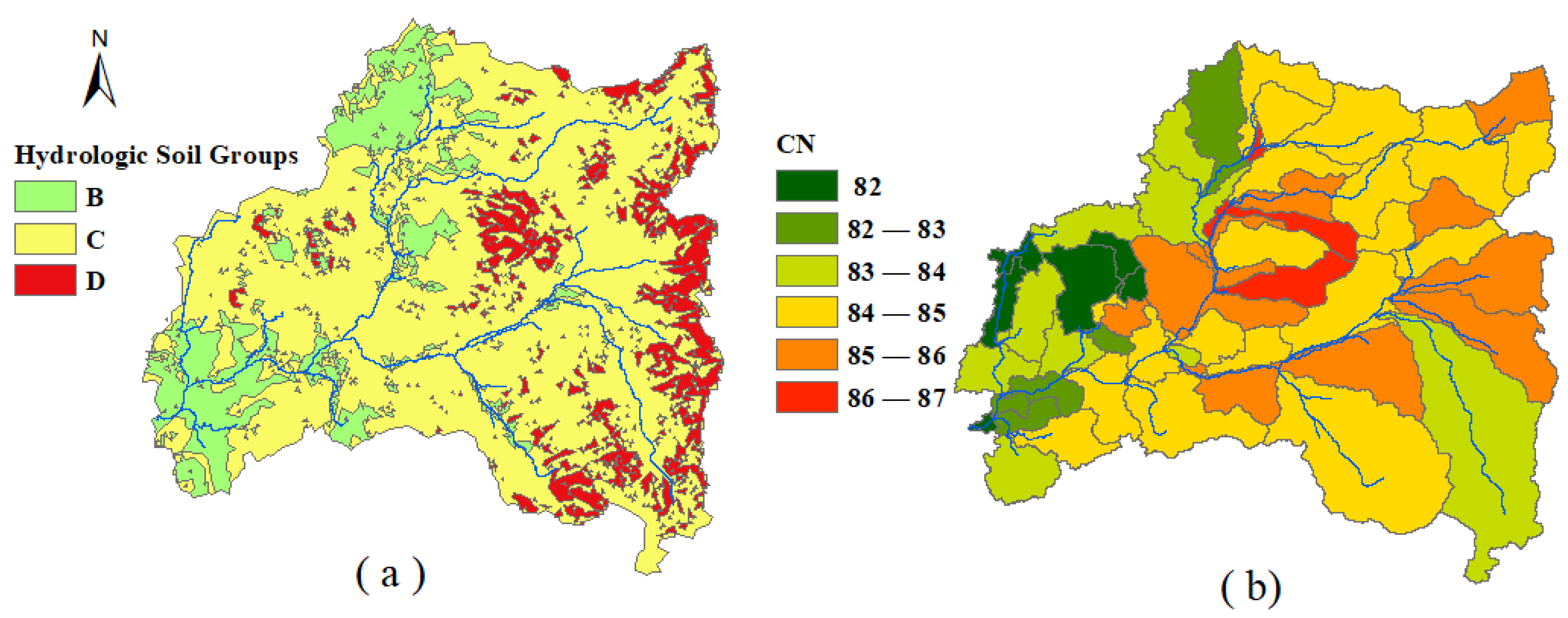
5. Watershed Data
6. Methodology
7. Results
7.1. Models Calibration
7.2. Models’ Validation
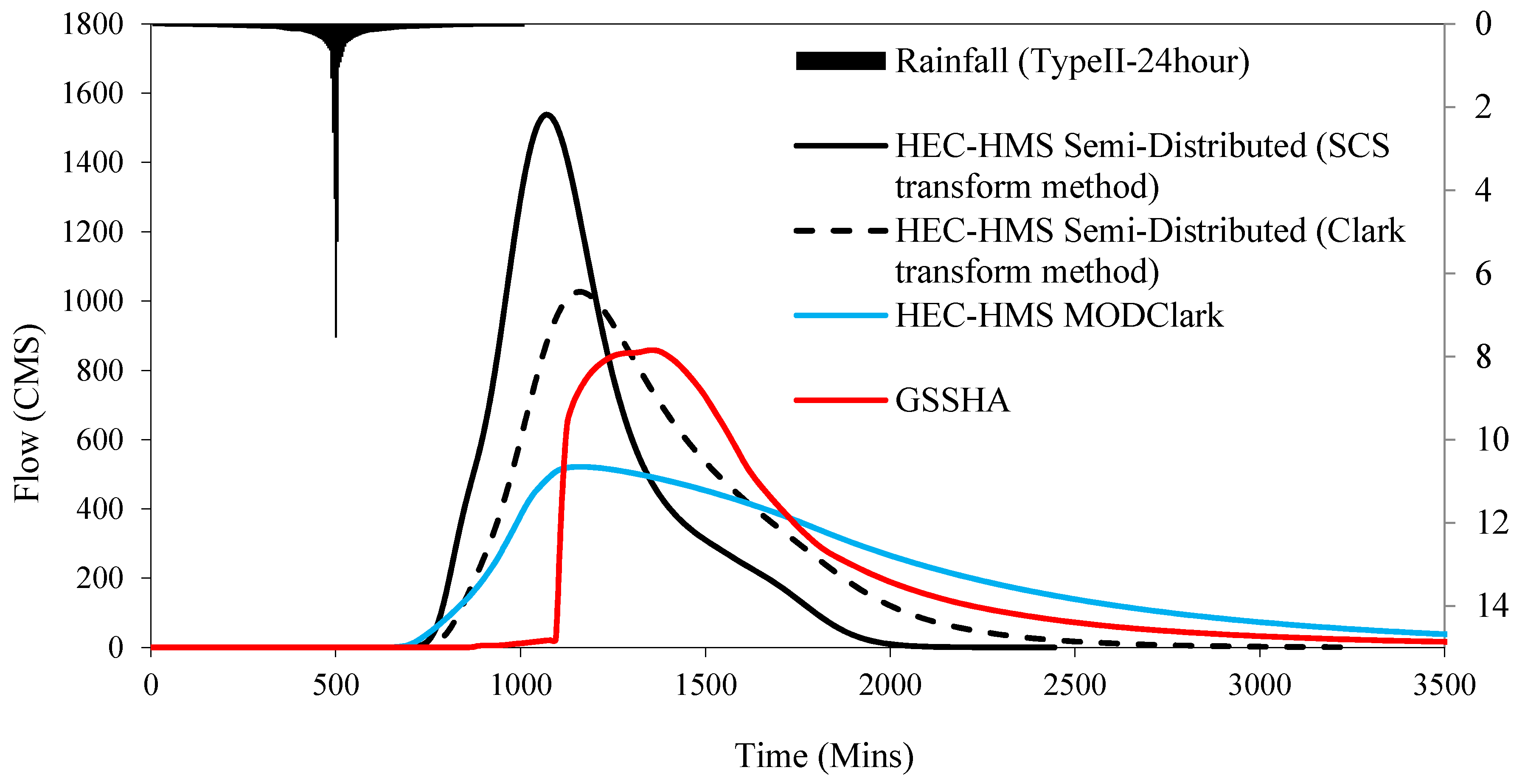
7.3. Models’ Outputs Comparison
7.4. Effect of Topography on HEC-HMS Simulations
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, Q.; Ding, Y.; Wang, J.; Gao, H.; Zhang, S.; Zhao, C.; Xu, J.; Han, H.; Shangguan, D. Projecting Climate Change Impacts on Hydrological Processes on the Tibetan Plateau with Model Calibration against the Glacier Inventory Data and Observed Streamflow. J. Hydrol. 2019, 573, 60–81. [Google Scholar] [CrossRef]
- Umair, M.; Kim, D.; Ray, R.L.; Choi, M. Estimating Land Surface Variables and Sensitivity Analysis for CLM and VIC Simulations Using Remote Sensing Products. Sci. Total Environ. 2018, 633, 470–483. [Google Scholar] [CrossRef]
- Santos, R.M.B.; Sanches Fernandes, L.F.; Moura, J.P.; Pereira, M.G.; Pacheco, F.A.L. The Impact of Climate Change, Human Interference, Scale and Modeling Uncertainties on the Estimation of Aquifer Properties and River Flow Components. J. Hydrol. 2014, 519, 1297–1314. [Google Scholar] [CrossRef]
- Zhang, Z.; Koren, V.; Smith, M.; Reed, S.; Wang, D. Use of Next Generation Weather Radar Data and Basin Disaggregation to Improve Continuous Hydrograph Simulations. J. Hydrol. Eng. 2004, 9, 103–115. [Google Scholar] [CrossRef] [Green Version]
- Furl, C.; Ghebreyesus, D.; Sharif, H.O. Assessment of the Performance of Satellite-Based Precipitation Products for Flood Events across Diverse Spatial Scales Using GSSHA Modeling System. Geosciences 2018, 8, 191. [Google Scholar] [CrossRef] [Green Version]
- Al-Zahrani, M.; Al-Areeq, A.; Sharif, H.O. Estimating Urban Flooding Potential near the Outlet of an Arid Catchment in Saudi Arabia. Geomat. Nat. Hazards Risk 2017, 8, 672–688. [Google Scholar] [CrossRef] [Green Version]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.-J. DMIP Participants, and Overall Distributed Model Intercomparison Project Results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Biftu, G.; Gan, T. Semi-Distributed, Physically Based, Hydrologic Modeling of the Paddle River Basin, Alberta, Using Remotely Sensed Data. J. Hydrol. 2001, 244, 137–156. [Google Scholar] [CrossRef]
- Refsgaard, J.C. Parameterisation, Calibration and Validation of Distributed Hydrological Models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
- Donnelly-Makowecki, L.; Moore, R. Hierarchical Testing of Three Rainfall–Runoff Models in Small Forested Catchments. J. Hydrol. 1999, 219, 136–152. [Google Scholar] [CrossRef]
- Shrestha, M.N. Spatially Distributed Hydrological Modelling Considering Land–Use Changes Using Remote Sensing and GIS. In Proceedings of the Map Asia Conference, Kuala Lumpur, Malaysia, 13–15 October 2003. [Google Scholar]
- Bobba, A.G.; Singh, V.P.; Bengtsson, L. Application of Environmental Models to Different Hydrological Systems. Ecol. Modell. 2000, 125, 15–49. [Google Scholar] [CrossRef]
- Schumann, A.H. Development of Conceptual Semi-Distributed Hydrological Models and Estimation of Their Parameters with the Aid of GIS. Hydrol. Sci. J. 1993, 38, 519–528. [Google Scholar] [CrossRef]
- Jones, J.A.A. Global Hydrology: Processes, Resources and Environmental Management; Routledge: Oxfordshire, UK, 2014; ISBN 9781315844398. [Google Scholar]
- Vázquez, R.F.; Feyen, L.; Feyen, J.; Refsgaard, J.C. Effect of Grid Size on Effective Parameters and Model Performance of the MIKE-SHE Code. Hydrol. Process. 2002, 16, 355–372. [Google Scholar] [CrossRef]
- Sharif, H.O.; Sparks, L.; Hassan, A.A.; Zeitler, J.; Xie, H. Application of a Distributed Hydrologic Model to the November 17, 2004, Flood of Bull Creek Watershed, Austin, Texas. J. Hydrol. Eng. 2010, 15, 651–657. [Google Scholar] [CrossRef]
- Paudel, M.; Nelson, E.J.; Downer, C.W.; Hotchkiss, R. Comparing the Capability of Distributed and Lumped Hydrologic Models for Analyzing the Effects of Land Use Change. J. Hydroinformatics 2011, 13, 461–473. [Google Scholar] [CrossRef]
- Sith, R.; Nadaoka, K. Comparison of SWAT and GSSHA for High Time Resolution Prediction of Stream Flow and Sediment Concentration in a Small Agricultural Watershed. Hydrology 2017, 4, 27. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.L.; Zhang, H.L.; Wang, Y.J.; Wang, Y.Q.; Li, D.X.; Wang, X.K. Quantitative Comparison of Semi- and Fully-Distributed Hydrologic Models in Simulating Flood Hydrographs on a Mountain Watershed in Southwest China. J. Hydrodyn. 2013, 25, 877–885. [Google Scholar]
- El-Nasr, A.A.; Arnold, J.G.; Feyen, J.; Berlamont, J. Modelling the Hydrology of a Catchment Using a Distributed and a Semi-Distributed Model. Hydrol. Process. 2005, 19, 573–587. [Google Scholar] [CrossRef]
- Meselhe, E.A.; Habib, E.H.; Oche, O.C.; Gautam, S. Sensitivity of Conceptual and Physically Based Hydrologic Models to Temporal and Spatial Rainfall Sampling. J. Hydrol. Eng. 2009, 14, 711–720. [Google Scholar] [CrossRef]
- Ogden, F.L.; Downer, C.W.; Meselhe, E. U.S. Army Corps of Engineers Gridded Surface/Subsurface Hydrologic Analysis (GSSHA) Model: Distributed-Parameter, Physically Based Watershed Simulations. In Proceedings of the World Water & Environmental Resources Congress 2003, Philadelphia, PA, USA, 23–26 June 2003; American Society of Civil Engineers: Reston, VA, USA, 2003; pp. 1–10. [Google Scholar]
- El Hassan, A.A.; Sharif, H.O.; Jackson, T.; Chintalapudi, S. Performance of a Conceptual and Physically Based Model in Simulating the Response of a Semi-Urbanized Watershed in San Antonio, Texas. Hydrol. Process. 2013, 27, 3394–3408. [Google Scholar] [CrossRef]
- Al Abdouli, K.; Hussein, K.; Ghebreyesus, D.; Sharif, H.O. Coastal Runoff in the United Arab Emirates-the Hazard and Opportunity. Sustainability 2019, 11, 5406. [Google Scholar] [CrossRef] [Green Version]
- Sharif, H.; Al-Zahrani, M.; Hassan, A. Physically, Fully-Distributed Hydrologic Simulations Driven by GPM Satellite Rainfall over an Urbanizing Arid Catchment in Saudi Arabia. Water 2017, 9, 163. [Google Scholar] [CrossRef]
- Embaby, A.; Halawa, A.A.; Ramadan, M. Integrating Geotechnical Investigation with Hydrological Modeling for Mitigation of Expansive Soil Hazards in Tabuk City, Saudi Arabia. Mod. Hydrol. 2017, 7, 11–37. [Google Scholar] [CrossRef] [Green Version]
- Fathy, I.; Negm, A.M.; El-fiky, M.; Nassar, M.; El-Sayed, E.A.H. Runoff Hydrograph Modeling for Arid Regions: Case Study—Wadi Sudr-Sinai. Int. Water Technol. J. IWTJ 2015, 5, 58–68. [Google Scholar]
- Abdelkarim, A.; Gaber, A.F.D. Flood Risk Assessment of the Wadi Nu’man Basin, Mecca, Saudi Arabia (During the Period, 1988–2019) Based on the Integration of Geomatics and Hydraulic Modeling: A Case Study. Water 2019, 11, 1887. [Google Scholar] [CrossRef] [Green Version]
- Elfeki, A.; Masoud, M.; Niyazi, B. Integrated Rainfall–Runoff and Flood Inundation Modeling for Flash Flood Risk Assessment under Data Scarcity in Arid Regions: Wadi Fatimah Basin Case Study, Saudi Arabia. Nat. Hazards 2017, 85, 87–109. [Google Scholar] [CrossRef]
- El Bastawesy, M.; Habeebullah, T.; Balkhair, K.; Ascoura, I. Modelling Flash Floods in Arid Urbanized Areas: Makkah (Saudi Arabia). Sécheresse 2013, 24, 171–181. [Google Scholar] [CrossRef]
- Dawod, G.M.; Mirza, M.N.; Al-Ghamdi, K.A. Assessment of Several Flood Estimation Methodologies in Makkah Metropolitan Area, Saudi Arabia. Arab. J. Geosci. 2013, 6, 985–993. [Google Scholar] [CrossRef]
- Al-ghamdi, K.A.; Elzahrany, R.A.; Mirza, M.N.; Dawod, G.M. Impacts of Urban Growth on Flood Hazards in Makkah City, Saudi Arabia. Int. J. Water Resour. Environ. Eng. 2012, 4, 23–34. [Google Scholar]
- Al Saud, M. Morphometric Analysis of Wadi Aurnah Drainage System, Western Arabian Peninsula. Open Hydrol. J. 2009, 3, 1–10. [Google Scholar]
- GAS Population. Available online: https://www.stats.gov.sa/en/852 (accessed on 31 August 2020).
- Subyani, A.M. Hydrologic Behavior and Flood Probability for Selected Arid Basins in Makkah Area, Western Saudi Arabia. Arab. J. Geosci. 2011, 4, 817–824. [Google Scholar] [CrossRef]
- Alahmadi, M.; Atkinson, P.M. Three-Fold Urban Expansion in Saudi Arabia from 1992 to 2013 Observed Using Calibrated DMSP-OLS Night-Time Lights Imagery. Remote Sens. 2019, 11, 2266. [Google Scholar] [CrossRef] [Green Version]
- Al Jabri, N.; Alhazmi, R. Observing and Monitoring the Urban Expansion of Makkah Al-Mukarramah Using the Remote Sensing and GIS. J. Eng. Sci. Inf. Technol. 2017, 1, 103–125. [Google Scholar]
- Tan, J.; Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. IMERG V06: Changes to the Morphing Algorithm. J. Atmos. Ocean. Technol. 2019, 36, 2471–2482. [Google Scholar] [CrossRef]
- Chow, V.T. A General Formula for Hydrologic Frequency Analysis. Trans. Am. Geophys. Union 1951, 32, 231. [Google Scholar] [CrossRef]
- Lautenbach, S.; Voinov, A.; Seppelt, R. Localization Effects of Land Use Change on Hydrological Models. In Proceedings of the iEMSs Third Biennial Meeting, Summit on Environmental Modelling and Software, Burlington, VT, USA, 9–13 July 2006; Voinov, A., Jakeman, A., Rizzoli, A., Eds.; International Environmental Modelling and Software Society: Burlington, VT, USA, 2006. [Google Scholar]
- Scharffenberg, W.A. Hydrologic Modeling System HEC-HMS–User’s Manual; Institute for Water Resources, Hydrologic Engineering Center: Davis, CA, USA, 2013; p. 442. [Google Scholar]
- Mishra, S.K.; Singh, V. Soil Conservation Service Curve Number (SCS-CN) Methodology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003; p. 513. [Google Scholar]
- Urban Hydrology for Small Watersheds; No. 55. Engineering Division, Soil Conservation Service, US Department of Agriculture: Washington, DC, USA, 1986.
- Kent, K.M. Section 4–Hydrology. In National Engineering Handbook (NEH); Soil Conservation Service, U.S. Department of Agriculture: Washington, DC, USA, 1985. [Google Scholar]
- Downer, C.W.; James, W.F.; Byrd, A.; Eggers, G.W. Gridded Surface Subsurface Hydrologic Analysis (GSSHA) Model Simulation of Hydrologic Conditions and Restoration Scenarios for the Judicial Ditch 31 Watershed, Minnesota; Engineer Research and Development Center: Vicksburg, MS, USA, 2002; pp. 1–27. [Google Scholar]
- Downer, C.W.; Ogden, F.L. GSSHA: Model To Simulate Diverse Stream Flow Producing Processes. J. Hydrol. Eng. 2004, 9, 161–174. [Google Scholar] [CrossRef]
- Downer, C.W.; Ogden, F.L. System-Wide Water Resources Program Gridded Surface Subsurface Hydrologic Analysis (GSSHA) User’s Manual Version 1.43 for Watershed Modeling System 6.1; US Army Corps of Engineers, Engineer Research and Development Center: Vicksburg, MS, USA, 2006. [Google Scholar]
- GSSHA Primer Gssha/GSSHA Primer–Gsshawiki. Available online: https://gsshawiki.com/Gssha/GSSHA_Primer#Description (accessed on 15 September 2018).
- What is GIS? ESRI (Environmental Systems Research Institute). Available online: https://www.esri.com/en-us/what-is-gis/overview (accessed on 11 November 2020).
- Ross, C.W.; Prihodko, L.; Anchang, J.; Kumar, S.; Ji, W.; Hanan, N.P. HYSOGs250m, Global Gridded Hydrologic Soil Groups for Curve-Number-Based Runoff Modeling. Sci. Data 2018, 5, 180091. [Google Scholar] [CrossRef]
- Deliman, P.N.; Ruiz, C.E.; Manwaring, C.T.; Nelson, E.J. Watershed Modeling System (WMS) Version 11 Tutorial; EMRL (Environmental Modeling Research Laboratory); US Army Corps of Engineers, Engineers Research and Development Center: Vicksburg, MS, USA, 2002. [Google Scholar]
- Al-Baroudi, M.; Mirza, M.; Dawood, G. The Use of GIS in Estimating the Volumes of Floods and the Extent of Their Development at the Lower Reaches of Wadi Nu’man South of Makkah City by the Application of the Snyder Model and the Model of Digital Heights. In Proceedings of the International Geography Conference Geography Contemporary Global Changing, Medina, Saudi Arabia, 20–23 May 2013; Res. Bookl. C Part C. Faculty of Arts and Humanities, University Thebes Medina: Medina, Saudi Arabia, 2013; pp. 757–783. [Google Scholar]
- Clark, C.O. Storage and the Unit Hydrograph. Trans. Am. Soc. Civ. Eng. 1945, 110, 1419–1446. [Google Scholar] [CrossRef]
- Paudel, M.; Nelson, E.J.; Scharffenberg, W. Comparison of Lumped and Quasi-Distributed Clark Runoff Models Using the SCS Curve Number Equation. J. Hydrol. Eng. 2009, 14, 1098–1106. [Google Scholar] [CrossRef]
- Halwatura, D.; Najim, M.M.M. Application of the HEC-HMS Model for Runoff Simulation in a Tropical Catchment. Environ. Model. Softw. 2013, 46, 155–162. [Google Scholar] [CrossRef]
- Walega, A.; Salata, T.; Cover, C.L. In Fl Uence of Land Cover Data Sources on Estimation of Direct Runo Ff According to SCS-CN and Modi Fi Ed SME Methods. Catena 2019, 172, 232–242. [Google Scholar] [CrossRef]

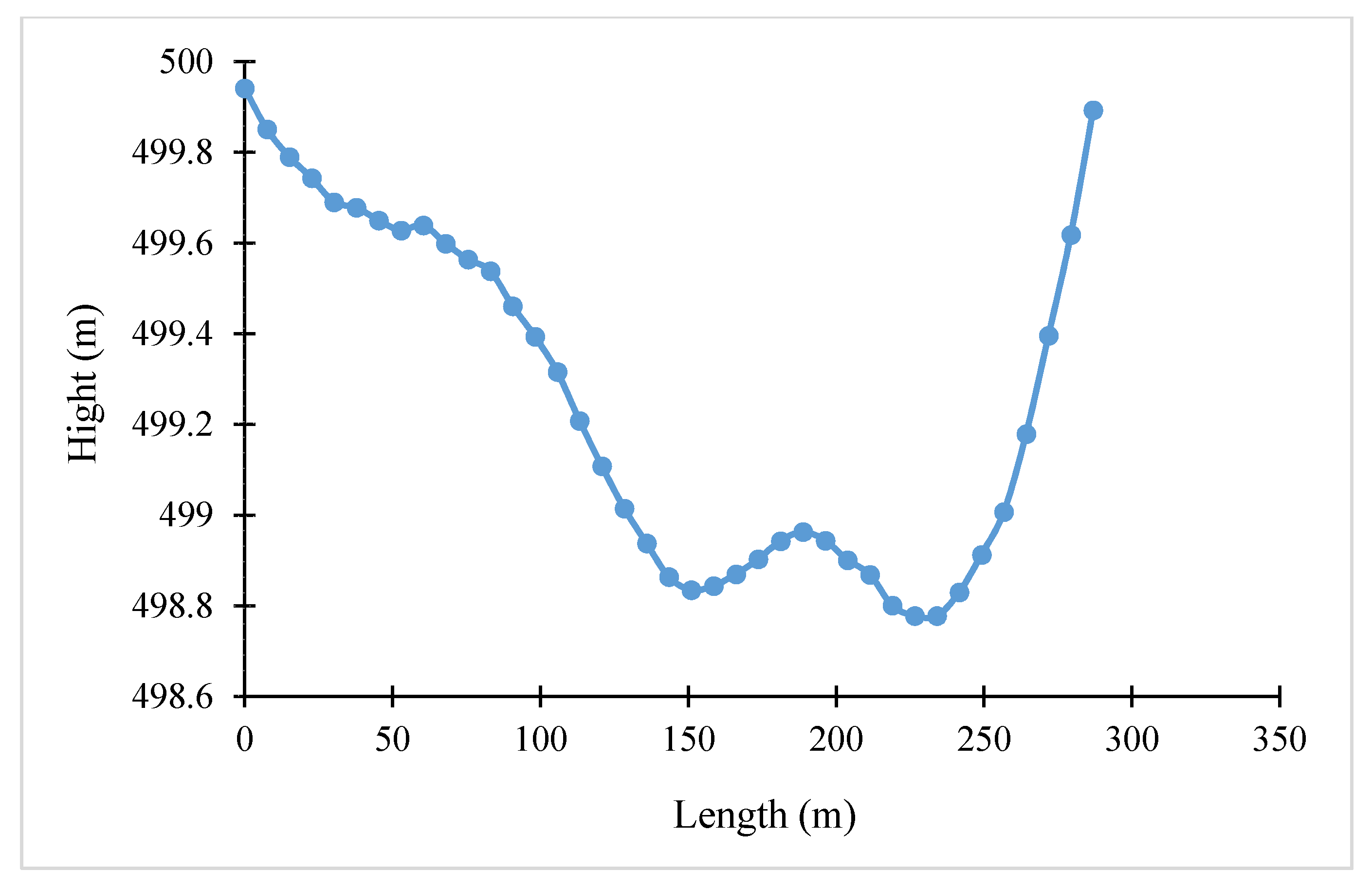
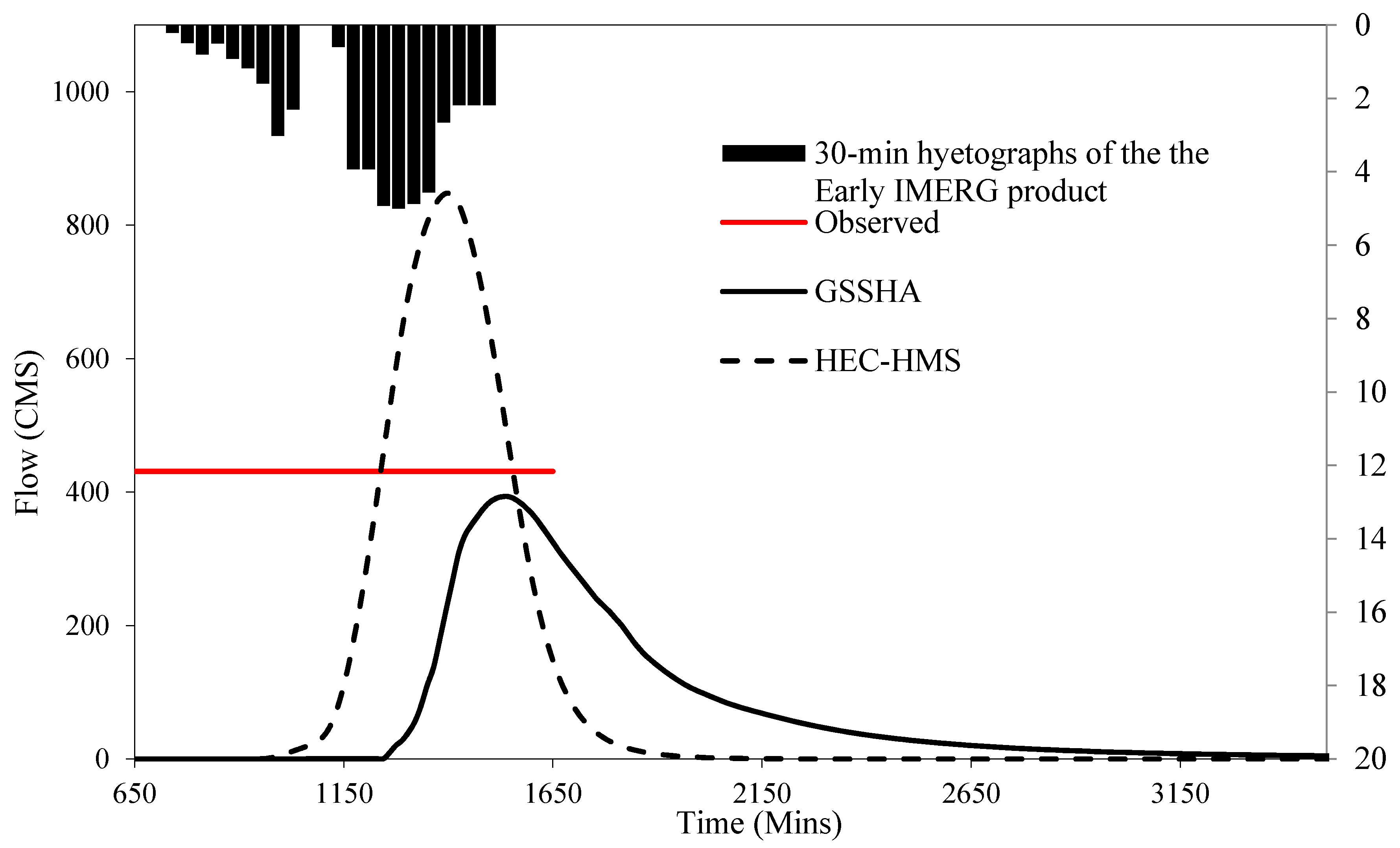
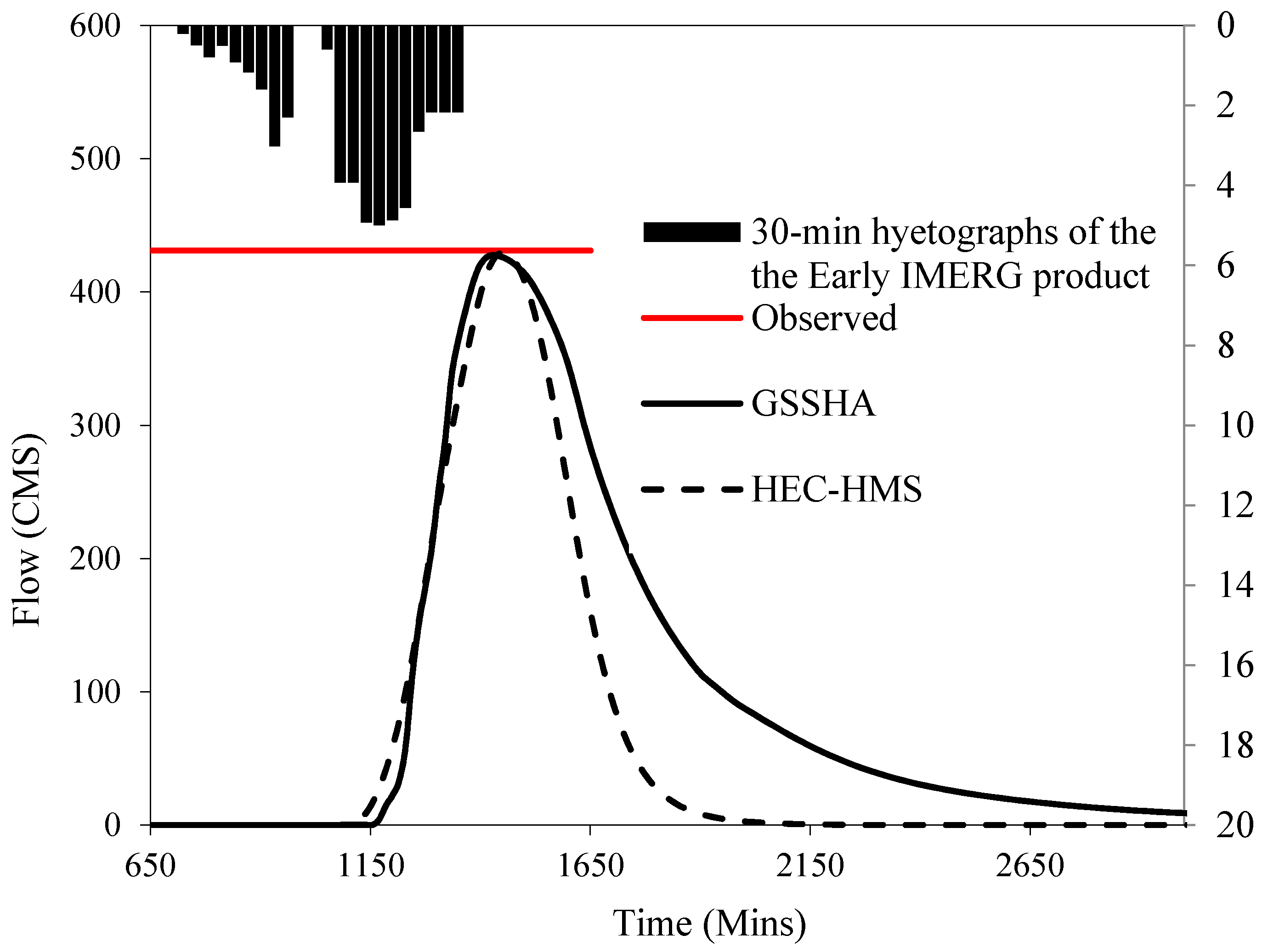
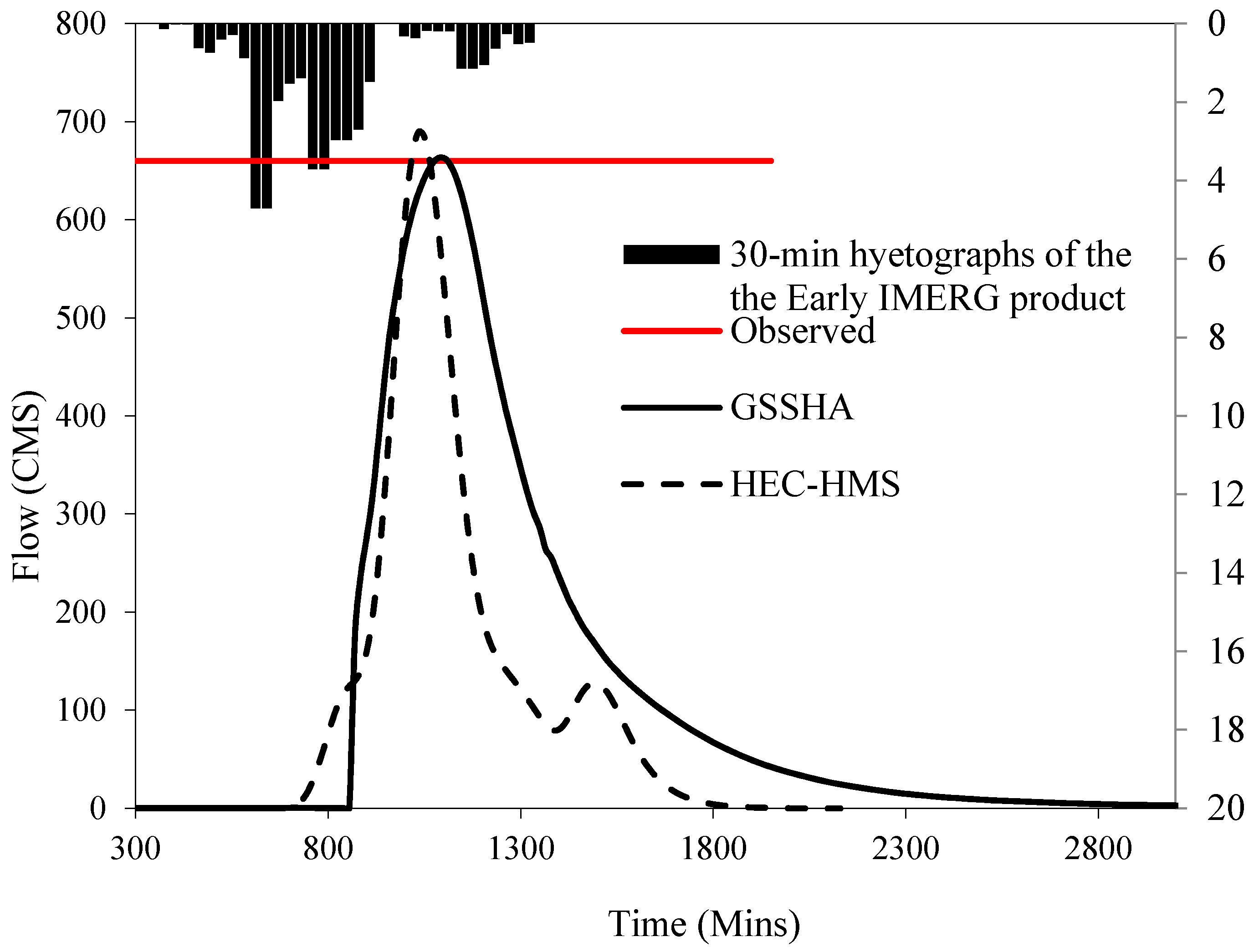

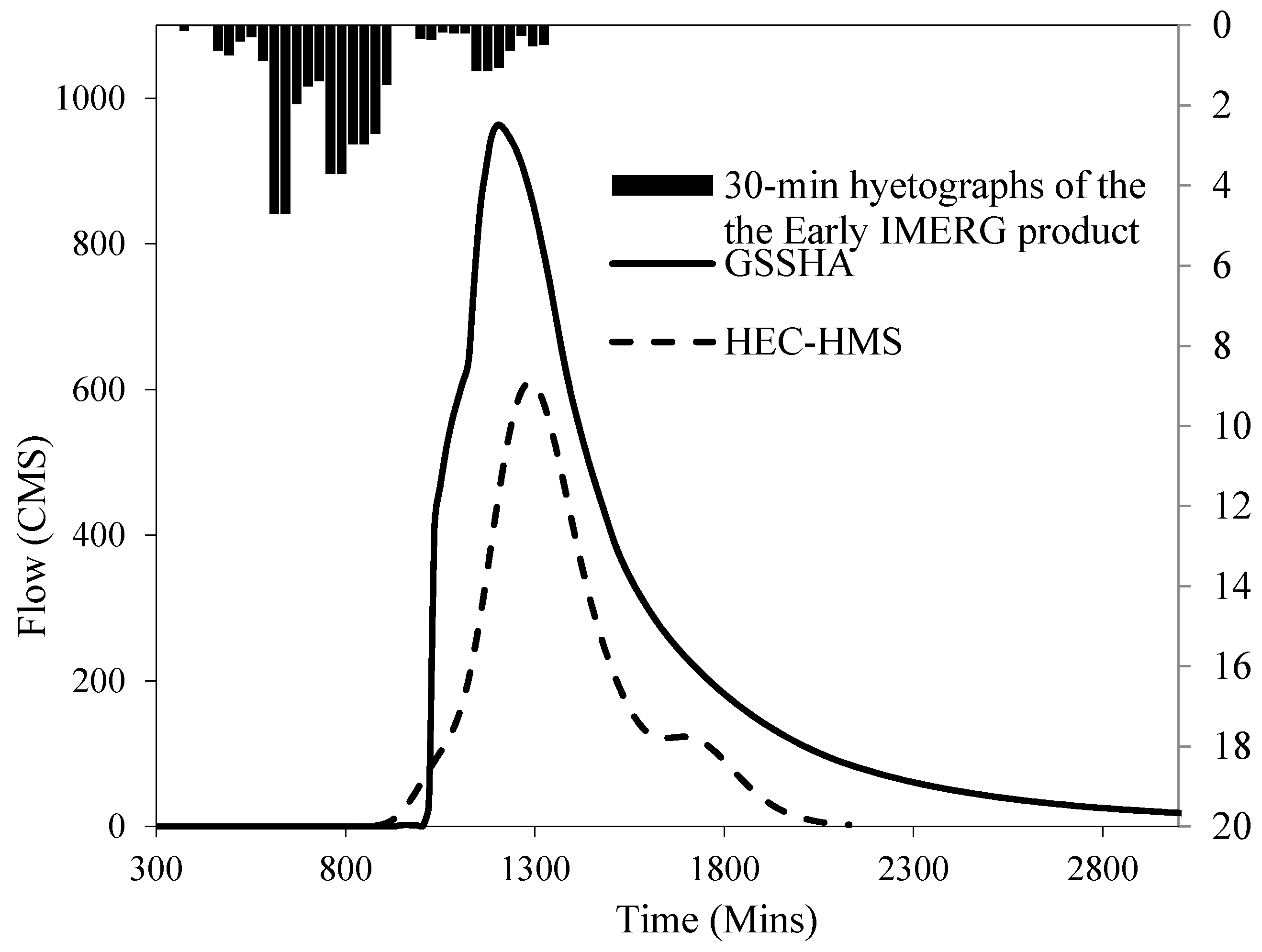
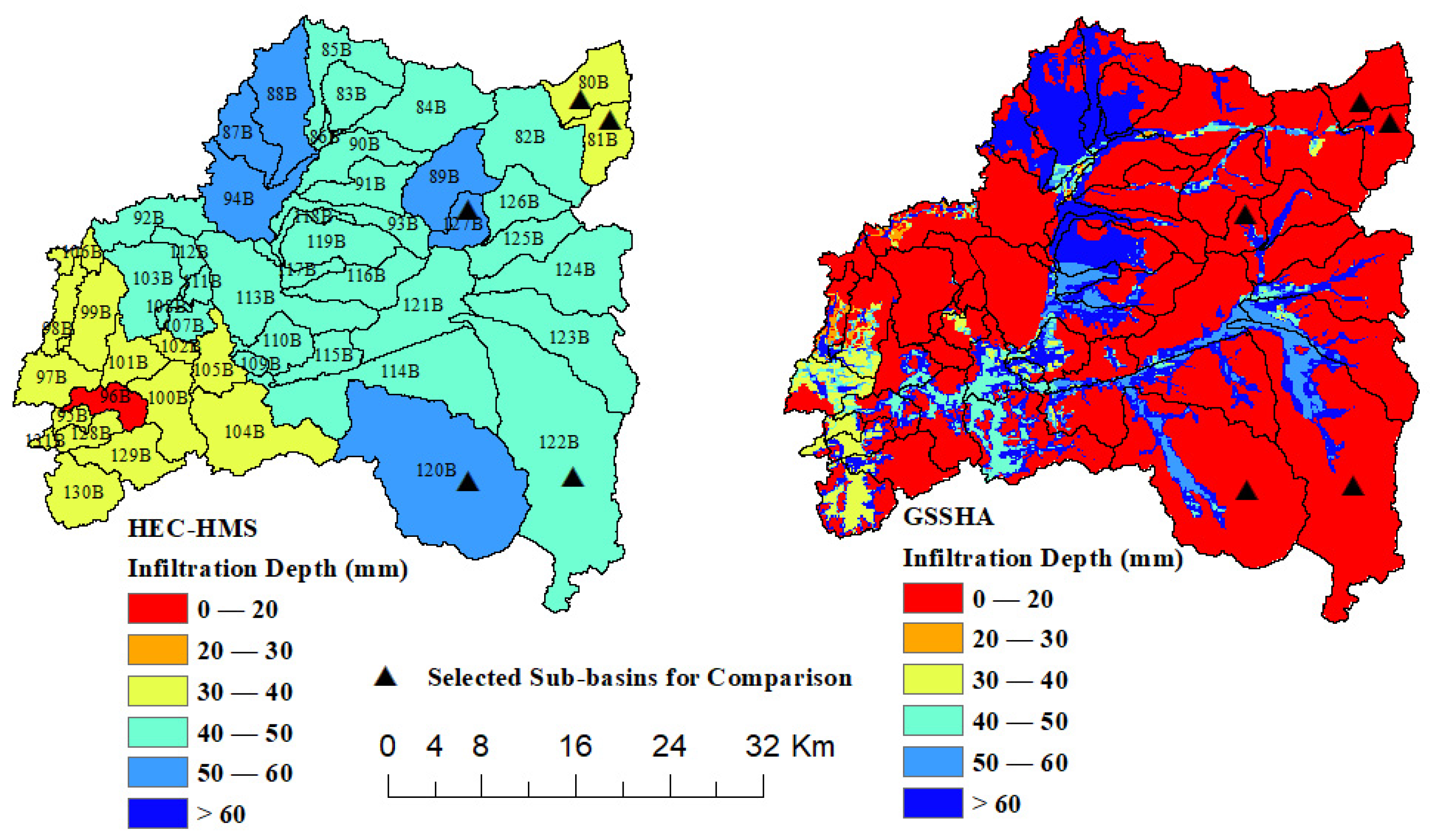
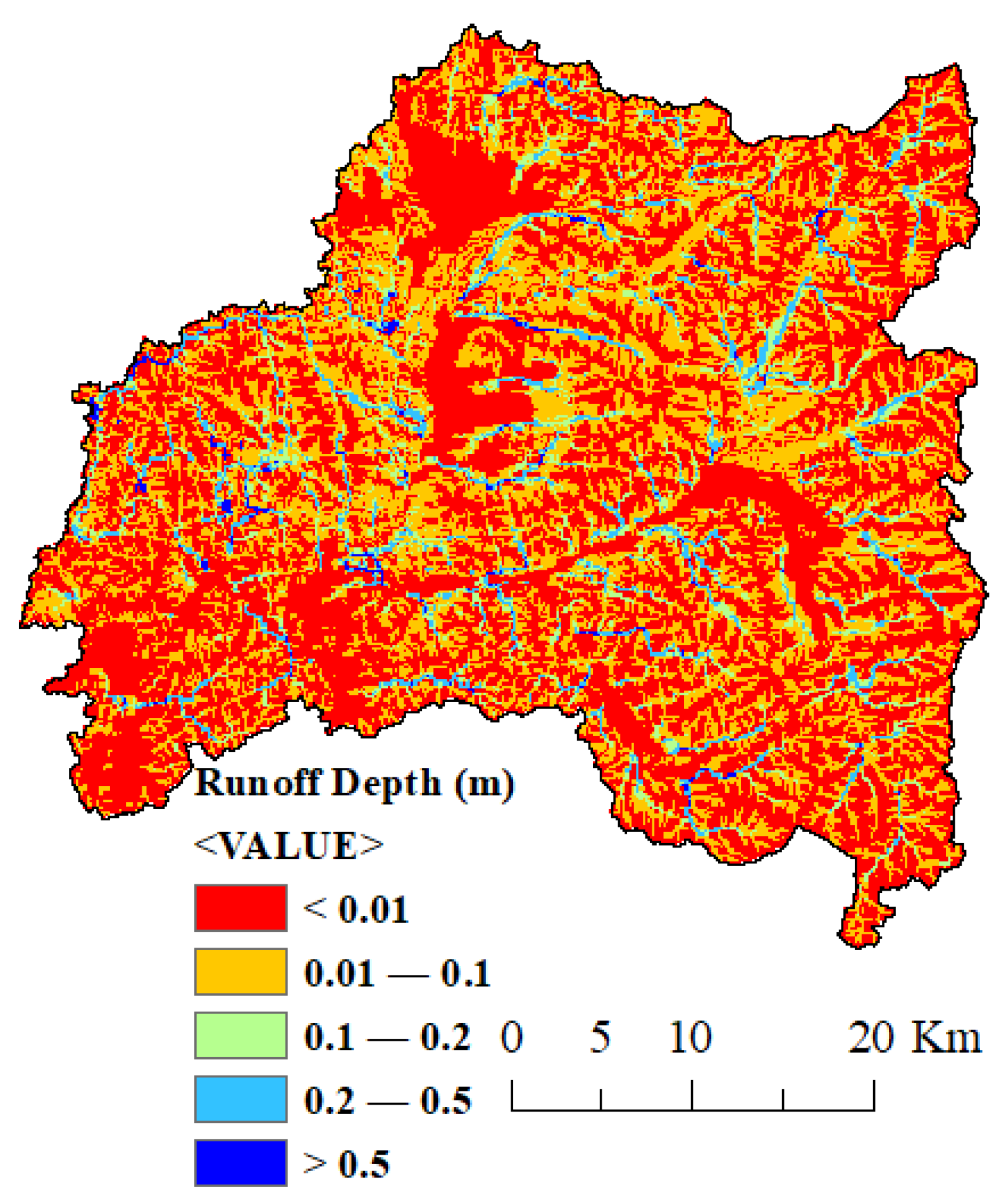
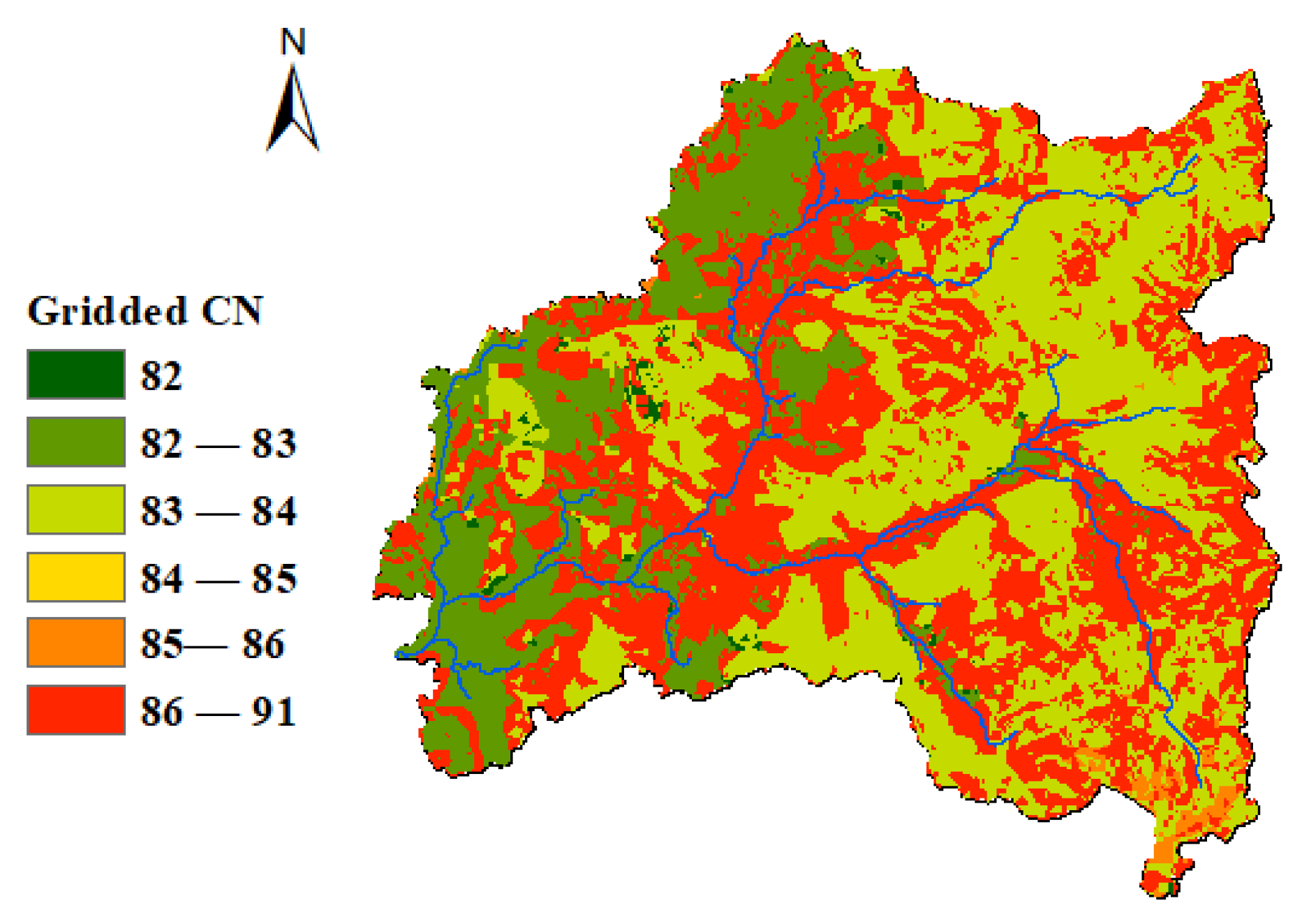
| Return Period | 2 | 5 | 10 | 25 | 50 | 100 |
|---|---|---|---|---|---|---|
| Rainfall (mm) | 28 | 48 | 64 | 88 | 107 | 129 |
| Model | Peak Discharge (m3/s) | Runoff Volume (m3) | Error in Peak Discharge (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 13 February 2010 | 3 November 2018 | 13 February 2010 | 3 November 2018 | 13 February 2010 | 3 November 2018 | ||||
| Before Calibration | After Calibration | Validation | Before Calibration | After Calibration | Validation | Before Calibration | After Calibration | Validation | |
| GSSHA | 393.2 | 427.6 | 663.6 | 12,866,921 | 14,311,943.5 | 19,455,825.4 | 8.8 | −0.8 | 0.6 |
| HEC-HMS | 847.9 | 429.5 | 689.8 | 17,150,300 | 8,882,200 | 11,933,600 | 96.7 | 0.3 | 4.5 |
| Basin | Model | Peak Discharge (m3) | Runoff Volume (m3) | Differences (%) | |
|---|---|---|---|---|---|
| Peak Discharge | Runoff Volume | ||||
| 80B | HEC-HMS | 8.1 | 78,300 | 78.5 | 92.9 |
| GSSHA | 37.6 | 1,097,316 | |||
| 81B | HEC-HMS | 9.1 | 90,100 | 78 | 90.8 |
| GSSHA | 41.3 | 978,141 | |||
| 127B | HEC-HMS | 23.4 | 335,400 | 59.2 | 77.7 |
| GSSHA | 57.3 | 1,505,590 | |||
| 120B | HEC-HMS | 135.4 | 1,882,000 | 26.9 | 59.5 |
| GSSHA | 185.1 | 4,646,771 | |||
| 122B | HEC-HMS | 131 | 1,907,500 | 41.8 | 63 |
| GSSHA | 225.1 | 5,152,439 | |||
| Model | Direct Runoff/Overland Flow Routing | Runoff Volume Computation/Infiltration | Channel Flow Routing |
|---|---|---|---|
| HEC-HMS semi-distributed (SCS-UH) | SCS unit hydrograph | SCS curve number | Muskingum |
| HEC-HMS semi-distributed(C-UH) | Clark unit hydrograph | SCS curve number | Muskingum |
| HEC-HMS ModClark | Clark unit hydrograph | Gridded SCS curve number | Muskingum |
| GSSHA | Two-dimensional diffusive wave routing | Green and Ampt with redistribution (GAR) | One-dimensional diffusive wave |
| Model Type | Rainfall (m3) | Runoff Volume (m3) | Runoff (%) | Losses (m3) | Losses (%) | Peak Discharge (m3/s) |
|---|---|---|---|---|---|---|
| GSSHA | 94,788,583 | 37,622,799 | 39.7 | 53,142,119 | 56.1 | 858.6 |
| HEC-HMS ModClark | 94,963,200 | 40,485,600 | 42.6 | 54,241,500 | 57.1 | 521.5 |
| HEC-HMS (Semi-distributed using SCS transform method) | 94,894,200 | 39,013,400 | 41.1 | 55,880,800 | 58.9 | 1536.1 |
| HEC-HMS (Semi-distributed using Clark transform method) | 94,894,200 | 39,013,400 | 41.1 | 55,880,800 | 58.9 | 1026.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Areeq, A.M.; Al-Zahrani, M.A.; Sharif, H.O. The Performance of Physically Based and Conceptual Hydrologic Models: A Case Study for Makkah Watershed, Saudi Arabia. Water 2021, 13, 1098. https://doi.org/10.3390/w13081098
Al-Areeq AM, Al-Zahrani MA, Sharif HO. The Performance of Physically Based and Conceptual Hydrologic Models: A Case Study for Makkah Watershed, Saudi Arabia. Water. 2021; 13(8):1098. https://doi.org/10.3390/w13081098
Chicago/Turabian StyleAl-Areeq, Ahmed M., Muhammad A. Al-Zahrani, and Hatim O. Sharif. 2021. "The Performance of Physically Based and Conceptual Hydrologic Models: A Case Study for Makkah Watershed, Saudi Arabia" Water 13, no. 8: 1098. https://doi.org/10.3390/w13081098
APA StyleAl-Areeq, A. M., Al-Zahrani, M. A., & Sharif, H. O. (2021). The Performance of Physically Based and Conceptual Hydrologic Models: A Case Study for Makkah Watershed, Saudi Arabia. Water, 13(8), 1098. https://doi.org/10.3390/w13081098







