Numerical Investigation on the Kinetic Characteristics of the Yigong Debris Flow in Tibet, China
Abstract
:1. Introduction
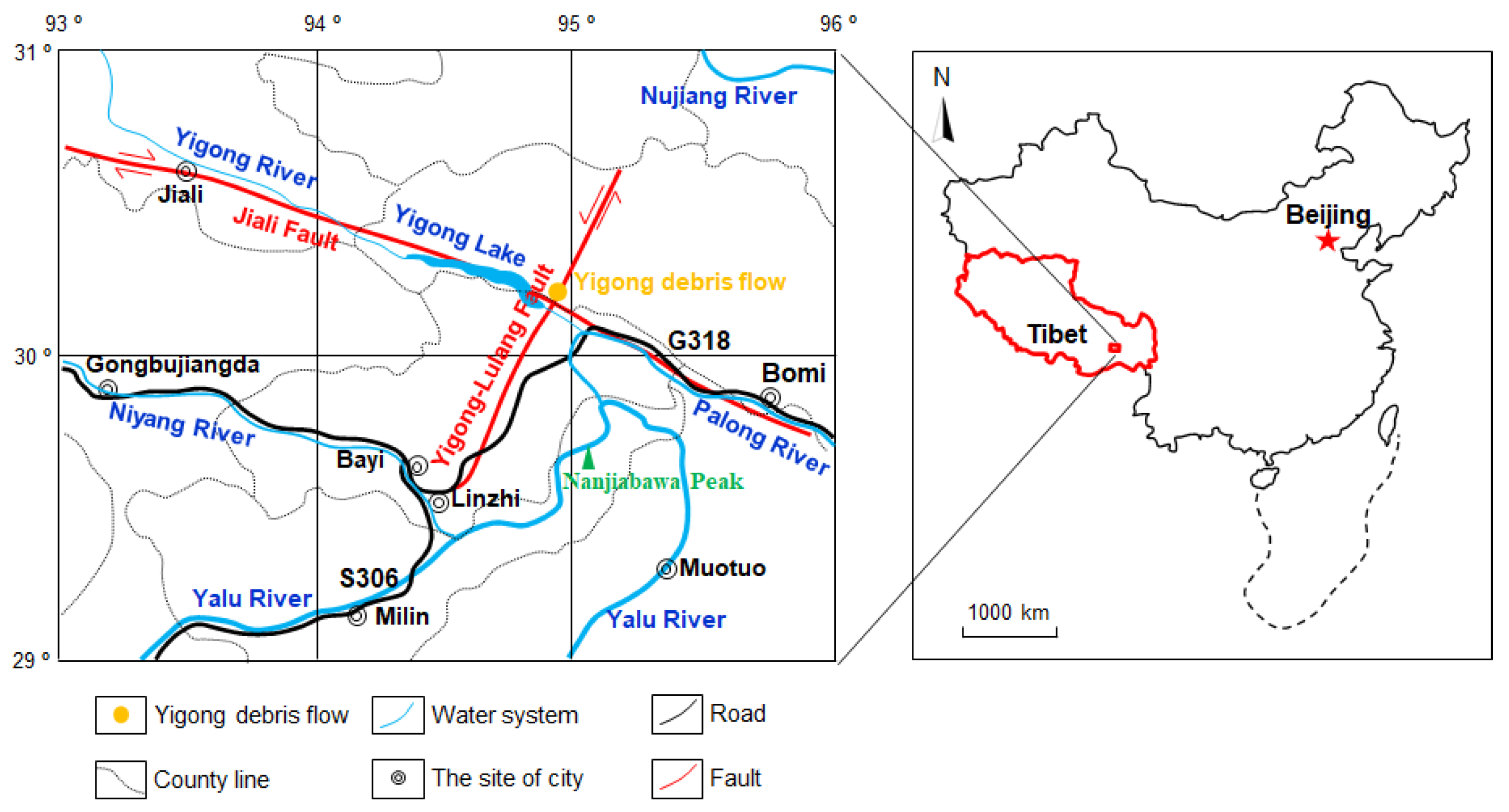
2. Geological Setting and Debris Flow Features
2.1. Geological Setting
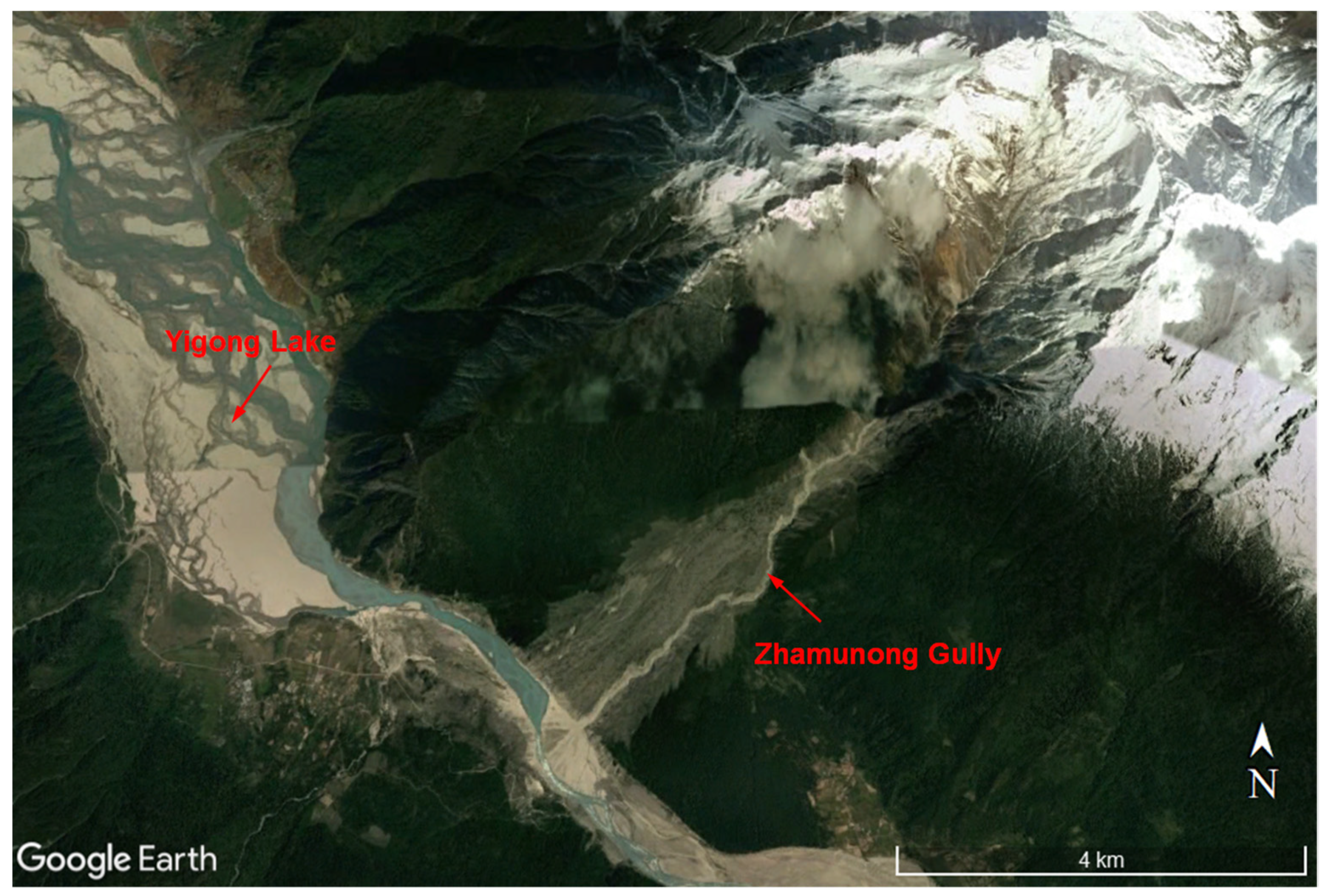
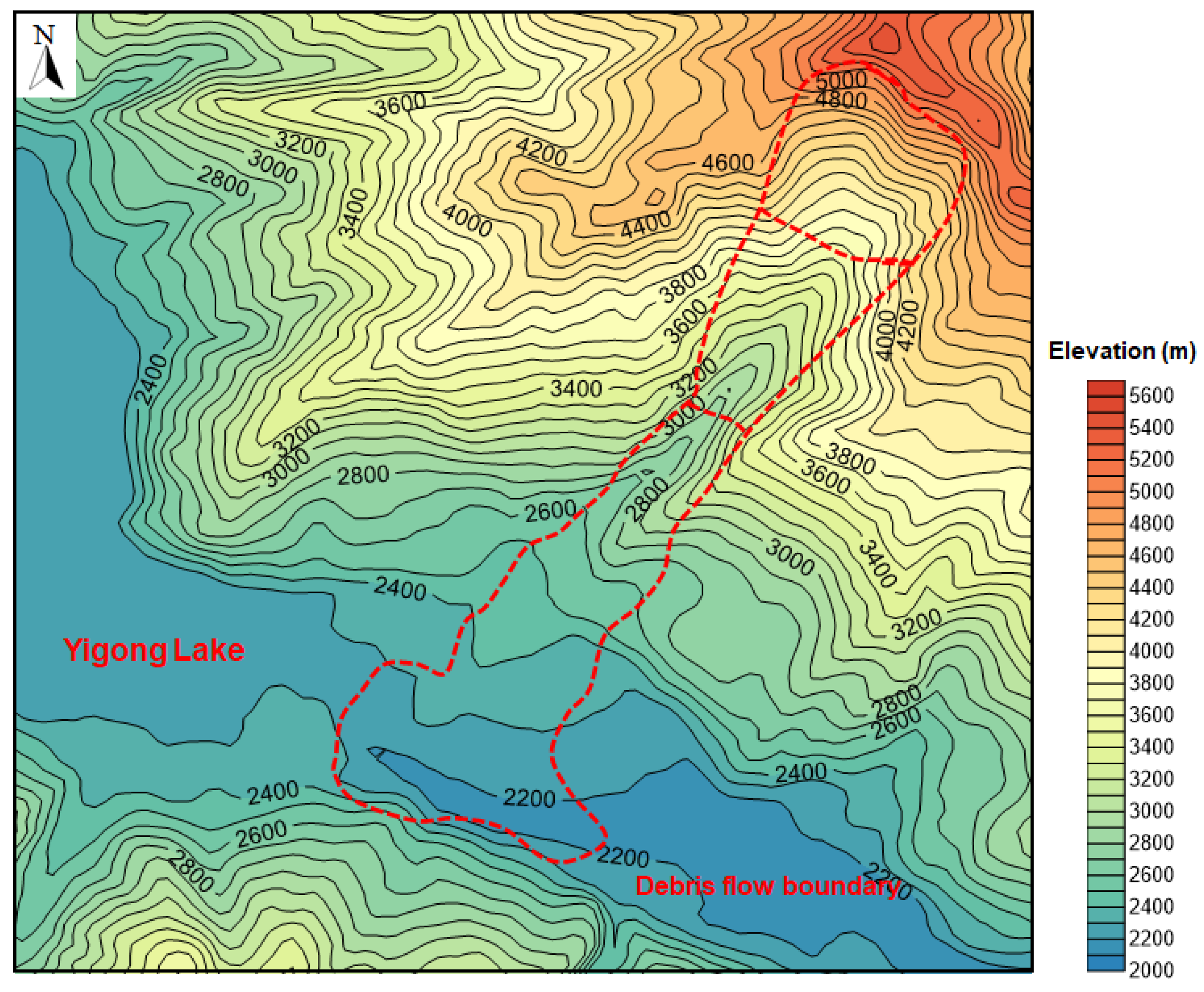
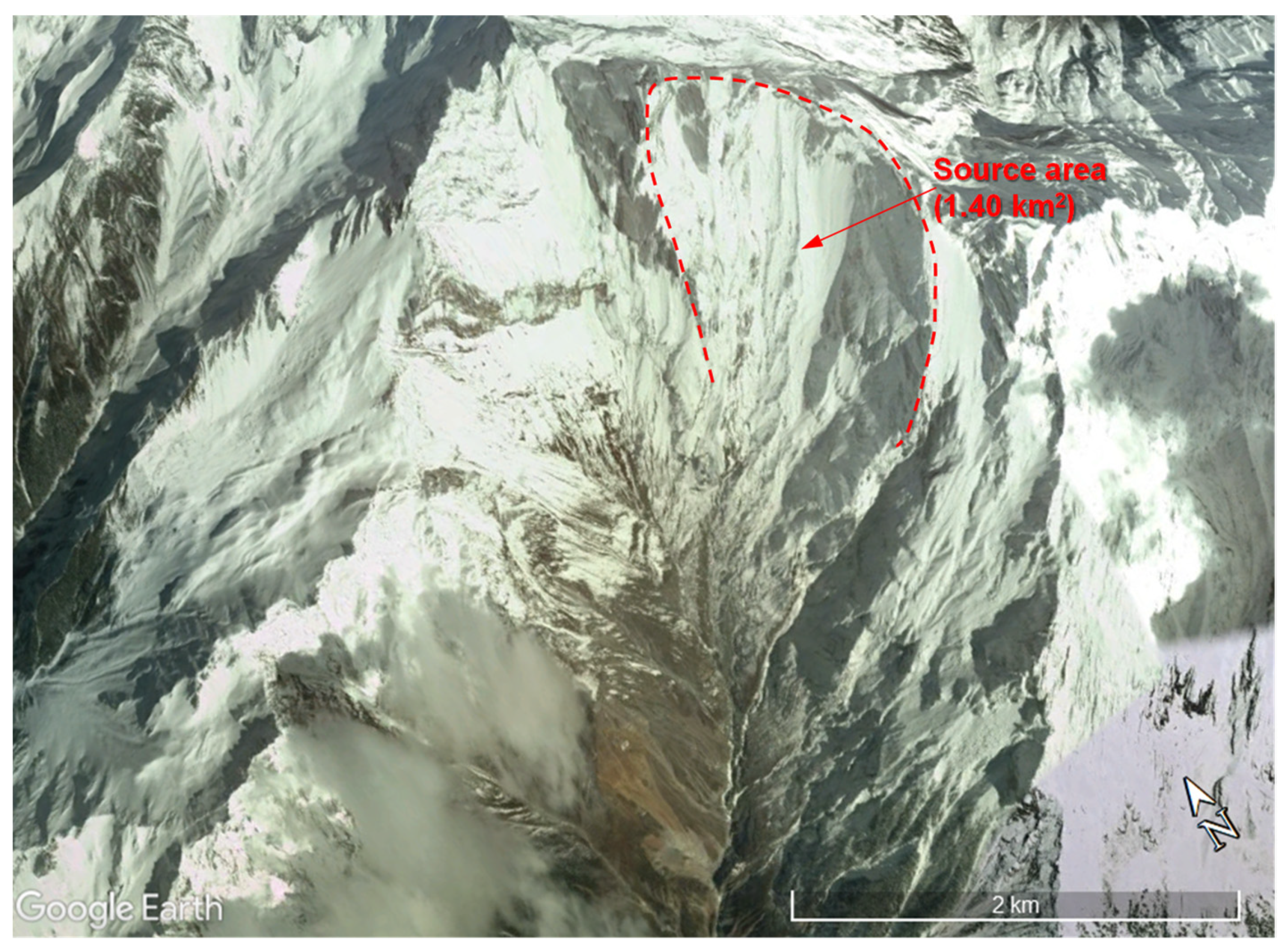
2.2. Debris Flow Features
2.2.1. Source Zone
2.2.2. Propagation Zone
2.2.3. Deposit Zone
3. Numerical Model
3.1. SPH Algorithm
3.2. SPH Model of the Yigong Debris Flow
3.2.1. Material Model
3.2.2. Boundary Treatment
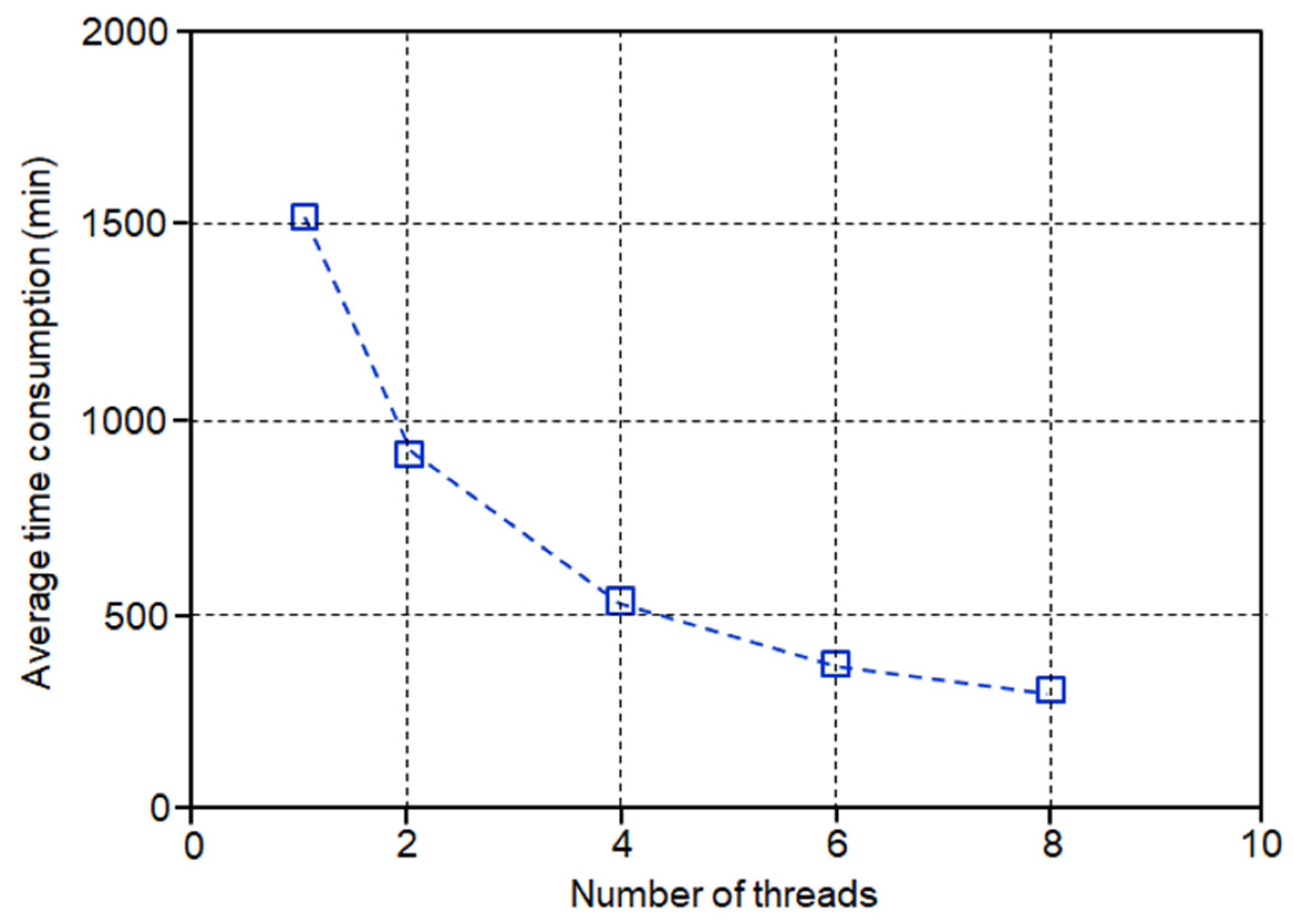
3.2.3. OpenMP Parallelism
3.2.4. Time Integration
4. Kinetic Characteristics of the Yigong Debris Flow
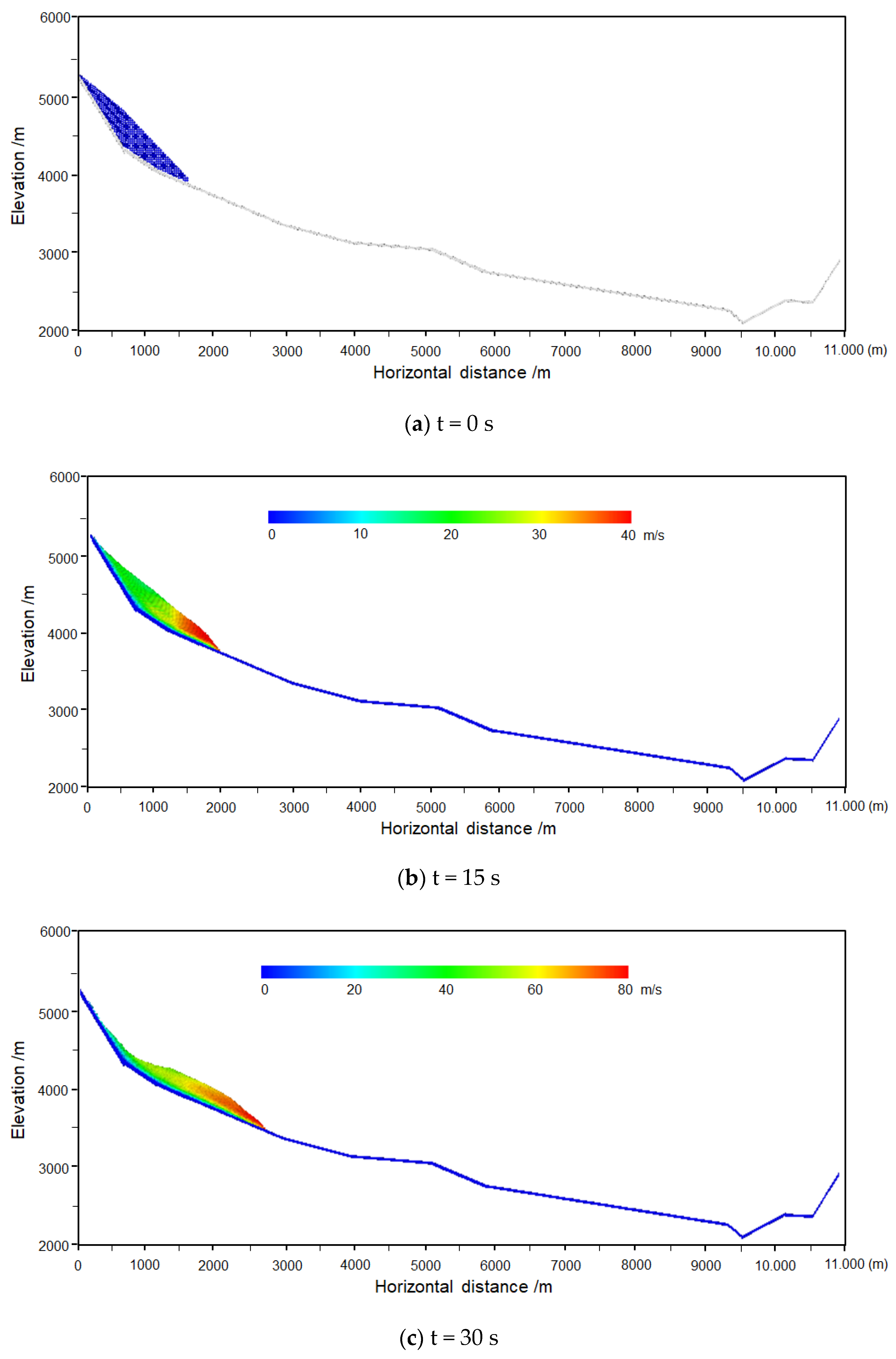
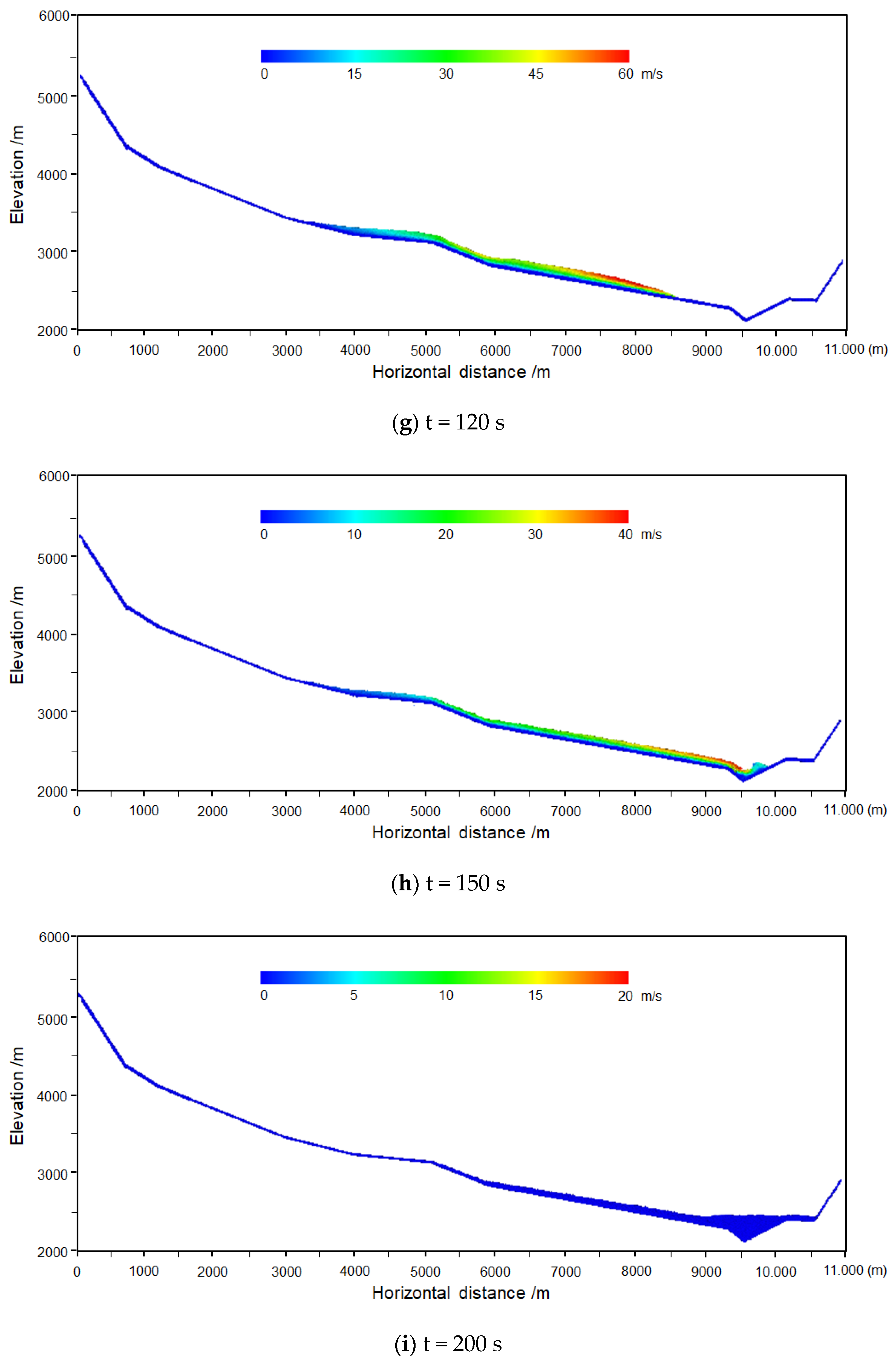
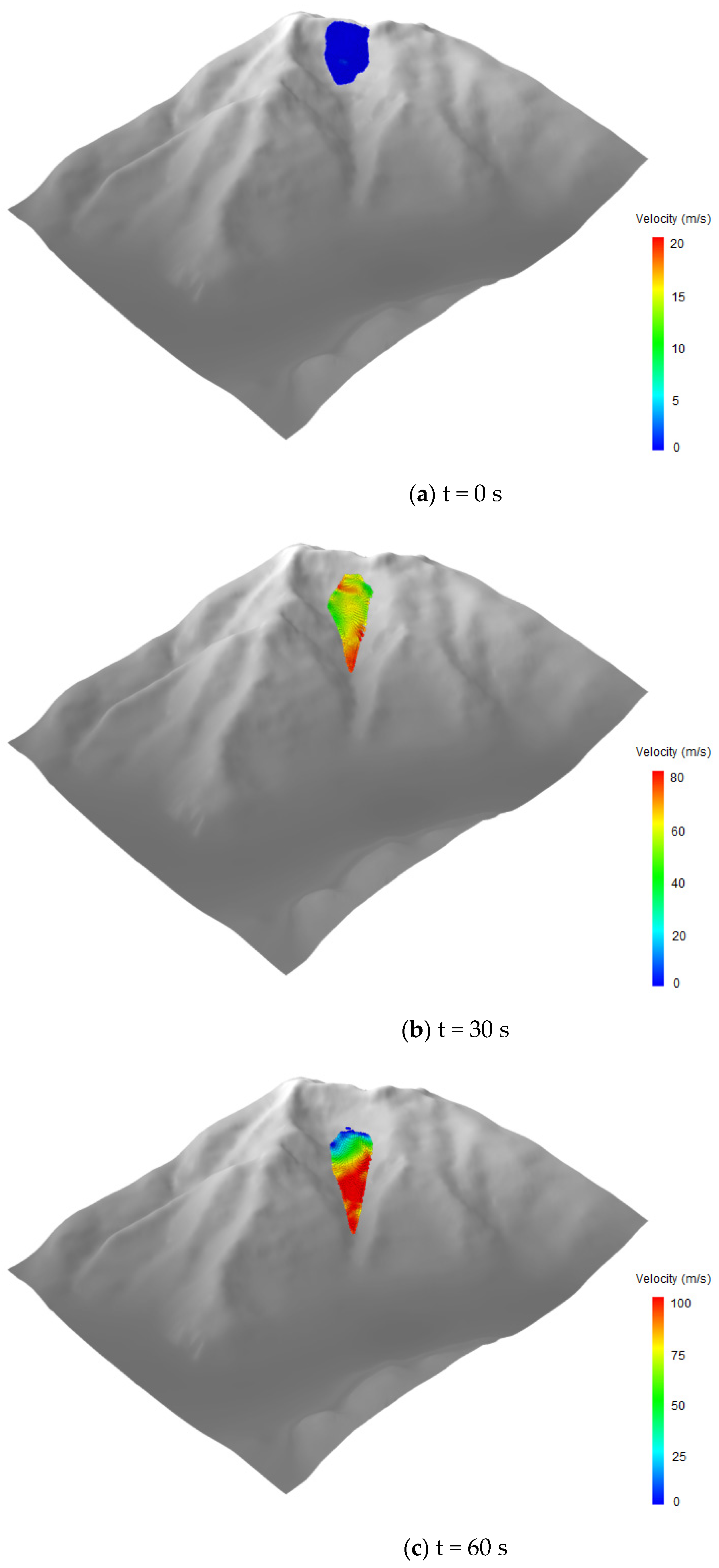
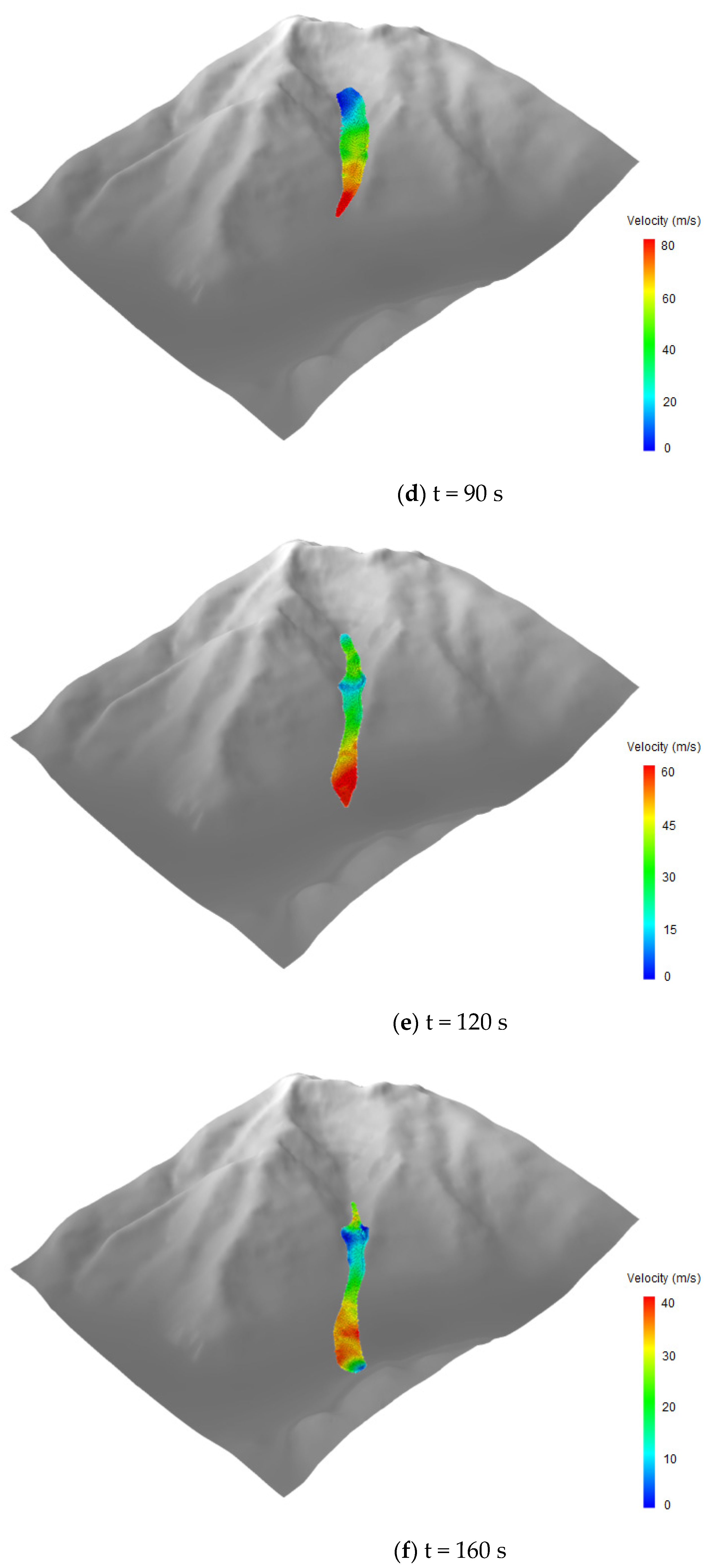
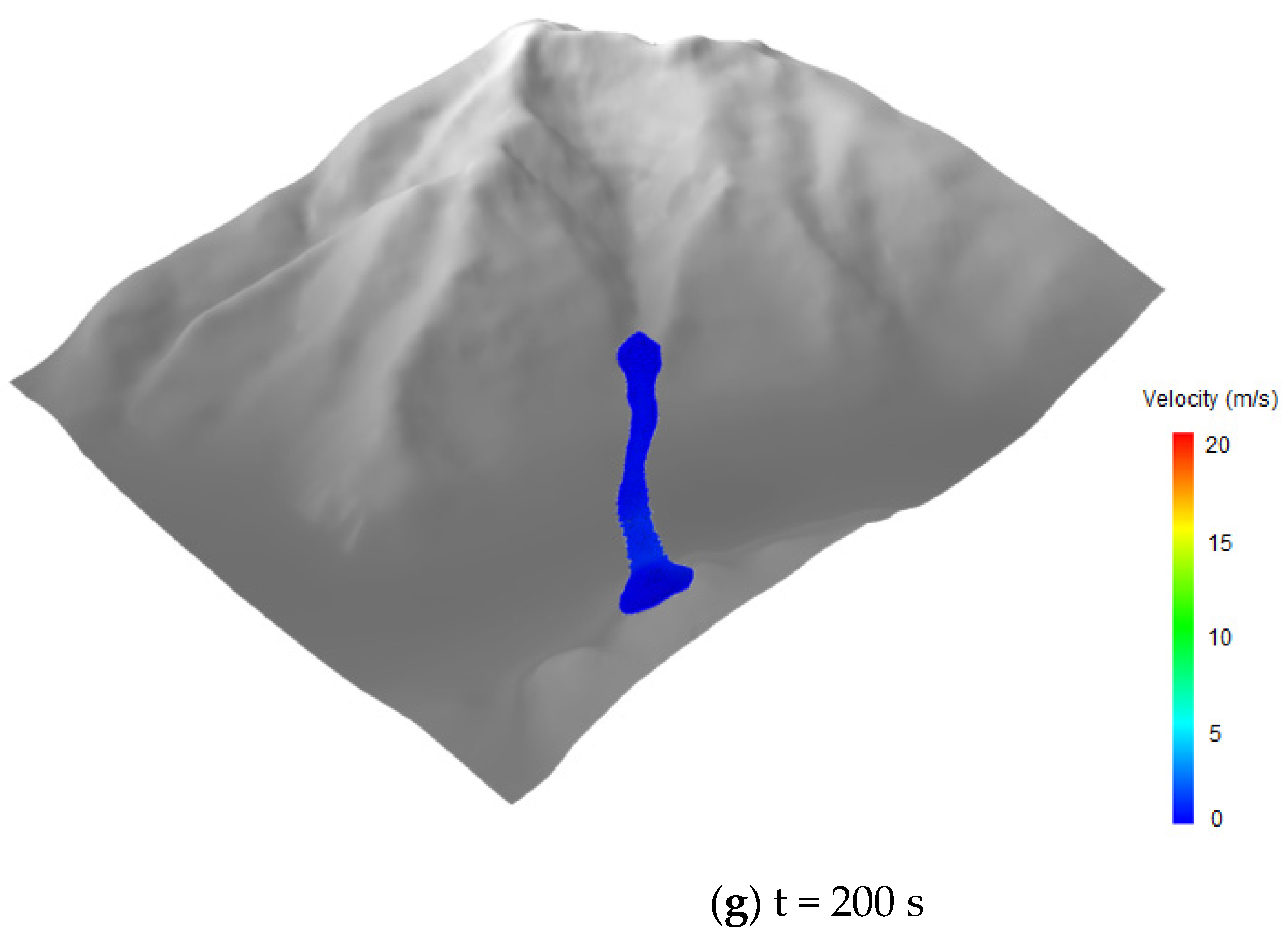
4.1. Two-Dimensional Modeling
4.2. Three-Dimensional Modeling
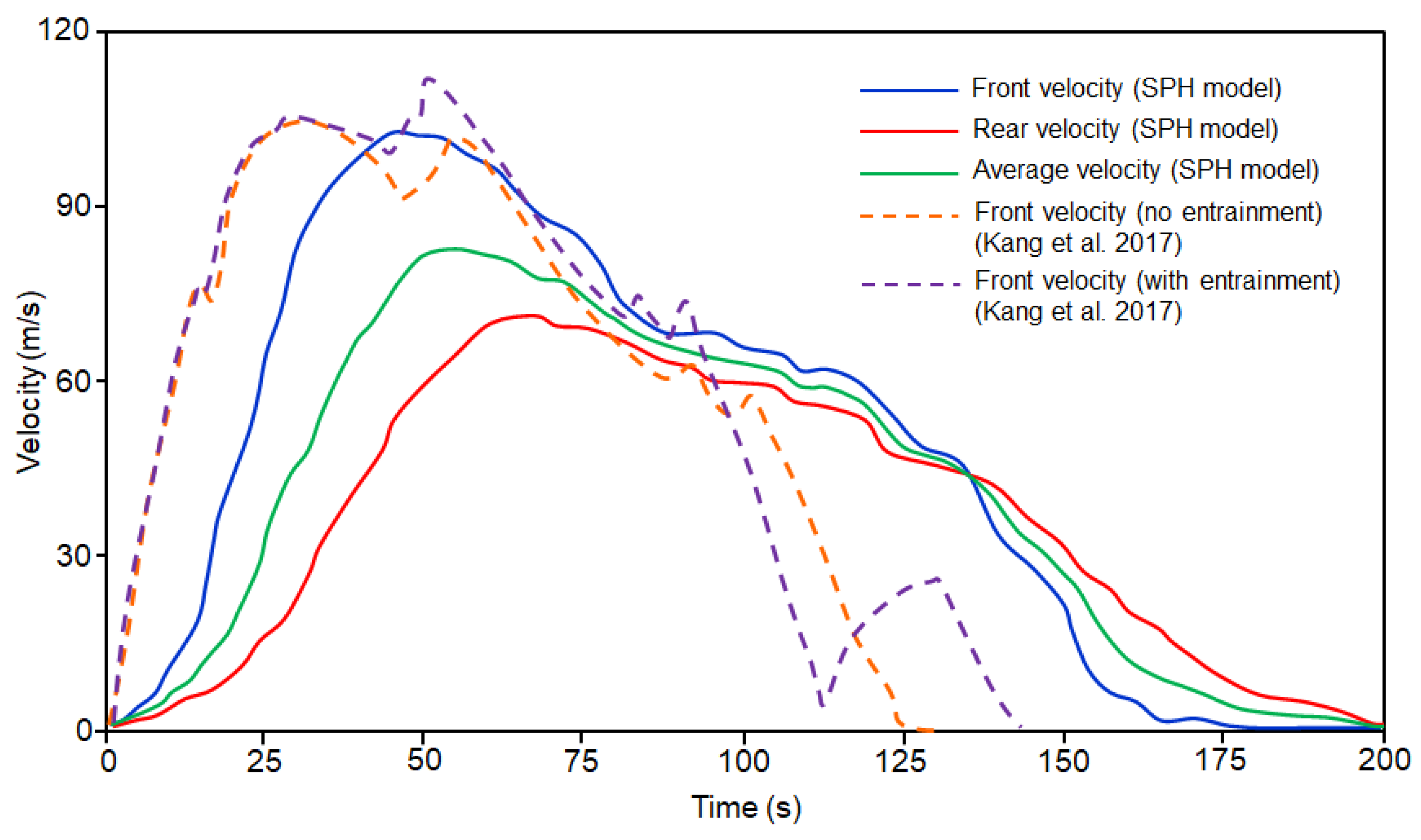
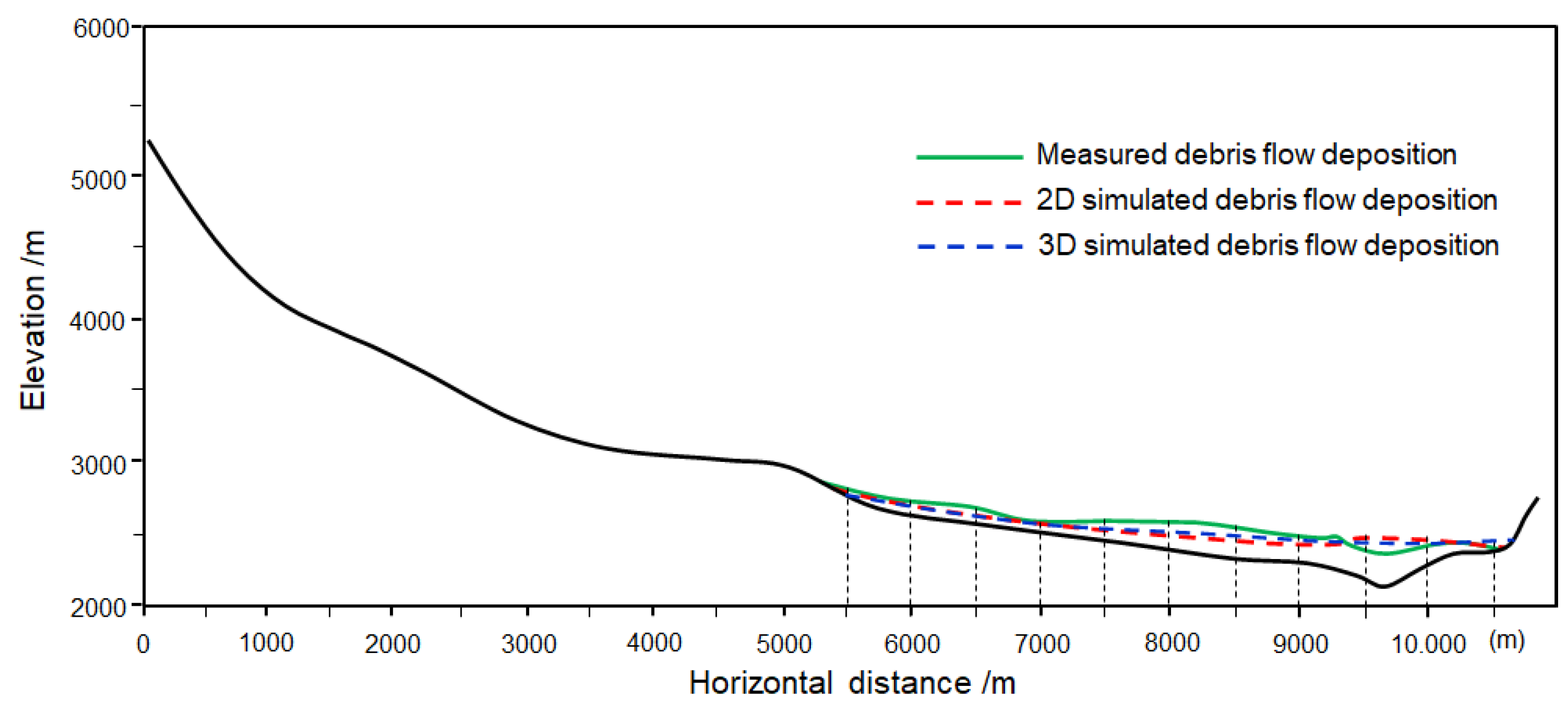
4.3. Analysis of Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zou, Q.; Cui, P.; Jiang, H.; Wang, J.; Li, C.; Zhou, B. Analysis of regional river blocking by debris flows in response to climate change. Sci. Total Environ. 2020, 741, 140262. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.Q. Large-scale landslides and their sliding mechanisms in China since the 20th century. Chin. J. Rock Mech. Eng. 2007, 26, 433–454, (In Chinese with English abstract). [Google Scholar]
- Shang, Y.J.; Yue, Z.Q.; Yang, Z.F.; Wang, Y.C.; Liu, D.A. Addressing severe slope failure hazards along Sichuan-Tibet highway in southwestern China. Epis. Newsmag. Int. Union Geol. Sci. 2003, 26, 94–104. [Google Scholar]
- Zou, Z.X.; Tang, H.M.; Xiong, C.R.; Su, A.J.; Criss, R.E. Kinetic characteristics of debris flows as exemplified by field investigations and discrete element simulation of the catastrophic Jiweishan rockslide, China. Geomorphology 2017, 295, 1–15. [Google Scholar] [CrossRef]
- Leonardi, A.; Pirulli, M. Analysis of the load exerted by debris flows on filter barriers: Comparison between numerical results and field measurements. Comput. Geotech. 2020, 118, 103311. [Google Scholar] [CrossRef]
- Liu, S.L.; Zhang, J.C.; Cheng, X.; Wang, W.B.; Jiang, H.T. Gradation and Rheological Characteristics of Glacial Debris Flow along the Kangding-Linzhi Section of Sichuan-Tibet Railway. Adv. Civ. Eng. 2020, 2020, 8886137. [Google Scholar]
- Chang, M.; Liu, Y.; Zhou, C.; Che, H.X. Hazard assessment of a catastrophic mine waste debris flow of Hou Gully, Shimian, China. Eng. Geol. 2020, 275, 105733. [Google Scholar] [CrossRef]
- Ma, C.; Deng, J.Y.; Wang, R. Analysis of the triggering conditions and erosion of a runoff-triggered debris flow in Miyun County, Beijing, China. Landslides 2018, 15, 2475–2485. [Google Scholar] [CrossRef]
- Xiong, J.; Tang, C.; Chen, M.; Zhang, X.Z.; Shi, Q.Y.; Gong, L.F. Activity characteristics and enlightenment of the debris flow triggered by the rainstorm on 20 August 2019 in Wenchuan County, China. Bull. Eng. Geol. Environ. 2021, 80, 873–888. [Google Scholar] [CrossRef]
- Fannin, R.J.; Wise, M.P. An empirical-statistical model for debris flow travel distance. Can. Geotech. J. 2001, 38, 982–994. [Google Scholar] [CrossRef]
- Tang, C.; Zhu, J.; Chang, M.; Ding, J.; Qi, X. An empirical-statistical model for predicting debris-flow runout zones in the Wenchuan earthquake area. Quat. Int. 2012, 250, 63–73. [Google Scholar] [CrossRef]
- Huang, J.; Hales, T.C.; Huang, R.Q.; Ju, N.P.; Li, Q.; Huang, Y. A hybrid machine-learning model to estimate potential debris-flow volumes. Geomorphology 2020, 367, 107333. [Google Scholar] [CrossRef]
- Fang, Q.S.; Tang, C.; Chen, Z.H.; Wang, S.Y.; Yang, T. A calculation method for predicting the runout volume of dam-break and non-dam-break debris flows in the Wenchuan earthquake area. Geomorphology 2019, 327, 201–214. [Google Scholar] [CrossRef]
- Zhou, G.G.D.; Li, S.; Song, D.R.; Choi, C.E.; Chen, X.Q. Depositional mechanisms and morphology of debris flow: Physical modelling. Landslides 2019, 16, 315–332. [Google Scholar] [CrossRef]
- Wang, D.P.; Chen, Z.; He, S.M.; Chen, K.J.; Liu, F.M.; Li, M.Q. Physical model experiments of dynamic interaction between debris flow and bridge pier model. Rock Soil Mech. 2019, 40, 3363–3372. [Google Scholar]
- Tan, D.Y.; Yin, J.H.; Qin, J.Q.; Zhu, Z.H.; Feng, W.Q. Experimental study on impact and deposition behaviours of multiple surges of channelized debris flow on a flexible barrier. Landslides 2020, 17, 1577–1589. [Google Scholar] [CrossRef]
- Brighenti, R.; Spaggiari, L.; Segalini, A.; Savi, R.; Capparelli, G. Debris flow impact on a flexible barrier: Laboratory flume experiments and force-based mechanical model validation. Nat. Hazards 2021, 106, 735–756. [Google Scholar] [CrossRef]
- Bowman, E.T.; Laue, J.; Imre, B.; Springman, S.M. Experimental modelling of debris flow behaviour using a geotechnical centrifuge. Can. Geotech. J. 2010, 47, 742–762. [Google Scholar] [CrossRef]
- Milne, F.D.; Brown, M.J.; Knappett, J.A.; Davies, M.C.R. Centrifuge modelling of hillslope debris flow initiation. Catena 2012, 92, 162–171. [Google Scholar] [CrossRef]
- Zhou, J.W.; Cui, P.; Yang, X.G. Dynamic process analysis for the initiation and movement of the Donghekou landslide-debris flow triggered by the Wenchuan earthquake. J. Asian Earth Sci. 2013, 76, 70–84. [Google Scholar] [CrossRef]
- Chen, R.D.; Liu, X.N.; Cao, S.Y.; Guo, Z.X. Numerical simulation of deposit in confluence zone of debris flow and mainstream. Sci. China Technol. Sci. 2011, 54, 2618–2628. [Google Scholar] [CrossRef]
- Cascini, L.; Cuomo, S.; Pastor, M.; Rendina, I. SPH-FDM propagation and pore water pressure modelling for debris flows in flume tests. Eng. Geol. 2016, 213, 74–83. [Google Scholar] [CrossRef]
- Shen, W.; Li, T.L.; Li, P.; Lei, Y.L. Numerical assessment for the efficiencies of check dams in debris flow gullies: A case study. Comput. Geotech. 2020, 122, 103541. [Google Scholar] [CrossRef]
- Lei, M.; Yang, P.; Wang, Y.K.; Wang, X.K. Numerical analyses of the influence of baffles on the dynamics of debris flow in a gully. Arab. J. Geosci. 2020, 13, 1052. [Google Scholar] [CrossRef]
- Zhou, G.G.D.; Du, J.H.; Song, D.R.; Choi, C.E.; Hu, H.S.; Jiang, C.H. Numerical study of granular debris flow run-up against slit dams by discrete element method. Landslides 2020, 17, 585–595. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Sun, D.A.; Xu, Y.F. A new thermal analysis model with three heat conduction layers in the nuclear waste repository. Nucl. Eng. Des. 2021, 317, 110929. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Y.X.; Jia, M.C.; Li, C.N. Numerical Simulation of Failure Behavior of Granular Debris Flows Based on Flume Model Tests. Sci. World J. 2013, 2013, 603130. [Google Scholar] [CrossRef] [Green Version]
- Dai, Z.L.; Huang, Y.; Cheng, H.L.; Xu, Q. SPH model for fluid–structure interaction and its application to debris flow impact estimation. Landslides 2017, 14, 917–928. [Google Scholar] [CrossRef]
- Huang, Y.; Cheng, H.L.; Dai, Z.L.; Xu, Q.; Liu, F.; Sawada, K.; Moriguchi, S.; Yashima, A. SPH-based numerical simulation of catastrophic debris flows after the 2008 Wenchuan earthquake. Bull. Eng. Geol. Environ. 2015, 74, 1137–1151. [Google Scholar] [CrossRef]
- Coussot, P.; Piau, J.M. A large-scale field coaxial cylinder rheometer for the study of the rheology of natural coarse suspensions. J. Rheol. 1995, 39, 105–124. [Google Scholar] [CrossRef]
- Pellegrino, A.M.; Di Santolo, A.S.; Schippa, L. The sphere drag rheometer: A new instrument for analysing mud and debris flow materials. Int. J. Geomate 2016, 11, 2512–2519. [Google Scholar] [CrossRef]
- Pellegrino, A.M.; Scotto di Santolo, A.; Schippa, L. An integrated procedure to evaluate rheological parameters to model debris flows. Eng. Geol. 2015, 196, 88–98. [Google Scholar] [CrossRef]
- Portilla, M.; Chevalier, G.; Hürlimann, M. Description and analysis of the debris flows occurred during 2008 in the Eastern Pyrenees. Nat. Hazards Earth Syst. Sci. 2010, 10, 1635–1645. [Google Scholar] [CrossRef] [Green Version]
- Han, Z.; Su, B.; Li, Y.; Wang, W.; Wang, W.; Huang, J.; Chen, G. Numerical simulation of debris-flow behavior based on the SPH method incorporating the Herschel-Bulkley-Papanastasiou rheology model. Eng. Geol. 2019, 255, 26–36. [Google Scholar] [CrossRef]
- Wang, Z.; You, Y.; Zhang, G.; Feng, T.; Liu, J.; Lv, X.; Wang, D. Superelevation analysis of the debris flow curve in Xiedi gully, China. Bull. Eng. Geol. Environ. 2021, 80, 967–978. [Google Scholar] [CrossRef]
- Xu, Q.; Shang, Y.; van Asch, T.; Wang, S.; Zhang, Z.; Dong, X. Observations from the large, rapid Yigong rock slide—debris avalanche, southeast Tibet. Can. Geotech. J. 2012, 49, 589–606. [Google Scholar] [CrossRef]
- Shang, Y.J.; Yang, Z.F.; Li, L.H.; Liu, D.; Liao, Q.L.; Wang, Y.C. A super-large landslide in Tibet in 2000: Background, occurrence, disaster, and origin. Geomorphology 2003, 4, 225–243. [Google Scholar] [CrossRef]
- Zhou, J.W.; Cui, P.; Hao, M.H. Comprehensive analyses of the initiation and entrainment processes of the 2000 Yigong catastrophic landslide in Tibet, China. Landslides 2016, 13, 39–54. [Google Scholar] [CrossRef]
- Lee, H.Y.; Chung, S.L.; Wang, J.R.; Wen, D.J.; Lo, C.H.; Yang, T.F.; Zhang, Y.; Xie, Y.; Lee, T.Y.; Wu, G.; et al. Miocene Jiali faulting and its implications for Tibetan tectonic evolution. Earth Planet. Sci. Lett. 2003, 205, 185–194. [Google Scholar] [CrossRef] [Green Version]
- Kang, C.; Chan, D.; Su, F.; Cui, P. Runout and entrainment analysis of an extremely large rock avalanche—A case study of Yigong, Tibet, China. Landslides 2017, 14, 123–139. [Google Scholar] [CrossRef]
- Li, J.; Chen, N.S.; Zhao, Y.D.; Liu, M.; Wang, W.Y. A catastrophic landslide triggered debris flow in China’s Yigong: Factors, dynamic processes, and tendency. Earth Sci. Res. J. 2020, 24, 71–82. [Google Scholar] [CrossRef] [Green Version]
- Yin, Y.P. Characteristics of Bomi–Yigong huge high speed landslide in Tibet and the research on disaster prevention. Hydrogeol. Eng. Geol. 2000, 4, 8–11, (In Chinese with English abstract). [Google Scholar]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherial stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Dai, Z.L.; Huang, Y.; Cheng, H.L.; Xu, Q. 3D numerical modeling using smoothed particle hydrodynamics of flow-like landslide propagation triggered by the 2008 Wenchuan earthquake. Eng. Geol. 2014, 180, 21–33. [Google Scholar] [CrossRef]
- Dai, Z.L.; Huang, Y.; Xu, Q. A hydraulic soil erosion model based on a weakly compressible smoothed particle hydrodynamics method. Bull. Eng. Geol. Environ. 2019, 78, 5853–5864. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A. Frequency analysis and control of sloshing coupled by elastic walls and foundation with smoothed particle hydrodynamics method. J. Sound Vib. 2020, 476, 115310. [Google Scholar] [CrossRef]
- Price, D.J.; Laibe, G. A solution to the overdamping problem when simulating dust-gas mixtures with smoothed particle hydrodynamics. Mon. Not. R. Astron. Soc. 2020, 495, 3929–3934. [Google Scholar] [CrossRef]
- Ma, C.; Iijima, K.; Oka, M. Nonlinear waves in a floating thin elastic plate, predicted by a coupled SPH and FEM simulation and by an analytical solution. Ocean Eng. 2020, 204, 107243. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Monaghan, J.J.; Gingold, R.A. Shock simulation by the particle method SPH. J. Comput. Phys. 1983, 52, 374–389. [Google Scholar] [CrossRef]
- Zheng, B.; Chen, Z. A multiphase smoothed particle hydrodynamics model with lower numerical diffusion. J. Comput. Phys. 2019, 382, 177–201. [Google Scholar] [CrossRef]
- Zhang, W.J.; Ji, J.; Gao, Y.F. SPH-based analysis of the post-failure flow behavior for soft and hard interbedded earth slope. Eng. Geol. 2020, 267, 105446. [Google Scholar] [CrossRef]
- Hungr, O. A model for the runout analysis of rapid flow slides, debris flows, and avalanches. Can. Geotech. J. 1995, 32, 610–623. [Google Scholar] [CrossRef]
- Rickenmann, D.; Laigle, D.; McArdell, B.W.; Hübl, J. Comparison of 2D debris-flow simulation models with field events. Comput. Geosci. 2006, 10, 241–264. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Chen, G.Q.; Han, Z.; Zhou, S.H.; Zhang, H. 3d numerical simulation of debris-flow motion using sph method incorporating non-newtonian fluid behavior. Nat. Hazards 2016, 81, 1981–1998. [Google Scholar] [CrossRef]
- Fávero Neto, A.H.; Askarinejad, A.; Springman, S.M.; Borja, R.I. Simulation of debris flow on an instrumented test slope using an updated Lagrangian continuum particle method. Acta Geotech. 2020, 15, 2757–2777. [Google Scholar] [CrossRef]
- Schippa, L.; Pavan, S. Numerical modelling of catastrophic events produced by mud or debris flows. Int. J. Saf. Secur. Eng. 2011, 1, 403–423. [Google Scholar] [CrossRef]
- Chen, H.; Lee, C.F. Runout analysis of slurry flows with Bingham model. J. Geotech. Geoenviron. Eng. 2002, 128, 1032–1042. [Google Scholar] [CrossRef]
- Dai, Z.L.; Wang, F.W.; Huang, Y.; Song, K.; Iio, A. SPH-based numerical modeling for the post-failure behavior of the landslides triggered by the 2016 Kumamoto earthquake. Geoenviron. Disasters 2016, 3, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Shen, W.; Hou, X.; Li, T. Numerical simulation of the propagation process of a rapid flow-like landslide considering bed entrainment: A case study. Eng. Geol. 2019, 263, 105287. [Google Scholar] [CrossRef]
- Wang, Y.F.; Dong, J.J.; Cheng, Q.G. Velocity-dependent frictional weakening of large rock avalanche basal facies: Implications for rock avalanche hypermobility? J. Geophys. Res. Solid Earth 2017, 122, 1648–1676. [Google Scholar] [CrossRef]
- Hu, M.J.; Pan, H.L.; Zhu, C.Q.; Wang, F.W. High-speed ring shear tests to study the motion and acceleration processes of the Yigong landslide. J. Mt. Sci. 2015, 12, 1534–1541. [Google Scholar] [CrossRef]
- Marr, J.G.; Elverhøi, A.; Harbitz, C.; Imran, J.; Harff, P. Numerical simulation of mud-rich subaqueous debris flows on the glacially active margins of the Svalbard–Barents Sea. Mar. Geol. 2002, 188, 351–364. [Google Scholar] [CrossRef]
- Beguerı´a, S.; Van Asch, T.W.J.; Malet, J.P.; Gro¨ndahl, S. A GIS based numerical model for simulating the kinematics of mud and debris flows over complex terrain. Nat. Hazards Earth Syst. Sci. 2009, 9, 1897–1909. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.H.; Yue, Z.Q.; Lee, C.F.; Zhu, B.Q.; Wang, Z.H. Satellite image analysis of a huge landslide at Yi Gong, Tibet, China. Q. J. Eng. Geol. Hydrogeol. 2001, 34, 325–332. [Google Scholar] [CrossRef] [Green Version]




| Case | Rheological Parameters of Debris Flow | Relative Error Norm | ||
|---|---|---|---|---|
| η (Pa·s) | c (kPa) | φ (°) | εL2 | |
| 1 | 200 | 0 | 5 | 0.235 |
| 2 | 200 | 0 | 10 | 0.227 |
| 3 | 200 | 0 | 20 | 0.205 |
| 4 | 200 | 10 | 10 | 0.174 |
| 5 | 200 | 20 | 20 | 0.183 |
| 6 | 100 | 10 | 20 | 0.243 |
| 7 | 400 | 10 | 20 | 0.267 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Z.; Xu, K.; Wang, F.; Yang, H.; Qin, S. Numerical Investigation on the Kinetic Characteristics of the Yigong Debris Flow in Tibet, China. Water 2021, 13, 1076. https://doi.org/10.3390/w13081076
Dai Z, Xu K, Wang F, Yang H, Qin S. Numerical Investigation on the Kinetic Characteristics of the Yigong Debris Flow in Tibet, China. Water. 2021; 13(8):1076. https://doi.org/10.3390/w13081076
Chicago/Turabian StyleDai, Zili, Kai Xu, Fawu Wang, Hufeng Yang, and Shiwei Qin. 2021. "Numerical Investigation on the Kinetic Characteristics of the Yigong Debris Flow in Tibet, China" Water 13, no. 8: 1076. https://doi.org/10.3390/w13081076







