Compressor Scheduling and Pressure Control for an Alternating Aeration Activated Sludge Process—A Simulation Study Validated on Plant Data
Abstract
1. Introduction
1.1. The Aeration Process
1.2. State-of-the-Art
1.3. Objectives & Contribution
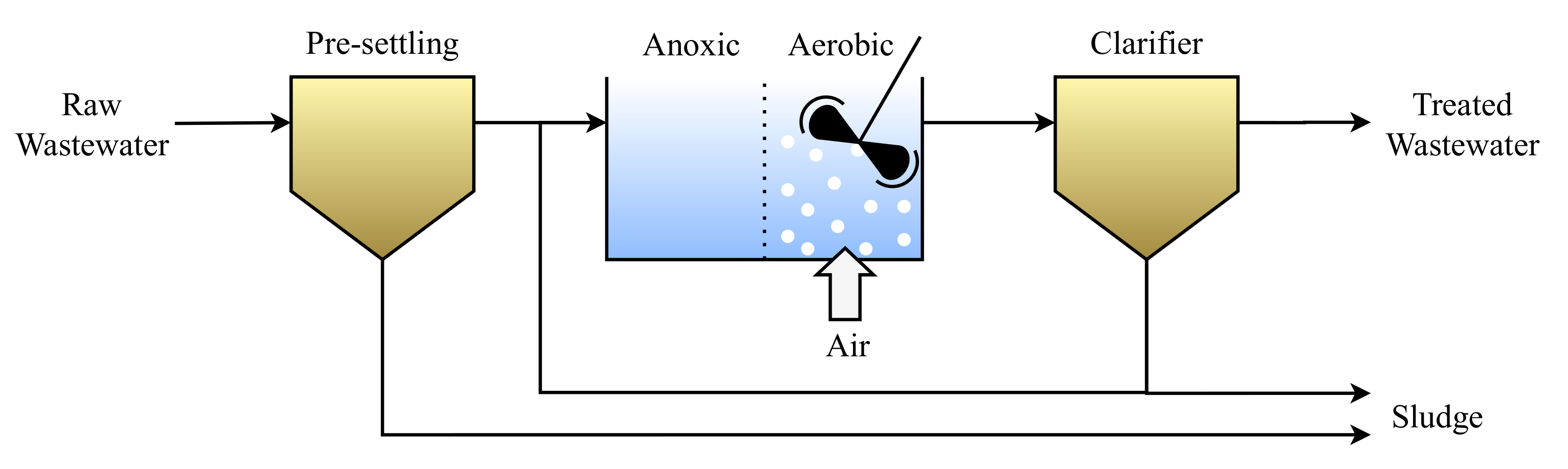
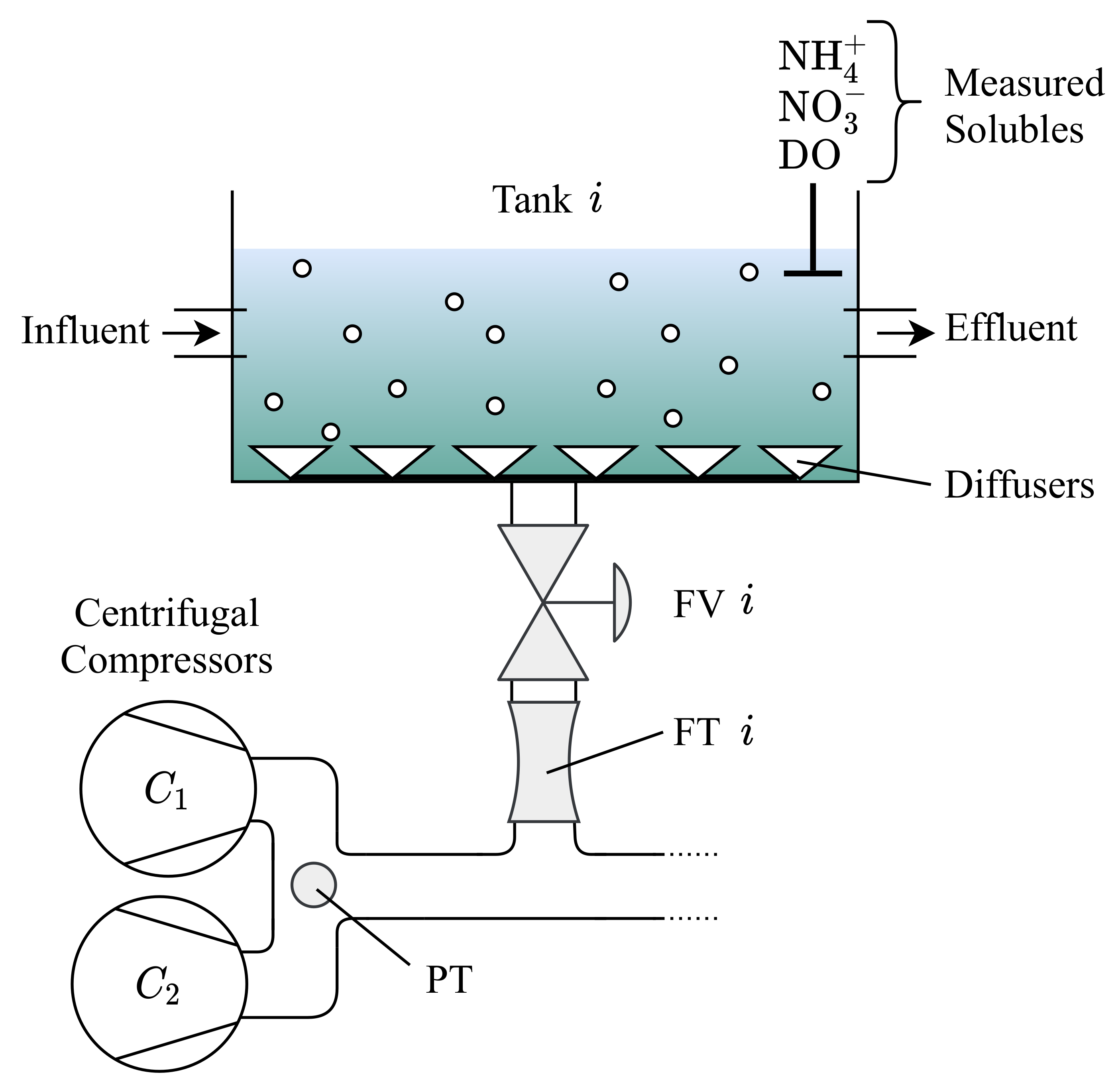
2. Case Plant: Grindsted Wastewater Treatment Plant
- Algorithm 1
- A relational operator determines which compressor to activate depending on the number of completely open valves.
- Algorithm 2
- The DO controller is a relational operator between DO feedback and set-point, meaning the valves are either set completely open or closed.
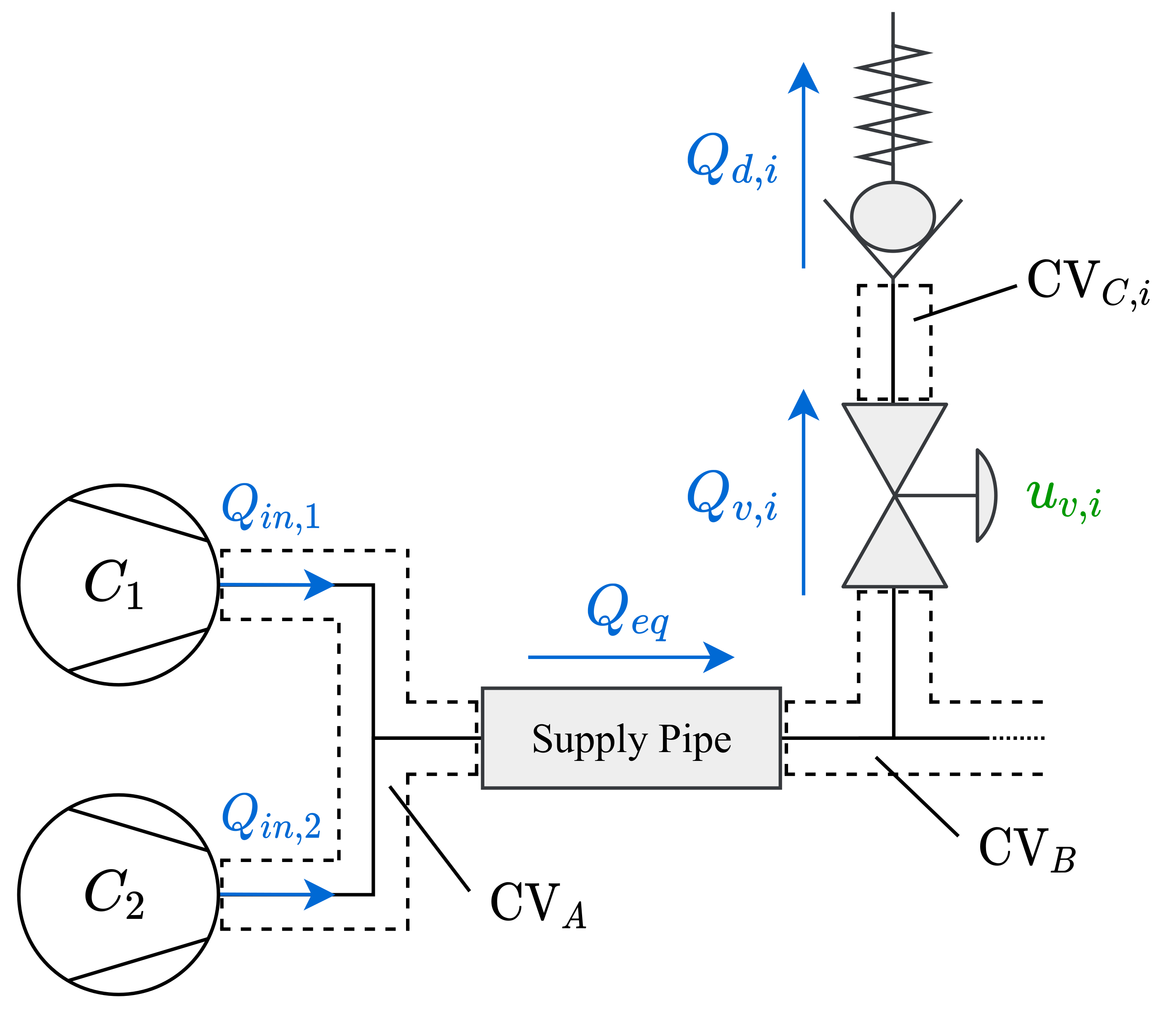
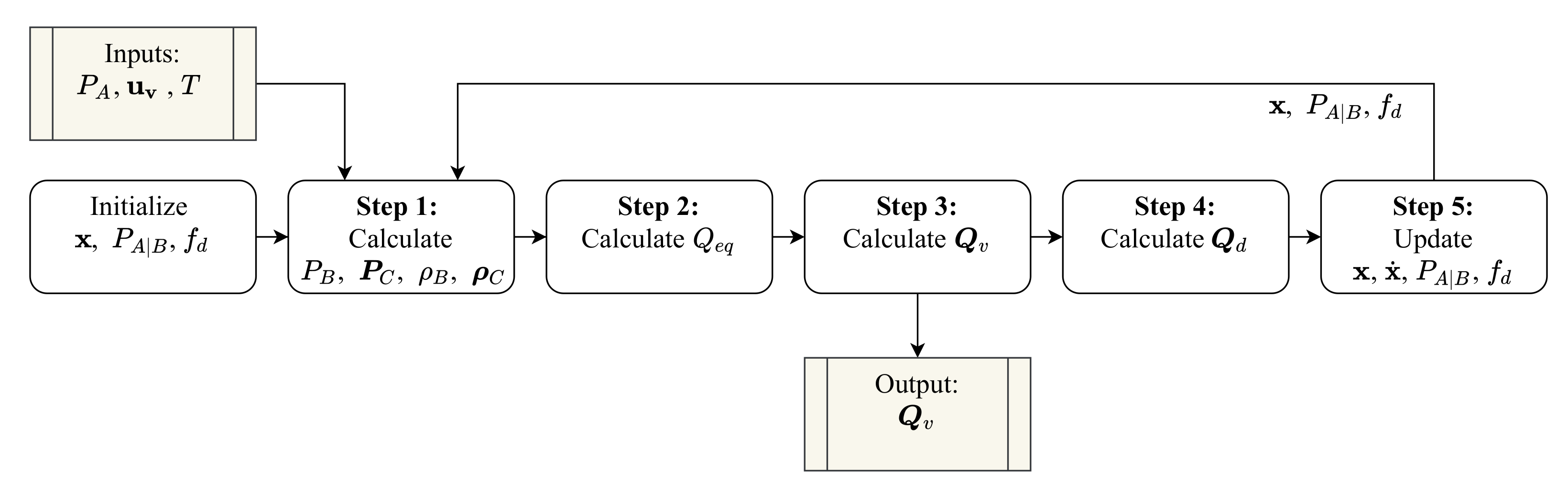
3. Modelling of the Airflow Distribution Network
3.1. Mass Balances
3.2. Pipe Friction Losses
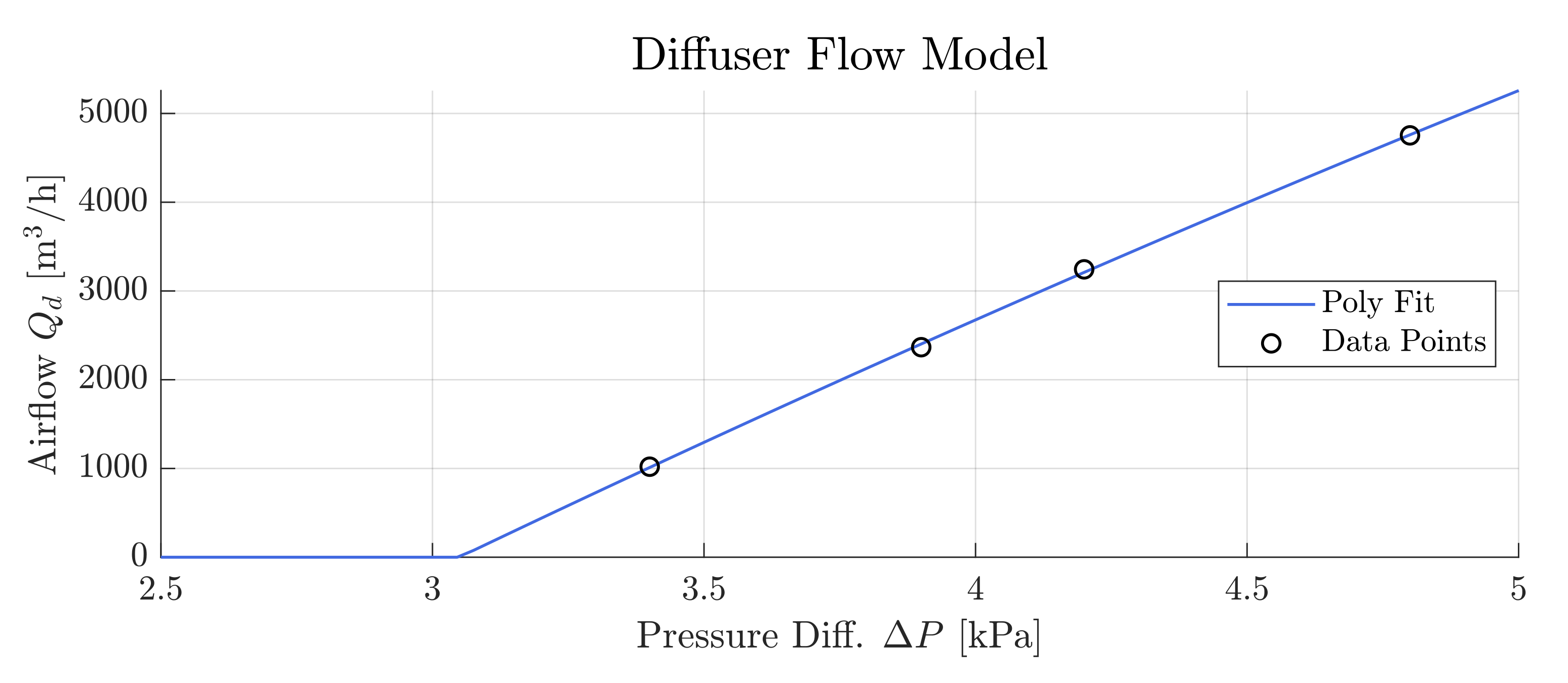
3.3. Diffuser Model
3.4. Valve and Flow Sensor Models
- Assumption 1
- The gas is an ideal gas and the flow through the orifice is steady.
- Assumption 2
- Flow through the orifice is an adiabatic process; there is no heat exchange with the surroundings.
- Assumption 3
- The upstream flow velocity (inlet) is much smaller than the downstream flow velocity.
- Assumption 4
- The discharge coefficient, , is constant.
3.5. Combined Model
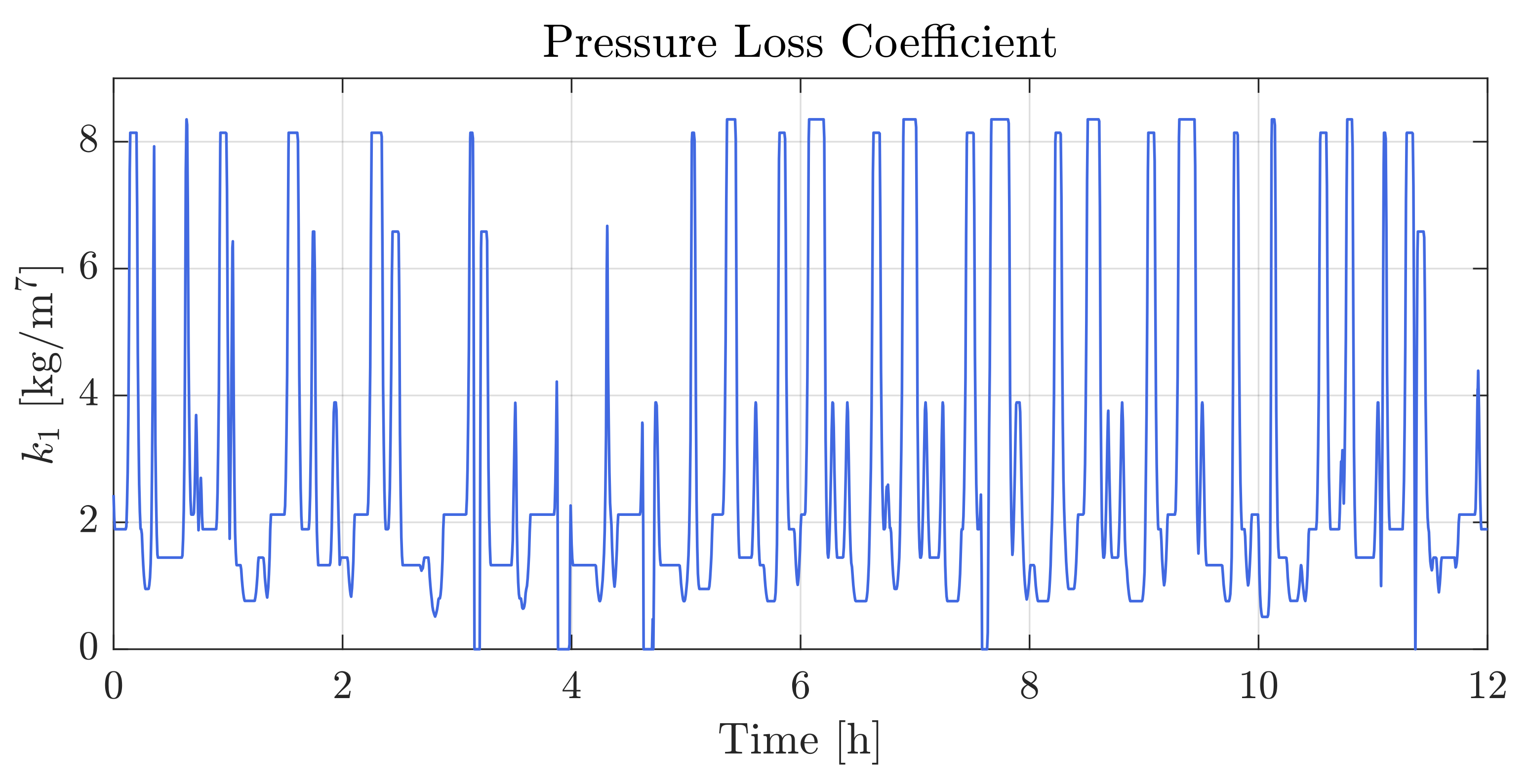
3.6. Parameter Identification
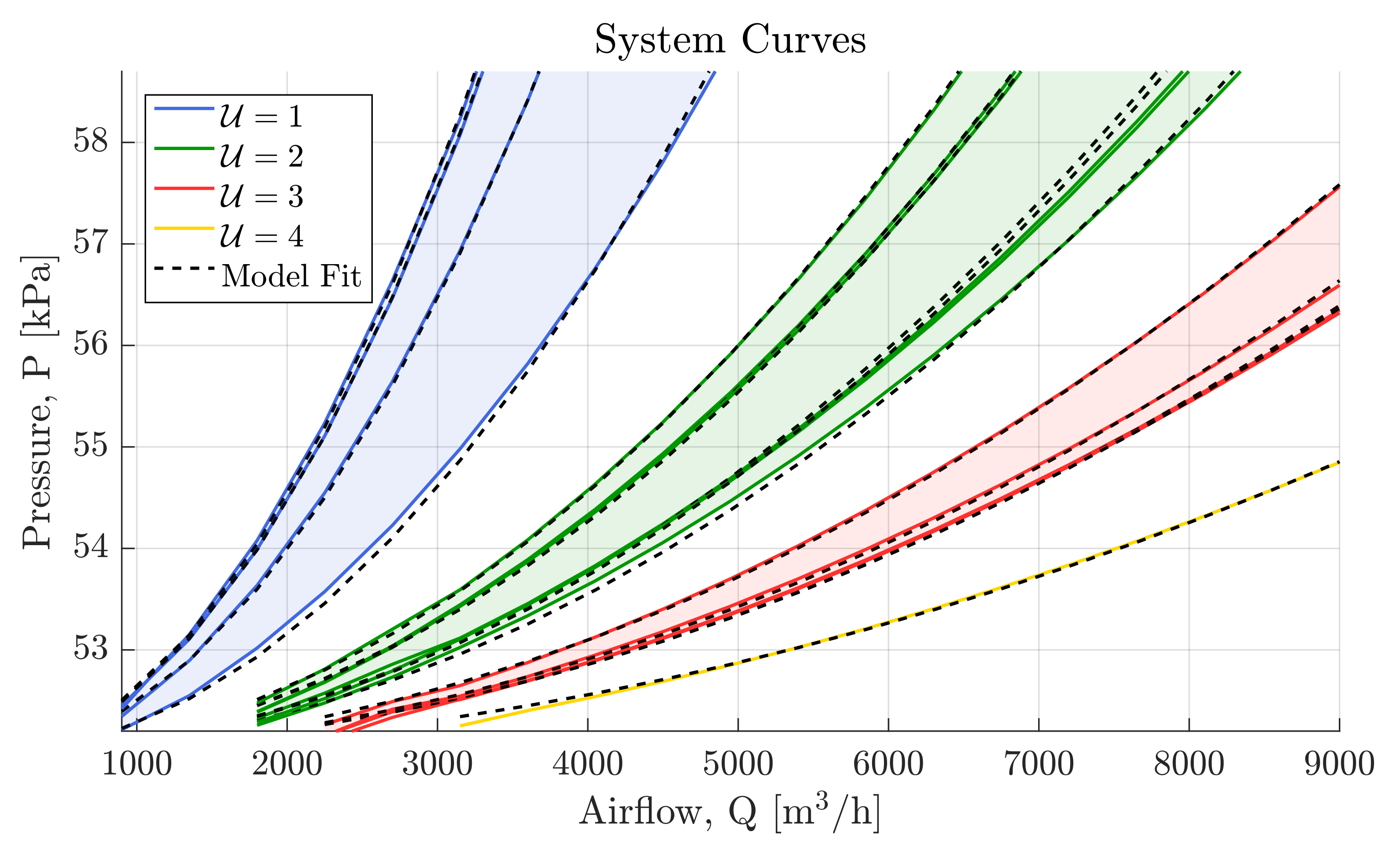
3.7. System Curves
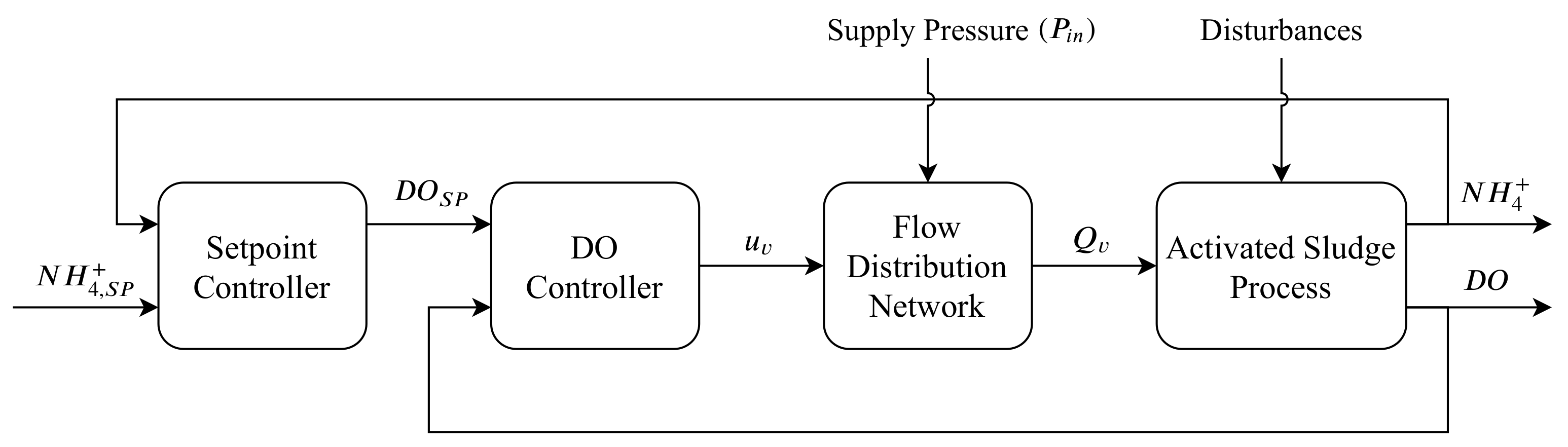
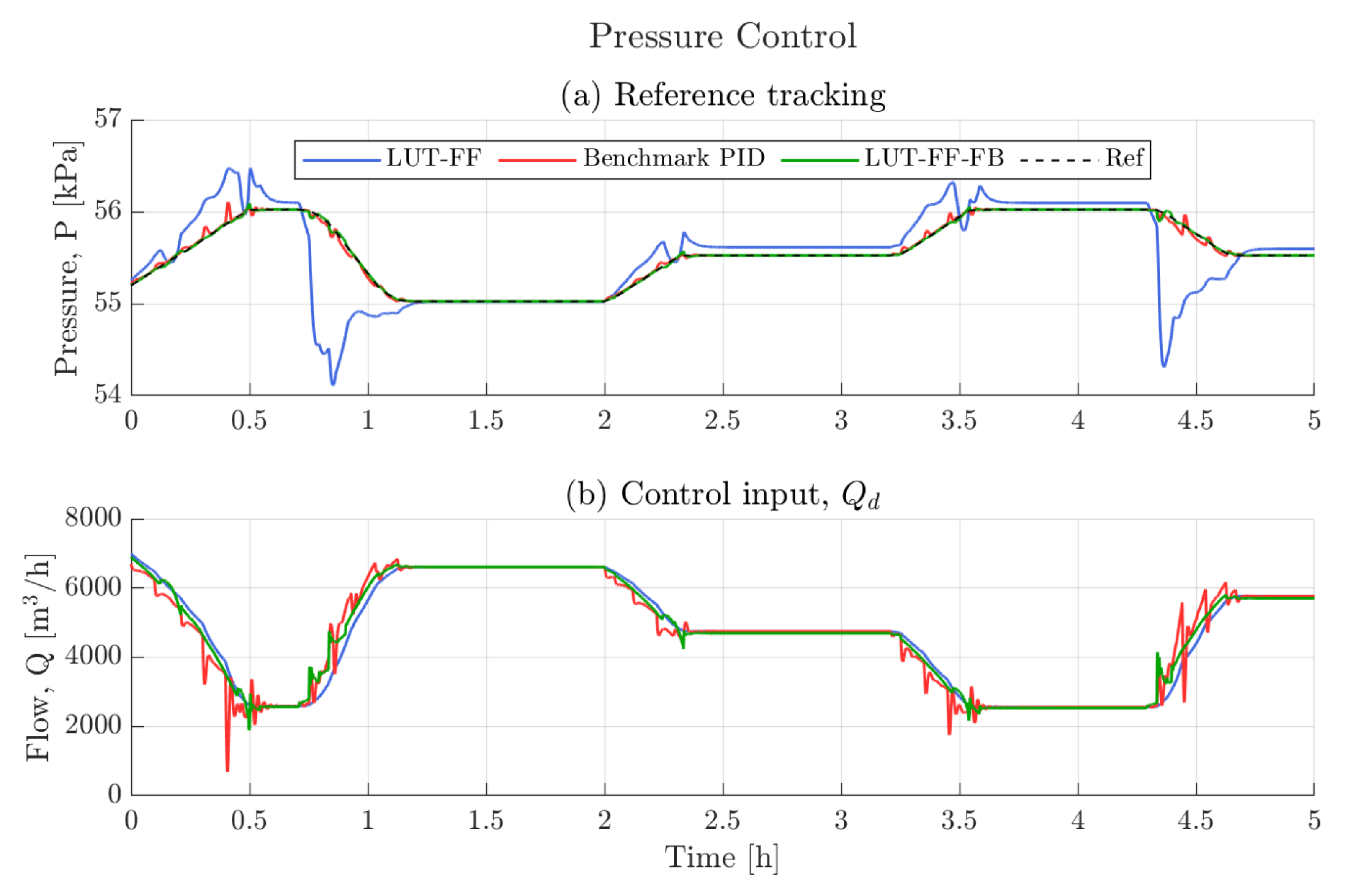
4. Pressure Control
4.1. Benchmark PID Controller (Benchmark PID)
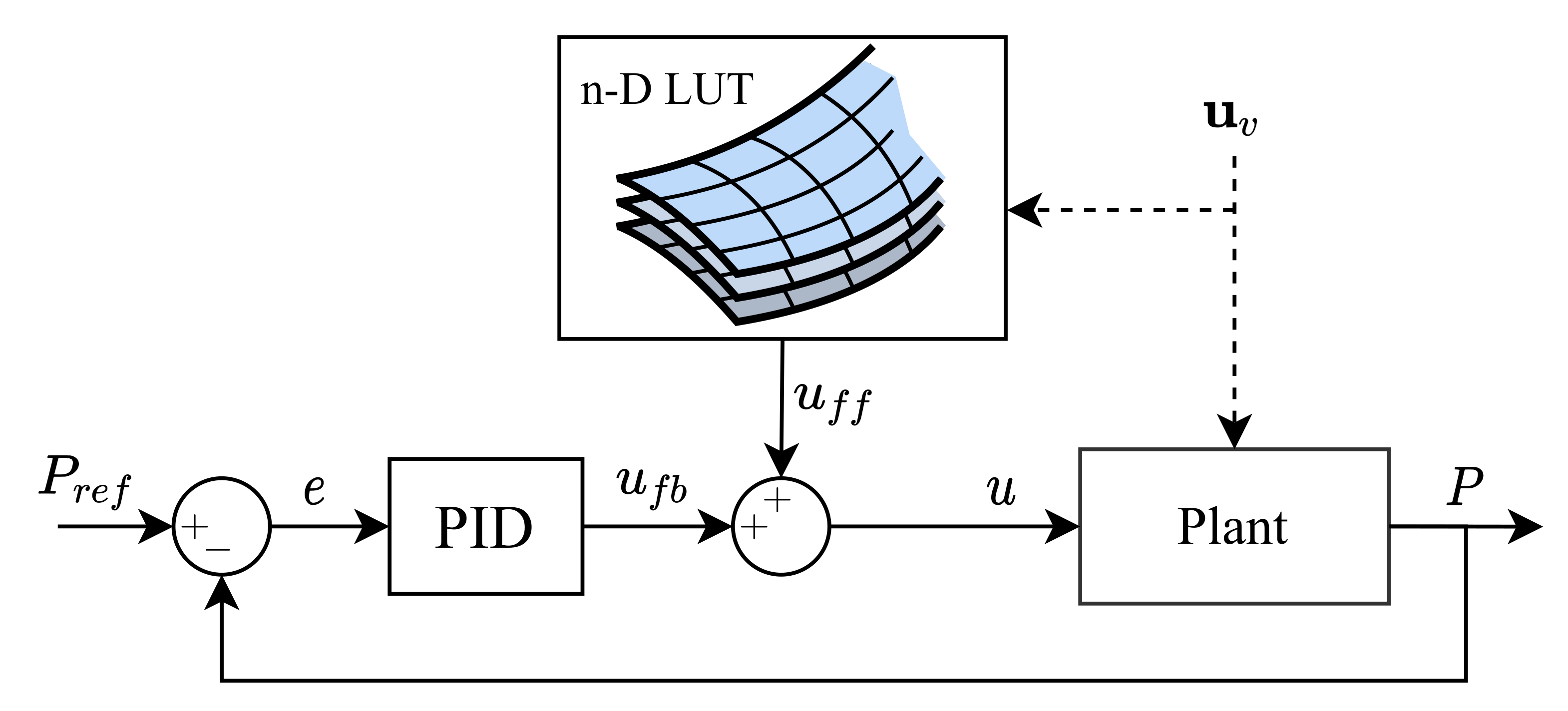
4.2. LUT-Feedforward Controller (LUT-FF)
4.3. LUT-Feedforward-Feedback Controller (LUT-FF-FB)
5. Compressor Scheduling
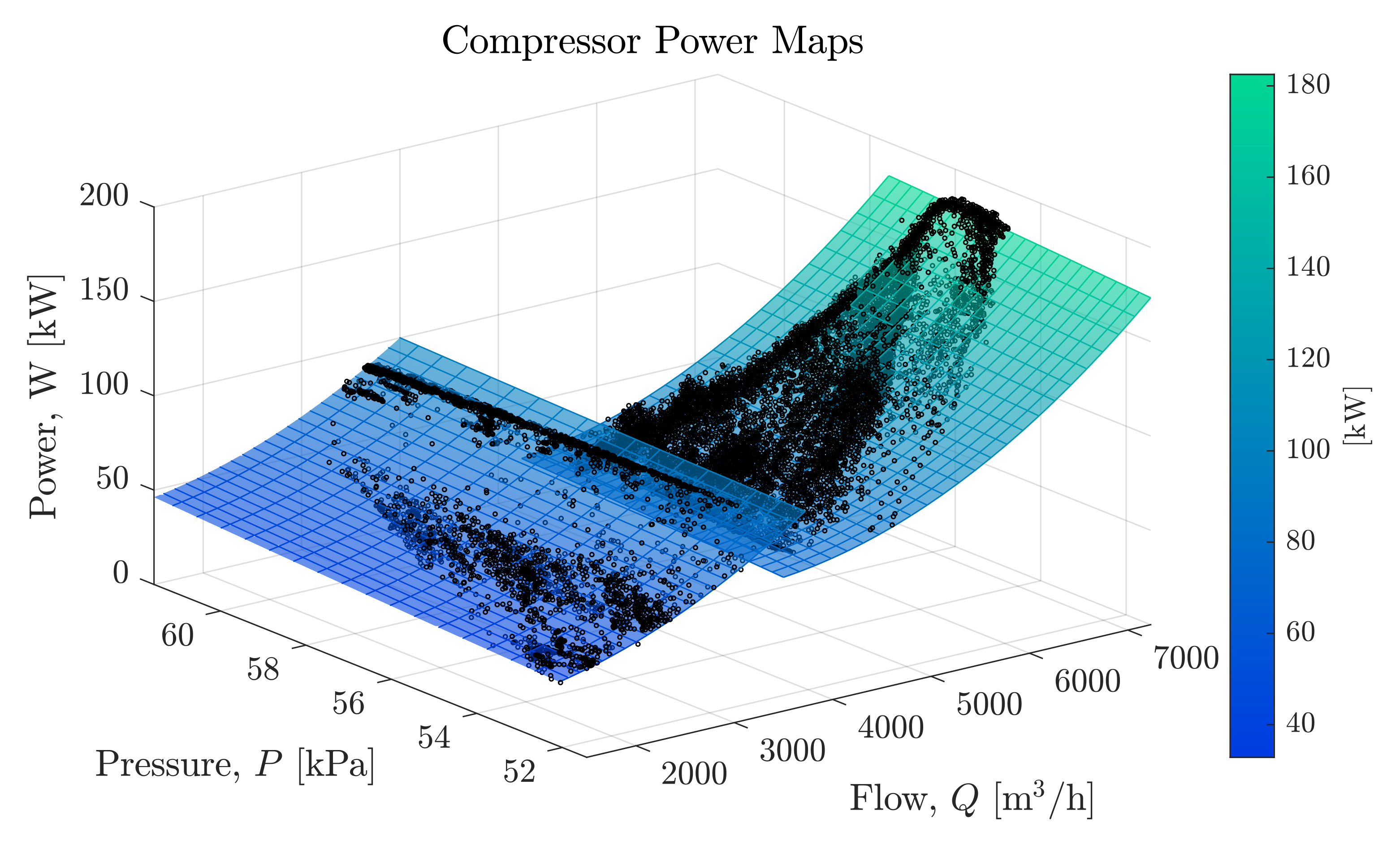
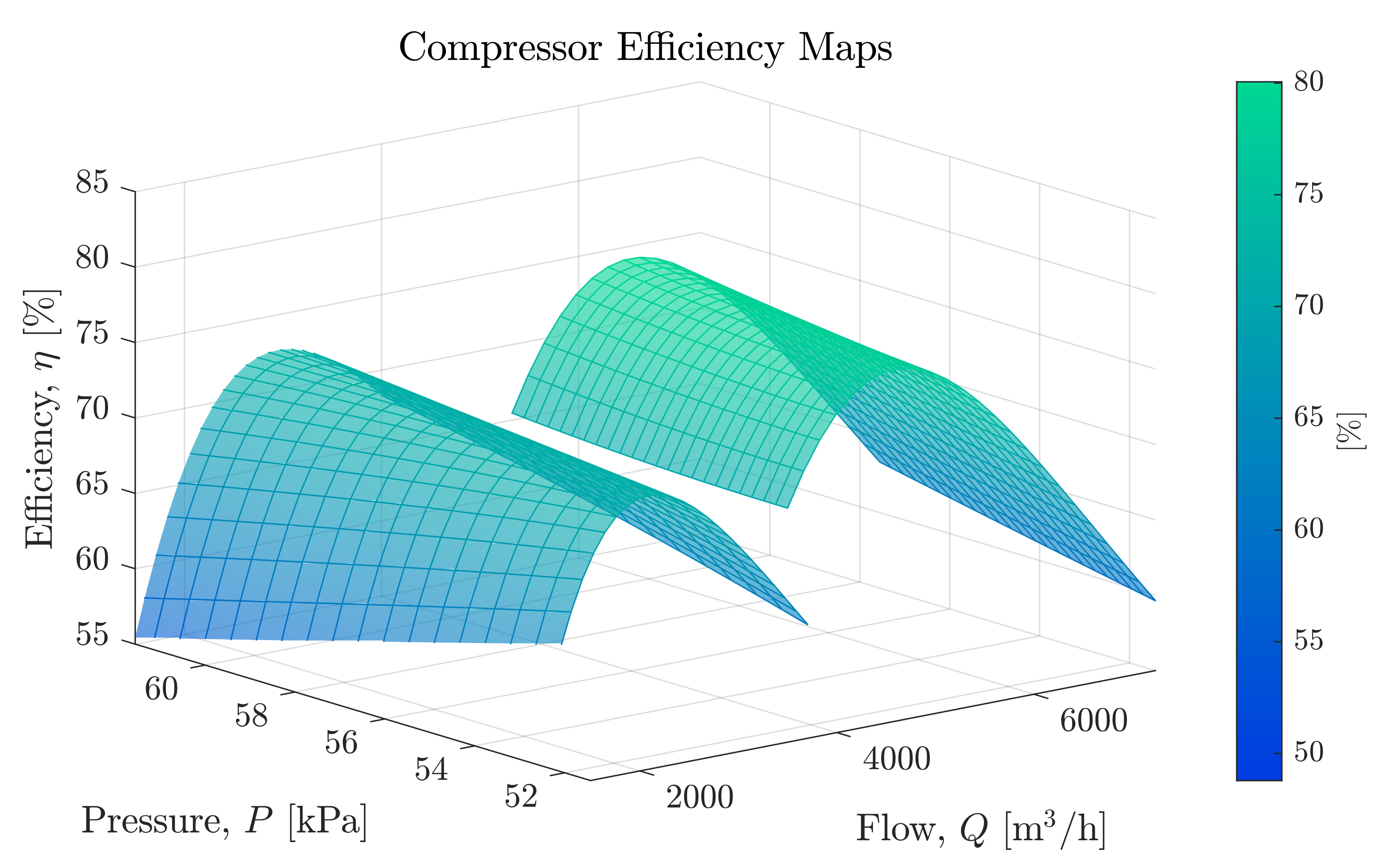
5.1. Static Power Model
- Assumption 1
- The transient dynamics of the compressors are assumed fast enough to be neglected, meaning that static models are adequate to describe the system.
- Assumption 2
- The efficiency of the motor and motor driver is constant. This implies that the system efficiency, , can be defined as the ratio of hydraulic power to electric power [65].
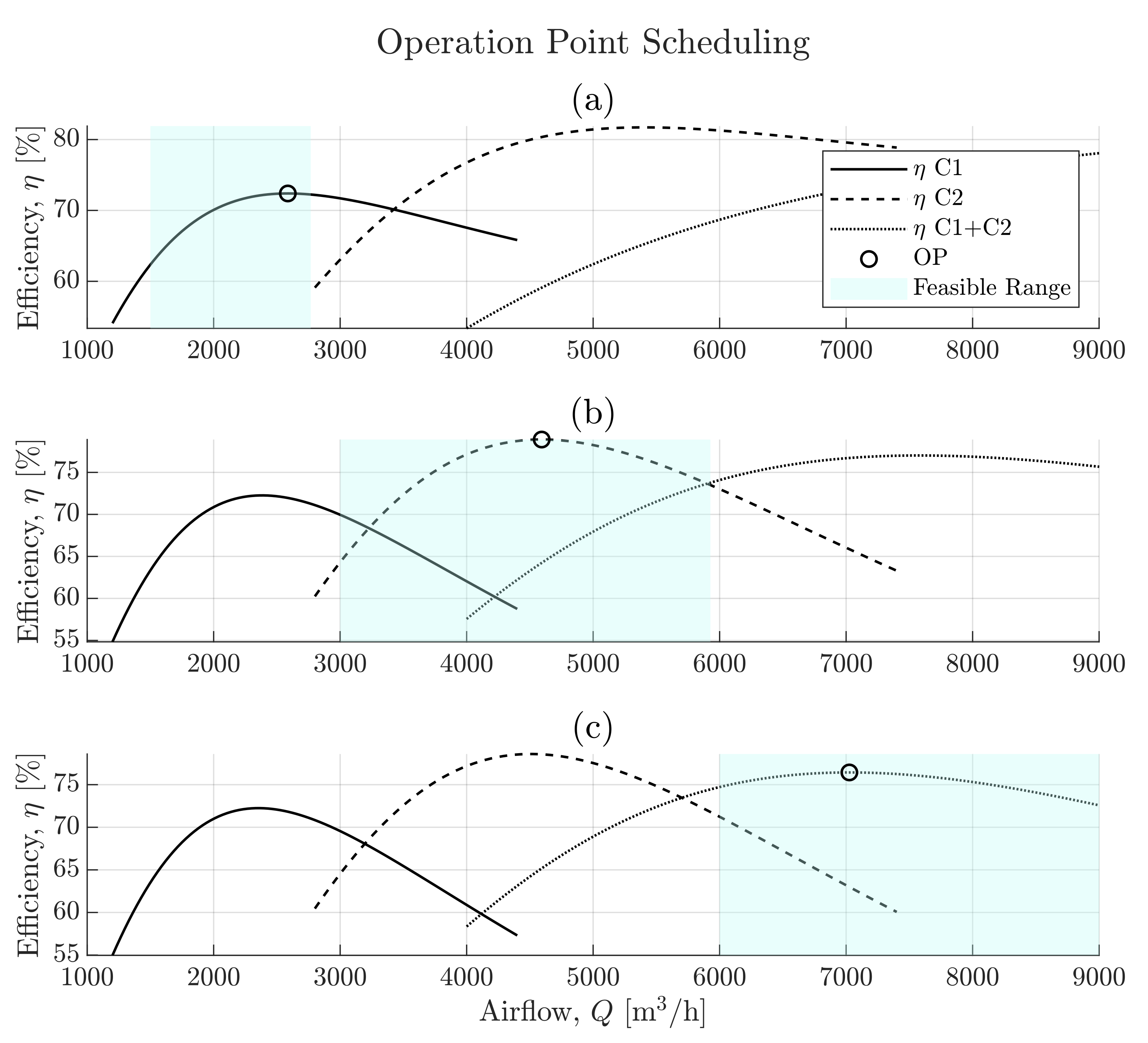
5.2. Compressor Load Sharing
5.3. Scheduling Algorithm
- Constraint 1
- The solution should be within the flow and pressure ranges defined in Equation (17). This constraint ensures that the air supply system never exceeds the physical limitations in pressure drop across the diffusers or approaches the limits of operation (surge/stall) for the compressors.
- Constraint 2
- To facilitate biochemical treatment a minimum airflow supply for each reactor is required (), therefore, the air supply is subject to:
| Algorithm 1: Compressor scheduling algorithm pseudo code. |
 |
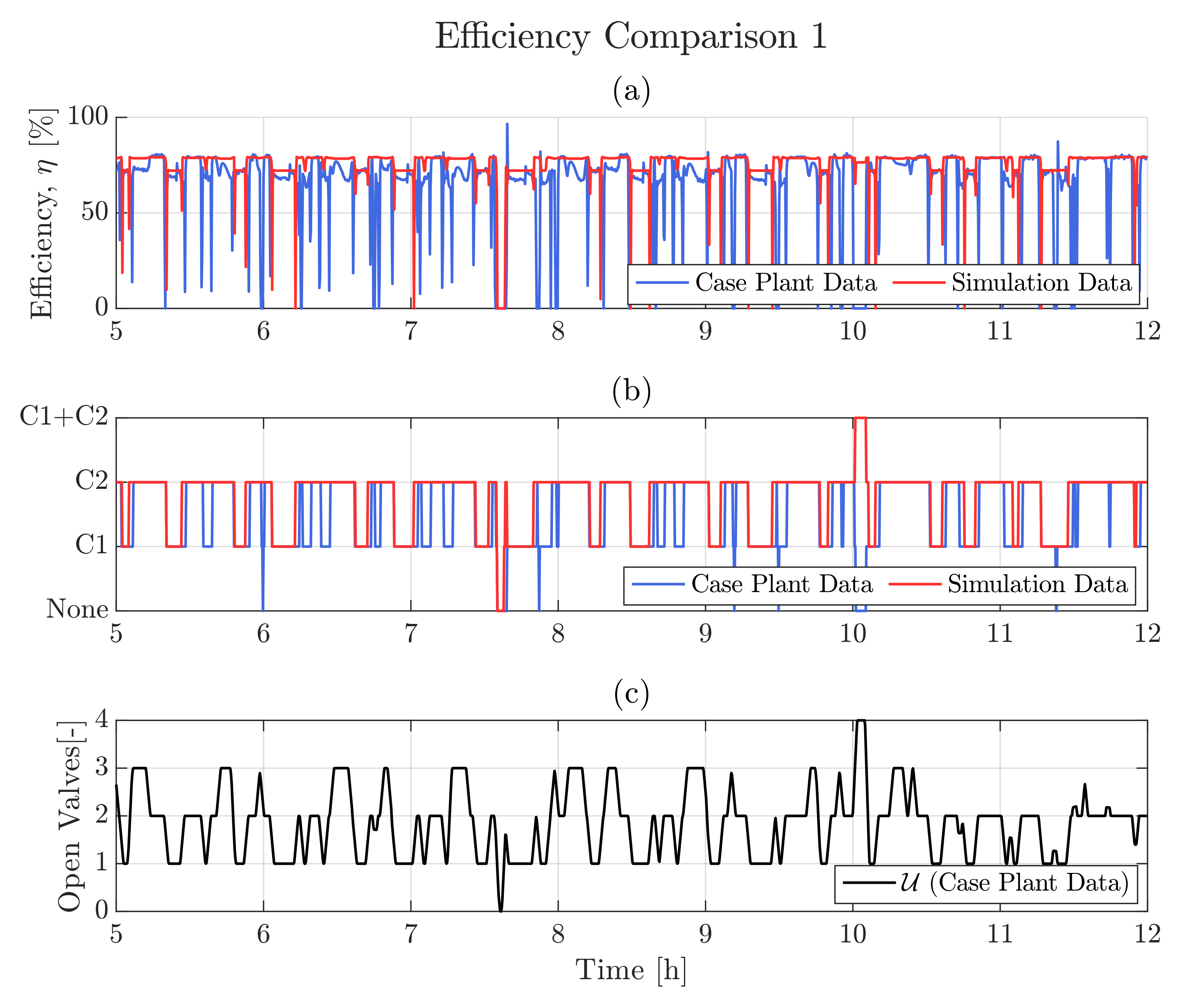
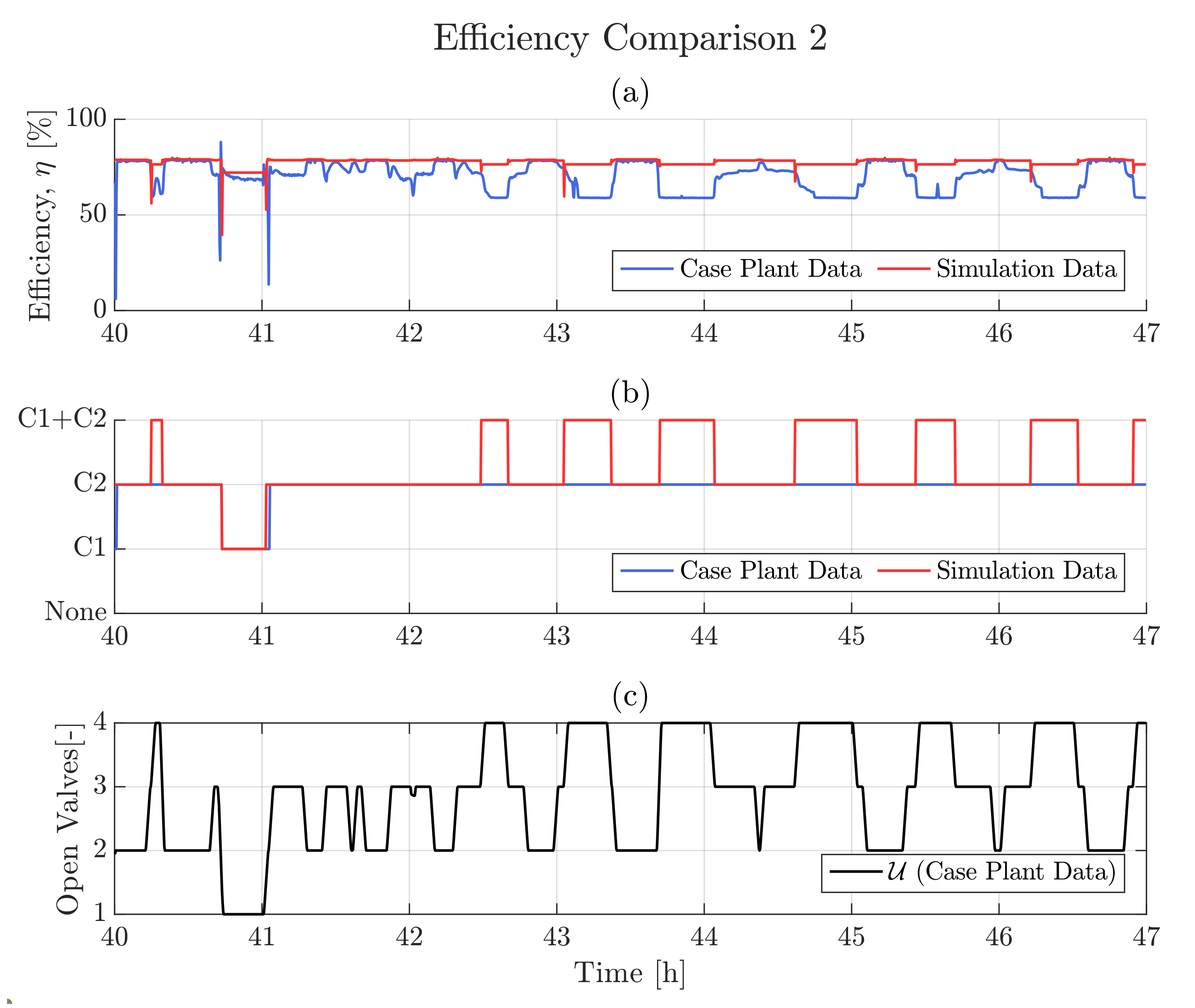
6. Results
- Control Rule 1
- one valve is completely open → start C1
- Control Rule 2
- two valves are completely open → start C2
7. Discussion
- Flow sensor dynamics are approximated assuming a first-order filter, resulting in the model being fitted to the damped sensor measurements rather than the actual flows. This is however a necessity as there is no other option for validating the airflow distribution model without changing the system setup and implementing another sensor. Should another, faster sensor (like a pressure transmitter) be implemented, the sensor dynamics should still be modelled despite the faster dynamics, as these dynamics most likely would contribute to the over-all system dynamics.
- Valve discharge coefficients which are estimated using a numerical method minimizing a cost function. By using this approach, the estimated parameters are not identified to fit the actual discharge coefficients of the valves alone, but instead an estimate of a general “loss coefficient” for the entire system, compensating for and eliminating many of the uncertainties introduced when modelling other flow elements.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol | Description | Value | Unit |
|---|---|---|---|
| D | Main pipe diameter | 460 | mm |
| L | Main pipe length | 16.5 | m |
| Main pipe cross-sectional area | 0.1662 | ||
| Volume in | 4.00 | ||
| Volume in | 12.00 | ||
| Volume in | 4.00 | ||
| Pressure at diffusers | 149.9 | kPa | |
| Leakage flow coefficient |
References
- Lofrano, G.; Brown, J. Wastewater management through the ages: A history of mankind. Sci. Total Environ. 2010, 408, 5254–5264. [Google Scholar] [CrossRef] [PubMed]
- Vuorinen, H.S.; Juuti, P.S.; Katko, T.S. History of water and health from ancient civilizations to modern times. Water Supply 2007, 7, 49–57. [Google Scholar] [CrossRef]
- Lens, P.; Zeeman, G.; Lettinga, G. Decentralised Sanitation and Reuse: Concepts, Systems and Implementation; IWA Publishing: London, UK, 2005. [Google Scholar]
- Brown, J.A. The Early History of Wastewater Treatment and Disinfection. In Proceedings of the World Water and Environmental Resources Congress, Anchorage, AK, USA, 15—19 May 2005; pp. 1–7. [Google Scholar]
- Englande, A.; Krenkel, P.; Shamas, J. Wastewater Treatment & Water Reclamation; Elsevier Inc.: Amsterdam, The Netherlands, 2015; pp. 1–32. [Google Scholar]
- Rosenfeld, P.E.; Feng, L.G.H. Risks of Hazardous Wastes; William Andrew Publishing: Norwich, NY, USA, 2011; pp. 269–284. [Google Scholar]
- Henze, M.; Grady, C.P.; Gujer, W.; Marais, G.V.; Matsuo, T. A general model for single-sludge wastewater treatment systems. Water Res. 1987, 21, 505–515. [Google Scholar] [CrossRef]
- Henze, M.; Odegaard, H. An Analysis of Waste-water Treatment Strategies for Eastern and Central-Europe. Water Sci. Technol. 1994, 30, 25–40. [Google Scholar] [CrossRef]
- Coen, F.; Vanderhaegen, B.; Boonen, I.; Vanrolleghem, P.A.; Van Meenen, P. Improved Design and Control of Industrial and Municipal Nutrient Removal Plants using Dynamic Models. Wat. Sci. Tech. 1997, 35, 53–61. [Google Scholar] [CrossRef]
- Fikar, M.; Chachuat, B.; Latifi, M.A. Optimal operation of alternating activated sludge processes. Control Eng. Pract. 2005, 13, 853–861. [Google Scholar] [CrossRef][Green Version]
- Scholz, M. Chapter 15—Activated Sludge Processes; Elsevier: Amsterdam, The Netherlands, 2016; pp. 91–105. [Google Scholar]
- Henze, M.; Gujer, W.; Mino, T.; van Loosedrecht, M. Activated Sludge Models ASM1, ASM2, ASM2d and ASM3; IWA Publishing: London, UK, 2000; Volume 5. [Google Scholar]
- Sotomayor, O.A.; Park, S.W.; Garcia, C. Software sensor for on-line estimation of the microbial activity in activated sludge systems. ISA Trans. 2002, 41, 127–143. [Google Scholar] [CrossRef]
- Halvgaard, R.F.; Munk-Nielsen, T.; Tychsen, P.; Grum, M.; Madsen, H. Stochastic Greybox Modeling of an Alternating Activated Sludge Process. In Proceedings of the 9th IWA Symposium on Systems Analysis and Integrated Assessment (Watermatex 2015), Gold Coast, QLD, Australia, 11–14 June 2015; Volume 8. [Google Scholar]
- Busby, J.B.; Andrews, J.F. Dynamic modeling and control strategies for the activated sludge process. J. Water Pollut. Control. Fed. 1975, 47, 1055–1080. [Google Scholar]
- Olsson, G.; Andrews, J.F. The dissolved oxygen profile-A valuable tool for control of the activated sludge process. Water Res. 1978, 12, 985–1004. [Google Scholar] [CrossRef]
- Gernaey, K.V.; Van Loosdrecht, M.C.; Henze, M.; Lind, M.; Jørgensen, S.B. Activated Sludge Wastewater Treatment Plant Modelling and Simulation: State of the Art. Environ. Model. Softw. 2004, 19, 763–783. [Google Scholar] [CrossRef]
- Lindberg, C.F. Control and Estimation Strategies Applied to the Activated Sludge Process. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 1997. [Google Scholar]
- Schraa, O.; Rieger, L.; Alex, J. Development of a Model for Activated Sludge Aeration Systems: Linking Air Supply, Distribution, and Demand. Water Sci. Technol. 2017, 75, 552–560. [Google Scholar] [CrossRef]
- Holenda, B.; Domokos, E.; Redey, A.; Fazakas, J. Dissolved Oxygen Control of the Activated Sludge Wastewater Treatment Process Using Model Predictive Control. Comput. Chem. Eng. 2008, 32, 1270–1278. [Google Scholar] [CrossRef]
- Silva, F.J.; Catunda, S.Y.; Van Haandel, A.C.; Fonseca Neto, J.V. Dissolved Oxygen PWM Control and Oxygen Uptake Rate Estimation Using Kalman Filter in Activated Sludge Systems. In Proceedings of the 2010 IEEE International Instrumentation and Measurement Technology Conference, I2MTC 2010, Austin, TX, USA, 3–6 May 2010; pp. 579–584. [Google Scholar]
- Lukasse, L.; Keesman, K.; van Straten, G. Grey-Box Identification of Dissolved Oxygen Dynamics in Activated Sludge Processes. IFAC Proc. Vol. 1996, 29, 6804–6809. [Google Scholar] [CrossRef]
- Hreiz, R.; Latifi, M.A.; Roche, N. Optimal design and operation of activated sludge processes: State-of-the-art. Chem. Eng. J. 2015, 281, 900–920. [Google Scholar] [CrossRef]
- Robert, P. Comparison of Two Nonlinear Predictive Control Algorithms for Dissolved Oxygen Tracking Problem at WWTP. J. Autom. Mob. Robot. Intell. Syst. 2016, 10, 8–16. [Google Scholar]
- Wahab, N.A.; Katebi, R.; Balderud, J. Multivariable PID Control Design for Activated Sludge Process with Nitrification and Denitrification. Biochem. Eng. J. 2009, 45, 239–248. [Google Scholar] [CrossRef]
- Stentoft, P.A.; Guericke, D.; Munk-Nielsen, T.; Mikkelsen, P.S.; Madsen, H.; Vezzaro, L.; Møller, J.K. Model predictive control of stochastic wastewater treatment process for smart power, cost-effective aeration. IFAC Pap. 2019, 52, 622–627. [Google Scholar] [CrossRef]
- Brok, N.B.; Munk-Nielsen, T.; Madsen, H.; Stentoft, P.A. Flexible Control of Wastewater Aeration for Cost-Efficient, Sustainable Treatment. IFAC Pap. 2019, 52, 494–499. [Google Scholar] [CrossRef]
- Arnell, M. Performance Assessment of Wastewater Treatment Plants – Multi-Objective Analysis Using Plant-Wide Models. Ph.D. Thesis, Lund University, Lund, Sweden, 2016. [Google Scholar]
- Rieger, L.; Alex, J.; Gujer, W.; Siegrist, H. Modelling of aeration systems at wastewater treatment plants. Water Sci. Technol. 2006, 53, 439–447. [Google Scholar] [CrossRef]
- Al Ba’ba’a, H.B.; Amano, R.S. A study of optimum aeration efficiency of a lab-scale air-diffused system. Water Environ. J. 2017, 31, 432–439. [Google Scholar] [CrossRef]
- Olsson, G.; Nielsen, M.; Yuan, Z.; Lynggaard-Jensen, A.; Steyer, J.P. Instrumentation, Control and Automation in Wastewater Systems; IWA Publishing: London, UK, 2005. [Google Scholar]
- Nielsen, M.K.; Önnerth, T.B. Improvement of a recirculating plant by introducing STAR control. Water Sci. Technol. 1995, 31, 171–180. [Google Scholar] [CrossRef]
- Önnerth, T.B.; Nielsen, M.K.; Stamer, C. Advanced computer controlbased on real and software sensors. Water Sci. Technol. 1996, 33, 237–245. [Google Scholar] [CrossRef]
- Kuriqi, A. Simulink Application On Dynamic Modeling Of Biological Waste Water Treatment For Aerator Tank Case. Int. J. Sci. Technol. Res. 2014, 3, 69–72. [Google Scholar]
- Kuriqi, A.; Kuriqi, I.; Poci, E. Simulink Programing for Dynamic Modelling of Activated Sludge Process: Aerator and Settler Tank Case. Fresenius Environ. Bull. 2016, 25, 2891–2899. [Google Scholar]
- Andrews, J.F. Dynamic models and control strategies for wastewater treatment processes. Water Res. 1974, 8, 261–289. [Google Scholar] [CrossRef]
- Andrews, J.F.; Stenstrom, M.K. Dynamic Models and Control Strategies for Wastewater Treatment Plants—An Overview. IFAC Proc. Vol. 1977, 10, 443–452. [Google Scholar] [CrossRef]
- Durdevic, P.; Raju, C.S.; Yang, Z. Potential for Real-Time Monitoring and Control of Dissolved Oxygen in the Injection Water Treatment Process. IFAC Pap. 2018, 51, 170–177. [Google Scholar] [CrossRef]
- Durdevic, P.; Yang, Z. Potential use of real-time dissolved oxygen sensors for oxygen scavenging feedback control. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kazimierz Dolny, Poland, 21–23 November 2019; Volume 504, p. 012098. [Google Scholar]
- Lee, I.; Lim, H.; Jung, B.; Colosimo, M.F.; Kim, H. Evaluation of aeration energy saving in two modified activated sludge processes. Chemosphere 2015, 140, 72–78. [Google Scholar] [CrossRef] [PubMed]
- Martín de la Vega, P.T.; Jaramillo, M.A.; Martínez de Salazar, E. Upgrading the biological nutrient removal process in decentralized WWTPs based on the intelligent control of alternating aeration cycles. Chem. Eng. J. 2013, 232, 213–220. [Google Scholar] [CrossRef]
- Åmand, L.; Olsson, G.; Carlsson, B. Aeration control - A review. Water Sci. Technol. 2013, 67, 2374–2398. [Google Scholar] [CrossRef]
- Saidur, R.; Rahim, N.A.; Hasanuzzaman, M. A review on compressed-air energy use and energy savings. Renew. Sustain. Energy Rev. 2010, 14, 1135–1153. [Google Scholar] [CrossRef]
- Vrečko, D.; Zupančič, U.; Babič, R. Improving Aeration Control at the Ljubljana Wastewater Treatment Plant. Water Sci. Technol. 2014, 69, 1395–1402. [Google Scholar] [CrossRef] [PubMed]
- Bellman, R.; Glicksberg, I.; Gross, O. On the “bang-bang” control problem. Q. Appl. Math. 1956, 14, 11–18. [Google Scholar] [CrossRef]
- Durdevic, P.; Pedersen, S.; Yang, Z. Challenges in modelling and control of offshore de-oiling hydrocyclone systems. In Proceedings of the Journal of Physics: Conference Series, Lille, France, 17–18 November 2016; Volume 783012048, pp. 1–10. [Google Scholar]
- Durdevic, P.; Yang, Z. Application of h∞ robust control on a scaled offshore oil and gas de-oiling facility. Energies 2018, 11, 287. [Google Scholar] [CrossRef]
- Åmand, L.; Carlsson, B. Optimal Aeration Control in a Nitrifying Activated Sludge Process. Water Res. 2012, 46, 2101–2110. [Google Scholar] [CrossRef] [PubMed]
- Zhai, Z.; El Mankibi, M.; Zoubir, A. Review of Natural Ventilation Models. Energy Procedia 2015, 78, 2700–2705. [Google Scholar] [CrossRef]
- Fariborz, H.; Li, H. Building Airflow Movement - Validation of Three Airflow Models. J. Archit. Plan. Res. 2004, 21, 331–349. [Google Scholar]
- Ai, Z.T.; Mak, C.M. Pressure Losses Across Multiple Fittings in Ventilation Ducts. Sci. World J. 2013, 1–10. [Google Scholar] [CrossRef]
- Yang, Z.; Pedersen, S.; Durdevic, P. Control of variable-speed pressurization fan for an offshore HVAC system. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 458–463. [Google Scholar]
- Kopanos, G.M.; Xenos, D.P.; Cicciotti, M.; Pistikopoulos, E.N.; Thornhill, N.F. Optimization of a network of compressors in parallel: Operational and maintenance planning—The air separation plant case. Appl. Energy 2015, 146, 453–470. [Google Scholar] [CrossRef]
- Krawczyk, W.; Piotrowski, R.; Brdys, M.A.; Chotkowski, W. Modelling and identification of aeration systems for model predictive control of dissolved oxygen—Swarzewo wastewater treatment plant case study. IFAC Proc. Vol. Ifac Pap. 2007, 40, 43–48. [Google Scholar] [CrossRef]
- Amaral, A.; Schraa, O.; Rieger, L.; Gillot, S.; Fayolle, Y.; Bellandi, G.; Amerlinck, Y.; Mortier, S.T.; Gori, R.; Neves, R.; et al. Towards Advanced Aeration Modelling: From Blower to Bubbles to Bulk. Water Sci. Technol. 2017, 75, 507–517. [Google Scholar] [CrossRef]
- Gerhart, P.M.; Gerhart, A.L.; Hochstein, J.I. Munson’s Fluid Mechanics, global edition; John Wiley & Sons, Inc.: Singapore, 2017. [Google Scholar]
- Egeland, O.; Gravdahl, J. Modeling and Simulation for Automatic Control; Marine Cybernetics AS: Trondheim, Norway, 2002. [Google Scholar]
- Walker, I.S.; Wilson, D.J.; Sherman, M.H. A Comparison of the Power Law to Quadratic Formulations for Air Infiltration Calculations. Energy Build. 1998, 27, 293–299. [Google Scholar] [CrossRef]
- Yin, Y. High Speed Pneumatic Theory and Technology Volume I: Servo System, 1st ed.; Springer: Singapore, 2019. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder–Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Niegodajew, P.; Marek, M.; Elsner, W.; Kowalczyk, L. Power Plant Optimisation—Effective Use of the Nelder-Mead Approach. Processes 2020, 8, 357. [Google Scholar] [CrossRef]
- Fan, S.K.S.; Zahara, E. A hybrid simplex search and particle swarm optimization for unconstrained optimization. Eur. J. Oper. Res. 2007, 181, 527–548. [Google Scholar] [CrossRef]
- Wang, P.C.; Shoup, T.E. Parameter sensitivity study of the Nelder-Mead Simplex Method. Adv. Eng. Softw. 2011, 42, 529–533. [Google Scholar] [CrossRef]
- Yang, Z.; Børsting, H. Optimal Scheduling and Control of a Multi-Pump Boosting System. IEEE Conf. Control Appl. Proc. 2010, 2010, 2071–2076. [Google Scholar]
- Yang, Z.; Børsting, H. Energy efficient control of a boosting system with multiple variable-speed pumps in parallel. In Proceedings of the IEEE Conference on Decision and Control, Atlanta, GA, USA, 15–17 December 2010; pp. 2198–2203. [Google Scholar]
- Nandong, J. A unified design for feedback-feedforward control system to improve regulatory control performance. Int. J. Control. Autom. Syst. 2014, 13, 91–98. [Google Scholar] [CrossRef]
- Zurbriggen, F.; Ott, T.; Onder, C.H. Fast and robust adaptation of lookup tables in internal combustion engines: Feedback and feedforward controllers designed independently. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2016, 230, 723–735. [Google Scholar] [CrossRef]
- de Vries, T.J.A.; Velthuis, W.J.R.; van Amerongen, J. Learning Feed-Forward Control: A Survey and Historical Note. IFAC Proc. Vol. 2000, 33, 881–886. [Google Scholar] [CrossRef]
- Jepsen, K.L.; Hansen, L.; Mai, C.; Yang, Z. Power consumption optimization for multiple parallel centrifugal pumps. In Proceedings of the 1st Annual IEEE Conference on Control Technology and Applications, CCTA. Kohala Coast, HI, USA, 27–30 August 2017; pp. 806–811. [Google Scholar]
- Cortinovis, A.; Zovadelli, M.; Mercangoz, M.; Pareschi, D.; De Marco, A.; Bittanti, S. Online adaptation of performance maps for centrifugal gas compressors. In Proceedings of the 2014 European Control Conference, ECC 2014, Strasbourg, France, 24–27 June 2014; pp. 1036–1041. [Google Scholar]
- Tengesdal, N.; Kristoffersen, T.; Holden, C. Applied Nonlinear Compressor Control with Gain Scheduling and State Estimation. IFAC Pap. 2018, 51, 151–157. [Google Scholar] [CrossRef]
- Gülich, J.F. Centrifugal Pumps, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Kurz, R.; Lubomirsky, M.; Brun, K. Gas compressor station economic optimization. Int. J. Rotating Mach. 2012, 2012, 1–9. [Google Scholar] [CrossRef]
- Han, I.S.; Han, C.; Chung, C.B. Optimization of the air- and gas-supply network of a chemical plant. Chem. Eng. Res. Des. 2004, 82, 1337–1343. [Google Scholar] [CrossRef]
- Booysen, W.; Kleingeld, M.; Van Rensburg, J. Optimising compressor control strategies for maximum energy savings. Energize 2009, 32, 65–68. [Google Scholar]
- Nguyen, H.H.; Chan, C.W. Applications of artificial intelligence for optimization of compressor scheduling. Eng. Appl. Artif. Intell. 2006, 19, 113–126. [Google Scholar] [CrossRef]
- Nguyen, H.H.; Uraikul, V.; Chan, C.W.; Tontiwachwuthikul, P. A comparison of automation techniques for optimization of compressor scheduling. Adv. Eng. Softw. 2008, 39, 178–188. [Google Scholar] [CrossRef]
- Nguyen, H.H.; Chan, C.W. Optimal scheduling of gas pipeline operation using genetic algorithms. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Saskatoon, SK, Canada, 1–4 May 2005; pp. 2195–2198. [Google Scholar]

| Symbol | Description | Unit |
|---|---|---|
| Compressor load percentage | % | |
| Airflow delivered by compressors | ||
| Airflow through airflow distribution network | ||
| Valve airflow | ||
| Diffuser airflow | ||
| Dissolved oxygen | mg/L | |
| Nitrate concentration | mg/L | |
| Ammonium concentration | mg/L |
| Symbol | Description | Unit |
|---|---|---|
| Upstream supply pipe pressure | kPa | |
| Valve state | % | |
| Valve airflow | /h | |
| Dissolved oxygen | mg/L | |
| Dissolved oxygen setpoint | mg/L | |
| Ammonium concentration | mg/L | |
| Ammonium concentration setpoint | mg/L |
| Symbol | Description | Unit |
|---|---|---|
| Airflow from compressor j | ||
| Total airflow through the supply pipe | ||
| Airflow through a control valve | ||
| Airflow through diffusers | ||
| Pressure (absolute) in control volume n | ||
| Air density in control volume n | ||
| State of flow regulating valve | % | |
| Valve discharge coefficient | − |
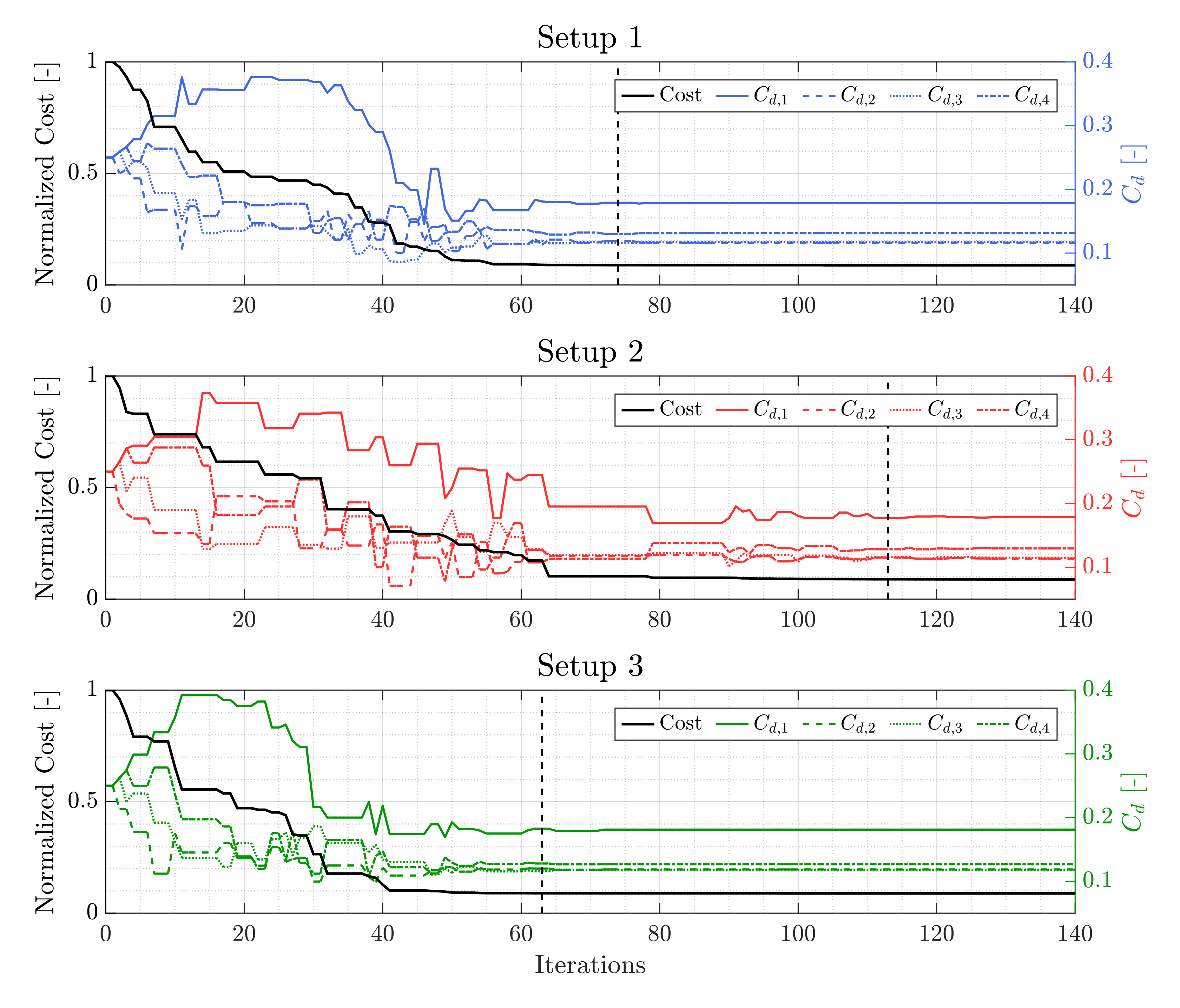
| NM Coefficient | Original NM | Fan and Zahara [63] | Wang and Shoup [64] |
|---|---|---|---|
| Setup 1 | Setup 2 | Setup 3 | |
| Reflection () | 1.00 | 1.50 | 1.29 |
| Expansion () | 2.00 | 2.75 | 2.29 |
| Contraction () | 0.50 | 0.75 | 0.47 |
| Simplex size () | 0.50 | 0.50 | 0.57 |
| Final cost (normalized) | |||
| Final values |
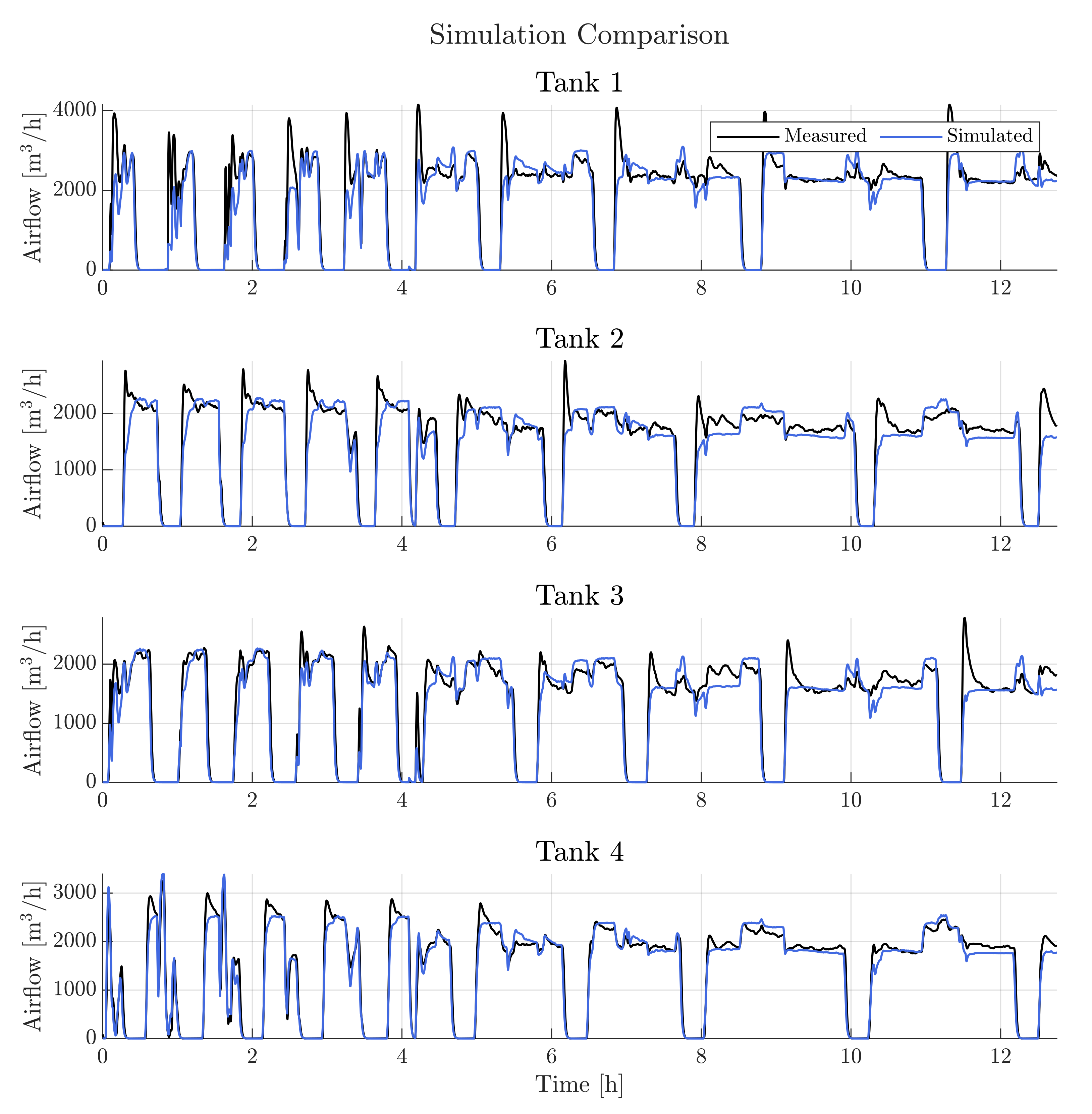
| Tank | 1 | 2 | 3 | 4 | Mean GOF |
|---|---|---|---|---|---|
| Identification Data (16 h) [GOF] | 60.29 | 64.46 | 69.08 | 79.60 | 68.63 |
| Validation Data (9 days) [GOF] | 58.17 | 63.69 | 72.73 | 77.29 | 67.97 |
| Efficiency [%] | Restarts pr. Day | ||||
|---|---|---|---|---|---|
| 1 Valve | 2 Valves | 3 Valves | 4 Valves | ||
| Current | 69.7 | 77.3 | 71.6 | 61.4 | 93.4 |
| Proposed | 74.8 | 78.8 | 78.2 | 76.4 | 65.8 |
| Difference | 5.1 | 1.6 | 6.6 | 15.0 | −27.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hansen, L.D.; Veng, M.; Durdevic, P. Compressor Scheduling and Pressure Control for an Alternating Aeration Activated Sludge Process—A Simulation Study Validated on Plant Data. Water 2021, 13, 1037. https://doi.org/10.3390/w13081037
Hansen LD, Veng M, Durdevic P. Compressor Scheduling and Pressure Control for an Alternating Aeration Activated Sludge Process—A Simulation Study Validated on Plant Data. Water. 2021; 13(8):1037. https://doi.org/10.3390/w13081037
Chicago/Turabian StyleHansen, Laura Debel, Morten Veng, and Petar Durdevic. 2021. "Compressor Scheduling and Pressure Control for an Alternating Aeration Activated Sludge Process—A Simulation Study Validated on Plant Data" Water 13, no. 8: 1037. https://doi.org/10.3390/w13081037
APA StyleHansen, L. D., Veng, M., & Durdevic, P. (2021). Compressor Scheduling and Pressure Control for an Alternating Aeration Activated Sludge Process—A Simulation Study Validated on Plant Data. Water, 13(8), 1037. https://doi.org/10.3390/w13081037






