Advanced Graphical–Analytical Method of Pipe Tank Design Integrated with Sensitivity Analysis for Sustainable Stormwater Management in Urbanized Catchments
Abstract
:1. Introduction
2. Materials and Methods
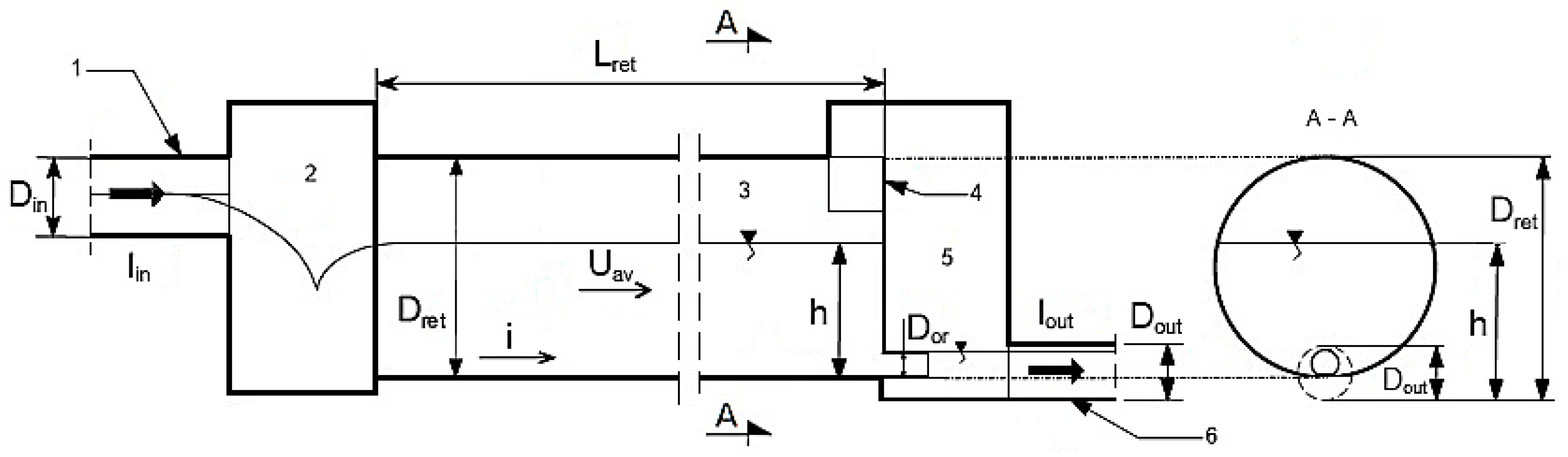
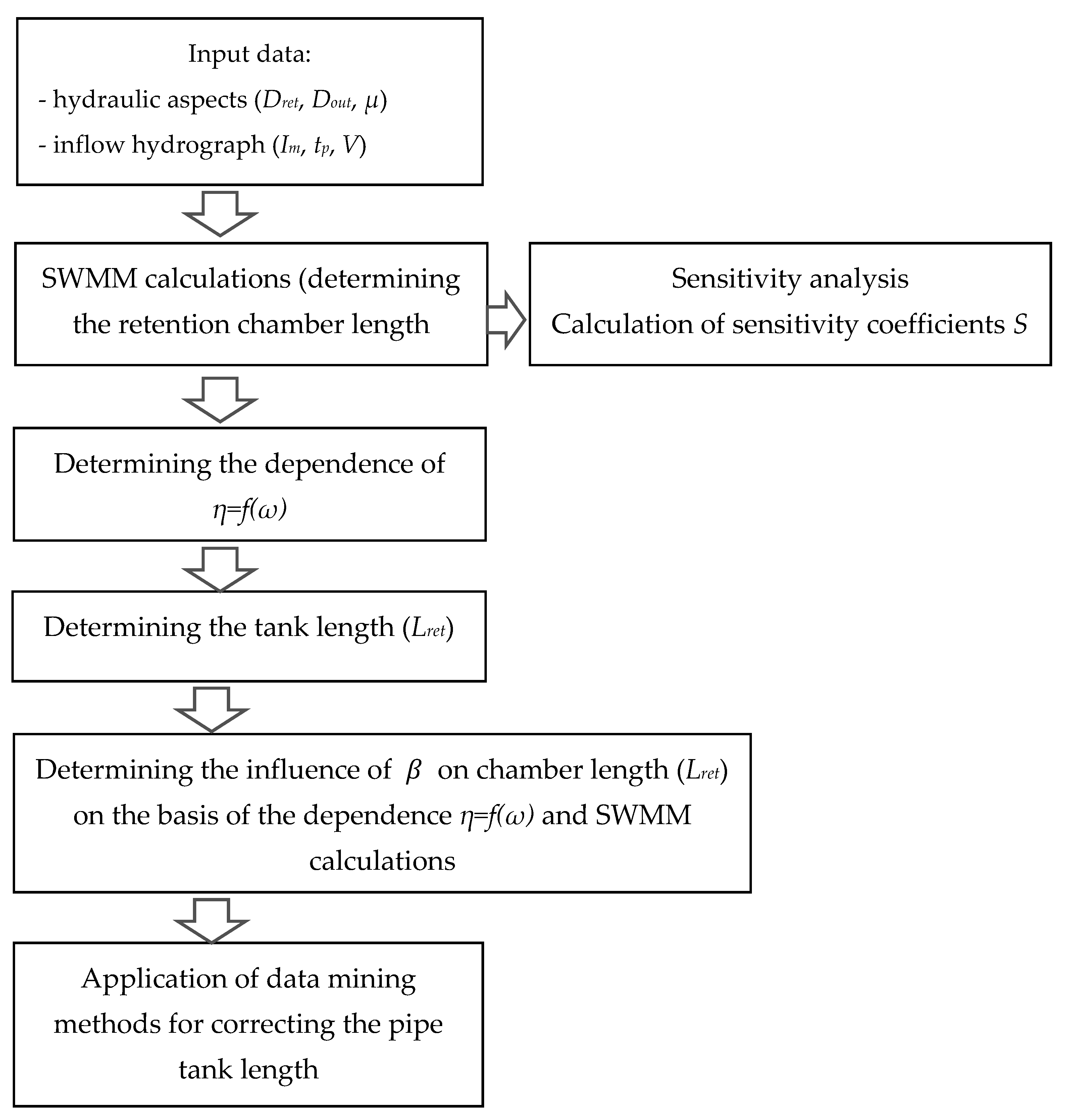
2.1. Calculation Algorithm Concept
2.2. Differential Equation of Stormwater Volume Balance
2.3. Dimensionless Differential Equation of Volume Balance
- -
- Dimensionless time from the start (t*):
- -
- Dimensionless flow rate (I*):
- -
- Dimensionless tank volume (V*):
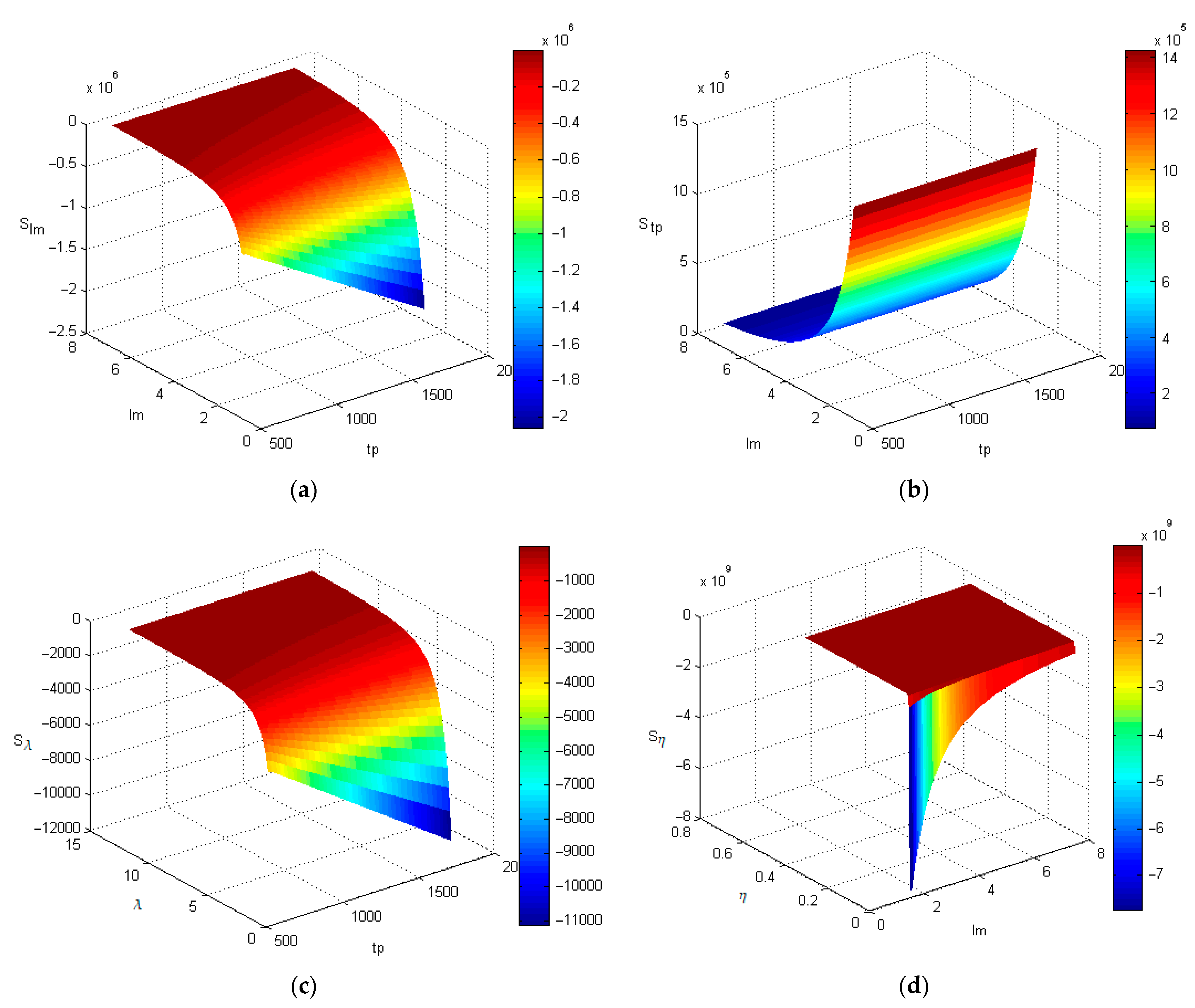
2.4. Local Sensitivity Analysis
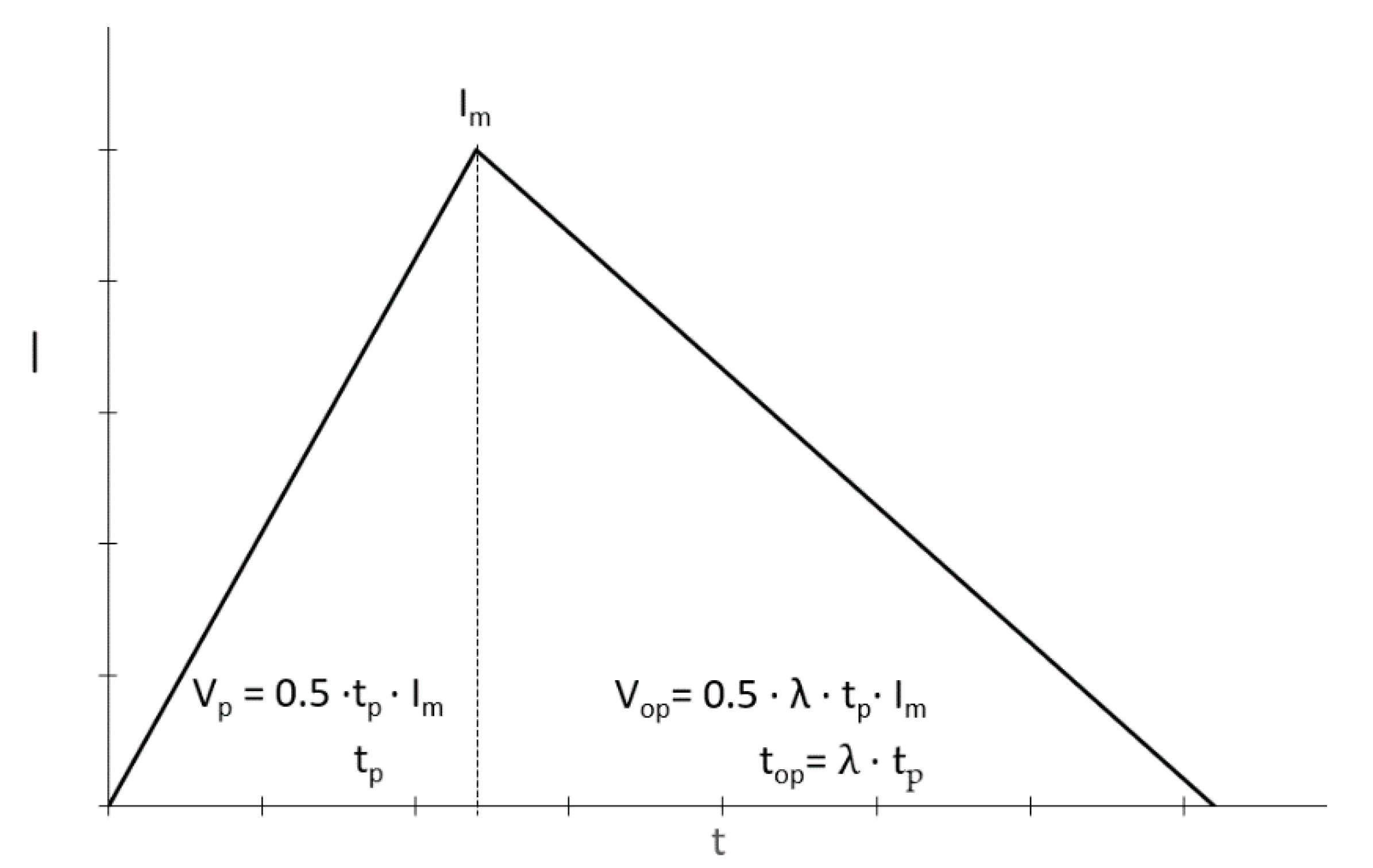
2.5. Influence of Hydrograph Parameters and Outlet Devices on Calculation Errors
2.6. Modeling of the Errors in the Predicted Tank Length Using Data Mining Methods
3. Results and Discussion
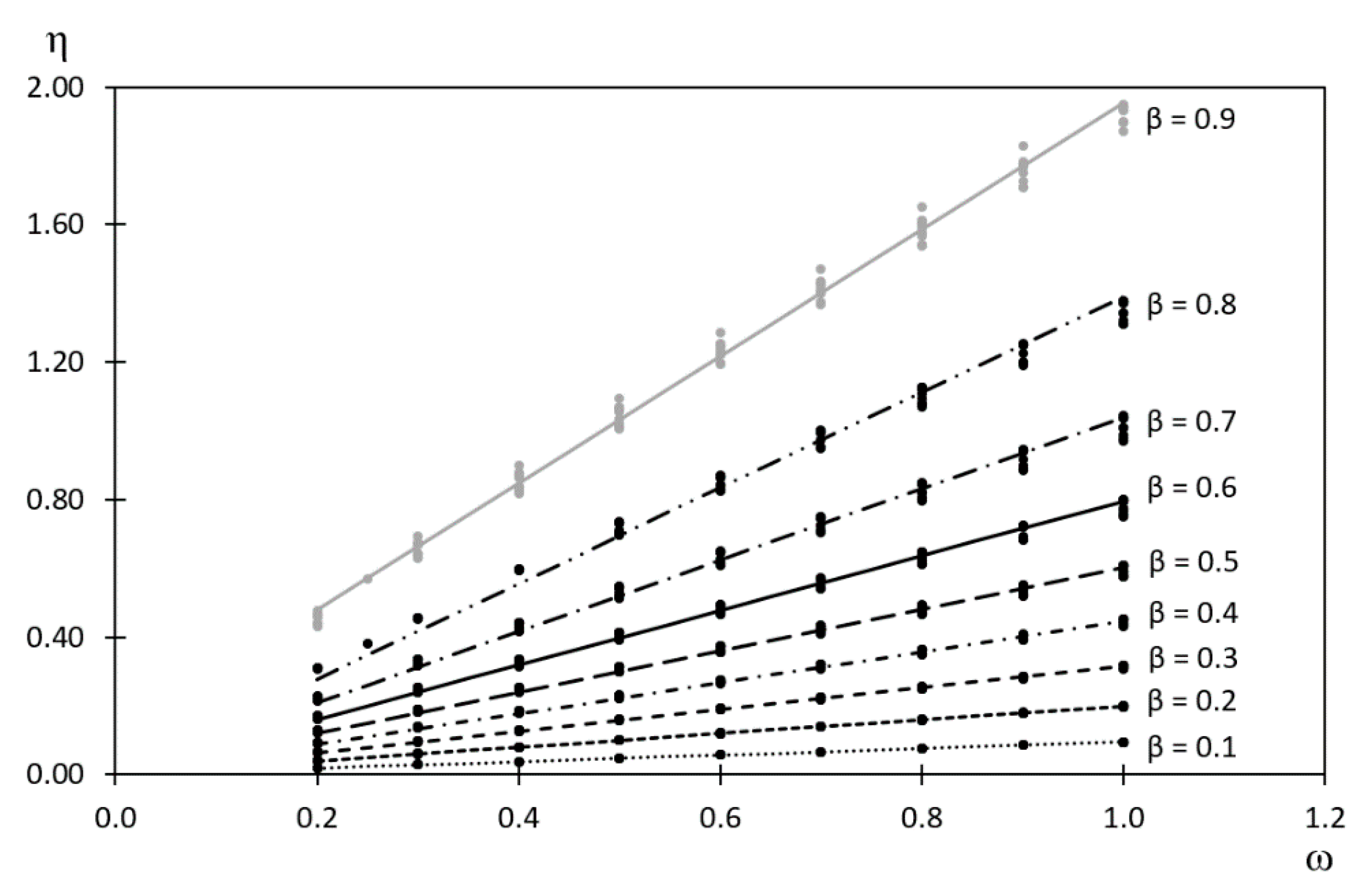
3.1. Dependence η = f(ω, β)
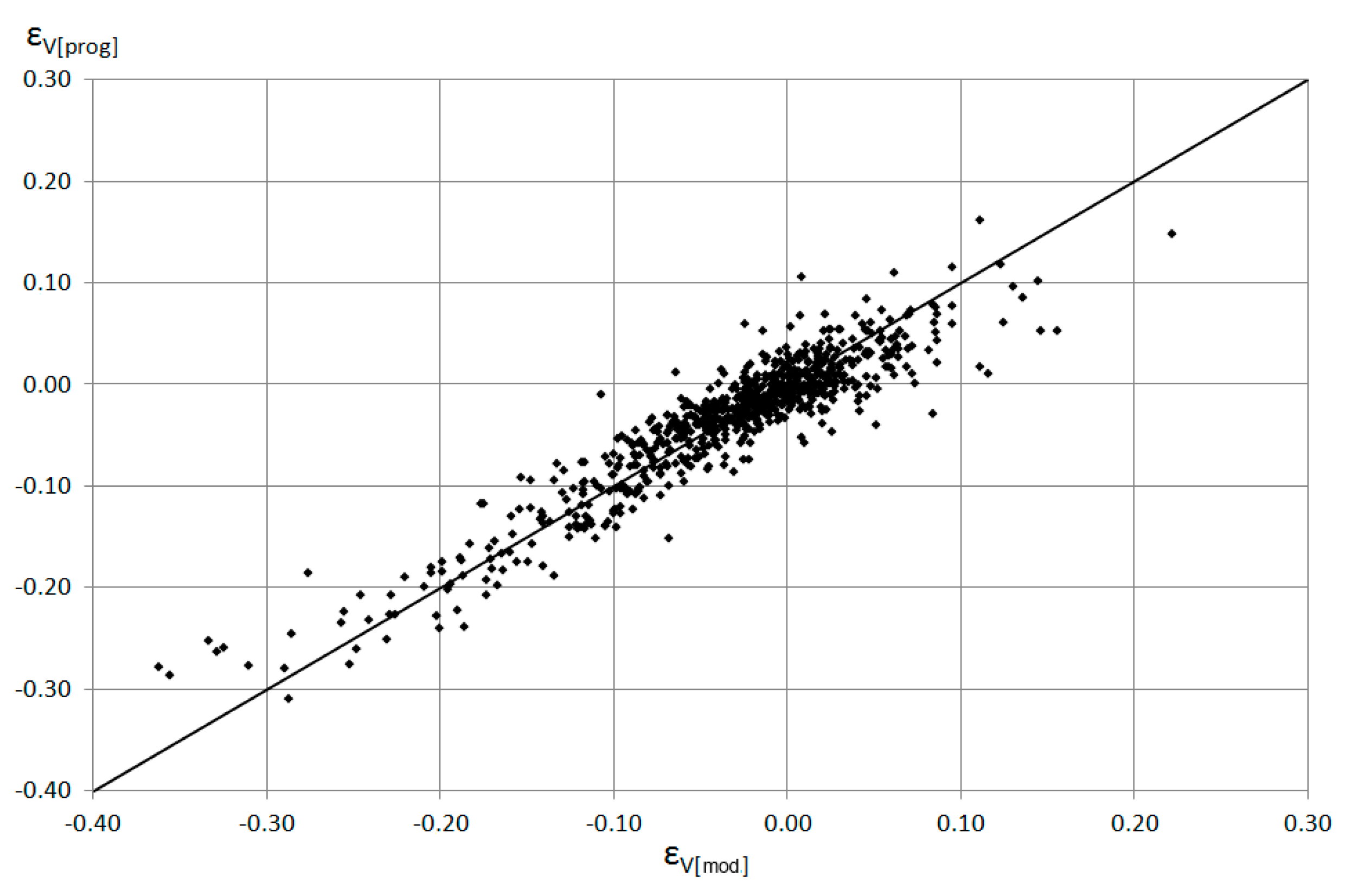
3.2. Influence of the Influent Hydrograph Parameters and Tank Characteristics on the Errors in the Prediction of Its Volume
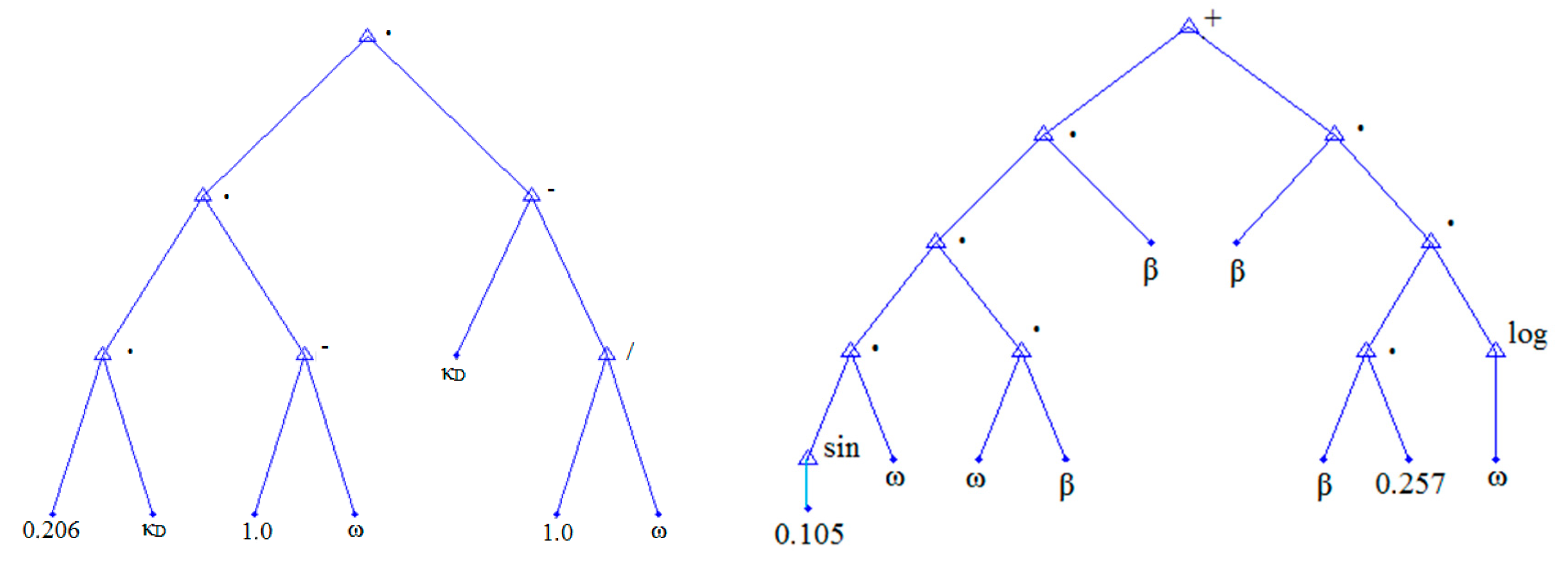
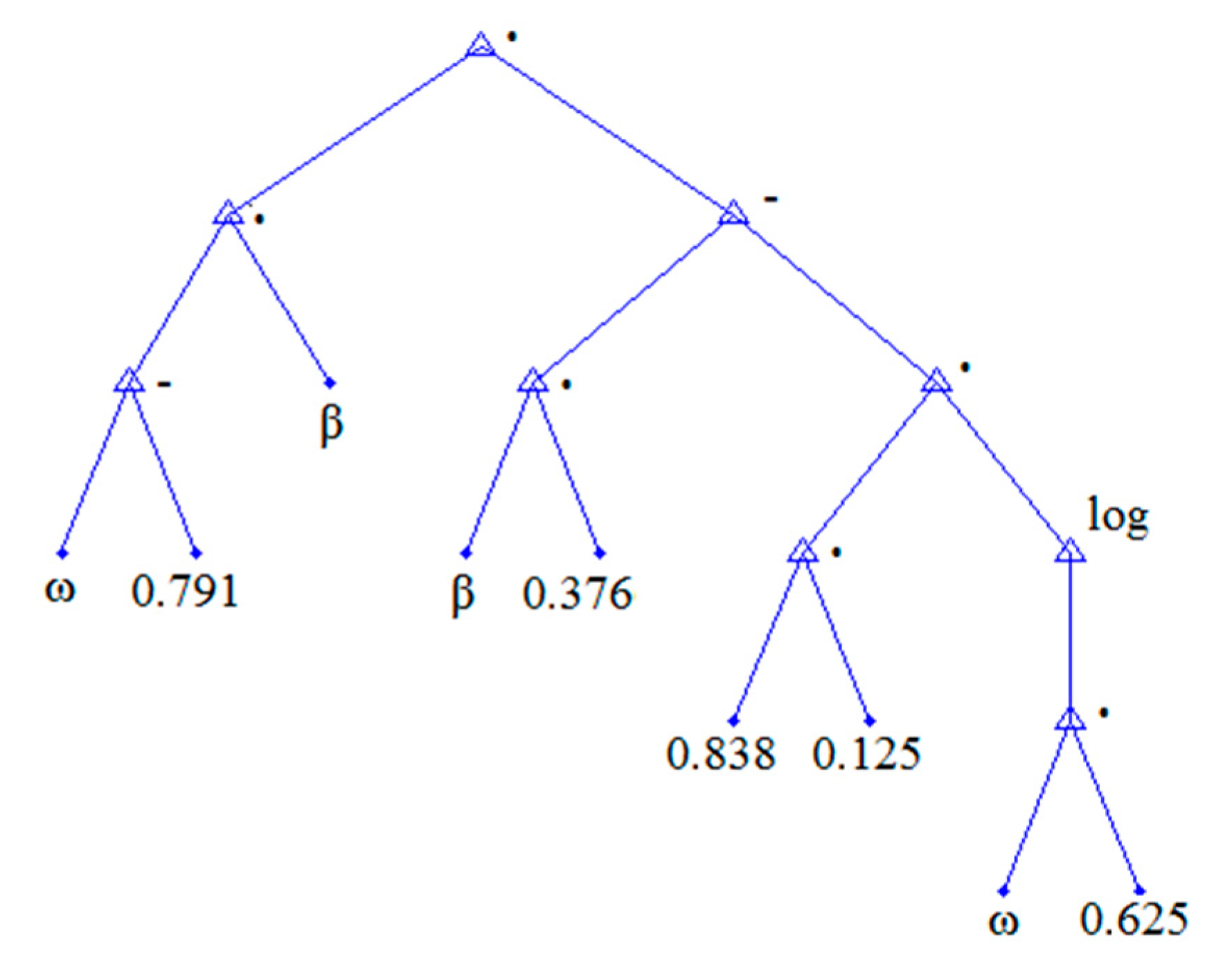
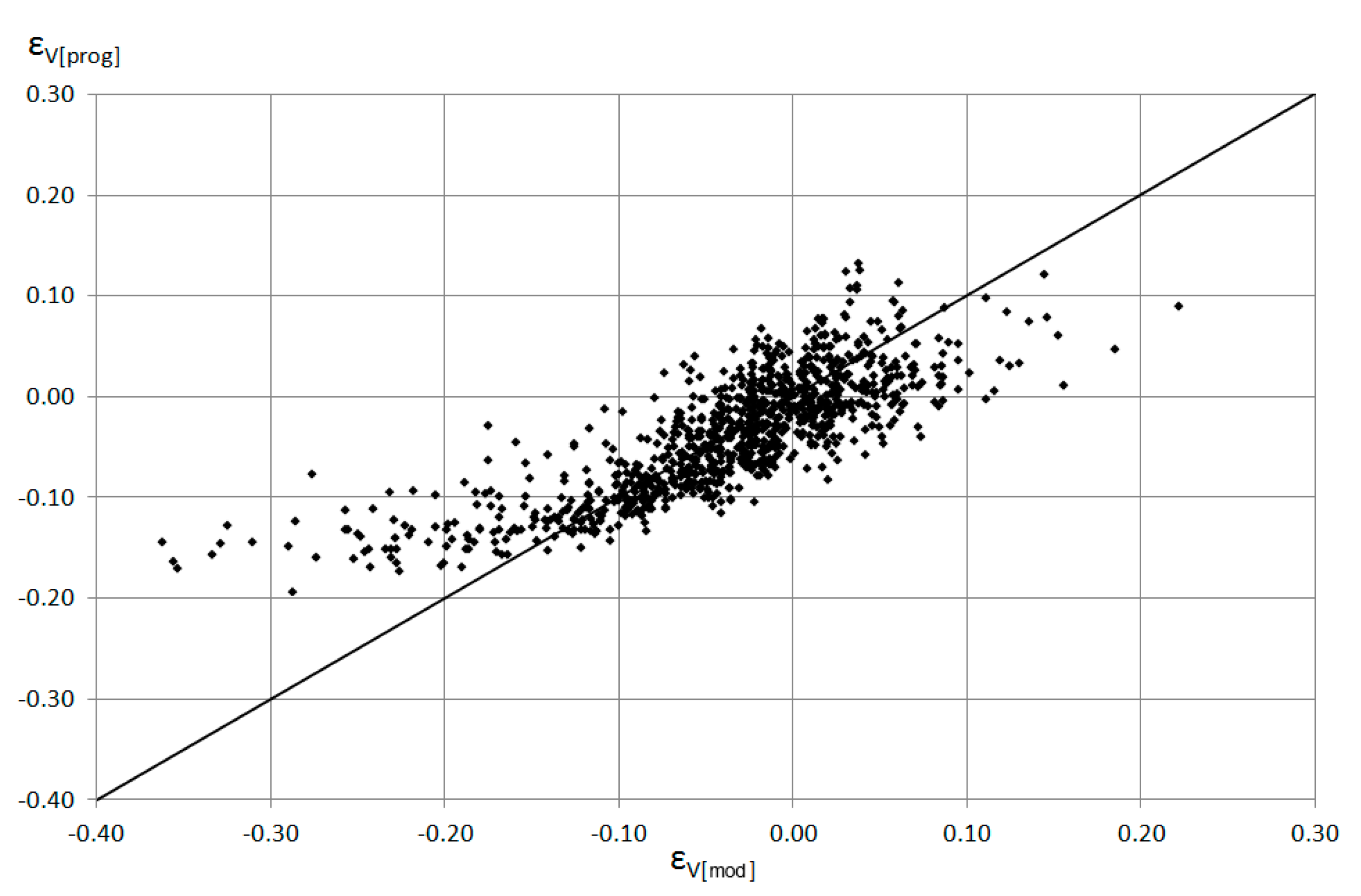
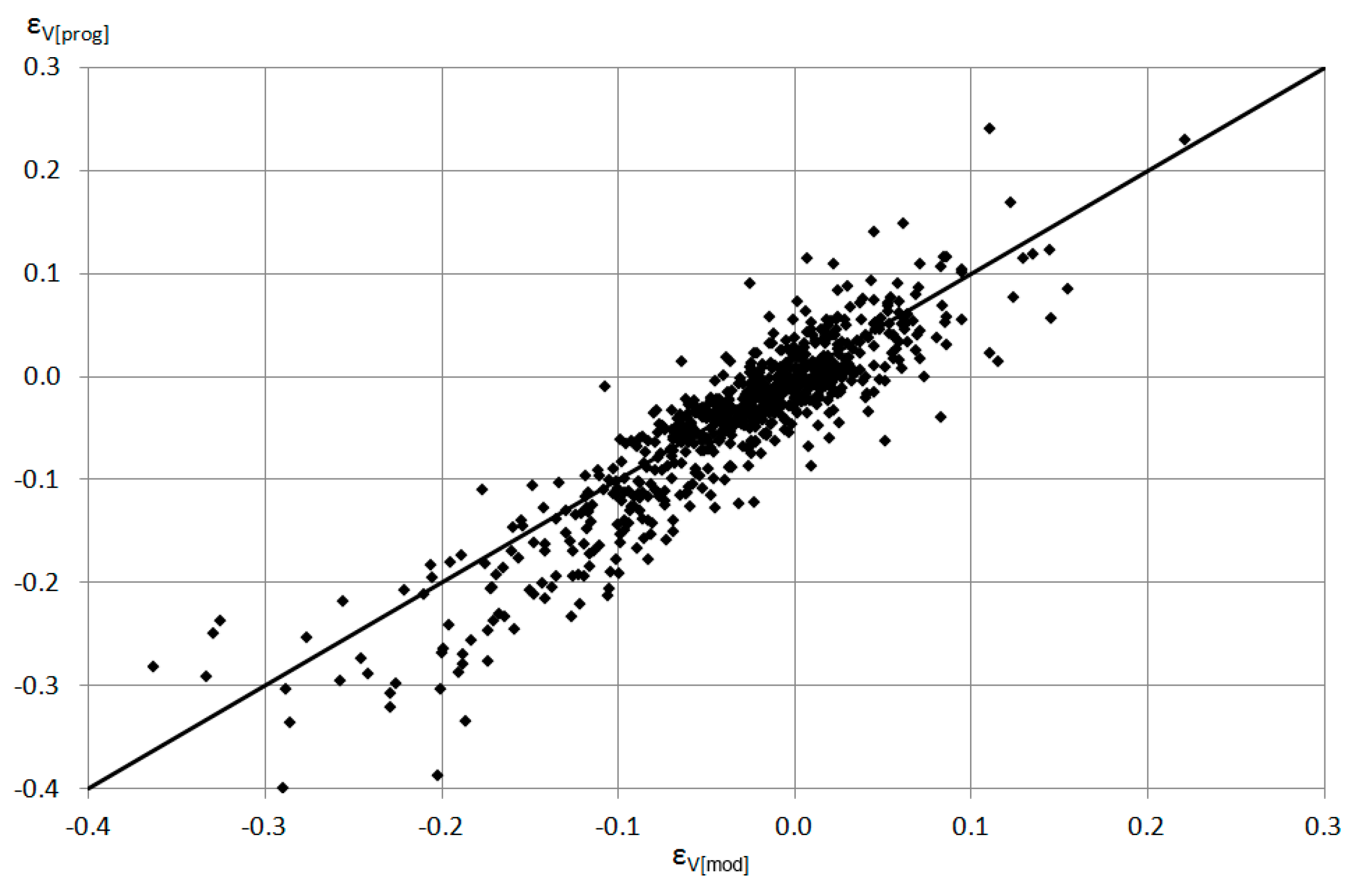
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arfanuzzaman, M.; Atiq Rahman, A. Sustainable water demand management in the face of rapid urbanization and ground water depletion for social–ecological resilience building. Glob. Ecol. Conserv. 2017, 10, 9–22. [Google Scholar] [CrossRef]
- Nagypál, V.; Mikó, E.; Hodúr, C. Sustainable Water Use Considering Three Hungarian Dairy Farms. Sustainability 2020, 12, 3145. [Google Scholar] [CrossRef] [Green Version]
- Özerol, G.; Dolman, N.; Bormann, H.; Bressers, H.; Lulofs, K.; Böge, M. Urban water management and climate change adaptation: A self-assessment study by seven midsize cities in the North Sea Region. Sustain. Cities Soc. 2020, 55, 102066. [Google Scholar] [CrossRef]
- Kärrman, E. Strategies towards sustainable wastewater management. Urban. Water 2001, 3, 63–72. [Google Scholar] [CrossRef]
- Garrick, D.; Iseman, T.; Gilson, G.; Brozovic, N.; O’Donnell, E.; Matthews, N.; Miralles-Wilhelm, F.; Wight, C.; Young, W. Scalable solutions to freshwater scarcity: Advancing theories of change to incentivise sustainable water use. Water Secur. 2020, 9, 100055. [Google Scholar] [CrossRef]
- Willuweit, L.; O’Sullivan, J.J. A decision support tool for sustainable planning of urban water systems: Presenting the Dynamic Urban Water Simulation Model. Water Res. 2013, 47, 7206–7220. [Google Scholar] [CrossRef]
- Paithankar, D.N.; Taji, S.G. Investigating the hydrological performance of green roofs using storm water management model. Mater. Today Proc. 2020, 32, 943–950. [Google Scholar] [CrossRef]
- Simon, D. Our Common Future: Report of the World Commission on Environment and Development (Book Review). Third World Plan. Rev. 1987, 9, 285. [Google Scholar] [CrossRef]
- Demuzere, M.; Orru, K.; Heidrich, O.; Olazabal, E.; Geneletti, D.; Orru, H.; Bhave, A.G.; Mittal, N.; Feliu, E.; Faehnle, M. Mitigating and adapting to climate change: Multi-functional and multi-scale assessment of green urban infrastructure. J. Environ. Manag. 2014, 146, 107–115. [Google Scholar] [CrossRef]
- La Rosa, D.; Pappalardo, V. Planning for spatial equity - A performance based approach for sustainable urban drainage systems. Sustain. Cities Soc. 2020, 53, 101885. [Google Scholar] [CrossRef]
- Wakode, H.B.; Baier, K.; Jha, R.; Azzam, R. Impact of urbanization on groundwater recharge and urban water balance for the city of Hyderabad, India. Int. Soil Water Conserv. Res. 2018, 6, 51–62. [Google Scholar] [CrossRef]
- Tapia Silva, F.O.; Wehrmann, A.; Henze, H.-J.; Model, N. Ability of plant-based surface technology to improve urban water cycle and mesoclimate. Urban. For. Urban. Green. 2006, 4, 145–158. [Google Scholar] [CrossRef]
- Paul, M.J.; Meyer, J.L. Streams in the Urban Landscape. Annu. Rev. Ecol. Syst. 2001, 32, 333–365. [Google Scholar] [CrossRef]
- Mielby, S.; Eriksson, I.; Campbell, D.; De Beer, H.; Bonsor, H.; Le Guern, C.; van der Krogt, R.; Lawrence, D.; Ryzynski, G.; Schokker, J. Opening up the Subsurface for the Cities of Tomorrow. Considering the Access to Subsurface Knowledge-Evaluation of Practices and Techniques; COST Action TU1206 Sub-Urban Report; TU1206-WG2-001; TNO Publications; 2016, p. 119. Available online: http://sub-urban.squarespace.com/s/TU1206-WG2-001-Opening-up-the-subsurface-for-the-cities-of-tomorrow_Summary-Report.pdf (accessed on 13 September 2020).
- Timm, A.; Kluge, B.; Wessolek, G. Hydrological balance of paved surfaces in moist mid-latitude climate—A review. Landsc. Urban. Plan. 2018, 175, 80–91. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H. Extending the Rational Method for assessing and developing sustainable urban drainage systems. Water Res. 2018, 144, 112–125. [Google Scholar] [CrossRef]
- Cheng, M.-S.; Coffman, L.S.; Clar, M.L. Low-Impact Development Hydrologic Analysis. In Urban Drainage Modeling, Proceedings of the Specialty Symposium of the World Water and Environmental Resources Congress, Orlando, FL, USA, 20–24 May 2001; American Society of Civil Engineers: Reston, VA, USA, 2001; pp. 659–681. [Google Scholar]
- Dietz, M.E. Low Impact Development Practices: A Review of Current Research and Recommendations for Future Directions. Water Air Soil Pollut. 2007, 186, 351–363. [Google Scholar] [CrossRef]
- Ahiablame, L.M.; Engel, B.A.; Chaubey, I. Effectiveness of Low Impact Development Practices: Literature Review and Suggestions for Future Research. Water Air Soil Pollut. 2012, 223, 4253–4273. [Google Scholar] [CrossRef]
- Kaykhosravi, S.; Khan, U.; Jadidi, A. A Comprehensive Review of Low Impact Development Models for Research, Conceptual, Preliminary and Detailed Design Applications. Water 2018, 10, 1541. [Google Scholar] [CrossRef] [Green Version]
- Khan, U.; Valeo, C.; Chu, A.; He, J. A Data Driven Approach to Bioretention Cell Performance: Prediction and Design. Water 2013, 5, 13–28. [Google Scholar] [CrossRef]
- Elliott, A.; Trowsdale, S. A review of models for low impact urban stormwater drainage. Environ. Model. Softw. 2007, 22, 394–405. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.-L.; et al. SUDS, LID, BMPs, WSUD and more—The evolution and application of terminology surrounding urban drainage. Urban. Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
- Ishaq, S.; Hewage, K.; Farooq, S.; Sadiq, R. State of provincial regulations and guidelines to promote low impact development (LID) alternatives across Canada: Content analysis and comparative assessment. J. Environ. Manag. 2019, 235, 389–402. [Google Scholar] [CrossRef] [PubMed]
- Ghodsi, S.H.; Zahmatkesh, Z.; Goharian, E.; Kerachian, R.; Zhu, Z. Optimal design of low impact development practices in response to climate change. J. Hydrol. 2020, 580, 124266. [Google Scholar] [CrossRef]
- Gaffin, S.; Khanbilvardi, R.; Rosenzweig, C. Development of a Green Roof Environmental Monitoring and Meteorological Network in New York City. Sensors 2009, 9, 2647–2660. [Google Scholar] [CrossRef] [PubMed]
- Abdollahian, S.; Kazemi, H.; Rockaway, T.; Gullapalli, V. Stormwater Quality Benefits of Permeable Pavement Systems with Deep Aggregate Layers. Environments 2018, 5, 68. [Google Scholar] [CrossRef] [Green Version]
- Šijanec Zavrl, M.; Tanac Zeren, M. Sustainability of Urban Infrastructures. Sustainability 2010, 2, 2950–2964. [Google Scholar] [CrossRef] [Green Version]
- Sartipi, M.; Sartipi, F. Stormwater retention using pervious concrete pavement: Great Western Sydney case study. Case Stud. Constr. Mater. 2019, 11, e00274. [Google Scholar] [CrossRef]
- Boogaard, F.; Lucke, T. Long-Term Infiltration Performance Evaluation of Dutch Permeable Pavements Using the Full-Scale Infiltration Method. Water 2019, 11, 320. [Google Scholar] [CrossRef] [Green Version]
- Saadeh, S.; Ralla, A.; Al-Zubi, Y.; Wu, R.; Harvey, J. Application of fully permeable pavements as a sustainable approach for mitigation of stormwater runoff. Int. J. Transp. Sci. Technol. 2019, 8, 338–350. [Google Scholar] [CrossRef]
- Zhu, H.; Yu, M.; Zhu, J.; Lu, H.; Cao, R. Simulation study on effect of permeable pavement on reducing flood risk of urban runoff. Int. J. Transp. Sci. Technol. 2019, 8, 373–382. [Google Scholar] [CrossRef]
- Nordbo, A.; Järvi, L.; Haapanala, S.; Wood, C.R.; Vesala, T. Fraction of natural area as main predictor of net CO 2 emissions from cities. Geophys. Res. Lett. 2012, 39, 2012GL053087. [Google Scholar] [CrossRef]
- Morakinyo, T.E.; Lam, Y.F.; Hao, S. Evaluating the role of green infrastructures on near-road pollutant dispersion and removal: Modelling and measurement. J. Environ. Manage. 2016, 182, 595–605. [Google Scholar] [CrossRef] [PubMed]
- Capotorti, G.; Alós Ortí, M.M.; Copiz, R.; Fusaro, L.; Mollo, B.; Salvatori, E.; Zavattero, L. Biodiversity and ecosystem services in urban green infrastructure planning: A case study from the metropolitan area of Rome (Italy). Urban. For. Urban. Green. 2019, 37, 87–96. [Google Scholar] [CrossRef]
- Bressy, A.; Gromaire, M.-C.; Lorgeoux, C.; Saad, M.; Leroy, F.; Chebbo, G. Efficiency of source control systems for reducing runoff pollutant loads: Feedback on experimental catchments within Paris conurbation. Water Res. 2014, 57, 234–246. [Google Scholar] [CrossRef] [Green Version]
- Palermo, S.A.; Talarico, V.C.; Turco, M. On the LID systems effectiveness for urban stormwater management: Case study in Southern Italy. IOP Conf. Ser. Earth Environ. Sci. 2020, 410, 012012. [Google Scholar] [CrossRef]
- Dabas, R.; Kumar, S.; Kumar, M. Applications of Low Impact Development for Managing the Storm Water Surface Runoff in Urban Areas; Springer: Singapore, 2021; pp. 275–283. [Google Scholar]
- Kevern, J.T. Green Building and Sustainable Infrastructure: Sustainability Education for Civil Engineers. J. Prof. Issues Eng. Educ. Pract. 2011, 137, 107–112. [Google Scholar] [CrossRef]
- Winz, I.; Brierley, G.; Trowsdale, S. Dominant perspectives and the shape of urban stormwater futures. Urban. Water, J. 2011, 8, 337–349. [Google Scholar] [CrossRef]
- Russo, A.; Escobedo, F.J.; Cirella, G.T.; Zerbe, S. Edible green infrastructure: An approach and review of provisioning ecosystem services and disservices in urban environments. Agric. Ecosyst. Environ. 2017, 242, 53–66. [Google Scholar] [CrossRef]
- Starzec, M.; Dziopak, J. A Case Study of the Retention Efficiency of a Traditional and Innovative Drainage System. Resources 2020, 9, 108. [Google Scholar] [CrossRef]
- Piro, P.; Carbone, M.; Morimanno, F.; Palermo, S.A. Simple flowmeter device for LID systems: From laboratory procedure to full-scale implementation. Flow Meas. Instrum. 2019, 65, 240–249. [Google Scholar] [CrossRef]
- Sepehri, M.; Malekinezhad, H.; Ilderomi, A.R.; Talebi, A.; Hosseini, S.Z. Studying the effect of rain water harvesting from roof surfaces on runoff and household consumption reduction. Sustain. Cities Soc. 2018, 43, 317–324. [Google Scholar] [CrossRef]
- Soonthornnonda, P.; Christensen, E.R. Source apportionment of pollutants and flows of combined sewer wastewater. Water Res. 2008, 42, 1989–1998. [Google Scholar] [CrossRef]
- Park, M.-H.; Swamikannu, X.; Stenstrom, M.K. Accuracy and precision of the volume–concentration method for urban stormwater modeling. Water Res. 2009, 43, 2773–2786. [Google Scholar] [CrossRef]
- Oviedo-Ocaña, E.R.; Dominguez, I.; Ward, S.; Rivera-Sanchez, M.L.; Zaraza-Peña, J.M. Financial feasibility of end-user designed rainwater harvesting and greywater reuse systems for high water use households. Environ. Sci. Pollut. Res. 2018, 25, 19200–19216. [Google Scholar] [CrossRef] [Green Version]
- Burns, M.J.; Fletcher, T.D.; Duncan, H.P.; Hatt, B.E.; Ladson, A.R.; Walsh, C.J. The performance of rainwater tanks for stormwater retention and water supply at the household scale: An empirical study. Hydrol. Process. 2015, 29, 152–160. [Google Scholar] [CrossRef]
- Xu, W.; Fletcher, T.; Duncan, H.; Bergmann, D.; Breman, J.; Burns, M. Improving the Multi-Objective Performance of Rainwater Harvesting Systems Using Real-Time Control Technology. Water 2018, 10, 147. [Google Scholar] [CrossRef] [Green Version]
- Musz-Pomorska, A.; Widomski, M.K.; Gołębiowska, J. Financial Sustainability of Selected Rain Water Harvesting Systems for Single-Family House under Conditions of Eastern Poland. Sustainability 2020, 12, 4853. [Google Scholar] [CrossRef]
- Suleiman, L.; Olofsson, B.; Saurí, D.; Palau-Rof, L. A breakthrough in urban rain-harvesting schemes through planning for urban greening: Case studies from Stockholm and Barcelona. Urban. For. Urban. Green. 2020, 51, 126678. [Google Scholar] [CrossRef]
- Melville-Shreeve, P.; Ward, S.; Butler, D. Rainwater Harvesting Typologies for UK Houses: A Multi Criteria Analysis of System Configurations. Water 2016, 8, 129. [Google Scholar] [CrossRef] [Green Version]
- Lazarova, V.; Hills, S.; Birks, R. Using recycled water for non-potable, urban uses: A review with particular reference to toilet flushing. Water Supply 2003, 3, 69–77. [Google Scholar] [CrossRef]
- GhaffarianHoseini, A.; Tookey, J.; GhaffarianHoseini, A.; Yusoff, S.M.; Hassan, N.B. State of the art of rainwater harvesting systems towards promoting green built environments: A review. Desalin. Water Treat. 2015, 1–10. [Google Scholar] [CrossRef]
- Oberascher, M.; Zischg, J.; Palermo, S.A.; Kinzel, C.; Rauch, W.; Sitzenfrei, R. Smart Rain Barrels: Advanced LID Management through Measurement and Control; Springer: Cham, Switzerland, 2019; pp. 777–782. [Google Scholar]
- Palermo, S.A.; Talarico, V.C.; Pirouz, B. Optimizing Rainwater Harvesting Systems for Non-potable Water Uses and Surface Runoff Mitigation; Springer: Cham, Switzerland, 2020; pp. 570–582. [Google Scholar]
- Taji, S.G.; Saraf, V.R.; Regulwar, D.G. Smart Rain Water Harvesting for Smart Cities, In Studies in Systems, Decision and Control.; Springer: Cham, Switzerland, 2021; Volume 308, pp. 91–116. [Google Scholar]
- Campisano, A.; Creaco, E.; Modica, C. Application of Real-Time Control Techniques to Reduce Water Volume Discharges from Quality-Oriented CSO Devices. J. Environ. Eng. 2016, 142, 04015049. [Google Scholar] [CrossRef]
- Akan, A.O.; Houghtalen, R.J. Urban Hydrology, Hydraulics, and Stormwater Quality: Engineering Applications and Computer Modeling; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003; ISBN 0471431583. [Google Scholar]
- Mrowiec, M. The Effective Dimensioning and Dynamic Regulation Sewage Reservoirs; Wydawnictwo Politechniki Częstochowskiej: Częstochowa, Poland, 2009; ISBN 9788371934247. [Google Scholar]
- De Paola, F.; De Martino, F. Stormwater Tank Performance: Design and Management Criteria for Capture Tanks Using a Continuous Simulation and a Semi-Probabilistic Analytical Approach. Water 2013, 5, 1699–1711. [Google Scholar] [CrossRef] [Green Version]
- Starzec, M.; Dziopak, J.; Słyś, D.; Pochwat, K.; Kordana, S. Dimensioning of Required Volumes of Interconnected Detention Tanks Taking into Account the Direction and Speed of Rain Movement. Water 2018, 10, 1826. [Google Scholar] [CrossRef] [Green Version]
- Szeląg, B.; Kiczko, A.; Dąbek, L. Stormwater Reservoir Sizing in Respect of Uncertainty. Water 2019, 11, 321. [Google Scholar] [CrossRef] [Green Version]
- Kisiel, A.; Kisiel, J.; Malmur, R.; Mrowiec, M. Retention tanks as key elements of modern drainage systems. Tech. J. Environ. 2008, 105, 41–63. [Google Scholar]
- Mrowiec, M. A tubular tank for stormwater storage in the stormwater collection system. Gas. Water Sanit. Eng. 2002, 7, 236–239. [Google Scholar]
- Guo, J.C.Y. Detention Storage Volume for Small Urban Catchments. J. Water Resour. Plan. Manag. 1999, 125, 380–382. [Google Scholar] [CrossRef]
- Hong, Y.-M.; Yeh, N.; Chen, J.-Y. The simplified methods of evaluating detention storage volume for small catchment. Ecol. Eng. 2006, 26, 355–364. [Google Scholar] [CrossRef]
- Hong, Y.-M. Graphical estimation of detention pond volume for rainfall of short duration. J. Hydro-environ. Res. 2008, 2, 109–117. [Google Scholar] [CrossRef]
- Szeląg, B.; Kiczko, A. The graphic method of sizing pipe reservoir for short, high-intensity rainfalls. Ann. Warsaw Univ. Life Sci. L. Reclam. 2014, 46, 221–232. [Google Scholar] [CrossRef] [Green Version]
- Rutkowska, D.; Piliński, M.; Rutkowski, L. Neural Networks, Genetic Algorithms and Fuzzy Systems; Wydaw. Naukowe PWN: Warszawa; Łódź, Poland, 1997; ISBN 978-83-01-12304-8.
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Szelag, B.; Barbusinski, K.; Studzinski, J. Activated sludge process modelling using selected machine learning techniques. Desalin. WATER Treat. 2018, 117, 78–87. [Google Scholar] [CrossRef]
- Capodaglio, A. Sludge bulking analysis and forecasting: Application of system identification and artificial neural computing technologies. Water Res. 1991, 25, 1217–1224. [Google Scholar] [CrossRef]
- Rutkowski, L. Arificial Intellignce Methods and Techniques; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2006. [Google Scholar]
- Szeląg, B.; Mrowiec, M. The methods of evaluating storage volume for single-chamber reservoir in urban catchments. Arch. Environ. Prot. 2016, 42, 20–25. [Google Scholar] [CrossRef] [Green Version]
- Froehlich, D.C. Graphical Sizing of Small Single-Outlet Detention Basins in the Semiarid Southwest. J. Irrig. Drain. Eng. 2009, 135, 779–790. [Google Scholar] [CrossRef]
- Guo, J.C.Y. Hydrology-Based Approach to Storm Water Detention Basin Design Using New Routing Schemes. J. Hydrol. Eng. 2004, 9, 333–336. [Google Scholar] [CrossRef]
- McEnroe, B.M. Preliminary Sizing of Detention Reservoirs to Reduce Peak Discharges. J. Hydraul. Eng. 1992, 118, 1540–1549. [Google Scholar] [CrossRef]
- Starzec, M.; Dziopak, J.; Słyś, D. An Analysis of Stormwater Management Variants in Urban Catchments. Resources 2020, 9, 19. [Google Scholar] [CrossRef] [Green Version]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Kiczko, A.; Szeląg, B.; Kozioł, A.P.; Krukowski, M.; Kubrak, E.; Kubrak, J.; Romanowicz, R.J. Optimal Capacity of a Stormwater Reservoir for Flood Peak Reduction. J. Hydrol. Eng. 2018, 23, 4018008. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model. User’s Manual Version 5.1; National Risk Management Research Laboratory Office of Research and Development, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2015; Volume 352. [Google Scholar]
- Zhang, S.; Guo, Y. SWMM Simulation of the Storm Water Volume Control Performance of Permeable Pavement Systems. J. Hydrol. Eng. 2015, 20, 06014010. [Google Scholar] [CrossRef]
- El-Sharif, A.; Hansen, D. Application of SWMM to the Flooding Problem in Truro, Nova Scotia. Can. Water Resour. J. 2001, 26, 439–459. [Google Scholar] [CrossRef]
- Sañudo, E.; Cea, L.; Puertas, J. Modelling Pluvial Flooding in Urban Areas Coupling the Models Iber and SWMM. Water 2020, 12, 2647. [Google Scholar] [CrossRef]
- TIBCO Software Inc. Statistica (Automated Neural Network); Version 10; TIBCO Software Inc.: Palo Alto, CA, USA, 2011. [Google Scholar]
- Paik, K. Analytical derivation of reservoir routing and hydrological risk evaluation of detention basins. J. Hydrol. 2008, 352, 191–201. [Google Scholar] [CrossRef]
| β | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|
| εVmax | 3.77 | 5.75 | 6.16 | 6.31 | 9.45 | 11.19 | 12.92 | 18.44 | 22.13 |
| εVmin | −7.01 | −7.28 | −9.79 | −12.07 | −18.08 | −20.51 | −22.93 | −25.03 | −36.33 |
| Method | RRE | MPE | r | AIC |
|---|---|---|---|---|
| Regression | 0.0442 | 47.51 | 0.6851 | −3553 |
| ANN | 0.0272 | 5.60 | 0.9310 | −3010 |
| GP(ω, η) | 0.0345 | 8.02 | 0.8872 | −3321 |
| GP(ω, β) | 0.0312 | 7.89 | 0.8953 | −3299 |
| GP(ω, β) | 0.0296 | 7.21 | 0.9010 | −3236 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szeląg, B.; Kiczko, A.; Musz-Pomorska, A.; Widomski, M.K.; Zaburko, J.; Łagód, G.; Stránský, D.; Sokáč, M. Advanced Graphical–Analytical Method of Pipe Tank Design Integrated with Sensitivity Analysis for Sustainable Stormwater Management in Urbanized Catchments. Water 2021, 13, 1035. https://doi.org/10.3390/w13081035
Szeląg B, Kiczko A, Musz-Pomorska A, Widomski MK, Zaburko J, Łagód G, Stránský D, Sokáč M. Advanced Graphical–Analytical Method of Pipe Tank Design Integrated with Sensitivity Analysis for Sustainable Stormwater Management in Urbanized Catchments. Water. 2021; 13(8):1035. https://doi.org/10.3390/w13081035
Chicago/Turabian StyleSzeląg, Bartosz, Adam Kiczko, Anna Musz-Pomorska, Marcin K. Widomski, Jacek Zaburko, Grzegorz Łagód, David Stránský, and Marek Sokáč. 2021. "Advanced Graphical–Analytical Method of Pipe Tank Design Integrated with Sensitivity Analysis for Sustainable Stormwater Management in Urbanized Catchments" Water 13, no. 8: 1035. https://doi.org/10.3390/w13081035





