Principles for Distributing Infiltration-Based Stormwater Control Measures in Series
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theory
2.1.1. Step 1: Defining the Baseline
2.1.2. Step 2: Calculating Limiting Values of Upstream SCMs
2.1.3. Step 3: Redistributing Volume Among SCM Elements
2.2. Hypothetical Case Study
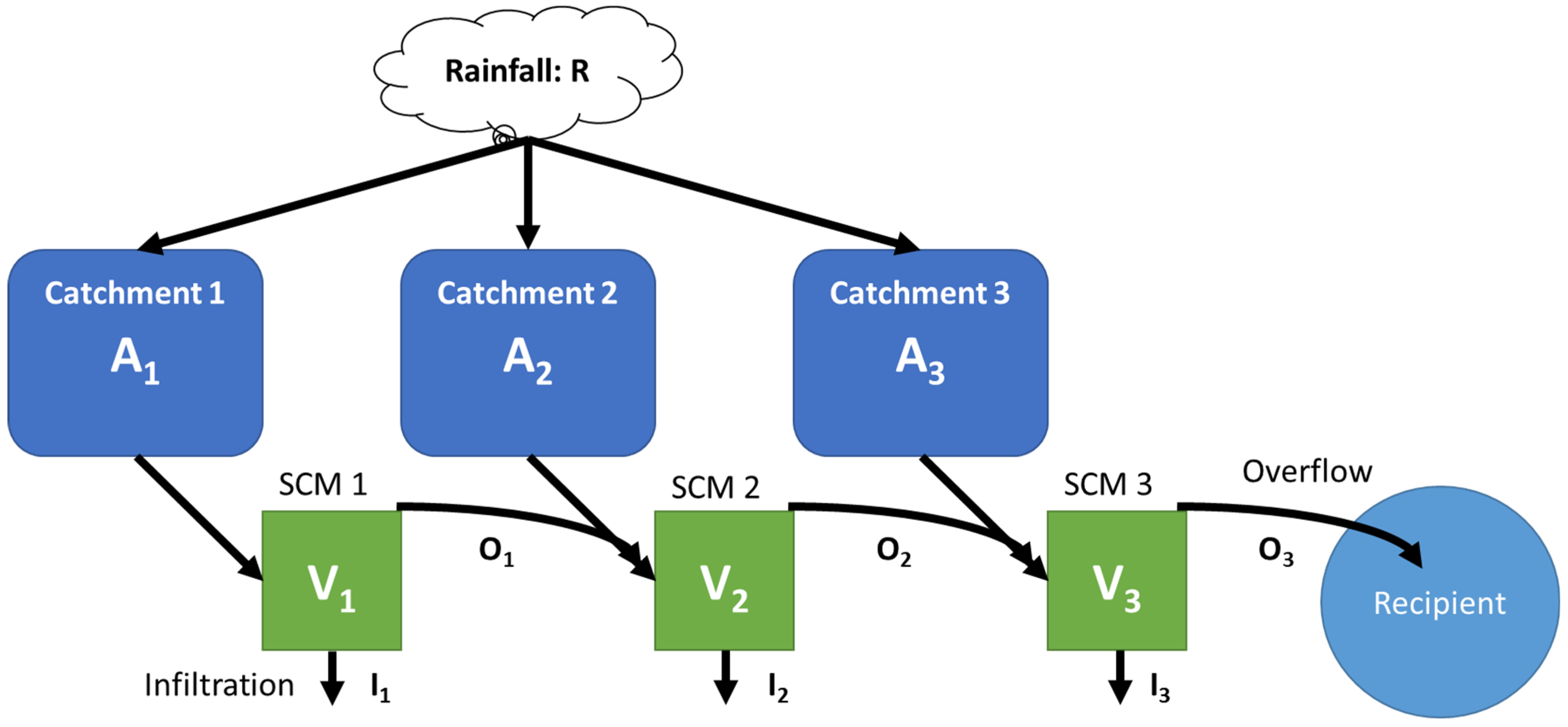
- The volume of water in SCM 1, V1, is calculated as the sum of the volume from the previous time step plus the runoff generated by multiplying the rainfall rate, R, with the area of sub-catchment 1, A1, minus the volume lost to infiltration, I1. If the calculated volume is more than the maximum volume of SCM 1, the excess is transferred to overflow, O1, and the stored volume is reduced to the maximum volume. If the calculated volume is less than zero, infiltration, I1, is reduced to balance the equation and the stored volume is set to zero.
- The volume of SCM 2 is calculated in the same way as for SCM 1, with the addition of the overflow from SCM 1, O1, to the first step as inflow.
- The volume of SCM 3 is calculated in the same way as for SCM 2 with the overflow from SCM 2, O2, replacing the overflow from SCM 1.
- The overflow from SCM 3, O3, represents the outflow from the catchment to the recipient, where we expect a threshold on the return period of outflow to apply. The frequency of overflow serves as main performance indicator for comparing the scenarios.
- The total number of calendar days where overflow occurs, nOi.
- The total volume of overflow in m3 for the duration of the simulation, VOi.
- The total volume infiltrated in m3 for the duration of the simulation, Ii.
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-davies, A.; Mikkelsen, P.S.; Rivard, G.; et al. SUDS, LID, BMPs, WSUD and more—The evolution and application of terminology surrounding urban drainage. Urban Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
- Barbosa, A.E.; Fernandes, J.N.; David, L.M. Key issues for sustainable urban stormwater management. Water Res. 2012, 46, 6787–6798. [Google Scholar] [CrossRef]
- Lerer, S.M.; Arnbjerg-Nielsen, K.; Mikkelsen, P.S. A Mapping of Tools for Informing Water Sensitive Urban Design Planning Decisions—Questions, Aspects and Context Sensitivity. Water 2015, 7, 993–1012. [Google Scholar] [CrossRef] [Green Version]
- Sørup, H.J.D.; Lerer, S.M.; Arnbjerg-Nielsen, K.; Mikkelsen, P.S.; Rygaard, M. Efficiency of stormwater control measures for combined sewer retrofitting under varying rain conditions: Quantifying the Three Points Approach (3PA). Environ. Sci. Policy 2016, 63, 19–26. [Google Scholar] [CrossRef] [Green Version]
- Jurga, A.; Pacak, A.; Pandelidis, D.; Kaźmierczak, B. A Long-Term Analysis of the Possibility of Water Recovery for Hydroponic Lettuce Irrigation in an Indoor Vertical Farm. Part 2: Rainwater Harvesting. Appl. Sci. 2020, 11, 310. [Google Scholar] [CrossRef]
- Godskesen, B.; Hauschild, M.; Rygaard, M.; Zambrano, K.; Albrechtsen, H.J. Life-cycle and freshwater withdrawal impact assessment of water supply technologies. Water Res. 2013, 47, 2363–2374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Faragò, M.; Brudler, S.; Godskesen, B.; Rygaard, M. An eco-efficiency evaluation of community-scale rainwater and stormwater harvesting in Aarhus, Denmark. J. Clean. Prod. 2019, 219, 601–612. [Google Scholar] [CrossRef]
- Andersen, J.S.; Lerer, S.M.; Backhaus, A.; Jensen, M.B.; Sørup, H.J.D. Characteristic Rain Events: A Methodology for Improving the Amenity Value of Stormwater Control Measures. Sustainability 2017, 9, 1793. [Google Scholar] [CrossRef] [Green Version]
- Brudler, S.; Arnbjerg-Nielsen, K.; Hauschild, M.Z.; Rygaard, M. Life cycle assessment of stormwater management in the context of climate change adaptation. Water Res. 2016, 106, 394–404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lerer, S.M.; Righetti, F.; Rozario, T.; Mikkelsen, P.S. Integrated hydrological model-based assessment of stormwater management scenarios in Copenhagen’s first climate resilient neighbourhood using the three point approach. Water 2017, 9, 883. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Q.; Panduro, T.E.; Thorsen, B.J.; Arnbjerg-Nielsen, K. Adaption to Extreme Rainfall with Open Urban Drainage System: An Integrated Hydrological Cost-Benefit Analysis. Environ. Manag. 2013, 51, 586–601. [Google Scholar] [CrossRef] [Green Version]
- Wolch, J.R.; Byrne, J.; Newell, J.P. Urban green space, public health, and environmental justice: The challenge of making cities ‘just green enough’. Landsc. Urban Plan. 2014, 125, 234–244. [Google Scholar] [CrossRef] [Green Version]
- Belmeziti, A.; Cherqui, F.; Kaufmann, B. Improving the multi-functionality of urban green spaces: Relations between components of green spaces and urban services. Sustain. Cities Soc. 2018, 43, 1–10. [Google Scholar] [CrossRef]
- Sørup, H.J.D.; Fryd, O.; Liu, L.; Arnbjerg-Nielsen, K.; Jensen, M.B. An SDG-based framework for assessing urban stormwater management systems. Blue Green Syst. 2019, 1, 102–108. [Google Scholar] [CrossRef] [Green Version]
- Bastien, N.; Arthur, S.; Wallis, S.; Scholz, M. The best management of SuDS treatment trains: A holistic approach. Water Sci. Technol. 2010, 61, 263–272. [Google Scholar] [CrossRef] [PubMed]
- Åstebøl, S.O.; Hvitved-Jacobsen, T.; Simonsen, Ø. Sustainable stormwater management at Fornebu—From an airport to an industrial and residential area of the city of Oslo, Norway. Sci. Total Environ. 2004, 334–335, 239–249. [Google Scholar] [CrossRef] [PubMed]
- Bach, P.M.; Deletic, A.; Urich, C.; Sitzenfrei, R.; Kleidorfer, M.; Rauch, W.; McCarthy, D.T. Modelling Interactions Between Lot-Scale Decentralised Water Infrastructure and Urban Form—A Case Study on Infiltration Systems. Water Resour. Manag. 2013, 27, 4845–4863. [Google Scholar] [CrossRef]
- Bach, P.M.; Mccarthy, D.T.; Deletic, A. Can we model the implementation of water sensitive urban design in evolving cities? Water Sci. Technol. 2015, 71, 149–156. [Google Scholar] [CrossRef] [PubMed]
- Löwe, R.; Urich, C.; Kulahci, M.; Radhakrishnan, M.; Deletic, A.; Arnbjerg-Nielsen, K. Simulating flood risk under non-stationary climate and urban development conditions—Experimental setup for multiple hazards and a variety of scenarios. Environ. Model. Softw. 2018, 102, 155–171. [Google Scholar] [CrossRef] [Green Version]
- Radhakrishnan, M.; Löwe, R.; Ashley, R.M.; Gersonius, B.; Arnbjerg-Nielsen, K.; Pathirana, A.; Zevenbergen, C. Flexible adaptation planning process for urban adaptation in Melbourne, Australia. Proc. Inst. Civ. Eng. Eng. Sustain. 2019, 172, 393–403. [Google Scholar] [CrossRef]
- Van Uytven, E.; Wampers, E.; Wolfs, V.; Willems, P. Evaluation of change factor-based statistical downscaling methods for impact analysis in urban hydrology. Urban Water J. 2020, 17, 785–794. [Google Scholar] [CrossRef]
- Sørup, H.J.D.; Davidsen, S.; Löwe, R.; Thorndahl, S.L.; Borup, M.; Arnbjerg-Nielsen, K. Evaluating catchment response to artificial rainfall from four weather generators for present and future climate. Water Sci. Technol. 2018, 77, 2578–2588. [Google Scholar] [CrossRef] [PubMed]
- Lerer, S.M.; Sørup, H.J.D.; Arnbjerg-nielsen, K.; Mikkelsen, P.S. A new tool for quantifying the impacts of water sensitive urban design—The power of simplicity. In Proceedings of the 10th International Conference on Urban Drainage Modelling, Mont-Sainte-Anne, QC, Canada, 20–23 September 2015; pp. 285–289. [Google Scholar]
- Sohn, W.; Kim, J.-H.; Li, M.-H.; Brown, R.D.; Jaber, F.H. How does increasing impervious surfaces affect urban flooding in response to climate variability? Ecol. Indic. 2020, 118, 106774. [Google Scholar] [CrossRef]
- Guan, M.; Sillanpää, N.; Koivusalo, H. Storm runoff response to rainfall pattern, magnitude and urbanization in a developing urban catchment. Hydrol. Process. 2016, 30, 543–557. [Google Scholar] [CrossRef]
- Penna, D.; Tromp-van Meerveld, H.J.; Gobbi, A.; Borga, M.; Dalla Fontana, G. The influence of soil moisture on threshold runoff generation processes in an alpine headwater catchment. Hydrol. Earth Syst. Sci. 2011, 15, 689–702. [Google Scholar] [CrossRef] [Green Version]
- BOYD, M.J.; BUFILL, M.C.; KNEE, R.M. Pervious and impervious runoff in urban catchments. Hydrol. Sci. J. 1993, 38, 463–478. [Google Scholar] [CrossRef]
- Davidsen, S.; Löwe, R.; Ravn, N.H.; Jensen, L.N.; Arnbjerg-Nielsen, K. Initial conditions of urban permeable surfaces in rainfall-runoff models using Horton’s infiltration. Water Sci. Technol. 2018, 77, 662–669. [Google Scholar] [CrossRef]
- Woods Ballard, B.; Wilson, S.; Udale-Clarke, H.; Illman, S.; Scott, T.; Ashley, R.; Kellagher, R. The SuDS Manual; CIRIA: London, UK, 2015; ISBN 978-0-86017-759-3. [Google Scholar]
- Melbourne Water. WSUD Engineering Procedures: Stormwater; CSIRO Publishing: Clayton, Australia, 2005; ISBN 9780643092235. [Google Scholar]
- SEMCOG. Low Impact Development Manual for Michigan–A Design Guide for Implementers and Reviewers; SEMCOG: Detroit, MI, USA, 2008. [Google Scholar]
- Gregersen, I.B.; Madsen, H.; Rosbjerg, D.; Arnbjerg-Nielsen, K. A regional and nonstationary model for partial duration series of extreme rainfall. Water Resour. Res. 2017, 53, 2659–2678. [Google Scholar] [CrossRef] [Green Version]
- Jensen, D.M.R.; Thomsen, A.T.H.; Larsen, T.; Egemose, S.; Mikkelsen, P.S. From EU Directives to Local Stormwater Discharge Permits: A Study of Regulatory Uncertainty and Practice Gaps in Denmark. Sustainability 2020, 12, 6317. [Google Scholar] [CrossRef]

| Case | A1 [m2] | A2 [m2] | A3 [m2] | Max V1 [m3] | Max V2 [m3] | Max V3 [m3] | D1 [mm] | D2 [mm] | D3 [mm] |
|---|---|---|---|---|---|---|---|---|---|
| Case 0 | 1000 | 0 | 0 | VBaseline = 60 | 0 | 0 | dBaseline = 20 | ||
| Case 1 | 20 | 20 | 20 | 20 | 20 | 20 | |||
| Case 2 | 10 | 20 | 30 | 10 | 15 | 20 | |||
| Case 3 | 5 | 10 | 45 | 5 | 7.5 | 20 | |||
| Case 4 | 30 | 20 | 10 | 30 | 25 | 20 | |||
| Case 5 | 45 | 10 | 5 | 45 | 27.5 | 20 | |||
| Case 6 | 20 | 30 | 40 | 20 | 25 | 30 | |||
| Case 7 | 40 | 30 | 20 | 40 | 35 | 30 | |||
| Case | nO1 [-] | nO2 [-] | nO3 [-] | VO1 [m3] | VO2 [m3] | VO3 [m3] | I1 [m3] | I2 [m3] | I3 [m3] | Total I [m3] |
|---|---|---|---|---|---|---|---|---|---|---|
| Case 0 | - | - | 152 | - | - | 4323 | - | - | 69,557 | 69,557 |
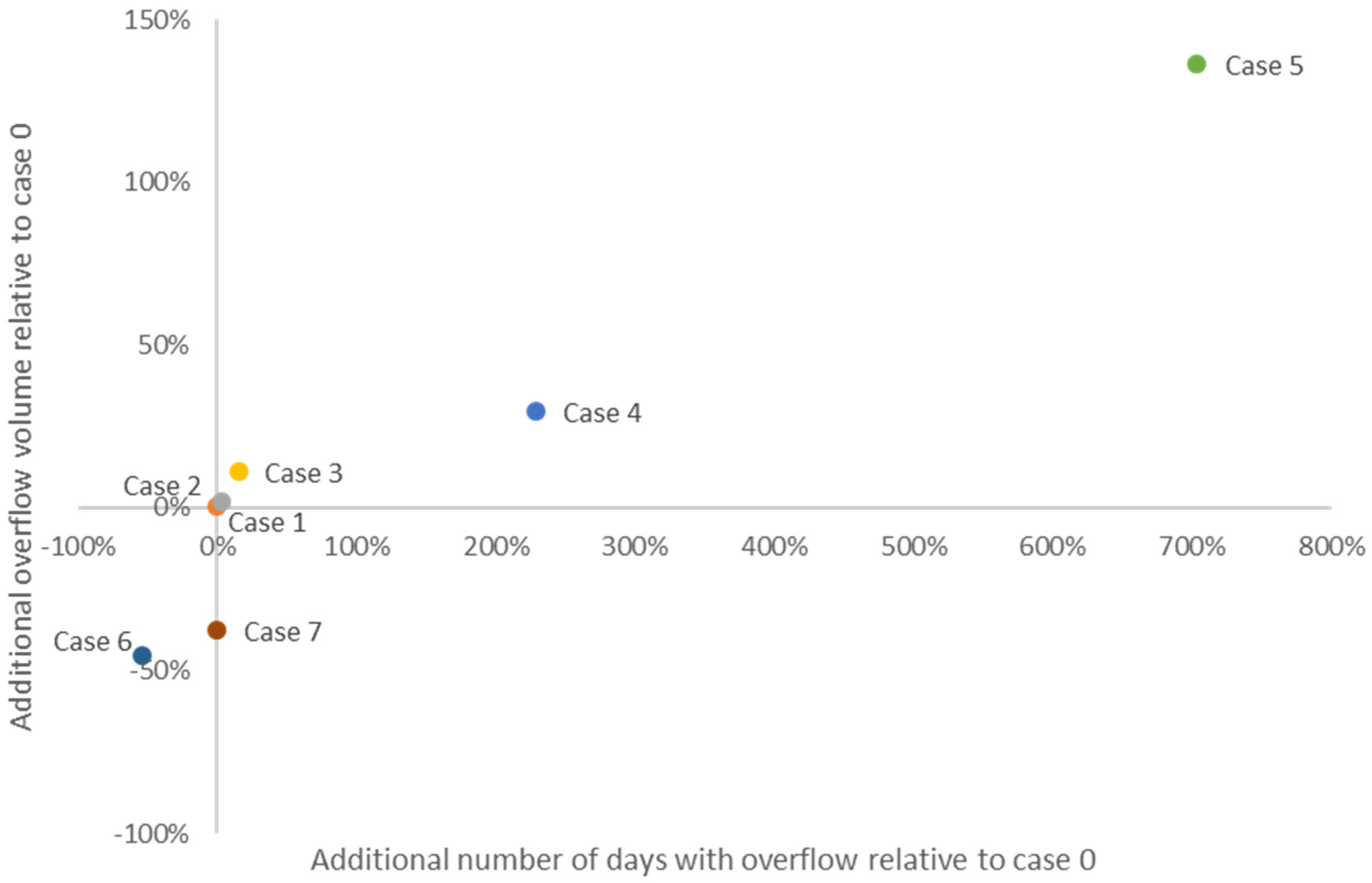
| Case 1 | 152 | 152 | 152 (+0%) | 1441 | 2882 | 4323 (+0%) | 23,186 | 23,186 | 23,186 | 69,557 (+0%) |
| Case 2 | 500 | 258 | 156 (+3%) | 3384 | 4215 | 4402 (+2%) | 21,242 | 23,796 | 24,440 | 69,478 (−0%) |
| Case 3 | 1223 | 777 | 175 (+15%) | 6456 | 9169 | 4803 (+11%) | 18,171 | 21,914 | 28,992 | 69,076 (−1%) |
| Case 4 | 68 | 152 | 500 (+229%) | 775 | 2216 | 5600 (+30%) | 23,851 | 23,186 | 21,242 | 68,279 (−2%) |
| Case 5 | 29 | 500 | 1223 (+705%) | 378 | 3762 | 10,218 (+136%) | 24,248 | 21,242 | 18,171 | 63,661 (−8%) |
| Case 6 | 152 | 106 | 70 (−54%) | 1441 | 2081 | 2354 (−46%) | 23,186 | 23,987 | 24,353 | 71,526 (+2%) |
| Case 7 | 40 | 68 | 152 (+0%) | 479 | 1254 | 2695 (−38%) | 24,148 | 23,851 | 23,186 | 71,185 (+3%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sørup, H.J.D.; Lerer, S.M. Principles for Distributing Infiltration-Based Stormwater Control Measures in Series. Water 2021, 13, 1029. https://doi.org/10.3390/w13081029
Sørup HJD, Lerer SM. Principles for Distributing Infiltration-Based Stormwater Control Measures in Series. Water. 2021; 13(8):1029. https://doi.org/10.3390/w13081029
Chicago/Turabian StyleSørup, Hjalte Jomo Danielsen, and Sara Maria Lerer. 2021. "Principles for Distributing Infiltration-Based Stormwater Control Measures in Series" Water 13, no. 8: 1029. https://doi.org/10.3390/w13081029
APA StyleSørup, H. J. D., & Lerer, S. M. (2021). Principles for Distributing Infiltration-Based Stormwater Control Measures in Series. Water, 13(8), 1029. https://doi.org/10.3390/w13081029






