Theoretical Estimation of Energy Balance Components in Water Networks for Top-Down Approach
Abstract
:1. Introduction
2. Theoretical Analysis of Energy Balance
2.1. Single Pipe Network
- Input energy ()
- Outgoing energy through water loss ()
- Friction energy loss ()
- Friction energy loss for a water loss-free network ()
- Energy associated with water loss ()where is specific weight of water.
- Normalized input energy ()
- Normalized outgoing energy through water loss ()
- Normalized friction energy loss ()
- Normalized friction energy loss for a water loss-free network ()
- Normalized energy associated with water loss ()
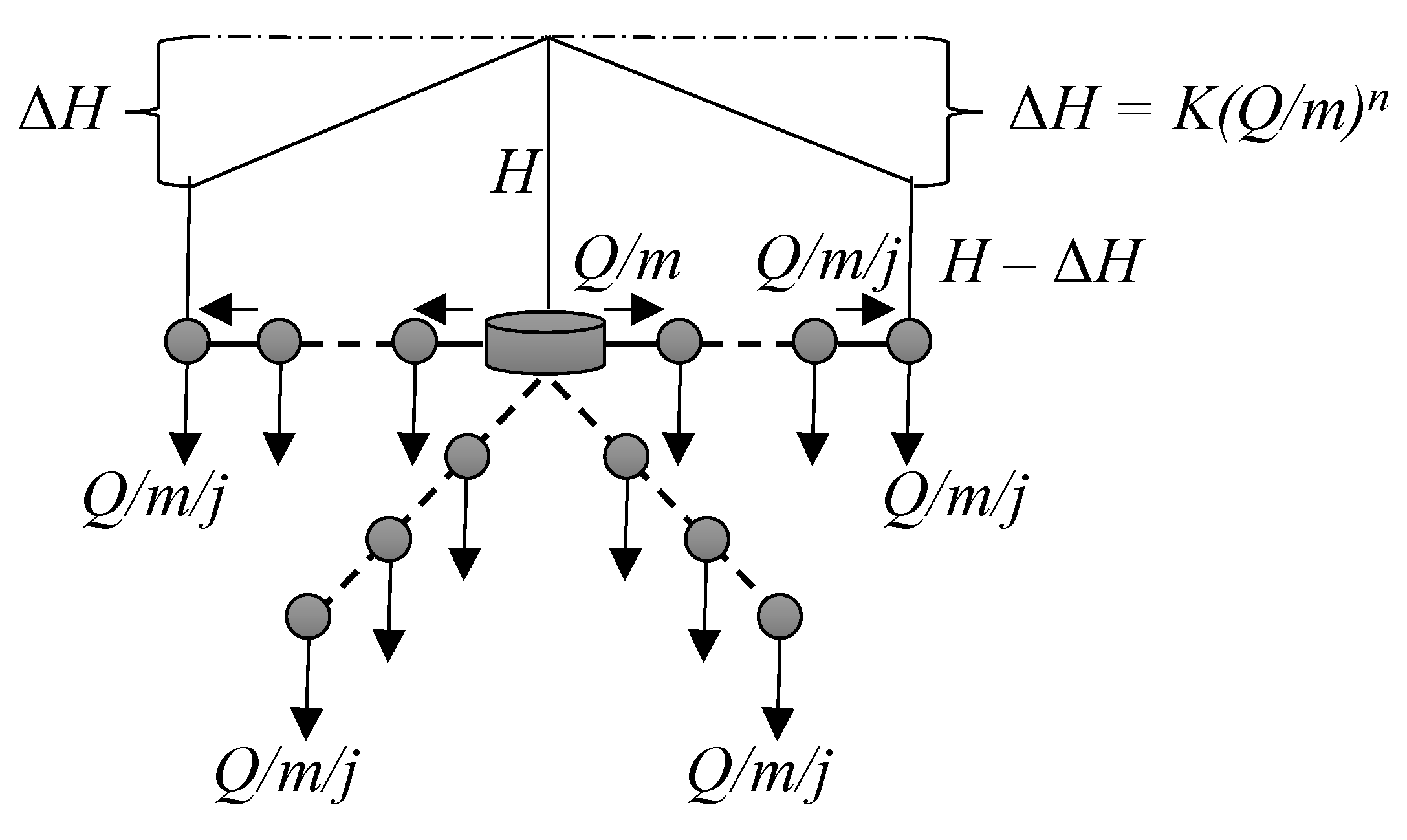
2.2. Branched Pipe Network with Uniformly Distributed Demand Nodes
- Input energy ()
- Outgoing energy through water loss ()
- Friction energy loss ()
- Friction energy loss for a water loss-free network ()
- Energy associated with water loss ()
- Normalized input energy ()
- Normalized outgoing energy through water loss ()
- Normalized friction energy loss ()
- Normalized friction energy loss for a water loss-free network ()
- Normalized energy associated with water loss ()where
2.3. Utilization of Theory to Real Networks
3. Application to Real Water Networks
3.1. Characteristics of Water Networks
3.2. Basic Relationship for Energy Balance Components
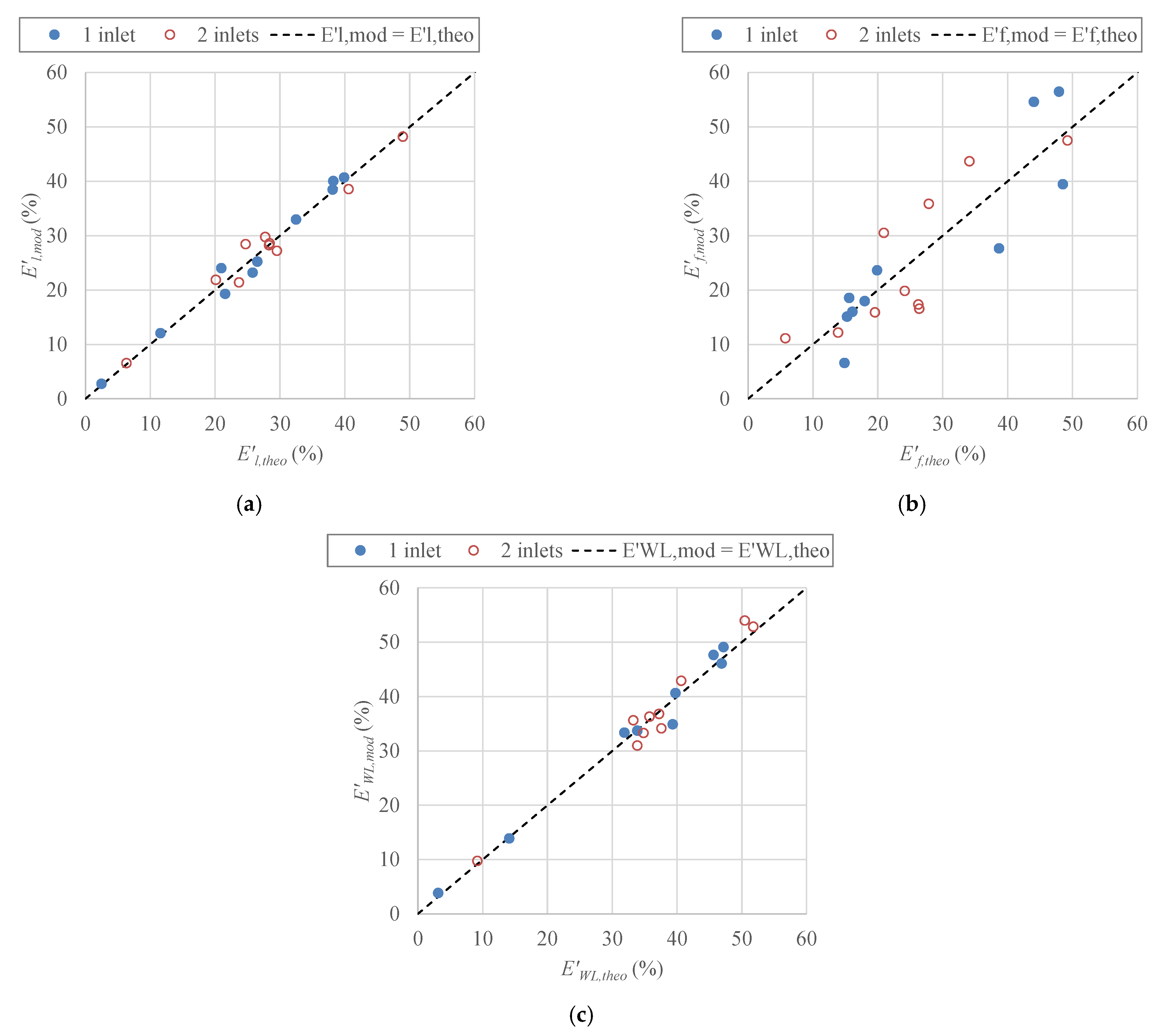
4. Estimation of Energy Balance Components
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DMA | district metering area |
| IWA | International Water Association |
| MWA | Metropolitan Waterworks Authority, Thailand |
| parameter in Equation (26) | |
| D | pipe diameter |
| energy associated with authorized consumption | |
| friction energy loss | |
| normalized friction energy loss | |
| normalized friction energy loss evaluated by mathematical model | |
| normalized friction energy loss estimated by theory | |
| friction energy loss for a water loss-free network | |
| normalized friction energy loss for a water loss-free network | |
| input energy | |
| normalized input energy | |
| outgoing energy through water loss | |
| normalized outgoing energy through water loss | |
| normalized outgoing energy through water loss by mathematical model | |
| normalized outgoing energy through water loss by theory | |
| energy associated with water loss | |
| normalized energy associated with water loss | |
| normalized energy associated with water loss by mathematical model | |
| normalized energy associated with water loss by theory | |
| H | input energy head |
| j | number of demand nodes in each branch |
| K | loss coefficient |
| m | number of branches |
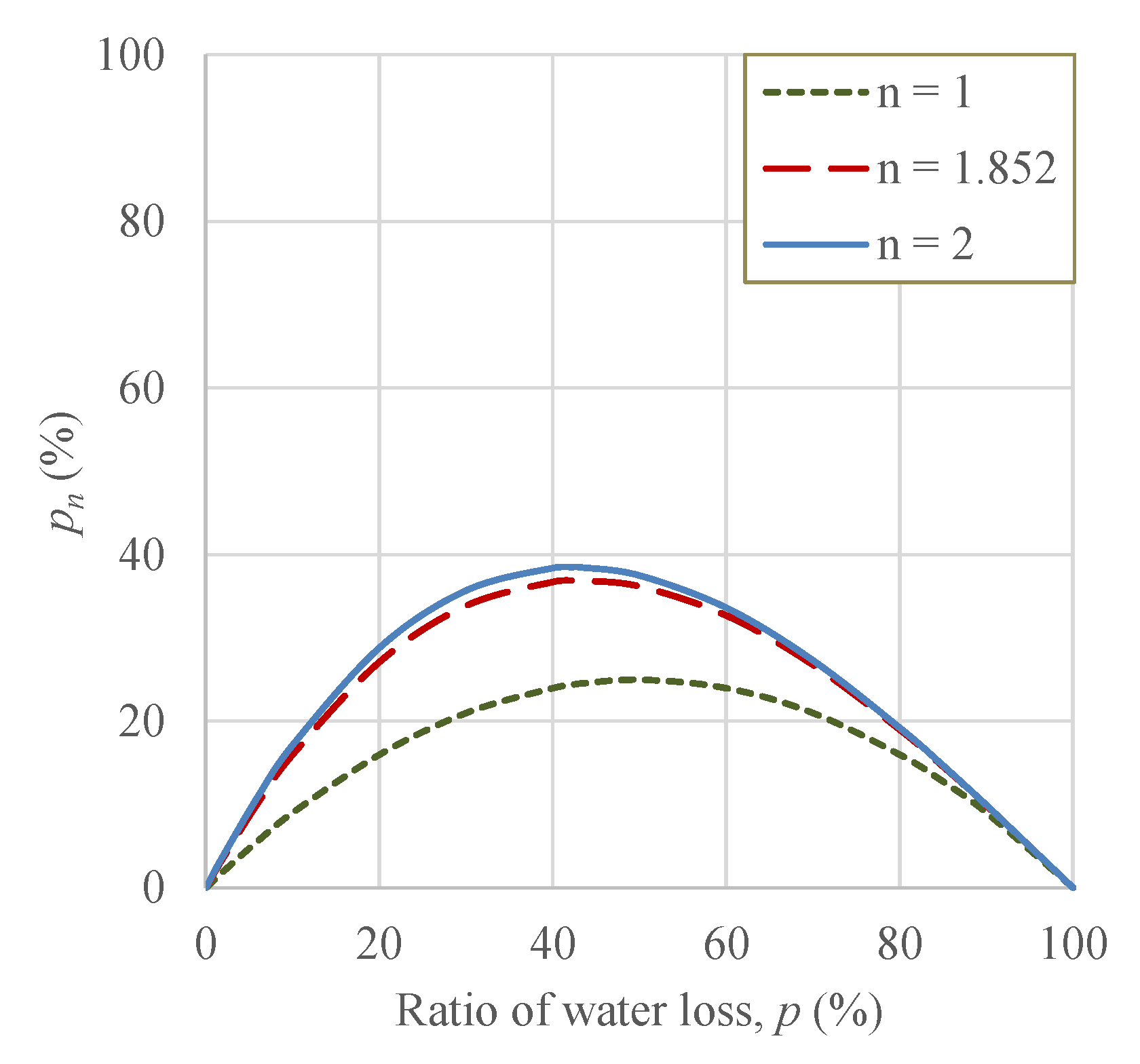
| n | flow exponent in head loss formula |
| ratio of water loss | |
| coefficient as a function of | |
| inflow | |
| flow in subarea i | |
| flow due to water loss | |
| flow to supply authorized consumption | |
| Sf | friction slope |
| SIV | system input volume |
| WL | water loss |
| specific gravity | |
| head loss between the source and the minimum energy point | |
| normalized head loss between the source and the minimum energy point | |
| renormalized head loss in Equation (30) | |
| head loss in subarea i |
References
- International Energy Agency (IEA). Water Energy Nexus-Excerpt from the World Energy Outlook 2016; World Energy Outlook; IEA: Paris, France, 2016; p. 60. [Google Scholar]
- Loureiro, D.; Silva, C.; Cardoso, M.A.; Mamade, A.; Alegre, H.; Rosa, M.J. The Development of a Framework for Assessing the Energy Efficiency in Urban Water Systems and Its Demonstration in the Portuguese Water Sector. Water 2020, 12, 134. [Google Scholar] [CrossRef] [Green Version]
- Vilanova, M.R.N.; Balestieri, J.A.P. Exploring the water-energy nexus in Brazil: The electricity use for water supply. Energy 2015, 85, 415–432. [Google Scholar] [CrossRef]
- Pelli, T.; Hitz, H. Energy indicators and savings in water supply. J. Am. Water Work. Assoc. 2000, 92, 55–62. [Google Scholar] [CrossRef]
- World Bank. A Primer on Energy Efficiency for Municipal Water and Wastewater Utilities; Technical Report; 001.12. 2012b; ESMAP: Washington, DC, USA, 2012. [Google Scholar]
- WWAP. The United Nations World Water Development Report 2014: Water and Energy; UNESCO: Paris, France, 2014; Volume 1. [Google Scholar]
- Colombo, A.F.; Karney, B.W. Energy and Costs of Leaky Pipes: Toward Comprehensive Picture. J. Water Resour. Plan. Manag. 2002, 128, 441–450. [Google Scholar] [CrossRef] [Green Version]
- Colombo, A.F.; Karney, B.W. Impacts of Leaks on Energy Consumption in Pumped Systems with Storage. J. Water Resour. Plan. Manag. 2005, 131, 146–155. [Google Scholar] [CrossRef]
- Bylka, J.; Mroz, T. A Review of Energy Assessment Methodology for Water Supply Systems. Energies 2019, 12, 4599. [Google Scholar] [CrossRef] [Green Version]
- Cabrera, E.; Pardo, M.A.; Cobacho, R. Energy Audit of Water Networks. J. Water Resour. Plan. Manag. 2010, 136, 669–677. [Google Scholar] [CrossRef]
- Cabrera, E.; Cobacho, R.; Soriano, J. Towards an Energy Labelling of Pressurized Water Networks. Procedia Eng. 2014, 70, 209–217. [Google Scholar] [CrossRef] [Green Version]
- Cabrera, E.; Gomez, E.; Cabrera, E., Jr.; Soriano, J. Calculating the Economic Level of Friction in Pressurized Water Systems. Water 2018, 10, 763. [Google Scholar] [CrossRef] [Green Version]
- Cabrera, E.; Gómez, E.; Soriano, J.; Del Teso, R. Eco-Layouts in Water Distribution Systems. J. Water Resour. Plan. Manag. 2019, 145, 04018088. [Google Scholar] [CrossRef]
- Cabrera, E.; Gomez, E.; Soriano, J.; Espert, V. Energy Assessment of Pressurized Water Systems. J. Water Resour. Plan. Manag. 2015, 141, 04014095. [Google Scholar] [CrossRef]
- Gomez, E.; Cabrera, E.; Balaguer, M.; Soriano, J. Direct and Indirect Water Supply: An Energy Assessment. Procedia Eng. 2015, 119, 1088–1097. [Google Scholar] [CrossRef] [Green Version]
- Hashemi, S.; Filion, Y.R.; Speight, V.L. Pipe-level Energy Metrics for Energy Assessment in Water Distribution Networks. Procedia Eng. 2015, 119, 139–147. [Google Scholar] [CrossRef] [Green Version]
- Sarbu, I. A Study of Energy Optimisation of Urban Water Distribution Systems Using Potential Elements. Water 2016, 8, 593. [Google Scholar] [CrossRef] [Green Version]
- Gómez, E.; Del Teso, R.; Cabrera, E.; Cabrera, J.E.; Soriano, J. Labeling Water Transport Efficiencies. Water 2018, 10, 935. [Google Scholar] [CrossRef] [Green Version]
- Mamade, A.; Sousa, C.; Marques, A.; Loureiro, D.; Alegre, H.; Covas, D. Energy Auditing as a Tool for Outlining Major Inefficiencies: Results from a Real Water Supply System. Procedia Eng. 2015, 119, 1098–1108. [Google Scholar] [CrossRef] [Green Version]
- Mamade, A.; Loureiro, D.; Alegre, H.; Covas, D. A comprehensive and well tested energy balance for water supply systems. Urban Water J. 2017, 14, 853–861. [Google Scholar] [CrossRef]
- Mamade, A.; Loureiro, D.; Alegre, H.; Covas, D. Top-Down and Bottom-Up Approaches for Water-Energy Balance in Portuguese Supply Systems. Water 2018, 10, 577. [Google Scholar] [CrossRef] [Green Version]
- Cabrera, E.; Del Teso, R.; Gómez, E.; Cabrera, E.; Estruch-Juan, E. Deterministic Model to Estimate the Energy Requirements of Pressurized Water Transport Systems. Water 2021, 13, 345. [Google Scholar] [CrossRef]
- Lenzi, C.; Bragalli, C.; Bolognesi, A.; Artina, S. From energy balance to energy efficiency indicators including water losses. Water Supply 2013, 13, 889–895. [Google Scholar] [CrossRef]
- Dziedzic, R.; Karney, B.W. Energy Metrics for Water Distribution System Assessment: Case Study of the Toronto Network. J. Water Resour. Plan. Manag. 2015, 141, 04015032. [Google Scholar] [CrossRef] [Green Version]
- Wong, H.G.; Speight, V.L.; Filion, Y.R.; Wong, H.G. Impact of Urban Development on Energy Use in a Distribution System. J. Am. Water Work. Assoc. 2017, 109, E10–E18. [Google Scholar] [CrossRef]
- Lapprasert, S.; Pornprommin, A.; Lipiwattanakarn, S.; Chittaladakorn, S. Energy Balance of a Trunk Main Network in Bangkok, Thailand. J. Am. Water Work. Assoc. 2018, 110, E18–E27. [Google Scholar] [CrossRef]
- Lipiwattanakarn, S.; Kaewsang, S.; Pornprommin, A.; Wongwiset, T. Real benefits of leak repair and increasing the number of inlets to energy. Water Pract. Technol. 2019, 14, 714–725. [Google Scholar] [CrossRef]
- Alegre, H.; Baptista, J.M.; Cabrera, E.; Cubillo, F.; Duarte, P.; Hirner, W.; Merkel, W.; Parena, R. Performance Indicators for Water Supply Services; IWA Publishing: London, UK, 2006. [Google Scholar]
- Rossman, L.A. EPANET 2 Users Manual, Water Supply and Water Resources Division; USEPA: Cincinnati, OH, USA, 2000.


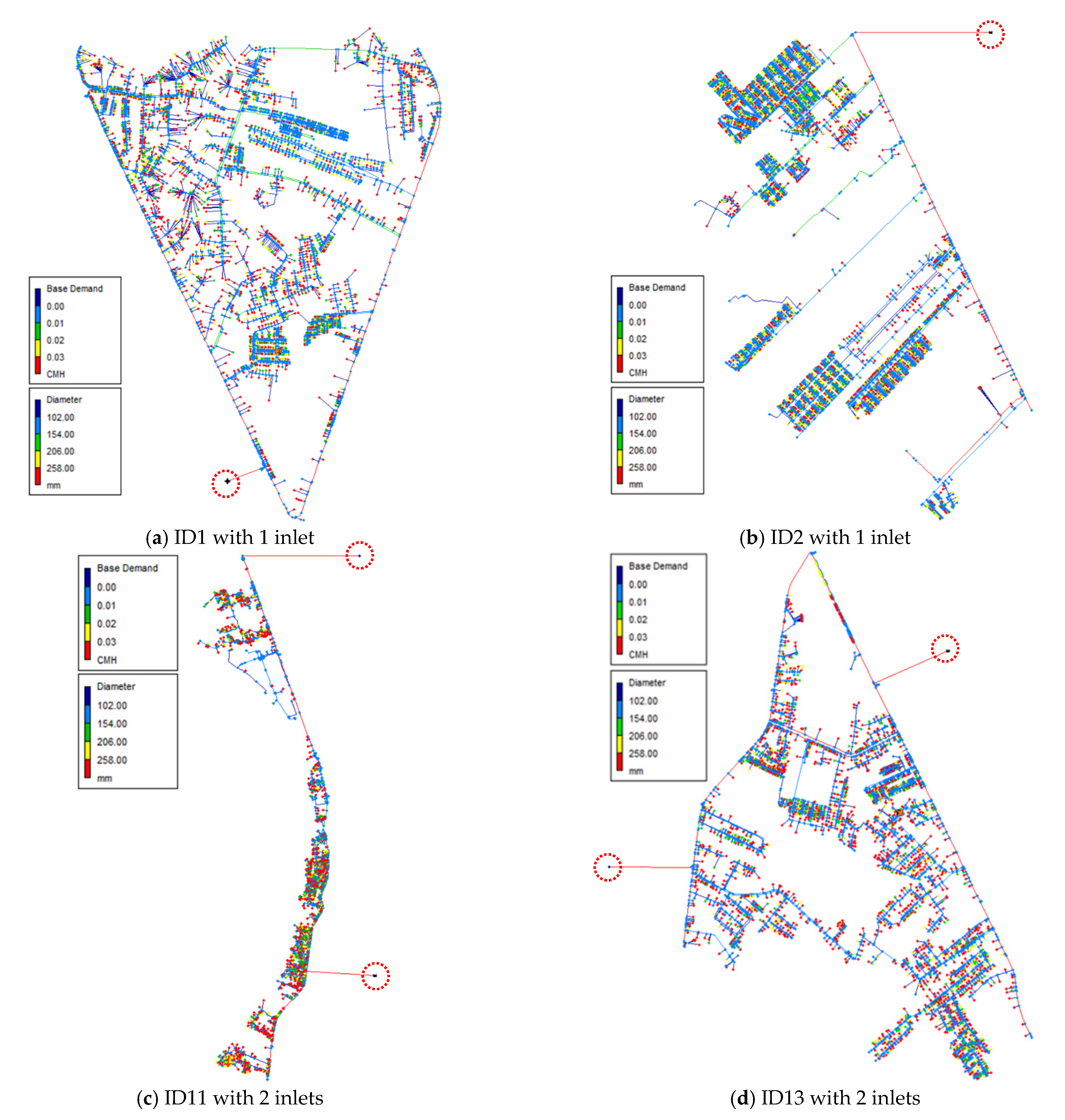

| ID | No. of Inlets | No. of Customers | Length | Avg. D | Avg. Sf | Water Loss, p | ΔH* |
|---|---|---|---|---|---|---|---|
| (km) | (mm) | (m/km) | (%) | (%) | |||
| 1 | 1 | 2669 | 24.5 | 161 | 0.17 | 37.1 | 16.6 |
| 2 | 1 | 2657 | 26.4 | 147 | 0.17 | 28.6 | 35.7 |
| 3 | 1 | 4399 | 52.3 | 148 | 0.08 | 44.6 | 14.1 |
| 4 | 1 | 2626 | 46.4 | 174 | 0.20 | 38.5 | 44.2 |
| 5 | 1 | 3594 | 54.7 | 139 | 0.11 | 44.2 | 18.4 |
| 6 | 1 | 4812 | 51.0 | 143 | 0.36 | 54.9 | 40.7 |
| 7 | 1 | 4607 | 43.2 | 130 | 0.17 | 32.4 | 44.8 |
| 8 | 1 | 1695 | 28.8 | 208 | 0.09 | 12.9 | 13.7 |
| 9 | 1 | 3634 | 18.1 | 183 | 0.16 | 29.7 | 14.4 |
| 10 | 1 | 1820 | 22.5 | 132 | 0.14 | 2.8 | 14.8 |
| 11 | 2 | 1921 | 22.2 | 166 | 0.50 | 30.0 | 35.0 |
| 12 | 2 | 2151 | 19.0 | 154 | 0.16 | 50.9 | 7.6 |
| 13 | 2 | 2297 | 24.9 | 154 | 0.22 | 31.9 | 25.9 |
| 14 | 2 | 739 | 17.3 | 191 | 0.33 | 33.9 | 32.0 |
| 15 | 2 | 1468 | 15.9 | 178 | 0.70 | 7.7 | 34.8 |
| 16 | 2 | 4204 | 47.4 | 153 | 0.48 | 36.3 | 37.0 |
| 17 | 2 | 11,545 | 129.6 | 150 | 0.14 | 30.7 | 45.3 |
| 18 | 2 | 4460 | 73.7 | 180 | 0.15 | 30.0 | 65.3 |
| 19 | 2 | 4957 | 51.5 | 143 | 0.07 | 31.2 | 18.4 |
| 20 | 2 | 3897 | 47.4 | 154 | 0.28 | 47.2 | 27.8 |
| Avg. | 1.5 | 3508 | 40.8 | 159 | 0.23 | 32.8 | 29.3 |
| Component | Equation | No. of Inlets | r | RMSE (%) | |||
|---|---|---|---|---|---|---|---|
| Before | After | Before | After | ||||
| (27) | 1 | 0.7466 | 0.939 | 0.990 | 8.57 | 1.65 | |
| 2 | 0.5047 | 0.957 | 0.985 | 6.02 | 1.91 | ||
| (28) | 1 | 1.0833 | 0.905 | 0.905 | 7.32 | 6.92 | |
| 2 | 0.7538 | 0.834 | 0.834 | 11.30 | 6.99 | ||
| (29) | 1 | 0.4219 | 0.992 | 0.994 | 4.75 | 1.83 | |
| 2 | 0.3095 | 0.978 | 0.984 | 4.46 | 2.17 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lipiwattanakarn, S.; Kaewsang, S.; Charuwimolkul, N.; Changklom, J.; Pornprommin, A. Theoretical Estimation of Energy Balance Components in Water Networks for Top-Down Approach. Water 2021, 13, 1011. https://doi.org/10.3390/w13081011
Lipiwattanakarn S, Kaewsang S, Charuwimolkul N, Changklom J, Pornprommin A. Theoretical Estimation of Energy Balance Components in Water Networks for Top-Down Approach. Water. 2021; 13(8):1011. https://doi.org/10.3390/w13081011
Chicago/Turabian StyleLipiwattanakarn, Surachai, Suparak Kaewsang, Natchapol Charuwimolkul, Jiramate Changklom, and Adichai Pornprommin. 2021. "Theoretical Estimation of Energy Balance Components in Water Networks for Top-Down Approach" Water 13, no. 8: 1011. https://doi.org/10.3390/w13081011





