Modeling Flood Peak Discharge Caused by Overtopping Failure of a Landslide Dam
Abstract
1. Introduction
2. Materials and Methods
2.1. Landslide Dam Failure Data
2.2. Modeling Dam-Break Peak Discharge
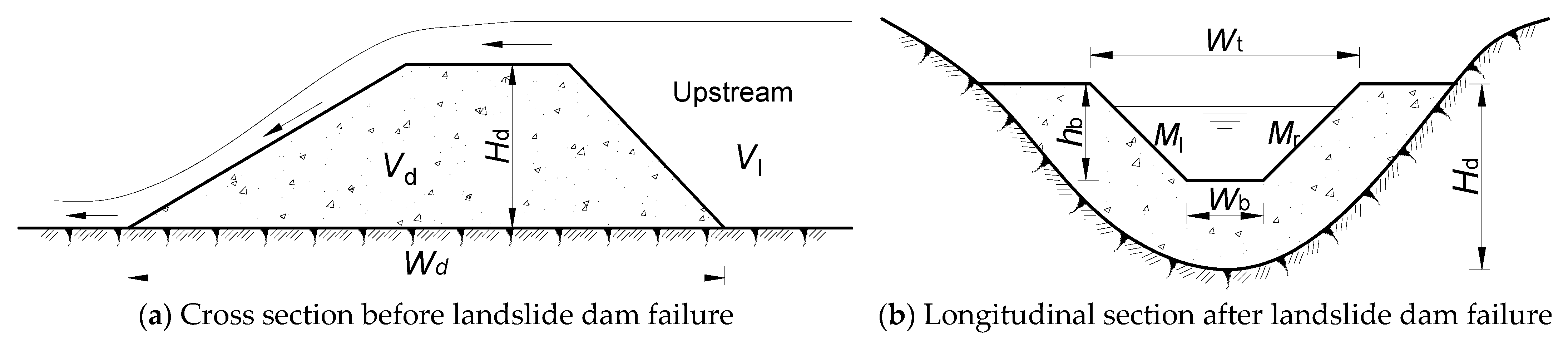
2.2.1. Calculation of Breach Size
2.2.2. Calculation of Peak Discharge of Dam Failure
3. Results and Discusions
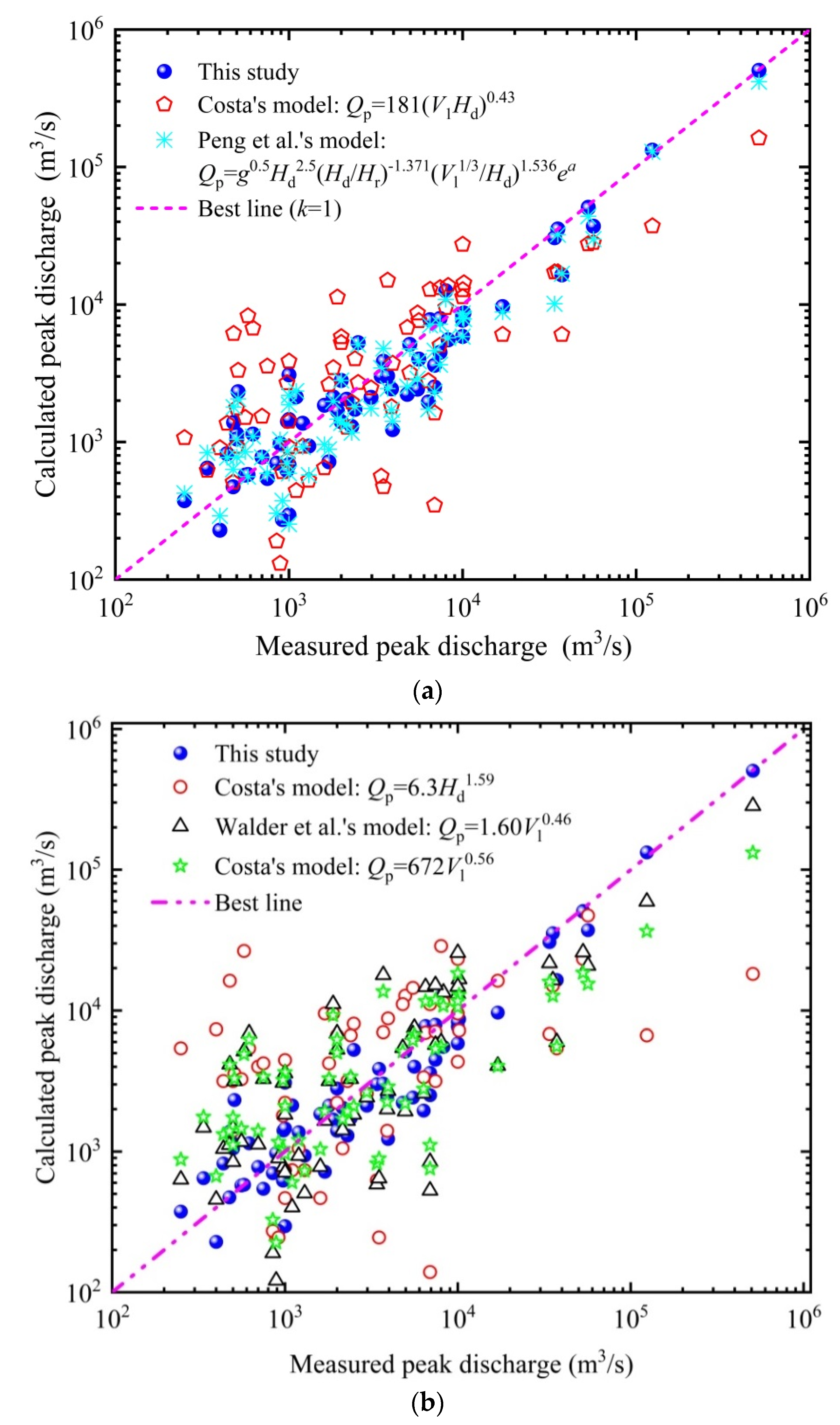
3.1. Model Verification and Comparison
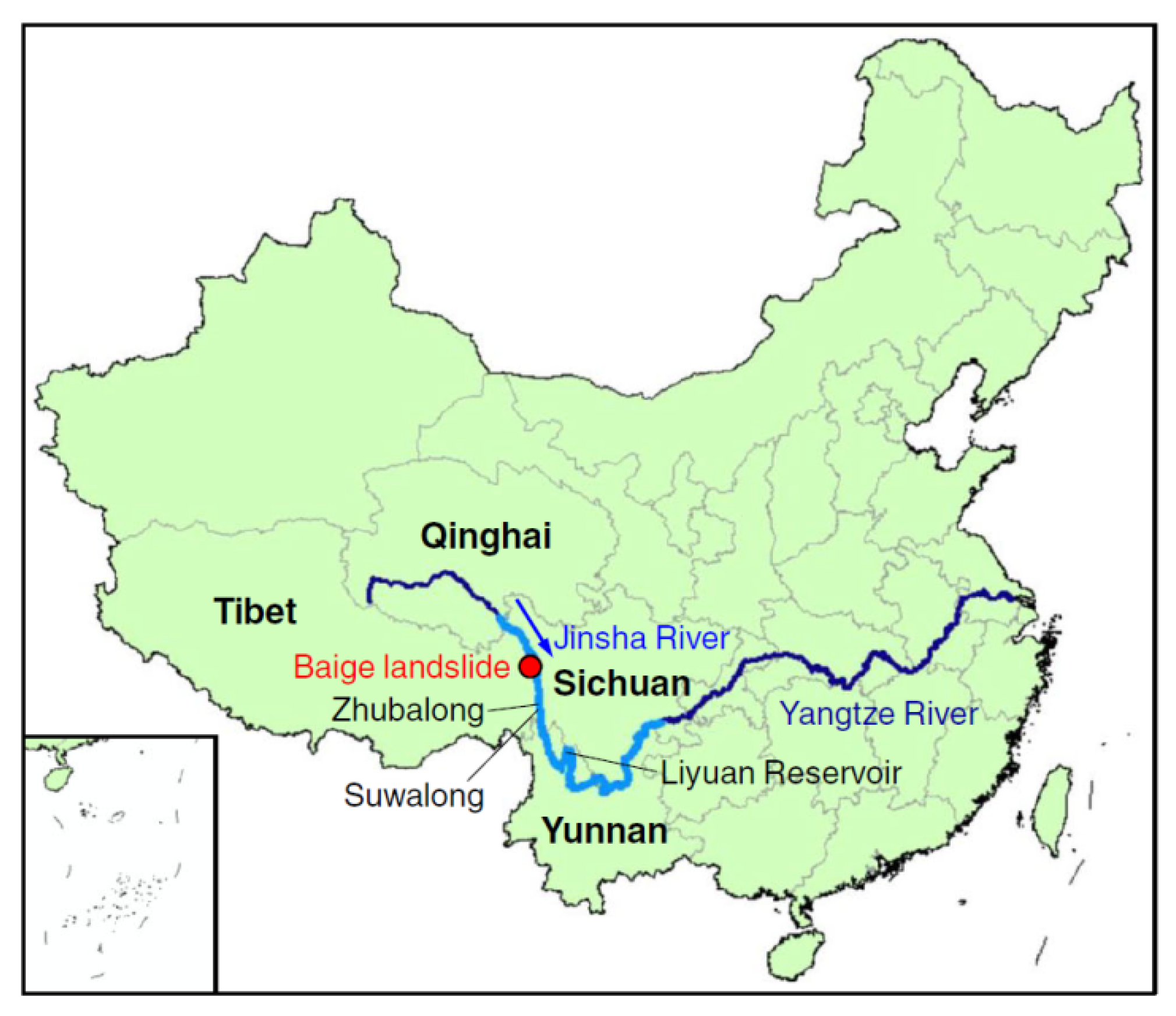
3.2. Example Application
4. Conclusions
- (1)
- The calculated model for peak discharge of landslide dam failure is proposed, which can consider the dam erodibility, the final shape of the breach, the shape of the dam, the lake volume and other parameters at the same time.
- (2)
- Compared with other models, the calculated peak discharge of this model are more close to measured peak discharge. In addition, the model needs 12 parameters to calculate the breach depth, breach bottom width, breach top width and breach peak discharge, whereas the model proposed by Peng et al. needs 17 parameters.
- (3)
- The model proposed in this paper is used to simulate the peak discharge of two dam failure events of Baige landslide in Jinsha River (10 October 2018 and 3 November 2018). The relative error of peak discharge simulation of the two events is 0.73% and 6.68%, respectively, which is obviously better than other models, indicating that the simulated effect of the model is reasonable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Hd | Dam height |
| V1 | Volume of dammed lake |
| Wd | Dam width |
| Vd | Volume of landslide dam |
| hb | Breach depth |
| Wt | Breach top width |
| Wb | Breach bottom width |
| Qp | Peak discharge of landslide dam failure |
| PE | Potential energy of water |
| d | Height at which the water level drops during a dam outbreak |
| g | Acceleration of gravity |
| a | Erodibility coefficient of landslide dam |
| H | High erodibility of the landslide dam |
| M | Moderate erodibility of the landslide dam |
| L | Low erodibility of the landslide dam |
| Hr | Unit length, Hr = 1 m |
| q | Combinative parameter of the cross section of breach |
| Ml | Slope ratio of left side of the breach |
| Mr | Slope ratio of right side of the breach |
| Wu | Characteristic parameterof initial breach water depth |
| W | Characteristic parameter of the breach water depth |
| λ | Parameter determined by the erodibility of landslide dam |
| ξ | Parameter determined by the erodibility of landslide dam |
| α | Parameter determined by the erodibility of landslide dam |
| β | Parameter determined by the erodibility of landslide dam |
| MRE | Mean relative error |
| RMSE | Standard deviation |
| R2 | Coefficient of determination |
Appendix A
| No. | Name | Location | Data of Formation | Dam Height Hd (m) | Dam Width Wd (m) | Dam Volume Vd (×106 m3) | Lake Volume Vl (×106 m3) | Dam Erodbility | Breach Depth hb (m) | Breach Top Width Wt(m) | Breach Bottom Width Wb(m) | Peak Discharge Qp (m3/s) | References |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Tsatichhu | Bhutan | 10 September 2003 | 110 | 700 | 5 | 1.5 | H | - | - | - | 6900 | [56] |
| 2 | Arida River, Hanazono Village | Papua New Guinea | 11 November 1985 | 200 | 3000 | 200 | 50 | H | 70 | - | - | 8000 | [57] |
| 3 | Bireh-Ganga River | India | 22 September 1983 | 274 | 2750 | 286 | 460 | H | 97.5 | - | - | 56,650 | [39,42] |
| 4 | Mantaro River | Peru | 16 August 1945 | 133 | 580 | 3.5 | 301 | H | 56 | - | - | 35,400 | [58] |
| 5 | Mt Adams | New Zealand | 6 October 1999 | 90 | 700 | 12.5 | 6 | H | 45 | 125 | 45 | 2500 | [59,60] |
| 6 | Nishi River, Totsugawa Village | Japan | 20 August 1889 | 20 | 120 | 0.63 | 0.4 | H | - | 1100 | [18,61] | ||
| 7 | Tanggudong | China | 8 June 1967 | 175 | 3000 | 68 | 680 | H | - | 55 | 53,000 | [62] | |
| 8 | Tegermach River | USSR | 1853 | 120 | 60 | 20 | 6.6 | H | - | 310 | 55 | 4960 | [39,63] |
| 9 | Totsu River, Daito Village | Japan | 20 August 1889 | 18 | 450 | 0.036 | 0.78 | H | - | - | - | 3400 | [18,61] |
| 10 | Totsu River, Daito VIllage | Japan | 20 August 1889 | 10 | 380 | 0.23 | 0.93 | H | - | - | - | 3500 | [18,61] |
| 11 | Totsu River, Nakatotsugawa Village | Japan | 20 August 1889 | 7 | 250 | 0.073 | 0.65 | H | - | - | - | 6900 | [18,61] |
| 12 | Arida River, Hanazono Village | Japan | 18 July 1953 | 10 | 150 | 0.18 | 0.047 | H | - | - | - | 890 | [18,61] |
| 13 | Yigong | China | 9 April 2000 | 80 | 2350 | 300 | 3000 | H | 58.39 | - | 128 | 124,000 | [64] |
| 14 | Tanggudong | China | 8 June 1967 | 175 | 3000 | 68 | 680 | H | 53,000 | [12] | |||
| 15 | Lantianwang | China | 10 June 1786 | 70 | 1400 | 40 | 50 | H | 37,345 | [12,65] | |||
| 16 | Cordillera de Santa Cruz | Argentina | November 2005 | 15 | 355 | 12 | 0.0041 | H | 1000 | [66] | |||
| 17 | Ambon Island | Indonesia | July 2012 | 140 | 1660 | 170 | 25 | H | 17,000 | [67] | |||
| 18 | Indus valleynear the Nanga Parbat | Pakistan | December 1840 | 150 | 30,000 | 30,000~50,000 | H | 509,000 | [68] | ||||
| 19 | Donghekou | China | 12 May 2008 | 20 | 750 | 12 | 6 | M | 10 | 25 | 15 | 1000 | [69] |
| 20 | East Fork Hood River | America | 25 December 1980 | 10.7 | 225 | 0.085 | 0.105 | M | - | - | - | 850 | [18,39] |
| 21 | Hime River | Japan | 9 August 1911 | 60 | 500 | 1.9 | 16 | M | - | - | - | 1800 | [18,61] |
| 22 | Hongshihe | China | 12 May 2008 | 50 | 500 | 18 | 4 | M | 10 | 9 | 500 | [69] | |
| 23 | Iketsu River | Japan | 19 August 1889 | 140 | 180 | 3.4 | 26 | M | - | - | - | 480 | [18,61] |
| 24 | Kaminirau River | America | 26 July 1788 | 50 | 500 | 2 | 2.2 | M | - | - | - | 440 | [18,61] |
| 25 | Kano River, Kitatotsugawa Village | Japan | 20 August 1889 | 15 | 130 | 0.094 | 1.3 | M | - | - | - | 1600 | [18,61] |
| 26 | Kano River, Totsugawa Village | Japan | 20 August 1889 | 20 | 120 | 0.1 | 0.6 | M | - | - | - | 1300 | [18,61] |
| 27 | La Josefina | Ecuado | 29 March 1993 | 100 | 1100 | 20 | 200 | M | 43 | - | - | 10,000 | [42,70] |
| 28 | Mantaro River | Peru | 25 April 1974 | 175 | 3800 | 1300 | 670 | M | 107 | 243 | - | 10,000 | [71] |
| 29 | Naka River, Kaminaka Town | Japan | 25 July 1892 | 80 | 330 | 3.3 | 75 | M | - | - | - | 5600 | [18,61] |
| 30 | Nishi River, Totsugawa Village | Japan | 20 August 1889 | 20 | 200 | 0.6 | 1.3 | M | - | - | - | 980 | [18,61] |
| 31 | Nishi River, Totsugawa Village | Japan | 20 August 1889 | 25 | 250 | 0.63 | 1.8 | M | - | - | - | 1200 | [18,61] |
| 32 | Pilsque River | Ecuado | 2 January 1990 | 58 | 450 | 1 | 2.5 | M | 30 | 50 | 700 | [42,72] | |
| 33 | Ram Creek | New Zealand | 24 May 1968 | 40 | 1200 | 2.8 | 1.1 | M | 30 | - | 30 | 1000 | [73] |
| 34 | Rio Paute | Ecuado | 29 March 1993 | 112 | 800 | 25 | 210 | M | - | - | 8250 | [74] | |
| 35 | Rio Toro River | Costa Rica | 13 June 1992 | 85 | 600 | 3 | 0.5 | M | 40 | 60 | - | 400 | [75] |
| 36 | Susobana River | Japan | 24 March 1847 | 54 | 250 | 1.2 | 16 | M | - | - | - | 510 | [18,61] |
| 37 | Tangjiashan | China | 12 May 2008 | 82 | 611.8 | 20.37 | 246.6 | M | 30 | 190 | 90 | 6500 | [4,76] |
| 38 | Totsu River, Amakawa Village | Japan | 20 August 1889 | 80 | 350 | 2.5 | 17 | M | - | - | - | 2400 | [18,61] |
| 39 | Totsu River, Daito Village | Japan | 21 August 1889 | 80 | 750 | 13 | 40 | M | - | - | - | 2000 | [18,61] |
| 40 | Totsu River, Kitatotsugawa Village | Japan | 20 August 1889 | 110 | 690 | 3.1 | 42 | M | - | - | - | 4800 | [18,61] |
| 41 | Unawaea Landslide Dam | New Zealand | 17 August 1991 | 70 | 550 | 4 | 0.9 | M | - | - | - | 250 | [42] |
| 42 | Upstream Xiaogangjian | China | 12 May 2008 | 95 | 300 | 2 | 12 | M | 30 | 80 | - | 3950 | [77] |
| 43 | Xiaojiaqiao | China | 12 May 2008 | 62 | 200 | 2.42 | 20 | M | 37.3 | 131.6 | 8 | 1000 | [78] |
| 44 | Zepozhu, Dong River | China | 27 October 1965 | 51 | 650 | 29 | 2.7 | M | - | - | - | 560 | [39,62] |
| 45 | Hongshiyan | China | 3 August 2014 | 83~96 | 262 | 12 | 260 | M | - | - | - | 7420 | [7] |
| 46 | Sunkoshi landslide dam | Nepal | 2 August 2014 | 52 | 300 | 2 | 11.1 | M | - | - | - | 6346 | [79] |
| 47 | Hsiaolin village | China | 9 August 2009 | 44 | 1500 | 15.4 | 9.9 | M | - | - | - | 2974 | [5] |
| 48 | Tsao-Ling | China | 21 September 1999 | 50 | 150 | 120 | 46 | M | - | - | - | 7422 | [80] |
| 49 | Xuelongnang | China | Ancient | 84 | 680 | - | 310 | M | 33 | - | - | 10,168~16,091 | [53] |
| 50 | Wenjaiba | China | 12 May 2008 | 50 | 700 | 6 | 5 | M | - | - | - | 2300 | [81] |
| 51 | Yibadao | China | 12 May 2008 | 25 | 100 | 0.15 | 3.79 | M | - | - | - | 2153/2355 | [82] |
| 52 | Laoyingyan | China | 12 May 2008 | 100 | 500 | 4.7 | 5 | M | - | - | - | 1700 | [83] |
| 53 | Qingyandong | China | 21 June 2005 | 30 | 0.3 | 1.5 | M | 6.5 | - | 30 | 500 | [84] | |
| 54 | Downstream Xiaogangjian | China | 12 May 2008 | 30 | 150 | 3.5 | 7 | M | - | 34.6 | - | 3900 | [85] |
| 55 | Hattian Bala Landslide Dam | Pakistan | 8 October 2005 | 130 | 1587 | 65 | 62 | M | - | - | - | 5500 | [6,86] |
| 56 | Baige 1 | China | 10 October 2018 | 61 | 1500 | - | 249 | M | - | - | - | 10,000 | [9] |
| 57 | Baige 2 | China | 3 November 2018 | 81 | 1000 | - | 494 | M-L | - | - | - | 33,900 | [9] |
| 58 | Arida River, Hanazono Village | Japan | 20 July 1953 | 60 | 500 | 2.6 | 17 | L | - | - | - | 750 | [18,61] |
| 59 | Jackson Creek Lake | America | 18 May 1980 | 4.5 | 302.5 | 0.77 | 2.47 | L | - | - | - | 477 | [18] |
| 60 | Ojika River | Japan | 1 August 1683 | 70 | 400 | 3.8 | 64 | L | - | - | - | 620 | [18,61] |
| 61 | Sai River | Japan | 24 March 1847 | 82.5 | 1000 | 21 | 350 | L | - | - | - | 3700 | [18,61] |
| 62 | Shiratani River, Totsugawa Village | Japan | 21 August 1889 | 190 | 500 | 10 | 38 | L | - | - | - | 580 | [18,61] |
| 63 | Sho River | Japan | 29 November 1586 | 100 | 600 | 19 | 150 | L | - | - | - | 1900 | [18,61] |
| 64 | Tangjiawang | China | 12 May 2008 | 35 | 800 | 4 | 7/15.2 | L | - | - | - | 974 | [87] |
| 65 | Suya | China | 17 July 2012 | 4.3 | 300 | 0.6 | 4.1 | L | - | - | - | 338 | [88] |
| 66 | Kuitun River | China | 15 July 1978 | 10 | 150 | 0.75 | 1.67 | L | - | - | - | 917 | [89] |
| 67 | Paree Chu | India | 26 June 2005 | 40 | 1100 | - | 64 | L | - | - | - | 2000 | [90] |
References
- Ali, R.; Kuriqi, A.; Kisi, O. Human-Environment Natural Disasters Interconnection in China: A Review. Climate 2020, 8, 48. [Google Scholar] [CrossRef]
- Shen, G.; Sheng, J.; Xiang, Y.; Zhong, Q.; Yang, D. Numerical Modeling of Overtopping-Induced Breach of Landslide Dams. Nat. Hazards Rev. 2020, 21, 04020002. [Google Scholar] [CrossRef]
- Singh, K. Rainfall Thresholds Triggering Landslides: A Review. In Sustainable Environment and Infrastructure; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Hu, X.W.; Huang, R.; Shi, Y.B.; Lu, X.P.; Zhu, H.Y.; Wang, X.R. Analysis of blocking river mechanism of tangjiashan landslide and dam-breaking mode of its barrier dam. Chin. J. Rock Mech. Eng. 2009, 28, 181–189. [Google Scholar]
- Dong, J.-J.; Li, Y.-S.; Kuo, C.-Y.; Sung, R.-T.; Li, M.-H.; Lee, C.-T.; Chen, C.-C.; Lee, W.-R. The formation and breach of a short-lived landslide dam at Hsiaolin village, Taiwan—part I: Post-event reconstruction of dam geometry. Eng. Geol. 2011, 123, 40–59. [Google Scholar] [CrossRef]
- Konagai, K.; Sattar, A. Partial breaching of Hattian Bala Landslide Dam formed in the 8th October 2005 Kashmir Earthquake, Pakistan. Landslides 2011, 9, 1–11. [Google Scholar] [CrossRef]
- Wang, L.; Li, S.Y.; Yu, S.; Du, X.H.; Deng, G. Key techniques for the emergency disposal of Hongshiyan landslide dam. J. China Inst. Water Resour. Hydropower Res. 2015, 13, 284–289. [Google Scholar]
- Zhong, Q.; Chen, S.; Mei, S.; Cao, W. Numerical simulation of landslide dam breaching due to overtopping. Landslides 2018, 15, 1183–1192. [Google Scholar] [CrossRef]
- Zhang, L.; Xiao, T.; He, J.; Chen, C. Erosion-based analysis of breaching of Baige landslide dams on the Jinsha River, China, in 2018. Landslides 2019, 16, 1965–1979. [Google Scholar] [CrossRef]
- Zhong, Q.; Chen, S.; Shan, Y. Prediction of the overtopping-induced breach process of the landslide dam. Eng. Geol. 2020, 274, 105709. [Google Scholar] [CrossRef]
- Islam, A.R.M.; Talukdar, S.; Mahato, S.; Kundu, S.; Eibek, K.U.; Pham, Q.; Kuriqi, A.; Limh, N. Flood susceptibility modelling using advanced ensemble machine learning models. Geosci. Front. 2021, 12, 101075. [Google Scholar] [CrossRef]
- Dai, F.C.; Lee, C.F.; Deng, J.H.; Tham, L.G. The 1786 earthquake-triggered landslide dam and subsequent dam-break flood on the Dadu River, southwestern China. Geomorphology 2005, 65, 205–221. [Google Scholar] [CrossRef]
- Delaney, K.B.; Evans, S.G. The 2000 Yigong landslide (Tibetan Plateau), rockslide-dammed lake and outburst flood: Review, remote sensing analysis, and process modelling. Geomorphology 2015, 246, 377–393. [Google Scholar] [CrossRef]
- Xu, W.-J.; Xu, Q.; Wang, Y.-J. The mechanism of high-speed motion and damming of the Tangjiashan landslide. Eng. Geol. 2013, 157, 8–20. [Google Scholar] [CrossRef]
- Xiong, Z.; Feng, G.; Feng, Z.; Miao, L.; Wang, Y.; Yang, D.; Luo, S. Pre- and post-failure spatial-temporal deformation pattern of the Baige landslide retrieved from multiple radar and optical satellite images. Eng. Geol. 2020, 279, 105880. [Google Scholar] [CrossRef]
- Shi, Z.M.; Zhang, G.D.; Peng, M.; Liu, S.Y. Study on the pemeability and stability of landslide dam materials. J. Eng. Geol. 2017, 25, 1182–1189. [Google Scholar]
- Costa, J.; Schuster, R. Formation and failure of natural dams. Geol. Soc. Am. Bull. 1988, 100, 1054–1068. [Google Scholar] [CrossRef]
- Costa, J.E.; Schuster, R.L. Documented historical landslide dams from around the world. US Geol. Surv. Open File Rep. 1991, 91–239. [Google Scholar]
- Peng, M.; Zhang, L. Breaching parameters of landslide dams. Landslides 2012, 9, 13–31. [Google Scholar] [CrossRef]
- Fread, D.L. The Development and Testing of a Dam-Break Flood Forecasting Model. In Proceedings of the Dam-Break Flood Routing Model Workshop, Bethesda, MD, USA, 18–20 October 1977; pp. 164–197. [Google Scholar]
- Fread, D. BREACH: An Erosion Model for Earthen Dam Failures; US National Weather Service, Office of Hydrology: Silver Spring, MD, USA, 1988; p. 35.
- Singh, V.; Quiroga, C. A dam-breach erosion model: I. Formulation. Water Resour. Manag. 1987, 1, 177–197. [Google Scholar] [CrossRef]
- Visser, P. Breach growth in sand-dikes. Elibrary 1998, 98, 465. [Google Scholar]
- Tingsanchali, T.; Chinnarasri, C. Numerical modelling of dam failure due to flow overtopping. Hydrol. Sci. J. 2001, 46, 113–130. [Google Scholar] [CrossRef]
- Bowles, D. Estimating Life Loss for Dam Safety Risk Assessment—A Review and New Approach; Institute For Water Resources Us Army Corps Of Engineers: Washington, DC, USA, 2002. [Google Scholar]
- Hanson, G.J.; Cook, K.R.; Hunt, S.L. Physical modeling of overtopping erosion and breach formation of cohesive embankments. Trans. Am. Soc. Agric. Eng. 2005, 48. [Google Scholar] [CrossRef]
- Temple, D.M.; Hanson, G.J.; Neilsen, M.; Cook, K.R. Simplified breach analysis model for homogeneous embankments: Part I, Background and model components. In Proceedings of the 25th Annual USSD Conference, Denver, CO, USA, 6–10 June 2005; pp. 151–161. [Google Scholar]
- Wang, Z.; Bowles, D. Three-dimensional non-cohesive earthen dam breach model. Part 1: Theory and methodology. Adv. Water Resour. 2006, 29, 1528–1545. [Google Scholar] [CrossRef]
- Zhu, Y. Breach Growth in Clay Dikes. Trans. Am. Soc. Agric. Eng. 2005, 48. [Google Scholar] [CrossRef]
- Faeh, R. Numerical Modeling of Breach Erosion of River Embankments. J. Hydraul. Eng. Asce 2007, 133. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S. One-Dimensional Modeling of Dam-Break Flow Over Movable Beds. J. Hydraul. Eng. Asce 2007, 133. [Google Scholar] [CrossRef]
- Ponce, V.; Tsivoglou, A. Modeling Gradual Dam Breaches. Asce J. Hydraul. Div. 1981, 107, 829–838. [Google Scholar] [CrossRef]
- Chang, D.S.; Zhang, L. Simulation of the Erosion Process of Landslide Dams Due to Overtopping Considering Variations in Soil Erodibility along Depth. Nat. Hazards Earth Syst. Sci. 2010, 10. [Google Scholar] [CrossRef]
- Cao, Z.; Yue, Z.; Pender, G. Landslide dam failure and flood hydraulics. Part I: Experimental investigation. Nat. Hazards 2011, 59, 1003–1019. [Google Scholar] [CrossRef]
- Liu, J. The investigation of earth dam-breaking sediment hydrograph (1)—Impact factors and secondary fluctuations. Chin. J. Appl. Mech. 2020, 37, 2257–2264. [Google Scholar]
- Kirkpatrick, G.W. Evaluation guidelines for spillway adequacy. Eval. Dam Saf. 1977, 3, 395–414. [Google Scholar]
- Macdonald, T.C.; Langridge-Monopolis, J. Breaching characteristics of dam failures. J. Hydraul. Eng. 1984, 110, 567–586. [Google Scholar] [CrossRef]
- Singh, K.; Snorrason, Á. Sensitivity of outflow peaks and flood stages to the selection of dam breach parameters and simulation models. J. Hydrol. 1984, 68, 295–310. [Google Scholar] [CrossRef]
- Costa, J.E. Floods from dam failures. Open File Rep. 1985, 5, 85–560. [Google Scholar]
- Froehlich, D.C.; Froehlich, D.C.; Froehlich, D. Peak Outflow from Breached Embankment Dam. J. Water Resour. Plan. Manag. 1995, 121, 90–97. [Google Scholar] [CrossRef]
- Webby, M.G. Discussion of Peak Outflow from Breached Embankment Dam by David, C. Froehlich. J. Water Resour. Plan. Manag. 1996, 122, 316–317. [Google Scholar] [CrossRef]
- Walder, J.; O’Connor, J. Methods for Predicting Peak Discharge of Floods Caused by Failure of Natural and Constructed Dams. Water Resour. Res. 1997, 33. [Google Scholar] [CrossRef]
- Pierce, M.W.; Thornton, C.I.; Abt, S.R. Predicting Peak Outflow from Breached Embankment Dams. J. Hydrol. Eng. 2010, 15, 338–349. [Google Scholar] [CrossRef]
- Hakimzadeh, H.; Nourani, V.; Amini, A.B. Genetic Programming Simulation of Dam Breach Hydrograph and Peak Outflow Discharge. J. Hydrol. Eng. 2014, 19, 757–768. [Google Scholar] [CrossRef]
- Zhou, G.G.D.; Zhou, M.; Shrestha, M.S.; Song, D.; Choi, C.E.; Cui, K.F.E.; Peng, M.; Shi, Z.; Zhu, X.; Chen, H. Experimental investigation on the longitudinal evolution of landslide dam breaching and outburst floods. Geomorphology 2019, 334, 29–43. [Google Scholar] [CrossRef]
- Zhou, M.-j.; Zhou, G.G.D.; Cui, K.F.E.; Song, D.-R.; Lu, X.-Q. Influence of inflow discharge and bed erodibility on outburst flood of landslide dam. J. Mt. Sci. 2019, 16, 778–792. [Google Scholar] [CrossRef]
- Briaud, J.-L. Case Histories in Soil and Rock Erosion: Woodrow Wilson Bridge, Brazos River Meander, Normandy Cliffs, and New Orleans Levees. J. Geotech. Geoenviron. Eng. 2008, 134, 1425–1447. [Google Scholar] [CrossRef]
- Cui, P.; Zhu, Y.-Y.; Han, Y.-S.; Chen, X.-Q.; Zhuang, J.-Q. The 12 May Wenchuan earthquake-induced landslide lakes: Distribution and preliminary risk evaluation. Landslides 2009, 6, 209–223. [Google Scholar] [CrossRef]
- Froehlich, D. Embankment dam breach parameters revisited. Int. Water Resour. Eng. Conf. Proc. 1995, 1, 887–891. [Google Scholar]
- Froehlich, D. Embankment Dam Breach Parameters and Their Uncertainties. J. Hydraul. Eng. Asce 2008, 134. [Google Scholar] [CrossRef]
- Elmazoghi, H. Fuzzy algorithm for estimating average breach widths of embankment dams. Nat. Hazards 2013, 68. [Google Scholar] [CrossRef][Green Version]
- Wang, B.; Chen, Y.; Wu, C.; Dong, J.; Ma, X.; Song, J. A semi-analytical approach for predicting peak discharge of floods caused by embankment dam failures: Semi-Analytical Model for Predicting Peak Discharge of Dam-Break Flood. Hydrol. Process. 2016, 30. [Google Scholar] [CrossRef]
- Liu, H. The Numerical Simulation Study of Outburst Floodevolution for Xuelongnang Paleolandslide Dam; China University of Geosciences: Beijing, China, 2016. [Google Scholar]
- Tacconi Stefanelli, C.; Segoni, S.; Casagli, N.; Catani, F. Geomorphic indexing of landslide dams’ evolution. Eng. Geol. 2016, 208. [Google Scholar] [CrossRef]
- Tacconi Stefanelli, C.; Segoni, S.; Casagli, N.; Catani, F. Assessing Landslide Dams Evolution: A Methodology Review; Springer: Cham, Switerland, 2017; pp. 253–257. [Google Scholar]
- Dunning, S.; Rosser, N.; Petley, D.; Massey, C. Formation and failure of the Tsatichhu landslide dam, Bhutan. Landslides 2006, 3, 107–113. [Google Scholar] [CrossRef]
- King, J.; Loveday, I.; Schuster, R. The 1985 Bairaman landslide dam and resulting debris flow, Papua New Guinea. Q. J. Eng. Geol. Hydrogeol. 1989, 22, 257–270. [Google Scholar] [CrossRef]
- Snow, D.T. Landslide of Cerro Condor-Sencca, Department of Ayacucho, Peru. Geol. Soc. Am. Rev. Eng. Geol. 1964, 5, 1–6. [Google Scholar] [CrossRef]
- Becker, J.; Johnston, D.; Paton, D.; Hancox, G.; Davies, T.; McSaveney, M.; Manville, V. Response to Landslide Dam Failure Emergencies: Issues Resulting from the October 1999 Mount Adams Landslide and Dam-Break Flood in the Poerua River, Westland, New Zealand. Nat. Hazards Rev. 2007, 8. [Google Scholar] [CrossRef]
- Hancox, G.T.; McSaveney, M.J.; Manville, V.R.; Davies, T.R. The October 1999 Mt Adams rock avalanche and subsequent landslide dam-break flood and effects in Poerua river, Westland, New Zealand. N. Z. J. Geol. Geophys. 2005, 48, 683–705. [Google Scholar] [CrossRef]
- Tong, Y.X. Quantitative Analysis for Stability of Landslide Dams; National Central University: Taoyuan, Taiwan, 2008. (In Chinese) [Google Scholar]
- Li, T.C.; Schuster, R.L.; Wu, J.S. Landslide dams in south-central China. Landslide Dams Process. Risk Mitig. 1986, 3, 146–162. [Google Scholar]
- Glazyrin, G.Y.; Reyzvikh, V.N. Computation of the flow hydrograph for the breach of landslide lakes. Sov. Hydrol. 1968, 5, 592–596. [Google Scholar]
- Shang, Y.; Yang, Z.; Li, L.; Liu, D.a.; Liao, Q.; Wang, Y. A super-large landslide in Tibet in 2000: Background, occurrence, disaster, and origin. Geomorphology 2003, 54, 225–243. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Y.S.; Cao, W.Z.; Zhang, L.; Huang, J.L.; He, J.X.; Liu, Y. Formation mechanism and motion process of lantianwan landslide triggered by the 1786 Moxi earthquake. Mt. Res. 2016, 34, 520–529. [Google Scholar]
- Perucca, L.P.; Esper Angillieri, M.Y. Evolution of a debris-rock slide causing a natural dam: The flash flood of Río Santa Cruz, Province of San Juan—12 November 2005. Nat. Hazards 2009, 50, 305–320. [Google Scholar] [CrossRef]
- Ishizuka, T.; Kaji, A.; Morita, K.; Mizuyama, T. Analysis for a Landslide Dam Outburst Flood in Ambon Island, Indonesia. Int. J. Eros. Control Eng. 2017, 10, 32–38. [Google Scholar] [CrossRef][Green Version]
- Schneider, J.; Gruber, F.; Mergili, M. Recent Cases and Geomorphic Evidence of Landslide-Dammed Lakes and Related Hazards in the Mountains of Central Asia. Landslide Sci. Pract. Risk Assess. Manag. Mitig. 2013, 6. [Google Scholar] [CrossRef]
- Chang, D.S.; Zhang, L.; Xu, Y. Analysis of overtopping failure of Hongshihe Landslide dam after Wenchuan earthquake. J. Eng. Geol. 2009, 17, 51–55. [Google Scholar]
- Plaza, G.; Zevallos, O. The 1993 La Josefina rockslide and Rio Paute landslide dam, Ecuador. Landslide News 1994, 8, 4–6. [Google Scholar]
- Lee, K.L.; Duncan, J.M. Landslide of April 25, 1974, on the Mantaro River, Peru: Report of Inspection; The National Academies Press: Washington, DC, USA, 1975; p. 81. [Google Scholar] [CrossRef]
- Plaza-Nieto, G.; Yepes, H.; Schuster, R.L. Landslide dam on the Plsque river, northern Ecuador. Landslide News 1990, 4, 2–4. [Google Scholar]
- Nash, T.; Bell, D.; Davies, T.; Nathan, S. Analysis of the formation and failure of Ram Creek landslide dam, South Island, New Zealand. N. Z. J. Geol. Geophys. 2008, 51, 187–193. [Google Scholar] [CrossRef]
- Canuti, A.; Frassoni, A.; Natale, L. Failure of the Rio Paute landslide dam. Landslide News 1993, 8, 6–7. [Google Scholar]
- Mora Castro, S. The 1992 Río Toro landslide dam, Costa Rica. Landslide News 1993, 7, 19–22. [Google Scholar]
- Huang, M.H.; Jin, F.; Yang, W.J. Breaching flood simulation of tangjiashan landslide dam. In Proceedings of the 2008 Annual Conference of Chinese Hydraulic Engineering Society, Beijing, China, 4 July 2008; pp. 964–966. [Google Scholar]
- Liu, N.; Zhang, J.; Lin, W.; Cheng, W.; Chen, Z. Draining Tangjiashan Barrier Lake after Wenchuan Earthquake and the flood propagation after the dam break. Technol. Sci. 2009, 52, 801–809. [Google Scholar] [CrossRef]
- Liang, J. Formation of seismic barrier lake and its harnessing scheme. In Proceedings of the Analysis and Investigation on Seismic Damages to Projects Subjected to Wenchuan Earthquake, Wenchuan, China, 12 May 2009; pp. 1056–1061. [Google Scholar]
- Shrestha, B.B.; Nakagawa, H. Hazard assessment of the formation and failure of the Sunkoshi landslide dam in Nepal. Nat. Hazards 2016, 82, 2029–2049. [Google Scholar] [CrossRef]
- Li, M.-H.; Hsu, M.-H.; Hsieh, L.-S.; Teng, W.-H. Inundation Potentials Analysis for Tsao-Ling Landslide Lake Formed by Chi-Chi Earthquake in Taiwan. Nat. Hazards 2002, 25, 289–303. [Google Scholar] [CrossRef]
- Dai, R.Q.; Yan, K.A.; Zhou, F. Construction of emergency danger removal project of Wenjiaba barrier lake in Pingwu, Sichuan. Yangtze River 2008, 39, 7–8. [Google Scholar]
- Jiang, L.K.; Zhang, S.S.; Huang, L.W.; Liu, F. Preliminary study on engineering geology of yibadao barrier lake and its emergency treatment. In Proceedings of the Investigation and Analysis of Earthquake Damage in Wenchuan Earthquake Engineering, Wenchuan, China, 12 May 2009; pp. 1041–1049. [Google Scholar]
- He, X.R. Summary on emergency disposal of laoyingyan dammed lake in Anxian County. In Proceedings of the Investigation and Analysis of Earthquake Damage in Wenchuan Earthquake Engineering, Wenchuan, China, 8 January 2009; pp. 1019–1022. [Google Scholar]
- Xu, T.H. Example of danger removal of Qingyandong landslide dam in Daning River. Resour. Environ. Eng. 2008, 22, 162–163. [Google Scholar]
- He, B.S.; Wang, Y.J.; Wei, J.J.; Zhang, S.C. Site investigation and analysis of 14 barrier lakes in Sichuan earthquake stricken area. China Flood Drought Manag. 2010, 20, 36–42. [Google Scholar]
- Dunning, S.A.; Mitchell, W.A.; Rosser, N.J.; Petley, D.N. The Hattian Bala rock avalanche and associated landslides triggered by the Kashmir Earthquake of 8 October 2005. Eng. Geol. 2007, 93, 130–144. [Google Scholar] [CrossRef]
- Shi, D.G.; Wang, M.T.; Yin, D.L.; Li, Q.C.; Chen, S.Y. Formation mechanism and stability evaluation of Tangjiawan barrier dam. In Proceedings of the Investigation, Analysis and Research on Engineering Damage of Wenchuan Earthquake, Wenchuan, China, 5 February 2009; pp. 1066–1073. [Google Scholar]
- Bao, G.H. Hydrological emergency monitoring and thinking of Suya barrier lake in Mile County. In Proceedings of the 3rd 9th Council of Yunnan Water Conservancy Society and 2013 academic exchange meeting, Yuxi, China, 11 February 2013. [Google Scholar]
- Tang, S.Z. Preliminary study on sudden flood of “87.7” barrier lake in Kuitun River of Tianshan Mountain. Xinjiang Water Resour. 2011, 2011, 37–42. [Google Scholar]
- Vikram Gupta, M.P.S. Impact of flood discharge from a barrier lake across the Himalayas in the Satluj basin of Himachal Pradesh, India. Inf. Hydrogeol. Eng. Geol. Technol. 2008, 1, 1–8. [Google Scholar]

| Dam Erodibility | λ | ξ | α | β |
|---|---|---|---|---|
| H | 0.27 | 4.554 | 0.283 | 0.433 |
| M | 0.15 | 5.641 | 0.047 | 0.532 |
| L | 0.07 | 0.7247 | 0.404 | 0.612 |
| Empirical Formula | Note | References |
|---|---|---|
| Hd: Dam height (m). | Costa (1985) [39] | |
| V1: Volume of dammed lake (m3). | Costa (1985) [39] | |
| Hd: Dam height (m). V1: Volume of dammed lake (m3). | Costa (1985) [39] | |
| Vl: Volume of dammed lake (m3). | Walder and O’Connor (1997) [42] | |
| g: The acceleration of gravity (m/s2). Hd: Dam height (m). Hr = 1 m; V1: Volume of dammed lake (m3). a: Erodibility coefficient. When the dam erodibility is high, medium and low, a is 1.236, −0.380 and −1.615 respectively. | Peng and Zhang (2012) [19] |
| Model | References | MRE | RMSE (m3/s) | R2 |
|---|---|---|---|---|
| This study | - | 0.48 | 4387 | 0.995 |
| Peng and Zhang (2012) [19] | 0.50 | 12,227 | 0.963 | |
| Costa (1985) [39] | 1.49 | 44,479 | 0.510 | |
| Costa (1985) [39] | 1.34 | 29,943 | 0.778 | |
| Costa (1985) [39] | 3.12 | 62,412 | 0.035 | |
| Walder and O’Connor (1997) [42] | 1.32 | 48,278 | 0.423 |
| Dam Failure Events | Dam Erodibility | Dam Height hd (m) | Volume of Dammed Lake Vl (×106 m3) | Data Sources |
|---|---|---|---|---|
| 10 October 2018 | M | 61 | 49 | Zhang et al. [9] |
| 3 November 2018 | M-H | 81 | 494 |
| Prediction Model | Peak Discharge (m3/s) | Relative Error (%) | ||
|---|---|---|---|---|
| 10 October 2018 | 3 November 2018 | 10 October 2018 | 3 November 2018 | |
| This study | 9927 | 31,634 | 0.73 | 6.68 |
| 7999 | 30,528 | 20.01 | 9.95 | |
| 11,369 | 17,244 | 13.69 | 94.91 | |
| 14,765 | 21,670 | 47.65 | 93.61 | |
| 4345 | 6821 | 56.55 | 97.99 | |
| 11,651 | 15,967 | 16.51 | 95.29 | |
| Measured peak discharge | 10,000 | 33,900 | -- | -- |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, H.; Chen, H.; Wang, T.; Chen, J.; Li, H. Modeling Flood Peak Discharge Caused by Overtopping Failure of a Landslide Dam. Water 2021, 13, 921. https://doi.org/10.3390/w13070921
Ruan H, Chen H, Wang T, Chen J, Li H. Modeling Flood Peak Discharge Caused by Overtopping Failure of a Landslide Dam. Water. 2021; 13(7):921. https://doi.org/10.3390/w13070921
Chicago/Turabian StyleRuan, Hechun, Huayong Chen, Tao Wang, Jiangang Chen, and Huibin Li. 2021. "Modeling Flood Peak Discharge Caused by Overtopping Failure of a Landslide Dam" Water 13, no. 7: 921. https://doi.org/10.3390/w13070921
APA StyleRuan, H., Chen, H., Wang, T., Chen, J., & Li, H. (2021). Modeling Flood Peak Discharge Caused by Overtopping Failure of a Landslide Dam. Water, 13(7), 921. https://doi.org/10.3390/w13070921







