Assessing the TSS Removal Efficiency of Decentralized Stormwater Treatment Systems by Long-Term In-Situ Monitoring
Abstract
1. Introduction
- (i)
- Is turbidity a sufficiently useful surrogate parameter for concentration and composition in the influent and effluent of DS?
- (ii)
- How high are the TSS and TSS63 removal efficiencies during in situ long-term operation and how do they vary?
- (iii)
- What are the deterministic and stochastic components of the efficiencies?
2. Materials and Methods
2.1. Monitoring Sites
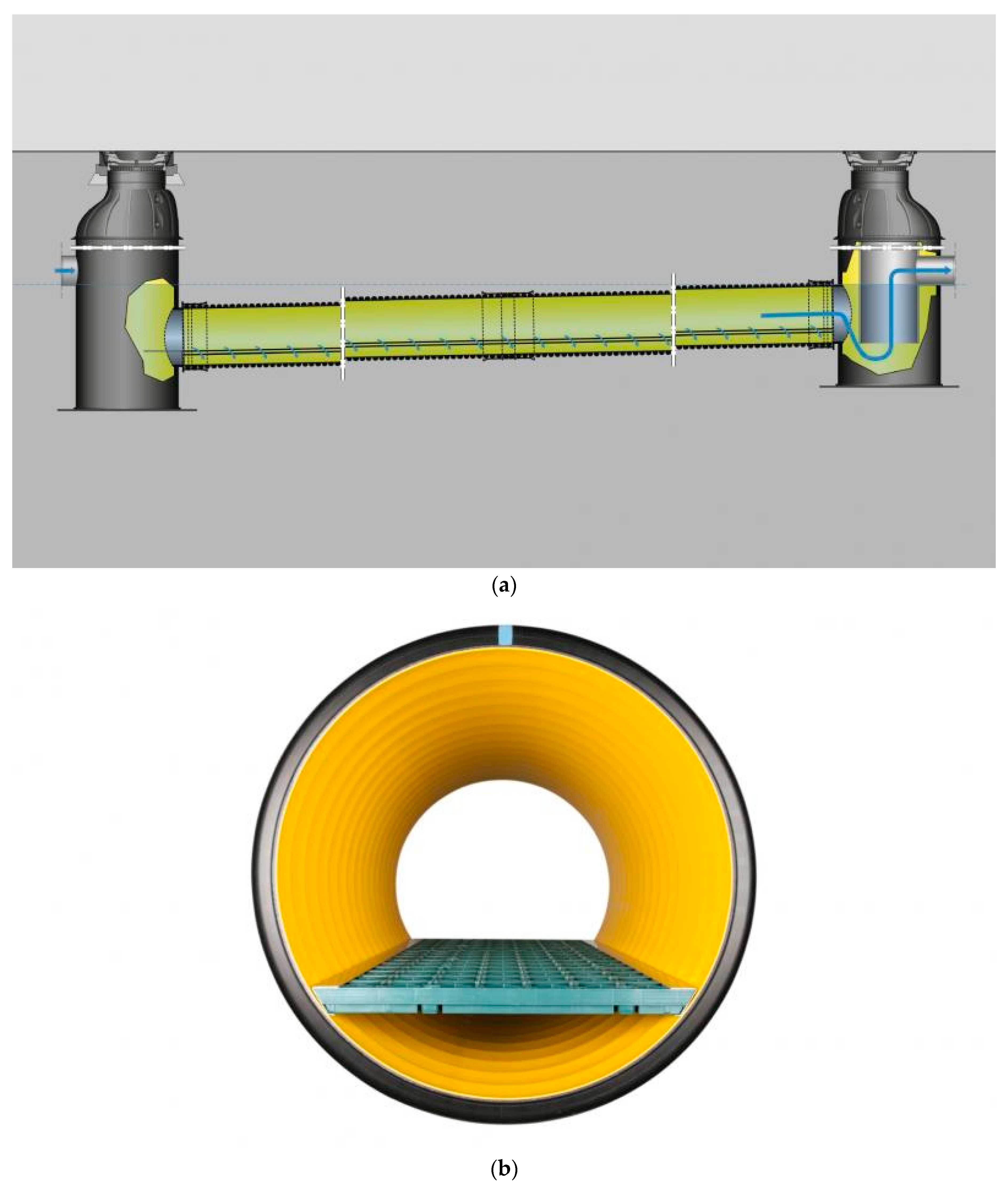
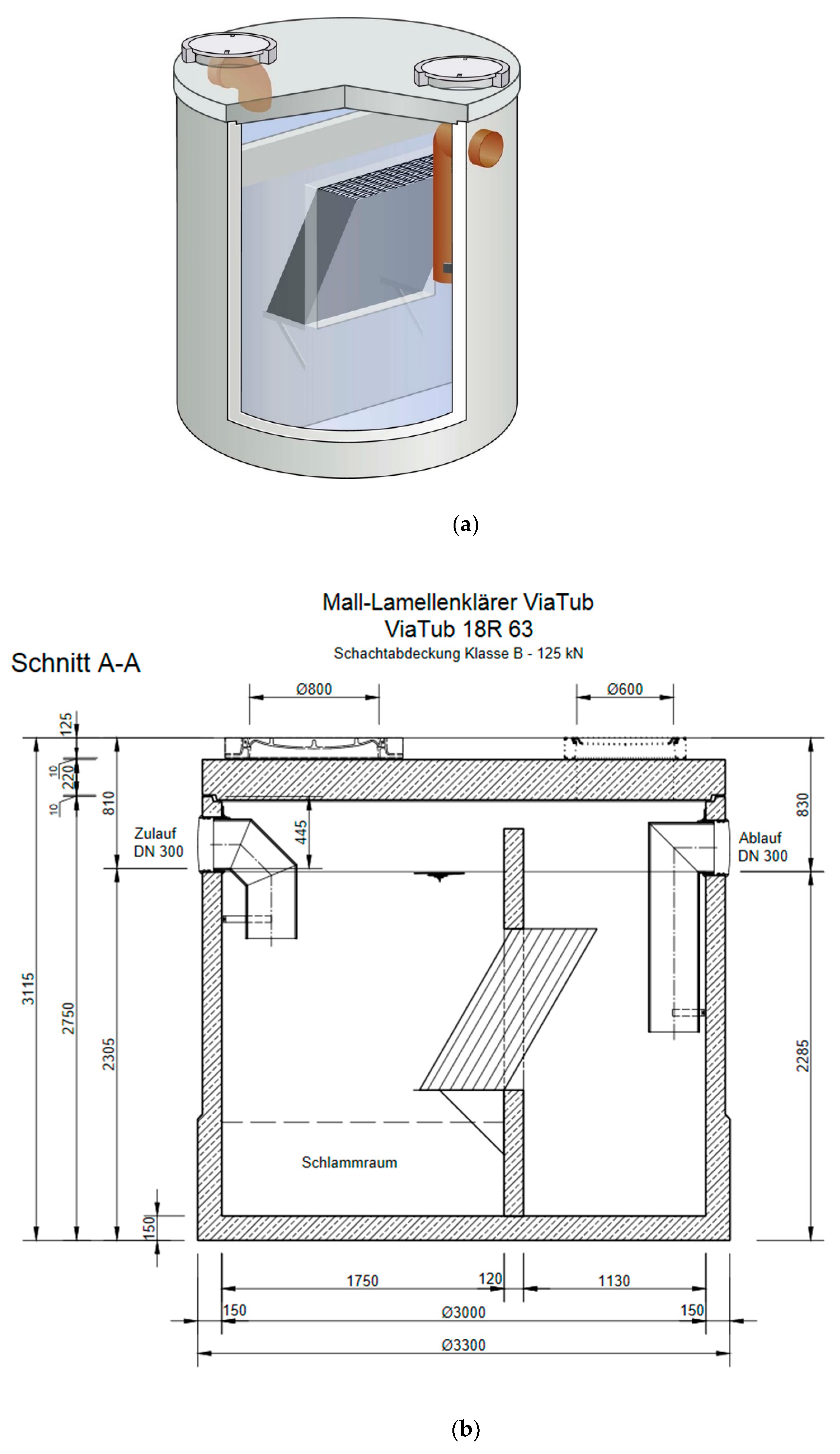
2.2. Decentralized Stormwater Treatment Systems
2.3. Measurement Equipment
2.4. Sampling Method and TSS Analysis
2.5. Data Processing and Management
2.6. Determination of Load Removal Efficiencies
2.7. Determination of Uncertainties
3. Results
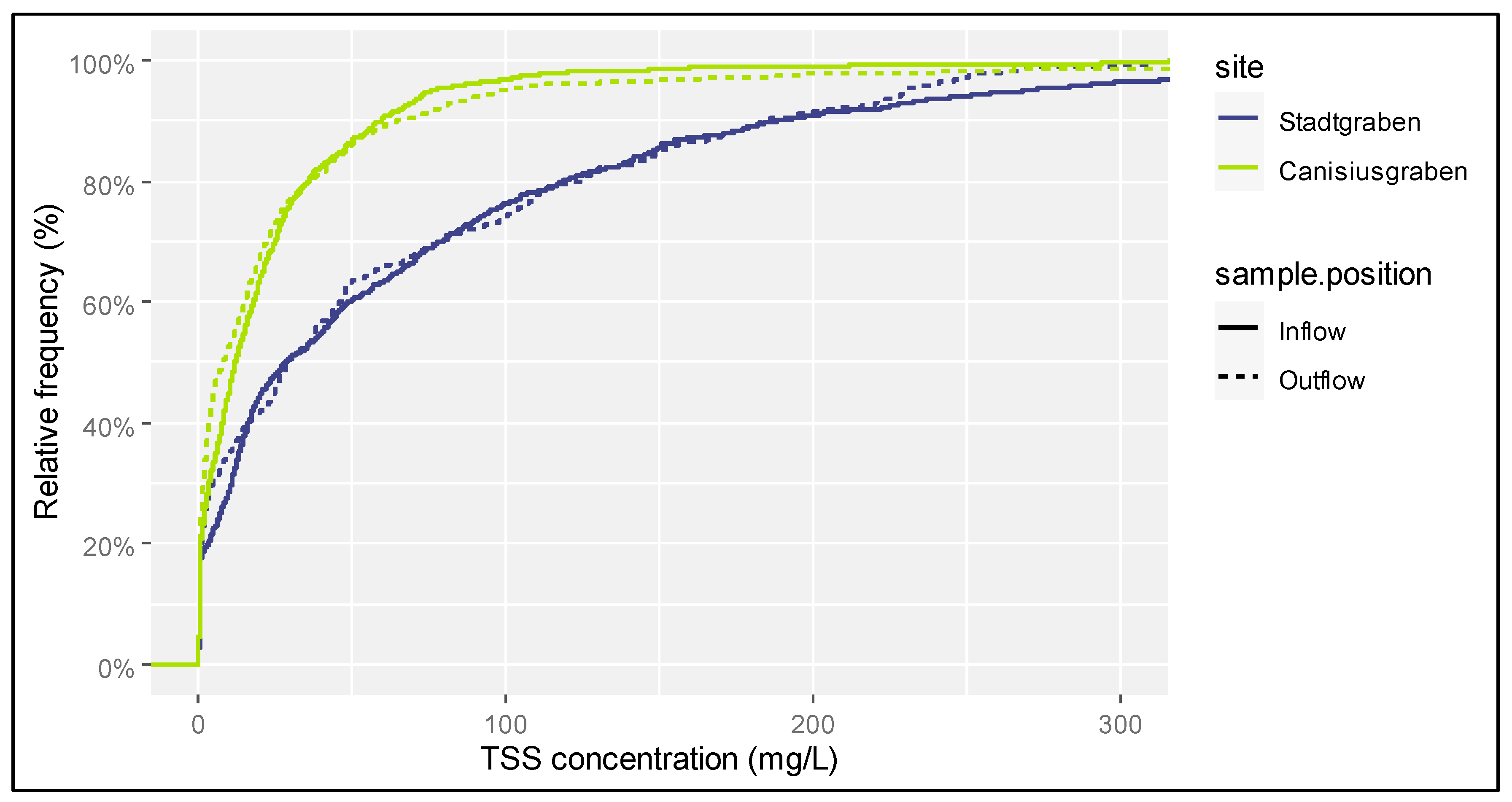
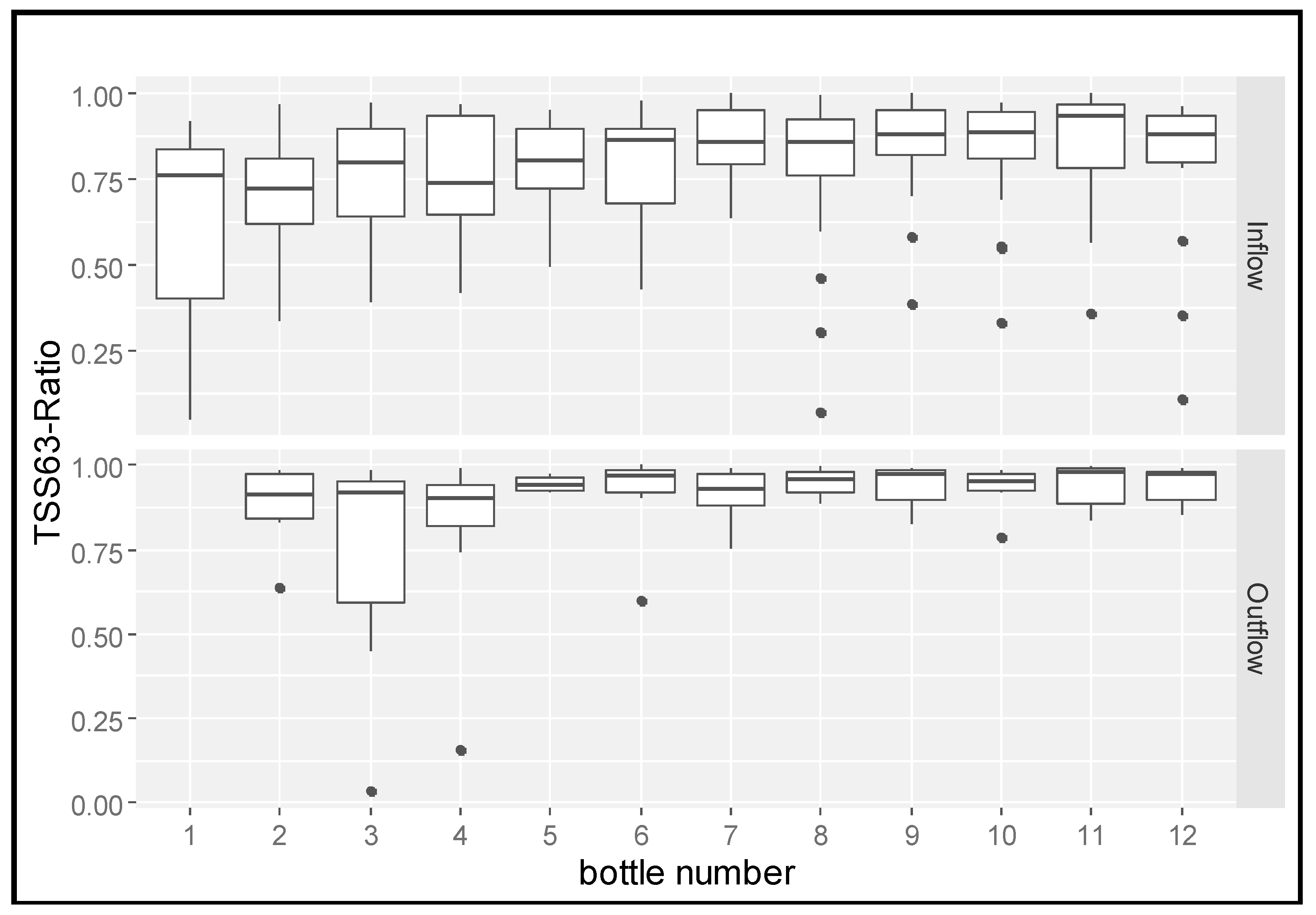
3.1. Analysis of TSS and TSS63
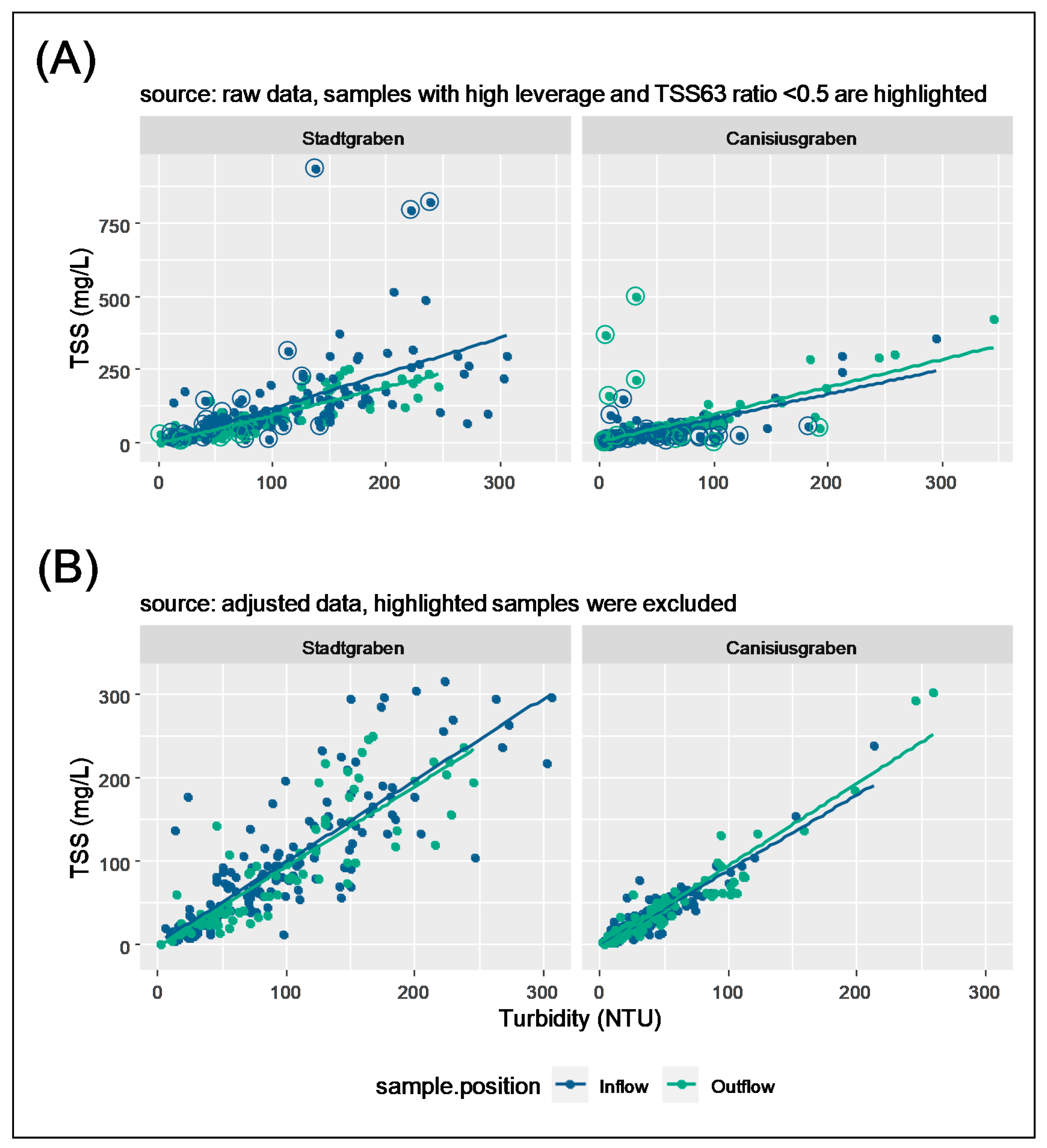
3.2. Relation between TSS and Turbidity
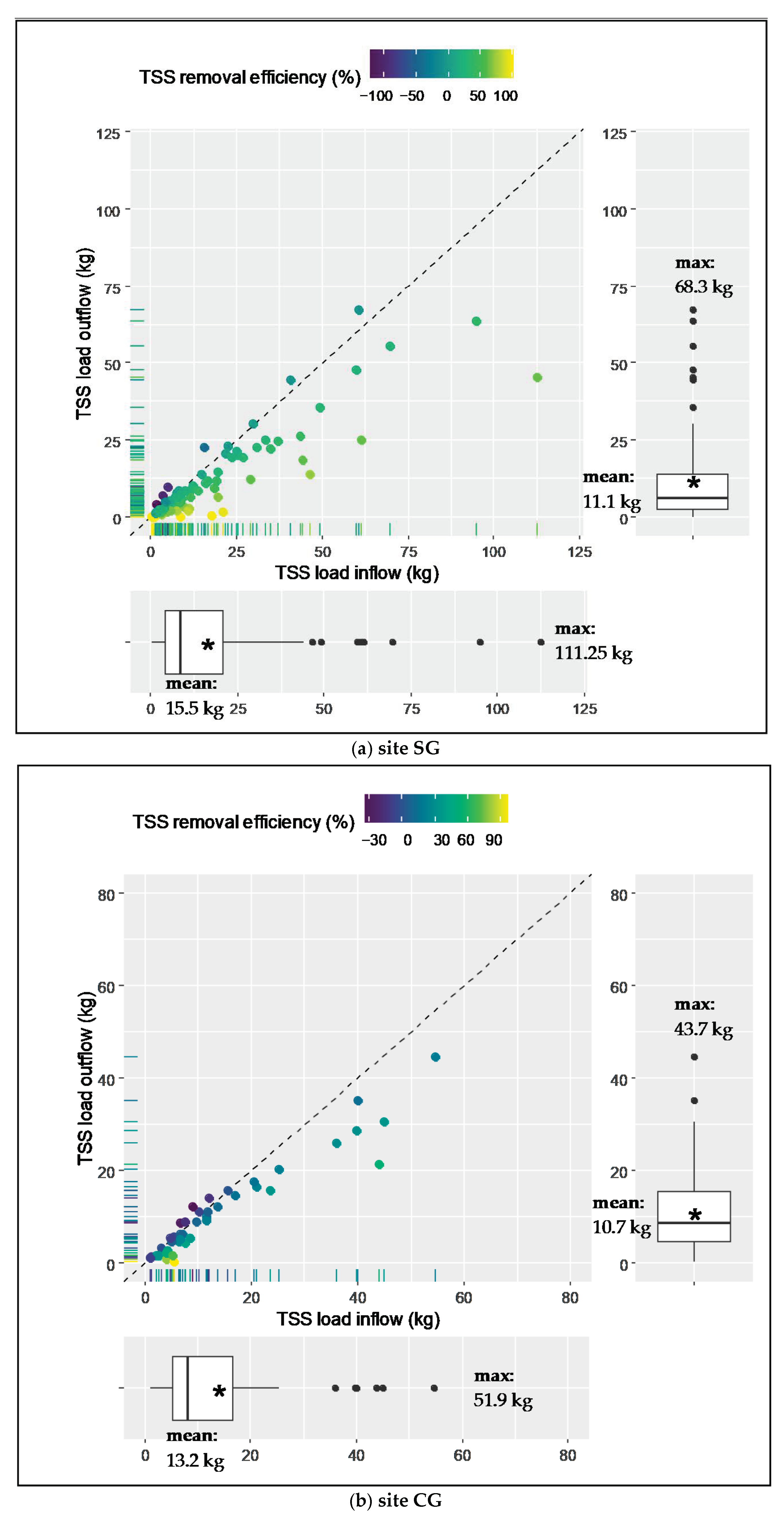
3.3. TSS Load Removal Efficencies
3.4. Uncertainty of TSS Load Removal Efficency
3.5. Mass Balance
4. Discussion
4.1. Relation between TSS and Turbidity
4.2. TSS Load Removal Efficencies and Uncertainties
4.3. TSS and TSS63 in Urban Stormwater Runoff
4.4. Indications for Further Planning and Operation of DS
4.5. Improvement of DS Evaluation
5. Conclusions
- In situ treatment is not at par with lab results. Even with constant hydraulic conditions, high variability of efficiency was observed.
- For the two monitored sites with a high mean TSS63 ratio of 0.8, sedimentation treatment does not meet the treatment objective to adequately protect the receiving water and exposed organisms.
- The significant TSS63 ratio shift from inflow to outflow indicated that DS with an exclusive sedimentation treatment can achieve better removal efficiencies with respect to coarser particles (>63 µm).
- The TSS63 as a new stormwater design parameter and especially its fraction of TSS should be given more attention to characterize stormwater quality as it affects the correlation to turbidity.
- It is well known that using turbidity as a proxy of TSS introduces uncertainties. However, as the explorative results indicated, further investigations especially when evaluating the removal efficiency of DS are strongly recommended.
- Due to the physics of sedimentation and its limits, treatment of urban stormwater runoff with high TSS63 pollution requires additional techniques, such as filtering to retain fine particles more effective.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Rain Event | |||||
|---|---|---|---|---|---|
| Site | Date | Duration | Sum | Mean | Imax60 |
| - | - | h | mm | mm | mm/h |
| Canisiusgraben | 10 May 2018 | 6.7 | 3.1 | 0.5 | 1.4 |
| 29 August 2018 | 9.9 | 11.9 | 1.2 | 5.3 | |
| 30 August 2018 | 9.9 | 11.9 | 1.2 | 5.3 | |
| 6 September 2018 | 2.8 | 5.0 | 1.8 | 3.4 | |
| 21 September 2018 | 0.8 | 3.8 | 4.9 | 4.9 | |
| 06 October 2018 | 0.4 | 0.4 | 3.6 | 1.0 | |
| 24 October 2018 | 29.7 | 7.6 | 0.3 | 1.2 | |
| 26 October 2018 | 2.6 | 3.5 | 1.3 | 3.0 | |
| 10 November 2018 | 1.2 | 1.0 | 0.8 | 0.9 | |
| 14 November 2018 | 0.0 | 0.1 | 1.5 | 1.5 | |
| 20 November 2018 | 3.0 | 1.9 | 0.6 | 1.4 | |
| 28 November 2018 | 2.4 | 0.8 | 0.3 | 0.5 | |
| 4 December 2018 | 5.2 | 3.1 | 11.4 | 0.6 | |
| 17 December 2018 | 10.6 | 2.0 | 0.2 | 0.4 | |
| 6 January 2019 | 35.9 | 8.1 | 0.2 | 1.1 | |
| 1 February 2019 | 2.6 | 1.7 | 0.7 | 1.2 | |
| 4 February 2019 | 0.0 | 0.1 | 2.4 | 2.4 | |
| 10 February 2019 | 20.4 | 22.0 | 12.6 | 1.1 | |
| 24 April 2019 | 0.3 | 1.9 | 19.2 | 7.2 | |
| 26 April 2019 | 3.0 | 1.5 | 0.5 | 1.3 | |
| 2 May 2019 | 1.9 | 0.5 | 0.3 | 0.3 | |
| 3 May 2019 | 2.8 | 1.5 | 6.6 | 0.6 | |
| 19 May 2019 | 1.6 | 0.8 | 0.5 | 0.5 | |
| 21 May 2019 | 0.6 | 0.4 | 0.7 | 0.7 | |
| 6 July 2019 | 4.1 | 4.9 | 1.2 | 2.7 | |
| Stadtgraben | 1 January 2018 | 2.3 | 5.3 | 2.3 | 3.4 |
| 31 January 2018 | 15.4 | 13.6 | 0.9 | 5.0 | |
| 8 March 2018 | 5.5 | 8.1 | 1.5 | 4.2 | |
| 10 March 2018 | 7.3 | 4.4 | 0.6 | 1.0 | |
| 13 March 2018 | 5.5 | 1.3 | 0.2 | 0.5 | |
| 23 March 2018 | 2.5 | 0.2 | 0.1 | 0.1 | |
| 28 March 2018 | 7.9 | 14.1 | 1.8 | 4.0 | |
| 26 April 2018 | 2.6 | 1.8 | 0.7 | 1.7 | |
| 28 July 2018 | 0.6 | 2.8 | 5.0 | 5.0 | |
| 8 August 2018 | 2.3 | 0.3 | 5.4 | 0.13 | |
| 20 December 2018 | 11.3 | 5.9 | 0.5 | 2.9 | |
| 10 January 2019 | 10.4 | 2.7 | 3.6 | 0.26 | |
| 17 January 2019 | 13.8 | 5.4 | 0.4 | 2.2 | |
| 28 January 2019 | 17.8 | 9.0 | 0.5 | 5.0 | |
| 1 February 2019 | 2.6 | 1.7 | 0.7 | 1.2 | |
| 1 March 2019 | 5.1 | 1.7 | 0.3 | 1.1 | |
| 6 March 2019 | 0.8 | 1.3 | 1.6 | 1.6 | |
| 24 April 2019 | 0.3 | 1.9 | 7.2 | 7.2 | |
| 6 June 2019 | 3.4 | 4.2 | 1.2 | 3.1 | |
| Site | Sample Position | Parameter | n | TSS Concentration (mg/L) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Sd | 0% | 5% | 10% | 25% | 50% | 75% | 90% | 95% | 100% | ||||
| SG | Inflow | TSS63/TSS | 210 | 0.78 | 0.19 | 0.051 | 0.37 | 0.53 | 0.69 | 0.84 | 0.93 | 0.96 | 0.98 | 1 |
| TSS63 | 210 | 94.4 | 101 | 2.84 | 8.82 | 12.2 | 18.6 | 62.6 | 134 | 229 | 328 | 513 | ||
| TSS | 210 | 27.1 | 168 | 5.21 | 13.5 | 14.7 | 27.0 | 81.2 | 155 | 276 | 381 | 1398 | ||
| TSS in Turb | 210 | 97.9 | 127 | 4.03 | 10.4 | 11.2 | 20.1 | 63.2 | 121 | 220 | 296 | 938 | ||
| Turbidity | 210 | 84.2 | 69.7 | 5.70 | 11.8 | 15.0 | 26.1 | 69.5 | 126 | 181 | 226 | 306 | ||
| Outflow | TSS63/TSS | 91 | 0.89 | 0.17 | 0.034 | 0.61 | 0.74 | 0.89 | 0.94 | 0.98 | 0.99 | 0.99 | 1 | |
| TSS63 | 91 | 97.9 | 86.1 | 0.68 | 4.92 | 12.0 | 26.6 | 67.6 | 162 | 235 | 260 | 315 | ||
| TSS | 91 | 03.3 | 86.8 | 1.07 | 13.9 | 17.8 | 31.6 | 69.2 | 171 | 241 | 269 | 324 | ||
| TSS in Turb | 91 | 82.0 | 70.6 | 0.81 | 11.2 | 13.4 | 25.3 | 57.8 | 119 | 201 | 220 | 250 | ||
| Turbidity | 91 | 88.1 | 63.7 | 1.50 | 14.2 | 18.0 | 40.0 | 71.0 | 130 | 185 | 220 | 246 | ||
| CG | Inflow | TSS63/TSS | 221 | 0.79 | 0.19 | 0.05 | 0.46 | 0.51 | 0.67 | 0.87 | 0.93 | 0.97 | 0.98 | 1 |
| TSS63 | 221 | 31.0 | 43.6 | 0.55 | 2.40 | 4.58 | 9.81 | 19.6 | 37.1 | 65.6 | 76.1 | 410 | ||
| TSS | 221 | 38.4 | 49.7 | 1.55 | 3.60 | 7.57 | 13.5 | 25.4 | 47.0 | 74.9 | 104 | 432 | ||
| TSS in Turb | 221 | 29.9 | 39.7 | 1.25 | 2.88 | 5.73 | 10.5 | 19.3 | 35.4 | 58.1 | 77.2 | 356 | ||
| Turbidity | 221 | 36.8 | 38.4 | 2.50 | 4.50 | 7.00 | 12.0 | 25.7 | 48.0 | 73.0 | 102 | 295 | ||
| Outflow | TSS63/TSS | 189 | 0.82 | 0.19 | 0.0055 | 0.46 | 0.61 | 0.76 | 0.88 | 0.95 | 0.98 | 0.99 | 1 | |
| TSS63 | 189 | 34.2 | 56.3 | 0.36 | 1.48 | 2.17 | 5.15 | 16.8 | 39.2 | 74.7 | 98.2 | 456 | ||
| TSS | 189 | 46.0 | 81.4 | 1.06 | 2.02 | 2.96 | 7.90 | 21.2 | 46.4 | 89.8 | 179 | 579 | ||
| TSS in Turb | 189 | 37.8 | 68.8 | 0.89 | 1.69 | 2.48 | 5.95 | 17.0 | 39.0 | 75.9 | 136 | 498 | ||
| Turbidity | 189 | 36.9 | 49.0 | 2.20 | 3.48 | 4.28 | 7.20 | 20.1 | 44.0 | 94.0 | 113 | 345 | ||
References
- Ellis, J.; Hvitved-Jacobsen, T. Urban drainage impacts on receiving waters. J. Hydraul. Res. 1996, 34, 771–783. [Google Scholar] [CrossRef]
- Walsh, C.J.; Fletcher, T.D.; Burns, M.J. Urban Stormwater Runoff: A New Class of Environmental Flow Problem. PLoS ONE 2012, 7, e45814. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.-Y.; Lusk, M.G. Nutrients in Urban Stormwater Runoff: Current State of the Science and Potential Mitigation Options. Curr. Pollut. Rep. 2018, 4, 112–127. [Google Scholar] [CrossRef]
- Chebbo, G.; Gromaire, M.; Ahyerre, M.; Garnaud, S. Production and transport of urban wet weather pollution in combined sewer systems: The “Marais” experimental urban catchment in Paris. Urban Water 2001, 3, 3–15. [Google Scholar] [CrossRef]
- Göbel, P.; Dierkes, C.; Coldewey, W. Storm water runoff concentration matrix for urban areas. J. Contam. Hydrol. 2007, 91, 26–42. [Google Scholar] [CrossRef] [PubMed]
- Becouze-Lareure, C.; Dembélé, A.; Coquery, M.; Cren-Olivé, C.; Barillon, B.; Bertrand-Krajewski, J.-L. Source characterisation and loads of metals and pesticides in urban wet weather discharges. Urban Water J. 2016, 13, 600–617. [Google Scholar] [CrossRef]
- Ellis, J.; Revitt, D.; Harrop, D.; Beckwith, P. The contribution of highway surfaces to urban stormwater sediments and metal loadings. Sci. Total Environ. 1987, 59, 339–349. [Google Scholar] [CrossRef]
- Launay, M.A.; Dittmer, U.; Steinmetz, H. Organic micropollutants discharged by combined sewer overflows—Characterisation of pollutant sources and stormwater-related processes. Water Res. 2016, 104, 82–92. [Google Scholar] [CrossRef] [PubMed]
- Zgheib, S.; Moilleron, R.; Chebbo, G. Priority pollutants in urban stormwater: Part 1—Case of separate storm sewers. Water Res. 2012, 46, 6683–6692. [Google Scholar] [CrossRef]
- Aryal, R.; Vigneswaran, S.; Kandasamy, J.; Naidu, R.; Vigneswaran, S. Urban stormwater quality and treatment. Korean J. Chem. Eng. 2010, 27, 1343–1359. [Google Scholar] [CrossRef]
- Sansalone, J.J.; Buchberger, S.G. Characterization of Solid and Metal Element Distributions in Urban Highway Stormwater. Water Sci. Technol. 1997, 36, 155–160. [Google Scholar] [CrossRef]
- Hilliges, R.; Endres, M.; Tiffert, A.; Brenner, E.; Marks, T. Characterization of road runoff with regard to seasonal variations, particle size distribution and the correlation of fine particles and pollutants. Water Sci. Technol. 2017, 75, 1169–1176. [Google Scholar] [CrossRef]
- DWA-A 102-1. Grundsätze zur Bewirtschaftung und Behandlung von Regenwasserabflüssen zur Einleitung in Oberflächengewässer—Teil 1: Allgemeines; Deutsche Vereinigung für Wasserwirtschaft, Abwasser und Abfall e. V. (DWA): Hennef, Germany, 2020; ISBN 978-3-96862-044-2. [Google Scholar]
- Dierschke, M.; Welker, A. Bestimmung von Feststoffen in Niederschlagsabflüssen. GWF Wasser Abwasser 2015, 156, 440–446. [Google Scholar]
- Zhao, H.; Li, X.; Wang, X.; Tian, D. Grain size distribution of road-deposited sediment and its contribution to heavy metal pollution in urban runoff in Beijing, China. J. Hazard. Mater. 2010, 183, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Selbig, W.R. Characterizing the distribution of particles in urban stormwater: Advancements through improved sampling technology. Urban Water J. 2013, 12, 111–119. [Google Scholar] [CrossRef]
- Sommer, H.; Post, M.; Estupinan, F.; Ingenieurgesellschaft Prof. D. Sieker mbH. Dezentrale Behandlung von Straßenabflüssen—Übersicht Verfügbarer Anlagen. 2016. Available online: https://www.sieker.de/fileadmin/sieker/Buero/veroeffentlichungen/Broschuere_Dezentrale_Regenwasserbehandlung_2016.pdf (accessed on 25 March 2021).
- Geosyntec Consultants; Wright Water Engineers, Inc. Urban Stormwater BMP Performance Monitoring; US Environmental Protection Agency: Washington, DC, USA, 2009.
- Department of Ecology State of Washington. Technical Guidance Manual for Evaluating Emerging Stormwater Treatment Technologies. Technology Assessment Protocol—Ecology (TAPE). Available online: https://ecology.wa.gov/Regulations-Permits/Guidance-technical-assistance/Stormwater-permittee-guidance-resources/Emerging-stormwater-treatment-technologies (accessed on 13 December 2020).
- VSA-Leistungsprüfung für Behandlungsanlagen, Merkblatt «Leistungsprüfung für Adsorbermaterialien und Dezentrale Technische Anlagen zur Behandlung von Niederschlagswasser». Available online: https://vsa.ch/Mediathek/vsa-leistungspruefung-fuer-behandlungsanlagen/ (accessed on 11 February 2021).
- DIBt (Deutsches Institut für Bautechnik). Zulassungsgrundsätze für Niederschlagswasserbehandlungsanlagen; Teil 1: Anlagen zur dezentralen Behandlung des Abwassers von Kfz-Verkehrsflächen zur anschließenden Versickerung in Boden und Grundwasser; DIBt (Deutsches Institut für Bautechnik): Berlin, Germany, 2015. [Google Scholar]
- Lucke, T.; Nichols, P.; Shaver, E.; Lenhart, J.; Welker, A.; Huber, M. Pathways for the Evaluation of Stormwater Quality Improvement Devices—The Experience of Six Countries. CLEAN Soil Air Water 2017, 45, 1600596. [Google Scholar] [CrossRef]
- Leutnant, D.; Muschalla, D.; Uhl, M. Stormwater Pollutant Process Analysis with Long-Term Online Monitoring Data at Micro-Scale Sites. Water 2016, 8, 299. [Google Scholar] [CrossRef]
- Gruber, G.; Winkler, S.; Pressl, A. Quantification of pollution loads from CSOs into surface water bodies by means of online techniques. Water Sci. Technol. 2004, 50, 73–80. [Google Scholar] [CrossRef]
- Bertrand-Krajewski, J.-L. TSS concentration in sewers estimated from turbidity measurements by means of linear regression accounting for uncertainties in both variables. Water Sci. Technol. 2004, 50, 81–88. [Google Scholar] [CrossRef]
- Caradot, N.; Sonnenberg, H.; Rouault, P.; Gruber, G.; Hofer, T.; Torres, A.; Pesci, M.; Bertrand-Krajewski, J.-L. Influence of local calibration on the quality of online wet weather discharge monitoring: Feedback from five international case studies. Water Sci. Technol. 2014, 71, 45–51. [Google Scholar] [CrossRef]
- Métadier, M.; Bertrand-Krajewski, J.-L. The use of long-term on-line turbidity measurements for the calculation of urban stormwater pollutant concentrations, loads, pollutographs and intra-event fluxes. Water Res. 2012, 46, 6836–6856. [Google Scholar] [CrossRef] [PubMed]
- Bertrand-Krajewski, J.-L.; Chebbo, G.; Saget, A. Agnes Distribution of Pollutant Mass vs. Volumen in Stormwater Discharges and the First Flush Phenomen. Water Res. 1998, 32, 2341–2356. [Google Scholar] [CrossRef]
- Bertrand-Krajewski, J.-L. Stormwater pollutant loads modelling: Epistemological aspects and case studies on the influence of field data sets on calibration and verification. Water Sci. Technol. 2007, 55, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Uhl, M.; Mohn, R.; Maus, C.; Schnieders, A.; Sommer, M.; Voßwinkel, N.; Ebbert, S.; Tenbeitel, J.-G. Weitergende Regenwasserbehandlung Im Trennsystem (WEREBE); FH Münster Institut für Wasser·Ressourcen·Umwelt (IWARU): Münster, Germany, 2013. [Google Scholar]
- WTW GmbH. Operating Manual VisoTurb 700 IQ (SW). 2017. Available online: https://www.xylemanalytics.com/en/File%20Library/Resource%20Library/WTW/01%20Manuals/ba57301e09_VisoTurb_700_IQ_SW_WTW.pdf (accessed on 25 March 2020).
- Nivus GmbH. Technical Instructions for Correlation Sensors and External Electronic Box. 2019. Available online: http://www.nivus.de/ximages/1404786_sasba02en.pdf (accessed on 11 February 2021).
- OTT Hydromet GmbH. Betriebsanleitung Niederschlagssensor OTT Pluvio2 L. 2013. Available online: https://www.lufft.com/de-de/produkte/download-de/betriebsanleitung-ott-pluvio2-l-de/ (accessed on 25 March 2021).
- DIN 38409-2. Summarische Wirkungs—Und Stoffkenngrößen (Gruppe H)—Bestimmung Der Abfiltrierbaren Stoffe Und Des Glührückstandes (H 2); Beuth Verlag GmbH: Berlin, Germany, 1987. [Google Scholar]
- NEMI Method Summary-160.2—Residue. Non-Filterable (Gravimetric. Dried at 103–105 °C). Available online: https://www.nemi.gov/methods/method_summary/5213/ (accessed on 13 December 2020).
- 2540 Solids. Available online: https://www.standardmethods.org/doi/ref/10.2105/SMWW.2882.030 (accessed on 13 December 2020).
- Baum, P.; Benisch, J.; Blumensaat, F.; Dierschke, M.; Dittmer, U.; Gelhardt, L.; Gruber, G.; Grüner, S.; Heinz, E.; Hofer, T.; et al. AFS63—Harmonisierungsbedarf Und Empfehlungen Für Die Labortechnische Bestimmung Des Neuen Parameters. In Proceedings of the Regenwasser in urbanen Räumen—Aqua urbanica trifft RegenwasserTage 2018, Landau in der Pfalz, Germany, 18–19 June 2018; Schmitt, T.G., Ed.; Technische Universität Kaiserslautern: Landau in der Pfalz, Germany, 2018; Volume 1. [Google Scholar]
- Leutnant, D.; Henrichs, M.; Muschalla, D.; Uhl, M. OSCAR—An Online Supervisory Control and Urban Drainage Data Acquisition System with R. In Proceedings of the 10th International Conference on Urban Drainage Modelling, Mont-Sainte-Anne, QC, Canada, 20–23 September 2015; Maere, T., Tik, S., Duchesne, S., Vanrolleghem, P., Eds.; pp. 135–138. [Google Scholar]
- InfluxData. InfluxDB; Manual: San Francisco, CA, USA, 2020. [Google Scholar]
- Grafana Labs. Grafana; Manual: New York, NY, USA; Stockholm, Sweden, 2020. [Google Scholar]
- Leutnant, D.; Kleckers, J.; Haberkamp, J.; Uhl, M. Assessing the Performance of Decentralised Stormwater Management Measures by Means of Continuous Turbidity Measurement. In Proceedings of the Novatech 2019—10th International Conference on Urban Water—Strategies and Solutions for Sustainable Management, Lyon, France, 1–5 July 2019; p. 4. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Leutnant, D.; Schleifenbaum, R.; Rickert, G.; Grüning, H.; Uhl, M. Stofftransport Und –Behandlung in Der Siedlungshydrologie (STBMOD); Fachhochschule Münster, Institut für Wasser·Ressourcen·Umwelt (IWARU): Münster, Germany, 2016. [Google Scholar]
- Hannouche, A.; Chebbo, G.; Ruban, G.; Tassin, B.; Lemaire, B.J.; Joannis, C. Relationship between turbidity and total suspended solids concentration within a combined sewer system. Water Sci. Technol. 2011, 64, 2445–2452. [Google Scholar] [CrossRef]
- JCGM 101. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. 2008. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 25 March 2021).
- Leutnant, D.; Uhl, M. Leistungsfähigkeit Großer Dezentraler Niederschlagswasserbehandlungsanlagen Unter Realen Betriebsbedingungen. In Proceedings of the 52. ESSENER TAGUNG—Wasser in einer sich Verändernden Welt, Aachen, Germany, 20–22 March 2019; Pinnekamp, J., Ed.; Gesellschaft zur Förderung des Instituts für Siedlungswasserwirtschaft an der RWTH Aachen e. V.: Aachen, Germany, 2020. [Google Scholar]
- Rommel, S.; Gelhardt, L.; Welker, A.; Helmreich, B. Settling of Road-Deposited Sediment: Influence of Particle Density, Shape, Low Temperatures, and Deicing Salt. Water 2020, 12, 3126. [Google Scholar] [CrossRef]
- Mall GmbH. Lamellenklaerer ViaTub. Available online: https://www.mall.info/produkte/regenwasserbewirtschaftung/regenwasserbehandlung/viatub-lamellenklaerer/ (accessed on 9 March 2021).
- Fränkische Rohrwerke Gebr. Kirchner GmbH & Co. KG SediPipe XL. Available online: https://www.fraenkische.com/en/product/sedipipe-xl (accessed on 9 March 2021).
| Site | Total Size | Impervious Area | Slope | Traffic Load | |||
|---|---|---|---|---|---|---|---|
| Sum (Cover) | Roofs | Sidewalks | Streets | ||||
| - | ha | ha (%) | ha | ha | ha | ‰ | Vehicles per day |
| Stadtgraben (SG) | 2.63 | 2.5, (95) | 0.63 | 0.27 | 1.6 | 5.5 | 30,000 |
| Canisiusgraben (CG) | 10.7 | 5.7, (53) | 2.51 | 0.83 | 2.36 | 10 to 13 | 9000 and 13,000 |
| Site | Sample Position | Year | n | |||||
|---|---|---|---|---|---|---|---|---|
| - | - | - | - | mg/L | mg/L | mg/L | - | - |
| Sewer | 2015 | 85 | 63.7 | 31.7 | 67.1 | - | - | |
| SG | Inflow | 2018 | 107 | 172 | 184 | 123 | 0.80 | - |
| 2019 | 103 | 80.4 | 135 | 32.1 | 0.76 | - | ||
| all | 210 | 127 | 168 | 81.2 | 0.78 | 0.19 | ||
| Outflow | 2018 | 67 | 127 | 88.4 | 110 | 0.91 | - | |
| 2019 | 24 | 36.1 | 25.2 | 29.5 | 0.84 | - | ||
| all | 91 | 103 | 86.8 | 69.2 | 0.89 | 0.17 | ||
| CG | Inflow | 2018 | 128 | 47.4 | 60.4 | 29.2 | 0.83 | - |
| 2019 | 93 | 26.1 | 24.6 | 18.2 | 0.73 | - | ||
| all | 221 | 38.4 | 49.7 | 25.4 | 0.79 | 0.19 | ||
| Outflow | 2018 | 103 | 56.1 | 81.9 | 29.2 | 0.86 | - | |
| 2019 | 86 | 34.0 | 79.6 | 10.0 | 0.78 | - | ||
| all | 189 | 46.0 | 81.4 | 21.2 | 0.82 | 0.19 |
| Site | Sample Position | n | R2 (Adjusted) | Intercept (a) | Slope (b) | st.error |
|---|---|---|---|---|---|---|
| Stadtgraben | inflow | 210 1 | 0.44 | −3.84 | 1.21 | 0.09 |
| outflow | 91 1 | 0.75 | −2.68 | 0.96 | 0.06 | |
| Canisiusgraben | inflow | 221 1 | 0.65 | −0.78 | 0.84 | 0.04 |
| outflow | 189 1 | 0.44 | 3.25 | 0.94 | 0.08 | |
| Stadtgraben | inflow | 182 2 | 0.75 | 2.31 | 0.99 | 0.04 |
| outflow | 83 2 | 0.75 | −0.41 | 0.95 | 0.06 | |
| Canisiusgraben | inflow | 181 2 | 0.86 | −1.94 | 0.91 | 0.03 |
| outflow | 166 2 | 0.92 | −3.96 | 0.99 | 0.02 |
| TSS Load Inflow | TSS Load Outflow | TSS | |||||
|---|---|---|---|---|---|---|---|
| Site | Period | Events | Median | Total | Median | Total | Removal Efficiency |
| From– to | |||||||
| SG | - | kg | kg | kg | kg | % | |
| November 2017–July 2019 | 51 | 7.9 | 812 | 4.4 | 485 | 40 | |
| November 2017–November 2020 | 91 | 7.6 | 1413 | 5.16 | 1006 | 29 | |
| CG | May 2018– July 2019 | 26 1 | 10.3 | 442 | 11.7 | 357 | 19 |
| May 2018– November 2020 | 42 1 | 8.3 | 556 | 8.4 | 452 | 19 | |
| Site | Sample Position | TSS | TSS63 | TSScoarse | |||
|---|---|---|---|---|---|---|---|
| Total Load | Ratio TSS63/TSS | Total Load | Removal Efficiency | Total Load | Removal Efficiency | ||
| - | - | kg | - | kg | % | kg | % |
| SG | Inflow | 1413 | 0.78 | 1102 | 19 | 242 | 59 |
| Outflow | 1006 | 0.89 | 895 | 98 | |||
| CG | Inflow | 556 | 0.79 | 439 | 16 | 92 | 28 |
| Outflow | 452 | 0.82 | 370 | 66 | |||
| Year | Rain Sum | Effective Rain Sum | Site SG | Site CG | ||
|---|---|---|---|---|---|---|
| Treated Rain | Treatment Ratio | Treated Rain | Treatment Ratio | |||
| From - to | mm | mm | mm | - | mm | - |
| November 2017-> | 189 | 137 | 69.0 | 0.51 | - | - |
| 2018 | 578 | 403 | 246 | 0.61 | 71.9 | 0.27 1 |
| 2019 | 762 | 630 | 226 | 0.36 | 224 | 0.36 |
| ->December 2020 | 597 | 483 | 266 | 0.55 | 71.6 | 0.15 2 |
| Total | 2126 | 1653 | 806 | 0.49 | 387 | 0.27 1 |
| Events per Season | SG (n = 91) Spring n = 18 Summer n = 21 Fall n = 24 Winter n = 28 | |||||
| CG (n = 51) Spring n = 7 Summer n = 15 Fall n = 16 Winter n = 13 | ||||||
| SG Inflow | SG Outflow | CG Inflow | CG Outflow | |
|---|---|---|---|---|
| n | 182 | 83 | 181 | 166 |
| Mean | 0.000904 | 0.00711 | 0.261 | 0.0774 |
| 0.824 | 0.554 | 1.03 | 1.80 | |
| Event | Duration | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| site-ID | g/s | g/s | - | - | % | % | % | % | hh:mm |
| SG-1 | 59.3 | 46.6 | 3.17 | 1.71 | 21.0 | 5 | 5 | 24 | 04:26 |
| SG-159 | 261 | 192 | 8.81 | 4.24 | 26.4 | 3 | 3 | 11.3 | 08:01 |
| CG-15 | 41.2 | 28.3 | 2.77 | 3.35 | 31 | 9 | 9 | 30 | 07:55 |
| CG-109 | 80.3 | 76.0 | 11.0 | 11.0 | 5 | 19 | 19 | 353 | 11:35 |
| Events | Sample Pairs | Q Sampled | Removal Efficiency | TSS63 Ratio Sum In | TSS63 Ratio Sum Out | TSS63 Ratio Shift | ||
|---|---|---|---|---|---|---|---|---|
| - | - | m3 | kg | kg | % | - | - | % |
| 9 | 75 | 270 | 63.0 | 33.5 | 47 | 63.3 | 66.7 | 5.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lieske, C.; Leutnant, D.; Uhl, M. Assessing the TSS Removal Efficiency of Decentralized Stormwater Treatment Systems by Long-Term In-Situ Monitoring. Water 2021, 13, 908. https://doi.org/10.3390/w13070908
Lieske C, Leutnant D, Uhl M. Assessing the TSS Removal Efficiency of Decentralized Stormwater Treatment Systems by Long-Term In-Situ Monitoring. Water. 2021; 13(7):908. https://doi.org/10.3390/w13070908
Chicago/Turabian StyleLieske, Christian, Dominik Leutnant, and Mathias Uhl. 2021. "Assessing the TSS Removal Efficiency of Decentralized Stormwater Treatment Systems by Long-Term In-Situ Monitoring" Water 13, no. 7: 908. https://doi.org/10.3390/w13070908
APA StyleLieske, C., Leutnant, D., & Uhl, M. (2021). Assessing the TSS Removal Efficiency of Decentralized Stormwater Treatment Systems by Long-Term In-Situ Monitoring. Water, 13(7), 908. https://doi.org/10.3390/w13070908







