Improving Radar-Based Rainfall Forecasts by Long Short-Term Memory Network in Urban Basins
Abstract
1. Introduction
2. Study Area and Data Processing
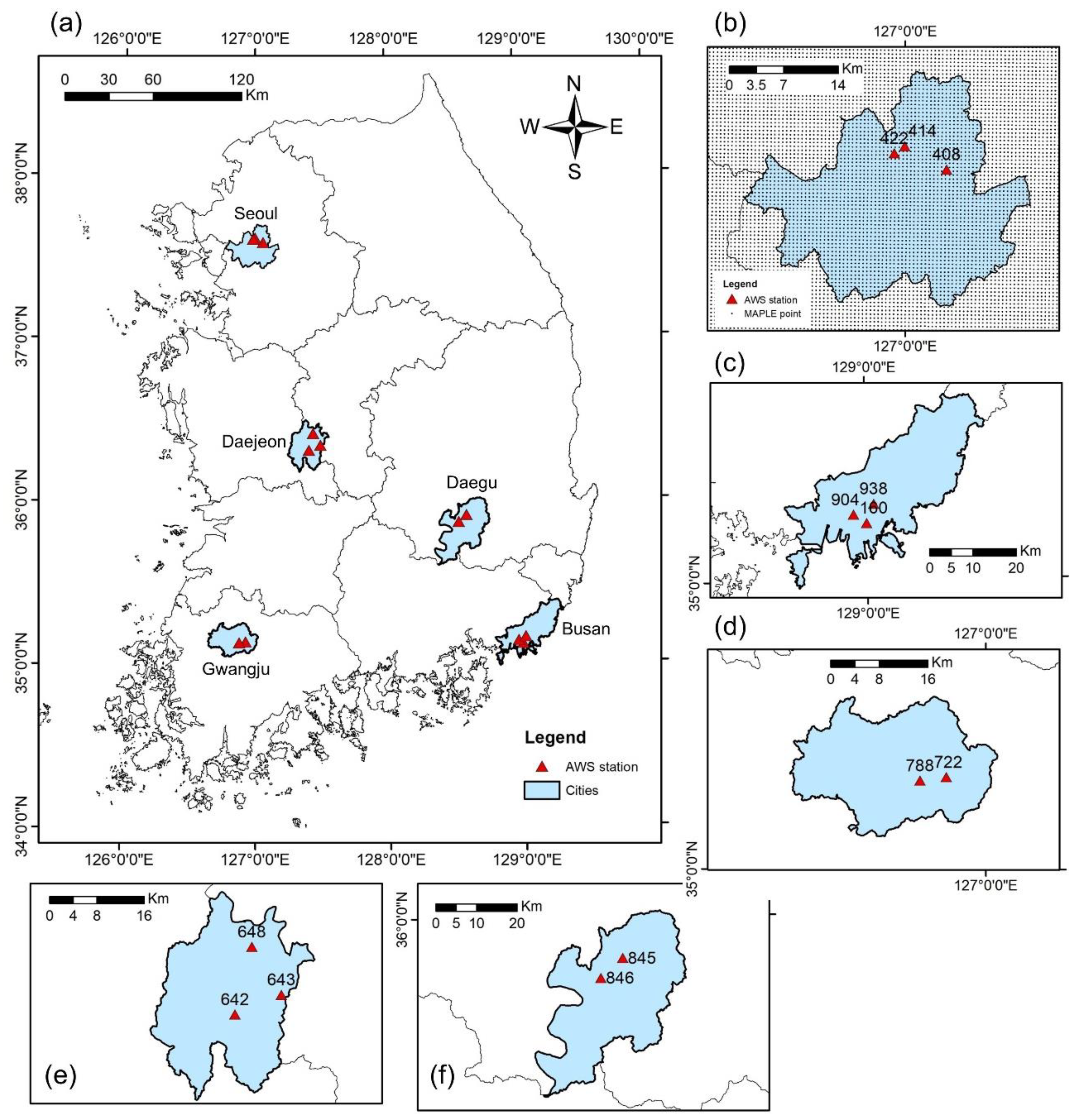
2.1. Study Area
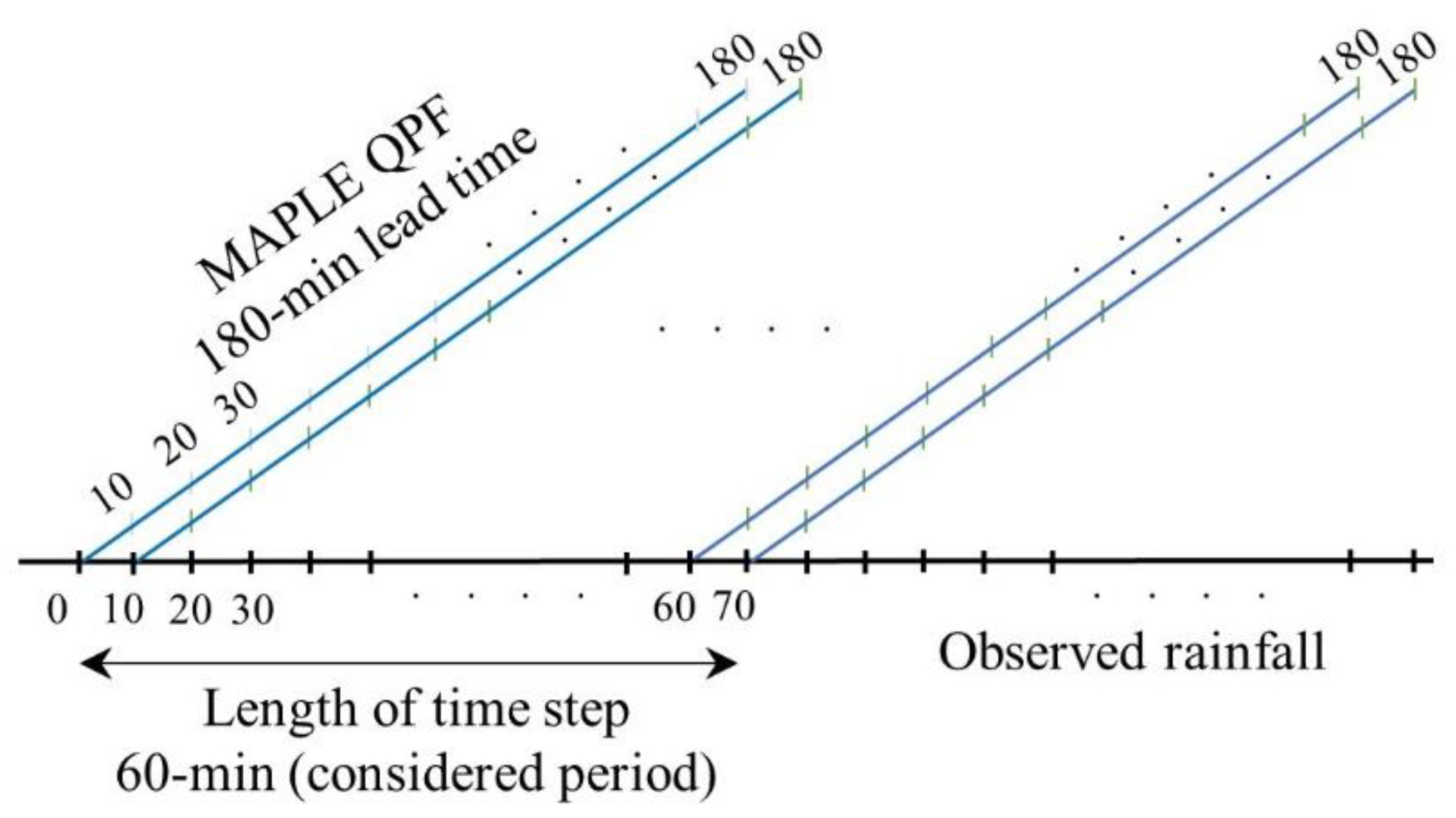
2.2. Data Collection
3. Methodology
3.1. Multivariate Adaptive Regression Splines (MARS)
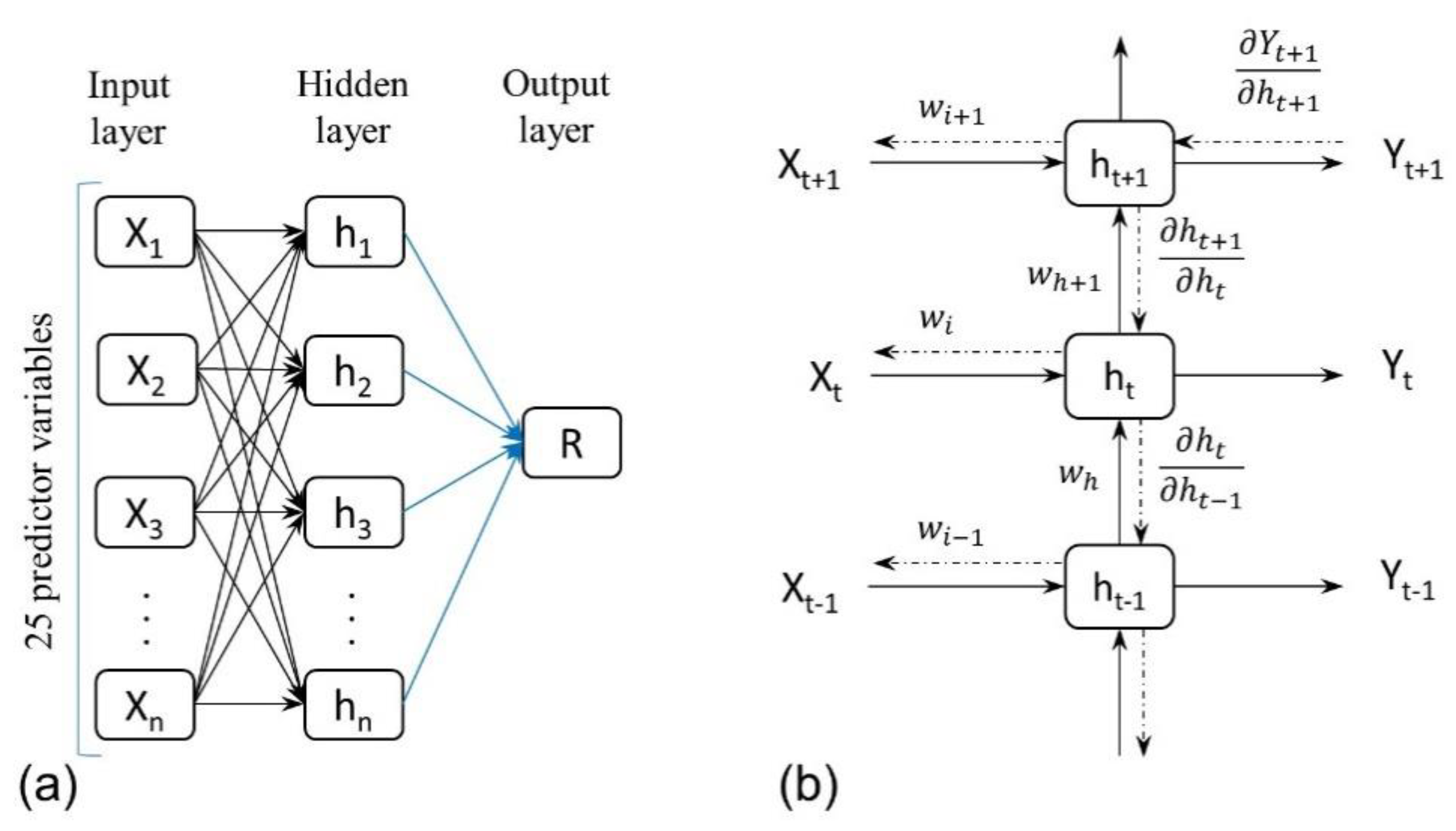
3.2. Multi-Layer Perceptron (MLP)
3.3. Basic RNN and Long-Term Dependencies Problem
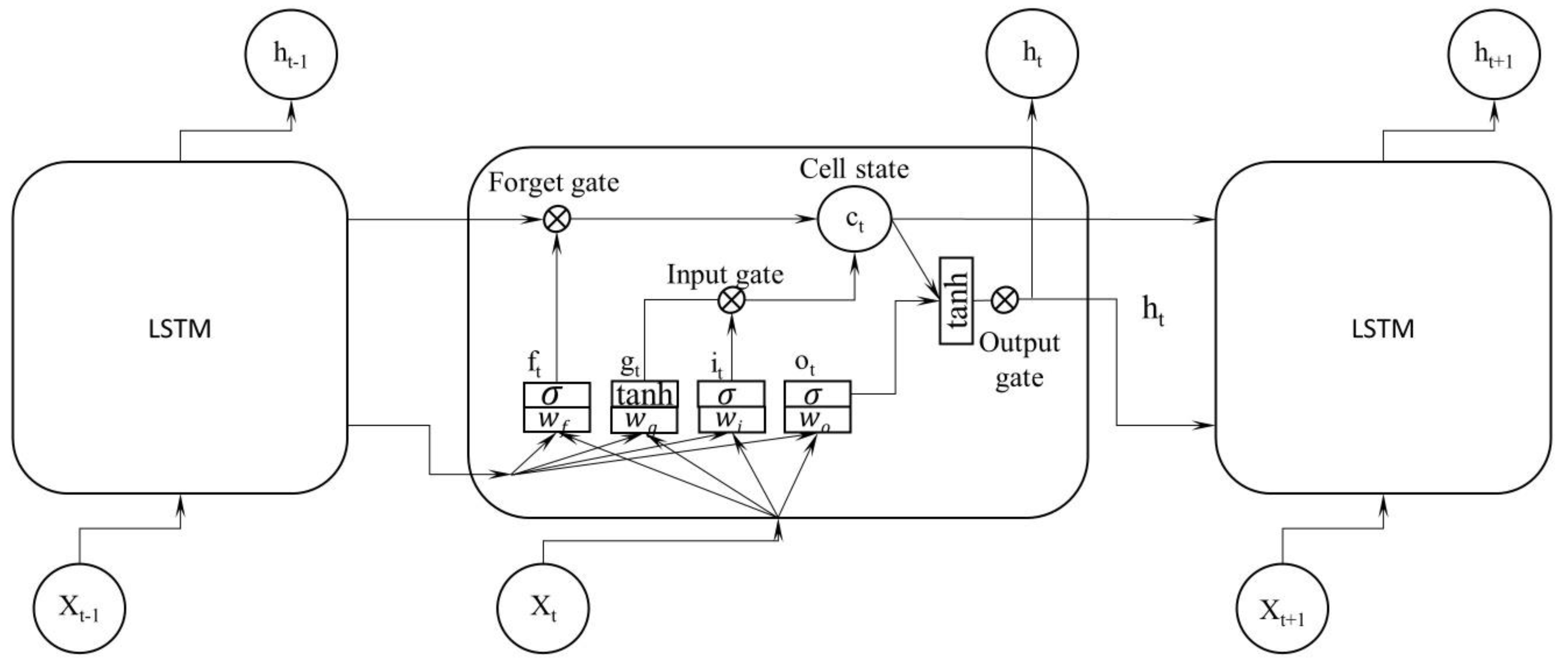
3.4. LSTM Network
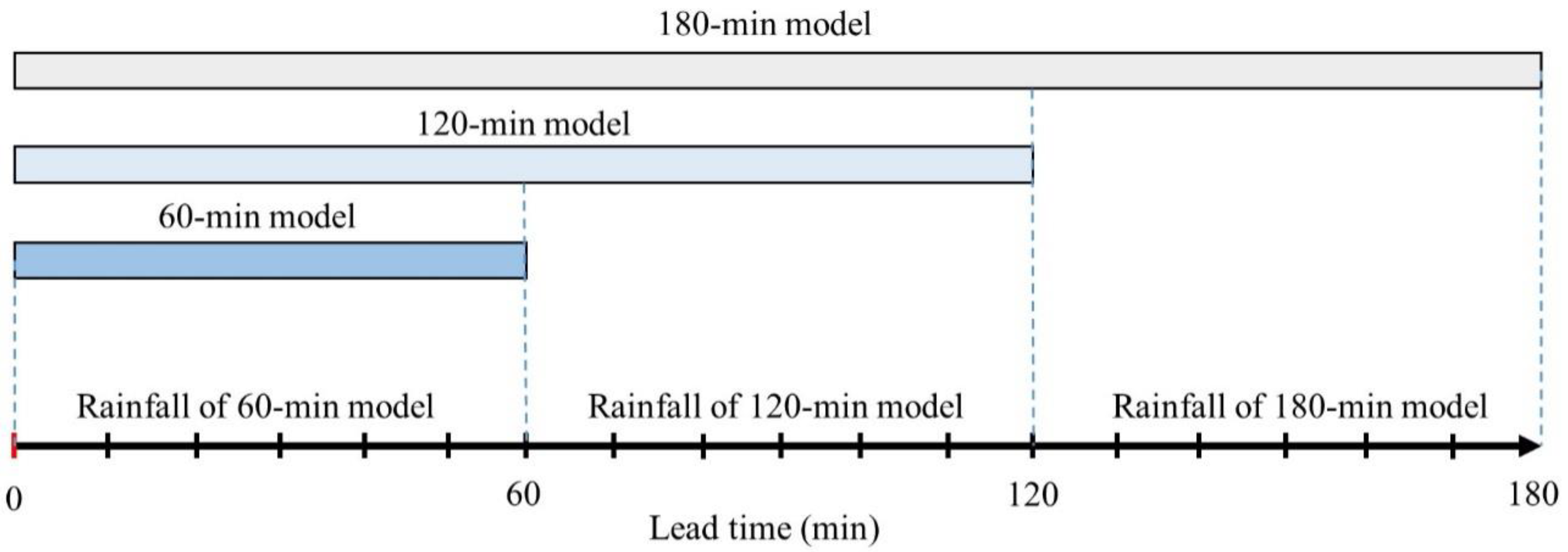
3.5. Training Datasets and Model Implementation
3.6. Model Performance Parameters
4. Results and Discussions
4.1. Training of ANN Models
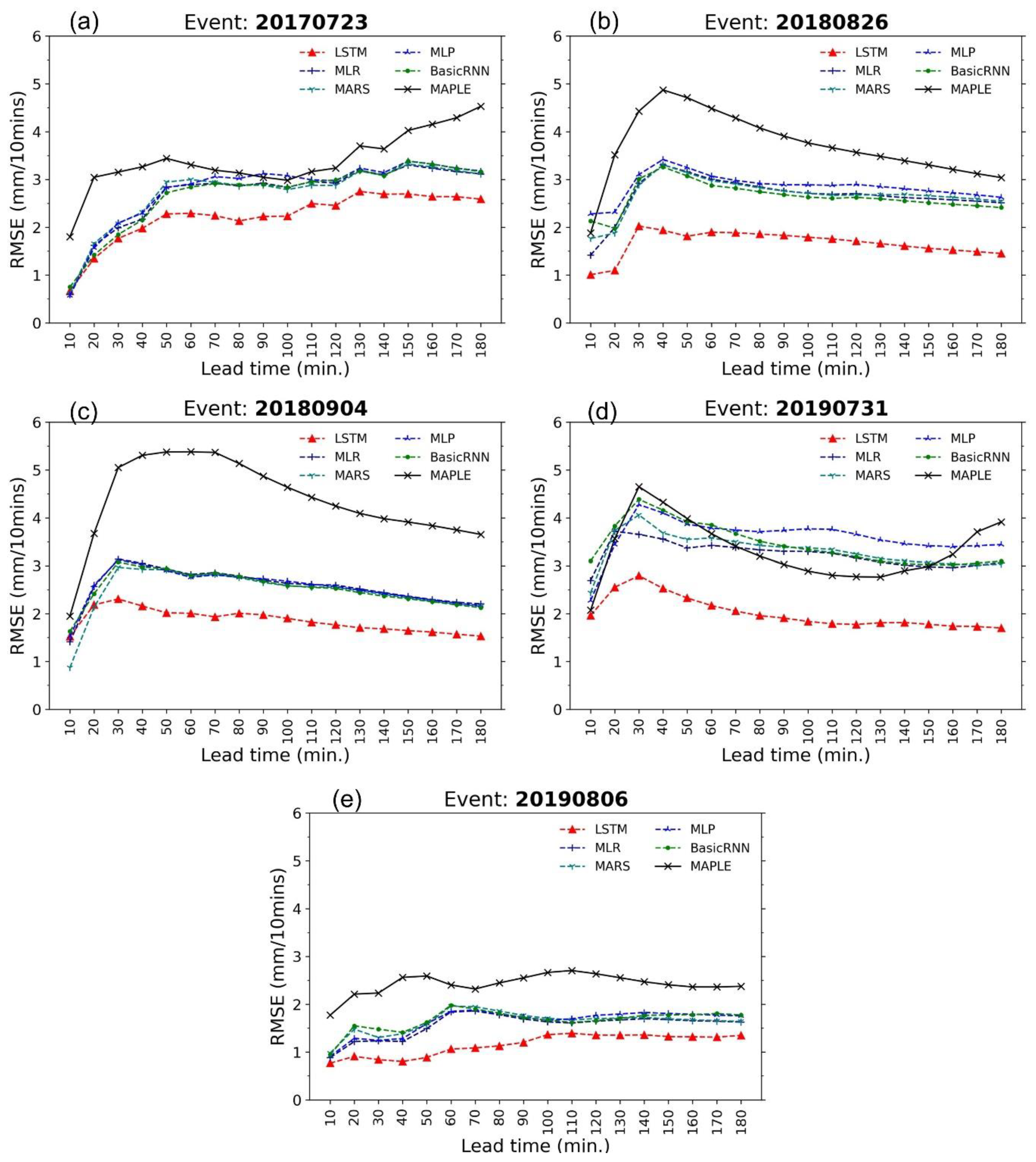
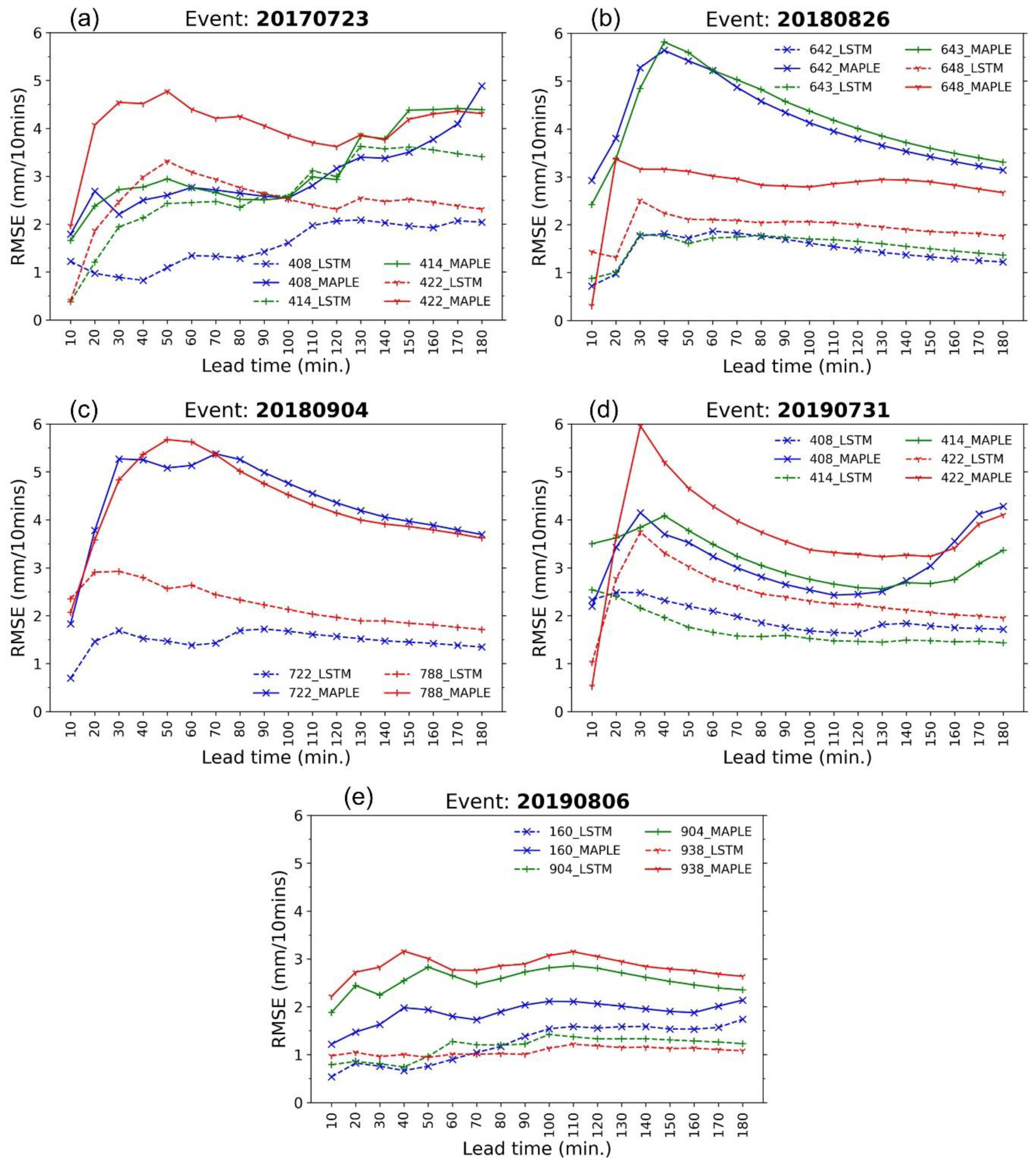
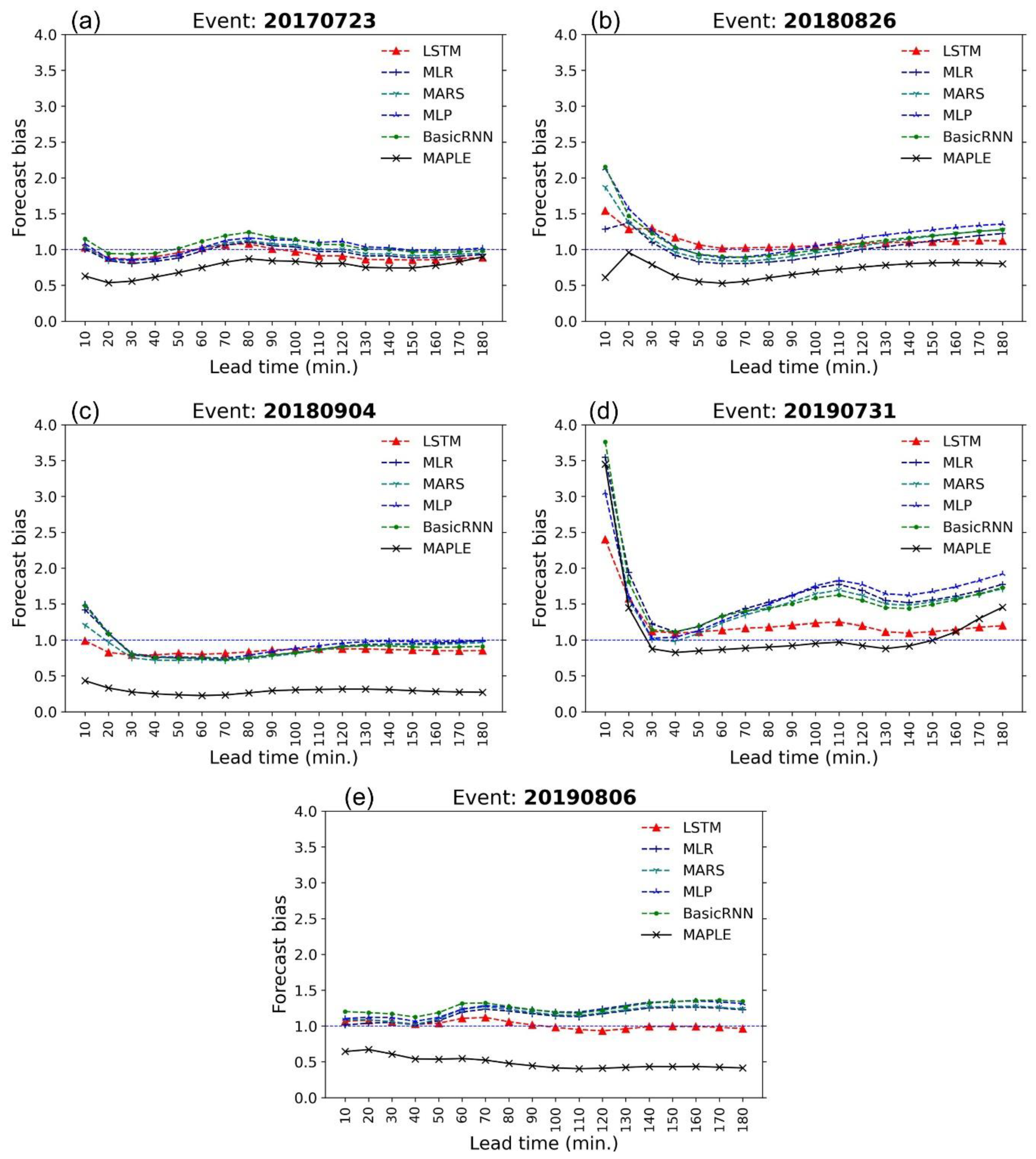
4.2. Performance of Data-Driven Models
5. Conclusions
- (1)
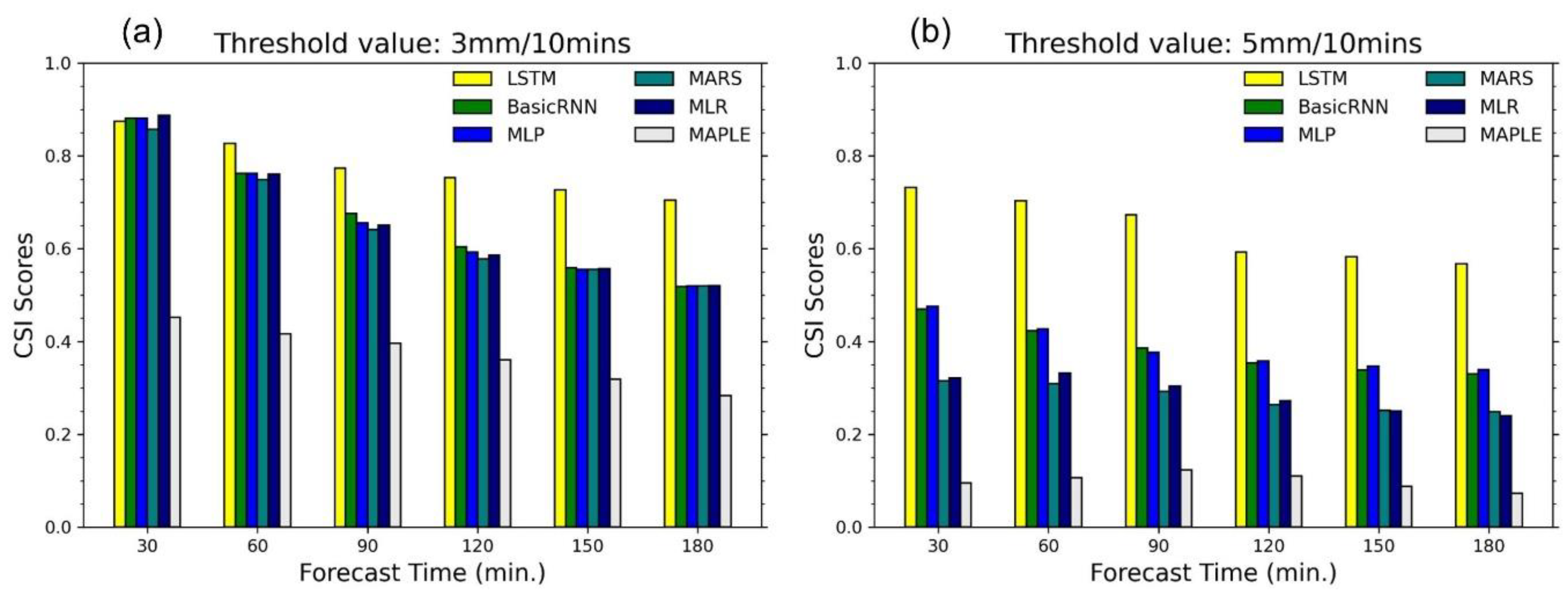
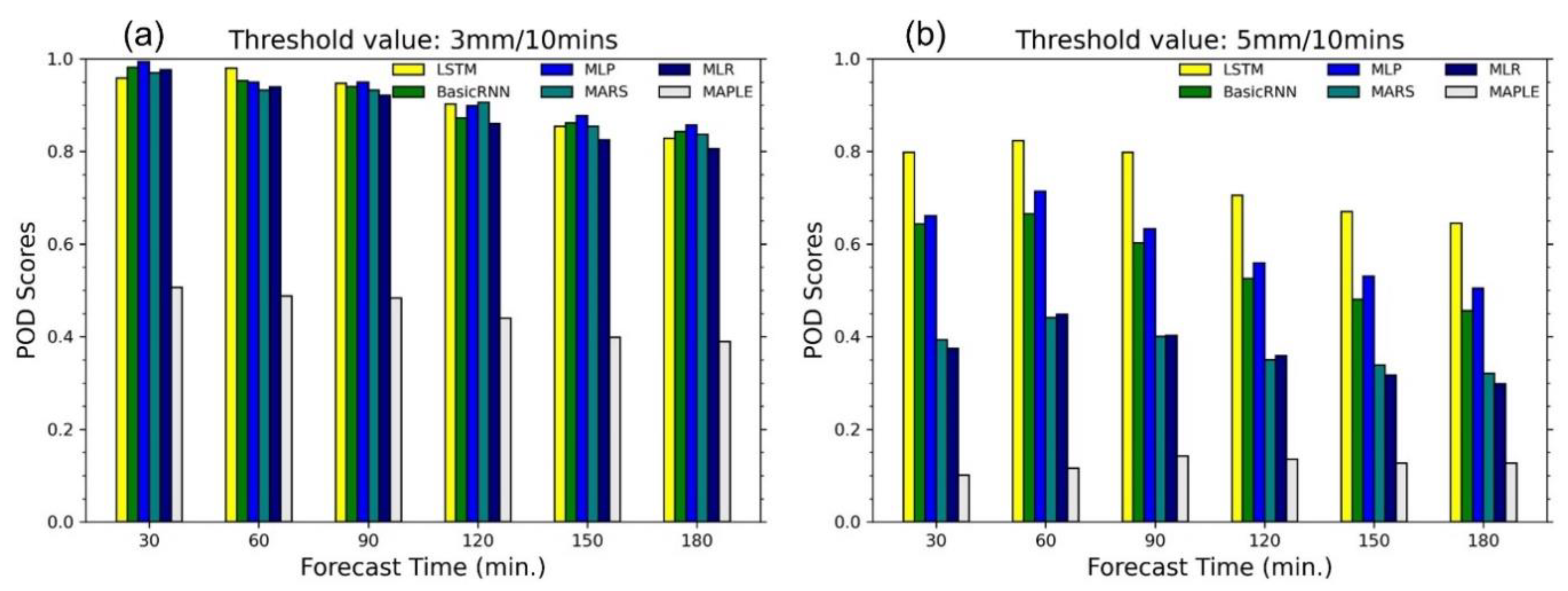
- The models are compared with MAPLE using the RMSE, FB, R, PEMR, CSI, and POD criteria. All of the models were able to improve the rainfall forecasts to a certain extent.
- (2)
- The four models named basic RNN, MLP, MARS, and MLP showed similar corrections for the test events in terms of RMSE and FB performances. However, the basic RNN and MLP can provide better performance in terms of CSI and POD value, which showed substantially higher accuracy for high rainfall predictions.
- (3)
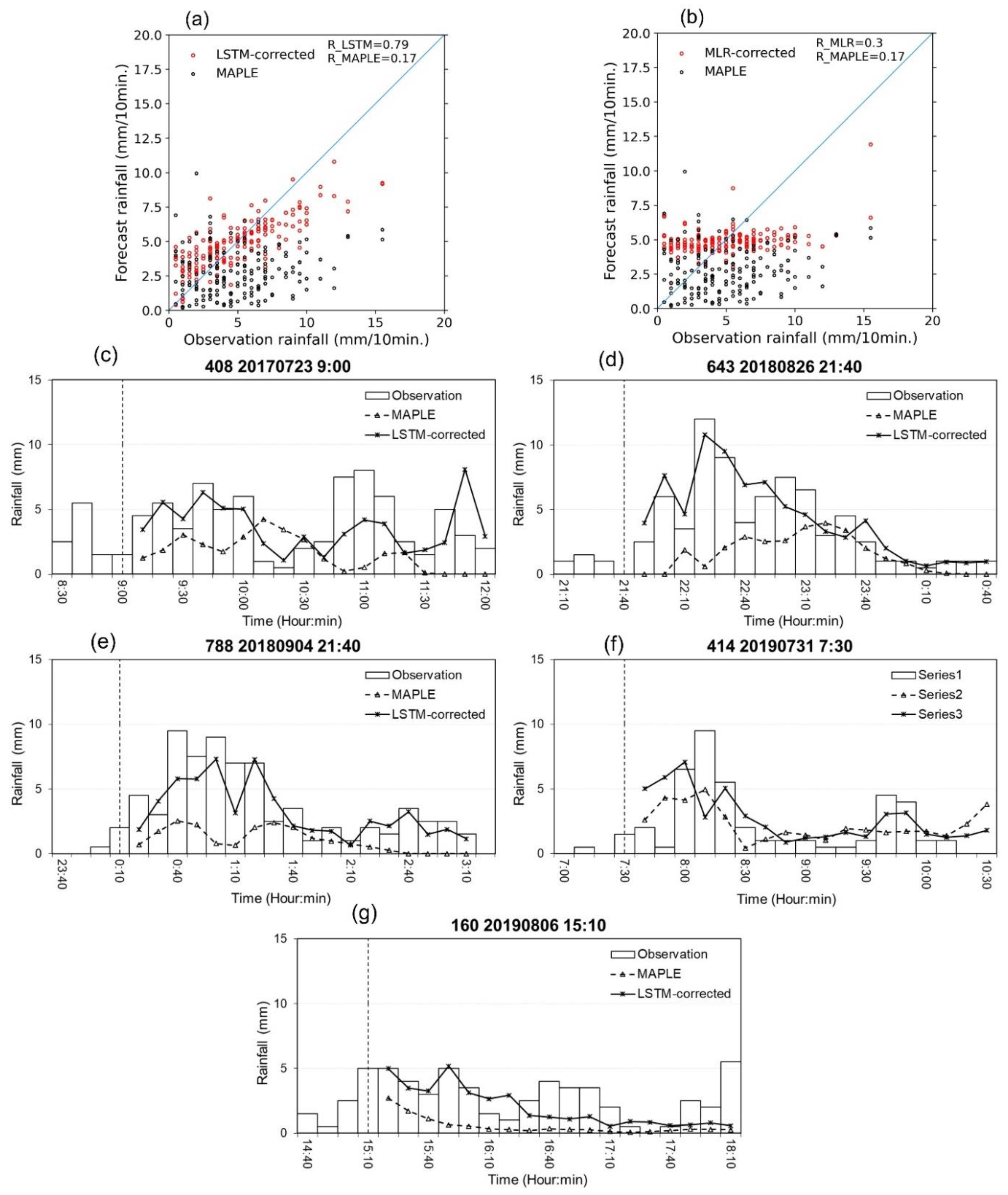
- Because of the gating structures of the neurons, the LSTM outperformed the basic RNN, MLP, MARS, and MLR, especially for predicting high rainfall values, reducing RMSE, and improving forecast bias. The LSTM could reproduce the rainfall forecasts with sufficient accuracy within 60 min forecast time at the stations. This advanced AI technique, therefore, has high practicability for improving rainfall forecasts of the radar-based system. The LSTM model can be considered an optional approach in real practice.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cuo, L.; Pagano, T.C.; Wang, Q.J. A Review of Quantitative Precipitation Forecasts and Their Use in Short- to Medium-Range Streamflow Forecasting. J. Hydrometeorol. 2011, 12, 713–728. [Google Scholar] [CrossRef]
- Chung, K.S.; Yao, I.A. Improving radar echo lagrangian extrapolation nowcasting by blending numerical model wind information: Statistical performance of 16 typhoon cases. Mon. Weather Rev. 2020, 148, 1099–1120. [Google Scholar] [CrossRef]
- Foresti, L.; Sideris, I.V.; Nerini, D.; Beusch, L.E.A.; Germann, U.R.S. Using a 10-year radar archive for nowcasting precipitation growth and decay: A probabilistic machine learning approach. Weather Forecast. 2019, 34, 1547–1569. [Google Scholar] [CrossRef]
- Wang, G.; Yang, J.; Wang, D.; Liu, L. A quantitative comparison of precipitation forecasts between the storm-scale numerical weather prediction model and auto-nowcast system in Jiangsu, China. Atmos. Res. 2016, 181, 1–11. [Google Scholar] [CrossRef]
- Sokol, Z.; Mejsnar, J.; Pop, L.; Bližňák, V. Probabilistic precipitation nowcasting based on an extrapolation of radar reflectivity and an ensemble approach. Atmos. Res. 2017, 194, 245–257. [Google Scholar] [CrossRef]
- Bellon, A.; Zawadzki, I.; Kilambi, A.; Lee, H.C.; Lee, Y.H.; Lee, G. McGill algorithm for precipitation nowcasting by lagrangian extrapolation (MAPLE) applied to the South Korean radar network. Part I: Sensitivity studies of the Variational Echo Tracking (VET) technique. Asia-Pacific J. Atmos. Sci. 2010, 46, 369–381. [Google Scholar] [CrossRef]
- Lee, H.C.; Lee, Y.H.; Ha, J.-C.; Chang, D.-E.; Bellon, A.; Zawadzki, I.; Lee, G. McGill Algorithm for Precipitation Nowcasting by Lagrangian Extrapolation (MAPLE) Applied to the South Korean Radar Network. Part II: Real-Time Verification for the Summer Season. Asia-Pacific J. Atmos. Sci. 2010, 46, 383–391. [Google Scholar] [CrossRef]
- Sokol, Z.; Pesice, P. Nowcasting of precipitation-Advective statistical forecast model (SAM) for the Czech Republic. Atmos. Res. 2012, 103, 70–79. [Google Scholar] [CrossRef]
- Heuvelink, D.; Berenguer, M.; Brauer, C.C.; Uijlenhoet, R. Hydrological application of radar rainfall nowcasting in the Netherlands. Environ. Int. 2020, 136, 105431. [Google Scholar] [CrossRef] [PubMed]
- Atencia, A.; Zawadzki, I. A Comparison of Two Techniques for Generating Nowcasting Ensembles. Part I: Lagrangian Ensemble Technique. Mon. Weather Rev. 2014, 4036–4052. [Google Scholar] [CrossRef]
- He, S.; Raghavan, S.V.; Nguyen, N.S.; Liong, S.Y. Ensemble rainfall forecasting with numerical weather prediction and radar-based nowcasting models. Hydrol. Process. 2013, 27, 1560–1571. [Google Scholar] [CrossRef]
- Seed, A.W.; Pierce, C.E.; Norman, K. Formulation and evaluation of a scale decomposition-based stochastic precipitation nowcast scheme. Water Resour. Res. 2013, 49, 6624–6641. [Google Scholar] [CrossRef]
- Yoon, S.-S. Adaptive Blending Method of Radar-Based and Numerical Weather Prediction QPFs for Urban Flood Forecasting. Remote Sens. 2019, 11, 642. [Google Scholar] [CrossRef]
- Wang, G.; Wong, W.K.; Hong, Y.; Liu, L.; Dong, J.; Xue, M. Improvement of forecast skill for severe weather by merging radar-based extrapolation and storm-scale NWP corrected forecast. Atmos. Res. 2015, 154, 14–24. [Google Scholar] [CrossRef]
- Nguyen, H.M.; Bae, D.H. An approach for improving the capability of a coupled meteorological and hydrological model for rainfall and flood forecasts. J. Hydrol. 2019, 577, 124014. [Google Scholar] [CrossRef]
- Wong, W.K.; Yeung, L.; Wang, Y.C.; Chen, M.X. Towards the blending of NWP with nowcast: Operation experience in B08FDP. In Proceedings of the World Weather Research Program Symposium on Nowcasting, Whistler, BC, Canada, 30 August–4 September 2009. [Google Scholar]
- Wilson, J.; Xu, M. Experiments in blending radar echo extrapolation and NWP for nowcasting convective storms. In Proceedings of the Fourth European Conference on Radar in Meteorology and Hydrology, Barcelona, Spain, 18–22 September 2006; pp. 519–522. [Google Scholar]
- Kober, K.; Craig, G.C.; Keil, C.; Dörnbrack, A. Blending a probabilistic nowcasting method with a high-resolution numerical weather prediction ensemble for convective precipitation forecasts. Q. J. R. Meteorol. Soc. 2012, 138, 755–768. [Google Scholar] [CrossRef]
- Dai, Q.; Rico-Ramirez, M.A.; Han, D.; Islam, T.; Liguori, S. Probabilistic radar rainfall nowcasts using empirical and theoretical uncertainty models. Hydrol. Process. 2015, 29, 66–79. [Google Scholar] [CrossRef]
- Sokol, Z. Utilization of regression models for rainfall estimates using radar-derived rainfall data and rain gauge data. J. Hydrol. 2003, 278, 144–152. [Google Scholar] [CrossRef]
- Tien Bui, D.; Hoang, N.D.; Pham, T.D.; Ngo, P.T.T.; Hoa, P.V.; Minh, N.Q.; Tran, X.T.; Samui, P. A new intelligence approach based on GIS-based Multivariate Adaptive Regression Splines and metaheuristic optimization for predicting flash flood susceptible areas at high-frequency tropical typhoon area. J. Hydrol. 2019, 575, 314–326. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Heddam, S.; Zounemat-Kermani, M.; Kisi, O.; Li, B. Least square support vector machine and multivariate adaptive regression splines for streamflow prediction in mountainous basin using hydro-meteorological data as inputs. J. Hydrol. 2019, 124371. [Google Scholar] [CrossRef]
- Chiang, Y.M.; Chang, F.J.; Jou, B.J.D.; Lin, P.F. Dynamic ANN for precipitation estimation and forecasting from radar observations. J. Hydrol. 2007, 334, 250–261. [Google Scholar] [CrossRef]
- Foresti, L.; Kanevski, M.; Pozdnoukhov, A. Kernel-Based Mapping of Orographic Rainfall Enhancement in the Swiss Alps as Detected by Weather Radar. IEEE Trans. Geosci. Remote. Sens. 2012, 50, 2954–2967. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Kisi, O.; Singh, V.P. Daily water level forecasting using wavelet decomposition and artificial intelligence techniques. J. Hydrol. 2015, 520, 224–243. [Google Scholar] [CrossRef]
- Zadeh, M.R.; Amin, S.; Khalili, D.; Singh, V.P. Daily Outflow Prediction by Multi Layer Perceptron with Logistic Sigmoid and Tangent Sigmoid Activation Functions. Water Resour. Manag. 2010, 24, 2673–2688. [Google Scholar] [CrossRef]
- Lin, G.F.; Chen, L.H. Application of an artificial neural network to typhoon rainfall forecasting. Hydrol. Process. 2005, 19, 1825–1837. [Google Scholar] [CrossRef]
- Lin, G.; Wu, M. A hybrid neural network model for typhoon-rainfall forecasting. J. Hydrol. 2009, 375, 450–458. [Google Scholar] [CrossRef]
- Karamouz, M.; Razavi, S.; Araghinejad, S. Long-lead seasonal rainfall forecasting using time-delay recurrent neural networks: A case study. Hydrol. Process. 2008, 241, 229–241. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A Critical Review of Recurrent Neural Networks for Sequence Learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Zaytar, M.A.; Amrani, C. El Sequence to Sequence Weather Forecasting with Long Short-Term Memory Recurrent Neural Networks. Int. J. Comput. Appl. 2016, 143, 7–11. [Google Scholar] [CrossRef]
- Zhang, D.; Lindholm, G.; Ratnaweera, H. Use long short-term memory to enhance Internet of Things for combined sewer overflow monitoring. J. Hydrol. 2018, 556, 409–418. [Google Scholar] [CrossRef]
- Asanjan, A.A.; Yang, T. Short-Term Precipitation Forecast Based on the PERSIANN System and LSTM Recurrent Neural Networks. J. Geophys. Res. Atmos. 2018, 543–563. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep Learning with a Long Short-Term Memory Networks Approach for Rainfall-Runoff Simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Zhang, C.J.; Zeng, J.; Wang, H.Y.; Ma, L.M.; Chu, H. Correction model for rainfall forecasts using the LSTM with multiple meteorological factors. Meteorol. Appl. 2020, 27, 1–15. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Bae, D.H. Correcting mean areal precipitation forecasts to improve urban flooding predictions by using long short-term memory network. J. Hydrol. 2020, 584, 124710. [Google Scholar] [CrossRef]
- Swain, M.; Pattanayak, S.; Mohanty, U.C. Characteristics of occurrence of heavy rainfall events over Odisha during summer monsoon season. Dyn. Atmos. Ocean. 2018, 82, 107–118. [Google Scholar] [CrossRef]
- Salack, S.; Saley, I.A.; Lawson, N.Z.; Zabré, I.; Daku, E.K. Scales for rating heavy rainfall events in the West African Sahel. Weather Clim. Extrem. 2018, 21, 36–42. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Borga, M.; Creutin, J.D.; Marra, F. Estimation of debris flow triggering rainfall: Influence of rain gauge density and interpolation methods. Geomorphology 2015, 243, 40–50. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Emamgolizadeh, S.; Bateni, S.M.; Shahsavani, D.; Ashrafi, T.; Ghorbani, H. Estimation of soil cation exchange capacity using Genetic Expression Programming (GEP) and Multivariate Adaptive Regression Splines (MARS). J. Hydrol. 2015, 529, 1590–1600. [Google Scholar] [CrossRef]
- Ishak, S.; Kotha, P.; Alecsandru, C. Optimization of Dynamic Neural Network Performance for Short-Term Traffic Prediction. Transp. Res. Rec. J. Transp. Res. Board 2003, 1836, 45–56. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Hoogi, A.; Mishra, A.; Gimenez, F.; Dong, J.; Rubin, D. Natural Language Generation Model for Mammography Reports Simulation. IEEE J. Biomed. Health Inform. 2020, 24, 2711–2717. [Google Scholar] [CrossRef]
- Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- van der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- Pedregosa, F.; Weiss, R.; Brucher, M. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
| Acronym | Explanation |
|---|---|
| MAPLE | The McGill Algorithm for Precipitation nowcasting by Lagrangian Extrapolation system |
| KMA | The Korean Meteorological Administration |
| AWS | The Automatic Weather System operated by KMA |
| HRFCO | The Han River Flood Control Office |
| QPF | Quantitative precipitation forecasts |
| ANN | Artificial neural network |
| MLR | Multiple linear regression model |
| MLP | Multi-layer perceptron model |
| MARS | Multivariate adaptive regression splines model |
| RNN | Recurrent neural network model |
| LSTM | Long Short-Term Memory model |
| BP | The backpropagation technique |
| BPTT | The backpropagation through time technique |
| X | Model input that includes twenty-five predictor variables (mm/10 min) |
| No. | Event | Duration (hour:min) | Maximum Rainfall in AWS Stations (mm/10 min) | City | Configuration |
|---|---|---|---|---|---|
| 1 | 20160701 | 19:00–22:30 | 8.5 | Seoul | Training and Validation |
| 2 | 20160704 | 1:00–7:00 | 16.0 | Busan | |
| 3 | 20160705 | 8:00–11:00 | 18.5 | Seoul | |
| 4 | 20160729 | 6:00–9:00 | 13.5 | Seoul | |
| 5 | 20170702 | 21:00–2:00 | 15.5 | Seoul | |
| 6 | 20170710 | 19:00–23:00 | 13.5 | Seoul | |
| 7 | 20170715 | 3:00–7:00 | 12.5 | Seoul | |
| 8 | 20170815 | 9:00–16:00 | 8.0 | Seoul | |
| 9 | 20170820 | 21:00–24:00 | 12.5 | Seoul | |
| 10 | 20170825 | 4:00–7:00 | 15.0 | Gwangju | |
| 11 | 20180628 | 4:00–16:00 | 8.5 | Busan | |
| 12 | 20180810a | 2:00–8:00 | 11.0 | Daegu | |
| 13 | 20180810b | 18:00–22:00 | 15.0 | Gwangju | |
| 14 | 20180827 | 9:00–16:00 | 15.5 | Gwangju | |
| 15 | 20180828 | 15:30–21:30 | 17.5 | Seoul | |
| 16 | 20180829 | 16:00–7:00 | 9.0 | Seoul | |
| 17 | 20180831 | 9:00–12:00 | 19.0 | Gwangju | |
| 18 | 20190720 | 1:00–18:00 | 8.0 | Busan | |
| 19 | 20190726 | 6:00–13:00 | 7.5 | Seoul | |
| 20 | 20190804 | 17:00–19:00 | 14.0 | Seoul | |
| 21 | 20200610 | 22:00–3:00 | 8.5 | Daejeon | |
| 22 | 20200629 | 16:00–2:00 | 7.0 | Busan | |
| 23 | 20170723 | 7:00–12:00 | 13.5 | Seoul | Test |
| 24 | 20180826 | 17:00–1:00 | 12.0 | Daejeon | |
| 25 | 20180904 | 0:00–4:00 | 10.0 | Gwangju | |
| 26 | 20190731 | 6:00–10:30 | 15.5 | Seoul | |
| 27 | 20190806 | 14:00–21:00 | 6.5 | Busan |
| Event | Station | Model | 10 min | 20 min | 30 min | 60 min | 90 min | 120 min |
|---|---|---|---|---|---|---|---|---|
| 20170723 | 408 | LSTM | 0.811 | 0.92 | 0.89 | 0.93 | 0.60 | 0.51 |
| MAPLE | 0.01 | 0.41 | 0.31 | 0.47 | −0.05 | −0.06 | ||
| 414 | LSTM | 0.996 | 0.81 | 0.47 | 0.45 | 0.24 | 0.29 | |
| MAPLE | 0.68 | 0.22 | 0.08 | 0.34 | 0.47 | 0.08 | ||
| 422 | LSTM | 0.994 | 0.81 | 0.80 | 0.86 | 0.87 | 0.82 | |
| MAPLE | 0.52 | −0.12 | −0.15 | 0.57 | 0.48 | 0.27 | ||
| 20180826 | 642 | LSTM | 0.98 | 0.97 | 0.97 | 0.95 | 0.92 | 0.94 |
| MAPLE | 0.83 | 0.60 | 0.59 | 0.58 | 0.30 | 0.48 | ||
| 643 | LSTM | 0.99 | 0.99 | 0.98 | 0.95 | 0.92 | 0.90 | |
| MAPLE | 0.85 | 0.62 | 0.48 | 0.65 | 0.51 | 0.47 | ||
| 648 | LSTM | 0.35 | 0.65 | 0.93 | 0.62 | 0.61 | 0.65 | |
| MAPLE | 0.99 | 0.89 | 0.83 | 0.43 | 0.24 | 0.11 | ||
| 20180904 | 722 | LSTM | 0.98 | 0.91 | 0.97 | 0.96 | 0.87 | 0.87 |
| MAPLE | 0.50 | 0.33 | 0.62 | 0.42 | 0.12 | 0.25 | ||
| 788 | LSTM | 0.53 | 0.32 | 0.69 | 0.74 | 0.78 | 0.83 | |
| MAPLE | 0.07 | −0.18 | 0.29 | −0.03 | −0.12 | 0.20 | ||
| 20190731 | 408 | LSTM | 0.93 | 0.90 | 0.78 | 0.80 | 0.80 | 0.80 |
| MAPLE | 0.94 | 0.63 | 0.18 | 0.29 | 0.38 | 0.39 | ||
| 414 | LSTM | 0.04 | 0.73 | 0.87 | 0.90 | 0.91 | 0.91 | |
| MAPLE | 0.03 | 0.28 | 0.31 | 0.39 | 0.46 | 0.47 | ||
| 422 | LSTM | 0.98 | 0.99 | 0.95 | 0.92 | 0.92 | 0.91 | |
| MAPLE | 0.998 | 0.81 | 0.68 | 0.69 | 0.73 | 0.70 | ||
| 20190806 | 160 | LSTM | 0.01 | 0.90 | 0.82 | 0.92 | 0.58 | 0.60 |
| MAPLE | 0.78 | 0.73 | 0.48 | 0.67 | 0.59 | 0.59 | ||
| 904 | LSTM | 0.98 | 0.87 | 0.84 | 0.77 | 0.71 | 0.67 | |
| MAPLE | 0.48 | −0.04 | −0.04 | 0.18 | 0.13 | 0.11 | ||
| 938 | LSTM | 0.99 | 0.85 | 0.88 | 0.91 | 0.83 | 0.74 | |
| MAPLE | 0.75 | 0.37 | −0.18 | 0.32 | 0.25 | 0.20 |
| Event | Station | PEMR (%) | |||||
|---|---|---|---|---|---|---|---|
| MLR | MARS | MLP | RNN | LSTM | MAPLE | ||
| 20170723 | 408 | −33.5 | −28.1 | −13.9 | −26.8 | 1.3 | 140.7 |
| 414 | −50.5 | −57.2 | −45.0 | −54.5 | −40.5 | −43.7 | |
| 422 | −54.7 | −55.5 | −42.8 | −52.4 | −39.4 | −36.3 | |
| 20180826 | 642 | −50.8 | −50.2 | −46.2 | −46.4 | −18.5 | −51.9 |
| 643 | −51.6 | −54.1 | −56.8 | −51.6 | −10.2 | −60.8 | |
| 648 | −12.1 | −23.2 | −27.6 | −10.2 | 16.0 | 42.0 | |
| 20180904 | 722 | −47.3 | −45.9 | −48.8 | −46.1 | −26.0 | −75.8 |
| 788 | −44.9 | −40.2 | −47.0 | −39.4 | −23.1 | −61.2 | |
| 20190731 | 408 | −34.9 | −18.4 | −34.8 | −24.4 | −16.7 | 77.1 |
| 414 | −28.8 | −35.0 | 3.8 | −32.4 | −17.5 | 2.9 | |
| 422 | −23.1 | −46.1 | −47.2 | −59.9 | −40.4 | −15.9 | |
| 20190806 | 160 | −7.0 | −3.1 | −8.5 | 6.8 | 8.2 | −24.7 |
| 904 | −21.4 | −17.8 | −22.5 | −11.2 | 16.3 | −34.6 | |
| 938 | −24.5 | −17.8 | −22.5 | −8.5 | −9.3 | −37.0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, D.H.; Kim, J.-B.; Bae, D.-H. Improving Radar-Based Rainfall Forecasts by Long Short-Term Memory Network in Urban Basins. Water 2021, 13, 776. https://doi.org/10.3390/w13060776
Nguyen DH, Kim J-B, Bae D-H. Improving Radar-Based Rainfall Forecasts by Long Short-Term Memory Network in Urban Basins. Water. 2021; 13(6):776. https://doi.org/10.3390/w13060776
Chicago/Turabian StyleNguyen, Duc Hai, Jeong-Bae Kim, and Deg-Hyo Bae. 2021. "Improving Radar-Based Rainfall Forecasts by Long Short-Term Memory Network in Urban Basins" Water 13, no. 6: 776. https://doi.org/10.3390/w13060776
APA StyleNguyen, D. H., Kim, J.-B., & Bae, D.-H. (2021). Improving Radar-Based Rainfall Forecasts by Long Short-Term Memory Network in Urban Basins. Water, 13(6), 776. https://doi.org/10.3390/w13060776






