Abstract
Process-based models are commonly used to design management strategies to reduce excessive algal growth and subsequent hypoxia. However, management targets typically focus on phosphorus control, under the assumption that successful nutrient reduction will solve hypoxia issues. Algal responses to nutrient drivers are not linear and depend on additional biotic and abiotic controls. In order to generate a comprehensive assessment of the effectiveness of nutrient control strategies, independent nutrient, dissolved oxygen (DO), temperature and algal models must be coupled, which can increase overall uncertainty. Here, we extend an existing process-based phosphorus model (INtegrated CAtchment model of Phosphorus dynamics) to include biological oxygen demand (BOD), dissolved oxygen (DO) and algal growth and decay (INCA-PEco). We applied the resultant model in two eutrophied mesoscale catchments with continental and maritime climates. We assessed effects of regional differences in climate and land use on parameter importance during calibration using a generalised sensitivity analysis. We successfully reproduced in-stream total phosphorus (TP), suspended sediment, DO, BOD and chlorophyll-a (chl-a) concentrations across a range of temporal scales, land uses and climate regimes. While INCA-PEco is highly parameterized, model uncertainty can be significantly reduced by focusing calibration and monitoring efforts on just 18 of those parameters. Specifically, calibration time could be optimized by focusing on hydrological parameters (base flow, Manning’s n and river depth). In locations with significant inputs of diffuse nutrients, e.g., in agricultural catchments, detailed data on crop growth and nutrient uptake rates are also important. The remaining parameters provide flexibility to the user, broaden model applicability, and maximize its functionality under a changing climate.
1. Introduction
Low dissolved oxygen (hypoxia) in rivers and lakes has been an increasing global concern since the 1980s. Hypoxia occurs within a water body, where oxygen consumption during aerobic decomposition of organic matter (i.e., biological oxygen demand, or BOD) exceeds re-aeration [1]). This can be triggered by excess nutrient availability supporting high rates of vegetation growth and decay; wastewater discharge; high water temperatures; or slow rates of water movement. Nutrient management has been a primary method of hypoxia control, where reductions in phosphorus (P) loading have been found to be particularly effective in many riverine systems, attributable to its control over phytoplankton growth [2].
Current global trends of increasing air and water temperatures, excessive fertilizer use, extreme drought events, and rising human populations are significant concerns for hypoxia management, as each have the potential to increase BOD within rivers [3] and lakes [4]. The ability to identify regions particularly susceptible to hypoxia, and to develop and apply management strategies which are sustainable under future climate and land use change, is essential for the protection of aquatic ecosystems. Tracking these drivers and responses across catchments quickly becomes complex, however. Nutrients and organic matter originate from both end-of-pipe (e.g., sewage and stormwater outflows) and diffuse sources; the latter of which might include atmospheric deposition, fertilizer application, plant decay, and septic system discharge. Transport of nutrients and organic matter to receiving waters differs across soil and land use types [5], by season and even during individual rainfall events [6]. Interactions between P, BOD and DO along flow pathways add to this complexity.
Process based models are commonly used to design and implement management strategies for such complex systems. Although the aim of these strategies is to reduce hypoxia or algal growth, management targets are frequently designed around nutrient control, most frequently P. It is typically assumed that solutions to hypoxia and algal blooms will also follow suit. Research demonstrates, however, that algal responses to nutrient drivers vary both spatially and temporally, depending on additional biotic and abiotic controls [7]. As riverine nutrient models are rarely designed to simulate algal responses [8], and as comprehensive phytoplankton models are commonly focused on the waterbody component with a disconnect from terrestrial processes (e.g., QUAL2K [9]; PROTECH [10]), then in order to generate a comprehensive assessment of the effectiveness of nutrient control strategies, nutrient models must often be coupled to independent DO, temperature and algal models [11].
This method of linking disparate models can however result in the forward propagation of uncertainty [12], which can become particularly large where the linked models are dissimilar in spatial and temporal scale [13]. Research has shown that as a result, models used in combination are often unable to simulate chemical and ecological processes at a comparable level of detail as they could in isolation, e.g., where linked sewer network and river quality models are unable to simulate seasonal variability in DO concentrations and water quality status [12]. By integrating chemical and ecological processes into a single model with identical spatial and temporal resolution, this ‘explosion’ of uncertainty can be avoided.
Despite the regular use of models in environmental decision-making [13] there are few catchment scale modelling tools available which offer managers the capacity to simulate nutrient reduction strategies across the terrestrial (urban and rural) and aquatic environment, and evaluate the ecological results using a more systems scale approach. A model’s ability to meet management goals is of course dependent upon the context to which it is applied [14], however as eutrophication problems increase, the call for integrated catchment scale biochemical models is growing.
The objectives of this study were (1) to address the research gap associated with systems modelling, by elaborating an existing process-based phosphorus model (INCA-P) to simulate BOD, DO and algal growth and decay; (2) to use Generalized Sensitivity Analysis (GSA) for identification of the most sensitive model parameters which should be constrained by field measurements; (3) to identify how regional differences in model application affect parameter importance during calibration.
2. Methods
The dynamic process based INtegrated CAtchment model of Phosphorus dynamics (INCA-P) has been applied to over 40 catchments across Europe, North America and Asia. Originally described in Wade et al. [15] the model can simulate fully branched river networks, with an unlimited number of tributaries and stream orders. The model simulates P pools and fluxes through subcatchments comprised of different land use types, to networks of multiple reaches and tributaries. A full mass balance is imposed at each level. Until recently, INCA-P was limited to simulating flows of water, nutrients and sediment [16]. In this study, a new model named INCA-Phosphorus Ecology (INCA-PEco), expands the utility of INCA-P to include dissolved oxygen (DO), biological oxygen demand (BOD), and in-stream phytoplankton concentrations (chl-a) through the integration of new process-based equations.
INCA is a semi-distributed process-based model, meaning it can be calibrated independently to observations made in different land uses, subcatchments and river reaches [17]. The flexibility that this affords is a significant advantage when applying models under such different conditions, where plausibility of parameter values chosen can be constrained by expert judgement, literature values and field observations. With over 280 parameters within the INCA suite of models however, calibration can be time consuming, and if the resolution of monitoring data is low, then where parameters are highly sensitive, model uncertainty can be high [18]. It is therefore essential to identify and prioritize parameters which have the greatest impact on model output. A complete sensitivity analysis (SA) has not previously been carried out on INCA-P, and to this end a SA of the models is conducted below.
2.1. Model Development
INCA-P includes both land and water phases (Figure 1), within which inputs, transport and storage of water, nutrients and sediment are simulated. In INCA-PEco dissolved oxygen (DO) and biological oxygen demand (BOD) have been added to both of these phases, and phytoplankton growth added to the in-stream water phase.
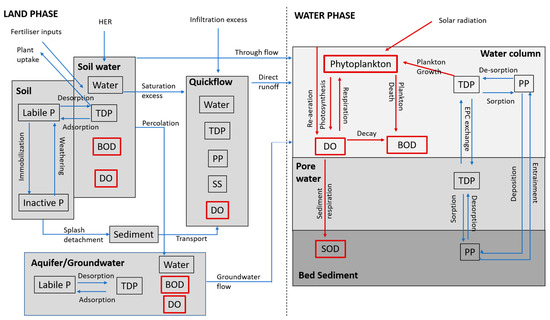
Figure 1.
Conceptual diagram of the functionality of the INCA-PEco model (adapted from Jackson-Blake et al. (2016)). Boxes in red indicate new processes and variables added to INCA-P to create INCA-PEco.
Within the land phase there are three primary stores of water and nutrients; soil water (SW), quickflow (QF) and groundwater (GW). Nutrients and oxygen move between these stores via quickflow, saturation excess flow and percolation; and ultimately are transported to the water phase via throughflow, direct runoff and groundwater flow. Once in the water phase, nutrients and DO are influenced by solar radiation, water temperature and hydrology to support phytoplankton growth, which in turn acts as an additional control on BOD. Processes occurring in upstream and tributary catchments influence those downstream, in a semi-distributed setup. An unlimited number of land uses, subcatchments and tributaries can be modelled, facilitating the simulation of catchment dynamics at any scale desired by the user. A full description of all equations contained within INCA-PEco is documented within SI 1, and only a summary of the new equations is provided here. Units for all parameters are listed in Table SI 2.
2.1.1. Terrestrial Phase
BOD and DO are simulated as user-defined constants in the land phase (soilwater, groundwater and quickflow boxes) which are subsequently adjusted by temporal variations in water volumes within the respective flow pathways. BOD can also be input through fertiliser additions, and adjusted via user specified decay rates. BOD and DO from the land phase are output to river reaches as a ‘starting point’ for processing in the water column, and are important for catchment mass balance purposes.
Soil water
Calculations for the change in water flow within the soil water (QSW_out) and the total soil water volume (VSW) are detailed in SI 1.1.1. For each land use category, the user enters an initial soil water BOD concentration (mg/L). The soil water BOD concentration can be reduced by a user-specified daily decay rate (RSW_BODdecay), or increased through terrestrial inputs of organic material, e.g., manure and plant residue (RBODfert) at user specified times and durations throughout the year. Change in soil water BOD mass (MBOD_SW, g km−2) is therefore calculated as BOD additions associated with organic material or fertiliser (RBODfert, g km−2 day−1); BOD removals specified through the decay rate; and as advective transport out of the soil water box:
where rT is a soil temperature factor, which increases the rate of BOD decay under higher temperatures:
The user may also specify a constant DO value within the soilwater box (RDO_SW). Change in soil water DO mass ( g km−2) is then primarily associated with advective flow:
Quickflow
Calculations for the change in water flow from the quickflow box (QQF) and the total quickflow volume (VQF) are detailed in SI 1.1.2. BOD is not simulated within quickflow as it is assumed that any surface runoff will be sufficiently aerated to have a BOD of zero. A constant DO value (RDO_QF) may be specified, similar to the mechanism used within the soilwater box, to simulate change in mass of DO within the quickflow box:
Groundwater
Calculations for the change in water flow from the groundwater box (QGW) and the total groundwater volume (VGW) are detailed in SI 1.1.3. Initial BOD concentrations are specified by the user. Change in groundwater BOD mass (MBOD_GW, g km−2) is equal to BOD additions from percolation of soil water, decay of BOD and advective transport out of the groundwater. Where BOD percolating from the soilwater store is calculated as:
Additionally, BOD groundwater flux from each land use category is calculated as:
where RGW_BODdecay is a user defined decay rate for groundwater BOD.
Groundwater DO is simulated as a user-defined concentration constant (RDO_GW), and daily flux within a land use class associated with advective flux:
Flux
The flux of BOD (MBODLUclass) and DO (MDOLUclass) to the river from each land use class (kg km−2 day−1) is calculated by summing exports from soil water, groundwater and quickflow:
The total mass of DO and BOD exported to the river reach (MBODtotal, MDOtotal) is calculated by summing totals from each land use class within each subcatchment (MBODLUclass, MDOLUclass):
2.1.2. Water Phase
Instream biological oxygen demand
Oxidation and decay of organic matter present in the water column may reduce DO concentrations. This is known as the biological oxygen demand (BOD) and represents the amount of oxygen respired by micro-organisms during their consumption of organic matter [19]. Simulating changes in water column BOD (MBOD_WC) are essential for determination of water column DO. In INCA-PEco BOD is input from upstream reaches (MBODus), wastewater treatment effluent (MBODww), the land phase (MBODtotal), and from dying phytoplankton (BODphyto). It is output from the reach via settling (BODsettle) and advection:
where QreachOut is reach outflow (m3s−1) and Sreach is daily river water volume (m3), detailed in SI 1.6.
Microbial consumption of dead phytoplankton removes oxygen from the water column. In INCA-PEco this mass of phytoplankton oxygen demand is included in the BOD calculation as (BODphyto; g km−2). RPhytoBOD is a user defined parameter of the dead algae contribution to the BOD (mg O2 µg−1 Chl-a−1 day−1) and CPhytoDeath is concentration of phytoplankton dying per day (µg chl-a day−1).
As organic matter settles and is buried within the bed sediment, it is deactivated as a source of oxygen demand. It is possible however that the decaying organic matter could later be re-suspended, and re-integrated as a BOD input. Therefore, in INCA-PEco, the amount of BOD which has been buried (g O2 km−2 day−1) is calculated using a net settling velocity (burial minus resuspension) of m day−1 which varies with reach depth:
where Rnetv is a user defined parameter.
Instream dissolved oxygen
Within the water column, changes in mass of DO (g km−2) are calculated by taking into consideration the major sources and sinks (Cox; 2002) including influx from upstream reaches (MDOus g km−2) and the land phase (MDOtotal g km−2), phytoplankton oxygen contributions (DOphytox, g O2 km−2 day−1), and re-aeration (DOatmox, g O2 km−2 day−1). Losses of DO are from uptake through BOD (MBOD_decay_WC, g km−2) sediment oxygen demand (DOsod, g O2 km−2 day−1), and advection. Temperature is perhaps the most significant driver of DO concentration in water, and as such is a key factor used in calculating each parameter (see SI Equations (130), (132) and (133)).
Inputs of DO through atmospheric re-aeration (DOatmox) can be calculated either by the model, or set using a user-defined parameter. A full description of the atmospheric re-aeration calculations is provided in SI 1.10.1. In summary, re-aeration is a function of the rate that aeration occurs (DOatmox/day), a temperature-dependent, calculated, total concentration of DO which the water column can hold (Abssat) and the DO mass currently within the water column (MDO_WC). Oxygen contributions from algae (DOphytox) are calculated as a function of O2 supplied by photosynthesis (DOptsyn, g O2 km2 day−1) and consumed through microbial respiration (DOptResp, g O2 km2 day−1):
Threshold ‘low’ and ‘high’ rates of photosynthesis are applied, determined by phytoplankton concentrations and daylight hours (SI 1.10.2). Removal of DO through phytoplankton respiration (DOptResp) is determined by phytoplankton concentration (Equation (24)), and a single user defined respiration slope and offset:
Chemical oxidation of compounds may also occur within riverbed sediments where organic matter is incorporated in the channel bed, exerting a significant oxygen demand and influencing the in-stream DO. This ‘uptake’ of dissolved oxygen is expressed as:
where Sedox is determined by a user defined rate of oxidation (Rox) and water temperature:
Decay and oxidation of organic matter in the water column (MBOD_decay_WC) reduces DO concentrations. A key mechanism for removal of DO from the water column is therefore associated with MBOD_WC (Equation (12)).
The amount of DO removed by the BOD is positively related to stream depth and temperature of the water column, where if the water depth is >2.4 m:
Otherwise
where ‘Oxid’ is a user defined parameter, determining the rate of organic matter oxidation. The concentration of dissolved oxygen in the water column is expressed as:
To ensure that BOD cannot cause the DO concentration to become negative, oxygen loss is set to zero if there is insufficient DO to satisfy the BOD requirements. DO is also limited to 300% of the DO saturation value (DOsat%). Water column DO saturation is dependent upon the following relationship with water column temperature (Tempwc) (SI 1.10)
In-stream phytoplankton
The concentration of phytoplankton in the water column is critical for calculations of DO and BOD mass; considering the influence of phytoplankton respiration, photosynthesis and death on instream processes (Equations (15) and (16)). In INCA-PEco, phytoplankton is represented in units of chlorophyll (µg L−1).
There are no direct land phase additions of phytoplankton to the water column. Instead the model is first balanced by calculating the change in phytoplankton inputs from the upstream, minus the outputs from the downstream; referred to here as advection (CphytoAdv).
Subsequently, phytoplankton inputs and outputs associated with growth and death, respectively, are calculated. It is important that at least one upstream reach is initialized with Cphyto > 0, in order for phytoplankton growth to propagate throughout the model.
Phytoplankton response to light, temperature and nutrient availability varies with the morphology of species within the algal community [20]. The phytoplankton growth (CPhytoGrowth) equation has therefore been designed to enable the user to specify phytoplankton community response to each of light, temperature, nutrients and self-shading. User-defined thresholds can also be set to initiate or cut-off specific drivers. This makes the phytoplankton component of the model particularly adaptable to environments with seasonal blooms, ice-on and ice-off events, extreme light reductions, extreme temperature changes, or with blooms of particularly dominant species.
where rT and rSR are thresholds below which temperature and light become a limiting factor on algal growth; where:
When
Otherwise
Additionally, when
Otherwise
where Rsolar is a user-defined light threshold for growth, expressed as a fraction of annual maximum solar radiation (0–1); and where SolarRad, and SolarRadmax are calculated parameters (SI 1.11.1). Rsrpmax is a user defined SRP threshold at which phytoplankton growth is not limited by nutrient availability; Rgrowth is a user defined rate of phytoplankton growth, and Rphytoshade is the user-defined chl-a concentration at which phytoplankton growth becomes self-limiting.
Death of phytoplankton (CPhytoDeath) is controlled by a user defined daily rate (RphytodDeath), which should be considered a synecological representation (i.e., death including that by foraging of higher order consumers):
2.2. Model Applications
To assess robustness and transferability of the model, INCA PEco was applied to two mesoscale catchments, one representative of a continental climate, and one of a maritime climate; each located on different continents and run during separate time periods (Table 1). Catchments and model run periods were selected to allow calibration across the widest possible range of conditions, while being supported by the greatest spatial and temporal availably of observed data. The Beaver River catchment, Ontario, Canada has a continental climate. It was selected based on its availability of high frequency monitoring data across all variables of interest and occurrence of freeze–thaw events (Table 1). A detailed site map can be found in SI 3 and Crossman and Elliot [21]. The Beaver River is fed by tributaries from 26 sub-catchments and is in turn a tributary of Lake Simcoe (722 km2), to which the Beaver River contributes some of the largest P loads. Lake Simcoe drains into Lake Huron via the Severn River and Georgian Bay. As a significant water resource both economically and societally, Lake Simcoe has historically supported fishing, tourism and drinking water supplies. Declining water quality was first noticed around the 1970s associated with excess P, algal blooms and reduced availability of dissolved oxygen. Since this time, Lake Simcoe and its tributaries have been the focus of collaborative restoration efforts between federal, provincial and municipal managers. The catchment is dominated by agricultural land (65%), with significant low-lying wetland areas (20%). As urban coverage is low (5%), there are just two sewage treatment works in the area, with rural dwellings predominantly connected to septic systems. The catchment has a high proportion of low-permeability clayey soils and a high density of tile drains, associated with high runoff rates and macropore flow, respectively.

Table 1.
Catchment characteristics as represented in INCA PEco.
To compliment the high frequency, short duration application of INCA PEco to the Beaver catchment, the model was also applied to the Trent catchment, UK, in which measurements of DO and BOD have been conducted since 2000 [22]. A detailed site map can be found in SI 3 and Bussi and Whitehead [23]. The UK experiences a maritime climate. The Trent catchment is over 25 times larger than the Beaver catchment, and flows into the North Sea via the Humber Estuary. Land use in the catchment consists of a mixture of arable agriculture, pasture and grassland (75%), with an urban coverage of 15%, draining the major UK cities of Birmingham, Derby, Nottingham and Leicester. Throughout its course, the river serves a population of over 7 million [23] and performs several important functions. In the northwest it drains the Peak District, a National Park and area of geological, ecological and cultural significance. To the south, the river receives sewage effluent contributions from Birmingham and Leicester. Water quality concerns surrounding the Trent have persisted since the 19th century, associated with storm-sewer overflows, untreated runoff, and discharge from industrial and sewage treatment works [24].
The 30 year climate of the two regions (1985–2015) is very different. The Beaver catchment in Ontario is situated in Köppen-Geiger climatic zone Dfb, or ‘humid continental’, compared to the Trent catchment in the UK which is located in Köppen-Geiger climatic zone Cfb, or ‘temperate oceanic’ [25]. In the Beaver catchment, peak temperatures occur in summer (June–August) and are between 27–30 °C, versus just 17.3 to 26.7 °C in the Trent River catchment. Minimum temperatures occur in winter (December–February) and are at between −23.5 to −28 °C (Beaver) and −7.5 to 0.6 °C (Trent). Differences in annual precipitation in the two catchments are smaller, at an average of 777 mm in the Beaver and 747 mm in the Trent. However, the Beaver River catchment receives a large seasonal input of snow, of between 92 cm during winter, and 27 cm during spring (or 92 mm and 27 mm of rainwater equivalent).
Model Setup
Earlier INCA-P applications for the Beaver [21] and the Trent [23] were re-calibrated within the new INCA-PEco model, using additional observations of phytoplankton (chl-a), DO and BOD. Details of forcing data, model setup and calibration strategy are provided in Crossman and Elliot [21] and Bussi and Whitehead [23]; and only a summary of the process is given here. The two study catchments were subdivided into their constituent subcatchment networks (26 for the Beaver, and 20 for Trent) using ArcHydro GIS software, and hydrological networks developed from 50 m digital elevation models. The following land use classes were employed: urban, intensive-agriculture, non-intensive-agriculture, wetlands and forest (Beaver); and woodland, grassland, improved grassland, arable, urban and water (Trent). INCA-PEco is forced using a daily time series of precipitation, temperature, soil moisture deficit (SMD) and hydrologically effective rainfall (HER). For both model applications, the SMD and HER time series were generated using the process-based rainfall-runoff model PERSiST [26]. Meteorological data for the Beaver catchment was obtained from the Daymet daily surface weather data [27]; and for the Trent catchment from the UK met office [28].
In the Beaver, fertilizer P application rates to agricultural lands were estimated using a combination of provincial legislation [29] and crop growth statistics [30]. Septic system inputs to soils were calculated using average household P load [31], combined with numbers of households connected to septic systems in the catchment [32]. Wet and dry atmospheric deposition was calculated using monitoring data reported in Ramwekellan et al. [33]. Initial soil P concentrations were based on literature values [34]. Soil equilibrium coefficients were calculated using laboratory values [35,36,37]. In rivers, effluent inputs from sewage treatment works were obtained from XCG and KMK consultants, and groundwater P concentrations were calibrated using observed monitoring data from the Provincial Groundwater Monitoring Network [38]. Monitoring of flow, total phosphorus (TP), dissolved phosphorus (DP) and soluble reactive phosphorus (SRP) has been conducted in the Beaver River, across all subcatchments since the early 1980s. These data were used for model calibration.
For the Trent simulation, arable fertilizer applications had been found to be a minor source of P to this watercourse [23] and so in the model no P was added to soils via fertilisers. Furthermore, septic systems are uncommon in the UK and were also not included in the model calibration. Atmospheric P deposition was calculated using UK estimates of soil nutrient balances [39]. Wastewater inputs were calculated as a proportion of the population living in each sub-catchment [40]. Groundwater P concentrations were calibrated using water quality data provided by the Environment Agency Water Quality Data Archive. Consistent water quality data is available from 2010–2016, and the model was calibrated to SRP and flow data in one of the last non-tidal reaches proximal to the catchment outflow.
The empirical data required for BOD, DO and phytoplankton modelling (e.g., chl-a, temperature and DO) within the Beaver River were available at an almost daily time-step for a 12-month period between 2015 and 2016, for a relatively short stretch of river proximal to Lake Simcoe. No daily BOD data was available in the Beaver catchment. For the Trent, all data was available for the full time period (2010–2014); albeit at a lower resolution (maximum of twice per month). Calibration coefficients (R2 and mean absolute error; MAE) were calculated for all variables, at a monthly timescale.
2.3. Sensitivity Analysis
An SA of both model applications was conducted to determine how climate and land use-related differences between the catchments might affect prioritization of parameters in the calibration process. For instance, climatic extremes (freeze–thaw in the Beaver vs. milder conditions in the Trent) and land use differences (higher agricultural influence in the Beaver vs. point-source urban influence in the Trent) could affect the significance of overland flow processes in spring. Both model applications were run through 50,000 simulations, under 50,000 different parameter sets which were generated by randomly varying 33 of the model parameters using uniform sampling. Kling and Gupta Efficiency (KGE) goodness-of-fit statistics were calculated for each model run at the catchment outflow (Beaver) or at one of the last non-tidal reaches (Trent) using observed daily flow, in-stream P concentration (TP, TDP or SRP depending on availability of observed data), phytoplankton concentration, and dissolved oxygen concentration (SI 4). Model performances were grouped into either good (behavioural) or bad (non-behavioural) results; where good behaviours were defined as the 98th percentile of all KGE values obtained in the 50K simulations. The sensitivity of model performance to parameter variance was then measured by calculating the Kolmogorov–Smirnov (KS) of the difference between the behavioural distribution and a uniform distribution. The sensitivity results (KS) for flow, phosphorus, phytoplankton, and dissolved oxygen were plotted and compared for both model applications, using a sensitivity heat map developed in the open-source online graphing tool Plotly (http://chart-studio.plotly.com accessed on 2 February 2021), similar to those used in Harman et al. [41], and Niida et al. [42].
3. Results and Discussion
3.1. Calibration
In the Beaver model, flow simulations were excellent, with an R2 of 0.96 and mean absolute error (MAE) of −0.28. TP and TDP concentrations modelled at the mouth of the river corresponded with observed data (Figure 2A,B) with an R2 of 0.1 and 0.6, respectively, and MAE of −0.09 and −0.26. Dissolved oxygen concentrations were well represented by INCA PEco (Figure 2D) with an R2 value of 0.7 and MAE of >0.01. Although available at a very high temporal resolution (once every two days), observed chlorophyll-a data in the Beaver River were available for only a short time period, and over a limited spatial resolution. An R2 value of 0.7 was achieved, with MAE of >0.2, with 80% of observed data points lying within 1 SD of the modelled values (Figure 2C).
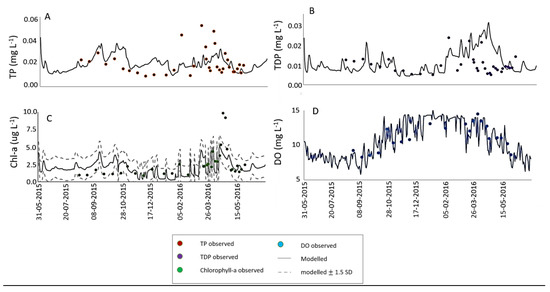
Figure 2.
Calibration results of (A) TP concentration (B) TDP concentration, (C) chl-a concentration and (D) DO concentration within the river mouth of the Beaver River catchment between 2015 and 2017.
The model does an excellent job of simulating the low phytoplankton concentrations from late fall to early spring (Figure 2C) in the Beaver River, when growth is limited by temperature and light availability, particularly from December to February where light is restricted due to ice cover. During spring melt (beginning around 2 February and ending on 25 May), a rise in in-stream chl-a concentrations occurred in both observed and modelled data. Increases in phytoplankton following ice break-up is known as a ‘spring bloom’, a phenomena which is commonly observed in seasonally ice-covered lakes [10,43], although sensitivity to ice-cover is also not uncommon in rivers [44]. During ice cover, nutrient concentrations build up due to limited photosynthetic activity which would otherwise act to reduce them. During spring, as ice melts, temperature and light availability increase, and phytoplankton growth accelerates [45]. This growth is initially not limited by nutrients due to the large available store, and hydrologic flushing of soils by snowmelt [46]. The bloom rapidly subsides as nutrients are either washed away by large volumes of spring meltwater, or are used up by algal growth. A second peak in chl-a is observed in summer in the Beaver River, when terrestrial P from fertilizer applications is washed into rivers during precipitation events [47] (Figure 2C). Nutrients, however, appear to remain the limiting factor for chl-a concentrations until late fall, when declining temperatures and shorter daylight hours once again begin to limit phytoplankton growth. The interactions of temperature and light in limiting algal growth have been well documented in the literature (e.g., [48]). DO concentrations begin to drop during higher chl-a concentrations in summer (Figure 2D), likely associated with an increase in BOD from decaying phytoplankton. Further exploration of this is provided in the sensitivity analysis.
Trent
In the Trent application, flow simulations were also good, with an R2 of 0.88 and mean absolute error (MAE) of <0.01. The observed patterns of TDP nutrient concentrations, which were highest during periods of low flow, were also well simulated (Figure 3A) with R2 of 0.63 and MAE of 0.08. Similarly, dissolved oxygen concentrations (Figure 3D) had an R2 value of 0.74 and MAE of −0.02. In the Trent, chlorophyll-a data (Figure 3C) were available at a much lower temporal resolution, but for a longer time period (4 years) and here an R2 value of 0.49 was achieved, with MAE of 0.57, where 89% of observed data points lay within 1 SD of the modelled values. In this catchment, observed BOD data was available for calibration (Figure 3B), and with an R2 of 0.3, and an MAE of 0.41.
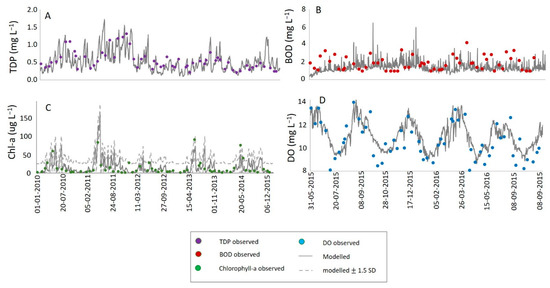
Figure 3.
Calibration results of (A) TP concentration (B) TDP concentration, (C) chl-a concentration and (D) DO concentration in the Trent River between 2010 and 2015.
In the Trent, spring phytoplankton blooms are well captured by INCA PEco (Figure 3C), followed by periods of lower concentrations in summer with a winter minima. The spring blooms occur during periods of lower flow, as light availability and temperatures begin to increase [49]. Point sources are the dominant nutrient input in this catchment, and low discharge results in concurrent increases in availability of bioavailable phosphorus [23]. These ideal conditions for phytoplankton growth, combined with reduced rates of hydraulic flushing [50] and associated reduced advection (Equation (26)), explain the rapid increase in phytoplankton concentrations during April and May. In winter, high discharges are associated with higher rates of flushing, and greater loss of phytoplankton mass through advection; and with lower availability of nutrients due to dilution. In addition, algal growth rates can be limited by cool winter temperatures and shorter daylight hours [48].
The lower summer phytoplankton concentrations in the Trent have been discussed since the 1980s. The summer discharge minima, combined with light, temperature and phosphorus maxima would suggest ideal conditions for algal growth, and it has been posited that some form of subsequent ‘loss’ mechanism is responsible, for example high death rates [49]. The precise process has however remained unclear. INCA-PEco reproduces these low summer phytoplankton concentrations in the Trent primarily through the mechanism of ‘self shading’ (Equation (27)), suggesting that in summer, phytoplankton mass becomes limited by water volume. Following spring blooms, as water volumes approach a summer minima, algae concentrations are higher than the water volume can support, and despite high incident solar radiation, algae within the water column of the Trent cannot access that light due to obstruction by the presence of phytoplankton around them [51]. Rather than a ‘loss’ process therefore, INCA PEco suggests that lower-than-expected summer blooms in the Trent are caused by in situ limitations on growth. In the Trent, peak BOD occurs during the spring, coinciding with algal blooms; however minimum DO is still observed during the summer low flow minima. Summer hypoxia in this river is therefore unlikely to be caused by phytoplankton blooms or by BOD, and is more likely associated with high summer water column temperatures during these periods of low flow.
Through placing user-defined thresholds upon the temperature and solar-radiation equations, within the phytoplankton growth equations, these models applied to different continents and climatic regions demonstrate that algal growth can be limited below certain temperatures and light conditions (e.g., during winter or under low flow conditions), while enabling significant growth responses to excess nutrient availability in the absence of those limiting factors (in spring and summer). The successful calibration of the model to both the Trent and Beaver catchments highlight the benefits provided by the flexibility of these user-defined thresholds, facilitating application both to systems which are temporarily ice-covered, and to those which are open year round.
3.2. Sensitivity Analysis
3.2.1. Flow and P
The sensitivity analysis (Figure 4) demonstrates that the accuracy of the Beaver River and Trent model calibrations are highly sensitive to variations in base-flow index value (KS > 0.6, P < 0.1), which likely reflects their high contributions from groundwater (40% Trent, 65% Beaverton). The Beaver application, however, also demonstrates a high sensitivity of flow to maximum infiltration rates of soils (KS > 0.7, P < 0.1), which is not observed in the Trent. This is likely due to higher infiltration excess characteristics and shorter soil water residence times within the Beaver catchment. The accuracy of flow calibrations (and by association, the in-stream nutrient concentrations) in both models are highly sensitive to the stream bed roughness co-efficient (Manning’s n) and river depth. These parameters are components of the Manning’s equation (SI 1.6, Equations (79)–(86)), which controls changes in river flow, volume, water depth and channel width. In the Trent application, concentrations of nutrients are highly sensitive only to these flow parameters.
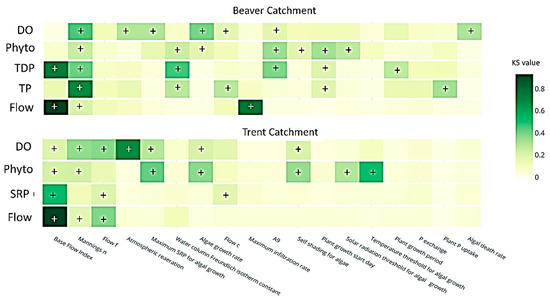
Figure 4.
A sensitivity heat map for the Beaver and Trent model applications, using Kolmogorov–Smirnov (KS) values to indicate sensitivity of model performance to parameter variance.
P concentrations (TDP and TP) in the Beaver application show additional sensitivity to several terrestrial parameters associated with agricultural management, including plant growth start day (TP and TDP, KS > 0.18, P < 0.06), plant growth period (TDP, KS > 0.25, P < 0.01), and plant nutrient uptake rate (TP, KS > 0.32, P < 0.01). This stark contrast in sensitivity with the Trent application is likely due to the higher fertilizer applications and significant diffuse sources of P in the Beaver catchment. The Beaver is 65% agriculture, with annual P application rates of 0.5 kg ha−1. Uptake of soil P through vegetation growth (SI 1.3.1 Equations (50)–(55)) is therefore a primary nutrient control where the model is applied in agriculturally dominant regions. Similar sensitivities to vegetation growth have been found of the Soil Water Assessment Tool (SWAT) model [52]. In contrast, previous studies conducted on the Trent have shown diffuse terrestrial P contributions to be negligible compared to direct P inputs from sewage effluent, owing to the large populations living within the catchment [23]. The Trent model was therefore simulated without fertilizer P inputs, and as a result, primary nutrient contributions in this model are from end-of-pipe sources, e.g., sewage effluent; bypassing these terrestrial processes.
In the Beaver River application, TDP and TP calibration accuracy is also sensitive to the water column Freudlinch isotherm constant (FIC), and in-stream concentration of small clay particles, known in the model as ‘background sediment release’ (TDP). The FIC controls P transfer rates between the dissolved and particulate phase (SI 1.8.2 Equation (115)), and background sediment release simulates the sustained mobilisation of fine-grained sediments from the stream channel during low flow conditions (SI 1.7.3 Equation (96)). The particles act as sites for TDP absorption in the water column, thus also impacting conversion rates between TDP and PP. The Beaver was calibrated using observed data of TP, TDP, sediment and PP; meaning the conversion between these fractions is carefully constrained. In this catchment, 45% of TP was attributed to PP. In the Trent however, less than 0.1% of the modelled TP was attributed to PP. In the Trent, TP data is not regularly available, and it is therefore not possible to calculate either the FIC or background sediment release rates. It is likely that the assumed low contribution of PP to instream processes is the reason for the low sensitivity of these parameters in the Trent applications.
3.2.2. Phytoplankton Concentration
In both catchments, phytoplankton concentration was highly sensitive to parameters associated with the phytoplankton growth equation (Figure 4; Equation (27) and SI 1.11 Equation (154)), including algal growth rate (KS > 0.18, P < 0.08); self-shading (KS > 0.19, P < 0.06) and solar radiation (KS > 0.27, P < 0.01). The Trent application however demonstrated a much higher sensitivity to self-shading than that seen in the Beaver River (Figure 4). Phytoplankton concentrations are 10 times higher in the Trent than in the Beaver; indicating that the importance of self-shading as a limiting factor will to some extent be dependent upon relative in-stream concentrations. The spatial variance in self-shading influence was similarly noted in a study by Whitehead et al. [8]. In both applications the accuracy of phytoplankton concentration calibrations was also highly sensitive to flow volume through the Manning’s roughness coefficient (KS > 0.22, P < 0.01), and, in the case of Trent, also the base-flow index (KS > 0.21, P < 0.02). River discharge controls the transport of phytoplankton from upstream reaches, residence time of phytoplankton within the water column (flushing rates), and phytoplankton outflow (Equations (25) and (26); and SI 1.11 Equations (152) and (153)). Both model applications also demonstrated sensitivity of phytoplankton growth to nutrient limitation, defined in Equation (27) as:
where CSRP is the concentration of SRP, and RSRPmax is a user defined threshold concentration of SRP at which phytoplankton growth is uninhibited by nutrient availability. The Trent was directly limited through a sensitivity to ‘maximum SRP for algal growth’, or RSRPmax (KS > 0.43, P < 0.01). The Beaverton application demonstrated a more indirect sensitivity to nutrient limitation, where phytoplankton concentration was sensitive to multiple parameters which also control the concentration of in-stream phosphorus or the ‘CSRP’ component of the equation; including FIC (KS > 0.24, P < 0.01), background sediment release (KS > 0.32, P < 0.01), and plant growth start date (KS > 0.31, P < 0.01). The Trent application was more sensitive to the temperature threshold component of the phytoplankton growth equation. This threshold represents a limit below which algal growth becomes restricted, and indicates a sharp change in accuracy at between 8 and 9 °C. Several reasons for this difference in temperature sensitivity are plausible. As a region with no seasonal ice cover, phytoplankton communities within the Trent are more exposed to cool winter conditions which may become the limiting factor on algae population size. These results correspond with previous findings in the UK [53] where algal growth was inhibited at temperatures below 10 °C. In contrast, during cooler conditions in the Beaver catchment, ice cover frequently topped with snow shields phytoplankton communities from extreme temperature conditions; and instead, restricts light which may then become a primary limiting factor during winter [54].
3.2.3. Dissolved Oxygen
In both model applications, the accuracy of DO calibrations were highly sensitive to the same parameters that influenced flow (Figure 4), including Manning’s n (Beaver and Trent; KS > 0.35, P < 0.01) and river depth (KS > 0.17, P < 0.1). Manning’s n and river depth parameters control in-stream velocity, which is a primary component of the atmospheric re-aeration calculation (SI 1.10 Equation (132)). Indeed, the accuracy of DO calibrations in both models are highly sensitive to the calculated re-aeration parameter (KS in the Trent and Beaver 0.65 and 0.29, respectively; P < 0.1). Again the predominantly groundwater-fed Trent catchment had a higher sensitivity to base-flow (KS > 0.18, P < 0.1), likely reflecting a higher input concentration of DO from this source.
The DO in both applications were also highly sensitive to parameters associated with phytoplankton concentration, including maximum SRP (KS > 0.28, P < 0.01) and algal growth rate (KS > 0.21, P < 0.03). DO sensitivity in the Trent was additionally strongly associated with self-shading (KS > 0.21, P < 0.03); whereas the Beaverton was associated with algal death rates (KS > 0.29, P < 0.01). The similarities in application sensitivities here reflect the importance of oxygen contributions from photosynthesis (Equations (16) and (17), and SI 1.10 Equation (141)–(145)), which in turn are reliant on phytoplankton concentration, which can be limited by growth rates and the availability of nutrients (Equation (27) and SI 1.11 Equation (154)). The ‘self-shading’ sensitivity exhibited by the Trent is a self-limiting component of the phytoplankton growth equation.
The high sensitivity of DO concentrations to algal death rates in the Beaver application is not represented in the catchments’ phytoplankton sensitivities, indicating that the influence of death rate is through an increase in BOD (Equation (12) and SI 1.9 Equations (124) and (125)), rather than through a decline in photosynthesis (Equation (25) and SI 1.11 Equation (152)). The Trent does not exhibit a strong DO sensitivity to algal death rates, indicating a weaker influence of BOD over DO in the Trent catchment. A possible reason for this is the contrast in seasonal bloom behaviours between the sites. In the Beaver, phytoplankton peak in summer, when temperatures are highest, decay rates fastest and DO at a minima. In a slow flowing water body, and with phytoplankton concentrations predominantly below the self-shading threshold, dying algae would have a long residence time, and optimal opportunity to impact BOD (e.g., [55]). In contrast in the Trent, phytoplankton blooms occur only in spring, when temperatures are lower, flow rates and DO concentration are not at their minimum. During this period dying algae are more rapidly flushing into the estuary, and they have less of an impact on BOD. In the Trent during the lowest flow periods, algae exceed the self-shading threshold and are unable to bloom.
Despite some differences in responses between model applications, the sensitivity analysis of INCA-PEco generally indicates similar dominant model responses. Both terrestrial and in-stream hydrology appears to be the key influential driving mechanism throughout INCA-PEco, influencing concentrations of phosphorus, phytoplankton, DO and the impact of phytoplankton death on BOD. It is therefore critical that hydrological parameters be carefully calibrated prior to the assessment of other variables within the model. Terrestrial management strategies have a similar model-wide influence where diffuse applications of nutrients are found.
3.3. Study Limitations and Further Research
The inclusion of DO, BOD and phytoplankton in the INCA model presents multiple advantages over coupling different process-based models; including, but not limited to, the ability to assess the direct impact of nutrient management strategies on ecosystem health. There remain however several opportunities for further development of INCA-PEco.
First, high frequency datasets were selected for the calibration of the study catchments, as lower temporal resolution data such as monthly grab samples have been demonstrated to be insufficient to identify causes of variations in phytoplankton biomass [53]. Using these data, assessment of model accuracy can be performed to a more management-relevant timescale, e.g., weekly or daily. As such high-resolution data has only recently become available, the lengths of these datasets are insufficient to support performance assessments on broader timescales (e.g., seasonal or annual). Future research might include additional model performance across longer timescales, as further observed data becomes available.
Second, INCA-PEco currently simulates the total phytoplankton concentration within the water column, but does not simulate different species which make up that community. While it has been established that total biovolume is closely associated with environmental conditions [56], it is more difficult to predict community composition [57]. The community composition is important however, as individual phytoplankton groups differ in their effects (e.g., toxicity, decay rates, nutrient requirements). As such, INCA PEco’s current focus on biovolume does pose some limitations in applicability for long term modelling efforts, e.g., under climate simulations. As water temperature conditions change over time, so too can the dominance of particular algal communities [58] as their relative competitive advantages are either enhanced or suppressed. Changes in community dominance driven by climate change, could alter a community’s sensitivity to other stressors (e.g., nutrient availability), meaning thresholds of sensitivity established during calibration periods may vary under future climates. While it is not the intention of INCA-PEco to simulate the biomass of a specific algal species, but to simulate the BOD and DO concentrations resulting from phytoplankton community growth, accurate modelling of community growth assemblages can also be important. As a next step, to enable more specific assessments of the impact of a changing climate on particular bloom types, the modelling of individual communities could be adapted (e.g., diatoms, microcystis, dinoflagellates). These communities may be grouped by their sensitivity to specific thresholds such as temperature resilience and nutrient requirements (e.g., [20]).
INCA-PEco in its current form, however, can still successfully be used as a management tool to identify sources and causes of current bloom events, and to assess potential effectiveness of considered nutrient control strategies under a changing climate.
4. Conclusions
INCA-PEco provides the functionality to integrate point and diffuse transport of DO and BOD to rivers, simultaneously with phosphorus and sediments, and to simulate subsequent instream interactions with seasonal phytoplankton blooms. These additional processes bridge the gap between phosphorus management strategies and ecological responses, enabling users to simulate how policy objectives might best be achieved.
Sensitivity analyses indicate that calibration time might be optimized in all models by initially focusing on the hydrological parameters of base flow, Manning’s n and river depth. An accurate calculation of the base flow index is critical in minimizing model uncertainty. In applications where diffuse inputs of nutrients are significant, e.g., in heavily fertilized catchments, detailed data on terrestrial vegetation growth and crop type (nutrient uptake rates) are also recommended. Furthermore, where surface flow and soil throughflow are dominant, historic datasets of regional infiltration rates would be beneficial.
In summary, while INCA-PEco comprises more than 268 parameters, model uncertainty can be significantly reduced by focusing calibration efforts and watershed monitoring resources on just 18 of those parameters. This does not render the other parameters ineffective however, as they provide flexibility to the user, broadening the applicability of the model, and maximizing its functionality under a changing climate. For instance, as temperatures increase, the limiting temperature threshold for growth will be crossed less frequently and blooms will be limited by other factors (e.g., nutrients or light). In systems where low winter temperatures are a dominant driving factor (the Trent), this will have significant implications for phytoplankton and DO concentrations. The user-defined thresholds provided in INCA-PEco ensure that the impact of these changing climatological conditions on ecological processes will be included when simulating sustainability of management options.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4441/13/5/723/s1, SI1: INCA-PEco supplementary equations documentation; SI2: Full list of INCA PEco parameters with units; SI3 Site map of (a) Beaver River catchment boundaries, Ontario and (b) Trent River catchment boundaries, UK. The black dot indicates the location of INCA PEco application; SI4 Figure S1 Kling Gupta Efficiency statistics (Sensitivity analysis) for Beaver land phase analysis; SI4 Figure S2 Kling Gupta Efficiency statistics (Sensitivity analysis) for Beaver aquatic phase analysis; SI4 Figure S3 Kling Gupta Efficiency statistics (Sensitivity analysis) for Trent River land phase analysis; SI4 Figure S4 Kling Gupta Efficiency statistics (Sensitivity analysis) for Trent River aquatic phase analysis.
Author Contributions
Conceptualization: J.C. and P.G.W.; Methodology: J.C., P.G.W., G.B., M.N.F. and D.B.; Software: M.N.F., D.B. and P.G.W.; Validation: J.C., E.L. and G.B.; Formal Analysis: J.C., D.B., P.G.W., G.B. and M.N.F.; Resources: J.C. and P.G.W.; Data Curation: J.C. and G.B.; Writing—original draft preparation: J.C.; Writing—review and editing: J.C., G.B., P.G.W., E.L., D.B. and M.N.F.; Supervision: J.C. and M.N.F.; Project Administration: J.C.; Funding Acquisition: J.C. and P.G.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Environment Canada Lake Simcoe Georgian Bay Clean Up Fund [grant number GCXE 16R150].
Institutional Review Board Statement
No applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study (the model equations which comprise INCA PEco) are provided in full in the Supplementary Materials.
Acknowledgments
The authors would like to thank the Lake Simcoe Region Conservation Authority, and Ministry of Conservation and Parks for collection of historic water quality monitoring data. This work was supported by the Environment Canada Lake Simcoe Georgian Bay Clean Up Fund [grant number GCXE 16R150]. We would also like to thank Brian Cox, whose published work on dynamic modelling of dissolved oxygen and biological oxygen demand in the Thames River, formed the conceptual framework for some of the equations developed in INCA Peco.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rabalais, N.N.; Diaz, R.J.; Levin, L.A.; Turner, R.E.; Gilbert, D.; Zhang, J. Dynamics and distribution of natural and human-caused hypoxia. Biogeosciences 2010, 7, 585–619. [Google Scholar] [CrossRef]
- Tian, R. Factors Controlling Hypoxia Occurrence in Estuaries, Chester River, Chesapeake Bay. Water 2020, 12, 1961. [Google Scholar] [CrossRef]
- Wen, Y.; Schoups, G.; van de Giesen, N. Organic pollution of rivers: Combined threats of urbanization, livestock farming and global climate change. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- Mallin, M.A.; Johnson, V.L.; Ensign, S.H.; MacPherson, T.A. Factors contributing to hypoxia in rivers, lakes, and streams. Limnol. Oceanogr. 2006, 51, 690–701. [Google Scholar] [CrossRef]
- Jang, G.-S.; An, K.-G. Physicochemical water quality characteristics in relation to land use pattern and point sources in the basin of the Dongjin River and the ecological health assessments using a fish multi-metric model. J. Ecol. Environ. 2016, 40, 6. [Google Scholar] [CrossRef][Green Version]
- Liu, C.; Li, Z.; Dong, Y.; Chang, X.; Nie, X.; Liu, L.; Xiao, H.; Wang, D.; Peng, H. Response of sedimentary organic matter source to rainfall events using stable carbon and nitrogen isotopes in a typical loess hilly-gully catchment of China. J. Hydrol. 2017, 552, 376–386. [Google Scholar] [CrossRef]
- Nelson, N.G.; Muñoz-Carpena, R.; Phlips, E.J.; Kaplan, D.; Sucsy, P.; Hendrickson, J. Revealing Biotic and Abiotic Controls of Harmful Algal Blooms in a Shallow Subtropical Lake through Statistical Machine Learning. Environ. Sci. Technol. 2018, 52, 3527–3535. [Google Scholar] [CrossRef] [PubMed]
- Whitehead, P.G.; Bussi, G.; Bowes, M.J.; Read, D.S.; Hutchins, M.G.; Elliott, J.A.; Dadson, S.J. Dynamic modelling of multiple phytoplankton groups in rivers with an application to the Thames river system in the UK. Environ. Model. Softw. 2015, 74, 75–91. [Google Scholar] [CrossRef]
- Chapra, S.; Pelletier, G.; Tao, H. Qualk2K: A Modelling Framework for Simulating River and Stream Water Quality (Version 2.11). Documentation and Users Manual; Civil and Environmental Engineering Department, Tufts University: Medford, MA, USA, 2008; Available online: http://www.ecs.umass.edu/cee/reckhow/courses/577/Qual2/Q2KDocv2_11b8%20v211.pdf (accessed on 15 February 2021).
- Elliott, J.A.; Persson, I.; Thackeray, S.J.; Blenckner, T. Phytoplankton modelling of Lake Erken, Sweden by linking the models PROBE and PROTECH. Ecol. Model. 2007, 202, 421–426. [Google Scholar] [CrossRef]
- Crossman, J.; Futter, M.; Elliott, J.; Whitehead, P.; Jin, L.; Dillon, P. Optimizing land management strategies for maximum improvements in lake dissolved oxygen concentrations. Sci. Total. Environ. 2019, 652, 382–397. [Google Scholar] [CrossRef]
- Moreno-Rodenas, A.M.; Tscheikner-Gratl, F.; Langeveld, J.G.; Clemens, F.H. Uncertainty analysis in a large-scale water quality integrated catchment modelling study. Water Res. 2019, 158, 46–60. [Google Scholar] [CrossRef] [PubMed]
- Tscheikner-Gratl, F.; Bellos, V.; Schellart, A.; Moreno-Rodenas, A.; Muthusamy, M.; Langeveld, J.; Clemens, F.; Benedetti, L.; Rico-Ramirez, M.A.; de Carvalho, R.F.; et al. Recent insights on uncertainties present in integrated catchment water quality modelling. Water Res. 2019, 150, 368–379. [Google Scholar] [CrossRef]
- Getz, W.M.; Marshall, C.R.; Carlson, C.J.; Giuggioli, L.; Ryan, S.J.; Romañach, S.S.; Boettiger, C.; Chamberlain, S.D.; Larsen, L.; D’Odorico, P.; et al. Making ecological models adequate. Ecol. Lett. 2018, 21, 153–166. [Google Scholar] [CrossRef]
- Wade, A.J.; Whitehead, P.G.; Butterfield, D. The Integrated Catchments model of Phosphorus dynamics (INCA-P), a new approach for multiple source assessment in heterogeneous river systems: Model structure and equations. Hydrol. Earth Syst. Sci. 2002, 6, 583–606. [Google Scholar] [CrossRef]
- Jackson-Blake, L.A.; Wade, A.J.; Futter, M.N.; Butterfield, D.; Couture, R.M.; Cox, B.A.; Crossman, J.; Ekholm, P.; Halliday, S.J.; Jin, S.; et al. The INtegrated CAtchment model of phosphorus dynamics (INCA-P); Description and demonstra-tion of new model structure and equations. Environ. Model. Softw. 2016, 83, 356–386. [Google Scholar] [CrossRef]
- Whitehead, P.G.; Wilson, E.J.; Butterfield, D. A semi-distributed Integrated Nitrogen model for multiple source as-sessment in Catchments (INCA): Part I—model structure and process equations. Sci. Total Environ. 1998, 210, 547–558. [Google Scholar] [CrossRef]
- Wang, A.; Solomatine, D.P. Practical Experience of Sensitivity Analysis: Comparing Six Methods, on Three Hydrological Models, with Three Performance Criteria. Water 2019, 11, 1062. [Google Scholar] [CrossRef]
- Cox, B.A. Dynamic Modelling of Dissolved Oxygen: A Case-Study for the River Thames. Ph.D. Thesis, University of Reading, Reading, UK, 2016. [Google Scholar]
- Elliott, J.A.; Reynolds, C.S.; Irish, A.E.; Tett, P. Exploring the potential of the PROTECH model to investigate phyto-plankton community theory. Hydrobiologia 1999, 414, 37–43. [Google Scholar] [CrossRef]
- Crossman, J.; Elliott, J. Bridging the gap between terrestrial, riverine and limnological research: Application of a model chain to a mesotrophic lake in North America. Sci. Total. Environ. 2018, 622–623, 1363–1378. [Google Scholar] [CrossRef] [PubMed]
- Environment Agency Water Quality Archive. Available online: https://environment.data.gov.uk/water-quality/view/download/new (accessed on 8 January 2020).
- Bussi, G.; Whitehead, P.G. Impacts of droughts on low flows and water quality near power stations. Hydrol. Sci. J. 2020, 65, 898–913. [Google Scholar] [CrossRef]
- Rivett, M.O.; Ellis, P.A.; Mackay, R. Urban groundwater baseflow influence upon inorganic river-water quality: The River Tame headwaters catchment in the City of Birmingham, UK. J. Hydrol. 2011, 400, 206–222. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmerman, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Kö ppen-Geiger climate classification maps at 1km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- Futter, M.N.; Erlandsson, M.A.; Butterfield, D.; Whitehead, P.G.; Oni, S.K.; Wade, A.J. PERSiST: A flexible rainfall-runoff modelling toolkit for use with the INCA family of models. Hydrol. Earth Syst. Sci. 2014, 18, 855–873. [Google Scholar] [CrossRef]
- Thornton, M.M.; Shrestha, Y.W.; Thornton, P.E.; Kao, S.; Wilson, B.E. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 4; ORNL DAAC: Oak Ridge, TN, USA, 2020. [CrossRef]
- Met Office. Met Office Integrated Data Archive System (MIDAS) Land and Marine Surface Stations Data (1853-Current). Center for Environmental Data Analyais. 2012. Available online: https://catalogue.ceda.ac.uk/uuid/dbd451271eb04662beade68da43546e1 (accessed on 8 January 2020).
- OMAFRA. Ontario Ministry of Agriculture, Food and Rural Affairs: Agronomy Guide for Field Crops. 2009. Available online: http://www.omafra.gov.on.ca/english/crops/pub811/p811toc.html (accessed on 30 January 2021).
- Statistics Canada. Farm and Operator Data. Census of Agriculture. 2011. Available online: https://www.statcan.gc.ca/eng/ca2011/index (accessed on 30 January 2021).
- Stephens, S.L.S. Optimising Agricultural and Urban Pollution Remediation Measures Using Watershed Modelling: Review, Calibration, Validation and Applications of the CANWET Model in the Lake Simcoe Watershed. Master’s Thesis, Trent University, Trent, ON, Canada, 2007. [Google Scholar]
- Louis Berger Group Inc. Estimation of the Phosphorus Loadings to Lake Simcoe; The Louis Berger Group Inc.: Washington, DC, USA, 2020. [Google Scholar]
- Ramwakellan, J.; Gharabaghi, B.; Winder, J.G. Application of weather radar in estimation of bulk atmospheric deposition of total phosphorus over Lake Simcoe. J. Can. Water Resour. 2009, 34, 37–60. [Google Scholar] [CrossRef]
- Fournier, R.E.; Morrison, I.K.; Hopkin, A.A. Short range variability of soil chemistry in three acid soils in Ontario, Canada. Commun. Soil Sci. Plant Anal. 1994, 25, 3069–3082. [Google Scholar] [CrossRef]
- Peltouvouri, T. Phosphorus in Agricultural Soils of Finland—Characterisation of Reserves and Retention in Mineral Soil Profiles, Pro Terra No. 26. Ph.D. Thesis, University of Helsinki, Helsinki, Finland, 2006. [Google Scholar]
- Vaananen, R. Phosphorus Retention in Forest Soils and the Functioning of Buffer Zones Used in Forestry. Ph.D. Thesis, Department of Forest Ecology, University of Helsinki, Helsinki, Finland, 2008; p. 42. [Google Scholar] [CrossRef]
- Koski–Vähälä, J. Role of Resuspension and Silicate in Internal Phosphorus Loading. Master’s Thesis, Department of Limnology and Environmental Protection, Department of Applied Chemistry and Microbiology, University of Helsinki, Helsinki, Finland, 2001. [Google Scholar]
- Provincial Groundwater Monitoring Network. Provincial Groundwater Monitoring Network Program: Groundwater Level Data, Groundwater Chemistry Data, and Precipitation Data, Ministry of Environment. 2012. Available online: https://www.javacoeapp.lrc.gov.on.ca/geonetwork/srv/en/metadata (accessed on 8 November 2019).
- DEFRA. Soil Nutrient Balances. UK Provisional Estimates for 2012. Available online: https://www.farminguk.com/content/knowledge/Soil%20nutrient%20balances%20UK%20provisional%20estimates%20for%202012(335).pdf (accessed on 10 January 2020).
- CIESIN. University, Center for International Earth Science Information Network—CIESIN—Columbia. Documentation for the Gridded Population of the World, Version 4 (GPWv4); NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2016. [Google Scholar] [CrossRef]
- Harman, M.; Krinke, J.; Ren, J.; Yoo, S. Search Based Data Sensitivity Analysis Applied to Requirement Engineering. In Proceedings of the 11th Annual conference on Genetic and evolutionary computation, Montreal, QC, Canada, 8–12 July 2009; pp. 1681–1688. [Google Scholar]
- Niida, A.; Hasegawa, T.; Miyano, S. Sensitivity analysis of agent-based simulation utilizing massively parallel computation and interactive data visualization. PLoS ONE 2019, 14, e0210678. [Google Scholar] [CrossRef]
- Arvola, L. Spring phytoplankton of 54 small lakes in southern Finland. Hydrobiologia 1986, 137, 125–134. [Google Scholar] [CrossRef]
- Akomeah, E.; Chun, K.P.; Lindenschmidt, K. Dynamic water quality modelling and uncertainty analysis of phyto-plankton and nutrient cycles for the upper South Saskatchewan River. Environ. Sci. Pollut. Res. 2015, 22, 18239–18251. [Google Scholar] [CrossRef] [PubMed]
- Peters, F.; Dietmar, S.; Lorke, A.; Livingstone, D.M. Earlier onset of the spring phytoplankton bloom in lakes of the t emperate zone in a warmer climate. Glob. Chang. Biol. 2007, 13, 1898–1909. [Google Scholar] [CrossRef]
- O’Donnell, J.; Douglas, T.; Barker, A.; Guo, L. Changing Biogeochemical Cycles of Organic Carbon, Nitrogen, Phosphorus, and Trace Elements in Arctic Rivers. In Arctic Hydrology, Permafrost and Ecosystems; Springer: Cham, Switzerland, 2021; pp. 315–348. [Google Scholar]
- Crossman, J.; Futter, M.N.; Whitehead, E.; Stainsby, E.; Baulch, H.M.; Jin, L.; Oni, S.K.; Wilby, R.L.; Dillon, P.J. Flow pathways and nutrient transport mechanisms drive hydrochemical sensitivity to climate change across catchments with different geology and topography. Hydrol. Earth Syst. Sci. 2014, 18, 5125–5148. [Google Scholar] [CrossRef]
- Edwards, K.F.; Thomas, M.K.; Klausmeier, A.; Litchman, E. Phytoplankton growth and the interaction of light and temperature: A synethesissynthesis at the species and community level. Limnol. Oceanogr. 2016, 61, 1232–1244. [Google Scholar] [CrossRef]
- Skidmore, R.E.; Maberly, S.C.; Whitton, B.A. Patterns of spatial and temporal variation in phytoplankton chloro-phyll a in the River Trent and its tributaries. Sci. Total Environ. 1998, 210–211, 357–365. [Google Scholar] [CrossRef]
- Pinder, A.; Marker, A.F.H.; Pinder, A.C.; Ingram, J.K.G.; Leach, D.V.; Collet, G.D. Concentrations of suspended chlorophyll a in the Humber Rivers. Sci. Total Environ. 1997, 194–195, 373–378. [Google Scholar] [CrossRef]
- Shigesada, N.; Akira, O. Analysis of the self-shading effect on algal vertical distribution in natural waters. J. Math. Biol. 1981, 12, 311–326. [Google Scholar] [CrossRef]
- Trybula, E.M.; Cibin, R.; Burks, J.L.; Chaubey, I.; Brouder, S.M.; Volenec, J.J. Perennial rhizomatous grasses as bioenergy feedstock in SWAT: Parameter development and model improvement. Gcb Bioenergy 2015, 7, 1185–1202. [Google Scholar] [CrossRef]
- Bowes, M.J.; Loewenthal, M.; Read, D.S.; Hutchins, M.G.; Prudhomme, C.; Armstrong, L.K.; Harman, S.A.; Wickham, H.D.; Gozzard, E.; Carvalho, L. Identifying multiple stressor controls on phytoplankton dynamics in the River Thames (UK) using high-frequency water quality data. Sci. Total Environ. 2016, 569–570, 1489–1499. [Google Scholar] [CrossRef] [PubMed]
- Wright, R.T. Dynamics of a phytoplankton community in an ice-covered lake1. Limnol. Oceanogr. 1964, 9, 163–178. [Google Scholar] [CrossRef]
- Radwan, M.; Willems, P.; El-Sadek, A.; Berlamont, J. Modelling of dissolved oxygen and biochemical oxygen de-mand in river water using a detailed and a simplified model. Int. J. River Basin Manag. 2003, 1, 97–103. [Google Scholar] [CrossRef]
- Scheffer, M.; Rinaldi, S.; Huisman, J.; Weissing, F.J. Why plankton communities have no equilibrium: Solutions to the paradox. Hydrobiol. 2003, 491, 9–18. [Google Scholar] [CrossRef]
- Kruk, C.; Peeters, E.T.H.M.; Van Nes, E.H.; Huszar, V.L.M.; Costa, L.S.; Scheffer, M. Phytoplankton community com-position can be predicted best in terms of morphological groups. Limnol. Oceanogr. 2011, 56, 110–118. [Google Scholar] [CrossRef]
- Striebel, M.; Schabhuttl, S.; Hodapp, D.; Hinsamer, P.; Hillebrand, H. Phytoplankton responses to temperature in-creases are constrained by abiotic conditions and community composition. Oecologia 2016, 182, 815–827. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).