A Novel Physically Based Distributed Model for Irrigation Districts’ Water Movement
Abstract
:1. Introduction
2. Methodology
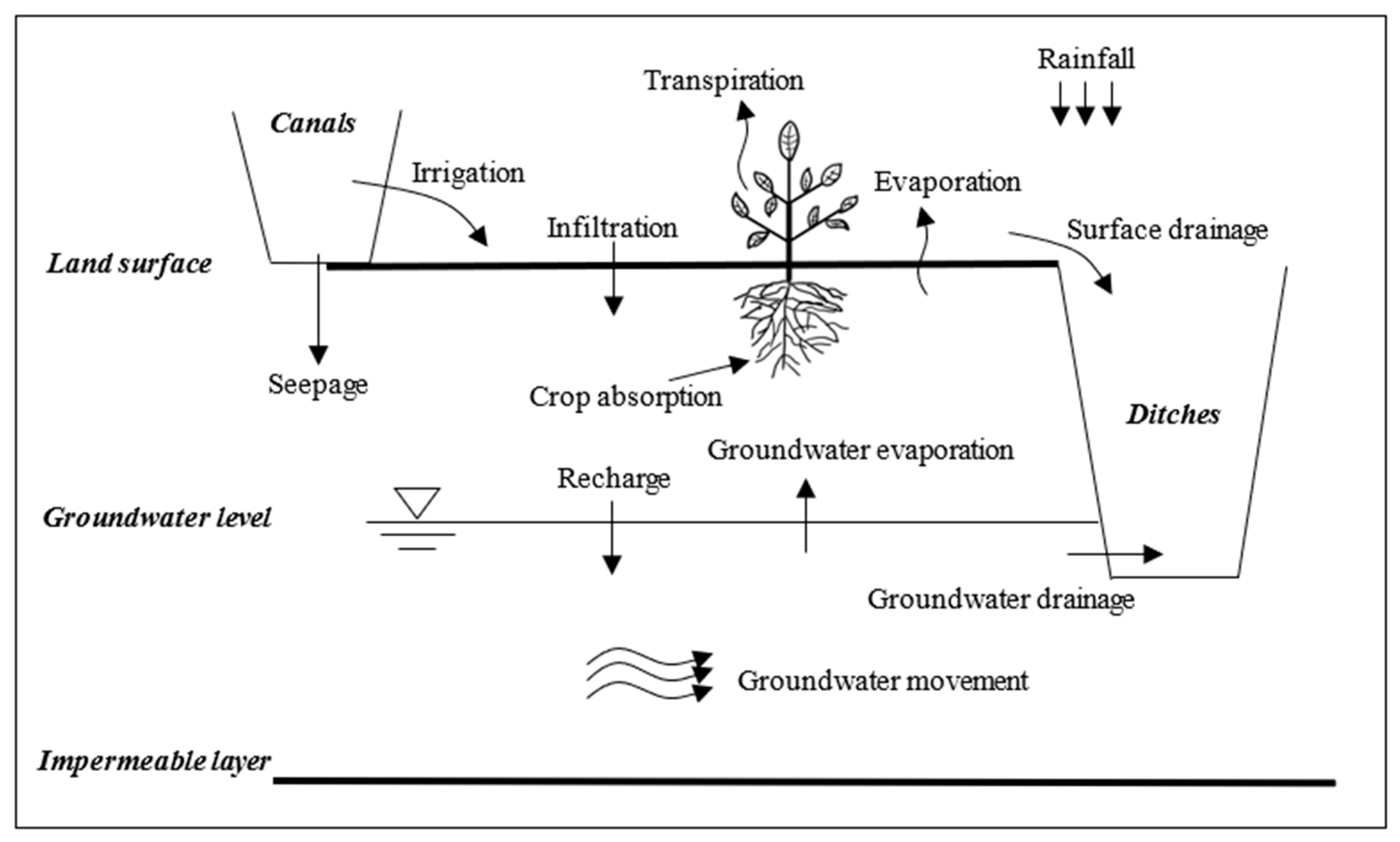
2.1. Soil Water Movement
2.2. Groundwater Movement
2.3. Channel Flow
2.4. Model Coupling
2.5. Model Inputs and Outputs
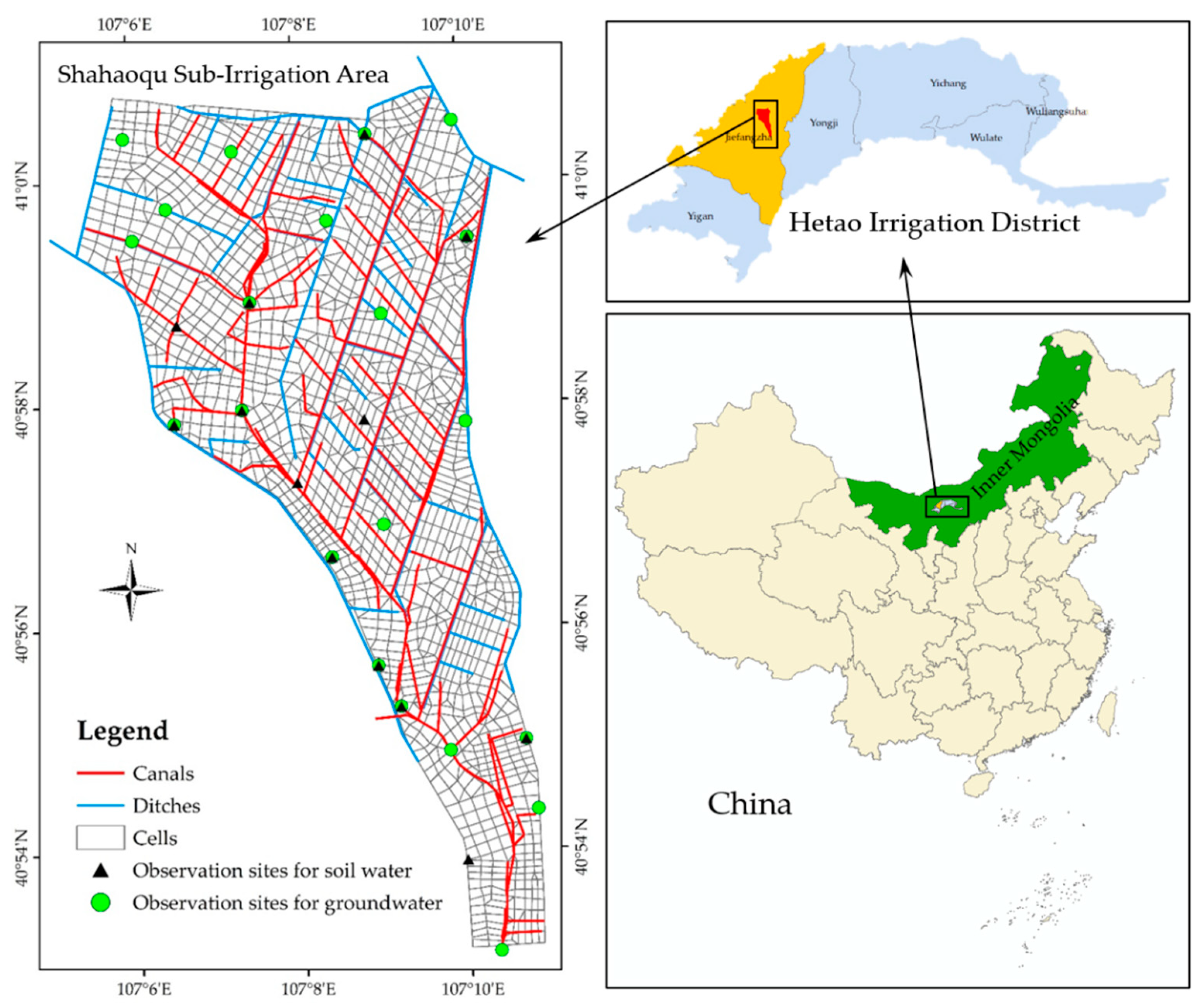
3. Test Case
3.1. Input Data
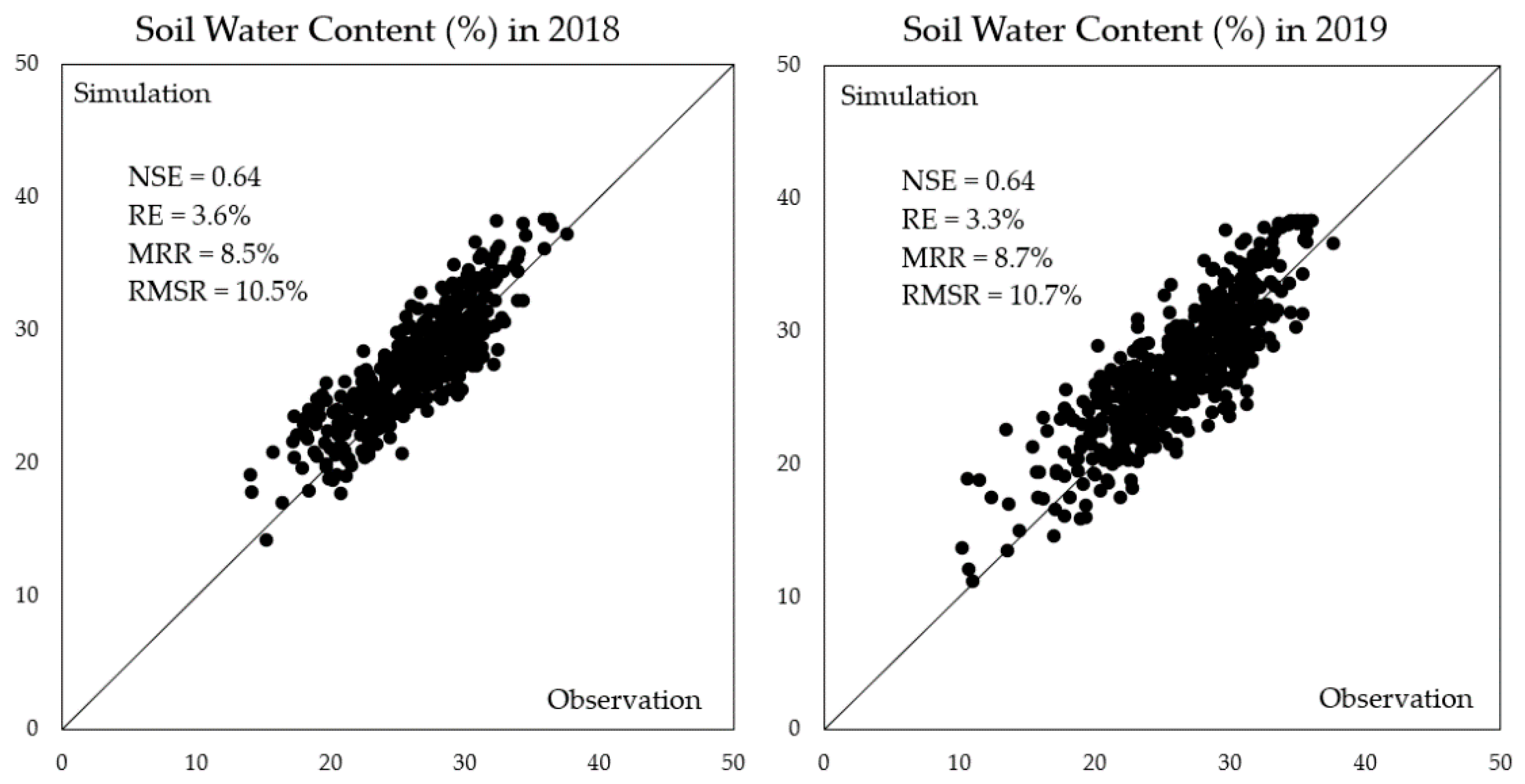
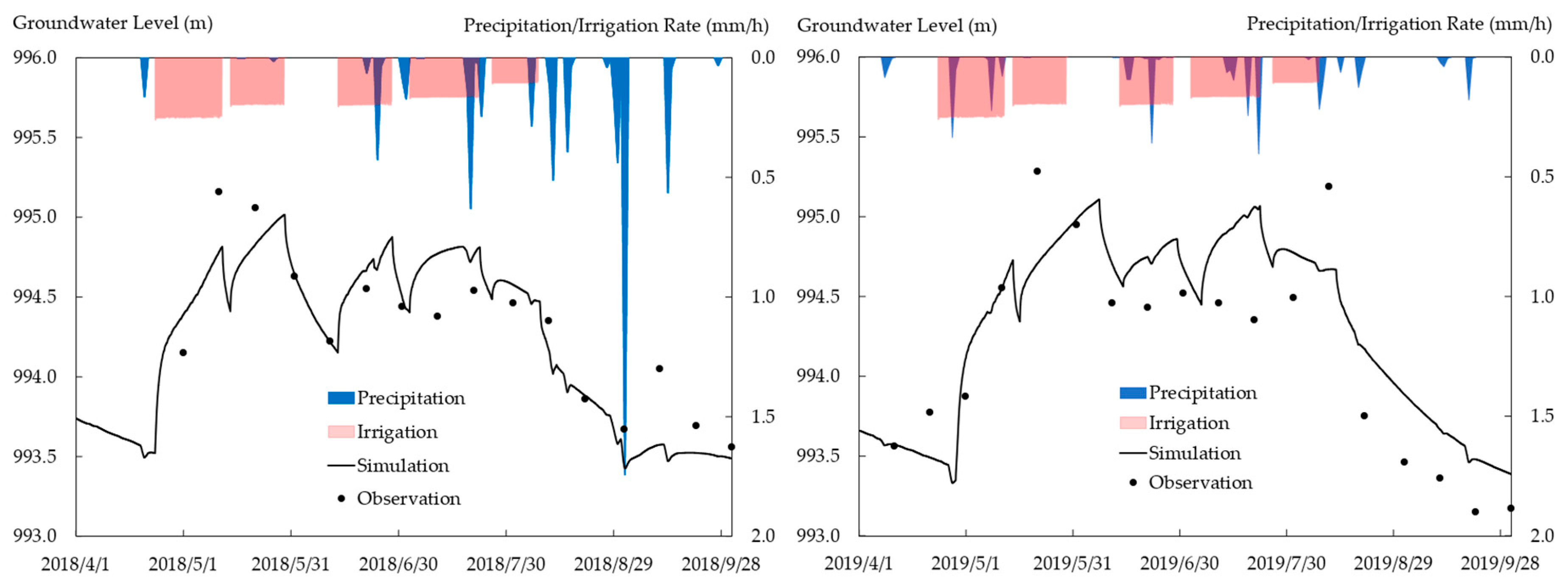
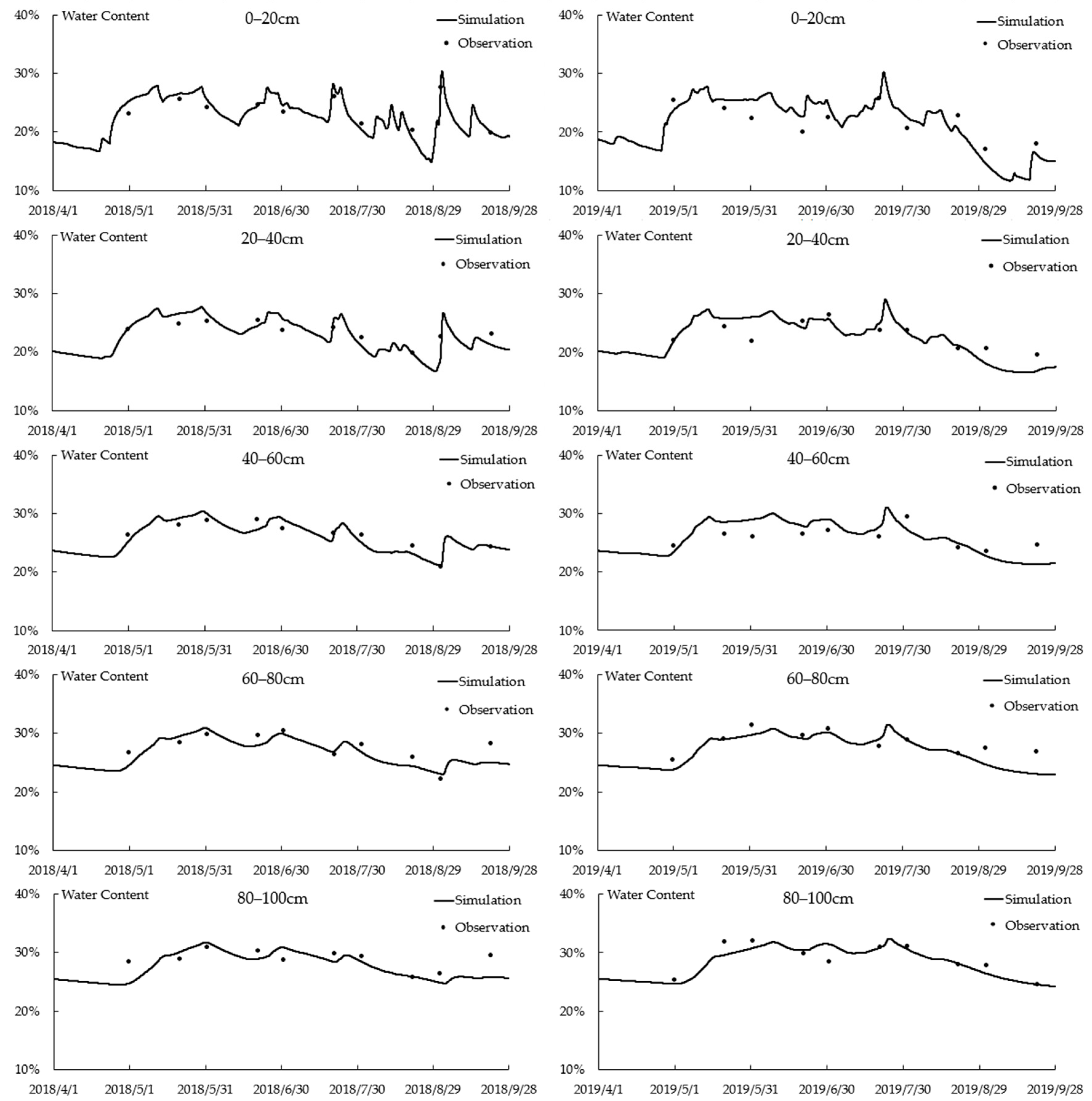
3.2. Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, S.; Wu, P.; Wang, Y.; Zhao, X.; Liu, J.; Zhang, X. The impacts of interannual climate variability and agricultural inputs on water footprint of crop production in an irrigation district of China. Sci. Total Environ. 2013, 444, 498–507. [Google Scholar] [CrossRef]
- Paniconi, C.; Putti, M. Physically based modeling in catchment hydrology at 50: Survey and outlook. Water Resour. Res. 2015, 51, 7090–7129. [Google Scholar] [CrossRef] [Green Version]
- Lin, L.; Jin-Zhong, Y.; Zhang, B.; Yan, Z. A simplified numerical model of 3-D groundwater and solute transport at large scale area. J. Hydrodyn. Ser. B 2010, 22, 319–328. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Griensven, A.V.; Liew, M.W.V. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1345–1352. [Google Scholar] [CrossRef]
- Zheng, J.; Li, G.-Y.; Han, Z.-Z.; Meng, G.-X. Hydrological cycle simulation of an irrigation district based on a SWAT model. Math. Comput. Model. 2010, 51, 1312–1318. [Google Scholar] [CrossRef]
- Xie, X.; Cui, Y. Development and test of SWAT for modeling hydrological processes in irrigation districts with paddy rice. J. Hydrol. 2011, 396, 61–71. [Google Scholar] [CrossRef]
- Gao, H.; Tang, Q.; Shi, X.; Zhu, C.; Bohn, T.; Su, F.; Sheffield, J.; Pan, M.; Lettenmaier, D.; Wood, E.F. Water Budget Record from Variable Infiltration Capacity (VIC) Model. 2010. Available online: http://hydrology.princeton.edu/~mpan/academics/uploads/content/articles/Water_Cycle_MEaSUREs_ATBD_Combined_v1.0.pdf (accessed on 20 October 2020).
- Dai, Y.; Zeng, X.; Dickinson, R.E.; Baker, I.; Bonan, G.B.; Bosilovich, M.G.; Denning, A.S.; Dirmeyer, P.A.; Houser, P.R.; Niu, G. The common land model. Bull. Am. Meteorol. Soc. 2003, 84, 1013–1024. [Google Scholar] [CrossRef] [Green Version]
- Leng, G.; Huang, M.; Tang, Q.; Gao, H.; Leung, L.R. Modeling the Effects of Groundwater-Fed Irrigation on Terrestrial Hydrology over the Conterminous United States. J. Hydrometeorol. 2014, 15, 957–972. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. A dynamic TOPMODEL. Hydrol. Process. 2001, 15, 1993–2011. [Google Scholar] [CrossRef]
- Gironás, J.; Roesner, L.A.; Rossman, L.A.; Davis, J. A new applications manual for the Storm Water Management Model (SWMM). Environ. Model. Softw. 2010, 25, 813–814. [Google Scholar] [CrossRef]
- Kim, H.D.; Kim, J.T.; Nam, W.H.; Kim, S.J.; Choi, J.Y.; Koh, B.S. Irrigation Canal Network Flow Analysis by a Hydraulic Model. Irrig. Drain. 2016, 65, 57–65. [Google Scholar] [CrossRef]
- D’Urso, G. Simulation and Management of on-Demand Irrigation Systems: A Combined Agrohydrological and Remote Sensing Approach; Wageningen University: Wageningen, The Netherlands, 2001. [Google Scholar]
- Ventrella, D.; Di Giacomo, E.; Costanza, F.; Giglio, L.; Raffaele, L.; Guastaferro, F.; Castrignanò, A. Soil Water Balance and Irrigation Strategies in an Agricultural District of Southern Italy. Ital. J. Agron. 2010, 5, 193–204. [Google Scholar] [CrossRef] [Green Version]
- Harbaugh, A.W. MODFLOW-2005, the US Geological Survey Modular Ground-Water Model: The Ground-Water Flow Process; US Department of the Interior: Washington, DC, USA; US Geological Survey: Reston, VA, USA, 2005.
- Trefry, M.G.; Muffels, C. FEFLOW: A finite-element ground water flow and transport modeling tool. Groundwater 2007, 45, 525–528. [Google Scholar] [CrossRef]
- Zhang, J.; Xuebin, Q.I.; Nurolla, M.; Ping, L.I.; Huang, Z.; Yanling, H.U. Appropriate Well-canal Irrigation Proportion in Irrigation District Based on MODFLOW and GIS. J. Irrig. Drain. 2017, 36, 58–63. [Google Scholar]
- Khalid Awan, U.; Tischbein, B.; Martius, C. Simulating Groundwater Dynamics Using Feflow-3D Groundwater Model Under Complex Irrigation and Drainage Network of Dryland Ecosystems of Central Asia. Irrig. Drain. 2015, 64, 283–296. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Van Genuchten, M.T. New features of version 3 of the HYDRUS (2D/3D) computer software package. J. Hydrol. Hydromech. 2018, 66, 133–142. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Zha, Y.-Y.; Tong, J.-X.; Yang, J.-Z. Method of coupling 1-D unsaturated flow with 3-D saturated flow on large scale. Water Sci. Eng. 2011, 4, 357–373. [Google Scholar]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and application of the integrated SWAT–MODFLOW model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Aliyari, F.; Bailey, R.T.; Tasdighi, A.; Dozier, A.; Arabi, M.; Zeiler, K. Coupled SWAT-MODFLOW model for large-scale mixed agro-urban river basins. Environ. Model. Softw. 2019, 115, 200–210. [Google Scholar] [CrossRef]
- Simunek, J.; Saito, H.; Sakai, M.; Genuchten, T.M. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media; International Ground Water Modeling Center, Colorado School of Mines: Golden, CO, USA, 1998; Volume 68. [Google Scholar]
- Van Dam, J.C. Field-Scale Water Flow and Solute Transport: SWAP Model Concepts, Parameter Estimation and Case Studies=[Waterstroming en Transport van Opgeloste Stoffen op Veldschaal]; [sn]; Wageningen University: Wageningen, The Netherlands, 2000. [Google Scholar]
- Flerchinger, G.N. The Simultaneous Heat and Water (SHAW) Model: Technical Documentation; Northwest Watershed Research Center, USDA Agricultural Research Service: Boise, ID, USA, 2000.
- Tan, X.; Shao, D.; Liu, H. Simulating soil water regime in lowland paddy fields under different water managements using HYDRUS-1D. Agric. Water Manag. 2014, 132, 69–78. [Google Scholar] [CrossRef]
- Ma, Y.; Feng, S.; Huo, Z.; Song, X. Application of the SWAP model to simulate the field water cycle under deficit irrigation in Beijing, China. Math. Comput. Model. 2011, 54, 1044–1052. [Google Scholar] [CrossRef]
- Li, R.; Shi, H.; Takeo, A.; Zhang, Y.; Zhang, X.; GN, F. Scheme of water saving irrigation in autumn based on SHAW model in Inner Mongolia Hetao irrigation district. Trans. Chin. Soc. Agric. Eng. 2010, 26, 31–36. [Google Scholar]
- Haj-Amor, Z.; Bouri, S. Use of HYDRUS-1D–GIS tool for evaluating effects of climate changes on soil salinization and irrigation management. Arch. Agron. Soil Sci. 2020, 66, 193–207. [Google Scholar] [CrossRef]
- Xu, X.; Huang, G.; Zhan, H.; Qu, Z.; Huang, Q. Integration of SWAP and MODFLOW-2000 for modeling groundwater dynamics in shallow water table areas. J. Hydrol. 2012, 412, 170–181. [Google Scholar] [CrossRef]
- Achu, A.; Reghunath, R.; Thomas, J. Mapping of groundwater recharge potential zones and identification of suitable site-specific recharge mechanisms in a tropical river basin. Earth Syst. Environ. 2020, 4, 131–145. [Google Scholar] [CrossRef]
- Masoud, M. Groundwater Resources Management of the Shallow Groundwater Aquifer in the Desert Fringes of El Beheira Governorate, Egypt. Earth Syst. Environ. 2020, 4, 147–165. [Google Scholar] [CrossRef]
- Kadhem, G.M.; Zubari, W.K. Identifying Optimal Locations for Artificial Groundwater Recharge by Rainfall in the Kingdom of Bahrain. Earth Syst. Environ. 2020, 4, 551–566. [Google Scholar] [CrossRef]
- Refshaard, J.C.; Storm, B.; Singh, V.P. MIKE SHE. In Computer Models of Watershed Hydrology; Water Resources Publications: Lone Tree, CO, USA, 1995; pp. 809–846. [Google Scholar]
- Brunner, P.; Simmons, C.T. HydroGeoSphere: A Fully Integrated, Physically Based Hydrological Model. Ground Water 2012, 50, 170–176. [Google Scholar] [CrossRef] [Green Version]
- Schulla, J.; Jasper, K. Modell Description WaSiM-ETH; Institute for Atmospheric and Climate Science, Swiss Federal Institute of Technology: Zürich, Switzerland, 2000. [Google Scholar]
- Walsum, P.E.V.V.; Veldhuizen, A.A.; Bakel, P.J.T.V.; Bolt, F.J.E.V.D.; Dik, P.E.; Groenendijk, P.; Querner, E.P.; Smit, M.F.R. SIMGRO 5.0. 1; Theory and Model Implementation (No. 913.1); Wageningen University: Wageningen, The Netherlands, 2004; Volume 64, pp. 393–413. [Google Scholar]
- Yue, W.; Zhan, C. Study on Sustainable Utilization Coupled Management Model for Water Resources in an Arid Irrigation District (China). In Proceedings of the 2010 4th International Conference on Bioinformatics and Biomedical Engineering, Chengdu, China, 18–20 June 2010; pp. 1–4. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Van Genuchten, M.T. A Numerical Model for Water and Solute Movernent; Unpublished Research Report; U.S. Salinity Laboratory: Riverside, CA, USA, 1987.
- Hoffman, G.J.; Van Genuchten, M.T. Soil properties and efficient water use: Water management for salinity control. Limit. Effic. Water Use Crop Prod. 1983, 73–85. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and drainage paper No. 56. Rome Food Agric. Organ. U. N. 1998, 56, e156. [Google Scholar]
- Lawrence, D.M.; Thornton, P.E.; Oleson, K.W.; Bonan, G.B. The partitioning of evapotranspiration into transpiration, soil evaporation, and canopy evaporation in a GCM: Impacts on land–atmosphere interaction. J. Hydrometeorol. 2007, 8, 862–880. [Google Scholar] [CrossRef]
- Panday, S.; Langevin, C.D.; Niswonger, R.G.; Ibaraki, M.; Hughes, J.D. MODFLOW–USG Version 1: An Unstructured Grid Version of MODFLOW for Simulating Groundwater Flow and Tightly Coupled Processes Using a Control Volume Finite-Difference Formulation; 2328-7055; US Geological Survey: Reston, VA, USA, 2013.
- Xian, C.; Qi, Z.; Tan, C.S.; Zhang, T.-Q. Modeling hourly subsurface drainage using steady-state and transient methods. J. Hydrol. 2017, 550, 516–526. [Google Scholar] [CrossRef]
- Ren, D.; Xu, X.; Hao, Y.; Huang, G. Modeling and assessing field irrigation water use in a canal system of Hetao, upper Yellow River basin: Application to maize, sunflower and watermelon. J. Hydrol. 2016, 532, 122–139. [Google Scholar] [CrossRef]
- Hao, Y.; Xu, X.; Ren, D.; Huang, Q.; Huang, G. Distributed modeling of soil water-salt dynamics and crop yields based on HYDRUS-EPIC model in Hetao Irrigation District. Trans. Chin. Soc. Agric. Eng. 2015, 31, 110–116. [Google Scholar]





| Item | Value | ||||
|---|---|---|---|---|---|
| Groundwater | Ksg [m·d−1] | 14.4 | |||
| μ [-] | 0.03 | ||||
| Soil water | Layer depth [cm] | 0~40 | 40~170 | 170~250 | 250~300 |
| θr [-] | 0.050 | 0.043 | 0.073 | 0.043 | |
| θs [-] | 0.413 | 0.460 | 0.500 | 0.450 | |
| α [cm−1] | 0.010 | 0.012 | 0.007 | 0.012 | |
| n [-] | 1.567 | 1.467 | 1.200 | 1.700 | |
| Kss [cm·d−1] | 10.333 | 17.467 | 6.000 | 28.100 | |
| Canal flow | Nm [m−1/3·s] | 0.022 | |||
| Ditch flow | Nm [m−1/3·s] | 0.029 | |||
| Year | Round | Time | Water Amount [104 m3] | Crops to Irrigate |
|---|---|---|---|---|
| 2018 | 1 | 4/23~5/14 | 577.4 | wheat, sunflower, melon |
| 2 | 5/14~5/25 | 365.6 | wheat, sunflower | |
| 3 | 6/13~6/26 | 368.3 | wheat, maize, sunflower | |
| 4 | 7/3~7/19 | 398.9 | maize, sunflower | |
| 5 | 7/26~8/4 | 173.6 | maize, sunflower | |
| 2019 | 1 | 4/28~5/16 | 530.4 | wheat, sunflower, melon |
| 2 | 5/16~5/30 | 500.7 | wheat, sunflower | |
| 3 | 6/14~6/23 | 194.6 | wheat, maize | |
| 4 | 7/6~7/20 | 424.8 | maize, sunflower | |
| 5 | 7/26~8/9 | 259.1 | maize, sunflower |
| Item | 2018 | 2019 | |
|---|---|---|---|
| Precipitation | 827.7 | 408.8 | |
| Irrigation | Inlet | 1820.9 | 1834.3 |
| To fields | 1197.3 | 1210.7 | |
| Seepage | 513.3 | 513.5 | |
| Evaporated | 18.7 | 11.4 | |
| Discarded | 93.8 | 100.9 | |
| Surface evaporation | 883.8 | 856.8 | |
| Crop transpiration | 1335.0 | 1241.8 | |
| Groundwater drainage | 218.8 | 222.4 | |
| Groundwater boundary flow 1 | −119.7 | −119.9 | |
| Water storage change 2 | −71.1 | −337.1 | |
| Balance error 3 | 52.1 (2.9%) | 29.1 (1.6%) | |
| Item | 2018 | 2019 |
|---|---|---|
| Precipitation | 827.7 | 408.8 |
| Irrigation | 1197.3 | 1210.7 |
| Evapotranspiration | 2218.8 | 2098.6 |
| Net recharge from 1 m depth below | 196.5 | 309.5 |
| Water storage change 1 | 2.7 | −169.6 |
| Number of Threads | 1 | 2 | 4 | 8 |
|---|---|---|---|---|
| Total time consumed | 1 | 0.75 | 0.50 | 0.35 |
| Time for canals | 0.01 | 0.01 | 0.01 | 0.01 |
| Time for ditches | 0.01 | 0.01 | 0.01 | 0.01 |
| Time for soil water | 0.81 | 0.56 | 0.33 | 0.19 |
| Time for groundwater | 0.08 | 0.08 | 0.08 | 0.08 |
| Time for output | 0.10 | 0.08 | 0.06 | 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, B.; Chen, H.; Wang, S.; Jin, Y.; Jia, J.; Chang, X.; Fu, X.; Chai, R.; Wei, M. A Novel Physically Based Distributed Model for Irrigation Districts’ Water Movement. Water 2021, 13, 692. https://doi.org/10.3390/w13050692
Mi B, Chen H, Wang S, Jin Y, Jia J, Chang X, Fu X, Chai R, Wei M. A Novel Physically Based Distributed Model for Irrigation Districts’ Water Movement. Water. 2021; 13(5):692. https://doi.org/10.3390/w13050692
Chicago/Turabian StyleMi, Boyu, Haorui Chen, Shaoli Wang, Yinlong Jin, Jiangdong Jia, Xiaomin Chang, Xiaojun Fu, Ronghua Chai, and Meiling Wei. 2021. "A Novel Physically Based Distributed Model for Irrigation Districts’ Water Movement" Water 13, no. 5: 692. https://doi.org/10.3390/w13050692
APA StyleMi, B., Chen, H., Wang, S., Jin, Y., Jia, J., Chang, X., Fu, X., Chai, R., & Wei, M. (2021). A Novel Physically Based Distributed Model for Irrigation Districts’ Water Movement. Water, 13(5), 692. https://doi.org/10.3390/w13050692








