Distributed-Framework Basin Modeling System: I. Overview and Model Coupling
Abstract
:1. Introduction
1.1. The Issue of the Distributed Hydrological Model
1.2. The Issue of the Integration of the Geographic Information System and Hydrological Models
2. Materials and Methods
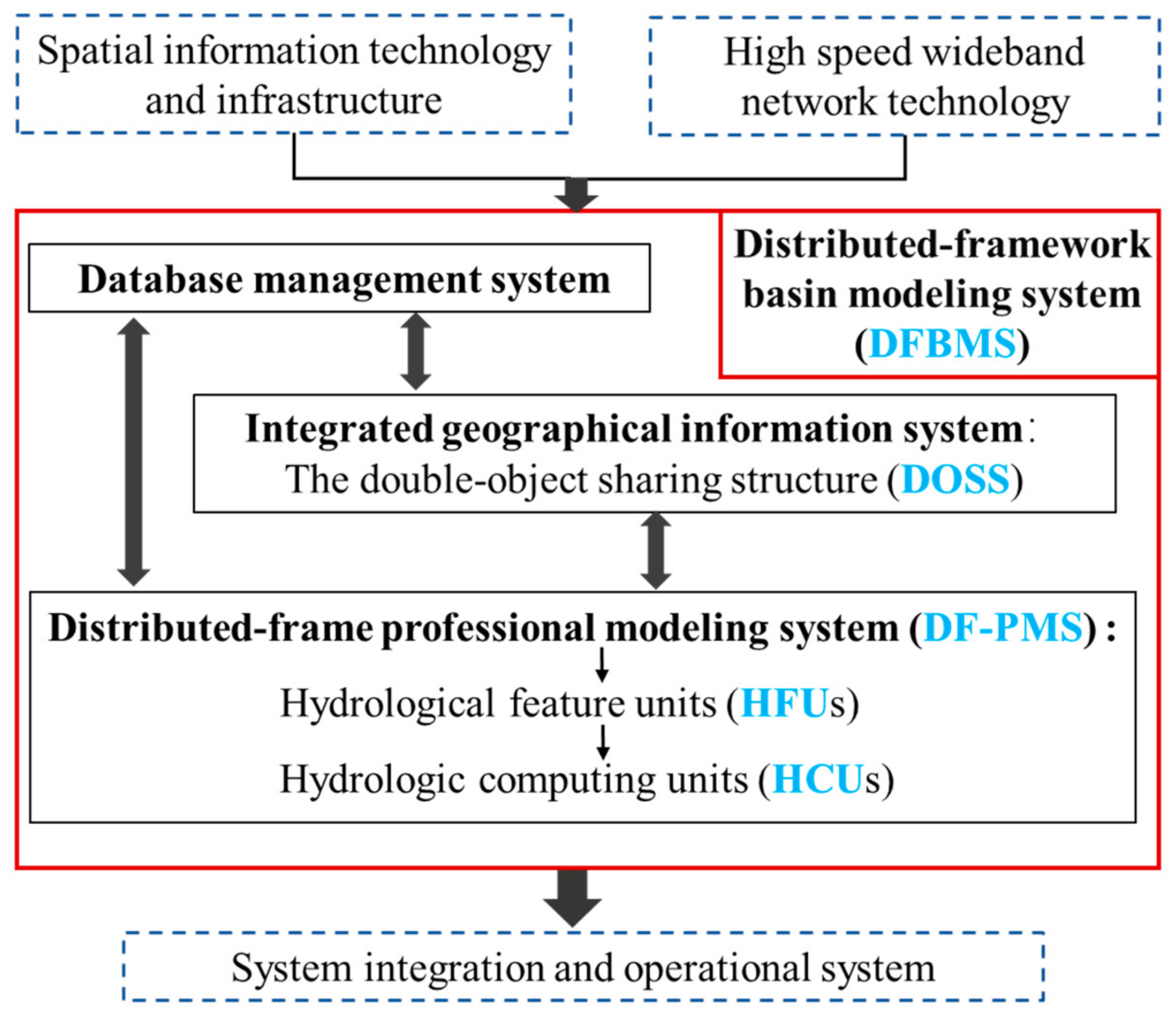
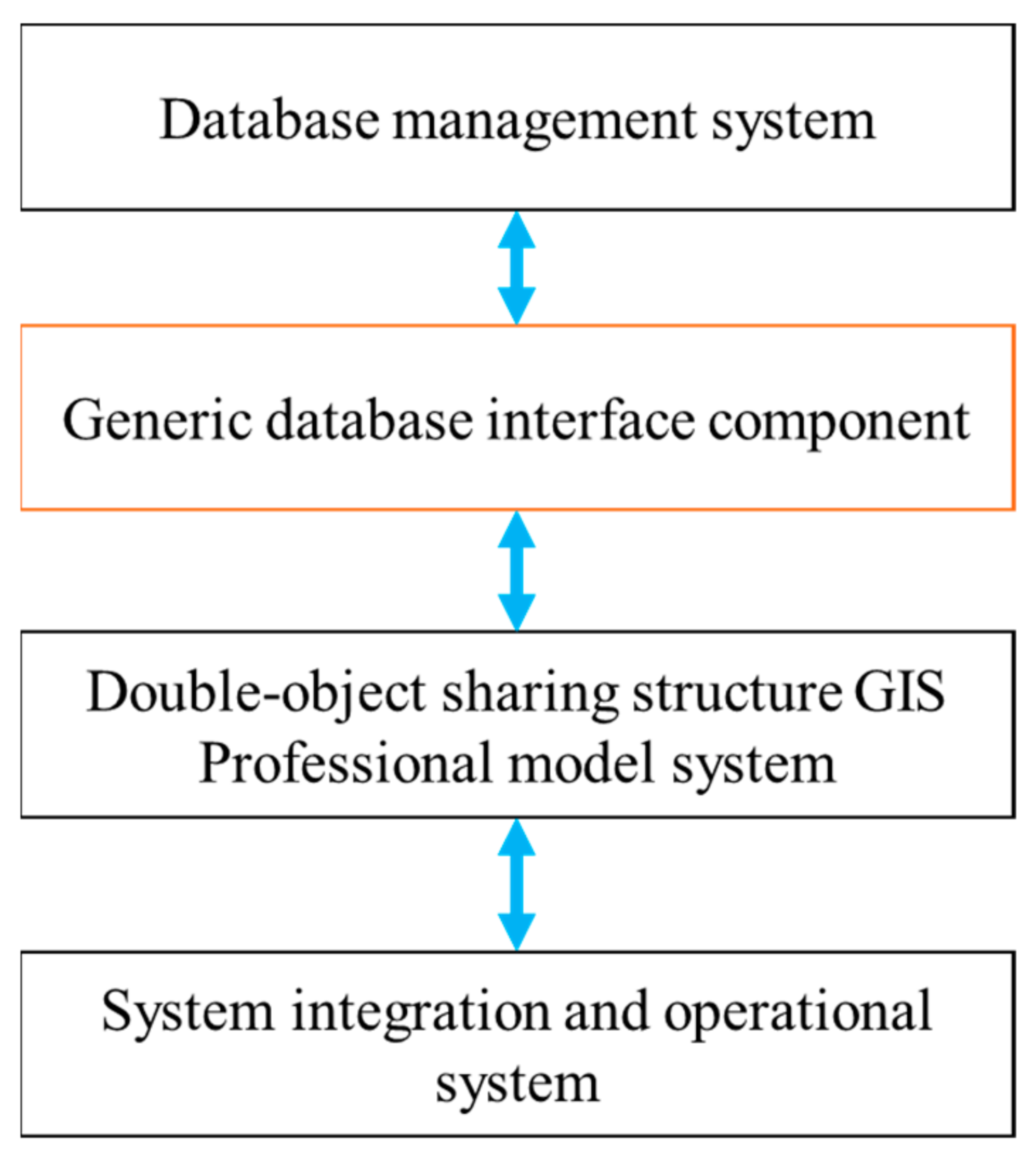
2.1. The Structure of the Distributed-Framework Basin Modeling System
- Database management system: The basic system for DFBMS. This contains the technology for data management, mass data memory and management, data mining, and the data warehouse.
- Geographical integrated system: The core part of DFBMS that carries out the visualization of model results and information. The capabilities and functions of GIS in the DFBMS are completely self-developed, which is the main role of the geographical integrated system. It not only provides the spatial information required by DFBMS, but also supplies a visual representation of spatial information and model results. The GIS can interpret remote sensing data as being one of four different types of underlying surface that will be used for rainfall runoff.
- Professional model system: A modeling system that can be used to simulate changes in the geographical environment in the past, present, and future. The professional model system is another kernel for DFBMS, containing various professional models, such as the hydrologic model, hydraulic model, digital basin generating model, water quality model, and sediment yield model. In this study, we only introduce the hydrologic and hydraulic model.
2.2. Distributed-Framework Professional Modeling System (DF-PMS)
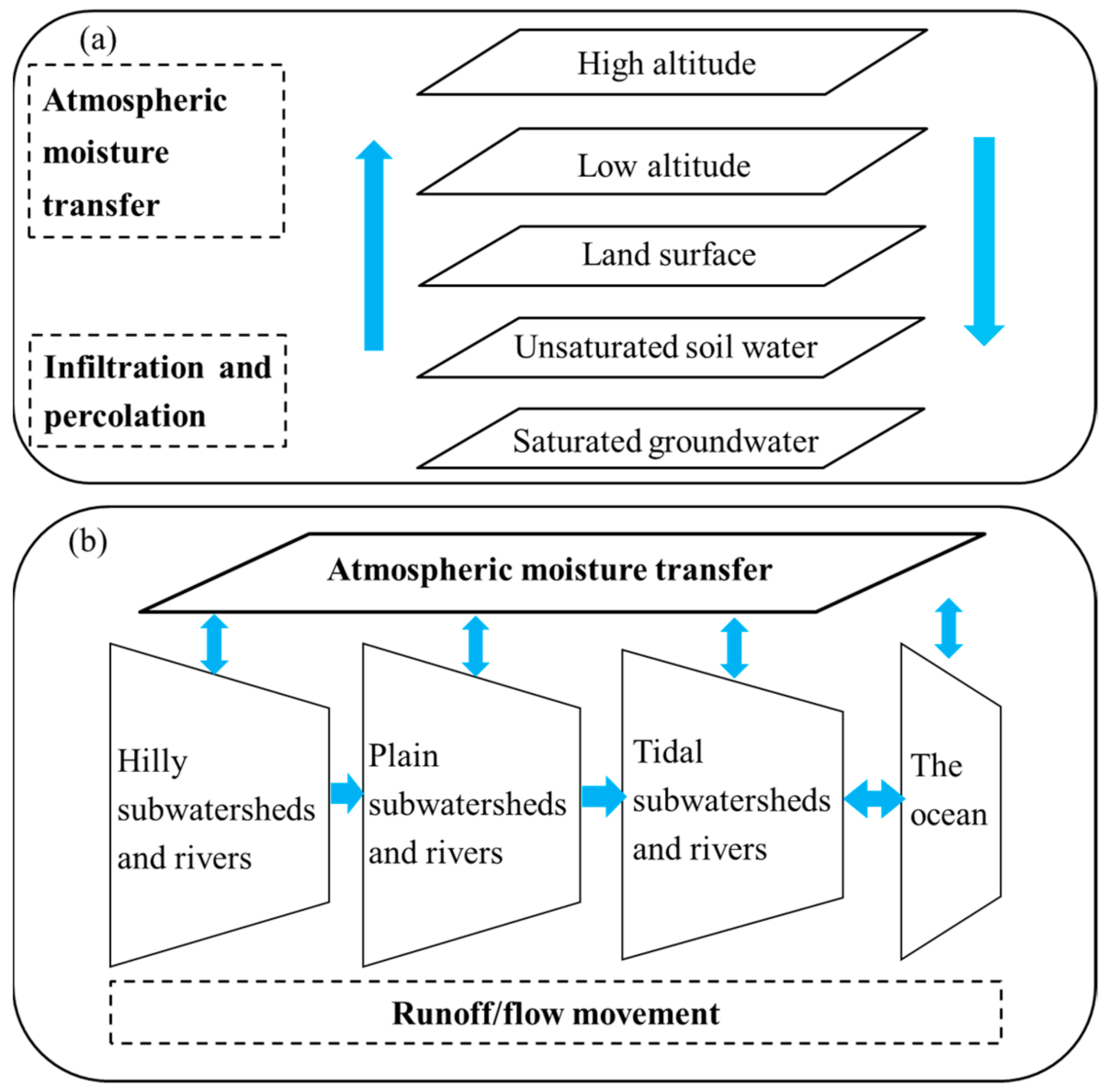
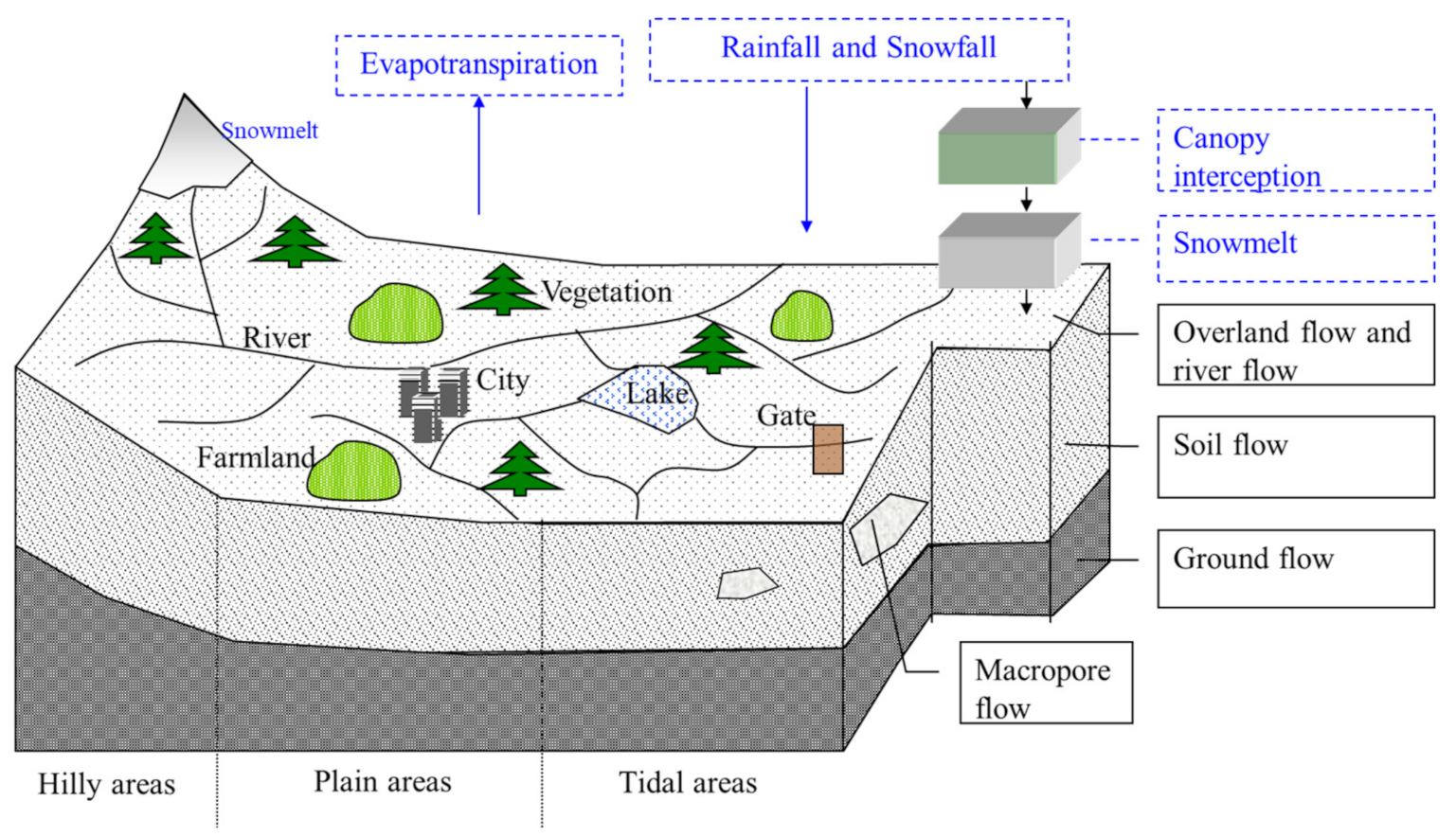
2.2.1. Hydrological Processes
2.2.2. Distributed-Frame Professional Modeling System
2.2.3. Hydrological Feature Unit (HFU)
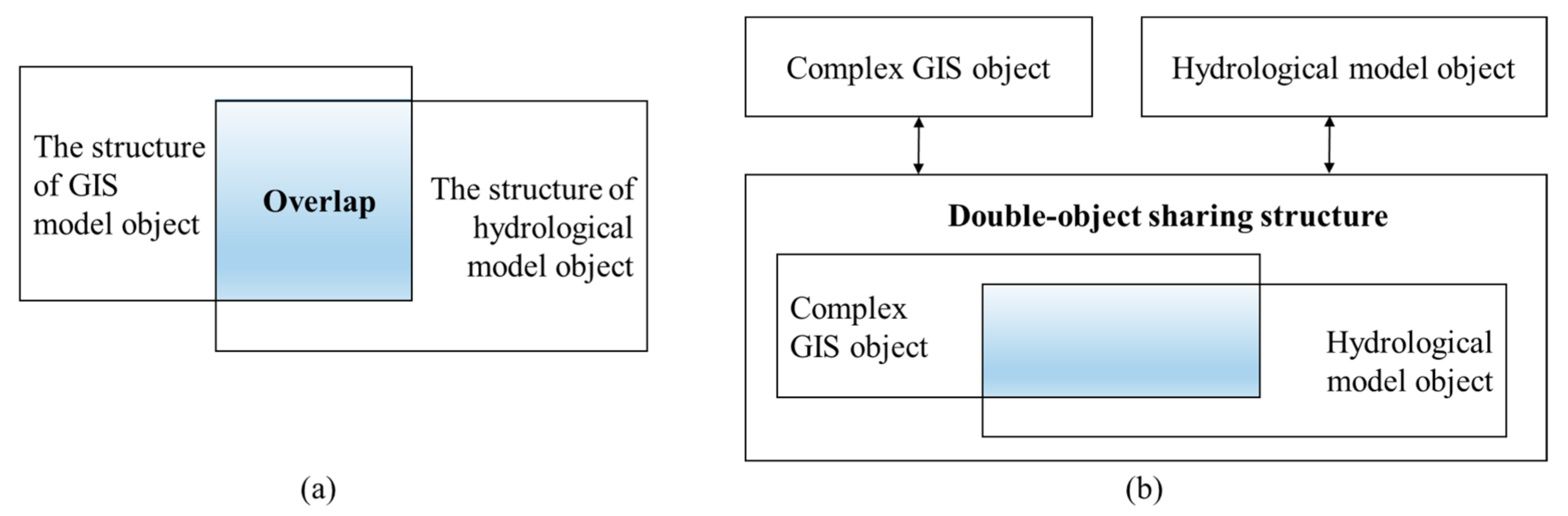
2.3. Systems Integration for GIS and the Professional Model System
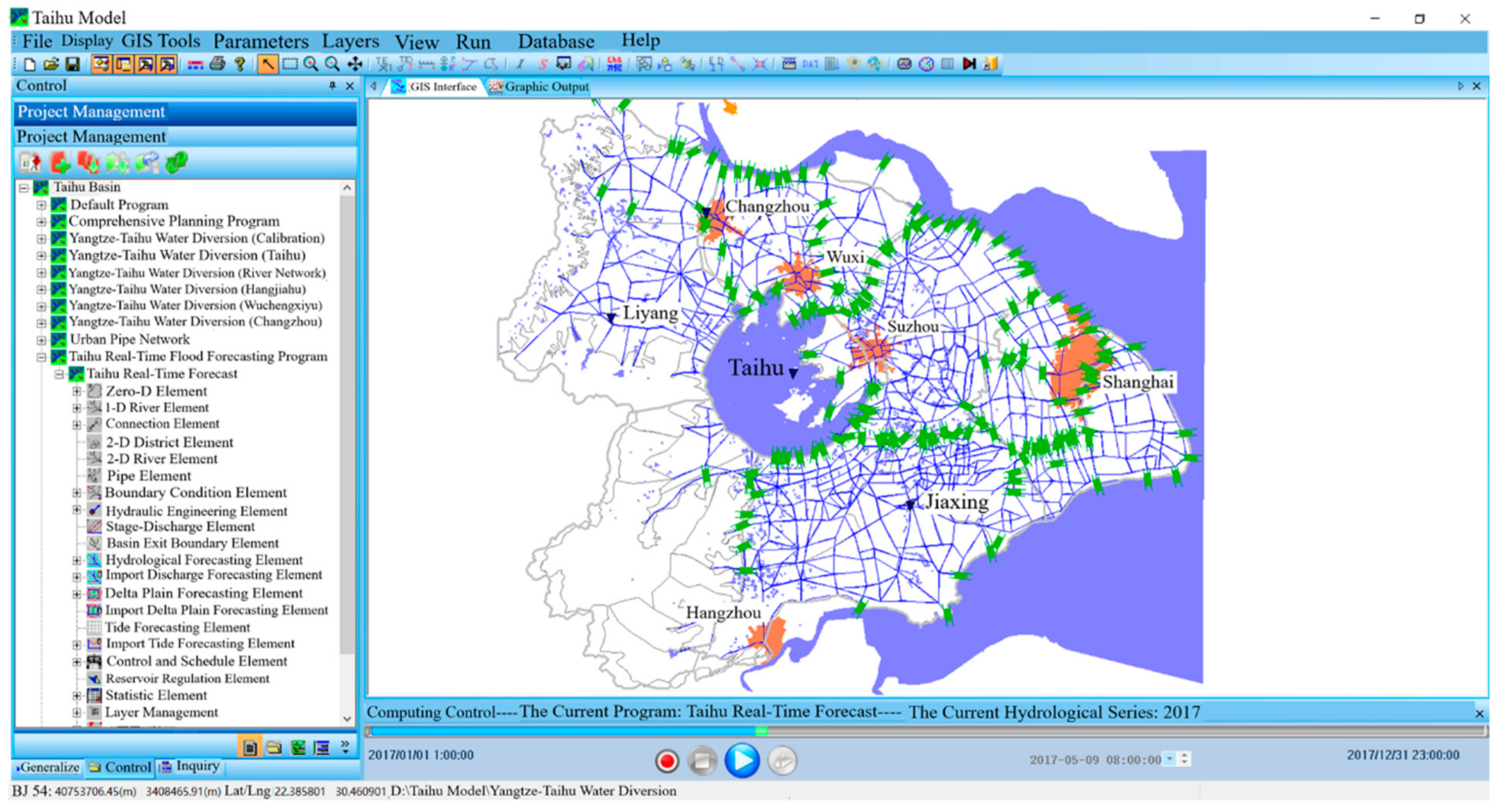
2.4. Development of the Distributed-Framework Basin Modeling System
3. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, E.; Merwade, V.; Heathman, G.C. Implementation of surface soil moisture data assimilation with watershed scale distributed hydrological model. J. Hydrol. 2012, 416–417, 98–117. [Google Scholar] [CrossRef]
- Freeze, A.R.; Harlan, R.L. Blueprint for a physically-based, digitally-simulated hydrologic response model. J. Hydrol. 1969, 9, 237–258. [Google Scholar] [CrossRef]
- Götzinger, J.; Bárdossy, A. Comparison of four regionalisation methods for a distributed hydrological model. J. Hydrol. 2007, 333, 374–384. [Google Scholar] [CrossRef]
- Fenicia, F.; Kavetski, D.; Savenije, H.H.; Pfister, L. From spatially variable streamflow to distributed hydrological models: Analysis of key modeling decisions. Water Resour. Res. 2016, 52, 954–989. [Google Scholar] [CrossRef] [Green Version]
- Skoulikaris, C.; Filali-Meknassi, Y.; Aureli, A.; Amani, A.; Jiménez-Cisneros, B. Information-Communication Technologies as an Integrated Water Resources Management (IWRM) Tool for Sustainable Development. In Achievements and Challenges of Integrated River Basin Management; IntechOpen: London, UK, 2018. [Google Scholar]
- Christian Refsgaard, J.; Storm, B.; Clausen, T. Systeme hydrologique Europeen (SHE): Review and perspectives after 30 years development in distributed physically-based hydrological modelling. Hydrol. Res. Int. J. 2010, 41, 355–377. [Google Scholar] [CrossRef]
- Metcalfe, P.; Beven, K.; Freer, J. Dynamic TOPMODEL. Environ. Model. Softw. 2015, 72, 155–172. [Google Scholar] [CrossRef] [Green Version]
- Shekhar, S.; Xiong, H. Soil and water assessment tool “SWAT”. Encycl. GIS 2008. [Google Scholar] [CrossRef]
- Yao, C.; Li, Z.; Yu, Z.; Zhang, K. A priori parameter estimates for a distributed, grid-based Xinanjiang model using geographically based information. J. Hydrol. 2012, 468–469, 47–62. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. Asabe 2012, 55, 1345–1352. [Google Scholar] [CrossRef]
- Habets, F.; Boone, A.; Champeaux, J.L.; Etchevers, P.; Franchistéguy, L.; Leblois, E.; Ledoux, E.; le Moigne, P.; Martin, E.; Morel, S.; et al. The SAFRAN-ISBA-MODCOU hydrometeorological model applied over France. J. Geophys. Res. Atmos. 2008. [Google Scholar] [CrossRef] [Green Version]
- Skoulikaris, C.; Anagnostopoulou, C.; Lazoglou, G. Hydrological modeling response to climate model spatial analysis of a South Eastern Europe international basin. Climate 2020, 8, 1. [Google Scholar] [CrossRef] [Green Version]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.J.; DMIP Participants. Overall distributed model intercomparison project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Carpenter, M.T.; Georgakakos, K.P.; Sperfslagea, J.A. On the parametric and NEXRAD-radar sensitivities of a distributed hydrologic model suitable for operational use. J. Hydrol. 2001, 253, 169–193. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Z.; Li, Z. Performance of WASMOD and SWAT on hydrological simulation in Yingluoxia watershed in northwest of China. Hydrol. Process. 2011, 25, 2001–2008. [Google Scholar] [CrossRef]
- Smith, M.B.; Seo, D.J.; Koren, V.I.; Reed, S.M.; Zhang, Z.; Duan, Q.; Cong, S. The distributed model intercomparison project (DMIP): Motivation and experiment design. J. Hydrol. 2004, 298, 4–26. [Google Scholar] [CrossRef]
- Beven, K. Towards an alternative blueprint for a physically based digitally simulated hydrologic response modelling system. Hydrol. Process. 2002, 16, 189–206. [Google Scholar] [CrossRef] [Green Version]
- Dutta, D.; Herath, S.; Musiake, K. Flood inundation simulation in a river basin using a physically based distributed hydrologic model. Hydrol. Process. 2000, 14, 497–519. [Google Scholar] [CrossRef]
- Kavvas, M.L. Nonlinear hydrologic processes: Conservation equations for determining their means and probability distributions. J. Hydrol. Eng. 2003, 8, 44–53. [Google Scholar] [CrossRef]
- James, W. Perspectives in hydrologic modeling and simulation. In Simulation Modeling for Watershed Management; Springer: Berlin/Heidelberg, Germany, 2001; pp. 41–49. [Google Scholar] [CrossRef]
- Akbari, A.; Samah, A.A.; Othman, F. Integration of SRTM and TRMM date into the GIS-based hydrological model for the purpose of flood modelling. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 4747–4775. [Google Scholar]
- Masutomi, Y.; Inui, Y.; Takahashi, K.; Matsuoka, Y. Development of highly accurate global polygonal drainage basin data. Hydrol. Process. 2010, 23, 572–584. [Google Scholar] [CrossRef]
- Goodchild, M.; Haining, R.; Wise, S. Integrating GIS and spatial data analysis: Problems and possibilities. Int. J. Geogr. Inf. Syst. 1992, 6, 407–423. [Google Scholar] [CrossRef]
- Payne, M.S.; Woessner, W.W. An aquifer classification system and geographical information system-based analysis tool for watershed managers in the Western U.S. JAWRA J. Am. Water Resour. Assoc. 2010, 46, 1003–1023. [Google Scholar] [CrossRef]
- Mcdonnell, A.R.; Lloyd, C.; Burrough, P. Principles of Geographical Information Systems; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Holt, A.E.; McCune, B.; Neitlich, P. Spatial scale of GIS-derived categorical variables affects their ability to separate sites by community composition. Appl. Veg. Sci. 2008, 11, 421–430. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z.; Chen, Z. Implementation of object-oriented GIS data model with topological relations between spatial objects. In Proceedings of the International Conference on Graphic and Image Processing (ICGIP 2012), Singapore, 5–7 October 2012. [Google Scholar]
- Goodchild, M.F. The future of digital earth. Geogr. Inf. Sci. 2012, 18, 93–98. [Google Scholar] [CrossRef]
- Viessman, W.; Lewis, G.L. Introduction to hydrology:United States edition. Archaea 2003, 2013, 810286. [Google Scholar]
- Kumar, M.; Marks, D.; Dozier, J.; Reba, M.; Winstral, A. Evaluation of distributed hydrologic impacts of temperature-index and energy-based snow models. Adv. Water Resour. 2013, 56, 77–89. [Google Scholar] [CrossRef]
- Tobin, C.; Schaefli, B.; Nicótina, L.; Simoni, S.; Barrenetxea, G.; Smith, R.; Rinaldo, A. Improving the degree-day method for sub-daily melt simulations with physically-based diurnal variations. Adv. Water Resour. 2013, 55, 149–164. [Google Scholar] [CrossRef] [Green Version]
- Perumal, M. Multilinear Muskingum flood routing method. J. Hydrol. 1992, 133, 259–272. [Google Scholar] [CrossRef]
- Trefry, G.M.; Muffels, C. FEFLOW: A finite-element groundwater flow and transport modeling tool. Groundwater 2007, 45, 525–528. [Google Scholar] [CrossRef]
- Maloszewski, P.; Zuber, A. A general lumped parameter model for the interpretation of tracer data and transit time calculation in hydrologic systems: Comments. J. Hydrol. 1998, 204, 297–300. [Google Scholar] [CrossRef]
- Yao, C.; Li, Z.J.; Bao, H.J.; Yu, Z.B. Application of a developed grid-xinanjiang model to Chinese watersheds for flood forecasting purpose. J. Hydrol. Eng. 2009, 14, 923–934. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Cent. Agric. Rural Dev. Publ. 2007, 50, 1211–1250. [Google Scholar] [CrossRef] [Green Version]
| No. | HFUs | Type | Influencing Factors | Discrete Scale in Simulation | Vertical Circulation | Transverse Circulation | Simulation Models or Methods | Primary Reference | |
|---|---|---|---|---|---|---|---|---|---|
| Time Scale | Spatial Scale (HCUs Division) | ||||||||
| 1 | Snowfield | Runoff generation | Snow depth, area, terrain, perennial average temperature, meteorological condition, etc. | 1 day | Distributed according to the actual type, no more division for the HCUs. | Snowmelt | Hilly areas | The energy-balance method, or the diurnal temperature-index method | [30,31] |
| 2 | Hilly sub-watershed | Runoff generation and confluence | Subwatershed, landuse, collecting area, soil type, vegetation type, etc. | hour, up to day | The area according to the time scale, and the HCU division based on the distribution of underlying information, usually in kilometers. | Overland flow and river flow, soil flow, ground flow | Hilly areas, plain areas | Xinanjiang model, or TOPMODEL | [7,9] |
| 3 | Hilly river | Confluence | Flow regime (sub- or supercritical flow) | hour | The reach length for HCUs (cross-section) according to the time scale, usually the distance for cross sections is in kilometers. | Overland flow and river flow | Hilly areas, plain areas | Muskingum model | [32] |
| 4 | Plain overland flow | Runoff generation and confluence | Subwatershed, landuse, collecting area, soil type, vegetation type, etc. | 1 hour to 1 day | The area according to the time scale, and the HCU division based on the distribution of underlying information, from meters to kilometers. | Overland flow and river flow, soil flow, ground flow | Plain areas, tidal areas | Rainfall-runoff model in water area, rain-fed land, paddy field and construction land | In Section 2.2.3 of the 2nd paper in this series |
| 5 | Plain river | Routing | Flow regime, flow direction, hydraulic engineering structures, intake and drainage, etc. | seconds to hours | The reach length for HCUs (cross-section) according to the time scale, usually the distance for cross-sections is from meters to kilometers. | Overland flow and river flow | Plain areas, tidal areas | One or two dimensional hydrodynamic model | In the 3rd paper in this series |
| 6 | Urban pipe network | Routing | Distribution of pipe network, design parameter, sediment in the pipe, etc. | seconds to hours | Spatial scale according to major inspection well, usually from meters to kilometers | Overland flow and pipe flow | Plain areas, tidal areas | Urban pipe network model | Further paper |
| 7 | Lakes and reservoirs (including flood plains and paddy fields) | Routing | Natural topography, wind speed, etc. | seconds to hours | Usually from the meters to kilometers for two-dimensional simulation, but no grid for zero-dimensional simulation | Overland flow | Hilly areas, plain areas, tidal areas | Zero-, or two dimensional model | In the 3rd paper in this series |
| 8 | Hydraulic engineering structures | Routing | According to type of engineering, overflowing type, etc. | Same as connected hydrological feature unit | Same as the engineering scale | Overland flow and river flow | Hilly areas, plain areas, tidal areas | Gate and dam simulation | In the 3rd paper in this series |
| 9 | Unsaturated soil water zones | Runoff generation | Soil type, initial water content, etc. | minutes to hours | According to different calculated modes, from meters to kilometers | Unsaturated soil water | Hilly areas, plain areas, tidal areas | Finite element subsurface FLOW system (FEFLOW) | [33] |
| 10 | Saturated groundwater zones | Confluence | According to the groundwater table: Deep or shallow | 1 day to 1 month | Grid divided according to the distribution of underground rock | Saturated groundwater | Hilly areas, plain areas, tidal areas | FEFLOW | [33] |
| 11 | Karst regions | Confluence | According to macropore flow and underground river region | 1 h | The area according to the time scale, and the HCU division based on the distribution of underground river region | Interflow | Hilly areas | Not applied in this stage | _ |
| Type of Variable | Name of Variable | Variable Information | Classify |
|---|---|---|---|
| CArray < UINT, UINT> | m_LineNumber | Multiply connected boundary information | Public |
| LONG | M_NumofXgrid | The total grid number in X direction | Public |
| LONG | M_NumofYgrid | The total grid number in Y direction | Public |
| Double | m_XX | X-coordinate | Public |
| Double | m_YY | Y-coordinate | Public |
| Double | m_ZD | Elevation of grid nodes | Public |
| Double | m_AVV | Velocity V | Model object |
| Double | m_AUU | Velocity U | Model object |
| Double | m_TZZ | Water surface elevation Z | Model object |
| Double | m_CTT | Concentration field | Model object |
| BOOL | m_bLineType | Type of line element | GIS object |
| UINT | m_LineWidth | Width of line element | GIS object |
| SymbolInfo | m_LSymbolInfo | The pattern of line element | GIS object |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Hua, W.; Chen, G.; Fang, X.; Li, X. Distributed-Framework Basin Modeling System: I. Overview and Model Coupling. Water 2021, 13, 678. https://doi.org/10.3390/w13050678
Wang C, Hua W, Chen G, Fang X, Li X. Distributed-Framework Basin Modeling System: I. Overview and Model Coupling. Water. 2021; 13(5):678. https://doi.org/10.3390/w13050678
Chicago/Turabian StyleWang, Chuanhai, Wenjuan Hua, Gang Chen, Xing Fang, and Xiaoning Li. 2021. "Distributed-Framework Basin Modeling System: I. Overview and Model Coupling" Water 13, no. 5: 678. https://doi.org/10.3390/w13050678
APA StyleWang, C., Hua, W., Chen, G., Fang, X., & Li, X. (2021). Distributed-Framework Basin Modeling System: I. Overview and Model Coupling. Water, 13(5), 678. https://doi.org/10.3390/w13050678








