The FLOod Probability Interpolation Tool (FLOPIT): A Simple Tool to Improve Spatial Flood Probability Quantification and Communication
Abstract
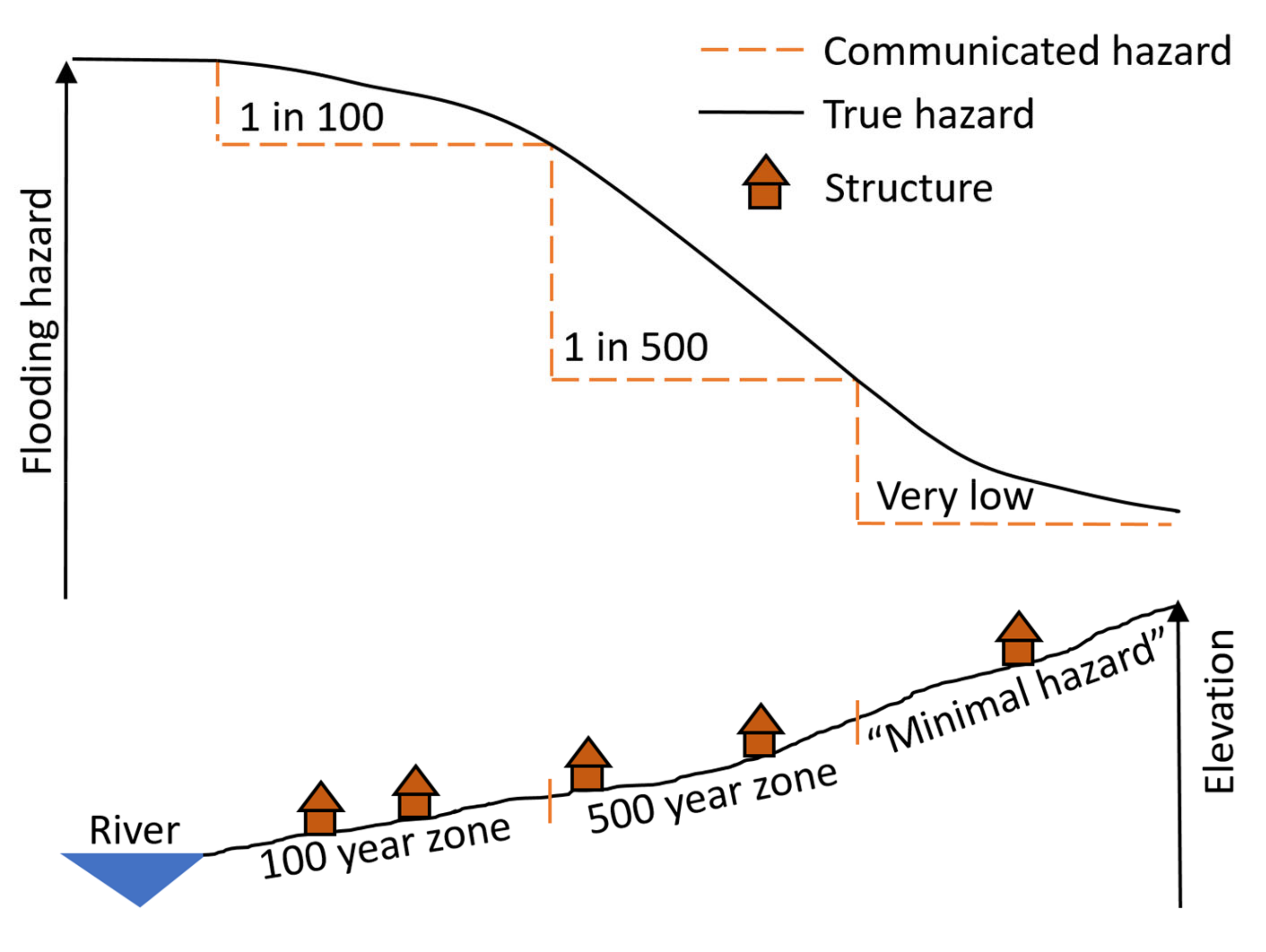
:1. Introduction
2. Materials and Methods
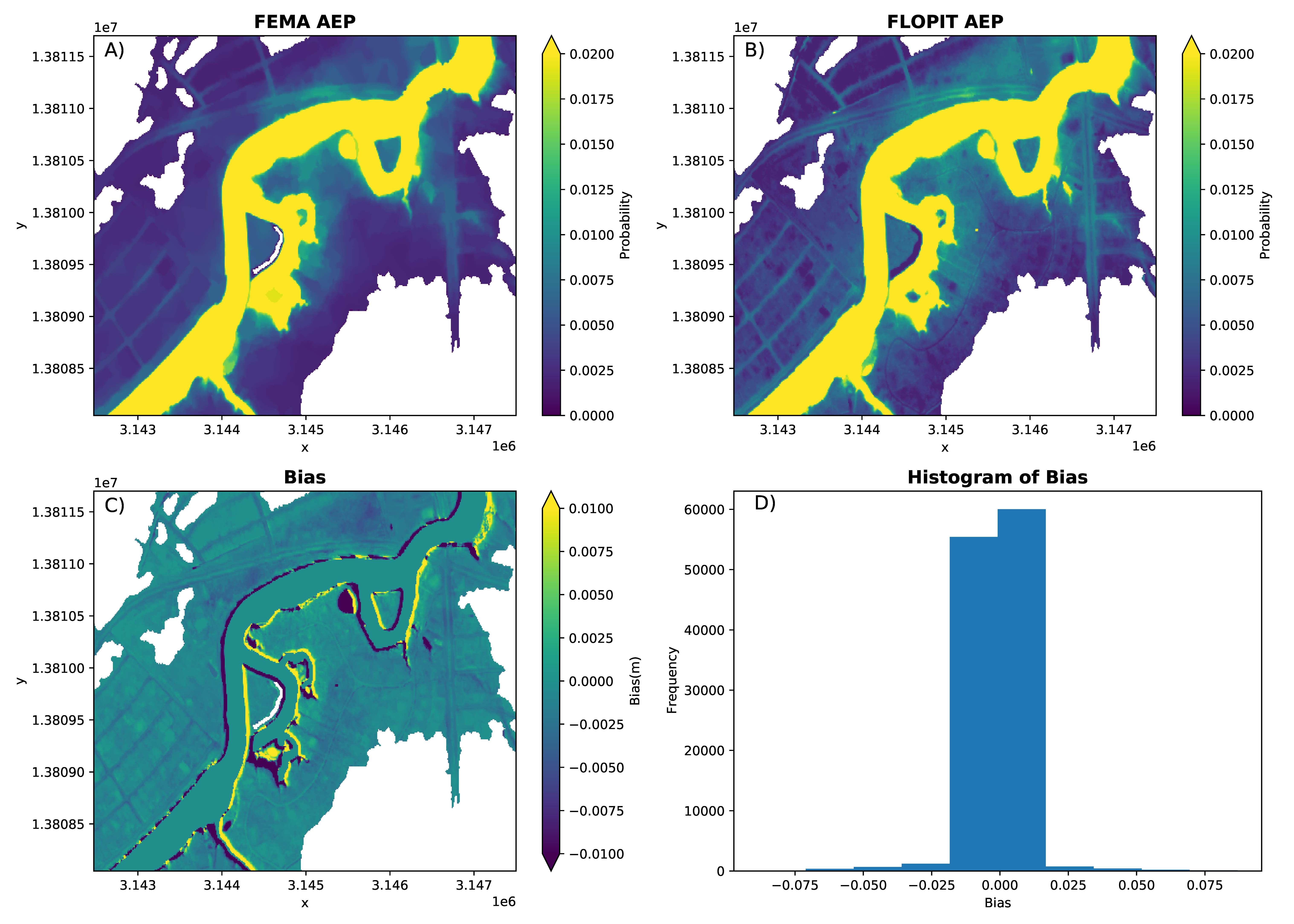
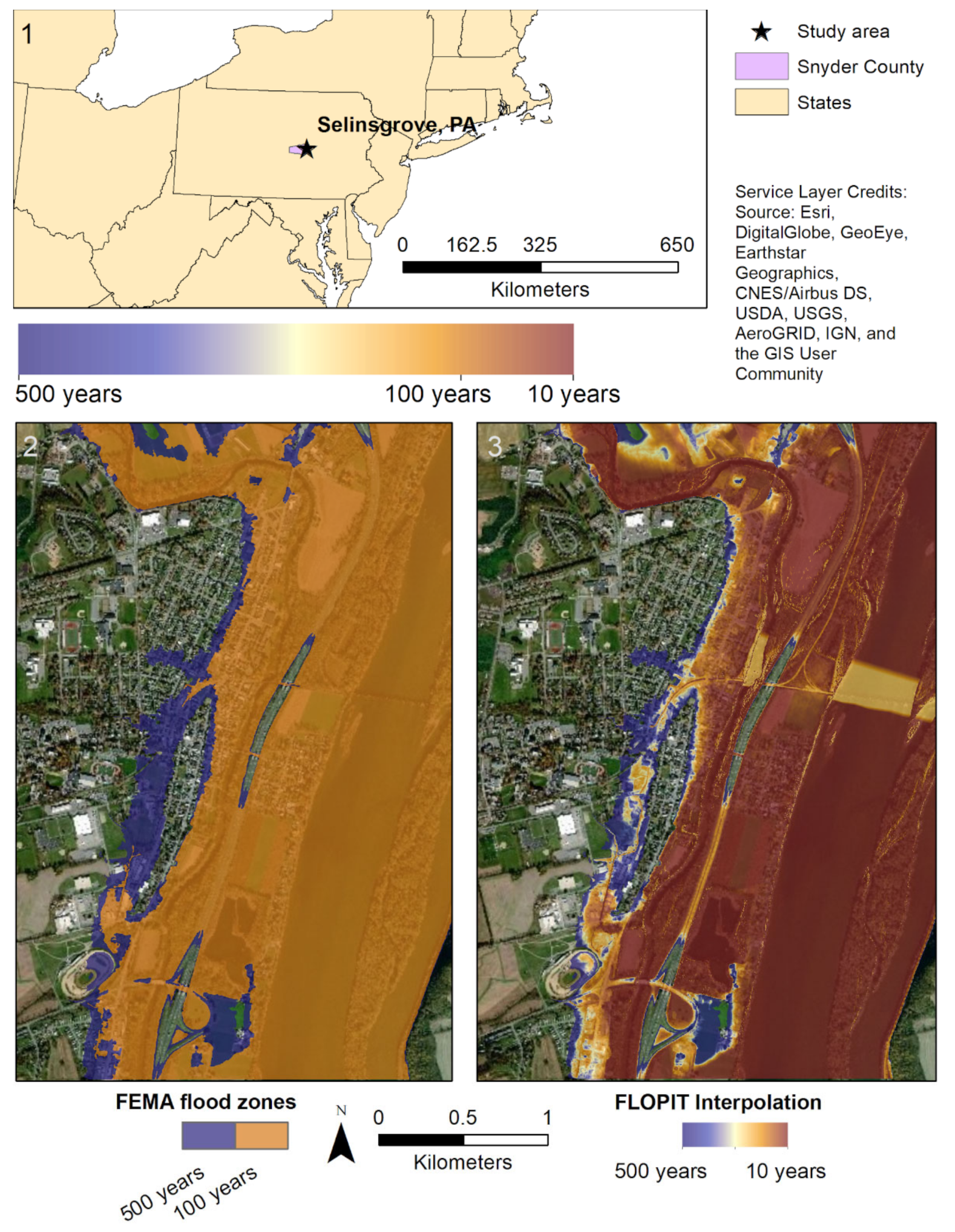
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Disclaimer
References
- Strömberg, D. Natural Disasters, Economic Development, and Humanitarian Aid. J. Econ. Perspect. 2007, 21, 199–222. [Google Scholar] [CrossRef]
- (IFRC) International Federation of Red Cross and Red Crescent Societies. World Disasters Report 2016; IFRC: Paris, France, 2016; Available online: https://www.ifrc.org/Global/Documents/Secretariat/201610/WDR 2016-FINAL_web.pdf (accessed on 3 July 2020).
- Winsemius, H.C.; Aerts, J.C.J.H.; Van Beek, L.P.H.; Bierkens, M.F.P.; Bouwman, A.; Jongman, B.; Kwadijk, J.C.J.; Ligtvoet, W.; Lucas, P.L.; Van Vuuren, D.P.; et al. Global drivers of future river flood risk. Nat. Clim. Chang. 2016, 6, 381–385. [Google Scholar] [CrossRef]
- Wing, O.E.J.; Bates, P.D.; Smith, A.M.; Sampson, C.C.; Johnson, K.A.; Fargione, J.; Morefield, P. Estimates of present and future flood risk in the conterminous United States. Environ. Res. Lett. 2018, 13, 034023. [Google Scholar] [CrossRef]
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. Available online: http://www.nature.com/nclimate/journal/v3/n9/full/nclimate1979.html%5Cnhttp://www.nature.com/nclimate/journal/v3/n9/pdf/nclimate1979.pdf (accessed on 1 July 2020). [CrossRef]
- Hirabayashi, Y.; Mahendran, R.; Koirala, S.; Konoshima, L.; Yamazaki, D.; Watanabe, S.; Kim, H.; Kanae, S. Global flood risk under climate change. Nat. Clim. Chang. 2013, 3, 816–821. [Google Scholar] [CrossRef]
- Godschalk David, R. Urban Hazard Mitigation: Creating Resilient Cities. Nat. Hazards Rev. 2003, 4, 136–143. [Google Scholar] [CrossRef]
- Kjellgren, S. Exploring local risk managers’ use of flood hazard maps for risk communication purposes in Baden-Württemberg. Nat. Hazards Earth Syst. Sci. 2013, 13, 1857–1872. [Google Scholar] [CrossRef]
- Zarekarizi, M.; Srikrishnan, V.; Keller, K. Neglecting uncertainties biases house-elevation decisions to manage riverine flood risks. Nat. Commun. 2020, 11, 1–11. [Google Scholar] [CrossRef]
- (FEMA) The Federal Emergency Management Agency. Percent Annual Chance Data; FEMA: Washington, DC, USA, 2015. Available online: https://www.fema.gov/media-library-data/1522157767608-ed99f04df13b5b7239922b3e77b7f8ea/FactSheet-PercentAnnualChanceData.pdf (accessed on 3 July 2020).
- Ludy, J.; Kondolf, G.M. Flood risk perception in lands “protected” by 100-year levees. Nat. Hazards 2012, 61, 829–842. [Google Scholar] [CrossRef]
- Smith, D.I. Floodplain management: Problems, issues and opportunities. Floods 2000, 1, 254–267. [Google Scholar]
- Alfieri, L.; Salamon, P.; Bianchi, A.; Neal, J.C.; Bates, P.D.; Feyen, L. Advances in pan-European flood hazard mapping. Hydrol. Process. 2014, 28, 4067–4077. [Google Scholar] [CrossRef]
- Jafarzadegan, K.; Merwade, V.; Saksena, S. A geomorphic approach to 100-year floodplain mapping for the Conterminous United States. J. Hydrol. 2018, 561, 43–58. [Google Scholar] [CrossRef]
- Woznicki, S.A.; Baynes, J.; Panlasigui, S.; Mehaffey, M.; Neale, A. Development of a spatially complete floodplain map of the conterminous United States using random forest. Sci. Total. Environ. 2019, 647, 942–953. [Google Scholar] [CrossRef]
- (FEMA) The Federal Emergency Management Agency. Guidance for Flood Risk Analysis and Mapping; FEMA: Washington, DC, USA, 2018. Available online: https://www.fema.gov/media-library-data/1523562952942-4c54fdae20779bb004857f1915236e6c/Flood_Depth_and_Analysis_Grids_Guidance_Feb_2018.pdf (accessed on 3 July 1998).
- Luke, A.; Sanders, B.F.; Goodrich, K.A.; Feldman, D.L.; Boudreau, D.; Eguiarte, A.; Serrano, K.; Reyes, A.; Schubert, J.E.; AghaKouchak, A.; et al. Going beyond the flood insurance rate map: Insights from flood hazard map co-production. Nat. Hazards Earth Syst. Sci. 2018, 18, 1097–1120. [Google Scholar] [CrossRef] [Green Version]
- Soden, R.; Sprain, L.; Palen, L. Thin Grey Lines. In Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems, Denver, CO, USA, 6–11 May 2017; pp. 2042–2053. [Google Scholar]
- McClelland, G.H.; Schulze, W.D.; Coursey, D.L. Insurance for low-probability hazards: A bimodal response to unlikely events. J. Risk Uncertain. 1993, 7, 95–116. [Google Scholar] [CrossRef]
- Oberholzer-Gee, F. Learning to Bear the Unbearable: Towards an Explanation of Risk Ignorance; Mimeo, Wharton School, University of Pennsylvania: Philadelphia, PA, USA, 1998. [Google Scholar]
- (FEMA) The Federal Emergency Management Agency. Guidance for Flood Risk Analysis and Mapping; FEMA: Washington, DC, USA, 2020. Available online: https://www.fema.gov/sites/default/files/documents/fema_flood-depth-and-analysis-guidance.pdf (accessed on 3 July 2020).
- Yamazaki, D.; Ikeshima, D.; Sosa, J.; Bates, P.D.; Allen, G.H.; Pavelsky, T.M. MERIT Hydro: A High-Resolution Global Hydrography Map Based on Latest Topography Dataset. Water Resour. Res. 2019, 55, 5053–5073. [Google Scholar] [CrossRef] [Green Version]
- Fritsch, F.N.; Carlson, R.E. Monotone Piecewise Cubic Interpolation. SIAM J. Numer. Anal. 1980, 17, 238–246. [Google Scholar] [CrossRef]
- Gesch, D.; Oimoen, M.; Greenlee, S.; Nelson, C.; Steuck, M.; Tyler, D. The National Elevation Dataset. Photogramm. Eng. Remote. Sens. 2002, 68, 5–32. [Google Scholar]
- (PAMAP, 2020) Pennsylvania Spatial Data Access. PAMAP Program. Available online: https://www.dcnr.pa.gov/Geology/PAMAP/Pages/default.aspx (accessed on 3 July 2020).
- Taheri, S.; Briggs, I.; Burtscher, M.; Gopalakrishnan, G. DiffTrace: Efficient Whole-Program Trace Analysis and Diffing for Debugging. In Proceedings of the 2019 IEEE International Conference on Cluster Computing (CLUSTER), Albuquerque, NM, USA, 23–26 September 2019; pp. 1–12. [Google Scholar]
- Taheri, S.; Devale, S.; Gopalakrishnan, G.; Burtscher, M. ParLoT: Efficient Whole-Program Call Tracing for HPC Applications. In Computer Vision; Springer International Publishing: Dallas, TX, USA, 2019; pp. 162–184. [Google Scholar]
- Kron, W. Flood Risk = Hazard ×·Values ×·Vulnerability. Water Int. 2005, 30, 58–68. [Google Scholar] [CrossRef]
- Schumann, G.; Hostache, R.; Puech, C.; Hoffmann, L.; Matgen, P.; Pappenberger, F.; Pfister, L. High-Resolution 3-D Flood Information From Radar Imagery for Flood Hazard Management. IEEE Trans. Geosci. Remote. Sens. 2007, 45, 1715–1725. [Google Scholar] [CrossRef]
- Cohen, S.; Brakenridge, G.R.; Kettner, A.; Bates, B.; Nelson, J.; McDonald, R.; Huang, Y.-F.; Munasinghe, D.; Zhang, J. Estimating Floodwater Depths from Flood Inundation Maps and Topography. JAWRA J. Am. Water Resour. Assoc. 2018, 54, 847–858. [Google Scholar] [CrossRef]
- Scorzini, A.R.; Radice, A.; Molinari, D. A New Tool to Estimate Inundation Depths by Spatial Interpolation (RAPIDE): Design, Application and Impact on Quantitative Assessment of Flood Damages. Water 2018, 10, 1805. [Google Scholar] [CrossRef] [Green Version]
- Frazier, T.; Boyden, E.E.; Wood, E. Socioeconomic implications of national flood insurance policy reform and flood insurance rate map revisions. Nat. Hazards 2020, 1–18. [Google Scholar] [CrossRef]
- Karamouz, M.; Fereshtehpour, M.; Ahmadvand, F.; Zahmatkesh, Z. Coastal Flood Damage Estimator: An Alternative to FEMA’s HAZUS Platform. J. Irrig. Drain. Eng. 2016, 142, 04016016. [Google Scholar] [CrossRef]
- Kousky, C.; Kunreuther, H.; LaCour-Little, M.; Wachter, S. Flood Risk and the U.S. Housing Market. J. Hous. Res. 2020, 29, S3–S24. [Google Scholar] [CrossRef]
- Thaler, T.; Hartmann, T. Justice and flood risk management: Reflecting on different approaches to distribute and allocate flood risk management in Europe. Nat. Hazards 2016, 83, 129–147. [Google Scholar] [CrossRef] [Green Version]

| Log-Linear | Log-Spline | Linear | Spline |
|---|---|---|---|
| 0.766 | 0.729 | 1.414 | 1.313 |
| Study Area | Sims Bayou | Muncy | Selinsgrove | |
|---|---|---|---|---|
| Resolution (Total Area) | 10 m (18 km2) | 16 m (400 km2) | 6 m (100 km2) | |
| Interpolation Method | Log-Linear | 12.55 | 119.75 | 233.13 |
| Spline | 21.61 | 117.40 | 311.67 | |
| Log-Spline | 25.04 | 140.97 | 364.26 | |
| Linear | 10.07 | 97.92 | 179.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zarekarizi, M.; Roop-Eckart, K.J.; Sharma, S.; Keller, K. The FLOod Probability Interpolation Tool (FLOPIT): A Simple Tool to Improve Spatial Flood Probability Quantification and Communication. Water 2021, 13, 666. https://doi.org/10.3390/w13050666
Zarekarizi M, Roop-Eckart KJ, Sharma S, Keller K. The FLOod Probability Interpolation Tool (FLOPIT): A Simple Tool to Improve Spatial Flood Probability Quantification and Communication. Water. 2021; 13(5):666. https://doi.org/10.3390/w13050666
Chicago/Turabian StyleZarekarizi, Mahkameh, K. Joel Roop-Eckart, Sanjib Sharma, and Klaus Keller. 2021. "The FLOod Probability Interpolation Tool (FLOPIT): A Simple Tool to Improve Spatial Flood Probability Quantification and Communication" Water 13, no. 5: 666. https://doi.org/10.3390/w13050666






