Integration of 2D Lateral Groundwater Flow into the Variable Infiltration Capacity (VIC) Model and Effects on Simulated Fluxes for Different Grid Resolutions and Aquifer Diffusivities
Abstract
1. Introduction
2. Materials and Methods
2.1. Implementation of Groundwater Flow Model in VIC
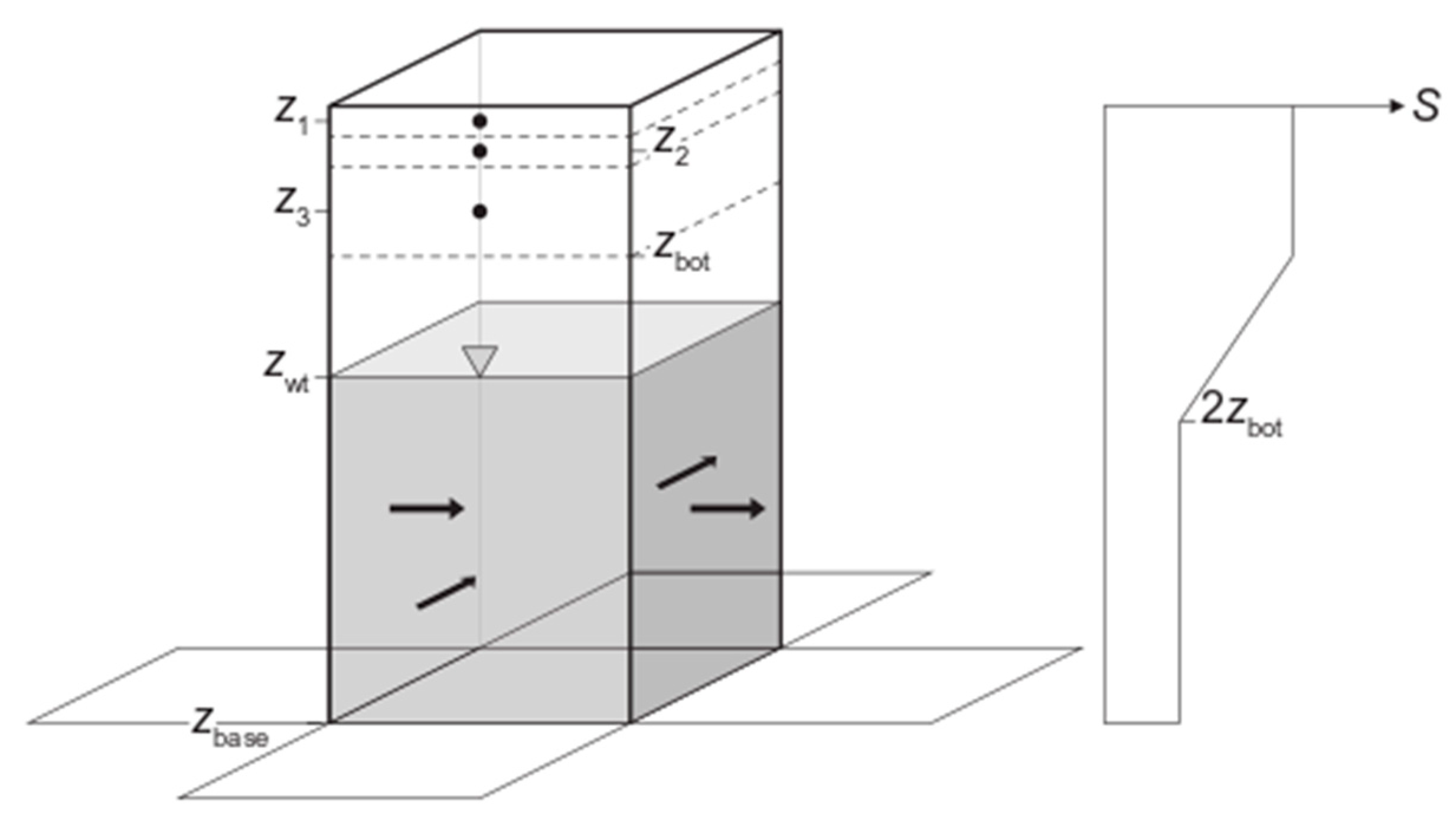
2.1.1. Groundwater Model Formulation
2.1.2. Vertical Soil Water–Groundwater Interaction
2.1.3. River–Groundwater Interaction
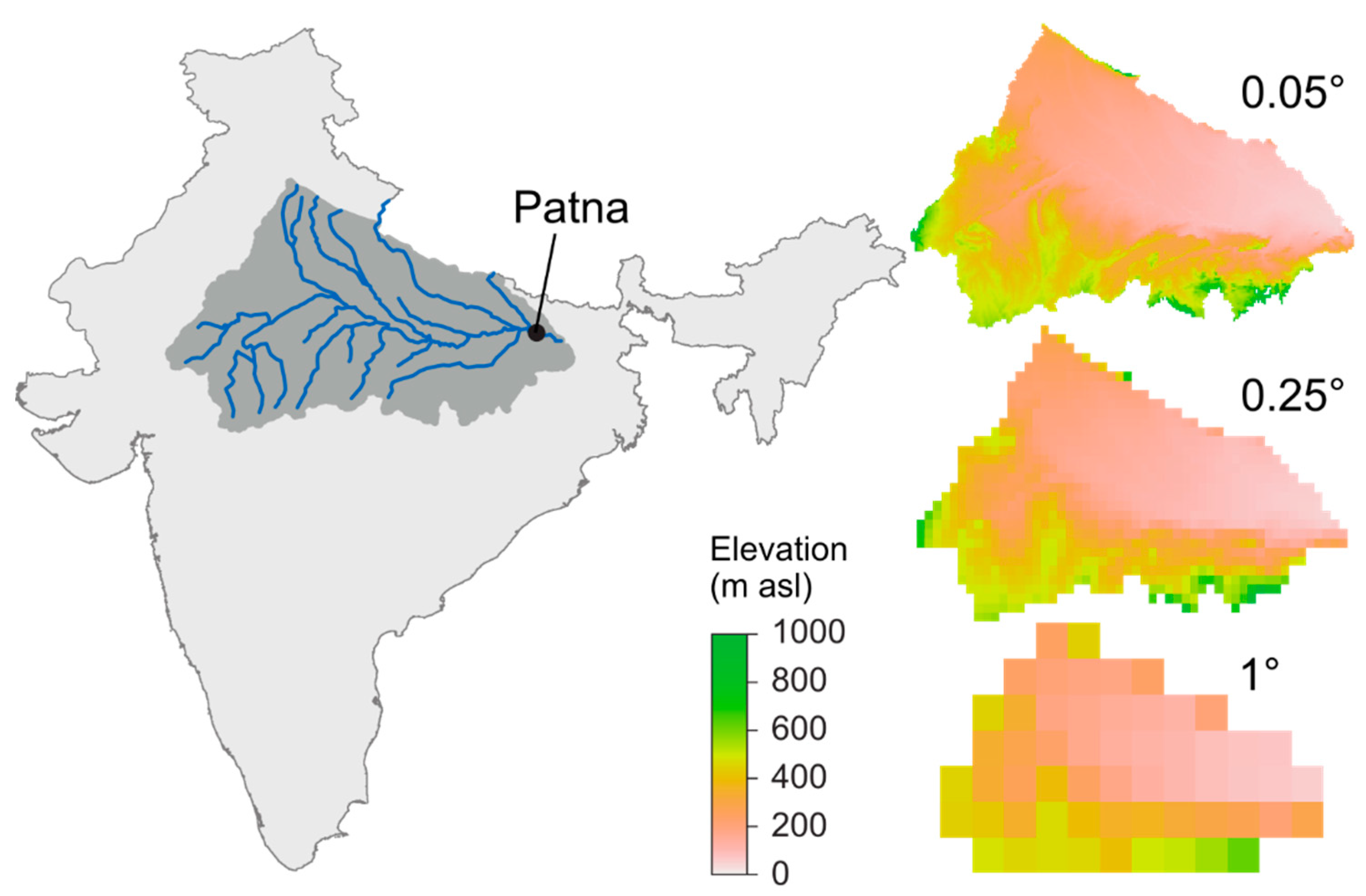
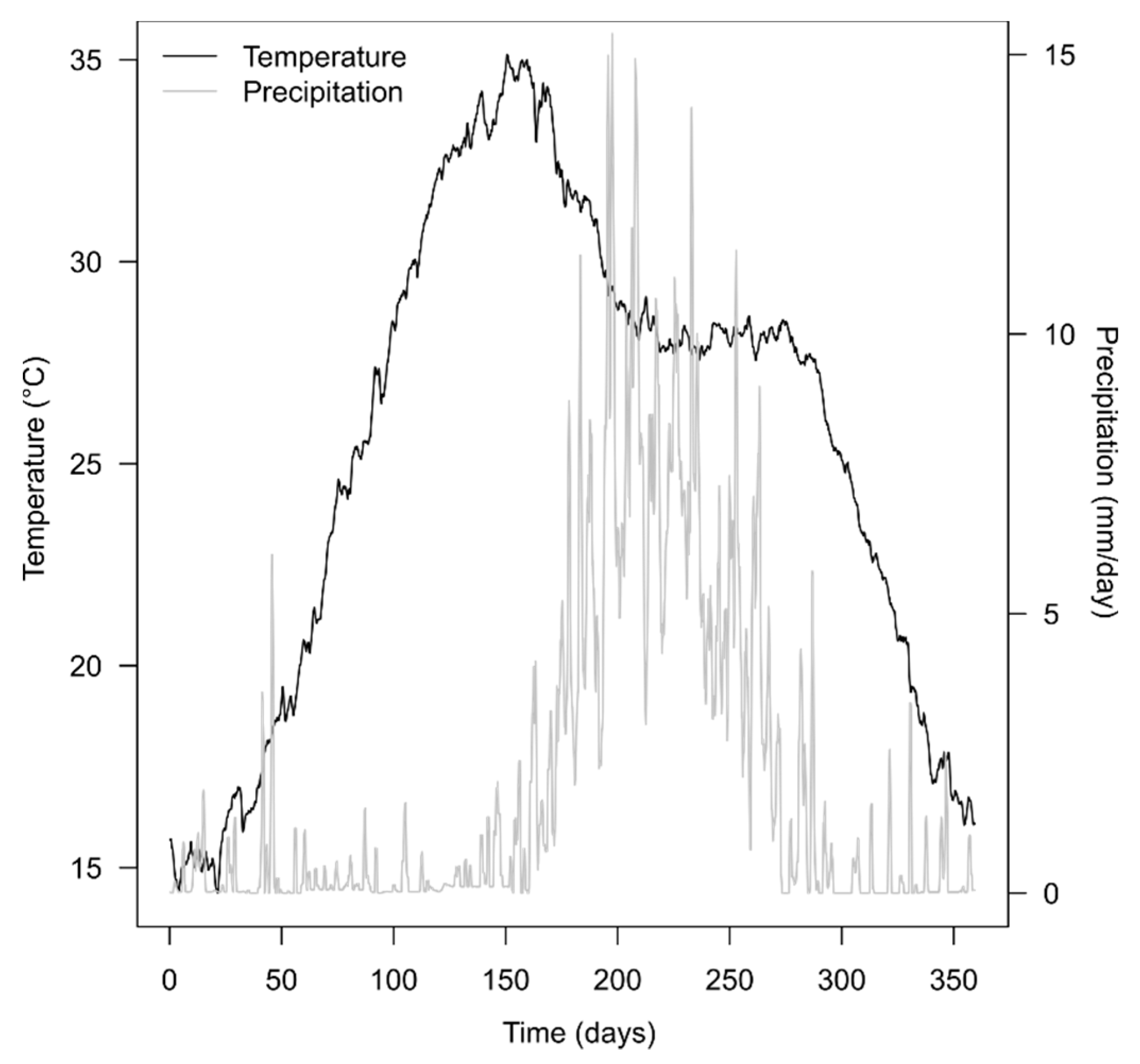
2.2. Model Application
3. Results
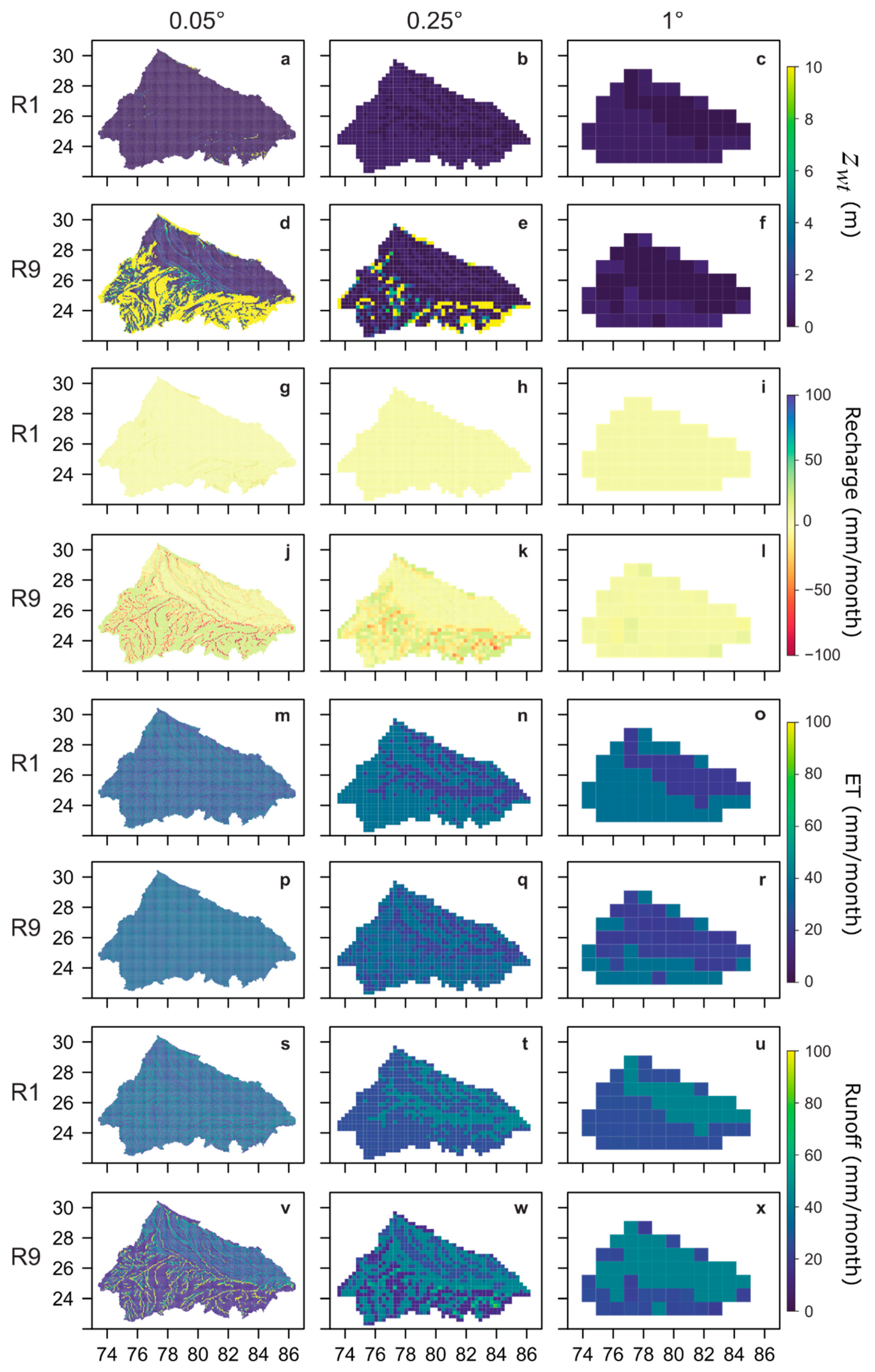
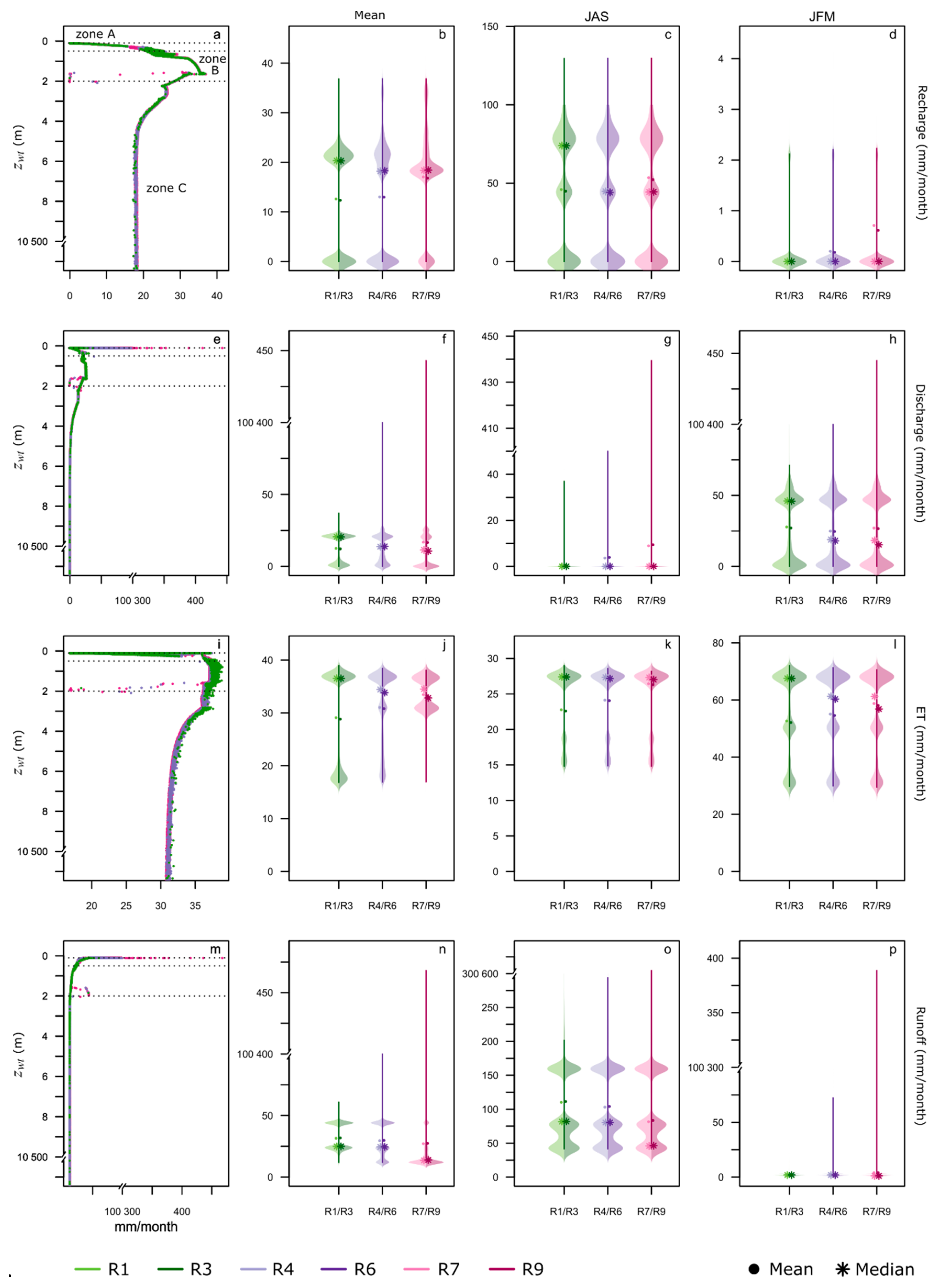
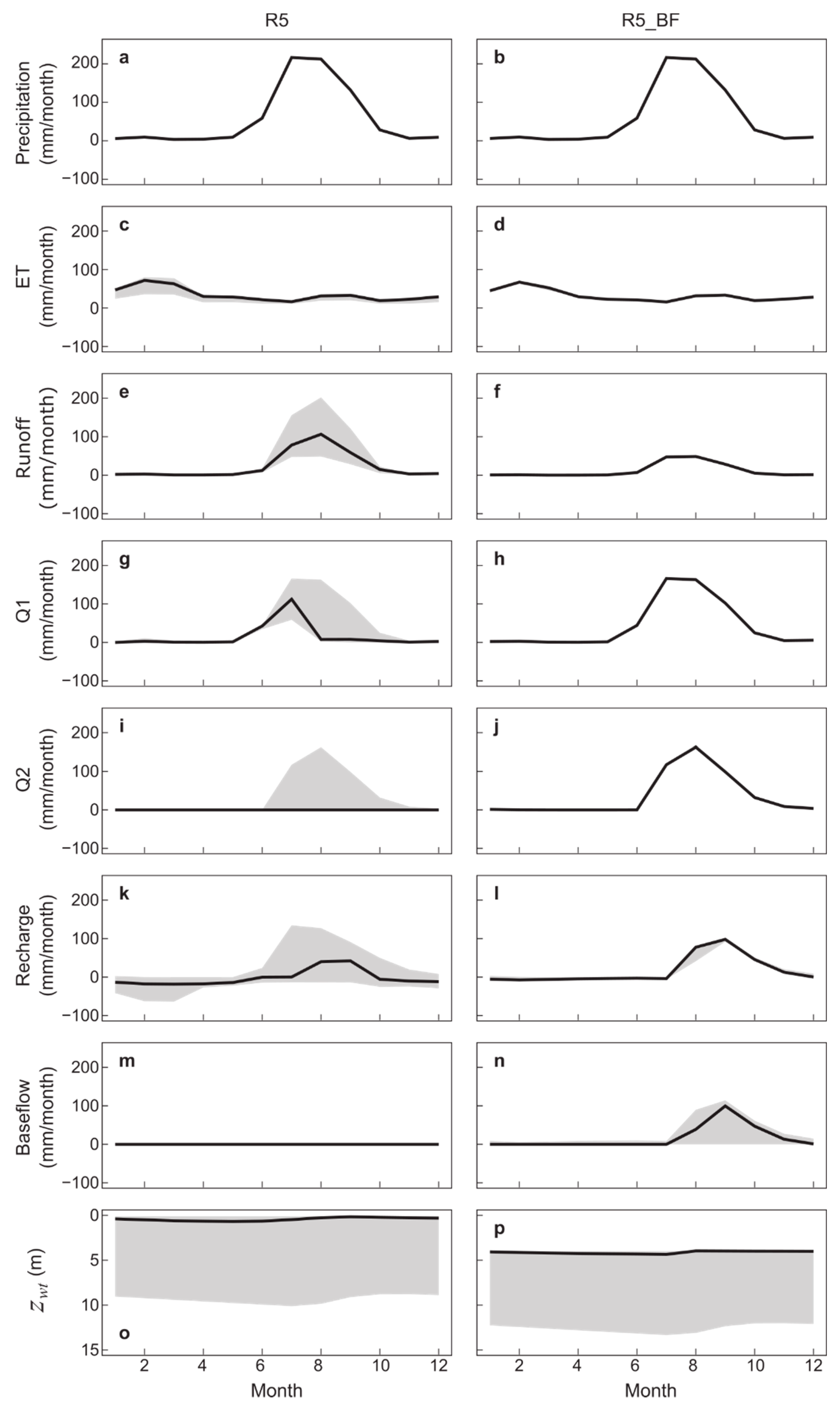
3.1. Effect of Aquifer Properties on Water Table Depth and Fluxes at 0.05 Resolution
3.1.1. Water Table Depth
3.1.2. Groundwater Recharge
3.1.3. Evapotranspiration
3.1.4. Runoff
3.2. Impact of Grid Resolution on Water Table Depth and Water Fluxes
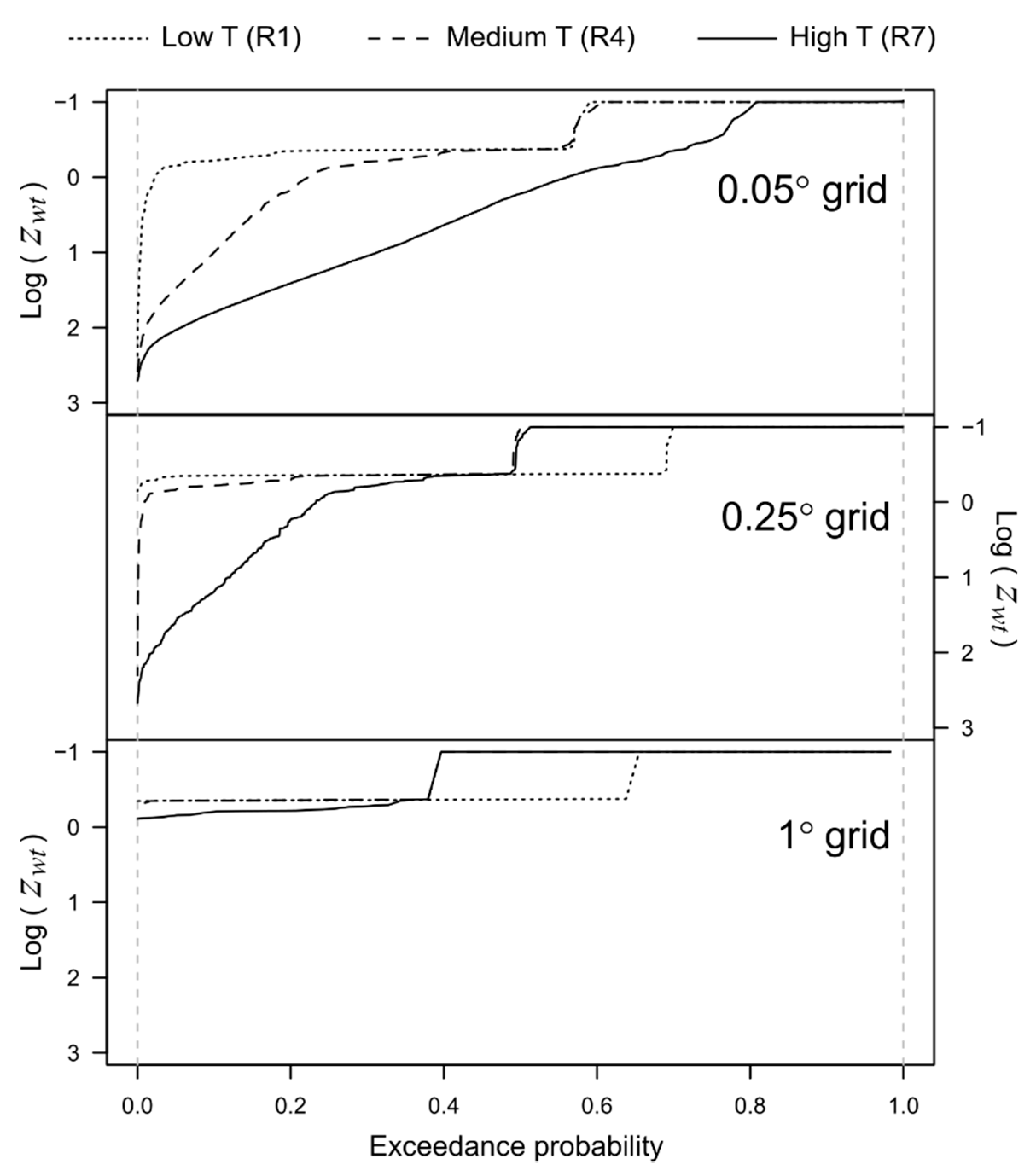
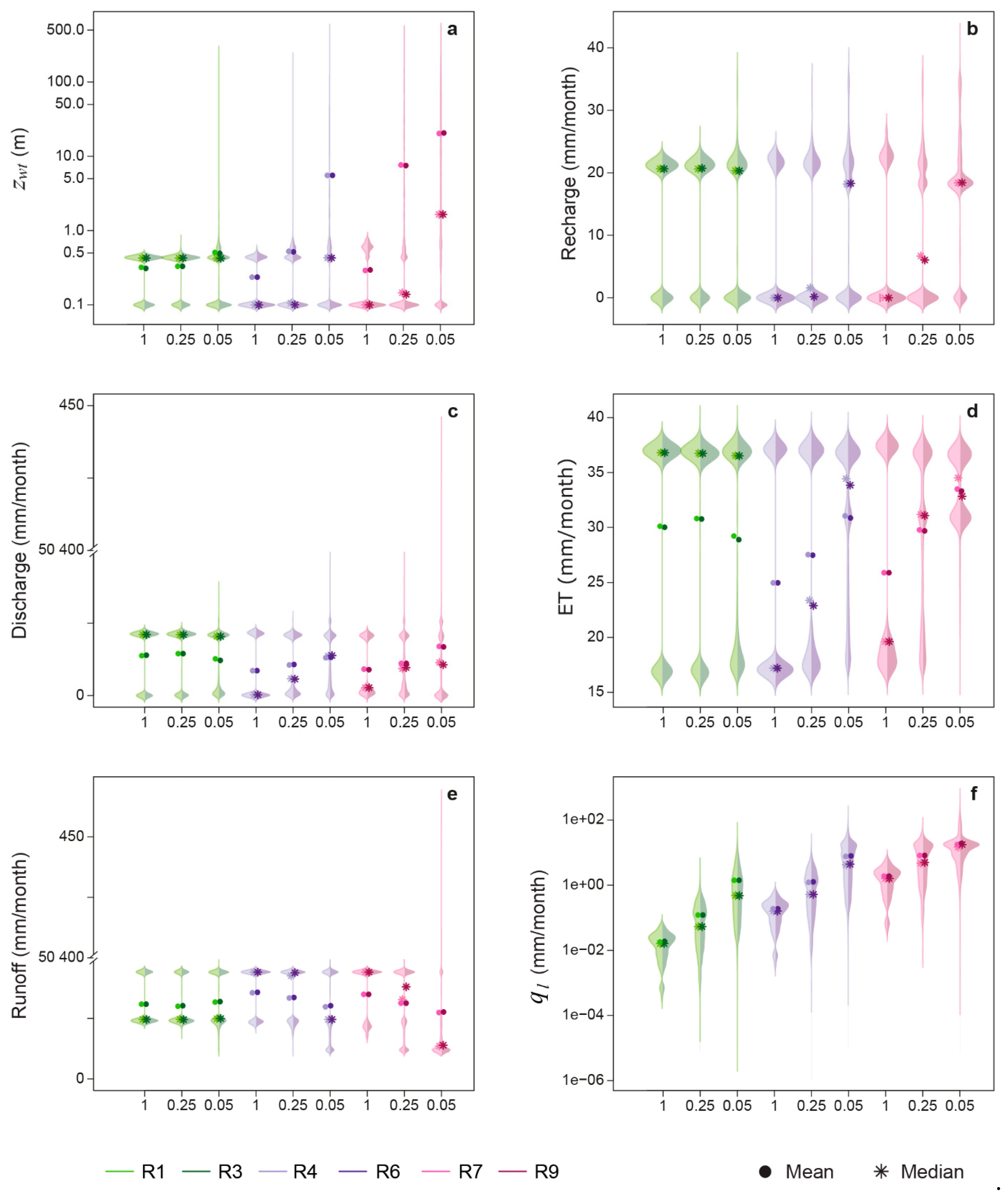
3.2.1. Water Table Depth
3.2.2. Groundwater Recharge
3.2.3. Evapotranspiration
3.2.4. Runoff
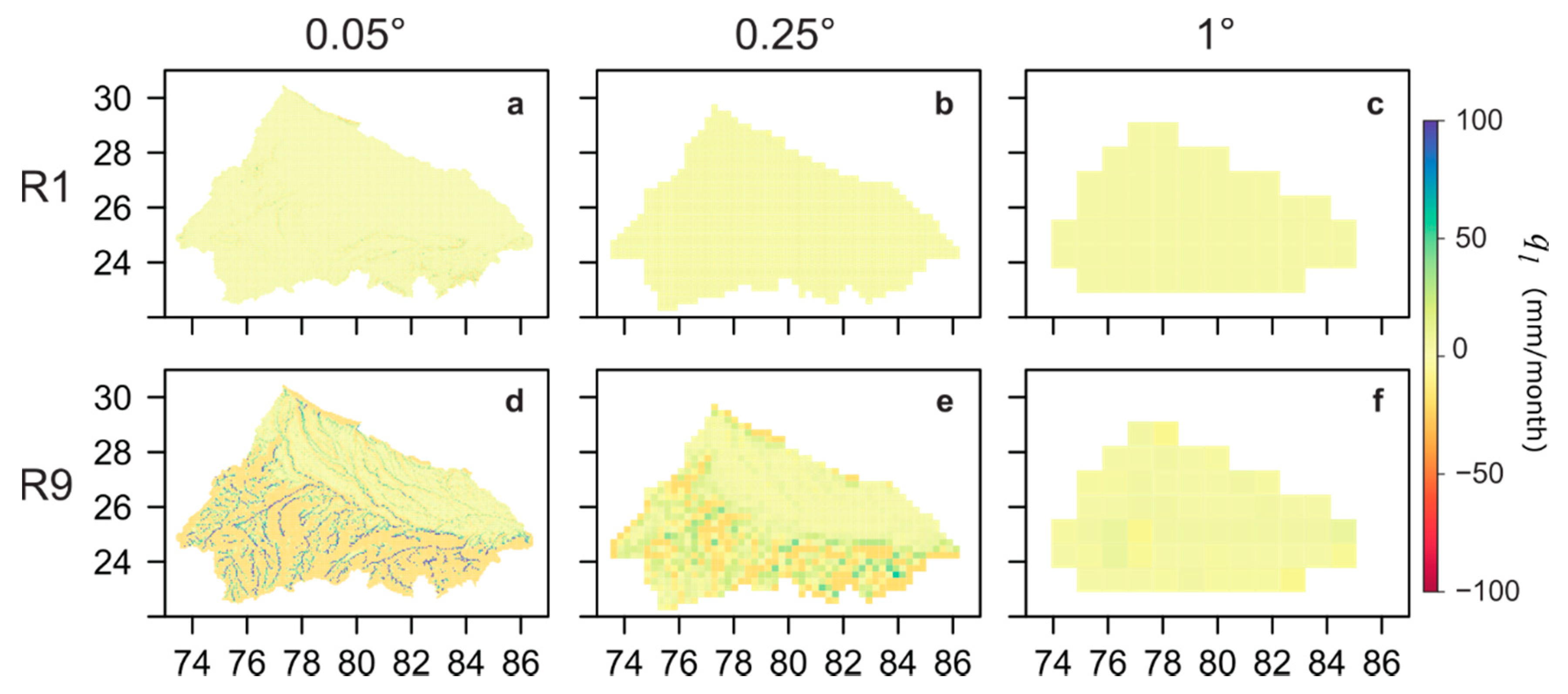
3.2.5. Lateral Groundwater Flow
3.3. Comparison of Groundwater Discharge through Capillary Rise and River Baseflow
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nazemi, A.; Wheater, H.S. On inclusion of water resource management in Earth system models -Part 1: Problem definition and representation of water demand. Hydrol. Earth Syst. Sci. 2015, 19, 33–61. [Google Scholar] [CrossRef]
- Wada, Y.; Bierkens, M.F.P.; De Roo, A.; Dirmeyer, P.A.; Famiglietti, J.S.; Hanasaki, N.; Konar, M.; Liu, J.; Schmied, H.M.; Oki, T.; et al. Human-water interface in hydrological modelling: Current status and future directions. Hydrol. Earth Syst. Sci. 2017, 21, 4169–4193. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Chang. 2012, 3, 322. [Google Scholar] [CrossRef]
- Condon, L.E.; Maxwell, R.M. Groundwater-fed irrigation impacts spatially distributed temporal scaling behavior of the natural system: A spatio-temporal framework for understanding water management impacts. Environ. Res. Lett. 2014, 9, 034009. [Google Scholar] [CrossRef]
- Leng, G.; Huang, M.; Tang, Q.; Gao, H.; Leung, L.R. Modeling the effects of groundwater-fed irrigation on terrestrial hydrology over the conterminous United States. J. Hydrometeorol. 2014, 15, 957–972. [Google Scholar] [CrossRef]
- Nazemi, A.; Wheater, H.S. On inclusion of water resource management in Earth system models Part 2: Representation of water supply and allocation and opportunities for improved modeling. Hydrol. Earth Syst. Sci. 2015, 19, 63–90. [Google Scholar] [CrossRef]
- Siebert, S.; Döll, P.; Hoogeveen, J.; Faures, J.M.; Frenken, K.; Feick, S. Development and validation of the global map of irrigation areas. Hydrol. Earth Syst. Sci. 2005, 9, 535–547. [Google Scholar] [CrossRef]
- Pokhrel, Y.N.; Koirala, S.; Yeh, P.J.F.; Hanasaki, N.; Longuevergne, L.; Kanae, S.; Oki, T. Incorporation of groundwater pumping in a global Land Surface Model with the representation of human impacts. Water Resour. Res. 2015, 51, 78–96. [Google Scholar] [CrossRef]
- Keune, J.; Sulis, M.; Kollet, S.; Siebert, S.; Wada, Y. Human Water Use Impacts on the Strength of the Continental Sink for Atmospheric Water. Geophys. Res. Lett. 2018, 45, 4068–4076. [Google Scholar] [CrossRef]
- MacDonald, A.M.; Bonsor, H.C.; Ahmed, K.M.; Burgess, W.G.; Basharat, M.; Calow, R.C.; Dixit, A.; Foster, S.S.D.; Gopal, K.; Lapworth, D.J.; et al. Groundwater quality and depletion in the Indo-Gangetic Basin mapped from in situ observations. Nat. Geosci. 2016, 9, 762–766. [Google Scholar] [CrossRef]
- Döll, P.; Mueller Schmied, H.; Schuh, C.; Portmann, F.T.; Eicker, A. Global-scale assessment of groundwater depletion and related groundwater abstractions: Combining hydrological modeling with information from well observations and GRACE satellites. Water Resour. Res. 2014, 50, 5698–5720. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Dickinson, R.E.; Gulden, L.E.; Su, H. Development of a simple groundwater model for use in climate models and evaluation with Gravity Recovery and Climate Experiment data. J. Geophys. Res. Atmos. 2007, 112, D07103. [Google Scholar] [CrossRef]
- Rosenberg, E.A.; Clark, E.A.; Steinemann, A.C.; Lettenmaier, D.P. On the contribution of groundwater storage to interannual streamflow anomalies in the Colorado River basin. Hydrol. Earth Syst. Sci. 2013, 17, 1475–1491. [Google Scholar] [CrossRef]
- Yeh, P.J.F.; Eltahir, E.A.B. Representation of Water Table Dynamics in a Land Surface Scheme. Part I: Model Development. J. Clim. 2005, 18, 1861–1880. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Miller, N.L. Development of a coupled land surface and groundwater model. J. Hydrometeorol. 2005, 6, 233–247. [Google Scholar] [CrossRef]
- Yang, H.W.; Xie, Z.H. A new method to dynamically simulate groundwater table in land surface model VIC. Prog. Nat. Sci. 2003, 13, 819–825. [Google Scholar] [CrossRef]
- Ruiz, L.; Varma, M.R.R.; Kumar, M.S.M.; Sekhar, M.; Maréchal, J.-C.; Descloitres, M.; Riotte, J.; Kumar, S.; Kumar, C.; Braun, J.-J. Water balance modelling in a tropical watershed under deciduous forest (Mule Hole, India): Regolith matric storage buffers the groundwater recharge process. J. Hydrol. 2010, 380, 460–472. [Google Scholar] [CrossRef]
- Chang, L.-L.; Dwivedi, R.; Knowles, J.F.; Fang, Y.-H.; Niu, G.-Y.; Pelletier, J.D.; Rasmussen, C.; Durcik, M.; Barron-Gafford, G.A.; Meixner, T. Why Do Large-Scale Land Surface Models Produce a Low Ratio of Transpiration to Evapotranspiration? J. Geophys. Res. Atmos. 2018, 123, 9109–9130. [Google Scholar] [CrossRef]
- Chawla, I.; Mujumdar, P.P. Isolating the impacts of land use and climate change on streamflow. Hydrol. Earth Syst. Sci. 2015, 19, 3633–3651. [Google Scholar] [CrossRef]
- Hamman, J.J.; Nijssen, B.; Bohn, T.J.; Gergel, D.R.; Mao, Y.X. The Variable Infiltration Capacity model version 5 (VIC-5): Infrastructure improvements for new applications and reproducibility. Geosci. Model. Dev. 2018, 11, 3481–3496. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. 1994, 99, 14,415–414,428. [Google Scholar] [CrossRef]
- Mishra, V.; Shah, R.; Azhar, S.; Shah, H.; Modi, P.; Kumar, R. Reconstruction of droughts in India using multiple land-surface models (1951–2015). Hydrol. Earth Syst. Sci. 2018, 22, 2269–2284. [Google Scholar] [CrossRef]
- Shah, R.; Sahai, A.K.; Mishra, V. Short to sub-seasonal hydrologic forecast to manage water and agricultural resources in India. Hydrol. Earth Syst. Sci. 2017, 21, 707–720. [Google Scholar] [CrossRef]
- Madhusoodhanan, C.G.; Sreeja, K.G.; Eldho, T.I. Assessment of uncertainties in global land cover products for hydro-climate modeling in India. Water Resour. Res. 2017, 53, 1713–1734. [Google Scholar] [CrossRef]
- Fan, Y.; Miguez-Macho, G.; Weaver, C.P.; Walko, R.; Robock, A. Incorporating water table dynamics in climate modeling: 1. Water table observations and equilibrium water table simulations. J. Geophys. Res. Atmos. 2007, 112, D10125. [Google Scholar] [CrossRef]
- Miguez-Macho, G.; Fan, Y.; Weaver, C.P.; Walko, R.; Robock, A. Incorporating water table dynamics in climate modeling: 2. Formulation, validation, and soil moisture simulation. J. Geophys. Res. Atmos. 2007, 112, D13108. [Google Scholar] [CrossRef]
- Zeng, Y.; Xie, Z.; Liu, S.; Xie, J.; Jia, B.; Qin, P.; Gao, J. Global Land Surface Modeling Including Lateral Groundwater Flow. J. Adv. Modeling Earth Syst. 2018, 10, 1882–1900. [Google Scholar] [CrossRef]
- de Graaf, I.E.M.; Sutanudjaja, E.H.; Van Beek, L.P.H.; Bierkens, M.F.P. A high-resolution global-scale groundwater model. Hydrol. Earth Syst. Sci. 2015, 19, 823–837. [Google Scholar] [CrossRef]
- de Graaf, I.E.M.; van Beek, R.L.P.H.; Gleeson, T.; Moosdorf, N.; Schmitz, O.; Sutanudjaja, E.H.; Bierkens, M.F.P. A global-scale two-layer transient groundwater model: Development and application to groundwater depletion. Adv. Water Resour. 2017, 102, 53–67. [Google Scholar] [CrossRef]
- Sutanudjaja, E.H.; Van Beek, R.; Wanders, N.; Wada, Y.; Bosmans, J.H.C.; Drost, N.; Van Der Ent, R.J.; De Graaf, I.E.M.; Hoch, J.M.; De Jong, K.; et al. PCR-GLOBWB 2: A 5 arcmin global hydrological and water resources model. Geosci. Model. Dev. 2018, 11, 2429–2453. [Google Scholar] [CrossRef]
- Harbaugh, A. MODFLOW-2005, The U.S. Geological Survey Modular Ground-Water Model.—The Ground-Water Flow Process.; U.S. Geological Survey Techniques and Methods 6-A16; U.S. Geological Survey: Reston, VA, USA, 2005. [CrossRef]
- Sridhar, V.; Billah, M.M.; Hildreth, J.W. Coupled Surface and Groundwater Hydrological Modeling in a Changing Climate. Groundwater 2018, 56, 618–635. [Google Scholar] [CrossRef]
- Kang, H.; Sridhar, V. Drought assessment with a surface-groundwater coupled model in the Chesapeake Bay watershed. Environ. Model. Softw. 2019, 119, 379–389. [Google Scholar] [CrossRef]
- Brandmeyer, J.E.; Karimi, H.A. Coupling methodologies for environmental models. Environ. Model. Softw. 2000, 15, 479–488. [Google Scholar] [CrossRef]
- Franchini, M.; Pacciani, M. Comparative analysis of several conceptual rainfall-runoff models. J. Hydrol. 1991, 122, 161–219. [Google Scholar] [CrossRef]
- Foster, T.; Brozović, N.; Butler, A.P. Modeling irrigation behavior in groundwater systems. Water Resour. Res. 2014, 50, 6370–6389. [Google Scholar] [CrossRef]
- Frija, A.; Chebil, A.; Speelman, S. Farmers’ Adaptation to Groundwater Shortage in the Dry Areas: Improving Appropriation or Enhancing Accommodation? Irrig. Drain. 2016, 65, 691–700. [Google Scholar] [CrossRef]
- O’Keeffe, J.; Buytaert, W.; Mijic, A.; Brozović, N.; Sinha, R. The use of semi-structured interviews for the characterisation of farmer irrigation practices. Hydrol. Earth Syst. Sci. 2016, 20, 1911–1924. [Google Scholar] [CrossRef]
- O’Keeffe, J.; Moulds, S.; Bergin, E.; Brozović, N.; Mijic, A.; Buytaert, W. Including Farmer Irrigation Behavior in a Sociohydrological Modeling Framework With Application in North India. Water Resour. Res. 2018, 54, 4849–4866. [Google Scholar] [CrossRef]
- Shah, T.; Singh, O.P.; Mukherji, A. Some aspects of South Asia’s groundwater irrigation economy: Analyses from a survey in India, Pakistan, Nepal Terai and Bangladesh. Hydrogeol. J. 2006, 14, 286–309. [Google Scholar] [CrossRef]
- Wood, E.F.; Lettenmaier, D.P.; Zartarian, V.G. A land-surface hydrology parameterization with subgrid variability for general circulation models. J. Geophys. Res. 1992, 97, 2717–2728. [Google Scholar] [CrossRef]
- Gao, H.; Tang, Q.; Shi, X.; Zhu, C.; Bohn, T.J.; Su, F.; Sheffield, J.; Pan, M.; Lettenmaier, D.P.; Wood, E.F. Water Budget Record from Variable Infiltration Capacity (VIC) Model. Algorithm Theor. Basis Doc. Terr. Water Cycle Data Rec. 2010. (in review). [Google Scholar]
- Lohmann, D.; Nolte-Holube, R.; Raschke, E. A large-scale horizontal routing model to be coupled to land surface parametrization schemes. Tellusseries A: Dyn. Meteorol. Oceanogr. 1996, 48, 708–721. [Google Scholar] [CrossRef]
- Tomer, S.; Muddu, S.S.; Mehta, V.K.; Yegina, S.; Thiyaku, S. Package ‘ambhasGW’. Available online: https://cran.r-project.org/web/packages/ambhasGW/index.html (accessed on 2 December 2020).
- Wang, H.F.; Anderson, M.P. Introduction to Groundwater Modeling: Finite Difference and Finite Element Methods; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Holden, H.; Karlsen, K.H.; Lie, K.-A. Splitting Methods for Partial Differential Equations with Rough Solutions: Analysis and MATLAB Programs; European Mathematical Society Series of Lectures in Mathematics. 2010, Volume 11. Available online: https://bookstore.ams.org/emsserlec-11 (accessed on 2 December 2020).
- Smith, G.D.; Smith, G.D.; Smith, G.D.S. Numerical Solution of Partial Differential Equations: Finite Difference Methods; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Kiehl, J.T.; Gent, P.R. The community climate system model, version 2. J. Clim. 2004, 17, 3666–3682. [Google Scholar] [CrossRef][Green Version]
- Campbell, G.S. Soil Physics with BASIC: Transport. Models for Soil-Plant. Systems; Elsevier: Amsterdam, The Netherlands, 1985; Volume 14. [Google Scholar]
- DHI, M. FEFLOW 7.0 User Guide; DHI: Copenhagen, Denmark, 2016. [Google Scholar]
- Jackson, C.; Spink, A. User’s Manual for the Groundwater Flow Model ZOOMQ3D; IR/04/140; British Geological Survey: Keyworth, UK, 2004.
- Miguez-Macho, G.; Fan, Y. The role of groundwater in the Amazon water cycle: 1. Influence on seasonal streamflow, flooding and wetlands. J. Geophys. Res. Atmos. 2012, 117, D15113. [Google Scholar] [CrossRef]
- Hiscock, K. Hydrogeology: Principles and Practice; Blackwell Science Ltd.: Oxford, UK, 2005. [Google Scholar]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4; CGIAR-CSI SRTM 90 m Database. Available online: http://srtm.csi.cgiar.org/ (accessed on 2 December 2020).
- Mazumder, R.; Eriksson, P.G. Chapter 1 Precambrian basins of India: Stratigraphic and tectonic context. Geol. Soc. Lond. Mem. 2015, 43, 1. [Google Scholar] [CrossRef]
- Nijssen, B.; Schnur, R.; Lettenmaier, D.P. Global Retrospective Estimation of Soil Moisture Using the Variable Infiltration Capacity Land Surface Model, 1980–1993. J. Clim. 2001, 14, 1790–1808. [Google Scholar] [CrossRef]
- Weedon, G.P.; Gomes, S.; Viterbo, P.; Österle, H.; Adam, J.C.; Bellouin, N.; Boucher, O.; Best, M. The WATCH forcing data 1958-2001: A Meteorological Forcing Dataset for Land Surface- and Hyrological-Models. Available online: https://catalogue.ceh.ac.uk/documents/ba6e8ddd-22a9-457d-acf4-d63cd34f2dda (accessed on 2 December 2020).
- Krakauer, N.Y.; Li, H.; Fan, Y. Groundwater flow across spatial scales: Importance for climate modeling. Environ. Res. Lett. 2014, 9, 034003. [Google Scholar] [CrossRef]
- Snowdon, A.P.; Sykes, J.F.; Normani, S.D. Topography scale effects on groundwater-surface water exchange fluxes in a Canadian Shield setting. J. Hydrol. 2020, 585, 124772. [Google Scholar] [CrossRef]
- Condon, L.E.; Atchley, A.L.; Maxwell, R.M. Evapotranspiration depletes groundwater under warming over the contiguous United States. Nat. Commun. 2020, 11, 873. [Google Scholar] [CrossRef]
- Marchionni, V.; Daly, E.; Manoli, G.; Tapper, N.J.; Walker, J.P.; Fatichi, S. Groundwater Buffers Drought Effects and Climate Variability in Urban Reserves. Water Resour. Res. 2020, 56, e2019WR026192. [Google Scholar] [CrossRef]
- Martínez-de la Torre, A.; Miguez-Macho, G. Groundwater influence on soil moisture memory and land–atmosphere fluxes in the Iberian Peninsula. Hydrol. Earth Syst. Sci. 2019, 23, 4909–4932. [Google Scholar] [CrossRef]
- Choi, H.I.; Kumar, P.; Liang, X.-Z. Three-dimensional volume-averaged soil moisture transport model with a scalable parameterization of subgrid topographic variability. Water Resour. Res. 2007, 43, W04414. [Google Scholar] [CrossRef]
- Singh, R.S.; Reager, J.T.; Miller, N.L.; Famiglietti, J.S. Toward hyper-resolution land-surface modeling: The effects of fine-scale topography and soil texture on CLM4.0 simulations over the Southwestern U.S. Water Resour. Res. 2015, 51, 2648–2667. [Google Scholar] [CrossRef]
- Reinecke, R.; Wachholz, A.; Mehl, S.; Foglia, L.; Niemann, C.; Döll, P. Importance of spatial resolution in global groundwater modeling. Groundwater 2020, 58, 363–376. [Google Scholar] [CrossRef]
- Westerhoff, R.; White, P.; Miguez-Macho, G. Application of an improved global-scale groundwater model for water table estimation across New Zealand. Hydrol. Earth Syst. Sci. 2018, 22, 6449–6472. [Google Scholar] [CrossRef]
- Fan, Y.; Li, H.; Miguez-Macho, G. Global patterns of groundwater table depth. Science 2013, 339, 940–943. [Google Scholar] [CrossRef]
- Staudinger, M.; Stoelzle, M.; Cochand, F.; Seibert, J.; Weiler, M.; Hunkeler, D. Your work is my boundary condition!: Challenges and approaches for a closer collaboration between hydrologists and hydrogeologists. J. Hydrol. 2019, 571, 235–243. [Google Scholar] [CrossRef]
| Model | Hydraulic Conductivity (m/day) | Storage Coefficient (-) | Maximum Diffusivity (m2/day) |
|---|---|---|---|
| R1 | 0.1 | 0.01 | 5000 |
| R2 | 0.1 | 0.1 | 500 |
| R3 | 0.1 | 0.2 | 250 |
| R4 | 1 | 0.01 | 50,000 |
| R5 | 1 | 0.1 | 5000 |
| R6 | 1 | 0.2 | 2500 |
| R7 | 10 | 0.01 | 500,000 |
| R8 | 10 | 0.1 | 50,000 |
| R9 | 10 | 0.2 | 25,000 |
| Run | Mean WTD (m) | Mean Recharge (mm/month) | Mean ET (mm/month) | Mean Runoff (mm/month) | Mean Discharge Area Fraction |
|---|---|---|---|---|---|
| 1 | 0.52 | 12.7 | 29.19 | 31.89 | 0.63 |
| 2 | 0.51 | 12.44 | 28.94 | 32.14 | 0.63 |
| 3 | 0.51 | 12.42 | 28.92 | 32.17 | 0.63 |
| 4 | 5.65 | 13.11 | 31.11 | 29.97 | 0.51 |
| 5 | 5.59 | 13.05 | 30.9 | 30.18 | 0.51 |
| 6 | 5.59 | 13.07 | 30.89 | 30.19 | 0.51 |
| 7 | 20.41 | 17.13 | 33.55 | 27.55 | 0.29 |
| 8 | 20.34 | 16.93 | 33.35 | 27.75 | 0.29 |
| 9 | 20.34 | 16.89 | 33.27 | 27.82 | 0.29 |
| Run | Grid Size | Mean WTD (m) | Mean Recharge (mm/month) | Mean ET (mm/month) | Mean Runoff (mm/month) | Mean Lateral Groundwater Flow (mm/month) | Mean Discharge Area Fraction |
|---|---|---|---|---|---|---|---|
| 1 | 1° | 0.32 | 13.9 | 30.07 | 31.03 | 0.02 | 0.67 |
| 1 | 0.25° | 0.33 | 14.79 | 30.86 | 30.21 | 0.13 | 0.65 |
| 1 | 0.05° | 0.52 | 12.7 | 29.19 | 31.89 | 1.43 | 0.63 |
| 4 | 1° | 0.24 | 8.8 | 25.03 | 35.94 | 0.18 | 0.67 |
| 4 | 0.25° | 0.53 | 10.94 | 27.49 | 33.57 | 1.26 | 0.65 |
| 4 | 0.05° | 5.65 | 13.11 | 31.11 | 29.97 | 9.05 | 0.51 |
| 7 | 1° | 0.3 | 9.07 | 25.95 | 35.14 | 1.78 | 0.62 |
| 7 | 0.25° | 7.61 | 11.07 | 29.84 | 31.24 | 9.38 | 0.55 |
| 7 | 0.05° | 20.41 | 17.13 | 33.55 | 27.55 | 20.98 | 0.29 |
| Low T (R1) | Medium T (R4) | High T (R7) | Change R1 to R7 | |
|---|---|---|---|---|
| WTD (m) | 0.52 | 5.65 | 20.41 | +19.89 |
| Recharge (% rain) | 20.6 | 21.3 | 27.8 | +7.2 |
| ET (% rain) | 47.4 | 50.5 | 54.5 | +7.1 |
| Runoff (% rain) | 51.8 | 48.7 | 44.7 | −7.1 |
| Lateral groundwater flow (% rain) | 2.4 | 14.7 | 34.1 | 31.7 |
| Discharge area fraction | 0.63 | 0.51 | 0.29 | −0.34 |
| Low T (R1) | Medium T (R4) | High T (R7) | |
|---|---|---|---|
| WTD (m) | +0.2 | +5.41 | +20.11 |
| Recharge (% rain) | −1.9 | +7.0 | +13.1 |
| ET (% rain) | −1.4 | +9.8 | +12.3 |
| Runoff (% rain) | +1.4 | −9.8 | −12.3 |
| Lateral groundwater flow (% rain) | +2.4 | +14.4 | +31.2 |
| Discharge area fraction | −0.04 | −0.16 | −0.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scheidegger, J.M.; Jackson, C.R.; Muddu, S.; Tomer, S.K.; Filgueira, R. Integration of 2D Lateral Groundwater Flow into the Variable Infiltration Capacity (VIC) Model and Effects on Simulated Fluxes for Different Grid Resolutions and Aquifer Diffusivities. Water 2021, 13, 663. https://doi.org/10.3390/w13050663
Scheidegger JM, Jackson CR, Muddu S, Tomer SK, Filgueira R. Integration of 2D Lateral Groundwater Flow into the Variable Infiltration Capacity (VIC) Model and Effects on Simulated Fluxes for Different Grid Resolutions and Aquifer Diffusivities. Water. 2021; 13(5):663. https://doi.org/10.3390/w13050663
Chicago/Turabian StyleScheidegger, Johanna M., Christopher R. Jackson, Sekhar Muddu, Sat Kumar Tomer, and Rosa Filgueira. 2021. "Integration of 2D Lateral Groundwater Flow into the Variable Infiltration Capacity (VIC) Model and Effects on Simulated Fluxes for Different Grid Resolutions and Aquifer Diffusivities" Water 13, no. 5: 663. https://doi.org/10.3390/w13050663
APA StyleScheidegger, J. M., Jackson, C. R., Muddu, S., Tomer, S. K., & Filgueira, R. (2021). Integration of 2D Lateral Groundwater Flow into the Variable Infiltration Capacity (VIC) Model and Effects on Simulated Fluxes for Different Grid Resolutions and Aquifer Diffusivities. Water, 13(5), 663. https://doi.org/10.3390/w13050663







