Some Theoretical Aspects of Tertiary Treatment of Water/Oil Emulsions by Adsorption and Coalescence Mechanisms: A Review
Abstract
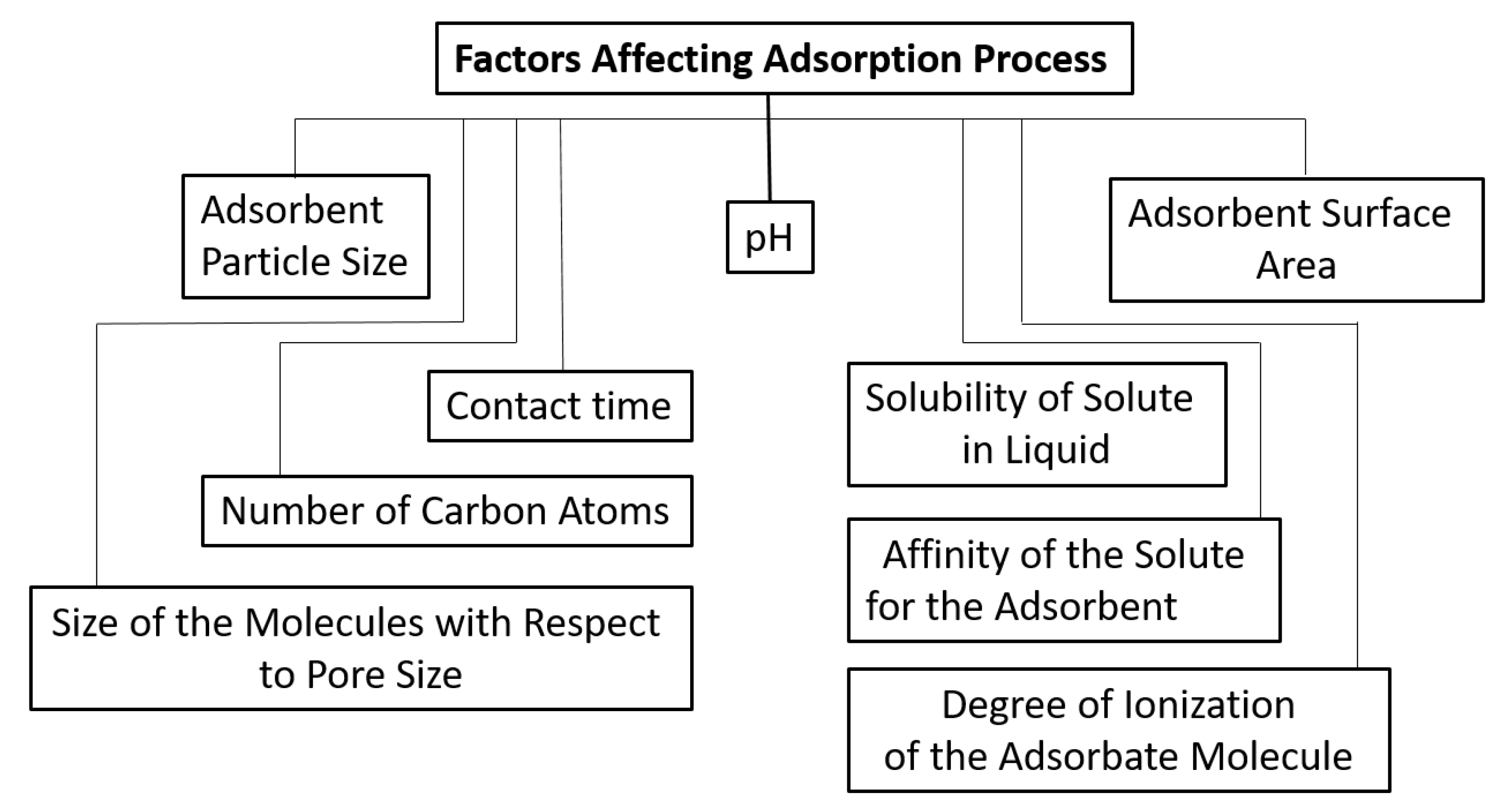
:1. Introduction
2. Adsorption Isotherms
2.1. Langmuir Isotherm (LI)
2.2. Brunauer–Emmet–Teller (BET) Isotherm
2.3. Freundlich Isotherm (FI)
2.4. Dubinin–Radushkevich (D-R) Isotherm
2.5. Error Analysis
3. Thermodynamics of Adsorption
4. Kinetics of Adsorption
4.1. Pseudo-First-Order Kinetic Model (PFOM)
4.2. Pseudo-Second-Order Kinetic Model (PSOM)
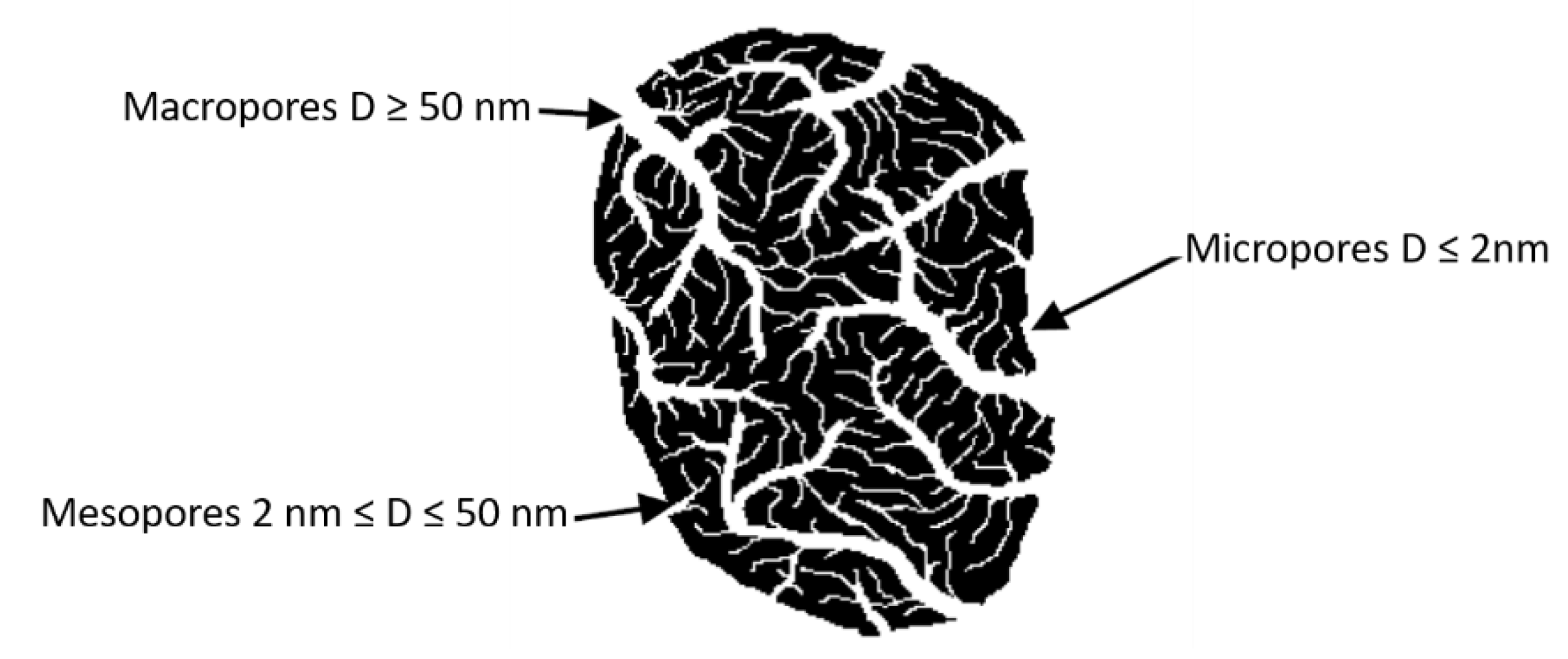
4.3. Diffusional Models
4.3.1. Douven’s Model
4.3.2. Weber–Morris Intra-Particle Diffusion (IPD) Model
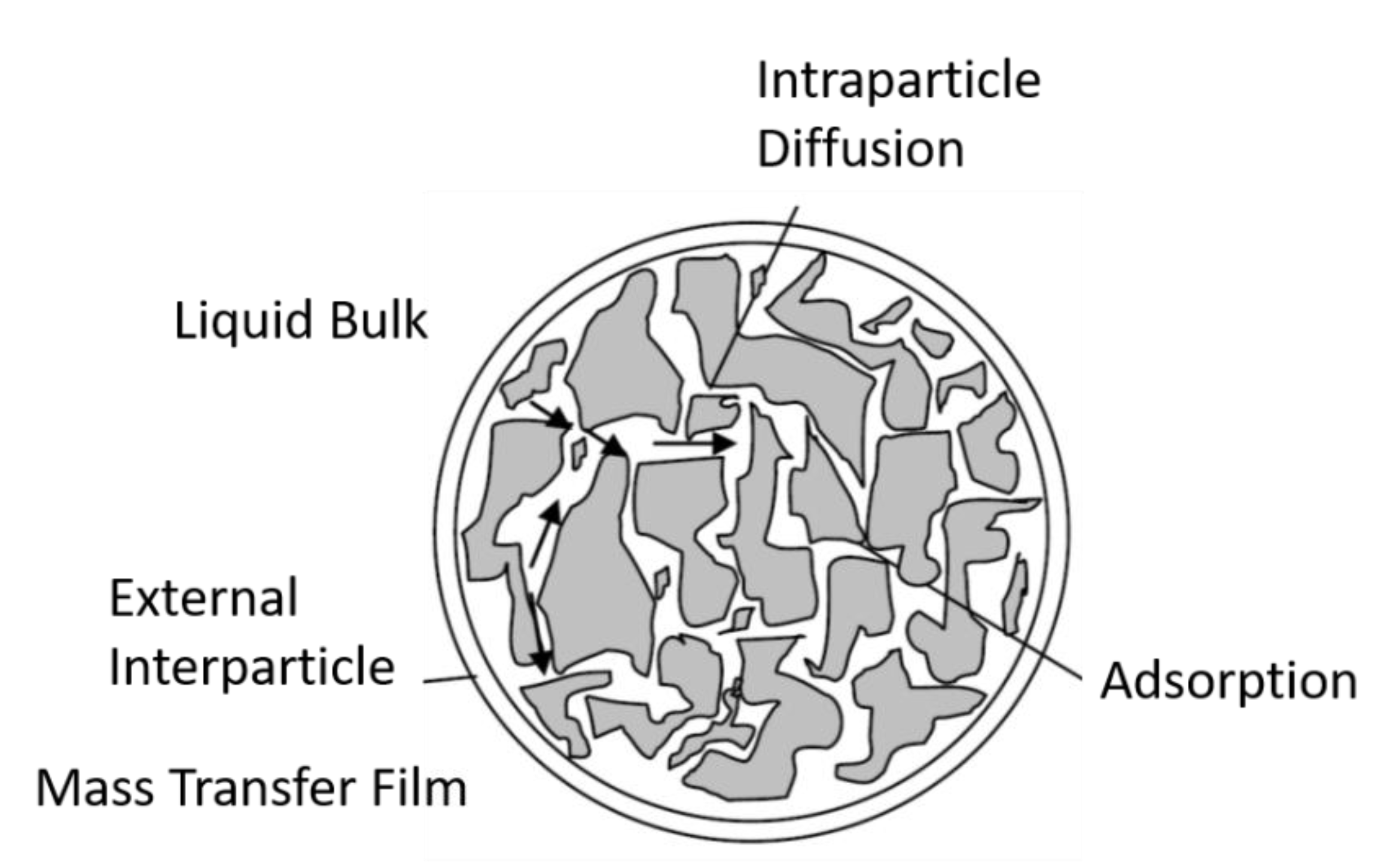
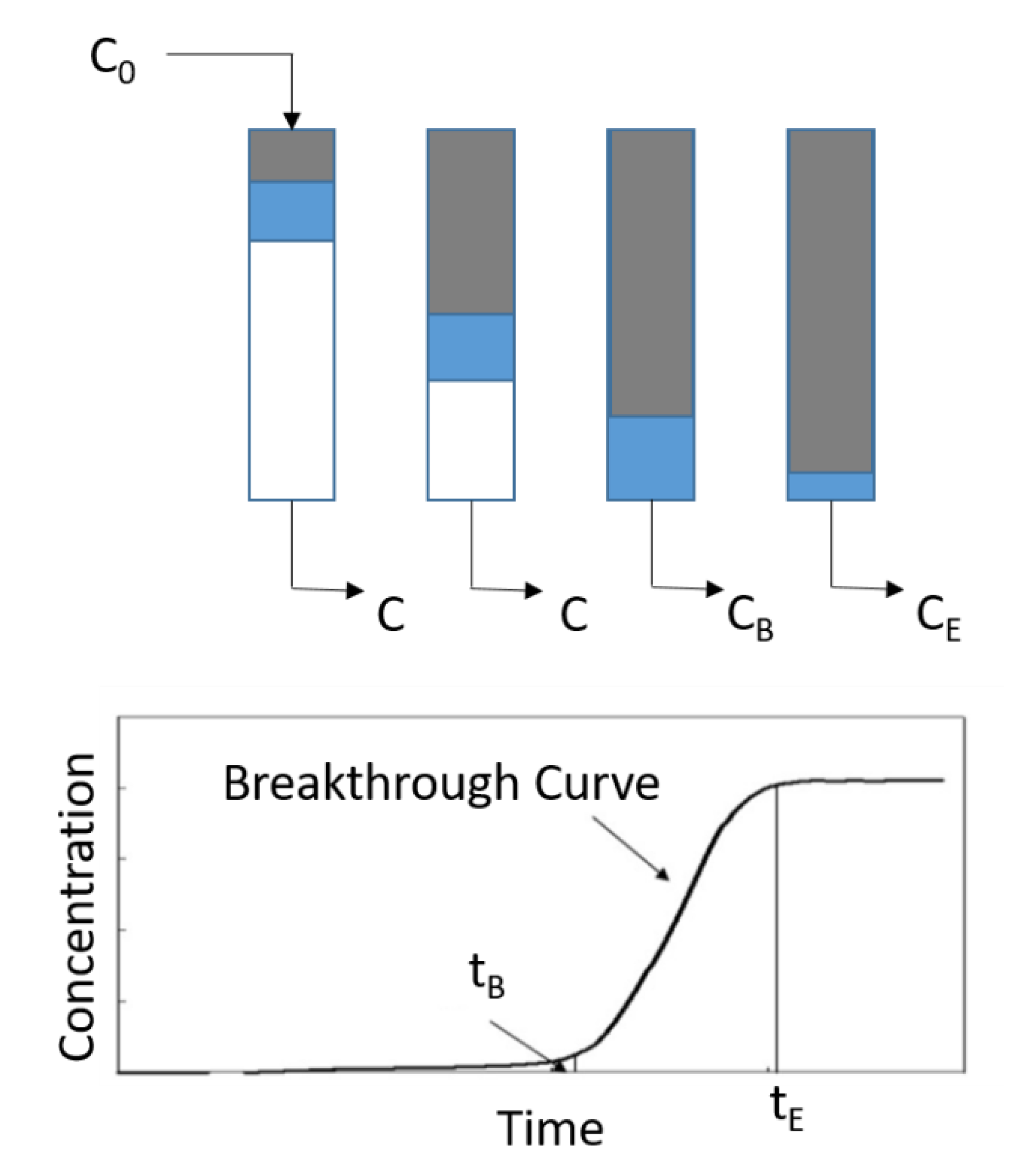
4.4. Adsorption Kinetics in Flow-through Systems (Fixed Bed Adsorption)
- A mass transfer from the bulk of the fluid to the surface of the adsorbent through the boundary layer around the particle.
- An internal diffusion through the pores of the adsorbent.
- An adsorption onto the surface of the adsorbent.
4.5. Bed Depth Service Time (BDST) Model
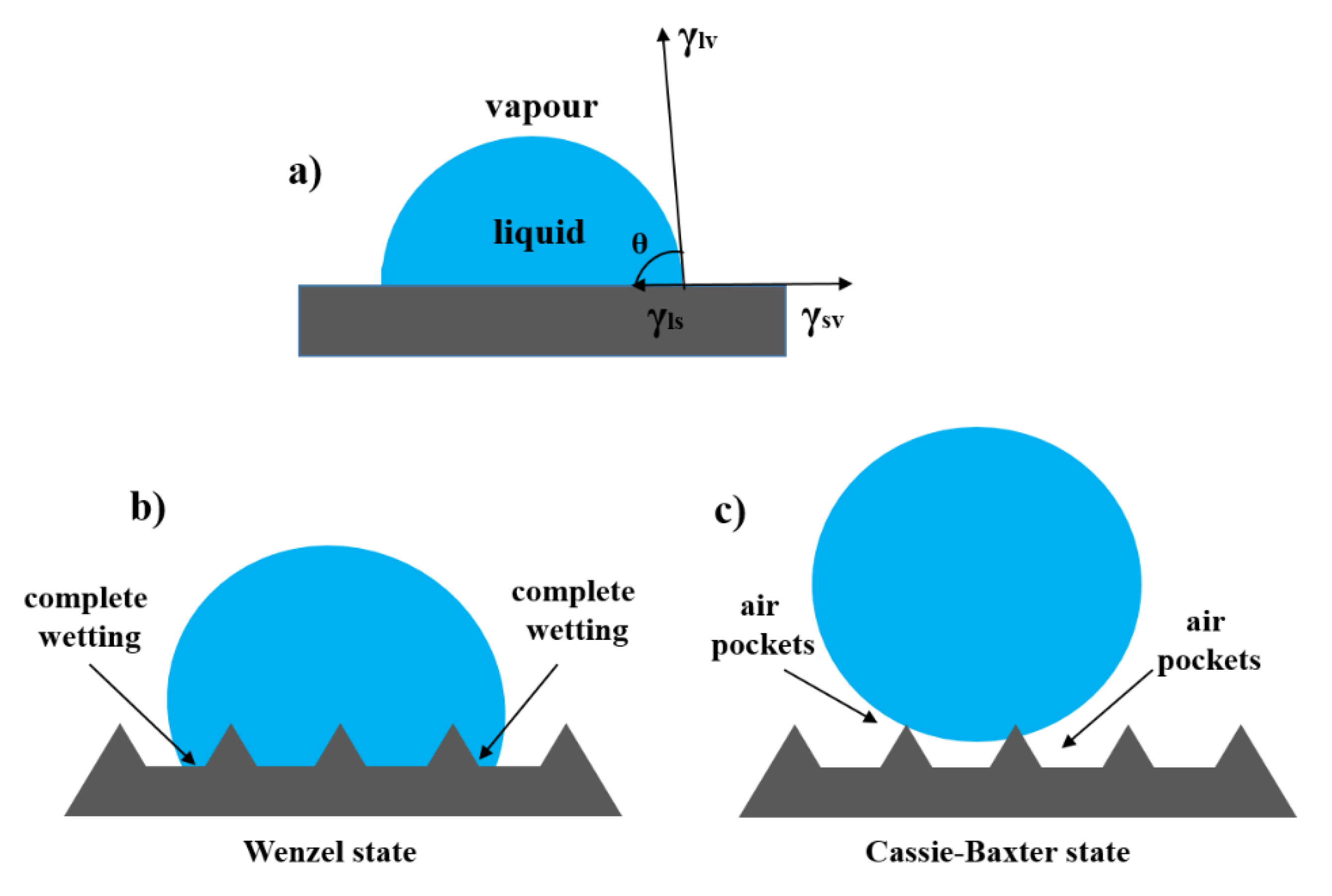
5. Interfacial interactions and Wettability of Surfaces
5.1. A Droplet Placed at a Smooth and Rough Surface in Air
5.2. A Droplet Placed at a Smooth and Rough Surface in Water
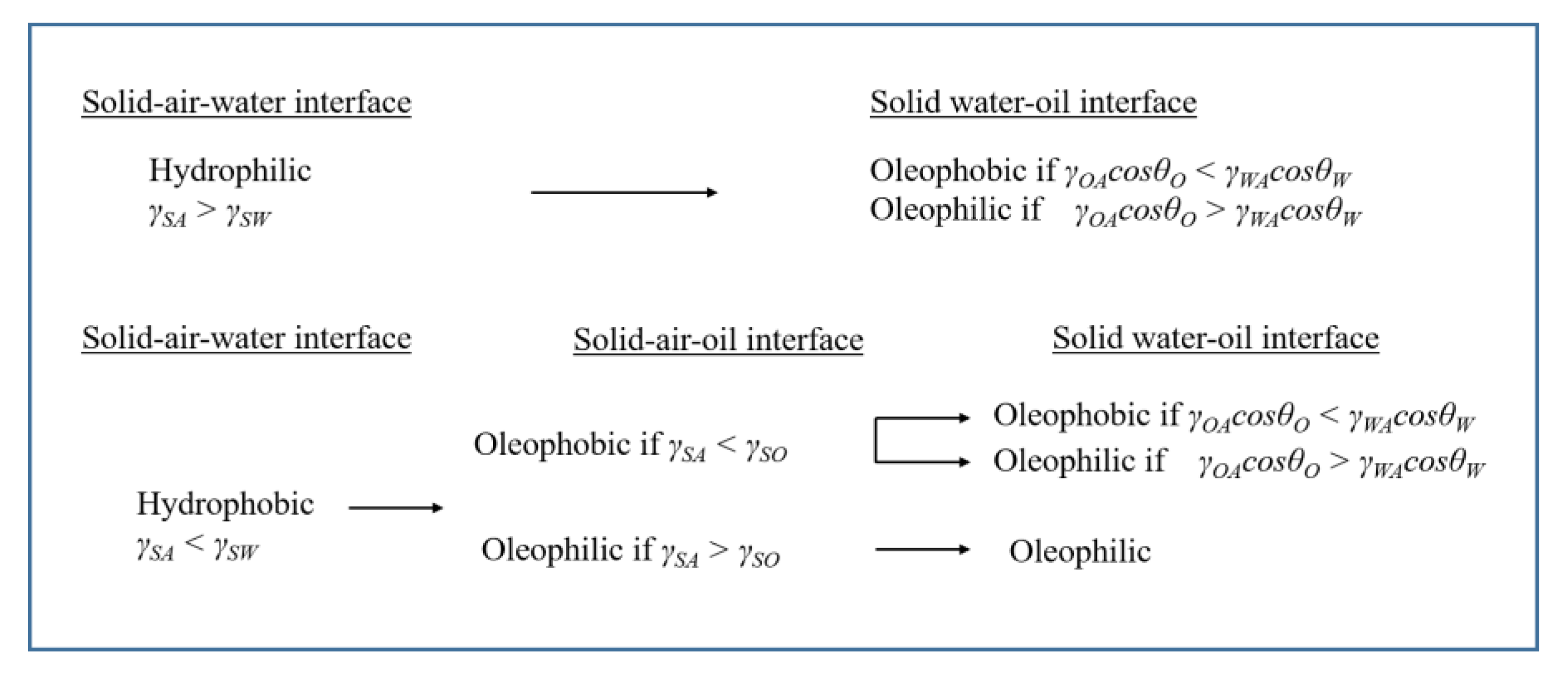
6. Oil/Water Separation Techniques according to the Wettability of Solid/Oil/Water Interfaces
6.1. Free (Stratified) Oil Separation from Water (Oil Spills): Superhydrophobic and Superoleophilic Surfaces
6.2. Oil/Water Emulsions—Separation of Oil Droplets by Membrane Filtration. Superoleophobic and Superhydrophilic Surfaces
6.3. Oil/Water Emulsions—Separation of Oil Droplets by Sorption (Preferable in Batch Systems). Superhydrophobic and Superoleophilic Surfaces
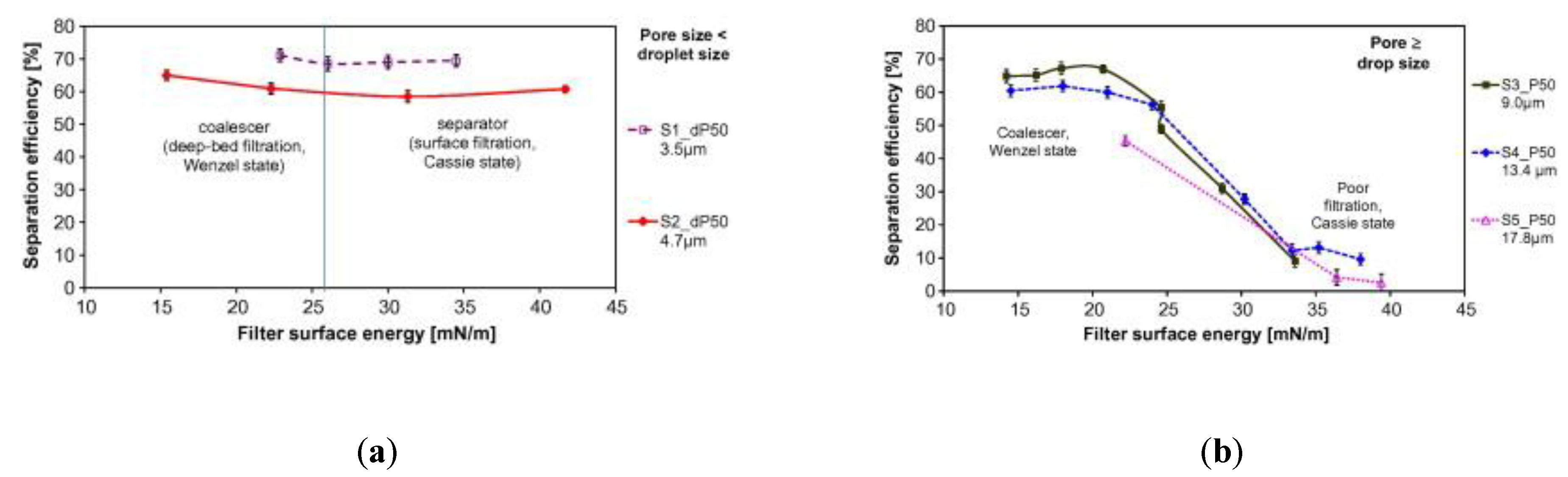
6.4. Oil/Water Emulsions—Separation of Oil Droplets by Demulsification-Coalescence (Deep-Bed Filtration). Balanced Hydrophobic and Oleophilic Surfaces
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pintor, A.M.A.; Vilar, V.J.P.; Botelho, C.M.S.; Boaventura, R.A.R. Oil and grease removal from wastewaters: Sorption treatment as an alternative to state-of-the-art technologies. A critical review. Chem. Eng. J. 2016, 297, 229–255. [Google Scholar] [CrossRef]
- El-Samak, A.A.; Ponnamma, D.; Hassan, M.K.; Ammar, A.; Adham, S.; Al-Maadeed, M.A.A.; Karim, A. Designing Flexible and Porous Fibrous Membranes for Oil Water Separation—A Review of Recent Developments. Polym. Rev. 2020, 60, 671–716. [Google Scholar] [CrossRef]
- Ponnamma, D.; Nair, S.S.; Parangusan, H.; Hassan, M.K.; Adham, S.; Karim, A.; Al-Maadeed, M.A.A. White graphene-cobalt oxide hybrid filler reinforced polystyrene nanofibers for selective oil absorption. Polymers (Basel) 2020, 12, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Samanta, A.; Bera, A.; Ojha, K.; Mandal, A. Comparative studies on enhanced oil recovery by alkali-surfactant and polymer flooding. J. Pet. Explor. Prod. Technol. 2012, 2, 67–74. [Google Scholar] [CrossRef] [Green Version]
- Esmaeilzadeh, P.; Bahramian, A.; Fakhroueian, Z. Adsorption of Anionic, Cationic and Nonionic Surfactants on Carbonate Rock in Presence of ZrO2 Nanoparticles. Phys. Procedia 2011, 22, 63–67. [Google Scholar] [CrossRef] [Green Version]
- Gbadamosi, A.O.; Junin, R.; Manan, M.A.; Agi, A.; Yusuff, A.S. An overview of chemical enhanced oil recovery: Recent advances and prospects. Int. Nano Lett. 2019, 9, 171–202. [Google Scholar] [CrossRef] [Green Version]
- Kamp, J.; Villwock, J.; Kraume, M. Drop coalescence in technical liquid/liquid applications: A review on experimental techniques and modeling approaches. Rev. Chem. Eng. 2017, 33, 1–47. [Google Scholar] [CrossRef] [Green Version]
- Danov, K.D.; Kralchevsky, P.A.; Ivanov, I.B. Encyclopedic Handbook of Emulsion Technology; Marcel Dekker: New York, NY, USA, 2001. [Google Scholar]
- Dickinson, E. Emulsion gels: The structuring of soft solids with protein-stabilized oil droplets. Food Hydrocoll. 2012, 28, 224–241. [Google Scholar] [CrossRef]
- McClements, D.J.; Jafari, S.M. Improving emulsion formation, stability and performance using mixed emulsifiers: A review. Adv. Colloid Interface Sci. 2018, 251, 55–79. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Xu, J.; Zhang, Y.; Wang, X.; Lorenzo, J.M.; Zhong, J. Gelatins as emulsifiers for oil-in-water emulsions: Extraction, chemical composition, molecular structure, and molecular modification. Trends Food Sci. Technol. 2020, 106, 113–131. [Google Scholar] [CrossRef]
- Zembyla, M.; Murray, B.S.; Sarkar, A. Water-in-oil emulsions stabilized by surfactants, biopolymers and/or particles: A review. Trends Food Sci. Technol. 2020, 104, 49–59. [Google Scholar] [CrossRef]
- Mathavan, G.N.; Viraraghavan, T. Coalescence/filtration of an oil-in-water emulsion in a peat bed. Water Res. 1992, 26, 91–98. [Google Scholar] [CrossRef]
- Gast, A.P.; Adamson, A.W. Physical Chemistry of Surfaces, 6th ed.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Jegatheesan, V.; Vigneswaran, S. Deep bed filtration: Mathematical models and observations. Crit. Rev. Environ. Sci. Technol. 2005, 35, 515–569. [Google Scholar] [CrossRef]
- El-Naas, M.; Alhailla, M.A. Modelling of adsorption processes. In Mathematical Modelling; Brennan, C.R., Ed.; Nova Science Publishers, Inc.: New York, NY, USA, 2011; pp. 579–600. [Google Scholar]
- Atkins, P.W.; De Paula, J.; Keeler, J. Atkins’ Physical Chemistry: Quantum Chemistry, Spectroscopy, and Statistical Thermodynamics, 11th ed.; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef] [Green Version]
- Albatrni, H.; Qiblawey, H.; Almomani, F.; Adham, S.; Khraisheh, M. Polymeric adsorbents for oil removal from water. Chemosphere 2019, 233, 809–817. [Google Scholar] [CrossRef] [PubMed]
- Senthil Kumar, P.; Varjani, S.J.; Suganya, S. Treatment of dye wastewater using an ultrasonic aided nanoparticle stacked activated carbon: Kinetic and isotherm modelling. Bioresour. Technol. 2018, 250, 716–722. [Google Scholar] [CrossRef]
- Saadi, R.; Saadi, Z.; Fazaeli, R.; Fard, N.E. Monolayer and multilayer adsorption isotherm models for sorption from aqueous media. Korean J. Chem. Eng. 2015, 32, 787–799. [Google Scholar] [CrossRef]
- Akperov, E.O.; Akperov, O.H. The wastage of the cotton stalks (Gossypium hirsutum L.) as low-cost adsorbent for removal of the Basic Green 5 dye from aqueous solutions. Appl. Water Sci. 2019, 9, 209–219. [Google Scholar] [CrossRef] [Green Version]
- Sumanjit; Rani, S.; Mahajan, R.K. Kinetic and Equilibrium Studies of Adsorption of Dye Congo Red from Aqueous Solutions on Bagasse Charcoal and Banana Peels. J. Surf. Sci. Technol. 2012, 28, 133–147. [Google Scholar] [CrossRef]
- Parker, G.R. Optimum isotherm equation and thermodynamic interpretation for aqueous 1,1,2-trichloroethene adsorption isotherms on three adsorbents. Adsorption 1995, 1, 113–132. [Google Scholar] [CrossRef]
- Ramakrishna, K.R.; Viraraghavan, T. Dye removal using low cost adsorbents. Water Sci. Technol. 1997, 36, 189–196. [Google Scholar] [CrossRef]
- Maurya, N.S.; Mittal, A.K. Applicability of equilibrium isotherm models for the biosorptive uptakes in comparison to activated carbon-based adsorption. J. Environ. Eng. 2006, 132, 1589–1599. [Google Scholar] [CrossRef]
- Edgehill, R.U.; Lu, G.Q. (Max) Adsorption characteristics of carbonized bark for phenol and pentachlorophenol. J. Chem. Technol. Biotechnol. 1998, 71, 27–34. [Google Scholar] [CrossRef]
- Vázquez, G.; González-Álvarez, J.; García, A.I.; Freire, M.S.; Antorrena, G. Adsorption of phenol on formaldehyde-pretreated Pinus pinaster bark: Equilibrium and kinetics. Bioresour. Technol. 2007, 98, 1535–1540. [Google Scholar] [CrossRef]
- Miller, C.O.M.; Clump, C.W. A liquid-phase adsorption study of the rate of diffusion of Phenol from aqueous solution into activated Carbon. AIChE J. 1970, 16, 169–172. [Google Scholar] [CrossRef]
- Ebadi, A.; Soltan Mohammadzadeh, J.S.; Khudiev, A. What is the correct form of BET isotherm for modeling liquid phase adsorption? Adsorption 2009, 15, 65–73. [Google Scholar] [CrossRef]
- Almeida, E.S.; Carvalho, A.C.B.; de Souza Soares, I.O.; Valadares, L.F.; Mendonça, A.R.V.; Silva, I.J.; Monteiro, S. Elucidating how two different types of bleaching earths widely used in vegetable oils industry remove carotenes from palm oil: Equilibrium, kinetics and thermodynamic parameters. Food Res. Int. 2019, 121, 785–797. [Google Scholar] [CrossRef] [Green Version]
- Rezvani, H.; Kazemzadeh, Y.; Sharifi, M.; Riazi, M.; Shojaei, S. A new insight into Fe3O4-based nanocomposites for adsorption of asphaltene at the oil/water interface: An experimental interfacial study. J. Pet. Sci. Eng. 2019, 177, 786–797. [Google Scholar] [CrossRef]
- Eskhan, A.; Banat, F. Removal of Oil from Water by Calcium Alginate Hydrogel Modified with Maleic Anhydride. J. Polym. Environ. 2018, 26, 2901–2916. [Google Scholar] [CrossRef]
- Elgawady, Y.; Ponnamma, D.; Adham, S.; Al-Maas, M.; Ammar, A.; Alamgir, K.; Al-Maadeed, M.A.A.; Hassan, M.K. Mesoporous silica filled smart super oleophilic fibers of triblock copolymer nanocomposites for oil absorption applications. Emergent Mater. 2020, 3, 1–12. [Google Scholar] [CrossRef]
- Yadav, V.B.; Gadi, R.; Kalra, S. Adsorption of lead on clay-CNT nanocomposite in aqueous media by UV-Vis-spectrophotometer: Kinetics and thermodynamic studies. Emergent Mater. 2019, 2, 441–451. [Google Scholar] [CrossRef]
- Alberti, G.; Amendola, V.; Pesavento, M.; Biesuz, R. Beyond the synthesis of novel solid phases: Review on modelling of sorption phenomena. Coord. Chem. Rev. 2012, 256, 28–45. [Google Scholar] [CrossRef]
- Inglezakis, V.J. Solubility-normalized Dubinin-Astakhov adsorption isotherm for ion-exchange systems. Microporous Mesoporous Mater. 2007, 103, 72–81. [Google Scholar] [CrossRef]
- Furmidge, C.G.L. Studies at phase interfaces. I. The sliding of liquid drops on solid surfaces and a theory for spray retention. J. Colloid Sci. 1962, 17, 309–324. [Google Scholar] [CrossRef]
- Suteu, D.; Malutan, T. Industrial cellolignin wastes as adsorbent for removal of methylene blue dye from aqueous solutions. BioResources 2013, 8, 427–446. [Google Scholar] [CrossRef] [Green Version]
- Hamdaoui, O.; Naffrechoux, E. Modeling of adsorption isotherms of phenol and chlorophenols onto granular activated carbon. Part II. Models with more than two parameters. J. Hazard. Mater. 2007, 147, 401–411. [Google Scholar] [CrossRef]
- Jain, M.; Garg, V.K.; Kadirvelu, K. Chromium(VI) removal from aqueous system using Helianthus annuus (sunflower) stem waste. J. Hazard. Mater. 2009, 162, 365–372. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, Z. Application of Dubinin–Radushkevich isotherm model at the solid/solution interface: A theoretical analysis. J. Mol. Liq. 2019, 277, 646–648. [Google Scholar] [CrossRef]
- Edgar, T.F.; Himmelblau, D.M.; Lasdon, L.S. Optimization of Chemical Processes, 2nd ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Hanna, O.T.; Sandall, O.C. Computational Methods in Chemical Engineering, Har/Dskt edition; Pearson College Div: Upper Saddle River, NJ, USA, 1995; p. 454. [Google Scholar]
- Kumar, K.V. Comparative analysis of linear and non-linear method of estimating the sorption isotherm parameters for malachite green onto activated carbon. J. Hazard. Mater. 2006, 136, 197–202. [Google Scholar] [CrossRef]
- Lataye, D.H.; Mishra, I.M.; Mall, I.D. Adsorption of 2-picoline onto bagasse fly ash from aqueous solution. Chem. Eng. J. 2008, 138, 35–46. [Google Scholar] [CrossRef]
- Kumar, K.V.; Porkodi, K.; Rocha, F. Isotherms and thermodynamics by linear and non-linear regression analysis for the sorption of methylene blue onto activated carbon: Comparison of various error functions. J. Hazard. Mater. 2008, 151, 794–804. [Google Scholar] [CrossRef] [PubMed]
- Kumar, K.V.; Sivanesan, S. Pseudo second order kinetics and pseudo isotherms for malachite green onto activated carbon: Comparison of linear and non-linear regression methods. J. Hazard. Mater. 2006, 136, 721–726. [Google Scholar] [CrossRef]
- Tan, I.A.W.; Ahmad, A.L.; Hameed, B.H. Adsorption isotherms, kinetics, thermodynamics and desorption studies of 2,4,6-trichlorophenol on oil palm empty fruit bunch-based activated carbon. J. Hazard. Mater. 2009, 164, 473–482. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.W.; Shen, B.X.; Sun, H.; Zhan, G.X.; Liu, J.C. Adsorption of dimethyl disulfide on ZSM-5 from methyl tert-butyl ether liquid: A study on equilibrium and kinetics. Fuel Process. Technol. 2016, 145, 14–19. [Google Scholar] [CrossRef]
- Ceylan, Z.; Mustafaoglu, D.; Malkoc, E. Adsorption of phenol by MMT-CTAB and WPT-CTAB: Equilibrium, kinetic, and thermodynamic study. Part. Sci. Technol. 2018, 36, 716–726. [Google Scholar] [CrossRef]
- Jung, Y.C.; Bhushan, B. Wetting behavior of water and oil droplets in three-phase interfaces for hydrophobicity/philicity and oleophobicity/philicity. Langmuir 2009, 25, 14165–14173. [Google Scholar] [CrossRef]
- Salvestrini, S.; Leone, V.; Iovino, P.; Canzano, S.; Capasso, S. Considerations about the correct evaluation of sorption thermodynamic parameters from equilibrium isotherms. J. Chem. Thermodyn. 2014, 68, 310–316. [Google Scholar] [CrossRef]
- Liu, Y. Some consideration on the Langmuir isotherm equation. Colloids Surfaces A Physicochem. Eng. Asp. 2006, 274, 34–36. [Google Scholar] [CrossRef]
- Ghosal, P.S.; Gupta, A.K. Determination of thermodynamic parameters from Langmuir isotherm constant-revisited. J. Mol. Liq. 2017, 225, 137–146. [Google Scholar] [CrossRef]
- Liu, Y. Is the free energy change of adsorption correctly calculated? J. Chem. Eng. Data 2009, 54, 1981–1985. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, X. The unit problem in the thermodynamic calculation of adsorption using the Langmuir equation. Chem. Eng. Commun. 2014, 201, 1459–1467. [Google Scholar] [CrossRef]
- Milonjić, S.K. A consideration of the correct calculation of thermodynamic parameters of adsorption. J. Serb. Chem. Soc 2007, 72, 1363–1367. [Google Scholar] [CrossRef]
- Azizian, S.; Eris, S.; Wilson, L.D. Re-evaluation of the century-old Langmuir isotherm for modeling adsorption phenomena in solution. Chem. Phys. 2018, 513, 99–104. [Google Scholar] [CrossRef]
- Lagergren, S. Zur Theorie der Sogenannten Adsorption Gelöster Stoffe, Kungliga Svenska Vetenskapsakademiens; Scientific Research Publishing: Handlingar, Sweden, 1898; pp. 1–39. [Google Scholar]
- Blanchard, G.; Maunaye, M.; Martin, G. Removal of heavy metals from waters by means of natural zeolites. Water Res. 1984, 18, 1501–1507. [Google Scholar] [CrossRef]
- Ho, Y.S. Second-order kinetic model for the sorption of cadmium onto tree fern: A comparison of linear and non-linear methods. Water Res. 2006, 40, 119–125. [Google Scholar] [CrossRef]
- Wang, Z.; Barford, J.P.; Hui, C.W.; McKay, G. Kinetic and equilibrium studies of hydrophilic and hydrophobic rice husk cellulosic fibers used as oil spill sorbents. Chem. Eng. J. 2015, 281, 961–969. [Google Scholar] [CrossRef]
- Hubbe, M.A.; Azizian, S.; Douven, S. Implications of apparent pseudo-second-order adsorption kinetics onto cellulosic materials: A review. BioResources 2019, 14, 7582–7626. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.J. Biosorption isotherms, kinetics and thermodynamics. Sep. Purif. Technol. 2008, 61, 229–242. [Google Scholar] [CrossRef]
- Azizian, S. Kinetic models of sorption: A theoretical analysis. J. Colloid Interface Sci. 2004, 276, 47–52. [Google Scholar] [CrossRef]
- Ho, Y.S.; McKay, G. Kinetic models for the sorption of dye from aqueous solution by wood. Process Saf. Environ. Prot. 1998, 76, 183–191. [Google Scholar] [CrossRef] [Green Version]
- Ho, Y.S.; McKay, G. The kinetics of sorption of basic dyes from aqueous solution by sphagnum moss peat. Can. J. Chem. Eng. 1998, 76, 822–827. [Google Scholar] [CrossRef]
- Ho, Y.S.; McKay, G. A kinetic study of dye sorption by biosorbent waste product pith. Resour. Conserv. Recycl. 1999, 25, 171–193. [Google Scholar] [CrossRef]
- Ho, Y.S.; McKay, G. Sorption of dye from aqueous solution by peat. Chem. Eng. J. 1998, 70, 115–124. [Google Scholar] [CrossRef]
- Canzano, S.; Iovino, P.; Leone, V.; Salvestrini, S.; Capasso, S. Use and misuse of sorption kinetic data: A common mistake that should be avoided. Adsorpt. Sci. Technol. 2012, 30, 217–225. [Google Scholar] [CrossRef]
- Douven, S.; Paez, C.A.; Gommes, C.J. The range of validity of sorption kinetic models. J. Colloid Interface Sci. 2015, 448, 437–450. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford University Press: London, UK, 1975; pp. 69–88. [Google Scholar]
- Weber, W.J.; Morris, J.C. Kinetics of Adsorption on Carbon from Solution. J. Sanit. Engineer. Div. 1963, 89, 31–60. [Google Scholar] [CrossRef]
- Réguer, A.; Sochard, S.; Hort, C.; Platel, V. Measurement and modelling of adsorption equilibrium, adsorption kinetics and breakthrough curve of toluene at very low concentrations on to activated carbon. Environ. Technol. 2011, 32, 757–766. [Google Scholar] [CrossRef]
- Thomas, H.C. Heterogeneous Ion Exchange in a Flowing System. J. Am. Chem. Soc. 1944, 66, 1664–1666. [Google Scholar] [CrossRef]
- Juang, R.S.; Kao, H.C.; Chen, W. Column removal of Ni(II) from synthetic electroplating waste water using a strong-acid resin. Sep. Purif. Technol. 2006, 49, 36–42. [Google Scholar] [CrossRef]
- Janson, A.; Minier-Matar, J.; Al-Shamari, E.; Hussain, A.; Sharma, R.; Rowley, D.; Adham, S. Evaluation of new ion exchange resins for hardness removal from boiler feedwater. Emergent Mater. 2018, 1, 77–87. [Google Scholar] [CrossRef]
- Pintor, A.M.A.; Martins, A.G.; Souza, R.S.; Vilar, V.J.P.; Botelho, C.M.S.; Boaventura, R.A.R. Treatment of vegetable oil refinery wastewater by sorption of oil and grease onto regranulated cork—A study in batch and continuous mode. Chem. Eng. J. 2015, 268, 92–101. [Google Scholar] [CrossRef]
- Bohart, G.S.; Adams, E.Q. Some aspects of the behavior of charcoal with respect to chlorine. J. Am. Chem. Soc. 1920, 42, 523–544. [Google Scholar] [CrossRef] [Green Version]
- Hutchins, R.A. New method simplifies design of activated carbon systems. Chem. Engineer. 1973, 80, 133–135. [Google Scholar]
- Elmobarak, W.F.; Almomani, F. Application of Fe3O4 magnetite nanoparticles grafted in silica (SiO2) for oil recovery from oil in water emulsions. Chemosphere 2021, 265, 129054. [Google Scholar] [CrossRef] [PubMed]
- Ewis, D.; Benamor, A.; Ba-Abbad, M.M.; Nasser, M.; El-Naas, M.; Qiblawey, H. Removal of Oil Content from Oil-Water Emulsions Using Iron Oxide/Bentonite Nano Adsorbents. J. Water Process Eng. 2020, 38, 2214–7144. [Google Scholar] [CrossRef]
- Diraki, A.; Mackey, H.; McKay, G.; Abdala, A.A. Removal of oil from oil–water emulsions using thermally reduced graphene and graphene nanoplatelets. Chem. Eng. Res. Des. 2018, 137, 47–59. [Google Scholar] [CrossRef]
- Lin, K.-Y.A.; Chen, Y.-C.; Phattarapattamawong, S. Efficient demulsification of oil-in-water emulsions using a zeolitic imidazolate framework: Adsorptive removal of oil droplets from water. J. Colloid Interface Sci. 2016, 478, 97–106. [Google Scholar] [CrossRef]
- Wang, D.; McLaughlin, E.; Pfeffer, R.; Lin, Y.S. Adsorption of oils from pure liquid and oil–water emulsion on hydrophobic silica aerogels. Sep. Purif. Technol. 2012, 99, 28–35. [Google Scholar] [CrossRef]
- Elanchezhiyan, S.S.; Prabhu, S.M.; Meenakshi, S. Effective adsorption of oil droplets from oil-in-water emulsion using metal ions encapsulated biopolymers: Role of metal ions and their mechanism in oil removal. Int. J. Biol. Macromol. 2018, 112, 294–305. [Google Scholar] [CrossRef]
- Okiel, K.; El-Sayed, M.; El-Kady, M.Y. Treatment of oil–water emulsions by adsorption onto activated carbon, bentonite and deposited carbon. Egypt. J. Pet. 2011, 20, 9–15. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.; Zhai, M.; Li, X. Adsorptive removal of oil drops from ASP flooding-produced water by polyether polysiloxane-grafted ZIF-8. Powder Technol. 2021, 378, 76–84. [Google Scholar] [CrossRef]
- Sharma, M.; Joshi, M.; Nigam, S.; Avasthi, D.K.; Adelung, R.; Srivastava, S.K.; Mishra, Y.K. Efficient oil removal from wastewater based on polymer coated superhydrophobic tetrapodal magnetic nanocomposite adsorbent. Appl. Mater. Today 2019, 17, 130–141. [Google Scholar] [CrossRef]
- Venkatesh, K.; Arthanareeswaran, G.; Bose, A.C.; Kumar, P.S. Hydrophilic hierarchical carbon with TiO2 nanofiber membrane for high separation efficiency of dye and oil-water emulsion. Sep. Purif. Technol. 2020, 241, 116709. [Google Scholar] [CrossRef]
- Knapik, E.; Stopa, J. Fibrous deep-bed filtration for oil/water separation using sunflower pith as filter media. Ecol. Eng. 2018, 121, 44–52. [Google Scholar] [CrossRef]
- El-Maghrabi, H.H.; Hosny, R.; Ramzi, M.; Zayed, M.A.; Fathy, M. Preparation and Characterization of Novel Magnetic ZnFe2O4–Hydroxyapatite Core–Shell Nanocomposite and Its Use as Fixed Bed Column System for Removal of Oil Residue in Oily Wastewater Samples. Egypt. J. Pet. 2019, 28, 137–144. [Google Scholar] [CrossRef]
- Akpomie, K.G.; Conradie, J. Ultrasonic aided sorption of oil from oil-in-water emulsion onto oleophilic natural organic-silver nanocomposite. Chem. Eng. Res. Des. 2021, 165, 12–24. [Google Scholar] [CrossRef]
- Elanchezhiyan, S.S.; Meenakshi, S. Synthesis and characterization of chitosan/Mg-Al layered double hydroxide composite for the removal of oil particles from oil-in-water emulsion. Int. J. Biol. Macromol. 2017, 104, 1586–1595. [Google Scholar] [CrossRef]
- Ben-Avraham, D. Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists. J. Stat. Phys. 2006, 123, 709–710. [Google Scholar] [CrossRef]
- An essay on the cohesion of fluids. Abstr. Pap. Print. Philos. Trans. R. Soc. London 1832, 1, 171–172. [CrossRef] [Green Version]
- Whyman, G.; Bormashenko, E.; Stein, T. The rigorous derivation of Young, Cassie-Baxter and Wenzel equations and the analysis of the contact angle hysteresis phenomenon. Chem. Phys. Lett. 2008, 450, 355–359. [Google Scholar] [CrossRef]
- Shafrin, E.G.; Zisman, W.A. Constitutive relations in the wetting of low energy surfaces and the theory of the retraction method of preparing monolayers. J. Phys. Chem. 1960, 64, 519–524. [Google Scholar] [CrossRef]
- Good, R.J.; van Oss, C.J. The Modern Theory of Contact Angles and the Hydrogen Bond Components of Surface Energies BT. In Modern Approaches to Wettability: Theory and Applications; Schrader, M.E., Loeb, G.I., Eds.; Springer Science + Business media: New York, NY, USA, 1992; pp. 1–27. [Google Scholar]
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- Marmur, A. Thermodynamic aspects of contact angle hysteresis. Adv. Colloid Interface Sci. 1994, 50, 121–141. [Google Scholar] [CrossRef]
- Gao, L.; McCarthy, T.J. Contact angle hysteresis explained. Langmuir 2006, 22, 6234–6237. [Google Scholar] [CrossRef]
- Ge, J.; Zhao, H.Y.; Zhu, H.W.; Huang, J.; Shi, L.A.; Yu, S.H. Advanced Sorbents for Oil-Spill Cleanup: Recent Advances and Future Perspectives. Adv. Mater. 2016, 28, 10459–10490. [Google Scholar] [CrossRef]
- Chen, C.; Weng, D.; Mahmood, A.; Chen, S.; Wang, J. Separation Mechanism and Construction of Surfaces with Special Wettability for Oil/Water Separation. ACS Appl. Mater. Interfaces 2019, 11, 11006–11027. [Google Scholar] [CrossRef]
- Hubbe, M.A.; Gardner, D.J.; Shen, W. Contact angles and wettability of cellulosic surfaces: A review of proposed mechanisms and test strategies. BioResources 2015, 10, 8657–8749. [Google Scholar] [CrossRef] [Green Version]
- Yong, J.; Chen, F.; Yang, Q.; Huo, J.; Hou, X. Superoleophobic surfaces. Chem. Soc. Rev. 2017, 46, 4168–4217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xue, Z.; Liu, M.; Jiang, L. Recent developments in polymeric superoleophobic surfaces. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 1209–1224. [Google Scholar] [CrossRef]
- Liu, M.; Wang, S.; Wei, Z.; Song, Y.; Jiang, L. Superoleophobic Surfaces: Bioinspired Design of a Superoleophobic and Low Adhesive Water/Solid Interface (Adv. Mater. 6/2009). Adv. Mater. 2009, 21, 665–669. [Google Scholar] [CrossRef]
- Järn, M.; Granqvist, B.; Lindfors, J.; Kallio, T.; Rosenholm, J.B. A critical evaluation of the binary and ternary solid-oil-water and solid-water-oil interaction. Adv. Colloid Interface Sci. 2006, 123–126, 137–149. [Google Scholar] [CrossRef] [PubMed]
- Hubbe, M.A.; Rojas, O.J.; Fingas, M.; Gupta, B.S. Cellulosic Substrates for Removal of Pollutants from Aqueous Systems: A Review. 3.Spilled Oil and Emulsified Organic Liquids. BioResources 2013, 8, 3038. [Google Scholar] [CrossRef] [Green Version]
- Parangusan, H.; Ponnamma, D.; Hassan, M.K.; Adham, S.; Al-Maadeed, M.A.A. Designing carbon nanotube-based oil absorbing membranes from gamma irradiated and electrospun polystyrene nanocomposites. Materials (Basel) 2019, 12, 709. [Google Scholar] [CrossRef] [Green Version]
- Fahim, M.A.; Othman, F.M. Coalescence of secondary dispersions in composite packed beds. J. Dispers. Sci. Technol. 1987, 8, 507–523. [Google Scholar] [CrossRef]
- Hadjiev, D.; Aurelle, Y.; Assenov, A. New separator for removal of organic liquids in water. Environ. Technol. (UK) 1992, 13, 267–274. [Google Scholar] [CrossRef]
- Kang, W.; Li, M.; Yang, H.; Kang, X.; Wang, F.; Jiang, H.; Zhang, M.; Zhu, T.; Sarsenbekuly, B. Coalescence behavior of aqueous drops in water-in-oil emulsions under high-frequency pulsed AC fields. J. Ind. Eng. Chem. 2021, 93, 415–422. [Google Scholar] [CrossRef]
- Head, B.A. Method of Filtering Oil from Oil-and-Water Emulsions. U.S. Patent 4309289A, 5 January 1982. [Google Scholar]
- Šećerov Sokolović, R.M.; Govedarica, D.D.; Sokolović, D.S. Separation of oil-in-water emulsion using two coalescers of different geometry. J. Hazard. Mater. 2010, 175, 1001–1006. [Google Scholar] [CrossRef]
- Rawlins, C.H. Experimental Study on Oil and Solids Removal in Nutshell Filters for Produced Water Treatment. In Proceedings of the SPE Western Regional Meeting, Garden Grove, CA, USA, 22–27 April 2018. [Google Scholar]
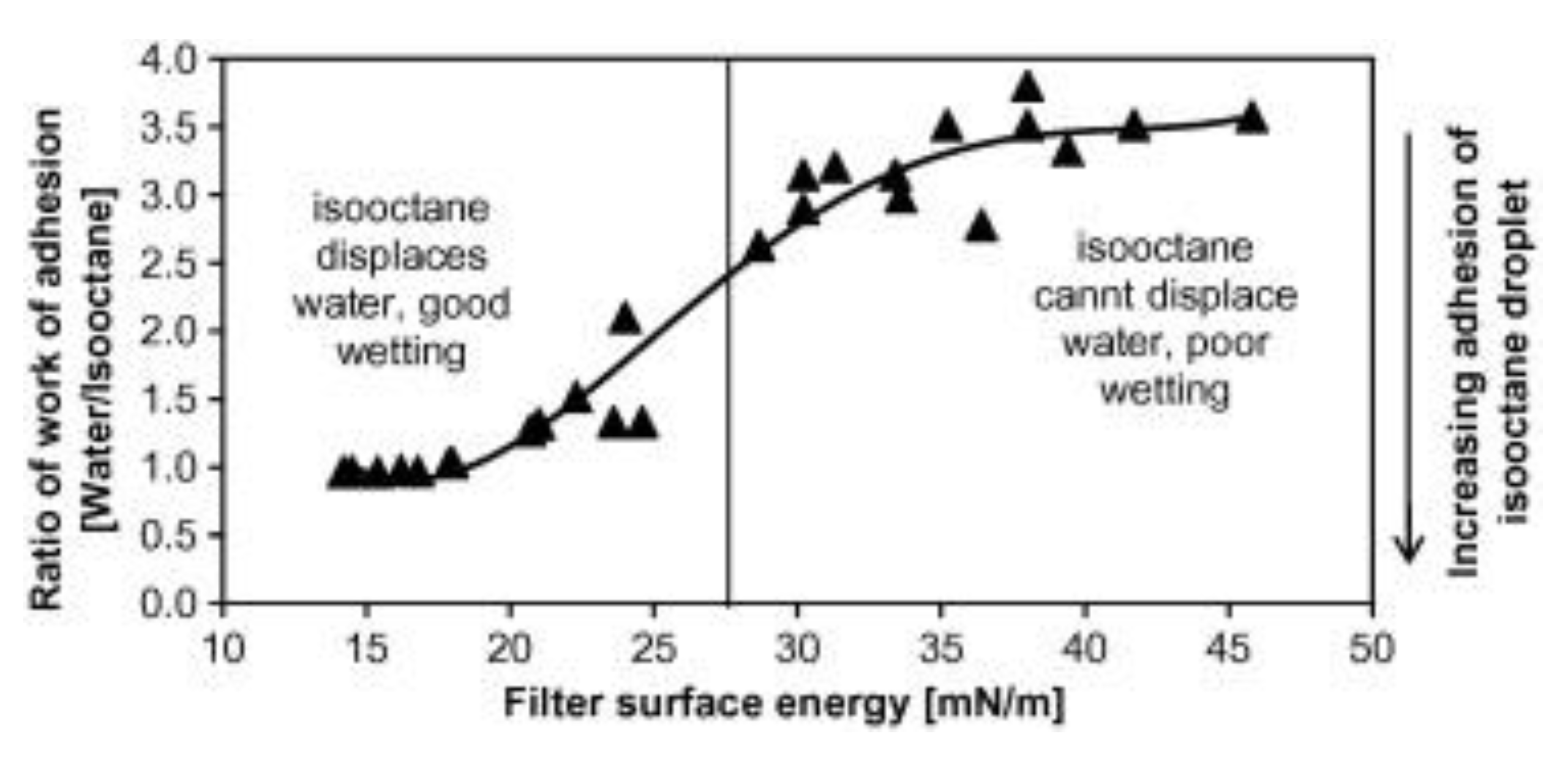
- Agarwal, S.; Von Arnim, V.; Stegmaier, T.; Planck, H.; Agarwal, A. Role of surface wettability and roughness in emulsion separation. Sep. Purif. Technol. 2013, 107, 19–25. [Google Scholar] [CrossRef]
- Agarwal, S.; Von Arnim, V.; Stegmaier, T.; Planck, H.; Agarwal, A. Effect of fibrous coalescer geometry and operating conditions on emulsion separation. Ind. Eng. Chem. Res. 2013, 52, 13164–13170. [Google Scholar] [CrossRef]
- Mino, Y.; Kagawa, Y.; Matsuyama, H.; Ishigami, T. Permeation of oil-in-water emulsions through coalescing filter: Two-dimensional simulation based on phase-field model. AIChE J. 2016, 62, 2525–2532. [Google Scholar] [CrossRef]
- Bansal, S.; von Arnim, V.; Stegmaier, T.; Planck, H. Effect of fibrous filter properties on the oil-in-water-emulsion separation and filtration performance. J. Hazard. Mater. 2011, 190, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Fredrick, E.; Walstra, P.; Dewettinck, K. Factors governing partial coalescence in oil-in-water emulsions. Adv. Colloid Interface Sci. 2010, 153, 30–42. [Google Scholar] [CrossRef] [PubMed]
- Soma, J.; Papadopoulos, K.D. Deposition of oil-in-water emulsions in sand beds in the presence of cetyltrimethylammonium bromide. Environ. Sci. Technol. 1997, 31, 1040–1045. [Google Scholar] [CrossRef]
- Shukla, A.; Zhang, Y.H.; Dubey, P.; Margrave, J.L.; Shukla, S.S. The role of sawdust in the removal of unwanted materials from water. J. Hazard. Mater. 2002, 95, 137–152. [Google Scholar] [CrossRef]
| The sum of the squares of the errors (SSE) | SSE = |
| The sum of the absolute errors (SAE) | SAE = |
| The average relative error (ARE) | ARE ) |
| The hybrid fractional error function (HYBRID) | HYBRID = |
| Marquardt’s percent standard deviation (MPSD) | MPSD = |
| Sorbent | Emulsion | Outputs | Models | Ref. |
|---|---|---|---|---|
| Optipore L493, Lewatit AF5, Amberlite IRA958 (synthetic resins), batch system | Synthetic PW emulsion, Octane 95, nonionic surfactant, 25–50 ppm | Below 2 ppm | Langmuir, Freundlich, Flor–Huggins isotherms, Toth, Dubinin–Radushkevich isotherms, PFO, PSO models, intra-particle diffusion model | [19] |
| Calcium alginate hydrogel modified by maleic anhydride, batch system | Crude oil, sonication, no surfactant, 1 M NaCl, 100–500 ppm | 80% removal efficiency | Freundlich, BET isotherms, PFO and PSO models, intra-particle, diffusion model | [33] |
| Fe3O4 magnetite nanoparticles grafted in silica (SiO2), batch system | Gasoline oil, 500–4000 ppm | >90% removal efficiency | Langmuir, Freundlich isotherms | [82] |
| Iron Oxide/ Bentonite Nano Adsorbents, batch system | Diesel oil, 66 to 170 ppm, non-ionic surfactant | 67% removal efficiency | Langmuir, Freundlich, Toth | [83] |
| Thermally reduced graphene and graphene nanoplatelets, batch system | 200 ppm and adjusted salinity | TRG: 1550 mg oil/g GNP: 805 mg oil/g | Langmuir, Freundlich, Dubinin–Radushkevich, Tempkin isotherms | [84] |
| Zeolitic imidazolate, batch system | Soybean oil, 5 wt% | 6633 mg/g | Langmuir, Freundlich isotherms, PFO and PSO | [85] |
| Hydrophobic silica aerogels, batch system | Vegetable oil, motor oil 10W30, light crude oil, Tween 80 | Freundlich isotherm | [86] | |
| https://www.sciencedirect.com/topics/biochemistry-genetics-and-molecular-biology/lanthanum (accessed on 26 February 2021), zirconium and cerium embedded chitosan/gelatin, batch system | 4 wt% cutting oil | Langmuir, Freundlich, Dubinin–Radushkevich, Tempkin isotherms | [87] | |
| Activated carbon, bentonite, deposited carbon, batch system | Produced wastewater from Gamasa Petroleum Company, 600–1012 ppm | Up to 98% removal efficiency | Langmuir, Freundlich isotherms | [88] |
| Polyether polysiloxane, batch system | Oil-flooding-produced water from the Daqing oil field, 400 ppm | 90% removal efficiency | Langmuir, Freundlich isotherms | [89] |
| Regranulated cork, flow system | Sunflower oil and saponified matter, 200 ppm | <15 ppm | Freundlich isotherms and linear partitioning models | [79] |
| Magnetic nanosorbent polydimethylsiloxane, zinc oxide, batch system | 2 wt% diesel, span 80 | 96% removal efficiency | PFO and PSO, intra-particle diffusion models | [90] |
| Hydrophilic hierarchical carbon with TiO2 nanofiber membrane, batch system | Engine oil, cooking oil, hexane, toluene, 1000 ppm, Surfactant SDS 200 ppm | 95.4% removal efficiency | BET isotherm | [91] |
| Sunflower pith, flow system | Artificial reservoir brine, 0.1, 2.0, and 20.0 g/L of oil | Over 99% removal efficiency | PFO, PSO, Modified logistic model | [92] |
| Magnetic ZnFe2O4–Hydroxyapatite Core–Shell Nanocomposite, flow system | Produced water containing oil from 100 to 10,000 ppm | 98% removal efficiency | Thomas–BDST model, Yoon–Nelson model | [93] |
| Oleophilic natural organic-silver nanocomposite, batch system | Motor oil, 200–1000 ppm | NA | Langmuir, Freundlich, Temkin isotherms, PFO and PSO | [94] |
| Chitosan/Mg-Al hydroxide composite, batch system | 4 wt.% cutting oil | 78% removal efficiency | Langmuir, Freundlich, Dubinin–Radushkevich, Tempkin isotherms | [95] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobolčiak, P.; Popelka, A.; Tanvir, A.; Al-Maadeed, M.A.; Adham, S.; Krupa, I. Some Theoretical Aspects of Tertiary Treatment of Water/Oil Emulsions by Adsorption and Coalescence Mechanisms: A Review. Water 2021, 13, 652. https://doi.org/10.3390/w13050652
Sobolčiak P, Popelka A, Tanvir A, Al-Maadeed MA, Adham S, Krupa I. Some Theoretical Aspects of Tertiary Treatment of Water/Oil Emulsions by Adsorption and Coalescence Mechanisms: A Review. Water. 2021; 13(5):652. https://doi.org/10.3390/w13050652
Chicago/Turabian StyleSobolčiak, Patrik, Anton Popelka, Aisha Tanvir, Mariam A. Al-Maadeed, Samer Adham, and Igor Krupa. 2021. "Some Theoretical Aspects of Tertiary Treatment of Water/Oil Emulsions by Adsorption and Coalescence Mechanisms: A Review" Water 13, no. 5: 652. https://doi.org/10.3390/w13050652
APA StyleSobolčiak, P., Popelka, A., Tanvir, A., Al-Maadeed, M. A., Adham, S., & Krupa, I. (2021). Some Theoretical Aspects of Tertiary Treatment of Water/Oil Emulsions by Adsorption and Coalescence Mechanisms: A Review. Water, 13(5), 652. https://doi.org/10.3390/w13050652







