Study of the Wet Bulb in Stratified Soils (Sand-Covered Soil) in Intensive Greenhouse Agriculture under Drip Irrigation by Calibrating the Hydrus-3D Model
Abstract
:1. Introduction
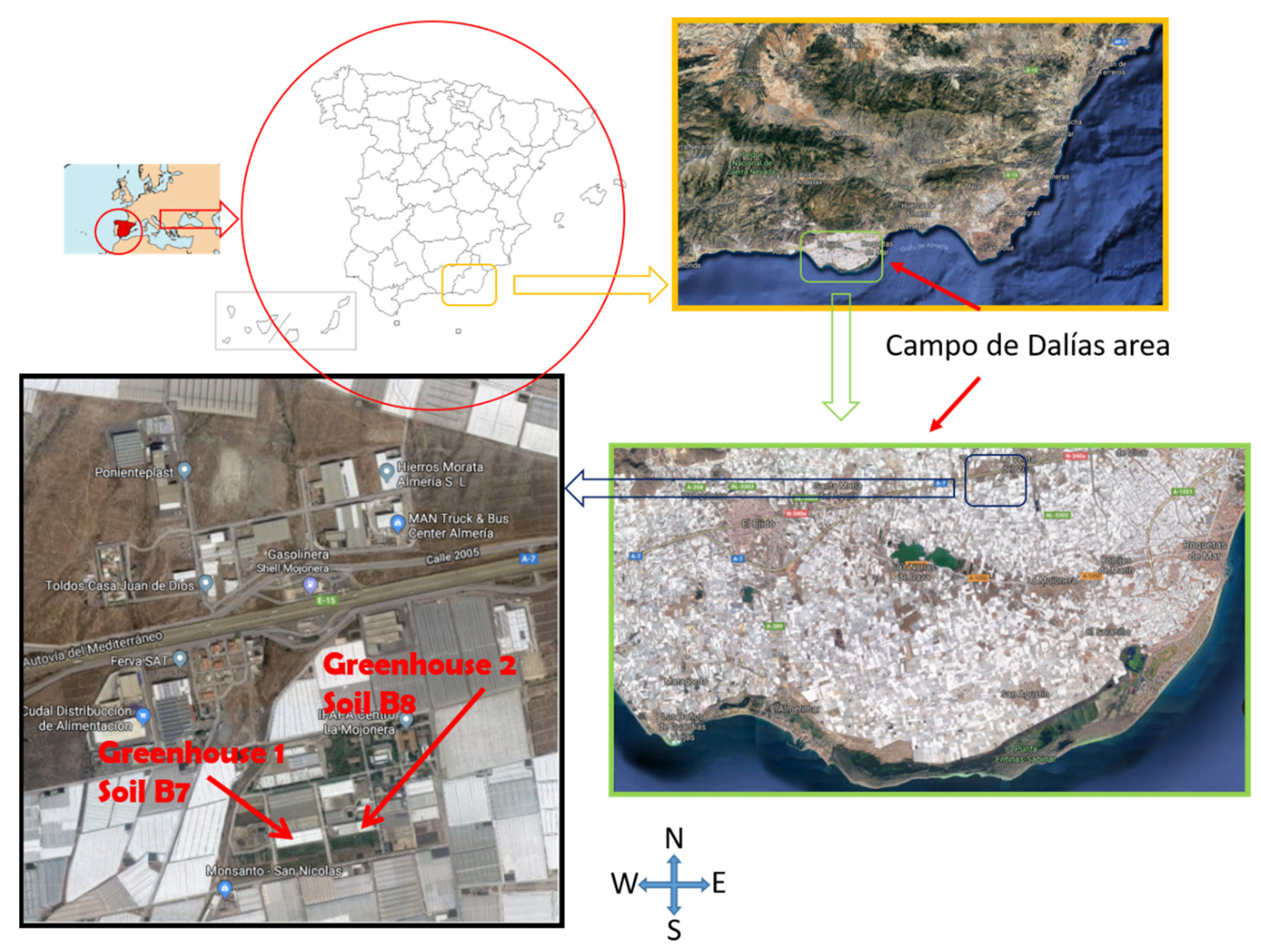
2. Materials and Methods
3. Results
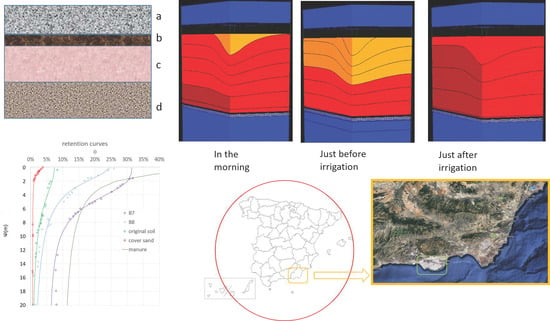
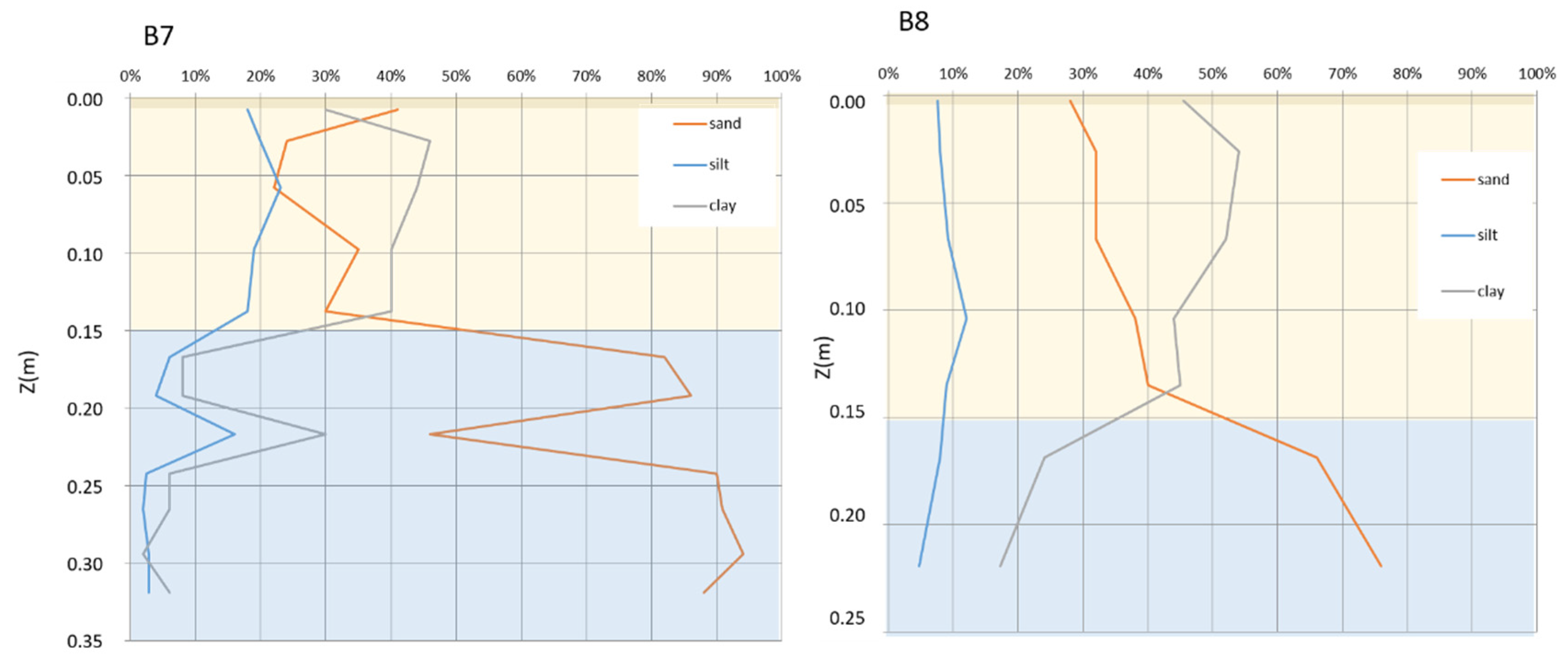
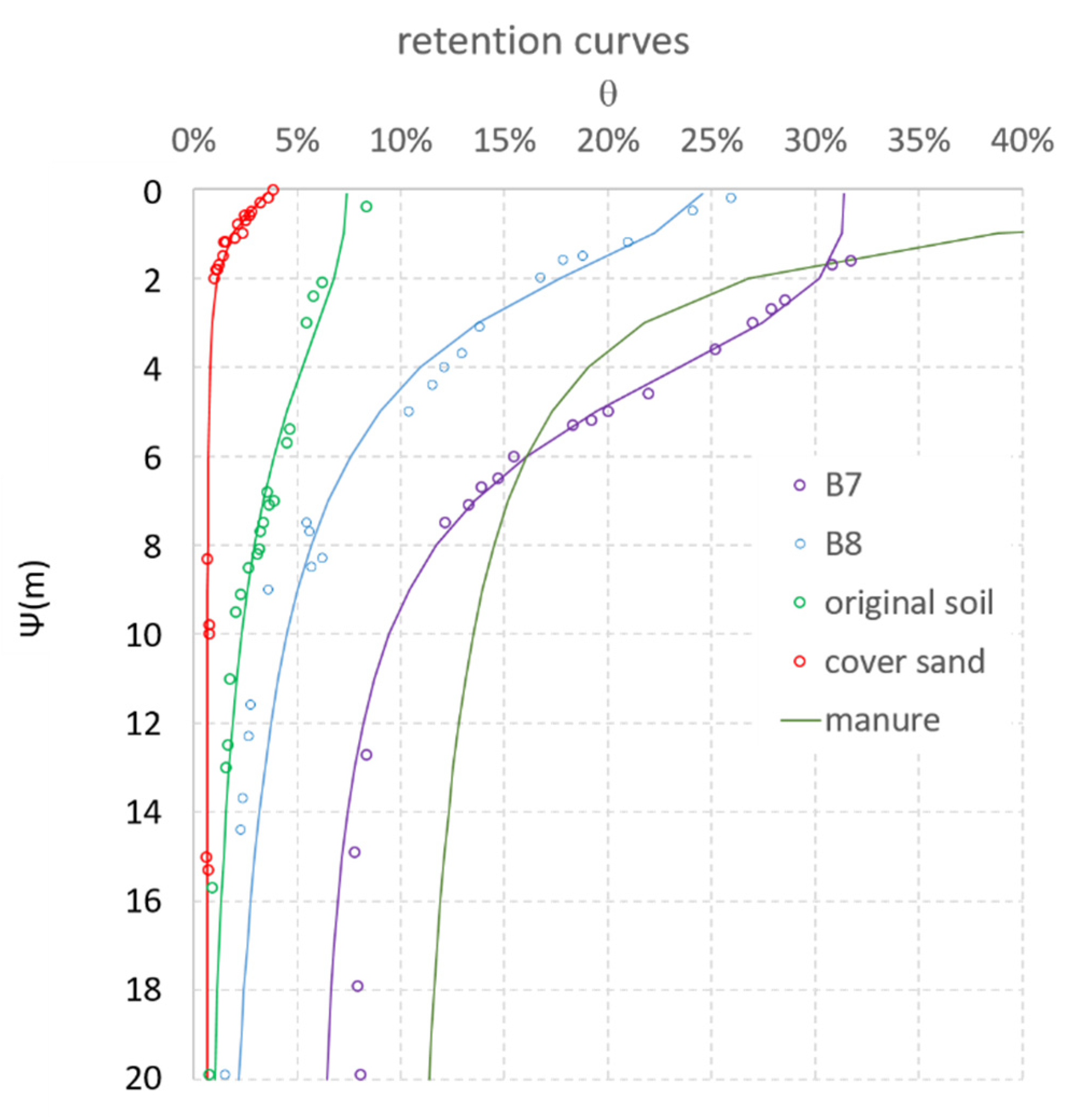
3.1. Moisture Retention Curve of Greenhouse Soils
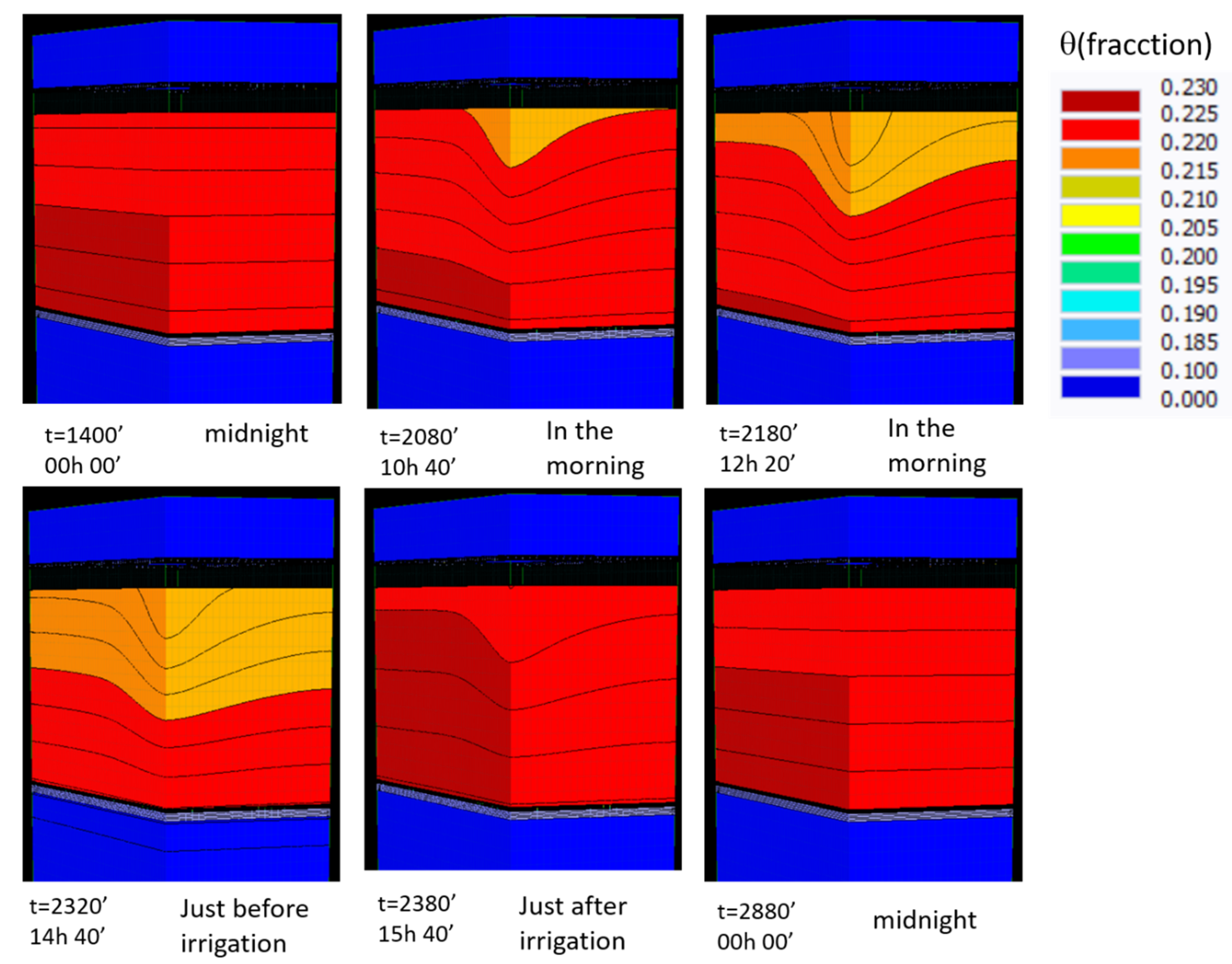
3.2. Estimation of Water Movement Using the Hydrus-3D Program
4. Discussion
4.1. Moisture Retention Curve of Greenhouse Soils
4.2. Estimation of Water Movement Using the Hydrus-3D Program
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chico, D.; Salmoral, G.; Llamas, M.R.; Garrido, A.; Aldaya, M.M. The Water Footprint and Virtual Water Exports of Spanish Tomatoes; Fundación Botín: Madrid, Spain, 2010; Volume 8. [Google Scholar]
- Neira, D.P.; Montiel, M.S.; Cabeza, M.D.; Reigada, A. Energy use and carbon footprint of the tomato production in heated multi-tunnel greenhouses in Almeria within an exporting agri-food system context. Sci. Total Environ. 2018, 628–629, 1627–1636. [Google Scholar] [CrossRef]
- Modaihsh, A.S.; Horton, R.; Kirkham, D. Soil Water Evaporation Suppression by Sand Mulches. Soil Sci. 1985, 139, 357–361. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, Z.; Sukhdev, S.; Vera, C.L.m.; Zhang, Y.; Guo, Z. Effects of gravel–sand mulch, plastic mulch and ridge and furrow rainfall harvesting system combinations on water use efficiency, soil temperature and watermelon yield in a semi-arid Loess Plateau of northwestern China. Agric. Water Manag. 2011, 101, 88–92. [Google Scholar] [CrossRef]
- Bonachela, S.; López, J.C.; Granados, M.R.; Magán, J.J.; Hernández, J.; Baille, A. Effects of gravel mulch on surface energy balance and soil thermal regime in an unheated plastic greenhouse. Biosyst. Eng. 2020, 192, 1–13. Available online: http://www.sciencedirect.com/science/article/pii/S1537511020300222 (accessed on 19 February 2021). [CrossRef]
- Pérez, J.; López, J.; Fernández, M.D. La Agricultura del Sureste: Situación Actual y Tendencias de las Estructuras de Producción en la Horticultura Almeriense 2a. Edición; Editorial Caja Rural Intermediterránea: Madrid, Spain, 2002. [Google Scholar]
- Arbat, G.; Puig-Bargués, J.; Duran-Ros, M.; Barragán, J.; De Cartagena, F.R. Drip-Irriwater: Computer software to simulate soil wetting patterns under surface drip irrigation. Comput. Electron. Agric. 2013, 98, 183–192. [Google Scholar] [CrossRef]
- Singh Lubana, P.P.; Narda, N.K. Soil and Water: Modelling Soil Water Dynamics under Trickle Emitters—A Review. J. Agric. Eng. Res. 2001, 78, 217–232. Available online: http://www.sciencedirect.com/science/article/pii/S0021863400906504 (accessed on 7 February 2013). [CrossRef]
- Schwartzman, M.; Zur, B. Emitter spacing and geometry of wetted soil volume. J. Irrig. Drain. Eng. 1986, 112, 242–253. [Google Scholar] [CrossRef]
- Amin, M.S.M.; Ekhmaj, A.I.M. DIPAC-Drip Irrigation Water Distribution Pattern Calculator. In Proceedings of the 7th International Micro Irrigation Congress, Pwtc, Kuala Lumpur, Malaysia, 10–16 September 2006. [Google Scholar]
- Kandelous, M.M.; Šimůnek, J. Comparison of numerical, analytical, and empirical models to estimate wetting patterns for surface and subsurface drip irrigation. Irrig. Sci. 2010, 28, 435–444. [Google Scholar] [CrossRef] [Green Version]
- Philip, J.R. Steady infiltration from buried, surface and perched point and line sources in heterogeneous soils, I. Analysis. Soil Sci. Soc. Am. Proc. 1972, 36, 268–273. [Google Scholar] [CrossRef]
- Chu, S.-T. Geen-Ampt Analysis of wetting patterns for surface emitters. J. Irrig. Drain Eng. 1994, 120, 414–421. [Google Scholar] [CrossRef]
- Hill, D.E.; Parlange, J.-Y. Wetting Front Instability in Layered Soils. Soil Sci. Soc. Am. J. 1972, 36, 697–702. [Google Scholar] [CrossRef]
- Li, Z.; VanderBorght, J.; Smits, K.M. The effect of the top soil layer on moisture and evaporation dynamics. Vadose Zone J. 2020, 19, 10. [Google Scholar] [CrossRef]
- Garcia-Caparros, P.; Contreras, J.I.; Baeza, R.; Segura, M.L.; Lao, M.T. Integral Management of Irrigation Water in Intensive Horticultural Systems of Almería. Sustainability 2017, 9, 2271. [Google Scholar] [CrossRef] [Green Version]
- Fernández, J.E.; Moreno, F.; Cabrera, F.; Arrúe, J.L.; Martin-Aranda, J. Drip irrigation, soil characteristics and the root distribution and root activity of olive trees. Plant Soil 1991, 133, 239–251. [Google Scholar] [CrossRef]
- Newman, E.I. A Method of Estimating the Total Length of Root in a Sample. J. Appl. Ecol. 1966, 3, 139. [Google Scholar] [CrossRef]
- Steudle, E. Water uptake by plant roots: An integration of views. Plant Soil 2000, 226, 45–56. [Google Scholar] [CrossRef]
- Prasad, R. A linear root water uptake model. J. Hydrol. 1988, 99, 297–306. [Google Scholar] [CrossRef]
- Šimunek, J.; Van Genuchten, M.T.; Šejna, M. HYDRUS: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1263–1274. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Simunek, J. Modeling Water Flow and Contaminant Transport in Soils and Groundwater Using the HYDRUS Computer Software Packages; International Groundwater Modeling Center, Colorado School of Mines: Golden, CO, USA, 2006; pp. 12–28. [Google Scholar]
- Sasidharan, S.; Bradford, S.A.; Šimůnek, J.; Kraemer, S.R. Groundwater recharge from drywells under constant head conditions. J. Hydrol. 2020, 583, 124569. [Google Scholar] [CrossRef]
- Crevoisier, D.; Popova, Z.; Mailhol, J.; Ruelle, P. Assessment and simulation of water and nitrogen transfer under furrow irrigation. Agric. Water Manag. 2008, 95, 354–366. [Google Scholar] [CrossRef] [Green Version]
- Honar, M.R.; Shamsnia, S.A.; Gholami, A. Evaluation of water flow and infiltration using HYDRUS model in sprinkler irrigation systems. In Proceedings of the 2nd International Conference on Environmental Engineering and Applications, Shanghai, China, 19 August 2011; Volume 17. [Google Scholar]
- Kandelous, M.M.; Šimůnek, J. Numerical simulations of water movement in a subsurface drip irrigation system under field and laboratory conditions using HYDRUS-2D. Agric. Water Manag. 2010, 97, 1070–1076. [Google Scholar] [CrossRef]
- Provenzano, G. Using HYDRUS-2D Simulation Model to Evaluate Wetted Soil Volume in Subsurface Drip Irrigation Systems. J. Irrig. Drain. Eng. 2007, 133, 342–349. [Google Scholar] [CrossRef]
- ElNesr, M.; Alazba, A. Computational evaluations of HYDRUS simulations of drip irrigation in 2D and 3D domains (ii-subsurface emitters). Comput. Electron. Agric. 2019, 163, 104879. [Google Scholar] [CrossRef]
- Domínguez-Niño, J.M.; Arbat, G.; Raij-Hoffman, I.; Kisekka, I.; Girona, J.; Casadesús, J. Parameterization of Soil Hydraulic Parameters for HYDRUS-3D Simulation of Soil Water Dynamics in a Drip-Irrigated Orchard. Water 2020, 12, 1858. [Google Scholar] [CrossRef]
- Shan, Y.; Wang, Q. Simulation of salinity distribution in the overlap zone with double-point-source drip irrigation using HYDRUS-3D. Aust. J. Crop Sci. 2012, 6, 238. [Google Scholar]
- Mao, X.M.; Shang, S.H. Method of minimum flux in saturation layer for calculating stable water infiltration through layered soil. J. Hydraul. Eng. 2010, 41, 810–817. [Google Scholar]
- Ma, Y.; Feng, S.; Su, D.; Gao, G.; Huo, Z. Modeling water infiltration in a large layered soil column with a modified Green–Ampt model and HYDRUS-1D. Comput. Electron. Agric. 2010, 71, S40–S47. [Google Scholar] [CrossRef]
- Tan, X.; Shao, D.; Gu, W.; Liu, H. Field analysis of water and nitrogen fate in lowland paddy fields under dif-ferent water managements using HYDRUS-1D. Agric. Water Manag. 2015, 150, 67–80. [Google Scholar] [CrossRef]
- Antonov, D.; Mallants, D.; Šimůnek, J.; Karastanev, D. Application of the HYDRUS (2D/3D) Inverse Solution Module for Estimating the Soil Hydraulic Parameters of a Quaternary Complex in Northern Bulgaria. In Proceedings of the HYDRUS Software Applications to Subsurface Flow and Contaminant Transport Problems, Prague, Czech Republic, 21–22 March 2013; p. 47. [Google Scholar]
- Mohammed, A.K.; Abed, B.S. Water distribution and interference of wetting front in stratified soil under a continues and an intermittent subsurface drip irrigation. J. Green Eng. 2020, 10, 268–286. [Google Scholar]
- Becerra, A.T.; Bravo, X.B.L.; Membrive, V.J.F. Huella hídrica y sostenibilidad del uso de los recursos hídricos. M A Rev. Electrónica Medioambiente 2013, 14, 56. [Google Scholar]
- Bouyoucos, G.J. Directions for making mechanical analyses of soils by the hydrometer method. Soil Sci. 1936, 42, 225–230. [Google Scholar] [CrossRef]
- Brooks, R.; Corey, T. Hydraulic Properties of Porous Media; Hydrology Papers n° 3, Fort Collings; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; Hopmans, J.W.; Šimůnek, J. Calibration of a Two-Dimensional Root Water Uptake Model. Soil Sci. Soc. Am. J. 2001, 65, 1027–1037. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Van Wijk, M.T.; Hopmans, J.W.; Šimunek, J. One-, two-, and three-dimensional root water uptake functions for transient modeling. Water Resour. Res. 2001, 37, 2457–2470. [Google Scholar] [CrossRef] [Green Version]
- Zapata-Sierra, A.; Pérez, M.M.; Requena, R.R.; Manzano-Agugliaro, F. Root distribution with the use of drip irrigation on layered soils at greenhouses crops. Sci. Total. Environ. 2021, 144944. [Google Scholar] [CrossRef]
- Willmott, C.J. ON THE VALIDATION OF MODELS. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Zapata-Sierra, A.J.; López-Segura, J.G.; Cánovas-Fernández, G.; Baeza-Cano, R. Caracterización del bulbo mojado por un gotero en suelos arenados mediante sondas fdr. In XXXVI Congreso Nacional de Riegos, Valladolid; Colegio Oficial de Ingenieros Agronomos de Centro y Canarias: Madrid, Spain, 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Zapata-Sierra, A.J.; Contreras, J.; Usero, F.; Baeza, R. Influencia de la textura del suelo en los bulbos húmedos desarrollados en suelo enarenado con emisores de riego localizado de bajo caudal. In XXXIII Congreso Nacional de Riegos; Universitat Politecnica de Valencia: Valencia, Spain, 2015; pp. 74–84. [Google Scholar] [CrossRef] [Green Version]
- Sutitarnnontr, P.; Hu, E.; Tuller, M.; Jones, S.B. Physical and Thermal Characteristics of Dairy Cattle Manure. J. Environ. Qual. 2014, 43, 2115–2129. [Google Scholar] [CrossRef]
- Zhou, Q.; Kang, S.; Zhang, L.; Li, F. Comparison of APRI and Hydrus-2D models to simulate soil water dynamics in a vineyard under alternate partial root zone drip irrigation. Plant Soil 2007, 291, 211–223. [Google Scholar] [CrossRef]
- Coelho, E.F.; Or, D. Root distribution and water uptake patterns of corn under surface and subsurface drip irrigation. Plant Soil 1998, 206, 123–136. [Google Scholar] [CrossRef]
- Tejedor, M.; Jimenez, C.; Díaz, F. Volcanic materials as mulches for water conservation. Geoderma 2003, 117, 283–295. [Google Scholar] [CrossRef]
- Caron, J.; Bonin, S.; Pepin, S.; Kummer, L.; Vanderleest, C.; Bland, W.L. Determination of irrigation set points for cranberries from soil- and plant-based measurements. Can. J. Soil Sci. 2016, 96, 37–50. [Google Scholar] [CrossRef] [Green Version]

 Indicates probes position.
Indicates probes position.
 Indicates probes position.
Indicates probes position.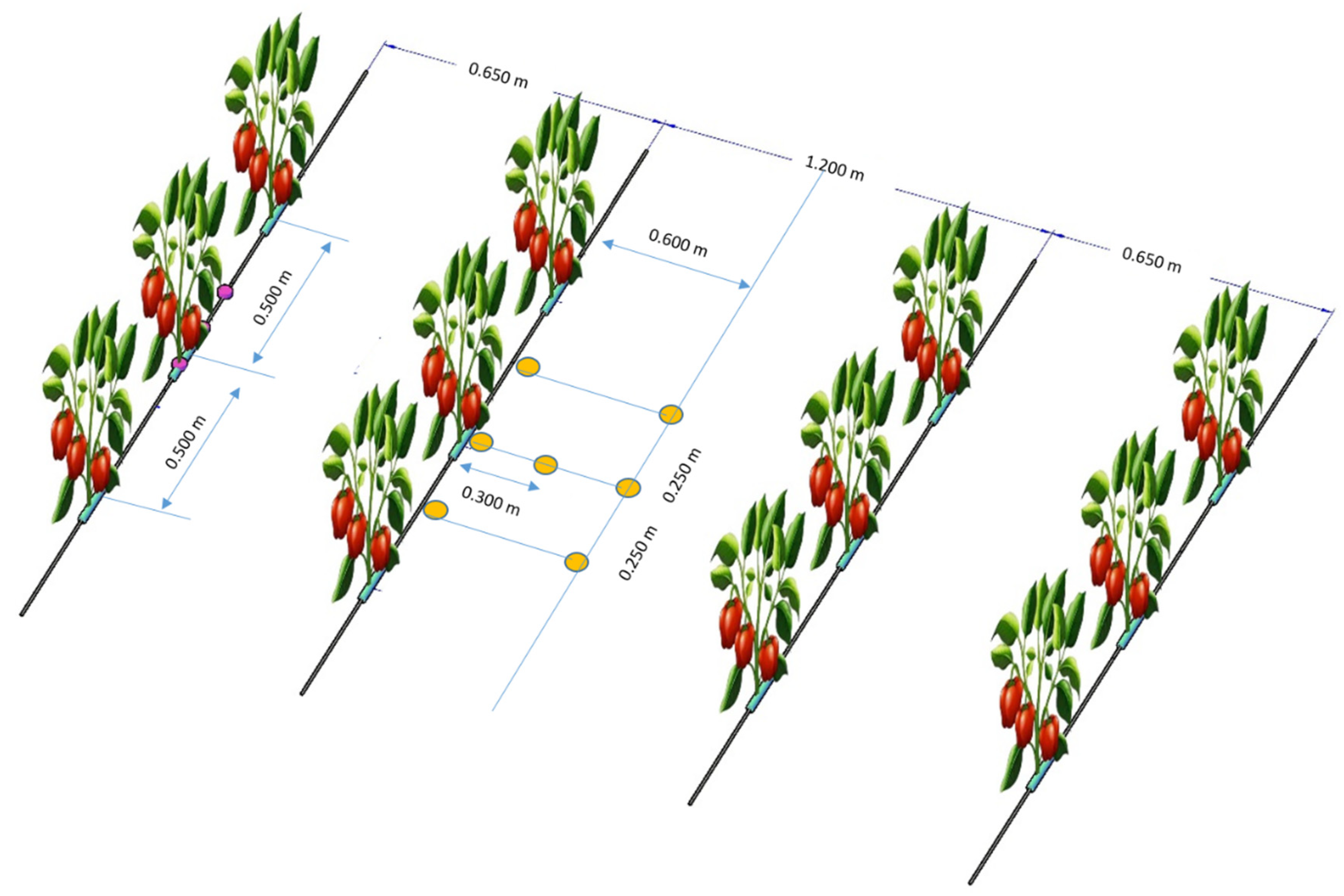
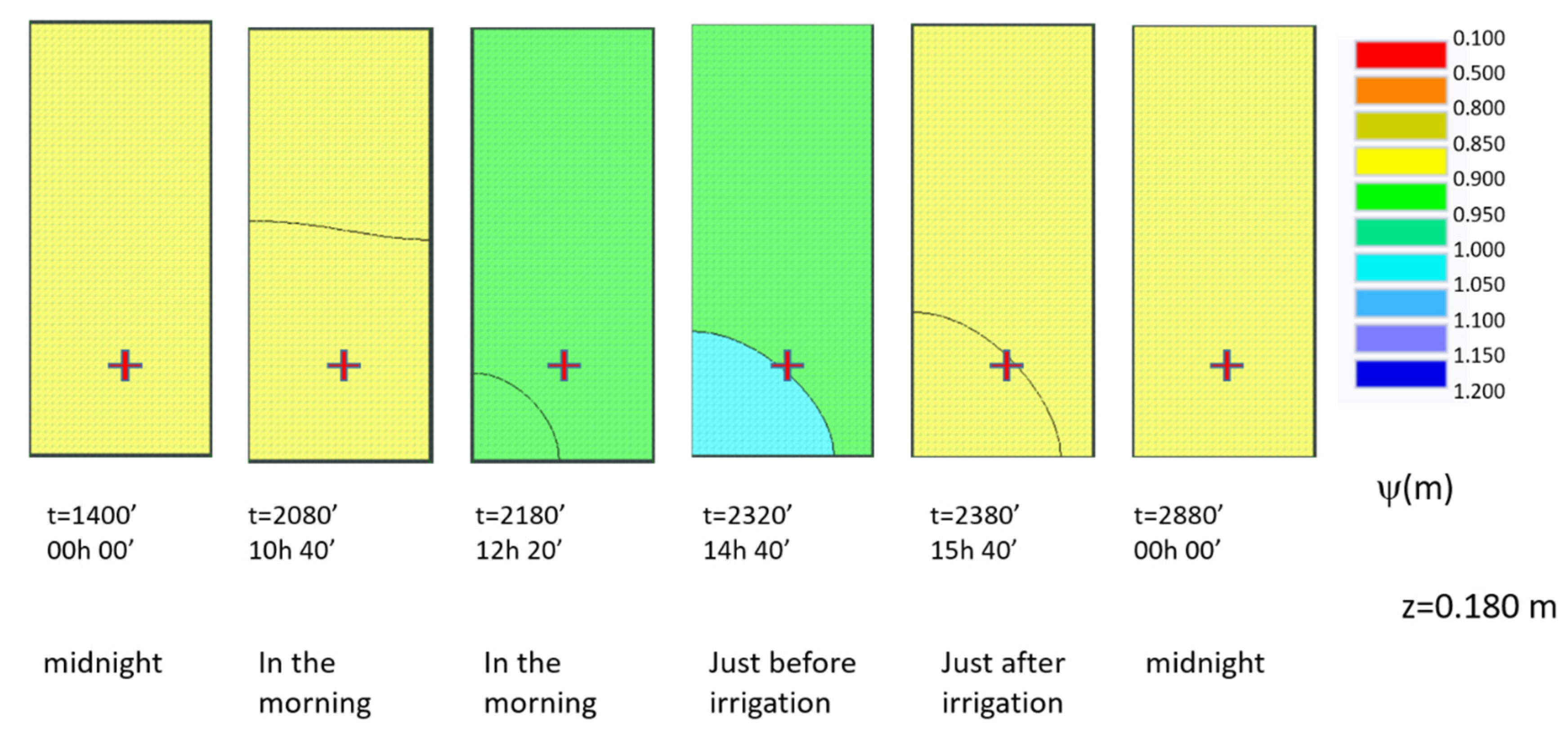
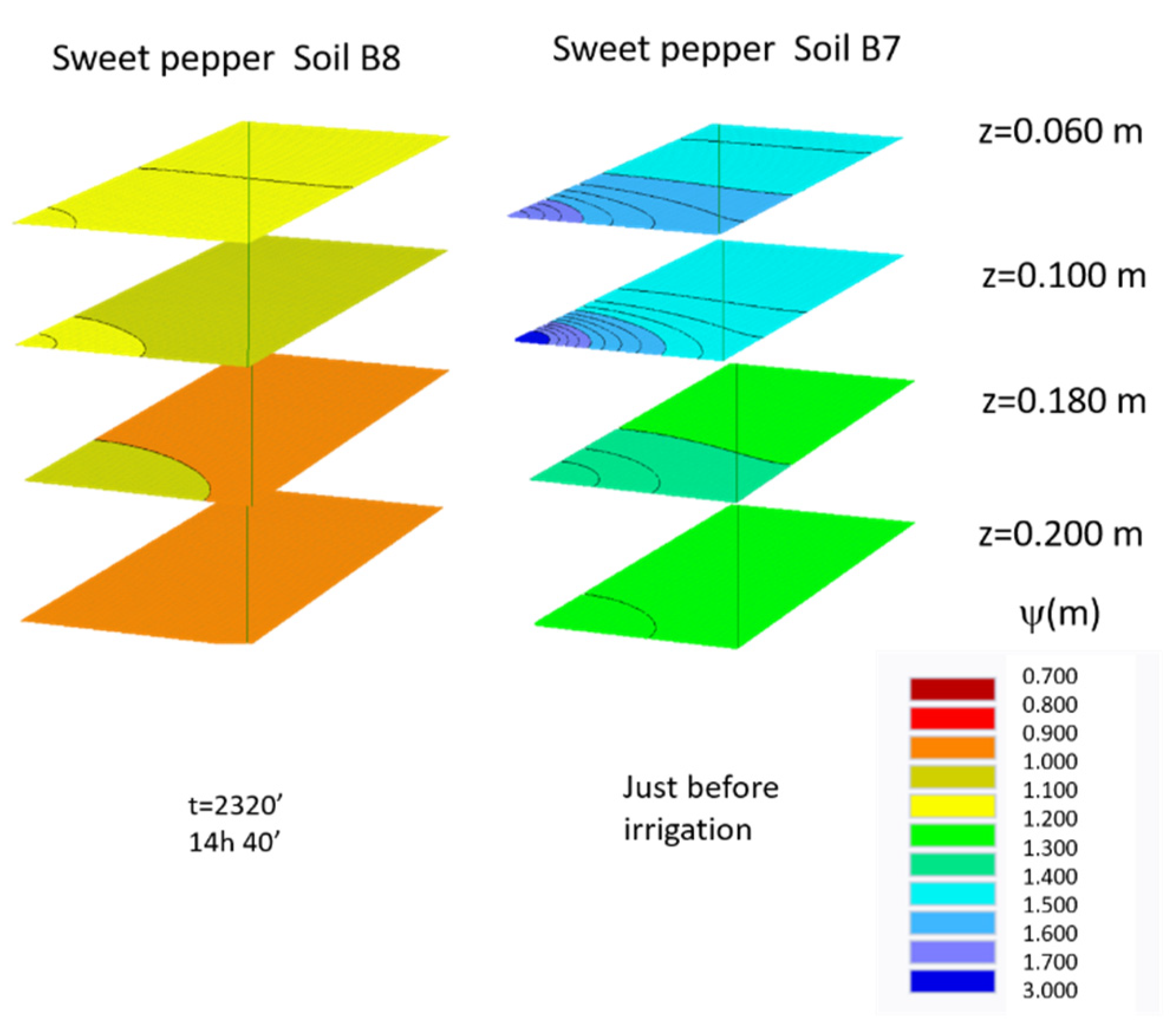
 z = 0.050 m,
z = 0.050 m,  , z = 0.150 m).
, z = 0.150 m).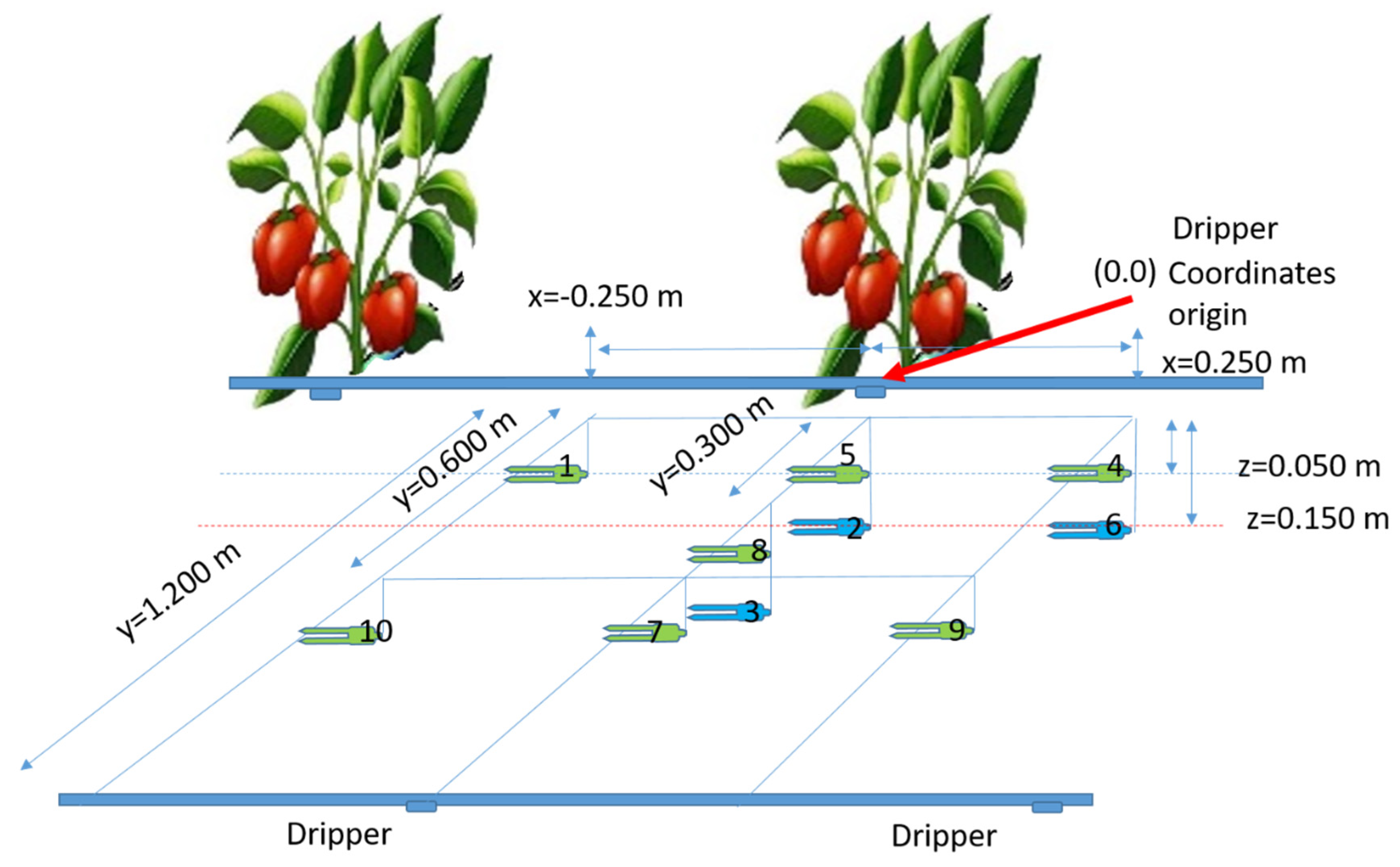

| Equipment 1 Soil B7 | Equipment 2 Soil B8 | ||||||
|---|---|---|---|---|---|---|---|
| Probe | x (m) | y (m) | z (m) | Probe | x (m) | y (m) | z (m) |
| 1 | 0.250 | 0 | 0.050 | 1 | −0.250 | 0 | 0.050 |
| 2 | −0.250 | 0 | 0.050 | 2 | 0 | 0 | 0.150 |
| 3 | 0 | 0.300 | 0.050 | 3 | 0 | 0.300 | 0.150 |
| 4 | −0.250 | 0 | 0.150 | 4 | 0.250 | 0 | 0.050 |
| 5 | −0.250 | 0 | 0.050 | 5 | 0 | 0 | 0.050 |
| 6 | 0.250 | 0 | 0.050 | 6 | 0.250 | 0 | 0.150 |
| 7 | 0 | 0 | 0.150 | 7 | 0 | 0.600 | 0.050 |
| 8 | 0 | 0 | 0.050 | 8 | 0 | 0.300 | 0.050 |
| 9 | 0 | 0.300 | 0.150 | 9 | 0.250 | 0.600 | 0.050 |
| 10 | 0 | 0.600 | 0.050 | 10 | −0.250 | 0.600 | 0.050 |
| B7 | B8 | Original Soil | Organic Matter | Cover Sand | |
|---|---|---|---|---|---|
| θs (%) | 31.99 | 24.56 | 7.403 | 89.50 | 3.51 |
| θr (%) | 5.62 | 0.00 | 0.00 | 8.69 | 0.63 |
| α (m−1) | 2.24 × 10−7 | 4.72 × 10−7 | 2.33 × 10−7 | 2.7 × 10−6 | 1.496 × 10−6 |
| n | 3.310 | 2.077 | 2.282 | 1.391 | 2.593 |
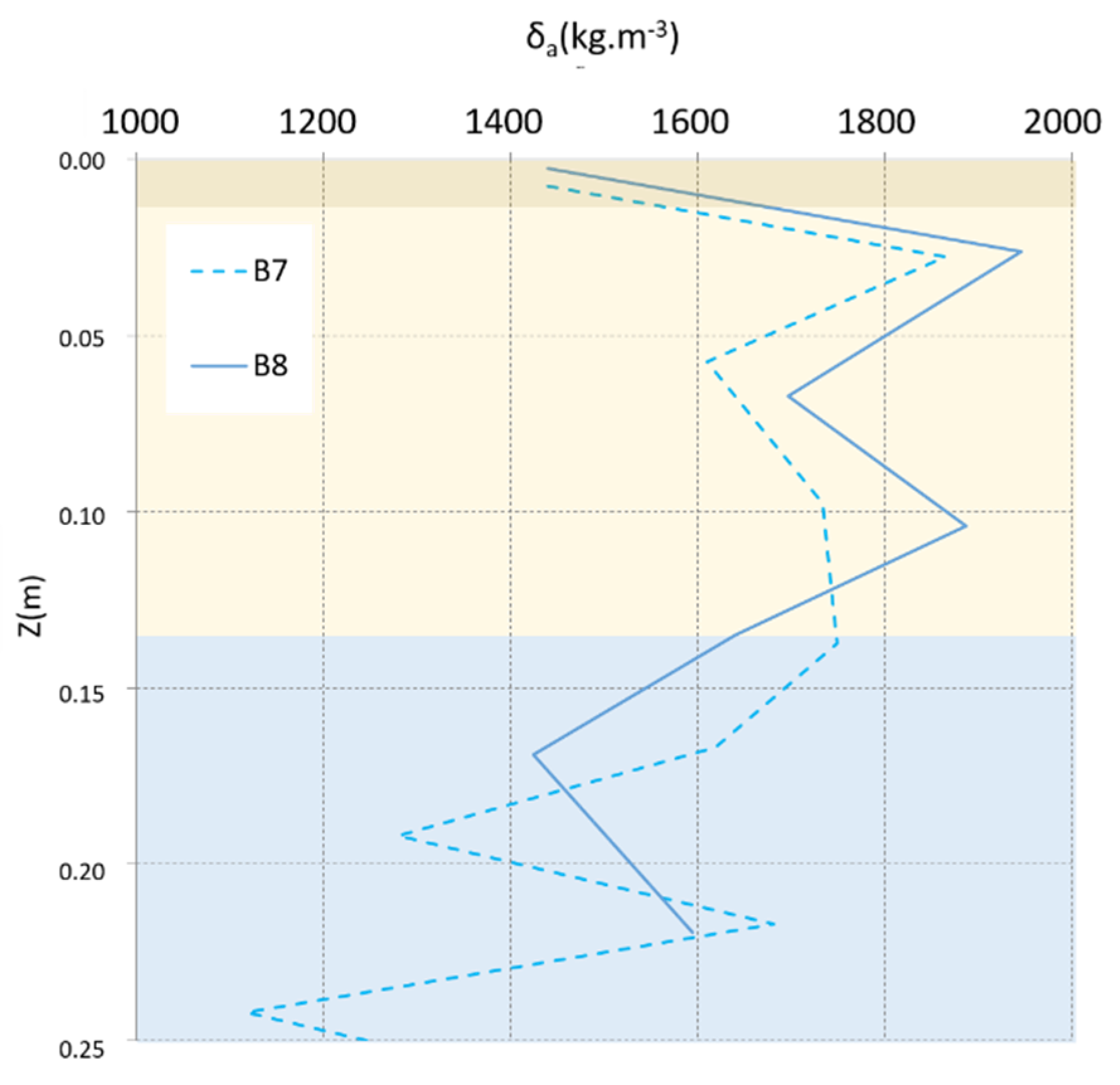
| δa (kg·m−3) | 1740 | 1490 | 1790 | 1440 | 1510 |
| ks(m·s−1) | 2.93 × 10−8 | 6 × 10−7 | 1.2858 × 10−5 | 2.199 × 10−5 | 9.334 × 10−4 |
| Ia (%) | 99.97 | 99.84 | 99.39 | 99.70 | 98.20 |
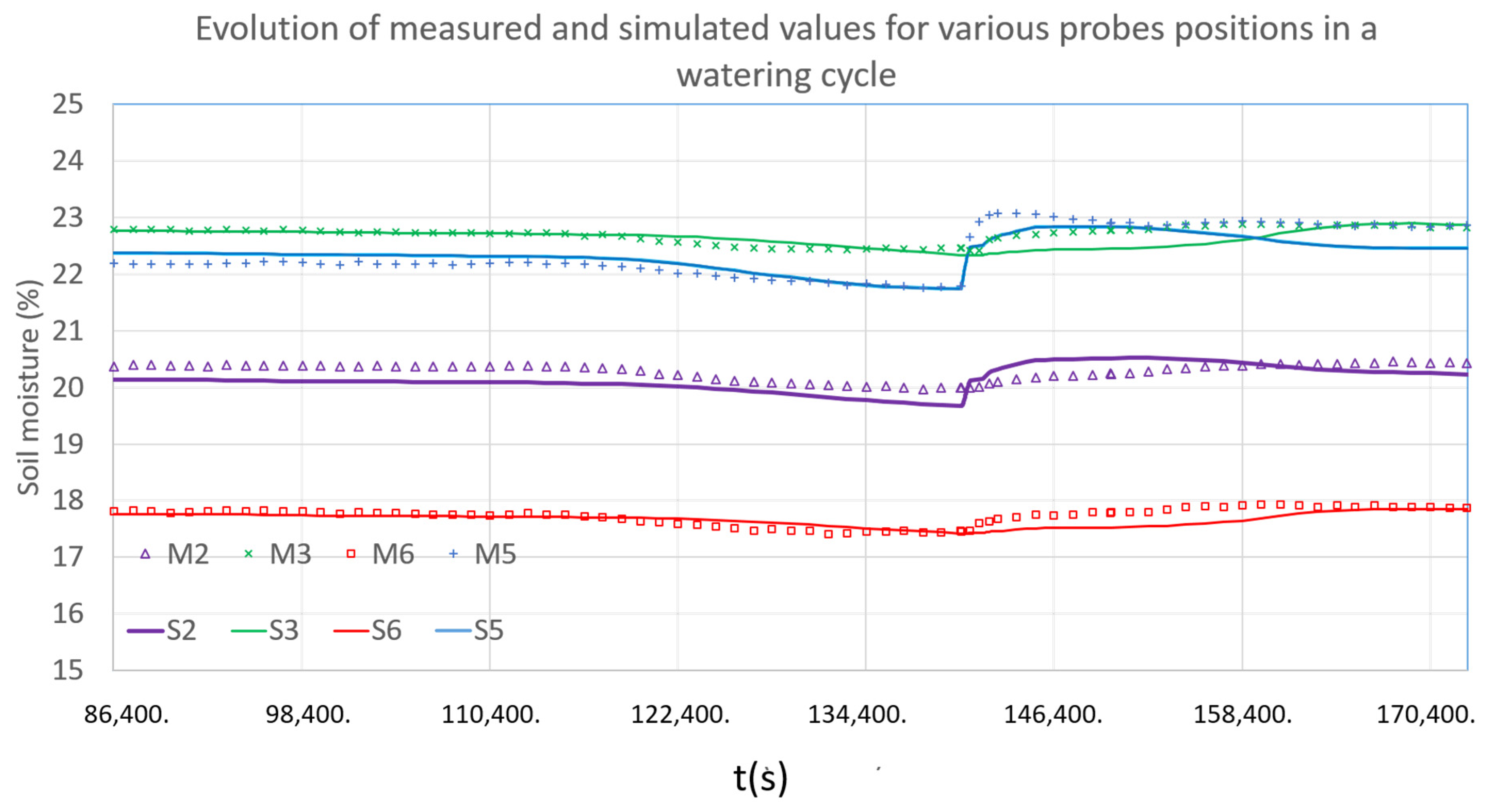
| P5 | P2 | P8 | P6 | P3 | P10–P9 | P7 | P4–P1 | |
|---|---|---|---|---|---|---|---|---|
| m(0,0) | 0.990 | 0.999 | 1.002 | 0.993 | 1.002 | 1.004 | 0.996 | 0.995 |
| Ia | 1.000 | 0.997 | 0.988 | 1.000 | 1.000 | 1.000 | 1.000 | 0.999 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zapata-Sierra, A.J.; Roldán-Cañas, J.; Reyes-Requena, R.; Moreno-Pérez, M.F. Study of the Wet Bulb in Stratified Soils (Sand-Covered Soil) in Intensive Greenhouse Agriculture under Drip Irrigation by Calibrating the Hydrus-3D Model. Water 2021, 13, 600. https://doi.org/10.3390/w13050600
Zapata-Sierra AJ, Roldán-Cañas J, Reyes-Requena R, Moreno-Pérez MF. Study of the Wet Bulb in Stratified Soils (Sand-Covered Soil) in Intensive Greenhouse Agriculture under Drip Irrigation by Calibrating the Hydrus-3D Model. Water. 2021; 13(5):600. https://doi.org/10.3390/w13050600
Chicago/Turabian StyleZapata-Sierra, Antonio Jesús, José Roldán-Cañas, Rafael Reyes-Requena, and María Fátima Moreno-Pérez. 2021. "Study of the Wet Bulb in Stratified Soils (Sand-Covered Soil) in Intensive Greenhouse Agriculture under Drip Irrigation by Calibrating the Hydrus-3D Model" Water 13, no. 5: 600. https://doi.org/10.3390/w13050600