Water Leak Localization Using High-Resolution Pressure Sensors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Database Formation
2.2. Data Analysis
2.3. Classification Algorithm
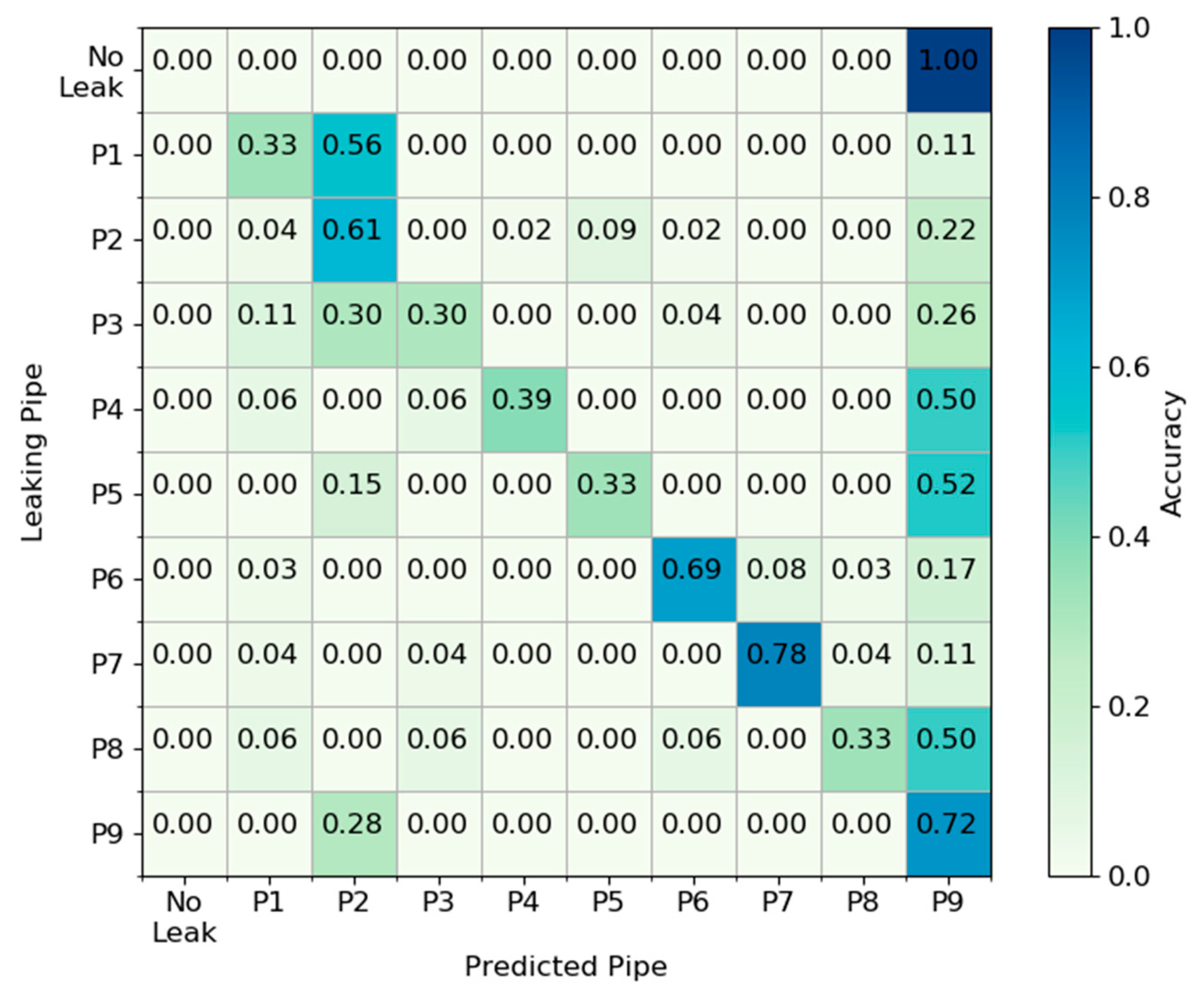
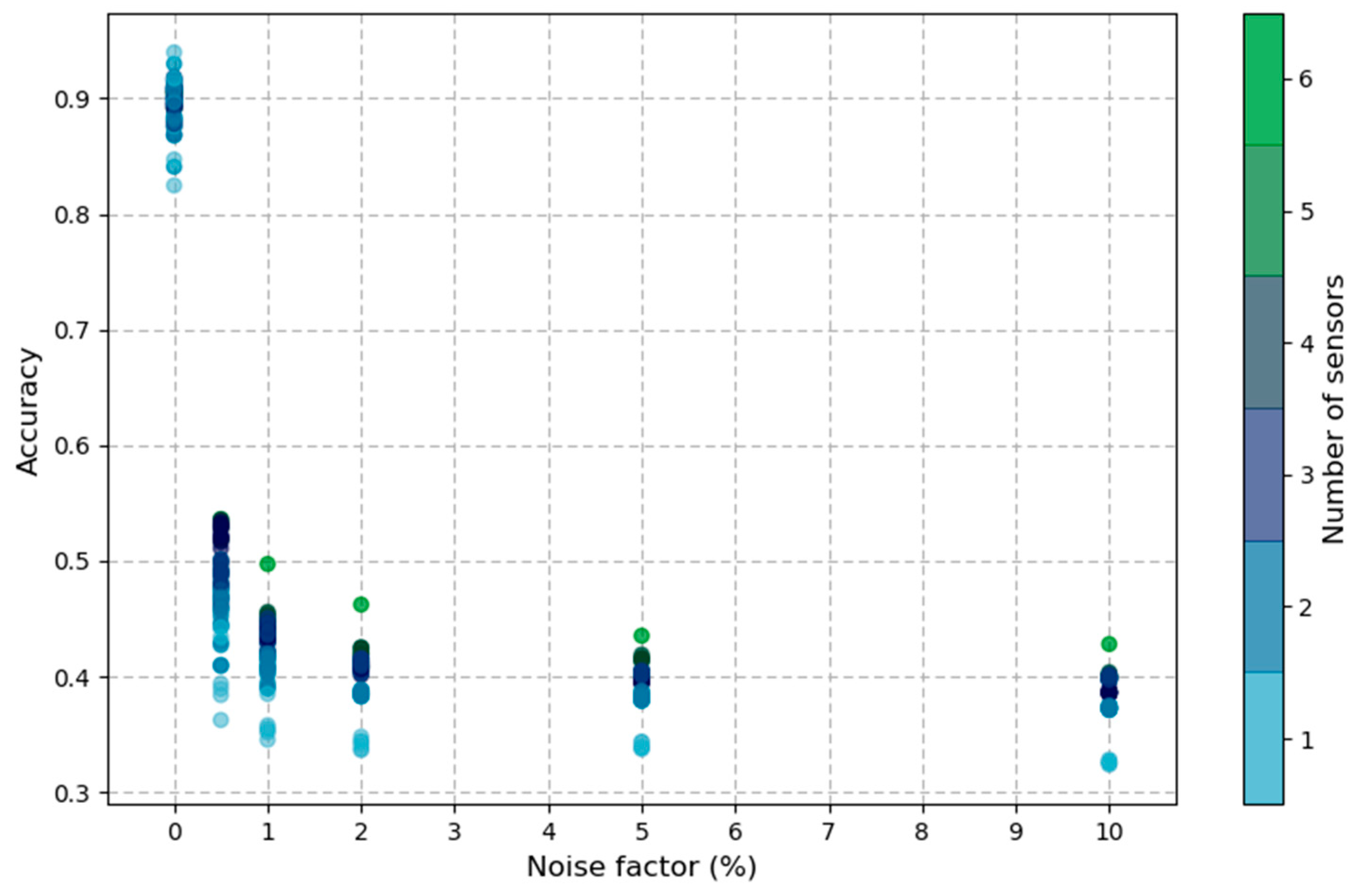
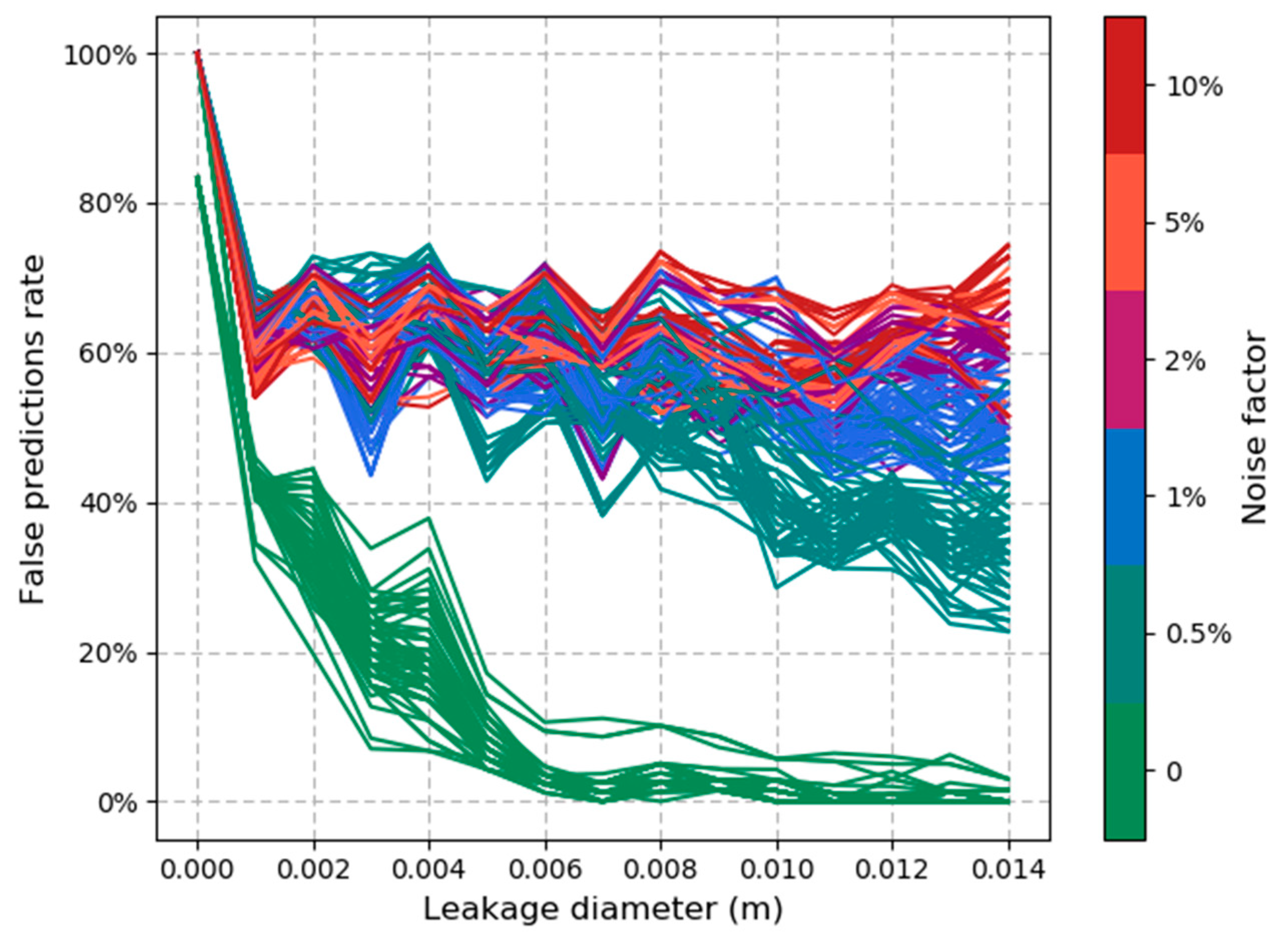
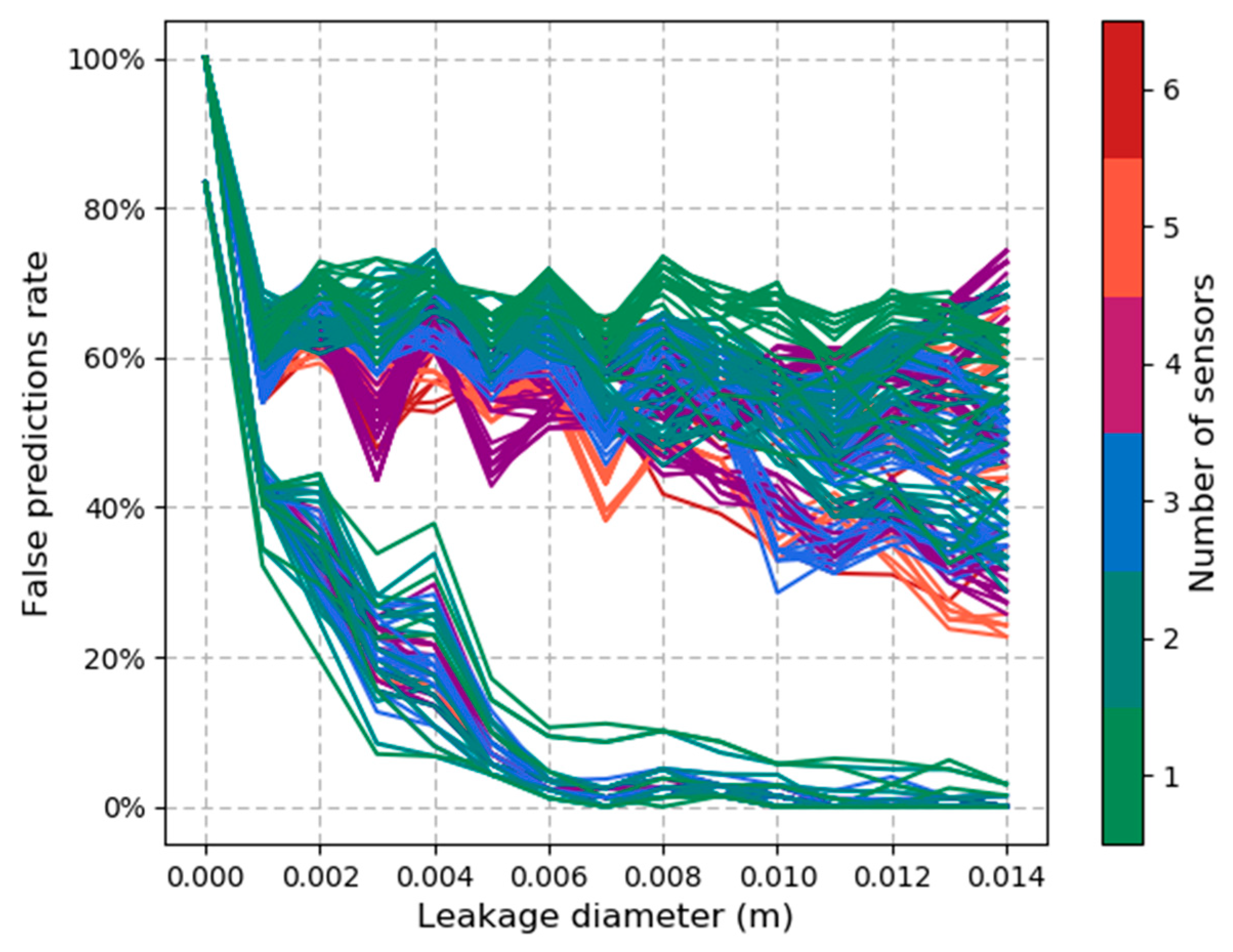
3. Results
3.1. Tnet1 Network
3.2. Sensitivity Analysis
4. Conclusions and Research Opportunities
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stephens, M.; Gong, J.; Zhang, C.; Marchi, A.; Dix, L.; Lambert, M.F. Leak-Before-Break Main Failure Prevention for Water Distribution Pipes Using Acoustic Smart Water Technologies: Case Study in Adelaide. J. Water Resour. 2020, 146, 05020020. [Google Scholar] [CrossRef]
- Cody, R.A.; Tolson, B.A.; Orchard, J. Detecting Leaks in Water Distribution Pipes Using a Deep Autoencoder and Hydroacoustic Spectrograms. J. Comput. Civ. Eng. 2020, 34, 04020001. [Google Scholar] [CrossRef]
- Choi, J.; Shin, J.; Song, C.; Han, S.; Park, D.I. Leak detection and location of water pipes using vibration sensors and modified ML prefilter. Sensors 2017, 17, 2104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, Y.; Brennan, M.J.; Joseph, P.F.; Muggleton, J.M.; Hunaidi, O. A model of the correlation function of leak noise in buried plastic pipes. J. Sound Vib. 2004, 277, 133–148. [Google Scholar] [CrossRef]
- Pérez, R.; Puig, V.; Pascual, J.; Peralta, A.; Landeros, E.; Jordanas, L. Pressure sensor distribution for leak detection in Barcelona water distribution network. Water Sci. Technol. Water Supply 2009, 9, 715–721. [Google Scholar] [CrossRef]
- Rocher, J.; Parra, L.; Lloret, J.; Mengual, J. An Unductive Sensor for Water Level Monitoring in Tubes for Water Grids. In Proceedings of the 2018 IEEE/ACS 15th International Conference on Computer Systems and Applications, Aqaba, Jordan, 28 October–1 November 2018. [Google Scholar]
- Zhang, X.; Yu, M.; Ma, Z.; Ouyang, H.; Zou, Y.; Zhang, S.L.; Niu, H.; Pan, X.; Xu, M.; Li, Z.; et al. Self-Powered Distributed Water Level Sensors Based on Liquid–Solid Triboelectric Nanogenerators for Ship Draft Detecting. Adv. Funct. Mater. 2019, 29, 1900327. [Google Scholar] [CrossRef]
- Wang, Z.; Song, H.; Watkins, D.W.; Ong, K.G.; Xue, P.; Yang, Q.; Shi, X. Cyber-Physical Systems for Water Sustainability: Challenges and Opportunities. IEEE Commun. Mag. 2015, 53, 216–222. [Google Scholar] [CrossRef] [Green Version]
- Kühnert, C.; Bernard, T.; Montalvo Arango, I.; Nitsche, R. Water quality supervision of distribution networks based on machine learning algorithms and operator feedback. Procedia Eng. 2014, 89, 189–196. [Google Scholar] [CrossRef]
- Aminravan, F.; Sadiq, R.; Hoorfar, M.; Rodriguez, M.J.; Najjaran, H. Multi-level information fusion for spatiotemporal monitoring in water distribution networks. Expert Syst. Appl. 2015, 42, 3813–3831. [Google Scholar] [CrossRef]
- Stephens, M.; Gong, J.; Marchi, A.; Dix, L.; Lambert, M. Field Testing of Adelaide CBD Smart Network Acoustic Technologies. In Proceedings of the 1st International WSDA/CCWI 2018 Joint Conference, Kingston, ON, Canada, 23–25 July 2018. [Google Scholar]
- Steffelbauer, D.B.; Deuerlein, J.; Gilbert, D.; Piller, O.; Abraham, E. A Dual Model For Leak Detection and Localization: BattLeDIM 2020-Battle of the Leakage Detection and Isolation Methods Team: Under Pressure. In Proceedings of the 2nd International CCWI / WDSA, Beijing, China, 30 June 2020. [Google Scholar] [CrossRef]
- Li, Z.; Xin, K. Fast Localization of Multiple Leaks in Water Distribution Network Jointly Driven By Simulation and Machine Learning. Zenodo 2020. [Google Scholar] [CrossRef]
- Izquierdo, J.; López, P.A.; Martínez, F.J.; Pérez, R. Fault detection in water supply systems using hybrid (theory and data-driven) modelling. Math. Comput. Model. 2007, 46, 341–350. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Z.Y.; Zhao, M.; Qi, J.; Huang, Y.; Zhao, H. Leakage Zone Identification in Large-Scale Water Distribution Systems Using Multiclass Support Vector Machines. J. Water Resour. 2016, 142, 04016042. [Google Scholar] [CrossRef]
- Fang, Q.S.; Zhang, J.X.; Xie, C.L.; Yang, Y.L. Detection of multiple leakage points in water distribution networks based on convolutional neural networks. Water Sci. Technol. Water Supply 2019, 19, 2231–2239. [Google Scholar] [CrossRef]
- Xing, L.; Sela, L. Transient simulations in water distribution networks: TSNet python package. Adv. Eng. Softw. 2020, 149, 102884. [Google Scholar] [CrossRef]
- Xing, L.; Sela, L. TSNet Documentation Release 0.2.0. Available online: https://www.researchgate.net/publication/341434146 (accessed on 23 February 2021).
- Klise, K.; Hart, D.; Moriarty, D.; Bynum, M.; Murray, R. Water Network Tool for Resilience (WNTR) User Manual, 2017, United States Environmental Protection Agency Office of Research and Development, Washington, DC, USA. Available online: https://cfpub.epa.gov/si/si_public_record_report.cfm?dirEntryId=337888&Lab=NRMRL (accessed on 23 February 2021).
- Crowl, D.A.; Louvar, J.F. Chemical Process Safety—Fundamentals with Applications, 2nd ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2019; pp. 112–116. ISBN 10:0130181765. [Google Scholar]
- Cover, T.M.; Hart, P.E. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
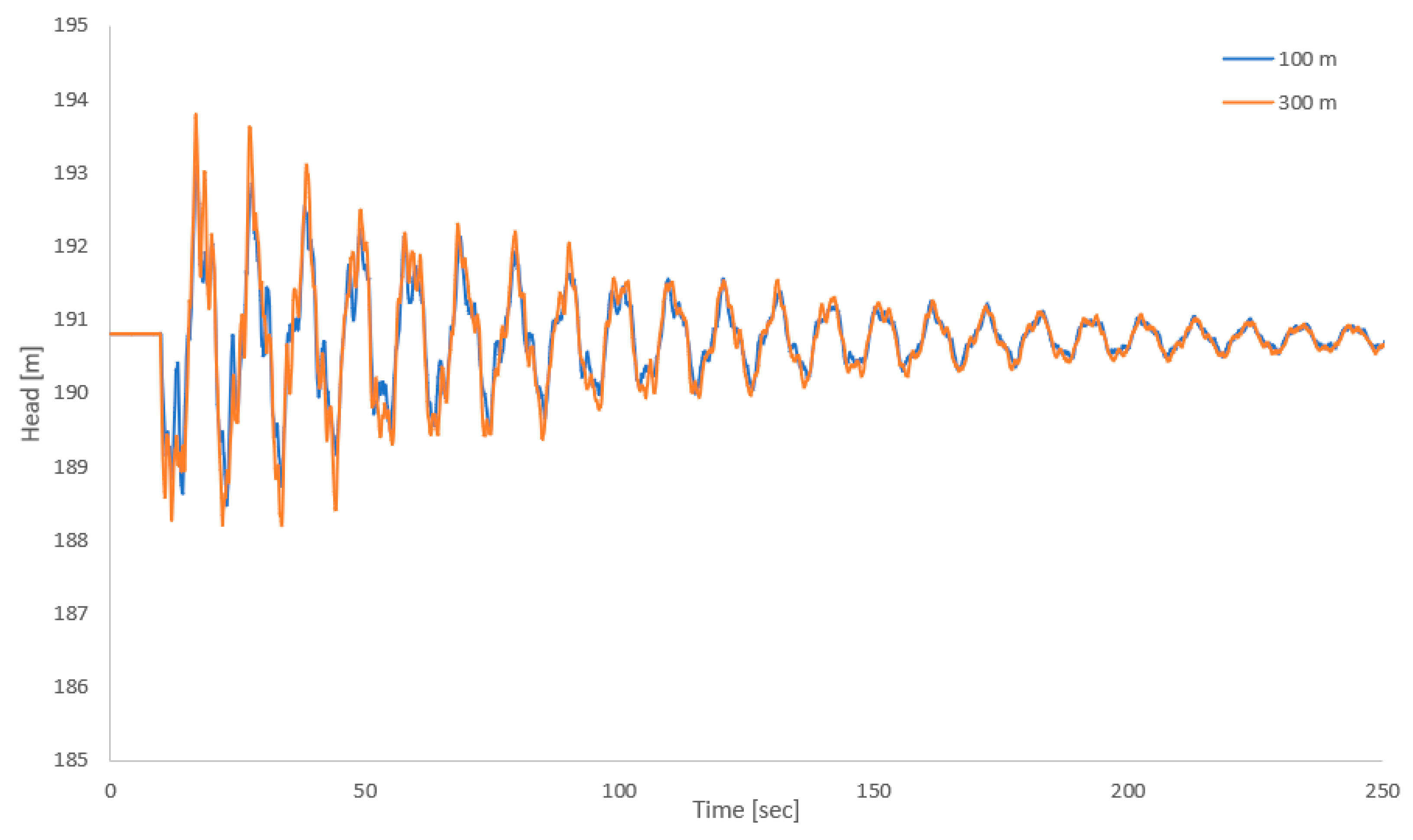
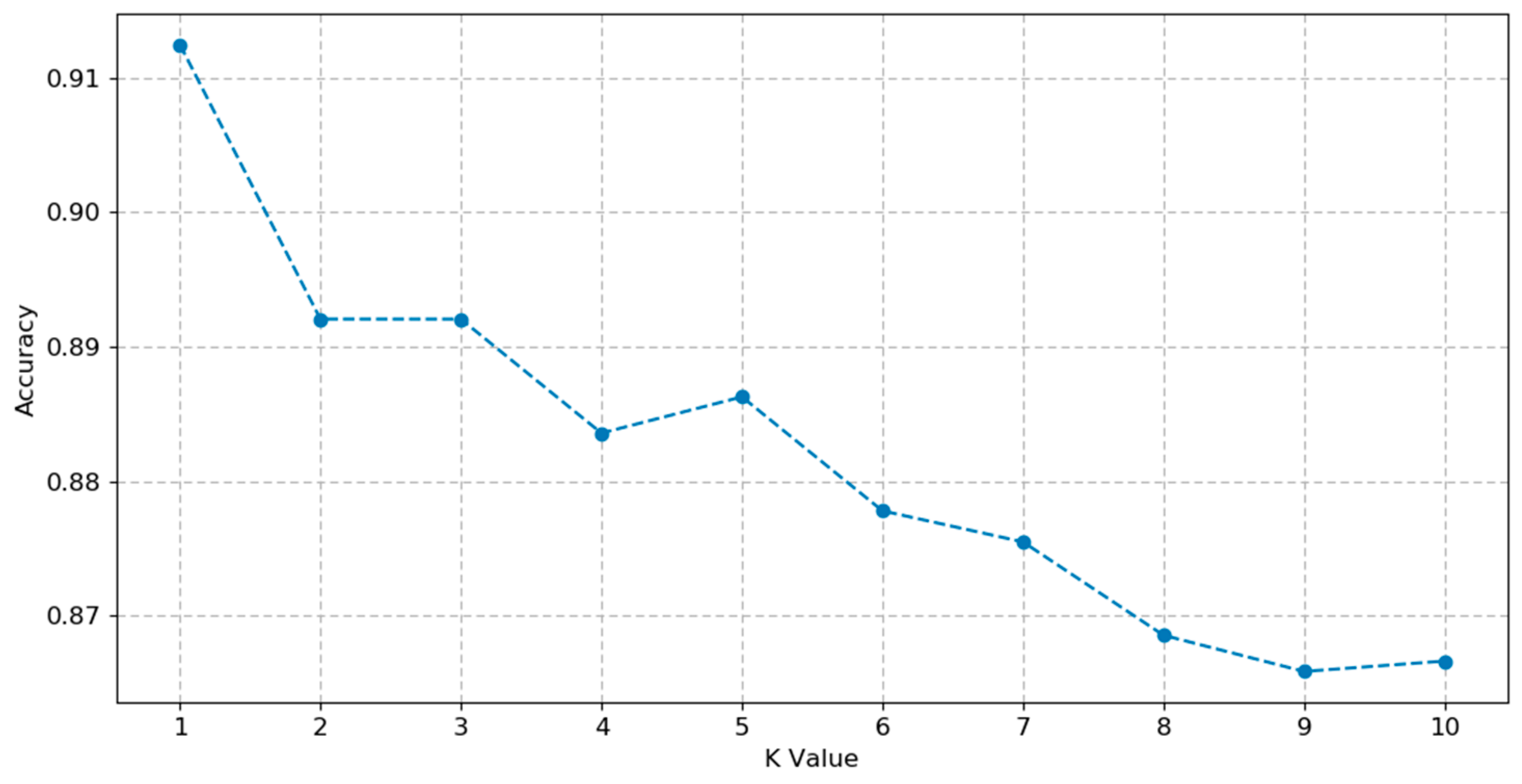
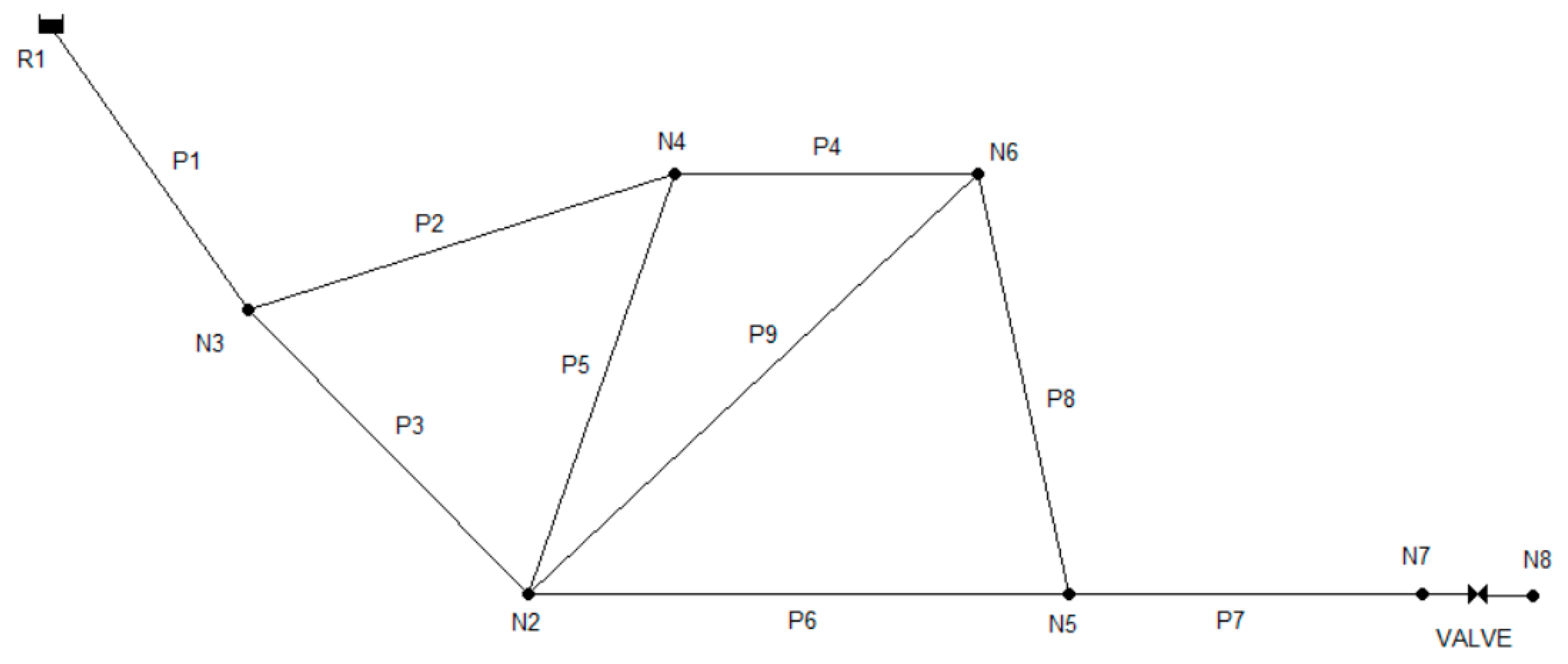
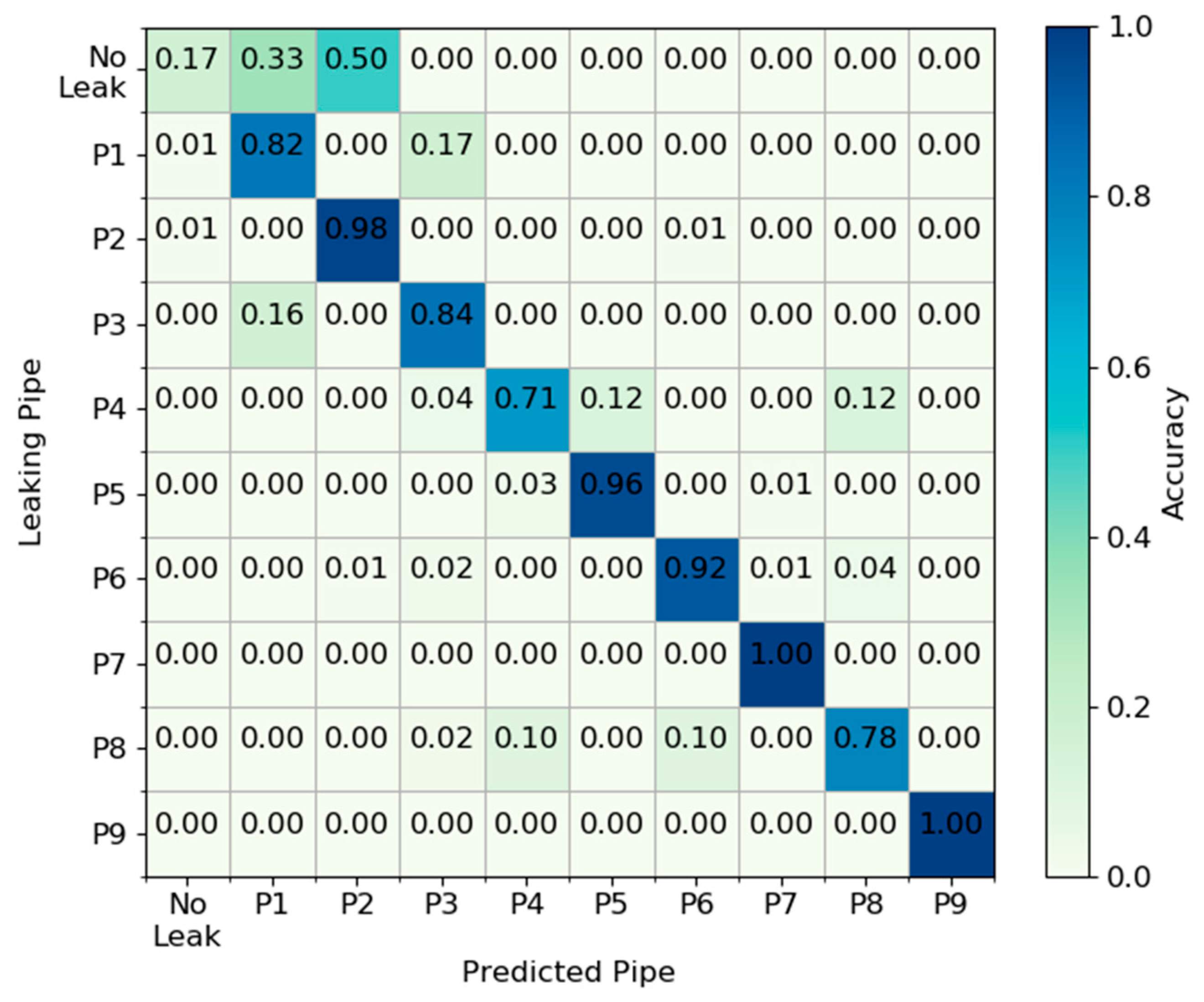


| N1, t1 | N1, t2 | … | N2, t1 | N2, t2 | … | Nn, t1 | Nn, T | Pipe | Distance | Diameter |
|---|---|---|---|---|---|---|---|---|---|---|
| 190.99 | 190.99 | 190.98 | 190.98 | 190.97 | 190.97 | P6 | 500 | 0.004 | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| Pipe ID | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| No Leakage | 0.25 | 0.17 | 0.2 | 6 |
| 1 | 0.83 | 0.82 | 0.82 | 128 |
| 2 | 0.98 | 0.98 | 0.98 | 195 |
| 3 | 0.78 | 0.84 | 0.81 | 124 |
| 4 | 0.81 | 0.71 | 0.76 | 73 |
| 5 | 0.92 | 0.96 | 0.94 | 101 |
| 6 | 0.91 | 0.92 | 0.92 | 127 |
| 7 | 0.99 | 1 | 0.99 | 196 |
| 8 | 0.83 | 0.78 | 0.8 | 89 |
| 9 | 1 | 1 | 1 | 73 |
| accuracy | 0.9 | 1112 | ||
| macro avg. | 0.83 | 0.82 | 0.82 | 1112 |
| weighted avg. | 0.9 | 0.9 | 0.9 | 1112 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levinas, D.; Perelman, G.; Ostfeld, A. Water Leak Localization Using High-Resolution Pressure Sensors. Water 2021, 13, 591. https://doi.org/10.3390/w13050591
Levinas D, Perelman G, Ostfeld A. Water Leak Localization Using High-Resolution Pressure Sensors. Water. 2021; 13(5):591. https://doi.org/10.3390/w13050591
Chicago/Turabian StyleLevinas, Daniel, Gal Perelman, and Avi Ostfeld. 2021. "Water Leak Localization Using High-Resolution Pressure Sensors" Water 13, no. 5: 591. https://doi.org/10.3390/w13050591








