Optimization Methodology for Estimating Pump Curves Using SCADA Data
Abstract
1. Introduction
2. Methodology
2.1. Problem Statement
2.2. Fixed Speed Pumps
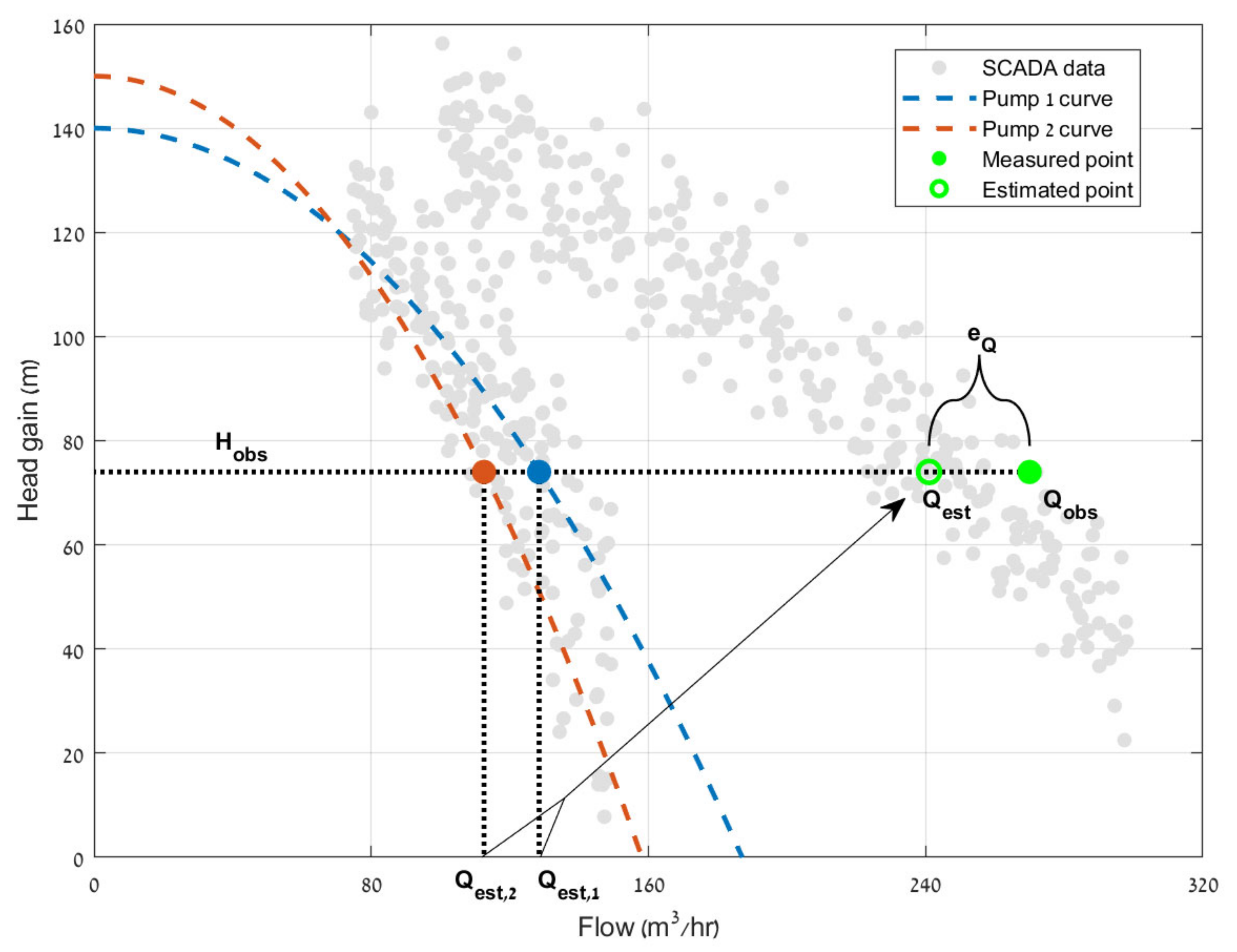
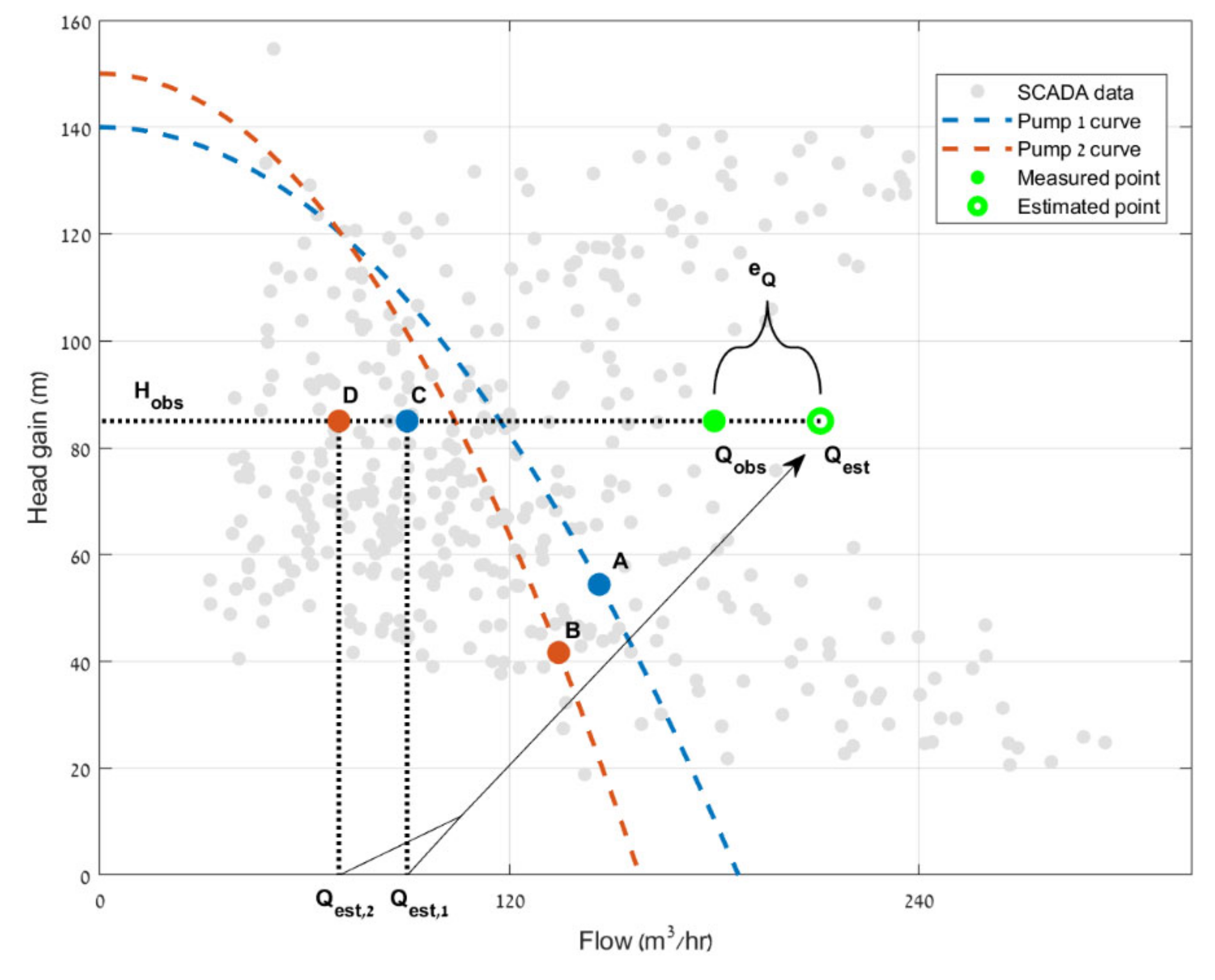
2.3. Variable Speed Pumps
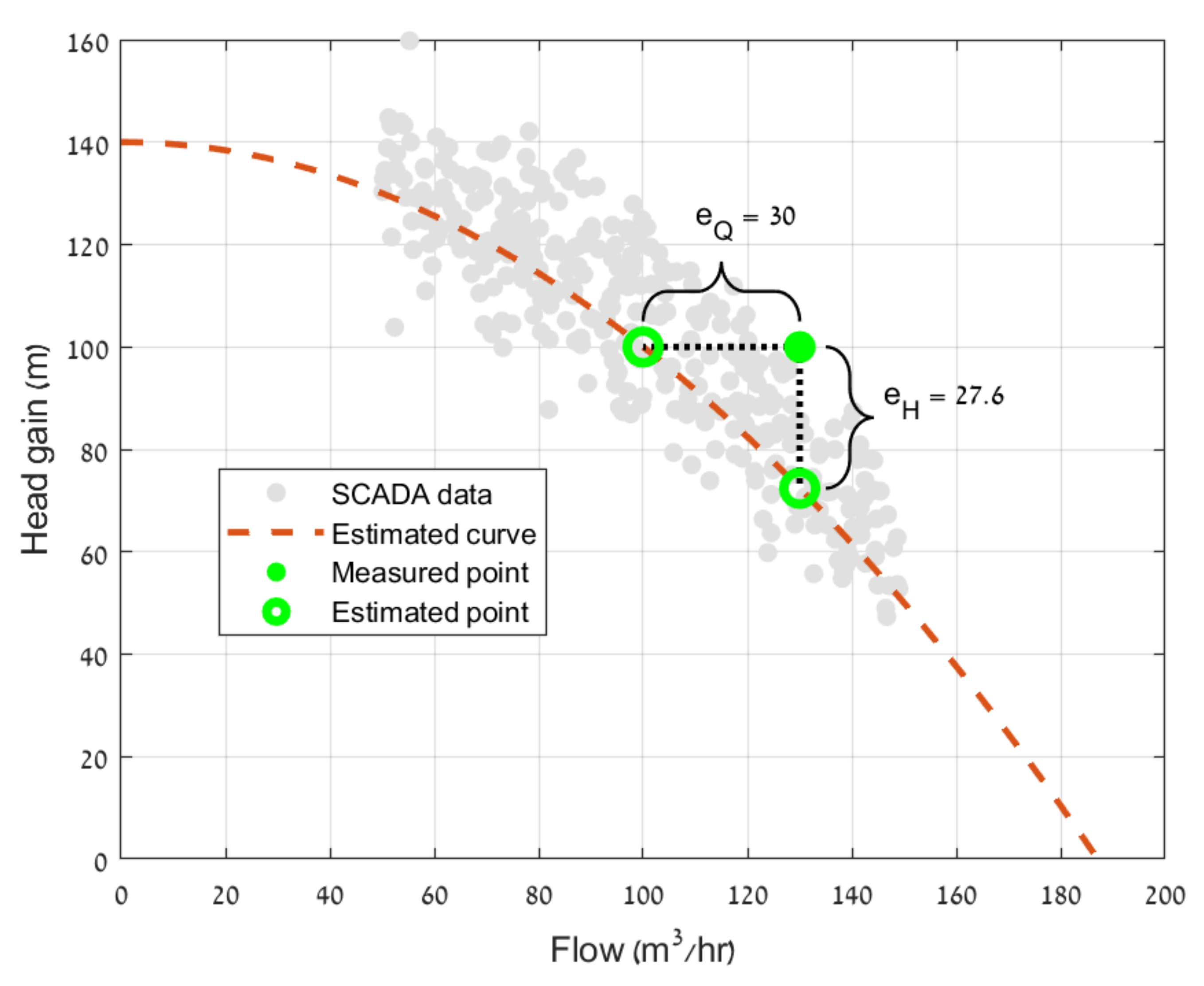
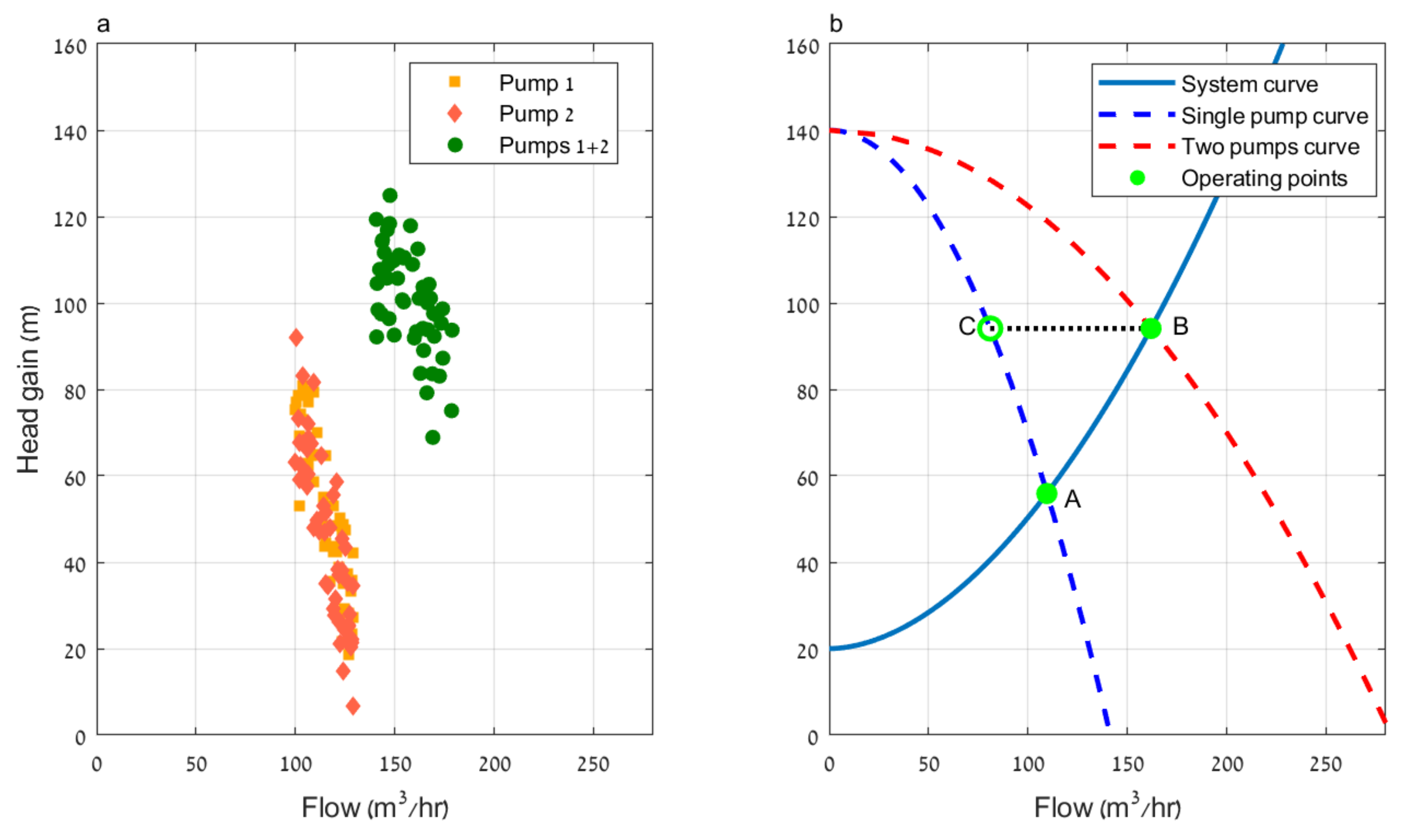
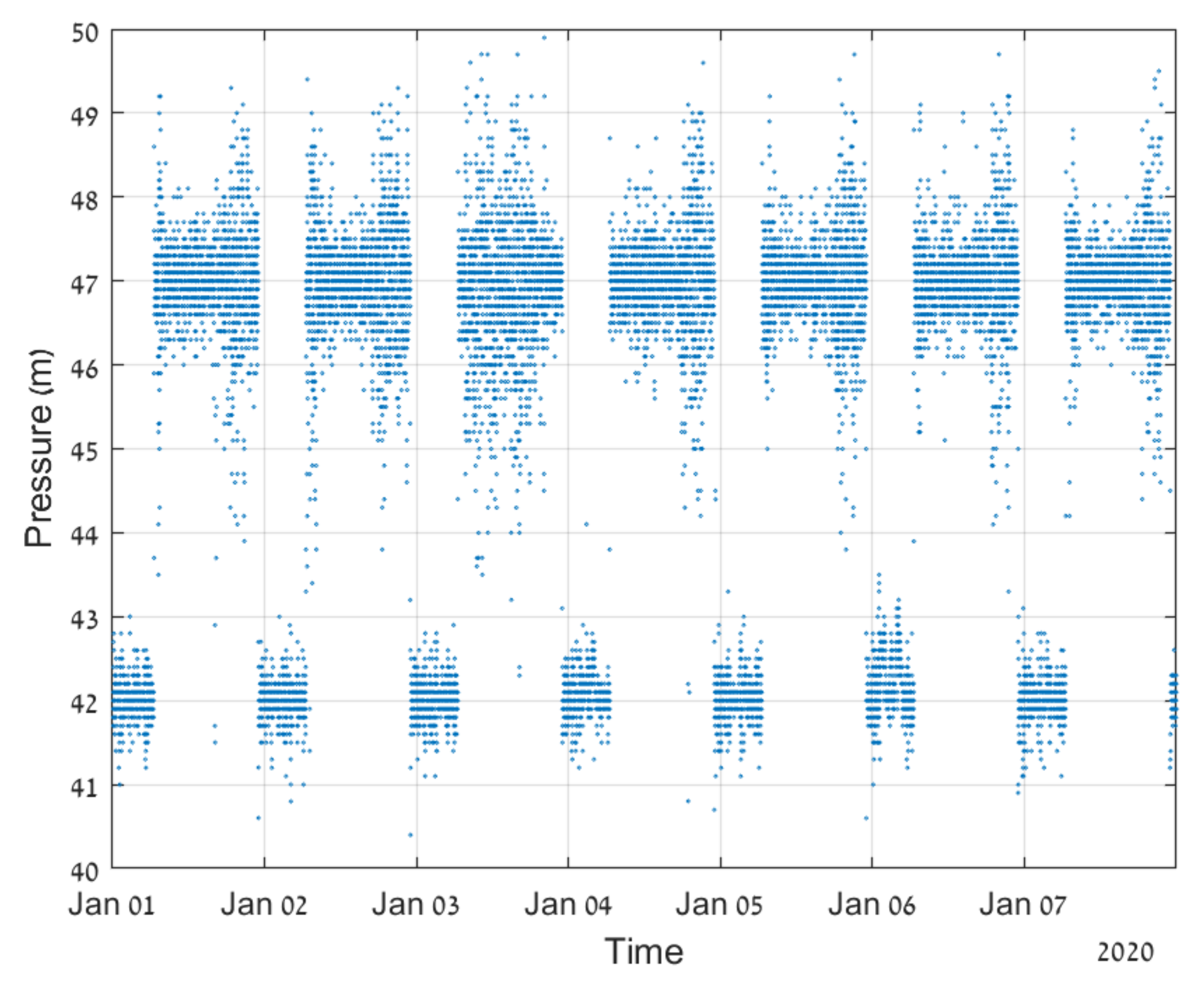
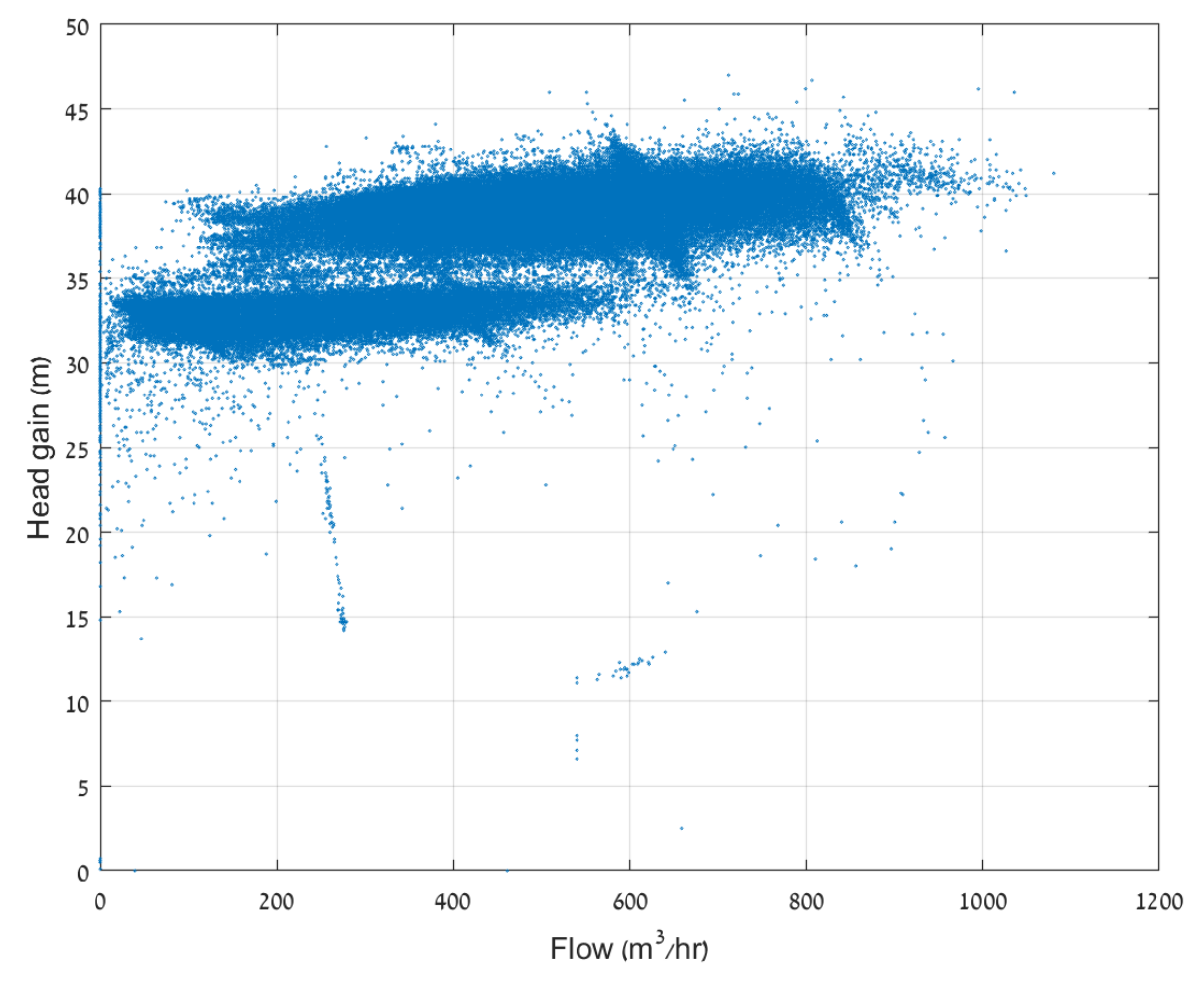
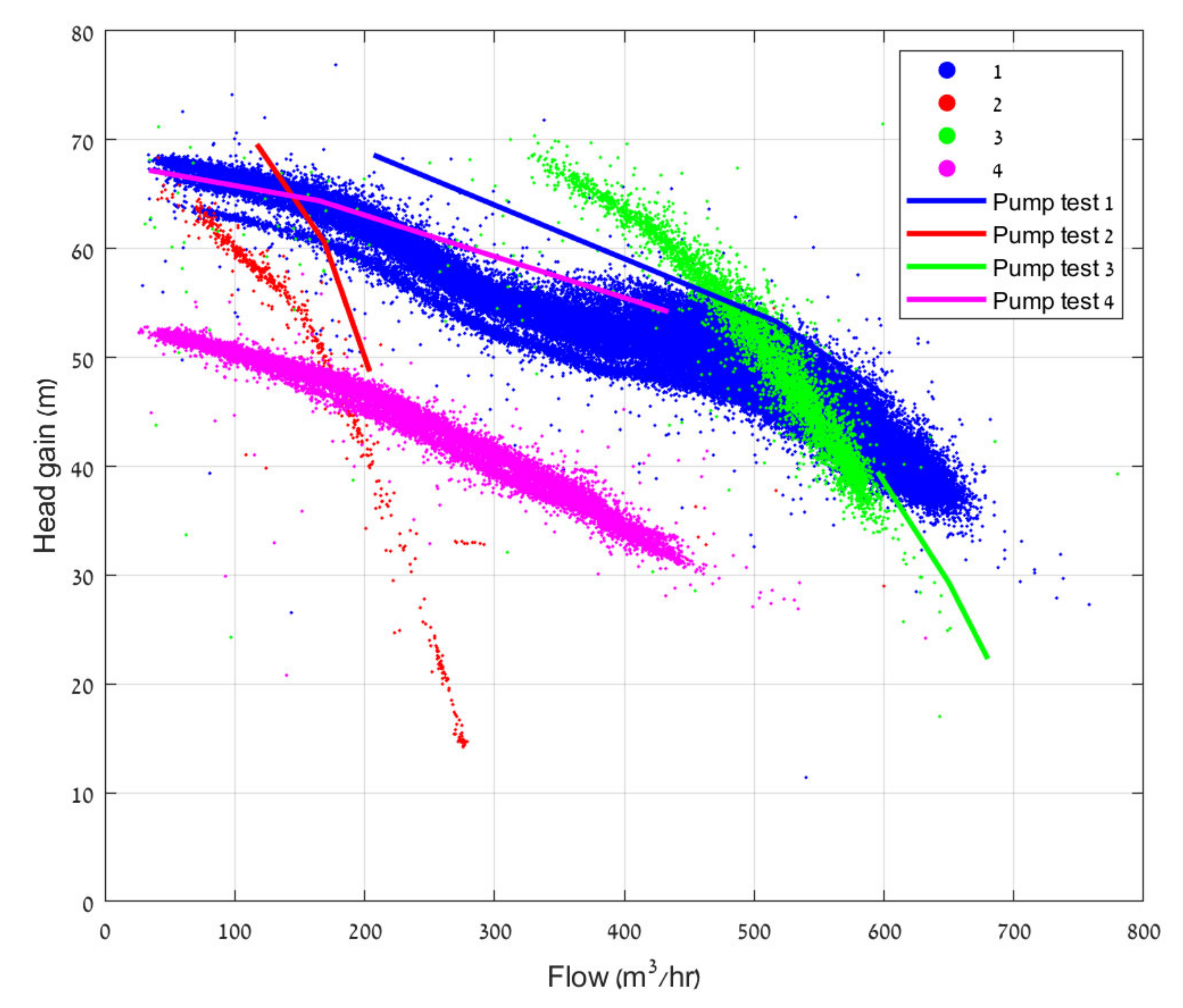
3. Test Case and Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Copeland, C.; Carter, N.T. Energy—Water Nexus: The Water Sector’ s Energy Use R43200. 2017. Available online: https://crsreports.congress.gov/product/pdf/R/R43200 (accessed on 25 January 2021).
- Sanders, K.T.; Webber, M.E. Evaluating the energy consumed for water use in the United States. Environ. Res. Lett. 2012, 7, 034034. [Google Scholar] [CrossRef]
- Lam, K.L.; Kenway, S.J.; Lant, P.A. Energy use for water provision in cities. J. Clean. Prod. 2017, 143, 699–709. [Google Scholar] [CrossRef]
- ETSU; CETIM; Reeves, D.T.; NESA; Technical University Darmstadt. Study on Improving the Energy Efficiency of Pumps. European Commission: UK, 2001. Available online: http://www.jakob-albertsen.dk/komposit/Darmstadtrapport.pdf (accessed on 25 January 2021).
- Bunn, S.M.; Reynolds, L. The energy-efficiency benefits of pumpscheduling optimization for potable water supplies. IBM J. Res. Dev. 2009, 53, 5:1–5:13. [Google Scholar] [CrossRef]
- Eaton, A.; D’Alessandro, F.; Ahmed, W.; Hassan, M. On the performance degradation of centrifugal pumps. In Proceedings of the International Conference on Fluid Flow, Heat and Mass Transfer, Niagara Falls, Canada, 7–9 June 2018; Avestia Publishing: Orléans, ON, Canada, 2018; p. 158. [Google Scholar]
- Sanks, R.L.; Tchobanoglous, G.; Bosserman Ii, B.E.; Jones, G.M. Pumping Station Design, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1998. [Google Scholar]
- Israeli Regulations: Energy Efficiency Test in Pumping Facilities. Available online: https://www.nevo.co.il/law_html/law01/999_315.htm (accessed on 10 December 2020).
- Costa, A.L.H.; De Medeiros, J.L.; Pessoa, F.L.P. Optimization of pipe networks including pumps by simulated annealing. Braz. J. Chem. Eng. 2000, 17, 887–895. [Google Scholar] [CrossRef]
- Stokes, C.S.; Simpson, A.R.; Maier, H.R. A computational software tool for the minimization of costs and greenhouse gas emissions associated with water distribution systems. Environ. Model. Softw. 2015, 69, 452–467. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E.; Ormsbee, L.; Uber, J.G.J.G.; Bros, C.M.C.M.; Kalungi, P.; Burd, R.; Zazula-Coetzee, B.; Belrain, T.; Kang, D.; et al. Battle of the Water Calibration Networks. J. Water Resour. Plan. Manag. 2012, 138, 523–532. [Google Scholar] [CrossRef]
- Housh, M.; Ohar, Z. Model-based approach for cyber-physical attack detection in water distribution systems. Water Res. 2018, 139, 132–143. [Google Scholar] [CrossRef]
- Marchi, A.; Simpson, A.R.; Lambert, M.F. Optimization of Pump Operation Using Rule-Based Controls in EPANET2: New ETTAR Toolkit and Correction of Energy Computation. J. Water Resour. Plan. Manag. 2016, 142, 04016012. [Google Scholar] [CrossRef]
- Khatavkar, P.; Mays, L.W. Model for real-time operations of water distribution systems under limited electrical power availability with consideration of water quality. J. Water Resour. Plan. Manag. 2018, 144, 04018071. [Google Scholar] [CrossRef]
- Shang, F.; Uber, J.G.; Rossman, L.A. Modeling reaction and transport of multiple species in water distribution systems. Environ. Sci. Technol. 2008, 42, 808–814. [Google Scholar] [CrossRef]
- Rossman, L. Modeling of chlorine residual in drinking water distribution system. J. Environ. Eng. ASCE 1995, 120, 803–820, ISSN 0733-9372/94/0004–0803. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Optimal layout of early warning detection stations for water distribution systems security. J. Water Resour. Plan. Manag. 2004, 130, 377–385. [Google Scholar] [CrossRef]
- Blinco, L.J.; Simpson, A.R.; Lambert, M.F.; Marchi, A. Comparison of Pumping Regimes for Water Distribution Systems to Minimize Cost and Greenhouse Gases. J. Water Resour. Plan. Manag. 2016, 142, 04016010. [Google Scholar] [CrossRef]
- Wood, D.J. Waterhammer Analysis—Essential and Easy (and Efficient). ASCE 2005, 131, 1123–1131. [Google Scholar] [CrossRef]
- Gottliebson, M.; Sanks, R.L.; Vause, A.; Abelin, S.M.; Benfell, R.S.; Bicknell, H.C.; Densmore, B.; Duncan, R.W.; Hong, S.S.; Jones, C.; et al. Variable-Speed Pumping. In Pumping Station Design; Elsevier Ltd.: Amsterdam, The Netherlands, 2008; ISBN 9781856175135. [Google Scholar]
- Lansey, K.; Awumah, K. Optimal Pump Operations Considering Pump Switches. J. Water Resour. Plan. Manag. 1994, 120, 17–35. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET2 User’s Manual; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2000. [Google Scholar]
- Marchi, A.; Simpson, A.R. Correction of the EPANET Inaccuracy in Computing the Efficiency of Variable Speed Pumps. J. Water Resour. Plan. Manag. 2013, 139, 456–459. [Google Scholar] [CrossRef]
- Ulanicki, B.; Kahler, J.; Coulbeck, B. Modeling the efficiency and power characteristics of a pump group. J. Water Resour. Plan. Manag. 2008, 134, 88–93. [Google Scholar] [CrossRef]
- Marchi, A.; Simpson, A.R.; Ertugrul, N. Assessing variable speed pump efficiency in water distribution systems. Drink. Water Eng. Sci. 2012, 5, 15–21. [Google Scholar] [CrossRef]
- Todini, E.; Tryby, M.E.; Wu, Z.Y.; Walski, T.M. Direct computation of Variable Speed Pumps for water distribution system analysis. In Proceedings of the Combined International Conference of Computing and Control for the Water Industry, CCWI2007 and Sustainable Urban Water Management, SUWM2007, Leicester, UK, 3–5 September 2007; pp. 411–418. [Google Scholar]
- AbdelMeguid, H.; Ulanicki, B. Feedback Rules for Operation of Pumps in a Water Supply System Considering Electricity Tariffs. Water Distrib. Syst. Anal. 2010. [Google Scholar] [CrossRef]
- Coulbeck, B.; Orr, C.H. Real-Time Optimized Control of a Water Distribution System. IFAC Proc. Vol. 1989, 22, 441–446. [Google Scholar] [CrossRef]
- Abdallah, M.; Kapelan, Z. Fast Pump Scheduling Method for Optimum Energy Cost and Water Quality in Water Distribution Networks with Fixed and Variable Speed Pumps. J. Water Resour. Plan. Manag. 2019, 145, 04019055. [Google Scholar] [CrossRef]
- Hashemi, S.S.; Tabesh, M.; Ataeekia, B. Ant-colony optimization of pumping schedule to minimize the energy cost using variable-speed pumps in water distribution networks. Urban Water J. 2014, 11, 335–347. [Google Scholar] [CrossRef]
- Bene, J.G.; Hos, C.J. Finding least-cost pump schedules for reservoir filling with a variable speed pump. J. Water Resour. Plan. Manag. 2012, 138, 682–686. [Google Scholar] [CrossRef]
- Wu, W.; Maier, H.R.; Dandy, G.C.; Arora, M.; Castelletti, A. The changing nature of the water–energy nexus in urban water supply systems: A critical review of changes and responses. J. Water Clim. Chang. 2020, 11, 1095–1122. [Google Scholar] [CrossRef]
- Lima, G.M.; Luvizotto, E.; Brentan, B.M.; Ramos, H.M. Leakage control and energy recovery using variable speed pumps as turbines. J. Water Resour. Plan. Manag. 2018, 144, 04017077. [Google Scholar] [CrossRef]
- Wu, W.; Simpson, A.R.; Maier, H.R.; Marchi, A. Incorporation of variable-speed pumping in multiobjective genetic algorithm optimization of the design of water transmission systems. J. Water Resour. Plan. Manag. 2012, 138, 543–552. [Google Scholar] [CrossRef]
- Huo, J.; Eckmann, D.H.; Hoskins, K.P. Hydraulic simulation and variable speed pump selection of a dual-function pumping station: Pumping treated water to a reclaimed water system or deep injection well system. In World Environmental and Water Resources Congress; American Society of Civil Engineers: Reston, VA, USA, 2007; pp. 1–7. [Google Scholar]
- Sunela, M.I.; Puust, R. A visual tool to calculate optimal control strategy for non-identical pumps working in parallel, taking motor and VSD efficiencies into account. Water Sci. Technol. Water Supply 2015, 15, 1115–1122. [Google Scholar] [CrossRef]
- Gostoli, C.; Spadoni, G. Linearization of the head-capacity curve in the analysis of pipe networks including pumps. Comput. Chem. Eng. 1985, 9, 89–92. [Google Scholar] [CrossRef]
- MATLAB 9.5.0.1033004 (R2018b); The MathWorks Inc.: Natick, MA, USA, 2018.
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Tawarmalani, M.; Sahinidis, N.V. A polyhedral branch-and-cut approach to global optimization. In Proceedings of the Mathematical Programming; Springer: Berlin/Heidelberg, Germany, 2005; Volume 103, pp. 225–249. [Google Scholar]
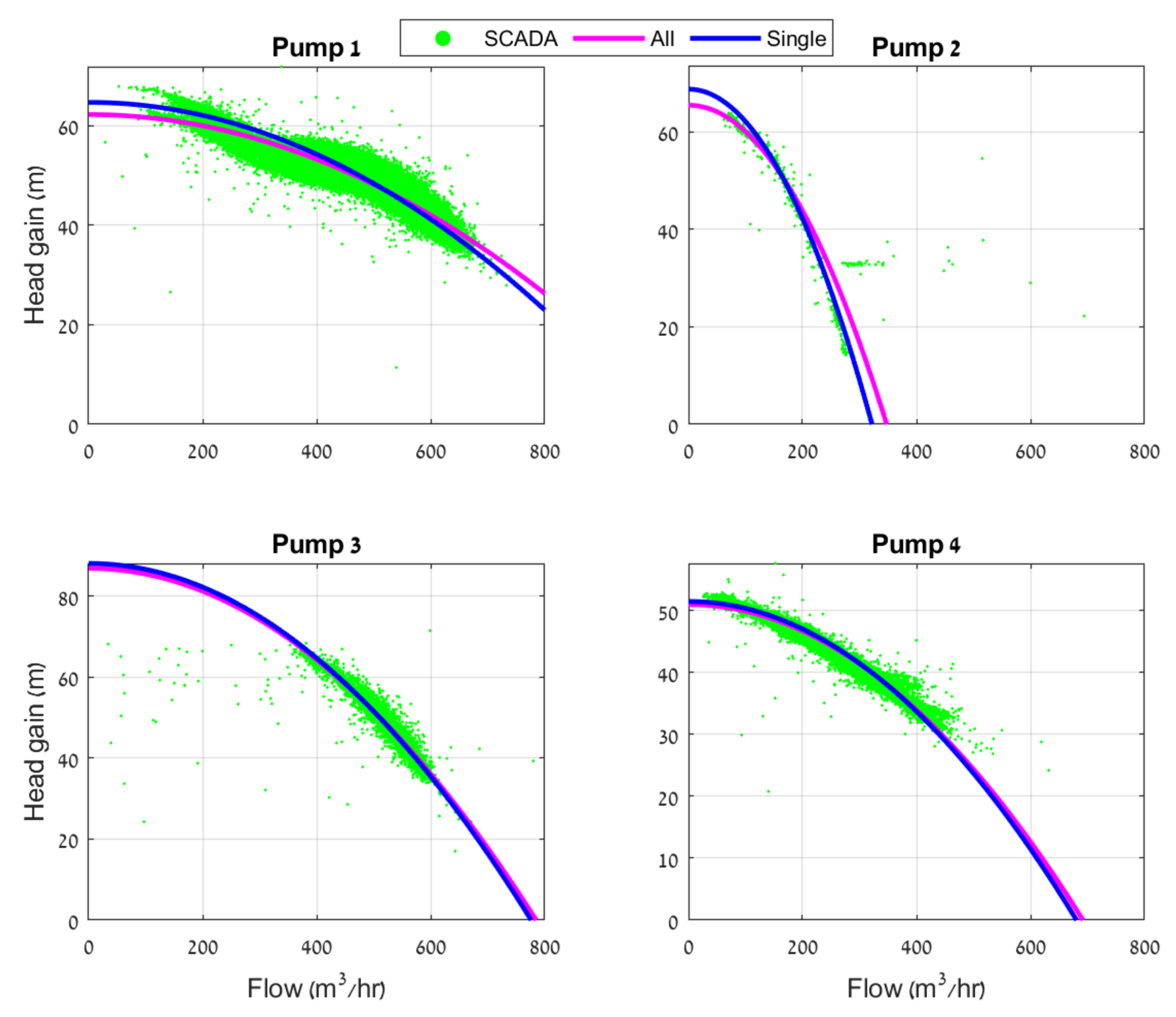
| Pump | Single | All | ||
|---|---|---|---|---|
| a | b (×10−4) | a | b (×10−4) | |
| 1 | 64.00 | 0.621 | 66.29 | 0.701 |
| 2 | 66.63 | 6.163 | 65.78 | 5.826 |
| 3 | 85.62 | 1.364 | 83.93 | 1.309 |
| 4 | 51.05 | 1.072 | 51.07 | 1.073 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salomons, E.; Shamir, U.; Housh, M. Optimization Methodology for Estimating Pump Curves Using SCADA Data. Water 2021, 13, 586. https://doi.org/10.3390/w13050586
Salomons E, Shamir U, Housh M. Optimization Methodology for Estimating Pump Curves Using SCADA Data. Water. 2021; 13(5):586. https://doi.org/10.3390/w13050586
Chicago/Turabian StyleSalomons, Elad, Uri Shamir, and Mashor Housh. 2021. "Optimization Methodology for Estimating Pump Curves Using SCADA Data" Water 13, no. 5: 586. https://doi.org/10.3390/w13050586
APA StyleSalomons, E., Shamir, U., & Housh, M. (2021). Optimization Methodology for Estimating Pump Curves Using SCADA Data. Water, 13(5), 586. https://doi.org/10.3390/w13050586







