Estimation of Groundwater Evapotranspiration of Different Dominant Phreatophytes in the Mu Us Sandy Region
Abstract
1. Introduction
2. Materials and Methods
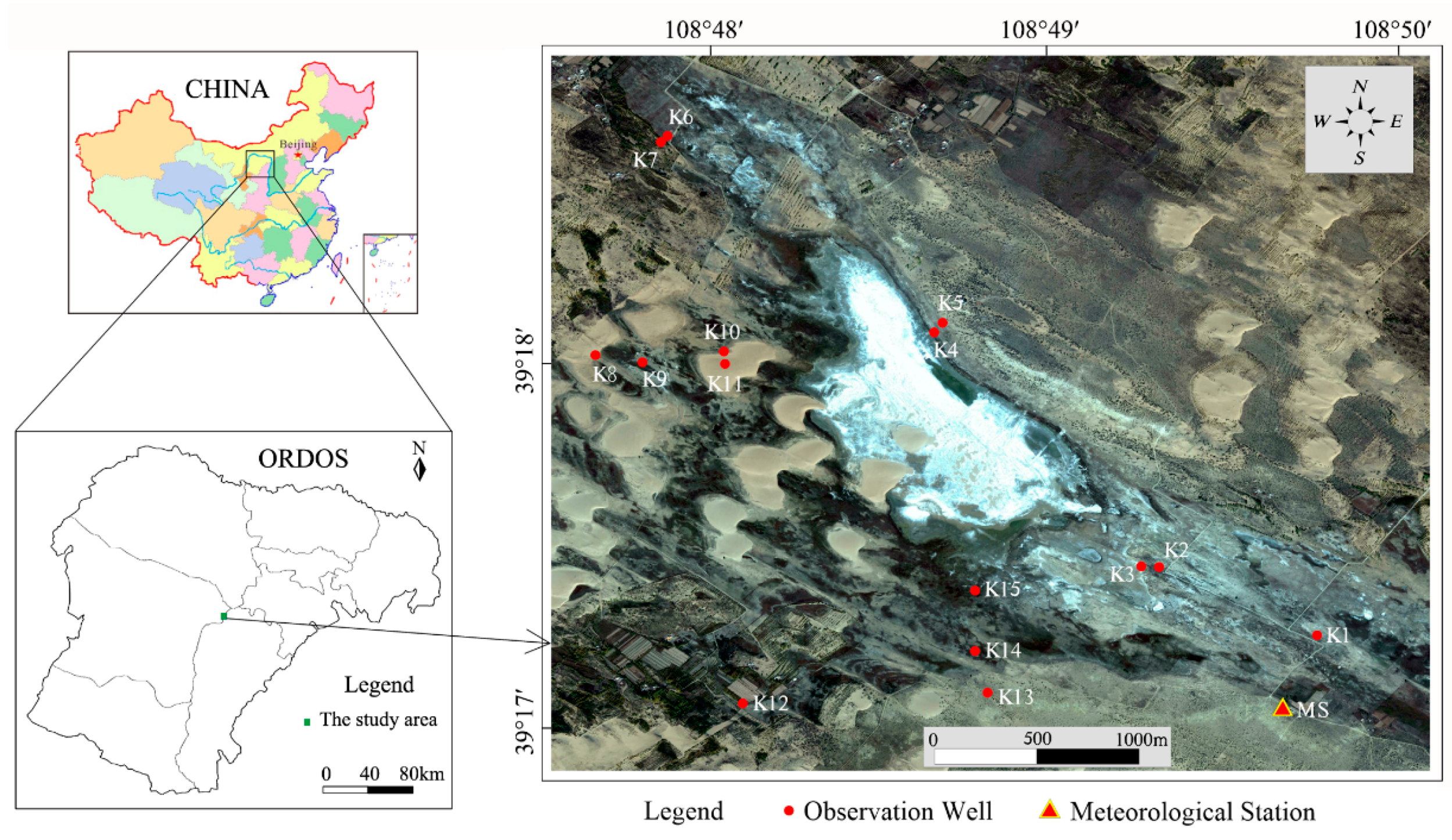
2.1. Site Description
2.2. Monitoring Design
2.3. Numerical Simulations
2.3.1. Soil Hydraulic Parameters Estimated by Inverse Modeling
2.3.2. Simulated Soil Moisture
2.3.3. Statistical Analysis
2.4. ETG Estimation
3. Results and Discussion
3.1. Soil Hydraulic Parameters
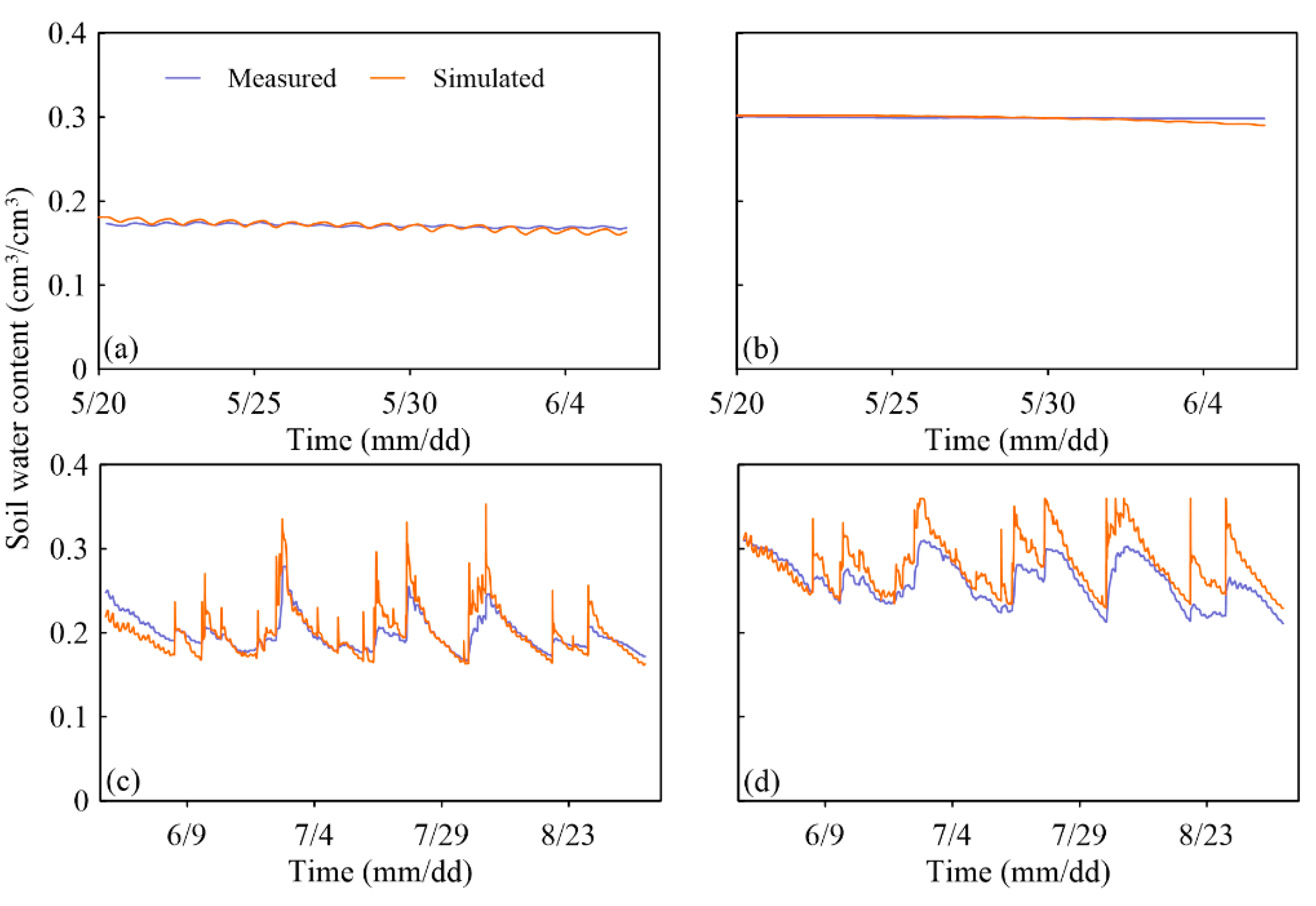
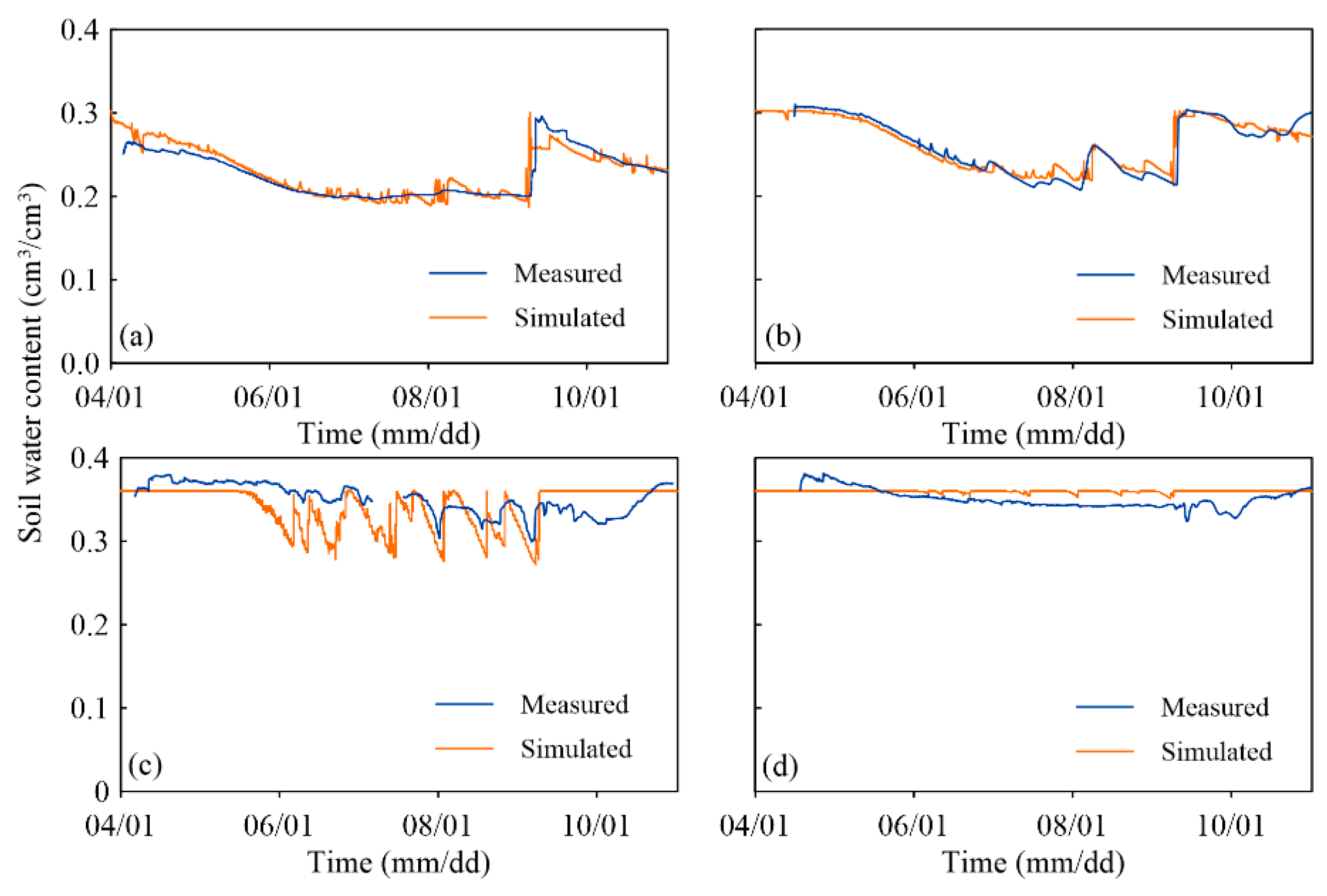
3.2. Validation of the Simulated Soil Moisture
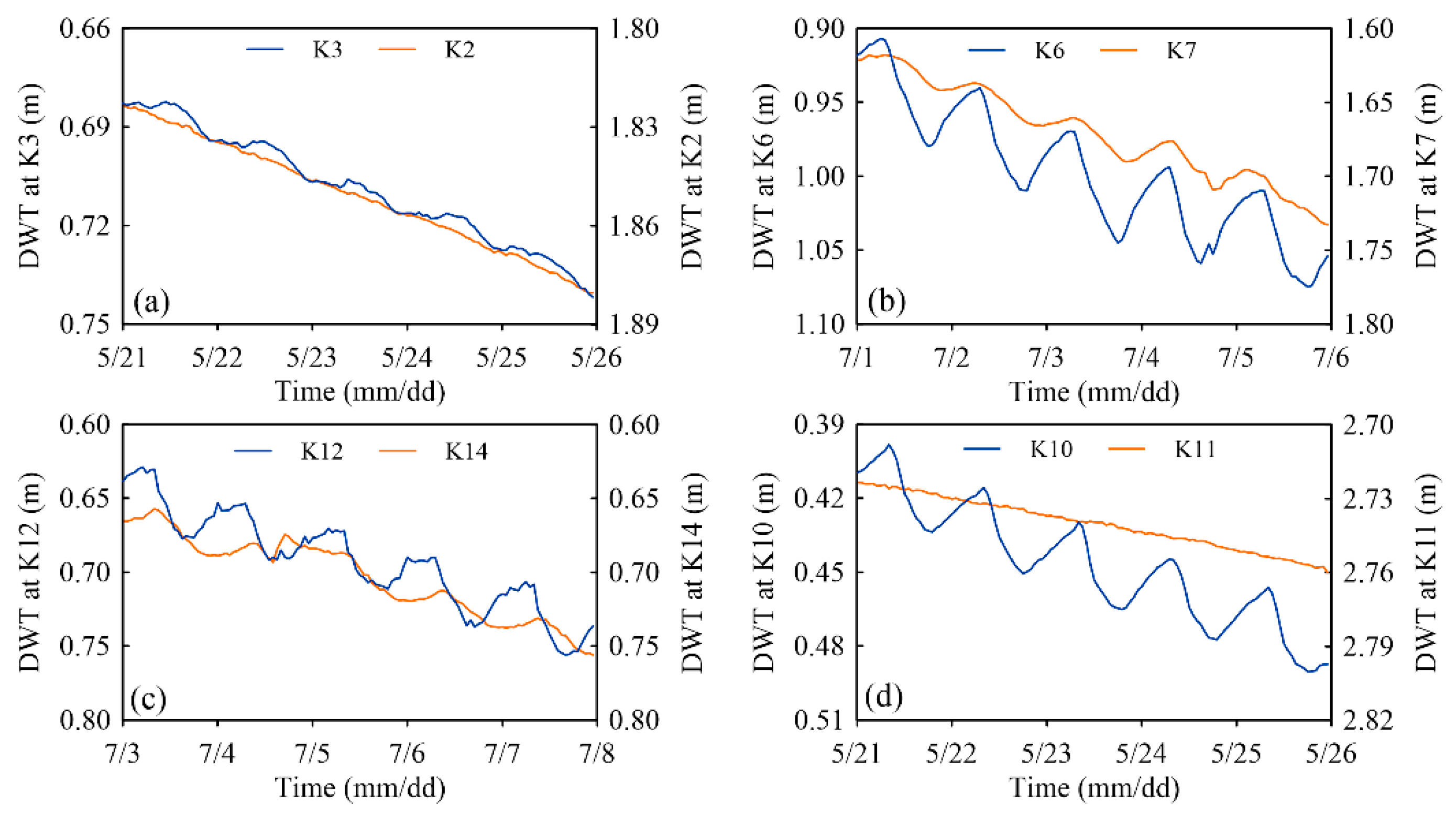
3.3. Temporal and Spatial Variations of Water Table
3.4. Groundwater Evapotranspiration
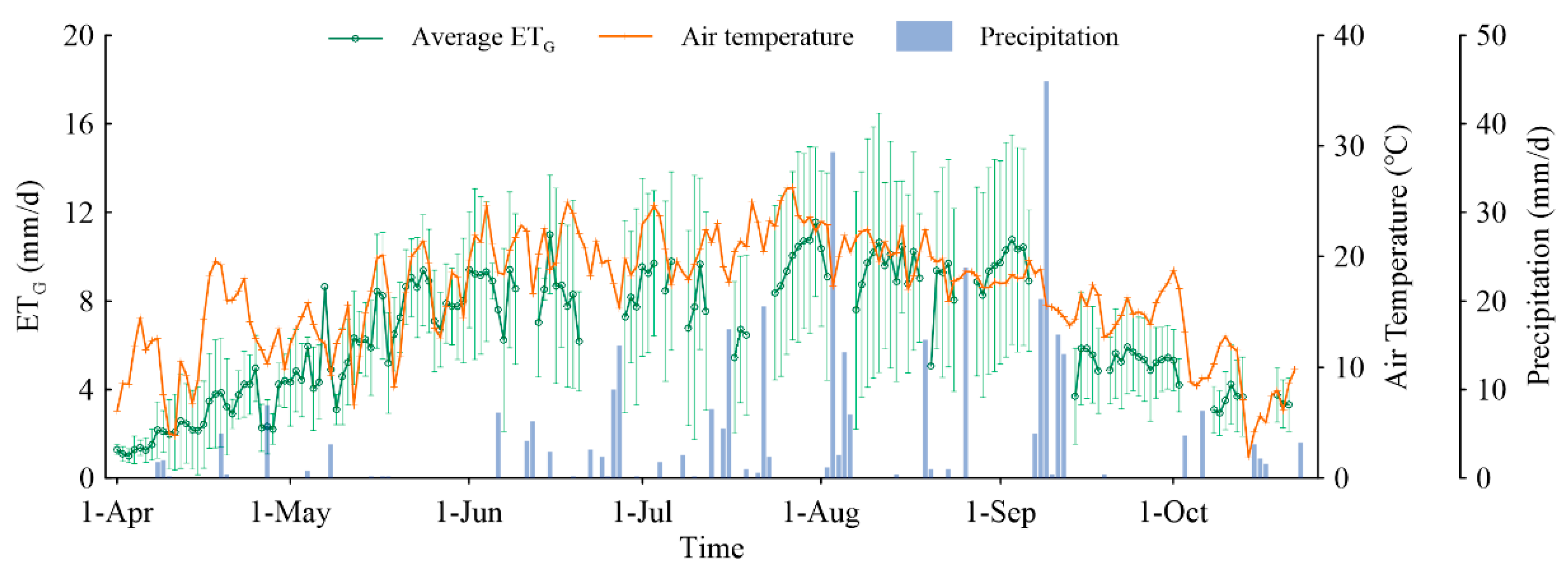
3.4.1. Temporal Variations of ETG
3.4.2. Spatial Variations of ETG
3.4.3. Average ETG in Different Vegetation Sites
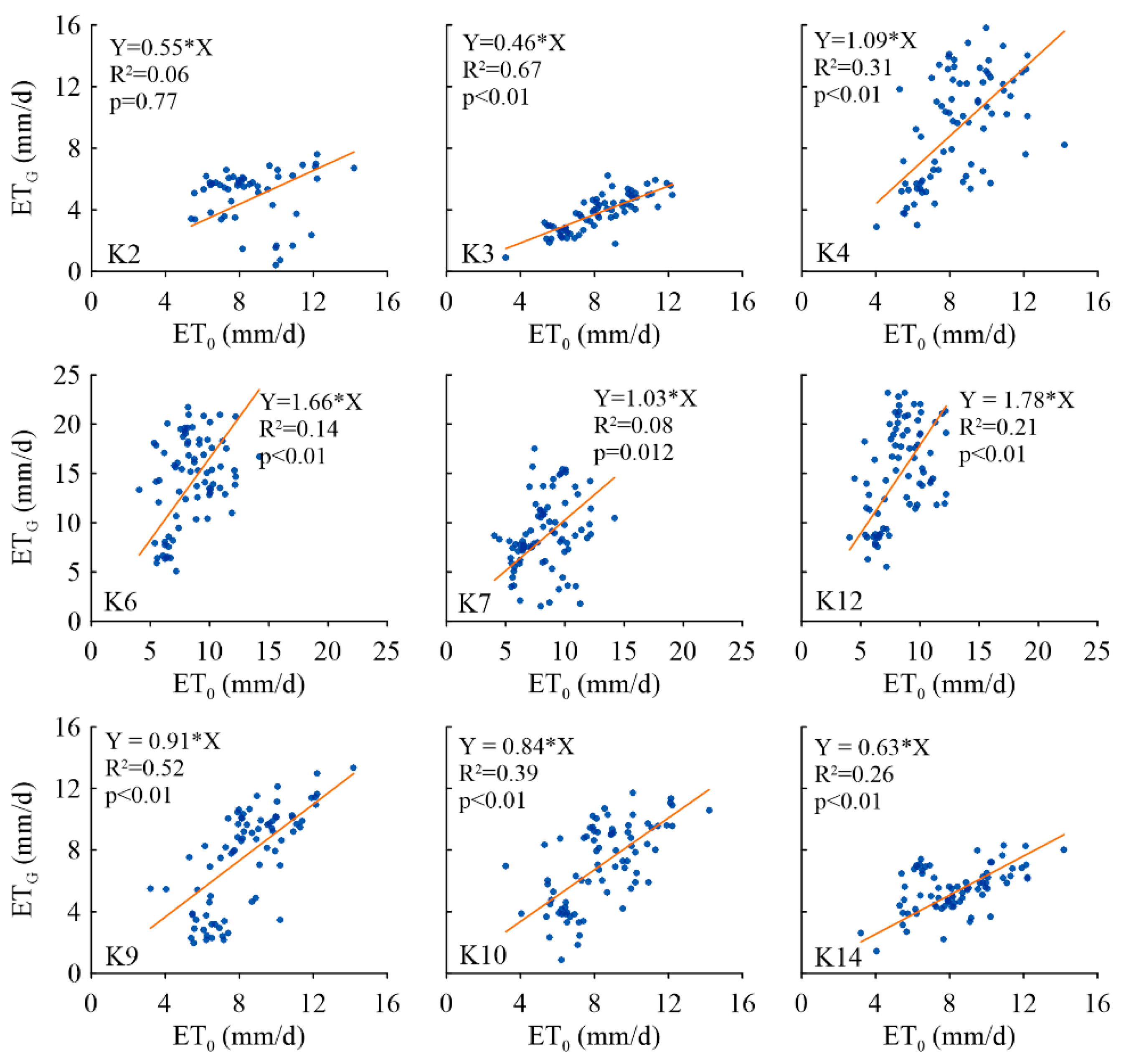
3.4.4. Sensitivity of ETG to Influencing Factors
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bullock, J.M.; Aronson, J.; Newton, A.C.; Pywell, R.F.; Rey-Benayas, J.M. Restoration of ecosystem services and biodiversity: Conflicts and opportunities. Trends Ecol. Evol. 2011, 26, 541–549. [Google Scholar] [CrossRef]
- Mvungi, A.; Mashauri, D.; Madulu, N. Management of water for irrigation agriculture in semi-arid areas: Problems and prospects. Phys. Chem. Earth Parts A/B/C 2005, 30, 809–817. [Google Scholar] [CrossRef]
- Alvarez, M.D.P.; Trovatto, M.M.; Hernández, M.A.; Gonzalez, N. Groundwater flow model, recharge estimation and sustainability in an arid region of Patagonia, Argentina. Environ. Earth Sci. 2012, 66, 2097–2108. [Google Scholar] [CrossRef]
- Wang, L.; Good, S.P.; Caylor, K. Global synthesis of vegetation control on evapotranspiration partitioning. Geophys. Res. Lett. 2014, 41, 6753–6757. [Google Scholar] [CrossRef]
- Li, X.; Gentine, P.; Lin, C.; Zhou, S.; Sun, Z.; Zheng, Y.; Liu, J.; Zheng, C. A simple and objective method to partition evapotranspiration into transpiration and evaporation at eddy-covariance sites. Agric. For. Meteorol. 2019, 265, 171–182. [Google Scholar] [CrossRef]
- Xiu, L.; Yan, C.; Li, X.; Qian, D.; Feng, K. Monitoring the response of vegetation dynamics to ecological engineering in the Mu Us Sandy Land of China from 1982 to 2014. Environ. Monit. Assess. 2018, 190, 543. [Google Scholar] [CrossRef]
- Lu, C.; Zhao, T.; Shi, X.; Cao, S. Ecological restoration by afforestation may increase groundwater depth and create potentially large ecological and water opportunity costs in arid and semiarid China. J. Clean. Prod. 2018, 176, 1213–1222. [Google Scholar] [CrossRef]
- Gribovszki, Z.; Kalicz, P.; Balog, K.; Szabó, A.; Tóth, T.; Csáfordi, P.; Metwaly, M.; Szalai, S. Groundwater uptake of different surface cover and its consequences in great Hungarian plain. Ecol. Process. 2017, 6, 39. [Google Scholar] [CrossRef]
- Yin, L.; Hu, G.; Huang, J.; Wen, D.; Dong, J.; Wang, X.; Li, H. Groundwater-recharge estimation in the Ordos Plateau, China: Comparison of methods. Hydrogeol. J. 2011, 19, 1563–1575. [Google Scholar] [CrossRef]
- Doody, T.M.; Benyon, R.G.; Theiveyanathan, S.; Koul, V.; Stewart, L. Development of pan coefficients for estimating evapotranspiration from riparian woody vegetation. Hydrol. Process. 2013, 28, 2129–2149. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Kar, S.K. Evapotranspiration Estimation with Remote Sensing and Various Surface Energy Balance Algorithms—A Review. Energies 2014, 7, 2821–2849. [Google Scholar] [CrossRef]
- Anapalli, S.S.; Fisher, D.K.; Reddy, K.N.; Wagle, P.; Gowda, P.H.; Sui, R. Quantifying soybean evapotranspiration using an eddy covariance approach. Agric. Water Manag. 2018, 209, 228–239. [Google Scholar] [CrossRef]
- White, W. A Method of Estimating Ground-Water Supplies Based on Discharge by Plants and Evaporation from Soil: Results of Investigations in Escalante Valley; US Geological Survey: Salt Lake, UT, USA, 1932. [Google Scholar]
- Cheng, D.-H.; Li, Y.; Chen, X.; Wang, W.-K.; Hou, G.-C.; Wang, C.-L. Estimation of groundwater evaportranspiration using diurnal water table fluctuations in the Mu Us Desert, northern China. J. Hydrol. 2013, 490, 106–113. [Google Scholar] [CrossRef]
- Yin, L.; Zhou, Y.; Ge, S.; Wen, D.; Zhang, E.; Dong, J. Comparison and modification of methods for estimating evapotranspiration using diurnal groundwater level fluctuations in arid and semiarid regions. J. Hydrol. 2013, 496, 9–16. [Google Scholar] [CrossRef]
- Gribovszki, Z.; Kalicz, P.; Szilágyi, J.; Kucsara, M. Riparian zone evapotranspiration estimation from diurnal groundwater level fluctuations. J. Hydrol. 2008, 349, 6–17. [Google Scholar] [CrossRef]
- Wang, T.-Y.; Wang, P.; Yu, J.-J.; Pozdniakov, S.P.; Du, C.-Y.; Zhang, Y.-C. Revisiting the White method for estimating groundwater evapotranspiration: A consideration of sunset and sunrise timings. Environ. Earth Sci. 2019, 78, 78. [Google Scholar] [CrossRef]
- Ii, S.P.L. A method for estimating subdaily evapotranspiration of shallow groundwater using diurnal water table fluctuations. Ecohydrology 2008, 1, 59–66. [Google Scholar] [CrossRef]
- Li, N.; Yan, C.; Xie, J. Remote sensing monitoring recent rapid increase of coal mining activity of an important energy base in northern China, a case study of Mu Us Sandy Land. Resour. Conserv. Recycl. 2015, 94, 129–135. [Google Scholar] [CrossRef]
- Liang, P.; Yang, X. Landscape spatial patterns in the Maowusu (Mu Us) Sandy Land, northern China and their impact factors. Catena 2016, 145, 321–333. [Google Scholar] [CrossRef]
- Cheng, D.-H.; Duan, J.; Qian, K.; Qi, L.; Yang, H.; Chen, X. Groundwater evapotranspiration under psammophilous vegetation covers in the Mu Us Sandy Land, northern China. J. Arid Land 2016, 9, 98–108. [Google Scholar] [CrossRef][Green Version]
- Satchithanantham, S.; Wilson, H.; Glenn, A.J. Contrasting patterns of groundwater evapotranspiration in grass and tree dominated riparian zones of a temperate agricultural catchment. J. Hydrol. 2017, 549, 654–666. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop. Evapotranspiration-Guidelines for Computing Crop. Water Requirements; FAO: Rome, Italy, 1998. [Google Scholar]
- Schelle, H.; Durner, W.; Iden, S.C.; Fank, J. Simultaneous Estimation of Soil Hydraulic and Root Distribution Parameters from Lysimeter Data by Inverse Modeling. Procedia Environ. Sci. 2013, 19, 564–573. [Google Scholar] [CrossRef]
- Nascimento, Í.V.; de Assis Júnior, R.N.; de Araújo, J.C.; de Alencar, T.L.; Freire, A.G.; Lobato, M.G.R.; da Silva, C.P.; Mota, J.C.A.; Nascimento, C.D.V. Estimation of van Genuchten Equation Parameters in Laboratory and through Inverse Modeling with Hydrus-1D. J. Agric. Sci. 2018, 10, 102. [Google Scholar] [CrossRef]
- Mavimbela, S.S.W.; Van Rensburg, L.D. Estimating Soil Hydraulic Parameters Characterizing Rainwater Infiltration and Runoff Properties of Dryland Floodplains. Comput. Water Energy Environ. Eng. 2019, 8, 11–40. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; Genuchten, M.T.V. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media; Version 4.17, HYDRUS Software Series 3; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2013. [Google Scholar]
- Li, Y.; Šimůnek, J.; Jing, L.; Zhang, Z.; Ni, L. Evaluation of water movement and water losses in a direct-seeded-rice field experiment using Hydrus-1D. Agric. Water Manag. 2014, 142, 38–46. [Google Scholar] [CrossRef]
- Ritchie, J.T. Model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef]
- Belmans, C.; Wesseling, J.; Feddes, R. Simulation model of the water balance of a cropped soil: SWATRE. J. Hydrol. 1983, 63, 271–286. [Google Scholar] [CrossRef]
- Zeng, X. Global Vegetation Root Distribution for Land Modeling. J. Hydrometeorol. 2001, 2, 525–530. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Numerical Model for Water and Solute Movement in and below the Root Zone; Unpublished Report; U.S. Salinity Laboratory, USDA, ARS: Riverside, CA, USA, 1987. [Google Scholar]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; LeGates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. Space Phys. 1985, 90, 8995–9005. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I-A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- LeGates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Laczniak, R.J.; Smith, J.L.; Elliott, P.E.; DeMeo, G.A.; Chatigny, M.A.; Roemer, G.J. Ground-Water Discharge Determined from Estimates of Evapotranspiration, Death Valley Regional Flow System, Nevada and California; Report 2001-4195; U.S. Geological Survey: Reston, VA, USA, 2001. [Google Scholar]
- Nachabe, M.H. Analytical expressions for transient specific yield and shallow water table drainage. Water Resour. Res. 2002, 38, 11-1–11-7. [Google Scholar] [CrossRef]
- Ii, S.P.L.; Butler, J.J., Jr.; Gorelick, S.M. Estimation of groundwater consumption by phreatophytes using diurnal water table fluctuations: A saturated-unsaturated flow assessment. Water Resour. Res. 2005, 41, 1–14. [Google Scholar] [CrossRef]
- Gribovszki, Z. Comparison of specific-yield estimates for calculating evapotranspiration from diurnal groundwater-level fluctuations. Hydrogeol. J. 2017, 26, 869–880. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Duke, H.R. Capillary Properties of Soils-Influence upon Specific Yield. Trans. ASAE 1972, 15, 0688–0691. [Google Scholar] [CrossRef]
- Butler, J.J.; Kluitenberg, G.J.; Whittemore, D.O.; Ii, S.P.L.; Jin, W.; Billinger, M.A.; Zhan, X. A field investigation of phreatophyte-induced fluctuations in the water table. Water Resour. Res. 2007, 43, 299–309. [Google Scholar] [CrossRef]
- Yue, W.; Wang, T.; Franz, T.E.; Chen, X. Spatiotemporal patterns of water table fluctuations and evapotranspiration induced by riparian vegetation in a semiarid area. Water Resour. Res. 2016, 52, 1948–1960. [Google Scholar] [CrossRef]
- Hughes, C.; Kalma, J.D.; Binning, P.J.; Willgoose, G.R.; Vertzonis, M. Estimating evapotranspiration for a temperate salt marsh, Newcastle, Australia. Hydrol. Process. 2001, 15, 957–975. [Google Scholar] [CrossRef]
- Senitz, S. Untersuchung und Anwendung kurzperiodischer Schwankungen des Grundwasserspiegels in Thüringen. Grundwasser 2001, 6, 163–173. [Google Scholar] [CrossRef]
- Jiang, X.-W.; Sun, Z.-C.; Zhao, K.-Y.; Shi, F.-S.; Wan, L.; Wang, X.; Shi, Z. A method for simultaneous estimation of groundwater evapotranspiration and inflow rates in the discharge area using seasonal water table fluctuations. J. Hydrol. 2017, 548, 498–507. [Google Scholar] [CrossRef]
- Scott, M.L.; Lines, G.C.; Auble, G.T. Channel incision and patterns of cottonwood stress and mortality along the Mojave River, California. J. Arid Environ. 2000, 44, 399–414. [Google Scholar] [CrossRef]
- Martín, D.; Chambers, J. Restoration of riparian meadows degraded by livestock grazing: Above- and belowground responses. Plant Ecol. 2002, 163, 77–91. [Google Scholar] [CrossRef]
- Shah, N.; Nachabe, M.; Ross, M. Extinction Depth and Evapotranspiration from Ground Water under Selected Land Covers. Groundwater 2007, 45, 329–338. [Google Scholar] [CrossRef] [PubMed]



| Wells | Soil Depth (cm) | Sand (%) | Silt (%) | Clay (%) |
|---|---|---|---|---|
| K1 | 40 | 82.9 | 17.1 | 0 |
| 60 | 83.4 | 16.6 | 0 | |
| 80 | 86.3 | 13.7 | 0 | |
| K3 | 50 | 85.0 | 15.0 | 0 |
| 70 | 85.1 | 14.9 | 0 | |
| K4 | 20 | 85.5 | 14.5 | 0 |
| 50 | 83.2 | 16.8 | 0 | |
| 70 | 81.9 | 18.1 | 0 | |
| K6 | 50 | 91.0 | 9.0 | 0 |
| 80 | 91.1 | 8.9 | 0 | |
| K9 | 20 | 85.6 | 14.4 | 0 |
| 50 | 85.2 | 14.8 | 0 | |
| K10 | 20 | 92.7 | 7.3 | 0 |
| 50 | 94.7 | 5.3 | 0 | |
| K12 | 50 | 92.4 | 7.6 | 0 |
| 80 | 92.9 | 7.1 | 0 | |
| 100 | 95.7 | 4.3 | 0 | |
| K14 | 30 | 98.0 | 2.0 | 0 |
| 60 | 98.4 | 1.6 | 0 | |
| 80 | 92.6 | 7.4 | 0 | |
| K15 | 20 | 87.2 | 12.8 | 0 |
| θr (cm3/cm3) | θs (cm3/cm3) | φ (1/cm) | n | Ks (cm/h) | |
|---|---|---|---|---|---|
| Initial Value | 0.057 | 0.41 | 0.124 | 2.28 | 14.5917 |
| Minimum | 0 | 0 | 0.016 | 1.37 | 0.25 |
| Maximum | 0.078 | 0.43 | 0.145 | 2.68 | 29.7 |
| Well | θr (cm3/cm3) | θs (cm3/cm3) | φ (1/cm) | n | Ks (cm/h) |
|---|---|---|---|---|---|
| K1 | 0.0453 | 0.302 | 0.0253 | 1.78 | 14.2 |
| K14 | 0.0532 | 0.387 | 0.0282 | 2.68 | 29.4 |
| RMSE (cm3/cm3) | NSE | PBIAS (%) | R2 | |
|---|---|---|---|---|
| K1 | 0.012 | 0.88 | 0.18 | 0.89 |
| K14 | 0.019 | 0.25 | −1.82 | 0.21 |
| Achnatherum splendens Site | Carex stenophylla Site | Salix psammophila Site | ||||
|---|---|---|---|---|---|---|
| Average ETG (mm/d) | Standard Deviation (mm/d) | Average ETG (mm/d) | Standard Deviation (mm/d) | Average ETG (mm/d) | Standard Deviation (mm/d) | |
| Apr-2019 | 3.11 | 2.40 | 2.05 | 0.86 | 6.58 | 0 |
| May-2019 | 4.07 | 1.82 | 6.71 | 1.48 | 8.76 | 1.76 |
| Jun-2019 | 3.69 | 2.20 | 7.75 | 2.18 | 10.51 | 5.60 |
| Jul-2019 | 4.31 | 1.32 | 7.96 | 2.38 | 10.70 | 3.80 |
| Aug-2019 | 4.54 | 1.45 | 7.93 | 2.58 | 12.60 | 5.45 |
| Sep-2019 | 4.18 | 1.66 | 6.07 | 2.21 | 9.25 | 2.31 |
| Oct-2019 | 3.19 | 1.49 | 3.71 | 1.53 | 4.29 | 1.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, W.; Yin, L.; Zhang, M.; Yu, K.; Wang, L.; Hu, F. Estimation of Groundwater Evapotranspiration of Different Dominant Phreatophytes in the Mu Us Sandy Region. Water 2021, 13, 440. https://doi.org/10.3390/w13040440
Jia W, Yin L, Zhang M, Yu K, Wang L, Hu F. Estimation of Groundwater Evapotranspiration of Different Dominant Phreatophytes in the Mu Us Sandy Region. Water. 2021; 13(4):440. https://doi.org/10.3390/w13040440
Chicago/Turabian StyleJia, Wuhui, Lihe Yin, Maosheng Zhang, Kun Yu, Luchen Wang, and Fusheng Hu. 2021. "Estimation of Groundwater Evapotranspiration of Different Dominant Phreatophytes in the Mu Us Sandy Region" Water 13, no. 4: 440. https://doi.org/10.3390/w13040440
APA StyleJia, W., Yin, L., Zhang, M., Yu, K., Wang, L., & Hu, F. (2021). Estimation of Groundwater Evapotranspiration of Different Dominant Phreatophytes in the Mu Us Sandy Region. Water, 13(4), 440. https://doi.org/10.3390/w13040440






