1. Introduction
The foundation pit is one major kind of underground structure in the massive construction of underground space [
1,
2,
3,
4]. Gradually increased excavation area and depth with the development of urban construction may result in environmental effects. There are high risks during construction in multi-aquifer–aquitard alternative strata which is rich in groundwater [
5,
6,
7,
8,
9]. To prevent water inrush accidents and ensure the safety of underground construction, groundwater control is essential and dewatering is a kind of common measurement [
10,
11,
12]. However, inappropriate dewatering may result in some negative impacts, such as soil deformation [
13,
14,
15], differential settlement [
16,
17,
18] and sand flow or piping phenomenon [
19]. To reduce the negative impacts of dewatering, waterproof curtains such as diaphragm walls [
20,
21], bored piles [
22] and mixing piles [
23] are constructed before the excavation. Waterproof curtains play a good role in blocking water seepage and extending the length of seepage distance [
24,
25], which can reduce the drawdown of groundwater level and ground settlement outside the pit.
The buried depth of the waterproof curtain is essential for the environmental effect outside the pit caused by foundation dewatering. Theoretically if the waterproof curtain fully cuts off the dewatering aquifer, which is called full penetrating waterproof curtain, the groundwater drawdown outside the pit is very small and the environmental effect caused by the foundation dewatering is slight. However, with the increase of the excavation depth, the depth of the watertight curtain also increases. Full penetrating waterproof curtains are faced with high construction cost and construction difficulty. Therefore, waterproof curtains that partially cut off the dewatering aquifer, called partial penetrating waterproof curtains, are always chosen in practical engineering [
26,
27,
28,
29,
30].
Anisotropic permeability widely exists in rock [
31], coal mines [
32] and soil layers [
33]. The degree of anisotropic permeability of the aquifer can be reflected by the ratio of horizontal and vertical hydraulic conductivity of the aquifer. The anisotropic permeability of the aquifer is different in different fields. For example, the value of anisotropic permeability always ranges from 2 to 4 and even as high as 10 in Shanghai [
26,
34], from 3 to 6 in Tianjin [
35] and from 4 to 10 in Ningbo [
36,
37]. The anisotropic permeability of the dewatering aquifer may influence the groundwater seepage inside and outside the pit during dewatering with a partial penetrating waterproof curtain. Some research also indicated that the buried depth of the waterproof curtain and the anisotropic permeability of the aquifer can both impact the environmental effect outside the pit [
38,
39]. The optimized method has been proved effectively to analyze the soil parameters [
40,
41], and it also can be used for considering the combination of these two factors in the design of dewatering. The objective of this paper is to evaluate the recommended depth of the waterproof curtain penetrating the dewatering aquifer considering the degree of anisotropic permeability based on an engineering case in Shanghai, China. Firstly, the project description is introduced. Secondly, a numerical model is established and the pumping test is used to correct the numerical model. Then, the effect of dewatering is investigated by considering the depth of waterproof curtain penetrating the dewatering aquifer and the degree of anisotropic permeability. Finally, the suggested depth of waterproof curtain is proposed via considering the anisotropic permeability.
2. Project Description
2.1. Engineering Overview
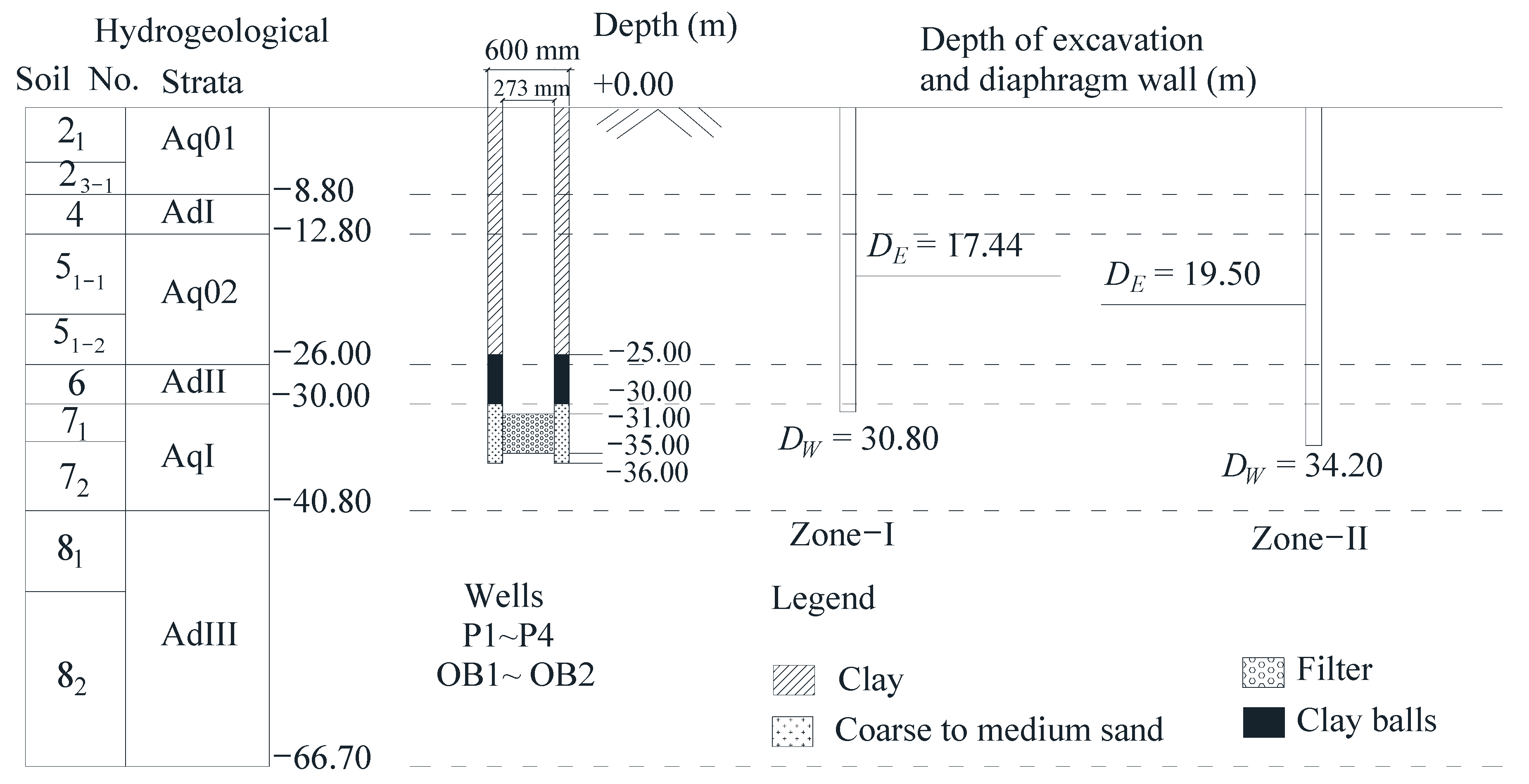
Figure 1 presents a plan view of the foundation pit of a certain metro line station in Shanghai. The pit is divided into two parts: the standard part (Zone-I) and the shield end well part (Zone-II). The length of Zone-I and Zone-II is 85.1 m and 16.3 m, and the width is 22.7 m and 27.1 m, respectively. The excavation depth (
DE) of Zone-I is 17.44 m and that of Zone-II is 19.50 m. A diaphragm wall with a thickness of 0.8 m is constructed as the waterproof curtain. The buried depth of the diaphragm wall (
DW) in Zone-I is 30.8 m, and 34.2m in Zone-II. Four pumping wells inside the pit and two observation wells outside the pit are arranged, which is shown in
Figure 1.
2.2. Engineering Geology and Hydrogeology
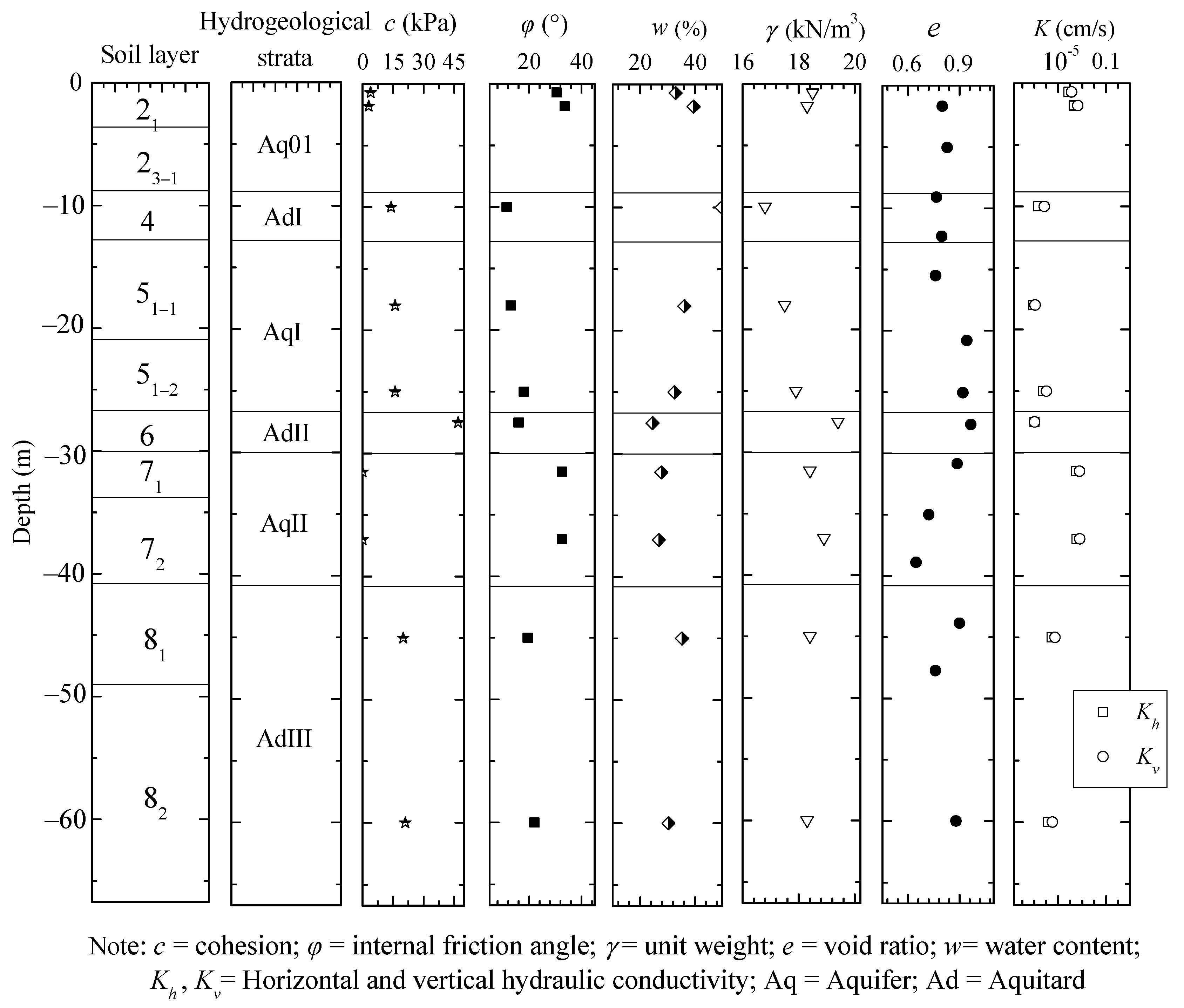
The soil layers from top to bottom are sandy silt with silty clay (labelled as 2
1), sandy silt (2
3–1), mucky clay (4), silty clay (5
1), silt (5
2), silty clay (6), mealy sand (7
1), fine sand (7
2), silty clay with mealy sand (8
1) and silty clay (8
2). The soil profile and properties of soil layers are presented in
Figure 2.
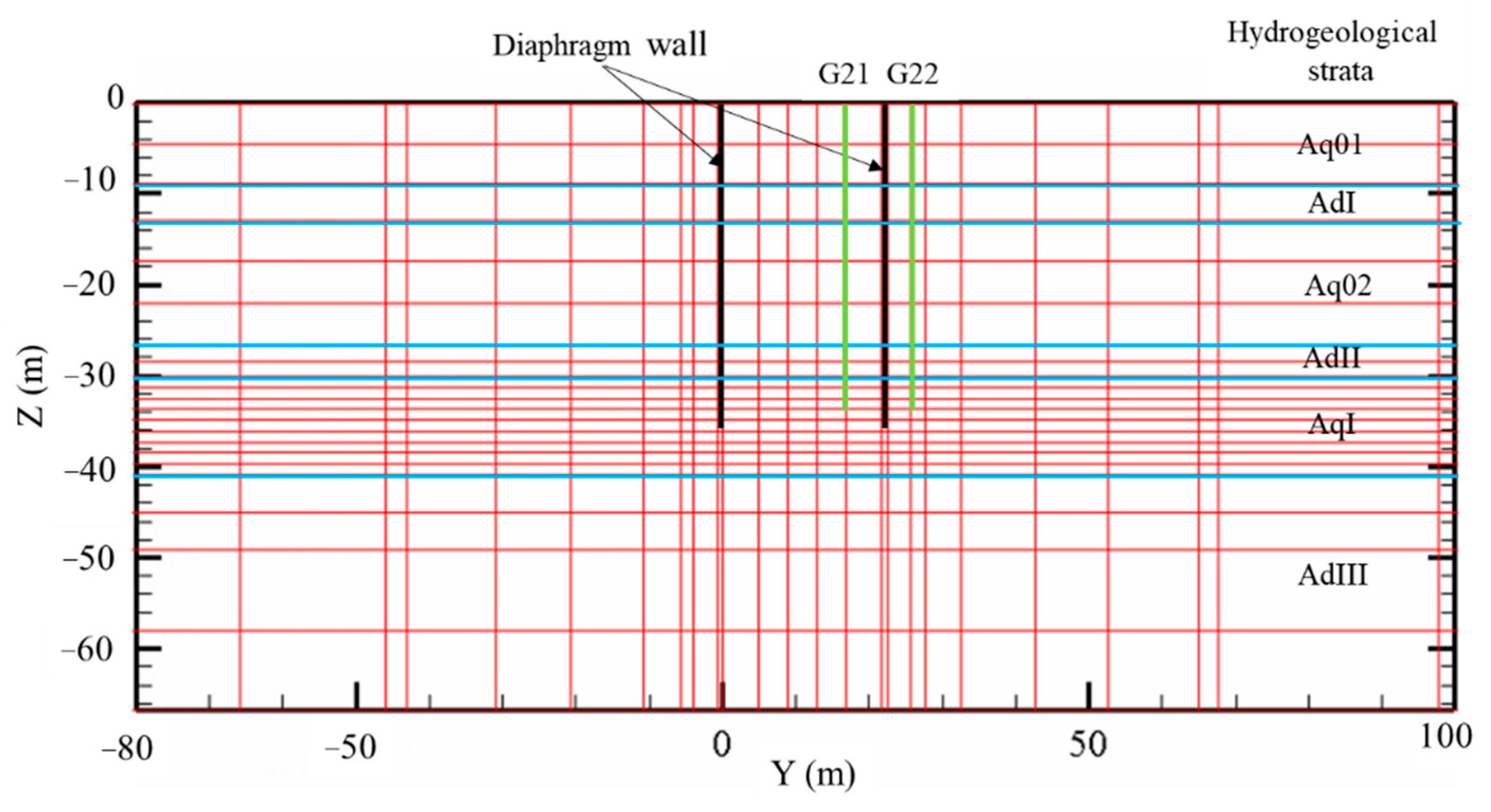
The hydrogeology of the project is multi-aquifer–aquitard alternative strata. The aquifer system of the project includes a phreatic aquifer (labelled as Aq01), and a confined aquifer I (labelled as AqI) and II (AqII). The aquitard layer is labelled as AdI to AdIII. Detailed information of the aquifers is described as follows:
(1) Aq01: the burial depth of the groundwater level of Aq01 is −0.5 to −1.0 m (a negative value implies that it is below ground surface); it lies within the Layers 21 and 23-1 and it is affected by rainfall, spring tides and surface water. The water inflow rate of a single well is 0.48–30 m3/d, and the hydraulic conductivity is 0.01–0.85 m/d;
(2) AqI: the burial depth of the groundwater level of AqI layer is −10.0 to −3.0 m and it lies within the Layers 51 and 52. The water inflow rate of a single well is 5–15 m3/d, and the hydraulic conductivity is 0.26–0.78 m/d;
(3) AqII: the burial depth of the groundwater level of AqII layer is −6.0 to −4.0 m; it lies within the Layers 7
1 and 7
2. The water inflow rate of a single well is 36–48 m
3/d, and the hydraulic conductivity is 0.18–4.1 m/d [
43].
2.3. Pumping Test
To prevent uprush by the underlying confined aquifer, groundwater level inside the pit should be lowered which can be calculated by the following equation [
44]:
where
Ps is the overburden pressure between the bottom surface of the foundation pit and the top surface of the underlying confined aquifer (kPa);
Pw is the uplift force of artesian water in the initial state (kPa);
hi is the thickness of each layer of soil between the bottom surface of foundation pit and top surface of the underlying confined aquifer (m);
hp is the difference between the groundwater level and top surface of the confined aquifer (m);
γsi is the unit weight of each soil layer between the bottom surface of the foundation pit and the top surface of the underlying confined aquifer (kN/m
3);
γw is the unit weight of water (kN/m
3); and
Fs is the safety coefficient, which is considered as 1.10 in this study [
44].
In this case, drawdown of AqII in Zone-I and II should be larger than 3.38m and 7.14m. To ensure the safety of construction and evaluate the dewatering effect on environment, the pumping test was conducted after the construction of the diaphragm wall. The placement of the pumping and observation wells are shown in
Figure 1 and the structure and burial depth of the wells are shown in
Figure 3. The pumping test contains two steps of dewatering, of which the pumping time and discharge rate is shown in
Table 1.
3. Numerical Analysis
3.1. Numerical Theory
The calculation method of software in the numerical simulation is a kind of finite different method [
13,
26,
45], which is three-dimensional (3D) groundwater seepage model. The basic equation of 3D groundwater seepage model is:
where
Kij = hydraulic conductivity of different direction, i, j = axes of
x,
y,
z in Cartesian coordinate system,
H = hydraulic head of groundwater,
q = external source/sink flux,
t = time, and
Ss = specific storage,
Ss ≈
γwmv,
γw = unit weight of water,
mv = soil coefficient of volume compressibility. Based on Terzaghi’s 1D consolidation theory, if the total vertical pressure is constant during the withdrawal or recharge of groundwater from an aquifer, the following equation could be applied:
where Δ
σ′ = change of effective stress.
3.2. Model Setup
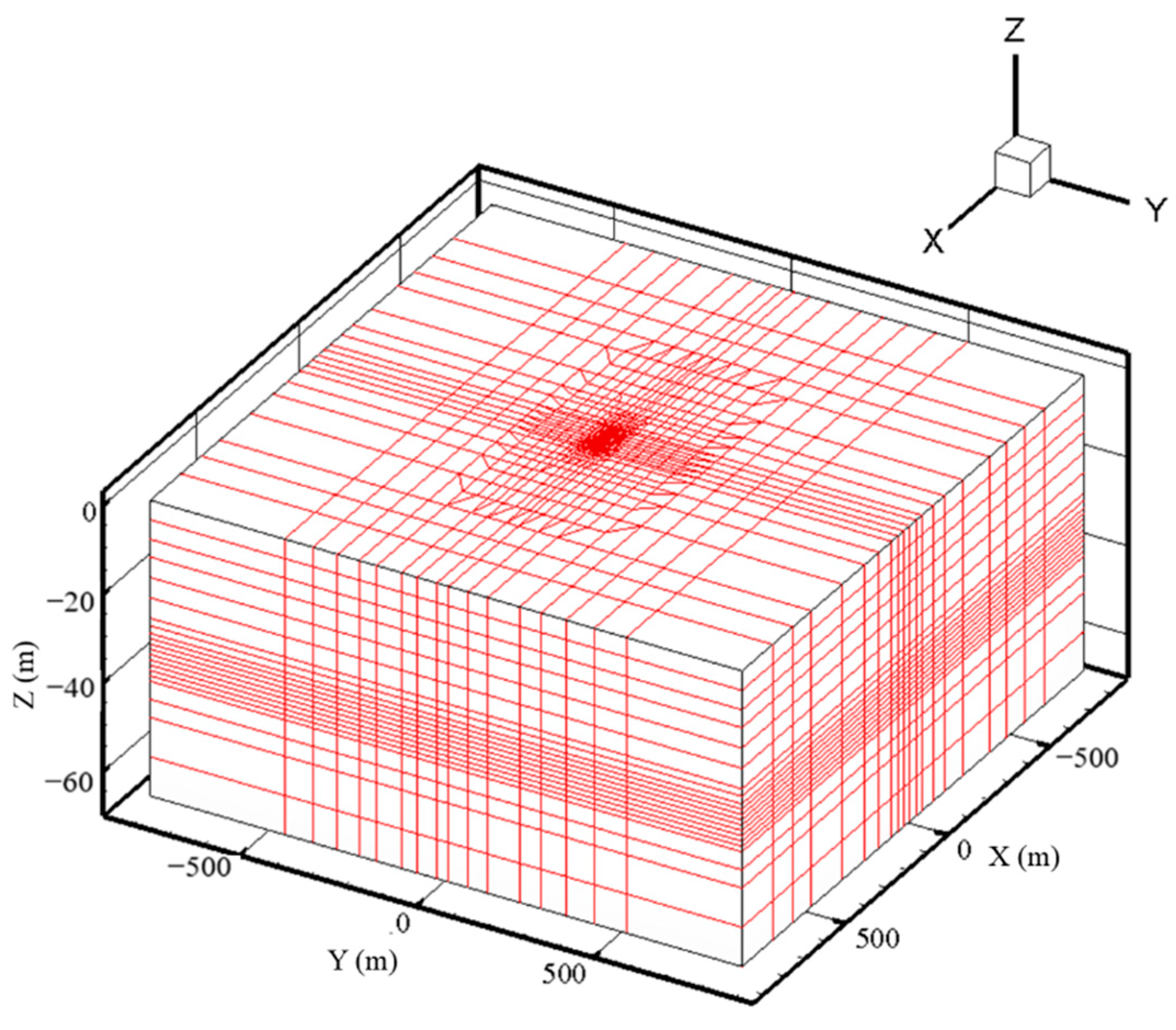
The plan size of the numerical model is required to be larger than the influence radius of dewatering. The length and width of the numerical model is 1670 m, and the depth is 66.7 m, which is the buried depth of the bottom face of layer AdIII.
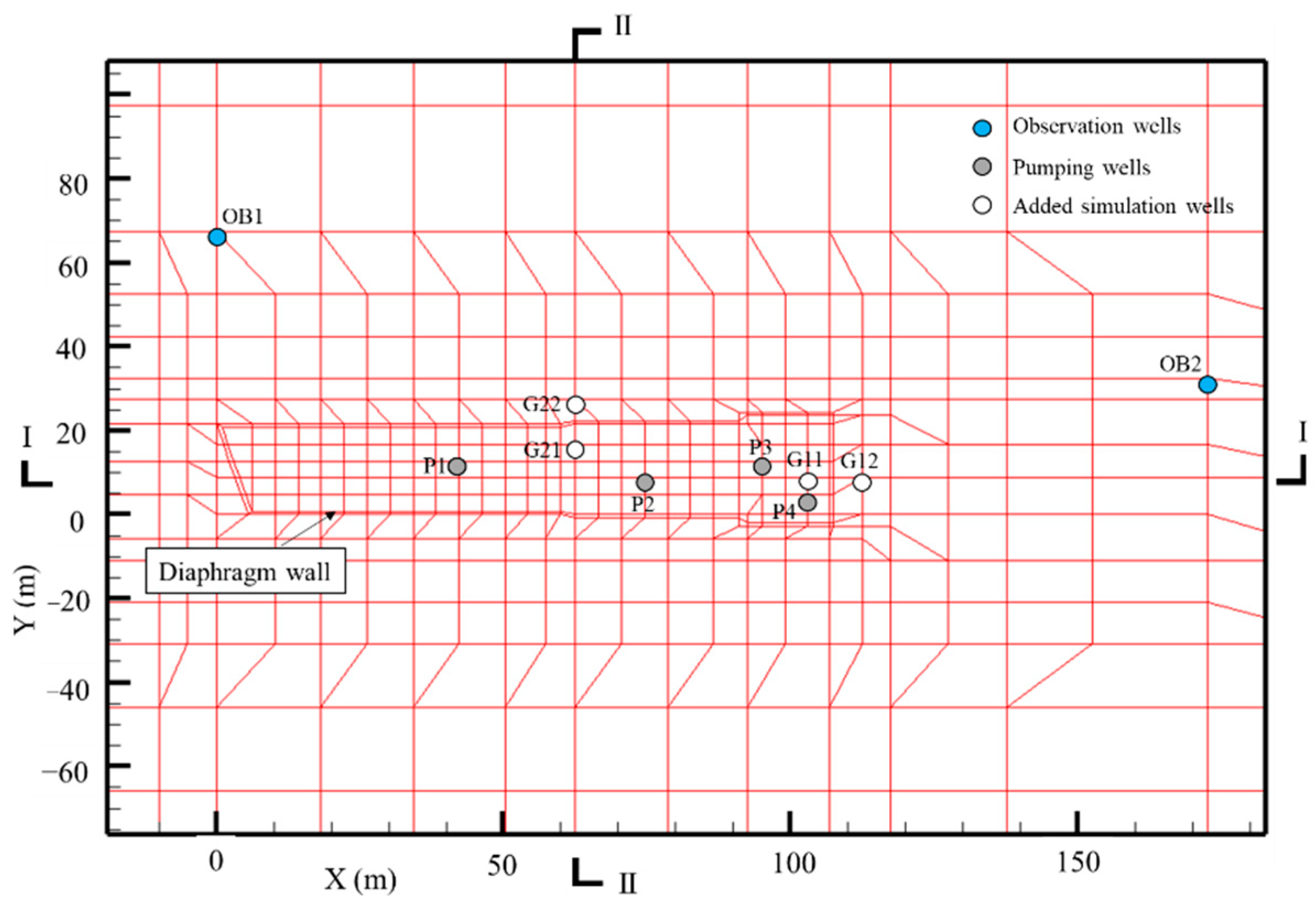
Figure 4 shows the three-dimensional model domain and the grid mesh. The number of nodes and elements in each plane is 1126 and 1148, respectively. The mesh size inside the foundation pit is 5 m × 5 m, and that is gradually enlarged to about 100 m × 100 m at the boundary of the model. The plan view of local enlarged mesh inside the foundation pit is presented in
Figure 5.
Figure 6 shows the profile of section II-II. The soil layer related to the construction is subdivided into 21 layers vertically. The total number of nodes and elements of the numerical model are 24,772 and 24,108, respectively.
The placement of the diaphragm wall, pumping and observation wells is shown in
Figure 5 according to the actual engineering case. Points G11, G12, G21 and G22 were added for further discussion of the simulation results. The initial groundwater level of Aq01, AqI and AqII layer is −0.5 m, −1.0 m and −2.8 m respectively. The groundwater level of four lateral boundaries is set as fixed hydraulic head boundary, which is equal to the initial groundwater level. The bottom boundary is set as the confining boundary.
3.3. Soil Parameters
Initial soil parameters in
Figure 2 are applied in the numerical model to simulate the pumping test. Then the soil parameters are inversed by fitting the results of the simulation to the observed data. When the results fit well enough and the maximum deviation between the measured data and simulated data is less than 5%, the parameters are thought to be appropriate for use in the simulation process. The final soil parameters determined by the aforementioned steps are tabulated in
Table 2.
3.4. Model Verification
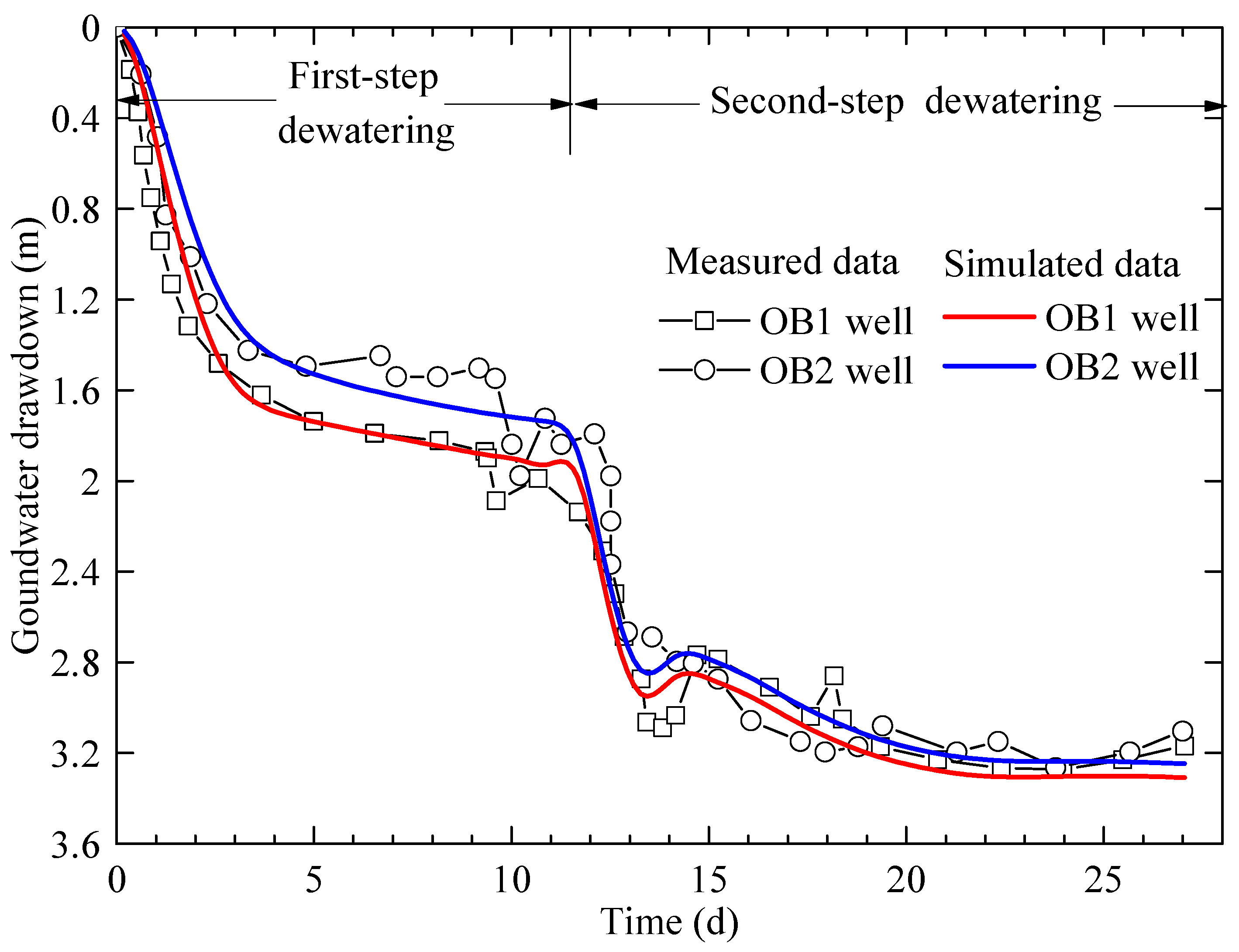
The comparison between measured data and simulated data is shown in
Figure 7. As shown in
Figure 7, the simulated groundwater drawdown decreases synchronously with the measured data. For the first step of dewatering, groundwater drawdown of observation wells OB1 and OB2 was 1.93 m and 1.74 m respectively, and that for simulated data was about 1.99 m and 1.72 m, of which the deviation is 3.1% and 1.2%. For the second step of dewatering, the final drawdown of wells OB1 and OB2 was 3.23 m and 3.20 m, and the simulated data was 3.30 m and 3.22 m. The deviation of the final drawdown was 2.2% and 0.63% respectively. These results demonstrate that the simulated results fit the measured data reasonably.
3.5. Simulation Results
To analyze the effect between the buried depth of the diaphragm wall and the anisotropic permeability of the dewatering aquifer, the penetrating depth of the diaphragm wall into the dewatering aquifer (D) and the ratio of horizontal and vertical hydraulic conductivity in dewatering confined aquifer (RC) are varied. The thickness of the dewatering confined aquifer (Ta) is set as 10.8 m in this case. D ranges from 0 to 10.8 m with an increment of 1.2 m, and RC changes from 1 to 10 with an increment of 1.
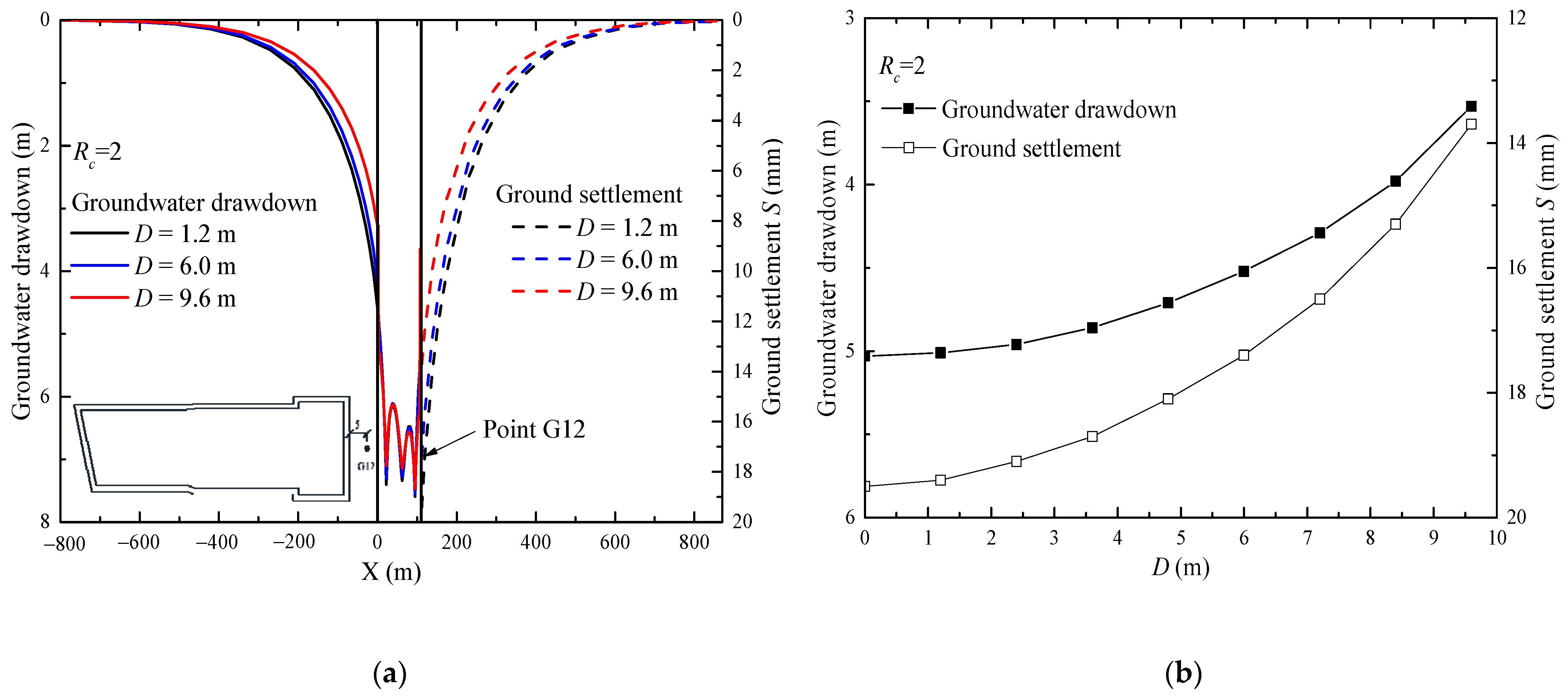
Figure 8a shows the groundwater drawdown and ground settlement with different values of
D when
RC equals 2. Groundwater drawdown outside the pit is obviously smaller than that inside the pit. The groundwater drawdown and ground settlement after dewatering of point G12, which is 5 m away outside the diaphragm wall is shown in
Figure 8b. With the increasing of
D, groundwater drawdown at point G12 decreases from 5.03 m (
D = 0 m) to 3.53 m (
D = 9.6 m). Ground settlement at point G12 decreases from 19.5 mm (
D = 0 m) to 13.70 mm (
D = 9.6 m). Both groundwater drawdown and ground settlement decrease gently initially and then change quickly.
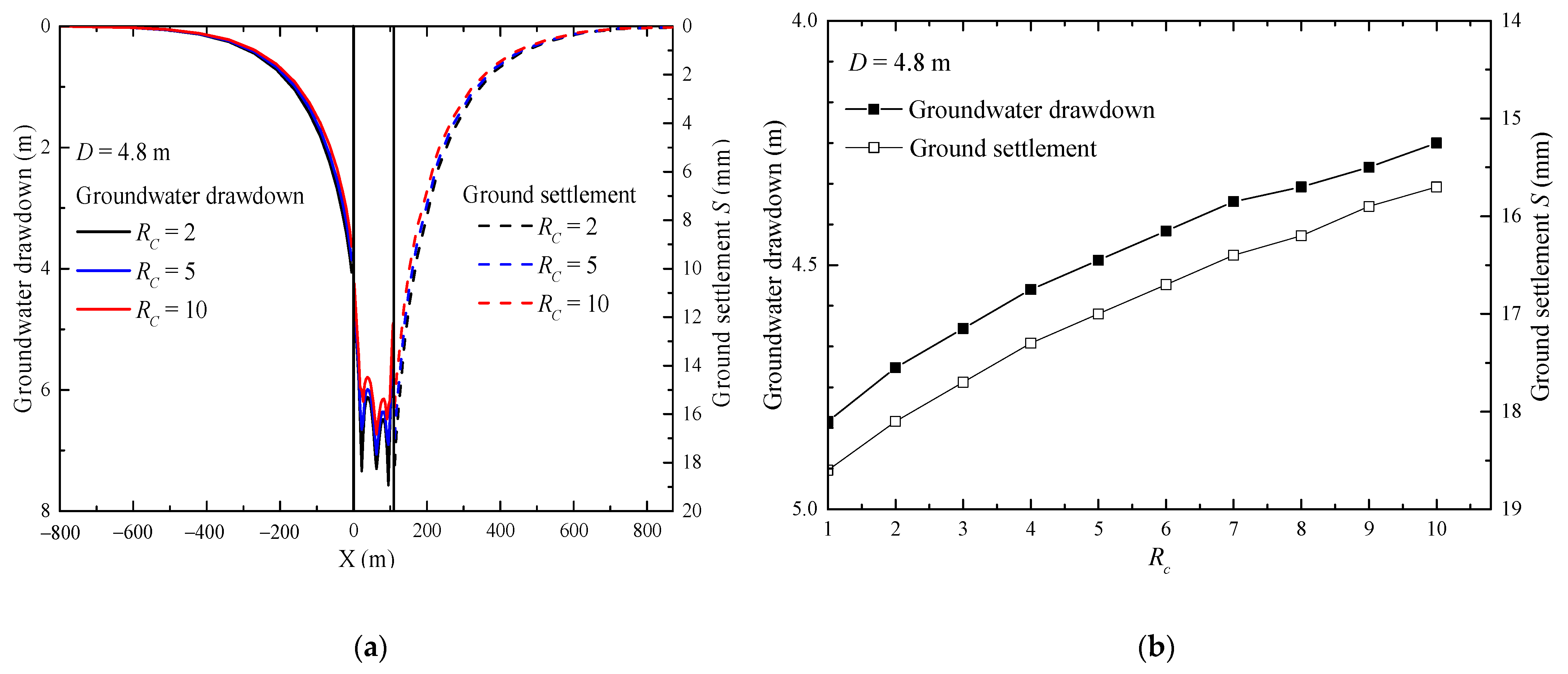
Figure 9a presents the groundwater drawdown and ground settlement with different value of
RC when
D is 4.8 m. Groundwater drawdown at point G12 is 4.71 m when
RC is 2 and 4.25 m when
RC is 10. Due to the decrease of vertical hydraulic conductivity, water supply from the boundary is more difficult which results in the decrease of groundwater drawdown and reduction of ground settlement outside the pit. The ground settlement at point G12 is 18.6 mm when
RC is 1 and 15.7 mm when
RC is 10. Moreover, comparing the change of groundwater drawdown and ground settlement outside the pit under different value of
D and
RC, the influence of
D on the groundwater drawdown outside the pit is much larger than that of
RC.
4. Discussion
4.1. Groundwater Drawdown at Two Sides of Diaphragm Wall
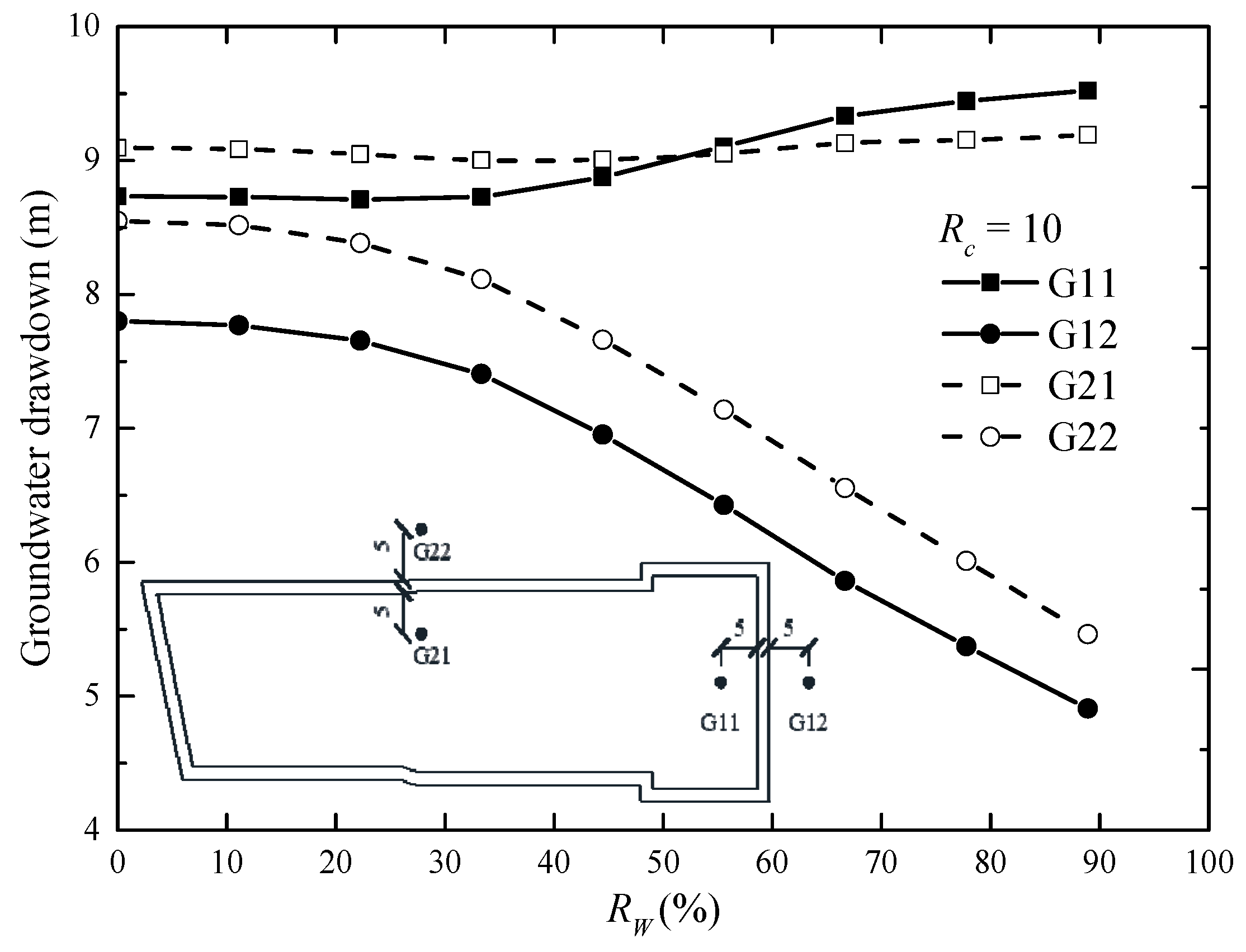
G11 with G12, and G21 with G22 are two groups of points at two sides of the diaphragm wall, of which the distance from diaphragm wall is 5 m.
Figure 10 shows the groundwater drawdown at two sides of the diaphragm wall when
RC is 10 with different
RW, which is defined as the ratio of
D to
Ta.
With the increasing of
RW, the seepage path lengthens and the blocking effect is more. Therefore, the supply volume from outside to inside the pit decreases, which results in decreased drawdown outside the pit obviously. Due to the drawdown inside the pit being required to stay the same, the drawdown inside the pit (G11 and G21) varies slightly. For example, the drawdown of G11 ranges from 9.52 m (
RW = 88.9%) to 8.73 m (
RW = 0), and the variation is 0.79 m. Drawdown of G12 ranges from 4.91 m (
RW = 88.9%) to 7.80 m (
RW = 0), and the variation is 2.89 m. Moreover, the effect of dewatering is dissymmetry in the rectangle foundation pit. The ground drawdown outside the pit along the short side (e.g., G12) is larger than that along the long side (e.g., G22) [
46,
47].
Approximate hydraulic gradient at two sides of the diaphragm wall (Δi) is defined as the quotient of the division of the difference in groundwater drawdown by seepage distance between the group of observation wells outside and inside the pit. Due to the seepage distance between G11 and G12 the well is a curve bypassing the bottom of the diaphragm wall, which is difficult to simulate accurately. Therefore, approximate seepage distance is calculated as the polyline length, which starts from the middle of the well filter outside the pit to the bottom of the diaphragm wall, and then to the middle of the well filter inside the pit. In the discussion process, Δi between observation well G11 and G12, and G21 and G22 is calculated.
4.2. Penetrating Depth of Diaphragm Wall
Figure 11 presents the relationship between Δ
i and
RW when
RC changes from 1 to 10. All the curves can be fitted by the Boltzmann curve, which is widely used in the simulation of different fields [
48,
49] and can be divided into three parts: initial gradual part (Part-I), middle sharp part (Part-II) and final gentle part (Part-III). With the increasing of
RW, Δ
i increases gradually, due to the blocking effect of the diaphragm wall on the groundwater seepage being stronger. When
D is larger than the filter length of pumping well, drawdown inside the pit changes little while drawdown outside decreases sharply, and this results in the sharp increase of Δ
i in Part-II. When
RW keeps increasing, since the difference of drawdown at two sides of diaphragm wall keeps constant while the seepage distance is much longer, Δ
i increases gently at the Part-III.
However, the fitted curve is different when comparing RC ranges from 4 to 10 with RC ranges from 1 to 3. Part-III is not so specific when RC ranges from 1 to 3, since the permeability anisotropy is not obvious enough. Vertical hydraulic conductivity is close to the horizontal conductivity and the water supply from outside is relatively easy, which shortens the seepage distance relatively. When RC ranges from 4 to 10, Part-III can be distinguished obviously, due to the difficulty of vertical seepage.
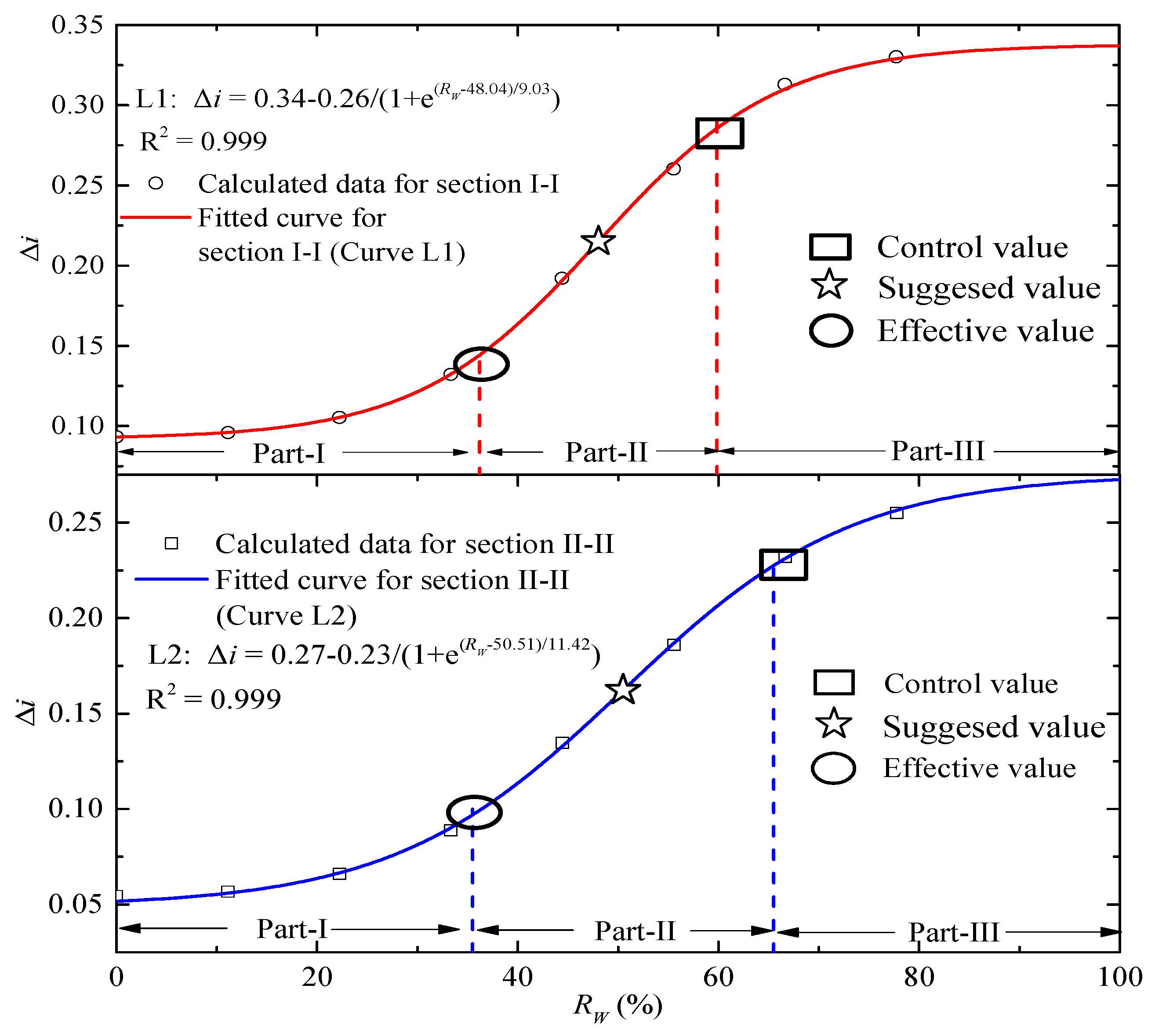
Figure 12 presents the relationship between Δ
i and
RW when
RC is 10 on section I-I and II-II, which is fitted by the Boltzmann curve. The x-coordinate of the maximum and minimum value of the second derivative of the curve is defined as the effective and control value of
RW, which are the demarcation points of the three parts. With the increase of
RW, Δ
i also increases due to the blocking effect of the diaphragm wall. Since
DW is above the bottom of the pumping wells filter, the increase of Δ
i is gradual. When
DW is over the effective value, Δ
i increases quickly, and the x-coordinate of the largest acceleration point (the contra-flexure point) is defined as the suggested value. If
RW is over the control value, drawdown at G11 increases and that at G12 decreases, while the seepage distance also increases and this results in the little increment of Δ
i.
As is shown in
Figure 12, the effective, suggested and control value of
RW is 36.2%, 48.0% and 59.9% for section I-I, and 35.9%, 50.6% and 65.4% for section II-II, respectively. By a comprehensive consideration of Δ
i on two sections, the effective, suggested and control value of
RW is 37%, 51% and 66% when
RC is 10.
4.3. Ratio of Horizontal and Vertical Hydraulic Conductivity
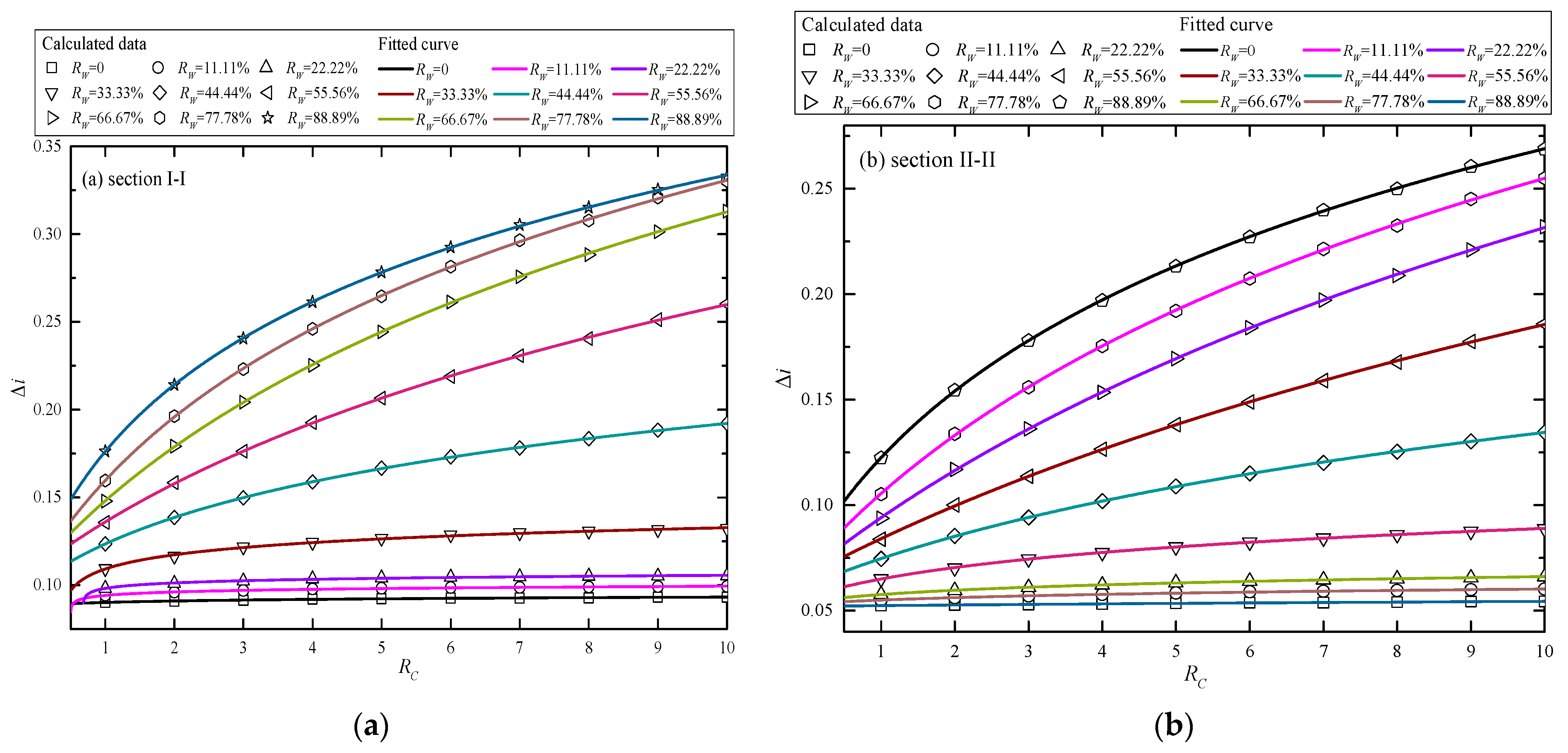
The relationship between Δ
i and
RC when
RW changes from 0 to 88.89% is shown in
Figure 13. Δ
i increases with the increase of
RC at all curves, because the permeability in vertical direction reduces and water supply from outside to inside is less. Therefore, the difference value of drawdown on the two sides of the diaphragm wall increases. When
RW is less than 33.33%, the increment of Δ
i is slight and the acceleration is slow. Since the buried depth of the diaphragm wall is above the filter of the pumping wells, the blocking effect is not obvious and drawdown at the two sides of the diaphragm wall varies little. When
RW is larger than 33.33%, the blocking effect of the diaphragm wall is obvious and the variation of Δ
i increases obviously.
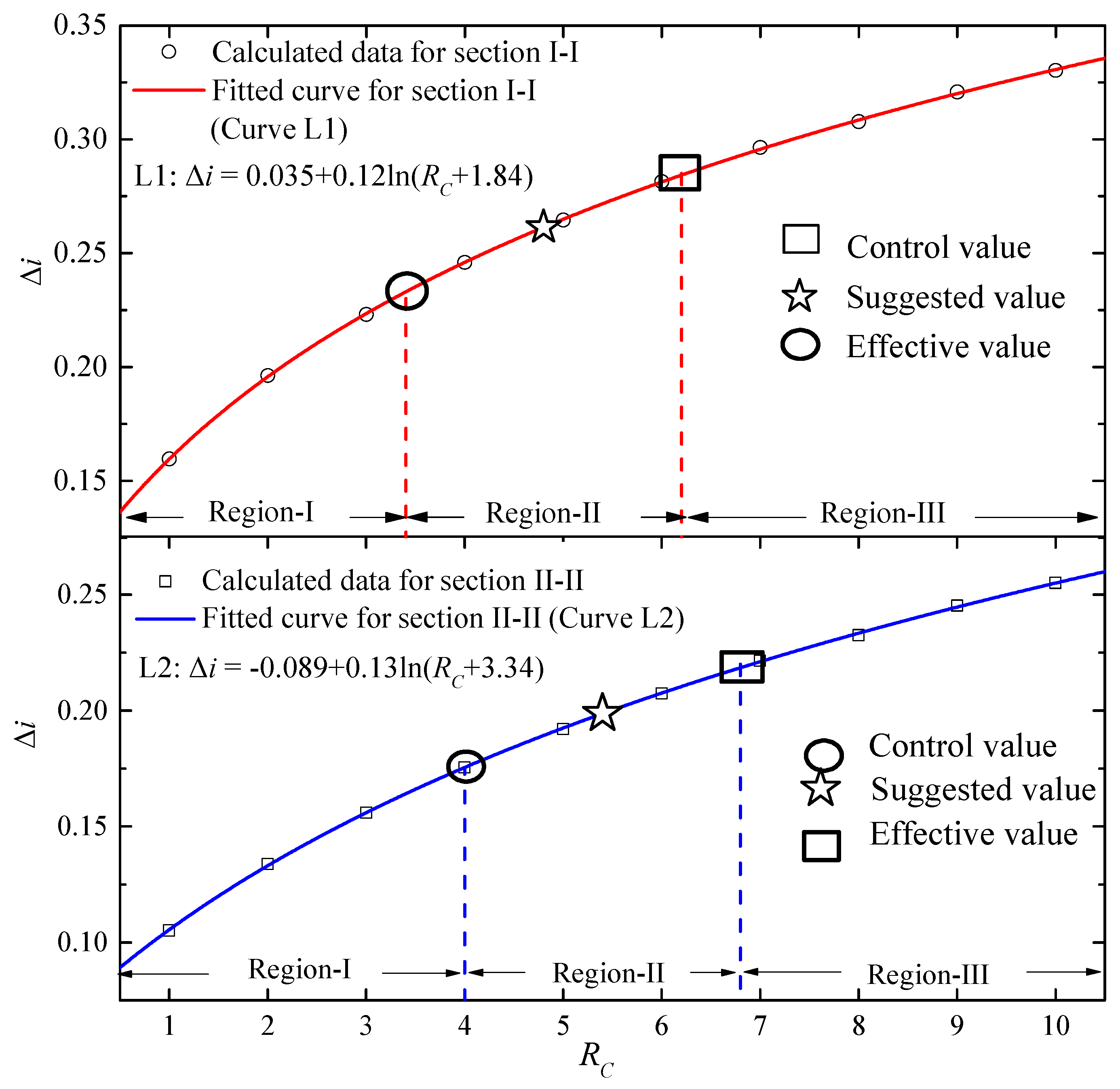
Figure 14 presents the relationship between Δ
i and
RC when
RW is 77.78%, of which all the relationship can be fitted by logarithmic curve. Groundwater supply from outside to inside requires flow from the bottom of the diaphragm wall, which means vertical permeability is important for the seepage process. Because of the large value of
RC and low vertical hydraulic conductivity, groundwater supply becomes difficult and Δ
i increases. The acceleration of Δ
i decreases, and due to the decrease of vertical hydraulic conductivity is limited.
Three regions are divided on the curve: poor effect region (Region-I), general effect region (Region-II) and good effect region (Region-III). The x-coordinate of demarcation points of three parts are defined as the effective value and control value, which represents the variation degree of Δi as 60% and 85%.
When RC is smaller than the effective value, Δi is small. The groundwater drawdown outside the pit is large and the environmental effect due to foundation dewatering is adverse. When RC is over the control value, water supply is difficult and the environment effect is good. If RC of the dewatering aquifer in the engineering field is small, some measurements can be adopted to increase RC to control the environment effect. By comprehensive consideration of economy and construction technology, the suggested value should be recommended. The suggested value is defined as the x-coordinate of midpoint of effective and control value. The effective, suggested and control value of RC is 3.4, 4.8 and 5.2 for section I-I, and those values are 4.0, 5.4 and 6.8 for section II-II when RW is 77.78%.
4.4. Relationship Between RW and RC
To determine the common relationship between control, suggested and effective
RW and
RC, all cases are conducted and the relationship is shown in
Figure 15. The control and suggested value of
RW decreases with the increase of
RC, while the effective value of
RW increases with the increase of
RC. All the relationships between
RW and
RC can be fitted by the logarithmic function, of which the characteristic is that the curve changes quickly firstly and the acceleration decreases. By the fitted equation, it is convenient to calculate the control, suggested and effective value of
RW according to different values of
RC.
For example, if the engineering is located at the place where the anisotropic permeability is not obvious, such as RC is 1.5, the control, suggested and effective value of RW for section I-I is 80.1%, 55.8% and 31.6% respectively. Those values are 93.9%, 63.9% and 34.2% for section II-II. Therefore, RW is recommended to be approximately 64% when RC is 1.5. As per the dissymmetry effect of the foundation pit mentioned above, control and suggested value of RW on section II-II is larger than that on section I-I, since the drawdown outside the diaphragm wall on section II-II is larger and drawdown inside the diaphragm wall is close.
5. Conclusions
This paper investigates the reasonable buried depth of diaphragm walls considering the anisotropic permeability of the dewatering aquifer for the control of groundwater drawdown outside the pit during foundation dewatering. The relationship among approximate hydraulic gradient at two sides of the diaphragm wall (Δi), the ratio of the penetrating depth of diaphragm wall and the thickness of the dewatering aquifer (RW), the ratio of horizontal and vertical hydraulic conductivity in dewatering confined aquifer (RC) are analyzed by numerical simulation based on an engineering case in Shanghai. The following conclusions can be obtained from this study:
(1) Δi increases with the increasing of RW, due to the increased blocking effect of the diaphragm wall. The relationship between Δi and RW can be fitted by the Boltzmann curve, which can be divided into three parts: initial gradual part, middle sharp part and final gentle part. The suggested value of RW is defined as the x-coordinate of the contra-flexure point of the curve. By comprehensive considering of Δi on two sections along the long and short sides of the foundation pit, the suggested value of RW is 51% when RC is 10.
(2) Δi increases with the increasing of RC, because the smaller vertical permeability makes the supply of groundwater from outside to inside the pit more difficult. The relationship between Δi and RC can be fitted by the logarithmic function, which also can be divided into three parts: poor effect part, general effect part and good effect part. X-coordinate of demarcation points of three parts are defined as the effective and control value of RC. The suggested value of RC is defined as the midpoint of effective and control value.
(3) If RC is small, measurements should be adopted to increase RC to the suggested value. By a comprehensive considering of Δi on two sections along the long and short sides of the foundation pit, suggested value of RC is 5.4 when RW is 77.78%.
(4) The relationship between the control, suggested and effective value of RW with RC is fitted by logarithmic function, and these values of RW can be calculated by the values of RC. By comprehensive consideration of the two sections along the long and short sides of the foundation pit, the suggested value of RW ranges from 48% to 65% when RC ranges from 1 to 10.
(5) This study proposes an optimized method to search suggested RW and RC, which can be used in foundation pit dewatering engineering in layered soil to obtain well dewatering effects and reduce environmental effects. Certainly, the specific value of suggested RW and RC may change in different engineering projects considering the different geometrical characteristics and hydrogeological strata in different place.
Author Contributions
Conceptualization, X.-w.W. and Y.-s.X.; methodology, Y.-s.X.; software, X.-w.W.; writing—original draft preparation, X.-w.W.; writing—review and editing, X.-w.W. and Y.-s.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (NSFC) (Grant No. 41877213). This financial support is gratefully acknowledged.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This study does not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liao, S.M.; Wei, S.F.; Shen, S.L. Structural responses of existing metro stations to adjacent deep excavations in Suzhou, China. J. Perform. Constr. Facil. ASCE 2016, 30, 04015089. [Google Scholar] [CrossRef]
- Liu, X.X.; Shen, S.L.; Xu, Y.S.; Yin, Z.Y. Analytical approach for time-dependent groundwater inflow into shield tunnel face in confined aquifer. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 655–673. [Google Scholar] [CrossRef]
- Tan, Y.; Wei, B.; Lu, Y.; Yang, B. Is basal reinforcement essential for long and narrow subway excavation bottoming out in Shanghai soft clay? J. Geotech. Geoenviron. Eng. ASCE 2019, 145, 05019002. [Google Scholar] [CrossRef]
- Liu, L.H.; Lei, M.F.; Cao, C.Y.; Shi, C.H. Dewatering Characteristics and Inflow Prediction of Deep Foundation Pits with Partial Penetrating Curtains in Sand and Gravel Strata. Water 2019, 11, 2182. [Google Scholar] [CrossRef]
- Xu, Y.S.; Shen, S.L.; Du, Y.J. Geological and hydrogeological environment in Shanghai with geohazards to construction and maintenance of infrastructures. Eng. Geol. 2009, 109, 241–254. [Google Scholar] [CrossRef]
- Xu, Y.S.; Shen, J.S.; Wu, H.N.; Zhang, N. Risk and impacts on the environment of free-phase biogas in Quaternary deposits along the coastal region of Shanghai. Ocean Eng. 2017, 137, 129–137. [Google Scholar] [CrossRef]
- Xu, Y.S.; Shen, J.S.; Zhou, A.N.; Arulrajan, A. Geological and hydrogeological environment with geohazards during underground construction in Hangzhou: A review. Arab. J. Geosci. 2018, 11, 1–18. [Google Scholar] [CrossRef]
- Zeng, C.F.; Xue, X.L.; Zheng, G.; Xue, T.Y.; Mei, G.X. Responses of retaining wall and surrounding ground to pre-excavation dewatering in an alternated multi-aquifer-aquitard system. J. Hydrol. 2018, 559, 609–626. [Google Scholar] [CrossRef]
- Zeng, C.F.; Zheng, G.; Xue, X.L.; Mei, G.X. Combined recharge: A method to prevent ground settlement induced by redevelopment of recharge wells. J. Hydrol. 2019, 568, 1–11. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, Y.Z.; Luo, L.H.; Liu, S.Q.; Sun, W.J.; Zeng, Y.F. Quantitative evaluation and prediction of water inrush vulnerability from aquifers overlying coal seams in Donghuantuo Coal Mine, China. Environ. Earth Sci. 2015, 74, 1429–1437. [Google Scholar] [CrossRef]
- Wang, J.X.; Liu, X.T.; Xiang, J.D.; Jiang, Y.H.; Feng, B. Laboratory model tests on water inrush in foundation pit bottom. Environ. Earth Sci. 2016, 75, 1–13. [Google Scholar] [CrossRef]
- Wang, W.; Faybishenko, B.; Jiang, T.; Dong, J.; Li, Y. Seepage Characteristics of a Single Ascending Relief Well Dewatering an Overlying Aquifer. Water 2020, 12, 919. [Google Scholar] [CrossRef]
- Xu, Y.S.; Ma, L.; Shen, S.L.; Sun, W.J. Evaluation of land subsidence by considering underground structures that penetrate the aquifers of Shanghai, China. Hydrogeol. J. 2012, 20, 1623–1634. [Google Scholar] [CrossRef]
- Cai, J.; Wang, P.; Shen, H.; Su, Y.; Huang, Y. Water Level Prediction of Emergency Groundwater Source and Its Impact on the Surrounding Environment in Nantong City, China. Water 2020, 12, 3529. [Google Scholar] [CrossRef]
- Pujades, E.; De Simone, S.; Carrera, J.; Vázquez-Suñé, E.; Jurado, A. Settlements around pumping wells: Analysis of influential factors and a simple calculation procedure. J. Hydrol. 2017, 548, 225–236. [Google Scholar] [CrossRef]
- Song, J.X.; Nie, X.H.; Zhang, J.Y. Prediction Technology of Adjacent Underground Pipelines Damage Caused by Excavations Dewatering. Build. Sci. 2014, 15, 74–79. (In Chinese) [Google Scholar]
- Tan, Y.; Lu, Y. Responses of shallowly buried pipelines to adjacent deep excavations in Shanghai soft ground. J. Pipel. Syst. Eng. Pract. ASCE 2018, 9, 05018002. [Google Scholar] [CrossRef]
- Wu, H.N.; Shen, S.L.; Yang, J. Identification of tunnel settlement caused by land subsidence in soft deposit of Shanghai. J. Perform. Constr. Facil. ASCE 2017, 31, 04017092. [Google Scholar] [CrossRef]
- Zhang, X.S.; Wang, J.X.; Wong, H.; Leo, C.J.; Liu, Q.; Tang, Y.Q.; Yan, X.L.; Sun, W.H.; Huang, Z.Q.; Hao, X.H. Land subsidence caused by internal soil erosion owing to pumping confined aquifer groundwater during the deep foundation construction in Shanghai. Nat. Hazards 2013, 69, 473–489. [Google Scholar] [CrossRef]
- Wu, Y.X.; Shen, J.S.; Chen, W.C.; Hino, T. Semi-analytical solution to pumping test data with barrier, wellbore storage, and partial penetration effects. Eng. Geol. 2017, 226, 44–51. [Google Scholar] [CrossRef]
- Pujades, E.; Vázquez-Suñé, E.; Carrera, J.; Jurado, A. Dewatering of a deep excavation undertaken in a layered soil. Eng. Geol. 2014, 178, 15–27. [Google Scholar] [CrossRef]
- Doan, L.V.; Lehane, B.M. Axial capacity of bored piles in very stiff intermediate soils. Can. Geotech. J. 2019, 57, 1417–1426. [Google Scholar] [CrossRef]
- Ma, L.; Xu, Y.S.; Shen, S.L.; Sun, W.J. Evaluation of the hydraulic conductivity of aquifers with piles. Hydrogeol. J. 2014, 22, 371–382. [Google Scholar] [CrossRef]
- Jiao, J.J.; Leung, C.; Ding, G.P. Changes to the groundwater system, from 1888 to present, in a highly-urbanized coastal area in Hong Kong, China. Hydrogeol. J. 2008, 16, 1527–1539. [Google Scholar] [CrossRef]
- Vilarrasa, V.; Carrera, J.; Jurado, A.; Pujades, E.; Vázquez-Suñé, E. A methodology for characterizing the hydraulic effectiveness of an annular low permeability barrier. Eng. Geol. 2011, 120, 68–80. [Google Scholar] [CrossRef]
- Shen, S.L.; Xu, Y.S. Numerical evaluation of land subsidence induced by groundwater pumping in Shanghai. Can. Geotech. J. 2011, 48, 1378–1392. [Google Scholar] [CrossRef]
- Shen, S.L.; Wu, Y.X.; Misra, A. Calculation of head difference at two sides of a cut-off barrier during excavation dewatering. Comput. Geotech. 2017, 91, 192–202. [Google Scholar] [CrossRef]
- Xu, Y.S.; Wu, H.N.; Wang, Z.F.; Yang, T.L. Dewatering induced subsidence during excavation in a Shanghai soft deposit. Environ. Earth Sci. 2017, 76, 351–365. [Google Scholar] [CrossRef]
- Xu, Y.S.; Yan, X.X.; Shen, S.L.; Zhou, A.N. Experimental investigation on the blocking of groundwater seepage from a waterproof curtain during pumped dewatering in an excavation. Hydrogeol. J. 2019, 27, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wang, J.H.; Chen, J.J.; Li, M.G. Numerical study on the responses of groundwater and strata to pumping and recharge in a deep confined aquifer. J. Hydrol. 2017, 548, 342–352. [Google Scholar] [CrossRef]
- Kawano, S.; Katayama, I.; Okazaki, K. Permeability anisotropy of serpentinite and fluid pathways in a subduction zone. Geology 2011, 39, 939–942. [Google Scholar] [CrossRef]
- Wang, K.; Zang, J.; Wang, G.; Zhou, A.T. Anisotropic permeability evolution of coal with effective stress variation and gas sorption: Model development and analysis. Int. J. Coal Geol. 2014, 130, 53–65. [Google Scholar] [CrossRef]
- Li, Y.Q.; Zhou, X. Study on the effect of anisotropic permeability on the behavior of an excavation. Chin. J. Undergr. Space Eng. 2017, 13, 1250–1257. (In Chinese) [Google Scholar]
- Li, M.G.; Chen, J.J.; Xia, X.H.; Zhang, Y.Q.; Wang, D.F. Statistical and hydro-mechanical coupling analyses on groundwater drawdown and soil deformation caused by dewatering in a multi-aquifer-aquitard system. J. Hydrol. 2020, 589, 125365. [Google Scholar] [CrossRef]
- Shen, S.L.; Wu, Y.X.; Xu, Y.S.; Hino, T.; Wu, H.N. Evaluation of hydraulic parameters from pumping tests in multi-aquifers with vertical leakage in Tianjin. Comput. Geotech. 2015, 68, 196–207. [Google Scholar] [CrossRef]
- Lin, N.S. Calculation of the permeability coefficient for layer sand (silt) of Ningbo area. Build. Struct. 2010, 40, 303–306. (In Chinese) [Google Scholar]
- Wang, X.W.; Yang, T.L.; Xu, Y.S.; Shen, S.L. Evaluation of optimized depth of waterproof curtain to mitigate negative impacts during dewatering. J. Hydrol. 2019, 577, 123969. [Google Scholar] [CrossRef]
- Ni, J.C.; Cheng, W.C.; Ge, L. A simple data reduction method for pumping tests with tidal, partial penetration, and storage effects. Soils Found. 2013, 53, 894–902. [Google Scholar] [CrossRef]
- Wu, Y.X.; Shen, S.L.; Yuan, D.J. Characteristics of dewatering induced drawdown curve under barrier effect of retaining wall in aquifer. J. Hydrol. 2016, 539, 554–566. [Google Scholar] [CrossRef]
- Yin, Z.Y.; Jin, Y.F.; Shen, S.L.; Huang, H.W. An efficient optimization method for identifying parameters of soft structured clay by an enhanced genetic algorithm and elastic-viscoplastic model. Acta Geotech. 2017, 12, 849–867. [Google Scholar] [CrossRef]
- Yin, Z.Y.; Jin, Y.F.; Shen, J.S.; Hicher, P.Y. Optimization techniques for identifying soil parameters in geotechnical engineering: Comparative study and enhancement. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 70–94. [Google Scholar] [CrossRef]
- Yang, T.L. Analysis of the land subsidence impact of dewatering of deep foundation pits. Shanghai Land Resour. 2012, 33, 41–44. (In Chinese) [Google Scholar]
- Sun, L.; Ju, J.; Miao, J.F.; Xu, L.P.; Chen, L.R. Zoning for structural type of confined water bearing layer in Shanghai downtown. Shanghai Geol. 2010, 1, 15–19. (In Chinese) [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of Building Foundation; GB50007-2011; MOHURD: Beijing, China, 2011. (In Chinese)
- Wu, Y.X.; Shen, S.L.; Wu, H.N.; Xu, Y.S.; Yin, Z.Y.; Sun, W.J. Environmental protection using dewatering technology in a deep confined aquifer beneath a shallow aquifer. Eng. Geol. 2015, 196, 59–70. [Google Scholar] [CrossRef]
- Ou, C.Y.; Chiou, D.C.; Wu, T.S. Three-dimensional finite element analysis of deep excavations. J. Geotech. Eng. 1996, 122, 337–345. [Google Scholar] [CrossRef]
- Finno, R.J.; Blackburn, J.T.; Roboski, J.F. Three-Dimensional Effects for Supported Excavations in Clay. J. Geotech. Geoenviron. Eng. 2007, 133, 30–36. [Google Scholar] [CrossRef]
- Green, M.E. A Resonance Model Gives the Response to Membrane Potential for an Ion Channel. J. Theor. Biol. 1998, 193, 475–483. [Google Scholar] [CrossRef]
- Janneke, K.; Dirk, V.D.E.; Drona, K.; Ruud, V.D.S.; Remko, B. Lattice Boltzmann simulation of 2D and 3D non-Brownian suspensions in Couette flow. Chem. Eng. Sci. 2006, 61, 858–873. [Google Scholar]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).