An Automated Approach to Groundwater Quality Monitoring—Geospatial Mapping Based on Combined Application of Gaussian Process Regression and Bayesian Information Criterion
Abstract
1. Introduction
2. Materials and Methods
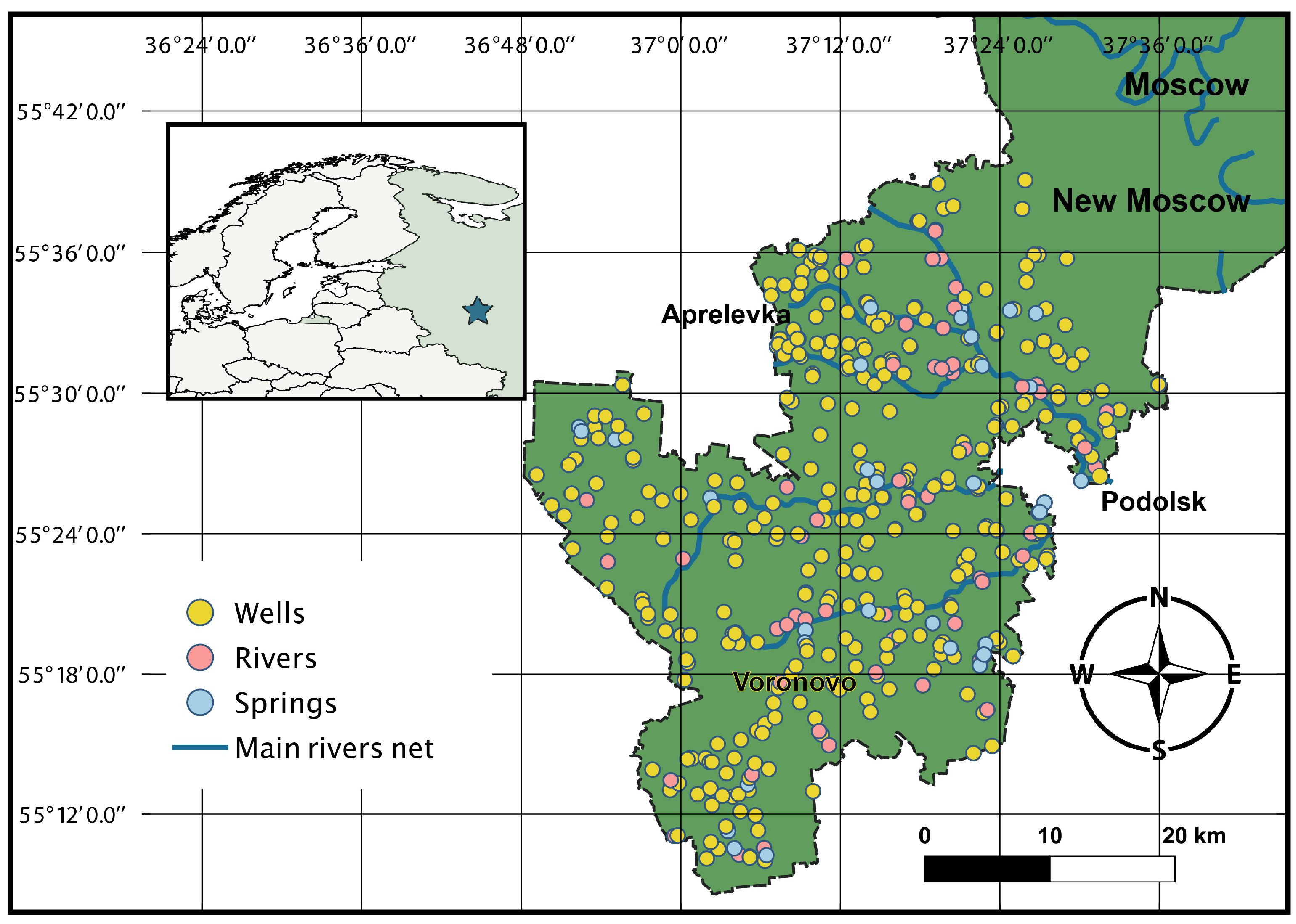
2.1. Site Description and Available Dataset
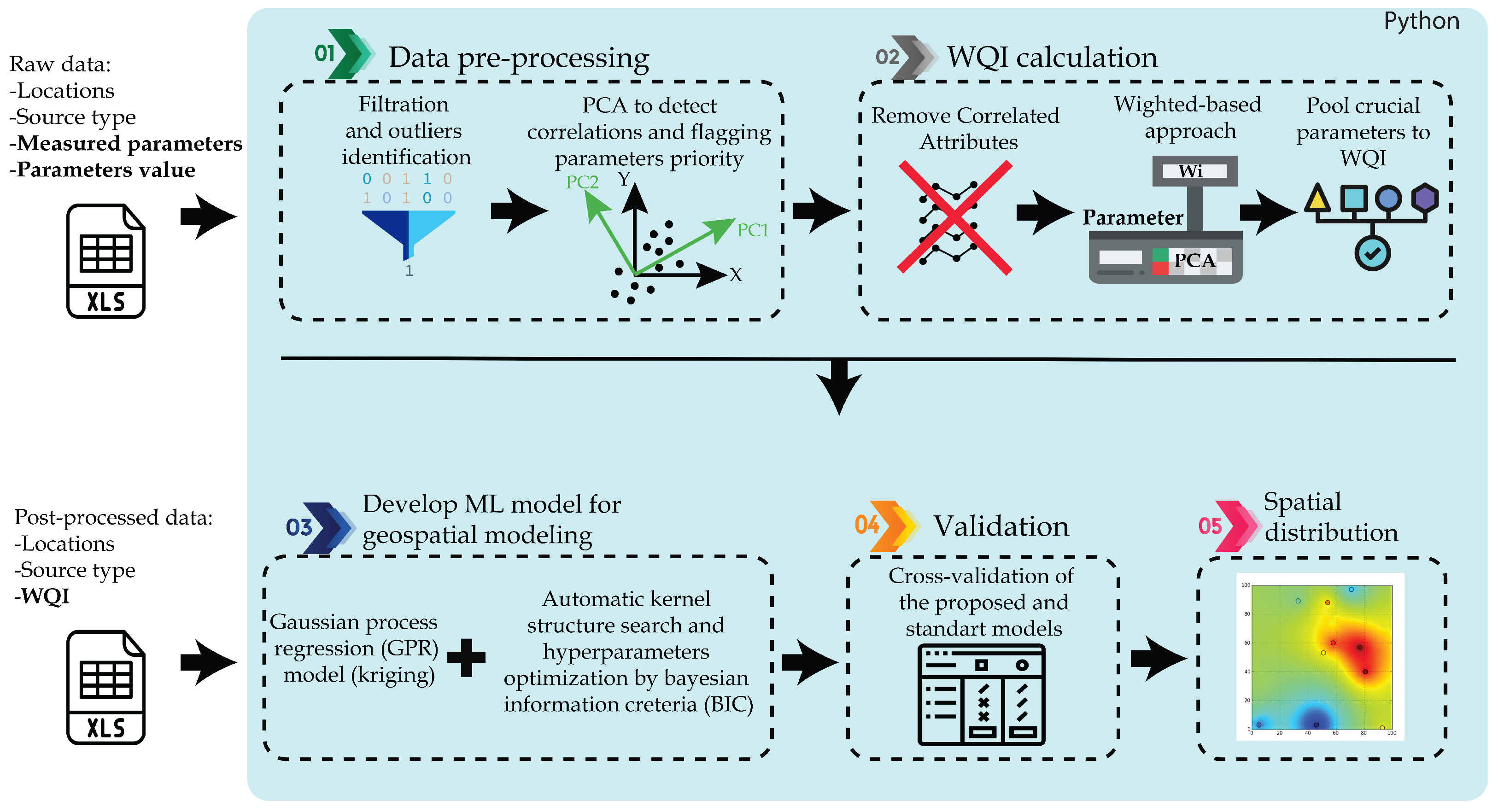
2.2. Data Preparation and Methodology
2.3. Water Quality Index Calculation Based on PCA and Weighted Factors
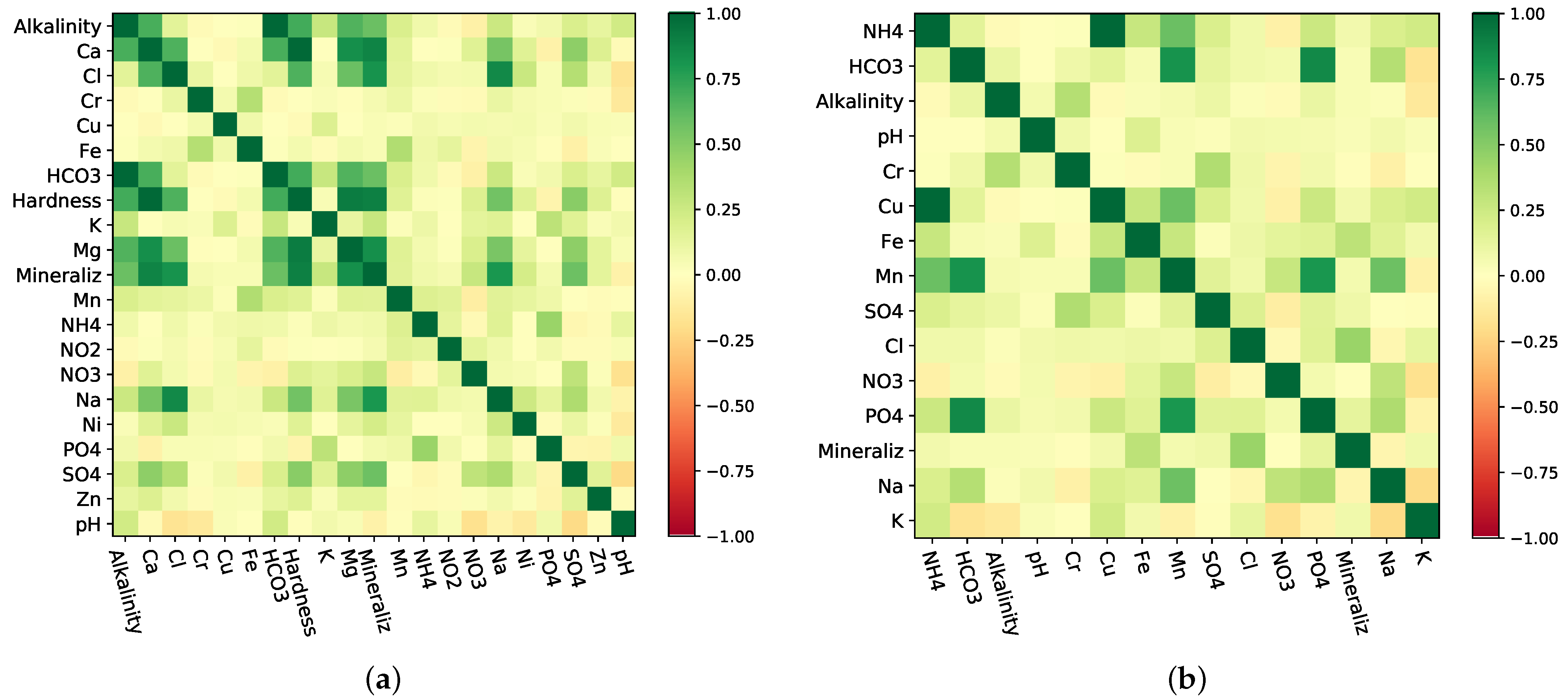
2.3.1. PCA Theory
2.3.2. Construction of WQI Based on PCA
2.4. Machine Learning Approach for Geospatial Modelling of WQI with Automatic Kernel Detection
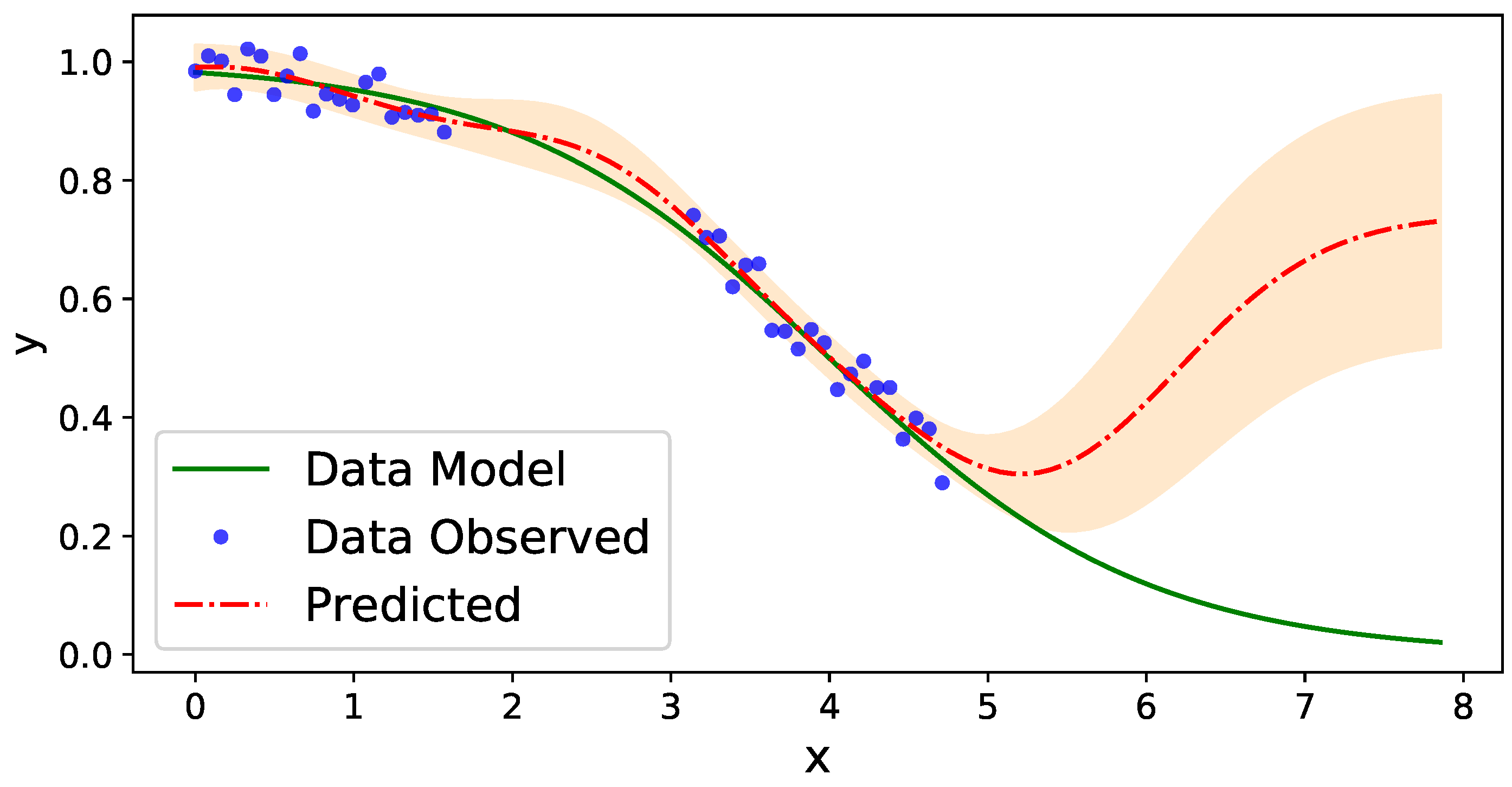
2.4.1. Gaussian Process Regression: General Overview of the Methodology
2.4.2. Hyper-Parameters Selection Using Bayesian Information Criterion
2.4.3. Universal and Ordinary Kriging
2.5. Approach to Geospatial Modelling
2.6. Validation Procedure
2.7. Software
3. Results and Discussion
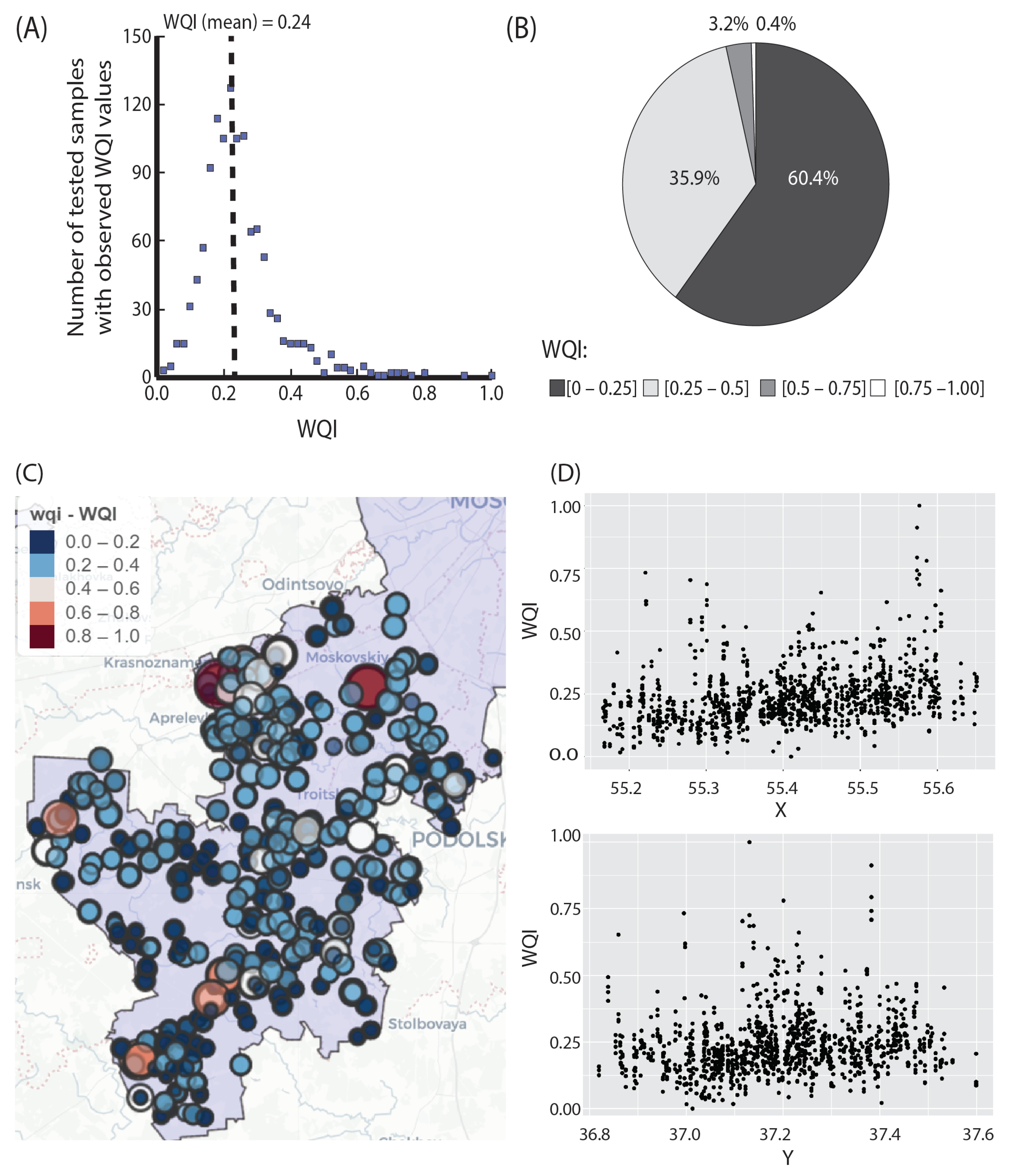
3.1. PCA-Based Weighted Water Quality Index
3.2. Geospatial Modeling
3.3. PCA-Weighted Approach in WQI Construction
3.4. Automatic Approach to Geospatial Mapping
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WQI | Water Quality Index |
| PCA | Principal Component Analysis |
| GPR | Gaussian Process Regression |
| BIC | Bayesian Information Criterion |
| OK | Ordinary Kriging |
| UK | Universal Kriging |
| ML | Machine Learning |
| FA | Factor Analysis |
| SVM | Support Vector Machine |
| ANN | Artificial Neural Network |
| ABC | Approximate Bayesian Computation |
| MLE | Maximum Likelihood Estimation |
| RMSE | Root Mean Square Error |
| DBSCAN | Density-based spatial clustering of applications with noise |
References
- Álvarez, X.; Valero, E.; Santos, R.M.; Varandas, S.; Fernandes, L.S.; Pacheco, F.A.L. Anthropogenic nutrients and eutrophication in multiple land use watersheds: Best management practices and policies for the protection of water resources. Land Use Policy 2017, 69, 1–11. [Google Scholar] [CrossRef]
- Brahney, J.; Mahowald, N.; Ward, D.S.; Ballantyne, A.P.; Neff, J.C. Is atmospheric phosphorus pollution altering global alpine Lake stoichiometry? Glob. Biogeochem. Cycles 2015, 29, 1369–1383. [Google Scholar] [CrossRef]
- Kashulin, N.A.; Dauvalter, V.A.; Denisov, D.B.; Valkova, S.A.; Vandysh, O.I.; Terentjev, P.M.; Kashulin, A.N. Selected aspects of the current state of freshwater resources in the Murmansk region, Russia. J. Environ. Sci. Health Part A 2017, 52, 921–929. [Google Scholar] [CrossRef]
- Dudgeon, D.; Arthington, A.H.; Gessner, M.O.; Kawabata, Z.I.; Knowler, D.J.; Lévêque, C.; Naiman, R.J.; Prieur-Richard, A.H.; Soto, D.; Stiassny, M.L.; et al. Freshwater biodiversity: Importance, threats, status and conservation challenges. Biol. Rev. 2006, 81, 163–182. [Google Scholar] [CrossRef]
- Foley, J.A.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K.; et al. Global consequences of land use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef] [PubMed]
- Tietenberg, T.H.; Lewis, L. Environmental and Natural Resource Economics; Routledge: London, UK, 2016. [Google Scholar]
- Tscheikner-Gratl, F.; Bellos, V.; Schellart, A.; Moreno-Rodenas, A.; Muthusamy, M.; Langeveld, J.; Clemens, F.; Benedetti, L.; Rico-Ramirez, M.A.; de Carvalho, R.F.; et al. Recent insights on uncertainties present in integrated catchment water quality modelling. Water Res. 2019, 150, 368–379. [Google Scholar] [CrossRef] [PubMed]
- Zwahlen, F. Vulnerability and Risk Mapping for the Protection of Carbonate (Karst) Aquifers; Office for Official Publications of the European Communities: Luxembourg, 2003. [Google Scholar]
- Hamdan, I.; Margane, A.; Ptak, T.; Wiegand, B.; Sauter, M. Groundwater vulnerability assessment for the karst aquifer of Tanour and Rasoun springs catchment area (NW-Jordan) using COP and EPIK intrinsic methods. Environ. Earth Sci. 2016, 75, 1474. [Google Scholar] [CrossRef]
- Daly, D.; Dassargues, A.; Drew, D.; Dunne, S.; Goldscheider, N.; Neale, S.; Popescu, I.; Zwahlen, F. Main concepts of the “European approach” to karst-groundwater-vulnerability assessment and mapping. Hydrogeol. J. 2002, 10, 340–345. [Google Scholar] [CrossRef]
- Ramakrishnaiah, C.; Sadashivaiah, C.; Ranganna, G. Assessment of water quality index for the groundwater in Tumkur Taluk, Karnataka State, India. J. Chem. 2009, 6, 523–530. [Google Scholar] [CrossRef]
- Sun, W.; Xia, C.; Xu, M.; Guo, J.; Sun, G. Application of modified water quality indices as indicators to assess the spatial and temporal trends of water quality in the Dongjiang River. Ecol. Indic. 2016, 66, 306–312. [Google Scholar] [CrossRef]
- Tripathi, M.; Singal, S.K. Use of Principal Component Analysis for parameter selection for development of a novel Water Quality Index: A case study of river Ganga India. Ecol. Indic. 2019, 96, 430–436. [Google Scholar] [CrossRef]
- Sakizadeh, M.; Mirzaei, R.; Ghorbani, H. Support vector machine and artificial neural network to model soil pollution: A case study in Semnan Province, Iran. Neural Comput. Appl. 2017, 28, 3229–3238. [Google Scholar] [CrossRef]
- Nourani, V.; Alizadeh, F.; Roushangar, K. Evaluation of a two-stage SVM and spatial statistics methods for modeling monthly river suspended sediment load. Water Resour. Manag. 2016, 30, 393–407. [Google Scholar] [CrossRef]
- Yang, K.; Yu, Z.; Luo, Y.; Yang, Y.; Zhao, L.; Zhou, X. Spatial and temporal variations in the relationship between lake water surface temperatures and water quality—A case study of Dianchi Lake. Sci. Total. Environ. 2018, 624, 859–871. [Google Scholar] [CrossRef] [PubMed]
- Dai, F.; Zhou, Q.; Lv, Z.; Wang, X.; Liu, G. Spatial prediction of soil organic matter content integrating artificial neural network and ordinary kriging in Tibetan Plateau. Ecol. Indic. 2014, 45, 184–194. [Google Scholar] [CrossRef]
- Mitrović, T.; Antanasijević, D.; Lazović, S.; Perić-Grujić, A.; Ristić, M. Virtual water quality monitoring at inactive monitoring sites using Monte Carlo optimized artificial neural networks: A case study of Danube river (Serbia). Sci. Total. Environ. 2019, 654, 1000–1009. [Google Scholar] [CrossRef] [PubMed]
- Ballabio, C.; Lugato, E.; Fernández-Ugalde, O.; Orgiazzi, A.; Jones, A.; Borrelli, P.; Montanarella, L.; Panagos, P. Mapping LUCAS topsoil chemical properties at European scale using Gaussian process regression. Geoderma 2019, 355, 113912. [Google Scholar] [CrossRef]
- Keskin, H.; Grunwald, S. Regression kriging as a workhorse in the digital soil mapper’s toolbox. Geoderma 2018, 326, 22–41. [Google Scholar] [CrossRef]
- McLeod, L.; Bharadwaj, L.; Epp, T.; Waldner, C.L. Use of principal components analysis and kriging to predict groundwater-sourced rural drinking water quality in Saskatchewan. Int. J. Environ. Res. Public Health 2017, 14, 1065. [Google Scholar] [CrossRef]
- Keshtegar, B.; Mert, C.; Kisi, O. Comparison of four heuristic regression techniques in solar radiation modeling: Kriging method vs. RSM, MARS and M5 model tree. Renew. Sustain. Energy Rev. 2018, 81, 330–341. [Google Scholar] [CrossRef]
- Liu, H.; Yang, C.; Huang, M.; Wang, D.; Yoo, C. Modeling of subway indoor air quality using Gaussian process regression. J. Hazard. Mater. 2018, 359, 266–273. [Google Scholar] [CrossRef]
- Cressie, N. The origins of kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Ebden, M. Gaussian processes: A quick introduction. arXiv 2015, arXiv:1505.02965. [Google Scholar]
- Van Stein, B.; Wang, H.; Kowalczyk, W.; Emmerich, M.; Bäck, T. Cluster-based Kriging approximation algorithms for complexity reduction. Appl. Intell. 2020, 50, 778–791. [Google Scholar] [CrossRef]
- Chiles, J.P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 731. [Google Scholar]
- Oliver, M.; Webster, R. A tutorial guide to geostatistics: Computing and modelling variograms and kriging. Catena 2014, 113, 56–69. [Google Scholar] [CrossRef]
- Aalto, J.; Pirinen, P.; Heikkinen, J.; Venäläinen, A. Spatial interpolation of monthly climate data for Finland: Comparing the performance of kriging and generalized additive models. Theor. Appl. Climatol. 2013, 112, 99–111. [Google Scholar] [CrossRef]
- Chica-Olmo, M.; Luque-Espinar, J.A.; Rodriguez-Galiano, V.; Pardo-Igúzquiza, E.; Chica-Rivas, L. Categorical Indicator Kriging for assessing the risk of groundwater nitrate pollution: The case of Vega de Granada aquifer (SE Spain). Sci. Total. Environ. 2014, 470, 229–239. [Google Scholar] [CrossRef]
- Al-Mudhafar, W.J. Bayesian kriging for reproducing reservoir heterogeneity in a tidal depositional environment of a sandstone formation. J. Appl. Geophys. 2019, 160, 84–102. [Google Scholar] [CrossRef]
- Pebesma, E.; Cornford, D.; Dubois, G.; Heuvelink, G.B.; Hristopulos, D.; Pilz, J.; Stöhlker, U.; Morin, G.; Skøien, J.O. INTAMAP: The design and implementation of an interoperable automated interpolation web service. Comput. Geosci. 2011, 37, 343–352. [Google Scholar] [CrossRef]
- Abdessalem, A.B.; Dervilis, N.; Wagg, D.J.; Worden, K. Automatic kernel selection for gaussian processes regression with approximate bayesian computation and sequential monte carlo. Front. Built Environ. 2017, 3, 52. [Google Scholar] [CrossRef]
- Megdal, S.B. Invisible water: The importance of good groundwater governance and management. npj Clean Water 2018, 1, 1–5. [Google Scholar] [CrossRef]
- Shishov, L.; Voinovich, N. Soils of Moscow Region and Their Use; Dokuchaev Soil Science Institute: Moscow, Russia, 2002. [Google Scholar]
- Dzhamalov, R.; Medovar, Y.A.; Yushmanov, I. Principles of MSW Landfill Sites’ Placement Depending on Geological and Hydrogeological Conditions of Territories (Based on Moscow Region). Water Resour. 2019, 46, S51–S58. [Google Scholar] [CrossRef]
- Klimanova, O.; Kolbowsky, E.; Illarionova, O. Impacts of urbanization on green infrastructure ecosystem services: The case study of post-soviet Moscow. Belg. Rev. Belg. Géographie 2018. [Google Scholar] [CrossRef]
- Pukalchik, M.; Shadrin, D.; Nikitin, A.; Jana, R.; Tregubova, P.; Matveev, S. Freshwater chemical properties for New Moscow region. 2020. Available online: https://figshare.com/articles/dataset/freshwater_chemical_properties_for_New_Moscow_region/10283225 (accessed on 2 February 2021).
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Richardson, M. Principal Component Analysis. 2009. Available online: http://www.dsc.ufcg.edu.br/~hmg/disciplinas/posgraduacao/rn-copin-2014.3/material/SignalProcPCA.pdf (accessed on 2 February 2021).
- Wall, M.E.; Rechtsteiner, A.; Rocha, L.M. Singular value decomposition and principal component analysis. In A Practical Approach to Microarray Data Analysis; Springer: Berlin/Heidelberg, Germany, 2003; pp. 91–109. [Google Scholar]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
- Cattell, R. The Scientific Use of Factor Analysis in Behavioral and Life Sciences; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Duvenaud, D.; Lloyd, J.R.; Grosse, R.; Tenenbaum, J.B.; Ghahramani, Z. Structure discovery in nonparametric regression through compositional kernel search. arXiv 2013, arXiv:1302.4922. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- MacCormack, K.E.; Brodeur, J.J.; Eyles, C.H. Evaluating the impact of data quantity, distribution and algorithm selection on the accuracy of 3D subsurface models using synthetic grid models of varying complexity. J. Geogr. Syst. 2013, 15, 71–88. [Google Scholar] [CrossRef]
- MacCormack, K.; Arnaud, E.; Parker, B.L. Using a multiple variogram approach to improve the accuracy of subsurface geological models. Can. J. Earth Sci. 2018, 55, 786–801. [Google Scholar] [CrossRef]
- Mueller, T.; Pusuluri, N.; Mathias, K.; Cornelius, P.; Barnhisel, R.; Shearer, S. Map quality for ordinary kriging and inverse distance weighted interpolation. Soil Sci. Soc. Am. J. 2004, 68, 2042–2047. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- GPy. GPy: A Gaussian Process Framework in Python. 2012. Available online: http://github.com/SheffieldML/GPy (accessed on 2 February 2021).
- Horton, R.K. An index number system for rating water quality. J. Water Pollut. Control. Fed. 1965, 37, 300–306. [Google Scholar]
- Esty, D.C.; Levy, M.; Srebotnjak, T.; De Sherbinin, A. Environmental Sustainability Index: Benchmarking National Environmental Stewardship; Yale Center for Environmental Law & Policy: New Haven, CT, USA, 2005; pp. 47–60. [Google Scholar]
- Mohd Ali, Z.; Ibrahim, N.A.; Mengersen, K.; Shitan, M.; Juahir, H. The Langat River water quality index based on principal component analysis. AIP Conf. Proc. 2013, 1522, 1322–1336. [Google Scholar] [CrossRef]
- Tyagi, S.; Sharma, B.; Singh, P.; Dobhal, R. Water quality assessment in terms of water quality index. Am. J. Water Resour. 2013, 1, 34–38. [Google Scholar] [CrossRef]
- Nardo, M.; Saisana, M.; Saltelli, A.; Tarantola, S. Tools for composite indicators building. Eur. Com. Ispra 2005, 15, 19–20. [Google Scholar]
- Tripathi, M.; Singal, S.K. Allocation of weights using factor analysis for development of a novel water quality index. Ecotoxicol. Environ. Saf. 2019, 183, 109510. [Google Scholar] [CrossRef]
- Hutcheson, G.D.; Sofroniou, N. The Multivariate Social Scientist: Introductory Statistics Using Generalized Linear Models; Sage: Thousand Oaks, CA, USA, 1999. [Google Scholar] [CrossRef]
- Ouyang, Y. Evaluation of river water quality monitoring stations by principal component analysis. Water Res. 2005, 39, 2621–2635. [Google Scholar] [CrossRef]
- Chen, Y.; Han, D. Water quality monitoring in smart city: A pilot project. Autom. Constr. 2018, 89, 307–316. [Google Scholar] [CrossRef]
- Gómez-Chova, L.; Muñoz-Marí, J.; Laparra, V.; Malo-López, J.; Camps-Valls, G. A review of kernel methods in remote sensing data analysis. In Optical Remote Sensing; Springer: Berlin/Heidelberg, Germany, 2011; pp. 171–206. [Google Scholar] [CrossRef]
- Lüscher, P.; Weibel, R. Exploiting empirical knowledge for automatic delineation of city centres from large-scale topographic databases. Comput. Environ. Urban Syst. 2013, 37, 18–34. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Z.; Li, D.; Cui, L. Data-driven soft sensor modeling for algal blooms monitoring. IEEE Sens. J. 2014, 15, 579–590. [Google Scholar] [CrossRef]

| Principal Components | Comp1 | Comp2 | Comp3 | Comp4 | Comp5 |
|---|---|---|---|---|---|
| Eigenvalues | 6.116 | 2.057 | 1.856 | 1.543 | 1.237 |
| Variance (%) | 29.12 | 9.79 | 8.84 | 7.35 | 5.89 |
| Cumulative variance (%) | 29.12 | 38.92 | 47.76 | 55.10 | 61.00 |
| Parameters loadings | |||||
| NH | 0.0794 | 0.0041 | 0.5602 | 0.0279 | −0.0603 |
| HCO | −0.0363 | 0.5385 | 0.0041 | 0.0229 | 0.0137 |
| Alkalinity | −0.0364 | 0.5386 | 0.0041 | 0.0228 | 0.0136 |
| pH | −0.1731 | 0.3074 | 0.2065 | −0.0889 | −0.1959 |
| Hardness of water | 0.2960 | 0.2583 | −0.1245 | −0.0123 | 0.0035 |
| Cr | 0.0076 | −0.0764 | −0.0718 | 0.5049 | 0.1270 |
| Cu | −0.1188 | 0.0103 | 0.0489 | 0.2093 | 0.4262 |
| Fe | −0.0179 | 0.0199 | −0.0408 | 0.6504 | −0.0269 |
| Mn | 0.0557 | 0.0913 | 0.1145 | 0.4557 | −0.1452 |
| Ni | 0.2217 | −0.1376 | −0.0030 | −0.1010 | −0.0475 |
| Zn | −0.0368 | 0.1017 | −0.1915 | 0.0638 | 0.1721 |
| SO | 0.1987 | −0.0145 | −0.1570 | −0.0894 | 0.3695 |
| Cl | 0.5033 | −0.1380 | 0.0726 | 0.0079 | −0.1002 |
| NO | 0.0666 | −0.1398 | −0.0800 | −0.1048 | 0.5048 |
| NO | 0.0518 | −0.0645 | 0.1705 | 0.1495 | 0.0442 |
| PO | 0.0223 | −0.0059 | 0.6047 | −0.0642 | 0.1163 |
| Mineralization | 0.3729 | 0.1255 | 0.0228 | −0.0215 | 0.1407 |
| Ca | 0.2973 | 0.2457 | −0.1414 | −0.0098 | −0.0152 |
| Mg | 0.2552 | 0.2604 | −0.0634 | −0.0169 | 0.0540 |
| Na | 0.4440 | −0.0817 | 0.1863 | 0.0101 | −0.0330 |
| K | −0.1235 | 0.1455 | 0.2777 | −0.0010 | 0.5150 |
| Parameter | Value |
|---|---|
| Gaussian kernel variance, | 0.0367 |
| Gaussian kernel length scale, l | 4.86 |
| Periodic kernel variance, | 0.0204 |
| Periodic kernel period, T | 5.67 |
| Periodic kernel length scale, s | 0.1 |
| 1 | 2 | 3 | 4 | 5 | Mean | std | ||
|---|---|---|---|---|---|---|---|---|
| Kriging with BIC | 0.729 | 0.487 | 0.609 | 0.641 | 0.702 | 0.637 | 0.098 | |
| approach | RMSE | 0.060 | 0.072 | 0.071 | 0.062 | 0.059 | 0.065 | 0.0063 |
| Ordinary Kriging | 0.580 | −0.075 | 0.599 | 0.625 | 0.575 | 0.461 | 0.300 | |
| Gaussian kernel | RMSE | 0.068 | 0.076 | 0.056 | 0.060 | 0.059 | 0.064 | 0.0085 |
| Universal Kriging | 0.610 | 0.014 | 0.604 | 0.646 | 0.622 | 0.499 | 0.271 | |
| Exponential kernel | RMSE | 0.070 | 0.077 | 0.056 | 0.060 | 0.058 | 0.064 | 0.0088 |
| Universal Kriging | 0.544 | −0.052 | 0.600 | 0.631 | 0.590 | 0.463 | 0.289 | |
| Gaussian kernel | RMSE | 0.071 | 0.076 | 0.055 | 0.059 | 0.058 | 0.064 | 0.0093 |
| Universal Kriging | −11.205 | −9.316 | −11.042 | −6.693 | −9.860 | −9.623 | 1.820 | |
| Polynomial kernel | RMSE | 0.129 | 0.113 | 0.109 | 0.097 | 0.103 | 0.110 | 0.0122 |
| Universal Kriging | 0.415 | −0.038 | 0.579 | 0.637 | 0.593 | 0.437 | 0.278 | |
| Periodic kernel | RMSE | 0.080 | 0.076 | 0.057 | 0.059 | 0.058 | 0.066 | 0.0114 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shadrin, D.; Nikitin, A.; Tregubova, P.; Terekhova, V.; Jana, R.; Matveev, S.; Pukalchik, M. An Automated Approach to Groundwater Quality Monitoring—Geospatial Mapping Based on Combined Application of Gaussian Process Regression and Bayesian Information Criterion. Water 2021, 13, 400. https://doi.org/10.3390/w13040400
Shadrin D, Nikitin A, Tregubova P, Terekhova V, Jana R, Matveev S, Pukalchik M. An Automated Approach to Groundwater Quality Monitoring—Geospatial Mapping Based on Combined Application of Gaussian Process Regression and Bayesian Information Criterion. Water. 2021; 13(4):400. https://doi.org/10.3390/w13040400
Chicago/Turabian StyleShadrin, Dmitrii, Artyom Nikitin, Polina Tregubova, Vera Terekhova, Raghavendra Jana, Sergey Matveev, and Maria Pukalchik. 2021. "An Automated Approach to Groundwater Quality Monitoring—Geospatial Mapping Based on Combined Application of Gaussian Process Regression and Bayesian Information Criterion" Water 13, no. 4: 400. https://doi.org/10.3390/w13040400
APA StyleShadrin, D., Nikitin, A., Tregubova, P., Terekhova, V., Jana, R., Matveev, S., & Pukalchik, M. (2021). An Automated Approach to Groundwater Quality Monitoring—Geospatial Mapping Based on Combined Application of Gaussian Process Regression and Bayesian Information Criterion. Water, 13(4), 400. https://doi.org/10.3390/w13040400







