Probabilistic Characterization of the Vegetated Hydrodynamic System Using Non-Parametric Bayesian Networks †
Abstract
:1. Introduction
| Study | Hydrodynamic Properties | Vegetation Characteristics | Drag Coefficient |
|---|---|---|---|
| Flume [34] | Regular waves m = 0.036–0.19 m | Polypropylene strips as artificial kelp m, 52 × 0.03 mm, = 1110–1490 m | – |
| Flume [6] | Used [34] | Used [34] | |
| Flume [35] | Used [34] | Used [34] and distinguished for rigid and flexible vegetation | Rigid Flex. |
| Flume [36] | Regular waves h = 0.4–1.0 m = 0.045–0.17 m | L. hyperborea m, mm, m | |
| Field (seagrass) [37] | Irregular waves h = 1–1.5 m m | Thalassia testundinum = 0.25–0.30 m, mm, m (Used relative velocity for drag calculation) | |
| Flume [8] | Both Regular & Irregular h = 0.3–0.8 m = 0.05–0.13 m (Reg.) = 0.03–0.13 m (Irreg.) | Posidonia oceanica m, mm, m | |
| Field (seagrass) [7] | Irregular waves 0.75–3.5 m 0.05–0.18 m | Zostera noltii m, m | |
| Field (Salt marsh) [38] | Irregular waves m m | Spartina alterniflora m, mm, m | |
| Field (Seagrass) [39] | Irregular waves (Storms) h = 6.5–16.5 m = 0.10–1.31 m | Posidonia oceanica m, mm, m | Used [8] |
| Field (Salt marsh) [40] | Irregular waves h = 0.4–0.82 m = 0.15–0.4 m | Spartina alterniflora m, mm, m | |
| Statistical [41] | Statistical evaluation of 35 studies | Statistical evaluation of kelp, seagrass, saltmarsh and mangroves | |
| Flume [42] Rigid Flexible | Regular waves h = 1.8–2.4 m = 0.4–0.5 m h = 0.4–1.0 m = 0.045–0.17 m | Posidonia oceanica (Polypropylene) m, mm, m Artificial seagrass (PVC strips) m, mm, m | |
| Flume [43] Rigid Flexible | Regular waves h = 0.4–0.7 m = 0.03–0.15 m Irregular waves h = 0.5–0.7 m = 0.03–0.10 m | Wooden cylinders (Rigid) = 0.48, 0.63 m, mm, m Spartina alterniflora (Flexible) m, mm, m Juncus roemerianus (Flexible) m, mm, m | Rigid Flexible |
| Flume [44] | Irregular waves h = 0.31–0.53 m = 0.05–0.19 m | Spartina alterniflora (Polyolefin tubes) = 0.41 m, mm, m | |
| Flume [45] | Regular waves & currents m = 0.04–0.20 m | Vegetation mimics (Wooden rods) m, mm, m | |
| Flume [11] | Irregular waves m = 0.2–0.7 m | Puccinellia maritima m, mm Elymus athericus m, mm | |
| Flume [46] | Both Regular & Irregular waves & currents m m (Regular) m (Irregular) Current vel. ms | Spartina anglica m, mm, m Puccinellia maritima m, mm, m | Irregular waves Irregular waves + current Irregular waves − current |
| Flume (Mangroves) [17] | Both Regular & Irregular m = 0.01–0.1 m Regular = 0.03–0.15 m Irreg. | Wooden cylinders (Rigid mangroves) m, mm, m | Used from [45] |
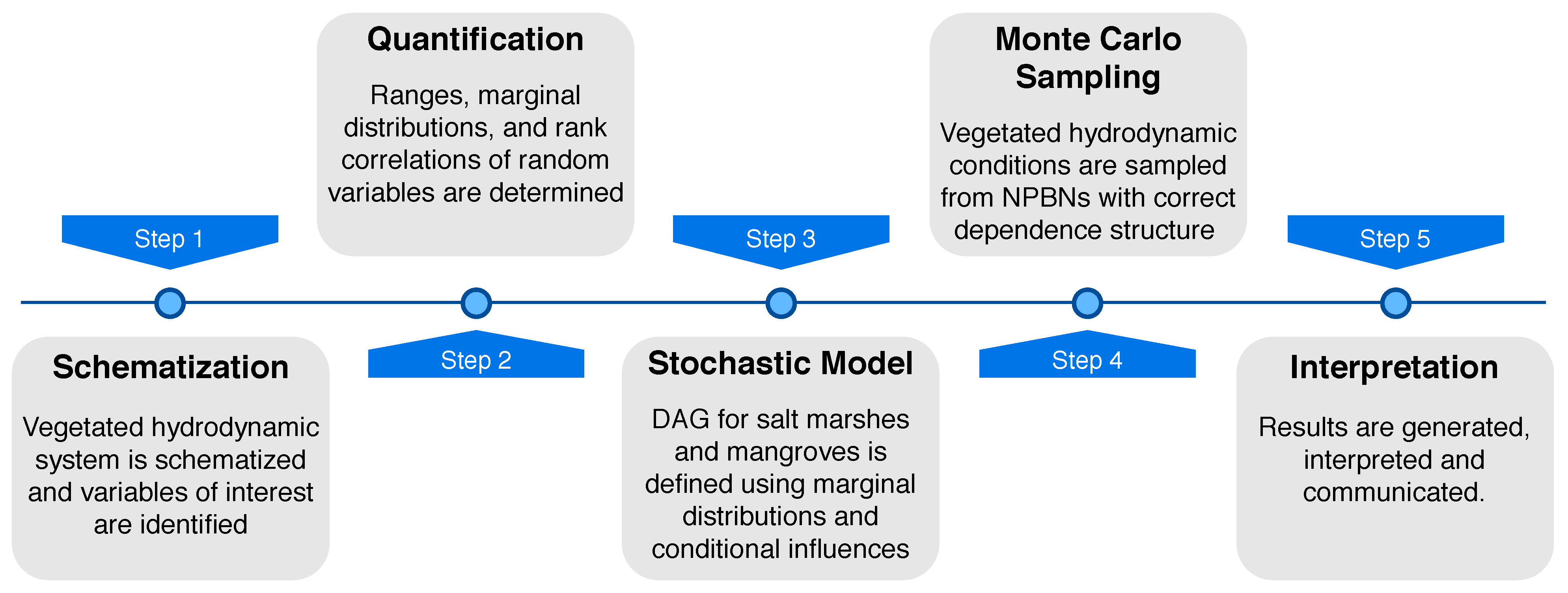
2. Methodology
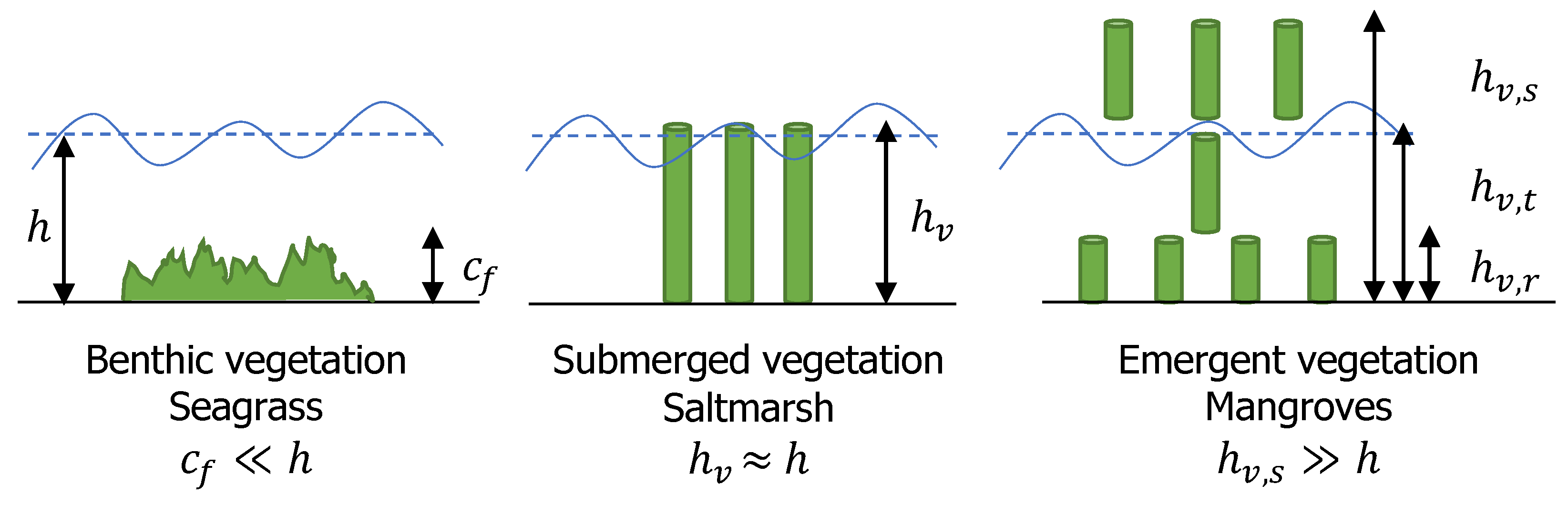
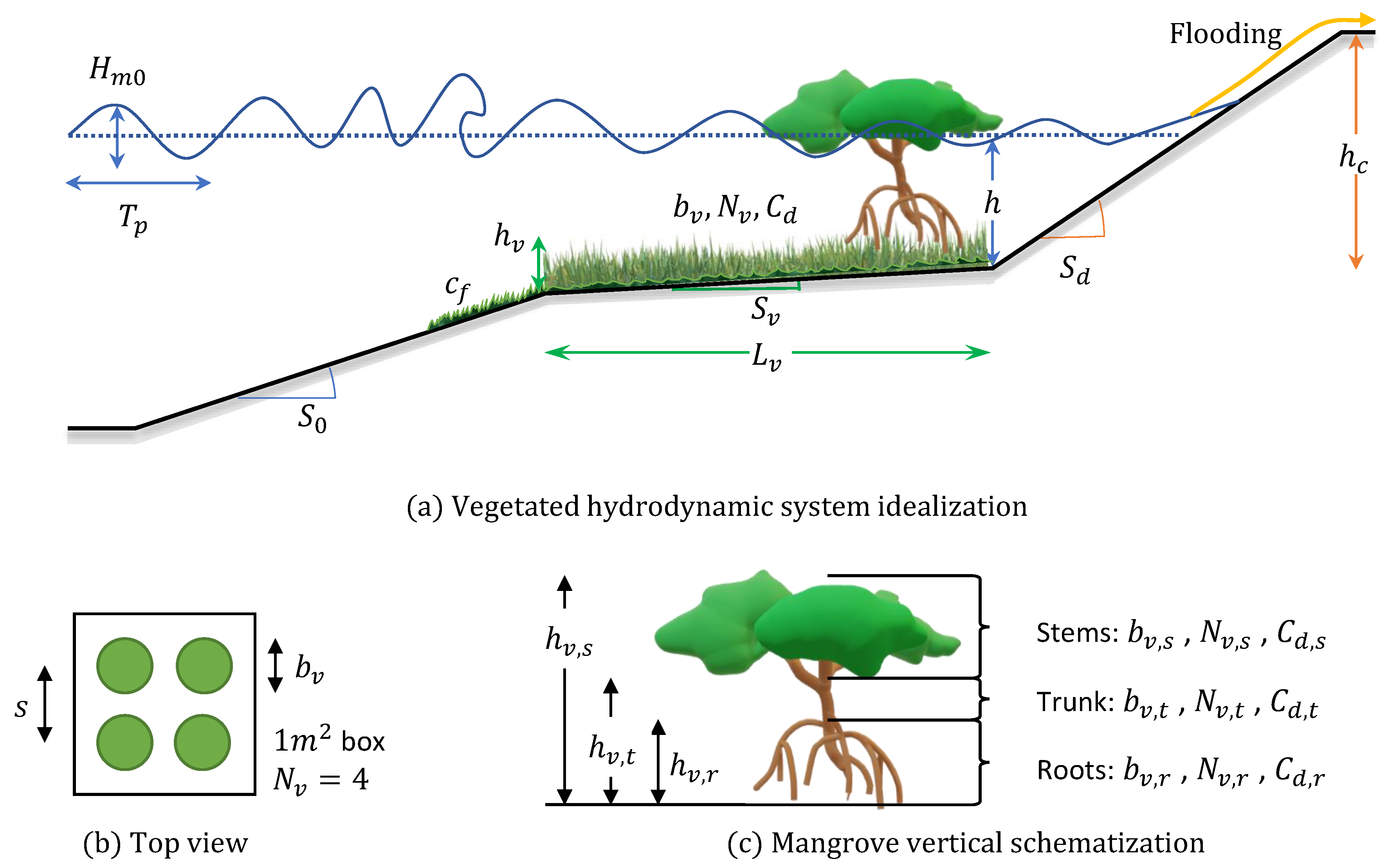
2.1. System Schematization and Parameterization
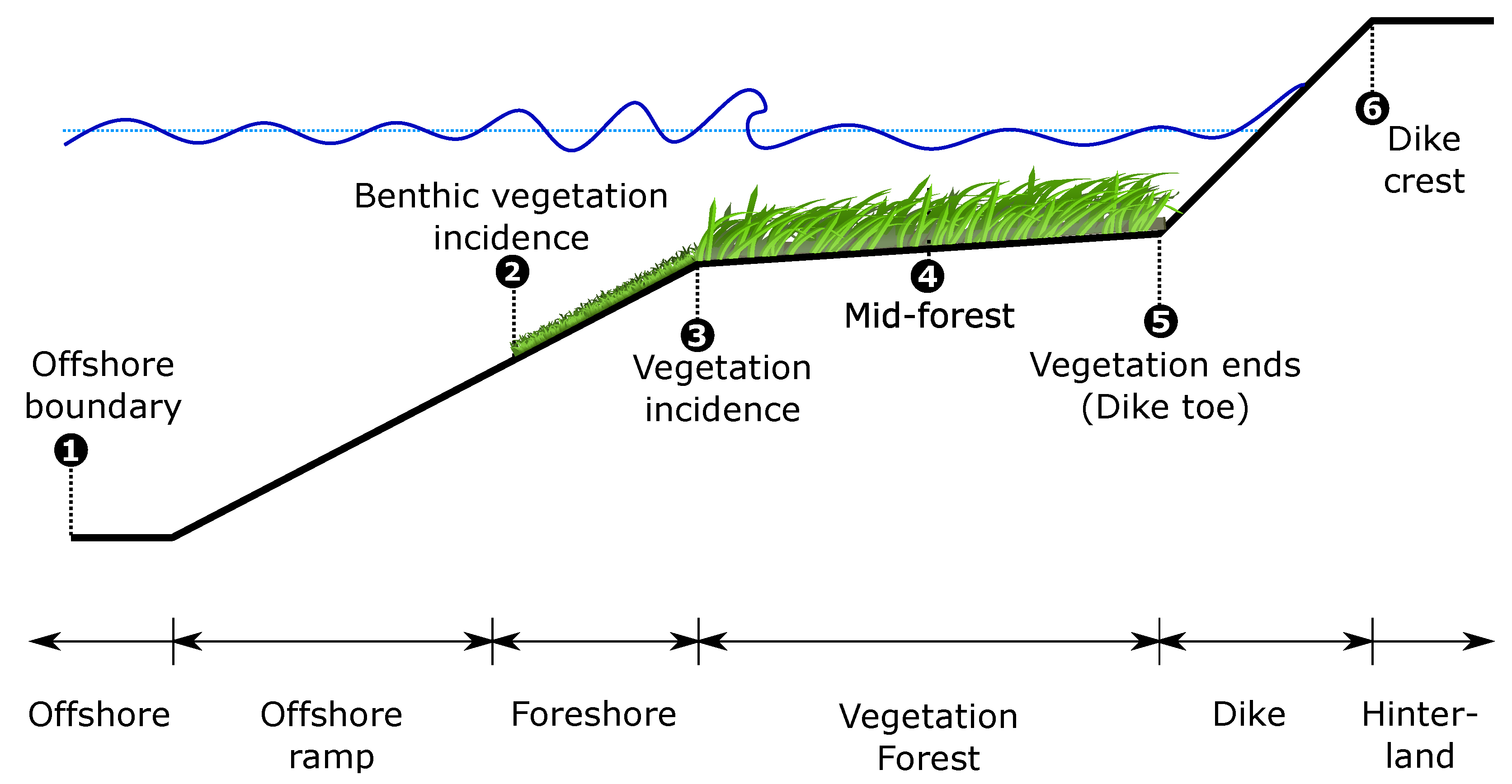
2.1.1. Schematization
2.1.2. Variable Families
- Hydrodynamic: Offshore wave height , peak wave period , water depth , and offshore slope were grouped as hydrodynamic variables.
- Vegetation: Vegetation forest length and vegetation slope were general vegetation variables which represented forest characteristics for both saltmarshes and mangroves.
- -
- Benthic vegetation was represented through dimensionless bed friction coefficient .
- -
- Submerged vegetation was parameterized by vegetation height , frontal width , vegetation density , and drag coefficient .
- -
- Emergent vegetation had three sub categories for each of the vertical layers.
- *
- Stem height , stem frontal width , stem density , and stem drag coefficient were put in place for the top layer of mangroves.
- *
- Trunk height , trunk frontal width , trunk density , and trunk drag coefficient were introduced to schematize the trunk.
- *
- Mangrove roots had height , frontal width , density , and drag coefficient .
- Hybrid: Lastly, dike slope and crest level were labeled as hybrid variables.
Hydrodynamic Variables
Vegetation Variables
Hybrid Variables
2.2. Stochastic Model Setup
2.2.1. Marginal Distributions
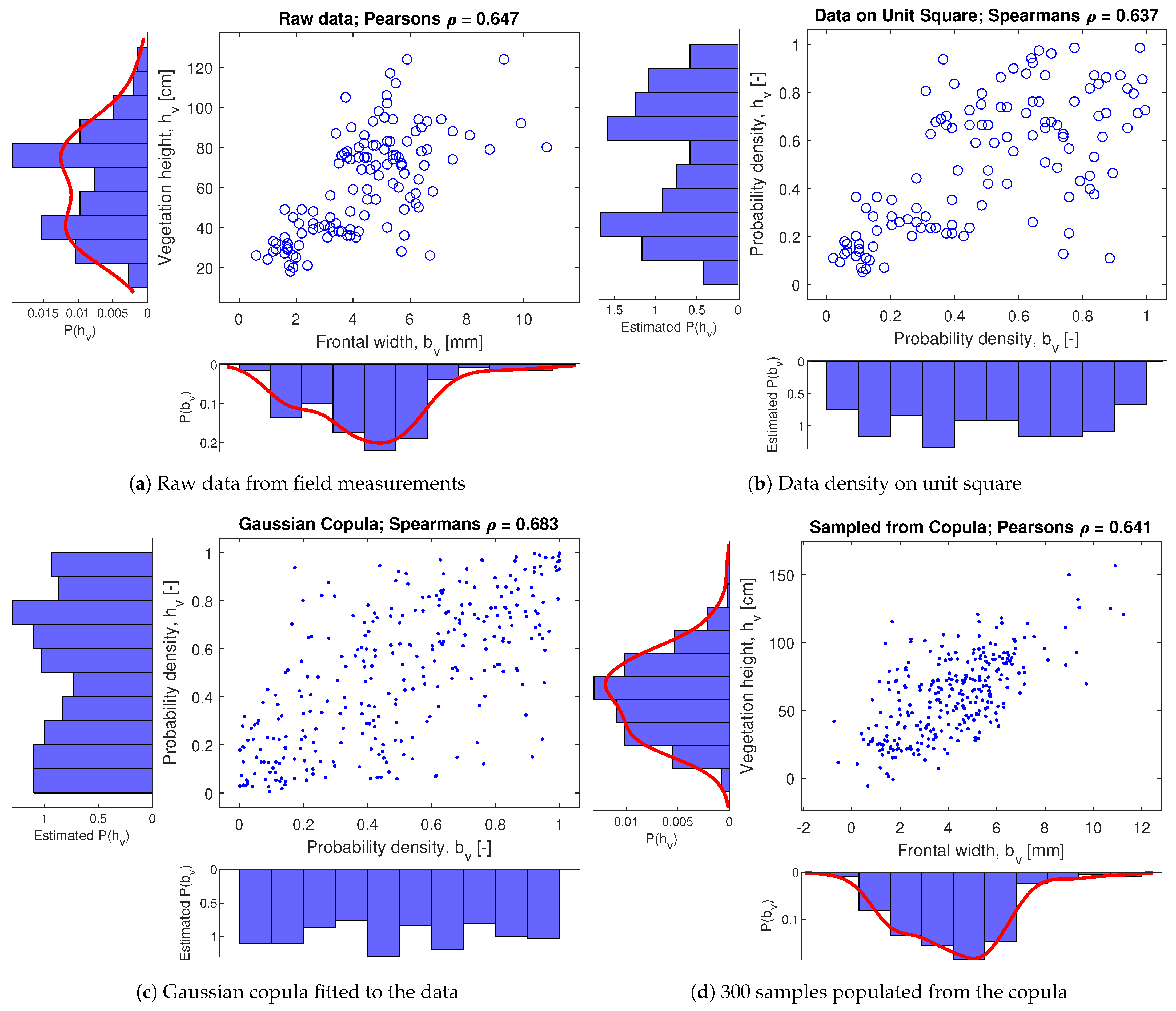
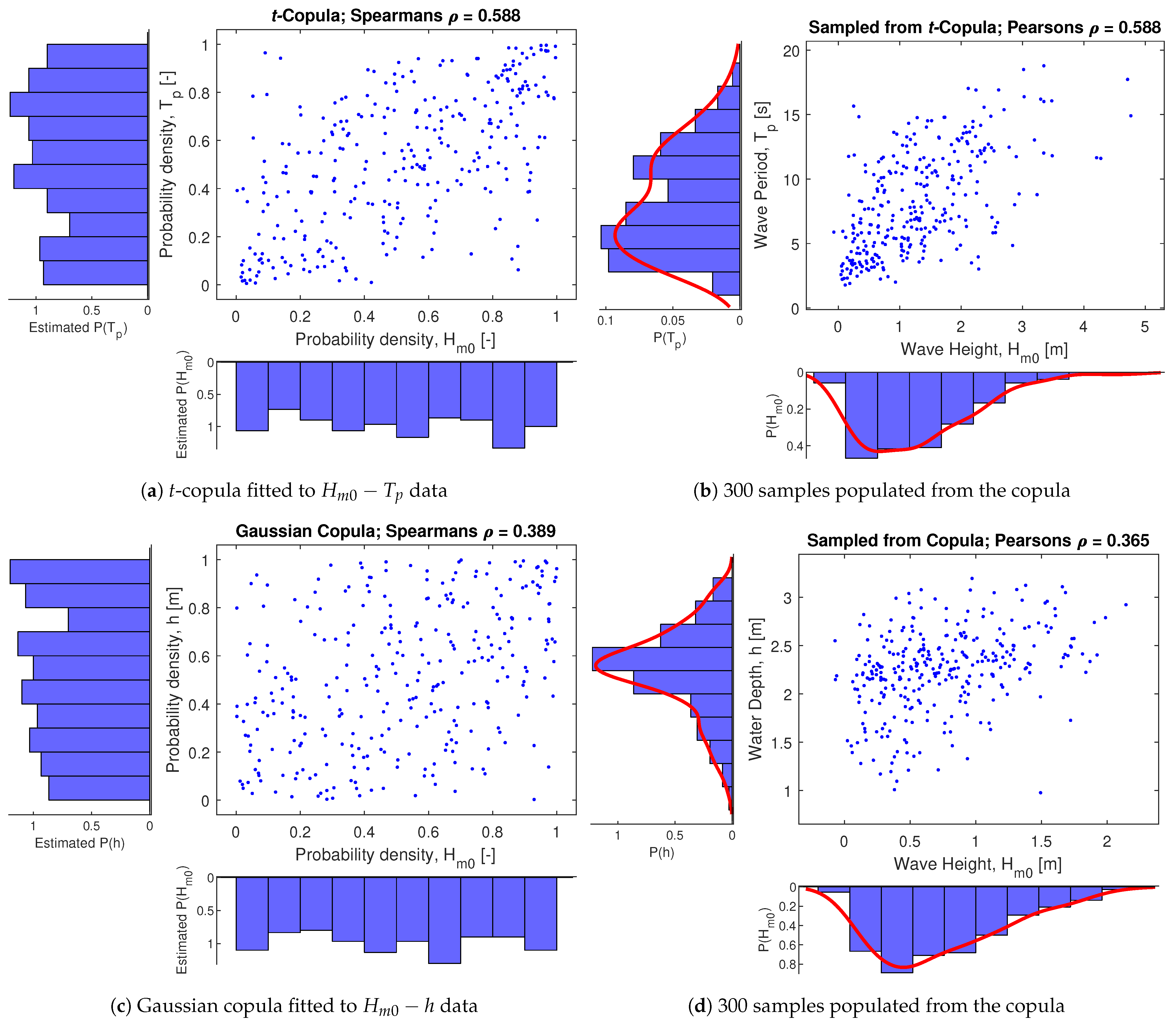
2.2.2. Correlations and Copulas
Data Processing
Expert Judgment

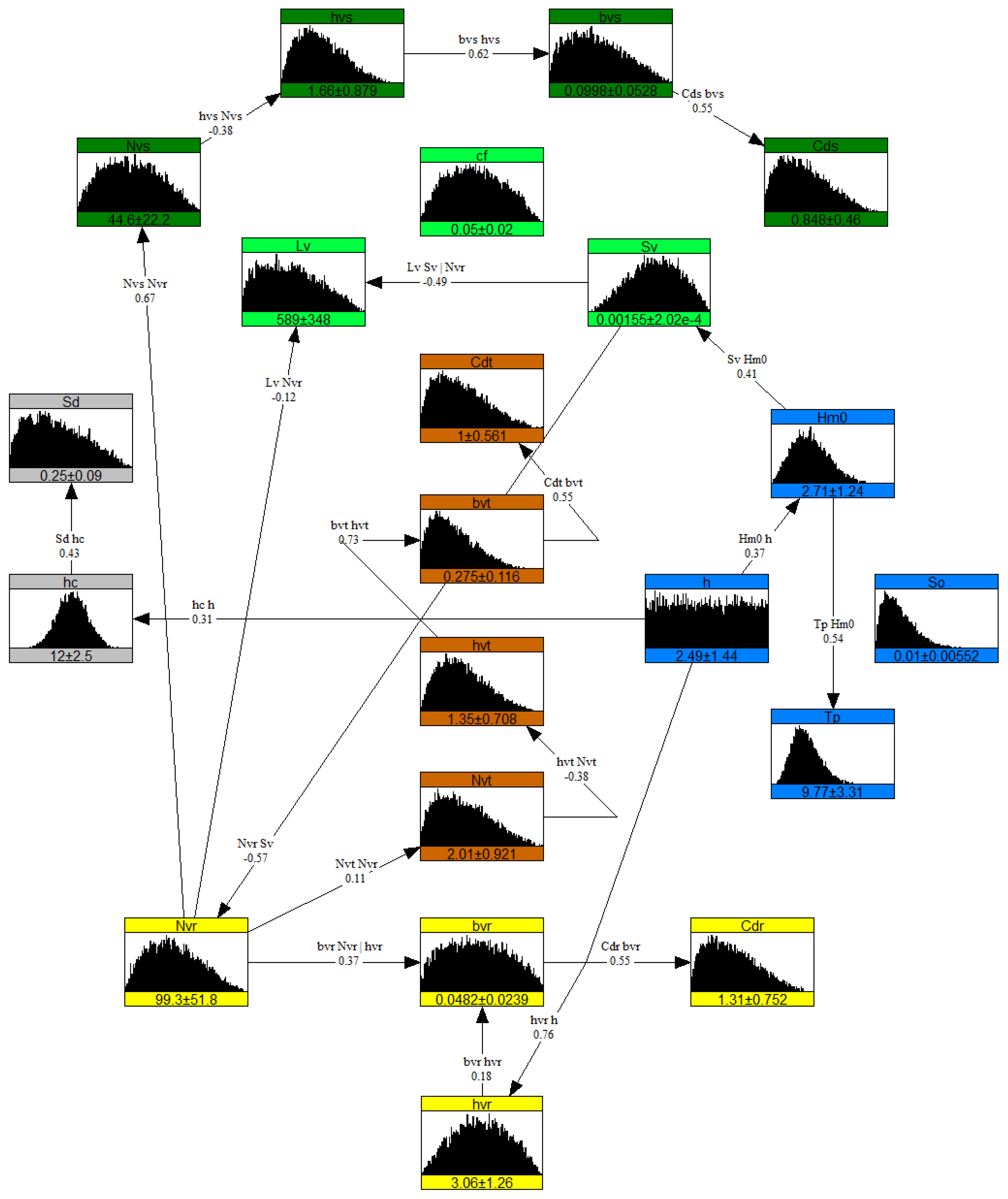
| Correlations | Nature | Coefficient | Source |
|---|---|---|---|
| + | 0.54 | Data | |
| + | 0.37 | Data | |
| + | 0.41 | Expert Judgment | |
| − | 0.33 | Expert Judgment | |
| − | 0.57 | Expert Judgment | |
| + | 0.62 | Data | |
| − | 0.38 | Data | |
| − | 0.48 | Data | |
| − | 0.12 | Expert Judgment | |
| + | 0.55 | Expert Judgment | |
| + | 0.31 | Expert Judgment | |
| + | 0.43 | Expert Judgment |
3. Results
3.1. Vegetated Hydrodynamic System
3.2. Dependence
3.3. Realistic Boundary Conditions
4. Discussion
4.1. Value of Dependence Modeling Using Nonparametric Bayesian Networks
4.1.1. Methodological Value
4.1.2. Reduced Numerical Simulations
4.1.3. Filling Information in Data-Scarce Environments
4.1.4. Better System-Based Response
4.2. Limitations and Way forward
- Rigid Cylindrical Vegetation: Vegetation was modeled as rigid cylinders which do not bend, undergo uprooting, or break in storm conditions which are critical for the system response [85].
- Data Availability: Ideally the statistical description should be derived from the data but due to limited data and responses, stochastic modeling was performed using in-house expert judgment for some of the variables.
- Gaussian Copula: Dependence analysis throughout the study was based on Gaussian copula. However, there is evidence of other dependence structures [80] for the variables in this study.
- New field data or data from global models could be obtained to expand the domain and scale of hydrodynamic and vegetation variables both spatially and temporally.
- Better dependence structure, e.g., vines, could be explored since the Gaussian copula is not the most accurate dependence description for some of the variables.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Meaning | Unit |
| Rank correlation | - | |
| Offshore wave height | m | |
| Peak wave period | s | |
| h | Water depth from diketoe | m |
| Reynolds number | – | |
| Keulegan–Carpenter number | – | |
| Offshore slope | - | |
| Bed friction coefficient | - | |
| Vegetation forest length | m | |
| Vegetation forest slope | - | |
| Vegetation height | m | |
| Stem frontal width | m | |
| Vegetation density | stems/m2 | |
| Bulk drag coefficient | - | |
| Dike crest level | m | |
| Dike slope | - | |
| Mangrove roots layer | - | |
| Mangrove trunk layer | - | |
| Mangrove stems layer | - | |
| No. of simulations | - |
Appendix A. Variable Table for Distributions
| Variable | Distribution | Bounds | Mean | SD | Percentiles | |||
|---|---|---|---|---|---|---|---|---|
| Min | Max | 5% | 50% | 95% | ||||
| Hydrodynamic | ||||||||
| Wave Height [m] | Weibull: | 2.69 | 1.24 | 0.86 | 2.58 | 4.91 | ||
| Peak wave period [s] | Gamma: | 1 | 9.77 | 3.31 | 5.12 | 9.36 | 15.83 | |
| Water depth h [m] | Uniform: | 5 | 2.5 | 1.44 | 0.25 | 2.5 | 4.75 | |
| Offshore slope [–] | Beta: | |||||||
| Seagrasses & Overall Forest | ||||||||
| Friction coefficient [–] | Beta: | 0.05 | 0.02 | 0.018 | 0.049 | 0.084 | ||
| Vegetation slope [–] | Beta: | |||||||
| Vegetation length [m] | Beta: | 1 | 1500 | 587 | 346 | 86 | 553 | 1205 |
| Satlmarshes | ||||||||
| Vegetation height [m] | Beta: | 0.79 | 0.43 | 0.13 | 0.76 | 1.52 | ||
| Frontal width [m] | Beta: | 0.011 | 0.006 | 0.002 | 0.011 | 0.022 | ||
| Veg. density | Beta: | 10 | 2000 | 697 | 415 | 115 | 645 | 1458 |
| Drag coefficient [–] | Beta: | 3 | 1 | 0.56 | 0.24 | 0.91 | 2.04 | |
| Mangroves | ||||||||
| Roots height [m] | Beta: | 0.2 | 6 | 3.06 | 1.25 | 1.02 | 3.05 | 5.12 |
| Roots width [m] | Beta: | 0.004 | 0.1 | 0.048 | 0.024 | 0.011 | 0.047 | 0.088 |
| Roots density | Beta: | 1 | 250 | 100 | 51.75 | 22.5 | 96 | 191.3 |
| Roots drag coeff. [–] | Beta: | 0.1 | 4 | 1.31 | 0.75 | 0.28 | 1.20 | 2.72 |
| Trunk height [m] | Beta: | 0.1 | 4 | 1.35 | 0.70 | 0.35 | 1.27 | 2.65 |
| Trunk width [m] | Beta: | 0.1 | 0.8 | 0.275 | 0.117 | 0.12 | 0.25 | 0.50 |
| Trunk density | Beta: | 0.5 | 5 | 2 | 0.92 | 0.73 | 1.88 | 3.70 |
| Trunk drag coeff. [–] | Beta: | 0.1 | 3 | 1 | 0.56 | 0.23 | 0.92 | 2.04 |
| Stems height [m] | Beta: | 0.1 | 5 | 1.675 | 0.90 | 0.42 | 1.57 | 3.31 |
| Stems width [m] | Beta: | 0.01 | 0.25 | 0.1 | 0.053 | 0.024 | 0.094 | 0.195 |
| Stems density | Beta: | 1 | 100 | 45 | 22.15 | 10.68 | 44 | 82.8 |
| Stems drag coeff. [–] | Beta: | 0.1 | 2.5 | 0.84 | 0.46 | 0.212 | 0.777 | 1.710 |
| Dike Variables | ||||||||
| Dike slope [–] | Beta: | |||||||
| Crest level [m] | Gaussian: | 1 | 20 | 12 | 2.5 | 7.88 | 12 | 16.11 |
References
- Niazi, M.H.K.; Morales Nápoles, O.; van Wesenbeeck, B.K. Vegetated Hydrodynamic System: Parameterization and Stochastic Dependence Modelling. Coast. Eng. Proc. 2020. [Google Scholar] [CrossRef]
- Spalding, M.D.; McIvor, A.L.; Beck, M.W.; Koch, E.W.; Möller, I.; Reed, D.J.; Rubinoff, P.; Spencer, T.; Tolhurst, T.J.; Woodroffe, C.D.; et al. Coastal Ecosystems: A Critical Element of Risk Reduction. Conserv. Lett. 2014, 7, 293–301. [Google Scholar] [CrossRef]
- Niazi, M.H.K.; Sigalas, N.; Scott, F.; Grossmann, F.; Damdam, K. Robust Flood Defence in Response to Climate Change; Report; Delft University of Technology: Delft, The Netherlands, 2018. [Google Scholar]
- Carrick, J.; Abdul Rahim, M.S.A.B.; Adjei, C.; Ashraa Kalee, H.H.H.; Banks, S.J.; Bolam, F.C.; Campos Luna, I.M.; Clark, B.; Cowton, J.; Domingos, I.F.N.; et al. Is planting trees the solution to reducing flood risks? J. Flood Risk Manag. 2018, 12, e12484. [Google Scholar] [CrossRef] [Green Version]
- Fonseca, M.S.; Cahalan, J.A. A preliminary evaluation of wave attenuation by four species of seagrass. Estuarine Coast. Shelf Sci. 1992, 35, 565–576. [Google Scholar] [CrossRef]
- Kobayashi, N.; Raichle, A.W.; Asano, T. Wave Attenuation by Vegetation. J. Waterw. Port Coastal Ocean. Eng. 1993, 119, 30–48. [Google Scholar] [CrossRef]
- Paul, M.; Amos, C.L. Spatial and seasonal variation in wave attenuation over Zostera noltii. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef]
- Sánchez-González, J.F.; Sánchez-Rojas, V.; Memos, C.D. Wave attenuation due to Posidonia oceanica meadows. J. Hydraul. Res. 2011, 49, 503–514. [Google Scholar] [CrossRef]
- Horstman, E.M.; Dohmen-Janssen, C.M.; Narra, P.M.F.; van den Berg, N.J.F.; Siemerink, M.; Hulscher, S.J.M.H. Wave attenuation in mangroves: A quantitative approach to field observations. Coast. Eng. 2014, 94, 47–62. [Google Scholar] [CrossRef]
- Marsooli, R.; Wu, W. Numerical investigation of wave attenuation by vegetation using a 3D RANS model. Adv. Water Resour. 2014, 74, 245–257. [Google Scholar] [CrossRef]
- Möller, I.; Kudella, M.; Rupprecht, F.; Spencer, T.; Paul, M.; van Wesenbeeck, B.K.; Wolters, G.; Jensen, K.; Bouma, T.J.; Miranda-Lange, M.; et al. Wave attenuation over coastal salt marshes under storm surge conditions. Nat. Geosci. 2014, 7, 727. [Google Scholar] [CrossRef] [Green Version]
- Van Rooijen, A.A.; De Vries, J.S.M.V.T.; Mccall, R.T.; Van Dongeren, A.R.; Roelvink, J.A.; Reniers, A.J.H.M. Modeling of Wave Attenuation by Vegetation with Xbeach. In Proceedings of the 36th Iahr World Congress, The Hague, The Netherlands, 28 June–3 July 2015; pp. 6749–6755. [Google Scholar]
- Vuik, V.; Jonkman, S.N.; Borsje, B.W.; Suzuki, T. Nature-based flood protection: The efficiency of vegetated foreshores for reducing wave loads on coastal dikes. Coast. Eng. 2016, 116, 42–56. [Google Scholar] [CrossRef] [Green Version]
- Reidenbach, M.A.; Thomas, E.L. Influence of the Seagrass, Zostera marina, on Wave Attenuation and Bed Shear Stress Within a Shallow Coastal Bay. Front. Mar. Sci. 2018, 5. [Google Scholar] [CrossRef]
- Mattis, S.A.; Kees, C.E.; Wei, M.V.; Dimakopoulos, A.; Dawson, C.N. Computational Model for Wave Attenuation by Flexible Vegetation. J. Waterw. Port Coastal Ocean. Eng. 2019, 145, 04018033. [Google Scholar] [CrossRef]
- Montgomery, J.M.; Bryan, K.R.; Mullarney, J.C.; Horstman, E.M. Attenuation of Storm Surges by Coastal Mangroves. Geophys. Res. Lett. 2019, 46, 2680–2689. [Google Scholar] [CrossRef] [Green Version]
- Phan, K.L.; Stive, M.J.F.; Zijlema, M.; Truong, H.S.; Aarninkhof, S.G.J. The effects of wave non-linearity on wave attenuation by vegetation. Coast. Eng. 2019, 147, 63–74. [Google Scholar] [CrossRef]
- Wu, W.C.; Ma, G.; Cox, D.T. Modeling wave attenuation induced by the vertical density variations of vegetation. Coast. Eng. 2016, 112, 17–27. [Google Scholar] [CrossRef]
- Karambas, T.; Koftis, T.; Prinos, P. Modeling of Nonlinear Wave Attenuation due to Vegetation. J. Coast. Res. 2016, 32, 142–152. [Google Scholar]
- Maza, M.; Lara, J.L.; Losada, I.J. Solitary wave attenuation by vegetation patches. Adv. Water Resour. 2016, 98, 159–172. [Google Scholar] [CrossRef]
- Chu, P.C.; Kuo, Y.; Galanis, G. Statistical Structure of the Global Significant Wave Heights. In Proceedings of the 20th Conference on Probability and Statistics in the Atmospheric Sciences, Atlanta, GA, USA, 16–21 January 2010. [Google Scholar]
- Xu, D.; Li, X.; Zhang, L.; Xu, N.; Lu, H. On the distributions of wave periods, wavelengths, and amplitudes in a random wave field. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef]
- Hawkes, P.J.; Gouldby, B.P.; Tawn, J.A.; Owen, M.W. The joint probability of waves and water levels in coastal engineering design. J. Hydraul. Res. 2002, 40, 241–251. [Google Scholar] [CrossRef]
- Guedes Soares, C.; Carvalho, A.N. Probability distributions of wave heights and periods in combined sea-states measured off the Spanish coast. Ocean. Eng. 2012, 52, 13–21. [Google Scholar] [CrossRef]
- Muraleedharan, G.; Lucas, C.; Martins, D.; Guedes Soares, C.; Kurup, P.G. On the distribution of significant wave height and associated peak periods. Coast. Eng. 2015, 103, 42–51. [Google Scholar] [CrossRef]
- Hu, Z.; Stive, M.; Zitman, T.; Suzuki, T. Drag coefficient of vegetation in flow modeling. In Proceedings of the International Conference on Coastal Engineering, Santander, Spain, 1–6 July 2012. [Google Scholar] [CrossRef] [Green Version]
- Simard, M.; Fatoyinbo, L.; Smetanka, C.; Rivera-Monroy, V.H.; Castañeda-Moya, E.; Thomas, N.; Van der Stocken, T. Mangrove canopy height globally related to precipitation, temperature and cyclone frequency. Nat. Geosci. 2019, 12, 40–45. [Google Scholar] [CrossRef]
- Reimann, S.; Husrin, S.; Strusińska, A.; Oumeraci, H. Damping Tsunami And Storm Waves By Coastal Forests – Parameterisation And Hydraulic Model Tests; Leibniz University Hannover: Hannover, Germany, 2019. [Google Scholar]
- Athanasiou, P.; van Dongeren, A.; Giardino, A.; Vousdoukas, M.; Gaytan-Aguilar, S.; Ranasinghe, R. Global distribution of nearshore slopes with implications for coastal retreat. Earth Syst. Sci. Data 2019, 11, 1515–1529. [Google Scholar] [CrossRef] [Green Version]
- Niazi, M.H.K. Flood Risk Prediction under Global Vegetated Hydrodynamics: A Bayesian Network. MSc Thesis, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- van Zelst, V. Global Flood Hazard Reduction by Foreshore Vegetation. MSc Thesis, Delft University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
- Chen, H.; Ni, Y.; Li, Y.; Liu, F.; Ou, S.; Su, M.; Peng, Y.; Hu, Z.; Uijttewaal, W.; Suzuki, T. Deriving vegetation drag coefficients in combined wave-current flows by calibration and direct measurement methods. Adv. Water Resour. 2018, 122, 217–227. [Google Scholar] [CrossRef] [Green Version]
- Henry, P.Y.; Myrhaug, D.; Aberle, J. Drag forces on aquatic plants in nonlinear random waves plus current. Estuarine Coast. Shelf Sci. 2015, 165, 10–24. [Google Scholar] [CrossRef]
- Asano, T.; Tsutsui, S.; Sakai, T. Wave damping characteristics due to seaweed. In Proceedings of the 35th Conference on Coastal Engineering, Kobe, Japan, 7 November 1988. [Google Scholar]
- Méndez, F.J.; Losada, I.J.; Losada, M.A. Hydrodynamics induced by wind waves in a vegetation field. J. Geophys. Res. Ocean. 1999, 104, 18383–18396. [Google Scholar] [CrossRef]
- Mendez, F.J.; Losada, I.J. An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields. Coast. Eng. 2004, 51, 103–118. [Google Scholar] [CrossRef]
- Bradley, K.; Houser, C. Relative velocity of seagrass blades: Implications for wave attenuation in low-energy environments. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef]
- Jadhav, R.S.; Chen, Q. Field Investigation of Wave Dissipation Over SaltMarsh Vegetation During Tropical Cyclone. In Proceedings of the 33rd Conference on Coastal Engineering, Santander, Spain, 1–6 July 2012. [Google Scholar] [CrossRef] [Green Version]
- Infantes, E.; Orfila, A.; Simarro, G.; Terrados, J.; Luhar, M.; Nepf, H. Effect of a seagrass (Posidonia oceanica) meadow on wave propagation. Mar. Ecol. Prog. Ser. 2012, 456, 63–72. [Google Scholar] [CrossRef] [Green Version]
- Jadhav, R.S.; Chen, Q.; Smith, J.M. Spectral distribution of wave energy dissipation by salt marsh vegetation. Coast. Eng. 2013, 77, 99–107. [Google Scholar] [CrossRef] [Green Version]
- Pinsky, M.L.; Guannel, G.; Arkema, K.K. Quantifying wave attenuation to inform coastal habitat conservation. Ecosphere 2013, 4, art95. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.L.; Losada, I.J. A coupled model of submerged vegetation under oscillatory flow using Navier–Stokes equations. Coast. Eng. 2013, 80, 16–34. [Google Scholar] [CrossRef]
- Ozeren, Y.; Wren, D.G.; Wu, W. Experimental Investigation of Wave Attenuation through Model and Live Vegetation. J. Waterw. Port Coast. Ocean. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Anderson, M.E.; Smith, J.M. Wave attenuation by flexible, idealized salt marsh vegetation. Coast. Eng. 2014, 83, 82–92. [Google Scholar] [CrossRef]
- Hu, Z.; Suzuki, T.; Zitman, T.; Uittewaal, W.; Stive, M. Laboratory study on wave dissipation by vegetation in combined current–wave flow. Coast. Eng. 2014, 88, 131–142. [Google Scholar] [CrossRef]
- Losada, I.J.; Maza, M.; Lara, J.L. A new formulation for vegetation-induced damping under combined waves and currents. Coast. Eng. 2016, 107, 1–13. [Google Scholar] [CrossRef]
- Plomaritis, T.A.; Costas, S.; Ferreira, Ó. Use of a Bayesian Network for coastal hazards, impact and disaster risk reduction assessment at a coastal barrier (Ria Formosa, Portugal). Coast. Eng. 2018, 134, 134–147. [Google Scholar] [CrossRef]
- Narayan, S.; Simmonds, D.; Nicholls, R.J.; Clarke, D. A Bayesian network model for assessments of coastal inundation pathways and probabilities. J. Flood Risk Manag. 2018, 11, S233–S250. [Google Scholar] [CrossRef]
- Jäger, W.S.; Christie, E.K.; Hanea, A.M.; den Heijer, C.; Spencer, T. A Bayesian network approach for coastal risk analysis and decision making. Coast. Eng. 2018, 134, 48–61. [Google Scholar] [CrossRef]
- Bolle, A.; das Neves, L.; Smets, S.; Mollaert, J.; Buitrago, S. An impact-oriented Early Warning and Bayesian-based Decision Support System for flood risks in Zeebrugge harbour. Coast. Eng. 2018, 134, 191–202. [Google Scholar] [CrossRef]
- Pearson, S.G.; Storlazzi, C.D.; van Dongeren, A.R.; Tissier, M.F.S.; Reniers, A.J.H.M. A Bayesian-Based System to Assess Wave-Driven Flooding Hazards on Coral Reef-Lined Coasts. J. Geophys. Res. Ocean. 2017, 122, 10099–10117. [Google Scholar] [CrossRef] [Green Version]
- Poelhekke, L.; Jäger, W.S.; van Dongeren, A.; Plomaritis, T.A.; McCall, R.; Ferreira, Ó. Predicting coastal hazards for sandy coasts with a Bayesian Network. Coast. Eng. 2016, 118, 21–34. [Google Scholar] [CrossRef]
- Den Heijer, C.; Knipping, D.T.J.A.; Plant, N.G.; Van Thiel De Vries, J.S.M.; Baart, F.; Van Gelder, P.H.A.J.M. Impact assessment of extreme storm events using a Bayesian network. Conf. Coast. Eng. 2012, 33, 4. [Google Scholar] [CrossRef] [Green Version]
- Plant, N.G.; Holland, K.T. Prediction and assimilation of surf-zone processes using a Bayesian network: Part I: Forward models. Coast. Eng. 2011, 58, 119–130. [Google Scholar] [CrossRef]
- Kurowicka, D.; Cooke, R. Non-Parametric Continuous Bayesian Belief Nets with Expert Judgement. Probab. Saf. Assess. Manag. 2004, 2784–2790. [Google Scholar]
- Hanea, A.M.; Kurowicka, D.; Cooke, R.M. Hybrid Method for Quantifying and Analyzing Bayesian Belief Nets. Qual. Reliab. Eng. Int. 2006, 22, 709–729. [Google Scholar] [CrossRef]
- Ababei, D.; Lewandowski, D.; Hanea, A.; Napoles, O.M.; Kurowicka, D.; Cooke, R. UNINET Help Documentation; Report; Delft University of Technology: Delft, The Netherlands, 2008. [Google Scholar]
- Morales Napoles, O.; Worm, D.; Haak, P.v.d.; Hanea, A.; Courage, W.; Miraglia, S. Reader for Course: Introduction to Bayesian Networks; Report; Netherlands Organisation for Applied Scientific Research: Delft, The Netherlands, 2013. [Google Scholar]
- Hanea, A.; Morales Napoles, O.; Ababei, D. Non-parametric Bayesian networks: Improving theory and reviewing applications. Reliab. Eng. Syst. Saf. 2015, 144, 265–284. [Google Scholar] [CrossRef]
- Genest, C.; Mackay, J. The Joy of Copulas: Bivariate Distributions with Uniform Marginals. Am. Stat. 1986, 40, 280–283. [Google Scholar] [CrossRef]
- Frees, E.W.; Valdez, E.A. Understanding Relationships Using Copulas. North Am. Actuar. J. 1998, 2, 1–25. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.C. Everything you always wanted to know about copula modeling but were afraid to ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Schweizer, B. Introduction to copulas. J. Hydrol. Eng. 2007, 12, 346. [Google Scholar] [CrossRef] [Green Version]
- Yule, G.U. An Introduction to the Theory of Statistics; Griffin, C., Ed.; Limited: London, UK, 1919. [Google Scholar]
- Songy, G. Wave Attenuation by Global Coastal Salt Marsh Habitats. MSc Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Holthuijsen, L.H. Waves in oceanic and coastal waters; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Young, I.R.; Zieger, S.; Babanin, A.V. Global Trends in Wind Speed and Wave Height. Science 2011, 332, 451. [Google Scholar] [CrossRef] [PubMed]
- Young, I.R. Global ocean wave statistics obtained from satellite observations. Appl. Ocean. Res. 1994, 16, 235–248. [Google Scholar] [CrossRef]
- Janssen, M. Flood Hazard Reduction by Mangroves. Msc Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Rahmeyer, W.; Werth, D. The Study of the Resistance and Stability of Vegetation Ecosystem Plant Groupings in Flood Control Channels; Report 148; UtahState Univeristy: Logan, UT, USA, 1996; Volume 1. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959; Volume 1. [Google Scholar]
- CIRIA; CUR; CETMEF. The Rock Manual. The Use of Rock in Hydraulic Engineering, 2nd ed.; C683; CIRIA: London, UK, 2007. [Google Scholar]
- Marek, P. Mangroves. 2019. Available online: www.mangrove.at (accessed on 15 July 2019).
- Moffett, K.B.; Nardin, W.; Silvestri, S.; Wang, C.; Temmerman, S. Multiple Stable States and Catastrophic Shifts in Coastal Wetlands: Progress, Challenges, and Opportunities in Validating Theory Using Remote Sensing and Other Methods. Remote Sens. 2015, 7, 10184–10226. [Google Scholar] [CrossRef] [Green Version]
- Cooke, R. Experts in Uncertainty: Opinion and Subjective Probability in Science; Oxford University Press on Demand: Oxford, UK, 1991. [Google Scholar]
- Morales Napoles, O.; Kurowicka, D.; Roelen, A. Eliciting conditional and unconditional rank correlations from conditional probabilities. Reliab. Eng. Syst. Saf. 2008, 93, 699–710. [Google Scholar] [CrossRef]
- Cooke, R.M.; Goossens, L.L.H.J. TU Delft expert judgment data base. Reliab. Eng. Syst. Saf. 2008, 93, 657–674. [Google Scholar] [CrossRef]
- Morales-Nápoles, O.; Delgado-Hernández, D.J.; De-León-Escobedo, D.; Arteaga-Arcos, J.C. A continuous Bayesian network for earth dams’ risk assessment: Methodology and quantification. Struct. Infrastruct. Eng. 2014, 10, 589–603. [Google Scholar] [CrossRef]
- Werner, C.; Bedford, T.; Cooke, R.M.; Hanea, A.M.; Morales-Nápoles, O. Expert judgement for dependence in probabilistic modelling: A systematic literature review and future research directions. Eur. J. Oper. Res. 2017, 258, 801–819. [Google Scholar] [CrossRef] [Green Version]
- Jäger, W.S.; Nápoles, O.M. A Vine-Copula Model for Time Series of Significant Wave Heights and Mean Zero-Crossing Periods in the North Sea. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part Civ. Eng. 2017, 3, 04017014. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez, G.R.; Guedes Soares, C. Correlation between successive wave heights and periods in mixed sea states. Ocean. Eng. 2001, 28, 1009–1030. [Google Scholar] [CrossRef]
- Antão, E.M.; Guedes Soares, C. Joint distributions of wave steepness in narrow band sea states. Ocean. Eng. 2015, 101, 201–210. [Google Scholar] [CrossRef]
- Memos, C.D. On the theory of the joint probability of heights and periods of sea waves. Coast. Eng. 1994, 22, 201–215. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. On the joint distribution of the periods and amplitudes of sea waves. J. Geophys. Res. 1975, 80, 2688–2694. [Google Scholar] [CrossRef]
- Vuik, V.; Suh Heo, H.Y.; Zhu, Z.; Borsje, B.W.; Jonkman, S.N. Stem breakage of salt marsh vegetation under wave forcing: A field and model study. Estuarine Coast. Shelf Sci. 2018, 200, 41–58. [Google Scholar] [CrossRef] [Green Version]
- Terefenko, P.; Paprotny, D.; Giza, A.; Morales-Nápoles, O.; Kubicki, A.; Walczakiewicz, S. Monitoring Cliff Erosion with LiDAR Surveys and Bayesian Network-based Data Analysis. Remote Sens. 2019, 11, 843. [Google Scholar] [CrossRef] [Green Version]
- Mendoza-Lugo, M.A.; Delgado-Hernández, D.J.; Morales-Nápoles, O. Reliability analysis of reinforced concrete vehicle bridges columns using non-parametric Bayesian networks. Eng. Struct. 2019, 188, 178–187. [Google Scholar] [CrossRef]
- Lee, D.; Pan, R. A nonparametric Bayesian network approach to assessing system reliability at early design stages. Reliab. Eng. Syst. Saf. 2018, 171, 57–66. [Google Scholar] [CrossRef]
- Couasnon, A.; Sebastian, A.; Morales-Nápoles, O. A Copula-Based Bayesian Network for Modeling Compound Flood Hazard from Riverine and Coastal Interactions at the Catchment Scale: An Application to the Houston Ship Channel, Texas. Water 2018, 10, 1190. [Google Scholar]
- Pearson, S. Predicting Wave-Induced Flooding on Low-Lying Tropical Islands Using a Bayesian Network. MSc Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Han, S.; Coulibaly, P. Bayesian flood forecasting methods: A review. J. Hydrol. 2017, 551, 340–351. [Google Scholar] [CrossRef]
- Jaeger, W. Multivariate Methods for Coastal and Offshore Risks. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
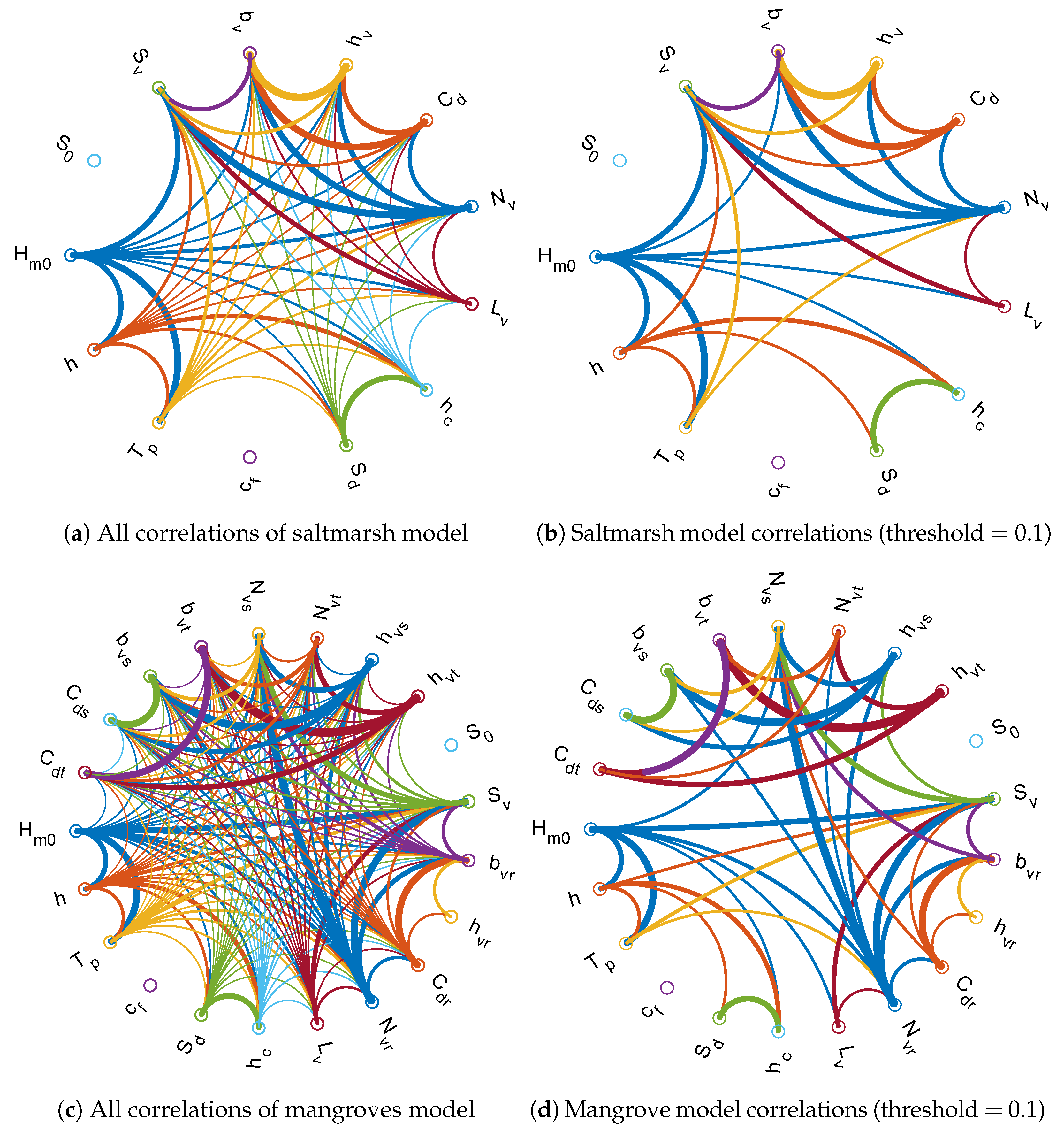
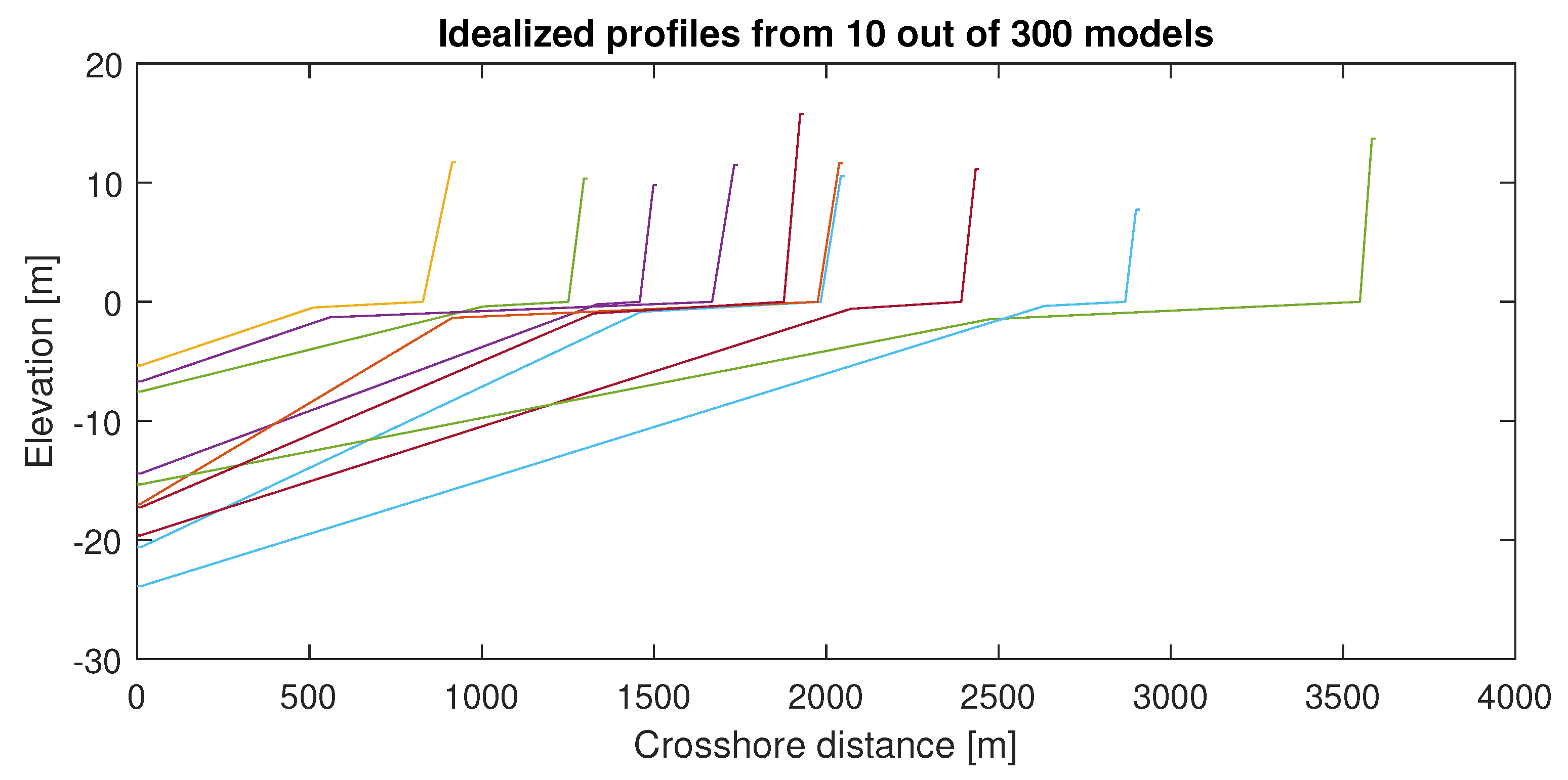
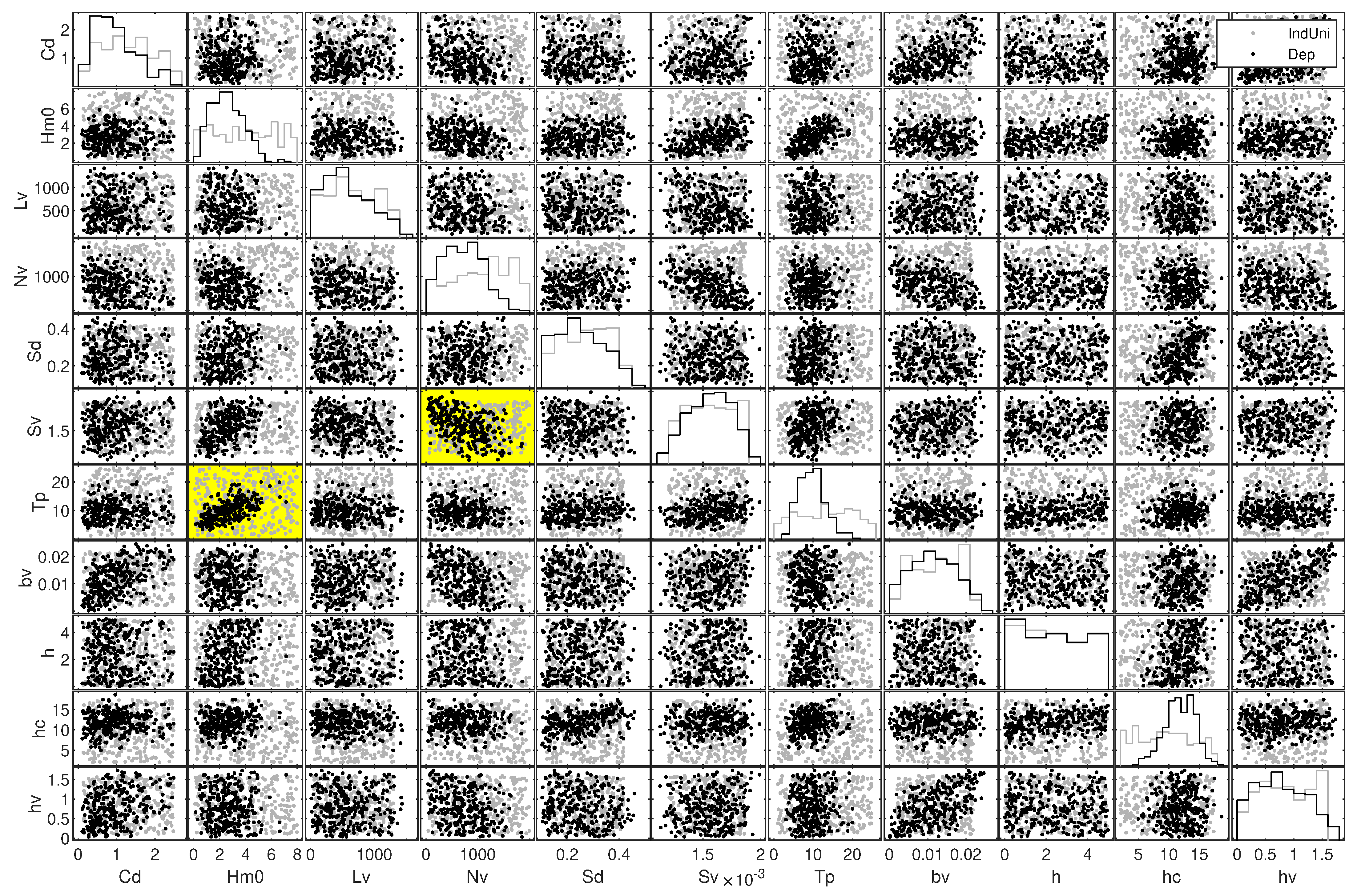
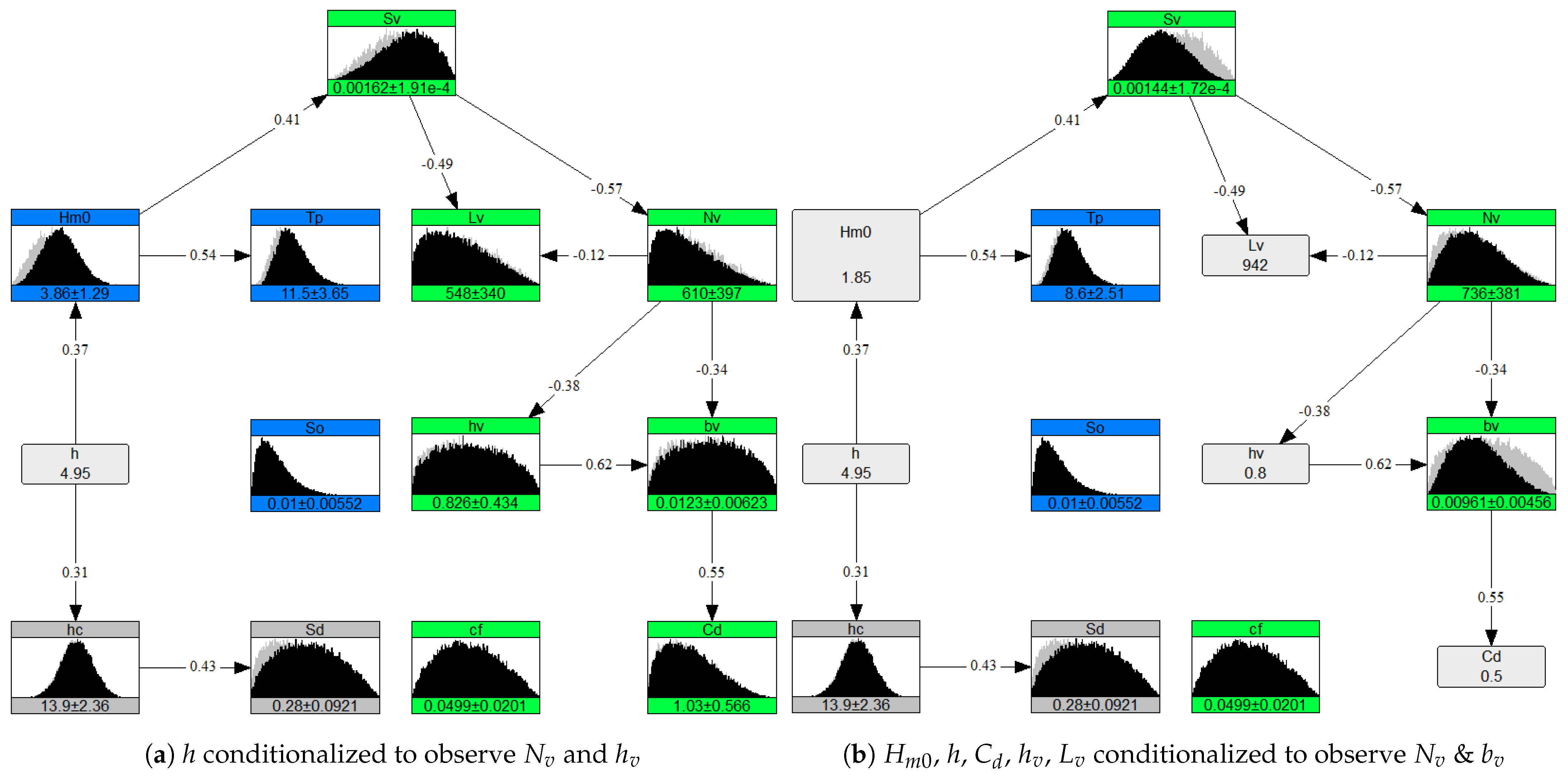
| Variable | Symbol | Unit | Range | Distribution | Source |
|---|---|---|---|---|---|
| Offshore Wave Height | m | to | Weibull | [21] | |
| Peak wave period | s | 1 to | Gamma | [22] | |
| Water depth | h | m | to 5 | Uniform | [23] |
| Offshore slope | – | to | Beta | Experts | |
| Vegetation forest length | m | 1 to 1500 | Beta | [65] | |
| Vegetation slope | – | to | Beta | Expert | |
| Benthic Seagrasses | |||||
| Friction coefficient | – | to | Beta | [70] | |
| Submerged Saltmarshes | |||||
| Vegetation height | m | to | Beta | [31] | |
| Frontal width | m | to | Beta | [31] | |
| Vegetation density | stems/m | 10 to 2000 | Beta | [31] | |
| Drag coefficient | – | to 3 | Beta | [26] | |
| Emergent Mangroves | |||||
| Stems height | m | to 5 | Beta | [27] | |
| Stems frontal width | m | to | Beta | [69] | |
| Stems density | stems/m | to 100 | Beta | [69] | |
| Stem drag coefficient | – | to | Beta | [26] | |
| Trunk height | m | to 4 | Beta | [27] | |
| Trunk frontal width | m | to | Beta | [73] | |
| Trunk density | trunk/m | to 5 | Beta | [69] | |
| Trunk drag coefficient | – | to 3 | Beta | [26] | |
| Roots height | m | to 6 | Beta | [27] | |
| Roots frontal width | m | to | Beta | [69] | |
| Roots density | roots/m | 1 to 250 | Beta | [69] | |
| Roots drag coefficient | – | to 4 | Beta | [26] | |
| Hybrid | |||||
| Dike slope | – | to | Beta | Experts | |
| Crest level | m | 1 to 20 | Gaussian | Expert | |
| City, Country | Location | Vegetation | Wave Height [m] | Wave Period [s] | ||
|---|---|---|---|---|---|---|
| Mean | Variance | Mean | Variance | |||
| Los Angeles, USA | 33° N 120° W | Saltmarsh | 2.17 | 0.73 | 11.99 | 9.73 |
| Mérida, Mexico | 21° N 090° W | Seagrass | 0.44 | 0.07 | 4.13 | 2.55 |
| São Luís, Brazil | 01° S 043° W | Mangroves | 1.63 | 0.15 | 8.71 | 6.77 |
| Texel, Netherlands | 53° N 005° E | Saltmarsh | 0.82 | 0.46 | 5.91 | 5.03 |
| Lagos, Nigeria | 05° N 003° E | Seagrass | 1.34 | 0.13 | 12.69 | 4.30 |
| Dubai, UAE | 25° N 054° E | Seagrass | 0.60 | 0.18 | 4.99 | 1.14 |
| Karachi, Pakistan | 24° N 067° E | Mangroves | 1.35 | 1.38 | 10.39 | 11.50 |
| Shanghai, China | 32° N 122° E | Saltmarsh | 0.95 | 0.32 | 5.45 | 3.40 |
| Surabaya, Indonesia | 06° S 113° E | Mangroves | 0.63 | 0.17 | 4.32 | 1.44 |
| Sydney, Australia | 34° S 152° E | Saltmarsh | 2.15 | 0.87 | 9.29 | 8.99 |
| h | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.00 | 0.37 | 0.54 | 0.00 | 0.05 | 0.12 | −0.14 | −0.24 | 0.07 | 0.09 | 0.12 | 0.41 | 0.00 | |
| h | 0.37 | 1.00 | 0.20 | 0.00 | 0.14 | 0.31 | −0.05 | −0.09 | 0.03 | 0.04 | 0.05 | 0.16 | 0.00 |
| 0.54 | 0.20 | 1.00 | 0.00 | 0.03 | 0.07 | −0.08 | −0.13 | 0.04 | 0.05 | 0.07 | 0.23 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.05 | 0.14 | 0.03 | 0.00 | 1.00 | 0.43 | −0.01 | −0.01 | 0.00 | 0.01 | 0.01 | 0.02 | 0.00 | |
| 0.12 | 0.31 | 0.07 | 0.00 | 0.43 | 1.00 | −0.02 | −0.03 | 0.01 | 0.01 | 0.01 | 0.05 | 0.00 | |
| −0.14 | −0.05 | −0.08 | 0.00 | −0.01 | −0.02 | 1.00 | −0.12 | 0.03 | 0.05 | 0.06 | −0.32 | 0.00 | |
| −0.24 | −0.09 | −0.13 | 0.00 | −0.01 | −0.03 | −0.12 | 1.00 | −0.27 | −0.38 | −0.48 | −0.57 | 0.00 | |
| 0.07 | 0.03 | 0.04 | 0.00 | 0.00 | 0.01 | 0.03 | −0.27 | 1.00 | 0.35 | 0.55 | 0.16 | 0.00 | |
| 0.09 | 0.04 | 0.05 | 0.00 | 0.01 | 0.01 | 0.05 | −0.38 | 0.35 | 1.00 | 0.62 | 0.22 | 0.00 | |
| 0.12 | 0.05 | 0.07 | 0.00 | 0.01 | 0.01 | 0.06 | −0.48 | 0.55 | 0.62 | 1.00 | 0.28 | 0.00 | |
| 0.41 | 0.16 | 0.23 | 0.00 | 0.02 | 0.05 | −0.32 | −0.57 | 0.16 | 0.22 | 0.28 | 1.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 |
| Run | h | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.32 | 11.5 | 0.39 | 0.024 | 0.259 | 0.006 | 417 | 0.00156 | 309.1 | 1.63 | 0.03 | 0.27 | 11.18 |
| 2 | 6.63 | 20.0 | 3.58 | 0.011 | 0.404 | 0.007 | 759 | 0.00165 | 342.7 | 1.52 | 0.072 | 0.29 | 13.05 |
| 3 | 3.37 | 14.2 | 4.86 | 0.006 | 0.911 | 0.012 | 1217 | 0.00131 | 1075.2 | 0.91 | 0.057 | 0.36 | 12.04 |
| 4 | 4.69 | 8.2 | 2.99 | 0.007 | 0.109 | 0.002 | 651 | 0.00175 | 478.2 | 0.72 | 0.061 | 0.3 | 14.8 |
| 5 | 0.15 | 5.1 | 0.53 | 0.007 | 0.667 | 0.013 | 1464 | 0.00118 | 168.3 | 1.73 | 0.079 | 0.12 | 12.69 |
| 6 | 1.29 | 8.5 | 0.81 | 0.021 | 0.653 | 0.021 | 372 | 0.00179 | 1310.3 | 1.98 | 0.052 | 0.15 | 11.63 |
| 7 | 1.95 | 8.9 | 0.84 | 0.021 | 0.147 | 0.010 | 125 | 0.00174 | 1224.4 | 1.37 | 0.093 | 0.16 | 13.17 |
| 8 | 7.14 | 13.0 | 2.23 | 0.005 | 1.625 | 0.024 | 504 | 0.00199 | 4.4 | 1.56 | 0.074 | 0.29 | 11.42 |
| 9 | 1.37 | 5.6 | 0.78 | 0.014 | 0.219 | 0.001 | 1311 | 0.00164 | 676.5 | 0.35 | 0.062 | 0.16 | 10.31 |
| 10 | 1.72 | 8.3 | 0.56 | 0.011 | 0.462 | 0.017 | 1086 | 0.00174 | 123.91 | 1.52 | 0.065 | 0.25 | 9.79 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 300 | 1.30 | 8.2 | 0.84 | 0.012 | 0.731 | 0.008 | 140 | 0.00164 | 1200.97 | 0.71 | 0.08 | 0.26 | 9.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niazi, M.H.K.; Morales Nápoles, O.; van Wesenbeeck, B.K. Probabilistic Characterization of the Vegetated Hydrodynamic System Using Non-Parametric Bayesian Networks. Water 2021, 13, 398. https://doi.org/10.3390/w13040398
Niazi MHK, Morales Nápoles O, van Wesenbeeck BK. Probabilistic Characterization of the Vegetated Hydrodynamic System Using Non-Parametric Bayesian Networks. Water. 2021; 13(4):398. https://doi.org/10.3390/w13040398
Chicago/Turabian StyleNiazi, Muhammad Hassan Khan, Oswaldo Morales Nápoles, and Bregje K. van Wesenbeeck. 2021. "Probabilistic Characterization of the Vegetated Hydrodynamic System Using Non-Parametric Bayesian Networks" Water 13, no. 4: 398. https://doi.org/10.3390/w13040398
APA StyleNiazi, M. H. K., Morales Nápoles, O., & van Wesenbeeck, B. K. (2021). Probabilistic Characterization of the Vegetated Hydrodynamic System Using Non-Parametric Bayesian Networks. Water, 13(4), 398. https://doi.org/10.3390/w13040398







