Next Article in Journal
Increase in Daily Household Water Demand during the First Wave of the Covid-19 Pandemic in Germany
Previous Article in Journal
Multi-Scale Target-Specified Sub-Model Approach for Fast Large-Scale High-Resolution 2D Urban Flood Modelling
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 13
Issue 3
10.3390/w13030257
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Climate Control of Multidecadal Variability in River Discharge and Precipitation in Western Europe

by
Isabel Jalón-Rojas
* and
Bruno Castelle
UMR5805 EPOC, CNRS, OASU, University Bordeaux, 33615 Pessac, France
*
Author to whom correspondence should be addressed.
Water 2021, 13(3), 257; https://doi.org/10.3390/w13030257
Submission received: 16 December 2020 / Revised: 11 January 2021 / Accepted: 19 January 2021 / Published: 21 January 2021
(This article belongs to the Section Hydrology)
Browse Figures
Versions Notes

Abstract

:
The influence of large-scale climate variability on winter river discharge and precipitation across western Europe is investigated. We analyze 60 years of monthly precipitation and river flow data from 18 major western-European rivers and its relationship with dominant teleconnection patterns and climate indices in this region. Results show that winter river flow is characterized by large interannual variability, best correlates with (a) the North Atlantic Oscillation (NAO) at the far-northern (R up to 0.56) and southern latitudes (R up to −0.72), and (b) the West Europe Pressure Anomaly (WEPA) at the middle and northern latitudes, from 42° N to 55° N (R up to 0.83). These indices also explain the interannual variability in autumn and spring discharge in rivers characterized by secondary floods. Compared to the other leading modes of atmospheric variability, WEPA increases the correlations with winter precipitation up to 0.8 in many regions of western and central Europe. A positive WEPA corresponds to a southward shift and an intensification of the Icelandic-Low/Azores-High dipole, driving enhanced precipitation and river discharge in these regions. The correlations with precipitation are slightly higher than those with river discharge, particularly in France, with clear latitudinal gradient. This trend suggests that water storage variability and other catchment characteristics may also influence the interannual variability of river discharge. Seasonal forecasting of the WEPA and NAO winter indices can become a powerful tool in anticipating hydrological risks in this region.

1. Introduction

The variations in water resources and hydrological variables on timescales of years to decades has become a critical issue because of water scarcity and the growth of global water demand [1,2]. In this context, it is essential to link local river streamflows with large-scale climate patterns of oceanographic and atmospheric variability; this is critical to predicting the evolution of the hydrological and ecological functioning of rivers [3], and therefore to improving the management of water resources and hydrological hazards [4,5].
Climate variability on interannual-to-multidecadal timescales, which refers to fluctuations in the climate system around the long-term trend, mostly results from the coupled interactions between oceanic and atmospheric components. Teleconnection patterns can explain this variability at global scale (e.g., [6]). Discharge records for major rivers around the world show multidecadal fluctuations linked to such large-scale climate patterns (review in [7]). For example, the El-Niño-Southern Oscillation (ENSO), which is a major driver of temperature and precipitation variability in the Pacific region, correlates well with river discharge in this region and beyond [8,9,10,11,12]. Chiew and McMahon [13] found a strong and consistent ENSO-discharge teleconnection in Australia and New Zealand, and Central and South America, as well as a weaker signal in some parts of Africa and North America. According to Ward et al. [9], floods are significantly longer during both El Niño and La Niña years at the global scale, compared to neutral years.
The large-scale atmospheric circulation over the North Atlantic has long been recognized as a critical driver of climate variability in Europe [14]. The North Atlantic Oscillation (NAO) is considered the dominant mode of decadal to interdecadal climate variability in this region [15], as shifts in the NAO phases change wind strength and direction, redistributing heat and moisture fluxes [16,17]. The NAO is known to influence precipitation, and consequently streamflow, over the Mediterranean basin, especially in Central European [18,19] and middle Eastern rivers [20,21]. During the positive phase of the NAO, which reflects an intensified Atlantic stream associated with a northward shift of storm tracks, flood occurrence increases in northern Europe while the opposite is observed in southern and eastern Europe [22]. In contrast, the links between hydrological variables and climate indices in western Europe are much less clear. Trigo et al. [23] and Lorenzo-Lacruz et al. [24] found that the winter NAO modulates the winter streamflow variability on the Iberian Peninsula. However, Giuntoli et al. [25] pointed out that France seems to be located in an area of weak influence of the winter NAO, after observing very little correlation between it and drought severity. Several studies have used wavelet analysis in attempts to find coherence between the temporal modes of variability of the winter NAO and the discharges of French rivers [26,27,28], but no strong correlations were highlighted. In the case of the United Kingdom, Burt and Howden [29] demonstrated a strong positive correlation between the winter NAO index, and river discharge and precipitation on the northwest coast, but a lower correlation in the rest of the country. In these previous studies, the winter months NAO index (DJFM) is most often used and related to interannual variations of river discharge, while summer NAO controls flash flood and droughts [30]. To our knowledge, there are no holistic studies at the scale of western Europe that have systematically investigated the links between climate variability, through all existing dominant teleconnection patterns in the region, and streamflow variability.
Natural modes of climate variability have a strong effect on rainfall, temperature, and storm tracks and intensity but also on wave energy propagating to the coast (e.g., [31]), and on the marine and terrestrial biosphere [32]. Winter mean wave energy has long been known to strongly and positively correlate with the NAO at the most northernly latitudes of the Atlantic coast of Europe [33]. However, this correlation drops off dramatically south of Ireland [34], which is similar in pattern to river discharge. A new climate index was developed by Castelle et al. [34], called the West Europe Pressure Anomaly (WEPA), which outperformed the conventional teleconnection indices, such as the NAO, Scandinavia (SCAN), and East Atlantic (EA) indices, in explaining the variability in winter wave height on the Atlantic coast of Europe, from Portugal to the UK (52° N). In line with the Hurrell definition of the NAO index as the gradient of normalized sea-level pressure between the Reykjavik station (Iceland) and a southern station (e.g., Lisbon, Portugal) [16], the WEPA index is defined as the normalized gradient of sea-level pressure between Valentia (Ireland) and Santa Cruz de Tenerife (Canary Islands, Spain) stations. A positive WEPA corresponds to a southward shift and an intensification of the Icelandic-Low/Azores-High dipole across the northeast Atlantic, driving severe storms and high-energy waves toward the Atlantic coast of Europe, south of 52° N [34]. Interestingly enough, WEPA was the only climate index able to capture the 2013/2014 winter, characterized by remarkable temporal and spatial clustering of extreme storms [35], driving widespread flooding in the west of Europe [36]. However, the link between the WEPA and river discharge, particularly in regions where information on correlation with all teleconnection patterns is lacking, has never been investigated.
The aim of this paper is to explain the multidecadal variability of river discharge and precipitation in western Europe, particularly during the wet season, and its link with climate variability. This study is based on an analysis of 60-year monthly precipitation and river flow data from 18 major western European rivers and its relationship with 11 climate indices. The correlations between winter river discharge and the climate indices are presented first. The interannual variability in seasonal river discharge is then analyzed, followed by analysis and discussion of the precipitation data.

2. Materials and Methods

2.1. Study Sites

Eighteen rivers were selected covering the west of Europe (10° W–7° E, 36° N–50° N), from Scotland in the north to southern Spain (Figure 1b–d, Table 1), according to two criteria: (1) availability of river-flow time series covering a common period between the 1950s and the present, recorded close to the outlet; (2) major basins were prioritized. Table 1 lists the main characteristics of the river basins, the gauges used in this study and the winter mean (DJFM) river discharge.
The UK rivers (Spey, Almond, Tyne, Trent, Severn, Wye, Thames, and Tamar) are relatively shorter than the rivers in southwest Europe, and characterized by relatively smaller basins (<14,000 km2) and weaker winter river discharges (9–147 m3/s, Table 1). The UK river-flow patterns are also less influenced by seasonal contrasts in precipitation and snowmelt. However, the seasonal variability in temperature, and therefore in evapotranspiration, imposes a marked seasonality on river discharge, with maximum and minimum values in winter and summer, respectively [37].
All the major French rivers, Seine, Loire, Rhône, Dordogne, Garonne, and Adour, were selected. They are characterized by large river basins (from 16,820 to 117,500 km2), which together cover approximately 70% of mainland France (Table 1). Consequently, winter river discharges are relatively larger, with means from 138 m3/s for the small Adour basin to 2050 m3/s for the large Rhône basin. These basins are characterized by a continental climate in the upland regions, with snowy winters and warm summers. An oceanic climate influences the middle and lower regions of the Loire, Seine, Garonne, and Adour River, characterized by moderate temperatures and heavy precipitations. The Rhône is influenced by a Mediterranean climate in its lower region [27,38]. Consequently, river flow varies seasonally, with maximum and minimum values in winter and summer, respectively. Nonetheless, the hydrological regimes can be complex. For example, the Garonne flow shows a second peak around April [39] and the maximum flows of the Rhône expand from November to March [27].
Four major Iberian rivers (Ebro, Douro, Tagus, and Guadalquivir) met the selection criteria. They are characterized by large river basins (57,020–97,480 km2) and moderate winter discharges (225–672 m3/s). In this region, the topography, together with large atmospheric circulation patterns, lead to a northwest-to-southeast gradient in annual precipitation. Basins in the northern section of the Atlantic watershed (Douro and Tagus) have an abundant flow compared to the southern basins (Guadalquivir) [24]. In general, the highly seasonal regime typical of the Mediterranean-Oceanic climate leads to maximum flows in winter, and long and dry summer periods with low river discharge [23].

2.2. Discharge, Precipitation, and Evapotranspiration Data

This work is based on monthly time series of river discharge from 1959 to 2018, the common period of available data at all river gauges. Table 1 lists the selected gauges for each river, together with the drained area at those locations. In the cases of the Seine, Dordogne, Douro, and Tagus Rivers, interspersed data collected at two nearby gauges were combined to cover the whole study period. In these cases, each pair of gauges covered practically the same drained area (Table 1, differences less than 10%); there was no significant difference between their common records (p > 0.05). There were only three missing values in the entire river-discharge dataset: the year 2010 for the Almond River; the years 2008 and 2015 for the Tagus River. The selected time series were extracted from the UK National River Flow Archive, the French National database Banque Hydro, the Portuguese Water Institute database, the Guadalquivir River Management Authority, and the Ebro River Management Authority.
Monthly-mean precipitation between 1959 and 2018 and monthly-mean evapotranspiration between 1959 and 2012 for Europe and northern Africa come from the Climatic Research Unit (CRU) dataset [40]. This high-resolution (0.5° latitude by 0.5° longitude) gridded dataset uses a dense network of observations. In particular, we use the monthly rainfall and evapotranspiration anomalies extracted from The Global Climate Monitor [41], which gives the difference from the 30-year average (1961–1990) for each month.

2.3. Climate Indices

The monthly teleconnection indices (NAO, EA, SCAND, WP, EP, PNA, WR, TNH, and POL) are calculated by applying the Rotated Principal Component Analysis to monthly mean standardized 500 mb height anomalies [42]. We used the normalized values provided by the NOAA Climate Prediction Center. The NAO of Jones et al. [43], which uses Gibraltar as the southern station, was also included, as it was used in prior works (e.g., [23]). The West Europe Pressure Anomaly (WEPA) is calculated as the normalized difference of sea-level pressure between Valentia (Ireland) and Santa Cruz de Tenerife (Spain, Figure 1) using in situ station data collected from 1942 to 2019 (see [34] for details).

2.4. Methodology

Consistent with previous hydroclimate studies (e.g., [23,29,44,45]), this work focused on the year-to-year variability in boreal winter streamflow, although monthly variability was also explored. Winter averages of the normalized climate indices, normalized river discharges, and grid-point precipitation and precipitation minus evapotranspiration anomalies were calculated by averaging the values of the Boreal winter months (December, January, February, and March, DJFM) from 1959 to 2018 (60 winters). Correlations between the time series of winter-averaged hydroclimatic variables and climate indices were quantified through the Pearson correlation coefficient R.

3. Results and Discussion

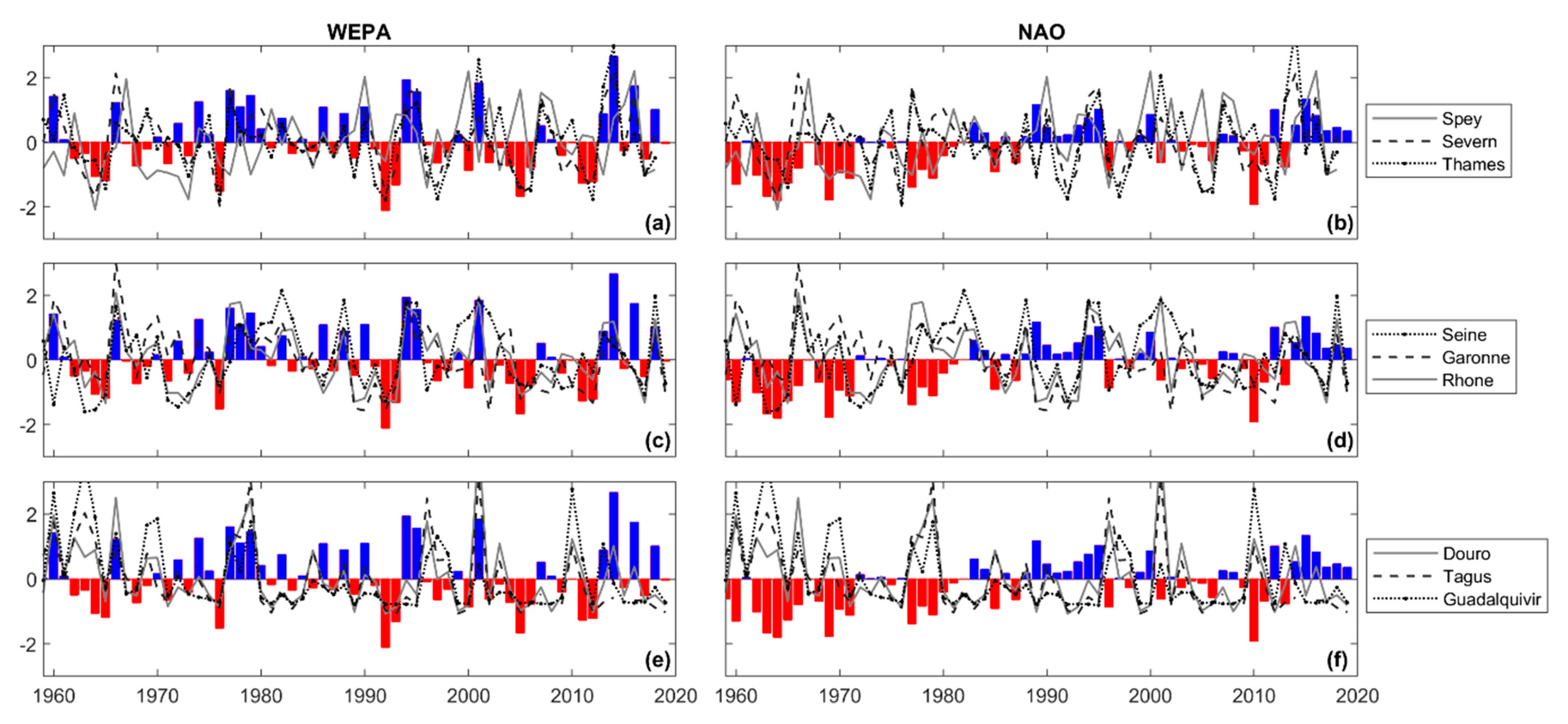
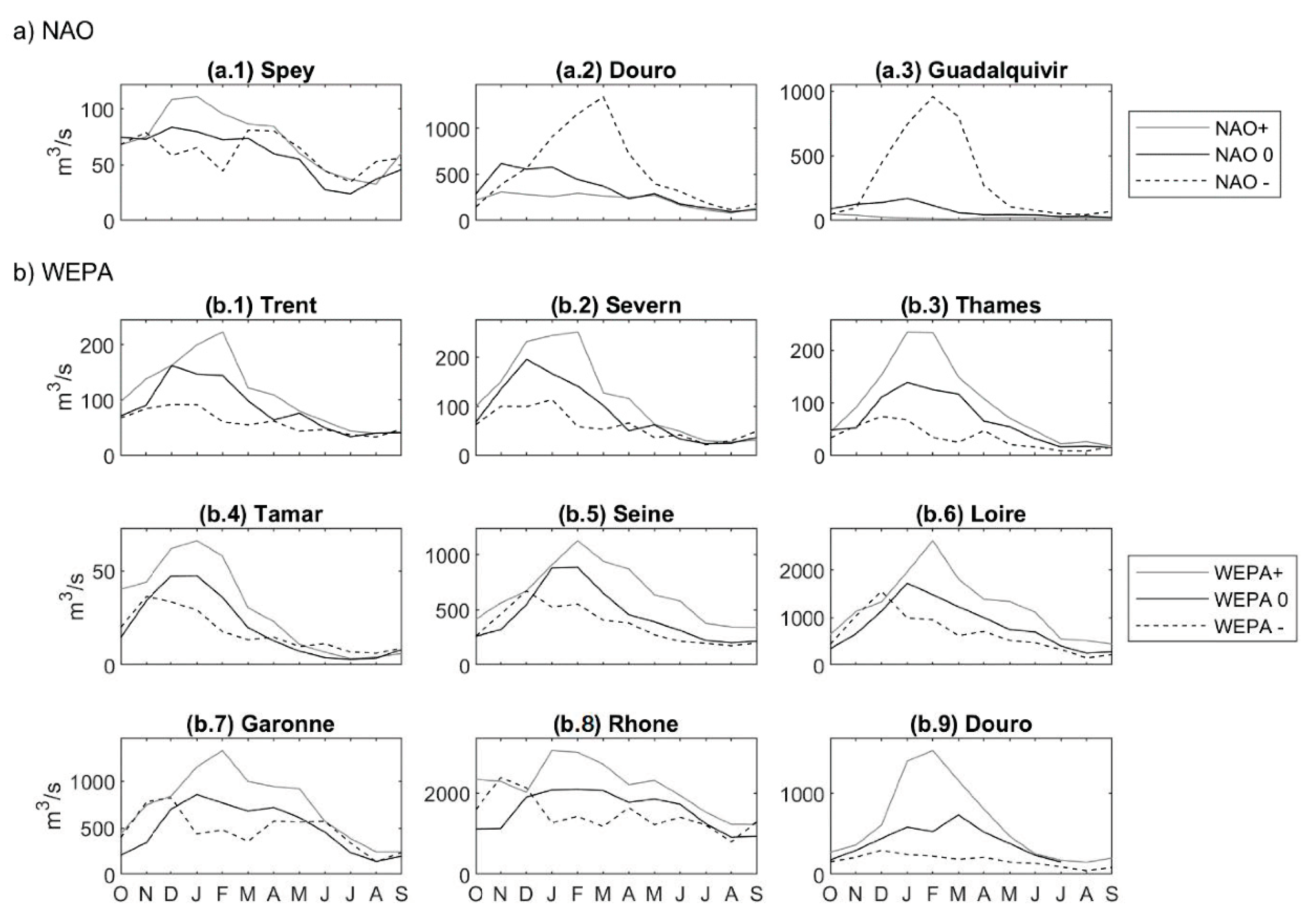
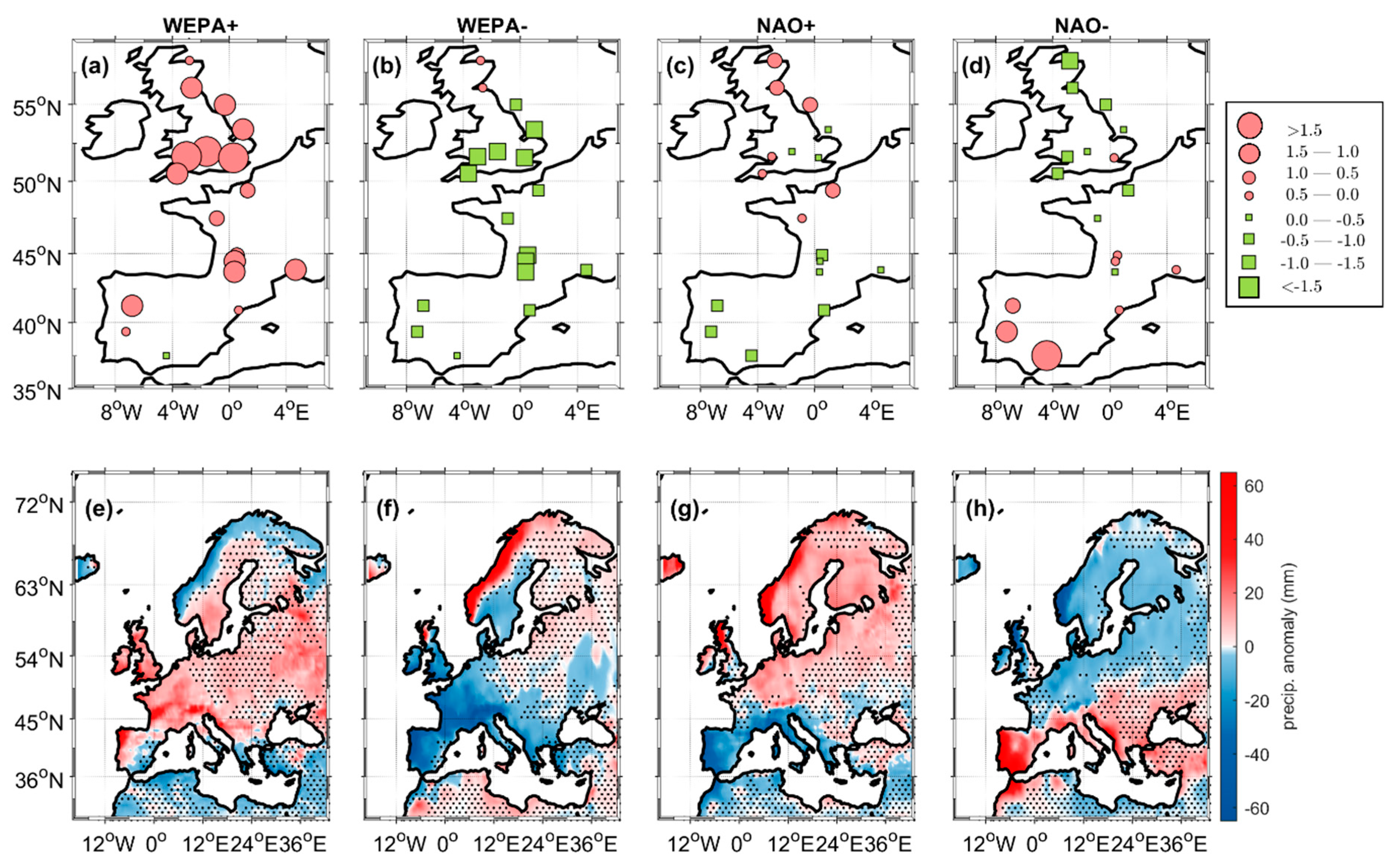
3.1. River-Discharge Variability

Table 2 shows the R values for the correlation between the winter mean climate indices and river discharges for the 18 river basins. The winter river-discharge variabilities in the Spey and Almond Rivers in the UK, at the more northerly latitudes, were well correlated with the NAO index (R = 0.56), and, in a lesser degree, with the SCAN index (R = 0.39–0.47); these R values dropped off dramatically south of 56° N, that is, south of Scotland. The WEPA index consistently showed the highest correlation with winter river discharge for the English, Welsh, and French rivers (Table 2). The correlation with WEPA was particularly strong for rivers in the middle and south of the UK, with R > 0.72; the correlation was significant (p < 0.01). In this region, winter river discharge variability also has a significant but weaker relationship with the EA (R = 0.46–0.59) and the POL index (R = −0.36–−0.43), except for the Thames Rivers.
French rivers were also characterized by a strong and significant correlation between WEPA and winter river discharge (R = 0.41–0.66). A significant but moderate correlation with the WR index (R = 0.27–0.38) was also found in this region. In contrast, there was an overall poor correlation between winter river discharge and the winter NAO index.
On the Iberian Peninsula, winter river-discharge variability was significantly and negatively correlated with NAO, with R increasing from the north (R = −0.44–−0.48 for the Ebro and Douro Rivers) to the south (R = 0.72 for Guadalquivir). In contrast, the relationship with WEPA and EA (significant for Douro and Tagus) decreased toward the south in this region, from R = 0.43–0.48 for the Dour River in the north to R = 0.07–0.12 for the Guadalquivir River in the south.
Therefore, the NAO and WEPA indices were the two main climate indices that best explained winter river-flow variability in western Europe, with WEPA proving the greatest R from 55° N (south Scotland) to 42° N (north Iberian Peninsula).
Figure 2 shows the temporal evolution of the normalized river discharge, WEPA and NAO for nine rivers. WEPA showed a large interannual variability, consistent with the alternating years of high and low discharge in the Welsh (e.g., Severn, Figure 2a), English (e.g., Thames, Figure 2a), French (e.g., Seine, Garonne, Rhône, Figure 2c) and, to a lesser extent, north Iberian (e.g., Douro, Figure 2e) rivers. Unlike NAO, WEPA (positive phase) captured the years characterized by important flooding events in these regions: the 2013/2014 floods in the UK (Figure 2a), in which the Thames discharge reached its highest peak on record [46,47]; the 2018 floods in France (Figure 2c) that flooded the city center of Paris [48]. NAO also showed some low-frequency variations but was mainly characterized by a marked trend toward the positive phase over the last few decades (Figure 2b,d,f). This trend is in line with the general decrease of winter discharge of the Iberian rivers from the 1980s (Figure 2f). In these southern latitudes, positive NAO phases corresponded to lower winter river discharges, while negative phases captured wet years (Figure 2f) such as 2010 that was characterized by dramatic floods in the Guadalquivir basin [49]. For rivers in the north of the UK, the positive (negative) NAO phases captured many, but not all, wet (dry) years (Figure 2b).
To gain further insight into the WEPA and NAO influences on the whole hydrological cycle, Figure 3 shows the monthly river flows from October to September of the years characterized by winters with positive (WEPA+/NAO+), neutral (WEPA0/NAO0), and negative (WEPA−/NAO−) phases of each index, calculated by averaging the river flow in the five years with the largest, closest-to-zero, and smallest values, respectively.
The Spey River in Scotland showed an obvious difference in river discharge for the winter months (DJFM) only between the NAO− years (44–65 m3/s) and the NAO+ years (86–111 m3/s) (Figure 3a.1). In the case of the Welsh and English rivers, the differences in mean river discharge between the WEPA− and WEPA+ years (Figure 3b.1–b.4) were remarkable in the winter months, and notable also in the spring months (April, May). For example, the mean discharge of the Thames River varied from 34 (WEPA−) to 234 m3/s (WEPA+) in February; from 47 to 107 m3/s in April (Figure 3b.3).
This was also the case for the French rivers; other than the major differences in the winter months (the mean discharge doubled between WEPA− and WEPA+ in most of the rivers), mean discharge was also slightly higher for the WEPA+ years in the autumn and spring months. This is related to the hydrological regime, characterized by secondary flow peaks from precipitation and snowmelt in these periods (Section 2.1). The mean summer discharge of the Seine and Loire Rivers was also slightly lower during the WEPA− years (e.g., 177 m3/s for Seine) than during WEPA+ years (348 m3/s).
The mean river discharge of the Iberian rivers showed major changes between the positive and negative NAO phases from January to May (Figure 3a.2,3). It is noticeable that the differences in mean discharge between the NAO+ years (e.g., 958 m3/s for the Guadalquivir in February) and the NAO0 years (117 m3/s) were much greater than the differences between the NAO− years (14 m3/s) and the NAO0 years. WEPA can also explain the differences in the Douro discharge between wet and dry years in the winter and spring months. In summary, WEPA and NAO mainly control the multidecadal variability in the winter river discharge, but can also impact, to a lesser extent, the hydrological variability in the other seasons, depending on the hydrological regime of the river.
From a hydroclimatic point of view, western Europe can be divided into three regions: river flow variability correlated with winter NAO in the southern and far-northern latitudes, and with winter WEPA in the middle and northern latitudes, from 42° N to 55° N; this is consistent with previous work. Burt and Howden [29] evaluated the interannual variability of seasonal discharge at 86 river-gauge stations in the UK but only found strong correlations with NAO at the northwest region for the winter discharges and, to a lesser extent, for the spring discharges. Lorenzo-Lacruz et al. [24] found a significant response of river discharge to the variability in the NAO index across the entire Iberian Peninsula in winter and autumn, particularly in the Atlantic watershed. This result was corroborated by Trigo et al. [23] for the Douro, Tagus, and Guadiana rivers. Chevalier et al. [27] found a strong coherence between river discharges in the four main French basins (Seine, Loire, Garonne, and Rhone), suggesting a common external forcing on hydrological variability They also found common modes of variability at multidecadal scales between the NAO and river discharge in these basins. However, the WEPA largely outperformed all the other climate indices tested in the previous studies in explaining discharge interannual variability in the UK and French rivers [22,26,27] and is the only index able to capture the wettest years. All these previous studies agreed that the river-flow variability is a direct consequence of the precipitation variability, which depends on the interannual shifts in the atmospheric dynamics on the North Atlantic region [7,22,23,28,29,50,51].

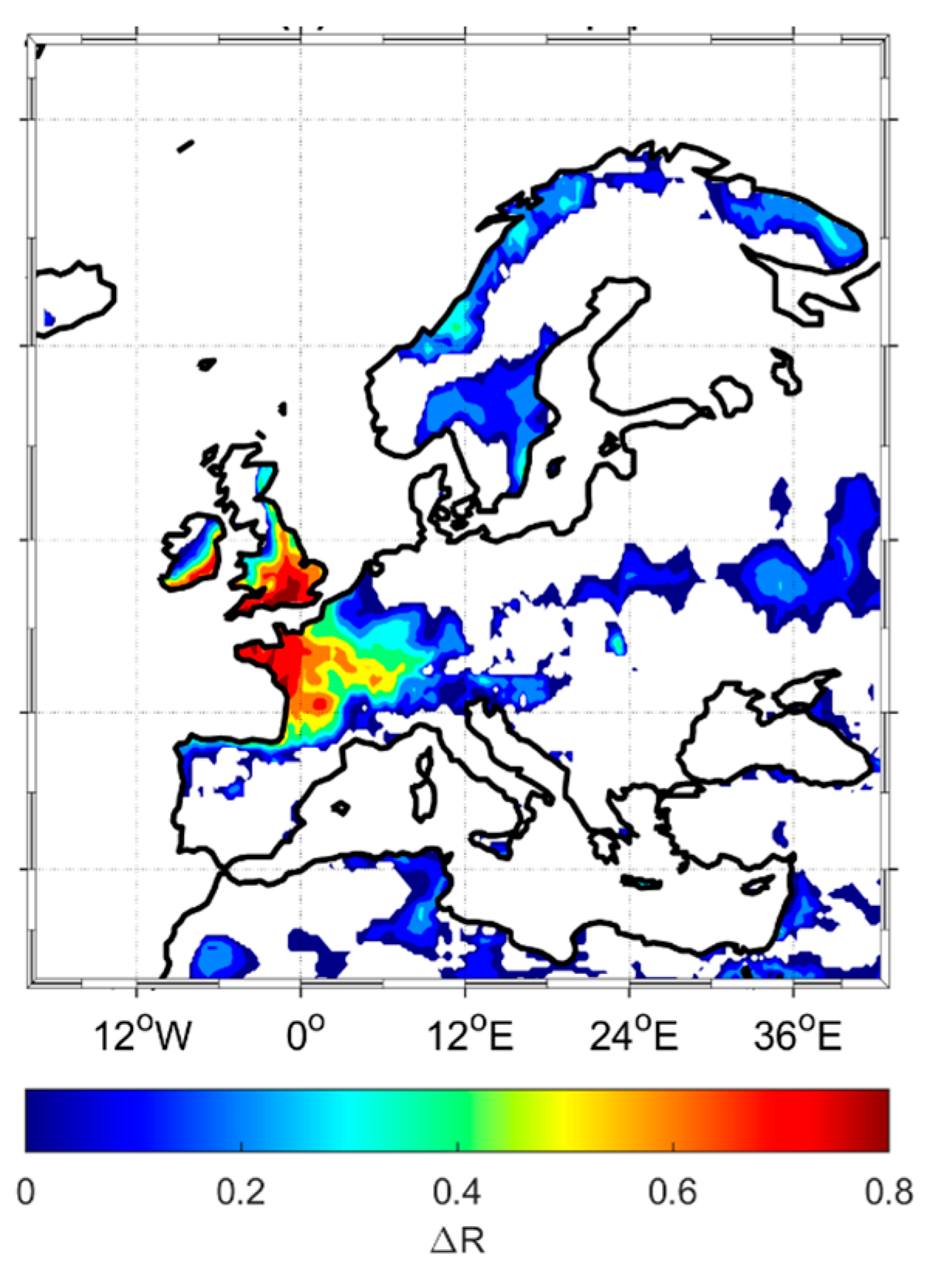
3.2. Precipitation Variability

To help further understanding the climate influence on river discharge and precipitation in western Europe, Figure 4 illustrates the spatial distribution of correlations between the winter mean precipitation anomaly and the four main climate indices that best correlated with river discharge in this region (Table 2), the WEPA, NAO, SCAN, and EA indices. The spatial patterns were consistent with the correlations found for winter river discharge. NAO and SCAN showed higher R with winter precipitation in northern Europe (up to 0.65 and −0.5, respectively, in Scotland). WEPA had the highest correlation in middle-to-south UK (R increased southwards from 0.40 to 0.85) and in France (R decreased southwards from 0.85 to 0.70); EA showed only moderate correlations in this region. On the Iberian Peninsula, WEPA (R ≈ 0.4–0.6) and NAO (R ≈ −0.4–−0.6) explained winter precipitation variability in the northwest, while NAO showed the highest correlation in the south (R up to 0.75). These results confirm the robust relationship between river discharge, precipitation, and the modes of large-scale atmospheric variability.
The spatial correlations between these main climate indices and the precipitation minus the evapotranspiration is given in Supplementary Materials. Results show similar patterns than correlations with precipitation. The correlation with the NAO index in the Iberian Peninsula and east of France was nonetheless enhanced. This is probably due to the effect of air temperature on the evapotranspiration. According to previous studies (e.g., [16,44,52]), the NAO explains the temperature variability over Europe by the advection of heat and the modulation of short-wave and long-wave radiation by cloud-cover variations.
The correlations with precipitation were slightly stronger than the corresponding correlations with river discharge, particularly in France, and showed clear north–south gradients. For example, the discharge of the Seine River had a lower correlation with WEPA than the southern French rivers (Table 2) while the precipitation correlation in France decreased toward the south (Figure 4a). The Thames River also broke the increasing correlation gradient toward the south between WEPA and river discharge (Table 2). These results suggest that water-storage variability and other catchment characteristics, such as the altitude [29,37] can also impact the interannual variability of river discharge.
To further emphasize the importance of WEPA to the hydrological regime of the western European rivers, Figure 4e–g shows the spatial distributions of the climate indices that best explain the winter precipitation variability in western Europe. The optimum climate index was defined as the index with the greatest |R| related to the local winter mean precipitation. Consistent with previous studies [22,23,29,51], if we disregard the WEPA index (Figure 4e), the two optimum climate indices explaining winter precipitation in western Europe were NAO (north of 56° N and south of 43° N) and EA. When WEPA was included (Figure 4f), this index outscored the other three indices in the west of Europe, from 41–42° N to 56° N. Compared to EA, WEPA had an increased correlation with inter precipitation, up by 0.3 and 0.45 in South UK and France, respectively (Figure 4g), corresponding in an increase of R locally exceeding 180%.
Given that most of the previous studies used the NAO index to explain the precipitation variability in these regions [28,53,54,55,56], Figure 5 shows the increase in R between the correlations of NAO (Figure 4b) and WEPA (Figure 4a) with winter precipitation. Compared to NAO, WEPA increased R by 0.8 in the southern UK, in the west of France, and in southern Ireland. The correlation with WEPA was also slightly higher in the Alps region (increase in R of up to 0.6), Belgium (up to 0.45), southern Germany (up to 0.30), the Cantabrian coast (northern Spain, up to 0.50), Tunisia (up to 0.30), and Ukraine (up to 0.30), which demonstrates that WEPA can also be used in these regions to address river-discharge variability.
To further gain insight into the hydroclimate patterns for both WEPA and NAO, Figure 6 shows the mean river-flow and precipitation anomalies for the years characterized by positive (WEPA/NAO+) and negative (WEPA/NAO−) phases of both indices, calculated by averaging the five years characterized by the greatest and smallest values, respectively. Storm tracks, SLP, and wind surface during these same years are available in Castelle et al. [34] and help to provide physical insight into the atmospheric phenomenon. During the NAO+ years, weaker and stronger river discharges were observed at southern and northern latitudes, respectively (Figure 6c). The opposite situation was observed during the NAO− years (Figure 6d). The positive phase of the NAO has long been associated with deep low-pressures crossing between Greenland and Scotland, higher W–SW wind over 60° N [16,34], and stronger precipitation over the northern latitudes (Figure 6g) [16]. During the NAO− years, there was higher precipitation over the southern Europe and dry winters in the north (Figure 6h) [50,51]. During the WEPA+ years, higher river discharges were observed through all western Europe, particularly from 41° N to 56° N (Figure 6a). As shown in Castelle et al. [34], the positive phase of WEPA reflects a southward-shifted and intensified Icelandic-Low/Azores-High dipole driving increased W–SW winds near 45°N across the Atlantic Ocean, bringing wetter winters at these latitudes (Figure 6e). In contrast, during the WEPA− years, fewer storms [34], lower precipitation, and river discharges were observed in this region (Figure 6b,f).

3.3. Implications and Future Work

The results of this study imply that the precipitation and river-discharge variability in western Europe is strongly influenced by changes in atmospheric circulation, best described by the WEPA index between latitudes 42° N to 55° N, and the NAO index below and above these latitudes. These two indices have already demonstrated a strong ability to explain ocean wave climate and coastal hazards along the Atlantic coast of Europe [57,58,59,60,61], and could help understand and predict other hydrological variables in this region. Future works linking river streamflow at regional or catchment scales with large-scale climate patterns may consider water storage, orographic effects, and the effect of temperature to reduce uncertainties. The outputs of this work could also help to understand and predict water-related hazards such as flooding [7,62], drought [63]; river-bank erosion [64]; economical parameters such as potential hydroelectricity production [23]; the variability in physico-chemical parameters affected by river discharge such as turbidity [65]. Recent climate-forecast systems have demonstrated improved seasonal predictions of the NAO [66,67,68]. The capacity of these climate models to forecast season-ahead winter WEPA and NAO indices will be key to anticipating hydrological hazards and risks in this region, improving the management of water resources.

4. Conclusions

The relationship between climate variability, described by leading climate indices, and winter river discharge variability in western Europe was investigated for the period 1959–2018. The relevance of the winter NAO index to explain the variability in winter river flow in far-northern (Scotland) and southern (Iberian Peninsula) latitudes was confirmed, while winter WEPA significantly outperformed all the other atmospheric modes in explaining river discharge in northern (UK) and middle (France) latitudes (R = 0.41–0.83). WEPA and NAO are also the most relevant indices to explain precipitation in these regions. WEPA increases the correlations with winter precipitation up to 0.8 in many regions of western and central Europe. The positive phase of WEPA reflects an intensification of the Icelandic-Low/Azores-High dipole, driving enhanced precipitation and river discharge in these regions. The differences in river discharge between positive, negative, and neutral phases of winter WEPA are also evident for autumn and spring river discharge. We anticipate that WEPA is an essential index to understand hydrodynamic hazards in western Europe. Further studies at regional or basin scales will allow considering specific catchment characteristic such as the water storage variability and orography in order to further explore the explanatory ability of this index for other seasons and other hydrological variables, such as flood timing and duration.

Supplementary Materials

The following are available online at https://www.mdpi.com/2073-4441/13/3/257/s1, Figure S1: Spatial correlation of winter-averaged (DJFM) precipitation minus evapotranspiration anomaly with winter-averaged (a) WEPA, (b) NAO, (c) SCAN and (d) EA. Dotted areas show statistically insignificant values (p = 0.05).

Author Contributions

Both authors designed the study. I.J.-R. performed the data analysis and drafted the manuscript. B.C. conceived the study concept and provided critical feedback on the analysis and manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

River-flow data were provided by the UK National River Flow Archive (NRFA, https://nrfa.ceh.ac.uk/), the French National database Banque Hydro (http://www.hydro.eaufrance.fr/selection.php), the Portuguese Water Institute database (SNIRH, http://snirh.pt), the Guadalquivir River management authority, and the Ebro River management authority. Precipitation data were developed by the Climatic Research Unit (CRU) dataset and available in the Global Climate Monitor (https://www.globalclimatemonitor.org/#). The North-Hemisphere monthly teleconnection indices are available in https://www.cpc.ncep.noaa.gov/data/teledoc/telecontents.shtml. The DJFM time series of WEPA used in this work will be included as supporting information in the accepted manuscript.

Acknowledgments

The authors thank Peter McIntyre for help with editing.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Alcamo, J.; Flörke, M.; Märker, M. Future Long-Term Changes in Global Water Resources Driven by Socio-Economic and Climatic Changes. Hydrol. Sci. J. 2007, 52, 247–275. [Google Scholar] [CrossRef]
  2. Sathasivan, A.; Korotta-Gamage, S.M.; Rahman, A. Uncertainties in Water Supplies Due to Changing Climate and Extreme Weather Events. In Sustainable Water: Resources, Management and Challenges; Gude, V.G., Gadhamshetty, V., Kandiah, R., Eds.; Nova Science Pub Inc.: Hauppauge, NY, USA, 2020; pp. 135–170. [Google Scholar]
  3. Naiman, R.J.; Latterell, J.J.; Pettit, N.E.; Olden, J.D. Flow Variability and the Biophysical Vitality of River Systems. Comptes Rendus Geosci. 2008, 342, 629–643. [Google Scholar] [CrossRef] [Green Version]
  4. IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
  5. Merz, B.; Aerts, J.; Arnbjerg-Nielsen, K.; Baldi, M.; Becker, A.; Bichet, A.; Blöschl, G.; Bouwer, L.M.; Brauer, A.; Cioffi, F.; et al. Floods and Climate: Emerging Perspectives for Flood Risk Assessment and Management. Nat. Hazards Earth Syst. Sci. 2014, 14, 1921–1942. [Google Scholar] [CrossRef] [Green Version]
  6. Liu, Z.; Alexander, M. Atmospheric Bridge, Oceanic Tunnel, and Global Climatic Teleconnections. Rev. Geophys. 2007, 45, RG2005. [Google Scholar] [CrossRef]
  7. Kundzewicz, Z.W.; Szwed, M.; Pińskwar, I. Climate Variability and Floods-A Global Review. Water 2019, 11, 1399. [Google Scholar] [CrossRef] [Green Version]
  8. Dettinger, M.D.; Cayan, D.R.; McCabe, G.J. Multiscale Streamflow Variability Associated with El Niño/Southern Oscillation. In El Nino and the Southern Oscillation; Diaz, H.F., Markgraf, V., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 113–147. [Google Scholar] [CrossRef]
  9. Ward, P.J.; Beets, W.; Bouwer, L.M.; Aerts, J.C.J.H.; Renssen, H. Sensitivity of River Discharge to ENSO. Geophys. Res. Lett. 2010, 37, L12402. [Google Scholar] [CrossRef] [Green Version]
  10. Ward, P.J.; Kummu, M.; Lall, U. Flood Frequencies and Durations and Their Response to El Niño Southern Oscillation: Global Analysis. J. Hydrol. 2016, 539, 358–378. [Google Scholar] [CrossRef] [Green Version]
  11. Dehghani, M.; Salehi, S.; Mosavi, A.; Nabipour, N.; Shamshirband, S.; Ghamisi, P. Spatial Analysis of Seasonal Precipitation over Iran: Co-Variation with Climate Indices. Int. J. Geo-Inf. 2020, 9, 73. [Google Scholar] [CrossRef] [Green Version]
  12. Le, J.A.; El-Askary, H.M.; Allali, M.; Sayed, E.; Sweliem, H.; Piechota, T.C.; Struppa, D.C. Characterizing El Niño-Southern Oscillation Effects on the Blue Nile Yield and the Nile River Basin Precipitation Using Empirical Mode Decomposition. Earth Syst. Environ. 2020, 4, 699–711. [Google Scholar] [CrossRef]
  13. Chiew, F.H.S.; McMahon, T.A. Global ENSO-Streamflow Teleconnection, Streamflow Forecasting and Interannual Variability. Hydrol. Sci. J. 2002, 47, 505–522. [Google Scholar] [CrossRef] [Green Version]
  14. Rodwell, M.J.; Rowell, D.P.; Folland, C.K. Oceanic Forcing of the Wintertime North Atlantic Oscillation and European Climate. Nature 1999, 398, 25–28. [Google Scholar] [CrossRef]
  15. Parker, D.; Folland, C.; Scaife, A.; Knight, J.; Colman, A.; Baines, P.; Dong, B. Decadal to Multidecadal Variability and the Climate Change Background. J. Geophys. Res. Atmos. 2007, 112, D18115. [Google Scholar] [CrossRef] [Green Version]
  16. Hurrell, J.W. Decadal Trends in the North Atlantic Oscillation: Regional Temperatures and Precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef] [Green Version]
  17. Hurrell, J.W.; Deser, C. North Atlantic Climate Variability: The Role of the North Atlantic Oscillation. J. Mar. Syst. 2009, 78, 28–41. [Google Scholar] [CrossRef]
  18. Rîmbu, N.; Boroneanţ, C.; Buţǎ, C.; Dima, M. Decadal Variability of the Danube River Flow in the Lower Basin and Its Relation with the North Atlantic Oscillation. Int. J. Climatol. 2002, 22, 1169–1179. [Google Scholar] [CrossRef]
  19. Stanev, E.V.; Peneva, E.L. Regional Sea Level Response to Global Climatic Change: Black Sea Examples. Glob. Planet. Chang. 2001, 32, 33–47. [Google Scholar] [CrossRef]
  20. Cullen, H.M.; DeMenocal, P.B. North Atlantic Influence on Tigris-Euphrates Streamflow. Int. J. Climatol. 2000, 20, 853–863. [Google Scholar] [CrossRef]
  21. Cullen, H.M.; Kaplan, A.; Arkin, P.A.; DeMenocal, P.B. Impact of the North Atlantic Oscillation on Middle Eastern Climate and Streamflow. Clim. Chang. 2002, 55, 315–338. [Google Scholar] [CrossRef]
  22. Nobre, G.G.; Jongman, B.; Aerts, J.; Ward, P.J. The Role of Climate Variability in Extreme Floods in Europe. Environ. Res. Lett. 2017, 12, 084012. [Google Scholar] [CrossRef]
  23. Trigo, R.M.; Pozo-Vázquez, D.; Osborn, T.J.; Castro-Díez, Y.; Gámiz-Fortis, S.; Esteban-Parra, M.J. North Atlantic Oscillation Influence on Precipitation, River Flow and Water Resources in the Iberian Peninsula. Int. J. Climatol. 2004, 24, 925–944. [Google Scholar] [CrossRef]
  24. Lorenzo-Lacruz, J.; Vicente-Serrano, S.M.; López-Moreno, J.I.; González-Hidalgo, J.C.; Morán-Tejeda, E. The Response of Iberian Rivers to the North Atlantic Oscillation. Hydrol. Earth Syst. Sci. 2011, 15, 2581–2597. [Google Scholar] [CrossRef] [Green Version]
  25. Giuntoli, I.; Renard, B.; Vidal, J.P.; Bard, A. Low Flows in France and Their Relationship to Large-Scale Climate Indices. J. Hydrol. 2013, 482, 105–118. [Google Scholar] [CrossRef] [Green Version]
  26. Massei, N.; Laignel, B.; Deloffre, J.; Mesquita, J.; Motelay, A.; Lafite, R.; Durand, A. Long-Term Hydrological Changes of the Seine River Flow (France) and Their Relation to the North Atlantic Oscillation over the Period 1950–2008. Int. J. Climatol. 2010, 30, 2146–2154. [Google Scholar] [CrossRef]
  27. Chevalier, L.; Laignel, B.; Massei, N.; Munier, S.; Becker, M.; Turki, I.; Coynel, A.; Cazenave, A. Hydrological Variability of Major French Rivers over Recent Decades, Assessed from Gauging Station and GRACE Observations. Hydrol. Sci. J. 2014, 59, 1844–1855. [Google Scholar] [CrossRef] [Green Version]
  28. Massei, N.; Dieppois, B.; Hannah, D.M.; Lavers, D.A.; Fossa, M.; Laignel, B.; Debret, M. Multi-Time-Scale Hydroclimate Dynamics of a Regional Watershed and Links to Large-Scale Atmospheric Circulation: Application to the Seine River Catchment, France. J. Hydrol. 2017, 546, 262–275. [Google Scholar] [CrossRef] [Green Version]
  29. Burt, T.P.; Howden, N.J.K. North Atlantic Oscillation Amplifies Orographic Precipitation and River Flow in Upland Britain. Water Resour. Res. 2013, 49, 3504–3515. [Google Scholar] [CrossRef]
  30. Shimura, T.; Mori, N.; Mase, H. Ocean Waves and Teleconnection Patterns in the Northern Hemisphere. J. Clim. 2013, 26, 8654–8670. [Google Scholar] [CrossRef] [Green Version]
  31. Wang, G.; Schimel, D. Climate Change, Climate Modes, and Climate Impacts. Annu. Rev. Environ. Resour. 2003, 28, 1–28. [Google Scholar] [CrossRef] [Green Version]
  32. Folland, C.K.; Knight, J.; Linderholm, H.W.; Fereday, D.; Ineson, S.; Hurrel, J.W. The Summer North Atlantic Oscillation: Past, Present, and Future. J. Clim. 2009, 22, 1082–1103. [Google Scholar] [CrossRef]
  33. Bacon, S.; Carter, D.J.T. A Connection between Mean Wave Height and Atmospheric Pressure Gradient in the North Atlantic. Int. J. Climatol. 1993, 13, 423–436. [Google Scholar] [CrossRef]
  34. Castelle, B.; Dodet, G.; Masselink, G.; Scott, T. A New Climate Index Controlling Winter Wave Activity along the Atlantic Coast of Europe: The West Europe Pressure Anomaly. Geophys. Res. Lett. 2017, 45, 3586–3596. [Google Scholar] [CrossRef] [Green Version]
  35. Davies, H.C. Weather Chains during the 2013/2014 Winter and Their Significance for Seasonal Prediction. Nat. Geosci. 2015, 8, 833–837. [Google Scholar] [CrossRef]
  36. Thorne, C. Geographies of UK Flooding in 2013/4. Geogr. J. 2014, 108, 297–309. [Google Scholar] [CrossRef]
  37. Wilson, D.; Hannah, D.M.; McGregor, G.R. A Large-Scale Hydroclimatological Perspective on Western European River Flow Regimes. Hydrol. Res. 2013, 44, 809–833. [Google Scholar] [CrossRef]
  38. Joly, D.; Brossard, T.; Cardot, H.; Cavailhes, J.; Hilal, M.; Wavresky, P. Les Types de Climats En France, Une Construction Spatiale. CyberGeo Eur. J. Geogr. 2010. [Google Scholar] [CrossRef]
  39. Jalón-Rojas, I.; Schmidt, S.; Sottolichio, A. Turbidity in the Fluvial Gironde Estuary (Southwest France) Based on 10-Year Continuous Monitoring: Sensitivity to Hydrological Conditions. Hydrol. Earth Syst. Sci. 2015, 19, 2805–2819. [Google Scholar] [CrossRef] [Green Version]
  40. Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated High-Resolution Grids of Monthly Climatic Observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef] [Green Version]
  41. Camarillo-Naranjo, J.M.; Álvarez-Francoso, J.I.; Limones-Rodríguez, N.; Pita-López, M.F.; Aguilar-Alba, M. The Global Climate Monitor System: From Climate Data-Handling to Knowledge Dissemination. Int. J. Digit. Earth 2019, 12, 394–414. [Google Scholar] [CrossRef]
  42. Barnston, A.G.; Livezey, R.E. Classification, Seasonality and Persistence of Low-Frequency Atmospheric Circulation Patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
  43. Jones, P.D.; Jonsson, T.; Wheeler, D. Extension to the North Atlantic Oscillation Using Early Instrumental Pressure Observations from Gibraltar and South-West Iceland. Int. J. Climatol. 1997, 17, 1433–1450. [Google Scholar] [CrossRef]
  44. Trigo, R.M.; Osborn, T.J.; Corte-Real, J.M. The North Atlantic Oscillation Influence on Europe: Climate Impacts and Associated Physical Mechanisms. Clim. Res. 2002, 20, 9–17. [Google Scholar] [CrossRef]
  45. Bokhari, S.A.A.; Ahmad, B.; Ali, J.; Ahmad, S.; Mushtaq, H.; Rasul, G. Future Climate Change Projections of the Kabul River Basin Using a Multi-Model Ensemble of High-Resolution Statistically Downscaled Data. Earth Syst. Environ. 2018, 2, 477–497. [Google Scholar] [CrossRef]
  46. Kendon, M.; McCarthy, M. The UK’s Wet and Stormy Winter of 2013/2014. Weather 2015, 70, 40–47. [Google Scholar] [CrossRef]
  47. Neumann, J.; Arnal, L.; Magnusson, L.; Cloke, H. The 2013/14 Thames Basin Floods: Do Improved Meteorological Forecasts Lead to More Skillful Hydrological Forecasts at Seasonal Time Scales? J. Hydrometeorol. 2018, 19, 1059–1075. [Google Scholar] [CrossRef]
  48. Garnier, E. Lessons Learned from the Past for a Better Resilience to Contemporary Risks. Disaster Prev. Manag. An Int. J. 2019, 28, 786–803. [Google Scholar] [CrossRef]
  49. Bohorquez, P.; del Moral-Erencia, J.D. 100 Years of Competition between Reduction in Channel Capacity and Streamflow during Floods in the Guadalquivir River (Southern Spain). Remote Sens. 2017, 9, 727. [Google Scholar] [CrossRef] [Green Version]
  50. Ulbrich, U.; Christoph, M.; Pinto, J.G.; Corte-Real, J. Dependence of Winter Precipitation over Portugal on NAO and Baroclinic Wave Activity. Int. J. Climatol. 1999, 19, 379–390. [Google Scholar] [CrossRef]
  51. Vicente-Serrano, S.M.; López-Moreno, J.I. Hydrological Response to Different Time Scales of Climatological Drought: An Evaluation of the Standardized Precipitation Index in a Mountainous Mediterranean Basin. Hydrol. Earth Syst. Sci. 2005, 9, 523–533. [Google Scholar] [CrossRef] [Green Version]
  52. Heape, R.; Hirschi, J.; Sinha, B. Asymmetric Response of European Pressure and Temperature Anomalies to NAO Positive and NAO Negative Winters. Weather 2013, 3, 73–80. [Google Scholar] [CrossRef]
  53. Fritier, N.; Massei, N.; Laignel, B.; Durand, A.; Dieppois, B.; Deloffre, J. Links between NAO Fluctuations and Inter-Annual Variability of Winter-Months Precipitation in the Seine River Watershed (North-Western France). Comptes Rendus Geosci. 2012, 344, 396–405. [Google Scholar] [CrossRef]
  54. Boé, J. Modulation of Soil Moisture-Precipitation Interactions over France by Large Scale Circulation. Clim. Dyn. 2013, 40, 875–892. [Google Scholar] [CrossRef]
  55. Hermida, L.; López, L.; Merino, A.; Berthet, C.; García-Ortega, E.; Sánchez, J.L.; Dessens, J. Hailfall in Southwest France: Relationship with Precipitation, Trends and Wavelet Analysis. Atmos. Res. 2015, 156, 174–188. [Google Scholar] [CrossRef]
  56. Hall, R.J.; Hanna, E. North Atlantic Circulation Indices: Links with Summer and Winter UK Temperature and Precipitation and Implications for Seasonal Forecasting. Int. J. Climatol. 2018, 38, e660–e677. [Google Scholar] [CrossRef]
  57. Burvingt, O.; Masselink, G.; Scott, T.; Davidson, M.; Russell, P. Climate Forcing of Regionally-Coherent Extreme Storm Impact and Recovery on Embayed Beaches. Mar. Geol. 2018, 401, 112–128. [Google Scholar] [CrossRef]
  58. Castelle, B.; Dodet, G.; Masselink, G.; Scott, T. Increased Winter-Mean Wave Height, Variability, and Periodicity in the Northeast Atlantic over 1949–2017. Geophys. Res. Lett. 2018, 45, 3586–3596. [Google Scholar] [CrossRef] [Green Version]
  59. Dodet, G.; Castelle, B.; Masselink, G.; Scott, T.; Davidson, M.; Floc’h, F.; Jackson, D.; Suanez, S. Beach Recovery from Extreme Storm Activity during the 2013–2014 Winter along the Atlantic Coast of Europe. Earth Surf. Process. Landf. 2019, 44, 393–401. [Google Scholar] [CrossRef] [Green Version]
  60. Scott, T.; Masselink, G.; McCarroll, R.J.; Castelle, B.; Dodet, G.; Saulter, A.; Scaife, A.A.; Dunstone, N. Atmospheric Controls and Long Range Predictability of Directional Waves in the United Kingdom & Ireland. Earth Sp. Sci. Open Arch. 2020, 1–27. [Google Scholar] [CrossRef] [Green Version]
  61. Wiggins, M.; Scott, T.; Masselink, G.; Russell, P.; McCarroll, R.J. Coastal Embayment Rotation: Response to Extreme Events and Climate Control, Using Full Embayment Surveys. Geomorphology 2019, 327, 385–403. [Google Scholar] [CrossRef]
  62. Tsanis, I.; Tapoglou, E. Winter North Atlantic Oscillation Impact on European Precipitation and Drought under Climate Change. Theor. Appl. Climatol. 2019, 135, 323–330. [Google Scholar] [CrossRef]
  63. Zanardo, S.; Nicotina, L.; Hilberts, A.G.J.; Jewson, S.P. Modulation of Economic Losses from European Floods by the North Atlantic Oscillation. Geophys. Res. Lett. 2019, 46, 2563–2572. [Google Scholar] [CrossRef]
  64. Dias, J.M.A.; Gonzalez, R.; Ferreira, Ó. Natural versus Anthropic Causes in Variations of Sand Export from River Basins: An Example from the Guadiana River Mouth (Southwestern Iberia). Polish Geol. Inst. Spec. Pap. 2004, 11, 95–102. [Google Scholar]
  65. Jalón-Rojas, I.; Schmidt, S.; Sottolichio, A. Comparison of Environmental Forcings Affecting Suspended Sediments Variability in Two Macrotidal, Highly-Turbid Estuaries. Estuar. Coast. Shelf Sci. 2017, 198, 529–541. [Google Scholar] [CrossRef]
  66. Dunstone, N.; Smith, D.; Scaife, A.; Hermanson, L.; Eade, R.; Robinson, N.; Andrews, M.; Knight, J. Skilful Predictions of the Winter North Atlantic Oscillation One Year Ahead. Nat. Geosci. 2016, 9, 809–814. [Google Scholar] [CrossRef]
  67. Scaife, A.A.; Comer, R.; Dunstone, N.; Fereday, D.; Folland, C.; Good, E.; Gordon, M.; Hermanson, L.; Ineson, S.; Karpechko, A.; et al. Predictability of European Winter 2015/2016. Atmos. Sci. Lett. 2017, 18, 38–44. [Google Scholar] [CrossRef]
  68. Smith, D.M.; Scaife, A.A.; Eade, R.; Athanasiadis, P.; Bellucci, A.; Bethke, I.; Bilbao, R.; Borchert, L.F.; Caron, L.P.; Counillon, F.; et al. North Atlantic Climate Far More Predictable than Models Imply. Nature 2020, 583, 796–809. [Google Scholar] [CrossRef]
Water 13 00257 g001 550
Figure 1. (a) Winter-averaged sea-level pressure (SLP) in the northeastern Atlantic Ocean. Dark-gray and light-gray circles indicate the North Atlantic Oscillation (NAO) and West Europe Pressure Anomaly (WEPA) indices, respectively, defined as the normalized gradient of sea-level pressure between two given stations. (b–d) Location of the eighteen rivers under study (Table 1) and their catchment boundaries (a) in United Kingdom, (b) France, and (c) Iberian Peninsula. Red dots indicate the locations of river-flow gauges.
Figure 1. (a) Winter-averaged sea-level pressure (SLP) in the northeastern Atlantic Ocean. Dark-gray and light-gray circles indicate the North Atlantic Oscillation (NAO) and West Europe Pressure Anomaly (WEPA) indices, respectively, defined as the normalized gradient of sea-level pressure between two given stations. (b–d) Location of the eighteen rivers under study (Table 1) and their catchment boundaries (a) in United Kingdom, (b) France, and (c) Iberian Peninsula. Red dots indicate the locations of river-flow gauges.
Water 13 00257 g001
Water 13 00257 g002 550
Figure 2. The 60−year time series of winter-averaged WEPA (a,c,e) and NAO (b,d,f) indices with superimposed normalized winter discharge at nine rivers: (a,b) the Spey, Severn, and Thames in the UK; (c,d) the Seine, Garonne, and Rhône in France; (e,f) the Douro, Tagus, and Guadalquivir in the Iberian Peninsula.
Figure 2. The 60−year time series of winter-averaged WEPA (a,c,e) and NAO (b,d,f) indices with superimposed normalized winter discharge at nine rivers: (a,b) the Spey, Severn, and Thames in the UK; (c,d) the Seine, Garonne, and Rhône in France; (e,f) the Douro, Tagus, and Guadalquivir in the Iberian Peninsula.
Water 13 00257 g002
Water 13 00257 g003 550
Figure 3. Mean monthly river discharge for the years characterized by strong positive (+), neutral (0), or negative (−) phases of the (a) NAO and (b) WEPA indices, calculated by averaging the discharges in the five years with the largest, closest-to-zero, and smallest indices, respectively: (NAO+) 1989, 1995, 200, 2012, and 2015; (NAO0) 1961, 1967, 1973, 1976, 1982; (NAO−) 1963, 1964, 1969, 1977, 2010; (WEPA+) 1977, 1994, 2001, 2014, 2016; (WEPA0) 1958, 1959, 1967, 2010, 1984; (WEPA−) 1953, 1976, 1992, 1993, 2005.
Figure 3. Mean monthly river discharge for the years characterized by strong positive (+), neutral (0), or negative (−) phases of the (a) NAO and (b) WEPA indices, calculated by averaging the discharges in the five years with the largest, closest-to-zero, and smallest indices, respectively: (NAO+) 1989, 1995, 200, 2012, and 2015; (NAO0) 1961, 1967, 1973, 1976, 1982; (NAO−) 1963, 1964, 1969, 1977, 2010; (WEPA+) 1977, 1994, 2001, 2014, 2016; (WEPA0) 1958, 1959, 1967, 2010, 1984; (WEPA−) 1953, 1976, 1992, 1993, 2005.
Water 13 00257 g003
Water 13 00257 g004 550
Figure 4. (a–d) Spatial correlation of winter-averaged (DJFM) precipitation anomaly with winter-averaged (a) WEPA, (b) NAO, (c) SCAN, and (d) EA. Dotted areas show statistically insignificant values (p = 0.05). (e–g) Spatial distribution of the climate indices that best explain the variability of local winter precipitation (e) ignoring and (f) including WEPA, with contours of the corresponding correlation coefficient R. (g) Corresponding spatial distribution of the increase (∆R) in R between (e) and (f).
Figure 4. (a–d) Spatial correlation of winter-averaged (DJFM) precipitation anomaly with winter-averaged (a) WEPA, (b) NAO, (c) SCAN, and (d) EA. Dotted areas show statistically insignificant values (p = 0.05). (e–g) Spatial distribution of the climate indices that best explain the variability of local winter precipitation (e) ignoring and (f) including WEPA, with contours of the corresponding correlation coefficient R. (g) Corresponding spatial distribution of the increase (∆R) in R between (e) and (f).
Water 13 00257 g004
Water 13 00257 g005 550
Figure 5. Spatial distribution of the difference (∆R) between the correlations of the NAO index and the WEPA index with winter-averaged precipitation.
Figure 5. Spatial distribution of the difference (∆R) between the correlations of the NAO index and the WEPA index with winter-averaged precipitation.
Water 13 00257 g005
Water 13 00257 g006 550
Figure 6. (a–d) Winter-averaged river discharge and (e–h) precipitation averaged over the five years of the strongest positive phases and of the strongest negative phases of the NAO and WEPA indices (details in the caption to Figure 3).
Figure 6. (a–d) Winter-averaged river discharge and (e–h) precipitation averaged over the five years of the strongest positive phases and of the strongest negative phases of the NAO and WEPA indices (details in the caption to Figure 3).
Water 13 00257 g006
Table
Table 1. Main characteristics of the 18 river basins under study.
Table 1. Main characteristics of the 18 river basins under study.
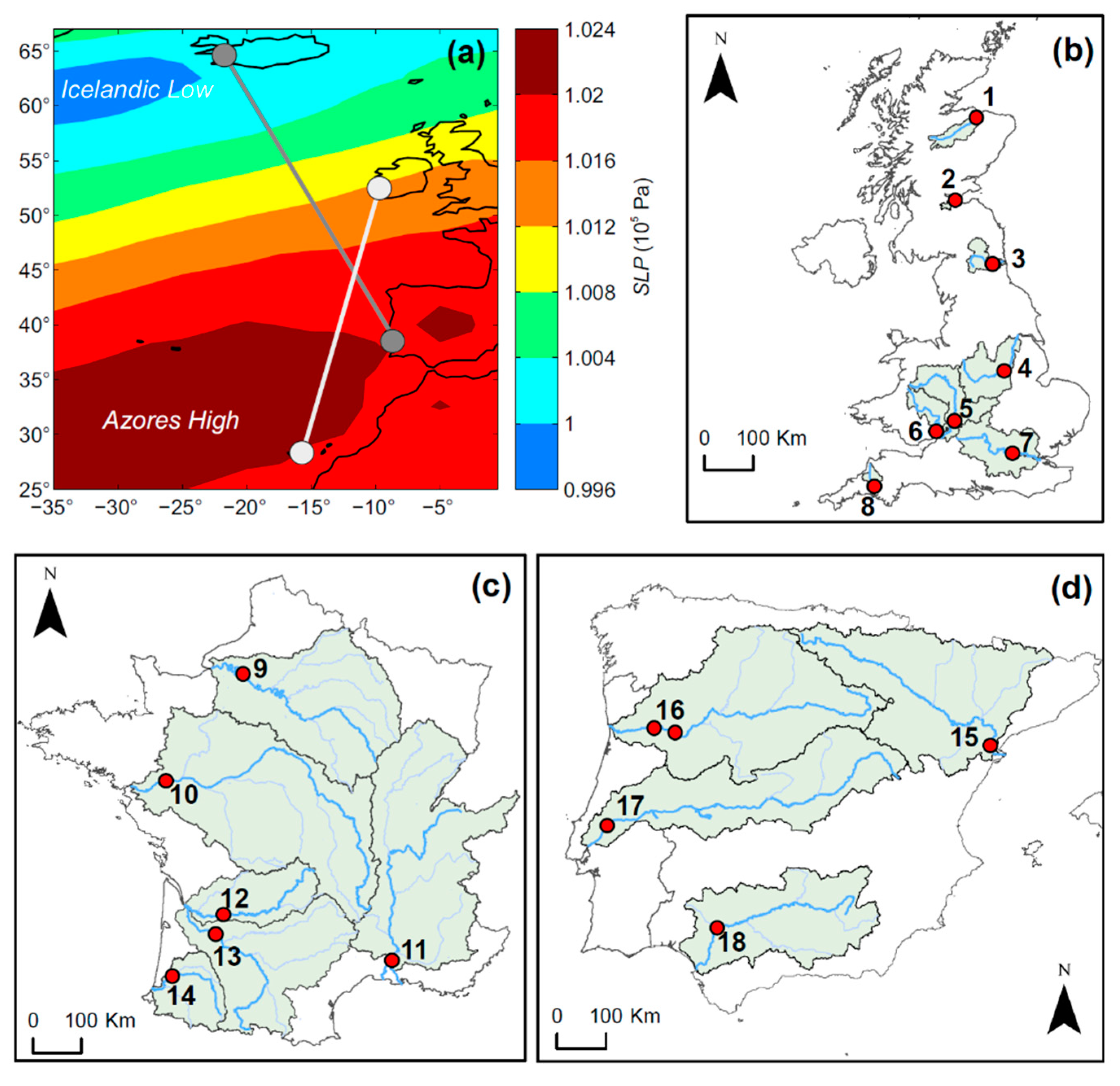
RiverGauging StationBasin Area
(103 km2, %)		Data GapsDJFM River Flow
(1959–2018) (m3/s)
TotalUpstream the StationMeanSD
1. SpeyBoat o Brig3.062.86 (93.5%)-83.520.1
2. AlmondCraigiehall0.380.37 (98.4%)20109.32.9
3. TyneBywell2.882.18 (75.7%)-67.517.1
4. TrentColwick10.397.49 (72.1/)-124.736.6
5. SevernSaxons-Upton11.426.85 (60%)-147.244.3
6. WyeRedbrook4.144.01 (96.9%)-123.237.7
7. ThamesKingston13.489.95 (73.8%)-110.051.4
8. TamarGunnislake0.960.92 (95.8%)-38.210.7
9. SeinePoses/Vernon76.2465/64.6 (85.2%/84.7%)-729.2282.3
10. LoireMontjean117.50109.93 (93.6%)-1428.8536.9
11. RhoneBeaucaire97.6395.59 (97.91%)-2049.2502.2
12. DordogneLamonzie/Bergerac24.0714.29/14.04 (59.4%/58.4%)-420.1146.0
13. GaronneTonneins56.5551.5 (91.1%)-869.0320.4
14. AdourSt. Vincent de Paul16.827.83 (46.6%)-137.952.4
15. EbroTortosa85.5284.23 (98.5%)-535.6287.4
16. DouroRegua/Pocinho97.4891.5/81.29 (93.87%/83.4%)-672.0498.1
17. TagusSantarem/Almourol71.6168.43/67.48 (95.6%/94.2%)2008, 2015611.52502.4
18. GuadalquivirAlcalá del Río57.0246.13 (80.9%)-225.4263.1
Table
Table 2. Correlation R between winter-mean (DFJM) river discharge and winter-averaged teleconnection indices, including the WEPA climate index. The strongest correlation for each river basin is highlighted in bold. * indicates statistically significant correlations at p < 0.01.
Table 2. Correlation R between winter-mean (DFJM) river discharge and winter-averaged teleconnection indices, including the WEPA climate index. The strongest correlation for each river basin is highlighted in bold. * indicates statistically significant correlations at p < 0.01.
River BasinRWEPARNAORNAO (Jones)REARSCANRWPREPRPNARWRRTNHRPOL
1. Spey0.090.56 *0.55 *0.20−0.47 *00.10.09−0.120.03−0.22
2. Almond0.300.56 *0.52 *0.45 *−0.39 *0.120.130.26−0.190−0.41 *
3. Tyne0.52 *0.37 *0.34 *0.46 *−0.180.100.210.20−0.25−0.04−0.38 *
4. Trent0.80 *0.020.100.47 *0.140.230.10.22−0.34 *−0.07−0.36 *
5. Severn0.83 *0.040.160.48 *0.140.120.090.09−0.34 *−0.06−0.36 *
6. Wye0.83 *0.240.310.59 *0.030.160.140.15−0.280.01−0.40 *
7. Thames0.72 *−0.080.030.50 *0.180.060.040.10−0.260.08−0.20
8. Tamar0.83 *0.220.260.46 *0.130.090.120.01−0.46 *0.06−0.43 *
9. Seine0.41 *0.28 *0.230.19−0.160.200.26 *0.17−0.27 *−0.09−0.30 *
10. Loire0.58 *−0.05−0.010.160.150.050.210.20−0.38 *−0.12−0.17
11. Rhone0.64 *−0.15−0.130.30 *0.230.120.190.17−0.34 *−0.09−0.25
12. Dordogne0.66 *−0.10−0.050.190.31 *0.050.200.17−0.38 *−0.16−0.16
13. Garonne0.56 *−0.21−0.190.050.45 *−0.040.22−0.02−0.30 *−0.12−0.01
14. Adour0.63 *−0.06−0.050.110.39 *−0.010.230.02−0.36 *−0.08−0.13
15. Ebro0.27 *−0.44 *−0.31−0.020.30−0.180.20−0.01−0.08−0.150.20
16. Douro0.48 *−0.48 *−0.40 *0.43 *0.31 *0.040.080.08−0.14−0.08−0.01
17. Tagus0.31 *−0.57 *−0.45 *0.31 *0.23−0.020.01−0.04−0.04−0.060.20
18. Guadalquivir0.07−0.72 *−0.60 *0.120.17−0.13−0.05−0.02−0.04−0.210.15
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Jalón-Rojas, I.; Castelle, B. Climate Control of Multidecadal Variability in River Discharge and Precipitation in Western Europe. Water 2021, 13, 257. https://doi.org/10.3390/w13030257

AMA Style

Jalón-Rojas I, Castelle B. Climate Control of Multidecadal Variability in River Discharge and Precipitation in Western Europe. Water. 2021; 13(3):257. https://doi.org/10.3390/w13030257

Chicago/Turabian Style

Jalón-Rojas, Isabel, and Bruno Castelle. 2021. "Climate Control of Multidecadal Variability in River Discharge and Precipitation in Western Europe" Water 13, no. 3: 257. https://doi.org/10.3390/w13030257

APA Style

Jalón-Rojas, I., & Castelle, B. (2021). Climate Control of Multidecadal Variability in River Discharge and Precipitation in Western Europe. Water, 13(3), 257. https://doi.org/10.3390/w13030257

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop