1. Introduction
River discharge data availability is of crucial interest for a variety of practical hydrological applications, such as the implementation, calibration and validation of hydrological models for water resources assessment and management [
1,
2], the monitoring of climate change impacts on water resources and runoff extremes [
3], the identification of the best criteria for the hydraulic infrastructures design and evaluation, the strategic planning and policies developing for both civil protection and water management activities.
In many practical applications, discharge estimation in natural rivers is conducted through a velocity-area method, based on: (i) the discrete point sampling of flow velocity along transects in a specific cross section of interest; (ii) the derivation of both average flow velocity and associated wetted area [
4,
5,
6]. This approach traditionally involves the use of current meters, requires a large employment of highly specialized personnel, and it is extremely expensive and time-consuming. Multiple field campaigns are often conducted on the same cross-section of a river with the ultimate objective of deriving the flow rating curve, which requires a consistent dataset of paired measures of discharge and river stage, with a consequent need of field campaigns conducted in different periods of the year in order to ensure a good flow regime representativeness. Moreover, cross sections may vary over time due to vegetation growth and river-bed movements [
7], and this implies the need for frequent replications of the field campaigns and periodic flow rating curve recalibrations.
Errors in river stage and velocity measurements during surveys have been regarded as considerable sources of uncertainties in discharge measurements using rating curves [
8,
9]. Moreover, these last are rarely adequate to evaluate discharge under severe flood conditions [
10] when extrapolation is often necessary. This last aspect is related to the difficulties in sampling discharge-stage couples under high flow conditions with traditional approaches and instruments, especially due to the increased safety risks for operators.
Although different and valid options are often considered, from the use of Doppler instrumentation [
11] to radar [
12,
13] and remote sensing observations [
14], these rarely reduce the problems related to both expensive equipment and need for prolonged and laborious field campaigns through expert personnel. There is an increased awareness that advances in flow monitoring towards easier and more accessible methods, allowing for higher spatial and temporal resolution, are still urgently needed.
Optical based techniques offer a great potential for river monitoring [
15], allowing for massive, easy and low-cost acquisitions of a wide range of measures in real time, at any flow conditions and at high spatial resolution. Such techniques are rapidly evolving also in consideration of the increasing availability of a new generation of optical sensors, digital cameras and methodologies. Recent years have been witnessing in fact a significant development of monitoring methods based on the elaboration of sequences of images captured by digital permanent gauge-cams installed close to the river, mobile-devices with operators standing on the banks and on bridges, or even cams installed on unmanned aerial vehicles (e.g., [
16,
17]).
Among the various image-based methods (e.g., [
18,
19,
20,
21,
22]), two different approaches have gained wide consensus for natural rivers monitoring: the large-scale particle image velocimetry (LSPIV) and particle tracking velocimetry (LSPTV) techniques. Both techniques, based on the analysis of floating tracers, were originally developed for laboratory experiments under controlled conditions and essentially enlarge the basic technique principles of the particle image velocimetry (PIV) and particle tracking velocimetry (PTV) technique to the large-scale cases; LSPIV adopts a Eulerian point of view, while LSPTV uses a Lagrangian point of view. The two techniques have several common characteristics, described for instance in [
23,
24], while the main differences lay in the adopted procedures for the evaluation of the recordings: LSPIV estimates the velocity at image sub-regions, while LSPTV reconstructs the trajectory of individual particles transiting in the field of view [
15].
The surface velocity field is indirectly obtained by measuring the velocity of floating tracer particles, naturally present or artificially introduced to the flow, which is assumed to move with the local flow velocity. The dynamics of the liquid surface are recorded by cameras, through a sequence of consecutive frames, reconstructing the local flow velocity starting from the identification of the tracer particles displacements between pairs of subsequent frames. Differently from the LSPTV, the here used LSPIV subdivides all frames into small regular sub-regions, called interrogation areas (IAs); local distribution patterns and the displacements are usually determined by cross-correlating the IAs of consecutive frames.
Measurements with LSPIV technique typically include the following four main phases:
“seeding”, i.e., introduction of tracer with adequate geometry and density in a well-lit area of the river, using particles that accurately describe the motion of the river, not interfering significantly with it; this is needed only if the characteristics of naturally occurring flow tracer are not appropriate for the scope (e.g., scarce concentration with non-uniform dispersion, inadequate dimensions, etc.);
“recording”, i.e., recording of images with an adequate temporal resolution;
“processing”, i.e., elaboration of recorded images, also including pre-processing procedures (e.g., images stabilization, orthorectification and manipulation to increase tracer brightness and the contrast between tracers and water) if needed, and estimation of the tracer displacements between pairs of consecutive images;
“evaluation”, i.e., velocity data post-processing to characterize the velocity field over the entire area of interest.
The estimation of the discharge is also possible by combining the bathymetry of a river cross section with the calculated surface velocity field and adopting simplified hypotheses on vertical velocity profiles [
25].
Monitoring approaches based on LSPIV pattern recognition technique show several advantages with respect to traditional methodologies. First of all, the simplicity: field campaigns are easier, faster and do not require personnel with specific skills; instruments are not submerged in the stream, limiting flow disturbance and, during floods, possible damages and risks for operators. Secondarily, the affordability: recent technological advancements have allowed commercially-available and inexpensive cameras for high resolution capabilities and equipment for extensive image storage and processing. Many software programs, based on LSPIV and LSPTV, are also widely available, user-friendly and freely available, such as FlowManager [
26], RIVeR [
27], FUDAA-LSPIV [
28,
29]. Despite the numerous and important advantages, image-based river flow monitoring is still rarely adopted in practical applications. The lack of consistent image acquisition and processing protocols feeds the urgent need for in-depth analyses that could offer, in the near future, the possibility of systematically implementing such methods in practical applications according to appropriate operational standards.
This work moves exactly along this direction, and it is aimed to analyze performance and sensitivity of a free and popular software based on PIV to the main factors, which typically influence the technique. In particular, an Image Sequence Generator (ISG) has been implemented ad-hoc with the aim to create, under fixed parametric scenarios, several replications of synthetic sequences of images with known and uniformly distributed tracers moving according to a known and stationary surface velocity profile simulating two possible flow velocity conditions (slow and fast).
The selected software for the analysis is PIVlab [
30], an open-source tool of MATLAB, which recently gained considerable attention for natural river flow monitoring (e.g., [
15,
31]). All the sequences generated by the ISG for each scenario are then processed in PIVlab, statistically analyzing the results, with particular emphasis on the error in the estimation of the surface velocity field characteristics.
The work is structured in two parts. The first considers a set of simulations dedicated to the analysis, for fixed number of processed frames, of the impact of different tracer characteristics under various flow velocity and environmental conditions. With regard to this last aspect, two alternative hypotheses are considered with the aim to investigate the influence of possible disturbances typical of environmental conditions. Some of the aspects investigated in the first set of simulations have been recently explored by [
32] with regard to the LSPTV technique (i.e., using PTVlab software [
33]). Differently from other existing synthetic studies on optical methods (e.g., [
32,
34,
35]), here, a realistic distribution of the flow velocity along the cross-section is considered.
The second part is constituted by simulations entirely focused on the role of the selected number of frames which depends on the selected duration of the video sequences and the frame elaboration frequency (frame-rate).
In real applications, the video duration should depend on different factors (e.g., tracer visibility and seeding density/dispersion characteristics in time, flow and illumination conditions and variability, etc.) and it is rather usual to acquire an overabundant sequence of images from which only a limited and representative subset is extracted and processed. The frame-rate of acquisition depends on the adopted device for recording. For instance, Charge-Coupled Devices, used in laboratory PIV experiments, can acquire video with frame-rate over 1000 fps. Commercial cameras, often used for LSPIV applications, typically record with frame-rate around 24–30 fps, while recent high-speed cameras acquisition frequency can reach up to about 250 fps. Many software for PIV analysis allow for modifying the processing frame-rate with respect to the frame-rate of acquisition. A high frame-rate could imply an excessively low frame-by-frame tracer displacement, especially under slow flow conditions, while the adoption of low frame-rate, especially under fast flow conditions, could imply excessive displacements, greater than the IA, with consequent loss of correlation due to in-plane motion [
36]. Both situations have to be avoided, since they negatively affect optical matching algorithms. The second set of simulations in this study is thus aimed to provide some indications about the choice of the frame-rate and the processed video sequence duration depending on the local flow velocity.
A general drawback in the full evaluation of the performances offered by software programs based on optical techniques is the absence of benchmarks, since current meter or Doppler measurements are not appropriate for massive comparing observations; for this reason, a synthetic image-based approach represents the only way to fully characterize a specific algorithm. This paper critically explores strengths and weakness of PIVlab capabilities and capitalizes our best present knowledge on this technique. Results of this work may be useful, on the one hand, in identifying possible source of errors in flow velocity estimations by LSPIV based methods and, on the other hand, in identifying the optimal experimental setup under different environmental circumstances. The numerical approach proposed could be used, for example, to preliminarily verify the operability of LSPIV on a given site. Information arising from our analyses could be useful in defining criteria and guidelines for practical applications.
2. Materials and Methods
2.1. PIVlab Software
PIVlab software, developed by the Energy and Sustainability Research Institute of Groningen, the Netherland [
30], is a free, open-source tool for performing digital PIV flow analysis in MATLAB environment. Apart from a very user-friendly graphical user interface, the program is accessible from the command line of MATLAB and this offers the possibility to easily automate the whole process, to include it in other applications and, in general, to benefit from all the MATLABs extensive plotting and data handling features.
PIVlab allows for importing image sequences and to choose the processing style between two available modes: type 1 (i.e., 1-2, 2-3, 3-4, etc.), so that the second image of each analyzed pair of images is also the first of the successive one; type 2 (i.e., 1-2, 3-4, 5-6, etc.), so that the cross-correlation analysis is applied only once per each image.
The typical PIVlab workflow consists of three main steps: (1) pre-processing; (2) image evaluation; (3) post-processing. The tool offers, in fact, various pre-processing techniques to enhance images quality and help tracers’ recognition (i.e., histogram equalization, intensity high-pass and intensity capping).
With regards to the images evaluation step, PIVlab provides the possibility to choose between two different correlation algorithms: D-CC (Direct Cross-Correlation) and FFT-CC (Fast Fourier Transform Cross-Correlation). Both are based on a cross correlation of small sub-images (interrogation areas, IAs) of an image pair. The former computes the correlation matrix between corresponding IAs in the spatial domain. The location of the intensity peak in the correlation matrix provides the most probable displacement of the particle from the first to the second IAs. With this approach the corresponding IAs in the two paired images can have different sizes. With the FFT-CC approach, which conversely uses IAs of identical size, the correlation matrix is computed in the frequency domain using FFT. Although the second approach has been demonstrated to create less accurate results than the D-CC [
37], especially when flow motion is not unidirectional, it reduces significantly the computational cost, especially when large IAs are considered, which actually is a very relevant drawback of D-CC. Moreover, the accuracy of the FFT can be offset by running several passes on the same dataset [
38] according to a methodology described in [
30] and based on a window deformation interpolator, using either a linear interpolation (faster) or a spline interpolation (higher precision, but slower).
The location of the intensity peak of the correlation matrix, which determines the displacement of IAs, can be refined with sub-pixel precision by using one of the two peak finding algorithms implemented in PIVlab: (i) 2·3-point fit and (ii) 9-point fit. The first consists in fitting two times a one-dimensional Gaussian (3-point fit) to the integer intensity distribution of the correlation matrix for both x and y axes independently, while with the second, a two-dimensional Gaussian function (9-point fit) is used.
Finally, the post-processing phase includes three steps: (i) filtering velocities and removing possible outliers; (ii) replacing missing vectors through a data interpolation technique based on a boundary value solver for interpolation; and, finally, (iii) removing measurements noise by applying a data smoothing technique based on a penalized least squared method [
39]. For further details on PIVlab, interested readers may refer to the original paper [
30].
Modelling Framework and PIVlab Setup
In order to allow for a statistical characterization of the results, several sequences for each considered scenario were created and processed; different scenarios were analyzed, leading to a wide number (i.e., 5200) of image sequences to be processed. This highlights the need for exploiting a not computational expensive automatic procedure.
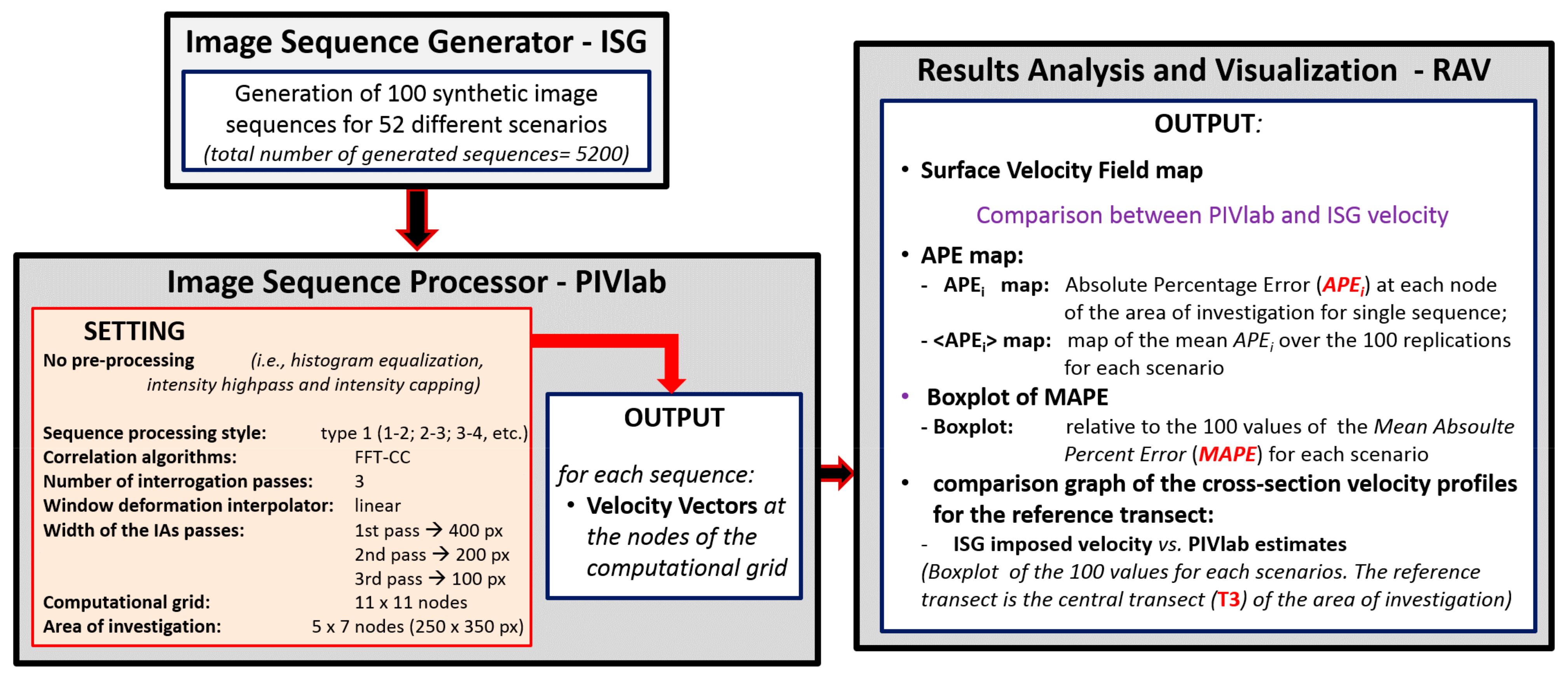
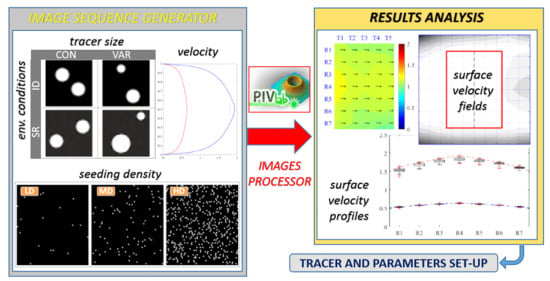
For this reason, despite PIVlab presents a very user-friendly GUI, in this work it was used through MATLAB command lines; the image processing by PIVlab was used as the core of an opportunely implemented modeling chain, schematically reported in
Figure 1, that also contains a code for the preliminary creation of the image sequences to be processed with the Image Sequence Generator—ISG (see
Section 2.2) and a code for the subsequent post-processing of PIVlab estimates to automatically achieve the desired indicators (Results Analysis and Visualization—RAV see
Section 2.3). Such modules have been separately developed in MATLAB and then fully integrated with PIVlab script.
PIVlab is forced with the output of the ISG. Since each sequence is formed by synthetically generated images, no pre-processing procedure is required by PIVlab. The adopted mode for the sequence processing style is type 1 (i.e., 1-2, 2-3, etc.) which, although more time consuming, is more performing than the alternative type 2 (i.e., 1-2, 3-4, etc.) for cases of sequences with a low frame-rate.
In order to reduce the calculation times, the FFT-CC algorithm was preferred to the D-CC, adopting the needed precautions to maintain an adequate accuracy of the results. In particular, three passes were set, using linear interpolation option as window deformation interpolator.
The width of the 1st pass IAs was selected by imposing three criteria suggested by PIVlab developers: (i) not lower than 50% of the minimum frame dimension; (ii) lower than the minimum frame dimension; (iii) higher than two times the maximum presumable frame-by-frame particle displacement. It is, in fact, desirable that the displacement of the particles remains within both the corresponding IAs of the image pair. The width of the 1st pass IAs was then set equal to 400 px (pixel) in consideration of the following aspects, which will be deepened in the following paragraphs: (i) squared frames of 600 × 600 px were generated; (ii) a maximum frame-by-frame displacement of 161 px was considered, i.e., the tracer displacement corresponding to the maximum velocity in the midstream for the fast velocity case and for frame-rate of 4 fps (frame per second).
The width of IAs for the following passes was obtained by halving the width relative to the previous pass, i.e., 200 and 100 px for the 2nd and 3rd pass, respectively. This setup allows the processing algorithm to create a grid of 11 × 11 computational nodes over the frame, with a total of 121 equidistant nodes placed at a distance of 50 px with each other and from the edges of the frame.
The results obtained by the cross-correlation algorithm application to each replication of a given scenario are point velocity vectors, computed node by node in the entire computational grid. Such data are then passed to the post-processor RAV by which: (i) all the results of interest at the level of single sequence per scenario are computed and stored; and (ii) a statistical analysis is carried out on the entire set of sequences per scenario, computing the main descriptive statistics and creating corresponding box-plots and tables.
2.2. Image Sequence Generator
An Image Sequence Generator (ISG) has been coded in MATLAB and implemented ad hoc for the scopes of this work. The code, after an opportune setup, is able to generate a desired number of synthetic image sequences, simulating a floating tracer moving under controlled conditions according to two different and alternative operational modalities: (1) ideal environmental condition (ID), by which the model reproduces a tracer moving on a black background; (2) semi-real environmental condition (SR), by which the tracer moves on a real background. In this last case, an actual image from a real river, representative of clear water conditions, is used as further input to the ISG.
Floater is simulated with disks of regular geometry having a uniform white color that, in the case of SR, is altered with white noise. The ISG creates tracers under two different modalities: CON (constant size) and VAR (variable size). In the CON case the particles have a uniform circular shape with a fixed diameter, while in the VAR case the disks have been generated with a diameter variable according to a Gaussian distribution with fixed parameters. Tracer is randomly distributed with a uniform concentration, according to a Poisson distribution with parameter λ (seeding density), on the grid lattice representing the background.
Once the grid lattice with the floating tracers is generated, a unidirectional motion is imposed to the floaters according to a realistic cross-section velocity profile that accounts for flow velocity reduction near the banks due to frictional forces. In particular, the model requires to impose a normalized velocity cross profile, which have to be multiplied by the desired mean flow velocity. A specific part of the code was implemented in order to exclude the possibility of particles’ overlap. Each particle keeps constant properties (i.e., shape and size) along its motion and results simply shifted from a frame to the next one.
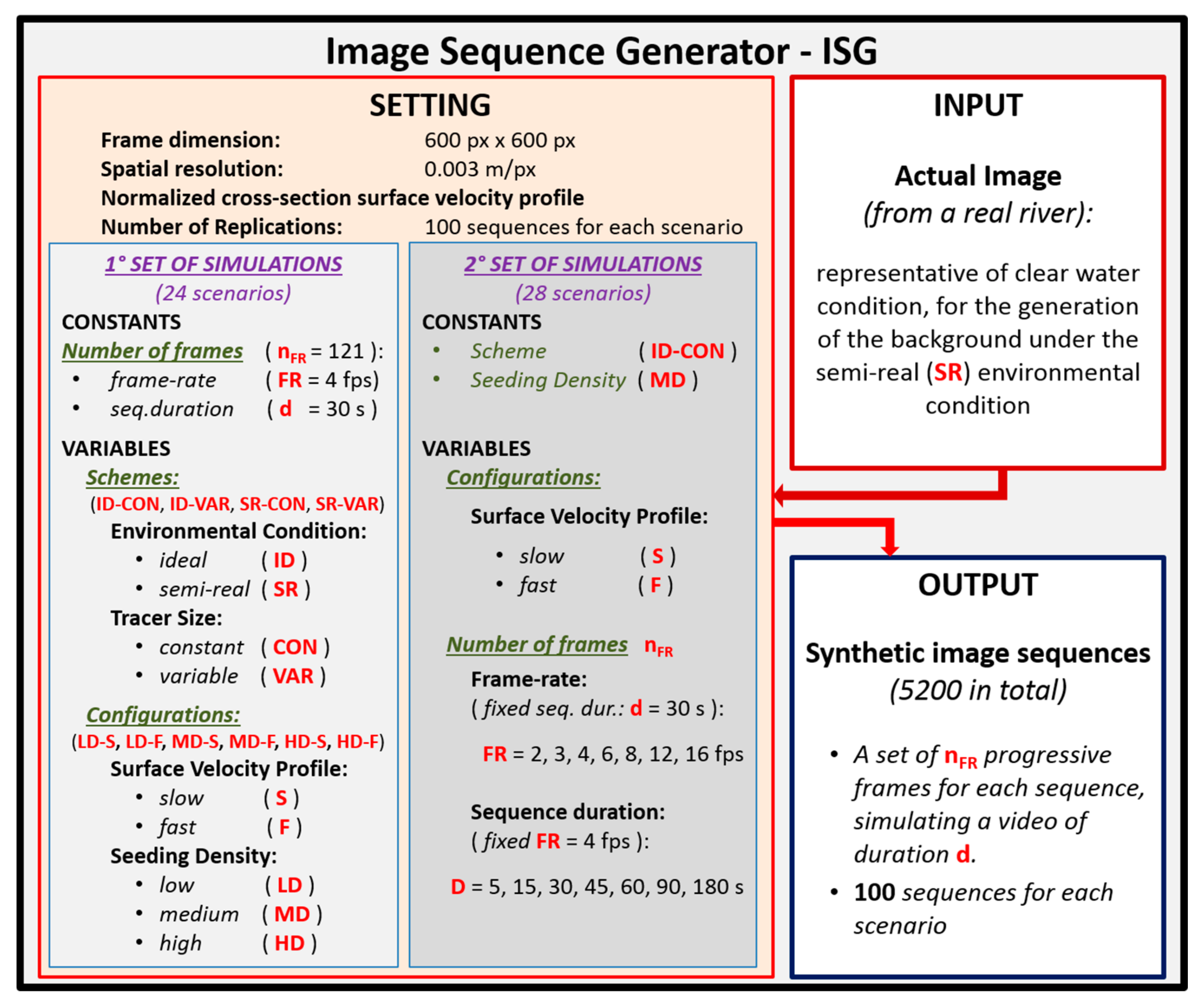
The ISG setup includes the setting of different parameters (
Figure 2). Considering the purposes of this work, it has been decided to keep some of these as constants over the different scenario, such as the frame dimension, the spatial resolution, the normalized cross-section flow velocity profile and the number of replications generated for each scenario. Then, the sensitivity of PIVlab to the remaining parameters has been explored by varying them according to a wide range of combinations.
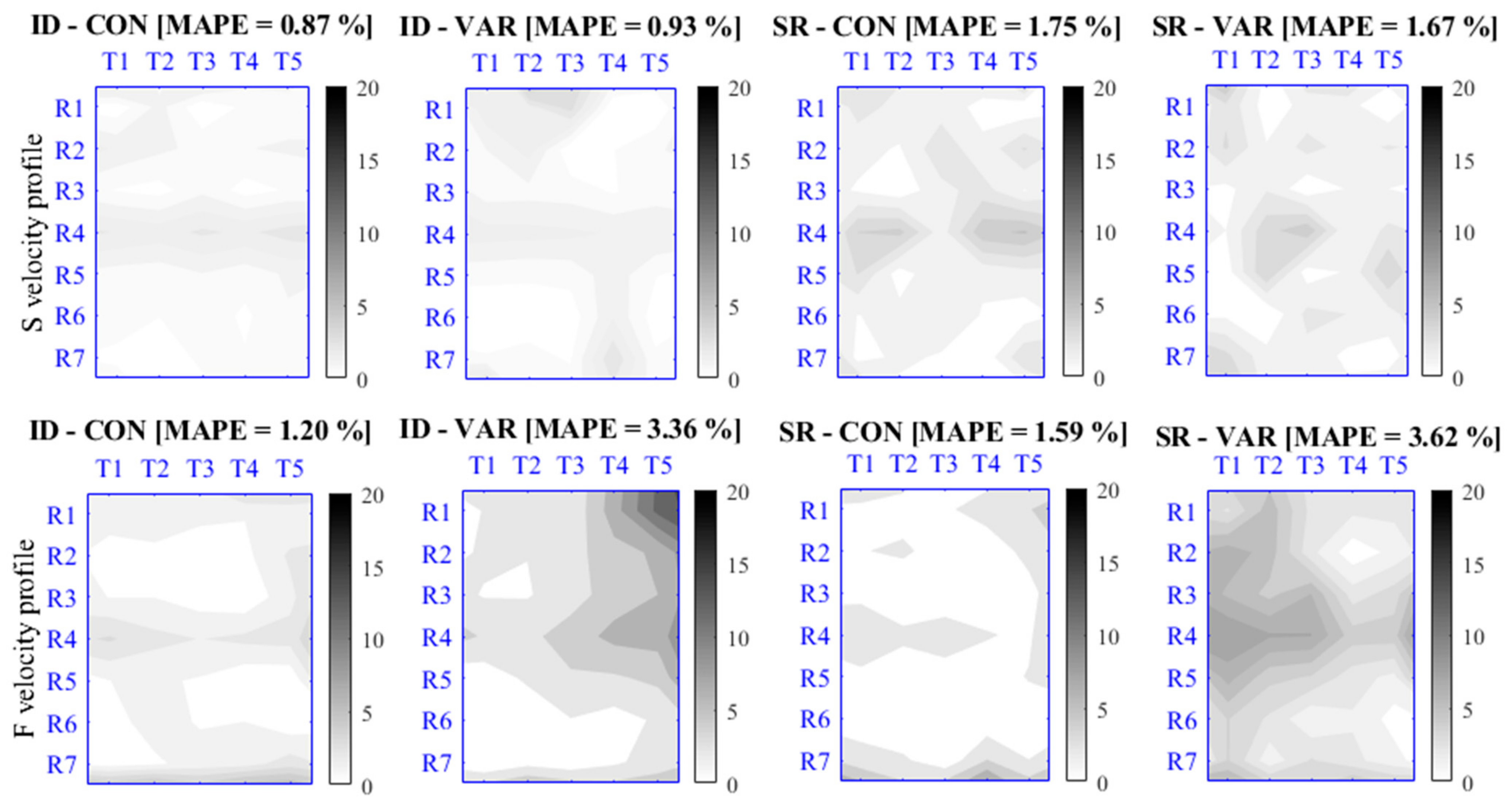
In particular, four different schemes have been created combining the two environmental conditions (i.e., ID and SR) with the two alternative hypotheses for the tracer size (CON and VAR): ID-CON, ID-VAR, SR-CON, SR-VAR.
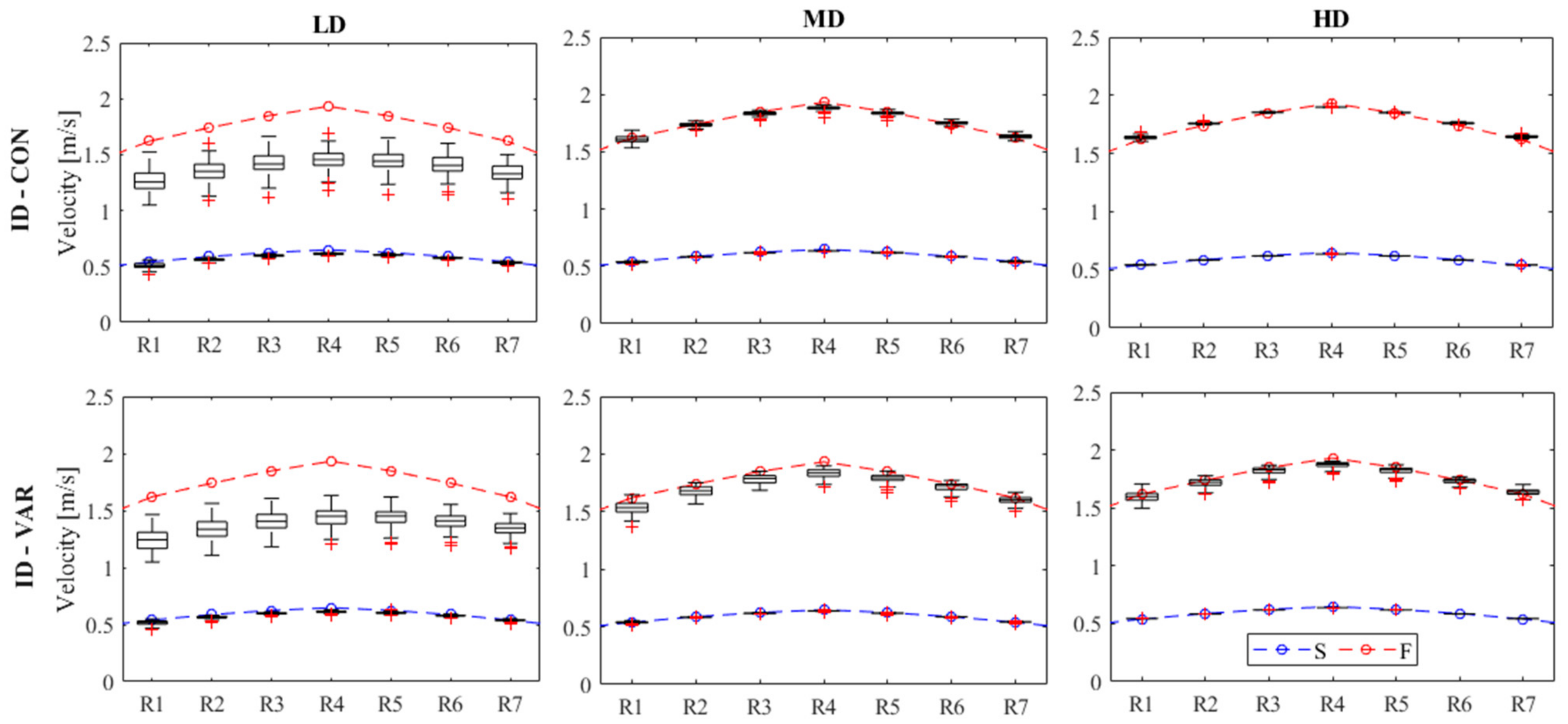
A first set of simulations has been carried out for all the aforementioned schemes, creating scenarios with sequences of fixed time duration and frame-rate under six different configurations, obtained by combining two flow velocity profiles (S = slow; F = fast) and three different seeding densities per frame (LD = low; MD = medium; HD = high). A second set of simulations has been carried on scenarios obtained by varying alternatively the frame-rate first (with fixed sequence duration) and, then, the sequence duration (with fixed frame-rate). These scenarios have been created considering only the ID-CON scheme and two seeding density-velocity configurations (MD-S and MD-F).
The different combinations of schemes and configurations for each set of simulations have generated a total of 52 different scenarios, as schematically represented in
Table 1. Some demonstrative synthetic image sequences are provided in the
Supplementary Materials.
ISG Setup
For the setting of the parameters under the different scenarios we referred to other works already present in literature and field observations (e.g., [
24,
29,
33,
35,
40,
41,
42,
43]). The parameters used in this work are synthesized in
Table 1.
In particular, a wide frame dimension (i.e., 600 × 600 px) was set since, as it will be discussed later, only a limited portion, centered in the middle of the image, will be used for avoiding possible disturbances in the contour region, i.e., border effects [
32].
For the generation of the grid lattice under the SR schemes, an actual image, which has been acquired and orthorectified (no other pre-processing procedures have been applied) during a past streamflow monitoring field campaign at the Oreto river (Italy) in 2018, has been used. This image was considered ideal for the scope since it was acquired in a perfect vertical condition by drone, hovering in stable position at 10 m above the river surface, under optimal daylight and clear water conditions. However, it is worth noting that the use of static background for the dynamic generation of a video sequence does not allow to include in the analysis some possible sources of error, neglected in this study, which usually occur in field conditions, such as the effects of glare and shadows or light intensity variation associated with free-surface deformations. The same spatial resolution of the image (i.e., 0.003 m/px), which is also similar to that adopted in [
35], was set in the ISG for the generation of all the synthetic sequences. For each scenario it has been decided to perform various replications, generating 100 independent sequences with the same parameter set, in order to allow for a statistical characterization of the results.
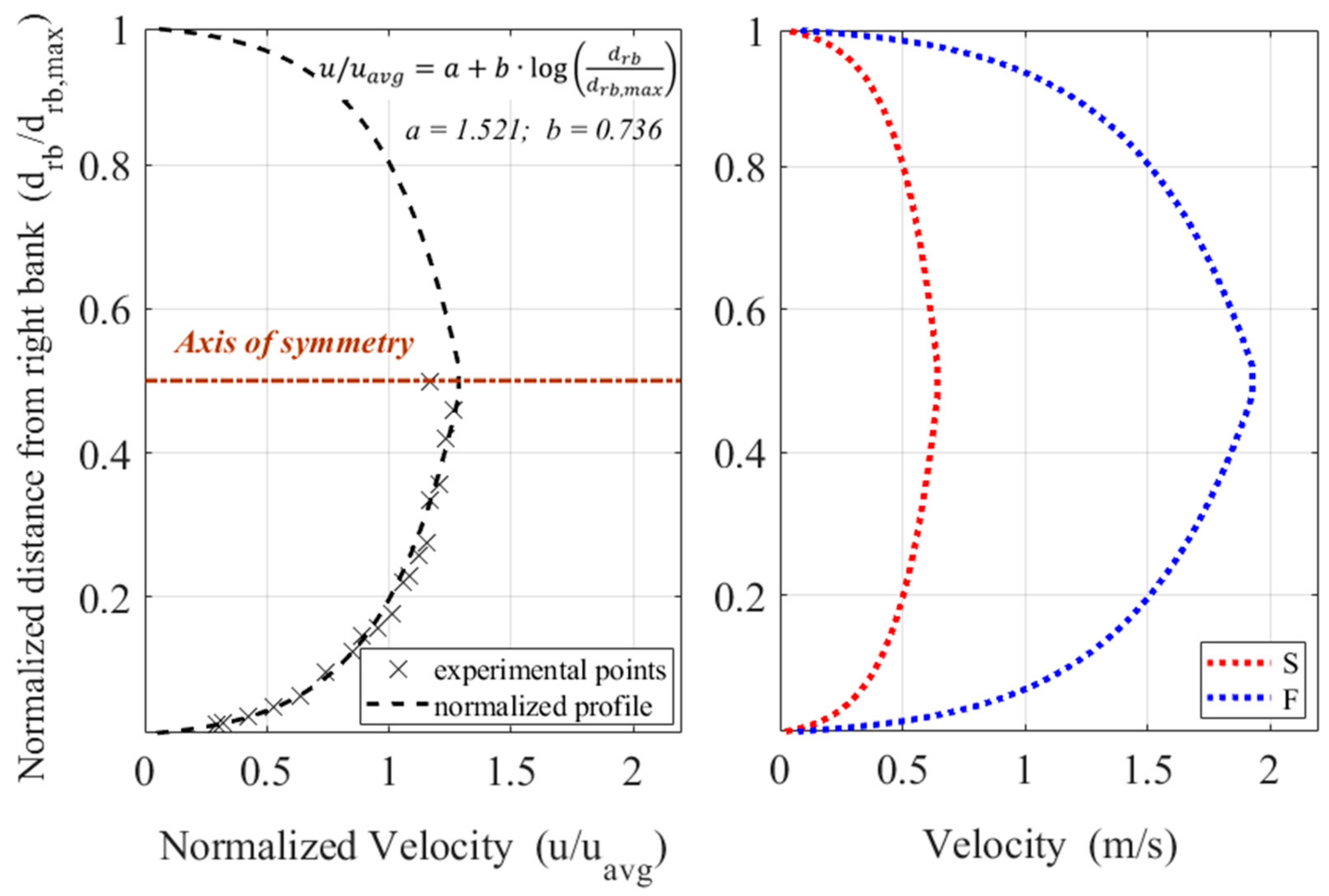
A unidirectional and stationary motion was imposed to the particles according to a synthetic and symmetric cross-section flow profile (
Figure 3). A reference profile was first derived starting from the results of field campaign in a real river [
44], retrieving experimental points for half section, formed by pairs of distance from the bank (normalized with respect to the total length of the cross-section) and the corresponding surface velocity, measured by the ADCP technique. Different functions were fitted to the experimental points, and the best fitting curve was found by a logarithmic function (R
2 = 0.985), which actually is one of the most widely used to characterize the horizontal velocity profile with the distance from the bank [
45], even if it does not account for possible effects of turbulence which could strongly influence real profiles.
The final normalized profile for the entire section, whose equation is reported in
Figure 3, was obtained by: (i) reflecting the obtained fitting function across the central axis of symmetry and (ii) rescaling the function so to obtain a unit average velocity. The obtained profile, characterizing the velocity (normalized with respect to the average velocity u
avg) distribution as a function of the normalized distance from the right bank (d
rb/d
rb,max), was finally used to generate the slow (S) and the fast (F) transverse velocity profiles, setting the average velocity u
avg equal to 0.5 m/s and 1.5 m/s for the velocity conditions S and F, respectively. The corresponding average frame-by-frame particle displacements, assuming a frame-rate of 4 fps, are equal to 42 px (S) and 126 px (F), with values ranging from about 32 px (S case close to the banks) to about 161 px (F case in the midstream).
In the CON case all the particles are characterized by a fixed diameter of 10 px, while in the VAR case the disks have different size, with diameters randomly ranging from 2 to 20 px, generated from a Gaussian distribution with mean and standard deviation equal to 10 and 3 px, respectively. The selected mean diameter of 10 px is rather common for both laboratory and field scales experiments [
32,
35,
42], since it is sufficiently large to avoid peak locking effects [
40,
41] and, at the same time, consistent with typical dimensions of tracers used in real applications [
22]. Under the ID schemes, the disks have a uniform white color, while, under the SR, the color was altered, frame by frame, by a white noise with standard deviation of 0.05 in order to simulate environmental signal noises, following the same approach used in [
32].
Figure 4a shows an example of tracers for four possible schemes ID-CON, ID-VAR, SR-CON and SR-VAR.
Moreover, for the choice of the seeding density, we referred to other works in literature (e.g., [
32,
43]) creating images with Poissonian distributed tracers, with parameter λ (corresponding to the mean seeding density for frame) equal to 6.4 × 10
−5 ppp (particles per pixel) for the case LD, 2.5 × 10
−5 ppp for the MD and 1.3E-03 ppp for the high density case (HD). Considering the selected size of the frame and mean diameter of the particles, the imposed seeding densities imply an average percentage of pixels with tracer over the entire frame of 0.5%, 2% and 10% of the frame, with a mean occurrence of 23, 91 and 459 disks per frame, for the LD, MD and HD cases, respectively. The explored seeding density range takes into account two limit cases: (i) the LD case could be considered as a lower limit, below which the matching algorithm could have problems related to frame regions with scarce or null presence of tracer; (ii) the HD case could be representative of an upper limit seeding density condition, over which individual particles could start forming clusters, causing a possible increment of the measuring uncertainties [
46]. In
Figure 4b an example for each case under the ID-CON scheme is reported.
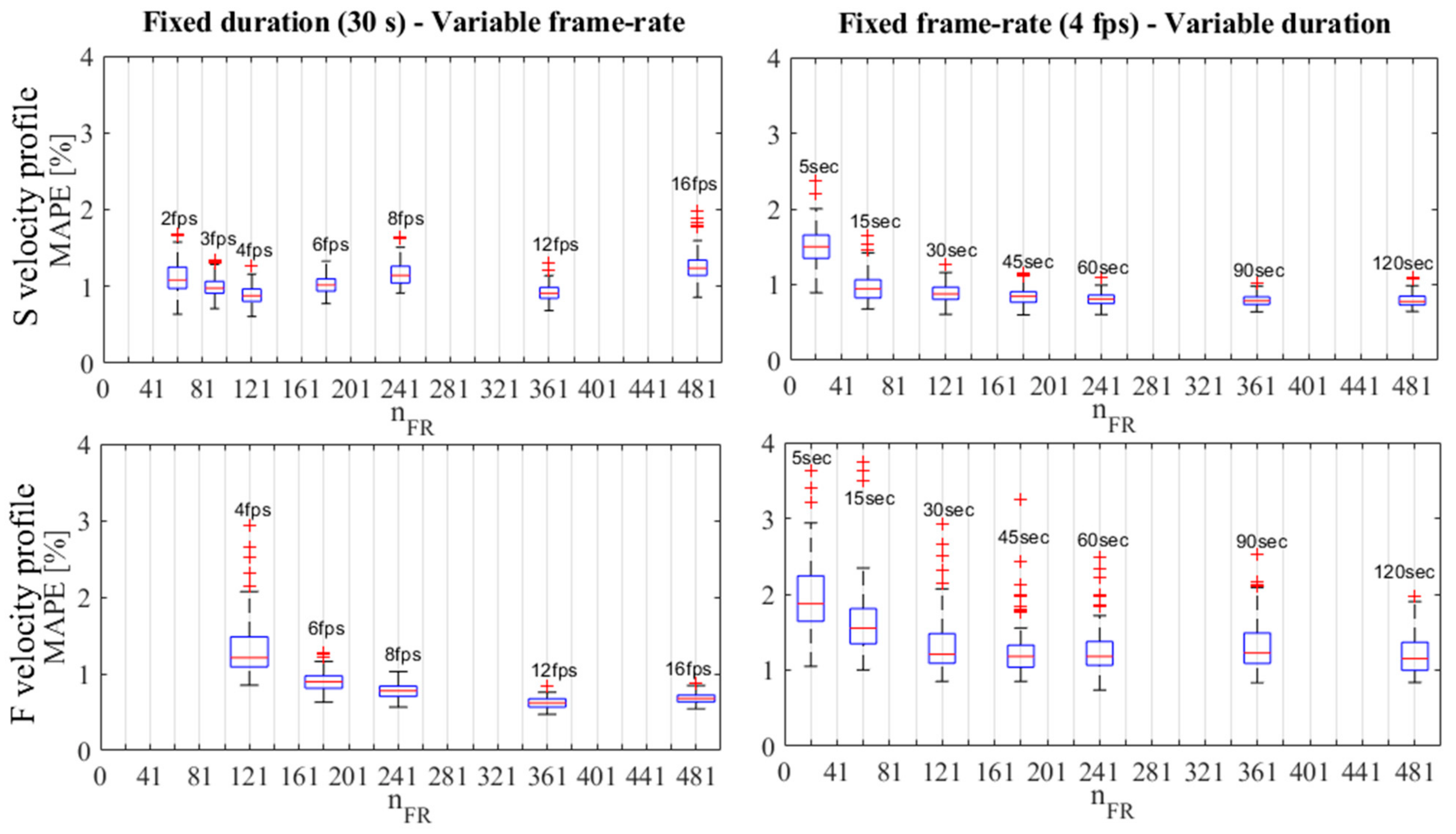
For the first set of simulations, we have set a constant frame-rate of 4 fps, and sequence duration equal to 30 s. Such settings provide a suitable displacement of particles between image pairs for both S and F velocity cases and ensure a number of processed frames (nFR) equal to 121 frames for each sequence and sufficient for a consistent characterization of the surface velocity field, limiting at the same time the associated computational times. Nevertheless, the second set of simulations was addressed to investigate the importance of the number of analyzed frames. With this aim, first the sequence duration was fixed equal to 30 s, altering the frame-rate (considering 2, 3, 4, 6, 8, 12 and 16 fps), and then, the frame-rate was fixed equal to 4 fps, considering different sequence durations (d = 5, 15, 30, 45, 60, 90 and 120 s), i.e., processing then a total number of frames ranging from nFR = 21 (for d = 5 s) to 481 frames (for d = 120 s).
2.3. Results Analysis and Visualization (RAV) Module
Although PIVlab offers a full suite of tools for results analysis and visualization, since in this work a considerable number of synthetic image sequences have to be managed, it has been preferred to create a specific MATLAB script, named Results Analysis and Visualization (RAV), dedicated to the analysis and the statistical characterization of the results relative to each parametric scenario.
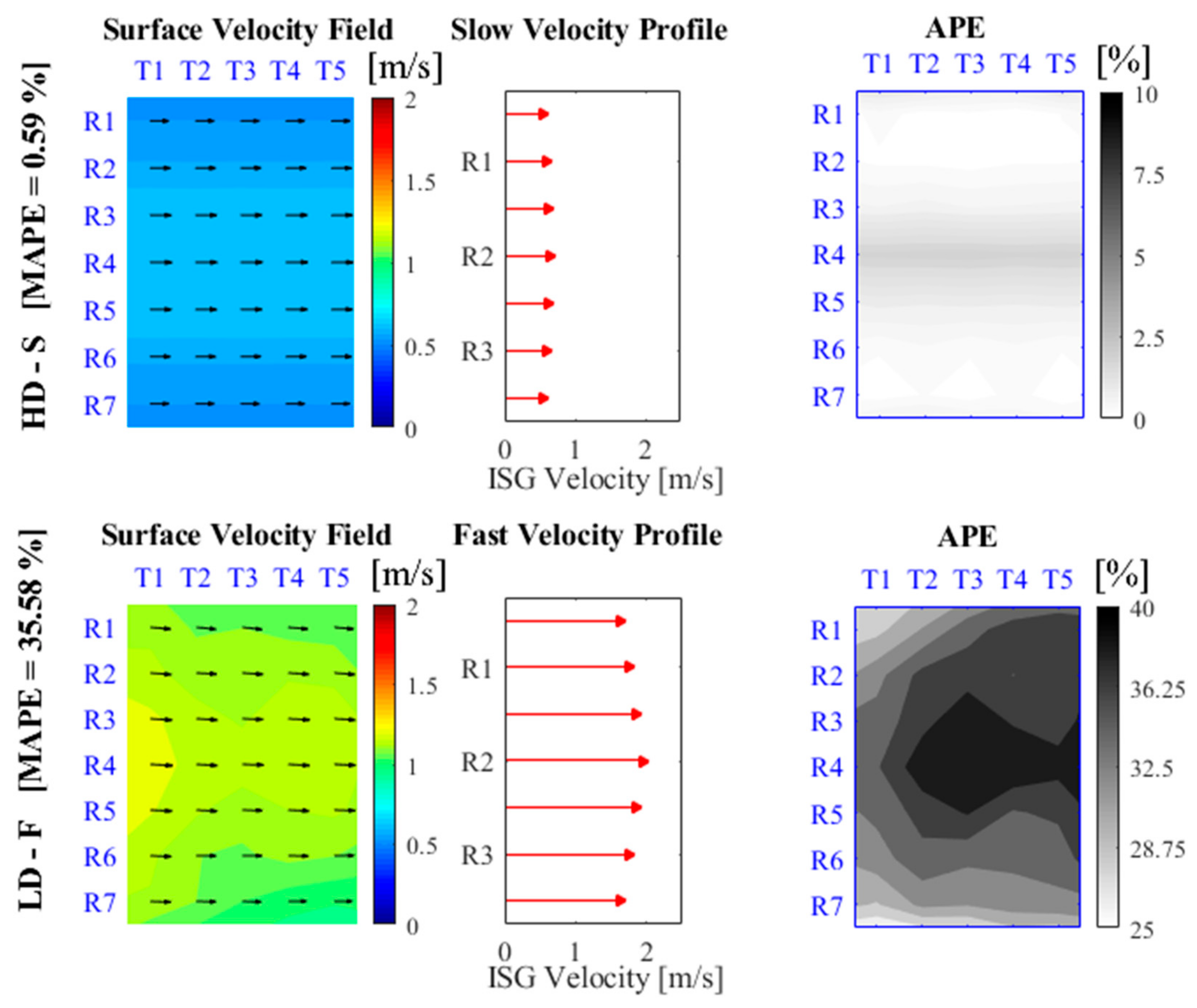
For each sequence, the estimated field of surface velocity is simply represented in a matrix form by a colored “heat map”, reporting the point velocity at any grid node.
A matrix, reporting the Absolute Percentage Error,
APEi (where
i refers to the generic
i-th node), has been associated to each sequence. The
APEi values arises from the comparison at each computational grid node between the surface velocity estimated by PIVlab (
) and the velocity imposed in the ISG (
), and are computed as:
Once the actual analysis area is selected, the script associates to each sequence an index, named
MAPE (Mean Absolute Percentage Error), that is the mean of all the
APEi over the analyzed area:
where
n refers to the total number of computational nodes within the analyzed area.
For each scenario, the script creates box-plots of all the MAPE values for the 100 corresponding realizations, with indications about the median, the interquartile range (IQR), the most extreme data points not considered outliers (whiskers) and the outliers (red marks). Moreover, it also generates maps reporting, again as colored heat map, the node-by-node mean values of the APEi over the 100 replications (<APEi>). Finally, for a reference cross-section transect within the analysis area (i.e., the central one), and for a given scenario, the script creates a comparison graph between the cross-section velocity profiles imposed by the ISG and that estimated by PIVlab; this last is displayed in the form of box-plots of the 100 surface velocity values estimated at each node of the transect for each replication of given scenario.
4. Discussion
The proposed work contributes to increase knowledge on optical methods for river monitoring and provides some useful indications towards the consolidation of operative protocols for the use of LSPIV technique in practical applications. Some of the evidences arising from this work, especially with regards to the ID-CON scheme, can be linked and compared to the results obtained by [
32], who carried out a similar study on the LSPTV technique considering a tracer with similar characteristics (i.e., shape, size and color). Our analyses, consistently with [
32], have shown an overall underestimation of the imposed velocity (see
Figure 10), with an error equal to about 0.5%, for the simulation with the best performance among all scenarios. Accuracy of field measurements may be affected by several factors neglected in our analysis, such as poor free-surface illumination, particles deformations and agglomeration processes, flow turbulence or adverse conditions acting on the free surface (e.g., strong winds), which might drastically reduce measurement accuracy; however, experimental field campaigns conducted with appropriate selections of parameters reveal mean velocity errors typically in the order of 3.5% [
51,
52], confirming how optical methods can reproduce flow velocity fields with accuracy comparable to conventional methods such as current meters and ADCP (e.g., [
22,
53]).
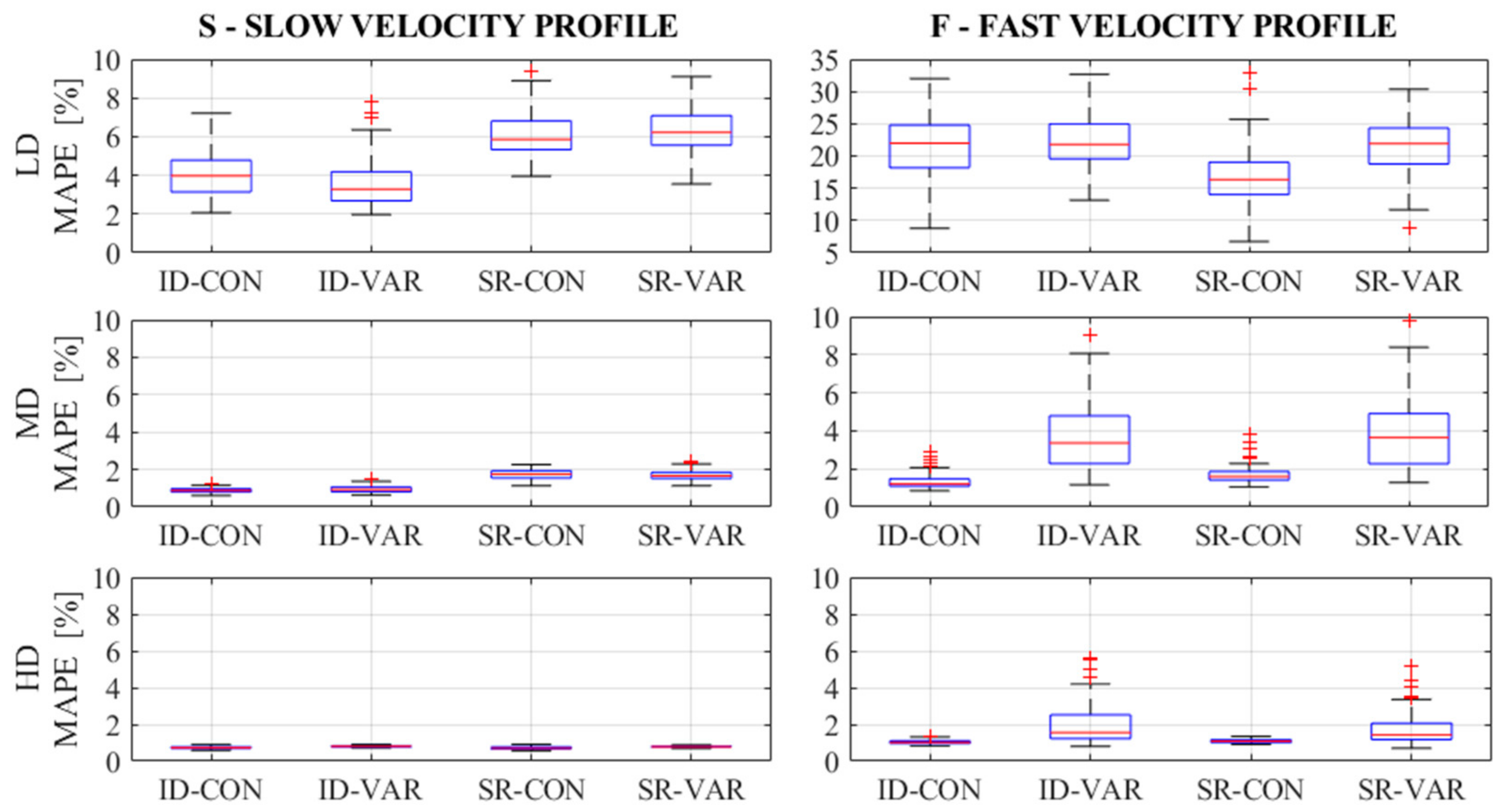
Our analyses on synthetic cases have identified the choice of an inappropriate seeding density as the main possible source of error and results uncertainty, consistently with what observed in field conditions in other works [
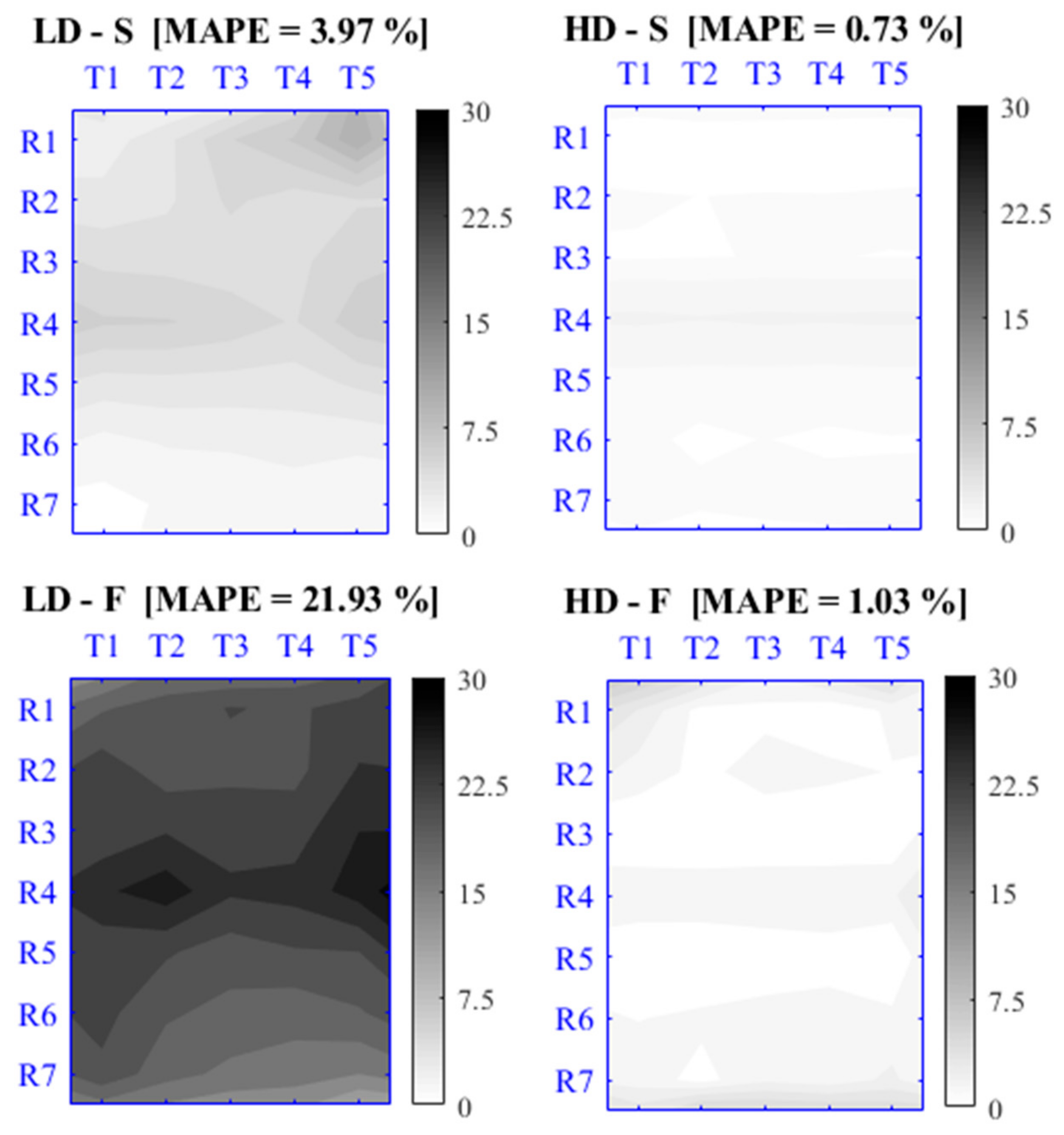
54]. More specifically, errors for the lowest seeding density cases (i.e., LD) are rather high also considering a high number of processed frames, while, for seeding density over 2.5 × 10
−4 ppp (i.e., MD), errors, in terms of magnitude and absolute variability over the various replications, reduce and stabilize, with no significant variations between the MD and the HD cases. Moreover, this result is strongly consistent with the quantitative estimate of the critical density value for errors stabilization given in [
32]. The first operative indication arising from this outcome is that, for the cases of artificial introduction of tracers, we should ensure a frame coverage with tracers of 2% at least, that implies the presence of about 30 floating particles per m
2 of liquid surface considering particles of area similar to that here considered (i.e., 7 × 10
−4 m
2).
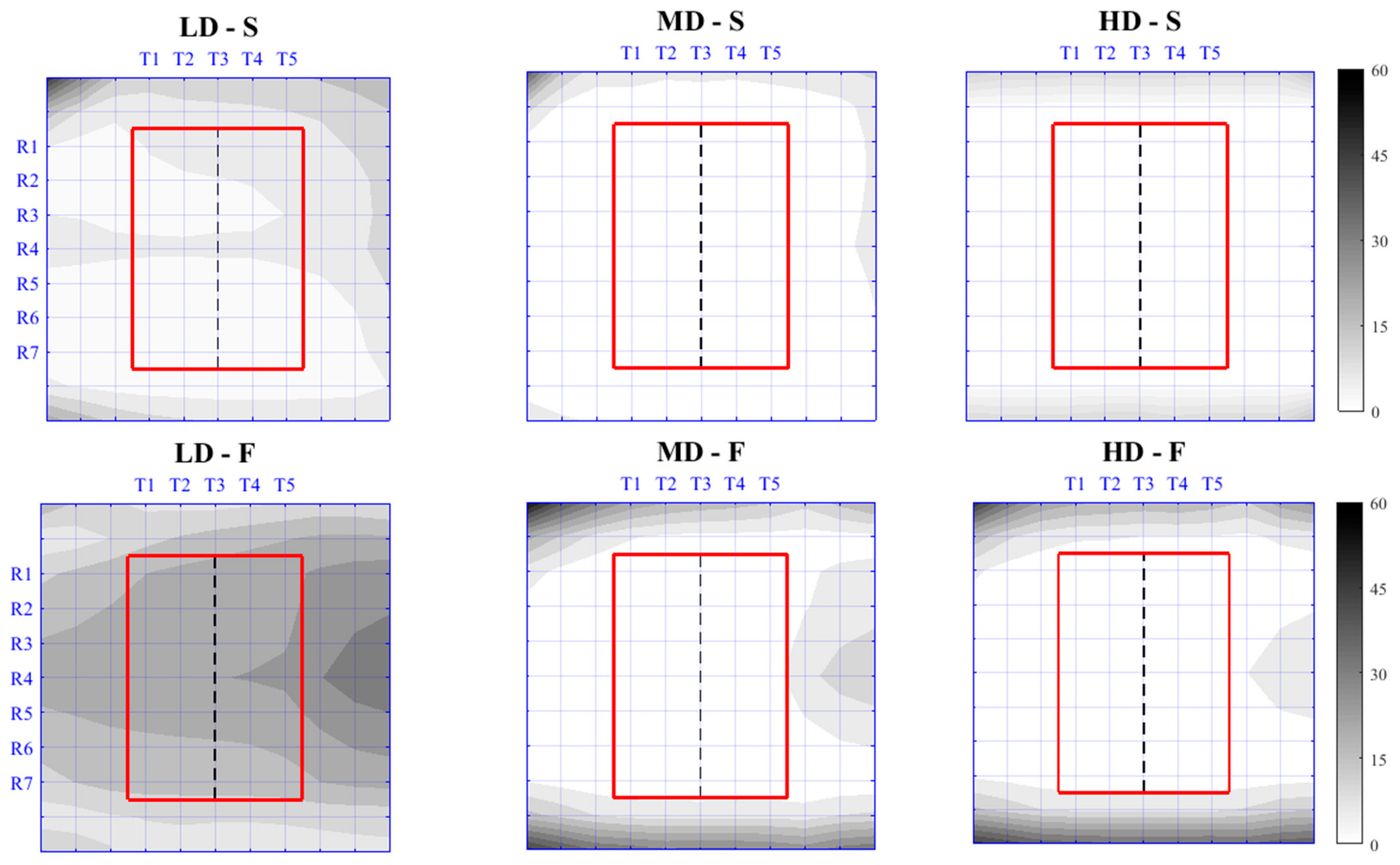
In the contour regions of the frames, especially in the tracer input and output zones, the border effect is known to produce important errors with loss of correlation, mainly due to in-plane motion and out-of-plane velocity gradients; our analysis in
Figure 5 represents the first attempt to quantitatively evaluate such errors for PIV technique.
The correct choice of the number of elaborated frames could be extremely important in real applications, where the tracer is often variable in concentration and not uniformly dispersed within the frames over the entire video sequence. The need of a number of frames sufficient to be processed is always contrasting with the needs for containing the computational time and the effects of possible disturbances related to seeding density, tracer distribution, illumination, flow conditions, etc. [
55]; for this reason, “compromise solutions” are often adopted. Our analysis demonstrates how key parameters that have to be taken into account in the choice of this trade-off solution are the frame-by-frame tracer displacement and density. In particular, such parameters should drive the choice of the selected frame-rate and video duration. Optimal setting for these two parameters should strictly depend on the local velocity conditions and the considered seeding density, together with its capacity to characterize the surface velocity field.
In real applications frame-by-frame displacement could be controlled by modifying the frame-rate during the processing phase with respect to the image acquisition frame-rate. An optimal frame-rate should be selected in relation to the sampling conditions; for instance, the use of high frame-rate with high velocities flow could avoid possible loss of detected particle and reduce possible errors due to particle deformation induced by the particle movement and camera settings [
32]. Several authors have suggested setting a frame-rate proportional to the flow velocity [
50]. According to [
56], for LSPIV measurements the maximum frame-by-frame particle displacement should be less than 50% of the IA. Considering the frame-rate here adopted for the first set of simulations (frame-rate = 4 fps), the maximum particles displacement for the F case reached, in the midstream, values up to 2/3 of the selected width for the first pass interrogation area, and this has produced frequent lack of image pairs with a sensible reduction of the performance and with higher results uncertainty with respect to the cases under the S case.
Figure 11 shows how, for high flow velocity, this issue can be easily overcome by increasing the frame-rate, with the consequent reduction of tracer displacements (see
Table 2). In particular, our analysis (
Figure 11) suggests that satisfying performance of PIVlab can be obtained when the frame-by-frame tracer displacements are lower than approximately 15% of the selected IA dimension along the flow direction; with our settings, this corresponds to a frame-by-frame displacement of about 50 px. It is worth emphasizing that, on the contrary, when the flow is characterized by a low velocity, a high frame-rate could drastically reduce frame-by-frame particles displacement, negatively affecting the matching algorithm between image pairs. This is here confirmed by the lowering of the performance under the scenario with fixed duration and maximum frame-rate (i.e., 16 fps) for the slow profile (top-left panel,
Figure 11).
The increment in the number of elaborated frames for longer video durations increases the number of velocity samples in space and this always produces a better characterization of the velocity field in numerical simulations, with consequent improvement in PIV based software performance (right graphs,
Figure 11). In real applications, especially when a natural tracer is used (e.g., boils, foam, free-surface waviness, leaves, etc.), seeding density could be rather low compared to the aforementioned critical value. In such cases, the use of longer sequence durations could become fundamental and strategical, allowing for counterbalancing the scarce presence of tracer within each frame and improving PIV capability to homogenously estimate the surface velocity field within the entire region of interest. Our analysis (top-left panel of
Figure 11) shows how, at same conditions of seeding density and frame-rate, PIVlab performances significantly improve passing from the elaboration of sequence duration of 5 s to that of 120 s, with a halving of
MAPE values. In real applications, where the tracer (naturally present or artificially introduced) could be not uniformly distributed and/or with not constant concentration over the entire duration of the analyzed video, an aspect that deserves particular attention is the selection of the most informative sequence of frames within the available video, which might lead to a significant error reduction in PIV estimates [
57]. With this regard, increasing the length of the video can be useful for searching the best seeding conditions.
5. Conclusions
Optical methods for river monitoring are recently gaining considerable attention, since they represent unexpansive and practical techniques that permit to overcome many of the difficulties related to traditional methods. For example, the use of optical sensors is crucial for monitoring surface velocity during floods, since alternative remote approaches, e.g., based on radar sensors, are still rather expensive and the field of view is limited. The synthetic approach presented in this study has demonstrated how accurate estimations of the surface velocity field can be obtained only paying particular attentions to the adopted experimental setup.
Many factors that determinates actual river flow conditions in real cases, such as the hydrodynamic effects of turbulence on tracers, are here explicitly neglected and, thus, the generated scenarios (also for the most realistic SR-VAR cases) could be rather far from real scenarios. Nevertheless, the creation of controlled conditions by a numerical approach has the advantage that allows one to conduct sensitivity analyses on specific factors of interest, minimizing the effects of external disturbances.
In this study, coherently with other works similarly conducted on alternative optical techniques (i.e., LSPTV), we have focused our attention on some factors which we can easily control during field surveys. Then, the numerical approach here discussed could be seen as a sort of preparatory activity that could drive experimental setup in real cases, providing useful suggestions for an appropriate parameterization in terms of seeding density, frame-rate and duration of the video-sequence depending on the presumable local flow and environmental conditions. With respect to synthetic approaches used in other works e.g., [
32,
35], here there is an attempt to make the numeric experiments closer to real conditions, considering a not uniform cross-section velocity profiles and adopting some schemes with tracers of different size (VAR). The robustness of our results has been tested by performing a high number of replications for each scenario.
Our main outcomes can be briefly synthesized in following points:
particular attention should be paid to the choice of an appropriate tracer concentration: low seeding densities produce larger errors in numerical simulations, while a sufficiently high seeding density of particles (i.e., percentage of pixels with tracers higher than 2% of the total number of pixels in the frame) ensures satisfying performance of LSPIV matching algorithms for a good range of typical flow velocities (lower than 1.5 m/s), reducing the errors in velocity estimation and, at the same time, results uncertainty. This suggests an operative criterion for choosing the proper seeding density in field campaigns, in which additional seeding particles could be artificially introduced to improve accuracy of LSPIV measurements in the case of low presence of natural tracers;
an important performance increment can be obtained increasing the duration of the processed video sequence. This is, in fact, a well-known strategy to compensate problems related to low seeding density, especially when flow velocity is rather low e.g., [
58,
59]. Nevertheless, it should be pointed out that longer durations also imply an increase of computational costs, and, in real cases, the occurrences of possible environmental disturbances over the video sequence;
the choice of the frame-rate for the processed sequence should be made with extreme care and according to the local flow conditions; in particular, the selected frame-rate should optimize the frame-by-frame tracer displacements. Our analyses suggest an optimal value for the frame-by-frame displacements in the order of about 15% of the selected interrogation area (IA) dimension along the flow direction. The frame-rate with respect to the typical image acquisition frame-rate (i.e., 24 fps) should be considerably reduced for very slow flows in order to avoid excessively small displacements, while, for very fast flows, it should be increased to limit the frame-by-frame displacements and the in-plain pairs loss. Considering our settings, an optimal value for the frame-rate (
Figure 11) could be around 12 fps for a river characterized by average velocities in the range between 0.5 and 1.5 m/s (i.e., expected average frame-by-frame particle displacements from 13 to 42 px,
Table 2);
the introduction of further disturbance elements in our simulations (i.e., SR-VAR scenarios) has slightly increased the errors in the velocity estimation with respect to the ideal conditions. Nevertheless, our analysis demonstrates that, when a tracer with different shaped particles of different size is used (for instance woodchips tracer, which is the most common and cheaper choice for practical applications, e.g., [
22]) and a more realistic background is considered, the expected software performance reduction with respect to an ideal case could be partially compensated again by increasing the seeding density and/or the number of processed frames. This aspect would deserve further investigations to take into account other disturbance factors, here neglected, that might have an important role in real applications, and, at the same time, the potential benefits arising from the adoption of image pre-processing procedures. For example, some pre-processing procedures incorporated in common PIV-based software could significantly reduce possible issues related to the environmental conditions, preliminarily enhancing tracer-background contrast and reducing background noise.
The numerical approach provides a useful tool also for studying the border effect in optical techniques, which is an aspect scarcely investigated in the past. Our analysis has confirmed the importance in removing the contour region of the frame, where the error is one order of magnitude higher than in the central part.
Our numerical investigation has quantitatively evaluated the importance of the aspect which usually has the highest impact on the resultant accuracy of LSPIV measurements, i.e., the seeding density [
54,
60], while it misses several important sources of errors. Our results refer to synthetic experiments that, although realistic, are not representative of any field conditions; moreover, the results here presented are unavoidably related to the PIV software selected. Further analyses, with a larger set of idealized circumstances, should be performed in order to generalize the obtained results.
Ref. [
60] identified twenty-seven possible sources of error that might affect the LSPIV measurements in field conditions, which are generated in each step of the measurement process: pre-processing (i.e., illumination, seeding, recording, transformation); processing or post-processing. Some of the aspects related to common practical difficulties, neglected in this work, that could deserve attention for future numerical investigations are related to the possible occurrence of: turbulence effects; not uniform distribution and/or inconstant concentration of the tracer within the liquid surface; tracer agglomeration and deformation processes; climate adverse conditions (e.g., scarce natural light conditions, sun-glint, rainfall, wind) that might affect the phase of pre-processing including image orthorectification, image resolution and camera stabilization.
The modeling framework here considered allows easy implementation and future improvements of the ISG that could include some of the aforementioned factors and that could be also extended to other types of sensors (e.g., radars).