Importance of Infiltration Rates for Fate and Transport of Benzene in High-Tiered Risk-Based Assessment Considering Korean Site-Specific Factors at Contaminated Sites
Abstract
:1. Introduction
2. Method
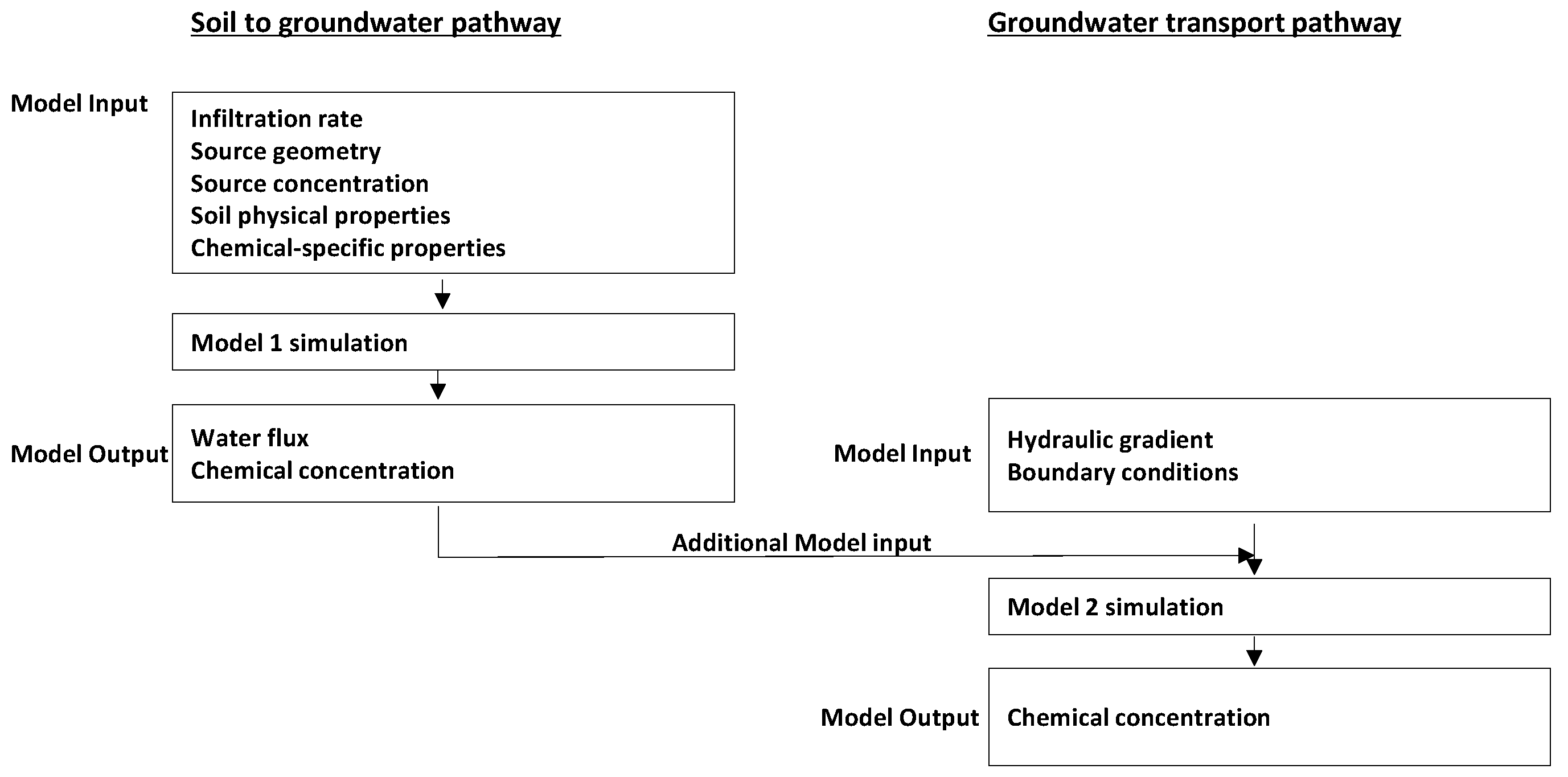
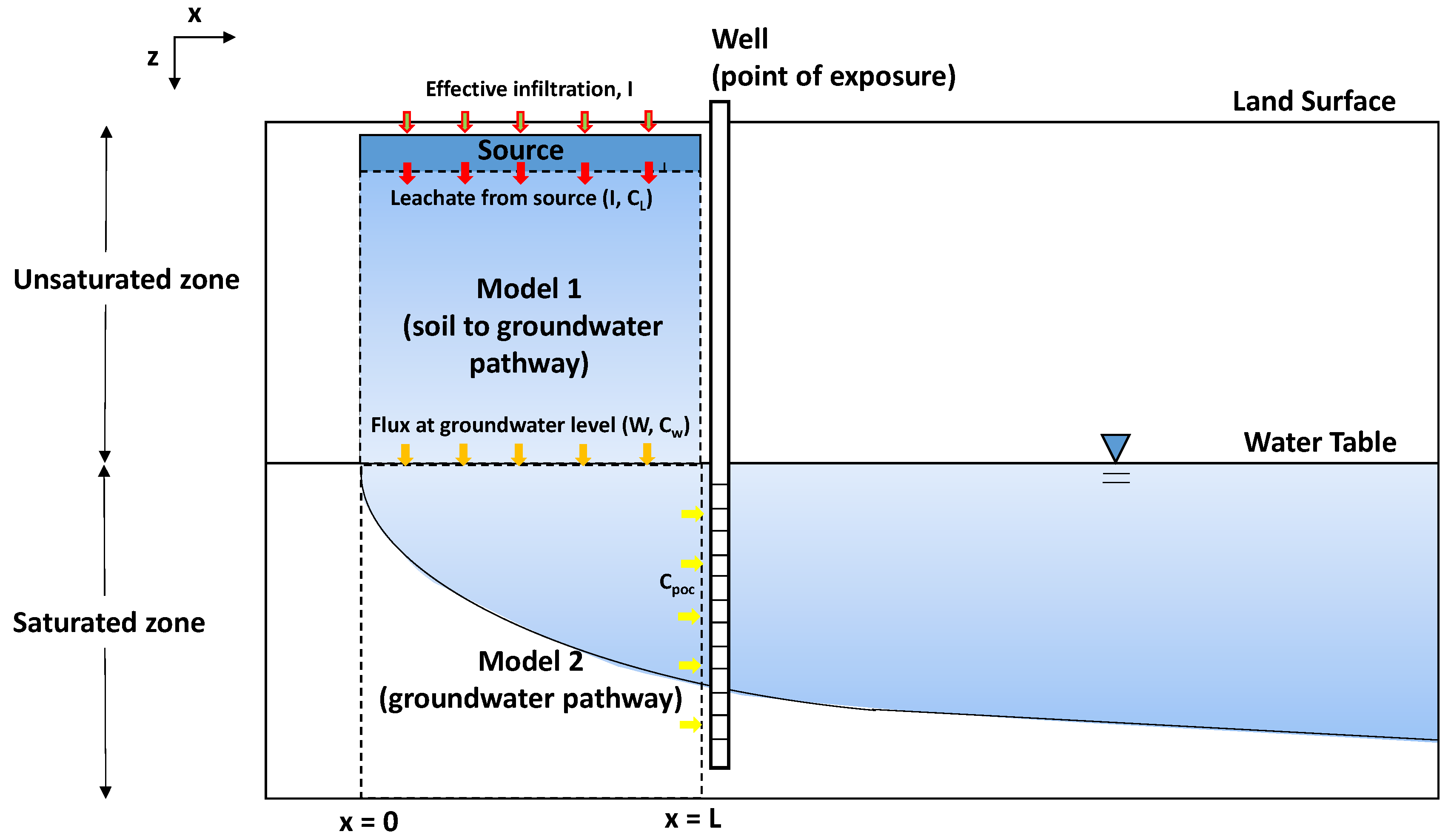
2.1. Conceptualized Numerical Model to Simulate Pathways in the Unsaturated and Saturated Zone
- (1)
- Leaching from source
- (2)
- Fate and transport in the unsaturated zone (Model 1)—Soil to groundwater pathway
- (3)
- Fate and transport in the saturated aquifer (Model 2)—Groundwater transport pathway
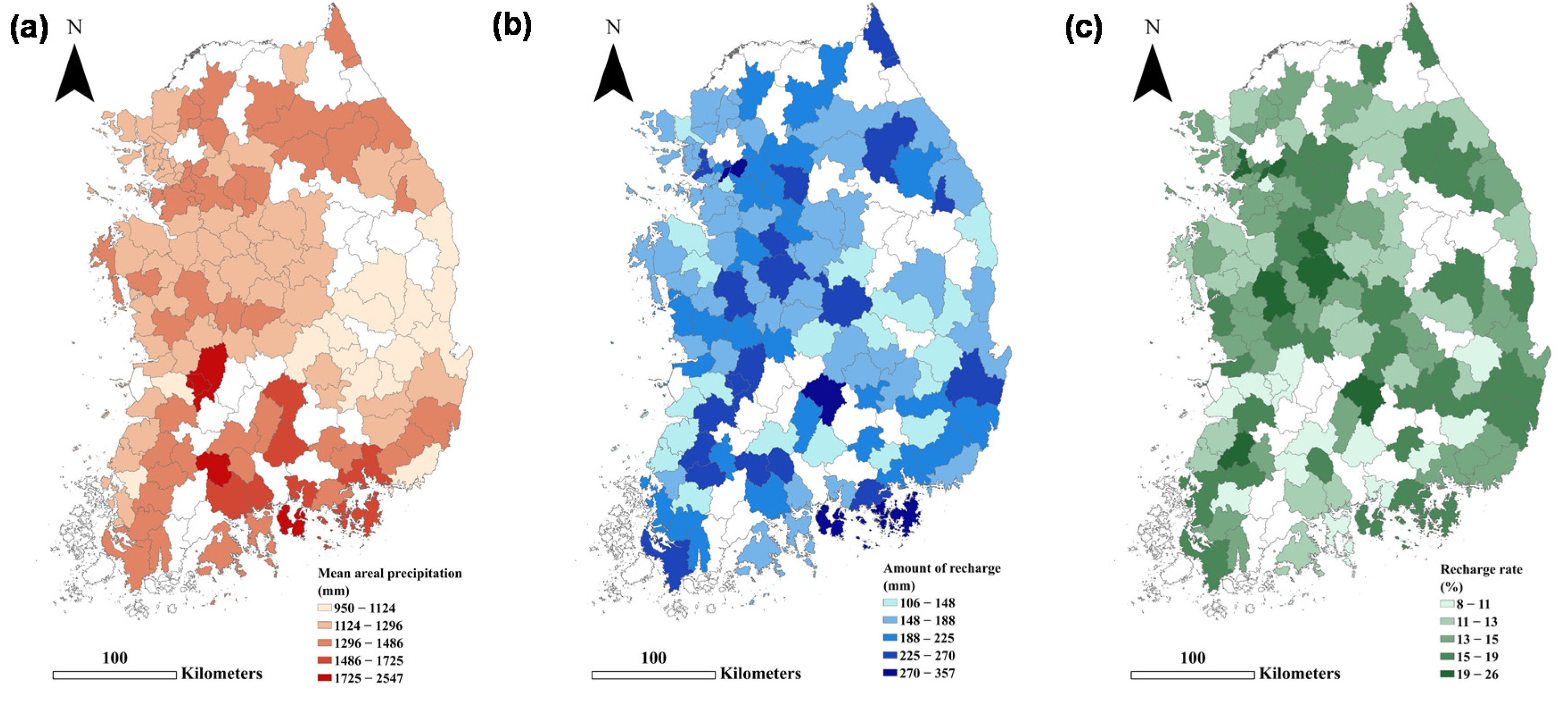
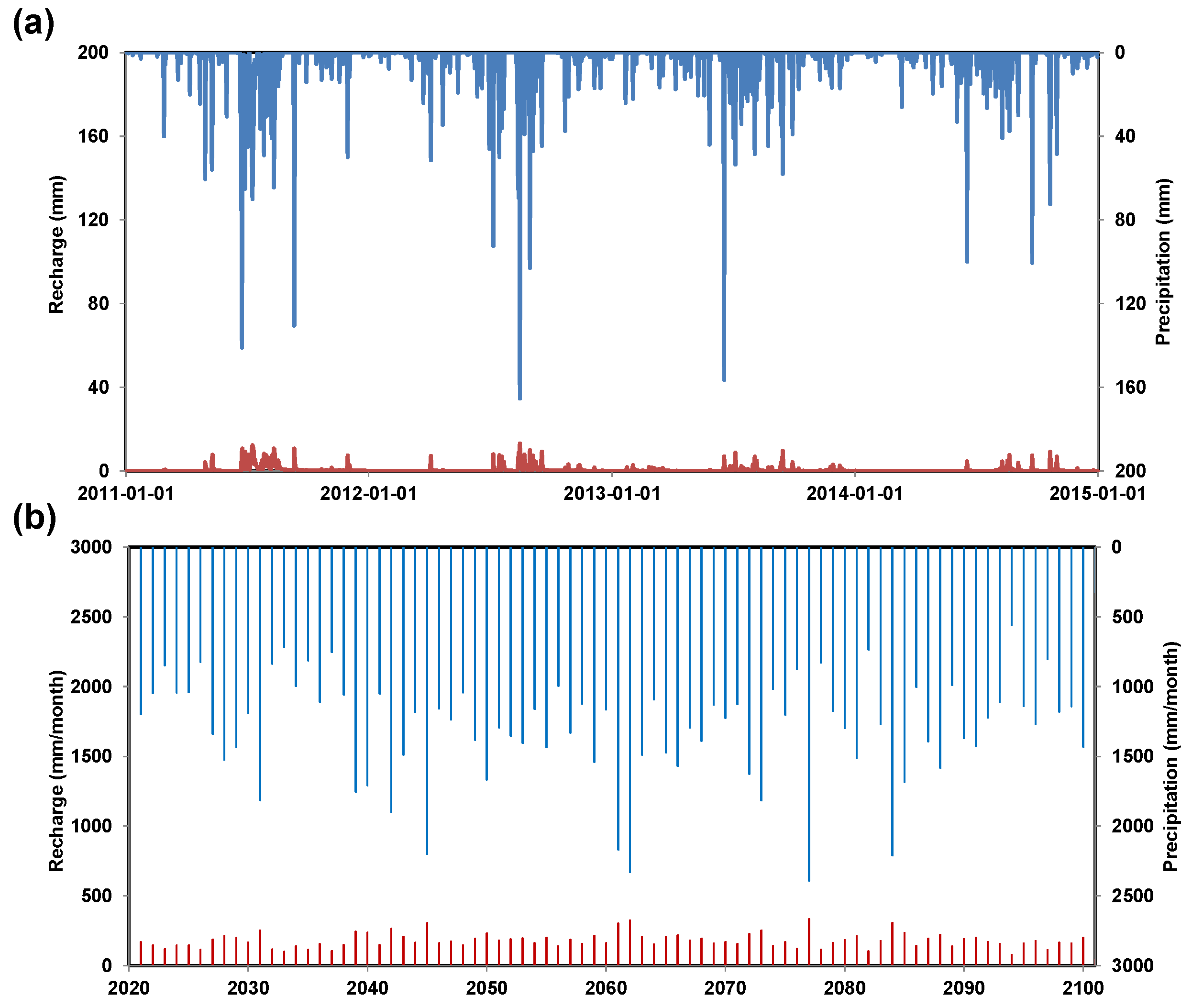
2.2. National Infiltration Data Acquisition for Model Input
3. Results and Discussion
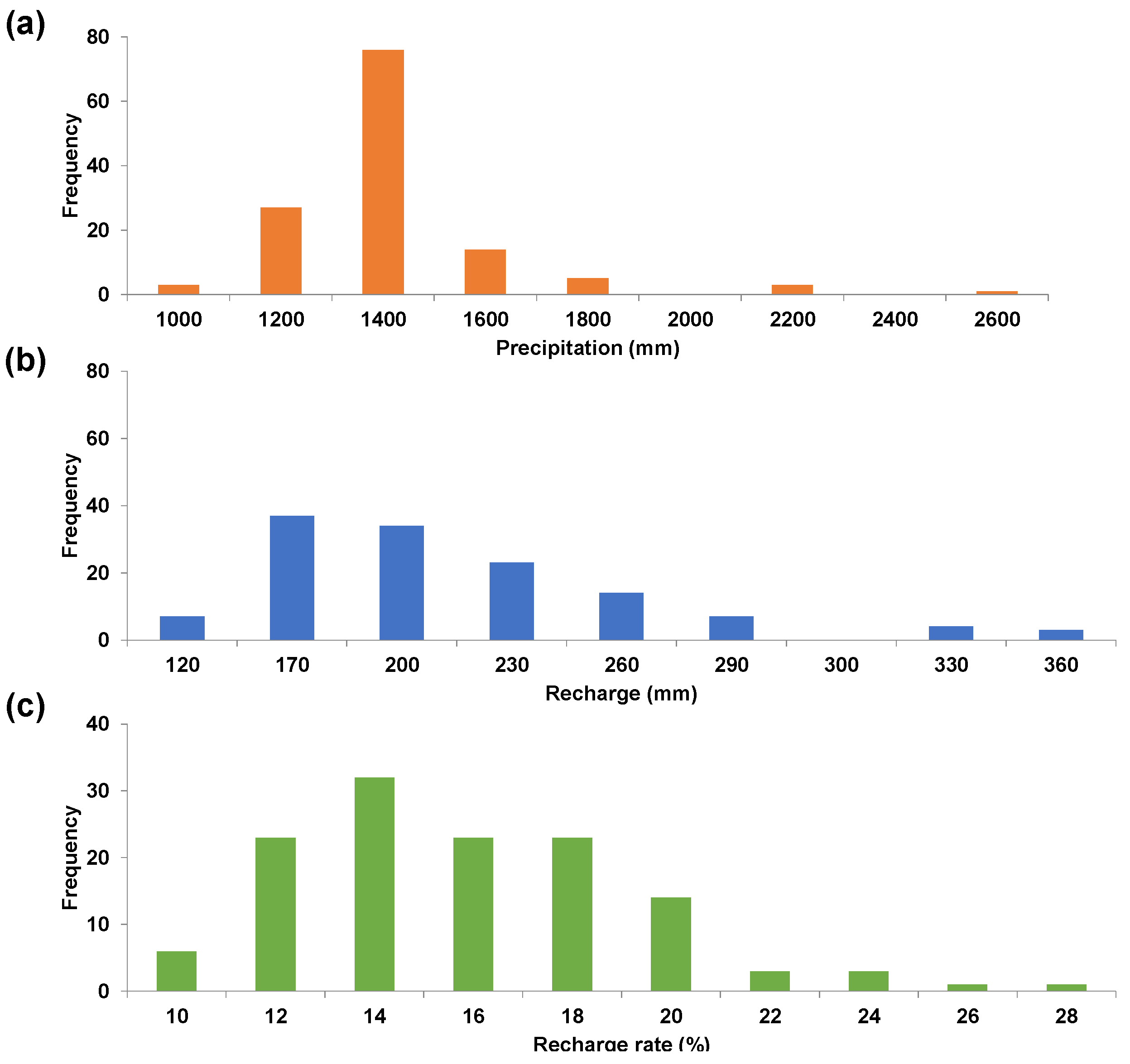
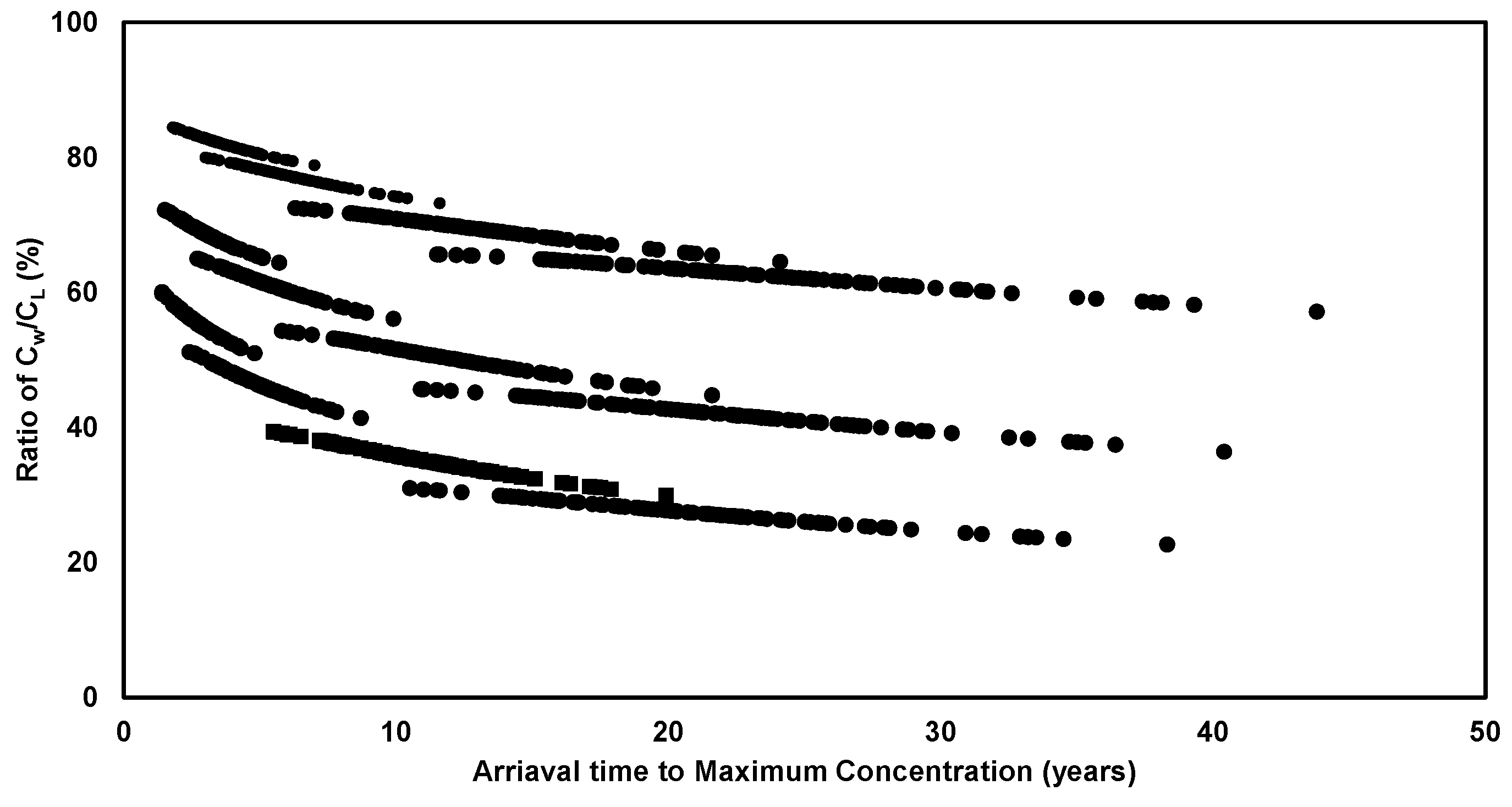
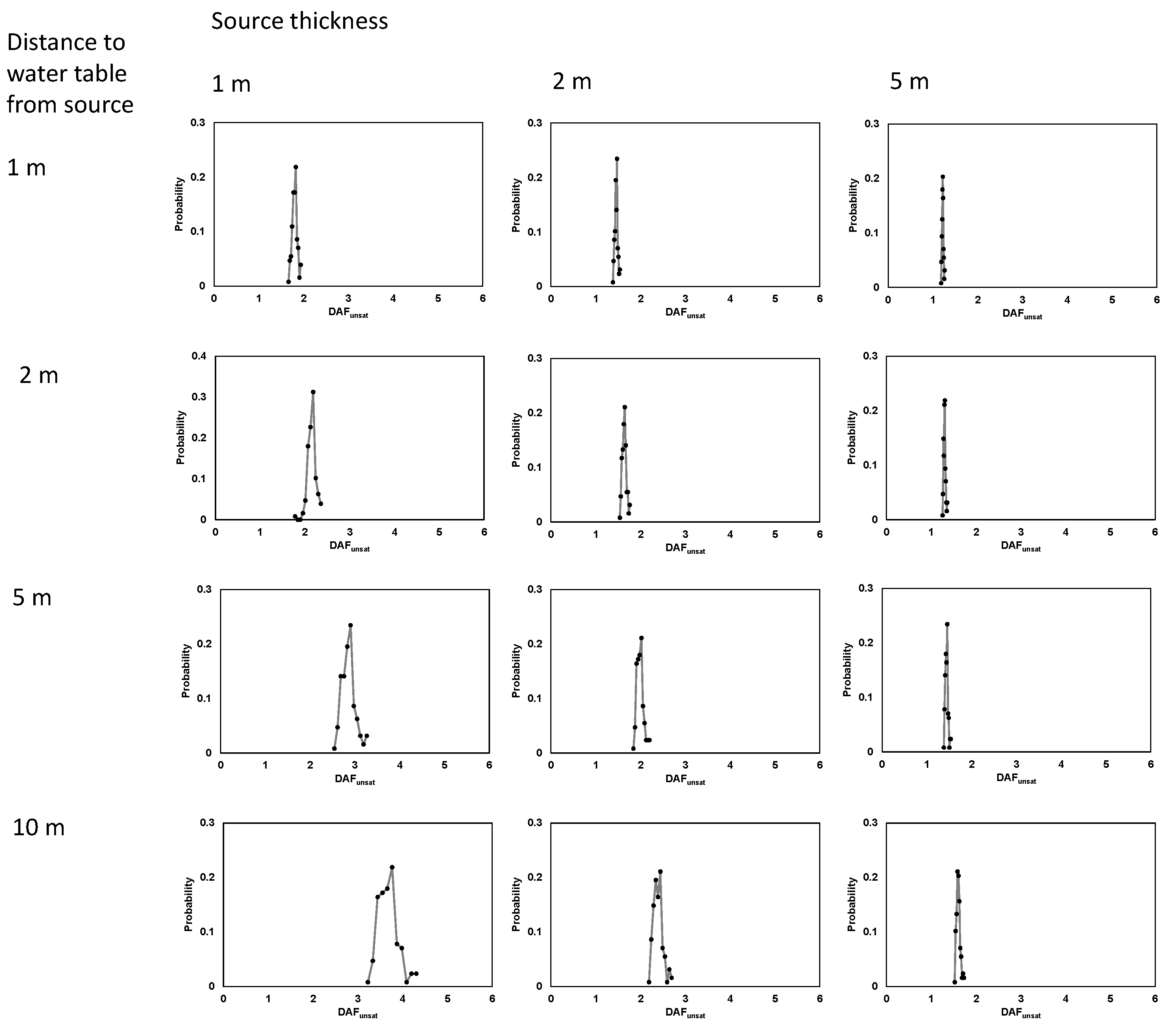
3.1. Estimation of the Probability Distribution of DAFunsat
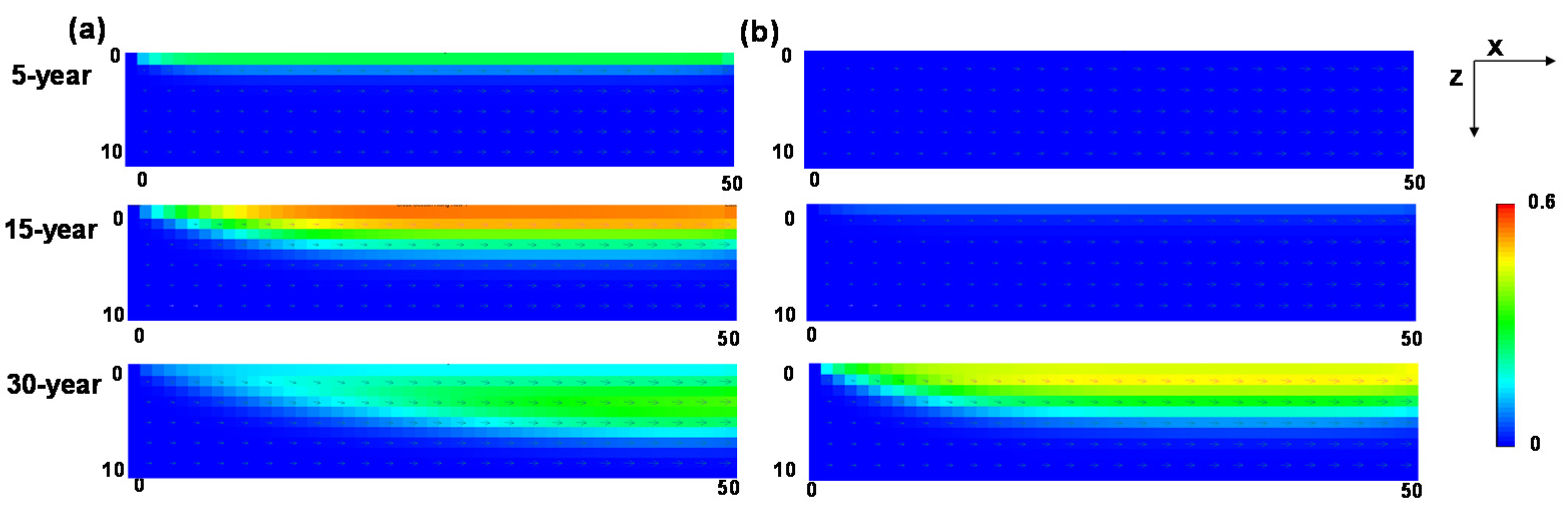
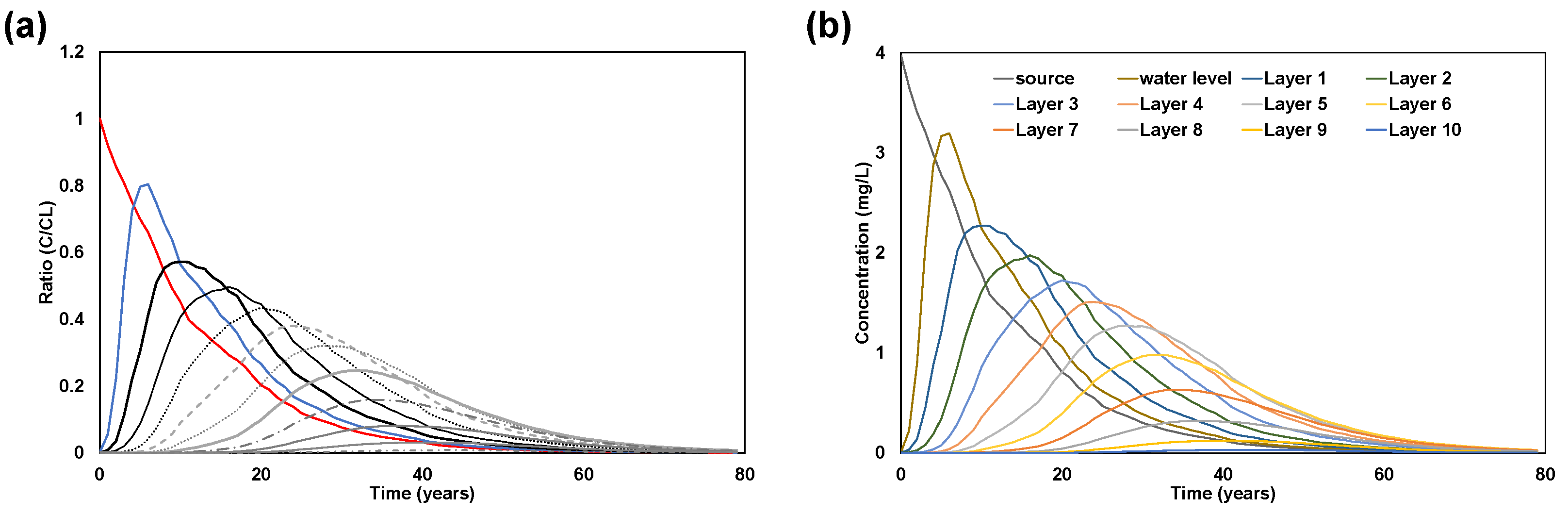
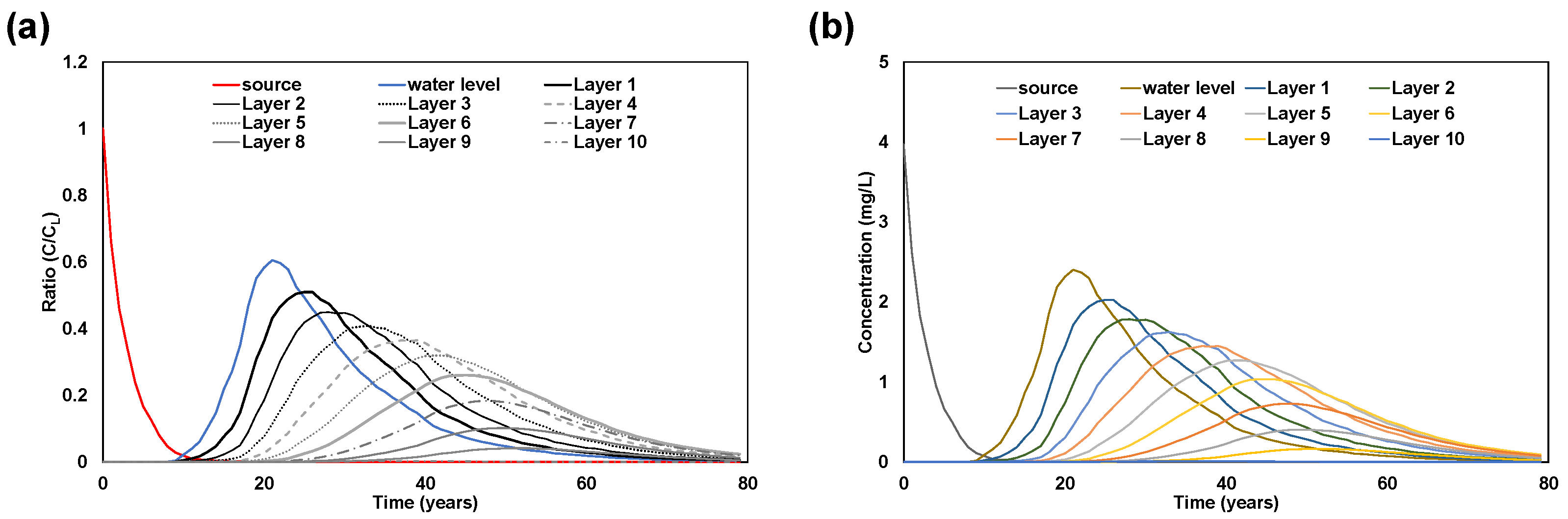
3.2. Case Study: Site Description and Simulation of the Benzene Pathway Using Hydrological Assessment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- U.S. EPA. Soil Screening Guidance: User’s Guide; U.S. EPA. Office of Emergency and Remedial Response: Washington, DC, USA, 1996.
- U.S. EPA. Soil Screening Guidance: Technical Background Document; U.S. EPA. Office of Emergency and Remedial Response: Washington, DC, USA, 1996.
- ASTM. Standard Guide for Risk-Based Corrective Action, Standard E2081-00; American Society for Testing Materials: West Conshohocken, PA, USA, 2000; p. 95. [Google Scholar]
- Kechavarzi, C.; Soga, K.; Illangasekare, T.H. Two-dimensional laboratory simulation of LNAPL infiltration and redistribution in the vadose zone. J. Contam. Hydrol. 2005, 76, 211–233. [Google Scholar] [CrossRef] [PubMed]
- Amiaz, Y.; Sorek, S.; Enzel, Y.; Dahan, O. Solute transport in the vadose zone and groundwater during flash floods. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Diamantopoulos, E.; Šimůnek, J.; Oberdörster, C.; Hammel, K.; Jene, B.; Schröder, T.; Harter, T. Assessing the Potential Exposure of Groundwater to Pesticides: A Model Comparison. Vadose Zone J. 2017, 16, vzj2017.2004.0070. [Google Scholar] [CrossRef] [Green Version]
- Ravi, V.; Johnson, J.A. A One-Dimensional Finite Difference Vadose Zone Leaching Model. Version 2.2; U.S. EPA. Office of Research and Development: Redding, CA, USA, 1997.
- Suk, H.-J.; Chae, B.-G. Analytical Solution of Multi-species Transport Equations Coupled with a First-order Reaction Network Under Various Boundary Conditions. J. Soil Groundw. Environ. 2011, 16, 46–57. [Google Scholar] [CrossRef]
- Jang, W.; Aral, M.M. Density-driven Transport of Volatile Organic Compounds and its Impact on Contaminated Groundwater Plume Evolution. Transp. Porous Media 2007, 67, 353–374. [Google Scholar] [CrossRef]
- Rivett, M.O.; Wealthall, G.P.; Dearden, R.A.; McAlary, T.A. Review of unsaturated-zone transport and attenuation of volatile organic compound (VOC) plumes leached from shallow source zones. J. Contam. Hydrol. 2011, 123, 130–156. [Google Scholar] [CrossRef] [PubMed]
- Köhne, J.M.; Köhne, S.; Šimůnek, J. A review of model applications for structured soils: A) Water flow and tracer transport. J. Contam. Hydrol. 2009, 104, 4–35. [Google Scholar] [CrossRef]
- Oostrom, M.; Truex, M.J.; Carroll, K.C.; Chronister, G.B. Perched-water analysis related to deep vadose zone contaminant transport and impact to groundwater. J. Hydrol. 2013, 505, 228–239. [Google Scholar] [CrossRef]
- Šimůnek, J.; Jarvis, N.J.; van Genuchten, M.T.; Gärdenäs, A. Review and comparison of models for describing non-equilibrium and preferential flow and transport in the vadose zone. J. Hydrol. 2003, 272, 14–35. [Google Scholar] [CrossRef]
- Sookhak Lari, K.; Davis, G.B.; Rayner, J.L.; Bastow, T.P.; Puzon, G.J. Natural source zone depletion of LNAPL: A critical review supporting modelling approaches. Water Res. 2019, 157, 630–646. [Google Scholar] [CrossRef] [PubMed]
- Essaid, H.I.; Bekins, B.A.; Cozzarelli, I.M. Organic contaminant transport and fate in the subsurface: Evolution of knowledge and understanding. Water Resour. Res. 2015, 51, 4861–4902. [Google Scholar] [CrossRef]
- Dobson, R.; Schroth, M.H.; Oostrom, M.; Zeyer, J. Determination of NAPL−Water Interfacial Areas in Well-Characterized Porous Media. Environ. Sci. Technol. 2006, 40, 815–822. [Google Scholar] [CrossRef] [PubMed]
- Luciano, A.; Mancini, G.; Torretta, V.; Viotti, P. An empirical model for the evaluation of the dissolution rate from a DNAPL-contaminated area. Environ. Sci. Pollut. Res. 2018, 25, 33992–34004. [Google Scholar] [CrossRef] [PubMed]
- Luciano, A.; Viotti, P.; Papini, M.P. On Morphometric Properties of DNAPL Sources: Relating Architecture to Mass Reduction. Water Air Soil Pollut. 2012, 223, 2849–2864. [Google Scholar] [CrossRef]
- Dobson, R.; Schroth, M.H.; Zeyer, J. Effect of water-table fluctuation on dissolution and biodegradation of a multi-component, light nonaqueous-phase liquid. J. Contam. Hydrol. 2007, 94, 235–248. [Google Scholar] [CrossRef] [PubMed]
- Teramoto, E.H.; Chang, H.K. Field data and numerical simulation of btex concentration trends under water table fluctuations: Example of a jet fuel-contaminated site in Brazil. J. Contam. Hydrol. 2017, 198, 37–47. [Google Scholar] [CrossRef] [Green Version]
- Legout, C.; Molenat, J.; Aquilina, L.; Gascuel-Odoux, C.; Faucheux, M.; Fauvel, Y.; Bariac, T. Solute transfer in the unsaturated zone-groundwater continuum of a headwater catchment. J. Hydrol. 2007, 332, 427–441. [Google Scholar] [CrossRef]
- Silliman, S.E.; Berkowitz, B.; Simunek, J.; van Genuchten, M.T. Fluid flow and solute migration within the capillary fringe. Ground Water 2002, 40, 76–84. [Google Scholar] [CrossRef]
- Haberer, C.M.; Rolle, M.; Liu, S.; Cirpka, O.A.; Grathwohl, P. A high-resolution non-invasive approach to quantify oxygen transport across the capillary fringe and within the underlying groundwater. J. Contam. Hydrol. 2011, 122, 26–39. [Google Scholar] [CrossRef]
- Verginelli, I.; Baciocchi, R. Role of natural attenuation in modeling the leaching of contaminants in the risk analysis framework. J. Environ. Manag. 2013, 114, 395–403. [Google Scholar] [CrossRef]
- Ryu, H. Development of Realistic Risk Assessment Framework for Organic Contaminants Incorporating Desoption-Limited Bioavailability and Dilution Attenuation Factors. Ph.D. Dissertation, Seoul National University, Seoul, Korea, 2010. [Google Scholar]
- Li, J.; Xi, B.; Cai, W.; Yang, Y.; Jia, Y.; Li, X.; Lv, Y.; Lv, N.; Huan, H.; Yang, J. Identification of dominating factors affecting vadose zone vulnerability by a simulation method. Sci. Rep. 2017, 7, 45955. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mazzieri, F.; Di Sante, M.; Fratalocchi, E.; Pasqualini, E. Modeling contaminant leaching and transport to groundwater in Tier 2 risk assessment procedures of contaminated sites. Environ. Earth Sci. 2016, 75, 1247. [Google Scholar] [CrossRef]
- Stoppiello, M.G.; Lofrano, G.; Carotenuto, M.; Viccione, G.; Guarnaccia, C.; Cascini, L. A Comparative Assessment of Analytical Fate and Transport Models of Organic Contaminants in Unsaturated Soils. Sustainability 2020, 12, 2949. [Google Scholar] [CrossRef] [Green Version]
- Park, K.S.; Sims, R.C.; Dupont, R.R.; Doucette, W.J.; Matthews, J.E. Fate of PAH compounds in two soil types: Influence of volatilization, abiotic loss and biological activity. Environ. Toxicol. Chem. 1990, 9, 187–195. [Google Scholar] [CrossRef]
- Freitas, J.G.; Barker, J.F. Oxygenated gasoline release in the unsaturated zone—Part 1: Source zone behavior. J. Contam. Hydrol. 2011, 126, 153–166. [Google Scholar] [CrossRef]
- Feenstra, S.; Mackay, D.M.; Cherry, J.A. A Method for Assessing Residual NAPL Based on Organic Chemical Concentrations in Soil Samples. Groundw. Monit. Remediat. 1991, 11, 128–136. [Google Scholar] [CrossRef]
- Garg, S.; Newell, C.J.; Kulkarni, P.R.; King, D.C.; Adamson, D.T.; Renno, M.I.; Sale, T. Overview of Natural Source Zone Depletion: Processes, Controlling Factors, and Composition Change. Groundw. Monit. Remediat. 2017, 37, 62–81. [Google Scholar] [CrossRef] [Green Version]
- Mackay, D.; Hathaway, E.; de Sieyes, N.; Zhang, H.; Rasa, E.; Paradis, C.; Schmidt, R.; Peng, J.; Buscheck, T.; Sihota, N. Comparing Natural Source Zone Depletion Pathways at a Fuel Release Site. Groundw. Monit. Remediat. 2018, 38, 24–39. [Google Scholar] [CrossRef]
- Park, E.; Parker, J.C. A simple model for water table fluctuations in response to precipitation. J. Hydrol. 2008, 356, 344–349. [Google Scholar] [CrossRef]
- Chang, S.W.; Kim, M.-G.; Chung, I.-M. Numerical Study of Contaminant Pathway based on Generic-scenarios and Contaminant-based Scenarios of Vadose Zone. KSCE J. Civ. Environ. Eng. Res. 2019, 39, 8. [Google Scholar]
- MOE. Soil Contamination Risk Aseessment Guildeline; Ministry of Environment: Sejong, Korea, 2006.
- Khan, F.I.; Husain, T. Risk-based monitored natural attenuation—A case study. J. Hazard. Mater. 2001, 85, 243–272. [Google Scholar] [CrossRef]
- MOE. National Groundwater Information Center. Available online: http://www.gims.go.kr (accessed on 2 September 2021).
- RCS. Hydrology: National Engineering handbook, Part 630 (Hydrology); USDA Soil Conservation Service: Washington, DC, USA, 2010.
- Healy, R.W.; Cook, P.G. Using groundwater levels to estimate recharge. Hydrogeol. J. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Park, E. Delineation of recharge rate from a hybrid water table fluctuation method. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Arnold, J.G.; Fohrer, N. SWAT2000: Current capabilities and research opportunities in applied watershed modelling. Hydrol. Processes 2005, 19, 563–572. [Google Scholar] [CrossRef]
- Chang, S.W.; Chung, I.-M. Analysis of Groudwater Budget in a Water Curtain Cultivation Site. J. Korean Soc. Civ. Eng. 2015, 35, 1259–1267. [Google Scholar] [CrossRef]
- About Risk Assessment. Available online: https://www.epa.gov/risk/about-risk-assessment (accessed on 6 October 2021).
| Input Parameter | Symbol | Unit | Default Values | Reference |
|---|---|---|---|---|
| Distance between the bottom of the source and water table | L | m | ||
| Thickness of the contaminant source | D | m | ||
| Effective infiltration | i | |||
| Total porosity | - | 0.396 | MOE [36] | |
| Volumetric water content | 0.16 | MOE [36] | ||
| Volumetric air content | 0.236 | MOE [36] | ||
| Soil bulk density | ρb | g/cm3 | 1.57 | MOE [36] |
| Fraction of organic carbon in soil | foc | - | 0.002 | MOE [36] |
| Distribution coefficient of benzene | KOC | L/kg | 62 | EPA [2] |
| Henry’s law constant | H | 0.228 | EPA [2] | |
| First-order decay (reaction) coefficient | 0 | |||
| Groundwater hydraulic gradient | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, S.W.; Chung, I.-M.; Kim, I.H.; Joo, J.C.; Moon, H.S. Importance of Infiltration Rates for Fate and Transport of Benzene in High-Tiered Risk-Based Assessment Considering Korean Site-Specific Factors at Contaminated Sites. Water 2021, 13, 3646. https://doi.org/10.3390/w13243646
Chang SW, Chung I-M, Kim IH, Joo JC, Moon HS. Importance of Infiltration Rates for Fate and Transport of Benzene in High-Tiered Risk-Based Assessment Considering Korean Site-Specific Factors at Contaminated Sites. Water. 2021; 13(24):3646. https://doi.org/10.3390/w13243646
Chicago/Turabian StyleChang, Sun Woo, Il-Moon Chung, Il Hwan Kim, Jin Chul Joo, and Hee Sun Moon. 2021. "Importance of Infiltration Rates for Fate and Transport of Benzene in High-Tiered Risk-Based Assessment Considering Korean Site-Specific Factors at Contaminated Sites" Water 13, no. 24: 3646. https://doi.org/10.3390/w13243646
APA StyleChang, S. W., Chung, I.-M., Kim, I. H., Joo, J. C., & Moon, H. S. (2021). Importance of Infiltration Rates for Fate and Transport of Benzene in High-Tiered Risk-Based Assessment Considering Korean Site-Specific Factors at Contaminated Sites. Water, 13(24), 3646. https://doi.org/10.3390/w13243646








