Motion Responses of a Berthed Tank under Resonance Coupling Effect of Internal Sloshing and Gap Flow
Abstract
:1. Introduction
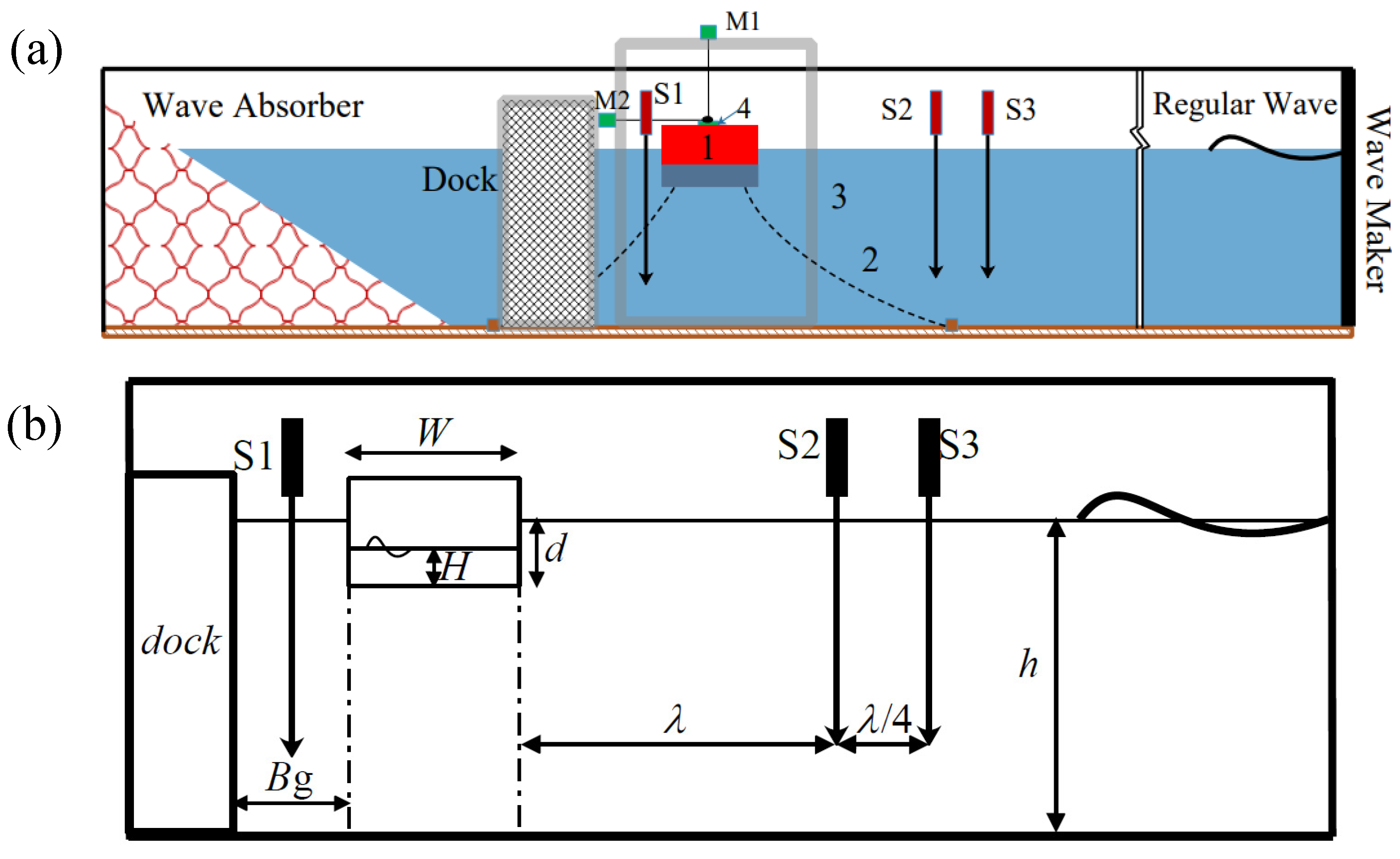
2. Experimental Setup
2.1. Experimental Condition
2.2. Problem Description
3. Results and Discussion
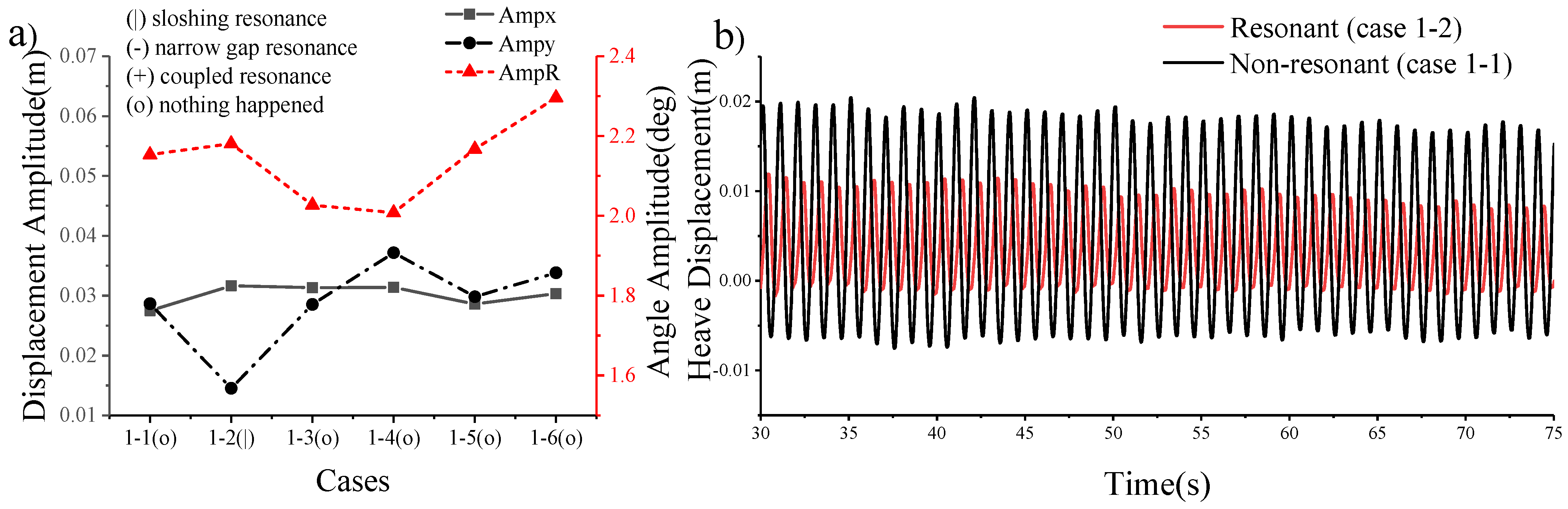
3.1. Motion Response of Floating Tank in Open Sea
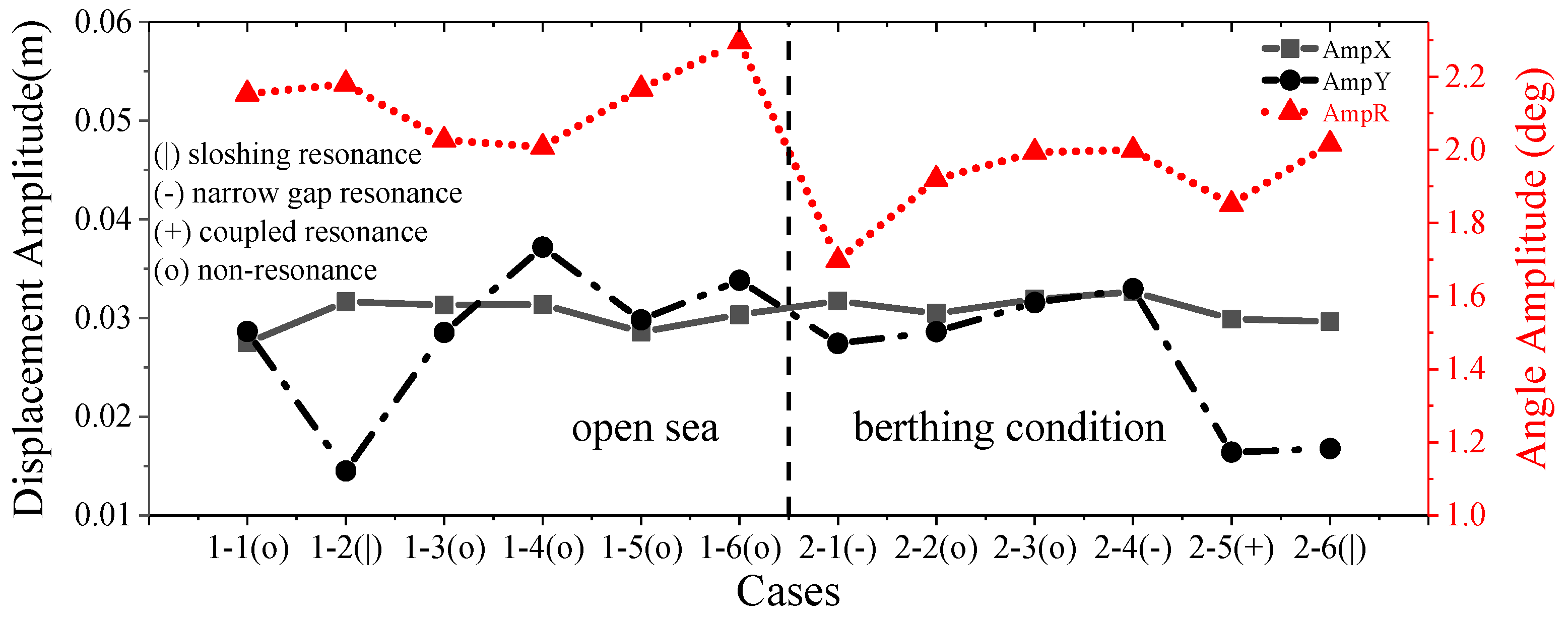
3.2. Motion Response of the Berthed Floating Tank
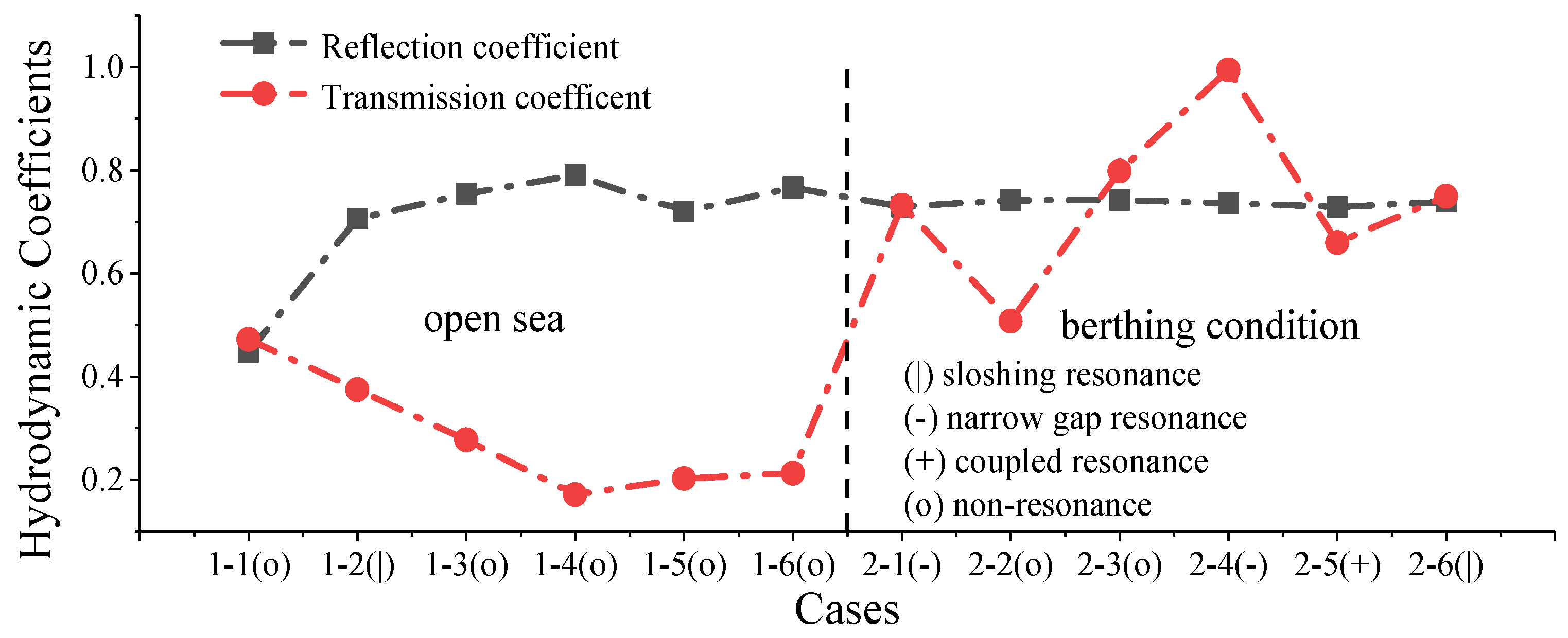
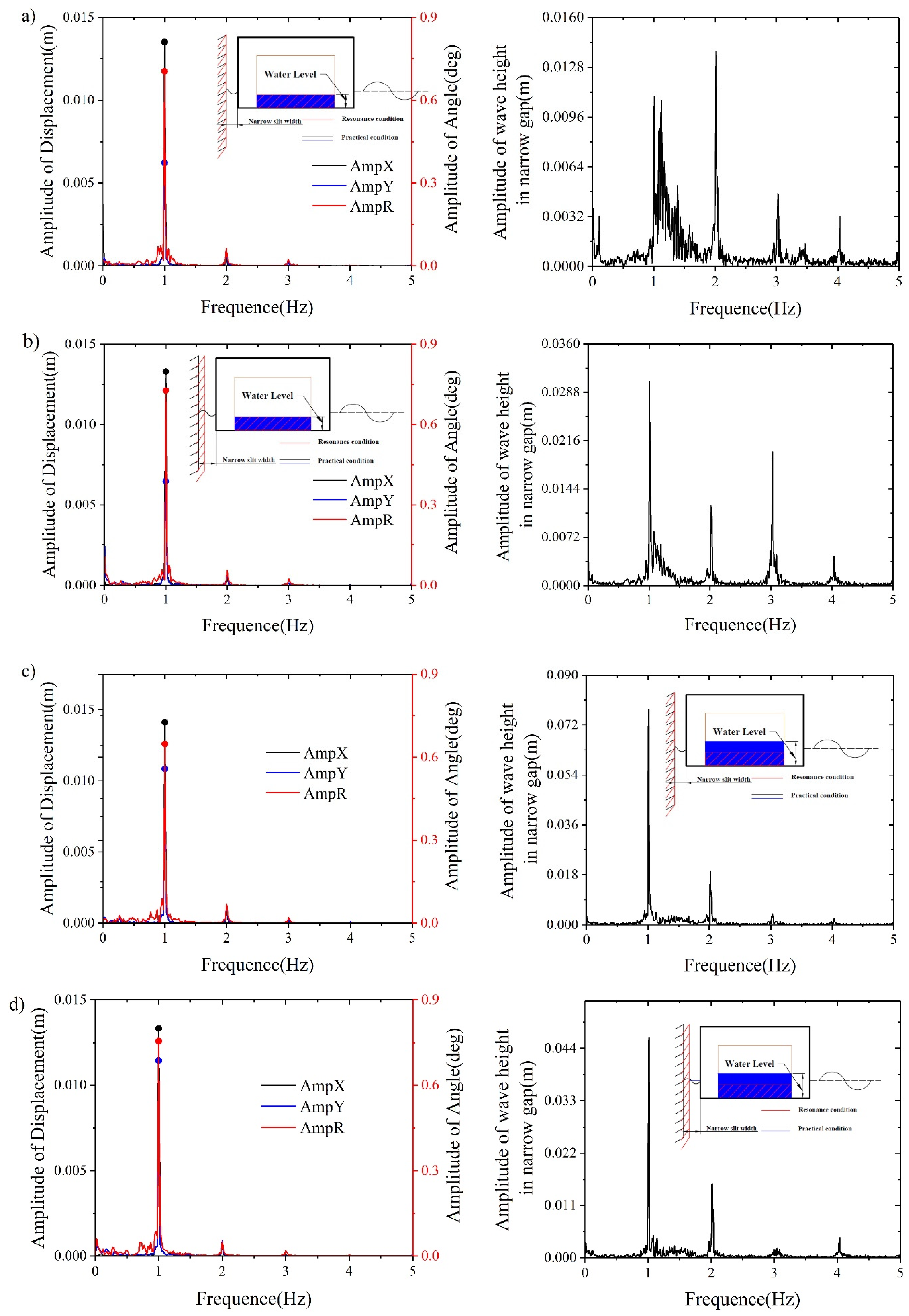
3.3. Motion Response of Berthed Floating Tank
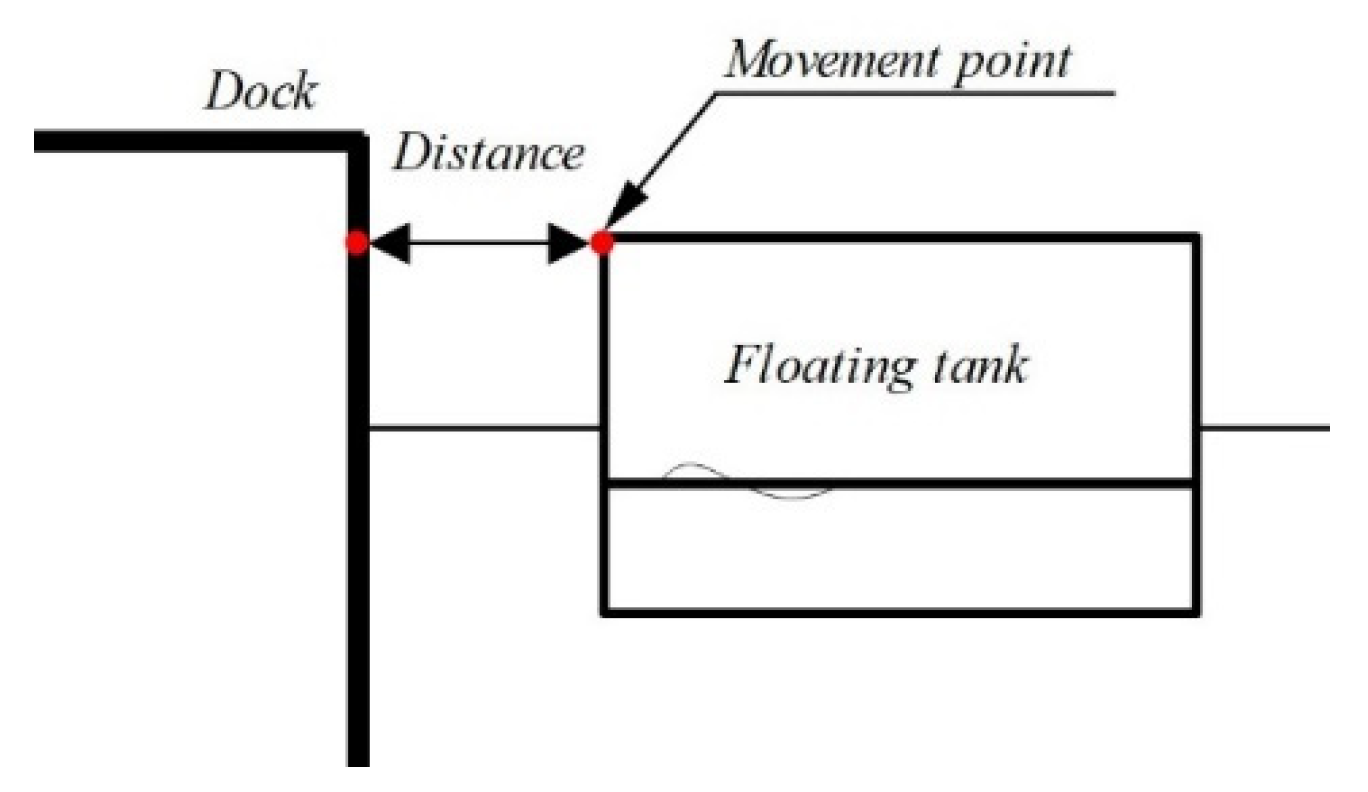
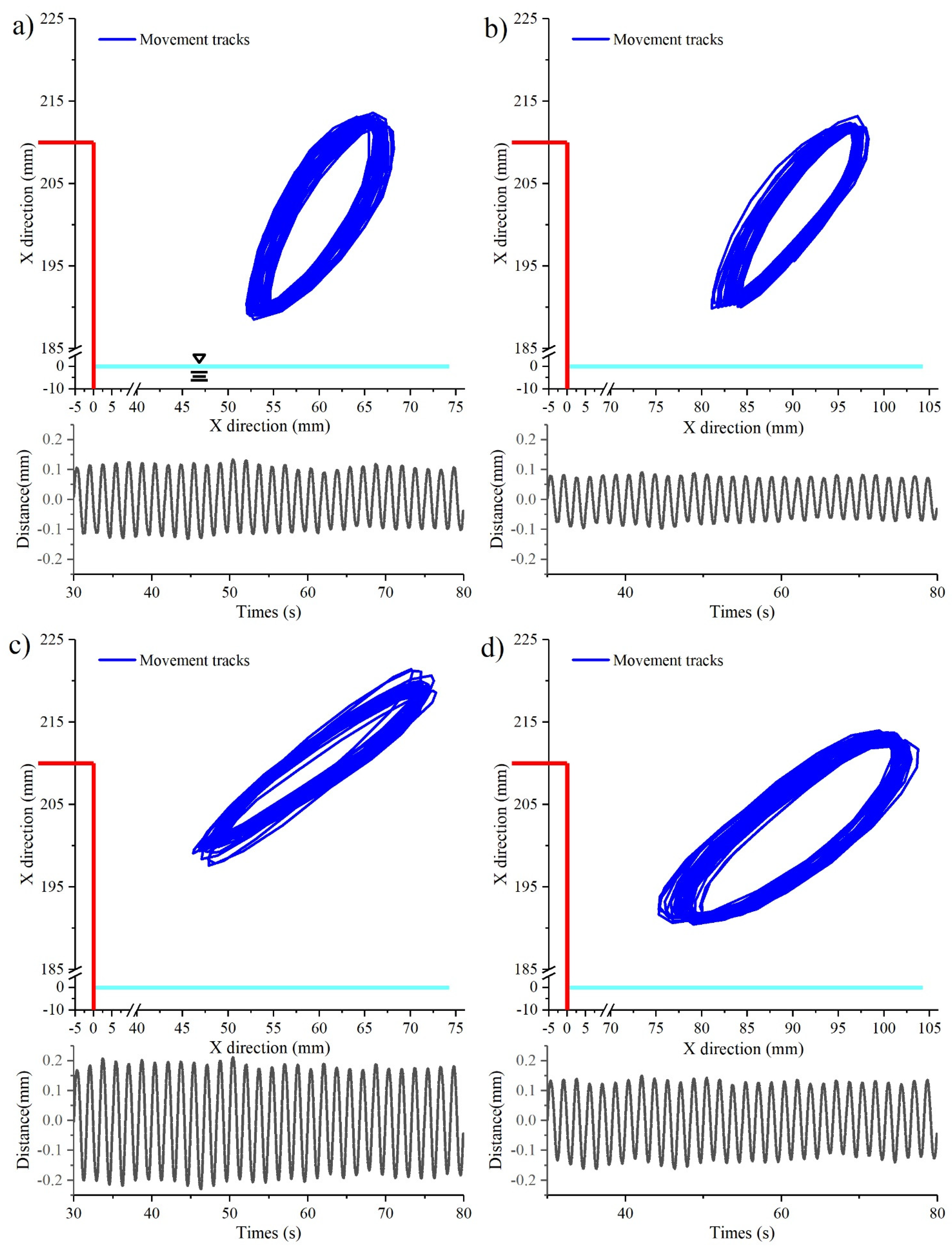
3.4. Collision Test of the Floating Tank with Dock
4. Conclusions
- A reasonable liquid tank design can reduce the amplitude of the heave response under wave action through tank resonance and improve the stability of the ship at anchor;
- When narrow gap resonance occurs, the wave height between the narrow gap increases significantly. The sloshing resonance has a beneficial effect on the stability of ships;
- The surge motion response of the floating tank is minimally affected when resonance occurs;
- The occurrence of the coupling resonance may be beneficial to the stability of the vessel when berthing;
- Based on the experimental cases in this paper, no collisions occurred in all cases and the resonance of sloshing and narrow gap contributed to avoiding a collision of the floating body with the dock.
Author Contributions
Funding
Conflicts of Interest
References
- Faltinsen, O.M.; Timokha, A.N. Sloshing with ship applications. In Proceedings of the 13th International Conference of Association of the Mediterranean, Istanbul, Turkey, 12–15 October 2009; Volume 1, pp. 25–38. [Google Scholar]
- Molin, B. LNG-FPSO’s: Frequency domain, coupled analysis of support and liquid cargo motion. In Proceedings of the IMAM Conference, Rethymnon, Greece, 13–17 May 2002. [Google Scholar]
- Lee, D.; Hong, S.Y.; Lee, G.-J. Theoretical and experimental study on dynamic behavior of a damaged ship in waves. Ocean Eng. 2007, 34, 21–31. [Google Scholar] [CrossRef]
- Brosset, L.; Mravak, Z.; Kaminski, M.; Collins, S.; Finnigan, T. Overview of Sloshel project. In Proceedings of the Nineteenth International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 July 2009. [Google Scholar]
- Bogaert, H.; Léonard, S.; Brosset, L.; Kaminsk, M.L. Sloshing and scaling: Results from the Sloshel project. In Proceedings of the Twentieth International Offshore and Polar Engineering Conference, International Society of Offshore and Polar Engineers, Beijing, China, 20–25 June 2010. [Google Scholar]
- Lafeber, W.; Bogaert, H.; Brosset, L. Elementary Loading Processes (ELP) involved in breaking wave impacts: Findings from the Sloshel project. In Proceedings of the Twenty-Second International Offshore and Polar Engineering Conference, International Society of Offshore and Polar Engineers, Rhodes, Greece, 17–22 June 2012. [Google Scholar]
- Maguire, J.R.; Whitworth, S.; Oguibe, C.N.; Radosavljevic, D.; Carden, E.P. Sloshing Dynamics-Numerical Simulations in Support of the Sloshel Project. In Proceedings of the Nineteenth International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 July 2009. [Google Scholar]
- Nam, B.W.; Kim, Y.; Kim, D.W.; Kim, Y.S. Experimental and numerical studies on ship motion responses coupled with sloshing in waves. J. Ship Res. 2009, 53, 68–82. [Google Scholar] [CrossRef]
- Jiang, S.C.; Bai, W. Coupling analysis for sway motion box with internal liquid sloshing under wave actions. Phys. Fluids 2020, 32, 072106. [Google Scholar] [CrossRef]
- Lee, S.; You, J.M.; Lee, H.H.; Lim, T.; Park, S.T.; Seo, J.; Rhee, K.P. Experimental study on the six degree-of-freedom motions of a damaged ship floating in regular waves. IEEE J. Ocean. Eng. 2015, 41, 40–49. [Google Scholar]
- Ahn, Y.; Kim, S.Y.; Kim, J.; Lee, J.; Kim, Y. Experimental Comparison of Sloshing Loads on Weather Side and Lee Side for LNG Carrier Cargo Tanks. Int. J. Offshore Polar Eng. 2019, 29, 249–256. [Google Scholar] [CrossRef]
- Xue, M.A.; Jiang, Z.; Hu, Y.A.; Yuan, X. Numerical study of porous material layer effects on mitigating sloshing in a membrane LNG tank. Ocean Eng. 2020, 218, 108240. [Google Scholar] [CrossRef]
- Kim, J.; Kim, Y.; Kim, S.Y.; Lee, K.M.; Sung, Y.J. Experimental Study of Slosh-induced Loads on an LNG Fuel Tank of a Container Ship. Int. J. Offshore Polar Eng. 2020, 30, 141–148. [Google Scholar] [CrossRef]
- Xue, M.A.; Lin, P. Numerical study of ring baffle effects on reducing violent liquid sloshing. Comput. Fluids 2011, 52, 116–129. [Google Scholar] [CrossRef]
- Xue, M.A.; Zheng, J.; Lin, P.; Yuan, X. Experimental study on vertical baffles of different configurations in suppressing sloshing pressure. Ocean Eng. 2017, 136, 178–189. [Google Scholar] [CrossRef]
- Xue, M.A.; Chen, Y.; Zheng, J.; Qian, L.; Yuan, X. Fluid dynamics analysis of sloshing pressure distribution in storage vessels of different shapes. Ocean Eng. 2019, 192, 106582. [Google Scholar] [CrossRef]
- Metherell, M.B.; Metherell, A.F. Apparatus and Method for Protecting Ships and Harbors from Attack by Vessels. U.S. Patent 6,591,774, 15 July 2003. [Google Scholar]
- Kashiwagi, M.; Endo, K.; Yamaguchi, H. Wave drift forces and moments on two ships arranged side by side in waves. Ocean Eng. 2005, 32, 529–555. [Google Scholar] [CrossRef]
- Teigen, P.; Niedzwecki, J.M. A Computational Study of Wave Effects Related to Side-by-Side LNG Offloading. In Proceedings of the Sixteenth International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 20 May–2 June 2006. [Google Scholar]
- Xiang, X.; Faltinsen, O.M. Time domain simulation of two interacting ships advancing parallel in waves. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; Volume 49484, pp. 357–369. [Google Scholar]
- Zhao, W.; Yang, J.; Hu, Z.; Tao, L. Prediction of hydrodynamic performance of an FLNG system in side-by-side offloading operation. J. Fluids Struct. 2014, 46, 89–110. [Google Scholar] [CrossRef]
- Pessoa, J.; Fonseca, N.; Soares, C.G. Numerical study of the coupled motion responses in waves of side-by-side LNG floating systems. Appl. Ocean Res. 2015, 51, 350–366. [Google Scholar] [CrossRef]
- Zhao, W.; Milne, I.; Efthymiou, M.; Wolgamot, H.; Draper, S.; Taylor, P.; Taylor, R.E. Current practice and research directions in hydrodynamics for FLNG-side-by-side offloading. Ocean Eng. 2018, 158, 99–110. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Pan, Z.; Lin, F.; Li, B.; Taylor, P.H.; Efthymiou, M. Estimation of gap resonance relevant to side-by-side offloading. Ocean Eng. 2018, 153, 1–9. [Google Scholar] [CrossRef]
- Iwata, H.; Saitoh, T.; Miao, G.P. Fluid resonance in narrow gaps of very large floating structure composed of rectangular modules. In Proceedings of the Fourth International Conference on Asian and Pacific Coasts, Nanjing, China, 21–24 September 2007; pp. 815–826. [Google Scholar]
- Moradi, N.; Zhou, T.; Cheng, L. Effect of inlet configuration on wave resonance in the narrow gap of two fixed bodies in close proximity. Ocean Eng. 2015, 103, 88–102. [Google Scholar] [CrossRef]
- Ning, D.; Zhu, Y.; Zhang, C.; Zhao, M. Experimental and numerical study on wave response at the gap between two barges of different draughts. Appl. Ocean Res. 2018, 77, 14–25. [Google Scholar] [CrossRef]
- Lu, L.; Teng, B.; Sun, L.; Chen, B. Modelling of multi-bodies in close proximity under water waves—Fluid forces on floating bodies. Ocean Eng. 2011, 38, 1403–1416. [Google Scholar] [CrossRef]
- Lu, L.; Tan, L.; Zhou, Z.; Zhao, M.; Ikoma, T. Two-dimensional numerical study of gap resonance coupling with motions of floating body moored close to a bottom-mounted wall. Phys. Fluids 2020, 32, 092101. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Timokha, A.N. Sloshing; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Goda, Y.; Suzuki, Y. Estimation of incident and reflected waves in random wave experiments. Coast. Eng. 1976, 1977, 828–845. [Google Scholar] [CrossRef] [Green Version]
| Cases | H (m) | Bg (m) | Tn (s) | Sloshing Resonance | Tg (s) | Narrow Gap Resonance | Coupled Resonance |
|---|---|---|---|---|---|---|---|
| 1-1 | 0.05 | o | 1.17 | o | o | o | o |
| 1-2 | 0.07 | o | 1.01 | | | o | o | o |
| 1-3 | 0.09 | o | 0.92 | o | o | o | o |
| 1-4 | 0.11 | o | 0.86 | o | o | o | o |
| 1-5 | 0.13 | o | 0.81 | o | o | o | o |
| 1-6 | 0.15 | o | 0.79 | o | o | o | o |
| 2-1 | 0.13 | 0.06 | 0.81 | o | 1.06 | - | o |
| 2-2 | 0.13 | 0.09 | 0.81 | o | 1.19 | o | o |
| 2-3 | 0.15 | 0.09 | 0.79 | o | 1.19 | o | o |
| 2-4 | 0.15 | 0.06 | 0.79 | o | 1.06 | - | o |
| 2-5 | 0.07 | 0.06 | 1.01 | | | 1.06 | - | + |
| 2-6 | 0.07 | 0.09 | 1.01 | | | 1.19 | o | o |
| Deviation Coefficient | Open Sea | Berthing Condition |
|---|---|---|
| AmpX | 0.052036 | 0.035876 |
| AmpY | 0.246216 | 0.259292 |
| AmpR | 0.045661 | 0.058453 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Jin, H.; Lou, M.; Wang, X.; Liu, Y. Motion Responses of a Berthed Tank under Resonance Coupling Effect of Internal Sloshing and Gap Flow. Water 2021, 13, 3625. https://doi.org/10.3390/w13243625
Wang T, Jin H, Lou M, Wang X, Liu Y. Motion Responses of a Berthed Tank under Resonance Coupling Effect of Internal Sloshing and Gap Flow. Water. 2021; 13(24):3625. https://doi.org/10.3390/w13243625
Chicago/Turabian StyleWang, Tengxiao, Heng Jin, Mengfan Lou, Xinyu Wang, and Yi Liu. 2021. "Motion Responses of a Berthed Tank under Resonance Coupling Effect of Internal Sloshing and Gap Flow" Water 13, no. 24: 3625. https://doi.org/10.3390/w13243625
APA StyleWang, T., Jin, H., Lou, M., Wang, X., & Liu, Y. (2021). Motion Responses of a Berthed Tank under Resonance Coupling Effect of Internal Sloshing and Gap Flow. Water, 13(24), 3625. https://doi.org/10.3390/w13243625






