Abstract
Scouring is one of the most common potential causes of bridge pile foundation failure with loss of life, economic and environmental impacts. Comprehensive studies on the numerical simulation of local scour around pile groups are still limited. This paper presents a numerical simulation using Flow-3D software to calculate the maximum sediment scour depth and investigate the mechanism around the groups of three cylinders in a tandem arrangement. A validation using the experimental study was carried out to confirm the reliability of the present numerical model. By using the Van Rijn transport rate equation and RNG k-ε turbulence model, the results of time evolution of scour depth and bed elevation contour show good agreement with the experimental study. The numerical simulation of three cylinders in a tandem arrangement were conducted with pile spacing ratios, G/D of 2 and 3. The local scour is affected by the horseshoe vortex from the downflow driven by the downward pressure gradient and rotates in front of the pile and the high bed shear stress, triggered by flow acceleration. The deepest maximum local scour depth is always obtained by the front pile as a shield pile, followed by the piles behind. The trend of the maximum local scour depth in a tandem arrangement is in accordance with the experimental studies and has a better agreement than previous numerical studies with the same model setup. This means that the numerical model used to simulate pile groups is accurate and capable of calculating the depth of sediment scour.
1. Introduction
Currently, the use of offshore pile foundations has become commonplace [1,2,3], especially for bridge construction due to its structural efficiency, low cost, and ease of construction [4,5,6]. In bridge construction, pile foundations are used to transmit the load of the superstructure and substructure to a lower level, which is a stronger soil layer in the soil mass [7]. However, several issues, including the scour phenomenon, must be addressed to ensure the safety and stability of the offshore pile foundation which will directly affect the bridge structure [8,9,10].
Scouring on bridge foundations is a natural phenomenon that occurs because the presence of pile foundations affects the flow pattern and increases turbulence around the pile foundation [11,12,13]. The blocked current in front of the pile triggers the formation of a horseshoe vortex which erodes and transports the bed particles, then begins to generate the scour [12,13,14,15]. Reported by Lagasse et al. [16], in the United States, there are 488,750 bridges spanning rivers with scour-related bridge failures, costing $30 million per year. Furthermore, over the last 30 years, about 823 total bridge failures were identified and about 60% were caused by hydraulic failure modes including scour in pile foundations [17]. One of the deadliest bridge collapse tragedies due to excessive scouring under bridge pile foundations was the collapse of the Schoharie Creek Bridge, NY State Thruway on 5 April 1987 as shown in Figure 1a, which claimed five vehicles which fell into the river, and 10 occupants died [18]. In Taiwan, six lives were lost due to the collapse of one of the most extremely scour-critical bridges, the Houfeng Bridge, on 14 September 2008 during extreme weather conditions with strong winds and heavy rain [19]. This shows that scour is one of the most common potential causes of bridge pile foundation failure which causes loss of life, economic and environmental impacts. Therefore, monitoring and assessment of the scour depth around bridge pile foundation is necessary during the design [20], operation and maintenance of hydraulic structures [21].

Figure 1.
Collapses of bridge pile foundations: (a) Schoharie Creek Bridge [18]; (b) Houfeng Bridge [19]. Copyright 1996–2021, American Society of Civil Engineers.
One way to avoid serious damage is to monitor local scour around the bridge pile foundation [22] and to ensure the safety and stability of the structure, thereby preventing the loss of life and financial loss. Monitoring means understanding the local scour process or mechanism around the bridge pile foundation, including the factors that influence the occurrence of scour. Most conventional monitoring methods that use depth measuring instrumentation such as bridge mounted sonar, acoustic doppler current profilers (ADCP), ground penetrating radar (GPR), fiber bragg grating (FBG) sensor, numbered bricks, sliding magnetic collar (SMC), and steel rod are based on the installation and maintenance of expensive underwater monitoring devices that can be destroyed during a flooding event, when the risk of scour is highest [23,24,25]. Therefore, experimental and numerical methods have been carried out for the study of scour around bridge pile foundations in recent decades. Due to limited computational capacity in the early years, researchers studied experimental methods of local scour around bridge pile foundations through laboratory investigations. However, laboratory results may vary depending on the laboratory conditions and cannot be used directly to guide design practice due to laboratory study simplifications and assumptions that may render the results inapplicable to field applications [26]. In addition, experimental studies only produce limited data output whereas large numbers of values obtained are required to obtain reasonable information.
At present, with the development of computer science, various fields including local scour have been applied in artificial intelligence (AI) and numerical methods. Homaei & Najafzadeh [10] studied the influence of different parameters including flow conditions, initial movement status of bed sediment, and piles arrangement on the reliability of the scour depth which resulted in several findings, e.g., marine structures should be assessed for scour under short period wave loading, and provided a recommendation to limit pile spacing to less than four times the pile diameter. Moreover, to increase the reliability of the safe scour depth around the piles, a higher number of piles should be considered in parallel with the flow rather than normal to the flow. Another study by Najafzadeh & Oliveto [27] conducted an assessment of four well-known AI models including Evolutionary Polynomial Regression (EPR), Gene-Expression Programming (GEP), Multivariate Adaptive Regression Spline (MARS), and M5 Model Tree (M5MT) for the prediction of local scour depth in pile groups which presents nonlinear equations when fed by a large number of datasets and benefits from automated procedures for selection of input variables. From this study, it was found that the most influential parameter to predict the scour depth at pile groups is the ratio U/Uc between the approach flow velocity, U, and the flow velocity, Uc, at the beginning of the sediment movement with Total Sobol Index (TSI) of 0.514, and the opposite trend of scour with a ratio m/n (TSI = 0.023), between the number, m, of piles inline with the flow and that, n, of piles perpendicular to the flow.
The other method is numerical, which offers several advantages such as low cost and low time consumption, high accuracy, and freedom from the modeling scale, making it an effective method for the prediction of probable failures [12]. Flow simulations processed with simulation software are similar in many ways to the setting up of experiments, where Computational Fluid Dynamics (CFD) is always used to solve Navier-Stokes and continuity equations for computational cells [23]. There are many types of CFD software that are able to model sediment scour, one of which is Flow-3D. Flow-3D is a commercial CFD software with a special hydraulic engineering applications module that solves fluid motion equations and provides transient, three-dimensional solutions to multi-scale, multi-physical flow problems using computational technologies [28]. Flow-3D, created by Flow Science Inc., has some advanced capabilities for numerically solving the Navier-Stokes equation for free surface flow, known as the volume of fluid (VOF-method), and meshing complex geometries, known as fractional area-volume obstacle representation (FAVOR method) [29]. Flow-3D provides the flexibility and utility for porous media flow, as well as easy setup for complex structures [30]. Jalal & Hasan [31] argue that Flow-3D should be used to model the scour processes around bridge pile foundations and has a good ability to analyze the behavior of special liquids and gasses in solving problems of transients, free-surfaces, and sediment transport. Therefore, Flow-3D software was chosen to model and simulate sediment scour around the bridge pile foundation.
However, most of the studies only simulate and analyze the scour depth around a single pile foundation. There are several studies tabulated in Table 1 related to numerical simulation of local scour around bridge pile foundations which have been verified with experimental results to examine the modeling setup and Table 2 for boundary conditions using Flow-3D only provides limited information about scour behavior. In fact, pile groups, as mostly used in offshore bridge pile foundations, also need to understand the scour mechanism in order to comprehend their mutual influence effect between on local scour. Only a few studies have looked at the numerical study of sediment scour around pile groups, particularly with Flow-3D v11.2 software.

Table 1.
Numerical model properties.

Table 2.
Boundary conditions.
In this study, a numerical simulation of three cylindrical piles with a tandem arrangement will be presented to calculate the sediment scour depth and analyze the mechanism. As a common pile group configuration, a tandem arrangement parallel to the direction of the water flow is recommended for design in terms of maximum scour, rather than piles arranged crosswise with flow [12,40], due to the shielding effect of the front pile upstream to downstream of the rear pile, which results in a smaller horseshoe vortex which then eventually generates minimum scour depth [41,42]. Mostafa [43] mentioned the advantages of the structural design aspects of the tandem pile group arrangement in supporting marine structures such as higher ultimate lateral capacity and lower displacement and bending moments compared to pile groups with side-by-side arrangement. Three piles were used in this numerical simulation because their composition consists of front, middle, and rear piles which will provide more information about the scour mechanism around the pile group compared to two tandem piles in a group. Due to limited numerical studies of scour around three piles in a tandem arrangement, this study is necessary.
Wang et al. [32] performed a numerical study of sediment scour depth of two piles in a tandem arrangement. The channel size of 2.7 m × 0.8 m × 1 m (L × W × H) with 0.03 m pile diameter and pile spacing of 2D was built using Flow-3D software. As for sediment properties, fine sand with an average grain size (d50) of 0.15 mm has a bulk density of 1990 kg/m3. The depth and velocity of the water were set to 0.25 m and 0.225 m/s, respectively. Uniform mesh of 0.008 m was generated in this study with a total of more than forty-two million cells. Due to its compromised model accuracy and the requirement for simulation power, k-ε turbulence model was chosen which can achieve reasonably high resolution with low CPU time requirement. The boundary conditions applied are the same as for the single pile study in Table 2. After running for 180 min, the maximum local scour depths around the front and rear piles were 0.058 m and 0.043 m.
Zhang et al. [12] modeled sediment scour around three cylindrical piles in a tandem arrangement with different spacing ratios, G/D of 2, 3, and 4 for pile diameters of 1.5 m using Flow-3D software. The geometry size of the channel is 40 m × 18 m × 7 m (L × W × H) with water depth of 3 m and velocity of 2 m/s. There are two types of sediment particle used including fine gravel and medium gravel with a size of 5 mm and 10 mm. RNG k-ε and Meyer, Peter and Müller eq. were used as turbulence model and bed-load transport rate equation, which are the same as the parameters used in the model verification of Gengsheng Wei et al. [36], as well as the applied boundary conditions. The minimum grid size of 0.1 m for x and y directions was applied around the piles, and 0.05 m for z direction in sediment and water layers. After running for 500 s, for G/D = 2, the maximum scour depth of the front, middle, and rear piles were around 0.59 m, 0.17 m, and 0.23 m respectively. For G/D = 3, the maximum scour depth were 0.61 m, 0.23 m, and 0.29 m, and for G/D = 4, the maximum scour depths were 0.53 m, 0.28 m, and 0.35 m.
Hassan et al. [44] simulated a numerical model of scour using Flow-3D software consisting of 2 cylindrical piles with a diameter of 0.055 m arranged in tandem. The spacing of the piles used varies from 2 to 10 times the pile diameter. The length of the domain was set at 52D with a fixed bed at the inlet to prevent upward movement at the beginning of the simulation. Uniform sand (d50) of 0.85 mm was placed as bed sediment with a thickness of 0.15 m. The minimum and maximum cell sizes used in this numerical study were 0.003 m and 0.025 m. The boundary conditions applied are similar to the previous study by Zhang et al. [12], the only difference being the wall boundary conditions on the front and back sides. However, this study does not clearly explain the maximum sediment scour depth generated for the front and rear piles. After running for 5 min for the flow of V/Vc = 0.91, Hassan et al. [44] reported that the scouring depth recorded at the rear pier was the smallest in all simulations.
Based on the literature review of previous related studies on numerical simulation of local scour around pile groups in tandem arrangement using the Flow-3D software above, all studies agree that the maximum scour depth generated by the front pile is always deeper than that of the rear pile. However, the scour depth around the three piles in a tandem arrangement by Zhang et al. [12] consisting of the front, middle, and rear piles showed an interesting trend, i.e., the scour depth around the middle pile is the smallest due to the shadow effects of the front pile, and flows to the lateral side of the front pile, leading to a lower flow velocity around the middle, then accelerating in the rear pile.
In this study, a verification model was developed to ensure applicability and accuracy by comparing the depth of sediment scour generated by the numerical model and the experimental model. Furthermore, this model will be used to simulate the scour depth around three cylindrical piles in a tandem arrangement and analyze the scour mechanism around the piles. In addition, the trend of the scour depth in this numerical result will be compared with the results of an experimental study of scour depth with a tandem arrangement as a re-verification.
2. Numerical Method
As the software used in this study, the Flow-3D v11.2 CFD package developed by Flow Science Inc. uses two methods to estimate the location of the free surface and obstacles: VOF and FAVOR. Since the free surface is one of the external boundaries of the liquid, a precise representation of the free-surface dynamics requires a good characterization of the boundary conditions at the free surface. Therefore, the VOF method is used to track the liquid/gas interface [45] which defines the fluid volume function, the method of solving the VOF transport equation, and determination of the boundary conditions at free surfaces, the three main components of Flow-3D. Secondly, the FAVOR method is a formula for defining general geometric area in a rectangular grid. This method models a complex geometric region with area and volume porosity functions and describes the obstacle surface in the mesh cell [28].
2.1. Governing Equations
In the Flow-3D software, the RANS (Reynolds-Averaged Navier-Stokes) equation is used as the equation governing the motion of an incompressible viscous fluid around a bridge pile foundation which describes the three-dimensional motion of viscous fluid substances. The motion equations for fluid velocity sections (u, v, and w) with some additional terms in the three x-, y-, and z-coordinates are as follows:
where is volume fraction, is area fraction, is fluid density, is average hydrodynamic pressure, and and are body acceleration and viscous acceleration.
2.2. Turbulence Model
Turbulence is a chaotic and unstable fluid motion caused by a lack of stabilizing force which consists of high-frequency oscillations and the development of several types of eddies with varying energies [28]. This is mainly determined by the Reynolds number. The natural instability that occurs in the flow at high Reynolds numbers does not reduce, resulting in the formation of eddies of different length scales. There are six turbulent flow models offered in Flow-3D software: the Prandtl mixing length model, the one-equation model, the two-equation (k-ε) model, renormalized group (RNG) model, two-equation (k-ω) model and the large eddy simulation (LES) model.
An assessment of turbulence models for modeling sediment scour around bridge pile foundations using Flow-3D software is provided by several studies which are summarized in Table 1, resulting in RNG k-ε as the most widely used turbulence model. In this study, the RNG k-ε turbulence model was chosen because of its accuracy in describing low-intensity turbulent flow which has a stronger shear region with greater precision, and can significantly reduce computation time compared to the Large Eddy Simulation (LES) model, which requires a very fine mesh [12,33]. The RNG k-ε turbulence model [46,47] applied statistical methods to the derivation of the averaged equations for turbulence quantities, such as turbulent kinetic energy and its dissipation rate. This model, which has a wider applicability than the k-ε model, uses equations similar to the k-ε model, in which the equation constants are derived explicitly in the RNG k-ε turbulence model. The governing equations of the RNG k-ε turbulence model are as follows:
where is the specific kinetic energy associated with turbulent velocity fluctuations in the flow (turbulent kinetic energy), , , , and are the FAVOR functions of Flow-3D, and and are the turbulent kinetic energy production and turbulent buoyancy production. and are the diffusion terms of turbulent kinetic energy and diffusion of dissipation, and is the rate of turbulent energy dissipation. CDIS1, CDIS2, and CDIS3 are all dimensionless user-adjustable parameters, and have defaults of 1.44, 1.92 and 0.2, respectively.
2.3. Sediment Transport Model
The sediment scour model assumes many species of non-cohesive sediment with varying properties, such as grain size, mass density, critical shear stress, angle of repose, and entrainment and transport parameters [12,31]. Sediment scour models predict the behavior of packed and suspended sediments, including sediment advection, erosion, settlement, and deposition [28] around bridge pile foundations in the three-dimensional flow capabilities of Flow-3D [48].
According to Hyperinfo Corp. [49], the sediment scour consists of five sediment transport mechanisms that can express all sediment transport processes. In the first stage called drift, the sediment will settle due to gravity. Then, it will move with the current flowing at a certain height above the packed bed. After that there will be scour where the sediment is trapped in the water flow and moves or settles with it. In the fourth stage called bed-load transport, in reaction to the shear stress of the fluid flow, the sediment rolls and slides along the packed bed surface. Lastly, the deposition if suspended grains on the sediment bed, known as deposits, will settle and solidify due to gravity, buoyancy, and friction. Several important parameters used to determine the sediment scour model include critical shields number definition, bed-load transport rate equation, maximum packing fraction, bed shear stress, and some parameters of sediment characteristics.
2.3.1. Critical Shields Number
Critical shields parameter θcr,i correlates with the minimum or critical bed shear stress τcr required to remove sediment particles from the packed bed interface [48]. Sediment erosion can occur depending on the size of the sediment, its density, and body forces acting on it [28].
where is gravity in absolute value, di is sediment grain size, and ρi and ρf are mass density of sediment grain and fluid density.
In the Flow-3D software, the critical shields number θcr,i can be defined as the prescribed value and calculated value using the Soulsby-Whitehouse equation. The prescribed value means that the critical shields number is calculated by Flow-3D itself, then the other is determined using the equation of Soulsby-Whitehouse below [50].
where is the dimensionless grain size with = ρi/ρf and is the fluid kinematic viscosity. The critical shields number θcr,i can be specified with a default value of 0.05 [36].
2.3.2. Bed-Load Transport
Bed-load transport is defined as the mode of sediment transport by rolling or bouncing across the packed sediment bed surface. Three formulas for the volumetric sediment transport rate per bed width are known in Flow-3D software, including:
Meyer, Peter and Müller equation [51]
where is the bed-load coefficient which has a value for low transport from 5.0 to 5.7, intermediate transport is 8.0, and very high transport is up to 13.0.
Nielsen equation [52]
where is the bed-load coefficient which has a default value of 12.0.
Van Rijn equation [53]
where is the bed-load coefficient which has a default value of 0.053. Then for all equations is the volume fraction of species i in the bed material.
In order to obtain the closest results in the numerical simulation of local scour around the bridge pile foundation, Omara et al. [54] modeled the bed-load transport parameters of sediment scour by comparing three equations, resulting in the Van Rijn equation model with results rather close to those obtained by Ahmed & Rajaratnam’s [37] experimental study. Therefore, the Van Rijn equation model is applied in this numerical study.
2.3.3. Maximum Packing Fraction
The maximum packing fraction is the fraction which is the volume of all sediment species/open volume in the cell, where the cell is ‘packed’ and the drag function in the cell goes to infinity (no flow). This is equivalent to (1—porosity) with the highest packing fraction set to 0.64 by default, as shown analytically for uniformly randomly packed spheres. The maximum packing fraction is 0.55 to 0.7 since the sand has a porosity of 0.3 to 0.45.
2.3.4. Bed Shear Stress
The shear stress applied to the packed bed’s surface by fluid is calculated using the standard wall function for 3D turbulence flow, considering the roughness of the wall. Crough is the user-definable coefficient obtained by the ratio of Nikuradse roughness ks to the median grain diameter in packed sediment d50 which has a recommended value of 2.5 [36].
2.3.5. Sediment Characteristics
Some parameters of sediment characteristics use for modeling sediment scour in the Flow-3D software, such as type of sediment, sediment diameter size, mass density, critical shields number, entrainment coefficient, bedload coefficient, and angle of repose (degree) must be determined by the user depending on the actual conditions in the field. The entrainment coefficient is needed to compute the lifting velocity, or the velocity at which the grains leave the packed bed, as well as to scale the scour rate which has a default value of 0.018 [36]. However, Omara et al. [54] found that 0.005 gave good results for numerical study of local scour around bridge pile foundations. Then, the angle of repose parameter is used to change the local critical shields value for a slope effect that represents the greatest slope angle of the bed before grains start to slide on their own, which is usually between 30 and 40 degrees with a default value of 32 degrees [36].
2.4. Meshing
As one of the important factors in modeling sediment scour to obtain accurate results, finer mesh cell size is needed to obtain better results. Mesh can be described as a grid block covering a range of geometric figures and fluid flow [49]. In Flow-3D, orthogonal meshes are specified in cartesian or cylindrical coordinates. This software uses the FAVOR method to smooth block fractional sections of grid cell faces and volumes, in order to eliminate the stairstep effect that can occur with a simple cartesian grid system [28]. To be effective, the mesh cell size must be checked for adequacy by clicking the FAVOR before running the simulation.
There are several requirements for the maximum cell size ratio in the meshing setup by [49] including that the aspect ratio (x:y:z) for individual cells does not exceed 3:1 in any two directions. For neighboring cells, the adjacent ratio (x:x, y:y, or z:z) must not exceed 1.25 in the same direction. The mesh setup between each block (nested or linked) should not exceed 2:1, while the best result can be generated by cells with a cell size ratio of 1:1.
2.5. Boundary Conditions
The geometry-based boundary conditions are addressed by the choice of component type or by other component-specific properties that are related to a specific physical model/equation as in several assessments of boundary conditions for modeling sediment scour from different studies, given in Table 2. In this study, the boundary conditions applied to the numerical model are shown in Figure 2.
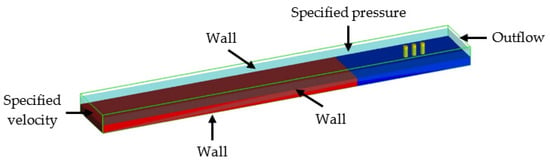
Figure 2.
Boundary conditions.
For the inlet, the fluid flow velocity is specified according to the real conditions in the field, and for the outlet the outflow boundary condition is a way to allow the fluid flow continuation through the boundary with a minimum of reflection. The specified pressure is applied at the top boundary to determine the pressure at the boundary which will follow the hydrostatic distribution if the fluid elevation is also defined, while the wall boundary conditions are applied to other boundaries which include the front side, back side, and the bottom boundary conditions in order to apply the no-slip and zero-velocity condition at the boundary.
3. Verification of the Present Model
To confirm the reliability of the present numerical model, a validation using the experimental study was carried out. The maximum sediment scour depth from the experimental results obtained by Khosronejad et al. [55] was used as a verification and then compared with the numerical results obtained using Flow-3D software. The numerical model was setup in the same way as the experimental study, representing actual field conditions, and then run until an equilibrium scour depth was reached.
3.1. Experimental Setup
The experiment was started under clear-water scour conditions with flat-bed elevation and continued until it reached an equilibrium depth. A high-definition digital camera was installed to observe the time evolution of scour, and was used to determine the final equilibrium scour depth [55]. This situation is thought to be obtained when the scour depth increases at a rate of less than 5% of the pile diameter over a 12-h period [56].
The dimensions of the channel were setup as 10 m long, 1.21 m wide and 4.5 m high with a pile diameter D of 0.1651 m which is located 4 m downstream of the inlet. The sediment particles have an average diameter d50 of 0.00085 m at a depth of 0.2 m. The experiment was carried out at a bulk inflow velocity of 0.25 m/s, which corresponds to a uniform flow depth of 0.186 m, a Reynolds number Re = 46,000 and a Froude number Fr = 0.18 for approximately 50 min until the equilibrium depth was reached. The maximum scour depth measured was about 0.076 m occurring at an angle of 45° from the upstream horizontal plane.
3.2. Numerical Setup
The numerical setup including geometry and other related parameters were modeled in the same way as the experiment conducted by Khosronejad et al. [55] to verify the applicability and accuracy of this numerical model by using Flow-3D software. The simulation time is set to 50 min or equal to 3000 s and uses the International System of Units (SI) as the simulation unit. Some of the important factors that must be considered in the numerical setup include sediment scour and turbulence, geometry, and meshing.
3.2.1. Sediment Scour and Turbulence
Several parameters are used to determine sediment for the validation model in this numerical study using Flow-3D software such as the critical shields number defined by Soulsby-Whitehouse equation, while the bed load transport rate equation uses the Van Rijn equation. The maximum packing fraction and bed roughness/d50 ratio are 0.64 and 2.5 for fine sand sediment with an average particle size diameter d50 of 0.00085 m which has a density of 1602 kg/m3, while the critical shields number, entrainment coefficient, bed load coefficient, and angle of repose are 0.05, 0.005, 0.053, and 32°, respectively.
Some of the parameters used such as maximum packing fraction, critical shields number, and angle of repose are based on the default values of the Flow-3D software. However, other parameters follow the recommendation of previous studies which proved to give the best results for sediment scour. For the validation model, the RNG k-ε turbulence model was used in this study because of its good performance in modeling sediment scour and its accuracy in describing low-intensity turbulence flows that have stronger shear regions with higher precision.
3.2.2. Geometry and Meshing
The geometry model including the dimensions of the channel bed and pile was setup in the same way as the experiment, with the same type of solid component for the pile and the same type of packed sediment for the channel bed. However, there is one more solid component that must be modeled at the outer side as the inlet before the fluid flow directly enters the channel bed to prevent the upward movement of sediment at the beginning of the simulation. The hydrodynamic entry length Lh in turbulent flow for an open channel with a rectangular cross sections is calculated using the equation of Cengel & Cimbala [57], yielding an entrance length of 6 m.
where Dh is hydraulic diameter, and and are water depth and channel width.
The geometry size of this numerical model in the validation stage exactly matches the experimental setup with the addition of a solid component to achieve a fully developed flow velocity which has an entry length Lh of 6 m. For the meshing setup, several grid tests were performed to check the sensitivity of the mesh modeled in this numerical study. In addition, two mesh planes in the x and y directions with finer resolution were applied to increase the accuracy of the model around the pile. The total number of 400,000 cells formed by 400 × 50 × 20 cells in x, y, and z directions have met the requirements as described in Table 3, assessed using the FAVOR option which produces a good solid geometry shape and surface model, showing that the number of cells is sufficient.

Table 3.
Mesh information.
3.3. Validation Result
Simulation was run on a 64-bit PC with eight processors using the Flow-3D solver version 11.2.0.16. The computational time required to calculate 50 min of physical time is approximately 2 days and 17 h. In this study, scour depth is the parameter used to verify the numerical model’s applicability and accuracy. Figure 3 shows that the present numerical result and the previous experimental result [55] are similar in terms of the time evolution of scour depth around a single pile. It is apparent that the current result and the experimental result are in good conformity.
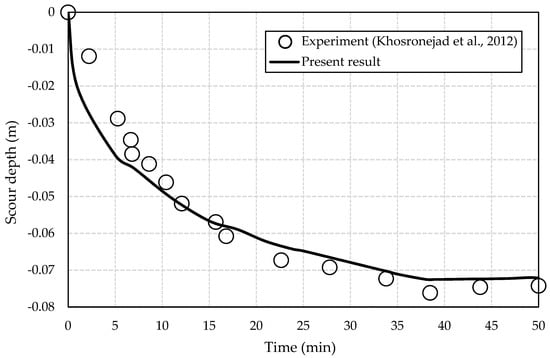
Figure 3.
Time evolution of scour depth between the present model and the experimental result [55] around a single pile. Copyright 2011 Elsevier Ltd. All rights reserved.
The local scour depth obtained from the experimental study increased significantly during the first 20 min, then gradually decreased until it reached equilibrium at 0.0742 m after approximately 50 min. However, the local scour depth obtained from this model increased slightly more than the experimental result in the first 16 min before decreasing, with a smaller scour depth than the experimental result until the end of the simulation at 0.0721 m. The maximum scour depths obtained for both experimental and numerical studies were 0.0762 m and 0.0725 m respectively at the same time after running for about 38 min. At the equilibrium stage, Figure 4 shows the present and experimental results in terms of bed elevation contours for local scour around a single pile with various colors representing the depth of scour and deposition.
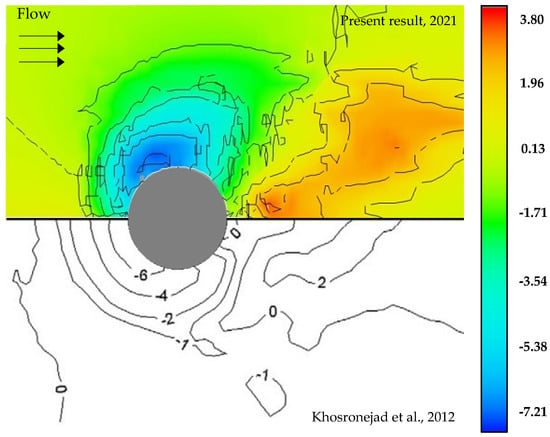
Figure 4.
The bed elevation contours at the equilibrium state between the present model and the experimental result [55] in units of cm. Copyright 2011 Elsevier Ltd. All rights reserved.
4. Numerical Simulation of Three Cylinders
In this study, numerical simulations of three cylinders were carried out in a tandem arrangement to calculate the scour depth and analyze its mechanism using Flow-3D software. The numerical setup of the previous validation model was applied to the geometric model of Zhang et al. [12] to give the same perception and used pile spacing ratios, G/D 2 and 3, as a comparison. Simulation time was set to 500 s and used the International System of Units (SI) as a simulation unit.
4.1. Sediment Scour and Turbulence
The sediment scour setup in the validation model is applied in this numerical study. However, other parameters such as sediment type, mean particle diameter d50, sand density, and angle of repose are described in Table 4 below.

Table 4.
Sediment properties.
As in the validation stage, the RNG k-ε was used in this study because of its good performance and accuracy in modeling sediment scour with high precision of the validation results in the previous simulation.
4.2. Geometry and Meshing
The geometry sizes for single and three cylinders with tandem arrangement in this numerical study are adopted from Zhang et al. [12] with channel dimensions of 40 m × 18 m × 7 m (L × W × H), while the entry length is calculated using the equation of Cengel and Cimbala [57], resulting in a length of 90 m. Cylindrical piles with a diameter of 1.5 m are placed 21 m downstream of the inlet on a 3 m deep sediment bed.
As the most important factor for modeling numerical simulation, the mesh should be structured with a finer cell size around the pile by two mesh planes in x and y directions to achieve good accuracy for scouring, then increasing to the edge of the channel. However, the efficiency of the simulation time also needs to be considered because of the large number of cells, especially for the pile groups. The minimum and maximum cell sizes are 0.12 m and 0.6 m, respectively, in this numerical model of single and tandem arrangements, with details tabulated in Table 5.

Table 5.
Meshing setup.
As seen in Table 5, both the maximum adjacent ratio and aspect ratio meet the requirements of not exceeding 1.25 and 3.
4.3. Boundary Conditions
The boundary conditions for all numerical models in this study were set to be the same as the validation model in the previous simulation. A specified velocity of 2 m/s with 3 m water depth is defined as the inlet and the outflow as the outlet. Wall boundary conditions are used for both left and right sides as well as the bottom of the channel, while the top free surface uses the specified pressure boundary condition.
4.4. Numerical Results and Discussion
The local scour mechanism around a single pile can be easily understood by observing the fluid flow motion as shown in Figure 5. Water flows from the inlet at fully developed velocity until it is obstructed by a solid cylindrical pile at x equal to 21 m then changes the direction of the flow to a vertical downward plane, which is called downflow. At that moment the flow velocity approaches zero at the upstream face of the cylinder, and the stagnation pressure also decreases since the approached flow velocity drops from the free surface to zero at the bed. The downflow driven by the downward pressure gradient causes the horseshoe vortex to rotate in front of the pile generating scour. In addition, the high bed shear stress triggered by flow acceleration is the main factor causing local scour around the pile, because when the bed shear stress exceeds the critical value, the sediment particles located at the top of the packed bed can be removed and taken into suspension.
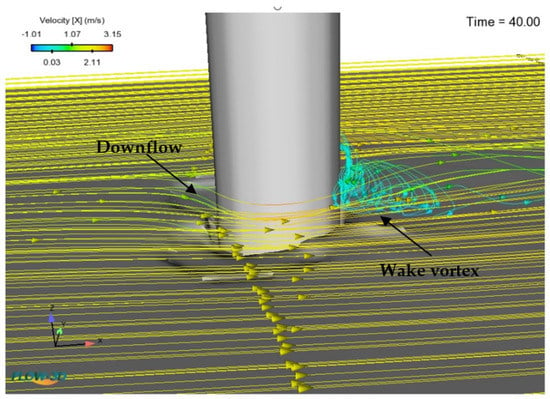
Figure 5.
Streamline around single pile.
Aside from downflow, the stagnation pressure accelerates flow through the cylinder in a sideways’ direction. The flow splits along the side of the cylinder, forming a wake downstream behind the pile. A discontinuity in the velocity profile from flow to wake causes the formation of concentrated vortices at the interface, known as cast-off vortices. These vortices interfere with the horseshoe vortex near the bed, causing the trailing regions of the horseshoe to fluctuate during vortex shedding. With a vertical low-pressure center, the cast-off vortices function like a mini-tornado, lifting sediment from the bed, resulting in sediment deposition [58].
The numerical results of the scour depth around a single pile are illustrated in Figure 6 where the maximum scour depth at t = 500 s is 0.79 m which occurs at an angle of approximately 45° from the flow direction. The local scour depth obtained increases significantly up to t = 340 s, then gradually decreases until the end of the simulation.
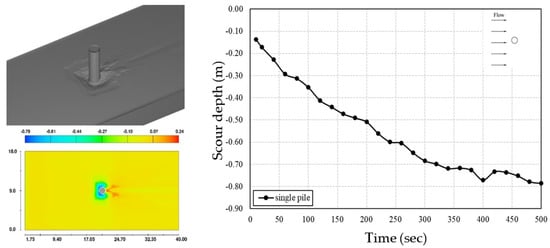
Figure 6.
Sediment scour depth around single pile.
In the group of three piles with a tandem arrangement, for the pile spacing ratio, G/D = 2, the scouring process is shown in Figure 7 from t = 0 s to the end of the simulation at t = 500 s. At the beginning of the simulation, after hitting the front pile, the current tends to slow down and flow sideways towards the rear pile due to the acceleration, resulting in a maximum scour depth that is deeper than the middle pile as shown by the line graph in Figure 8. However, approximately at t = 240 s the maximum scour depth for the middle pile increases slightly deeper than the rear pile until the end of the simulation. In this simulation, the maximum local scour depths generated from the front are 0.84 m, 0.42 m, 0.35 m, respectively, where the piles behind are smaller due to the sheltering effect of the pile in front, so that maximum local scour is always generated by the front pile in a tandem arrangement.
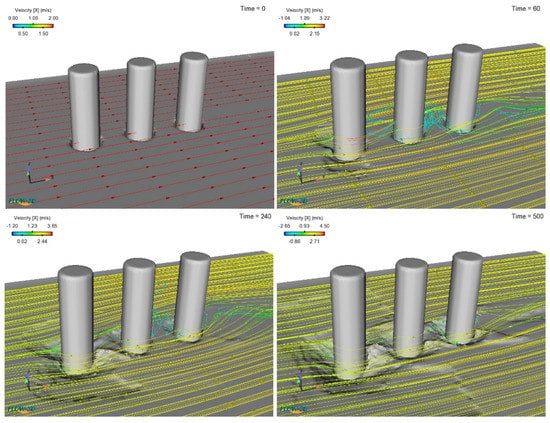
Figure 7.
Streamline around three piles in a tandem arrangement (G/D = 2).
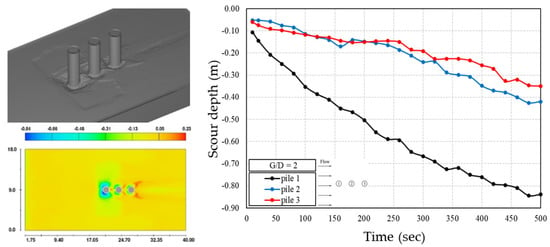
Figure 8.
Sediment scour depth around three piles in a tandem arrangement (G/D = 2).
Furthermore, the sediment scour mechanism around the three piles in tandem with the spacing ratio of 3 from the first simulation starts until t = 140 s seconds, and the local scour produced by the rear pile is deeper than the middle pile. Figure 9 shows at t = 60 s that the current flows at the lateral sides and through the middle pile with a lower velocity, then changes direction to downflow in front of the rear pile causing scour due to the acceleration. Nevertheless, this condition changes at approximate time t = 140 s with the local scour depth in the middle pile deeper than the rear pile until the end of the simulation. As shown in Figure 9 at t = 500 s, the wake vortex behind the middle pile produces sediment deposition and the particles move by the water flow so as to cover the scour in front of the rear pile.
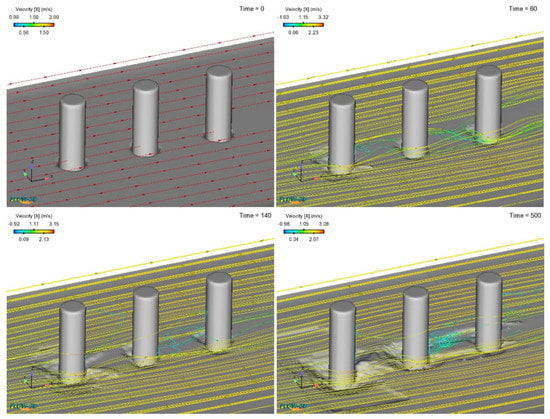
Figure 9.
Streamline around three piles in a tandem arrangement (G/D = 3).
As shown in Figure 10, the deepest maximum local scour depth obtained by the front pile is 0.83 m, followed by the middle and the rear piles with depths of 0.45 m and 0.23 m. Similar to the previous simulation, for pile spacing ratio equal to 3 the maximum local scour gradually decreases sequentially from the front to the rear pile.
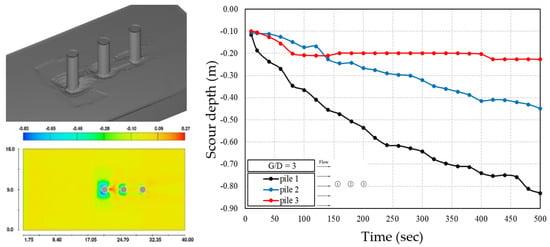
Figure 10.
Sediment scour depth around three piles in a tandem arrangement (G/D = 3).
In addition, as one of the main factors causing local scour, the contour of excess shear stress around three piles cylinders with G/D = 3 is given in Figure 11. This shows where scouring may occur with the highest value marked by a red color indicating the maximum local scour depth generated.
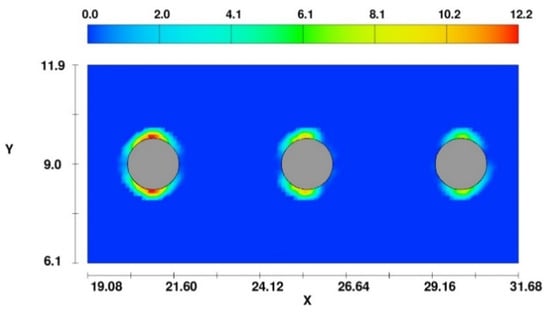
Figure 11.
Excess shear stress contour for G/D = 3 at t = 500 s.
Based on the numerical simulation results of local scour depths around groups of three piles in a tandem arrangement with pile spacing ratios 2 and 3, the scour mechanism around pile groups is more complex than that of single pile. There is interference movement between the front, middle, and rear piles which will affect the local scour depth. However, one interesting factor in these results is the trend of the maximum local scour depth obtained in a tandem arrangement which gradually decreases from the front pile to the rear pile. This is quite different from the results achieved by a previous numerical study of three piles in a tandem arrangement by Zhang et al. [12] which stated that the maximum local scour depth around the middle pile is smaller than that of the rear pile.
Several experimental studies on local scour around three piles in a tandem arrangement were figured out as a verification of the present numerical results. Wang et al. [59] conducted a local scour experiment around three piles with a diameter of 0.03 m in a tandem arrangement under different pile spacings and velocities. The pile spacing ratios, G/D of 2 and 3 with a velocity of 0.28 m/s were taken as an example which resulted in local scour depths at the front, middle, and rear piles of 0.041 m, 0.030 m, 0.016 m and 0.047 m, 0.031 m, 0.024 m, respectively. In addition, Zhou et al. [60] performed an experimental study of local scour around three piles in a tandem arrangement under different pile diameters, flow discharges, and pile spacings which resulted in the scouring depth gradually decreasing from the front to rear piles. They reported that the last pile has the least scour depth due to the hiding effect from upstream to downstream. These experimental results confirm the validity of the present numerical results on local scour depth around three cylindrical piles in a tandem arrangement.
5. Conclusions
A study of the numerical model of sediment scour around three cylindrical piles in a tandem arrangement has been carried out to calculate the local scour depth and analyze the mechanism. According to the results obtained, it can be concluded that Flow-3D is considered as effective software for simulating a numerical model of local scour around bridge piles since the result of the validation model has good agreement with the experimental study. This proves that the sediment scour model of Van Rijn equation as bed load transport rate equation and RNG k-ε model as turbulence model used in this study are accurate and capable to calculate the sediment scour depth.
Generally, the horseshoe vortex caused by the downflow driven by the downward pressure gradient rotation in front of the pile and the high bed shear stress triggered by flow acceleration are the main factors causing local scour around the pile. Moreover, in a tandem arrangement the scouring mechanism is more complex than in single pile because of the interference effect between the front, middle, and rear piles. The maximum local scour depth obtained for both pile spacing ratios, G/D of 2 and 3 gradually decreases from the front pile to the rear pile due to the sheltering effect of the pile in front. This trend is in better agreement with the related experimental studies of local scour around three cylindrical piles in a tandem arrangement, compared to the previous numerical study with the same model setup.
Author Contributions
Conceptualization, J.-H.T.; Methodology, J.-H.T. and A.D.P.; Software, A.D.P.; Validation, A.D.P.; Formal analysis, J.-H.T. and A.D.P.; Investigation, J.-H.T. and A.D.P.; Writing-original draft preparation, A.D.P.; writing-review and editing, J.-H.T. and A.D.P. All authors have read and agreed to the published version of the manuscript.
Funding
We thank the John Su Foundation for financial sponsorship.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Basack, S. Analysis and design of offshore pile foundation. In Advanced Materials Research; Trans Tech Publications, Ltd.: Stafa-Zurich, Switzerland, 2014; Volume 891–892, pp. 17–23. [Google Scholar]
- Zhang, Q.; Zhou, X.L.; Wang, J.H.; Guo, J.J. Wave-induced seabed response around an offshore pile foundation platform. Ocean Eng. 2017, 130, 567–582. [Google Scholar] [CrossRef]
- Jin, Y.F.; Yin, Z.Y.; Wu, Z.X.; Zhou, W.H. Identifying parameters of easily crushable sand and application to offshore pile driving. Ocean Eng. 2018, 154, 416–429. [Google Scholar] [CrossRef]
- AbdelSalam, S.; Sritharan, S.; Suleiman, M.T. Current Design and Construction Practices of Bridge Pile Foundations. J. Bridg. Eng. 2010, 15, 749–758. [Google Scholar] [CrossRef]
- DiMaggio, J.A.; Goble, G.G. Developments in Deep Foundation Highway Practice-The Last Quarter Century. In Current Practices and Future Trends in Deep Foundations; ASCE: Los Angeles, CA, USA, 2004; pp. 110–127. [Google Scholar]
- Ingham, T.J.; Rodriguez, S.; Donikian, R.; Chan, J. Seismic analysis of bridges with pile foundations. Comput. Struct. 1999, 72, 49–62. [Google Scholar] [CrossRef]
- Abdel-Mohti, A.; Khodair, Y. Analytical investigation of pile–soil interaction in sand under axial and lateral loads. Int. J. Adv. Struct. Eng. 2014, 54, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.; Han, J.; Bennett, C.; Parsons, R.L. Analysis of laterally loaded piles in soft clay considering scour-hole dimensions. Ocean Eng. 2016, 111, 461–470. [Google Scholar] [CrossRef]
- Qi, W.G.; Li, Y.X.; Xu, K.; Gao, F.P. Physical modelling of local scour at twin piles under combined waves and current. Coast. Eng. 2019, 143, 63–75. [Google Scholar] [CrossRef] [Green Version]
- Homaei, F.; Najafzadeh, M. A reliability-based probabilistic evaluation of the wave-induced scour depth around marine structure piles. Ocean Eng. 2020, 196, 106818. [Google Scholar] [CrossRef]
- Rasaei, M.; Nazari, S.; Eslamian, S. Experimental investigation of local scouring around the bridge piers located at a 90° convergent river bend. Sadhana-Acad. Proc. Eng. Sci. 2020, 45, 87. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, X.L.; Wang, J.H. Numerical investigation of local scour around three adjacent piles with different arrangements under current. Ocean Eng. 2017, 142, 625–638. [Google Scholar] [CrossRef]
- Jia, Y.; Altinakar, M.; Guney, M.S. Three-dimensional numerical simulations of local scouring around bridge piers. J. Hydraul. Res. 2018, 56, 351–366. [Google Scholar] [CrossRef]
- Ghaderi, A.; Abbasi, S. CFD simulation of local scouring around airfoil-shaped bridge piers with and without collar. Sādhanā 2019, 44, 216. [Google Scholar] [CrossRef] [Green Version]
- Xiong, W.; Tang, P.; Kong, B.; Cai, C.S. Computational Simulation of Live-Bed Bridge Scour Considering Suspended Sediment Loads. J. Comput. Civ. Eng. 2017, 31, 04017040. [Google Scholar] [CrossRef]
- Lagasse, P.F.; Richardson, E.V.; Schall, J.D.; Price, G.R. NCHRP Report 396: Instrumentation for Measuring Scour at Bridge Piers and Abutments; National Academies Press: Washington, DC, USA, 1997. [Google Scholar]
- Shirole, A.M.; Holt, R.C. Planning for a comprehensive bridge safety assurance program. Transp. Res. Rec. 1991, 1290, 137–142. [Google Scholar]
- LeBeau, K.H.; Wadia-Fascetti, S.J. Fault Tree Analysis of Schoharie Creek Bridge Collapse. J. Perform. Constr. Facil. 2007, 21, 320–326. [Google Scholar] [CrossRef]
- Hong, J.-H.; Chiew, Y.-M.; Lu, J.-Y.; Lai, J.-S.; Lin, Y.-B. Houfeng Bridge Failure in Taiwan. J. Hydraul. Eng. 2012, 138, 186–198. [Google Scholar] [CrossRef] [Green Version]
- Chris, S.; Norbert, D. Lessons from the Collapse of the Schoharie Creek Bridge. In Proceedings of the Forensic Engineering Congress, San Diego, CA, USA, 19–21 October 2003; ASCE: San Diego, CA, USA, 2003; pp. 158–167. [Google Scholar]
- Kayser, M.; Gabr, M. Assessment of scour on bridge foundations by means of in situ erosion evaluation probe. Transp. Res. Rec. 2013, 8, 72–78. [Google Scholar] [CrossRef]
- Elsebaie, I.H. An Experimental Study of Local Scour Around Circular Bridge Pier in Sand Soil. Int. J. Civ. Environ. Eng. 2013, 13, 23–28. [Google Scholar]
- Ghasemi, M.; Soltani, S. The Scour Bridge Simulation around a Cylindrical Pier Using Flow-3D. J. Hydrosci. Environ. 2017, 1, 46–54. [Google Scholar]
- Link, O.; Mignot, E.; Roux, S.; Camenen, B.; Escauriaza, C.; Chauchat, J.; Brevis, W.; Manfreda, S. Scour at bridge foundations in supercritical flows: An analysis of knowledge gaps. Water 2019, 11, 1656. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.-Y.; Hong, J.-H.; Su, C.-C.; Wang, C.-Y.; Lai, J.-S. Field Measurements and Simulation of Bridge Scour Depth Variations during Floods. J. Hydraul. Eng. 2008, 134, 810–821. [Google Scholar] [CrossRef] [Green Version]
- Deng, L.; Cai, C.S. Bridge Scour: Prediction, Modeling, Monitoring, and Countermeasures—Review. Pract. Period. Struct. Des. Constr. 2010, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Najafzadeh, M.; Oliveto, G. More reliable predictions of clear-water scour depth at pile groups by robust artificial intelligence techniques while preserving physical consistency. Soft Comput. 2021, 25, 5723–5746. [Google Scholar] [CrossRef]
- Flow Science. Flow-3D: Version 9.3: User Manual; Flow Science: Santa Fe, NM, USA, 2008. [Google Scholar]
- Abdelaziz, S.; Bui, M.D.; Rutschmann, P. Numerical simulation of scour development due to submerged horizontal jet. In River Flow; Bundesanstalt für Wasserbau: Karlsruhe, Germany, 2010; pp. 1597–1604. [Google Scholar]
- Nielsen, A.W.; Liu, X.; Sumer, B.M.; Fredsøe, J. Flow and bed shear stresses in scour protections around a pile in a current. Coast. Eng. 2013, 72, 20–38. [Google Scholar] [CrossRef]
- Jalal, H.K.; Hassan, W.H. Three-dimensional numerical simulation of local scour around circular bridge pier using Flow-3D software. IOP Conf. Ser. Mater. Sci. Eng. 2020, 745, 012150. [Google Scholar] [CrossRef]
- Wang, C.; Liang, F.; Yu, X. Experimental and numerical investigations on the performance of sacrificial piles in reducing local scour around pile groups. Nat. Hazards 2016, 85, 1417–1435. [Google Scholar] [CrossRef]
- Omara, H.; Tawfik, A. Numerical study of local scour around bridge piers. IOP Conf. Ser. Earth Environ. Sci. 2018, 151, 012013. [Google Scholar] [CrossRef]
- Nazari-Sharabian, M.; Nazari-Sharabian, A.; Karakouzian, M.; Karami, M. Sacrificial Piles as Scour Countermeasures in River Bridges A Numerical Study using Flow-3D. Civ. Eng. J. 2020, 6, 1091–1103. [Google Scholar] [CrossRef]
- Heidarpour, M.; Afzalimehr, H.; Izadinia, E. Reduction of local scour around bridge pier groups using collars. Int. J. Sediment Res. 2010, 25, 411–422. [Google Scholar] [CrossRef]
- Wei, G.; Brethour, J.; Grünzner, M.; Burnham, J. The Sediment Scour Model in Flow-3D. Flow Sci. Rep. 2014, FSR 03-14, 1–29. Available online: https://flow3d.co.kr/wp-content/uploads/FSR-03-14_sedimentation-scour-model.pdf (accessed on 14 September 2021).
- Ahmed, F.; Rajaratnam, N. Flow around Bridge Piers_Ahmed.pdf. J. Hydraul. Eng. 1998, 124, 288–300. [Google Scholar] [CrossRef]
- Melville, B.W. Local Scour at Bridge Sites. 1975. Available online: https://researchspace.auckland.ac.nz/handle/2292/2537 (accessed on 14 September 2021).
- Balouchi, M.; Chamani, M. Investigating the Effect of using a Collar around a Bridge Pier, on the Shape of the Scour Hole. In Proceedings of the First International Conference on Dams and Hydropower, Tehran, Iran, 8 February–13 February 2012. [Google Scholar]
- Abdeldayem, A.W.; Elsaeed, G.H.; Ghareeb, A.A. The effect of pile group arrangements on local scour using numerical models. Adv. Nat. Appl. Sci. 2011, 5, 141–146. [Google Scholar]
- Liang, F.; Wang, C.; Huang, M.; Wang, Y. Experimental observations and evaluations of formulae for local scour at pile groups in steady currents. Mar. Georesources Geotechnol. 2017, 35, 245–255. [Google Scholar] [CrossRef]
- Yang, Y.; Melville, B.W.; Macky, G.H.; Shamseldin, A.Y. Local scour at complex bridge piers in close proximity under clear-water and live-bed flow regime. Water 2019, 11, 1530. [Google Scholar] [CrossRef] [Green Version]
- Mostafa, Y.E. Design Considerations for Pile Groups Supporting Marine Structures with Respect to Scour. Engineering 2012, 4, 833–842. [Google Scholar] [CrossRef] [Green Version]
- Hassan, Z.F.; Karim, I.R.; Al-Shukur, A.-H.K. Numerical Simulation of Local Scour around Tandem Bridge Piers. J. Water Resour. Res. Dev. 2020, 3, 1–10. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Yakhot, V.; Smith, L.M. The renormalization group, the ɛ-expansion and derivation of turbulence models. J. Sci. Comput. 1992, 7, 35–61. [Google Scholar] [CrossRef]
- Brethour, J. Modeling Sediment Scour-Flow 3D Technical Notes; Flow Science, Inc.: Santa Fe, NM, USA, 2003; p. 6. [Google Scholar]
- Hyperinfo Corp. Flow-3D v11.2; Flow Science, Inc.: Santa Fe, NM, USA, 2016. [Google Scholar]
- Richard Soulsby. Dynamics of Marine Sands; Thomas Telford Publications: London, UK, 1997. [Google Scholar]
- Meyer-Peter, E.; Müller, R. Formulas for Bed-Load Transport. In Proceedings of the IAHSR 2nd Meeting, Stockholm, Sweden, 7–9 June 1948; pp. 39–64. [Google Scholar]
- Nielsen, P. Coastal Bottom Boundary Layers and Sediment Transport; World Scientific Publishing: Singapore, 1992; ISBN1 9810204728. ISBN2 9810204736. [Google Scholar]
- Van Rijn, L.C. Sediment transport, Part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef] [Green Version]
- Omara, H.; Elsayed, S.M.; Abdeelaal, G.M.; Abd-Elhamid, H.F.; Tawfik, A. Hydromorphological Numerical Model of the Local Scour Process Around Bridge Piers. Arab. J. Sci. Eng. 2018, 44, 4183–4199. [Google Scholar] [CrossRef]
- Khosronejad, A.; Kang, S.; Sotiropoulos, F. Experimental and computational investigation of local scour around bridge piers. Adv. Water Resour. 2012, 37, 73–85. [Google Scholar] [CrossRef]
- Melville, B.W.; Chiew, Y. Time Scale for Local Scour at Bridge Piers. J. Hydraul. Eng. 1999, 125, 59–65. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Cimbala, J.M. Fluid Mechanics: Fundamentals and Applications; McGraw-Hill: New York, NY, USA, 2014; ISBN 9780073380322. [Google Scholar]
- Raudkivi, A.J. Loose Boundary Hydraulics; August Aimé Balkema: Rotterdam, The Netherlands, 1998; ISBN 9054104473. [Google Scholar]
- Wang, H.; Tang, H.W.; Xiao, J.F.; Wang, Y.; Jiang, S. Clear-water local scouring around three piers in a tandem arrangement. Sci. China Technol. Sci. 2016, 59, 888–896. [Google Scholar] [CrossRef]
- Zhou, K.; Duan, J.G.; Bombardelli, F.A. Experimental and Theoretical Study of Local Scour around Three-Pier Group. J. Hydraul. Eng. 2020, 146, 04020069. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).


