Simple and Two-Level Hierarchical Bayesian Approaches for Parameter Estimation with One- and Two-Layer Evapotranspiration Models of Crop Fields
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sites and Observation
2.2. Evapotranspiration Model
2.2.1. Two-Layer Model Based on the SW Model
2.2.2. Traditional One-Layer PM Model
2.3. Simple and HB Approaches
2.4. Evaluation of the Performance of the SW Model Using Bayesian Approaches
3. Results and Discussion
3.1. Differences in Observation Conditions in a Dataset
3.2. Model Parameter Estimation Using the SB and HB Approaches
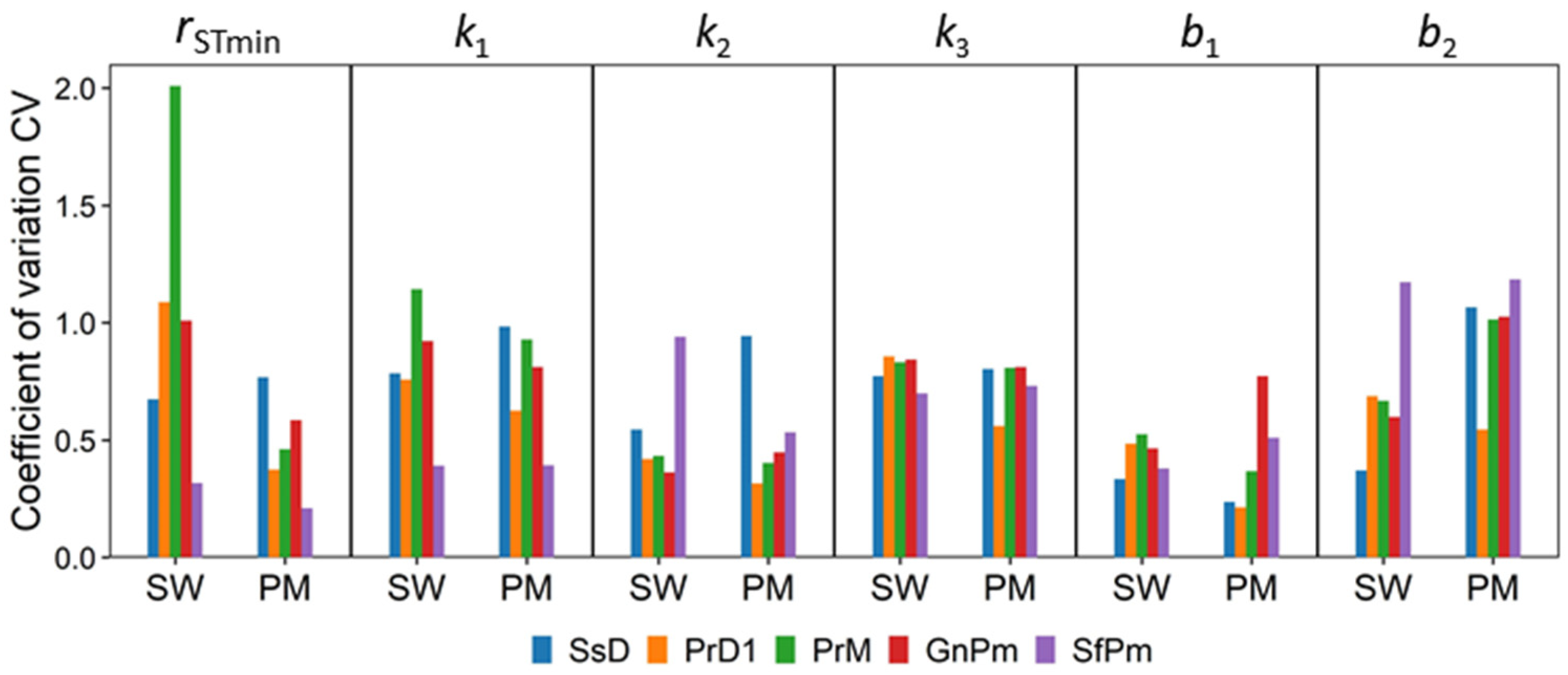
3.2.1. Comparison of Posterior Distributions of Model Parameters
3.2.2. Effect of Difference in Observation Conditions on Parameter Estimation
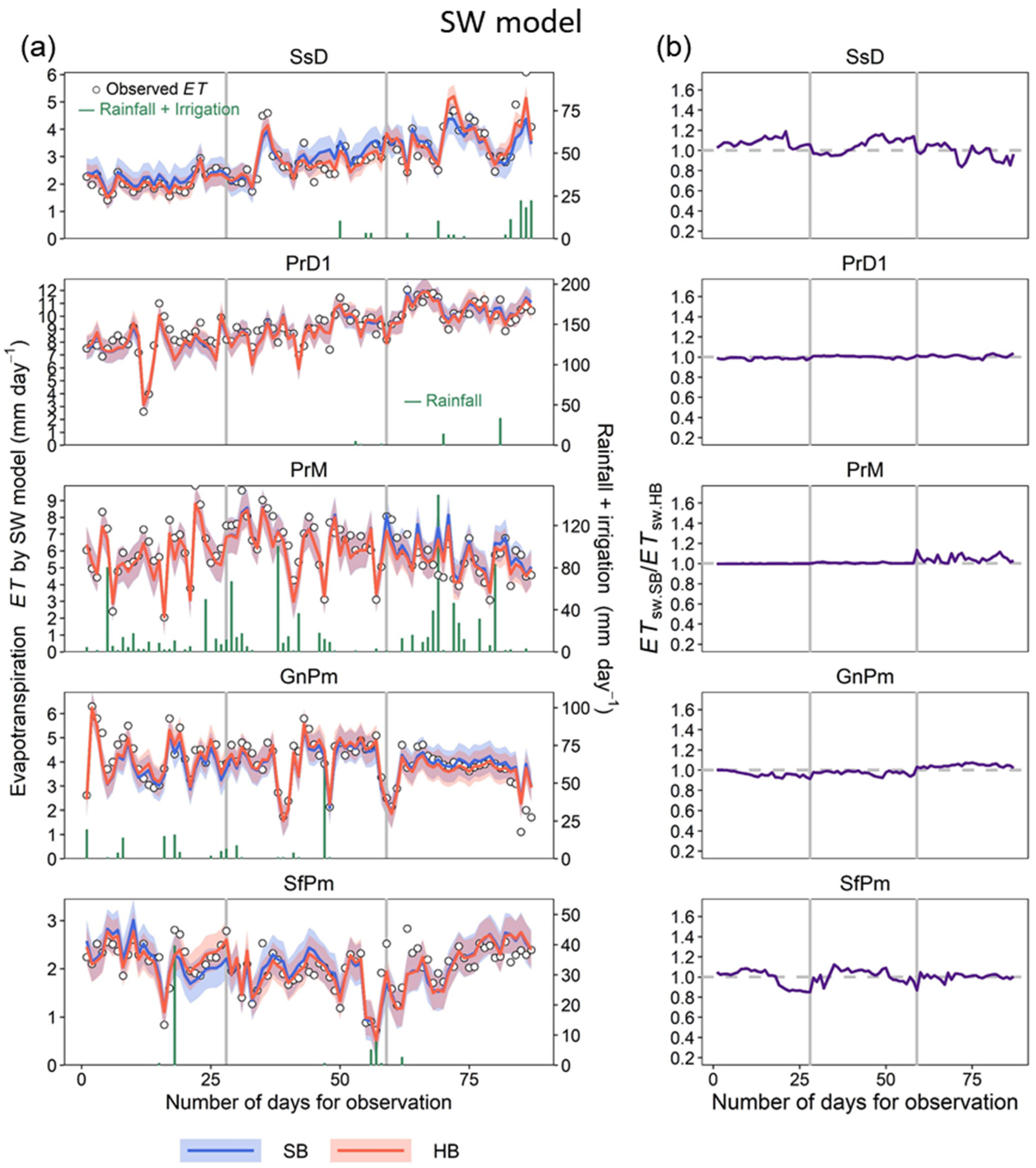
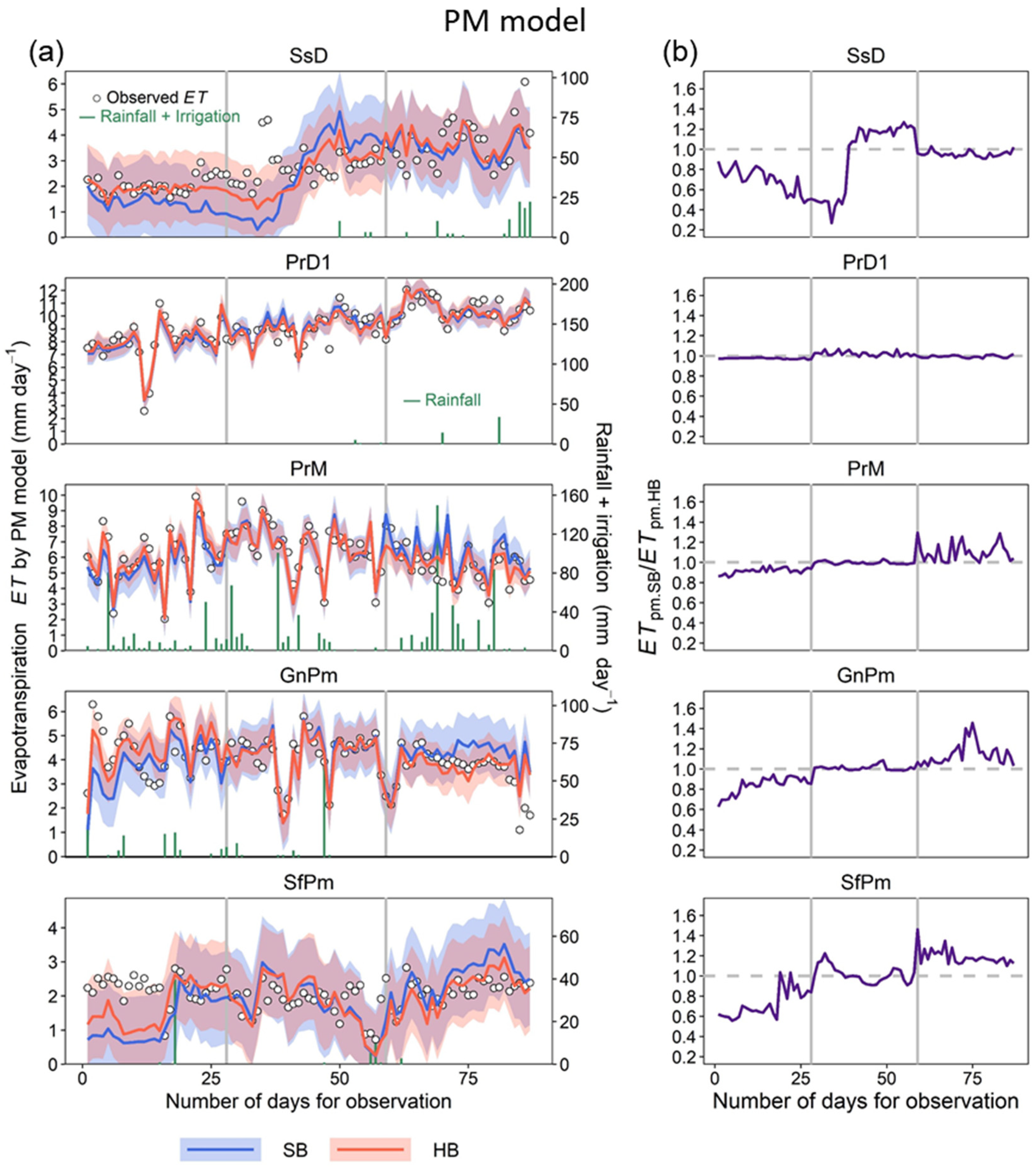
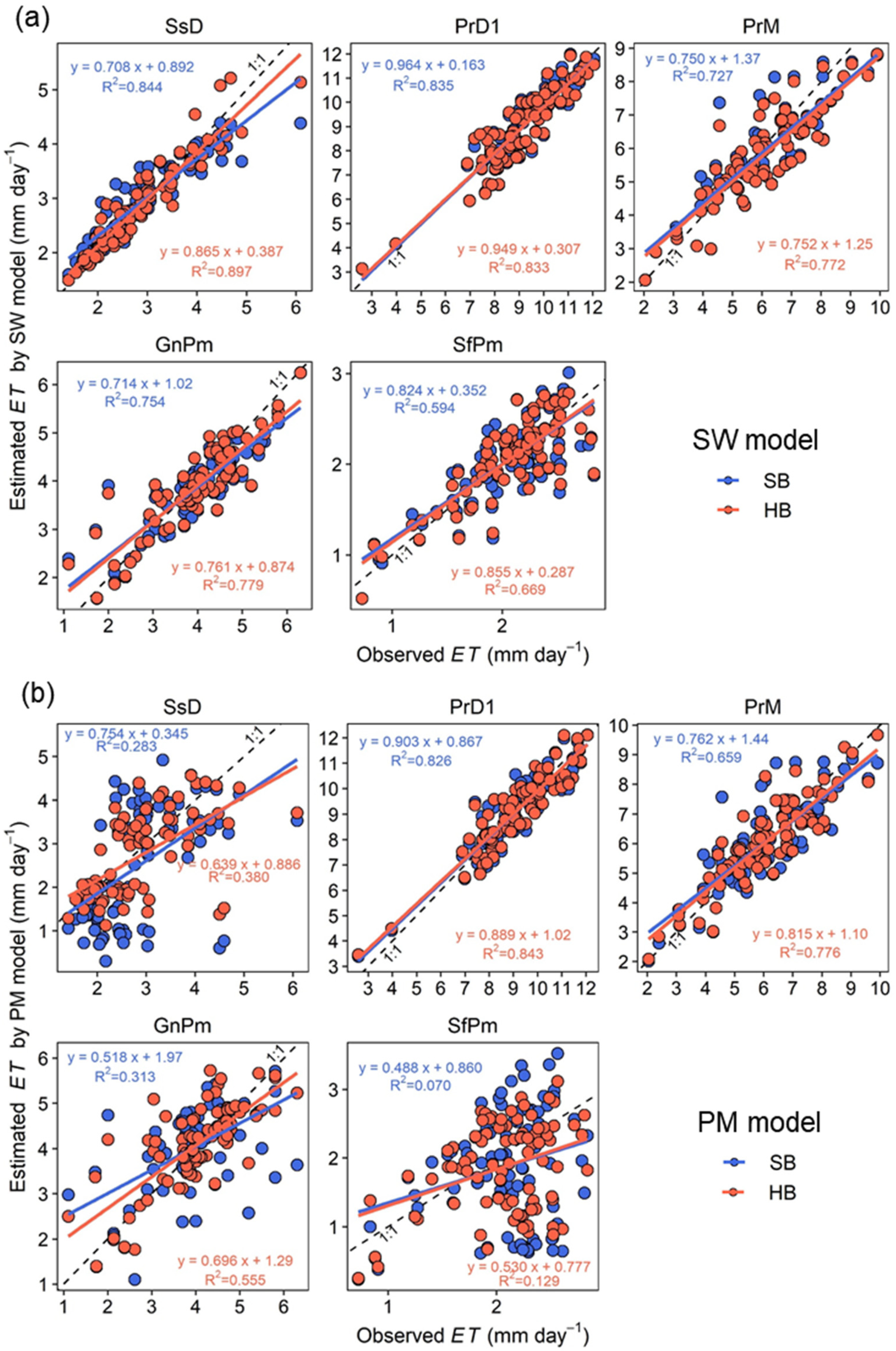
3.3. Comparison of ET Estimation by SW and PM Models Using SB and HB Approaches
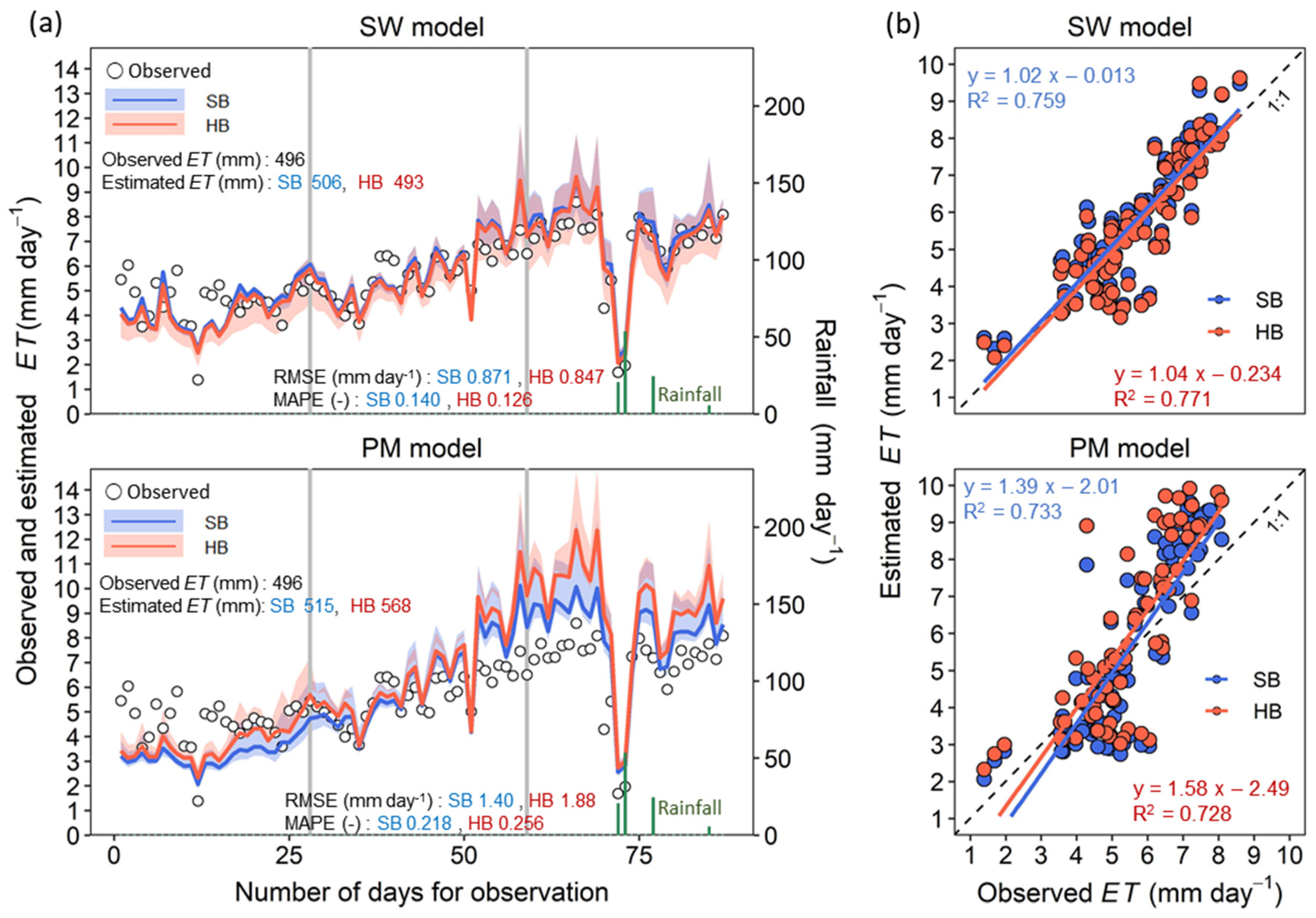
3.4. Validation of Model ET Estimation
4. Conclusions
- Parameterization using the SB and HB approaches was, in most cases, successful in reducing the uncertainties in the parameters. Using the HB approach to parameter estimation, we identified the parameters which are sensitive to seasonal fluctuations and differences in crop growth stages. The parameter k3, which is related to the water vapor pressure deficit, was not very susceptible to seasonal fluctuations, while rSTmin, which is related to stomatal resistance, was sensitive to variations in observation conditions.
- In the calibration of model parameters, the statistical criteria for all conditions observed indicated that the models with parameters calibrated using the HB approach had a better fit to the observed ET data than those with parameters calculated using the SB approach, indicating the potential importance of seasonal fluctuations and variability in crop growth stages for the calibration of model parameters. The performance of the SW models was superior to that of the PM model for most of the observation conditions, using both the SB and HB approaches.
- The SW model, with parameters calculated using the SB and HB approaches with only observed ET data, could provide an acceptable estimation of the ET. The PM model with parameters calculated using both SB and HB approaches overestimated the ET in the last half period; the ET estimates for the HB approach were slightly overestimated compared with the SB approach.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Aerodynamic Resistances
Appendix B. Posterior Probability Distributions of the Parameters
| Parameter | Model | Bayes | SsD | PrD1 | PrM | GnPm | SfPm |
|---|---|---|---|---|---|---|---|
| rSTmin (s m−1) | SW | SB | 45.8 (19.0, 59.5) | 5.60 (1.60, 15.2) | 2.10 (0.033, 10.4) | 33.9 (19.6, 57.0) | 54.4 (40.9, 59.8) |
| HB | 33.4 (5.40, 57.4) | 15.8 (2.30, 45.2) | 11.6 (0.41, 45.8) | 29.4 (4.48, 55.8) | 48.2 (19.1, 59.3) | ||
| PM | SB | 31.8 (9.46, 57.6) | 52.0 (37.6, 59.7) | 47.7 (22.3, 59.6) | 54.3 (41.5, 59.8) | 56.5 (47.7, 59.9) | |
| HB | 35.2 (5.95, 57.6) | 46.6 (16.4, 59.0) | 40.9 (11.8, 58.4) | 36.3 (8.55, 57.3) | 51.2 (27.8, 59.4) | ||
| k1 (W m−2) | SW | SB | 104 (2.10, 432) | 284 (70.3, 489) | 155 (2.30, 471) | 286 (104, 488) | 427 (266, 498) |
| HB | 256 (32.2, 473) | 250 (37.4, 470) | 185 (11.3, 453) | 257 (36.3, 471) | 381 (125, 492) | ||
| PM | SB | 214 (4.50, 483) | 317 (86.1, 492) | 197 (3.20, 479) | 378 (177, 495) | 446 (322, 498) | |
| HB | 209 (14.4, 463) | 309 (64.1, 483) | 225 (22.9, 464) | 254 (39.2, 470) | 378 (137, 490) | ||
| k2 (°C) | SW | SB | 8.41 (7.02, 10.6) | 12.9 (10.0, 17.2) | 21.6 (10.4, 29.6) | 26.2 (18.8, 29.9) | 9.70 (8.11, 11.0) |
| HB | 9.06 (5.55, 21.0) | 19.7 (9.23, 28.6) | 20.9 (8.76, 29.2) | 22.0 (9.96, 29.3) | 12.2 (5.82, 26.0) | ||
| PM | SB | 8.11 (6.66, 9.50) | 15.7 (14.5, 17.0) | 16.3 (10.95, 27.6) | 27.2 (19.8, 29.9) | 25.8 (11.6, 29.9) | |
| HB | 12.0 (5.77, 26.0) | 17.4 (10.2, 25.3) | 20.1 (9.23, 28.9) | 19.1 (8.34, 28.7) | 21.5 (7.94, 29.5) | ||
| k3 (kPa−1) | SW | SB | 0.063 (0.006, 0.099) | 0.045 (0.002, 0.096) | 0.049 (0.002, 0.097) | 0.052 (0.003, 0.098) | 0.069 (0.009, 0.099) |
| HB | 0.053 (0.006, 0.095) | 0.048 (0.005, 0.094) | 0.049 (0.005, 0.094) | 0.050 (0.005, 0.095) | 0.058 (0.008, 0.096) | ||
| PM | SB | 0.050 (0.003, 0.097) | 0.077 (0.024, 0.099) | 0.050 (0.002, 0.098) | 0.063 (0.006, 0.099) | 0.069 (0.009, 0.099) | |
| HB | 0.052 (0.006, 0.095) | 0.068 (0.015, 0.098) | 0.051 (0.006, 0.095) | 0.051 (0.005, 0.095) | 0.056 (0.007, 0.096) | ||
| b1 (s m−1) | SW | SB | 8.20 (6.39, 11.1) | 7.26 (4.13, 12.0) | 7.06 (4.12, 12.0) | 5.21 (4.04, 7.36) | 5.41 (4.92, 6.16) |
| HB | 9.42 (5.74, 13.2) | 8.32 (4.45, 13.6) | 8.00 (4.36, 13.6) | 6.33 (4.16, 11.8) | 6.22 (4.35, 10.6) | ||
| PM | SB | 12.9 (9.27, 14.9) | 11.6 (8.13, 14.8) | 12.0 (8.22, 14.9) | 7.81 (7.07, 8.67) | 6.29 (5.54, 7.05) | |
| HB | 12.3 (7.03, 14.8) | 10.9 (6.57, 14.5) | 10.8 (5.61, 14.5) | 9.06 (4.58, 14.2) | 7.39 (4.49, 12.3) | ||
| b2 (s m−1) | SW | SB | 3.65 (1.16, 7.66) | 4.93 (0.626, 7.88) | 5.18 (0.835, 7.89) | 6.13 (2.86, 7.93) | 0.774 (0.027, 2.33) |
| HB | 5.87 (2.23, 7.79) | 4.54 (0.685, 7.67) | 4.76 (0.789, 7.69) | 5.19 (0.616, 7.78) | 3.65 (0.40, 7.40) | ||
| PM | SB | 2.02 (0.072, 5.87) | 3.59 (0.192, 6.96) | 1.99 (0.069, 5.57) | 0.419 (0.010, 1.55) | 0.573 (0.013, 2.28) | |
| HB | 2.43 (0.183, 6.55) | 3.62 (0.359, 7.19) | 3.30 (0.329, 7.19) | 3.474 (0.315, 7.38) | 2.98 (0.230, 7.17) | ||
| σ (mm day−1) | SW | SB | 0.406 (0.348, 0.477) | 0.702 (0.603, 0.821) | 0.840 (0.723, 0.981) | 0.509 (0.438, 0.595) | 0.318 (0.273, 0.373) |
| HB | 0.310 (0.265, 0.364) | 0.705 (0.604, 0.825) | 0.806 (0.692, 0.943) | 0.479 (0.412, 0.561) | 0.285 (0.244, 0.336) | ||
| PM | SB | 1.20 (1.03, 1.40) | 0.676 (0.581, 0.792) | 0.948 (0.815, 1.11) | 0.897 (0.768, 1.05) | 1.05 (0.892, 1.23) | |
| HB | 1.06 (0.911, 1.24) | 0.646 (0.553, 0.760) | 0.768 (0.660, 0.899) | 0.701 (0.602, 0.820) | 0.944 (0.808, 1.11) |
References
- Flumignan, D.L.; Faria, R.T.; Prete, C.E.C. Evapotranspiration components and dual crop coefficients of coffee trees during crop production. Agric. Water Manag. 2011, 98, 791–800. [Google Scholar] [CrossRef]
- Williams, D.G.; Cable, W.; Hultine, K.; Hoedjes, J.C.B.; Yepez, E.A.; Simonneaux, V.; Er-Raki, S.; Boulet, G.; de Bruin, H.A.R.; Chehbouni, A.; et al. Evapotranspiration components determined by stable isotope, sap flow and eddy covariance techniques. Agric. For. Meteorol. 2004, 125, 241–258. [Google Scholar] [CrossRef]
- Moran, M.S.; Scott, R.L.; Keefer, T.O.; Emmerich, W.E.; Hernandez, M.; Nearing, G.S.; Paige, G.B.; Cosh, M.H.; O’Neill, P.E. Partitioning evapotranspiration in semiarid grassland and shrubland ecosystems using time series of soil surface temperature. Agric. For. Meteorol. 2009, 149, 59–72. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. In Symposia of the Society for Experimental Biology; Cambridge University Press (CUP): Cambridge, UK, 1965; Volume 19, pp. 205–234. [Google Scholar]
- Anadranistakis, M.; Liakatas, A.; Kerkides, P.; Rizos, S.; Gavanosis, J.; Poulovassilis, A. Crop water requirements model tested for crops grown in Greece. Agric. Water Manag. 2000, 45, 297–316. [Google Scholar] [CrossRef]
- Gardiol, J.M.; Serio, L.A.; Maggiora, A.D. Modelling evapotranspiration of corn (Zea mays) under different plant densities. J. Hydrol. 2003, 271, 188–196. [Google Scholar] [CrossRef]
- Kato, T.; Kimura, R.; Kamichika, M. Estimation of evapotranspiration, transpiration ratio and water-use efficiency from a sparse canopy using a compartment model. Agric. Water Manag. 2004, 65, 173–191. [Google Scholar] [CrossRef]
- Fisher, J.B.; Debiase, T.A.; Qi, Y.; Xu, M.; Goldstein, A.H. Evapotranspiration models compared on a Sierra Nevada forest ecosystem. Environ. Model. Softw. 2005, 20, 783–796. [Google Scholar] [CrossRef]
- Zhou, M.; Ishidaira, H.; Hapuarachchi, H.; Magome, J.; Kiem, A.; Takeuchi, K. Estimating potential evapotranspiration using Shuttleworth–Wallace model and NOAA-AVHRR NDVI data to feed a distributed hydrological model over the Mekong River basin. J. Hydrol. 2006, 327, 151–173. [Google Scholar] [CrossRef]
- Ortega-Farias, S.; Carrasco, M.; Olioso, A.; Acevedo, C.; Poblete, C. Latent heat flux over Cabernet Sauvignon vineyard using the Shuttleworth and Wallace model. Irrig. Sci. 2007, 25, 161–170. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops—An energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.L.; Sauer, T.J.; Ben-Gal, A. A review of approaches for evapotranspiration partitioning. Agric. For. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Samanta, S.; Mackay, D.S.; Clayton, M.K.; Kruger, E.L.; Ewers, B.E. Bayesian analysis for uncertainty estimation of a canopy transpiration model. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Reinds, G.J.; van Oijen, M.; Heuvelink, G.B.M.; Kros, H. Bayesian calibration of the VSD soil acidification model using European forest. Geoderma 2008, 146, 475–488. [Google Scholar] [CrossRef]
- Finsterle, S.; Najita, J. Robust estimation of hydrologic model parameters. Water Resour. Res. 1998, 34, 2939–2947. [Google Scholar] [CrossRef]
- Zhu, G.F.; Su, Y.H.; Li, X.; Zhang, K.; Li, C.B. Estimating actual evapotranspiration from an alpine grassland on Qinghai–Tibetan plateau using a two-source model and parameter uncertainty analysis by Bayesian approach. J. Hydrol. 2013, 476, 42–51. [Google Scholar] [CrossRef]
- Zhu, G.F.; Li, X.; Su, Y.H.; Zhang, K.; Bai, Y.; Ma, J.Z.; Li, C.B.; Hu, X.L.; He, J.H. Simultaneously assimilating multivariate data sets into the two-source evapotranspiration model by Bayesian approach: Application to spring maize in an arid region of northwestern China. Geosci. Model Dev. 2014, 7, 1467–1482. [Google Scholar] [CrossRef]
- Wei, G.; Zhang, X.; Ye, M.; Yue, N.; Kan, F. Bayesian performance evaluation of evapotranspiration models based on eddy covariance systems in an arid region. Hydrol. Earth Syst. Sci. 2019, 23, 2877–2895. [Google Scholar] [CrossRef]
- Chen, D.Y.; Wang, X.; Liu, S.Y.; Wang, Y.K.; Gao, Z.Y.; Zhang, L.L.; Wei, X.G.; Wei, X.D. Using Bayesian analysis to compare the performance of three evapotranspiration models for rainfed jujube (Ziziphus jujuba Mill) plantations in the Loess Plateau. Agric. Water Manag. 2015, 159, 341–357. [Google Scholar] [CrossRef]
- Song, Y.; Jin, L.; Zhu, G.; Ma, M. Parameter estimation for a simple two-source evapotranspiration model using Bayesian inference and its application to remotely sensed estimations of latent heat flux at the regional scale. Agric. For. Meteorol. 2016, 230–231, 20–32. [Google Scholar] [CrossRef]
- Clark, J.S.; Gelfand, A.E. Hierarchical Modelling for the Environmental Sciences. In Statistical Methods and Applications; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Nilsson, H.; Rieskamp, J.; Wagenmakers, E. Hierarchical Bayesian parameter estimation for cumulative prospect theory. J. Math. Psychol. 2011, 55, 84–93. [Google Scholar] [CrossRef]
- Morey, R.D.; Pratte, M.S.; Rouder, J.N. Problematic effects of aggregation in z ROC analysis and a hierarchical modeling solution. J. Math. Psychol. 2008, 52, 376–388. [Google Scholar] [CrossRef]
- Bowen, I.S. The ratio of heat losses by conduction and by evaporation from any water surface. Phys. Rev. 1926, 27, 779–787. [Google Scholar] [CrossRef]
- Weine, N.N.O. Review of Efforts to Combat Desertification and Arrest and Reverse Land Degradation in Myanmar. In Combating Desertification in Asia, Africa and the Middle East; Heshmati, G., Squires, V., Eds.; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Casanova, D.; Epema, G.F.; Goudriaan, J. Monitoring rice reflectance at field level for estimating biomass and LAI. Field Crop. Res. 1998, 55, 83–92. [Google Scholar] [CrossRef]
- Allen, R.G.; Jensen, M.E.; Wright, J.L.; Burman, R.D. Operational Estimates of Reference Evapotranspiration. Agron. J. 1989, 81, 650. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H.S. Neural networks and genetic algorithm approach for nonlinear evaporation and evapotranspiration modeling. J. Hydrol. 2008, 351, 299–317. [Google Scholar] [CrossRef]
- Shibayama, M.; Sakamoto, T.; Takada, E.; Inoue, A.; Morita, K.; Takahashi, W.; Kimura, A. Estimating Paddy Rice Leaf Area Index with Fixed Point Continuous Observation of Near Infrared Reflectance Using a Calibrated Digital Camera. Plant Prod. Sci. 2011, 14, 30–46. [Google Scholar] [CrossRef]
- Wei, Z.; Lee, X.; Wen, X.; Xiao, W. Evapotranspiration partitioning for three agro-ecosystems with contrasting moisture conditions: A comparison of an isotope method and a two-source model calculation. Agric. For. Meteorol. 2018, 252, 296–310. [Google Scholar] [CrossRef]
- Kar, G.; Kumar, A. Surface energy fluxes and crop water stress index in groundnut under irrigated ecosystem. Agric. For. Meteorol. 2007, 146, 94–106. [Google Scholar] [CrossRef]
- Banik, C.N.; Nath, R.; Chakraborty, P.K. Effect of dates of sowing on growth and yield of groundnut crop. J. Crop. Weed. 2009, 5, 59–62. [Google Scholar]
- Chapman, S.C.; Hammer, G.L.; Palta, J.A. Predicting leaf area development of sunflower. Field Crop. Res. 1993, 34, 101–112. [Google Scholar] [CrossRef]
- Chongdar, S.; Singharoy, A.; Saha, A.; Chhetri, B. Performance of summer sesame (Sesamum indicum L.) cultivars under varying dates of sowing in prevailing agro-climatic condition of North Bengal. Sci. Res. Essays 2015, 10, 411–420. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Gurney, R.J. The theoretical relationship between foliage temperature and canopy resistance in sparse crops. Q. J. R. Meteorol. Soc. 1990, 116, 497–519. [Google Scholar] [CrossRef]
- Jarvis, P.G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. B Biol. Sci. 1976, 273, 593–610. [Google Scholar] [CrossRef]
- Stewart, J.B. Modelling surface conductance of pine forest. Agric. For. Meteorol. 1988, 43, 19–35. [Google Scholar] [CrossRef]
- Li, S.; Kang, S.; Zhang, L.; Ortega-Farias, S.; Li, F.; Du, T.; Tong, L.; Wang, S.; Ingman, M.; Guo, W. Measuring and modeling maize evapotranspiration under plastic film-mulching condition. J. Hydrol. 2013, 503, 153–168. [Google Scholar] [CrossRef]
- Stewart, G.H. The influence of canopy cover on understorey development in forests of the western Cascade Range, Oregon, USA. Vegetatio 1988, 76, 79–88. [Google Scholar] [CrossRef]
- Brutsaert, W. Theory, History, and Applications. In Evaporation into the Atmosphere; Reidel: Dordrecht, The Netherlands, 1982; p. 299. [Google Scholar]
- Stan Modelling Language Users Guide and Reference Manual, Version 2.4. Available online: http://mc-stan.org/rstan (accessed on 23 October 2020).
- Sellers, P.J.; Heiser, M.D.; Hall, F.G. Relations between surface conductance and spectral vegetation indices at intermediate (100 m2 to 15 km2) length scales. J. Geophys. Res. 1992, 97, 19033–19059. [Google Scholar] [CrossRef]
- Meng, W.; Xihuan, S.; Juanjuan, M.; Xianghong, G.; Tao, L.; Ruofan, L. Measurement and simulation of the water storage pit irrigation trees evapotranspiration in the Loess Plateau. Agric. Water Manag. 2019, 226, 105804. [Google Scholar] [CrossRef]
- Gavilán, P.; Berengena, J. Accuracy of Bowen ratio-energy balance method for measuring latent heat flux in a semiarid advective environment. Irrig. Sci. 2007, 25, 127–140. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Wood, E.F. Impact of model structure and parameterization on Penman–Monteith type evaporation models. J. Hydrol. 2015, 525, 521–535. [Google Scholar] [CrossRef]
- Stannard, D.I. Comparison of Penman-Monteith, Shuttleworth-Wallace, and Modified Priestley-Taylor Evapotranspiration Models for wildland vegetation in semiarid rangeland. Water Resour. Res. 1993, 29, 1379–1392. [Google Scholar] [CrossRef]
- The, C.B.S.; Simmonds, L.P.; Wheeler, T.R. Modelling the partitioning of solar radiation capture and evapotranspiration intercropping systems. In Proceedings of the 2nd International Conference on Tropical Climatology, Meteorology and Hydrology TCMH-2001, Brussels, Belgium, 13–14 December 2001. [Google Scholar]
- Zhang, B.; Kang, S.; Li, F.; Zhang, L. Comparison of three evapotranspiration models to Bowen ratio-energy balance method for a vineyard in an arid desert region of northwest China. Agric. For. Meteorol. 2008, 148, 1629–1640. [Google Scholar] [CrossRef]
- Ortega-Farias, S.O.; Olioso, A.; Fuentes, S.; Valdes, H. Latent heat flux over a furrow-irrigated tomato crop using Penman–Monteith equation with a variable surface canopy resistance. Agric. Water Manag. 2006, 82, 421–432. [Google Scholar] [CrossRef]
- Burba, G.G.; Verma, S.B. Seasonal and interannual variability in evapotranspiration of native tallgrass prairie and cultivated wheat ecosystems. Agric. For. Meteorol. 2005, 135, 190–201. [Google Scholar] [CrossRef]
- Alves, I.; Cameira, M. Evapotranspiration estimation performance of root zone water quality model: Evaluation and improvement. Agric. Water Manag. 2002, 57, 61–73. [Google Scholar] [CrossRef]
- Denmead, O.T. Temperate Cereals. In Vegetation and the Atmosphere; Monteith, J.L., Ed.; Academic Press: New York, NY, USA, 1976; Volume 2, pp. 1–31. [Google Scholar]
- Uchijima, Z. Maize and rice. In Vegetation and the Atmosphere; Monteith, J.L., Ed.; Academic Press: New York, NY, USA, 1976; Volume 2, pp. 33–64. [Google Scholar]
- Monteith, J.L. Principles of Environmental Physics; Edward Arnold: London, UK, 1973; p. 241. [Google Scholar]

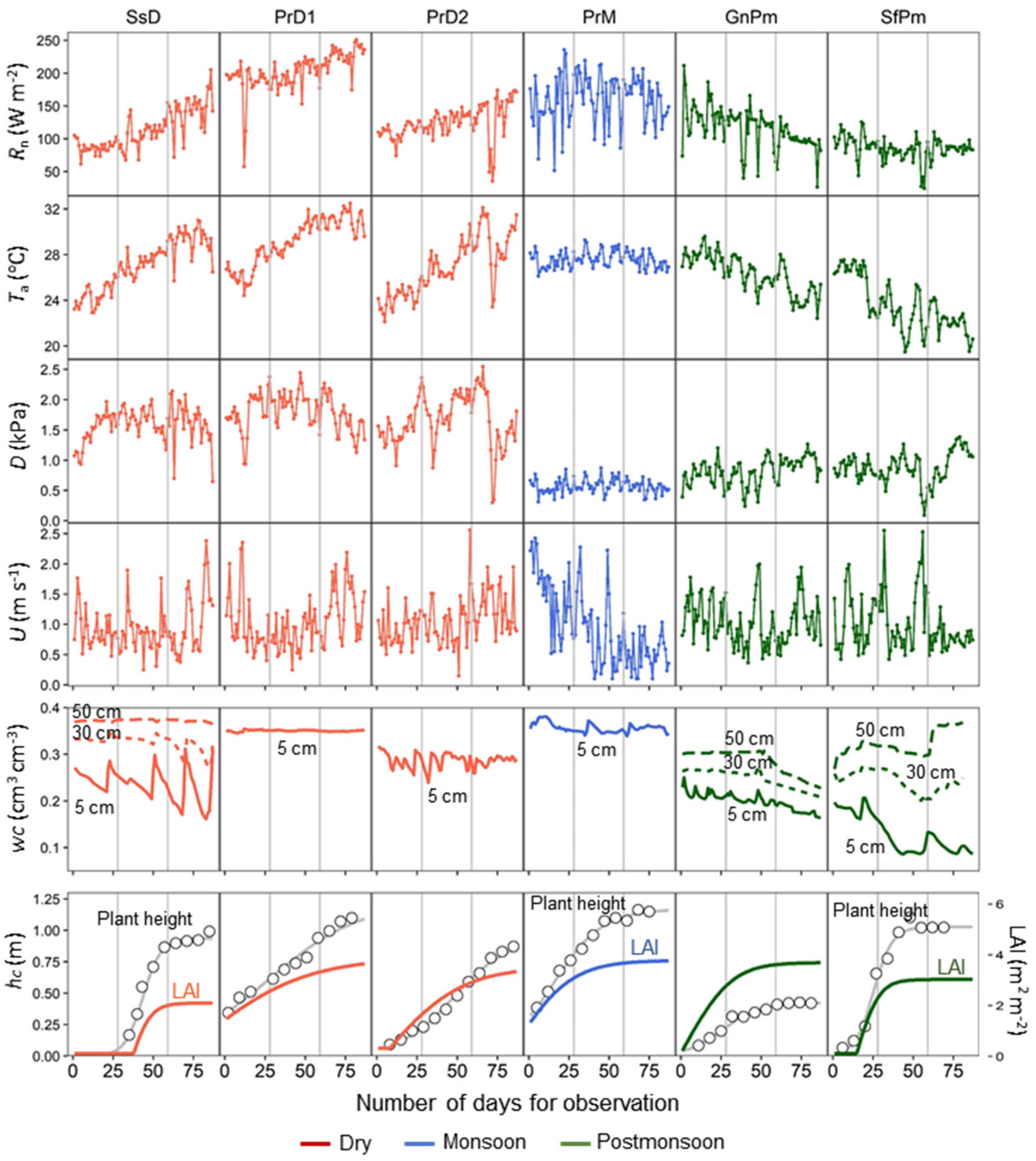
| Abbrev. | Crops | Seasons | Sown Day/Harvested Day | Soil Texture | Periods (87 Days) |
|---|---|---|---|---|---|
| Calibration | |||||
| SsD | Sesame | Dry | 5 February/15 May | Clay loam | 5 February–2 May 2018 |
| PrD1 | Paddy rice | Dry | 27 January/11 June | Sandy loam | 24 February–21 May 2019 |
| PrM | Paddy rice | Monsoon | 31 June/30 November | Sandy loam | 1 August–26 October 2017 |
| GnPm | Groundnut | Post-monsoon | 12 September/12 January | Sandy loam | 14 September–9 December 2018 |
| SfPm | Sunflower | Post-monsoon | 31 October/30 January | Sandy loam | 8 November 2017–2 February 2018 |
| Validation | |||||
| PrD2 | Paddy rice | Dry | 1 February/30 May | Sandy loam | 4 February–1 May 2017 |
| Model | Bayes Type | Condition | ETob (mm) | ETest (mm) | Eest (mm) | Test (mm) | MAE (mm d−1) | RMSE (mm d−1) | MAPE (%) | RMSPE (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| SW | SB | SsD | 248 | 253 | 182 | 71 | 0.275 | 0.388 | 0.099 | 0.120 |
| PrD1 | 798 | 783 | 110 | 673 | 0.562 | 0.684 | 0.065 | 0.087 | ||
| PrM | 529 | 516 | 43 | 473 | 0.663 | 0.825 | 0.112 | 0.142 | ||
| GnPm | 350 | 339 | 89 | 250 | 0.371 | 0.499 | 0.110 | 0.141 | ||
| SfPm | 180 | 179 | 124 | 55 | 0.239 | 0.309 | 0.117 | 0.170 | ||
| HB | SsD | 248 | 248 | 213 | 35 | 0.218 | 0.294 | 0.074 | 0.089 | |
| PrD1 | 798 | 784 | 94 | 690 | 0.557 | 0.679 | 0.065 | 0.086 | ||
| PrM | 529 | 506 | 43 | 463 | 0.642 | 0.786 | 0.106 | 0.140 | ||
| GnPm | 350 | 342 | 78 | 264 | 0.341 | 0.464 | 0.103 | 0.133 | ||
| SfPm | 180 | 179 | 129 | 49 | 0.205 | 0.272 | 0.102 | 0.153 | ||
| PM | SB | SsD | 248 | 217 | – | – | 0.921 | 1.17 | 0.333 | 1.37 |
| PrD1 | 798 | 796 | – | – | 0.529 | 0.657 | 0.062 | 0.077 | ||
| PrM | 529 | 528 | – | – | 0.731 | 0.927 | 0.125 | 0.151 | ||
| GnPm | 350 | 352 | – | – | 0.608 | 0.878 | 0.180 | 0.291 | ||
| SfPm | 180 | 163 | – | – | 0.661 | 0.838 | 0.317 | 1.01 | ||
| HB | SsD | 248 | 236 | – | – | 0.587 | 0.824 | 0.197 | 0.435 | |
| PrD1 | 798 | 797 | – | – | 0.497 | 0.615 | 0.058 | 0.073 | ||
| PrM | 529 | 527 | – | – | 0.597 | 0.737 | 0.102 | 0.126 | ||
| GnPm | 350 | 355 | – | – | 0.484 | 0.675 | 0.147 | 0.177 | ||
| SfPm | 180 | 163 | – | – | 0.535 | 0.669 | 0.266 | 0.627 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shiraki, S.; Thu, A.K.; Matsuno, Y.; Shinogi, Y. Simple and Two-Level Hierarchical Bayesian Approaches for Parameter Estimation with One- and Two-Layer Evapotranspiration Models of Crop Fields. Water 2021, 13, 3607. https://doi.org/10.3390/w13243607
Shiraki S, Thu AK, Matsuno Y, Shinogi Y. Simple and Two-Level Hierarchical Bayesian Approaches for Parameter Estimation with One- and Two-Layer Evapotranspiration Models of Crop Fields. Water. 2021; 13(24):3607. https://doi.org/10.3390/w13243607
Chicago/Turabian StyleShiraki, Shutaro, Aung Kyaw Thu, Yutaka Matsuno, and Yoshiyuki Shinogi. 2021. "Simple and Two-Level Hierarchical Bayesian Approaches for Parameter Estimation with One- and Two-Layer Evapotranspiration Models of Crop Fields" Water 13, no. 24: 3607. https://doi.org/10.3390/w13243607
APA StyleShiraki, S., Thu, A. K., Matsuno, Y., & Shinogi, Y. (2021). Simple and Two-Level Hierarchical Bayesian Approaches for Parameter Estimation with One- and Two-Layer Evapotranspiration Models of Crop Fields. Water, 13(24), 3607. https://doi.org/10.3390/w13243607






