Assessment of Climatic and Anthropogenic Controls on Bridge Deck Drainage and Sediment Removal
Abstract
:1. Introduction
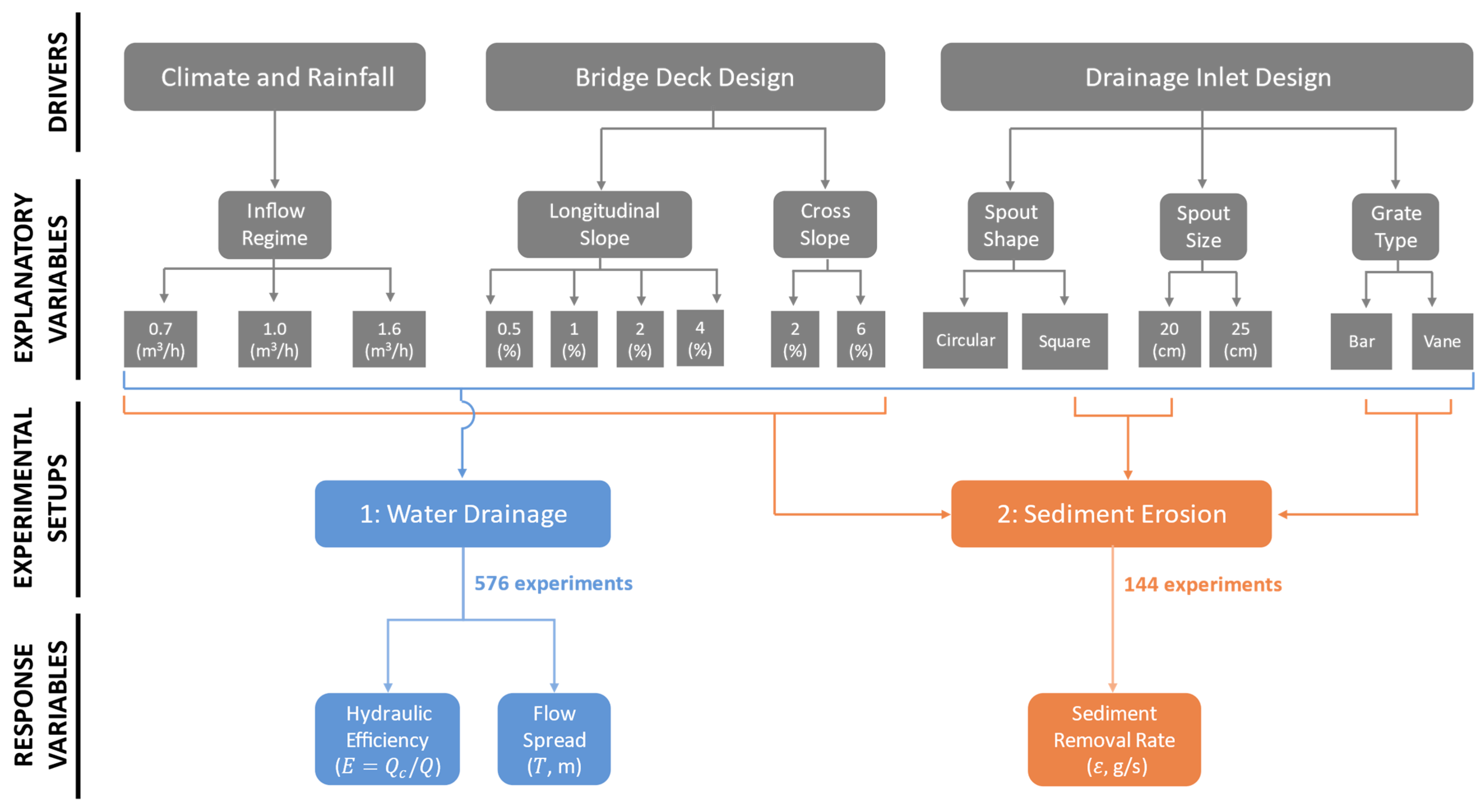
2. Materials and Methods
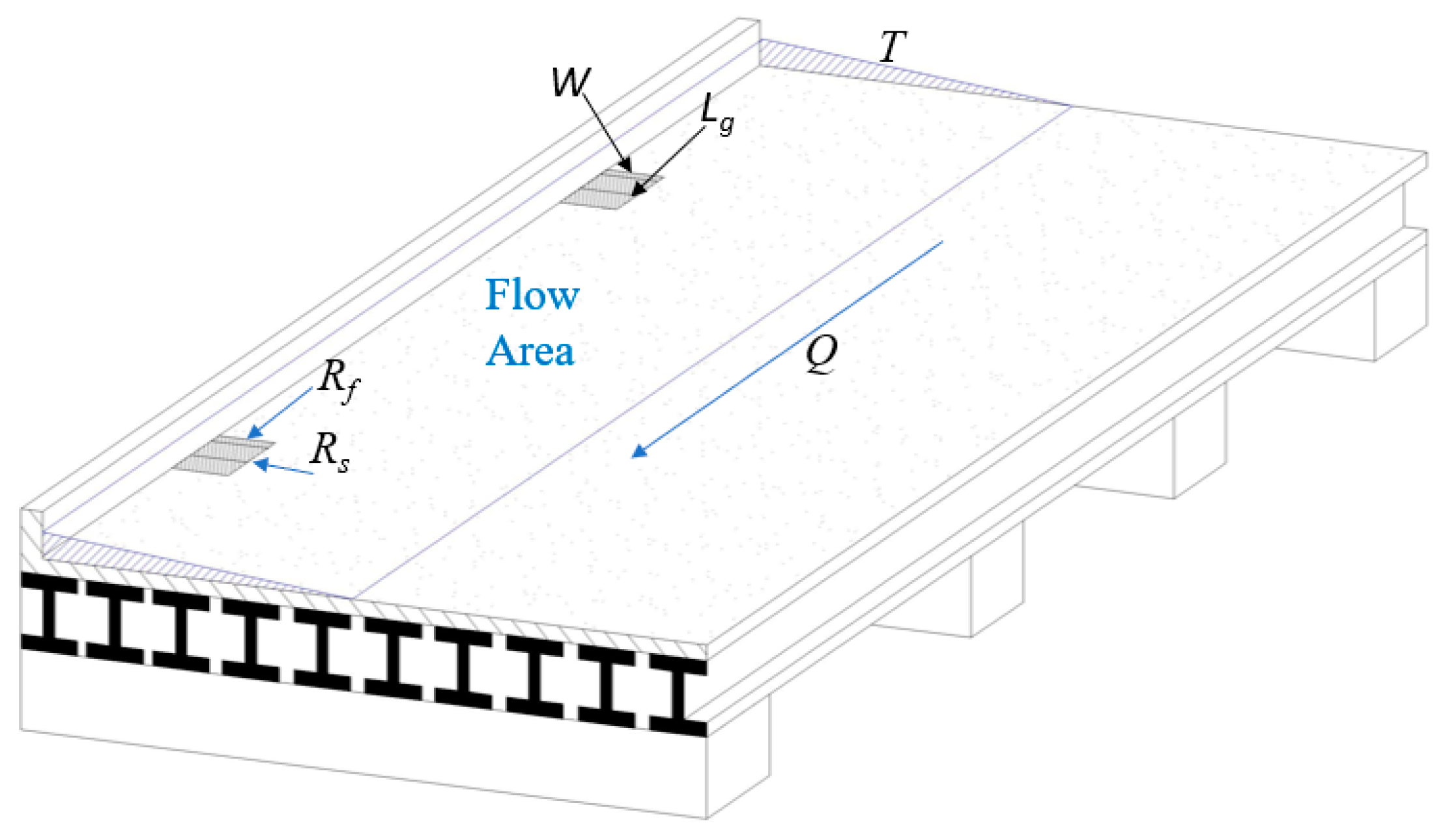
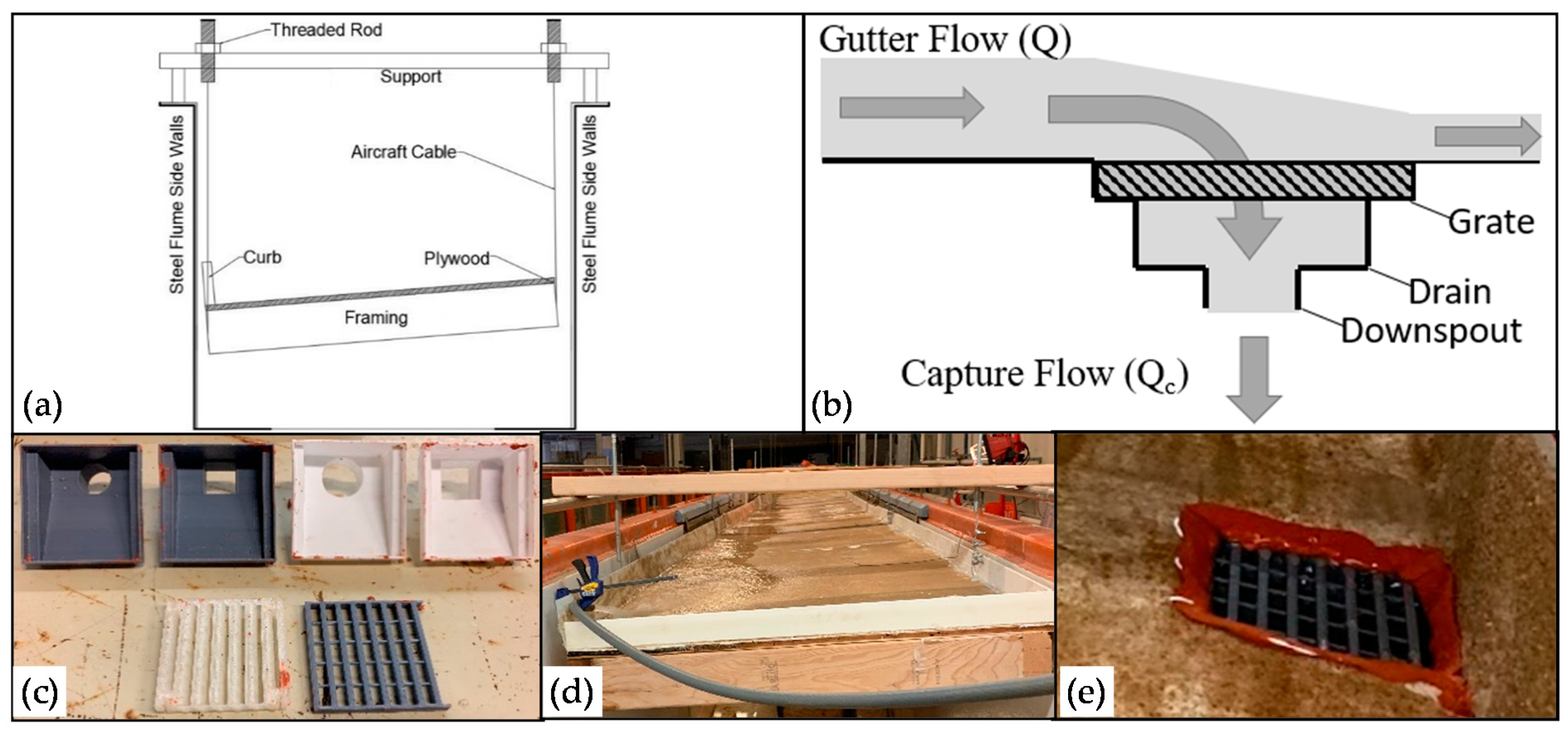
2.1. Laboratory Experimental Setup
2.1.1. Hydraulic Efficiency Experiment
2.1.2. Sediment Removal Experiment
2.1.3. Sediment Mixture Comparison
2.2. Precipitation Analysis
2.3. Statistical Analysis
3. Results
3.1. Climate: Inflow Regimes
3.1.1. Hydraulic Efficiency
3.1.2. Sediment Removal
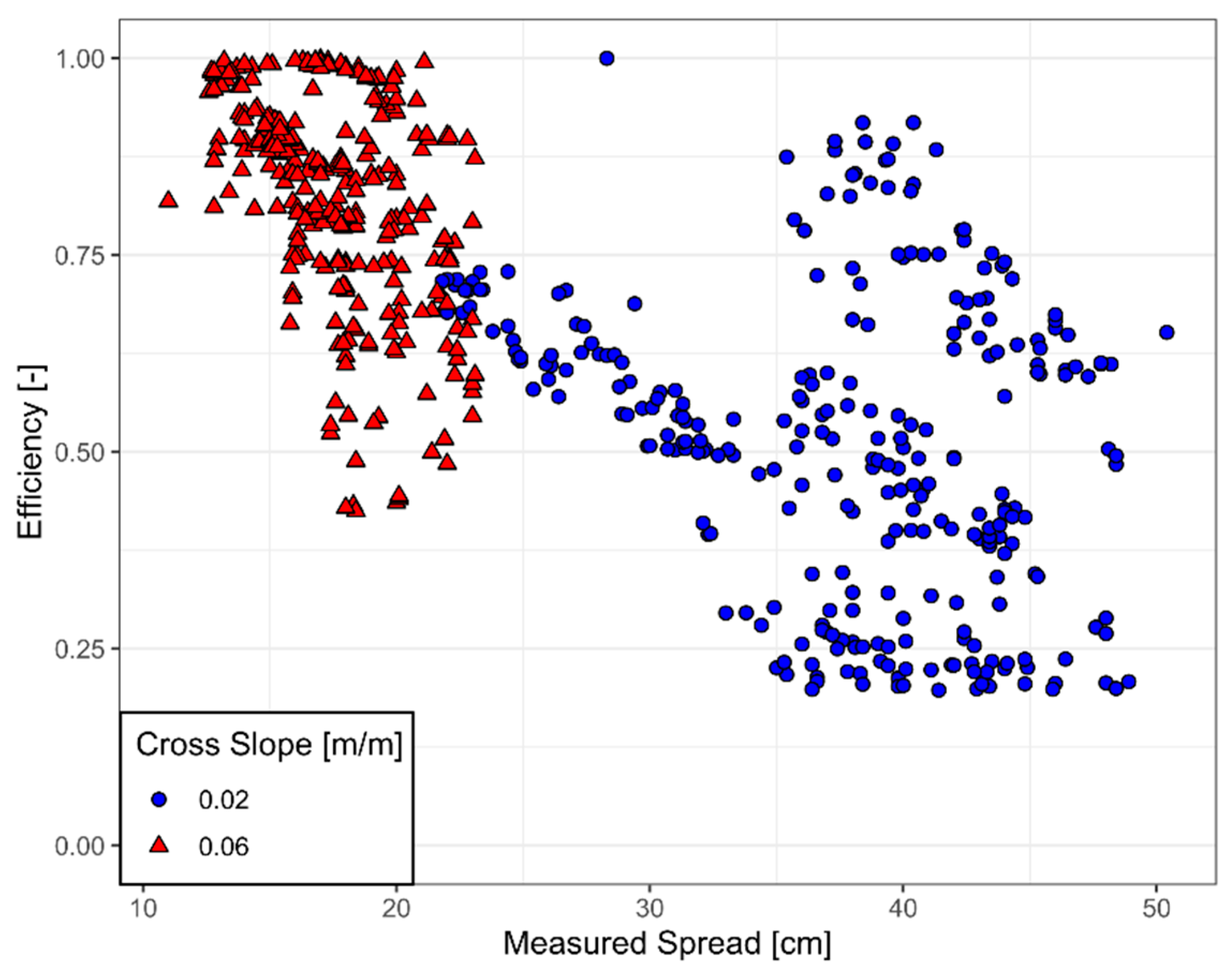
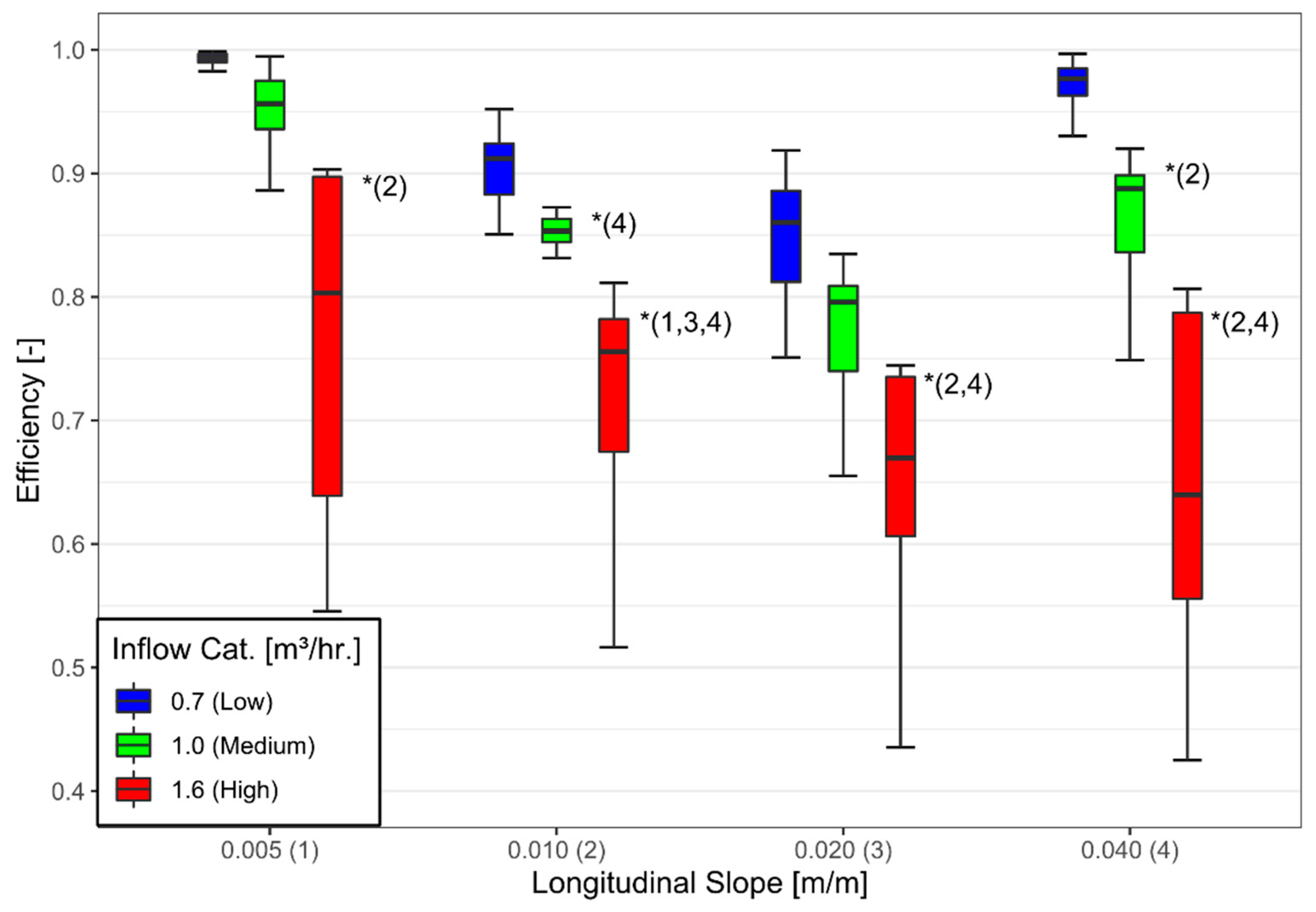
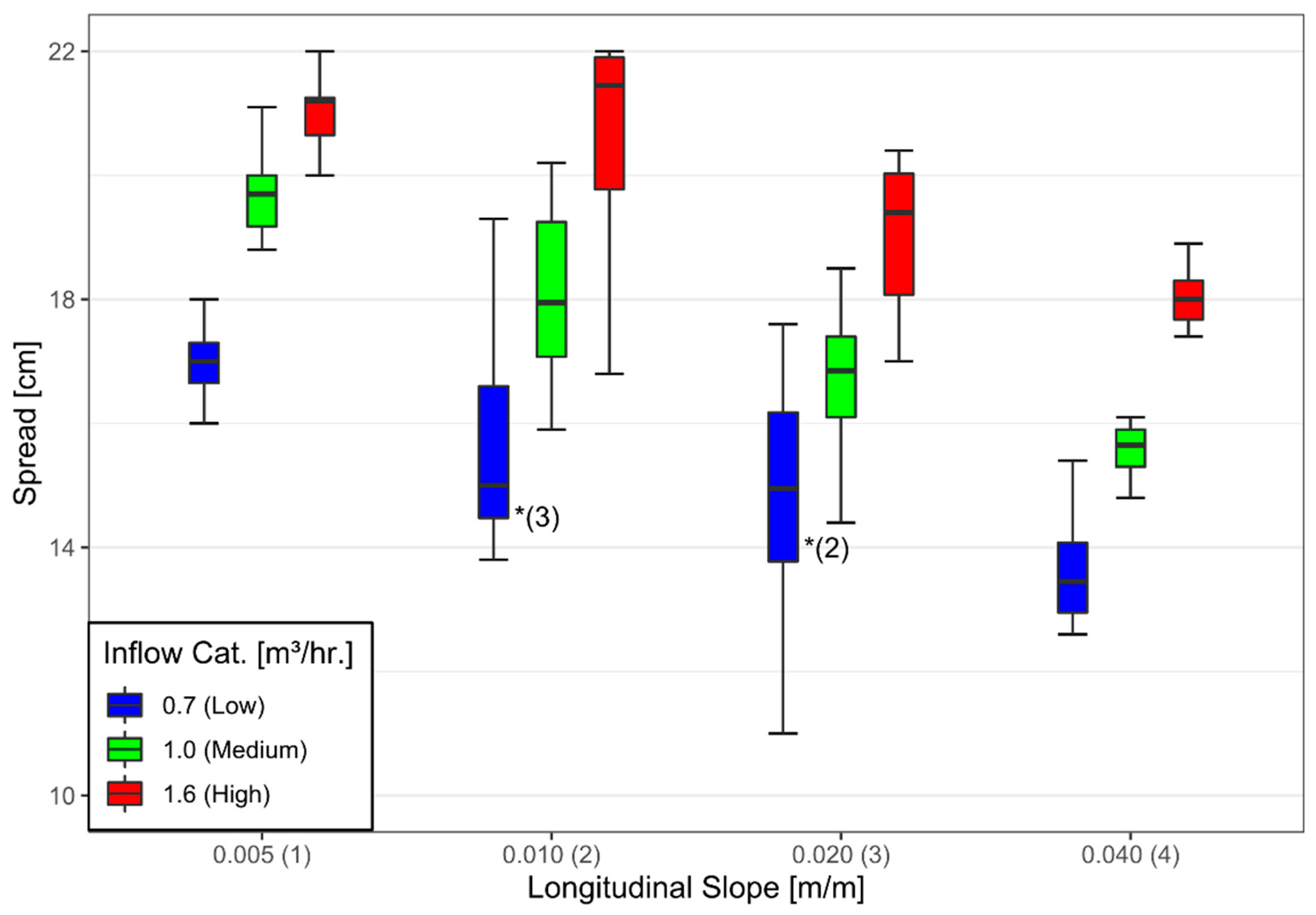
3.2. Bridge Deck Design: Longitudinal and Cross Slopes
3.2.1. Hydraulic Efficiency
3.2.2. Sediment Removal
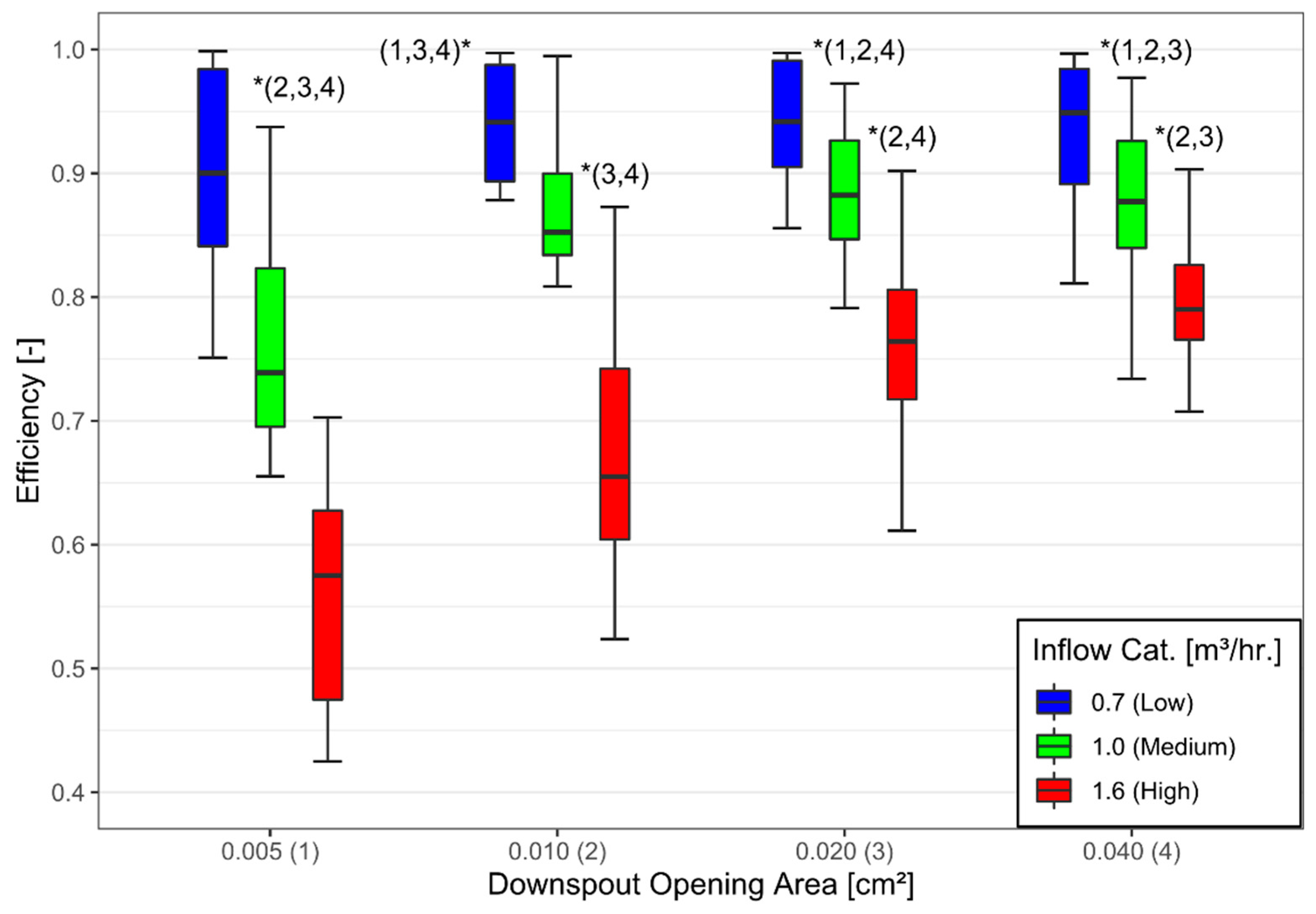
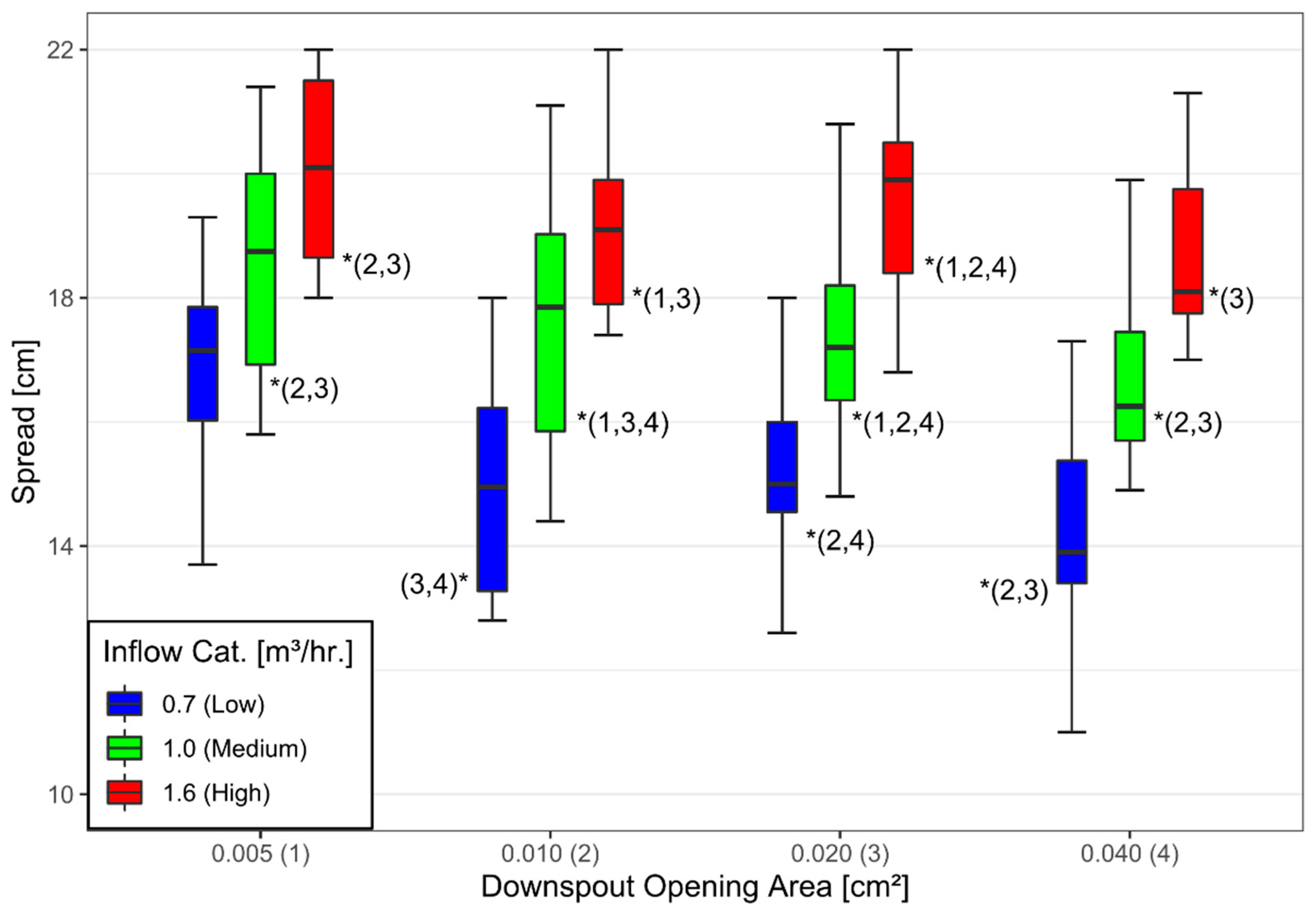
3.3. Inlet Design: Size, Shape, and Grate Type
3.3.1. Hydraulic Efficiency
3.3.2. Sediment Removal
4. Discussion
4.1. Controls and Implications
4.2. Sediment–Precipitation Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khasnabis, S.; Dhingra, S.L.; Mishra, S.; Safi, C. Mechanisms for transportation infrastructure investment in developing countries. J. Urban. Plann Dev. 2010, 136, 94–103. [Google Scholar] [CrossRef] [Green Version]
- Qian, Q.; Liu, X.; Barret, M.E.; Charbeneau, R.J. Physical modeling on hydraulic performance of rectangular bridge deck drains. Water 2016, 8, 67. [Google Scholar] [CrossRef] [Green Version]
- ASCE. 2021 Report Card for America’s Infrastructure; American Society of Engineers: Reston, VA, USA, 2021. [Google Scholar]
- IPCC. Climate Change. Synthesis Report; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2014. [Google Scholar]
- Kim, K.; Ha, S.; Kim, H. Using real options for urban infrastructure adaptation under climate change. J. Clean. Prod. 2017, 43, 40–50. [Google Scholar] [CrossRef]
- Mailhot, A.; Duchesne, S. Design criteria of urban drainage infrastructures under climate change. J. Water Resour. Pann. Manag. 2010, 136, 201–208. [Google Scholar] [CrossRef]
- Schweikert, A.; Chinowsky, P.; Kwiatkowski, K.; Espinet, X. The infrastructure planning support system: Analyzing the impact of climate change on road infrastructure and development. Transp. Policy 2014, 35, 146–153. [Google Scholar] [CrossRef]
- Hu, S.; Zhi-mao, G.; Jun-ping, Y. The impacts of urbanization on soil erosion in the Loess Plateau region. J. Geogr. Sci. 2001, 11, 282–290. [Google Scholar] [CrossRef]
- Fletcher, S.; Lickley, M.; Strzepek, K. Learning about climate change uncertainty enables flexible water infrastructure planning. Nat. Commun. 2019, 10, 1782. [Google Scholar] [CrossRef]
- Young, G.K.; Walker, S.E.; Chang, F. Design of Bridge Deck Drainage; FHWA-SA-92-010, Hydraulic Engineering Circular 21 (HEC 21); Federal Highway Administration (FHWA): Washington, DC, USA, 1993.
- Izzard, C.F. Hydraulics of runoff from developed surfaces. In Proceedings of the 26th Annual Meeting of Highway Research Board National Research Council, Washington, DC, USA, 5–8 December 1946; pp. 129–150. [Google Scholar]
- Izzard, C.F. Tentative Results on Capacity of Curb Opening Inlet; Research Report No. 11-B.; Highway Research Board: Washington, DC, USA, 1950; pp. 36–51. [Google Scholar]
- Schalla, F.E.; Ashraf, M.; Barrett, M.E. Limitations of traditional capacity equations for long curb inlets. Transp. Res. Rec. 2017, 2638, 97–103. [Google Scholar] [CrossRef]
- Kansas Department of Transportation. Design Manual Volume III—Bridge Section; Kansas Department of Transportation (KDOT): Topkeka, KS, USA, 2015.
- Illinois Department of Transportation. Bridge Manual; Illinois Department of Transporation (ILDOT): Springfield, IL, USA, 2012.
- Walder, J.S. Dimensionless Erosion Laws for Cohesive sediment. J. Hydraul. Eng. 2015, 142. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment pick-up functions. J. Hydraul. Eng. 1984, 110, 1494–1502. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. National Centers for Environmental Information Data Available on the World Wide Web. NOAA Climate Data Online. Available online: https://www.ncdc.noaa.gov/cdo-web/ (accessed on 4 February 2021).
- IBM Corp. IBM SPSS Statistics for Windows; Version 27.0; IBM Corp: Armonk, NY, USA, 2020. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Wilk, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: Oxford, UK, 2011; ISBN 978-0-12-3850255-5. [Google Scholar]
- Wang, F.; Huang, G.H.; Fan, Y.; Li, Y.P. Robust Subsampling ANOVA methods for sensitivity analysis of water resource and environmental models. Water Resour. Manag. 2020, 34, 3199–3217. [Google Scholar] [CrossRef]
- Blanca, M.J.; Alarcón, R.; Arnau, J.; Bono, R.; Bendayan, R. Non-Normal data: Is ANOVA still a valid option? Psicothema 2017, 29, 552–557. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Y. Experimental study on anisotropic attributes of surface roughness in watersheds. J. Hydrol. Eng. 2017, 22, 06017005. [Google Scholar] [CrossRef]
- Holley, E.R.; Woodward, C.; Brigneti, A.; Ott, C. Hydraulic Characteristics of Recessed Curb Inlets and Bridge Drains; Rep. No. FHWA/TX-92/0-1267-2F; Center for Transportation Research, the University of Texas at Austin: Austin, TX, USA, 1992. [Google Scholar]
- Hammons, M.A.; Holley, E.R. Hydraulic Characteristics of Flush Depressed Curb Inlets and Bridge Deck Drains; Rep. No. FHWA/TX-95/0-1409-01; Center for Transportation Research, the University of Texas at Austin: Austin, TX, USA, 1995. [Google Scholar]
- Hermange, C.; Todoroff, V.; Biesse, F.; Le-Chenadec, Y. Experimental investigation of the leading parameters influencing the hydroplaning phenomenon. Veh. Syst. Dyn. 2021, 1–18. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. The influence of time and other factors on soil loss produced by rain-impacted flow under artificial rainfall. J. Hydrol. 2020, 587, 125004. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, K.; Zhang, W. Detachment of road surface soil by flowing water. Catena 2009, 76, 155–162. [Google Scholar] [CrossRef]
- Johnson, F.L.; Chang, F. Drainage of Highway Pavement; Hydraulic Engineering Circular No. 12 (HEC-12); Federal Highway Administration (FHWA): Washington, DC, USA, 1984.
- Brown, S.A.; Schall, J.D.; Morris, J.L.; Doherty, C.L.; Stein, S.M.; Warner, J.C. Urban Drainage Design Manual: FHWA-NHI-10–009, Hydraulic Engineering Circular 22 (HEC-22), 3rd ed.; Federal Highway Administration (FHWA): Washington, DC, USA, 2009.
- Moustakis, Y.; Papalexiou, S.M.; Onof, C.J.; Paschalis, A. Seasonality, intensity, and duration of rainfall extremes change in a warmer climate. Earth’s Future 2021, 9, 1–15. [Google Scholar] [CrossRef]
- Awwad, M. Studying the effects of roads geometry and design parameters on the pavement drainage system. Civ. Eng. J. 2021, 7, 49–58. [Google Scholar] [CrossRef]
- Barreiro, J.; Lopes, R.; Ferreira, F.; Matos, J.S. Index-Based approach to evaluate city resilience in flooding scenarios. Civ. Eng. J. 2021, 7, 197–207. [Google Scholar] [CrossRef]
- Tao, W.; Wu, J.; Wang, Q. Mathematical model of sediment and solute transport along slope land in different rainfall pattern conditions. Sci. Rep. 2017, 7, 44082. [Google Scholar] [CrossRef]
- Naves, J.; Anta, J.; Suarez, J.; Puertas, J. Hydraulic, wash-off and sediment transport experiments in a full-scale urban drainage physical model. Sci. Data. 2020, 7, 44. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Mackenzie, K. Hydraulic Efficiency of Grate and Curb-Opening Inlets under Clogging Effect; Research Report CDOT-2012-3; DTD Applied Research and Innovation Branch, Colorado Department of Transportation (CDOT): Denver, CO, USA, 2012.
- Gomez, M.; Pares, J.; Russo, B.; Martinez-Gomariz, E. Methodology to quantify clogging coefficients for grated inlets. Application to SANT MARTI catchment. J. Flood Risk Manag. 2019, 12, e12479. [Google Scholar] [CrossRef] [Green Version]
- Ghodoosi, F.; Abu-Samra, S.; Zeynalian, M.; Zayed, T. Maintenance cost optimization for bridge structures using system reliability analysis and genetic algorithms. J. Constr. Eng. Manag. 2018, 144, 04017116. [Google Scholar] [CrossRef]
- Kim, K.H.; Nam, M.S.; Hwang, H.H.; Ann, K.Y. Prediction of remaining life for bridge decks considering deterioration factors and propose of prioritization process for bridge deck maintenance. Sustainability 2020, 12, 10625. [Google Scholar] [CrossRef]

| Inflow (m3/h) | Sediment Removal Rate (g/s) | |
|---|---|---|
| Bar Grate | Vane Grate | |
| 0.7 | 0.045 ± 0.015 | 0.049 ± 0.022 |
| 1.0 | 0.056 ± 0.023 | 0.075 ± 0.059 |
| 1.6 | 0.067 ± 0.045 | 0.059 ± 0.023 |
| Location | NOAA Station ID | Less than Test Flow (%) | Low-to-Medium Flow (%) | High Flow (%) | Optimal Grate Type |
|---|---|---|---|---|---|
| Iola, KS, USA | COOP:143984 | 25.1 | 30.2 | 44.7 | Bar |
| Lawrence, KS, USA | COOP:141612 | 24.3 | 35.7 | 40.0 | Bar |
| Smolan, KS, USA | COOP:147551 | 24.6 | 33.0 | 42.4 | Bar |
| Wilson, KS, USA | COOP:148946 | 26.3 | 28.9 | 44.8 | Bar |
| Chicago, IL, USA | COOP:111577 | 29.8 | 37.1 | 33.1 | Vane |
| Danville, IL, USA | COOP:112140 | 17.1 | 51.5 | 31.4 | Vane |
| Illinois City, IL, USA | COOP:114355 | 21.5 | 40.5 | 38.0 | Vane |
| Quincy, IL, USA | COOP:117077 | 26.9 | 30.9 | 42.2 | Bar |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michalek, A.; Husic, A.; Roundy, J.; Hansen, A.T. Assessment of Climatic and Anthropogenic Controls on Bridge Deck Drainage and Sediment Removal. Water 2021, 13, 3556. https://doi.org/10.3390/w13243556
Michalek A, Husic A, Roundy J, Hansen AT. Assessment of Climatic and Anthropogenic Controls on Bridge Deck Drainage and Sediment Removal. Water. 2021; 13(24):3556. https://doi.org/10.3390/w13243556
Chicago/Turabian StyleMichalek, Alexander, Admin Husic, Joshua Roundy, and Amy T. Hansen. 2021. "Assessment of Climatic and Anthropogenic Controls on Bridge Deck Drainage and Sediment Removal" Water 13, no. 24: 3556. https://doi.org/10.3390/w13243556
APA StyleMichalek, A., Husic, A., Roundy, J., & Hansen, A. T. (2021). Assessment of Climatic and Anthropogenic Controls on Bridge Deck Drainage and Sediment Removal. Water, 13(24), 3556. https://doi.org/10.3390/w13243556






