Study on Water Rights Allocation of Irrigation Water Users in Irrigation Districts of the Yellow River Basin
Abstract
1. Introduction
2. Materials and Methods
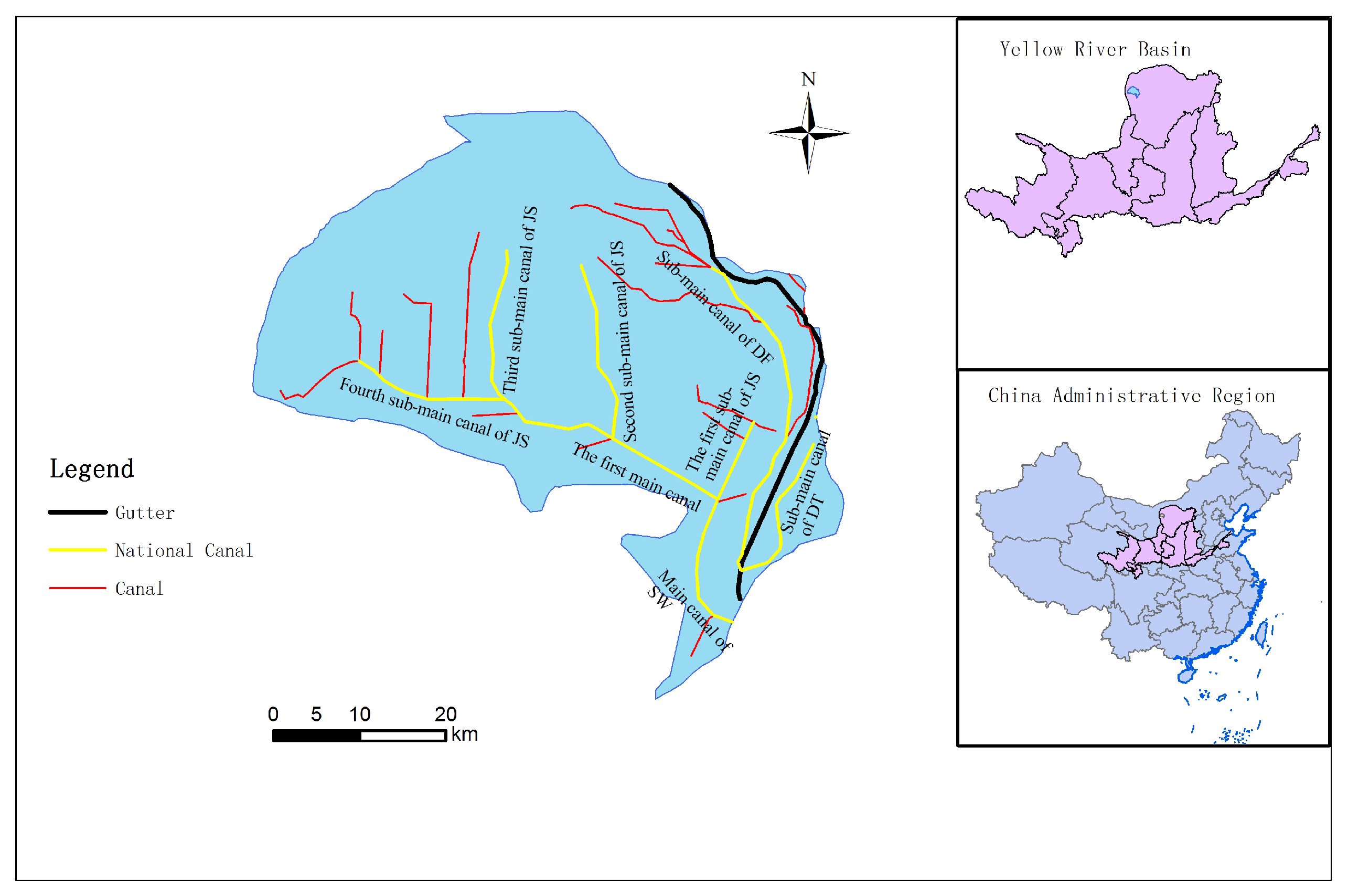
2.1. Overview of the Study Area and Data Sources
2.1.1. Overview of the Study Area
2.1.2. The Data Source
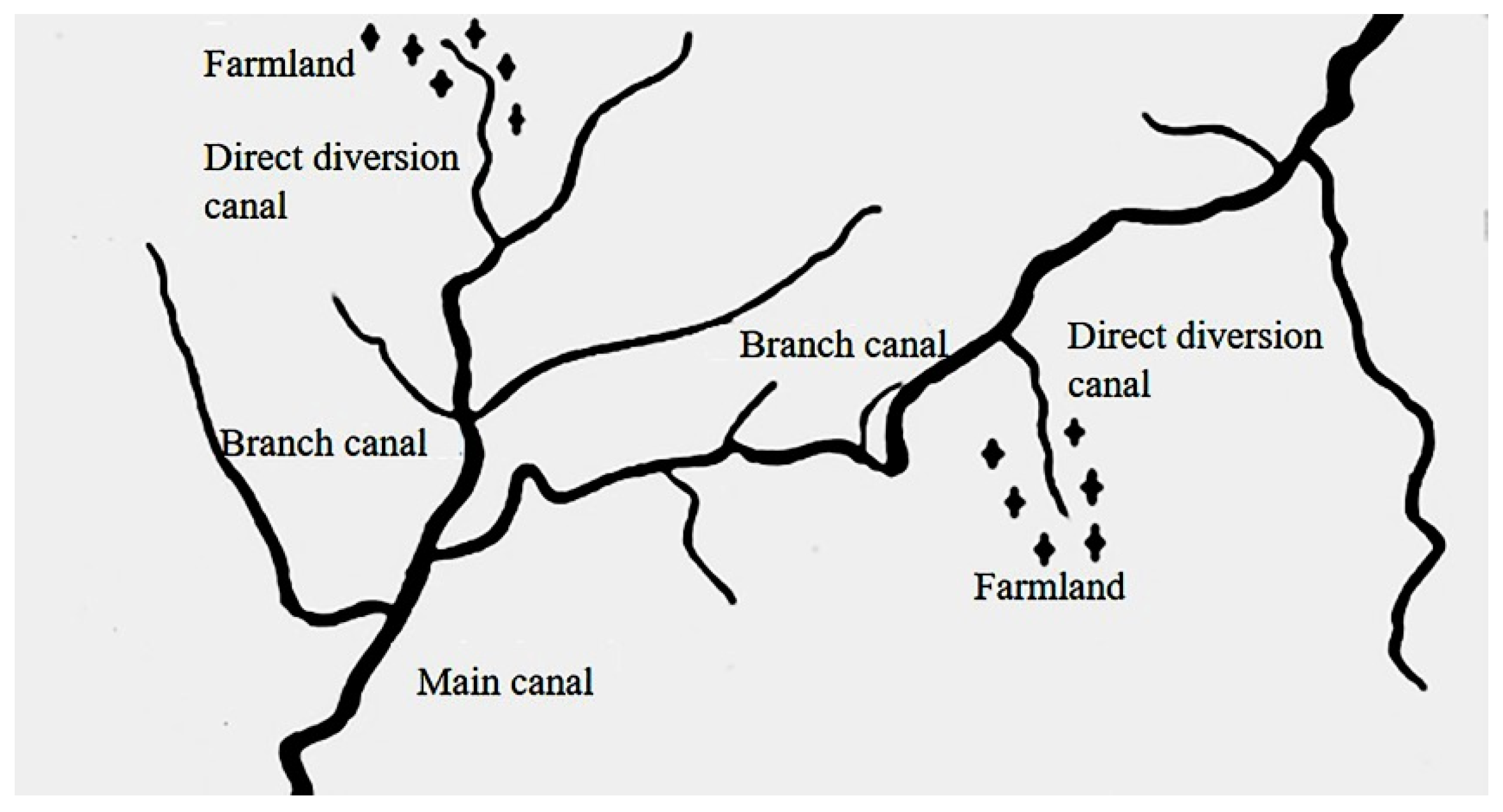
2.2. Double-Level Water Rights Allocation Model of the Irrigation District
2.2.1. Water Rights Allocation Model of National Canal System in Irrigation District
- (1)
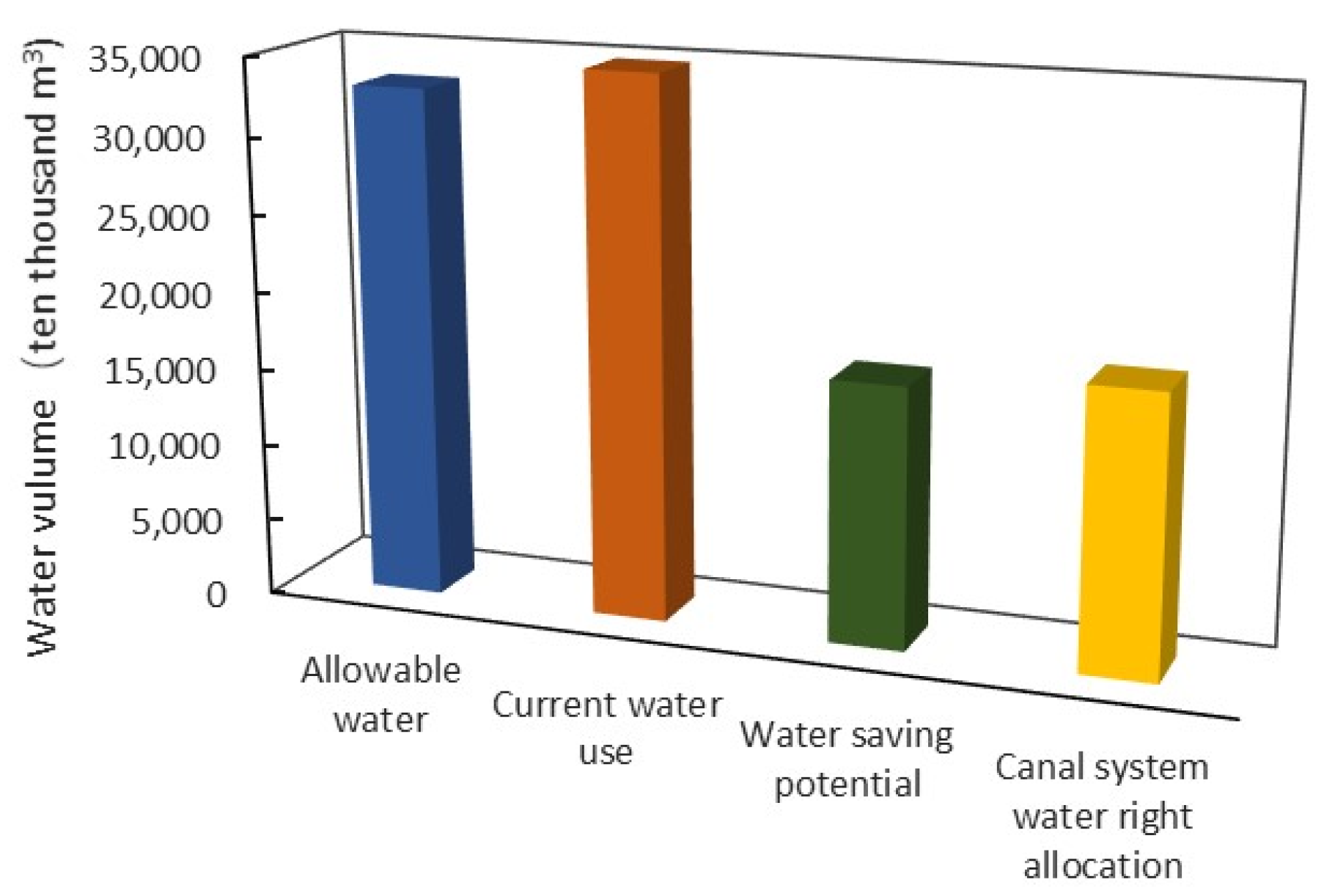
- Total amount of current water rights at the national canal system level. Generally, the total amount of canal system water rights is determined by the actual water diversion in the irrigation district and the average water consumption over the years.
- (2)
- Water-saving potential of the irrigation district. The main water-saving measures in the irrigation district are canal lining, border field reconstruction, and drip irrigation. The total water-saving amounts of water-saving projects in the irrigation district is the canal-level water-saving amount. The calculation formula is as follows:
- (3)
- Distribution of water rights of national canal system. By analyzing the total amount of current water rights of the canal system in the irrigation district and considering the potential water-saving amount of the canal system in the future, the canal-level water rights allocation model is determined. The calculation formula is as follows:
2.2.2. Water Rights Allocation Model among Farmer Households in Irrigation Districts
- (1)
- Select the indexes of water rights allocation among farmer households
- (2)
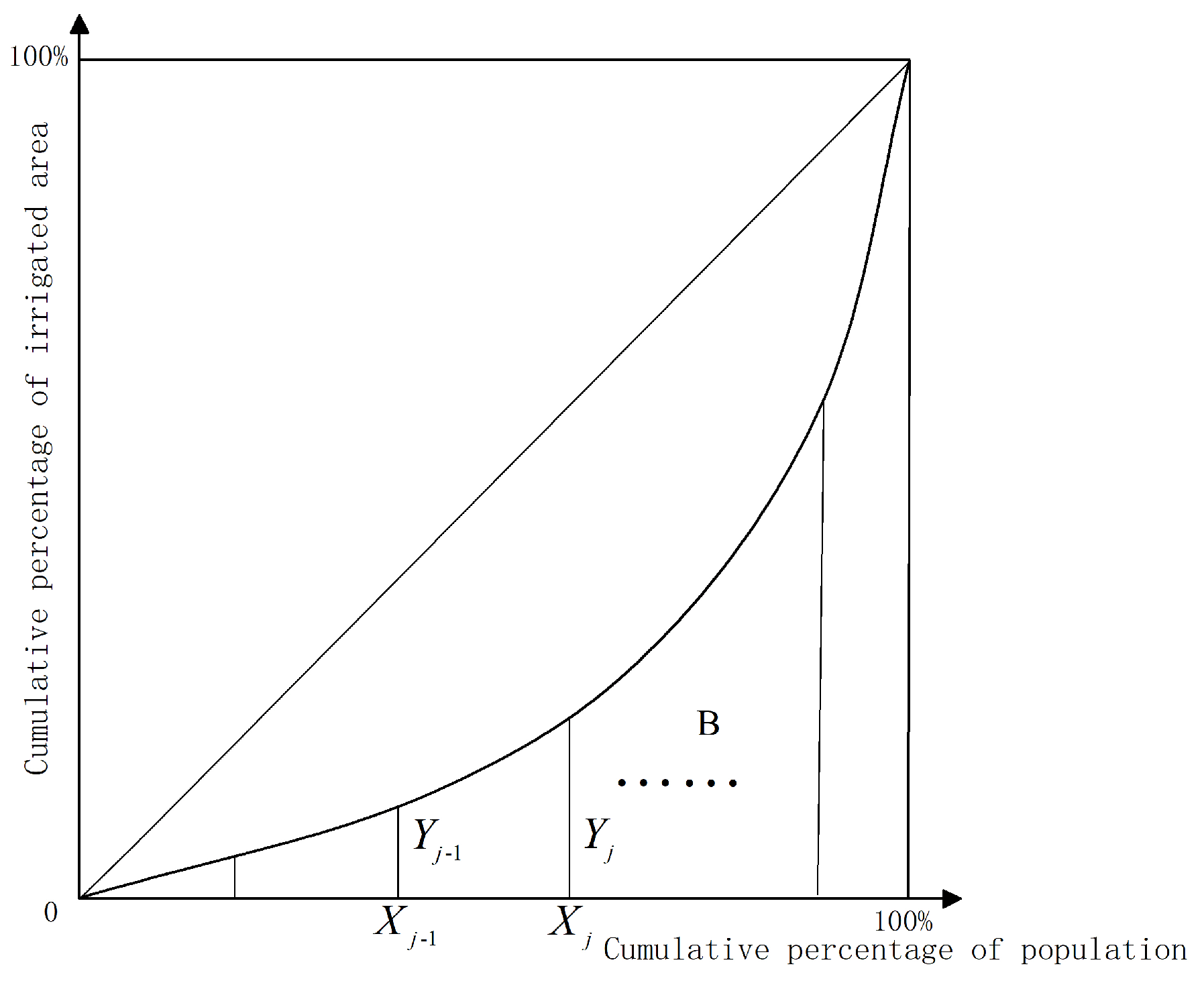
- Water rights allocation model among farmer households based on Gini coefficient method
3. Results
3.1. Distribution Results of Water Rights for the Canals Diverted Directly from the National Canal System
3.2. Results of the Water Rights Distribution among Farmer Households
4. Discussion
4.1. Analysis of Water Rights Distribution for the Canals Diverted Directly from the National Canal System
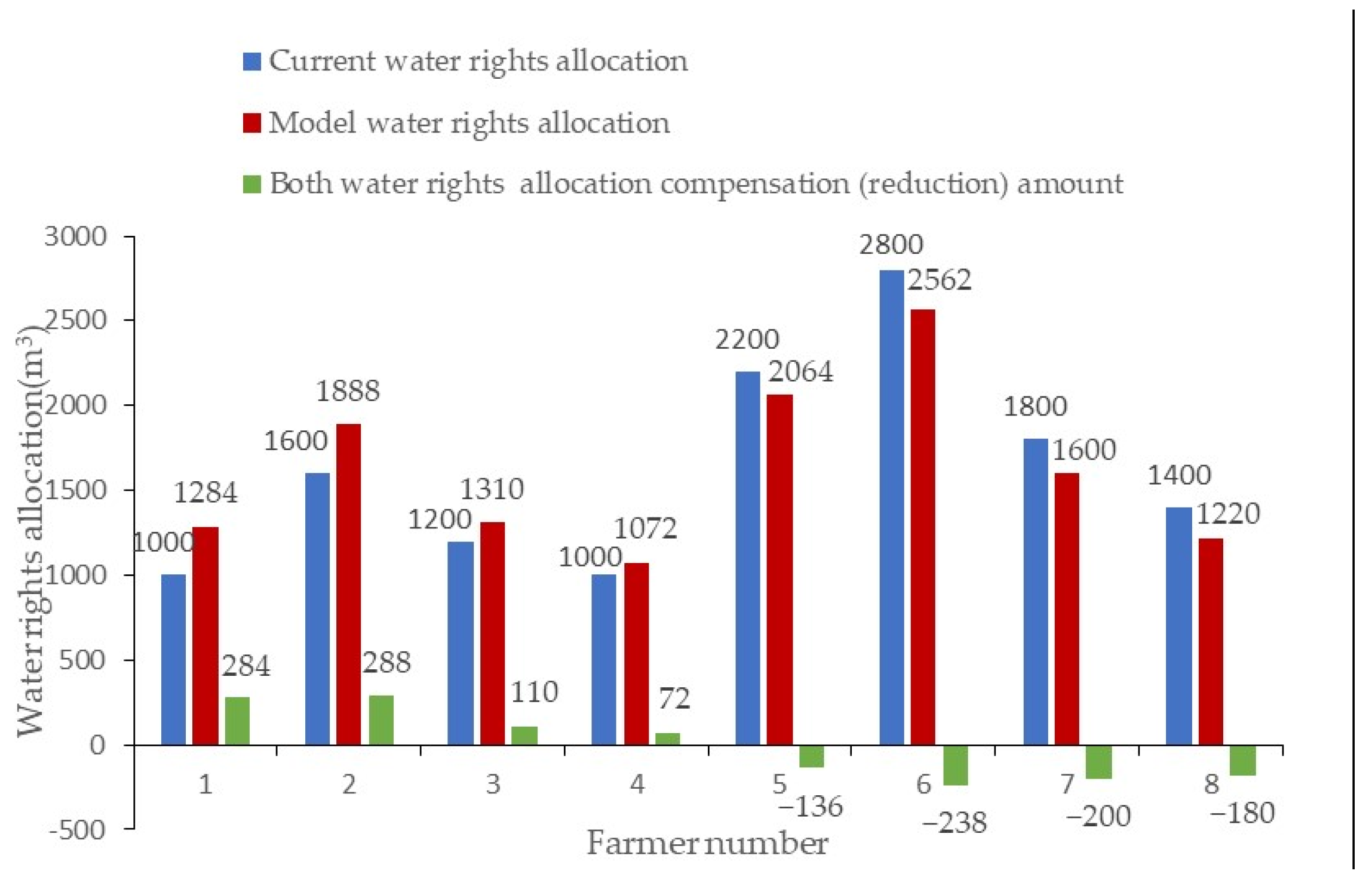
4.2. Performance Test of Water Rights Allocation Model among Farmer Households
4.3. Overall Analysis of Water Rights Distribution in the Irrigation District
5. Conclusions
- (1)
- Combined with the future water-saving potential of the canal system control area in the irrigation area, the canal system level water rights distribution model is established. Considering the factors of farmers’ agricultural population and irrigation area, the water rights distribution model at the farmers’ level based on the Gini coefficient method is established, which compensates the water users whose per capita irrigation area is less than that of the canal system, and fully reflects the fairness and enriches the existing theoretical system of initial water rights allocation.
- (2)
- The government should strengthen the investment in water-saving projects, promote efficient irrigation technology, and fully tap the water-saving potential. Farmers should pay attention to the implementation of field water-saving measures, adjust the planting structure, and actively respond to the government’s call to improve their self-awareness of water-saving. Realizing the economical utilization and sustainable development of water resources can provide a guarantee for the high-quality development of the Yellow River Basin.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Satoh, Y.; Fischer, G.; Burek, P. Development of future water use scenarios: Water Futures and Solutions (WFaS) initiative’s approaches. Jpn. Geosci. Union Meet. 2016, 1, 2–6. [Google Scholar]
- Zheng, H.; Wang, Z.J.; Hu, S.Y.; Wei, Y.P. A Comparative Study of the Performance of Public Water Rights Allocation in China. Water Resour. Manag. 2012, 26, 1107–1123. [Google Scholar] [CrossRef]
- Guo, P. The initial allocation system of water rights in China. Heihe J. 2009, 4, 88–90. [Google Scholar]
- Wu, D.; Wang, Y.H. Modeling for multi-layer hierarchical decision-making of initial water rights allocation in the river basin with water resources dual control action. China Popul. Resour. Environ. 2017, 27, 215–224. [Google Scholar]
- Wang, Z.J.; Zheng, H.; Wang, X.F. A Harmonious Water Rights Allocation Model for Shiyang River Basin, Gansu Province, China. Water Resour. Dev. 2002, 25, 355–371. [Google Scholar]
- John, F.; John, Q. Water Rights for Variable Supplies: Working Paper of Murray Darling Program; The University of Queensland: Brisbane, Australia, 2005. [Google Scholar]
- Coboum, K.M.; Ji, X.; Mooney, S. Water right seniority, economic efficiency and land allocation decisions. Agric. Appl. Econ. Assoc. 2017. [Google Scholar] [CrossRef]
- Veldwisch, G.J.; Beekman, W.; Bolding, A. Smallholder Irrigators, Water Rights and Investments in Agriculture: Three Cases from Rural Mozambique. Water Altern. 2013, 6, 125–141. [Google Scholar]
- Kreutzwiser, R.D.; de Loë, R.C.; Durley, J.; Priddle, C. Water Allocation and the Permit to Take Water Program in Ontario: Challenges and Opportunities. Can. Water Resour. J. 2004, 29, 135–146. [Google Scholar] [CrossRef][Green Version]
- Zhang, L.N.; Zhang, X.L.; Wu, F.P. Basin Initial Water Rights Allocation under Multiple Uncertainties: A Trade-off Analysis. Water Resour. Manag. 2020, 34, 955–988. [Google Scholar] [CrossRef]
- Sahebzadeh, A.; Kerachian, R.; Mohabbat, H.; Ashrafi, S. Developing a framework for water right allocation in inter-basin water transfer systems under uncertainty: The Solakan—Rafsanjan water transfer experience. Water Supply 2020, 20, 2658–2681. [Google Scholar] [CrossRef]
- Ramesh, D.; Robert, A.; Lin, X.M.; Shannon, K.; Paul, D. Restricted water allocations: Landscape-scale energy balance simulations and adjustments in agricultural water applications. Agric. Water Manag. 2020, 227, 105854. [Google Scholar] [CrossRef]
- Imron, F. Optimization of irrigation water allocation by using linear programming: Case study on Belitang irrigation system. IOP Conf. Ser. Earth Environ. Sci. 2021, 653, 12–23. [Google Scholar] [CrossRef]
- Chakraei, I.; Safavi, H.R.; Dandy, G.C.; Golmohammadi, M.H. Integrated Simulation-Optimization Framework for Water Allocation Based on Sustainability of Surface Water and Groundwater Resources. J. Water Resour. Plan. Manag. 2021, 147, 05021001. [Google Scholar] [CrossRef]
- Gebre, S.L.; Cattrysse, D.; Van, O. Multi-Criteria Decision-Making Methods to Address Water Allocation Problems: A Systematic Review. Water 2021, 13, 125. [Google Scholar] [CrossRef]
- Asimamaw, N.A.; Wondimagegn, Z.G. Assessment of hydrology and optimal water allocation under changing climate conditions: The case of Megech river sub basin reservoir, Upper Blue Nile Basin, Ethiopia. Modeling Earth Syst. Environ. 2020, 7, 2629–2642. [Google Scholar] [CrossRef]
- Mehdi, K.; Omid, B.H.; Elahe, F.M.; Hugo, A. Inter-basin hydropolitics for optimal water resources allocation. Environ. Monit. Assess. 2020, 192, 478. [Google Scholar] [CrossRef]
- Sri Legowo, W.D. A Mathematical Model on Water Resources Management Based on Regional Planning and Autonomous Region Planning (Case Study on Cimanuk River Basin-West Java). Civ. Eng. Dimens. 2007, 9, 90–97. [Google Scholar]
- Rao, K.; Dong, B.; Long, Z.X.; Huang, K.; Wu, W.X.; Zhang, T.Q. Application and comparison of fuzzy optimization and improved catastrophe model in water rights distribution of typical county. Water Sav. Irrig. 2019, 12, 95–101. [Google Scholar]
- Wu, D.; Wu, F.P. Industry-oriented initial water rights allocation system optimization. Adv. Sci. Technol. Water Resour. 2012, 32, 39–44. [Google Scholar] [CrossRef]
- Barrett, C.R.; Salles, M. On a Generalization of the Gini Coefficient. Math. Soc. Sci. 1995, 30, 235–244. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, Z.L. Initial allocation of agricultural water rights in water-deficient areas under the background of land circulation—Analysis of chaotic particle swarm optimization model based on projection pursuit. Chin. J. Agric. Resour. Reg. Plan. 2017, 38, 168–174. [Google Scholar]
- Rijswick, M.V. Mechanisms for water allocation and water rights in Europe and the Netherlands: Lessons from a general public law perspective. J. Water Law 2015, 24, 141–149. [Google Scholar]
- Shapiro, W.J. Fifth Amendment taking claims arising from restriction on the use and diversion of surface water. Vt. Law Rev. 2015, 39, 753–779. [Google Scholar]
| Gini Coefficient | <0.2 | 0.2~0.3 | 0.3~0.4 | 0.4~0.5 | >0.5 |
|---|---|---|---|---|---|
| Evaluation results | Absolute average | Comparative average | Relatively reasonable | Big gap | Wide disparity |
| Direct Diversion Canal Name | Township (Farm) | Five-Year Average Water Volume | Water Saving | Water Rights Allocation | ||
|---|---|---|---|---|---|---|
| Water Saving in Canal Lining | Water Saving in Border Field Reconstruction | Water Saving in Drip Irrigation | ||||
| Grazing team (4) | Bayangaole Town | 20.3 | 0 | 7.3 | 0 | 13.0 |
| Bayi canal | Wulanbuhe Farm | 1981.5 | 0 | 421.6 | 0 | 1559.8 |
| The fourth lateral canal | Hatengtaohai Farm | 843.5 | 229.6 | 151.4 | 0 | 462.5 |
| New third canal | Bayantauhai Farm | 169.5 | 61.0 | 80.8 | 0 | 27.6 |
| First canal of four groups | Sun Temple Farm | 336.7 | 0 | 264.4 | 0 | 72.3 |
| Susan canal 1 | Shajin Sumu | 137.4 | 0 | 61.7 | 0 | 75.7 |
| Two rounds of water 1 | Experiment Bureau | 354.2 | 0 | 122.4 | 0 | 231.8 |
| Western third lateral canal | Narintaohai Farm | 672.8 | 0 | 260.3 | 0 | 512.5 |
| The fourth brunch canal | Baoergai Farm | 5633.0 | 1463.2 | 0 | 2009.6 | 2160.2 |
| Zhao Duozhi | Bayin Maodao Gacha | 126.6 | 88.2 | 15.7 | 0 | 22.7 |
| Loess file one | Bulongnao Town | 213.9 | 0 | 0 | 36.8 | 177.1 |
| Tuanjie branch canal | San Tuan Farm | 3049.8 | 808.3 | 0 | 328.8 | 1912.7 |
| First lateral canal | Longsheng Hezhen | 365.1 | 0 | 70.0 | 0 | 295.1 |
| Farmer Household Number | Irrigation Area (hm2) | Agricultural Population | Current per Capita Irrigation Area (hm2/Person) | (Xj – Xj −1) * (Yj + Yj −1) |
|---|---|---|---|---|
| 1 | 0.333 | 6 | 0.056 | 0.0107 |
| 2 | 0.533 | 8 | 0.067 | 0.0515 |
| 3 | 0.400 | 5 | 0.080 | 0.0572 |
| 4 | 0.333 | 4 | 0.083 | 0.0615 |
| 5 | 0.733 | 6 | 0.122 | 0.1267 |
| 6 | 0.933 | 7 | 0.133 | 0.2104 |
| 7 | 0.600 | 4 | 0.150 | 0.1531 |
| 8 | 0.467 | 3 | 0.156 | 0.1320 |
| total | 4.333 | 43 | 0.8032 |
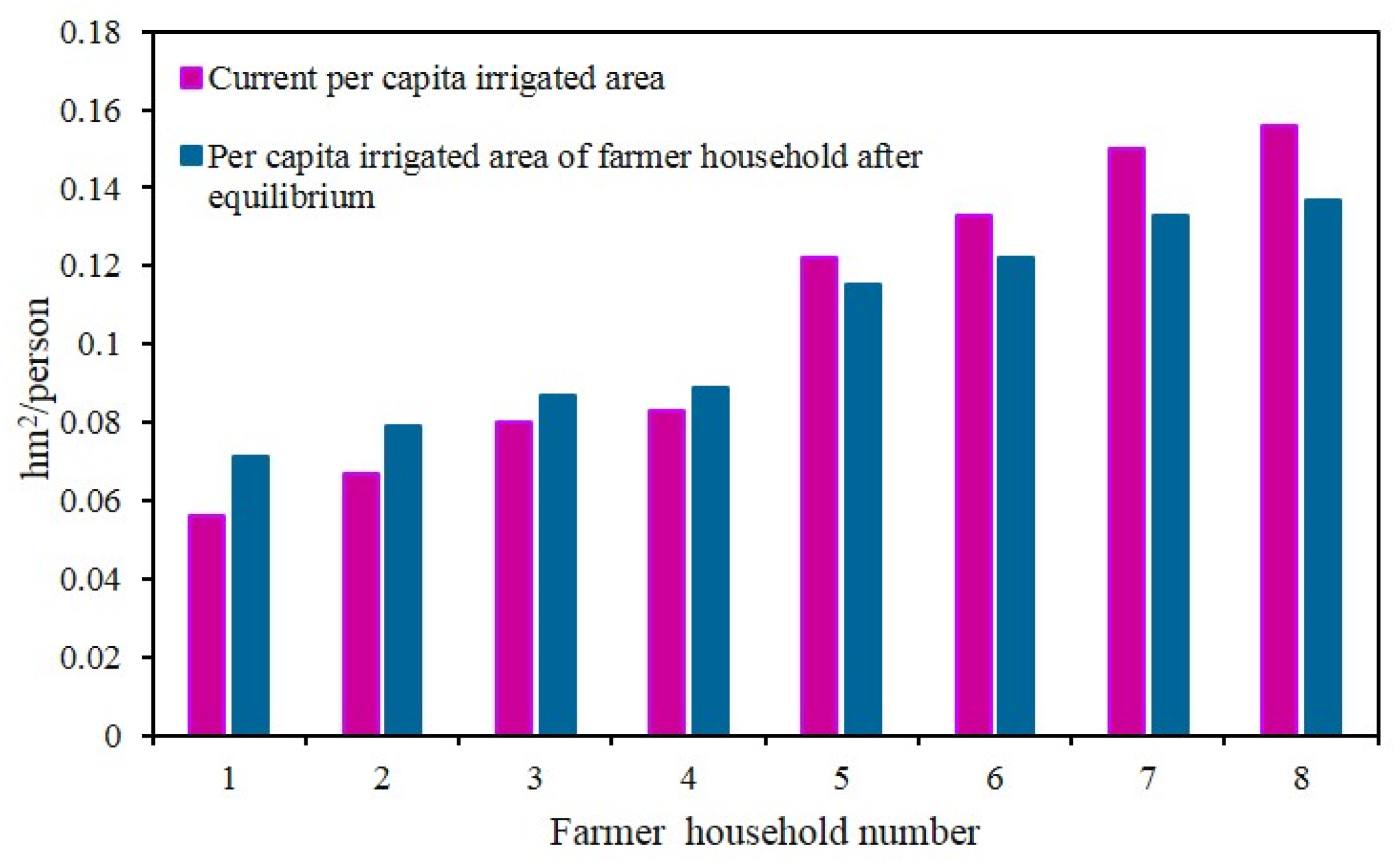
| Farmer Household Number | Area (hm2) | Agricultural Population | Per Capita Irrigation Area of Farmer Household (hm2/Person) | Per Capita Irrigation Area of Farmer Household after Equilibrium (hm2/Person) |
|---|---|---|---|---|
| 1 | 0.333 | 6 | 0.056 | 0.071 |
| 2 | 0.533 | 8 | 0.067 | 0.079 |
| 3 | 0.400 | 5 | 0.080 | 0.087 |
| 4 | 0.333 | 4 | 0.083 | 0.089 |
| 5 | 0.733 | 6 | 0.122 | 0.115 |
| 6 | 0.933 | 7 | 0.133 | 0.122 |
| 7 | 0.600 | 4 | 0.150 | 0.133 |
| 8 | 0.467 | 3 | 0.156 | 0.137 |
| Total | 4.333 | 43 |
| Farmer Household | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Water rights allocated by the model | 1284 | 1888 | 1310 | 1072 | 2064 | 2562 | 1600 | 1220 |
| Current allocated water rights | 1000 | 1600 | 1200 | 1000 | 2200 | 2800 | 1800 | 1400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, X.; Wang, B.; Zhang, W.; Du, Q. Study on Water Rights Allocation of Irrigation Water Users in Irrigation Districts of the Yellow River Basin. Water 2021, 13, 3538. https://doi.org/10.3390/w13243538
Guan X, Wang B, Zhang W, Du Q. Study on Water Rights Allocation of Irrigation Water Users in Irrigation Districts of the Yellow River Basin. Water. 2021; 13(24):3538. https://doi.org/10.3390/w13243538
Chicago/Turabian StyleGuan, Xinjian, Baoyong Wang, Wenge Zhang, and Qiongying Du. 2021. "Study on Water Rights Allocation of Irrigation Water Users in Irrigation Districts of the Yellow River Basin" Water 13, no. 24: 3538. https://doi.org/10.3390/w13243538
APA StyleGuan, X., Wang, B., Zhang, W., & Du, Q. (2021). Study on Water Rights Allocation of Irrigation Water Users in Irrigation Districts of the Yellow River Basin. Water, 13(24), 3538. https://doi.org/10.3390/w13243538





