Next Article in Journal
Comparison of the Applicability of Different Soil Erosion Models to Predict Soil Erodibility Factor and Event Soil Losses on Loess Slopes in Hungary
Next Article in Special Issue
River Stage Modeling with a Deep Neural Network Using Long-Term Rainfall Time Series as Input Data: Application to the Shimanto-River Watershed
Previous Article in Journal
Treatment of Textile Wastewater Using Advanced Oxidation Processes—A Critical Review
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 13
Issue 24
10.3390/w13243516
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Hydraulic Numerical Simulations of La Sabana River Floodplain, Mexico, as a Tool for a Flood Terrain Response Analysis

by
Rosanna Bonasia
1,* and
Mackendy Ceragene
2
1
CONACYT—Instituto Politécnico Nacional, ESIA, UZ, Miguel Bernard, S/N, Edificio de Posgrado, Mexico City 07738, Mexico
2
Instituto Politécnico Nacional, ESIA, UZ, Miguel Bernard, S/N, Edificio de Posgrado, Mexico City 07738, Mexico
*
Author to whom correspondence should be addressed.
Water 2021, 13(24), 3516; https://doi.org/10.3390/w13243516
Submission received: 10 November 2021 / Revised: 6 December 2021 / Accepted: 6 December 2021 / Published: 9 December 2021
(This article belongs to the Special Issue Application of Numerical Models and Data-Driven Intelligent Systems in Flood Forecasting)
Browse Figures
Versions Notes

Abstract

:
The floodplain of La Sabana River, Guerrero State, Mexico, was subject to disastrous floods due to the passage of extreme weather phenomena. This is a situation facing many ungauged rivers in Mexico, as well as in other developing countries, where increased urbanization and a lack of monitoring systems make many inhabited areas more vulnerable to flooding. The purpose of this work is to provide a tool for determining the flood terrain response to flooding based on a hydraulic study. This methodology combines a hydrological analysis of the river basin with the floodplain hydraulic study for the precise identification of overflow points and the resulting flood levels. Results show that, for an ungauged river, hydraulic analysis is an essential tool for determining the main potential flood points and establishing whether the river has the capacity to contain floods. Specifically, it is shown that La Sabana River is predisposed to overflow long before the river reaches its maximum flow, even in correspondence with more frequent flood scenarios. This study shows a further application that a hydraulic model can have to improve flood risk preparedness for ungauged rivers of regions where other types of monitoring tools cannot be used.

1. Introduction

The sub-basin of La Sabana River, located in Guerrero, a state in southern Mexico, occupies an inhabited area characterized by strong economic and social contrasts. The floodplain of this river has been almost completely covered by urban settlements of a medium–low socio-economic level in the northernmost regions, and of a higher level approaching the beach, where Acapulco, the famous tourist Mexican destination, is located. The population increase in the last 20 years has determined the uncontrolled growth of settlements that stick to the riverbed, which has led to an increase in vulnerability of this area [1]. Linked to this increase in urbanization is the fact that the Mexican territory loses hundreds of hectares of forest and jungle every year due to an intense deforestation [2,3]. In particular, from 1970 to 2010 the state of Guerrero lost 110 km2 of natural vegetation to produce building land, and it is estimated that the deforestation of the mountainous region of the state has doubled the susceptibility to flooding of the alluvial plains with particular consequences precisely on the Acapulco area [1]. This, along with other problems such as the increase in non-formal economic activities and hydro-meteorological effects caused by climate change, has caused an increase in the susceptibility of the area to flood events, especially in correspondence with the occurrence of extreme weather phenomena.
As a matter of fact, due to its particular geographical location in the Pacific Ocean, the coast of the Guerrero state has been subject, over the years, to the impact of several hurricanes, some of which formed in front of the coast and others that landed at the port of Acapulco [4]. In particular, for the period between 1970 and 2011, this state has suffered the direct impact of at least 24 tropical cyclones, highlighting the years 1974 and 1996 when three cyclones occurred in each season [5]. During the 2015 hurricane season, there were 18 hurricanes in the Pacific Ocean, some of which had a direct impact on the coast of Guerrero [6]. Among the events that occurred in the mentioned periods, the cases of hurricanes Pauline and Manuel are sadly well known. The first one occurred in October 1997. The global analysis of rainfall during this event indicates that in the La Sabana River Basin a maximum precipitation of 297 mm was recorded during a single day, equivalent to 1.9 times the average precipitation of the month of October [7]. This was an event that caused a high environmental, economic and social impact, due to violent floods, water erosion and high mass transport of sediments, which resulted in the loss of human life, as well as an economic loss of the order of $447.8 million of dollars [7].
In September 2013, two simultaneous hurricanes affected Mexico: Manuel on the Pacific Ocean side and Ingrid on the Gulf of Mexico. This meteorological phenomenon produced torrential rains over a large part of the country that led to the overflow of various rivers. According to information from the World Meteorological Organization [8], the antecedent of the presence of two tropical cyclones affecting both coasts of the country was in 1958, when Hurricane Alma, through the Gulf of Mexico, and Tropical Storm Number 2 in the Pacific ocean, struck at the same time in mid-June.
During the passage of Hurricane Manuel, the coast of Guerrero registered a considerable flood in various urban settlements and hotels located in the Acapulco tourist area. The accumulated rain sheet from 12 September to 17 September was 619.33 mm. The heavy rains forced the overflowing of La Sabana river towards the settlements located on the right bank, 6 km from the river mouth in the Tres Palos lagoon. The overflow verified after the first heavy rains, which suggests that the channel does not have sufficient hydraulic capacity to carry a volume like the one that accumulated during this hurricane [9]. The two cited extreme events caused enormous damage to the entire floodplain, affecting both urban settlements in the northern portion and tourist areas towards the coast.
Extreme weather phenomena capable of producing heavy rainfall are far from being unlikely or infrequent at present. Emanuel [10] finds an increase in the global average frequency of tropical cyclones in the range of 10–40% during the first three quarters of the 21st century. Along with the frequency, the average intensity of tropical cyclones is also increasing by ~15% [11]. Shamir et al. [12], in their review of current knowledge on climate change trends of precipitation, found that heavy rainfall events are expected to intensify as well as the frequency and intensity of large eastern pacific tropical cyclones. The increase of the storm and precipitation intensity are connected with an increase in the heat content of the oceans [13], so the combination of warmer air and cold water can lead to an increase in rainfall [14]. All these considerations are also in agreement with Knutson et al. [15], who find, through the global simulation of a tropical cyclone using a High-Resolution Atmospheric Model, that while the global number of tropical cyclones tends to decrease in the warmer climate of the late 21st century, their intensity increases as does the precipitation rate.
On the basis of these evidences, it is therefore clear that there is a need to develop and apply methodologies that make it possible to identify and propose possible solutions capable of minimizing the risk of flooding in areas like La Sabana River floodplain, which are highly exposed to extreme weather phenomena, and lack both meteorological and maximum flood level monitoring systems. Note that this need is even more significant in areas of developing countries, such as Mexico, susceptible to severe flooding, where there is a lack of an extensive know-how, resources are limited and the scarcity of data make the situation even more complicated. Moreover, in Mexico there is not a policy particularly dedicated to the prevention of damage caused by extreme weather phenomena and the decentralization policy of the organizations dedicated to people protection [16] makes the need to develop methodologies for the analysis of high-risk areas and for the determination of solutions aimed at the risk prevention and minimization more urgent. Areas at risk of flooding and without monitoring or extensive studies on the hydrological and hydraulic situation in Mexico are many, however, research focused at analyzing the individual and specific situations that cause flood risks is still few or fragmented. At the government level, the National Water Commission (CONAGUA), in 2014, established guidelines for the preparation of flood risk maps [17], which led to the creation of a national risk atlas, available online at the Water Information Systems Portal [18]. This portal provides hydro-meteorological information, vulnerability indices and flood susceptibility maps of some regions of the country. However, probabilistic studies aimed at characterizing the occurrence of the natural phenomenon, as well as at calculating the damage it can cause in the short and long range, are scarce, although this type of study is essential to provide the authorities with the necessary elements to define possible scenarios of risk and for adequate territorial planning. This derives from the hydrological complexity of the country, which makes an integral study of the whole territory very complex, but also from the lack, in many risk zones, of rivers monitoring.
Methodological approaches aimed to prevent damage caused by floods or to minimize them are varied: starting with the construction of hazard maps, which are a fundamental tool for prevention plans given their strong space-time component [19], then passing through the use of data driven models, which are useful for prediction purposes with the great advantage of requiring minimal inputs [20,21], arriving at hydrological, and hydrological and hydraulic combined models that allow, among other things, to determine rainfall thresholds and critical flood levels. Deriving rainfall thresholds is the most commonly used method for developing flash flood warning systems, because it provides information on the amount of rainfall that, for a given duration and a given basin, can cause a flood [22]. The methodologies developed in recent decades to calculate rainfall thresholds responsible for triggering floods are based on the use of distributed and semi-distributed hydrological models [23,24]. The combination of a hydrological study and a hydraulic model not only allows to accurately predict the design hydrographs of the basin but, very important, consent to simulate flooding in the alluvial plain in order to analyze the specific terrain response to flooding [25,26]. This combined methodological approach is particularly useful in the case of ungauged rivers where in-situ measurements of river critical levels as well as flood susceptibility maps are lacking.
The main objective of this study is therefore to demonstrate the usefulness of applying a hydrodynamic numerical model to characterize the terrain response to a river flood event in areas where there are no meteorological or flood levels monitoring systems. Hydraulic simulations can provide detailed information on the potential flood points of a river, even in correspondence with non-extreme weather events, and can also indicate which critical tie rods can lead to the flooding and the respective flood levels in the floodplain. The application of such methodology, in countries like Mexico where there is no free access or the availability of observations deriving, for example, from radar or meteorological satellites covering the whole territory, can certainly facilitate the characterization of flood zones, to improve the preparedness to flood scenarios. The application of a hydraulic model, therefore, can facilitate, both at the local and at the basin scale, the analysis of the area with respect to the risk of flooding, because it can identify the causes that can facilitate the runoff and the consequences that derive from it. This preliminary analysis of the territory can be carried out without the need for on-site inspections or without resorting to expensive on-site monitoring tools; a prospect that is advantageous in flood-prone areas of developing countries.The importance of demonstrating the reliability and practicality of the application of hydraulic models lies, finally, in the trend, for the future, to implement high-performance hydrodynamic models that predict full-scale river flood processes starting from the source, that is, using the rainfall data as input. In recent years, scientific advances in high-throughput computation, management and file format for data transfer have made the application of hydrodynamic numerical models more precise and widespread. Currently, there is a great variety of tools for simulating free-sheet water flows in two dimensions, among which the most consolidated are Mike-21 [27], and the various calculation modules of SMS which is equipped with 1D and 2D models for the calculation of flood levels, water quality and analysis of hydraulic structures [28,29]. Moreover, models that use finite volumes for solving the St. Venant equations in two dimensions [30] are, among others, the latest version of Mike-21 and the Iber software [31], which will be used for the hydraulic analysis of this work. The choice of this model is based on its extensive validation which has shown it to be adequate for solving various engineering problems and makes it particularly effective for the calculation of discontinuous flows and for areas with complex geometries.
Therefore, in this work a study of the alluvial plain of La Sabana River was carried out, applying a combined methodological approach (hydrological and hydraulic), with the aim of studying the terrain response of the floodplain in terms of flood levels and determining the main critical points of flooding and associate them with certain rainfall sheets and their duration. Specifically, the methodology of this work develops as follows: first of all, a hydrological study of La Sabana River basin was carried out, with the objective of calculating project hydrographs in correspondence with different return periods and different precipitation duration; these hydrographs were then be used as input for the hydraulic analysis of the study area using the Iber hydrodynamic model. Results not only provided the flood levels, but also allowed to identify the potential points of the river first flooding.
The reminder of this paper is organized as follows. Section 2 presents a description of the study area, the hydrological study applied for the estimation of flood discharges within La Sabana catchment, and the description of the methodology used for numerical simulations of different inundation scenarios. In this section, in order to validate the model in the study area, the numerical simulation of the hurricane Manuel hydrograph is also presented, and results of the calculated flood levels are compared with values measured on site. Results of this work are shown in Section 3, where inundation levels, first flood point and occurrence times in correspondence with two precipitation duration (10 and 30 min) and different return periods are described. Results discussion is presented in Section 4.

2. Materials and Methods

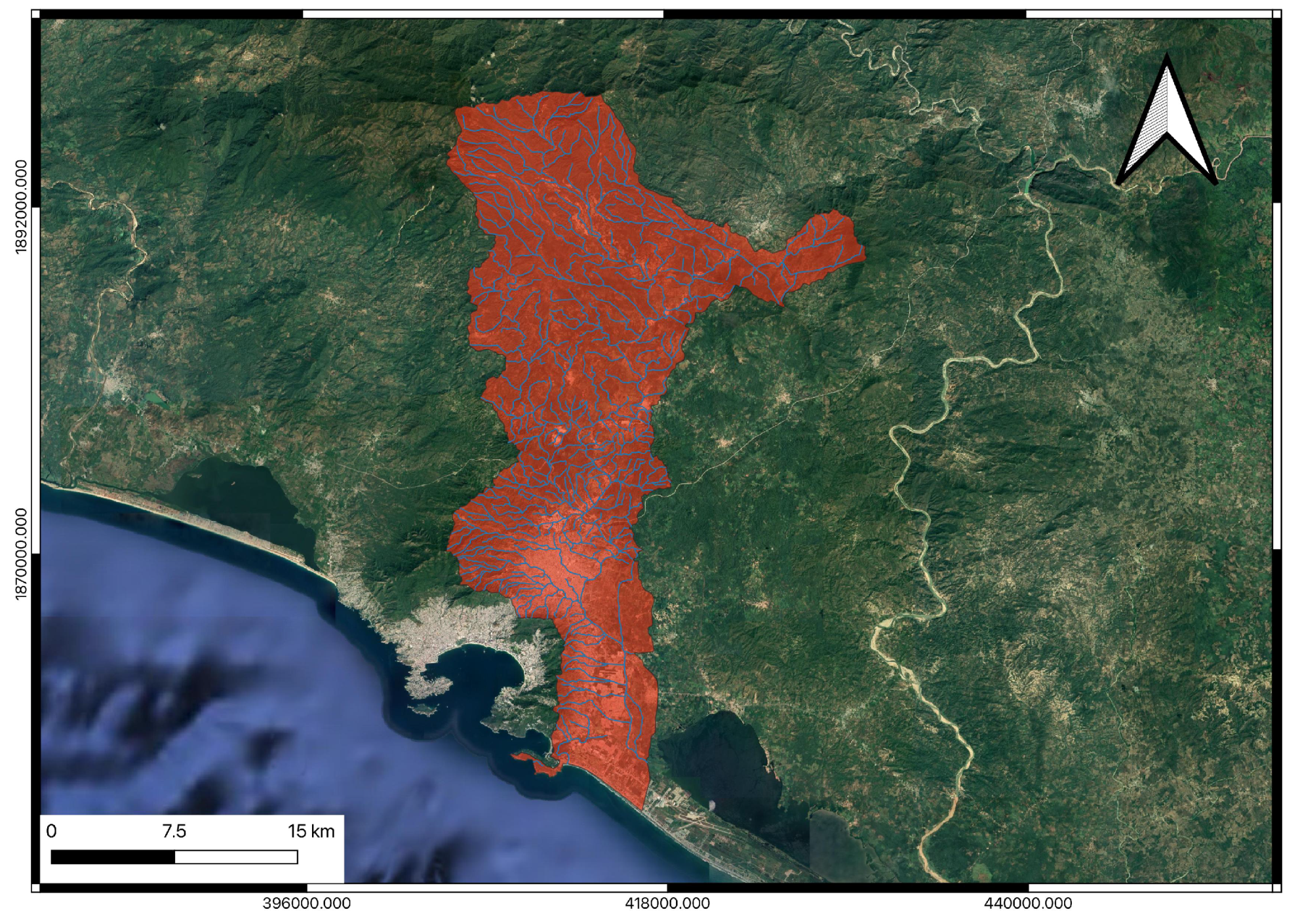
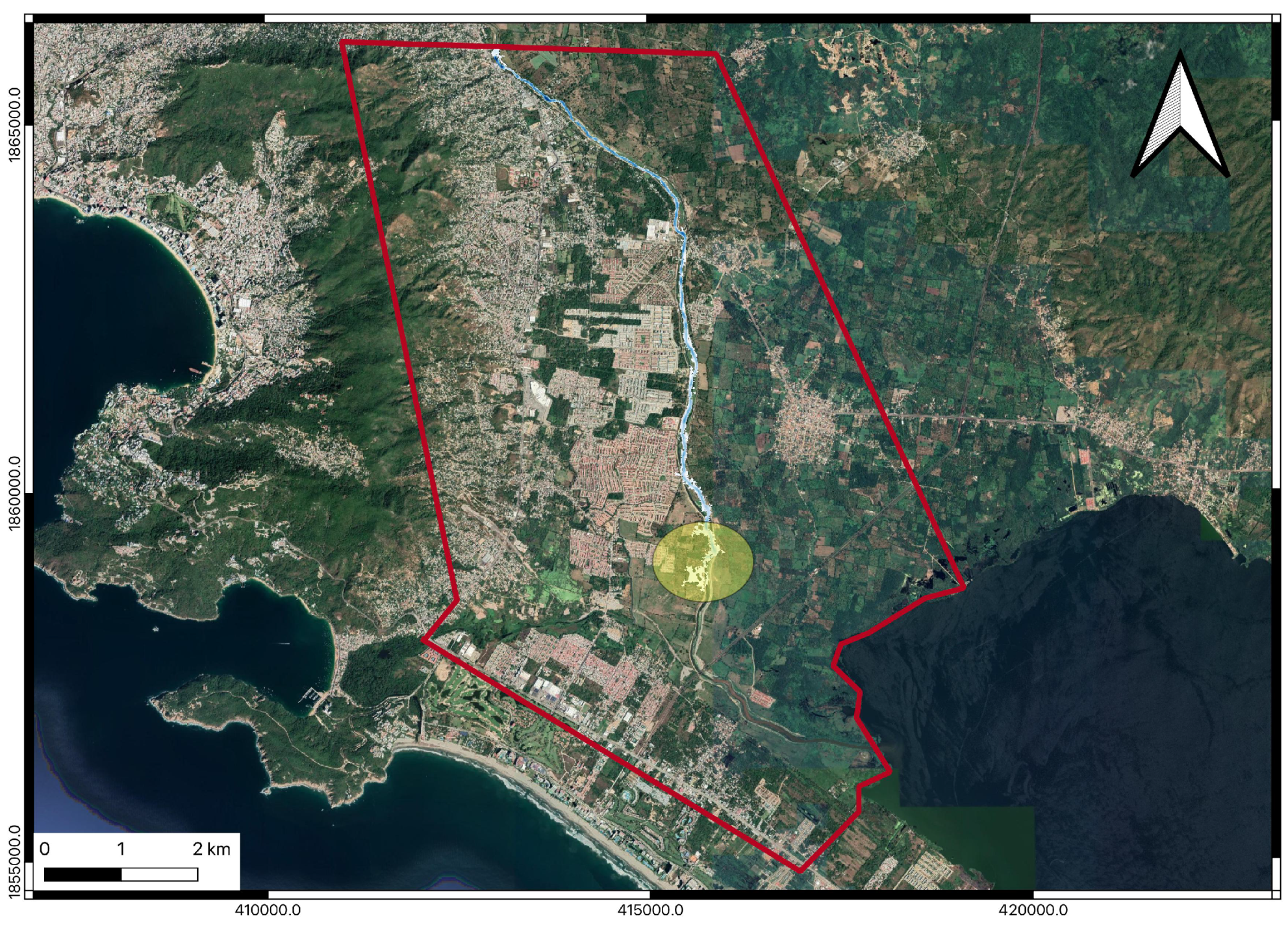
2.1. Study Area

La Sabana River is located in the hydrological region named “Costa Grande de Guerrero”. Its basin has an area of 762 km2 and a maximum elevation of 2250 m above sea level (Figure 1).
The channel has a length of of 72.72 km with an average slope of 2.1%. The floodplain of this river has a great socio-environmental peculiarity in the region. The increase in tourist activities and the urban transformation of the Acapulco city have impacted on the configuration of the sub-basin. Residential areas were built to shelter the inhabitants of the colonies located to the north of the city, which concentrated many migrants from different regions of the Guerrero state [32]. In fact, starting from the 1970s, when the first buildings were concentrated only in the area called “traditional Acapulco”, several urbanization plans led to the almost complete coverage of the flood plain. Figure 2 shows the urban distribution of the area under study. In the northern part of the flood plain, along the right edge of the river, there are urban settlements of a medium–low socio-economic level (e.g., “El Coloso” and “Llano Largo”), while, going down towards the coastal area, always on the right side of the river, there are higher-quality urban settlements (e.g., “La Marquesa” and “Las Gaviotas”), constructed very close to the edge of the river. Further south, separated by a river channel called “Canal Geo”, is the “Ciudad Luis Donaldo Colosio” urban unit, as well as a couple of shopping centers. These urban settlements are located in the areas of the alluvial plain that suffered the greatest floods during the 2013 event (Hurricane Manuel). The left bank of the river was left to be mainly used for agriculture. The southern part of the study area, close to the coast, is mostly destined for tourist, hotel and residential uses.
The prevailing climate within the study area is savanna, warm due to its temperature and sub-humid due to its precipitation. It ranges from warm sub-humid in the coastal plain to sub-humid semi-warm in the upper parts of the basin. This classification is based on the fact that the average annual temperature of the coldest month is greater than 18 °C, with rains in summer and a temperature oscillation of less than 5 °C, with June being the warmest month. The pluvial precipitation is more abundant in summer, extending until autumn (May–October) while the dry season occurs from November to May. The recorded precipitation values vary from 1017 to 1295 mm, with an annual average of 1035.5 mm [33]. The study area is located in a mangrove formation [34], however the land use that prevails throughout the La Sabana River region is urban settlement.

2.2. Estimation of Flood Discharges of La Sabana Catchment

The hydrological study of La Sabana River basin was carried out starting from the analysis of the meteorological stations that are located within a radius of 5 km in the study area and selecting the ones that have a minimum of 20 years of rainfall records. Based on these criteria, the operating climatological station number 12,183, “La Sabana”, was selected. Precipitation logs every 24 h were extracted from the Database of Surface Weather Stations of Mexico [35]. The maximum annual precipitation data were analyzed on the basis of independence and homogeneity tests and a frequency analysis was performed with a Gumbel-type distribution function. The analysis of Precipitation–Duration–Frequency was carried out using Chen’s method [36] to convert the maximum annual rainfall of 24 h into 60 min precipitations. Finally, applying the Bell’s method [37], precipitation was recalculated for short duration up to 240 min with time intervals of 5, 10, 15, 30, 60, 120 and 240 min for different return periods. River flood discharges were calculated in correspondence with the return periods of 10, 50, 100, 500 and 1000 years, using the Unit Hydrograph method of the Soil Conservation Service. To this end, peak flows related to each return period were calculated by means of the following formula:
Q p = 0.208 A P e t p ,
where A is the catchment area, t p the peak time and P e the effective precipitation. The effective precipitation was calculated as
P e = [ P − 508 n + 5.08 ] 2 P − 2032 n − 20.32 ,
being P the precipitation calculated as the intensity times duration ( P = I D ). The curve number n was calculated as a weighted average of the curve numbers associated with the soil types present in the basin (cambisol, phaeozem and regsol) and the slopes of the associated areas. The curve number used to calculate the excess precipitation is therefore n = 72.22 .
Catchment hydrological characteristics for flood discharges calculations, are shown in Table 1.
The excess precipitation and flood discharge values associated with each return period and calculated for a rain duration equal to 10 and 30 min, are shown in Table 2.
Hydrographs constructed for a precipitation lasting 10 min are shown in Figure 3, while Figure 4 shows hydrographs referring to a 30 min precipitation. These inflow scenarios will be used as inputs to simulate flood depths with the Iber hydrodynamic model.

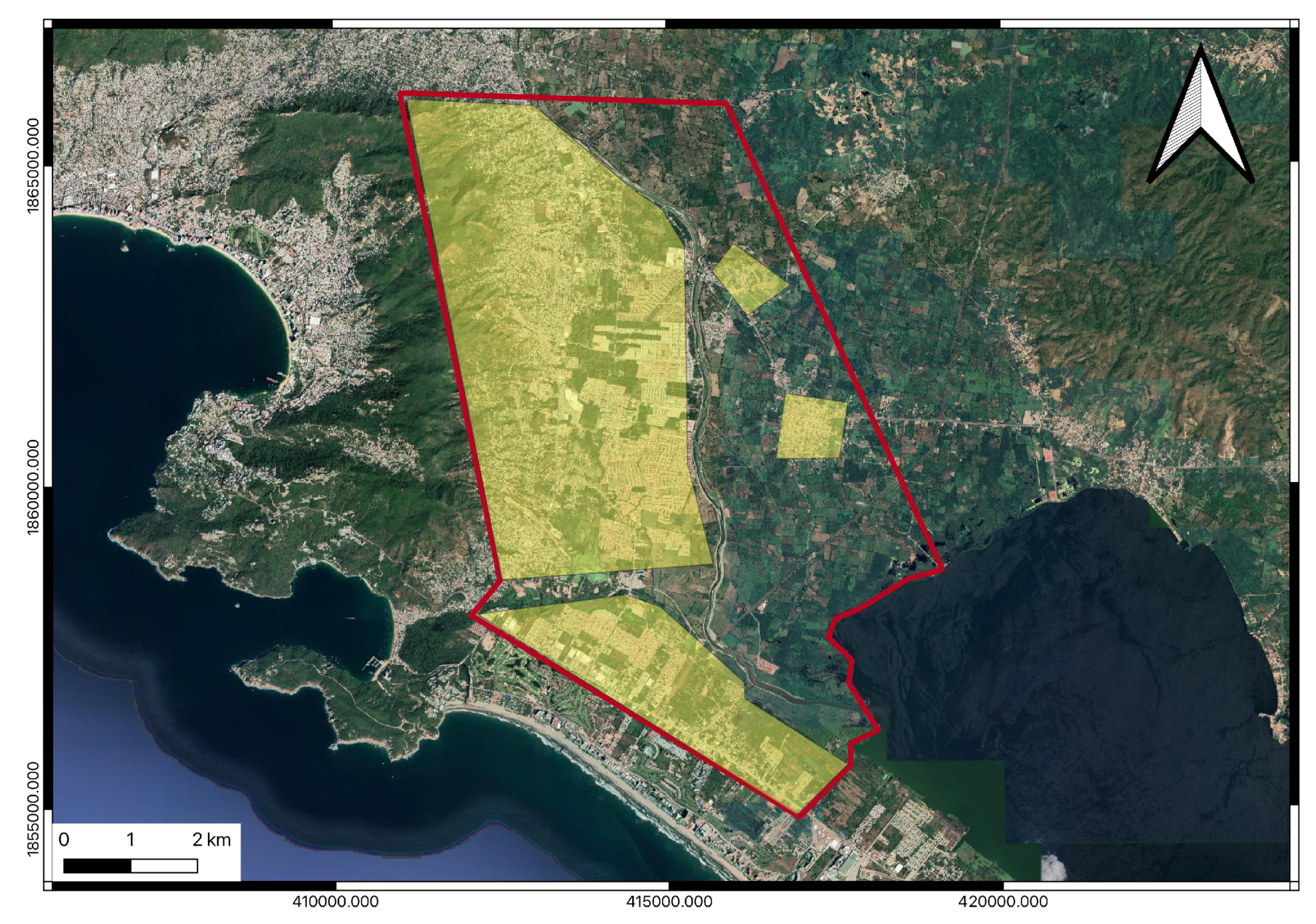
2.3. Numerical Simulations of Inundation Scenarios

Flood depths in La Sabana river floodplain were simulated in correspondence with different return periods and for precipitations lasting 10 and 30 min using the Iber software [31]. This model, that solves the shallow water equations in two dimensions on the basis of a finite volume numerical scheme, has been already extensively validated by the first author of this work in previous publications as well as in other previous studies applied to river floods and rainfall–runoff modeling [38,39,40]. However, to further validate the model in the study area of the present work, the precipitation produced during Hurricane Manuel was simulated using, as input, the hydrograph of the event reconstructed by Mejía [9]. From the project hydrograph shown on page 38 of the cited thesis, it can be observed that its peak was reached at 5.00 a.m. on 15 September 2013. For the hydrodynamic simulation of this event, the computational domain corresponds to the area enclosed by the red line shown in Figure 2. This area was defined considering the greatest effects in terms of damage to people and property caused by the hurricane in the river plain. The geometry of the study area was constructed using the digital surface-type elevation model with 5 m resolution derived from satellite remote sensor data provided by the National Institute of Statistics and Geography (available at https://www.inegi.org.mx/app/mapas/. Accessed on 2 September 2021). The area was subsequently discretized with an unstructured triangular mesh of 290,291 elements, in order to allow different levels of spatial resolution in the computation domain. This mesh was obtained by providing the following elements dimensions: 15 m for the river, 20 m for the rural area and 25 m for the urban area. The geometry has been assigned an initial condition of water depth equal to zero, since the river is dry for most of the year, the flow is intermittent so the water level can be considered minimum at the beginning of the precipitation event. Furthermore, three types of soil were considered: “river” for the canal, “urban vegetation” for the rural area and “residential” for the inhabited area. Geometry characteristics, initial condition and soil types, will also be maintained for flood scenarios determined by the hydrographs calculated in the previous section. The maximum simulation time for Hurricane Manuel is just over three days, 5 h after the maximum peak of the hydrograph had been reached and the river had flooded according to the observations. The result of this simulation, for maximum water depths, is shown in Figure 5.
From the figure, it can be seen that the water depths in the most affected area reach and in some cases exceed 5 m. This result is in agreement with the observations and measurements made by academic staff of the Institute of Engineering of the National Autonomous University of Mexico (IIUNAM), after the event, and described in [9]. In particular, the black line encloses the area of control points considered by the IIUNAM personnel in which water depth measurements were carried out after the event (see Figure 4.18, page 34 in [9]). In this area, flood levels measurements vary from 3.73 m to 5.43 m, values fairly coinciding with flood depths calculated with our simulation, which vary from 3.3 m to 6.6 m.
Once the model was validated in the study area, simulations of the project hydrogrphs calculated in the previous section were carried out for the considered return periods and in correspondence with two rainfall durations: 10 and 30 min. For these simulations the maximum simulation time was 9 h, about an hour and a half longer than the time required to reach the peak flow calculated in the hydrograph. This time allows the maximum flow to pass through the major risk zone during the entire simulation.

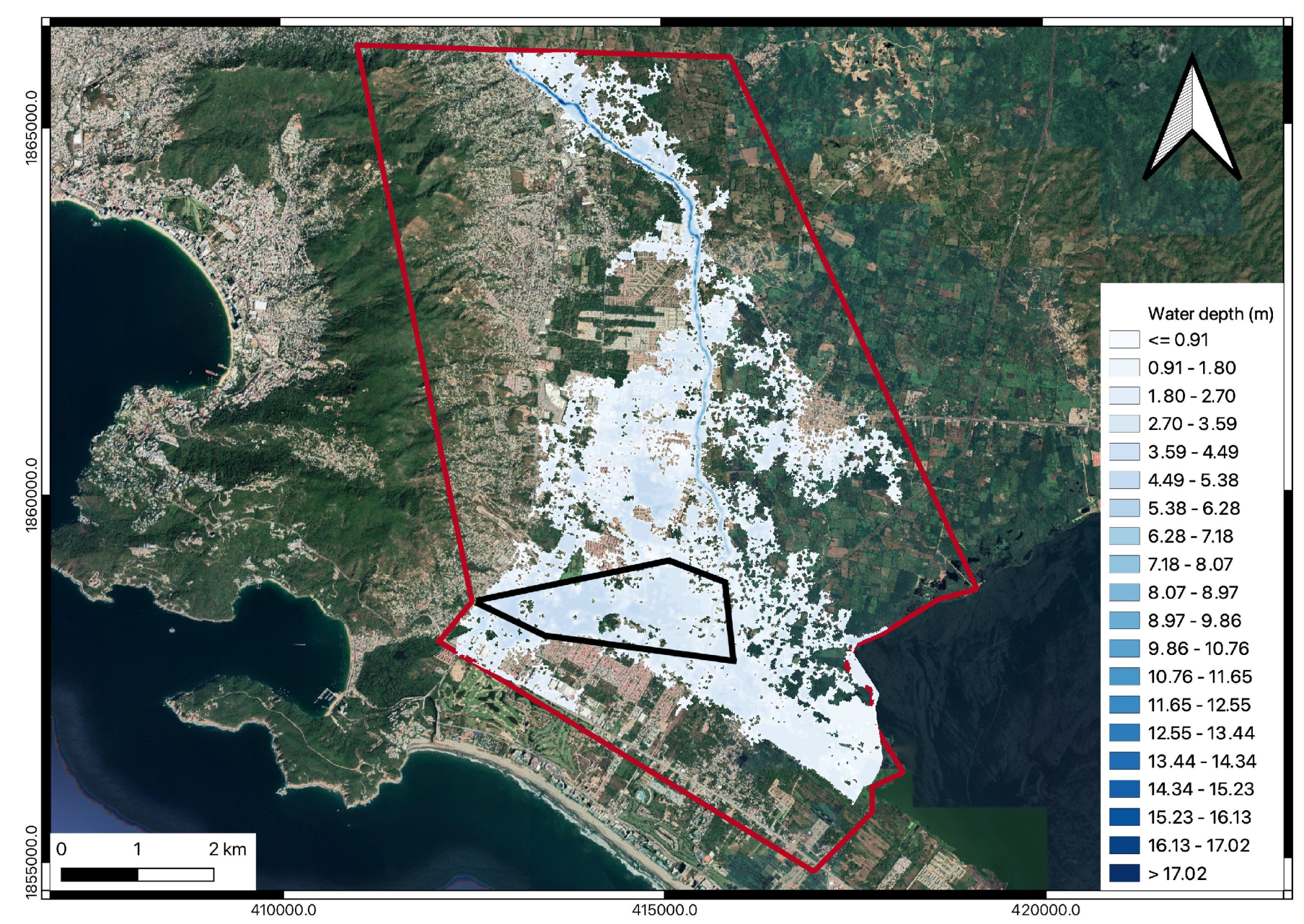
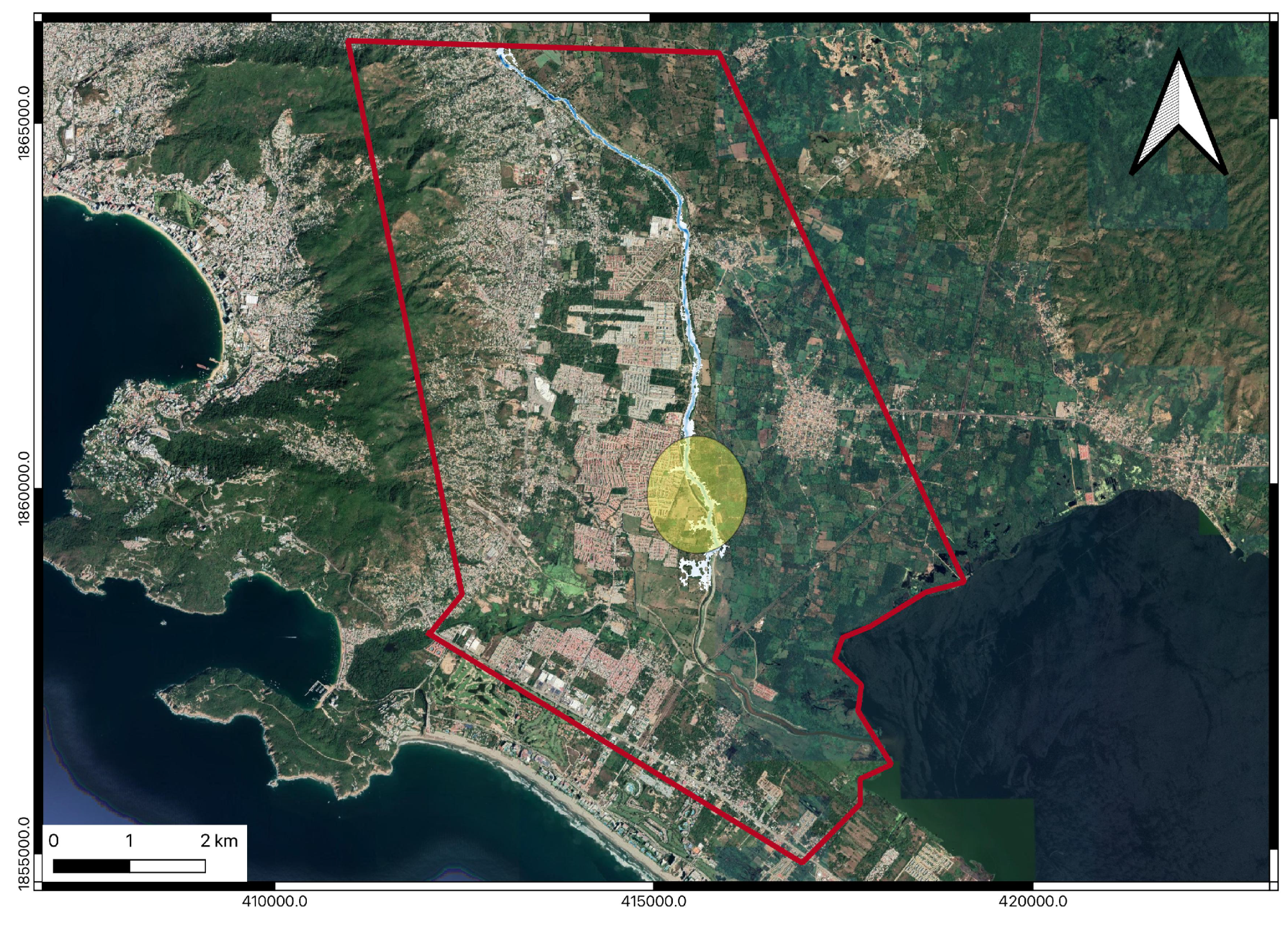
3. Results

Figure 6 shows the maximum flood levels calculated for a precipitation lasting 10 min, for the return periods 10 and 1000 years. Results obtained for the other return periods can be seen in the Appendix A. From a qualitative and general look at the two maps of Figure 6 it can be observed that for the lowest return period (10 years), the flooding is minimal, with depths mainly less than 50 cm. At the greatest return period (1000 years) the flooded area increases covering a predominantly rural zone, with flood levels ranging from 50 cm to more than 1 m.
As it would be expected, the situation changes if we look at the effects of a longer lasting precipitation (30 min). In Figure 7, it can be seen that, already in correspondence with the lowest return period (10 years), the flooded area is more extended, touching the inhabited areas in the southern part of the alluvial plain, with flood levels greater than 60 cm, while, still in the south, the rural area can be covered by flood levels that exceed 1 m in depth. Both the flooded area and the water depths increase in the highest return period (1000 years), with flood levels reaching 3 m in the inhabited area south of the river.
Simulations results also allowed the identification of the main potential river flood points and to obtain the time in which the first flood occurs based on the input hydrographs. Figure 8 is a snapshot of the moment when the first river flood occurs and refers to the simulation of a rain with a 10 min duration for the 10 years return period. The moment of the simulation corresponds to the time-step 28,800 s (8 h), shortly after the peak flow in the hydrograph has been reached.
The overflow point is located slightly south of the residential settlement “Las Gaviotas”, the area where the river first flooded during Hurricane Manuel. As the return period increases, the overflow time is anticipated, occurring up to 2 h before the maximum flow is reached in the corresponding hydrograph. By increasing the duration of precipitation (30 min), other two flood points can be identified (Figure 9), which correspond to the first area from which the river flooded during the hurricane of 2013.
With precipitation of longer duration, the overflow occurs about 2 h earlier than the time in which the peak flow is reached in the hydrograph, already with the lowest return period.

4. Discussion

Simulation results provided water depth values deriving from hydrographs constructed with two rainfall durations (10 and 30 min) and in correspondence with five return periods (10, 50, 100, 500 and 1000 years). The flood level maps shown in Figure 6 and Figure 7 and in Appendix A show that critical flood scenarios occur at high return periods, confirming the tendency of the area to suffer the effects of important floods only when extreme meteorological phenomena occur, which involve intense and long-lasting rainfall. During less frequent events (return periods from 100 years upwards), the urban settlements located in the southern part of the alluvial plain, in particular “Las Gaviotas” and “La Marquesa” neighborhoods, as well as part of the “Llano Largo”, can flood with levels ranging from 1 m to more than 2 m. The flood area increases when scenarios originated by precipitation of longer duration are simulated, reaching part of the tourist area south of the river. These are the areas that were most damaged during the hurricanes that hit the zone. However, even for the lowest return periods, with the increase in rainfall duration it is possible to notice that the river floods occur at very specific points, as it can be seen in Figure 9. The points identified by the hydrodynamic model actually correspond with the flooded areas during Hurricane Manuel, as reported in Mejía [9]. This result once again confirms the reliability of the Iber model for the hydraulic terrain response analysis to flood phenomena. Furthermore, results of the numerical simulations also provide the time of delays with respect to the input hydrograph in which the first flood occurs. This element is important to have information on the relationship between the moment in which the maximum peak discharge is reached and the moment when the overflow occurs. For short-term rainfall, during the most frequent events (return periods from 10 to 100 years), the flooding occurs when the peak flow of the hydrograph is reached, while for infrequent events (return periods from 100 to 1000 years) flooding can occur up to one hour before the river reaches its maximum discharge. For a longer precipitation duration, overflow may occur 2 h before the time of the maximum peak, even at the lowest return periods. This result is significant for the study area, as it indicates that the river does not have the capacity to contain the maximum flow when a precipitation occurs with a rain sheet greater than 20 mm falling for 30 min. These considerations can have an important implication for both long- and short-range prevention. For the purpose of long-term prevention, this result tells us that if the river is no longer able to contain the maximum design flow, this is probably due to the change in land use of the basin which has determined a decrease in infiltration, and therefore it serves to plan actions that can reduce superficial runoffs. The overflow of the river in specific points of the alluvial plain can also be a consequence of the expansion of the urban area which has reached the river margins in a few years. The study area has been heavily modified by anthropization over the last few decades, which has not only led to an increase in urban settlements, but also to the diversion of the river to obtain irrigation canals. The application of accurate numerical models and advanced methodologies aimed at combining the prediction of land use change with hydraulic models [41,42], in addition to methods that exploit analytical hierarchy processes for the construction of risk maps in urban areas [43], has greatly improved in recent years, with the aim of accurately determining peak flow rates according to the forecasts of urbanization. For the specific results of this work, the application of the hydrological model has allowed the identification of specific points of overflow of the river in the urban area, providing information on the attitude of the river in case of flood phenomena, information that is more precise than the one arising from observations made after an inundation event. This represents a useful result for an unmonitored river and further applications of a hydrodynamic model could be devoted to calculating how much flood levels would increase if urban sprawl increases in an uncontrolled way, as already done by [44], in another region of Mexico at high risk of flooding due to high urban expansion. For the purpose of short-range prevention, knowing the rain sheet that determines the first river overflow, represents another aspect that the application of a hydraulic model can have, as it could lay the basis for a study aimed at determining rainwater risk thresholds for the area.

5. Conclusions

This work aims to draw attention to the importance of applying hydrodynamic models in an increasingly widespread manner for the study of the terrain response to flooding and for the adequate preparedness to the consequences of such phenomena, particularly in areas lacking meteorological forecasts or flood levels monitoring. The advantage of applying these models lies in their high spatial and temporal resolution. Most of the hydraulic models currently in use, and specifically the Iber model, have been extensively validated showing their ability to solve 2D shallow water equations and to calculate water depths with high precision. On the other hand, the disadvantage of applying hydrodynamic models is represented by the possibility of not being able to have sufficient spatial resolutions for the construction of the problem geometry. However, digital elevation models, with resolution of at least 5 m, are currently available with a fairly global coverage, thanks to advances in remote sensing techniques. The high resolution of hydrodynamic models allows to study in detail the response to floods in highly critical areas, especially when monitoring systems are lacking or completely absent. This is the case in areas with high susceptibility to flooding in regions of developing countries. Results obtained in this work in addition to confirming that the area under study is susceptible to flooding as a result of extreme weather events, have above all highlighted the observation that, in the event of long-lasting precipitation, river flooding occurs long enough before the peak flow is reached in the design hydrographs, indicating that the river no longer has the ability to contain its maximum flow. Moreover, simulations allowed the identification of potential river overflow points, which suggest that an in-depth analysis of the conditions of the river margins in those areas must necessarily be carried out to avoid damage caused by a possible flood. Another important implication of this result is that a precise effective precipitation sheet can be associated with the overflow point, which suggests the application of the hydraulic model also for the possible determination of rain warning thresholds. Note that the area under study is a poor area, where there is a lack of resources and intentions on the part of the institutions to implement an in situ river monitoring system. The application of a hydraulic model made it possible to characterize the structure of the river without resorting to expensive tools that employ manpower. This is the reason why, with the result of this work, we want to emphasize the importance of applying hydrodynamic studies for an analysis of the areas at greatest risk of flooding for a systematic characterization of their problems.

Author Contributions

Conceptualization, R.B.; methodology, R.B.; validation, R.B. and M.C.; formal analysis, R.B.; investigation, R.B.; resources, R.B.; data curation, R.B. and M.C.; writing—original draft preparation, R.B.; writing—review and editing, R.B.; visualization, R.B.; supervision, R.B.; project administration, R.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: http://clicom-mex.cicese.mx/. Accessed on 15 January 2021.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Figure A1 shows maximum water depth results of the hydraulic simulations for a precipitation lasting 10 min and corresponding to the return periods 50, 100 and 500 years.
Water 13 03516 g0a1 550
Figure A1. Simulation results of maximum inundation waterdepths calculated for a precipitation duration of 10 min for the return periods: 50, 100 and 500 years.
Figure A1. Simulation results of maximum inundation waterdepths calculated for a precipitation duration of 10 min for the return periods: 50, 100 and 500 years.
Water 13 03516 g0a1
Figure A2 shows maximum water depth results of the hydraulic simulations for a precipitation lasting 30 min and corresponding to the return periods 50, 100 and 500 years.
Water 13 03516 g0a2 550
Figure A2. Simulation results of maximum inundation waterdepths calculated for a precipitation duration of 30 min for the return periods: 50, 100 and 500 years.
Figure A2. Simulation results of maximum inundation waterdepths calculated for a precipitation duration of 30 min for the return periods: 50, 100 and 500 years.
Water 13 03516 g0a2

References

  1. Zuñiga Tovar, M.; Magaña Rueda, V.O. Vulnerability and risk to intense rainfall in Mexico: The effect to land use cover change. Investig. Geogr. 2018, 95. [Google Scholar] [CrossRef]
  2. Mas, J.F.; Velázquez, A.; Díaz-Gallegos, J.R.; Mayorga Saucedo, R.; Alcántara, C.; Bocco, G.; Pérez-Vega, A. Assessing land use/cover changes: A nationwide multidate spatial database for Mexico. Int. J. Appl. Earth Obs. Geoinf. 1998, 37, 7–19. [Google Scholar] [CrossRef]
  3. Porter-Bolland, L.; Ellis, E.A.; Gholz, H.L. Land use dynamics and landscape history in La Montaña, Campeche, México. Landsc. Urban Plan. 2007, 82, 198–207. [Google Scholar] [CrossRef]
  4. Matías Ramírez, L.G. Algunos efectos de la precipitación del huracán Paulina en Acapulco, Guerrero. Investig. Geogr. 1998, 37, 7–19. [Google Scholar] [CrossRef]
  5. Base de datos de Ciclones Tropicales que Impactaron a México, 1970–2011, México: Comisión Nacional del Agua, Coordinación General del Servicio Meteorológico Nacional, Subgerencia de Pronóstico Meteorológico. Available online: http://smn.cna.gob.mx/ciclones/historia/ciclones1970-2011.pdf (accessed on 19 October 2021).
  6. Temporada de Ciclones 2015. México: Comisión Nacional del Agua, Servicio Meteorológico Nacional. Available online: http://smn.cna.gob.mx/index.php?option=com_content&view=article&id=276&Itemid=45 (accessed on 19 October 2021).
  7. Villegas-Romero, I.; Oropeza-Mota, J.L.; Martínez-Ménes, M.; Mejía-Sáenz, E. Path and relation rain-runoff caused by hurricane Pauline in the Sabana river, Guerrero, Mexico. Agrociencia 2009, 43, 345–356. [Google Scholar]
  8. WMO Statement on the Status of the Global Climate in 2013. Available online: https://library.wmo.int/index.php?lvl=notice_display&id=15957#.YW_gidlIAq0 (accessed on 20 October 2021).
  9. Mejía Estrada, P.I. Caracterización del Evento Hidrometeorológico Extremo en Acapulco, Guerrero, en Septiembre de 2013. Master’ Thesis, Universidad Nacional Autónoma de México, Mexico City, Mexico, June 2014. [Google Scholar]
  10. Emanuel, K.A. Downscaling CMIP5 climate models shows increased tropical cyclone activity over the 21st century. Proc. Natl. Acad. Sci. USA 2013, 110, 12219–12224. [Google Scholar] [CrossRef] [Green Version]
  11. Hong, C.; Tsou, C.; Hsu, P.; Chen, K.; Liang, H.; Hsu, H.; Tu, C.; Kitoh, A. Future Changes in Tropical Cyclone Intensity and Frequency over the Western North Pacific Based on 20-km HiRAM and MRI Models. J. Clim. 2021, 34, 2235–2251. [Google Scholar] [CrossRef]
  12. Shamir, E.; Tapia-Villaseñor, E.M.; Cruz-Ayala, M.B.; Megdal, S.B. A Review of Climate Change Impacts on the USA-Mexico Transboundary Santa Cruz River Basin. Water 2021, 13, 1390. [Google Scholar] [CrossRef]
  13. Trenberth, K.E.; Cheng, L.; Jacobs, P.; Zhang, Y.; Fasullo, J. Hurricane Harvey links to ocean heat content and climate change adaptation. Earth’s Future 2018, 6, 730–744. [Google Scholar] [CrossRef]
  14. Jan van Oldenborgh, G.; van der Wiel1, K.; Sebastian, A.; Singh, R.; Arrighi, J.; Otto, F.; Haustein, K.; Li, S.; Vecchi, G.; Cullen, H. Attribution of extreme rainfall from Hurricane Harvey, August 2017. Environ. Res. Lett. 2017, 12, 124009. [Google Scholar] [CrossRef]
  15. Knutson, T.R.; Sirutis, J.J.; Zhao, M.; Tuleya, R.E.; Bender, M.; Vecchi, G.A.; Villarini, G.; Chavas, D. Global Projections of Intense Tropical Cyclone Activity for the Late Twenty-First Century from Dynamical Downscaling of CMIP5/RCP4.5 Scenarios. J. Clim. 2015, 28, 7203–7224. [Google Scholar] [CrossRef] [Green Version]
  16. Bonasia, R.; Lucatello, S. Linking Flood Susceptibility Mapping and Governance in Mexico for Flood Mitigation: A Participatory Approach Model. Atmosphere 2019, 10, 424. [Google Scholar] [CrossRef] [Green Version]
  17. Lineamientos Para la Elaboración de Mapas de Peligro por Inundación. Available online: https://www.gob.mx/cms/uploads/attachment/file/469330/Lineamientos__para_la_elaboraci_n_de_mapas_de_peligro_por_inundaci_n.pdf (accessed on 21 October 2021).
  18. Portal de Sistemas de Información del Agua. Available online: https://app.conagua.gob.mx/sistemasdeagua/ (accessed on 21 October 2021).
  19. Dransch, D.; Rotzol, H.; Poser, K. The contribution of maps to the challenges of risk communication to the public. Int. J. Dig. Earth. 2010, 3, 292–311. [Google Scholar] [CrossRef]
  20. Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef] [Green Version]
  21. Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
  22. Forestieri, A.; Caracciolo, D.; Arnone, E.; Noto, L.V. Derivation of rainfall thresholds for flash flood warning in a Sicilian basin using a hydrological model. Procedia Eng. 2016, 154, 818–825. [Google Scholar] [CrossRef] [Green Version]
  23. Reed, S.; Schaake, J.; Zhang, Z. A distributed hydrologic model and threshold frequency-based method for flash flood forecasting at ungauged locations. J. Hydrol. 2007, 337, 402–420. [Google Scholar] [CrossRef]
  24. Norbiato, D.; Borga, M.; Degli Esposti, S.; Gaume, E.; Anquetin, S. Flash flood warning based on rainfall thresholds and soil moisture conditions: An assessment for gauged and ungauged basins. J. Hydrol. 2008, 362, 274–290. [Google Scholar] [CrossRef]
  25. Mai, D.T.; De Smedt, F. A Combined Hydrological and Hydraulic Model for Flood Prediction in Vietnam Applied to the Huong River Basin as a Test Case Study. Water 2017, 9, 879. [Google Scholar] [CrossRef] [Green Version]
  26. Dullo, T.T.; Gangrade, S.; Morales-Hernández, M.; Sharif, M.B.; Kao, S.C.; Kal-yanapu, A.J.; Ghafoor, S.; Evans, K.J. Simulation of Hurricane Harvey flood event through coupled hydrologic-hydraulic models: Challenges and next steps. J. Flood Risk Manag. 2021, 14, e12716. [Google Scholar] [CrossRef]
  27. Warren, I.R.; Bach, H.K. MIKE 21: A modelling system for estuaries, coastal waters and seas. Environ. Softw. 1991, 7, 229–240. [Google Scholar] [CrossRef]
  28. Gerstner, N.; Belzner, F.; Thorenz, C. Simulation of Flood Scenarios with Combined 2D/3D Numerical Models. In ICHE 2014, Proceedings of the 11th International Conference on Hydroscience & Engineering 2014, Hamburg, Germany, 28 September–2 October 2014; Rainer, L., Rebekka, K., Eds.; Bundesanstalt für Wasserbau: Karlsruhe, Germany, 2014; pp. 975–981. [Google Scholar]
  29. Lyubimova, T.; Lepikhin, A.; Parshakova, Y.; Tiunov, A.; Konovalov, V.; Shumilova, N. Numerical modelling of admixture transport in a turbulent flow at river confluence. Models. J. Phys. Conf. Ser. 2013, 416, 012028. [Google Scholar] [CrossRef] [Green Version]
  30. Vázquez-Cendón, M.E. Improved treatment of source terms in upwinds chemes for the shallow water equations in channels with irregular geometry. J. Comput. Phys. 1999, 148, 497–526. [Google Scholar] [CrossRef]
  31. Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, J.; Dolz, J.; Coll, A. IBER: Herramienta de simulación numérica de flujo en ríos. Rev. Int. Métodos Numer. Para Cálc. Diseño Ing. 2014, 30, 1–10. [Google Scholar] [CrossRef] [Green Version]
  32. Galán Castro, E.A.; Rodríguez Herrera, A.L.; Rosas-Acevedo, J.L. Gobernanza hídrica como securitización socioambiental en la subcuenca La Sabana–Tres Palos, Acapulco. Reg. Cohes. 2021, 11, 24. [Google Scholar] [CrossRef]
  33. Actualización de la Disponibilidad Media Anual de agua en el Acuífero La Sabana (1227) Estado de Guerrero. Available online: https://sigagis.conagua.gob.mx/gas1/Edos_Acuiferos_18/guerrero/DR_1227.pdf (accessed on 25 October 2021).
  34. Sistema Nacional de Información sobre Biodiversidad. Available online: http://www.conabio.gob.mx/informacion/gis/ (accessed on 25 October 2021).
  35. Base de Datos Climatológica Nacional (Sistema Clicom). Available online: http://clicom-mex.cicese.mx/ (accessed on 15 January 2021).
  36. Chen, C.I. Rainfall intensity-duration-frequency formulas. J. Hydraul. Eng. 1983, 109, 1603. [Google Scholar] [CrossRef]
  37. Bell, F.C. Generalized Rainfall-Duration-Frequency Relationships. J. Hydraul. Div. 1969, 95, 311–328. [Google Scholar] [CrossRef]
  38. Bladé, E.; Cea, L.; Corestein, G. Modelización numérica de inundaciones fluviales. Ing. Del Agua 2014, 16, 68. [Google Scholar]
  39. Cea, L.; Bladé, E.; Corestein, G. A simple and efficient unstructured finite volume scheme for solving the shallow water equations in overland flow applications. Water Resour. Res. 2015, 51, 5464–5486. [Google Scholar] [CrossRef] [Green Version]
  40. García-Feal, O.; González-Cao, J.; Gómez-Gesteira, M.; Cea, L.; Domínguez, J.; Formella, A. An accelerated tool for flood Modelling based on Iber. Water 2018, 10, 1459. [Google Scholar] [CrossRef] [Green Version]
  41. Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
  42. Ghimire, B.; Chen, A.S.; Guidolin, M.; Keedwell, E.C.; Djordjeviç, S.; Savic, D.A. Simulation of a fast 2D urban pluvial flood model using a cellular automata approach. J. Hydroinf. 2012, 15, 676–686. [Google Scholar] [CrossRef] [Green Version]
  43. Skilodimou, H.D.; Bathrellos, G.D.; Alexakis, D.E. Flood Hazard Assessment Mapping in Burned and Urban Areas. Sustainability 2021, 13, 4455. [Google Scholar] [CrossRef]
  44. Areu-Rangel, O.S.; Cea, L.; Bonasia, R.; Espinosa-Echavarria, V.J. Impact of Urban Growth and Changes in Land Use on River Flood Hazard in Villahermosa, Tabasco (Mexico). Water 2019, 11, 304. [Google Scholar] [CrossRef] [Green Version]
Water 13 03516 g001 550
Figure 1. Map of La Sabana River sub-basin. Hydrographic network, scale 1:50,000, of the National Institute of Statistics and Geography (INEGI).
Figure 1. Map of La Sabana River sub-basin. Hydrographic network, scale 1:50,000, of the National Institute of Statistics and Geography (INEGI).
Water 13 03516 g001
Water 13 03516 g002 550
Figure 2. Location map of the study area, delimited by the red line. Yellow polygons represent the areas covered by urban settlements.
Figure 2. Location map of the study area, delimited by the red line. Yellow polygons represent the areas covered by urban settlements.
Water 13 03516 g002
Water 13 03516 g003 550
Figure 3. Hydrographs of La Sabana catchment associated to different return periods for a precipitation with a 10 min duration.
Figure 3. Hydrographs of La Sabana catchment associated to different return periods for a precipitation with a 10 min duration.
Water 13 03516 g003
Water 13 03516 g004 550
Figure 4. Hydrographs of La Sabana catchment associated to different return periods for a precipitation with a 30 min duration.
Figure 4. Hydrographs of La Sabana catchment associated to different return periods for a precipitation with a 30 min duration.
Water 13 03516 g004
Water 13 03516 g005 550
Figure 5. Simulation results of maximum inundation waterdepths occurred as consequence of the hurricane Manuel. The red line delimits the computational domain; the black line delimits the area where the flood level measurements were made according to [9].
Figure 5. Simulation results of maximum inundation waterdepths occurred as consequence of the hurricane Manuel. The red line delimits the computational domain; the black line delimits the area where the flood level measurements were made according to [9].
Water 13 03516 g005
Water 13 03516 g006 550
Figure 6. Simulation results of maximum inundation waterdepths calculated for a precipitation duration of 10 min and the return periods: (a) 10 years and (b) 1000 years.
Figure 6. Simulation results of maximum inundation waterdepths calculated for a precipitation duration of 10 min and the return periods: (a) 10 years and (b) 1000 years.
Water 13 03516 g006
Water 13 03516 g007 550
Figure 7. Simulation results of maximum inundation waterdepths calculated for a precipitation duration of 30 min and the return periods: (a) 10 years and (b) 1000 years.
Figure 7. Simulation results of maximum inundation waterdepths calculated for a precipitation duration of 30 min and the return periods: (a) 10 years and (b) 1000 years.
Water 13 03516 g007
Water 13 03516 g008 550
Figure 8. Snapshot of the first flood of the river for a precipitation lasting 10 min and a 10 years return period. The moment of the simulation corresponds to the time-step 28,800 s. The yellow shaded area delimits the river overflow point.
Figure 8. Snapshot of the first flood of the river for a precipitation lasting 10 min and a 10 years return period. The moment of the simulation corresponds to the time-step 28,800 s. The yellow shaded area delimits the river overflow point.
Water 13 03516 g008
Water 13 03516 g009 550
Figure 9. Snapshot of the first flood of the river for a precipitation lasting 30 min and a 10 years return period. The moment of the simulation corresponds to the time-step 22,500 s. The yellow shaded area delimits two river overflow points that correspond to the first overflow area during hurricane Manuel.
Figure 9. Snapshot of the first flood of the river for a precipitation lasting 30 min and a 10 years return period. The moment of the simulation corresponds to the time-step 22,500 s. The yellow shaded area delimits two river overflow points that correspond to the first overflow area during hurricane Manuel.
Water 13 03516 g009
Table
Table 1. Hydrological characteristics of La Sabana River Basin.
Table 1. Hydrological characteristics of La Sabana River Basin.
Basin area (km2)446.05
Length of the main channel (m)72,720
Average slope of the main channel (%)2.10
Concentration time (h)7.97
Peak time (h)7.60
Peak flow rate (m3/s/mm)12.20
Table
Table 2. Accumulated precipitation, excess precipitation and flood discharges estimated for La Sabana Catchment for each return period and two precipitation duration: 10 and 30 min.
Table 2. Accumulated precipitation, excess precipitation and flood discharges estimated for La Sabana Catchment for each return period and two precipitation duration: 10 and 30 min.
Precipitation DurationReturn Period (Years)P (mm) P e (mm) Q d (m3/s)
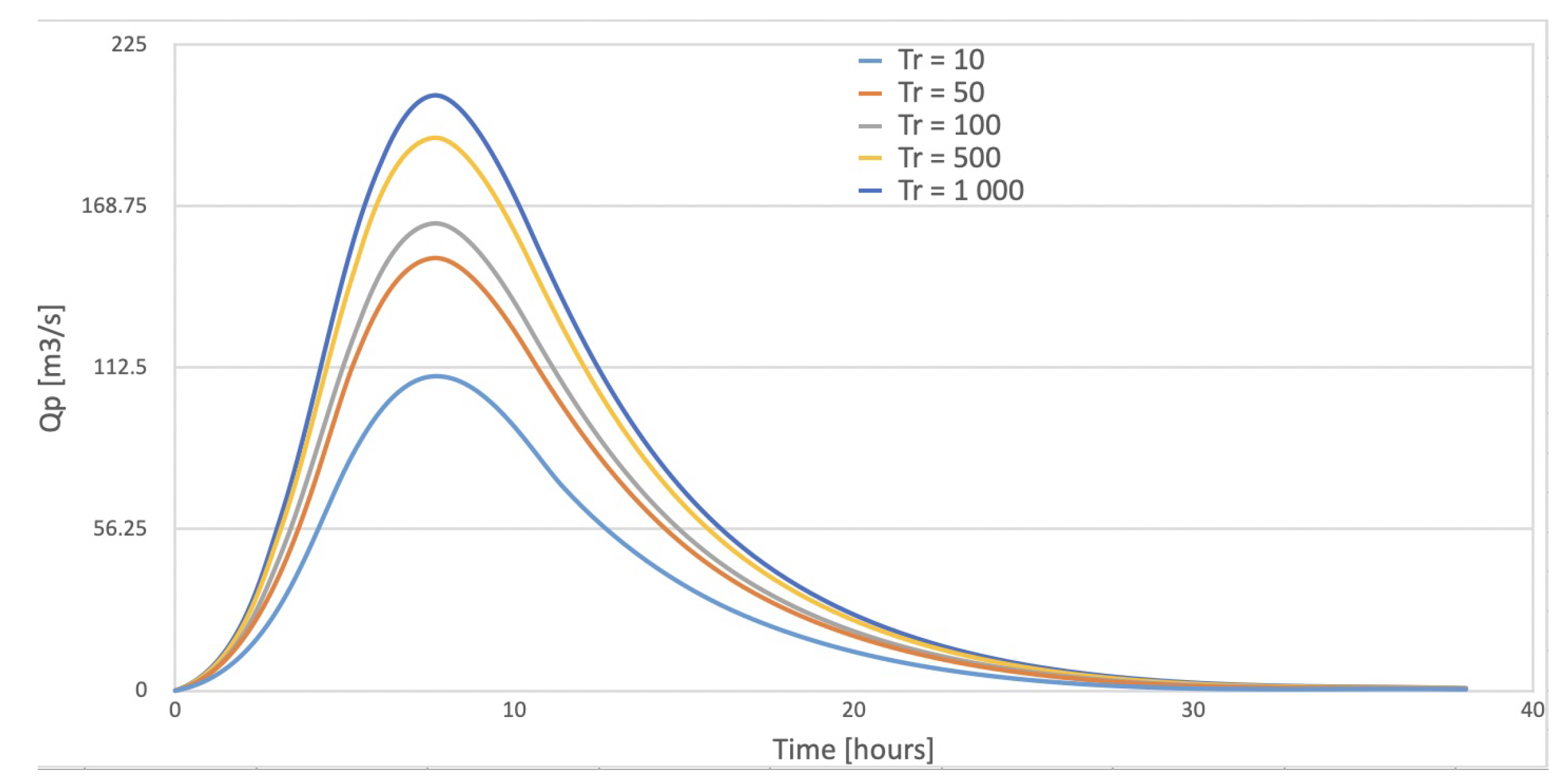
10 min1014.1046.734109.440
5017.1709.266150.598
10018.04110.008162.647
50020.15411.841192.449
100021.18412.751207.222
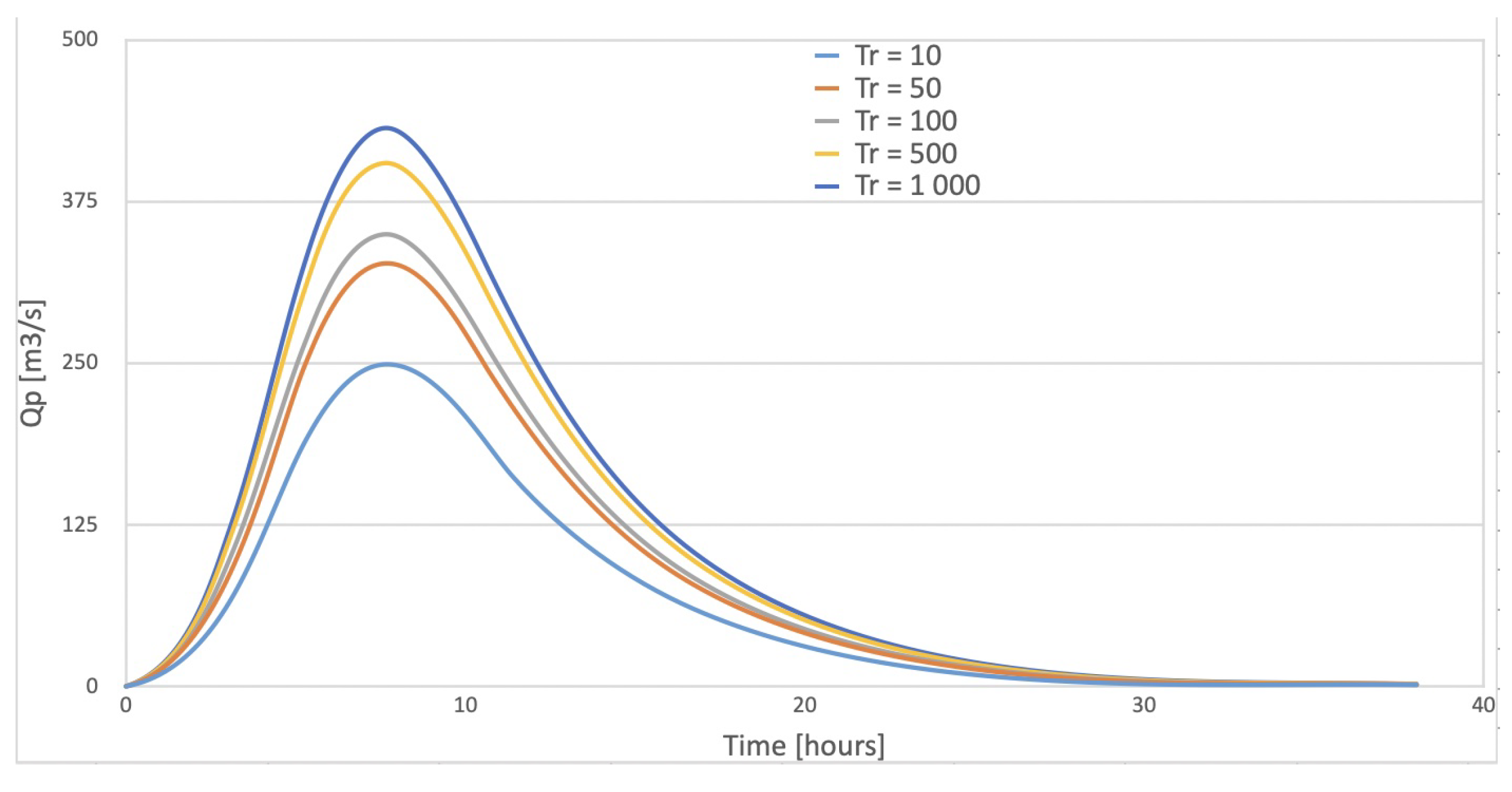
30 min1020.04515.317248.922
5029.27420.123327.021
10030.75821.508349.532
50034.36024.899404.633
100036.11626.565431.708
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Bonasia, R.; Ceragene, M. Hydraulic Numerical Simulations of La Sabana River Floodplain, Mexico, as a Tool for a Flood Terrain Response Analysis. Water 2021, 13, 3516. https://doi.org/10.3390/w13243516

AMA Style

Bonasia R, Ceragene M. Hydraulic Numerical Simulations of La Sabana River Floodplain, Mexico, as a Tool for a Flood Terrain Response Analysis. Water. 2021; 13(24):3516. https://doi.org/10.3390/w13243516

Chicago/Turabian Style

Bonasia, Rosanna, and Mackendy Ceragene. 2021. "Hydraulic Numerical Simulations of La Sabana River Floodplain, Mexico, as a Tool for a Flood Terrain Response Analysis" Water 13, no. 24: 3516. https://doi.org/10.3390/w13243516

APA Style

Bonasia, R., & Ceragene, M. (2021). Hydraulic Numerical Simulations of La Sabana River Floodplain, Mexico, as a Tool for a Flood Terrain Response Analysis. Water, 13(24), 3516. https://doi.org/10.3390/w13243516

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop