Comparison of the Applicability of Different Soil Erosion Models to Predict Soil Erodibility Factor and Event Soil Losses on Loess Slopes in Hungary
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site and Soil Properties
2.2. Rainfall Simulator and Experimental Design
2.3. Soil Erosion Modelling
2.4. Statistical Evaluation of the Model Performance
3. Results
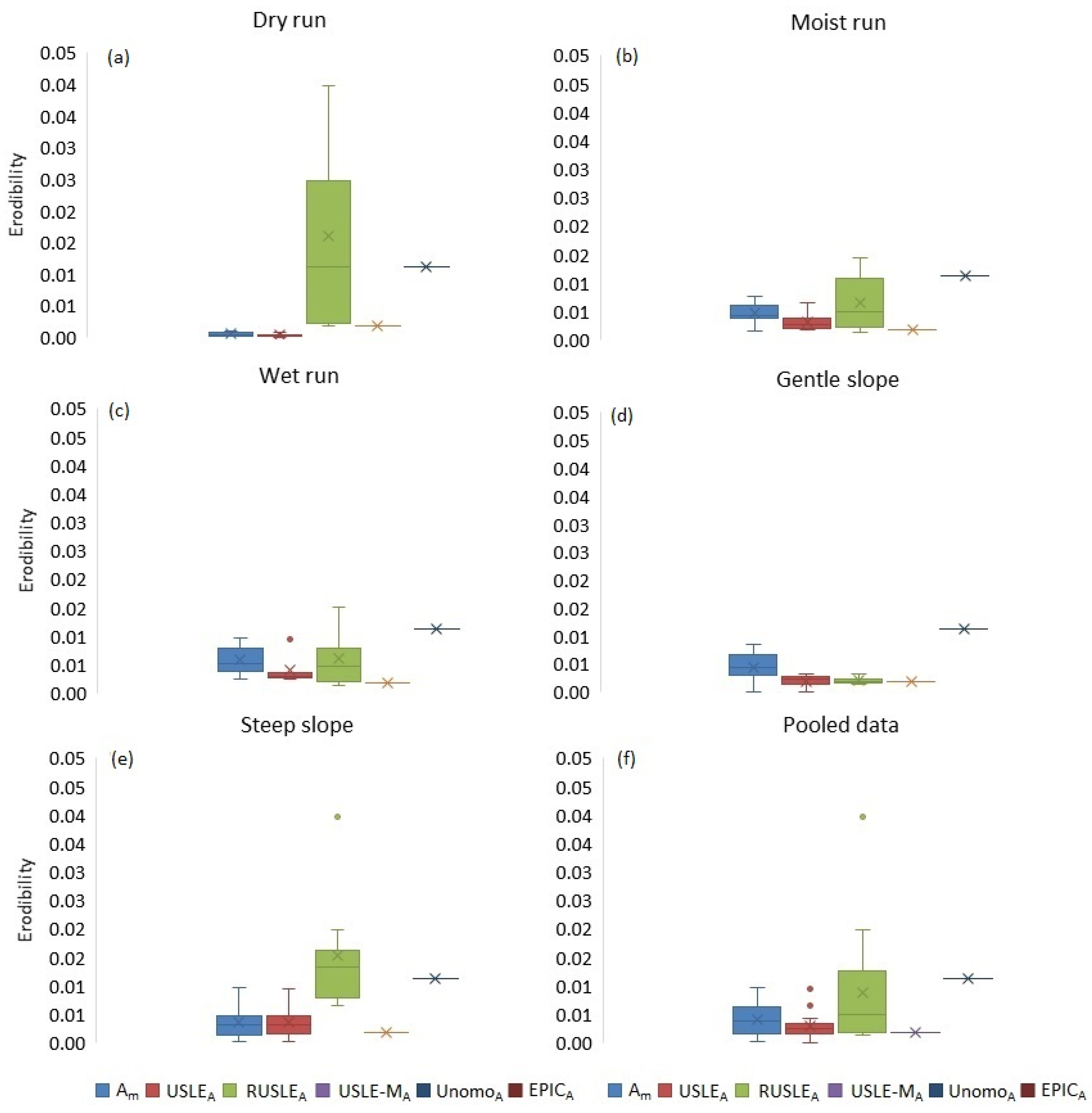
3.1. Evaluation of the Erodibility Estimated by the Applied Models
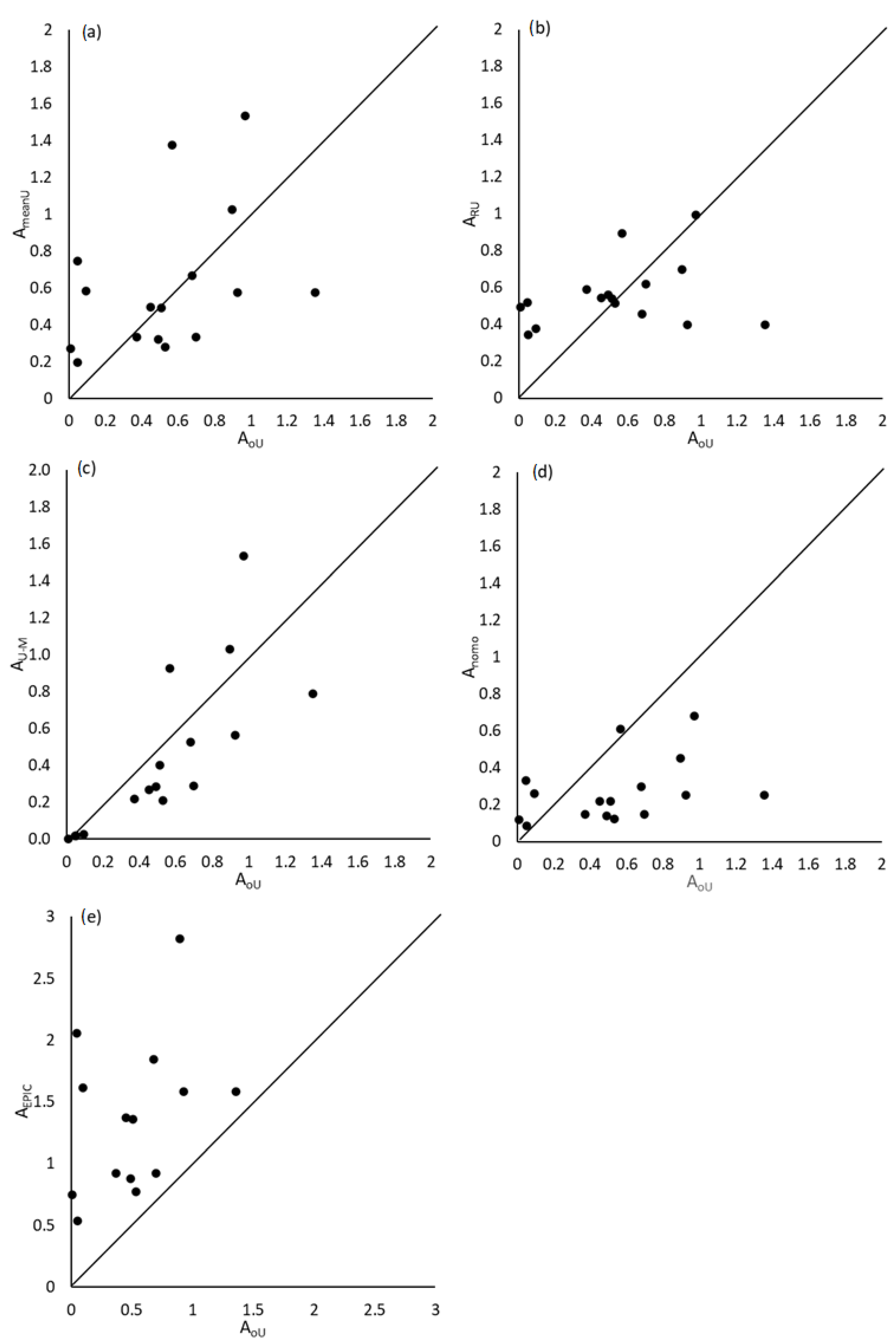
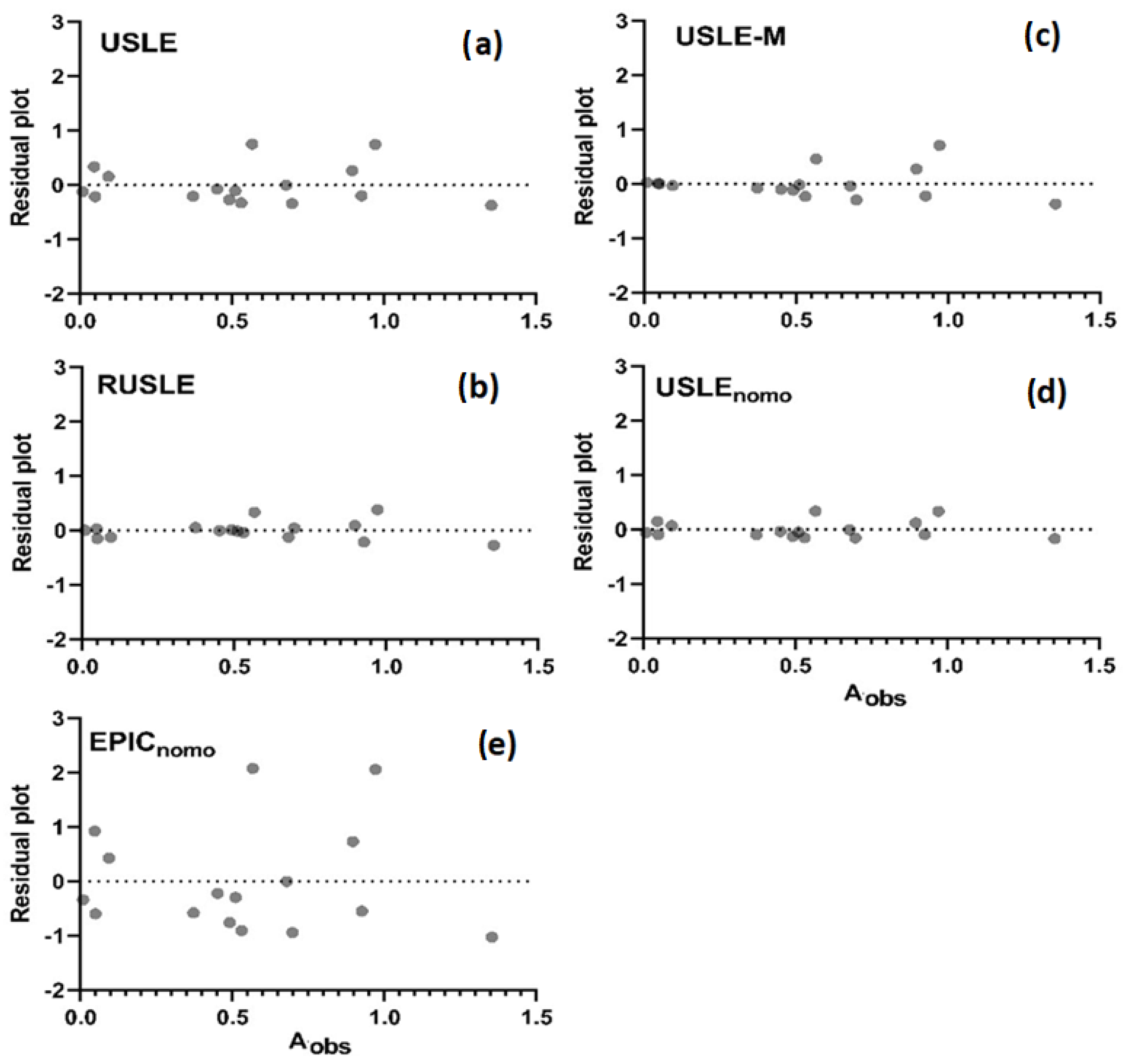
3.2. Evaluation of Event Soil Loss Estimation
4. Discussion
5. Conclusions
- (1)
- The K-values in Hungary for the loess-covered Koppány River Valley ranged from 0.0028 to 0.087 t ha h ha−1 MJ−1 mm−1. The calculated erodibility results vary with initial soil moisture content and slope degree. Regarding the pooled data, the CV% indicated less relative variability in the case of USLE and RUSLE, followed by USLE-M.
- (2)
- In respect to the event soil loss estimation, the results indicate high variance with the increase in initial soil moisture content and slope steepness. Based on the pooled data, the best estimations were obtained by RUSLE, USLE and USLE-M.
- (3)
- Both soil erodibility and soil loss estimation draw attention to the importance of the effect of soil moisture conditions.
- (4)
- Investigating the measured and estimated soil losses statistically, we found that RUSLE resulted in the best performance in event soil loss estimation. At the same time, RUSLE indicated sensitivity for the measured values.
- (5)
- Within these experiments, the USLE-type models’ capability for estimating event soil losses was confirmed. At the same time, we cannot emphasize enough that the non-standardized circumstances involving many affecting factors could result in high variance among the results.
- (6)
- This study points out the high variability of soil erodibility factors and soil loss estimation values in the case of event rainfall simulations. Besides, it draws attention to the importance of further studies on this topic, because rainfall simulation is necessary for the determination of each soil type’s erodibility and short or long time soil loss estimation. That is why we need to develop an accurate, standardized method for event soil loss measurements, where the observable parameters are not solely the type of soil and other soil properties because these methods cannot give satisfactory results.
- (7)
- This study focused on soils formed on loess parent material. These soils cover a wide range of geographical regions. Thus, this study can provide useful information for many areas that struggle with similar water erosion problems, suggesting using erosion modelling as a tool for finding a solution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Treatment | s | Soil Moisture Content | RIe | Pe | EI30 | Qe | QR | QREI30 | Aobs |
|---|---|---|---|---|---|---|---|---|---|
| % | mm h−1 | mm | MJ mm ha−1 h−1 | mm | MJ mm ha−1 h−1 | t ha−1 | |||
| FPG1 | 6.7 | moist | 56.24 | 16.81 | 256.93 | 4.22 | 0.25 | 64.53 | 0.45 |
| FPG2 | 6.7 | wet | 84.68 | 10.63 | 254.79 | 4.04 | 0.38 | 96.90 | 0.51 |
| FPG3 | 8 | dry | 22.65 | 28.96 | 155.66 | 1.20 | 0.04 | 6.43 | 0.05 |
| FPG4 | 8 | moist | 70.19 | 13.53 | 266.09 | 4.12 | 0.30 | 81.06 | 0.37 |
| FPG5 | 8 | wet | 86.12 | 10.41 | 253.61 | 4.36 | 0.42 | 106.22 | 0.49 |
| FPG6 | 7.7 | dry | 26.32 | 35.1 | 224.49 | 0.21 | 0.01 | 1.35 | 0.01 |
| FPG7 | 7.7 | moist | 56.92 | 15.19 | 235.44 | 5.28 | 0.35 | 81.79 | 0.53 |
| FPG8 | 7.7 | wet | 80.44 | 12.4 | 282.30 | 4.95 | 0.40 | 112.68 | 0.70 |
| FPS1 | 18.32 | dry | 20.87 | 26.64 | 130.20 | 0.53 | 0.02 | 2.61 | 0.09 |
| FPS2 | 18.32 | moist | 66.78 | 16.49 | 306.47 | 5.17 | 0.31 | 96.08 | 0.57 |
| FPS3 | 18.32 | wet | 103.48 | 11.67 | 341.76 | 5.42 | 0.46 | 158.82 | 0.97 |
| FPS4 | 17.26 | dry | 24.42 | 31.10 | 182.39 | 0.40 | 0.01 | 2.33 | 0.05 |
| FPS5 | 17.26 | moist | 49.89 | 10.53 | 140.42 | 4.81 | 0.46 | 64.11 | 0.93 |
| FPS6 | 17.26 | wet | 63.16 | 8.05 | 140.47 | 5.17 | 0.64 | 90.12 | 1.35 |
| FPS7 | 17.6 | moist | 44.05 | 13.86 | 158.61 | 5.03 | 0.37 | 58.11 | 0.68 |
| FPS8 | 17.6 | wet | 76.69 | 11.18 | 243.18 | 5.23 | 0.47 | 113.51 | 0.90 |
References
- Wang, B.; Zheng, F.; Guan, Y. Improved USLE-K factor prediction: A case study on water erosion areas in China. Int. Soil Water Conserv. Res. 2016, 4, 168–176. [Google Scholar] [CrossRef] [Green Version]
- Pimentel, D.; Harvey, C.; Resosudarmo, P.; Sinclair, K.; Kurz, D.; McNair, M. Environmental and economic costs of soil erosion and conservation benefits. Science 1995, 267, 1117–1123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pimentel, D. Soil erosion: A food and environmental threat Environment. Dev. Sustain. 2006, 8, 119–137. [Google Scholar] [CrossRef]
- Lal, R. Enhancing crop yield in the developing countries through restoration of soil organic carbon pool in agricultural lands. Land Degrad. Dev. 2006, 17, 197–209. [Google Scholar] [CrossRef]
- Miller, G.A.; Amemiya, M.; Jolly, R.W.; Melvin, S.W.; Nowak, P.J. Soil Erosion and the Iowa Soil 2000 Program; Iowa State University: Ames, IA, USA, 1988. [Google Scholar]
- Sharpley, A.N.; McDowell, R.W.; Kleinman, P.J.A. Phosphorus loss from land to water: Integrating agricultural and environmental management. Plant Soil 2001, 237, 287–307. [Google Scholar] [CrossRef]
- Smith, D.D. Interpretation of soil conservation data for field use. Agric. Eng. 1941, 22, 173–175. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting rainfall erosion losses. In A Guide to Conservation Planning. USDA Agriculture Handbook; USDA: Blacksburg, VA, USA, 1978. [Google Scholar]
- Mannering, J.V. The use of soil loss tolerances as a strategy for soil conservation. In Soil Conservation: Problems and Prospects; Morgan, R.P.C., Ed.; John Wiley and Sons: New York, NY, USA, 1981; pp. 337–349. [Google Scholar]
- Skidmore, E.L. Soil Loss Tolerance [Chapter 8], Determinants of Soil Loss Tolerance; ASA, SSSA: Madison, WI, USA, 1982; pp. 87–93. [Google Scholar] [CrossRef]
- Morgan, R.P.C. Soil Erosion and Conservation; Blackwell Publishing: Hoboken, NJ, USA, 2005; p. 299. [Google Scholar] [CrossRef]
- IPCC. Climate Change and Land. Intergovernmental Panel on Climate Change. 2019. Available online: https://www.ipcc.ch/site/assets/uploads/2019/08/4.-SPM_Approved_Microsite_FINAL.pdf (accessed on 6 September 2021).
- Edwards, W.M.; Owens, L.B. Large Storm Effects on Total Soil Erosion. J. Soil Water Conserv. 1991, 46, 75–78. Available online: https://www.jswconline.org/content/46/1/75.short (accessed on 28 October 2021).
- Bagarello, V.; Di Stefano, C.; Ferro, V.; Pampalone, V. Statistical distribution of soil loss and sediment yield at Sparacia experimental area, Sicily. Catena 2010, 82, 45–52. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Stefano, C.; Ferro, V.; Pampalone, V. Using plot loss distribution for soil conservation design. Catena 2011, 86, 172–177. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Stefano, C.; Ferro, V.; Kinnell, P.I.A.; Pampalone, V.; Porto, P.; Todisco, F. Predicting soil loss on moderate scope using an empirical model for sediment concentration. J. Hydrol. 2011, 400, 267–273. [Google Scholar] [CrossRef]
- Strohmeier, S.; Laaha, G.; Holzmann, H.; Klik, A. Magnitude and occurrence probability of soil loss: A risk analytical approach for the plot scale for two sites in lower Austria. Land Degrad. Dev. 2016, 27, 43–51. [Google Scholar] [CrossRef]
- Lang, K.; Prunty, L.; Schroeder, S.; Disrud, L. Interrill erosion as an index of mined land soil erodibility. Trans. ASAE 1984, 99, 109. [Google Scholar]
- Ali, S.A.; Hamelmal, H. Estimation of soil erosion using USLE and GIS in Awassa Catchment, Rift valley, Central Ethiopia. Geoderma Reg. 2016, 7, 159–166. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Varandas, S.G.P.; Sanches Fernandes, L.F.; Valle, R.F., Jr. Soil losses in rural watersheds with environmental land use conflicts. Sci. Total Environ. 2014, 485–486, 110–120. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Stefano, C.; Ferro, V.; Giordano, G.; Iovino, M.; Pampalone, V. Estimating the USLE Soil Erodibility Factor in Sicily, South Italy. Appl. Eng. Agric. 2012, 28, 199–206. [Google Scholar] [CrossRef]
- Borselli, L.; Cassi, P.; Sanchis, P. Soil Erodibility Assessment for Applications at Watershed Scale. In Manual of Methods for Soil and Land Evaluation; Springer: New York, NY, USA, 2009; pp. 98–117. [Google Scholar] [CrossRef]
- González-Hidalgo, J.C.; Batalla, R.J.; Cerdà, A.; de Luis, M. Contribution of the largest events to suspended sediment transport across the USA. Land Degrad. Dev. 2010, 21, 83–91. [Google Scholar] [CrossRef]
- González-Hidalgo, J.C.; Batalla, R.J.; Cerdà, A.; de Luis, M. A regional analysis of the effects of largest events on soil erosion. Catena 2012, 95, 85–90. [Google Scholar] [CrossRef]
- Larson, W.E.; Lindstrom, M.J.; Schumacher, T.E. The role of severe storms in soil erosion: A problem needing consideration. J. Soil Water Conserv. 1997, 52, 90–95. [Google Scholar]
- Iserloh, T.; Fister, W.; Seeger, M.; Willger, H.; Ries, J. A small portable rainfall simulator for reproducible experiments on soil erosion. Soil Tillage Res. 2012, 124, 131–137. [Google Scholar] [CrossRef]
- Iserloh, T.; Ries, J.; Arnáez, J.; Boix-Fayos, C.; Butzen, V.; Cerdà, A.; Echeverría, M.; Fernandez-Galvez, J.; Fister, W.; Geißler, C.; et al. European small portable rainfall simulators: A comparison of rainfall characteristics. Catena 2013, 110, 100–112. [Google Scholar] [CrossRef] [Green Version]
- Iserloh, T.; Pegoraro, D.; Schlösser, A.; Thesing, H.; Seeger, M.; Ries, J.B. Rainfall Simulation Experiments: Influence of Water Temperature, Water Quality and Plot Design on Soil Erosion and Runoff. Geophys. Res. Abstr. 2015, 17, EGU2015-5817. Available online: https://meetingorganizer.copernicus.org/EGU2015/EGU2015-5817.pdf (accessed on 28 October 2021).
- Risse, L.M.; Nearing, M.A.; Nicks, A.D.; Laflen, J.M. Error assessment in the Universal Soil Loss Equation. Soil Sci. Soc. Am. J. 1993, 57, 825–833. [Google Scholar] [CrossRef]
- Todisco, F.; Mannocchi, F.; Vergni, L.; Vinci, A. Plot Scale Measurements of Rainfall Erosion Losses in Central Italy. In Proceedings of the Role of Hydrology in Water Resources Management Symposium, Capri, Italy, 13–16 October 2008; Available online: http://www.scopus.com/inward/record.url?eid=2-s2.0-79551547410&partnerID=MN8TOARS (accessed on 28 October 2021).
- Todisco, F. The internal structure of erosive and non-erosive storm events for interpretation of erosive processes and rainfall simulation. J. Hydrol. 2014, 519, 3651–3663. [Google Scholar] [CrossRef]
- Todisco, F.; Brocca, L.; Termite, L.F.; Wagner, W. Use of satellite and modeled soil moisture data for predicting event soil loss at plot scale. Hydrol. Earth Syst. Sci. 2015, 19, 3845–3856. [Google Scholar] [CrossRef] [Green Version]
- Bagarello, V.; Di Piazza, G.V.; Ferro, V.; Giordano, G. Predicting unit plot soil loss in Sicily, south Italy. Hydrol. Process. 2008, 22, 586–595. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Stefano, C.; Ferro, V.; Pampalone, V. Comparing theoretically supported rainfall-runoff erosivity factors at the Sparacia [South Italy] experimental site. Hydrol. Process. 2018, 32, 507–515. [Google Scholar] [CrossRef]
- Kinnell, P. Runoff dependent erosivity and slope length factors suitable for modeling annual erosion using the Universal Soil Loss Equation. Hydrol. Process. 2007, 21, 2681–2689. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Event soil loss, runoff and the Universal Soil Loss Equation family of models: A review. J. Hydrol. 2010, 385, 384–397. [Google Scholar] [CrossRef]
- Boardman, J. Soil erosion science: Reflections on the limitations of current approaches. Catena 2006, 68, 2–3. [Google Scholar] [CrossRef]
- Foster, G.R.; Moldenhauer, W.C.; Wischmeier, W.H. Transferability of U.S. technology for prediction and control of erosion in the tropics. In Soil Erosion and Conservation in the Tropics; ASA: Madison, WI, USA, 1981; pp. 135–149. [Google Scholar] [CrossRef]
- Kinnell, P.; Wang, J.; Zheng, F. Comparison of the abilities of WEPP and the USLE-M to predict event soil loss on steep loessial slopes in China. Catena 2018, 171, 99–106. [Google Scholar] [CrossRef]
- Wischmeier, W.C.; Smith, D.D. Rainfall energy and its relationship to soil loss. Trans. Am. Geophys. Union 1958, 39, 285–291. [Google Scholar] [CrossRef]
- Williams, J.R. Sediment yield prediction with universal equation using runoff energy factor. In Present and Prospective Technology for Predicting Sediment Yields and Sources; USDA: Blacksburg, VA, USA, 1975. [Google Scholar]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting soil erosion by water: A guide to conservation planning with the Revised Universal Soil Loss Equation [RUSLE]. In USDA Agriculture Handbook; USDA: Blacksburg, VA, USA, 1997. [Google Scholar]
- Flanagan, D.C.; Nearing, M.A. USDA-Water Erosion Prediction Project: Hillslope Profile and Watershed Model Documentation; NSERL Report no.10; USDA-ARS National Soil Erosion Research Laboratory: West Lafayette, IN, USA, 1995. [Google Scholar]
- Nearing, M.A.; Foster, G.R.; Lane, L.J.; Finckner, S.C. A process-based soil erosion model for USDA—Water Erosion Prediction Project Technology. Trans. Am. Soc. Agric. Eng. 1989, 32, 1587–1593. [Google Scholar] [CrossRef]
- Kinnell, P.I.A.; Risse, L.M. USLE-M: Empirical modeling rainfall erosion through runoff and sediment concentration. Soil Sci. Soc. Am. J. 1998, 62, 1667–1672. [Google Scholar] [CrossRef]
- Bryan, R.B.; Govers, G.; Poesen, J. The concept of soil erodibility and some problems of assessment and application. Catena 1989, 16, 393–412. [Google Scholar] [CrossRef]
- Bryan, R.B. Soil erodibility and processes of water erosion on hillslope. Geomorphology 2000, 32, 385–415. [Google Scholar] [CrossRef]
- Wang, G.; Gertner, G.; Liu, X.; Anderson, A. Uncertainty assessment of soil erodibility factor for revised universal soil loss equation. Catena 2001, 46, 1–14. [Google Scholar] [CrossRef]
- Torri, D.; Poesen, J.; Borselli, L. Predictability and uncertainty of the soil erodibility factor using a global dataset. Catena 1997, 31, 1–22. [Google Scholar] [CrossRef]
- Jamshidi, R.; Dragovich, D.; Webb, A.A. Catchment scale geostatistical simulation and uncertainty of soil erodibility using sequential Gaussian simulation. Environ. Earth Sci. 2014, 71, 4965–4976. [Google Scholar] [CrossRef]
- Buttafuoco, G.; Conforti, M.; Aucelli, P.P.C.; Robustelli, G.; Scarciglia, F. Assessing spatial uncertainty in mapping soil erodibility factor using geostatistical stochastic simulation. Environ. Earth Sci. 2012, 66, 1111–1125. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Applying the QREI30 index within the USLE modelling environment. Hydrol. Process. 2013, 28, 591–598. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Accounting for the influence of runoff on event soil erodibilities associated with the EI 30 index in RUSLE2. Hydrol. Process. 2015, 29, 1397–1405. [Google Scholar] [CrossRef]
- Govers, G.; Takken, I.; Helming, K. Soil roughness and overland flow. Agronomie 2000, 20, 131–146. [Google Scholar] [CrossRef]
- Nearing, M.A. Soil erosion and conservation. In Environmental Modelling: Finding Simplicity in Complexity, 2nd ed.; Wainwright, J., Mulligan, M., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; pp. 365–378. [Google Scholar] [CrossRef] [Green Version]
- Cassol, E.A.; Silva, T.S.; Eltz, F.L.F.; Levien, R. Soil Erodibility under Natural Rainfall Conditions as the K Factor of the Universal Soil Loss Equation and Application of the Nomograph for a Subtropical Ultisol. Rev. Bras. Ciênc. Solo 2018, 42, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Römkens, M.J.M. The soil erodibility factor: A perspective. In Soil Erosion and Conservation; E1-Swaify, S.A., Moldenhauer, W.C., Lo, A., Eds.; Soil and Water Conservation Society: Ankeny, IA, USA, 1985; pp. 445–461. [Google Scholar]
- El-Swaify, S.A.; Dangler, E.W. Rainfall erosion in the tropics: A state of art. In Determinants of Soil Loss Tolerance; Krebs, D.M., Ed.; American Society of Agronomy: Madison, WI, USA, 1982; pp. 1–25. [Google Scholar]
- Wang, B.; Zheng, F.; Römkens, J.M. Comparison of soil erodibility factors in USLE, RUSLE2, EPIC and Dg models based on a Chinese soil erodibility database. Acta Agric. Scand. Sect. B Soil Plant Sci. 2013, 63, 69–79. [Google Scholar] [CrossRef]
- Williams, J.R.; Sharply, A.N. EPIC-Erosion Productivity Impact Calculator, I. In Model Documentation; US Department of Agriculture Technical Bulletin: Washington, DC, USA, 1990; p. 1768. [Google Scholar]
- Dövényi, Z. Inventory of Microregions in Hungary; MTAFKI: Budapest, Hungary, 2010. [Google Scholar]
- Szabó, B.; Centeri, C.; Szalai, Z.; Jakab, G.; Szabó, J. Comparison of soil erosion dynamics under extensive and intensive cultivation based on basic soil parameters. Növénytermelés 2015, 64, 23–26. [Google Scholar] [CrossRef]
- Szabó, J.A.; Centeri, C.; Keller, B.; Hatvani, I.G.; Szalai, Z.; Dobos, E.; Jakab, G. The use of various rainfall simulators in the determination of the driving forces of changes in sediment concentration and clay enrichment. Water 2020, 12, 2856. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Porter, J.P. RUSLE: Revised Universal Soil Loss Equation. J. Soil Water Conserv. 1991, 46, 30–33. [Google Scholar]
- Presbitero, A.L. Soil Erosion Studies on Steep Slopes of Humid-Tropic Philippines. In School of Environmental Studies; Nathan Campus, Griffith University: Queensland, Australia, 2003. [Google Scholar]
- Kinnell, P.I.A. Runoff ratio as a factor in the empirical modeling of soil erosion by individual rainstorms. Aus. J. Soil Res. 1997, 35, 1–14. [Google Scholar] [CrossRef]
- Rosewell, C.J.; Edwards, K. SOILOSS—A Program to Assist in the Selection of Management Practices to Reduce Erosion, Tech. Handbook No. 11; Soil Conservation Service of New South Wales: Sydney, Australia, 1998; p. 71.
- Ahmad, H.M.N.; Sinclair, A.; Jamieson, R.; Madani, A.; Hebb, B.; Havard, P.; Yiridoe, E.K. Modeling sediment and nitrogen export from a rural watershed in Eastern Canada Using the soil and water Assessment Tool. J. Environ. Qual. 2011, 40, 1182–1194. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.; Van Liew, M.; Bingner, R.; Harmel, R.D.; Veith, T. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Defersha, M.B.; Quraishi, S.; Melesse, A. The effect of slope steepness and antecedent moisture content on interrill erosion, runoff and sediment size distribution in the highlands of Ethiopia. Hydrol. Earth Syst. Sci. 2011, 15, 2367–2375. [Google Scholar] [CrossRef] [Green Version]
- Vermang, J.; Demeyer, V.; Cornelis, W.; Gabriels, D. Aggregate Stability and Erosion Response to Antecedent Water Content of a Loess Soil. Soil Sci. Soc. Am. J. 2009, 73, 718–726. [Google Scholar] [CrossRef]
- Ziadat, F.M.; Taimeh, A.Y. Effect of rainfall intensity, slope, land use and antecedent soil moisture on soil erosion in an arid environment. Land Degrad. Dev. 2013, 24, 582–590. [Google Scholar] [CrossRef]
- Centeri, C. In situ soil erodibility values versus calculations. In 25 Years of Assessment of Erosion—International Symposium; Gabriels, D., Cornelis, W., Eds.; International Center for Eremology—University of Ghent: Ghent, Belgium, 2003; pp. 135–140. [Google Scholar]
- Zhang, K.L.; Shu, A.P.; Xu, X.L.; Yang, Q.K.; Yu, B. Soil erodibility and its estimation for agricultural soils in China. J. Arid. Environ. 2008, 72, 1002–1011. [Google Scholar] [CrossRef]
- Bronstert, A.; Bárdossy, A. The role of spatial variability of soil moisture for modelling surface runoff generation at the small catchment scale. Hydrol. Earth Syst. Sci. 1999, 3, 505–516. [Google Scholar] [CrossRef]
- Zehe, E.; Blöschl, G. Predictability of hydrologic response at the plot and catchment scales: Role of initial conditions. Water Resour. Res. 2004, 40, W10202. [Google Scholar] [CrossRef] [Green Version]
- Nearing, M.A. Why soil erosion models over-predict small soil losses and under-predict large soil losses. Catena 1998, 32, 15–22. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Risse, L.M.; Nearing, M.A. Evaluation of WEPP and its comparison with USLE and RUSLE. Trans. ASAE 2000, 43, 1129–1135. [Google Scholar] [CrossRef]
- Di Stefano, C.; Ferro, V.; Pampalone, V. Applying the USLE Family of Models at the Sparacia (South Italy) Experimental Site. Land Degrad. Dev. 2016, 28, 994–1004. [Google Scholar] [CrossRef]
- Singh, M.J.; Khera, K.L. Nomographic estimation and evaluation of soil erodibility under simulated and natural rainfall conditions. Land Degrad. Dev. 2009, 20, 471–480. [Google Scholar] [CrossRef]
- Marques, V.S.; Ceddia, M.B.; Antunes, M.A.H.; Carvalho, D.F.; Anache, J.A.A.; Rodrigues, D.B.B.; Oliveira, P.T.S. USLE K-Factor method selection for a tropical catchment. Sustainability 2019, 11, 1840. [Google Scholar] [CrossRef] [Green Version]
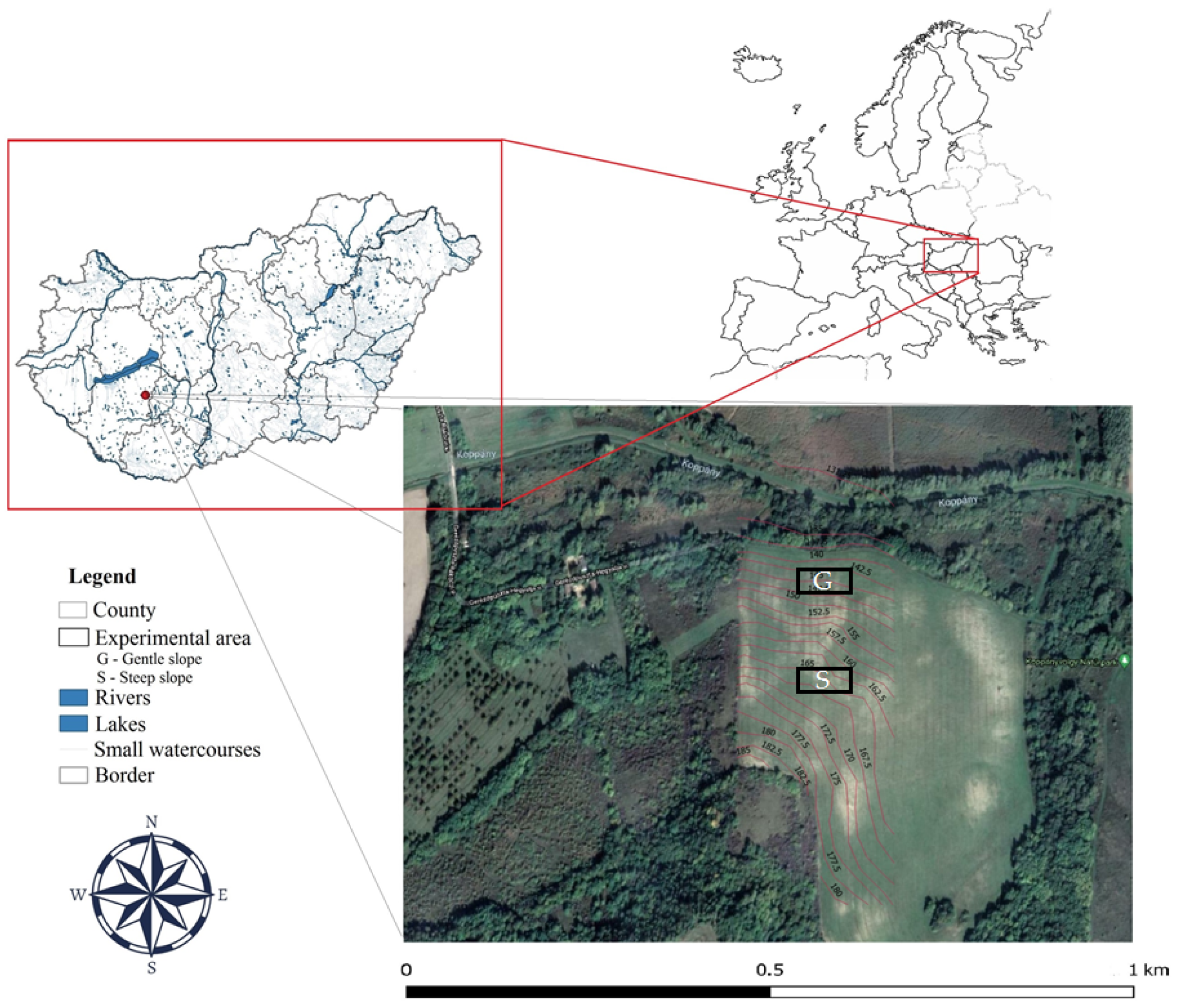

| Soil Properties | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Plasticity | pHH2O | CaCO3 | SOC | Coarse Sand | Fine Sand | Sand | Silt | Clay | Soil Permeability | Soil Structure Class | |
| (mm) | |||||||||||
| (%) | (%) | >0.25 | 0.25–0.0 | 0.05–0.02 | 0.02–0.002 | <0.002 | mm h−1 | ||||
| Gentle slope | 41 | 8.06 | 2.7 | 1.37 | 0.9 | 29 | 22 | 20.2 | 28 | 55.43 | fine granular |
| Steep slope | 44 | 8.22 | 13 | 1.39 | 1.1 | 26.5 | 19.2 | 23.8 | 29.3 | ||
| Treatment ID | s | Measured Rainfall Intensity | Rainfall | Rainfall Duration | Soil Moisture Content |
|---|---|---|---|---|---|
| (%) | (mm h−1) | (mm) | (s) | ||
| FPG1 | 6.7 | 15.06 | 19.18 | 4584 | dry |
| FPG2 | 6.7 | 56.24 | 16.81 | 1076 | moist |
| FPG3 | 6.7 | 84.68 | 10.63 | 452 | wet |
| FPG4 | 8 | 22.65 | 28.96 | 4603 | dry |
| FPG5 | 8 | 70.19 | 13.53 | 694 | moist |
| FPG6 | 8 | 86.12 | 10.41 | 435 | wet |
| FPG7 | 7.7 | 26.32 | 35.10 | 4801 | dry |
| FPG8 | 7.7 | 56.92 | 15.19 | 961 | moist |
| FPG9 | 7.7 | 80.44 | 12.4 | 555 | wet |
| FPS1 | 18.32 | 20.87 | 26.64 | 4595 | dry |
| FPS2 | 18.32 | 66.78 | 16.49 | 889 | moist |
| FPS3 | 18.32 | 103.48 | 11.67 | 406 | wet |
| FPS4 | 17.26 | 24.42 | 31.10 | 4585 | dry |
| FPS5 | 17.26 | 49.89 | 10.53 | 760 | moist |
| FPS6 | 17.26 | 63.16 | 8.05 | 459 | wet |
| FPS7 | 17.6 | 18.68 | 19.9 | 4627 | dry |
| FPS8 | 17.6 | 44.05 | 13.86 | 1121 | moist |
| FPS9 | 17.6 | 76.69 | 11.18 | 525 | wet |
| Pooled Data | |||||
|---|---|---|---|---|---|
| KU | KRU | KU-M | KEPIC | KNOMO | |
| MEAN | 0.0041 | 0.0028 | 0.0087 | 0.0112 | 0.0018 |
| SD | 0.0030 | 0.0024 | 0.0101 | ||
| Min | 0.0001 | 0.0000 | 0.0014 | ||
| Max | 0.0096 | 0.0095 | 0.0398 | ||
| Median | 0.0039 | 0.0026 | 0.0049 | ||
| CV% | 73.5113 | 86.3314 | 116.1762 | ||
| CV rel | 18.3778 | 21.5828 | 29.0440 | ||
| Moisture | Rainfall Intensity (mm h−1) | Runoff (mm h−1) | Suspended Sediment Concentration (g L−1) | Total Soil Loss (g m−2 h−1) |
|---|---|---|---|---|
| dry | 20.87–26.32 | 0.2–0.9 (0.5) | 3.6–10.3 (7.04) | 2.9–3.4 (3.21) |
| moist | 44.05–70.19 | 14.1–22.8 (19.2) | 9.01–19.25 (12.23) | 150.5–438.5 (237.88) |
| wet | 63.16–103.48 | 32.1–48.1 (37.5) | 11.26–26.19 (16.53) | 406.3–1061.5 (633.69) |
| AU | ARU | AU-M | Anomo | AEPIC | |
|---|---|---|---|---|---|
| r | 0.3988 | 0.2825 | 0.7706 | 0.3988 | 0.3988 |
| r2 | 0.1591 | 0.0798 | 0.5938 | 0.1591 | 0.1591 |
| NSEI | −0.2744 | 0.0431 | −1.7041 | −0.3745 | −15.5122 |
| RMSE | 0.1732 | 0.1300 | 0.3674 | 0.1868 | 2.2437 |
| RE | 0.1340 | 0.0359 | −0.1779 | −0.4970 | 2.1296 |
| PB | −13.3993 | −3.5878 | −50.9319 | 49.7031 | −212.9582 |
| p-value | 0.7520 | 0.8672 | 0.3414 | 0.0615 | <0.0001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keller, B.; Centeri, C.; Szabó, J.A.; Szalai, Z.; Jakab, G. Comparison of the Applicability of Different Soil Erosion Models to Predict Soil Erodibility Factor and Event Soil Losses on Loess Slopes in Hungary. Water 2021, 13, 3517. https://doi.org/10.3390/w13243517
Keller B, Centeri C, Szabó JA, Szalai Z, Jakab G. Comparison of the Applicability of Different Soil Erosion Models to Predict Soil Erodibility Factor and Event Soil Losses on Loess Slopes in Hungary. Water. 2021; 13(24):3517. https://doi.org/10.3390/w13243517
Chicago/Turabian StyleKeller, Boglárka, Csaba Centeri, Judit Alexandra Szabó, Zoltán Szalai, and Gergely Jakab. 2021. "Comparison of the Applicability of Different Soil Erosion Models to Predict Soil Erodibility Factor and Event Soil Losses on Loess Slopes in Hungary" Water 13, no. 24: 3517. https://doi.org/10.3390/w13243517
APA StyleKeller, B., Centeri, C., Szabó, J. A., Szalai, Z., & Jakab, G. (2021). Comparison of the Applicability of Different Soil Erosion Models to Predict Soil Erodibility Factor and Event Soil Losses on Loess Slopes in Hungary. Water, 13(24), 3517. https://doi.org/10.3390/w13243517









