Interpreting the Manning Roughness Coefficient in Overland Flow Simulations with Coupled Hydrological-Hydraulic Distributed Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Aggregated Hydrological Modelling
2.2. Distributed Hydrological Modelling
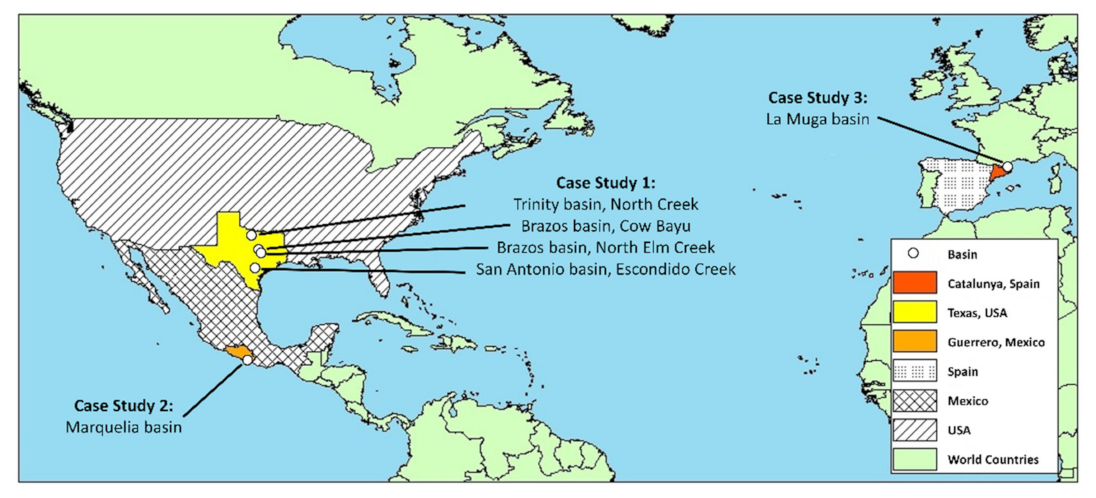
3. Case Studies
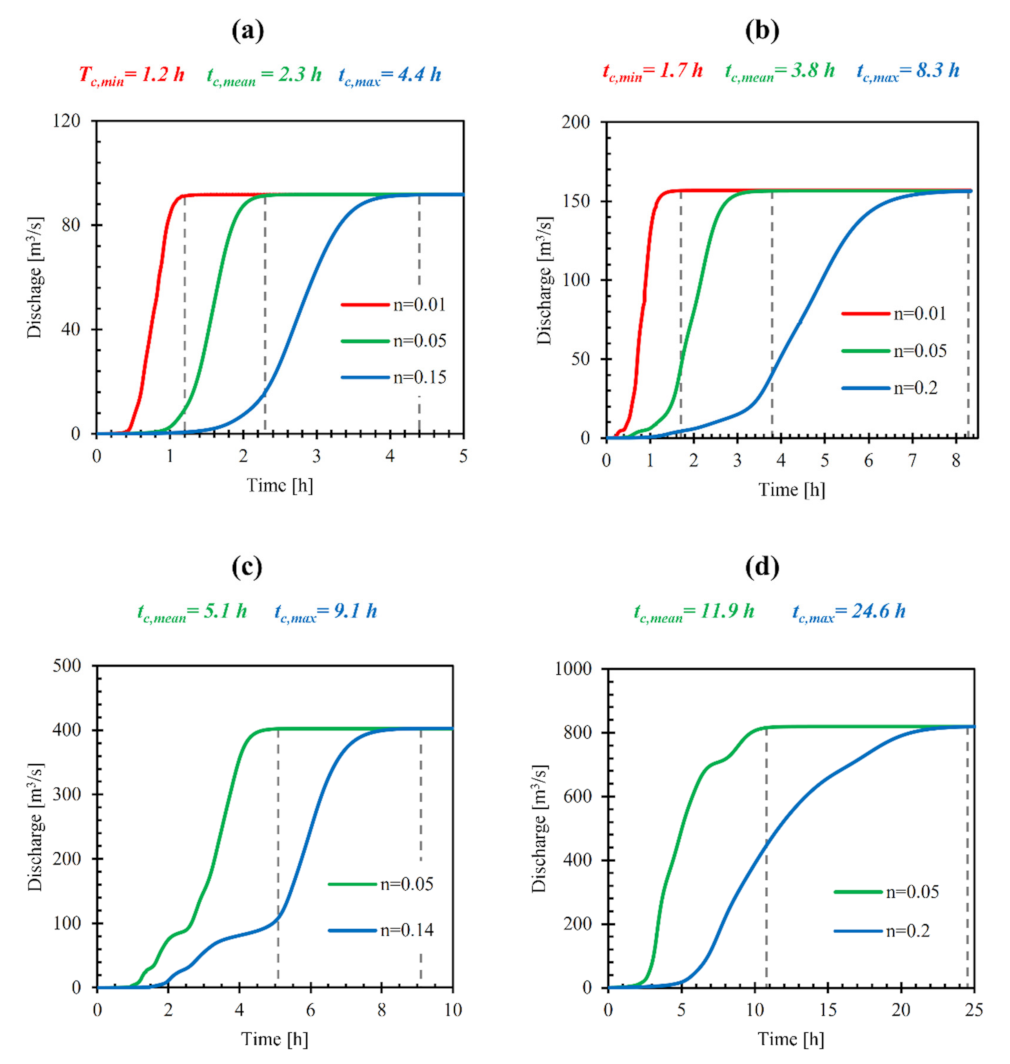
3.1. Case Study 1: Adjustment of the Roughness Coefficient Based on the Time of Concentration
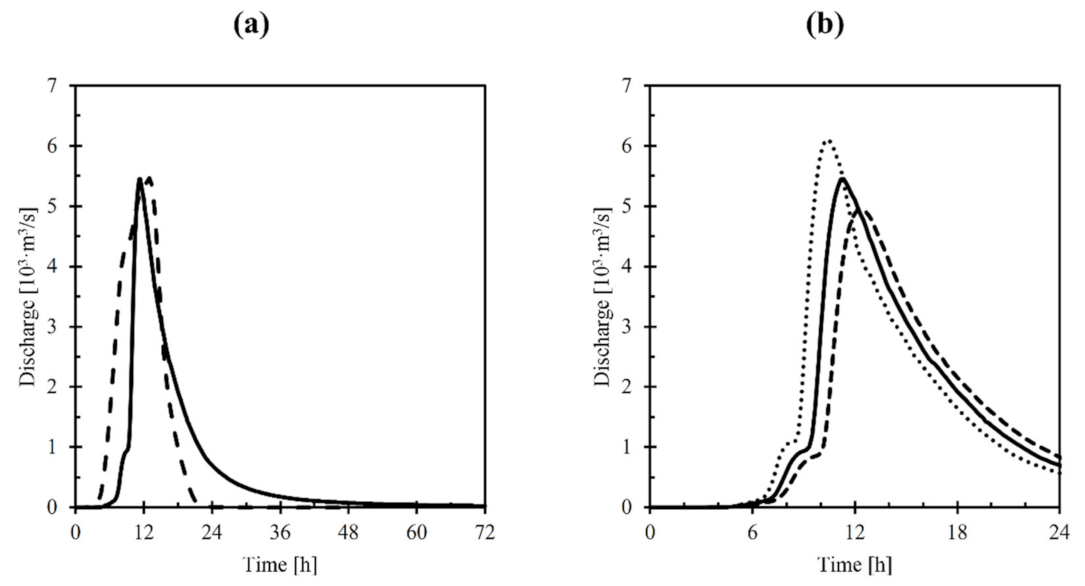
3.2. Case Study 2: Adjustment of the Roughness Coefficient Based on the Peak Time and Discharge from Aggregated Hydrological Models
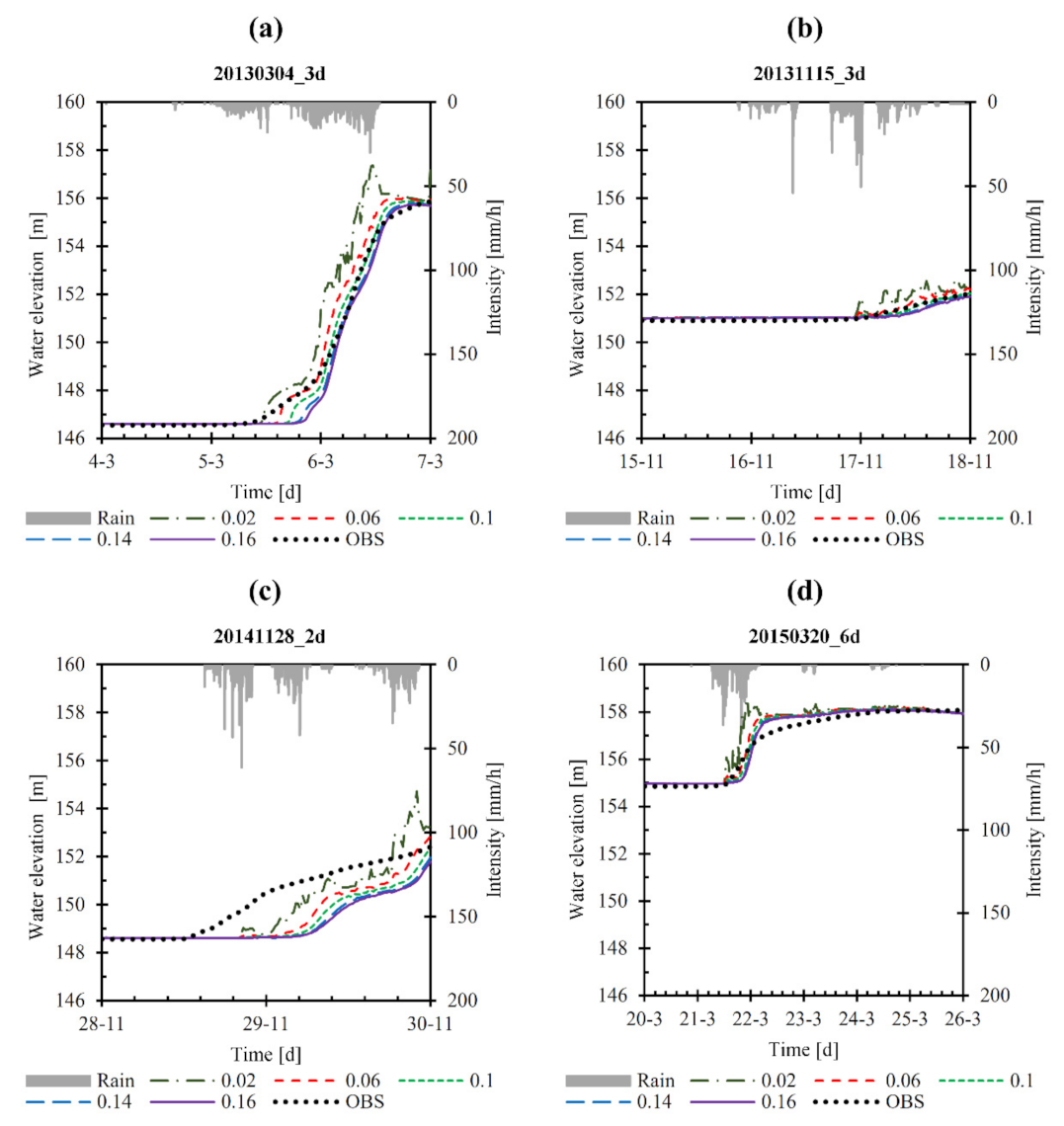
3.3. Case Study 3: Adjustment of the Roughness Coefficient Based on Observed Storm Events
4. Results
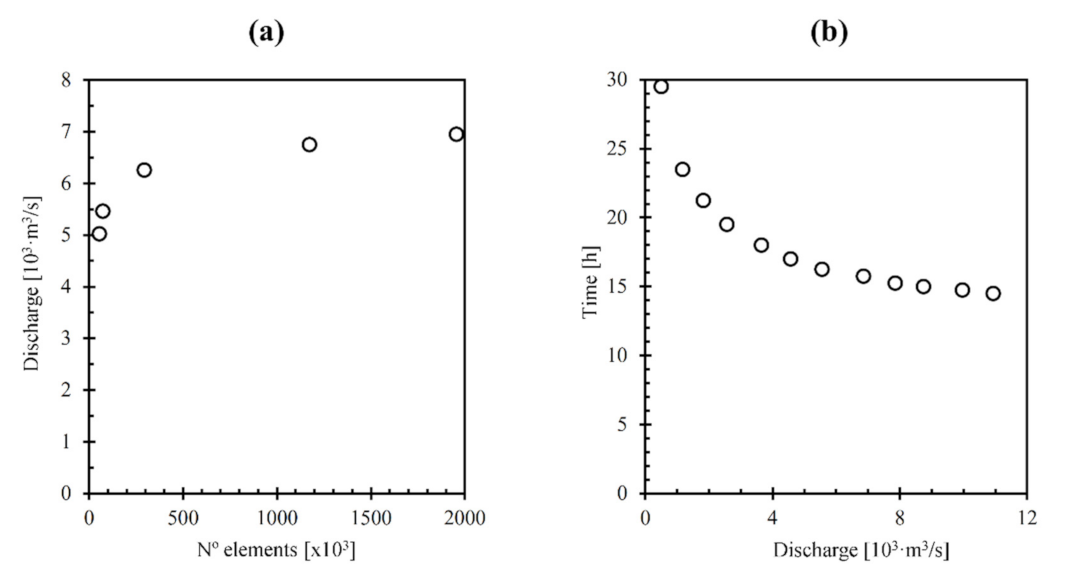
4.1. Case Study 1
4.2. Case Study 2
4.3. Case Study 3
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fonseca, A.R.; Santos, M.; Santos, J.A. Hydrological and flood hazard assessment using a coupled modelling approach for a mountainous catchment in Portugal. Stoch. Environ. Res. Risk Assess. 2018, 32, 2165–2177. [Google Scholar] [CrossRef]
- Kron, W. Flood Risk = Hazard + Values + Vulnerability. Water Int. 2005, 30, 58–68. [Google Scholar] [CrossRef]
- ISDR Global Assessment Report on Disaster Risk Reduction; United Nations: Geneva, Switzerland, 2009; ISBN 978-92-1-332019-8.
- Fraga, I.; Cea, L.; Puertas, J.; Mosqueira, G.; Quinteiro, B.; Botana, S.; Fernández, L.; Salsón, S.; Fernández-García, G.; Taboada, J. MERLIN: Una nueva herramienta para la predicción del riesgo de inundaciones en la demarcación hidrográfica Galicia-Costa. Ing. Agua 2021, 25, 215. [Google Scholar] [CrossRef]
- Thiemig, V.; Bisselink, B.; Pappenberger, F.; Thielen, J. A pan-African medium-range ensemble flood forecast system. Hydrol. Earth Syst. Sci. 2015, 19, 3365–3385. [Google Scholar] [CrossRef] [Green Version]
- Mure-Ravaud, M.; Binet, G.; Bracq, M.; Perarnaud, J.-J.; Fradin, A.; Litrico, X. A web based tool for operational real-time flood forecasting using data assimilation to update hydraulic states. Environ. Model. Softw. 2016, 84, 35–49. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Su, C.-H.; Crow, W.T.; Robertson, D.E.; Leahy, C. Improving operational flood ensemble prediction by the assimilation of satellite soil moisture: Comparison between lumped and semi-distributed schemes. Hydrol. Earth Syst. Sci. 2015, 19, 1659–1676. [Google Scholar] [CrossRef] [Green Version]
- Beven, K. Rainfall-Runoff Modelling. The Primer; John Wiley & Sons, Ltd.: Chichester, UK, 2012; ISBN 9780470714591. [Google Scholar]
- Paudel, M.; Nelson, E.J.; Downer, C.W.; Hotchkiss, R. Comparing the capability of distributed and lumped hydrologic models for analyzing the effects of land use change. J. Hydroinform. 2011, 13, 461–473. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Tauro, F.; Porfiri, M. Time of concentration: A paradox in modern hydrology. Hydrol. Sci. J. 2012, 57, 217–228. [Google Scholar] [CrossRef] [Green Version]
- Michailidi, E.M.; Antoniadi, S.; Koukouvinos, A.; Bacchi, B.; Efstratiadis, A. Timing the time of concentration: Shedding light on a paradox. Hydrol. Sci. J. 2018, 63, 721–740. [Google Scholar] [CrossRef] [Green Version]
- Beven, K.J. A history of the concept of time of concentration. Hydrol. Earth Syst. Sci. 2020, 24, 2655–2670. [Google Scholar] [CrossRef]
- Mulvany, T.J. On the use of self-registering rain and flood gauges in making observations of the relations of rainfall and flood discharges in a given catchment. Proc. Inst. Civ. Eng. Irel. 1851, 4, 18–33. [Google Scholar]
- W.M.O. International Glossary of Hydrology. Report No. 385; World Meteorological Organization (W.M.O.): Geneva, Switzerland, 1974. [Google Scholar]
- NCRS Hydrology. National Engineering Handbook; US Department of Agriculture: Washington, DC, USA, 1972. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; MCGRAW-HIL: New York, NY, USA, 1988; ISBN 9780071001748. [Google Scholar]
- Témez, J.R. Cálculo Hidrometeorológico de Caudales Máximos en Pequeñas Cuencas Naturales; Ministerio de Obras Públicas y Urbanismo, Dirección General de Carreteras: Madrid, España, 1978; ISBN 7433-457-8. [Google Scholar]
- Kirpich, Z.P. Time of concentration of small agricultural watersheds. Am. Soc. Civ. Eng. 1940, 10, 362. [Google Scholar]
- Mijares, A. Fundamentos de Hidrología de Superficie; Editorial Limusa, Grupo Noriega Editores: México D.F., México, 1998; ISBN 9681830148. [Google Scholar]
- CONAGUA. Manual de Agua Potable, Alcantarillado y Saneamiento: Drenaje Pluvial Urbano; Comisión Nacional del Agua. Naturales, Secretaría de Medio Ambiente y Recursos: Ciudad de México, México, 2016; ISBN 9786076260159. [Google Scholar]
- SCT. Estudios Hidráulico-Hidrológicos para Puentes: Manual de Análisis Hidrológicos; Secretaría de Comunicaciones y Transportes, Gobierno de México: Ciudad de México, México, 2000. [Google Scholar]
- Nanía, E.S.; Gomez-Valentín, M. Ingeniería Hidrológica, 2nd ed.; Grupo Editorial Universitario: Granada, España, 2014; ISBN 84-8491-636-7. [Google Scholar]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.J. Overall distributed model intercomparison project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Refsgaard, J.C. Parameterisation, calibration and validation of distributed hydrological models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
- Cea, L.; Bladé, E. A simple and efficient unstructured finite volume scheme for solving the shallow water equations in overland flow applications. Water Resour. Res. 2015, 51, 5464–5486. [Google Scholar] [CrossRef] [Green Version]
- Caro, C.A. Modelación Hidrológica Distribuida Basada en Esquemas de Volúmenes Finitos. Ph.D. Thesis, School of Civil Engineering, Universitat Politècnica de Catalunya, Barcelona, Spain, 2016. [Google Scholar]
- Kim, J.; Warnock, A.; Ivanov, V.Y.; Katopodes, N.D. Coupled modeling of hydrologic and hydrodynamic processes including overland and channel flow. Adv. Water Resour. 2012, 37, 104–126. [Google Scholar] [CrossRef]
- Cea, L.; Garrido, M.; Puertas, J. Experimental validation of two-dimensional depth-averaged models for forecasting rainfall–runoff from precipitation data in urban areas. J. Hydrol. 2010, 382, 88–102. [Google Scholar] [CrossRef]
- Viero, D.P.; Peruzzo, P.; Carniello, L.; Defina, A. Integrated mathematical modeling of hydrological and hydrodynamic response to rainfall events in rural lowland catchments. Water Resour. Res. 2014, 50, 5941–5957. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Duan, J. Simulation of Surface Runoff Using Hydrodynamic Model. J. Hydrol. Eng. 2017, 22, 04017006. [Google Scholar] [CrossRef]
- Nguyen, P.; Thorstensen, A.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Sanders, B.; Koren, V.; Cui, Z.; Smith, M. A high resolution coupled hydrologic–hydraulic model (HiResFlood-UCI) for flash flood modeling. J. Hydrol. 2016, 541, 401–420. [Google Scholar] [CrossRef] [Green Version]
- Panday, S.; Huyakorn, P.S. A fully coupled physically-based spatially-distributed model for evaluating surface/subsurface flow. Adv. Water Resour. 2004, 27, 361–382. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2009; Volume 40, ISBN 978-3-540-25202-3. [Google Scholar]
- Beven, K. Changing ideas in hydrology—The case of physically-based models. J. Hydrol. 1989, 105, 157–172. [Google Scholar] [CrossRef]
- Jakeman, A.J.; Hornberger, G.M. How much complexity is warranted in a rainfall-runoff model? Water Resour. Res. 1993, 29, 2637–2649. [Google Scholar] [CrossRef]
- Barnes, C.J. The art of catchment modeling: What is a good model? Environ. Int. 1995, 21, 747–751. [Google Scholar] [CrossRef]
- Beven, K. How far can we go in distributed hydrological modelling? Hydrol. Earth Syst. Sci. 2001, 5, 1–12. [Google Scholar] [CrossRef]
- Chow, V. Open Channel Hydraulics; McGraw-Hill Education: New York, NY, USA, 2006; ISBN 9780750668576. [Google Scholar]
- Barnes, H.H. Roughness characteristics of natural channels. J. Hydrol. 1969, 7, 354. [Google Scholar]
- Arcement, G.J.G.J.J.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; Paper 2339; 19. Books and Open-File Reports Section; U.S. Geological Survey, Federal Center: Denver, CO, USA, 1989. [Google Scholar]
- Kalyanapu, A.J.; Burian, S.J.; McPherson, T.N. Effect of land use-based surface roughness on hydrologic model output. J. Spat. Hydrol. 2009, 9, 51–71. [Google Scholar]
- Barnard, T.; Agnaou, M.; Barbis, J. Two Dimensional Modeling to Simulate Stormwater Flows at Photovoltaic Solar Energy Sites. J. Water Manag. Model. 2017, 25, 8. [Google Scholar] [CrossRef] [Green Version]
- USACE. Hydrologic Modeling System HEC-HMS. Technical Reference Manual; US Army Coprs of Engineers, Institute for Water Resources, Hydrologic Engineering Center: Dacis, CA, USA, 2000. [Google Scholar]
- USDA-SCS. SCS National Engineering Handbook, Hydrology, Section 4; US Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 1972. [Google Scholar]
- USDA-SCS. National Engineering Handbook, Supplement A, Section 4, Chapter 10: Hydrology; US Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 1985. [Google Scholar]
- USDA-NRCS. Part 630 Hydrology—Chapter 10. In National Engineering Handbook; US Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 2004; p. 79. [Google Scholar]
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de simulación numérica del flujo en ríos. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2014, 30, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Cea, L.; Bladé, E.; Corestein, G.; Fraga, I.; Espinal, M.; Puertas, J. Comparative analysis of several sediment transport formulations applied to dam-break flows over erodible beds. In Proceedings of the EGU General Assembly 2014, Vienna, Austria, 27 April–2 May 2014. [Google Scholar]
- Bladé, E.; Cea, L.; Corestein, G. Numerical modelling of river inundations. Ing. Agua 2014, 18, 68. [Google Scholar] [CrossRef]
- Anta Álvarez, J.; Bermúdez, M.; Cea, L.; Suárez, J.; Ures, P.; Puertas, J. Modelización de los impactos por DSU en el río Miño (Lugo). Ing. Agua 2015, 19, 105. [Google Scholar] [CrossRef]
- Cea, L.; Bermudez, M.; Puertas, J.; Blade, E.; Corestein, G.; Escolano, E.; Conde, A.; Bockelmann-Evans, B.; Ahmadian, R. IberWQ: New simulation tool for 2D water quality modelling in rivers and shallow estuaries. J. Hydroinform. 2016, 18, 816–830. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Villanueva, V.; Bladé, E.; Sánchez-Juny, M.; Marti-Cardona, B.; Díez-Herrero, A.; Bodoque, J.M. Two-dimensional numerical modeling of wood transport. J. Hydroinform. 2014, 16, 1077. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Bladé Castellet, E.; Palau Ibars, A.; Vericat Querol, D.; Ramos-Fuertes, A. IberHABITAT: Evaluación de la Idoneidad del Hábitat Físico y del Hábitat Potencial Útil para peces. Aplicación en el río Eume. Ribagua 2019, 6, 158–167. [Google Scholar] [CrossRef] [Green Version]
- Sanz-Ramos, M.; Bladé, E.; Torralba, A.; Oller, P. Las ecuaciones de Saint Venant para la modelización de avalanchas de nieve densa. Ing. Agua 2020, 24, 65–79. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Andrade, C.A.; Oller, P.; Furdada, G.; Bladé, E.; Martínez-Gomariz, E. Reconstructing the Snow Avalanche of Coll de Pal 2018 (SE Pyrenees). GeoHazards 2021, 2, 196–211. [Google Scholar] [CrossRef]
- Sañudo, E.; Cea, L.; Puertas, J. Modelling Pluvial Flooding in Urban Areas Coupling the Models Iber and SWMM. Water 2020, 12, 2647. [Google Scholar] [CrossRef]
- Aranda, J.Á.; Beneyto, C.; Sánchez-Juny, M.; Bladé, E. Efficient Design of Road Drainage Systems. Water 2021, 13, 1661. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Amengual, A.; Bladé, E.; Romero, R.; Roux, H. Flood forecasting using a coupled hydrological and hydraulic model (based on FVM) and highresolution meteorological model. E3S Web Conf. 2018, 40, 06028. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Martí-Cardona, B.; Bladé, E.; Seco, I.; Amengual, A.; Roux, H.; Romero, R. NRCS-CN Estimation from Onsite and Remote Sensing Data for Management of a Reservoir in the Eastern Pyrenees. J. Hydrol. Eng. 2020, 25, 05020022. [Google Scholar] [CrossRef]
- Roe, P.L. A basis for the upwind differencing of the two-dimensional unsteady Euler equations. Numer. Methods Fluid Dyn. II 1986, 55–80. [Google Scholar]
- Caro, C.A.A.; Lesmes, C.; Bladé, E. Drying and transport processes in distributed hydrological modelling based on finite volume schemes (IBER model). In Proceedings of the 9th Annual International Symposium on Agricultural Research, Athens, Greece, 11–14 July 2016; p. 33. [Google Scholar]
- Jenson, S.K.; Domingue, J.O. Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
- Bates, P.; De Roo, A.P. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Johnstone, D.; Cross, W.P. Elements of Applied Hydrology; Civil Engineering Series; Ronald Press Company: New York, NY, USA, 1949; ISBN 978-1124128436. [Google Scholar]
- DPW. California Culvert Practice, 2nd ed.; Department of Public Works, DPW, Division of Highways: Sacramento, CA, USA, 1995. [Google Scholar]
- Viparelli, C. Ricostruzione dell’idrogramma di Piena; Istituto di Idraulica dell’Università di Palermo, Stab. Tip. Genovese: Napoli, Italy, 1961; Volume 6. [Google Scholar]
- WRB-IUSS. World Reference Base for Soil Resources. World Soil Resources Reports 106; Food and Agriculture Organization of the United Nations: Rome, Italy, 2015; ISBN 9789251083697. [Google Scholar]
- Chen, C. Rainfall Intensity-Duration-Frequency Formulas. J. Hydraul. Eng. 1983, 109, 1603–1621. [Google Scholar] [CrossRef]
- Campos-Aranda, D.F. Introducción a la Hidrología Urbana; San Luis Potosí, México, 2010; ISBN 970-95118-1-5. Available online: https://bibliotecasibe.ecosur.mx/sibe/book/000051798 (accessed on 5 September 2021).
- Weiss, L.L. Ratio of true fixed-interval maximum rainfall. J. Hydraul. Div. 1964, 90, 77–82. [Google Scholar] [CrossRef]
- Roux, H.; Amengual, A.; Romero, R.; Bladé, E.; Sanz-Ramos, M. Evaluation of two hydrometeorological ensemble strategies for flash-flood forecasting over a catchment of the eastern Pyrenees. Nat. Hazards Earth Syst. Sci. 2020, 20, 425–450. [Google Scholar] [CrossRef] [Green Version]
- ACA. Planificació de l’Espai Fluvial. Estudis d’inundabilitat en l’àmbit del projecte PEFCAT-Memòria Específica Conca de La Muga; Agència Catalana de l’Aigua. Generalitat de Catalunya: Barcelona, España, 2007. [Google Scholar]
- Llasat, M.C.; Rodriguez, R. Extreme rainfall events in Catalonia. The case of 12 November 1988. Nat. Hazards 1992, 5, 133–151. [Google Scholar] [CrossRef]
- Martín-Vide, J. Geographical Factors in the Pluviometry of Mediterranean Spain: Drought and Torrential Rainfall; The University of Iowa, Iowa Institute of Hydraulic Research: Iowa, IA, USA, 1994. [Google Scholar]
- EEA. CORINE Land Cover 2006 Technical Guidelines; European Enviromental Agency, Technical Report No 17/2007; Office for Official Publications of the European Communities: Luxembourg, Luxembourg, 2007; ISBN 978-92-9167-968-3. [Google Scholar]
- Ramos-Fuertes, A.; Marti-Cardona, B.; Bladé, E.; Dolz, J. Envisat/ASAR Images for the Calibration of Wind Drag Action in the Doñana Wetlands 2D Hydrodynamic Model. Remote Sens. 2013, 6, 379–406. [Google Scholar] [CrossRef] [Green Version]
- Mateo Lázaro, J.; Sánchez Navarro, J.Á.; García Gil, A.; Edo Romero, V. Sensitivity analysis of main variables present in flash flood processes. Application in two Spanish catchments: Arás and Aguilón. Environ. Earth Sci. 2014, 71, 2925–2939. [Google Scholar] [CrossRef]
- Allison, S.V. Review of Small Basin Runoff Prediction Methods. J. Irrig. Drain. Div. 1967, 93, 1–6. [Google Scholar] [CrossRef]
- Fuentes, O.; Ravelo, A.; Ávila, A. Método Para Determinar Los Parámetros K, X Y Los Coeficentes De Tránsito Del Método De Muskingum-Cunge. In Proceedings of the XIX Congreso Nacional De Hidráulica; Asociación Mexicana de HIdráulcia: Cuernavaca, Mexico, 2006; p. 6. [Google Scholar]
- INEGI. Contínuo de Elevaciones Mexicano 3.0. Available online: https://www.inegi.org.mx/app/geo2/elevacionesmex/ (accessed on 15 July 2021).
- Sánchez-Juny, M.; Bladé, E.; Dolz, J. Analysis of pressures on a stepped spillway. J. Hydraul. Res. 2008, 46, 410–414. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Bladé, E.; Niñerola, D.; Palau-Ibars, A. Evaluación numérico-experimental del comportamiento histérico del coeficiente de rugosidad de los macrófitos. Ing. Agua 2018, 22, 109–124. [Google Scholar] [CrossRef] [Green Version]
- Bladé, E.; Sanz-Ramos, M.; Dolz, J.; Expósito-Pérez, J.M.; Sánchez-Juny, M. Modelling flood propagation in the service galleries of a nuclear power plant. Nucl. Eng. Des. 2019, 352, 110180. [Google Scholar] [CrossRef]
- ICGC Descàrregues. Available online: https://www.icgc.cat/Descarregues (accessed on 2 February 2021).
- Demissie, H.K.; Bacopoulos, P. Parameter estimation of anisotropic Manning’s n coefficient for advanced circulation (ADCIRC) modeling of estuarine river currents (lower St. Johns River). J. Mar. Syst. 2017, 169, 1–10. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Y. Experimental Study on Anisotropic Attributes of Surface Roughness in Watersheds. J. Hydrol. Eng. 2017, 22, 06017005. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Y.; Zhang, J.; Liu, Y. Simulation study of anisotropic flow resistance of farmland vegetation. Soil Water Res. 2017, 12, 220–228. [Google Scholar] [CrossRef] [Green Version]
- Anees, M.T.; Abdullah, K.; Nordin, M.N.M.; Rahman, N.N.N.A.; Syakir, M.I.; Kadir, M.O.A. One- and Two-Dimensional Hydrological Modelling and Their Uncertainties. Flood Risk Manag. 2017, 11, 221–244. [Google Scholar]
- Aureli, F.; Prost, F.; Vacondio, R.; Dazzi, S.; Ferrari, A. A GPU-accelerated shallow-water scheme for surface runoff simulations. Water 2020, 12, 637. [Google Scholar] [CrossRef] [Green Version]
- Ozcelik, C.; Gorokhovich, Y. An overland flood model for geographical information systems. Water 2020, 12, 2397. [Google Scholar] [CrossRef]
- Roux, H.; Labat, D.; Garambois, P.-A.; Maubourguet, M.-M.; Chorda, J.; Dartus, D. A physically-based parsimonious hydrological model for flash floods in Mediterranean catchments. Nat. Hazards Earth Syst. Sci. 2011, 11, 2567–2582. [Google Scholar] [CrossRef] [Green Version]
- Echeverribar, I.; Morales-Hernández, M.; Lacasta, A.; Brufrau, P.; García-Navarro, P. Simulación numérica con RiverFlow2D de posibles soluciones de mitigación de avenidas en el tramo medio del río Ebro. Ing. Agua 2017, 21, 53. [Google Scholar] [CrossRef] [Green Version]
- García-Feal, O.; González-Cao, J.; Gómez-Gesteira, M.; Cea, L.; Domínguez, J.M.; Formella, A. An Accelerated Tool for Flood Modelling Based on Iber. Water 2018, 10, 1459. [Google Scholar] [CrossRef] [Green Version]
- Liang, Q.; Xia, X.; Hou, J. Catchment-scale High-resolution Flash Flood Simulation Using the GPU-based Technology. Procedia Eng. 2016, 154, 975–981. [Google Scholar] [CrossRef] [Green Version]
- Sanz-Ramos, M.; Bladé, E.; Escolano, E. Optimización del cálculo de la Vía de Intenso Desagüe con criterios hidráulicos. Ing. Agua 2020, 24, 203. [Google Scholar] [CrossRef]
- USDA-NRCS. Part 630 Hydrology—Chapter 10. In National Engineering Handbook; US Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 2010; pp. 449–456. [Google Scholar]
| Characteristic | Brazos Basin (Cow Bayu) | San Antonio Basin (Escondido Creek) | Trinity Basin (North Creek) | Brazos Basin (North Elm Creek) |
|---|---|---|---|---|
| Area (km2) | 13.08 | 22.80 | 58.96 | 119.46 |
| Mean slope (%) | 5.90 | 2.90 | 5.20 | 1.40 |
| Main channel length (km) | 7.09 | 8.00 | 18.02 | 33.34 |
| Formula | Time of Concentration (h) | |||
|---|---|---|---|---|
| Brazos Basin (Cow Bayu) | San Antonio Basin (Escondido Creek) | Trinity Basin (North Creek) | Brazos Basin (North Elm Creek) | |
| Johnstone and Cross [64] | 1.98 | 3.05 | 3.35 | 9.07 |
| DPW [65] | 1.63 | 2.40 | 4.13 | 10.02 |
| NCRS [15] | 3.72 | 6.33 | 8.93 | 24.28 |
| Giandotti [65] | 4.77 | 8.20 | 9.23 | 17.77 |
| Kirpich [18] | 0.92 | 1.35 | 1.95 | 5.40 |
| Viparelli [66] | 1.37 | 1.60 | 3.42 | 6.58 |
| Témez [17] | 2.28 | 2.85 | 4.73 | 9.70 |
| Minimum | 0.92 | 1.35 | 1.95 | 5.40 |
| Mean | 2.38 | 3.68 | 5.10 | 11.83 |
| Maximum | 4.77 | 8.20 | 9.23 | 24.28 |
| Event | Cumulated Rainfall (mm) | Max. Intensity in 5-min (mm/h) | CN |
|---|---|---|---|
| 20130304_3d | 181.3 | 30.0 | 81 |
| 20131115_3d | 123.2 | 54.0 | 50 |
| 20141128_2d | 150.9 | 61.2 | 65 |
| 20150320_6d | 197.4 | 67.2 | 50 |
| Land Use | |
|---|---|
| Rainforest agriculture | 0.138 |
| Urban settlements | 0.051 |
| Pine and oak forest | 0.207 |
| Reservoir | 0.069 |
| Pastureland | 0.069 |
| River | 0.083 |
| Savanna | 0.138 |
| Event | Statistic | Manning Coefficient (s/m1/3) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.02 | 0.04 | 0.06 | 0.08 | 0.10 | 0.12 | 0.14 | 0.16 | ||
| 20130304_3d | RMSE | 0.512 | 0.361 | 0.263 | 0.258 | 0.236 | 0.297 | 0.352 | 0.352 |
| MAE | 0.262 | 0.130 | 0.069 | 0.067 | 0.056 | 0.088 | 0.124 | 0.124 | |
| R2 | 0.953 | 0.982 | 0.990 | 0.993 | 0.993 | 0.991 | 0.988 | 0.984 | |
| 20131115_3d | RMSE | 0.214 | 0.145 | 0.095 | 0.073 | 0.070 | 0.078 | 0.088 | 0.099 |
| MAE | 0.046 | 0.021 | 0.009 | 0.005 | 0.005 | 0.006 | 0.008 | 0.010 | |
| R2 | 0.903 | 0.964 | 0.979 | 0.973 | 0.962 | 0.945 | 0.925 | 0.902 | |
| 20141128_2d | RMSE | 0.485 | 0.521 | 0.580 | 0.630 | 0.669 | 0.703 | 0.732 | 0.758 |
| MAE | 0.235 | 0.272 | 0.336 | 0.397 | 0.447 | 0.494 | 0.536 | 0.575 | |
| R2 | 0.767 | 0.756 | 0.734 | 0.714 | 0.699 | 0.685 | 0.672 | 0.660 | |
| 20150320_6d | RMSE | 0.511 | 0.374 | 0.305 | 0.282 | 0.269 | 0.261 | 0.255 | 0.252 |
| MAE | 0.261 | 0.140 | 0.093 | 0.080 | 0.072 | 0.068 | 0.065 | 0.063 | |
| R2 | 0.255 | 0.282 | 0.298 | 0.303 | 0.306 | 0.309 | 0.311 | 0.314 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanz-Ramos, M.; Bladé, E.; González-Escalona, F.; Olivares, G.; Aragón-Hernández, J.L. Interpreting the Manning Roughness Coefficient in Overland Flow Simulations with Coupled Hydrological-Hydraulic Distributed Models. Water 2021, 13, 3433. https://doi.org/10.3390/w13233433
Sanz-Ramos M, Bladé E, González-Escalona F, Olivares G, Aragón-Hernández JL. Interpreting the Manning Roughness Coefficient in Overland Flow Simulations with Coupled Hydrological-Hydraulic Distributed Models. Water. 2021; 13(23):3433. https://doi.org/10.3390/w13233433
Chicago/Turabian StyleSanz-Ramos, Marcos, Ernest Bladé, Fabián González-Escalona, Gonzalo Olivares, and José Luis Aragón-Hernández. 2021. "Interpreting the Manning Roughness Coefficient in Overland Flow Simulations with Coupled Hydrological-Hydraulic Distributed Models" Water 13, no. 23: 3433. https://doi.org/10.3390/w13233433
APA StyleSanz-Ramos, M., Bladé, E., González-Escalona, F., Olivares, G., & Aragón-Hernández, J. L. (2021). Interpreting the Manning Roughness Coefficient in Overland Flow Simulations with Coupled Hydrological-Hydraulic Distributed Models. Water, 13(23), 3433. https://doi.org/10.3390/w13233433






